Pricing and risk of swing contracts in natural gas markets

Abstract

Motivated by the growing importance of swing contracts in natural gas markets, this article extends the literature on commodity price modelling as well as valuation methods and sensitivity analysis for swing options. While most previous studies focused on simple price models, we face the challenge of deriving option properties under more realistic commodity price dynamics. We begin by formulating a multi-factor price forward curve model with parametric volatility functions, which can capture uncertainty in both yearly seasonality and time-to-maturity effects, and propose a two-step calibration procedure to fit such models to empirical data. We then show how results from the literature can be combined to obtain swing option values and sensitivities in such a general framework. In this context, we also provide new theoretical results and a first numerical approach to efficiently estimate swing options’ gammas. For options’ deltas, we expand upon existing studies by including a larger variety of contract specifications and by focusing on a multidimensional variant of the Longstaff–Schwartz algorithm as an alternative option valuation method. With these contributions, we supply important tools for swing option sellers and buyers relying on accurate option value and risk estimates to maintain their business models, hedge option-related risks and adequately represent swing options in financial reporting.

Appendices

Appendix

Proofs

Proof of Lemma 2.4

Let $f_{\mu ,\Sigma }$ denote the probability density function of a multivariate normal distribution with mean $\mu$ and covariance $\Sigma$. The unconditional probability density function $\varphi _Y$ of Y is

$$\begin{aligned} \varphi _Y(y)&= \int \varphi _{X,Y}(x,y) dx = \int \varphi _{Y}(y|X=x) \varphi _X(x) dx \\&= \int f_{\mu _y + x, \Sigma _y}(y) f_{\mu _x, \Sigma _x}(x) dx = \int f_{\mu _y, \Sigma _y}(y-x) f_{\mu _x, \Sigma _x}(x) dx \\&= (f_{\mu _x, \Sigma _x} *f_{\mu _y, \Sigma _y})(y) = f_{\mu _x + \mu _y, \Sigma _x + \Sigma _y}(y), \end{aligned}$$

where $*$ denotes the convolution operator (see Klenke 2007, p. 277). For a detailed verification of the last equation, see Vinga (2004). $\square$

Proof of Proposition 2.5

With $\varepsilon _n \sim \mathcal {N}(0, \sigma _\varepsilon ^2 I)$, we have $\hat{a}_n | a_n \sim \mathcal {N}(a_n, \sigma _\varepsilon ^2 (X' X)^{-1})$ (see Johnson and Wichern 2007, p. 370). Under $\mathbb {P}_\Sigma$, we have $a_n \sim \mathcal {N}(\eta ,\Sigma )$ by definition. Thus, Lemma 2.4 implies

$$\begin{aligned} \hat{a}_n \sim \mathcal {N}(\eta , \Sigma + \sigma _\varepsilon ^2 (X' X)^{-1}). \end{aligned}$$

Considering the independence assumptions, the proposition follows by the definition of the Wishart distribution (see Johnson and Wichern 2007, p. 174). $\square$

Proof of Proposition 3.1

$\mathcal {Q}$, taking values in $[0,1]^T$ and being constrained by (3.3), is a bounded and closed subset of $\mathcal {L}^2 \cap \mathcal {L}^\infty$. Using the Banach-Alaoglu theorem (see, Brezis 2010, Theorem 3.16), we can deduce that it is a weak compact subset of $\mathcal {L}^2$ (see Bonnans et al. 2012). The objective function $\mathcal {J}: \mathcal {Q}\rightarrow \mathbb {R}$, defined by

$$\begin{aligned} \mathcal {J}(q) = \mathbb {E}\left[ \sum _{t=0}^{T -1} f_t(S_t) \cdot q_t \right] , \end{aligned}$$

is weakly continuous, such that the image of the compact space $\mathcal {Q}$ under the continuous mapping $\mathcal {J}$ is also compact. Because $\mathcal {J}(\mathcal {Q})$ is a closed and bounded subset of $\mathbb {R}$, the function $\mathcal {J}$ reaches its supremum. $\square$

Proof of Lemma 3.3

(based on, Bardou et al. 2010, Property P3) We only prove the concavity property because piecewise affinity can be verified by backward induction similar to the proof of Proposition 3.4, which handles the case $Q_{\min }, Q_{\max }\in \mathbb {N}_0$.

For fixed $t \in \{0,...,T -1\}$, let $Q_t, Q'_t \in {[}\underline{Q}_t, \overline{Q}_t]$, $\lambda \in [0,1]$ and $F_t$ be given. Additionally, let $(q_t) \in \mathcal {Q}$ be a feasible policy reached with $\sum _{s=0}^{t-1} q_t = Q_t$ (almost surely) and

$$\begin{aligned} \mathbb {E}\left[ \sum _{s=t}^{T -1} f_s(S_s) q_s \right] = \mathfrak {V}_{t}(Q_{t}, F_{t}), \end{aligned}$$

and let $q' \in \mathcal {Q}$ be a feasible policy with $\sum _{s=0}^{t-1} q'_t = Q'_t$ and

$$\begin{aligned} \mathbb {E}\left[ \sum _{s=t}^{T -1} f_s(S_s) q'_s \right] = \mathfrak {V}_{t}(Q'_{t}, F_{t}). \end{aligned}$$

Note that, since q and $q'$ are both [0, 1]-valued, $\lambda q + (1-\lambda ) q' := (\lambda q_t + (1-\lambda ) q'_t)_{0\le t \le T -1}$ is also [0, 1]-valued. Furthermore, $\lambda q + (1-\lambda ) q'$ reaches $\lambda Q_t + (1-\lambda ) Q'_t$ on day t and fulfills the global constraints, such that it is a feasible policy. We have

$$\begin{aligned}&\lambda \mathfrak {V}_{t}(Q_{t}, F_{t}) + (1-\lambda ) \mathfrak {V}_{t}(Q'_t, F_{t}) \\&\quad = \lambda \mathbb {E}\left[ \sum _{s=t}^{T -1} f_s(S_s) q_s\right] + (1-\lambda ) \mathbb {E}\left[ \sum _{s=t}^{T -1} f_s(S_s) q'_s\right] \\&\quad = \mathbb {E}\left[ \sum _{s=t}^{T -1} f_s(S_s) (\lambda q_s + (1-\lambda ) q'_s)\right] \\&\quad \le \mathfrak {V}_{t}(\lambda Q_{t} + (1-\lambda ) Q'_t, F_{t}), \end{aligned}$$

i.e., $\mathfrak {V}_{t}(Q_{t}, F_{t})$ is concave in $Q_t$. $\square$

Proof of Proposition 3.4

⁵⁷ For $Q_t \in [\underline{Q}_t, \overline{Q}_t] \cap \mathbb {N}_0$, we have $\underline{q}_t, \overline{q}_t \in \mathbb {N}_0$. We show that, in this case, the mapping

$$\begin{aligned} q_t \mapsto f_t(S_t) \cdot q_t + \mathbb {E}[\mathfrak {V}_{t+1}(Q_{t+1}, F_{t+1})|\mathcal {F}_t] \end{aligned}$$

(A.1)

is affine on $[\underline{q}_t, \overline{q}_t]$ for all $t\in \{0,...,T -1\}$ and $F_t\in \mathbb {R}^{T -t}_+$. Without loss of generality, we assume $Q_{t} \ge Q_{\min } - (T-t-1)$ and $Q_{t} \le Q_{\max }-1$, such that $[\underline{q}_t, \overline{q}_t]=[0,1]$. We proceed by backward induction on t.

Basis For $t = T - 1$, we have to consider $Q_{T -1} \in [\underline{Q}_{T -1}, \overline{Q}_{T -1}]$ and $q_{T -1} \in [\underline{q}_{T -1}, \overline{q}_{T -1}]$. Under these constraints, we have $Q_{\min } \le Q_T \le Q_{\max }$ such that mapping (A.1) becomes

$$\begin{aligned} q_{T -1} \mapsto f_{T -1}(S_{T -1}) \cdot q_{T -1}, \end{aligned}$$

which is linear.

Induction hypothesis Assume that, for some $t \in \{1,...,T -1\}$, we have: For all $Q_t \in [\underline{Q}_t, \overline{Q}_t]$ with $Q_t\in \mathbb {N}_0$ and all $F_t\in \mathbb {R}^{T -t}_+$, the mapping

$$\begin{aligned} q_t \mapsto f_t(S_t) \cdot q_t + \mathbb {E}[\mathfrak {V}_{t+1}(Q_t + q_t, F_{t+1})|\mathcal {F}_t] \end{aligned}$$

is affine on $[\underline{q}_t, \overline{q}_t]$.

Inductive step Now we move from t to $t-1$. Let $Q_{t-1} \in [0 \vee (Q_{\min } - (T-t)), (Q_{\max }-1) \wedge (t-1)] \cap \mathbb {N}_0$. Thus, we have to show the affinity of

$$\begin{aligned} q_{t-1} \mapsto&\ f_{t-1}(S_{t-1}) \cdot q_{t-1} + \mathbb {E}[\mathfrak {V}_{t}(Q_{t-1}+q_{t-1}, F_{t})|\mathcal {F}_{t-1}] \\&\quad = \ f_{t-1}(S_{t-1}) \cdot q_{t-1} + \mathbb {E}[\max _{q_t \in [0,1]} f_t(S_t) \cdot q_t\\&\qquad + \mathbb {E}[\mathfrak {V}_{t+1}(Q_{t-1}+q_{t-1}+q_t, F_{t+1})|\mathcal {F}_t]|\mathcal {F}_{t-1}] \end{aligned}$$

on [0, 1]. For $q_{t-1}$ and $F_t$ both fixed, we look closer at

$$\begin{aligned} q_t \mapsto f_t(S_t) \cdot q_t + \mathbb {E}[\mathfrak {V}_{t+1}(Q_{t-1}+q_{t-1}+q_t, F_{t+1})|\mathcal {F}_t] \end{aligned}$$

(A.2)

on $[\underline{q}_{t},\overline{q}_{t}]$. Note that $1-q_{t-1} \in [\underline{q}_{t},\overline{q}_{t}]$ because $Q_{\min } - (T-t) \le Q_{t-1} \le Q_{\max }-1$. We use the induction hypothesis to conclude that (A.2) is piecewise affine; more precisely, affine on $[\underline{q}_{t}, 1-q_{t-1}]$ and $[1-q_{t-1}, \overline{q}_{t}]$.

If $q_t \in [\underline{q}_{t}, 1-q_{t-1}]$, we have $q_{t-1}+q_t \le 1$. We define $\tilde{Q}_t := Q_{t-1}$. Since $\tilde{Q}_t \in [\underline{Q}_t, \overline{Q}_t] \cap \mathbb {N}_0$, the mapping

$$\begin{aligned} \tilde{q}_t \mapsto f_t(S_t) \cdot \tilde{q}_t + \mathbb {E}[\mathfrak {V}_{t+1}(\tilde{Q}_t+\tilde{q}_t, F_{t+1})|\mathcal {F}_t] \end{aligned}$$

(A.3)

is affine on $[0 \vee (Q_{\min }-Q_{t-1}-(T-t-1)), 1]$ by induction hypothesis. Setting $\tilde{q}_t = q_{t-1}+q_t$ then implies that mapping (A.2) is affine on $[\underline{q}_{t}, 1-q_{t-1}]$.

At the same time, we have $q_{t-1}+q_t \ge 1$ if $q_t \in [1-q_{t-1}, \overline{q}_{t}]$. We now set $\tilde{Q}_t := Q_{t-1} + 1 \in [\underline{Q}_t, \overline{Q}_t] \cap \mathbb {N}_0$. Again, the induction hypothesis states that (A.3) is affine on $[0, 1 \wedge (Q_{\max }-Q_{t-1}-1)]$, which implies that mapping (A.2) is affine on $[1-q_{t-1}, \overline{q}_{t}]$ by setting $\tilde{q}_t = q_{t-1}+q_t-1$.

It follows that (A.2) is piecewise affine with monotonicity breakpoint at $1-q_{t-1}$ such that the mapping reaches its maximum at the interval endpoints $\underline{q}_{t}, \overline{q}_{t}$ or at its monotonicity breakpoint. We have

$$\begin{aligned} \mathfrak {V}_{t}(Q_{t-1} + q_{t-1}, F_{t}) =&\max _{q_t\in \{\underline{q}_{t}, 1-q_{t-1}, \overline{q}_{t}\}} f_t(S_t) \cdot q_t \\&+ \mathbb {E}[\mathfrak {V}_{t+1}(Q_{t-1}+q_{t-1}+q_t, F_{t+1})|\mathcal {F}_t]. \end{aligned}$$

For fixed $F_{t}$, we consider the mappings

$$\begin{aligned} q_{t-1} \mapsto f_t(S_t) \cdot q_t + \mathbb {E}[\mathfrak {V}_{t+1}(Q_{t-1}+q_{t-1}+q_t, F_{t+1})|\mathcal {F}_t] \end{aligned}$$

(A.4)

on [0, 1] for $q_t \in \{\underline{q}_{t}, 1-q_{t-1}, \overline{q}_{t}\}$.

For $q_t = 1-q_{t-1}$, (A.4) becomes

$$\begin{aligned} q_{t-1} \mapsto f_t(S_t) \cdot (1-q_{t-1}) + \mathbb {E}[\mathfrak {V}_{t+1}(Q_{t-1}+1, F_{t+1})|\mathcal {F}_t], \end{aligned}$$

which is affine.

For $q_t = \underline{q}_{t} = 0 \vee (Q_{\min }-Q_{t-1}-q_{t-1}-(T-t-1))$, note that $Q_{\min }-Q_{t-1}-(T-t-1) \in \mathbb {Z}$, such that we have either $\underline{q}_{t} = 0$ or $\underline{q}_{t} = Q_{\min }-Q_{t-1}-q_{t-1}-(T-t-1) \ge 0$ on the entire interval $q_{t-1}\in [0,1]$. If $\underline{q}_{t} = 0$, (A.4) becomes

$$\begin{aligned} q_{t-1} \mapsto \mathbb {E}[\mathfrak {V}_{t+1}(Q_{t-1}+q_{t-1}, F_{t+1})|\mathcal {F}_t], \end{aligned}$$

which is affine by induction hypothesis (setting $\tilde{Q}_t := Q_{t-1} \in \mathbb {N}_0$). Otherwise, we have

$$\begin{aligned} q_{t-1} \mapsto&f_t(S_t) \cdot (Q_{\min }-Q_{t-1}-q_{t-1}-(T-t-1)) \\&+ \mathbb {E}[\mathfrak {V}_{t+1}(Q_{\min }-(T-t-1), F_{t+1})|\mathcal {F}_t], \end{aligned}$$

which is also affine. For $q_t = \underline{q}_{t} = 1 \wedge (Q_{\max } - Q_{t-1} - q_{t-1})$, we can similarly verify the affinity of (A.4).

It follows that $q_{t-1} \mapsto \mathfrak {V}_{t}(Q_{t-1} + q_{t-1}, F_{t})$ is convex as a pointwise maximum of affine mappings on [0, 1]. It is affine because we know from Lemma 3.3 that it is also concave. Taking conditional expectations with respect to $\mathcal {F}_{t-1}$ and adding $f_{t-1}(S_{t-1}) \cdot q_{t-1}$ completes the inductive step.

Starting at $t=0$ with $Q_0 = 0 \in \mathbb {N}_0$, we conclude by forward induction that taking $q_t$ from $\{\underline{q}_t, \overline{q}_t\} \subseteq \{0,1\}$ is always one optimal choice because (A.1) is affine in the case of $Q_t \in \mathbb {N}_0$. Hence, we can optimally exercise in digital fashion. $\square$

Proof of Corollary 3.6

(based on, Bonnans et al. 2012, Corollary 4.4) Because $\phi (x)$ is locally Lipschitz continuous by Danskin’s theorem, Rademacher’s theorem (see, Rockafellar and Wets 2009, Theorem 9.60) states that it is totally differentiable almost everywhere.

Now, let $x \in \mathbb {R}^n$ and $\phi (x)$ be totally differentiable at x. Assume Eq. (3.11) does not hold, i.e., there exist $v_1^*, v_2^* \in V^*(x)$ such that ${{\mathrm{d}}}_x \psi (x, v_1^*)\not ={{\mathrm{d}}}_x \psi (x, v_2^*)$. That is, the corresponding gradients differ in at least one entry with index i. Consider the direction $h = (0,...,0,1,0,...0)$ where 1 is placed at position i. With Eq. (3.9), we then have

$$\begin{aligned} \nabla _{h} \phi (x) \not = -(\nabla _{-h} \phi (x)). \end{aligned}$$

Thus, $\phi (x)$ is not totally differentiable at x and we have a contradiction. $\square$

Proof of Lemma 3.7

(based on, Bonnans et al. 2012, Lemma 4.1 and Proposition 4.2) In the first step, we show that, for every t, the partial derivative of $\mathcal {J}$ with respect to F(0, t) exists. We define $g(F(0,t), \omega ) := f_t(S_t(F(0,t), \omega ))\cdot q_t$. Let $x\in \mathbb {R}_+$ and $(x_n)$ be a sequence in $\mathbb {R}_+$ with $x_n \not = x$ for every $n\in \mathbb {N}$ and $\lim _{n\rightarrow \infty } x_n = x$. We now show that the corresponding sequence of difference quotients converges. To this end, set

$$\begin{aligned} \Delta g_n(\omega ) := \frac{g(x_n,\omega )-g(x,\omega )}{x_n - x} \end{aligned}$$

for every $\omega \in \Omega$. In view of the Lipschitz continuity of $f_t$, Rademacher’s theorem (see, Rockafellar and Wets 2009, Theorem 9.60) states that it is differentiable almost everywhere and that its derivative is bounded. Combined with the partial differentiability of $S_t$ in F(0, t), we know that $g(\cdot ,\omega )$ is differentiable for almost every $\omega$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Delta g_n = g'(x,\cdot ) \end{aligned}$$

almost surely. According to the mean value theorem (see, Rudin 1964, Theorem 5.10), for every $n \in \mathbb {N}$ and almost every $\omega \in \Omega$, there exists $y_n(\omega )\in \mathbb {R}_+$ such that $\Delta g_n(\omega )= g'(y_n(\omega ),\omega )$. In particular, $g_n$ is bounded almost everywhere for every n. Since $g(x,\cdot )$ is integrable for every x, we can apply the dominated convergence theorem (see, Klenke 2007, Corollary 6.26) to see that $g'(x, \cdot )$ is integrable and

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{\mathbb {E}[g(x_n)]-\mathbb {E}[g(x)]}{x_n-x} = \lim _{n\rightarrow \infty } \mathbb {E}[\Delta g_n] = \mathbb {E}[g'(x)]. \end{aligned}$$

Rewritten in our original terms, we have

$$\begin{aligned} \frac{\partial \mathcal {J}(F_0, q)}{\partial F(0,t)} = \frac{\partial \mathbb {E}[f_t(S_t(F_0)) \cdot q_t]}{\partial F(0,t)} = \mathbb {E}\left[ \frac{\partial f_t(S_t)}{\partial F(0,t)}(F_0) \cdot q_t\right] . \end{aligned}$$

In the second step, we verify the continuity of the partial derivatives. Again, let $x^*\in \mathbb {R}_+$ and $(x_n)$ be a sequence in $\mathbb {R}_+$ with $x_n \not = x^*$ for every $n\in \mathbb {N}$ and $\lim _{n\rightarrow \infty } x_n = x^*$. Furthermore, denote $\tilde{g}(F(0,t)) := S_t(F(0,t))$ and $S_t^n := \tilde{g}(x_n)$, $S_t^* := \tilde{g}(x^*)$. We have to show that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{\partial f_t(S^n_t)}{\partial F(0,t)} = \frac{\partial f_t(S^*_t)}{\partial F(0,t)} \end{aligned}$$

in $\mathcal {L}^1$. By the chain rule of differentiation, at the points where $f_t$ is differentiable, we have

$$\begin{aligned} \frac{\partial f_t(S_t)}{\partial F(0,t)} = \frac{\partial f_t(S_t)}{\partial S_t} \cdot \frac{\partial S_t}{\partial F(0,t)}. \end{aligned}$$

Denote $f_{\partial x} := \frac{\partial f}{\partial x}$. By assumption, the partial derivatives of $S_t^*$ and $S_t^n$ both have bounded density functions $\varphi _t^*$ and $\varphi _t^n$ with respect to the Lebesgue measure. Since $f_t$ is Lipschitz continuous, $\partial _{S_t} f_t \in \mathcal {L}^\infty (\Omega ,\mathcal {F},\mathbb {P}) \subseteq \mathcal {L}^q(\Omega ,\mathcal {F},\mathbb {P})$, $1\le q < \infty$. Because the space of continuous functions with compact support $C_c(\Omega )$ is dense in $\mathcal {L}^q(\Omega ,\mathcal {F},\mathbb {P})$, we have

$$\begin{aligned} \forall \varepsilon >0 \ \exists h: ||h-\partial _{S_t} f_t||_q \le \varepsilon . \end{aligned}$$

It follows that

$$\begin{aligned} ||h(S_t^n)-\partial _{S_t} f_t(S_t^n)||_q&= \left( \int _s |h(s)-\partial _s f_t(s)|^q \varphi _t^n(s) ds\right) ^{1/q} \\&\le ||\varphi _t^n||_\infty ^{1/q} \cdot ||h-\partial _{S_t} f_t||_q \\&\le ||\varphi _t^n||_\infty ^{1/q} \cdot \varepsilon \end{aligned}$$

and analogously

$$\begin{aligned} ||h(S_t^*)-\partial _{S_t} f_t(S_t^*)||_q \le ||\varphi _t^*||_\infty ^{1/q} \cdot \varepsilon . \end{aligned}$$

Moreover, $\lim _{n\rightarrow \infty } S_t^n = S_t^*$ almost surely and $\lim _{n\rightarrow \infty } \partial _{F(0,t)} S_t^n = \partial _{F(0,t)} S_t^*$ in $\mathcal {L}^p$, $1\le p<\infty$. By continuity of h and the dominated convergence theorem (see, Klenke 2007, Corollary 6.26), there exists a $N_h$ such that

$$\begin{aligned} ||h(S_t^n) - h(S_t^*)||_q \le \varepsilon \end{aligned}$$

for all $n\ge N_h$. Thus, we have

$$\begin{aligned}&||\partial _{S_t} f_t(S_t^n) - \partial _{S_t} f_t(S_t^*)||_q \\ \le \,&||\partial _{S_t} f_t(S_t^n) - h(S_t^n)||_q + ||h(S_t^n) - h(S_t^*)||_q + ||h(S_t^*) - \partial _{S_t} f_t(S_t^*)||_q \\ \le \,&(||\varphi _t^n||_\infty ^{1/q} + ||\varphi _t^*||_\infty ^{1/q}+ 1) \varepsilon \end{aligned}$$

for all $n\ge N_h$. Let $\varepsilon \rightarrow 0$. Then, we obtain $\lim _{n\rightarrow \infty } \partial _{S_t} f_t(S_t^n) = \partial _{S_t} f_t(S_t^*)$ in $\mathcal {L}^q$. Finally, taking $p^{-1}+q^{-1}=1$, $\lim _{n\rightarrow \infty } \partial _{F(0,t)} f_t(S_t^n) = \partial _{F(0,t)} f_t(S_t^*)$ in $\mathcal {L}^1$ follows by combining the convergence of $\partial _{S_t} f_t(S_t)$ in $\mathcal {L}^p$ and the convergence of $\partial _{F(0,t)} S_t$ in $\mathcal {L}^q$.

J having continuous partial derivatives is totally differentiable and its derivative is given by (3.12). In this perspective, $J'$ is weakly continuous with respect to q. $\square$

Proof of Proposition 3.8

To apply Danskin’s theorem (Theorem 3.5), we have to verify its assumptions. In view of Lemma 3.7, we only have to recall that the feasible solution space $\mathcal {Q}$ is weakly compact as argued in the proof of Proposition 3.1. Hence, Theorem 3.5 or rather Corollary 3.6 provides the result. $\square$

Proof of Proposition 3.9

We show by backward induction that $F_t \mapsto \mathfrak {V}_t(Q_t, F_t)$ is convex on $\mathbb {R}^{T -t}_+$ for every $t \in \{0,...,T -1\}$ and every valid quantity $Q_t$. Note that, for every t, we have $F(t,t) = S_t$ such that $F_t \mapsto f_t(S_t(F_t))$ is convex by assumption. For $t=T -1$ and $Q_{T -1} \in [\underline{Q}_{T -1}, \overline{Q}_{T -1}]$, we have

$$\begin{aligned} \mathfrak {V}_{T -1}(Q_{T -1}, F_{T -1})&= \max _{q_{T -1} \in [0,1]} f_{T -1}(S_{T -1}) \cdot q_{T -1} + \mathbb {E}[\mathfrak {V}_T (Q_T , F_ T )|\mathcal {F}_{T -1}] \\&= \max _{q_{T -1} \in [\underline{q}_{T -1},\overline{q}_{T -1}]} f_{T -1}(S_{T -1}) \cdot q_{T -1} , \end{aligned}$$

which, as a pointwise maximum over a set of convex functions, is convex in $F_{T -1}$.⁵⁸

We now move from t to $t-1$. Let $Q_{t-1} \in [\underline{Q}_{t-1}, \overline{Q}_{t-1}]$. By induction assumption, $F_{t} \mapsto \mathfrak {V}_{t}(Q_{t-1} + q_{t-1}, F_{t})$ is convex for every $q_{t-1} \in [\underline{q}_{t-1}, \overline{q}_{t-1}]$. For fixed $\Delta W(t-1)$, the function $g_{t-1}(F_{t-1}, \Delta W(t-1))$ is affine in $F_{t-1}$ by assumption, such that the mapping $F_{t-1} \mapsto \mathfrak {V}_{t}(Q_{t-1} + q_{t-1}, g_{t-1}(F_{t-1}, \Delta W(t-1)))$ is convex. Denote by $\varphi _{t-1}$ the density function of $\Delta W_{t-1}$. Then, it follows that

$$\begin{aligned}&F_{t-1} \mapsto \mathbb {E}[\mathfrak {V}_{t}(Q_{t-1} + q_{t-1}, F_{t})|\mathcal {F}_{t-1}] \\&\quad = \int _w \mathfrak {V}_{t}(Q_{t-1} + q_{t-1}, g_{t-1}(F_{t-1}, w)) \varphi _{t-1}(w) dw \end{aligned}$$

is convex. Since $F_{t-1} \mapsto f_{t-1}(S_{t-1})$ is convex by assumption and taking the pointwise maximum or adding functions of this kind are operations preserving convexity,

$$\begin{aligned} \mathfrak {V}_{t-1}(Q_{t-1}, F_{t-1})&= \max _{q_{t-1} \in [\underline{q}_{t-1},\overline{q}_{t-1}]} f_{t-1}(S_{t-1}) \cdot q_{t-1} \\&\quad + \mathbb {E}[\mathfrak {V}_{t}(Q_{t-1}+q_{t-1}, F_{t})|\mathcal {F}_{t-1}] \end{aligned}$$

is convex, which concludes the induction step.

Because $v: \mathbb {R}^T \rightarrow \mathbb {R}$ is convex, the theorem of Alexandrov (1939) ensures the twice totally differentiability almost everywhere. $\square$

Additional results

The following tables and figures present results extending our main analysis. They are ordered according to their line of occurrence/reference in the main text (Tables 9, 10, 11, 12 and Figs. 12, 13, 14, 15, 16).

Table 9 Single-factor model

Table 10 Principle component analysis

Table 11 Long-term gamma estimates for the benchmark approach with sample size $N = 5000$

Table 12 Benchmark approach with additive price shifts

Additional derivations and discussions

Derivation of drift term (2.26) Based on the solution (2.21) of the spot price process in the multi-factor framework, we obtain

$$\begin{aligned} \log S_t = \log F(0,t) + \sum _{k=1}^K \left( -\frac{1}{2} \int _0^t \sigma _k^2(s,t) ds + \int _0^t \sigma _k(s,t) dW_k(s) \right) , \end{aligned}$$

which implies

$$\begin{aligned} \int _0^t \sigma _2(s,t) dW_2(s)=&\log S_t - \log F(0,t) + \frac{1}{2} \sum _{k=1}^K \int _0^t \sigma _k^2(s,t) ds \\&- \sum _{k\not = 2} \int _0^t \sigma _k(s,t) dW_k(s). \end{aligned}$$

It follows that

$$\begin{aligned}&\sum _{k=1}^K \left( - \int _0^t \sigma _k(s,t) \frac{\partial \sigma _k(s,t)}{\partial t} ds + \int _0^t \frac{\partial \sigma _k(s,t)}{\partial t} dW_k(s) \right) \\&\quad = \sum _{k=2}^K \left( -\! \int _0^t \sigma _k(s,t) \frac{\partial \sigma _k(s,t)}{\partial t} ds\right) \! -\! \vartheta \int _0^t \sigma _2(s,t) dW_2(s) +\! \int _0^t \frac{\partial \sigma _3(s,t)}{\partial t} dW_3(s) \\&\quad = \sum _{k=2}^K \left( - \int _0^t \sigma _k(s,t) \frac{\partial \sigma _k(s,t)}{\partial t} ds\right) + \int _0^t \frac{\partial \sigma _3(s,t)}{\partial t} dW_3(s) \\&\qquad - \vartheta \left( \log S_t - \log F(0,t) + \frac{1}{2} \sum _{k=1}^K \int _0^t \sigma _k^2(s,t) ds - \sum _{k\not = 2} \int _0^t \sigma _k(s,t) dW_k(s)\right) \\&\quad = \frac{1}{2} \vartheta \sigma _2^2 \int _0^t \exp (-2\vartheta (t-s)) ds + a \sigma _3^2 \cos (a(t + c)) \sin (a(t + c)) t \\&\qquad - a \sigma _3 \sin (a(t + c)) W_3(t) - \vartheta \\&\qquad \left( \log S_t - \log F(0,t) + \frac{1}{2} \left( \sigma _1^2 t + \sigma _3^2 \cos ^2(a(t+c)) t \right) \right. \\&\qquad \left. - \sigma _1 W_1(t) - \sigma _3 \cos (a(t + c)) W_3(t)\right) . \end{aligned}$$

With $\int _0^t \exp (-2\vartheta (t-s)) ds = \frac{1}{2\vartheta }(1-\exp (-2\vartheta t))$, we get

$$\begin{aligned} \mu (t) = \frac{\partial F(0,t)}{\partial t} + \mu _{\text {seas}}(t) + \vartheta \left( \log \mu _{\text {lt}}(t) + \frac{\sigma _2^2}{4 \vartheta } (1-e^{-2\vartheta t}) - \log (S_t)\right) , \end{aligned}$$

where

$$\begin{aligned} \mu _{\text {seas}}(t)&= a \sigma _3^2 \cos (a(t + c)) \sin (a(t + c)) t - a \sigma _3 \sin (a(t + c)) W_3(t), \\ \mu _{\text {lt}}(t)&= F(0,t) \exp \left( - \frac{1}{2} \sigma _1^2 t + \sigma _1 W_1(t) - \frac{1}{2} \sigma _3^2 \cos ^2(a(t+c)) \right. \\&\quad \left. +\, \sigma _3 \cos (a(t+c)) W_3(t)\right) . \end{aligned}$$

Thus we have obtained the drift term (2.26). $\square$

Error propagation Uncertainty in continuation values (emerging from, for example, approximation error in the LSM) directly influences the exercise strategy and thus fair value and sensitivity estimates. To analyse the impact of such uncertainty in general, we perform a simple simulation study. That is, in our benchmark setting with three state variables and $N = 1000$, we set $^\epsilon \mathcal {C}_t^{r} = \mathcal {C}_t^{r} + \epsilon _t^r$, where $\epsilon _t^r$ are i.i.d. standard normal random variables.⁵⁹ Table 13 reports the consequences of this procedure for our estimates, e.g., the change in the option value $\Delta v := \,^\varepsilon v-v$. Besides changes in fair values, pathwise deltas and TFD long-term gammas, we present the changes in the expected consumption quantity $\mathbb {E}[q^*] := \mathbb {E}[\sum _{t=0}^{T -1}q^*_t]$. As expected, the value estimate is reduced in all cases. In most cases, expected consumption and deltas, which are closely related, also decrease. Gamma changes occur in both directions.

Fig. 12

Average $R^2$ in least-squares procedure dependent on $\vartheta$. a B-TSLS. b P-TSLS. For the basic (B-TSLS) and the piecewise (P-TSLS) two-stage least-squares procedures introduced in Sect. 2.2.3, this figure plots the resulting average regression $R^2$ dependent on the short-term volatility decay parameter $\vartheta$. We consider data for 48 front months in both cases. The maximization leads to optimal $\vartheta$ choices of 0.990 and 1.861 in the B-TSLS and P-TSLS approach, respectively

Fig. 13

Sample returns with fitted volatility functions (B-TSLS). a$R^2 = 0.7533$. b$R^2 = 0.9517$. c$R^2 = 0.8957$. d$R^2 =0.5843$. e$R^2 = 0.5092$. f$R^2 = 0.1186$. g$R^2 = 0.7288$. h$R^2 = 0.1270$. This figure plots sample log returns for 24 (a–f) and 48 (g, h) front months with volatility functions fitted according to our B-TSLS procedure and corresponding 95% confidence intervals

Fig. 14

Normalized piecewise seasonal volatility functions. a$f_3(t,T)$. b$f_4(t,T)$. c$f_5(t,T)$. d$f_6(t,T)$. e$f_7(t,T)$. f$f_8(t,T)$. In our P-TSLS regression approach, we capture the seasonal volatility for each season spread individually. Formally, we use six normalized volatility functions $f_k$ given by Eq. (2.18). We set $(c_{\min }, c_{\max }) = (0,18)$ for $k=3$, $(c_{\min }, c_{\max }) = (18,24)$ for $k=4$, $(c_{\min }, c_{\max }) = (30,36)$ for $k=5$, etc. The functions $f_k$, $k=3,...,8$, without correction term $\mu _k(t,T)$, are plotted above

Fig. 15

Sample returns with fitted volatility functions (P-TSLS). a$R^2 = 0.9479$. b$R^2 = 0.9855$. c$R^2 = 0.8802$. d$R^2 = 0.4870$. This figure plots sample log returns for 48 front months with volatility functions fitted according to our P-TSLS procedure and corresponding 95% confidence intervals

Fig. 16

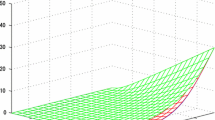
Simulated forward curves. a Path $n = 1$. b Path $n = 2$. c Path $n = 3$. This figure exemplarily plots forward prices derived from our simulation procedure which is based on the discretized version of the multi-factor PFC model (2.1) with volatility functions (2.6) and estimates taken from Table 3. For each day in the period from October 1, 2014 to September 30, 2016, we display the current forward prices (in €/MWh) of the respective next 36 months

Different random seeds In our analysis, we fix the random seed for two reasons. First, we ensure that the value, delta and gamma estimates correspond to each other because they are calculated based on the same price paths. Second, we opt for common random numbers because they are a variance reduction technique typically used when estimates are drawn from more than one simulated scenario. While finite differences derivative estimates are naturally biased (see, Glasserman 2003, chpt. 7.1), this dependent sampling method does not introduce additional bias.⁶⁰

To illustrate the variance reduction, we consider the forward difference of $\delta$, i.e.,

$$\begin{aligned} \text {Var}(v(F_0 + \Delta F_0) - v(F_0)) = {\left\{ \begin{array}{ll}\mathcal {O}(1), &{} \text {in case (i),} \\ \mathcal {O}(\varepsilon ), &{} \text {in case (ii),} \end{array}\right. } \end{aligned}$$

where $\Delta F_0 = \varepsilon \cdot dF_0$. Case (i) reflects the independent (with different random seeds) simulation of $v(F_0)$ and $v(F_0 + \Delta F_0)$. We then have

$$\begin{aligned} \text {Var}(v(F_0 + \Delta F_0) - v(F_0)) \rightarrow 2 \text {Var}(v(F_0)) \end{aligned}$$

under the assumption that $\text {Var}(v(F_0))$ is continuous in $\varepsilon$. Consequently, the variance of the estimator $(v(F_0 + \Delta F_0) - v(F_0))/\varepsilon$ explodes (converges to infinity at rate $1/\varepsilon ^2$) for $\varepsilon \rightarrow 0$ and there is no hope of obtaining reasonable sensitivity estimates. Case (ii) occurs (under some mild conditions) when common random numbers are used for the simulations at $F_0$ and $F_0 + \Delta F_0$ (see L’Ecuyer and Perron 1994). Here, the overall variance of the derivative estimator stays bounded for $\varepsilon \rightarrow 0$. These considerations similarly hold for the regression delta estimates and for our second-order sensitivity estimates.

Despite this advantage, using (fixed or variable) random numbers always introduces a Monte Carlo error. To quantify this error, we analyse the distributions of our estimators for different random seeds. Specifically, we obtain the sampling distributions of the fair value, pathwise delta and TFD long-term gamma estimators (of our benchmark approach) using $S = 1000$ distinct seeds. All other settings remain unchanged. That is, the Monte Carlo error corresponds to $N = 1000$ simulated price paths. Figure 17 presents our results for the contracts with $Q_{\min } = 60\cdot i$ and $Q_{\max } = 180$, $i = 0,1,2,3$.⁶¹

Table 13 Error propagation

Fig. 17

Estimator distributions under variable random seeds. For contracts with $Q_{\min } = 60\cdot i$ and $Q_{\max } = 180$, $i = 0,1,2,3$, and based on $S = 1000$ different random seeds, this figure shows the histograms of the fair value, pathwise delta and TFD long-term gamma estimators (of our benchmark approach) reflecting the Monte Carlo error related to $N = 1000$ simulated price paths

Because of our low number of $N = 1000$ simulated price paths, we can observe non-negligible Monte Carlo error. The standard deviation of our estimators is naturally related to the magnitude of the estimated sensitivity. For example, the pathwise delta estimator of the inflexible contract with $Q_{\min } = 180$ has a very low standard error because the option’s gamma is nearly zero. To obtain more precise estimates and more narrow distributions, we could increase N, which significantly increases computation time. However, as pointed out in Sect. 4.2, we can illustrate all features and the proper functioning of our approach based on this sample size.

Optimal bandwidth choice We assume that v is three times continuous (directional) differentiable in a neighborhood of $F_0$. We elaborate the estimation procedure for the overall gamma in the forwards approach, i.e., for the second-order derivative of v in the direction $d F_0 = (1,...,1)'$. We denote by $v', v''$ etc. the derivatives in this direction.

By Taylor expansion, we have $\delta (F_0 + \Delta F_0) = \delta (F_0) + \varepsilon _N \delta '(F_0) + \frac{1}{2} \varepsilon _N^2 \delta ''(F_0 + \xi dF_0)$, where $\xi \in [0, \varepsilon _N]$. Thus, for the estimator’s bias, we get

$$\begin{aligned} \mathbb {E}[\hat{\gamma }] - \gamma&= \mathbb {E}\left[ \sum _{t=0}^{T -1} \frac{\partial S_t}{\partial F(0, t)} \cdot \frac{\Delta q^*_t(F_0)}{\varepsilon _N}\right] - \gamma \\&= \frac{\delta (F_0 + \Delta F_0) - \delta (F_0)}{\varepsilon _N} - \delta '(F_0) \\&= \frac{\varepsilon _N^2}{2} \delta ''(F_0 + \xi dF_0) \\&= \frac{\varepsilon _N^2}{2} (\delta ''(F_0) + o(1)) \end{aligned}$$

as $N\rightarrow \infty$. We write $y_n = o(x_n)$, if $\lim _{n\rightarrow \infty } |\frac{y_n}{x_n}|=0$, and $y_n = \mathcal {O}(x_n)$, if $\limsup _{n\rightarrow \infty } |\frac{y_n}{x_n}|<\infty$. For the variance of the estimator, we have

$$\begin{aligned} \text {Var}(\hat{\gamma })&= \text {Var}\left( \frac{1}{N} \sum _{n=1}^N \sum _{t=0}^{T -1} \frac{\partial \, ^nS_t}{\partial F(0, t)} \cdot \frac{\Delta ^n q^*_t(F_0)}{\varepsilon _N}\right) \\&= \frac{1}{N\varepsilon _N^2} \text {Var}\left( \sum _{t=0}^{T -1} \frac{\partial S_t}{\partial F(0, t)} \cdot \Delta q^*_t(F_0)\right) \\&=: \frac{1}{N\varepsilon _N^2} \mathcal {V}_\gamma (\varepsilon _N). \end{aligned}$$

Furthermore, we define

$$\begin{aligned} X := \sum _{t=0}^{T -1} \frac{\partial S_t}{\partial F(0, t)} \cdot \Delta q^*_t(F_0). \end{aligned}$$

Because we use common random numbers, we have $\lim _{N\rightarrow \infty } q^*_t(F_0 + \Delta F_0) = q^*_t(F_0)$ almost surely for every t, which implies $\lim _{N\rightarrow \infty } \mathcal {V}_\gamma (\varepsilon _N) = 0$. Thus, what is left is to determine the speed of the convergence. Note that simulating $F_t(F_0)$ and $F_t(F_0 + \Delta F_0)$ with independent samples would cause $\mathcal {V}_\gamma (\varepsilon _N) = \mathcal {O}(1)$ because

$$\begin{aligned} \text {Var}(X(F_0+\Delta F_0) - X(F_0))&= \text {Var}(X(F_0+\Delta F_0)) + \text {Var}(X(F_0)) \\&\rightarrow 2 \text {Var}(X(F_0)). \end{aligned}$$

Because the payoff is pathwise discontinuous, we do not expect $\mathcal {V}_\gamma (\varepsilon _N) = \mathcal {O}(\varepsilon _N^2)$ such that the overall variance of the estimator stays bounded as $\varepsilon _N \rightarrow 0$.⁶²

We now present some heuristics to argue why we have at least $\mathcal {V}_\gamma (\varepsilon _N) = \mathcal {O}(\varepsilon _N)$. Because of

$$\begin{aligned} F(t, T) = F(0,T) \exp \left( \sum _{s=0}^{t-1}\sigma (s,T) \Delta W(s)\right) , \end{aligned}$$

we have $S_t(F_0 + \Delta F_0) - S_t(F_0) = \mathcal {O}(\varepsilon _N)$. For fixed $r_t$, it follows that $\mathcal {C}_t^{r_t}(F_t + \Delta F_t) - \mathcal {C}_t^{r_t}(F_t) = \mathcal {O}(\varepsilon _N)$ because $\mathcal {C}_t^{r_t}$ is differentiable in $F_t$ which can be seen by applying our previous results to the subproblem (3.5). Thus, toggling between $F_0$ and $F_0 + \Delta F_0$ shifts the exercise condition $S_t-\mathscr {K}+ \mathcal {C}_t^{r_t+1} - \mathcal {C}_t^{r_t}$ in $\mathcal {O}(\varepsilon _N)$. Since

$$\begin{aligned} \mathbb {P}(|S_t - \mathscr {K}+ \mathcal {C}_t^{r_t+1}-\mathcal {C}_t^{r_t}|<c\cdot \varepsilon _N) = \mathcal {O}(\varepsilon _N), \end{aligned}$$

the probability that the exercise condition crosses zero on day t for fixed $r_t$ is $\mathcal {O}(\varepsilon _N)$. Because we consider a discrete finite time horizon and a digital optimal control, there is only a finite number of exercise conditions which could lead to a discontinuous payoff. It follows that

$$\begin{aligned}&\mathbb {P}(X\text { is discontinuous in }[F_0, F_0 + \Delta F_0]) \\&\le \mathbb {P}\left( \bigcup _{t=0}^T \bigcup _{r_t=\underline{q}_t}^{\overline{q}_t} |S_t - \mathscr {K}+ \mathcal {C}_t^{r_t+1}-\mathcal {C}_t^{r_t}|<c\cdot \varepsilon _N\right) \\&\le \sum _{t=0}^T \sum _{r_t=\underline{q}_t}^{\overline{q}_t} \mathbb {P}(|S_t - \mathscr {K}+ \mathcal {C}_t^{r_t+1}-\mathcal {C}_t^{r_t}|<c\cdot \varepsilon _N) \\&= \mathcal {O}(\varepsilon _N), \end{aligned}$$

i.e., the probability that the overall payoff is discontinuous in $[F_0, F_0 + \Delta F_0]$ converges to zero as $\mathcal {O}(\varepsilon _N)$. Bridging discontinuities costs $\mathcal {O}(1)$, whereas we have $\mathcal {O}(\varepsilon _N)$ for a continuous payoff. Let $A := \{\omega \in \Omega : X(w)\text { is continuous in }[F_0, F_0 + \Delta F_0]\}$. It follows

$$\begin{aligned} \mathbb {E}[X]&= \mathbb {P}(\omega \in A) \mathbb {E}[X(\omega )|\omega \in A] + \mathbb {P}(\omega \not \in A) \mathbb {E}[X(\omega )|\omega \not \in A] \\&= \mathcal {O}(1)\mathcal {O}(\varepsilon _N) + \mathcal {O}(\varepsilon _N) \mathcal {O}(1) = \mathcal {O}(\varepsilon _N) \end{aligned}$$

and

$$\begin{aligned} \mathbb {E}[X^2]&= \mathbb {P}(\omega \in A) \mathbb {E}[X^2(\omega )|\omega \in A] + \mathbb {P}(\omega \not \in A) \mathbb {E}[X^2(\omega )|\omega \not \in A] \\&= \mathcal {O}(1) \mathcal {O}(\varepsilon _N^2) + \mathcal {O}(\varepsilon _N) \mathcal {O}(1) = \mathcal {O}(\varepsilon _N). \end{aligned}$$

Hence, we have

$$\begin{aligned} \mathcal {V}_\gamma = \text {Var}(X) = \mathbb {E}[X^2] - (\mathbb {E}[X])^2 = \mathcal {O}(\varepsilon _N). \end{aligned}$$

Table 14 Optimal bandwidth choice

We now turn to Monte Carlo methods. For $\varepsilon _N \in \{-2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2\}$, we use the corresponding pathwise delta estimates in the OLS regression

$$\begin{aligned} \mathbb {E}[\delta |F_0 + \Delta F_0] = \delta (F_0) + \delta '(F_0) \cdot \varepsilon + \frac{1}{2} \delta ''(F_0) \cdot \varepsilon ^2. \end{aligned}$$

(C.1)

In addition, we set $^n\delta (\varepsilon _N) := \sum _{t=0}^{T -1} \frac{\partial \,\, ^nS_t}{\partial F(0, t)} \cdot \,^n q^*_t(F_0 + \Delta F_0)$, calculate

$$\begin{aligned} \hat{\mathcal {V}}_\gamma (\varepsilon _N) = \text {Var}(^n\delta (\varepsilon _N) - \,^n\delta (0)) \end{aligned}$$

for each $\varepsilon _N$ and then perform the regression

$$\begin{aligned} \mathbb {E}[\mathcal {V}_\gamma (\varepsilon _N)|\varepsilon _N] = \mathcal {V}'_\gamma \cdot |\varepsilon _N|. \end{aligned}$$

(C.2)

We report the estimates of ${\delta }''(F_0)$ and ${\mathcal {V}}'_\gamma$ in Table 14. These values, related to the bias and variance of our gamma estimator, are then used to derive the optimal bandwidth parameter minimizing (4.10), which is also presented in Table 14. $\square$

Pseudo code