Introduction

Phenotypic plasticity is the difference in individual phenotypes due to the influence of the environment (Sultan and Stearns 2005; Miner et al. 2005). It can arise if individual behaviour or individual life history processes such as growth, reproduction and mortality depend on the environment. As population dynamics arises from the accumulation of individual life histories (Miller and Rudolf 2011), it is evident that plasticity in life history processes can strongly influence the dynamics of populations. Although plasticity is widely explored in the context of evolutionary dynamics, the effect of plasticity of life history traits on population dynamics is less well understood (Schmitz et al. 2003; Miner et al. 2005).

The population dynamic effects of plasticity in different life history processes cannot be considered separately, as many life history processes are linked through energy allocation schemes within an individual. It is therefore important to know the rules of within-individual energy allocation, when considering plasticity in life history processes (Nisbet et al. 2000; Brown et al. 2004). Different frameworks have been formulated to understand individual energy allocation (Kooijman 2000; West et al. 2001; Hou et al. 2008; Sousa et al. 2008). In general, assimilated energy is divided over maintenance, growth and reproduction, while a deficit in assimilated energy can lead to additional mortality due to starvation. If a life history process is entirely non-plastic, it does not depend on the environment and requires a predetermined amount of energy. The energy requirements of such a demand-driven process could be met through changes in behaviour to adapt the energy intake or by changes in the energy flow to other processes (Kooijman 2010). In contrast, a purely supply-driven process is by definition plastic, because it depends entirely on the amount of assimilated energy and therefore on the food conditions of the environment. Models for individual energy allocation mainly differ in the priority of different processes (Lika and Nisbet 2000; Kooijman 2000; Zhang et al. 2011; Jager et al. 2013), but commonly maintenance costs are considered as a non-plastic (demand driven) process while both growth and reproduction are considered as a plastic (supply driven) process (but see De Roos et al. (2009) for an example of a model in which growth is incorporated as a demand-driven process).

A life history process for which plasticity strongly differs between taxa is the individual growth in body size. Environment-dependent changes in individual growth rate are observed in a wide range of ectothermic species ranging from Daphnia (McCauley et al. 1990) and fish (Lorenzen and Enberg 2002; Zimmermann et al. 2018) to amphibians and reptiles (Halliday and Verrel 1988), although some specific species in these taxa are found to be endothermic (Dickson and Graham 2004). In addition, it is even suggested that the growth rate of some large fossil mammals was flexible (Köhler and Moyà-Solà 2009). This suggests that the growth rate in most ectotherms and early endotherms is plastic. In contrast, the growth rate of most modern endotherms (e.g. birds and mammals) is relatively independent of environmental influences. To maintain a constant growth rate in a fluctuating environment, it is necessary to regulate the amount of energy acquired and allocated to somatic growth. This can partly be achieved by the ability to maintain a constant homeostasis and adaptive behaviour (Kooijman 2010). Meanwhile, the resting metabolic expenditure of endotherms exceeds that of ectotherms by an order of magnitude, even when corrected for expenditure for thermoregulation or under conditions with limited energy demand such as during torpor or hibernation (Bennett and Ruben 1979). The additional resting metabolic expenditure in endotherms is likely used to maintain a constant energy flow to growth in order to maintain a constant somatic growth rate. This latter idea is supported by field observations of ungulates which experience delayed reproduction and decreased fecundity with low food abundance (Skogland 1986; Clutton-Brock et al. 1987; Festa-Bianchet et al. 1995; Coulson et al. 2000; Albon et al. 2000) and laboratory observations on house mice, which stopped ovulating while maintaining growth under reduced food conditions (Perrigo 1990). Altogether this suggests that the growth rate of endotherms is largely predetermined and non-plastic rather than supply driven.

Whereas the plasticity of life history characteristics can be considered as a continuous trait ranging from non-plastic to highly plastic (Sultan and Stearns 2005), the individual growth rate in models of structured populations is generally assumed to be either non-plastic or entirely plastic. This results in two categories of structured models with different dynamics. For example, age-based models, such as used in fisheries management (Schnute and Richards 1998), assume that individuals of the same age are of similar size. The growth rate of individuals is thus implicitly assumed to be independent of the environment, suggesting that individual growth is a non-plastic process (De Roos et al. 2003). In these models, the population structure is entirely determined by the individual reproduction and mortality rate. Population dynamic cycles in these models arise due to the delay between birth and maturation and the competition between different life stages (Gurney et al. 1983; Gurney and Nisbet 1985; De Roos et al. 2003; Pfaff et al. 2014). In contrast, most size-structured models are based on a dynamic energy budget model in which individual growth is modelled as a supply-driven process. As a consequence, the individual growth rate depends on the resource density and is therefore entirely plastic (De Roos et al. 1990; De Roos and Persson 2001). Due to the highly plastic individual growth rate, the size-structured models can show a range of population structures and different types of population dynamic cycles which mainly depend on the competitive strength of different life stages (De Roos et al. 2003; de Roos and Persson 2003). Due to the discrete differences between these two classes of structured models, it is largely unclear how predictions from (age-structured) models with non-plastic growth relate to (size-structured) models with entirely plastic growth.

Although we know most about the ecological dynamics when individual growth is either entirely plastic or non-plastic, it is more likely that for most species the actual level of plasticity in individual growth lies between these two extremes. At such intermediate levels of growth plasticity, individual growth would consist of a non-plastic part representing the baseline minimum growth rate of an individual, and a plastic part, which is an environment-dependent additional increase in individual growth. This raises the question how population dynamics changes when the plasticity in individual growth is at intermediate levels. Here we present a size-structured model in which we vary the individual growth rate from non-plastic to entirely plastic. We base this model on a simple Dynamic Energy Budget (DEB) model (Jager et al. 2013) to ensure a plausible scheme for energy allocation within an individual. Herewith we restrict ourselves to the simplest case in which the environment only consists of a single dynamic resource. Therefore, non-plastic growth in our model indicates that the individual growth rate is entirely independent of the resource density and requires a predetermined amount of energy, which could be set and regulated by genetic and chemical regulatory pathways within an individual. In contrast, entirely plastic growth indicates that the individual growth rate depends on the resource density, is completely supply driven and fluctuates accordingly. We will explore how the population dynamics in this model changes with respect to the level of growth plasticity as well as the maximum density of the resource, as an increase in the latter is generally known to destabilise the dynamics from structured population models, resulting in population dynamic cycles (De Roos et al. 1990).

Model formulation

Individual energy dynamics

As a basis for the individual energy dynamics, we use a simplified DEB model described by Jager et al. (2013). This model describes energy intake, somatic growth and reproduction in terms of energy stored in lean mass (\(E_m\)). In the DEB theory framework, it is generally assumed that individuals of all sizes and ages have the same shape and body composition and therefore both the mass and size of an individual scale with the energy stored in lean mass. Energy ingestion (I) is assumed to scale with the resource density (R) following a Holling type II functional response (\(f(R) = \frac{R}{R_h+R}\), with \(R_h\) the half saturation constant), the individual surface area (\(E_m^{2/3}\)) and the maximum ingestion rate per unit surface area (\(I_{R}\)):

$$\begin{aligned} I = I_R f(R) E_m^{2/3} = I_R \frac{R}{R_h+R} E_m^{2/3} \end{aligned}$$
(1)

We follow DEB theory and assume assimilation efficiency in the gut is a species-specific constant. The surface-specific maximum ingestion rate times the assimilation rate is represented by \(\alpha\). The original energetic model by Jager et al. (2013) assumes growth is plastic and follows a \(\kappa\)-rule in which a fraction \(\kappa\) of the assimilated energy is used for somatic growth and somatic maintenance costs. The somatic maintenance costs are assumed to be non-plastic and scale with the energy stored in lean mass through the energy-specific maintenance costs (b). Covering somatic maintenance costs has priority over somatic growth. This yields the following differential equation for plastic somatic growth:

$$\begin{aligned} \frac{d E_m}{dt} = \gamma _m \left( \kappa \alpha f(R) E_m^{2/3} - b E_m \right) \end{aligned}$$
(2)

With \(\gamma _m\) the conversion efficiency of assimilated energy to lean mass. These assumptions imply that individuals follow a von Bertalanffy type of growth curve when the resource density is constant. The maximum lean mass reached by an individual is proportional to \(f(R)^3\), whereas the growth rate is independent of resource density (Jager et al. 2013).

We assume individuals mature when reaching a predetermined amount of energy stored in lean mass (\(E_J\)). In adult individuals, a fraction \(1-\kappa\) of the assimilated energy is channelled to reproduction, while this fraction is used for maturation in juvenile individuals. This results in the following differential equation for the total amount of energy (\(E_r\)) invested by adults into the production of juveniles:

$$\begin{aligned} \frac{d E_r}{dt} = \gamma _r (1-\kappa ) \alpha f(R)E_m^{2/3} \end{aligned}$$
(3)

With \(\gamma _r\) the conversion efficiency of assimilated energy to energy in newborn lean mass.

To formulate a version of the model with non-plastic growth, the somatic growth rate has to be decoupled from the resource density. In other words, a constant amount of energy is used for somatic growth and somatic maintenance, independent of the current resource density. To stay close to the original model with plastic growth, non-plastic somatic growth is assumed to follow a von Bertalanffy growth trajectory as well. This results in the following differential equation for non-plastic somatic growth:

$$\begin{aligned} \frac{d E_m}{dt} = \gamma _m \left( \kappa \alpha \zeta E_m^{2/3} - b E_m \right) \end{aligned}$$
(4)

Here, we introduce a parameter \(\zeta\) as a scalar modulating the non-plastic growth rate to replace the scaled functional response (f(R)) in the plastic growth rate. Individuals following the non-plastic growth dynamics (Eq. (4)) will therefore grow at the same rate as individuals that follow the plastic growth dynamics (Eq. (2)) with a scaled functional response (f(R)) equal to \(\zeta\). To capture the entire spectrum from non-plastic growth to entirely plastic growth, we introduce the parameter \(\phi\), which represents the extent to which growth is plastic. This results in our general formula for somatic growth:

$$\begin{aligned} \frac{d E_m}{dt} = \gamma _m \left( \phi \kappa \alpha f(R) E_m^{2/3} + (1-\phi ) \kappa \alpha \zeta E_m^{2/3} -b E_m \right) \end{aligned}$$
(5)

We assume all energy not used for somatic processes is used by juveniles for maturation and by adults for reproduction, resulting in the following expression for the investment in reproductive energy:

$$\begin{aligned} \frac{d E_r}{dt} = {\left\{ \begin{array}{ll} 0 &{} \text { if } E_m < E_J \\ \gamma _r \left( \alpha f(R)E_m^{2/3} - \left( \phi \kappa \alpha f(R) E_m^{2/3} + (1-\phi ) \kappa \alpha \zeta E_m^{2/3} \right) \right) &{} \text { if } E_m > E_J \end{array}\right. } \end{aligned}.$$
(6)

With \(E_J\), the energy in lean mass corresponding to the size at which individuals mature.

Equations 5 and 6 simplify to the model described by Jager et al. (2013) if growth is entirely plastic (\(\phi =1\)). In addition, notice that the investment in growth in our model is higher compared to the \(\kappa\)-rule model with entirely plastic growth if \(f(R)<\zeta\), while investment in reproduction is higher if \(f(R)>\zeta\).

By comparing the equation for the assimilated energy (\(\alpha f(R) E_m^{2/3}\)) with the energy used for growth (Eq. 5), it is clear that the rate of energy supply may become insufficient to maintain the outlined energy allocation scheme. If energy supply becomes insufficient, we assume starvation and rechanneling of energy occur. An individual could encounter three types of starvation conditions (Fig. 1).

Fig. 1
figure 1

In addition to growth dynamics, individuals can encounter three types of starvation conditions, depending on the energy in lean mass and the scaled functional response of the resource density. The boundaries of these dynamics shift when growth shifts from non-plastic (\(\phi =0\)) to entirely plastic (\(\phi =1\)). Under severe starvation conditions (red area), assimilated energy is insufficient to cover maintenance costs. Under supply-driven starvation conditions (green area), the energy allocated to somatic processes is insufficient to cover maintenance costs. Under demand-driven starvation conditions (blue area), assimilated energy is insufficient to cover the costs for maintenance and demand-driven growth

Full size image

Under the most severe starvation condition as a consequence of very low resource densities, ingested energy is insufficient to cover somatic maintenance costs (red area in Fig. 1). This regime occurs when:

$$\begin{aligned} bE_m > \alpha f(R) E_m^{2/3} \end{aligned}$$
(7)

We will refer to this condition as severe starvation following De Roos et al. (1990) and we will assume individuals starve instantaneously when it occurs.

Under less severe starvation conditions, ingested energy is sufficient to cover somatic maintenance costs but the energy allocated to somatic processes is not (green area in Fig. 1):

$$\begin{aligned} \alpha f(R) E_m^{2/3}> b E_m > \phi \kappa \alpha f(R) E_m^{2/3} + (1-\phi ) \kappa \alpha \zeta E_m^{2/3}. \end{aligned}$$
(8)

De Roos et al. (1990) refers to this starvation condition as mild starvation but we will use the term supply-driven starvation, because the supply of energy to somatic processes is insufficient to cover maintenance costs.

The last type of starvation occurs if the assimilated energy is insufficient to cover all energy requirements for somatic growth and maintenance:

$$\begin{aligned} \phi \kappa \alpha f(R) E_m^{2/3} + (1-\phi ) \kappa \alpha \zeta E_m^{2/3}> \alpha f(R) E_m^{2/3} > b E_m. \end{aligned}$$
(9)

We will refer to this type of starvation as demand-driven starvation, because the energy demand for growth is too high for the energy supplied by assimilation. From inequality (9), it is clear that the boundary between growth conditions and demand-driven starvation is dependent on resource density, but not on individual size (Fig. 1, boundary of the blue area).

Comparison of the three starvation conditions shows that all three starvation boundaries intersect at a single point (\(E_m^{1/3} =\frac{\alpha \kappa }{b} \frac{1-\phi }{1-\phi \kappa } \zeta\), Fig. 1). If we do not take into account the conditions in which severe starvation occurs, individuals can only suffer demand-driven starvation if the energy stored in lean mass is below this critical value (\(E_m^{1/3} <\frac{\alpha \kappa }{b} \frac{1-\phi }{1-\phi \kappa } \zeta\)), while individuals can only suffer from supply-driven starvation if the energy stored in lean mass is above this critical value (\(E_m^{1/3} >\frac{\alpha \kappa }{b} \frac{1-\phi }{1-\phi \kappa } \zeta\)). In other words, small and large individuals are vulnerable to demand-driven and supply-driven starvation, respectively.

In general, we assume energy is rechanneled under starvation conditions from the energy flow with sufficient energy to the energy flow with the deficit (equation from maturation and reproduction to growth and somatic maintenance or vice versa). More specifically, this means that under supply-driven starvation, growth of all individuals stops and energy allocation to reproduction in adults is reduced:

$$\begin{aligned} \frac{d E_m}{dt}&= 0 \end{aligned}$$
(10)
$$\begin{aligned} \frac{d E_r}{dt}&= {\left\{ \begin{array}{ll} 0 &{} \text { if } E_m < E_J \\ \gamma _r \left( \alpha f(R) E_m^{2/3} - b E_m \right) &{} \text { if } E_m > E_J \end{array}\right. } \end{aligned}.$$
(11)

While under demand-driven starvation, energy allocation to reproduction by adults stops and growth of all individuals is reduced:

$$\begin{aligned} \frac{d E_m}{dt}&= \gamma _m \left( \alpha f(R) E_m^{2/3} - b E_m \right) \end{aligned}$$
(12)
$$\begin{aligned} \frac{d E_r}{dt}&= 0. \end{aligned}$$
(13)

These rechanneling rules imply that individuals below the species-specific threshold size (\(E_m^{1/3} =\frac{\alpha \kappa }{b} \frac{1-\phi }{1-\phi \kappa } \zeta\)) prioritise growth if experiencing (demand driven) starvation conditions, while individuals above the species-specific threshold size prioritise reproduction if experiencing (supply driven) starvation conditions (Fig. 1b).

It is likely that the re-channelling of energy will bring additional costs such as starvation mortality. We assume starvation mortality scales with the energy deficit and is zero at the supply-driven starvation boundary and the demand-driven starvation boundary. In addition, we assume starvation mortality approaches infinity if individual energetics approaches the severe starvation boundary. As a consequence, individuals will starve with certainty before entering severe starvation conditions. The starvation-induced mortality rate (\(\mu _s\)) under supply-driven starvation we therefore assume to follow:

$$\begin{aligned} \mu _s = q_s \text { max } \left( \frac{b E_m - \left( \phi \kappa \alpha f(R) E_m^{2/3} + (1-\phi ) \kappa \alpha \zeta E_m^{2/3} \right) }{\alpha f(R) E_m^{2/3} - b E_m} \text { , } 0 \right) \end{aligned}.$$
(14)

And under demand-driven starvation conditions:

$$\begin{aligned} \mu _s = q_s \text { max } \left( \frac{\left( \phi \kappa \alpha f(R) E_m^{2/3} + (1-\phi ) \alpha \kappa \zeta E_m^{2/3}\right) - \alpha f(R) E_m^{2/3} }{ \alpha f(R) E_m^{2/3} - b E_m } \text { , } 0 \right) \end{aligned}.$$
(15)

Growth dynamics

According to DEB theory (Kooijman 2010), the individual body mass can be expressed in terms of energy stored in lean mass by using the mass-specific energy density (\(d_m\)). In the same way, the volume can be related to the mass with the volume-specific mass (\(d_v\)) and the length can be related to the volume with a shape scaling constant (\(\delta _m\)).

$$\begin{aligned} W&= \frac{E_m}{d_m} = d_v V = d_v (\delta _m \ell ) ^3 \end{aligned}$$
(16)
$$\begin{aligned} \ell&= \frac{V^{1/3}}{\delta _m} = \frac{W^{1/3}}{d_v^{1/3} \delta _m} = \frac{E_m^{1/3}}{d_m^{1/3} d_v^{1/3} \delta _m}. \end{aligned}$$
(17)

Using these equalities, the individual dynamics can be expressed in terms of individual length instead of energy stored in lean mass (Table 1, see also the supplementary materials) (Murphy 1983; De Roos et al. 1990). To do so, we use expressions for the investments into somatic growth (\(F_g(R, \ell )\)), reproduction (\(F_r(R)\)) and growth and reproduction together (\(F_t(R, \ell )=F_g(R,\ell )+F_r(R)\)), which depend on the resource density, the ultimate size under unlimited food conditions (\(\ell _\infty\)) and possibly the actual length (\(\ell\)). Note that these investments are proportional to the energy allocation to growth and reproduction. In addition, these quantities are expressed per unit surface area and could therefore be interpreted as the (area specific) growth rate, fecundity and biomass production as well. The dynamics of the length-age relationship (\(\ell (t,a)\)) is defined in terms of the von Bertalanffy growth rate (\(r_B\)) times the investments into growth (\(F_g(R,\ell )\) or \(F_t(R,\ell )\)) in combination with the size at birth (\(\ell _b\)), which is a boundary condition needed to solve this differential equation. Individuals mature when reaching the size at maturation (\(\ell _J\)). The individual fecundity (\(\beta (R,\ell )\)) is defined in terms of the reproduction rate (\(r_F\)) times the investments into reproduction (\(F_r(R)\) or \(F_t(R,\ell )\)) and length squared. In this formulation, the parameters for the ultimate asymptotic size (\(\ell _\infty\)), von Bertalanffy growth rate (\(r_B\)) and the reproduction rate (\(r_F\)) are composite parameters consisting of the plastic energy assimilation constant (\(\kappa\)), the maximum ingestion and assimilation rate (\(\alpha\)), the energy-specific somatic maintenance costs (b), the size at birth (\(\ell _b\)) and the energy conversion efficiencies (\(\gamma _m\), \(\gamma _r\)) from the DEB formulation (Eq. (27)-(29)). Lastly, the dynamics of the population age distribution (n(t, a)) depends on the individual background mortality (\(\mu _b\)) and the individual starvation mortality (\(\mu _s(R, \ell )\)) in combination with the population birth rate (n(t, 0)) calculated as the total reproductive output of the population at a given time. We state that the mortality under extreme starvation conditions (\(F_t(R,\ell )\le 0\)) is infinitely large to indicate that the survival probability under this condition is zero and individuals are instantaneously removed from the population.

Table 1 Equations describing the population dynamics under growth conditions and supply-driven (\(F_g(R,\ell )<0\)), demand-driven (\(F_r(R)<0\)) and severe (\(F_t(R,\ell )<0\)) starvation conditions. Notice that as long as extreme starvation does not occur (\(F_t(R,\ell ) > 0\)) supply- and demand-driven starvation are mutually exclusive, such that\(F_r(R) \le 0\)implies\(F_g(R,\ell ) > 0\)and\(F_g(R,\ell ) \le 0\)implies\(F_r(R) > 0\)
Full size table

For simplicity, we will assume the resource to be unstructured and the dynamics of the resource without consumption to be described by semi-chemostat dynamics, with a turn-over rate \(\nu\) and a maximum resource density K:

$$\begin{aligned} \frac{d R}{d t} = \nu (K - R) - \int _0^{a_{max}} I_{max} f(R) \ell (t,a)^2 n(t,a) da \end{aligned}.$$
(18)

The parameter \(I_{max}\) is a scaled version of \(I_R\), representing the ingestion rate per unit surface area in terms of length instead of energy stored in lean mass.

Mathematical analysis

Model equilibria can be calculated following the procedure described by De Roos et al. (1990). At a constant resource density (\(R=\bar{R}\)) and hence a constant value of the functional response (\(f(\bar{R})\)) the consumer population can only persist if the functional response is sufficiently high for extreme and demand-driven starvation not to occur (\(F_t(\bar{R},\ell ), F_r(\bar{R}) > 0\)), because otherwise consumers would die instantaneously or never reproduce. With a constant functional response, investment in growth and the individual size can be solved explicitly as a function of age, which results in a von Bertalanffy growth curve:

$$\begin{aligned} F_g(\bar{R},\ell )&= \left( \left( \phi f(\bar{R}) + (1-\phi ) \zeta \right) \ell _\infty - \ell _b \right) e^{-r_B a} = F_{g\infty }(\bar{R}) e^{-r_B a} \end{aligned}$$
(19)
$$\begin{aligned} \ell (\bar{R}, a)=& \ell _b + \left( 1-e^{-r_B a} \right) F_{g\infty }(\bar{R}) \\ = & \ell _b e^{-r_B a} + \left( \phi f(\bar{R}) + (1-\phi ) \zeta \right) \left( 1-e^{-r_B a} \right) \ell _\infty \end{aligned}.$$
(20)

Herein, we introduce \(F_{g\infty }(\bar{R})\) as the lifetime investment in growth at the constant resource density \(\bar{R}\) given an individual survives, which we will use as an age independent quantity for energy investment in growth (Note that \(F_{g\infty }(\bar{R})\) equals the integral of the product \(r_BF_{g}(\bar{R},\ell (\bar{R}, a))\) over the entire lifetime for an individual living at resource density \(\bar{R}\)). From comparing the growth curve with the supply-driven starvation condition, it is clear that individuals do not experience supply-driven starvation when living at a constant resource density \(\bar{R}\) (\(F_g(\bar{R},\ell ) > 0\)). The von Bertalanffy growth curve also defines the age at maturation at the constant food density (\(\bar{a}_J\)), which is the age at which individuals reach the size at maturation (\(\ell (\bar{R}, \bar{a}_J) = \ell _J\)). For individuals to reach this maturation size at the constant resource density \(\bar{R}\) individuals of length \(\ell _J\) should not experience supply-driven starvation (\(F_g(\bar{R},\ell _J) > 0\)). When individuals do not experience starvation conditions, the dynamics of the population age distribution can be simplified and solved explicitly, resulting in an expression for the density of individuals at a given age:

$$\begin{aligned} \bar{n}(a) = \bar{n}(0) e^{-\mu _b a} \end{aligned}.$$
(21)

By substituting the von Bertalanffy growth curve (Eq. (20)) and the age distribution in equilibrium (Eq. (21)) in the expression for the population birth rate, we arrive at an expression for the lifetime reproductive output (LRO):

$$\begin{aligned} LRO &= r_F F_r(\bar{R}) \int _{\bar{a}_J}^{a_{max}} {\ell (\bar{R}, a)}^2 e^{-\mu a} da \\&= r_F F_r(\bar{R}) \int _{\bar{a}_J}^{a_{max}} \left( \ell _b + \left( 1-e^{-r_B a} \right) F_{g\infty }(\bar{R})\right) ^2 e^{-\mu a} da \end{aligned}.$$
(22)

The lifetime reproductive output represents the average number of offspring an individual is expected to produce during its lifetime. A population is in equilibrium if every individual on average replaces itself and therefore the lifetime reproductive output in equilibrium equals one. By setting the lifetime reproductive output to one, we can solve for the functional response in equilibrium, which we indicate with \(f(\tilde{R})\), because this is the only unknown in the lifetime reproductive output. The functional response and the resource density in equilibrium (\(\tilde{R}\)) are therefore completely determined by the growth, reproduction and mortality traits of the consumer population and hence independent of resource growth conditions.

The last step is to derive the population birth rate in equilibrium (\(\tilde{n}(0)\)) from the dynamics of the resource (Eq. (18)), which together with the resource density defines the complete equilibrium:

$$\begin{aligned} \tilde{n}(0) = \frac{ \nu \left( K - \tilde{R}\right) }{I_{max} f(\tilde{R}) \int _0^{a_{max}} {\ell (\tilde{R}, a)}^2 e^{-\mu a} da} \end{aligned}.$$
(23)

From Eq. (23), it follows that the resource density in equilibrium equals the maximum resource density (\(\tilde{R} = K\)) at the persistence boundary of the consumer population (\(\tilde{n}(0) = 0\)). Therefore, the persistence boundary is calculated by setting the lifetime reproductive output equal to one and substituting the resource density with the maximum resource density (Eq. (40)).

The stability boundary of the model can be calculated through linearisation of the dynamic equations around the equilibrium state as outlined by (De Roos et al. 1990). The derivation of the conditions determining the stability boundary is explained in detail in the supplementary materials (Eqs. ((48)-(80)).

Energetic trade-off

At a given, constant resource density \(\bar{R}\) both the investments into growth (\(F_{g\infty }(\bar{R})\)) and the investments into reproduction (\(F_r(\bar{R})\)) change with the growth plasticity (\(\phi\)). This change can be expressed as the derivative of these investments with respect to the level of growth plasticity:

$$\begin{aligned} \frac{\partial F_{g \infty }}{\partial \phi }&= \left( f(\bar{R}) - \zeta \right) \ell _\infty \end{aligned}$$
(24)
$$\begin{aligned} \frac{\partial F_r}{\partial \phi }&= - \left( f(\bar{R}) - \zeta \right) \ell _\infty \end{aligned}.$$
(25)

The direction of a change in energy allocation due to growth plasticity is determined by the non-plastic asymptotic size (\(\zeta \ell _\infty\)) compared to the plastic asymptotic size (\(f(\bar{R}) \ell _\infty\)). An increase in growth plasticity will lead to an increase in growth investments and a decrease in reproductive investments if the plastic asymptotic size exceeds the non-plastic asymptotic size (\(f(\bar{R}) \ell _\infty > \zeta \ell _\infty\)). In contrast, an increase in growth plasticity will lead to a decrease in growth investments and an increase in reproductive investments if the non-plastic asymptotic size exceeds the plastic asymptotic size (\(f(\bar{R}) \ell _\infty < \zeta \ell _\infty\)). It is also clear that the effect of the growth plasticity on the growth investments is always opposite to the effect on reproductive investments. This reveals a trade-off in which an increase in investment in growth will always lead to a decrease in investment in reproduction and vice versa.

A change in growth plasticity affects the lifetime reproductive output through both the growth investments and the reproductive investments:

$$\begin{aligned} \frac{d LRO}{d \phi } &= \frac{\partial LRO}{\partial F_{g\infty }} \frac{\partial F_{g\infty }}{\partial \phi } + \frac{\partial LRO}{\partial F_r} \frac{\partial F_r}{\partial \phi }\\& = \left( \frac{\partial LRO}{\partial F_{g\infty }} - \frac{\partial LRO}{\partial F_r} \right) \left( f(\tilde{R}) - \zeta \right) \ell _\infty \end{aligned}.$$
(26)

Explicit expressions for the partial derivatives \(\frac{\partial LRO}{\partial F_{g\infty }}\) and \(\frac{\partial LRO}{\partial F_r}\) are derived in the supplementary information. From Eq. (26), it is clear that the lifetime reproductive output of an individual is completely independent of the growth plasticity (\(\phi\)) if the plastic asymptotic size equals the non-plastic asymptotic size (\(f(\bar{R}) \ell _\infty = \zeta \ell _\infty\)). From Eqs.(19) and (22) we can furthermore infer that the lifetime reproductive output increases with both an increase in energy allocation to growth and energy allocation to reproduction (\(\frac{\partial LRO}{\partial F_{g\infty }} > 0\) and \(\frac{\partial LRO}{\partial F_r}>0\)). We therefore can distinguish a parameter region in which an increase in growth investments has a larger effect on lifetime reproductive output than a similar increase in reproductive investments (\(\frac{\partial LRO}{\partial F_{g\infty }} > \frac{\partial LRO}{\partial F_r}\)) and a parameter region in which an increase in reproductive investments has a larger effect on lifetime reproductive output than a similar increase in growth investments (\(\frac{\partial LRO}{\partial F_{g\infty }} < \frac{\partial LRO}{\partial F_r}\)). We will refer to the dynamics in these regions as growth-limited and reproduction-limited dynamics, respectively. Whether or not the lifetime reproductive output increases with an increase in growth plasticity depends on whether the dynamics are growth- or reproduction-limited in combination with whether the plastic growth asymptotic size (\(f(\bar{R}) \ell _\infty\)) is larger or smaller than the non-plastic asymptotic size (\(\zeta \ell _\infty\)). Furthermore, an increase in growth plasticity (\(\phi\)) results in a change from an increase to a decrease in lifetime reproductive output when the dynamics changes from growth to reproduction-limited, assuming that the plastic asymptotic size is larger than the non-plastic asymptotic size (\(f(\bar{R}) \ell _\infty > \zeta \ell _\infty\)). Alternatively, when the plastic asymptotic size is smaller than the non-plastic asymptotic size (\(f(\bar{R}) \ell _\infty < \zeta \ell _\infty\)) an increase in growth plasticity \(\phi\) results in a change from an increase to a decrease in lifetime reproductive output when the dynamics changes from reproduction to growth-limited. The value of the growth plasticity (\(\phi\)) at which the boundary between these two areas occurs, strongly depends on the plastic energy allocation constant (\(\kappa\)) but is also influenced by other parameters (Eqs. (41)-(47)).

Numerical analysis

The persistence boundary and the stability boundary have been studied numerically as a function of model parameters using general root finding and curve continuation procedures implemented in C (Findcurve software by De Roos (2019)). Time dynamics of the model have been computed using the Escalator Boxcar Train (EBT) method, especially designed for the numerical integration of physiologically structured population models (De Roos 1988; De Roos et al. 1992). For the numerical analysis of the model and corresponding figures, we use a parameter set representing Daphnia magna feeding on algae, comparable to the parameter values used by De Roos et al. (1990) (Table 2). We use slightly different definitions of the half saturation constant of the functional response (\(R_h\)) and the reproduction rate (\(r_F\)). Therefore, we recalculated the values of these parameters to ensure our model is numerically equivalent to the model analysed by De Roos et al. (1990) if growth is entirely plastic (\(\phi = 1\)). From here on we will refer to the structured Daphnia populations as consumers, while the unstructured algae community is referred to as the resource.

Table 2 Parameters used in the structured population model for Daphnia magna feeding on algae derived from De Roos et al. (1990)
Full size table

Equilibrium dynamics

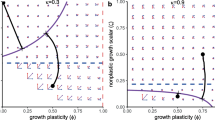
In general, four different configurations of the regions with growth-limited and reproduction-limited dynamics are possible (Derivation in supplementary materials Eqs. 41-47). (1) If the growth energy allocation constant \(\kappa\) is below a specific threshold value (\(\kappa \approx 0.857\) with our parameter set) and the plastic asymptotic size exceeds the non-plastic asymptotic size (\(f(\tilde{R}) \ell _\infty >\zeta \ell _\infty\), Fig. 2A), the dynamics is always growth-limited. (2) If the plastic growth energy allocation constant \(\kappa\) is below the threshold value and the non-plastic asymptotic size exceeds the plastic asymptotic size, (\(\kappa <0.857\), \(f(\tilde{R}) \ell _\infty <\zeta \ell _\infty\), Fig. 2B), the dynamics is growth-limited at high growth plasticity (high \(\phi\)) and reproduction-limited at low growth plasticity (low \(\phi\)). (3) In contrast, if the plastic growth energy allocation constant \(\kappa\) is above the threshold value and the plastic asymptotic size exceeds the non-plastic asymptotic size (\(\kappa >0.857\), \(f(\tilde{R}) \ell _\infty >\zeta \ell _\infty\), Fig. 2C), the dynamics is growth-limited at low growth plasticity (low \(\phi\)) and reproduction-limited at high growth plasticity (high \(\phi\)). (4) Lastly, the dynamics is always reproduction-limited if the plastic energy allocation constant \(\kappa\) exceeds the threshold value and the non-plastic asymptotic size exceeds the plastic asymptotic size (\(\kappa >0.857\), \(f(\tilde{R}) \ell _\infty <\zeta \ell _\infty\), Fig. 2D).

Fig. 2
figure 2

Persistence boundary (red line, numerically solved from Eq. (40)) and stability boundary (green, numerically solved from Eq. (80)) and the boundary between dynamics (yellow dashed, numerically solved from Eq. (44)) as a function of the growth plasticity (\(\phi\)) and the maximum resource density (K) when the plastic asymptotic size exceeds the non-plastic asymptotic size (\(f(\tilde{R}) \ell _\infty >\zeta \ell _\infty\)) (left panels) and when the non-plastic asymptotic size exceeds the plastic asymptotic size (\(\zeta \ell _\infty >f(\tilde{R}) \ell _\infty\)) (right panels). At the persistence boundaries (red lines), the maximum resource density is equal to the resource density in equilibrium

Full size image

With an increase or decrease in \(\phi\) the average lifetime reproductive output increases if the growth plasticity (\(\phi\)) approaches the boundary between growth-limited dynamics and reproduction-limited dynamics (Fig. 2B and C, yellow line). An increase in lifetime reproductive output with a change in \(\phi\) implies that the lifetime reproductive output will equal 1 at a lower resource density, which hence decreases in equilibrium, while equilibrium consumer population density increases. The maximum resource density (K) needed for the consumer population to persist decreases accordingly if the growth plasticity (\(\phi\)) approaches the boundary between the two regions (Fig. 2B and C, red line). In contrast, the lifetime reproductive output always increases with an increase in growth plasticity if the dynamics does not change between growth-limited dynamics and reproduction-limited dynamics. This leads to a decrease in resource density and an increase in population density at equilibrium with increasing growth plasticity. Again, the maximum resource density (K) needed for the consumer population to persist decreases accordingly (Fig. 2A and D, red line).

Population dynamic cycles

The bifurcation analysis revealed three parameter regions with cyclic dynamics (Fig. 2A and B, green lines). One of these regions occurred when the dynamics is limited by reproduction (Fig. 2B, low \(\phi\)). In these cycles (Fig. 3a), the area-specific investment in growth (\(F_{g\infty }\)) and therewith the maturation rate is relatively high and constant due to the high and largely non-plastic growth rate. As a result, individuals mature at a young age and the population consists of a low number of juveniles and a high number of adults. A peak in the number of juveniles occurs simultaneously with a peak in investment in reproduction (\(F_r\)). The high density of juveniles results in a depletion of the resource, which is directly followed by a decrease in fecundity. Although individuals mature at a young age, a new large reproductive event only occurs after the consumer density has sufficiently decreased by mortality for the resource density to recover. In other words, a new cycle starts if competition between adults is reduced. As a result, the resource density and the investment in reproduction fluctuate in phase with the juvenile density but out of phase with the adult density, with a period of several times the juvenile delay. It is clear that these cycles occur due to the fluctuations in fecundity. We therefore refer to these cycles as fecundity-driven cycles.

Fig. 3
figure 3

Population dynamic cycles for three combinations of \(\zeta\) and \(\phi\) with \(K=0.5\) and \(\kappa =0.3\). The surface-specific total investment in growth if individuals would not die (\(F_{g\infty }\)) and the surface-specific investment in reproduction are displayed as a measure of growth and fecundity. Note the different vertical axes for the consumer densities. The red vertical lines mark the occurrence of a peek in adult density to ease comparison between graphs

Full size image

The two other regions with cyclic dynamics occur when the dynamics is growth-limited (Fig. 2A and 2B for high \(\phi\)). During these cycles (Fig. 3b and c) the area-specific investment in growth (\(F_{g\infty }\)) and therewith the maturation rate is very low and shows periodic increases with a large amplitude. The investment in reproduction reaches a maximum simultaneously with the maturation rate. The occurrence of the high fecundity simultaneous with the high adult density results in the production of a large cohort of juveniles. This cohort decreases the resource density, which is followed by a decrease in the fecundity and maturation rate. The juvenile cohort matures and reproduces after the consumer density has sufficiently decreased by mortality for the resource density to recover. In other words, a new cycle starts as soon as competition between juveniles is sufficiently reduced. This results in cycles dominated by a single cohort from which all individuals mature simultaneously and directly produce a new dominant cohort. Consequently, the period of the cycles is approximately equal to the juvenile delay. In addition, the periodic and simultaneous maturation of a large group of juveniles contributes to the non-symmetric shape of these cycles in comparison with the fecundity-driven cycles (Fig. 3). This type of cycles also occurs when the individual fecundity is assumed to be independent of the resource density (Supplementary figure Fig. S1), which shows that these cycles are caused by the fluctuations in maturation rate rather than fluctuation in the fecundity. We therefore refer to this type of cycles as maturation-driven cycles.

Discussion

We analysed a model in which the individual growth rate could be varied between entirely non-plastic (\(\phi =0\)) to entirely plastic (\(\phi =1\)). Although the model was formulated at an individual level to ensure closed individual energy dynamics, the model was analysed at the population level. In the extreme case in which growth is entirely plastic (\(\phi =1\)), the model simplified to a classic size-structured model as analysed by De Roos et al. (1990) and Kooijman and Metz (1984). It has been shown that the well-posedness of this model is difficult to show because the fecundity (\(\beta (R,\ell )\)) of individuals jumps from zero to a positive value at the size of maturation and the fecundity at the size at maturation (\(\beta (R,\ell _J)\)) is therefore undefined (Thieme 1988). As a consequence, the model is undefined if the growth rate of a cohort is exactly zero at maturation and therefore remains at the size of maturation. Although unlikely, it is difficult to predict whether this specific condition will occur based on the starting conditions. Our model has the same properties and the well-posedness of our model is therefore difficult to prove. Nonetheless, these type of models is successfully used in a wide range of applications (Baas et al. 2018; De Roos and Persson 2001).

If growth is entirely plastic (\(\phi =1\)), the individual growth rate is fully coupled to the resource density and as a consequence the age-size relationship varies per cohort if the resource density fluctuates, for example during population dynamic cycles as is observed in classic size-structured models (Supplementary figure Fig. S2b). In contrast, if growth is completely non-plastic (\(\phi =0\)), the model is equivalent to an age-structured model given that there is a unique relationship between age and body size. Under this extreme condition, the individual growth rate in our model only changes if the demand-driven starvation condition (\(F_r<0\)) occurs, but the analysis of the model did not reveal any dynamic regimes in which individuals experienced demand-driven starvation. The growth rate is thus completely fixed if growth is non-plastic (\(\phi =0\)), which results in a fixed age-size relationship even during population dynamic cycles (Supplementary figure Fig. S2a). With the fixed age-size relationship, the model can be converted to an age-based model resembling our model with non-plastic growth. Besides linking energetic models with plastic and non-plastic growth, our model thus also connects classic age-structured models with classic size-structured models.

Our analysis divided the parameter space in a region with growth-limited and a region with reproduction-limited dynamics. In the region with growth-limited dynamics, changes in the area-specific investments in growth have a larger effect on the lifetime reproductive output than changes in the area-specific investments in reproduction. In contrast, in the region with reproduction-limited dynamics, changes in the area-specific investments in reproduction have a larger effect on lifetime reproductive output than changes in the area-specific investments in growth. At the boundary of the regions with different limiting mechanisms, the consumer population exploits the resource most efficiently and can persist on the lowest resource density (Fig. 2). In other words, on this boundary the energy allocation to growth and reproduction is most optimal. The location of this optimum is closely related to the classic trade-off regarding energy allocation to growth and reproduction (Stearns 1992), in which an optimal strategy arises through avoidance of severe limitation in growth or reproduction. Although this is a very intuitive trade-off, we tied it to the specific energy budget of individuals. Namely, an optimal energy allocation strategy can only occur if the plastic energy allocation constant is low (low \(\kappa\)) and the non-plastic asymptotic size exceeds the plastic asymptotic size in equilibrium (\(f(\tilde{R}) \ell _\infty < \zeta \ell _\infty\)) or if the plastic energy allocation constant is high (high \(\kappa\)) and the plastic asymptotic size exceeds the non-plastic asymptotic size in equilibrium (\(f(\tilde{R}) \ell _\infty > \zeta \ell _\infty\)). Hence, an optimal energy allocation can only occur when energy is relatively evenly distributed between growth and reproduction to avoid severe limitation through growth and reproduction. As a consequence, evolution cannot always reach an optimal energy allocation scheme if evolution only acts on growth plasticity.

The parameter regions in which the dynamics is limited by growth or reproduction show different kinds of population dynamics cycles. In the region with growth-limited dynamics, the cycles are caused by fluctuations in maturation, which is caused by fluctuations in growth rate. These maturation-driven cycles occur because a cohort of newborn individuals outcompetes the adult individuals. This results in single-cohort cycles, which are characterised by the synchronisation of a high resource density with the maturation of the dominant cohort. The oscillation period of these cycles is approximately equal to the juvenile delay (De Roos et al. 2003). Single-cohort cycles generally occur in models incorporating a juvenile delay and, based on the oscillation period, are mainly observed in generalist species (Murdoch et al. 2002). The type of single-cohort cycles found in our model is described in more detail by De Roos et al. (2003) as juvenile-driven cycles, which occur if juvenile individuals outcompete adults because they can survive on a lower resource density. The mechanism for these juvenile-driven cohort cycles is observed in various fish species (Townsend et al. 1990; Hamrin and Persson 1986; Townsend and Perrow 1989) and experimental Daphnia populations (Murdoch and McCauley 1985; McCauley 1993).

In the parameter region with reproduction-limited dynamics, the cycles are caused by fluctuations in average fecundity. These fecundity-driven cycles are characterised by low amplitude oscillations with a period of more than four times the juvenile delay of the consumer. In addition, the total consumer density lacks behind the resource density. These characteristics occur because a dominant cohort of newborn individuals depletes the resource, which causes fecundity to decrease. The dominant cohort of juveniles matures before the resource density is recovered, which delays their main reproductive event until the resource density is recovered, which is far beyond the age at maturation. The fecundity-driven cycles thus differ from the reproduction-driven cycles in that competition relaxes after instead of before the maturation of a dominant cohort.

The fecundity-driven cycles in our model show resemblances with various previously described types of cycles. The oscillation period of the fecundity-driven cycles is more than four times the juvenile delay of the consumer plus two times the juvenile delay of the resource, which is generally considered indicative of consumer–resource cycles (Murdoch et al. 2002). The fecundity-driven cycles indeed show an increase in resource density leading to an increase in consumer reproduction as is found in classic non-structured models with consumer–resource cycles (Rosenzweig and MacArthur 1963). In classic consumer–resource cycles this occurs because the resource periodically escapes the control of the consumer, which, however, cannot occur in our model, because in our model the resource follows semi-chemostat dynamics (De Roos et al. 1990). Instead, the increase in resource density in the fecundity-driven cycles is due to a relaxation of competition between consumers and are therefore different from classic consumer–resource cycles. The fecundity-driven cycles also show some resemblances with delayed-feedback cycles. One could argue that the depletion of the resource by a dominant cohort has a delayed effect, because it only affects the dominant cohort after maturation. Pfaff et al. (2014) suggested that delayed-feedback cycles can have a period of more than 4 times the juvenile delay and arise if the juvenile delay is decoupled from the resource density, which exactly occurs in the fecundity-driven cycles we found. Nonetheless, the fecundity-driven cycles do not correspond to the original description of delayed-feedback cycles from Gurney et al. (1983), because the depletion of the resource in the fecundity-driven cycles also has a direct effect on the consumer population, while Gurney et al. (1983) describe a complete separation of time between the moment of competition and the effect of competition. These resemblances between the fecundity-driven cycles, consumer–resource cycles and delayed-feedback cycles at least show that very detailed knowledge is needed to disentangle different types of cycles in structured populations Hastings (2020).

In this article, we presented a model in which we varied the plasticity in individual growth. More plastic growth is generally expected in ectotherms because the growth rate in these individuals is highly dependent on the environment, while less plastic growth is generally expected in endotherms because in these individuals growth is generally independent of the environment. Including a non-plastic growth rate results in an additional demand-driven process in the energy allocation scheme of individuals. We assumed that a potential deficit or surplus of energy from demand-driven growth is compensated by a change in energy allocation to reproduction. Another strategy to cover a deficit in ingested energy could be to increase energy ingestion by adaptive behaviour (Kooijman 2010). Although this strategy might weaken the trade-off between growth and reproduction, it is unlikely that adaptive behaviour could account for the entire deficit when individuals live in a natural ecosystem, as sufficient resource should be available to increase the consumption by adaptive behaviour. In our model, the resource density is regulated by competition between consumers. Therefore, an increase in consumption due to adaptive behaviour would lead to an increase in competition and a decrease in resource density which also could enlarge the energy deficit. Even if sufficient resource is available, ingested energy is limited by physiological and time constraints which are implemented in our model by using a type II functional response to model energy ingestion. It is therefore unlikely that adaptive behaviour can account for the full energy deficit caused by non-plastic growth and a trade-off between energy allocation to growth and reproduction occurs.

We showed that the trade-off between energy investment in growth and reproduction results in population dynamics regulated by, respectively, maturation or fecundity. Populations limited by maturation and the corresponding cohort cycles are widely explored in the context of ecological communities (De Roos et al. 2007; De Roos et al. 2008; Persson et al. 2007; Van Leeuwen et al. 2008; van Kooten et al. 2007), while the dynamics of populations limited by fecundity are less studied in structured populations (see De Roos et al. (2009) for an example) and is an open topic. In any case, our model analysis revealed how life history strategies of species in terms of energy allocation and plasticity affect the mechanisms which limit the population and determine the type of population dynamic cycles. In this way, we provide a new step in linking distinct ecological phenomena such as non-plastic growth and plastic growth, age and stage structure and populations limitation by individual growth and fecundity.