A sequential choice model for multiple discrete demand

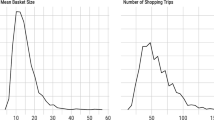
Abstract

Consumer demand in a marketplace is often characterized to be multiple discrete in that discrete units of multiple products are chosen together. This paper develops a sequential choice model for such demand and its estimation technique. Given an inherently high-dimensional problem to solve, a consumer is assumed to simplify it to a sequence of one-unit choices, which eventually leads to a shopping basket of multiple discreteness. Our model and its estimation method are flexible enough to be extended to various contexts such as complementary demand, non-linear pricing, and multiple constraints. The sequential choice process generally finds an optimal solution of a convex problem (e.g., maximizing a concave utility function over a convex feasible set), while it might result in a sub-optimal solution for a non-convex problem. Therefore, in case of a convex optimization problem, the proposed model can be viewed as an econometrician’s means for establishing the optimality of observed demand, offering a practical estimation algorithm for discrete optimization models of consumer demand. We demonstrate the strengths of our model in a variety of simulation studies and an empirical application to consumer panel data of yogurt purchase.

Appendices

Appendix A: Choice of removing one unit

Presented here is another example of a sequential choice process that involves a removal of a chosen item. Suppose a consumer makes her purchase decision for two goods (A and B) whose unit prices are 2 and 4 respectively (i.e., p_At = 2,p_Bt = 4) given her utility function that is specified as follows:

$$ \begin{array}{@{}rcl@{}} V\left( x_{At}, x_{Bt}\right) &=& \frac{\psi_{A} e^{\varepsilon_{At}}}{\gamma} \ln \left( \gamma x_{At}+1\right)+ \frac{\psi_{B} e^{\varepsilon_{Bt}}}{\gamma} \ln \left( \gamma x_{Bt}+1\right)\\ &&+ \ln \left( E - {p_{At}x_{At}} - {p_{Bt}x_{Bt}}+1\right) \end{array} $$

with the parameter values being ψ_A = 0.138,ψ_B = 0.272,ψ₀ = 1,γ = 0.052,E = 29.647. Provided ε_At = ε_Bt = 0, how the proposed sequential choice process unfolds is described in Table 15.

Table 15 Example of sequential choices with removal

We observe that one unit of B is removed from the cart in the sixth choice occasion. Note that two units of A (the 4th and 5th choices) are added between the latest addition of B in the third choice and its removal in the sixth, decreasing the remaining budget (=the amount of the outside good). As the remaining budget shrinks, the incremental utility of removing B increases due to the concave sub-utility of the outside good, which leads to a condition where removing one unit of B is the best choice option.

Appendix B: Bayesian MCMC procedure

The joint posterior distribution of all the model parameters is proportional to three components: (i) the prior distribution for the hyperparameters, (ii) the upper-level distribution for heterogeneity, and (iii) the model likelihood of the individual-level data.

$$ \begin{array}{@{}rcl@{}} &&p\left( \bar{\theta}, V_{\theta}, \{\theta_{i}\}_{i=1}^{N} | \{\{x_{i1t},x_{i2t},p_{i1t},p_{i2t}\}_{t=1}^{T}\}_{i=1}^{N} \right) \\ && \propto p\left( \bar{\theta}, V_{\theta} \right) \times p\left( \{\theta_{i}\}_{i=1}^{N} | \bar{\theta}, V_{\theta} \right)\\ &&\times \ell \left( \{\theta_{i}\}_{i=1}^{N} | \{\{x_{i1t},x_{i2t},p_{i1t},p_{i2t}\}_{t=1}^{T}\}_{i=1}^{N}\right) \\ && \propto p\left( \bar{\theta}, V_{\theta} \right) \times \prod\limits_{i=1}^{N} p\left( \theta_{i} | \bar{\theta}, V_{\theta} \right) \times \ell \left( \theta_{i} | \{x_{i1t},x_{i2t},p_{i1t},p_{i2t}\}_{t=1}^{T}\right) \end{array} $$

Adapting the standard procedure for a Bayesian multivariate linear regression, we employ a natural conjugate prior for the hyperparameters and make it diffuse that the influence of the prior distribution is minimal (e.g., ν₀ = 7,V₀ = 7I₍₄₎,𝜃₀ = (0, 0, 0, 0)^′,A = 0.01).

$$ \begin{array}{@{}rcl@{}} &&p\left( \bar{\theta}, V_{\theta} \right) = p\left( V_{\theta} \right) \times p\left( \bar{\theta} | V_{\theta} \right) \\ &&\text{where} \quad p\left( V_{\theta} \right) \sim IW \left( \nu_{0}, V_{0} \right) \\ &&\quad\qquad~ p\left( \bar{\theta} | V_{\theta} \right) \sim N \left( \theta_{0}, V_{\theta} \otimes A^{-1}\right) \end{array} $$

Then the joint posterior distribution is decomposed into a series of conditional distributions as follows:

$$ \begin{array}{@{}rcl@{}} && p\left( \theta_{i} | \bar{\theta}, V_{\theta} \right) \propto p\left( \theta_{i} | \bar{\theta}, V_{\theta} \right) \times \ell \left( \theta_{i} | \{x_{i1t},x_{i2t},p_{i1t},p_{i2t}\}_{t=1}^{T}\right),\\ && \forall i \in \{1,\cdots,N\} \\ && p\left( V_{\theta} | \{\theta_{i}\}_{i=1}^{N} \right) \sim IW \left( \nu_{0}+N, V_{0} +\tilde{S}\right) \\ && p\left( \bar{\theta} | V_{\theta}, \{\theta_{i}\}_{i=1}^{N} \right) \sim N \left( \tilde{ \theta}, V_{\theta} \otimes (N+A)^{-1}\right) \\ && \text{where} \quad \tilde{ \theta}=\text{vec}(\tilde{\Theta}), \quad \tilde{\Theta}=(N+A)^{-1}(N\bar{\Theta}+A {\Theta}_{0}) \\ && \quad \quad \quad \tilde{S}=({\Theta}-\tilde{\Theta})^{T}({\Theta}-\tilde{\Theta})+(\tilde{\Theta}-\bar{\Theta})^{T}A(\tilde{\Theta}-\bar{\Theta}) \end{array} $$

While the hyperparameters ($\bar {\theta }, V_{\theta }$) can be directly drawn from the standard distributions due to the conjugacy, we use the Metropolis–Hastings algorithm for drawing the individual-level parameters. Our Bayesian MCMC estimation algorithm follows the steps below:

(Step1):

(i) Set initial values for the model parameters ($\bar {\theta }^{(0)}, V_{\theta }^{(0)},\{\theta _{i}^{(0)}\}_{i=1}^{N}$). (ii) Compute the log-likelihood of the model for each individual.

$$ \begin{array}{@{}rcl@{}} {ll}_{i}^{(0)} = \ln \ell \left( \theta_{i}^{(0)} | \{x_{i1t},x_{i2t},p_{i1t},p_{i2t}\}_{t=1}^{T}\right), \quad \forall i \in \{1,\cdots,N\} \end{array} $$

(Step2):

Draw the individual level parameters ($\{\theta _{i}^{(r)}\}_{i=1}^{N}$) for r^th iteration. (i) Given $\{ \theta _{i}^{(r-1)}, {ll}_{i}^{(r-1)}, \bar {\theta }^{(r-1)},V_{\theta }^{(r-1)} \}$, draw $\theta _{i}^{(r)}$ by the Random Walk MH algorithm. (ii) Update the log-likelihood as well when the new parameter is accepted (${ll}_{i}^{(r)}$). (iii) Repeat (Step2)-(i)$\sim$(Step2)-(ii) for every individual (∀i ∈{1,⋯ ,N}).

(Step3):

Draw the hyperparameters ($\bar {\theta }^{(r)},V_{\theta }^{(r)}$) for r^th iteration. (i) Given $\{ \{\theta _{i}^{(r)}\}_{i=1}^{N},\nu _{0},V_{0} \}$, draw $V_{\theta }^{(r)}$ from the Inverse Wishart distribution. (ii) Given $\{ V_{\theta }^{(r)}, \{\theta _{i}^{(r)}\}_{i=1}^{N},\theta _{0},A \}$, draw $\bar {\theta }^{(r)}$ from from the multivariate Normal distribution.

(Step4):

Repeat (Step 2)$\sim$(Step3) for R iterations

It is noteworthy to mention that we reuse the log-likelihood value of the previous iteration (${ll}_{i}^{(r-1)}$) when implementing the MH algorithm for $\theta _{i}^{(r)}$ in (Step 2). Because our two-step approach approximates the model likelihood by the Monte Carlo integration rather than computing its exact value, the MCMC converges to the exact posterior only when the integration dummies used to simulate the likelihood become a part of the MCMC state space (Andrieu & Roberts, 2009).

Appendix C: Model specifications

• 1. Benchmark1: $\theta \equiv (\alpha _{2},\cdots ,\alpha _{J},\beta ,\ln \lambda )^{\prime }$ is estimated with α₁ = 0

  $$ \begin{array}{@{}rcl@{}} && Q_{t} \sim \text{Poisson} \left( \lambda \right) \\ && x_{1t},\cdots,x_{Jt} | Q_{t} \sim \text{Multinomial} \left( \pi_{1},\cdots,\pi_{J} \right), \quad \text{where} \pi_{j}=\frac{e^{\alpha_{j}+\beta \times p_{jt}}}{\sum \limits_{j=1}^{J} e^{\alpha_{j}+\beta \times p_{jt}}} \end{array} $$

• 2. Benchmark2: $\theta \equiv (\ln \psi _{1},\cdots ,\ln \psi _{J}, \ln \gamma ,\ln E)^{\prime }$ is estimated with ψ₀ = 1

  $$ \begin{array}{@{}rcl@{}} &\text{Maximize } \quad & V\left( x_{1t}, \cdots, x_{Jt}\right) = \sum\limits_{j = 1}^{J} \frac{\psi_{j} e^{\varepsilon_{jt}}}{\gamma} \ln \left( \gamma x_{jt}+1\right) + \psi_{0} \ln \left( E - \sum\limits_{j = 1}^{J} {{p_{jt}}{x_{jt}}} \right) \\ &\text{Subject to} \quad & x_{0t} = E - \sum\limits_{j = 1}^{J} {{p_{jt}}{x_{jt}}} \ge 0, x_{jt} \ge 0, \forall j \in \left\{ {1, {\cdots} ,J} \right\} \end{array} $$

• 3. Benchmark3: $\theta \equiv (\ln \psi _{1},\cdots ,\ln \psi _{J}, \ln \gamma )^{\prime }$ is estimated with ψ₀ = 1

  $$ \begin{array}{@{}rcl@{}} &\text{Maximize } \quad & V\left( x_{1t}, \cdots, x_{Jt}\right) = \sum\limits_{j = 1}^{J} \frac{\psi_{j} e^{\varepsilon_{jt}}}{\gamma} \ln \left( \gamma x_{jt}+1\right) + \psi_{0} \left( E - \sum\limits_{j = 1}^{J} {{p_{jt}}{x_{jt}}} \right) \\ &\text{Subject to} \quad & x_{0t} = E - \sum\limits_{j = 1}^{J} {{p_{jt}}{x_{jt}}} \ge 0, x_{jt} \in \left\{ {0,1,2, {\cdots} } \right\}, \forall j \in \left\{ {1, {\cdots} ,J} \right\} \end{array} $$

• 4. Proposed1: $\theta \equiv (\ln \psi _{1},\cdots ,\ln \psi _{J}, \ln \gamma ,\ln E)^{\prime }$ is estimated with ψ₀ = 1

  $$ \begin{array}{@{}rcl@{}} &\text{Maximize } \quad & V\left( x_{1t}, \cdots, x_{Jt}\right) = \sum\limits_{j = 1}^{J} \frac{\psi_{j} e^{\varepsilon_{jt}}}{\gamma} \ln \left( \gamma x_{jt}+1\right) + \psi_{0} \ln \left( E - \sum\limits_{j = 1}^{J} {{p_{jt}}{x_{jt}}} \right) \\ &\text{Subject to} \quad & x_{0t} = E - \sum\limits_{j = 1}^{J} {{p_{jt}}{x_{jt}}} \ge 0, x_{jt} \in \left\{ {0,1,2, {\cdots} } \right\}, \forall j \in \left\{ {1, {\cdots} ,J} \right\} \end{array} $$

• 5. Proposed2: $\theta \equiv (\ln \psi _{1},\cdots ,\ln \psi _{J}, \ln \gamma ,\ln E,\ln S)^{\prime }$ is estimated with ${\psi _{0}^{m}}={\psi _{0}^{s}}=1$

  $$ \begin{array}{@{}rcl@{}} \text{Maximize } &&\quad V\left( x_{1t}, \cdots, x_{Jt}\right)\\ &=& \sum\limits_{j = 1}^{J} \frac{\psi_{j} e^{\varepsilon_{jt}}}{\gamma} \ln \left( \gamma x_{jt}+1\right) + {\psi_{0}^{m}} \ln \left( E - \sum\limits_{j = 1}^{J} {{p_{jt}}{x_{jt}}} \right)\\ &&+ {\psi_{0}^{s}} \ln \left( S - \sum\limits_{j = 1}^{J} {{q_{j}}{x_{jt}}} \right) \\ \text{Subject to} \quad x_{0t}^{m} &=& E - \sum\limits_{j = 1}^{J} {{p_{jt}}{x_{jt}}} \ge 0, x_{0t}^{s} = S - \sum\limits_{j = 1}^{J} {{q_{j}}{x_{jt}}}\\ &\ge& 0, x_{jt} \in \left\{ {0,1,2, {\cdots} } \right\}, \forall j \in \left\{ {1, {\cdots} ,J} \right\} \end{array} $$

Appendix D: Parameter estimates of the models

Table 16 Parameter estimates

Table 17 Covariance matrix

Appendix E: Application of the proposed model to optimal demand of a non-convex problem

This section provides an additional simulation study that shows the limitation of the proposed sequential choice process in estimating optimal demand models of non-convex problems. Given the same utility function in Eq. 13, we simulate optimal demand of two complementary goods by comparing the attainable utilities of the entire feasible set. Then we apply our sequential choice model to the simulated data of optimal solutions for estimating the model parameters. Table 18 shows how our estimation algorithm works when it is applied to optimal demand of complementary goods. Because the sequential choice process embedded in the estimation algorithm does not guarantee an optimal solution of a non-convex problem, the parameter estimates fail to recover the true parameter values.

Table 18 Estimation result—optimal demand of complementary goods