Abstract
Transaction Memory (TM) is a concurrency control abstraction that allows the programmer to specify blocks of code to be executed atomically as transactions. However, since transactional code can contain just about any operation attention must be paid to the state of shared variables at any given time. E.g., contrary to a database transaction, if a TM transaction reads a stale value it may execute dangerous operations, like attempt to divide by zero, access an illegal memory address, or enter an infinite loop. Thus serializability is insufficient, and stronger safety properties are required in TM, which regulate what values can be read, even by transactions that abort. Hence, a number of TM safety properties were developed, including opacity, and TMS1 and TMS2. However, such strong properties preclude using prerelease as a technique for optimizing TM, because they virtually forbid reading from live transactions. On the other hand, properties that do allow prerelease are either not strong enough to prevent any of the problems mentioned above (recoverability), or add additional conditions on transactions that prerelease variables that limit their applicability (elastic opacity, live opacity, virtual world consistency). This paper introduces last-use opacity and strong last-use opacity, a pair of new TM safety properties meant to be a compromise between strong properties like opacity and minimal ones like serializability. The properties eliminate all but a small class of benign inconsistent views and pose no stringent conditions on transactions.
Similar content being viewed by others
1 Introduction
Writing concurrent programs using low-level synchronization primitives is notoriously difficult and error-prone. Over the past decade, there has been a growing interest in alternatives to lock-based synchronization by turning to the idea of software transactional memory (TM) [22, 39]. Basically, TM transplants the transaction abstraction from database systems and uses it to hide the details of synchronization. In particular, TM uses speculative execution to ensure that transactions in danger of reading inconsistent state abort and retry. This is a universal solution and means that the programmer must only specify where transactions begin and end, and the TM manages the execution so that the transactional code executes correctly and efficiently. Thus, the programmer avoids having to solve the problem of synchronization herself and can rely on any one of a plethora of TM systems (e.g., [1, 12, 19,20,21, 30, 31, 36, 37]).
TM allows transactional code to be mixed with non-transactional code and to contain virtually any operation, rather than just reads and writes like in its database predecessors. Therefore, greater attention must be paid to the state of shared variables at any given time. For instance, if a database transaction reads a stale value, it must simply abort and retry, and no harm is done. Whereas, if a TM transaction reads an inconsistent value it may execute an unanticipated dangerous operation, like dividing by zero, accessing an illegal memory address, entering an infinite loop or infinite recursion (see [11, 17]). Such erroneous behavior must be avoided or mitigated. Mitigation can be done comprehensively by sandboxing [11] transactions, that is isolating the system from the damaging effects of inconsistent views at the level of runtime or the operating system. This can mean applying such diverse techniques managing runtime exceptions, overloading fault signals, forcing periodic transaction validation to capture and contain a broad spectrum of possible errors, etc. [11, 32]. Other methods involve requiring programmers to place validation barriers on sensitive code, or deferring dangerous operations to commit [38].
However, in general, modern TM systems attempt to restrict the ability of transactions to view inconsistent state, as formally described by suitable TM safety properties. To that end, the safety property called opacity [16, 17] was introduced. This property stipulates as a criterion of correct execution that transactions do not read values written by other live (not completed) transactions. It also requires that the execution be both serializable [33] and real-time ordered. Opacity became the gold standard of TM safety properties, and most TM systems found in the literature are, in fact, opaque.
However, opacity precludes purposeful and controlled reading from live transactions, a technique we will refer to as prerelease, which involves transactions that technically conflict but nevertheless commit correctly, and produce a history that is also correct. This increases the amount of work transactions can do in parallel, which, improves the throughput of an implementation. Systems employing prerelease [9, 15, 26, 37] show that this yields a significant and worthwhile performance benefit in practice. This is particularly (but not exclusively) true for pessimistic concurrency control, where prerelease is vital to increased parallelism between transactions (see e.g., [40, 41]) and therefore essential for achieving high efficiency in applications with high contention.
In Fig. 1 we show an example, where transaction \(T_i\) writes values to variables \( x \) and \( y \), while \(T_j\), \(T_k\), and \(T_l\) show the behavior of transactions trying to read those variables under various example TM implementations. The first two implementations are opaque, illustrating typical behavior of TM systems. In an optimistic TM implementation, \(T_j\) reads x from before \(T_i\), but tries to read the value of y written by \(T_i\), conflicts, and needs to abort and restart to avoid reading inconsistent values of \( x \) and \( y \). In a lock-based pessimistic TM implementation, \(T_k\) waits for \(T_i\) to release a lock on \( x \) before reading it. The third implementation uses prerelease. Here, \(T_l\) reads live values of \( x \) and \( y \) from \(T_i\), allowing it to finish executing much earlier, leading to a shorter schedule overall and less duplicated effort. While this is just one example and the transaction interleavings do not always favor a prereleasing implementation, the performance gain is visible. However, this execution of \(T_l\) breaks opacity.
Opacity precludes prerelease, because in the general case reading from live transactions is unsafe. However, in certain limited circumstances the harmful operations caused by inconsistent states can be contained (e.g., by sandboxing), or harmful inconsistent states can be identified and eliminated by TM implementations. The question this paper is concerned with is whether the abandonment of prerelease in the context of safety is necessary or whether prerelease can be salvaged, and whether we can codify safe practices to dictate how to use prerelease safely.
We are, of course, not the first to argue undue restrictiveness on the part of opacity. A number of more relaxed properties were introduced that tweaked opacity’s various aspects to achieve a something more practical. These properties include virtual world consistency (VWC) [23] and transactional memory specification (TMS1 and TMS2) [13] which weaken the requirement for a consistent view of past operations among transactions, and elastic opacity [15] which allows splitting transactions into smaller fragments. The live opacity [14] property is even interested in allowing transactions to read from other uncommitted transactions while retaining the core guarantees of opacity while restricting the ability to abort.
The first contribution of this paper is to examine these properties and determine whether or not they allow the use of prerelease in TM, and, if so, what compromises they make with respect to consistency, and what additional assumptions they require. We then consider the applicability of these properties to TM systems that rely on prerelease. In addition to TM properties, we similarly examine common database consistency conditions: serializability [33], recoverability [18], cascadelessness (avoiding cascading aborts) [8], strictness [8], rigorousness [10] and commit-order preservation [44].
The second contribution of this paper is to introduce new TM safety properties called last-use opacity and strong last-use opacity that allow prerelease. Each of these is dedicated to a different transactional model (API). They both eschew stringent assumptions but nevertheless eliminate inconsistent views or restrict them to a benign minimum. This comes at the price of introducing considerations about the code of transactions and system invariants into the safety property. We give formal definitions, discuss example (strong) last-use opaque histories, and compare the new properties with other discussed properties, specifically showing they are stronger than serializability but weaker than opacity. We also specifically enumerate the guarantees given by the properties.
The paper is structured as follows. We present the definitions of basic terms in Sect. 2. We then discuss prerelease and construct a framework for examining properties through the lense of prerelease in Sect. 3. We follow by an examination of the TM property space in Sect. 4. Next, we define and discuss last-use opacity in Sect. 5 and strong last-use opacity in Sect. 6. Finally, we present the related work in Sect. 7 and conclude in Sect. 8. We also include an appendix containing additional proofs that we remove from the main text both due to their size and relative simplicity.
2 Preliminaries
We begin by introducing basic concepts pertaining to further discussion, including basic definitions describing transactional memory and execution of programs within it, as well as various system models, and properties. We also explain the convention we use for diagrams showing transactional executions.
2.1 Processes
The system is composed of processes \(\varPi = \{p_1, p_2, \ldots , p_n\}\) concurrently executing program \(\mathbb {P}\) which constitutes a set of sequential subprograms \(\mathbb {P}= \{ \mathcal {P}_1, \mathcal {P}_2, \ldots , \mathcal {P}_n \}\), where process \(p_i\) executes \(\mathcal {P}_i\). Each subprogram is a finite sequence of statements in some language \(\mathbb {L}\). The definition of \(\mathbb {L}\) can be whatsoever, as long as it provides constructs to execute transactional operations in accordance with the interface and assumptions described further in this section.
Given program \(\mathbb {P}\) and a set of processes \(\varPi \), we denote an execution of \(\mathbb {P}\) by \(\varPi \) as \(\mathcal {E}({\mathbb {P}},{\varPi })\). An execution entails each process \(p_k \in \varPi \) evaluating some prefix of subprogram \(\mathcal {P}_k \in \mathbb {P}\). The evaluation of each statement by a process is deterministic and follows the semantics of \(\mathbb {L}\). This evaluation produces a (possibly empty) sequence of events (steps) which we call a trace and denote \(\mathscr {T}\vdash \mathcal {E}({\mathbb {P}},{\varPi })\). \(\mathcal {E}({\mathbb {P}},{\varPi })\) is concurrent, i.e., while the statements in subprogram \(\mathcal {P}_k\) are evaluated sequentially by a single process, the evaluation of statements by different processes can be arbitrarily interleaved. Hence, given \(\mathscr {T}\vdash \mathcal {E}({\mathbb {P}},{\varPi })\) and \(\mathscr {T}' \vdash \mathcal {E}({\mathbb {P}},{\varPi })\), it is possible that \(\mathscr {T}\ne \mathscr {T}'\).
2.2 Shared variables
The system contains a set of shared variables (or just variables) \( Var = \{ x , y , z , \ldots \}\). A variable \( x \) is an entity that has state \(\mathtt{S}_{ x }\) and a specified interface consisting of the following two operations:
-
(a)
write operation \( w ^{}({ x }){ v }\) that sets \(\mathtt{S}_{ x }\) to value \( v \); the operation’s return value is the constant \( ok \) (indicating correct execution),
-
(b)
read operation \( r ^{}({ x }){}\) whose return value is the current value of \(\mathtt{S}_{ x }\).
Variables are hermetic, meaning that the state \(\mathtt{S}_{ x }\) of \( x \) can only be modified or read by executing write or read operations on \(x\). The state \(\mathtt{S}_{ x }\) can be defined however, but for simplicity we assume its domain is \(\mathbb {N}_0\).
Any process \(p_k \in \varPi \) can execute read and write operations on \( x \) as part of subprogram \(\mathcal {P}_k\). This results in the evaluation of some arbitrary sequence of statements (as part of \(\mathcal {P}_k\)) in language \(\mathbb {L}\) which have the ability to return and modify \(\mathtt{S}_{ x }\).
Whenever process \(p_k \in \varPi \) executes some operation \(\mathtt{m}( x )\) on variable \( x \) as part of \(\mathcal {P}_k\), this causes an invocation event \( inv _{}^{k}(\mathtt{m}( x ))\) and a subsequent response event \( res _{}^{k}( v )\) to be issued, where \( v \) is the return value of \(\mathtt{m}( x )\). The pair of these events (\( inv _{}^{k}(\mathtt{m}( x ))\), \( res _{}^{k}( v )\)) is called a complete operation execution and it is denoted \(\mathtt{m}^{k}( x )\rightarrow v \) in shorthand. For the sake of analogy we refer to an invocation event \( inv _{}^{k}(o)\) without the corresponding response event as a pending operation execution.
2.3 Transactions
Transactional memory (TM) is a programming paradigm that uses transactions to control concurrent execution of operations on shared variables by parallel processes.
A transaction \(T_i \in \mathbb {T}\) is some piece of code executed by process \(p_k\), as part of subprogram \(\mathcal {P}_k\). Hence, we say that \(p_k\) executes \(T_i\). Any transaction \(T_i\) is executed by exactly one process \(p_k\) and that each process executes transactions sequentially. Process \(p_k\) can execute local computations as well as operations on shared variables as part of the transaction. That is, given \( x \in Var \), the process can execute:
-
(a)
write (denoted \( w _{i}({ x }){ v }\), where i indicates transaction \(T_i\)) which sets \(\mathtt{S}_{ x }\) to \( v \) and returns \( ok _i\) if the operation is successful, and \( A _i\) otherwise,
-
(b)
read (denoted \( r _{i}({ x }){}\)) which returns the value of \(\mathtt{S}_{ x }\) if the execution is successful, or \( A _i\) otherwise.
In addition, the processes can execute the following transactional operations that do not pertain to any specific variable:
-
(c)
start (denoted \( start _i\)) which initializes transaction \(T_i\), and whose return value is the constant \( ok _i\),
-
(d)
commit (denoted \( tryC _i\)) which attempts to commit \(T_i\) and returns either the constant \( C _i\), which signifies a successful commitment of the transaction or the constant \( A _i\) in case of a forced abort,
Finally, there is also another operation allowed in some TM system models and not in others, which has great impact on consistency, and so we wish to separate it out. Namely, some TMs allow for a transaction to cause itself to roll back by executing an abort operation:
-
(e)
abort (denoted \( tryA _i\)) which aborts \(T_i\) and returns \( A _i\).
We call a TM system model where the abort operation is allowed (in addition to other operations) the arbitrary abort system model, as opposed to the commit-only model.
The operations a–e defined above are part of the so-called transactional interface (or transactional API). They can only be invoked within a transaction. Specifically, processes execute operations on shared variables only as part of a transaction.
Even though transactions are subprograms evaluated by processes, it is convenient to talk about them as separate and independent entities. Thus, rather than saying \(p_k\) executes some operation as part of transaction \(T_i\), we will simply say that \(T_i\) executes some operation. Hence we will also forgo the distinction of processes in transactional operation executions, and write simply: \( start _i \rightarrow ok _i\), \( r _{i}({ x })\!\rightarrow \!{ v }\), \( w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\), \( tryC _i \rightarrow C _i\), etc. By analogy, we also drop the superscript indicating processes in the notation of invocation and response events, unless the distinction is needed.
2.4 Sequential specification
Given variable \( x \), let sequential specification of \( x \), denoted \( Seq ( x )\), be a prefix-closed set of sequences containing invocation events and response events which specify the semantics of shared variables. (A set Q of sequences is prefix-closed if, whenever a sequence S is in Q, every prefix of S is also in Q.) Intuitively, a sequential specification enumerates all possible correct sequences of operations that can be performed on a variable in a sequential execution.
Specifically, in the case of any variable \( x \in Var \), given that D is the domain of \(\mathtt{S}_{ x }\), and assuming initially \(\mathtt{S}_{ x }= v _0\) for some \( v _0 \in D\), the sequential specification of \( x \) s.t., \( Seq ( x )\) is a set of sequences of the form \([\alpha _1 \rightarrow v _1, \alpha _2 \rightarrow v _2, \ldots , \alpha _m \rightarrow v _m]\), where each \(\alpha _j \rightarrow v _j\) (\(j=1, 2, \ldots , m\)) is either:
-
(a)
\( w _{i}({ x }){ v _j}\!\rightarrow \!{ ok _i}\), where \( v _j \in D\),
-
(b)
\( r _{i}({ x })\!\rightarrow \!{ v _0}\) and there are no preceding writes, or
-
(c)
\( r _{i}({ x })\!\rightarrow \!{ v _j}\) and the most recent preceding write operation is \( w _{l}({ x }){ v _j}\!\rightarrow \!{ ok _l}\).
From this point on, unless stated otherwise, we assume that the domain D of all transactional variables is the set of natural numbers \(\mathbb {N}_0\) and that the initial value \( v _0\) of each variable is 0.
2.5 Histories
Given a trace \(\mathscr {T}\vdash \mathcal {E}({\mathbb {P}},{\varPi })\), a TM history \(H\) is a subsequence of trace \(\mathscr {T}\) consisting only of executions of transactional operations s.t. for every event e, \(e \in H\) iff \(e \in \mathscr {T}\) and e is either an invocation or a response event specified by the transactional interface given in Sect. 2.3.
The sequence of events in a history \(H_j\) can be denoted as \(H_j = [ e_1, e_2, \ldots , e_m ]\). For instance, some history \(H_1\) below is a history of a run of some program that executes transactions \(T_i\) and \(T_j\):
Some subhistory \(H'\) of a history \(H\) is a subsequence of \(H\). Given any history \(H\), let \(H|T_i\) be the longest subhistory of \(H\) consisting only of invocations and responses executed by transaction \(T_i\). For example, \(H_1|T_j\) is defined as:
We say transaction \(T_i\) is in \(H\), which we denote \(T_i \in H\), iff \(H|T_i \ne \varnothing \).
Let \(H|x\) be the longest subhistory of \(H\) consisting only of invocations and responses executed on variable \( x \), but only those that form complete operation executions.
Given a complete operation execution \( op \) that consists of an invocation event \(e^i\) and a response event \(e^r\), we say \( op \) is in \(H\) (\( op \in H\)) iff \(e^i \in H\) and \(e^r \in H\). Given a pending operation execution \( op \) consisting of an invocation \(e^i\), we say \( op \) is in \(H\) (\( op \in H\)) iff \(e^i \in H\) and there is no other operation execution \( op '\) consisting of an invocation event \(e^i\) and a response event \(e^r\) s.t. \( op ' \in H\).
Given two complete operation executions \( op '\) and \( op ''\) in some history \(H\), where \( op '\) contains the response event \(\textit{res}'\) and \( op ''\) contains the invocation event \(\textit{inv}''\), we say \( op '\) precedes \( op ''\) (or \( op ''\) follows \( op '\)) in \(H\) if \(\textit{res}'\) precedes \(\textit{inv}''\) in \(H\). We denote this \( op ' \prec _H op ''\). For operations \( op ', op '' \in H\), we say \( op '\) directly precedes \( op ''\), denoted \( op ' \prec \!\!\!\prec _{H} op ''\) iff \( op ' \prec _{H} op ''\) and \(\not \exists { op '''\in H}\) s.t. \( op ' \prec _{H} op ''' \prec _{H} op ''\).
A history whose all operation executions are complete is a complete history.
Most of the time it will be convenient to denote any two adjoining events in a history that represent the invocation and response of a complete execution of an operation as that operation execution, using the syntax \(e \rightarrow e'\). Then, an alternative representation of \(H_1|T_j\) is denoted as follows:
In addition, sometimes the values written by particular operations, or returned by them will not be relevant to the discussion at hand. In those situations we use the placeholder value \(\square \) to indicate that whatever value was passed or returned. For instance, when the value returned by the read operation is irrelevant in \(H_1|T_j\), we denote it as follows:
2.5.1 Well-formedness
History \(H\) is well-formed if, for every transaction \(T_i\) in \(H\), \(H|T_i\) is an alternating sequence of invocations and responses s.t.,
-
(a)
\(H|T_i\) starts with an invocation \( inv _{i}^{}( start _i)\),
-
(b)
no events in \(H|T_i\) follow \( res _{i}^{}( C _i)\) or \( res _{i}^{}( A _i)\),
-
(c)
no invocation event in \(H|T_i\) follows \( inv _{i}^{}( tryC _i)\) or \( inv _{i}^{}( tryA _i)\),
-
(d)
for any two transactions \(T_i\) and \(T_j\) s.t., \(T_i\) and \(T_j\) are executed by the same process \(p_k\), the last event of \(H|T_i\) precedes the first event of \(H|T_j\) in \(H\) or vice versa.
In the remainder of the paper we assume that all histories are well-formed.
2.5.2 Unique writes
History \(H\) has unique writes if, given transactions \(T_i\) and \(T_j\) (where \(i\ne j\) or \(i=j\)), for any two write operation executions \( w _{i}({ x }){ v '}\!\rightarrow \!{ ok _i}\) and \( w _{j}({ x }){ v ''}\!\rightarrow \!{ ok _j}\) it is true that \( v ' \ne v ''\) and neither \( v ' = v _0\) nor \( v '' = v _0\).
2.5.3 Completion
Given history \(H\) and transaction \(T_i\), \(T_i\) is committed if \(H|T_i\) contains operation execution \( tryC _i \rightarrow C _i\). Transaction \(T_i\) is aborted if \(H|T_i\) contains response \( res _{i}^{}( A _i)\) to any invocation. Transaction \(T_i\) is commit-pending if \(H|T_i\) contains invocation \( tryC _i\) but it does not contain \( res _{i}^{}( A _i)\) nor \( res _{i}^{}( C _i)\). Finally, \(T_i\) is live if it is neither committed, aborted, nor commit-pending. We say a transaction is forcibly aborted if \(T_i\) is aborted and \(H|T_i\) does not contain an invocation \( inv _{i}^{}( tryA _i)\).
Given two histories \(H' = \big [e_1', e_2', \ldots , e_m'\big ]\) and \(H'' = [e_1'', e_2'', \ldots , e_m'']\), we define their concatenation as \(H' \cdot H'' = [e_1', e_2', \ldots , e_m', e_1'', e_2'', \ldots , e_m'']\). We say P is a prefix of \(H\) if \(H= P \cdot H'\). Then, let a completion \( Compl (H)\) of history \(H\) be any complete history s.t., \(H\) is a prefix of \( Compl (H)\) and for every transaction \(T_i \in H\) subhistory \( Compl (H)|T_i\) equals one of the following:
-
(a)
\(H|T_i\), if \(T_i\) finished committing or aborting,
-
(b)
\(H|T_i \cdot \bigg [ res _{i}^{}( C _i)\bigg ]\), if \(T_i\) is live and contains a pending \( tryC _i\),
-
(c)
\(H|T_i \cdot \bigg [ res _{i}^{}( A _i)\bigg ]\), if \(T_i\) is live and contains some pending operation,
-
(d)
\(H|T_i \cdot \bigg [ tryC _i \rightarrow A _i\bigg ]\), if \(T_i\) is live and contains no pending operations.
Note that, if all transactions in \(H\) are committed or aborted then \( Compl (H)\) and \(H\) are identical.
2.5.4 Equivalency
Two histories \(H'\) and \(H''\) are equivalent (denoted \(H' \equiv H''\)) if for every \(T_i \in \mathbb {T}\) it is true that \(H'|T_i = H''|T_i\). When we say \(H'\) is equivalent to \(H''\) we mean that \(H'\) and \(H''\) are equivalent.
2.5.5 Real-time order
A real-time order \(\prec _H\) is an order over history \(H\) s.t., given two transactions \(T_i, T_j \in H\), if the last event in \(H|T_i\) precedes in \(H\) the first event of \(H|T_j\), then \(T_i\) precedes \(T_j\) in \(H\), denoted \(T_i \prec _HT_j\). We then say that two transactions \(T_i, T_j \in H\) are concurrent if neither \(T_i \prec _HT_j\) nor \(T_j \prec _HT_i\). We say that history \(H'\) preserves the real-time order of \(H\) if \(\prec _H\subseteq \prec _{H'}\).
2.5.6 Sequential histories
A sequential history S is a history, s.t. no two transactions in S are concurrent in S. Some sequential history S is a sequential witness history of \(H\) if S is equivalent to \(H\) and S preserves the real time order of \(H\). We usually denote such a history \(\hat{S}_{H}\).
2.5.7 Accesses
Given a history \(H\) and a transaction \(T_i\) in \(H\), we say that \(T_i\) accesses some variable \(x\) in \(H\) iff there exists some invocation by \(T_i\) on \(x\) of any operation \(\mathtt{m}( x )\) in \(H|T_i\). In addition, let \(T_i\)’s access set, denoted \( ASet (i)\), in \(H\) be a set that contains every variable \(x\) such that \(T_i\) accesses \(x\) in \(H\).
With respect to variables specifically, \(T_i\) reads variable \( x \) in \(H\) if there exists an invocation \( inv _{i}^{}( r _{i}({ x }){})\) in \(H|T_i\). By analogy, we say that \(T_i\) writes to \( x \) in \(H\) if there exists an invocation \( inv _{i}^{}( w _{i}({ x }){ v })\) in \(H|T_i\). In addition, let \(T_i\)’s read set be a set that contains every variable \( x \) such that \(T_i\) reads \( x \). By analogy, \(T_i\)’s write set contains every \( x \) such that \(T_i\) writes to \( x \). A transaction’s access set, denoted \( ASet (i)\), is the union of its read set and its write set.
Given a history \(H\) (with unique writes) and a pair of transactions \(T_i, T_j \in H\), we say \(T_i\) reads from \(T_j\) if there is some variable \( x \), for which there is a complete operation execution \( w _{j}({ x }){ v }\!\rightarrow \!{ ok _j}\) in \(H|T_j\) and another complete operation execution \( r _{i}({ x })\!\rightarrow \!{ u }\) in \(H|T_i\), s.t. \( v = u \).
2.5.8 Locality
Given any transaction \(T_i\) in some history \(H,\) any operation execution on a variable \( x \) within \(H|T_i\) is either local or non-local. Read operation execution \( r _{i}({ x })\!\rightarrow \!{ v }\) in \(H|T_i\) is local if it is preceded in \(H|T_i\) by a write operation execution on \( x \), and it is non-local otherwise. Write operation execution \( w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) in \(H|T_i\) is local if it is followed in \(H|T_i\) by a write operation execution on \( x \), and non-local otherwise.
2.5.9 Conflicts
Following [17], transaction conflicts are defined for variables as follows. Given a history \(H\) and a pair of transactions \(T_i, T_j \in H\), we say \(T_i\) and \(T_j\) conflict on variable \( x \) in \(H\) if \(T_i\) and \(T_j\) are concurrent, both \(T_i\) and \(T_j\) access \( x \), and one or both of \(T_i\) and \(T_j\) write to \( x \). We call any two operation executions on some \( x \) that cause two transactions \(T_i\), \(T_j\) (\(i \ne j\)) to conflict on \( x \) conflicting operation executions.
2.6 Transaction legality
The definitions given above allow us to formulate the central concept that defines consistency of transactional execution: transaction legality. Intuitively, using variables as an example, we can say a transaction is legal in a sequential history if it only reads values of variables that were written by committed transactions or by itself.
More formally, let S be a sequential history that only contains committed transactions, with the possible exception of the last transaction, which can be aborted. We say that sequential history S is legal if for every \(x\in Var \), \(S|x\in Seq (x)\).
In addition, given any sequential history S and transaction \(T_i \in S\), let visible history \( Vis (S, T_i)\) be the longest subhistory of S s.t., for every transaction \(T_j \in Vis (S, T_i)\), either \(i=j\) or \(T_j\) is committed in S and \(T_j \prec _S T_i\). Then, given a sequential history S and a transaction \(T_i \in S\), we say that \(T_i\) is legal in S if \( Vis (S, T_i)\) is legal.
2.7 Safety properties
A property  is a condition that stipulates correct behavior. In relation to histories, a given history satisfies
is a condition that stipulates correct behavior. In relation to histories, a given history satisfies  if the condition is met for that history. Given property
if the condition is met for that history. Given property  , we call
, we call  the set of all
the set of all  -histories, defined such that
-histories, defined such that  if, and only if \(H\) satisfies
if, and only if \(H\) satisfies  . In relation to programs, program \(\mathbb {P}\) satisfies
. In relation to programs, program \(\mathbb {P}\) satisfies  if all histories produced by \(\mathbb {P}\) satisfy
if all histories produced by \(\mathbb {P}\) satisfy  .
.
Safety properties [28] are properties which guarantee that “something [bad] will not happen.” In the case of TM this means that, transactions will not observe concurrency of other transactions. Property  is a safety property if it meets the following definition (adapted from [6]):
is a safety property if it meets the following definition (adapted from [6]):
Definition 1
A property  is a safety property if, given the set
is a safety property if, given the set  of all histories that satisfy
of all histories that satisfy  :
:
-
(a)
Prefix-closure: every prefix \(H'\) of a history
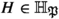 is also in
is also in  ,
, -
(b)
Limit-closure: for any infinite sequence \(H_0, H_1, \ldots \) of finite histories, s.t. for every \(h=0,1,\ldots \),
 and \(H_h\) is a prefix of \(H_{h+1}\), the infinite history that is the limit of the sequence is also in
and \(H_h\) is a prefix of \(H_{h+1}\), the infinite history that is the limit of the sequence is also in  .
.
For distinction, we use the term consistency condition to refer to properties that are not safety properties.
We compare properties with respect to their relative strength. Given two properties  and
and  we say
we say  is stronger than
is stronger than  if
if  (so
(so  is weaker than
is weaker than  ). If neither
). If neither  nor
nor  , then the properties are incomparable, which we denote
, then the properties are incomparable, which we denote  .
.
2.8 Invariants
An invariant expresses constant properties of a system. They can be provided by programmers writing transactional code or implemented as part of a TM implementation. Programmers can assume that invariants are true at the beginning of transactions and write their code to assure that they are true at the end of transactions. Invariants do not have to be maintained for the duration of the transaction, as long as they are true at their end. An invariant can be declared for all transactions or a set of specific transactions. Invariants can be expressed on a single variable (e.g., x> 0) or multiple variables (e.g., x == y == z).
We abstract from the semantics of invariants and only observe them as arbitrary black-box functions defined over sets of shared variables that apply to an explicitly stated set of transactions (including all transactions). For our purposes, an invariant is a pair consisting of a set of variables—its domain—and the set of transactions it applies to. We denote the set of all invariants in a system as  . Additionally, by \(\mathbb {I}^{ x }_{i}\) we denote the set containing variable \( x \) and all variables contained in the domain of any invariant that contains \( x \) and applies to transaction \(T_i\).
. Additionally, by \(\mathbb {I}^{ x }_{i}\) we denote the set containing variable \( x \) and all variables contained in the domain of any invariant that contains \( x \) and applies to transaction \(T_i\).
For the sake of subsequent discussion we define three specific examples of invariant sets.
 :
:-
denotes an empty invariant set. This refers to systems where programmers make no specific assumptions about values of shared variables or their relationships with other variables.
 :
:-
denotes a set containing only such invariants whose domains are either empty or singletons. This describes systems where there are no relationships between shared variables, but there are constraints on shared variables specified in terms of static values or local variables.
 :
:-
denotes a set containing an invariant that applies to all transactions and whose domain is \( Var \). This represents systems where no specific invariants are defined, but there is an overarching assumption that all variables are related. In the context of transactional execution it means that it is assumed that a transaction modifying a set of variables cannot expose the state of these variables to other transactions until it finishes all of its intended modifications.
Unless stated otherwise, we assume  .
.
2.9 Transaction diagrams
When talking about examples of histories, it is easier to understand the relationships between various events if the history is depicted using diagrams. For example, the following history is represented in the diagram in Fig. 2:
This and other diagrams each depict a history consisting of operations executed by transactions on a time axis. Every line depicts the operations executed by a particular transaction. The symbol  denotes a complete operation execution. The inscriptions above operation executions denote operations executed by the transactions, e.g. \( r _{i}({ x }){}\!\rightarrow \!0\) denotes that a read operation on variable \( x \) is executed by transaction \(T_i\) and returns 0, and \( w _{i}({ x }){1}\!\rightarrow \!{ ok _i}\) denotes that a write operation writing 1 to \( x \) is executed by \(T_i\), and \( tryC _i\!\rightarrow \! C _i\) indicates that \(T_i\) attempts to commit and succeeds because it returns \( C _i\), whereas \( tryA _i\!\rightarrow \! A _i\) indicates that the transaction attempts to abort and succeeds, etc. On the other hand, the symbol
denotes a complete operation execution. The inscriptions above operation executions denote operations executed by the transactions, e.g. \( r _{i}({ x }){}\!\rightarrow \!0\) denotes that a read operation on variable \( x \) is executed by transaction \(T_i\) and returns 0, and \( w _{i}({ x }){1}\!\rightarrow \!{ ok _i}\) denotes that a write operation writing 1 to \( x \) is executed by \(T_i\), and \( tryC _i\!\rightarrow \! C _i\) indicates that \(T_i\) attempts to commit and succeeds because it returns \( C _i\), whereas \( tryA _i\!\rightarrow \! A _i\) indicates that the transaction attempts to abort and succeeds, etc. On the other hand, the symbol  denotes an operation execution split into the invocation and the response event to indicate waiting, or that the execution takes a long time. In that case the inscription above is split between the events, e.g., a read operation execution would show \( r _{i}({ x }){}\) above the invocation, and \(\rightarrow \!1\) over the response.
denotes an operation execution split into the invocation and the response event to indicate waiting, or that the execution takes a long time. In that case the inscription above is split between the events, e.g., a read operation execution would show \( r _{i}({ x }){}\) above the invocation, and \(\rightarrow \!1\) over the response.
The diagram also adds additional information to the history to emphasize relationships between events. If waiting is involved, the arrow  is used to emphasize a happens before relation between two events. The same is used to indicate causality, e.g. whenever an abort event forces another operation to abort. Furthermore,
is used to emphasize a happens before relation between two events. The same is used to indicate causality, e.g. whenever an abort event forces another operation to abort. Furthermore,  denotes that the preceding transaction aborts (here, \(T_j\)) and a new transaction (\(T_{k}\)) is spawned. These elements are used as necessary to indicate particular scenarios and may be omitted.
denotes that the preceding transaction aborts (here, \(T_j\)) and a new transaction (\(T_{k}\)) is spawned. These elements are used as necessary to indicate particular scenarios and may be omitted.
3 Prerelease
The overall theme of this work is to examine safety properties and consistency conditions in terms of prerelease. What, then, is prerelease exactly and what impact does it have on consistency?
Prerelease pertains to a situation where conflicting transactions execute partially in parallel while accessing the same variable. In other words, prerelease is the ability of transactions to read from live transactions. The implied intent is for all such transactions to access these variables without losing consistency and thus for them all to finally commit. We show an example of this in Fig. 3 Here, transaction \(T_i\) writes value 1 to \( x \), and subsequently \(T_j\) reads 1 from \( x \), but does so without waiting for \(T_j\) to commit. Thus, \(T_i\) prereleased \( x \) for \(T_j\) to access.
The advantage of letting this happen is that the width of the schedule is shortened, which translates in some way into throughput. Then, if a TM system or a TM property allows it, there is a potential pragmatic benefit.
There are also pitfalls. What if \(T_i\) write to \( x \) again after \(T_j\) reads from \( x \)? Transactions are supposed to be atomic and isolated, so this behavior, reading a value from the middle of a transaction, should be treated as a clear violation.
But what if \(T_i\) eventually aborts instead of committing? Clearly \(T_j\) must then be forced to abort too. This can potentially cause other transactions to be forced to abort as well, which is a costly effect. On the other hand to prevent the situation we must either forbid prerelease or prevent \(T_i\) from aborting after prerelease. Creating such irrevocable transaction comes with its own problems, but, more importantly, is precluded in many classes of TM systems, including distributed TM, so at least that limitation should be considered too stringent.
3.1 Definition of prerelease
Our definitions are based on the observed effects of the release without reference to the actions of a concurrency control algorithm. That is a variable is considered to be prereleased by some transaction only when it is live and another transaction views the modifications applied to the variable by the first transaction. We define the concept of prerelease as follows:
Definition 2
(Prerelease) Given history \(H\) (with unique writes), transaction \(T_i \in H\) prereleases variable \( x \) in \(H\) iff there is some prefix P of \(H\), such that \(T_i\) is live in P and there exists some transaction \(T_j \in P\) such that there is a complete non-local read operation execution \( op _j = r _{j}({ x })\!\rightarrow \!{ v }\) in \(P|T_j\) and a complete write operation execution \( op _i = w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) in \(P|T_i\) such that \( op _i \prec _P op _j\).
3.2 Key questions
We begin our analysis by defining its key questions. The first and the most obvious is whether a particular property supports prerelease at all. Prerelease pertains to a situation where conflicting transactions execute partially in parallel while accessing the same variable. The implied intent is for all such transactions to access these variables without losing consistency and thus for them all to finally commit. We define prerelease formally in Definition 2. Then, the ability for a property to support prerelease is defined as follows:
Definition 3
(Prerelease Support) Property  supports prerelease iff given some history \(H\) that satisfies
supports prerelease iff given some history \(H\) that satisfies  there exists some transaction \(T_i \in H\), s.t. \(T_i\) prereleases some variable \( x \) in \(H\).
there exists some transaction \(T_i \in H\), s.t. \(T_i\) prereleases some variable \( x \) in \(H\).
If a property allows prerelease, it allows a significant performance boost (see e.g., [35, 41]) as transactions are executed with a higher degree of parallelism.
3.3 Overwriting support
Prerelease can give rise to some unwanted or unintuitive scenarios with respect to consistency. The most egregious of these is overwriting, where one transaction prereleases some variable, but proceeds to modify it afterward. In that case, any transaction that started executing operations on the released variable will observe an intermediate value with respect to the execution of the other transaction, ie., view inconsistent state.
An example of overwriting is shown in Fig. 4, where transaction \(T_i\) prereleases variable \( x \) but continues to write to \( x \) afterward. As a consequence, \(T_j\) first reads the value of \( x \) that is later modified. When \(T_j\) detects it is in conflict while executing a write operation it is aborted. This is a way for the TM to attempt to mitigate the consequences of viewing inconsistent state. The transaction is then restarted as a new transaction \(T_{k}\).
However, as argued in [17], simply aborting a transaction that views inconsistent state is not enough, since the transaction can potentially act in an unpredictable way on the basis of using an inconsistent value to perform local operations. For instance, if the value is used in pointer arithmetic it is possible for the transaction to access an unexpected memory location and crash the process. Alternatively, if the transaction uses the value within a loop condition, it can enter an infinite loop and become parasitic. Other dangerous behaviors are possible, including division by zero precluded by invariants that assume atomicity of transactions.
Thus, in our analysis of existing properties we ask the question whether, apart from allowing prerelease, the properties also forbid overwriting. In the light of the potential dangerous behaviors that can be caused by it, we consider properties that allow overwriting to be too weak to be practical.
Definition 4
(Overwriting Support) Property  supports overwriting iff
supports overwriting iff  supports prerelease, and given some history \(H\) (with unique writes) that satisfies
supports prerelease, and given some history \(H\) (with unique writes) that satisfies  , for some pair of transactions \(T_i, T_j \in H\) s.t.,
, for some pair of transactions \(T_i, T_j \in H\) s.t.,
-
(a)
\(T_i\) prereleases some variable \( x \),
-
(b)
\(H|T_i\) contains two write operation executions: \( w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) and \( w _{i}({ x }){ v '}\!\rightarrow \!{ ok _i}\), s.t. the former precedes the latter in \(H|T_i\),
-
(c)
\(H|T_j\) contains a read operation execution \( r _{j}({ x })\!\rightarrow \!{ v }\) that precedes \( w _{i}({ x }){ v '}\!\rightarrow \!{ ok _i}\) in \(H.\)
3.4 Aborting prerelease support
In addition, we look at whether or not a particular property forbids a transaction that prereleases some variable to abort. This is a precaution taken by many properties to prevent cascading aborts, another type of scenario involving inconsistent views. An example of this is shown in Fig. 5. In such a case a transaction, here \(T_i\), prereleases a variable and subsequently aborts. This can cause another transaction \(T_j\) that executed operations on that variable in the meantime to observe inconsistent state. In order to maintain consistency, a TM will then typically force \(T_j\) to abort and restart (as a new fresh transaction \(T_k\)).
However, while the condition that no transaction that prereleases a variable can abort, solves the problem of cascading aborts, it significantly limits the usefulness of any TM that satisfies it, since TM systems typically cannot predict whether any particular transaction eventually commits or aborts. In particular, there are important applications for TM, where a transaction can arbitrarily and uncontrollably abort at any time. Such applications include distributed TM and hardware TM, where aborts can be caused by outside stimuli, such as machine crashes.
An exception to this may be found in systems making special provisions to ensure that irrevocable transactions eventually commit (see e.g., [27, 45]). In such systems, prereleasing transactions could be ensured never to abort. However, case in point, these take drastic measures to ensure that, e.g., at most a single irrevocable transaction is present in the system at one time. Therefore, the requirement is too strict in the general case.
Definition 5
(Aborting Prerelease Support) Property  supports aborting prerelease iff
supports aborting prerelease iff  supports prerelease, and given some history \(H\) that satisfies
supports prerelease, and given some history \(H\) that satisfies  , for some transaction \(T_i \in H\) that prereleases some variable \( x \), \(H|T_i\) contains \( A _i\).
, for some transaction \(T_i \in H\) that prereleases some variable \( x \), \(H|T_i\) contains \( A _i\).
4 Properties and prerelease
In this section we analyze the extent to which various properties support prerelease, and what restrictions they apply to transactions that prerelease variables. The properties under consideration are the typical TM safety properties: serializability, opacity, markability, virtual world consistency, transactional memory specification, live opacity, and elastic opacity. We also consider some strong database consistency conditions that pertain to transactional processing: recoverability, commitment order preservation, cascadelessness, strictness, and rigorousness.
4.1 Serializability
The first property we discuss is serializability, a database property which can be regarded as a baseline TM safety property. It can be considered the minimal strong property acceptable in TM. It is also a property that can be grasped intuitively: a history is serializable if there is some sequential execution that would reflect the same behavior as shown in that history.
Serializability is defined formally in [33] in three variants: conflict serializability, view serializability, and final-state serializability. We follow a more general version of serializability defined in [43] (as global atomicity), which we adjust to account for non-atomicity of commits in our model.
Definition 6
(Serializability) History \(H\) is serializable iff there exists some sequential history S equivalent to a completion \( Compl (H)\) such that any committed transaction in S is legal in S.
Intuitively, the definition does not preclude prerelease, as long as illegal transactions are aborted. Serializability also makes no further stipulations on aborting transactions, so it permits both overwriting and cascading aborts.
Lemma 1
Serializability supports prerelease.
Proof
Let \(H\) be a transactional history as shown in Fig. 4. Note that since all transactions in \(H\) are committed or aborted then \(H= Compl (H)\). Then, let there be a sequential history \(\hat{S}_{H}= H|T_i \cdot H|T_j \cdot H|T_{k}\). Note that \(\hat{S}_{H}\equiv H\). Trivially, all the committed transactions, \(T_i\) and \(T_k\), in \(\hat{S}_{H}\) are legal in \(\hat{S}_{H}\), so \(H\) is serializable. Since, by Definition 2, \(T_i\) prereleases a variable in \(H\), then, by Definition 3, serializability supports prerelease. \(\square \)
Lemma 2
Serializability supports overwriting.
Proof
Let \(H\) be a serializable history as in the proof of Lemma 1 above. Transaction \(T_i\) writes 1 to \( x \) in \(H\) prior to \(T_j\) reading 1 from \( x \), and subsequently \(T_i\) writes 2 to \( x \). Thus, according to Definition 4, serializability supports overwriting. \(\square \)
Lemma 3
Serializability supports aborting prerelease.
Proof
Let \(H\) be a history such as the one in Fig. 5. Since all transactions in \(H\) are committed or aborted then \(H= Compl (H)\). Then, let \(\hat{S}_{H}\) be a sequential history equivalent to \(H\) such that \(\hat{S}_{H}= H|T_i \cdot H|T_j \cdot H|T_{k}\). \(\hat{S}_{H}\) contains only one committed transaction \(T_{k}\), which is trivially legal in \(\hat{S}_{H}\). Thus \(H\) is serializable. In addition, transaction \(T_i\) in \(\hat{S}_{H}\) both prereleases \( x \) (by Definition 2) and contains an abort (\( A _i \in H|T_i\)). Thus, by Definition 5, serializability supports aborting prerelease. \(\square \)
There is also a variant of serializability called strict serializability that adds the condition that the witness history S which justifies the serializability of history \(H\) must also preserve the real-time order of \(H\). The results above trivially extend to this variant.
4.2 Commitment order preservation
Commitment order preservation (CO) is a database consistency condition, which requires that transactions commit in the same order as the order in which the transactions accessed variables. It is often used as an additional condition to serializability. Formally, CO is defined as follows (adapted from [44]):
Definition 7
(Commitment Order Preservation) History \(H\) preserves commitment order iff for any two committed conflicting transactions \(T_i, T_j \,{\in }\, H\) s.t. \(i\,{\ne }\, j\) given any pair of conflicting operation executions \( op _i \in H|T_i\) and \( op _j\in H|T_j\), either \( op _i \prec _H op _j\) and \( res _{i}^{}( C _i) \prec _H res _{j}^{}( C _j)\), or \( op _j \prec _H op _i\) and \( res _{j}^{}( C _j) \prec _H res _{i}^{}( C _i)\).
CO maintains the order of their commits with respect to the order in which they access operations, but it makes no stipulations regarding aborted transactions, which allows them to read from live transactions. Thus, prerelease is generally allowed under commit ordering.
Lemma 4
Commitment order supports prerelease.
Proof
Let \(H\) be a transactional history as shown in Fig. 4. Here, all operations in \(T_i\) conflict with all operations in \(T_j\), and all operations in \(T_i\) conflict with all operations in \(T_k\). In addition, transactions \(T_i\) and \(T_k\) commit. Since \(T_k\) performs its operations on the shared variable after \(T_i\), then \(T_k\) must commit after \(T_i\). Since this is the case, \(H\) preserves commitment order (Definition 7). Since, by Definition 2, \(T_i\) prereleases a variable in \(H\), then, by Definition 3, commit ordering supports prerelease. \(\square \)
Lemma 5
Commitment order supports overwriting.
Proof
By analogy to Lemma 4. \(\square \)
Lemma 6
Commitment order supports aborting prerelease.
Proof
Let \(H\) be a history such as the one in Fig. 5. Here, only transaction \(T_k\) commits, so trivially, the history preserves commitment order by Definition 7. Transaction \(T_i\) in \(H\) prereleases \( x \) (Definition 2) and contains an abort (\( A _i \in H|T_i\)). Thus, by Definition 5, CO supports aborting prerelease. \(\square \)
Note that, a composition of CO with either serializability or recoverability (see below) trivially also allows prerelease, overwriting, and aborting prerelease.
4.3 Recoverability
Recoverability is another database consistency condition used in conjunction with serializability. Recoverability requires that transactions only commit after other transactions whose changes they read have committed. It is defined as below (following [18]):
Definition 8
(Recoverability) History \(H\) is recoverable iff for any \(T_i, T_j \in H\), s.t. \(i\ne j\) and \(T_j\) reads from \(T_i\), \(T_i\) commits in H before \(T_j\) commits.
Recoverability requires that transactions only commit after other transactions, whose changes they read, have committed, which does not impinge on the ability to prerelease.
Lemma 7
Recoverability supports prerelease.
Proof
Let \(H\) be a transactional history as shown in Fig. 4. Here, transaction \(T_j\) reads from \(T_i\) and \(T_k\) reads from \(T_i\), and no other transactions are in the reads-from relation. If \(H\) is recoverable, then, by Definition 8, \(T_i\) must commit before \(T_j\) commits and before \(T_k\) commits. This condition is true for \(T_i\) and \(T_j\), since \(T_j\) never commits. The condition is trivially true for \(T_i\) and \(T_k\). Hence, \(H\) is recoverable. Since, by Definition 2, \(T_i\) prereleases a variable in \(H\), then, by Definition 3, recoverability supports prerelease. \(\square \)
Lemma 8
Recoverability supports overwriting.
Proof
By analogy to Lemma 7. \(\square \)
Lemma 9
Recoverability supports aborting prerelease.
Proof
Let \(H\) be a history such as the one in Fig. 5. Here, transaction \(T_j\) reads from \(T_i\) and no other transactions are in the reads-from relation. Since \(T_i\) and \(T_j\) both abort, then, the condition in Definition 8 is trivially true for \(H\). Hence, \(H\) is recoverable. Transaction \(T_i\) in \(H\) prereleases \( x \) (Definition 2) and contains an abort (\( A _i \in H|T_i\)). Thus, by Definition 5, recoverability supports aborting prerelease. \(\square \)
Note that, a composition of recoverability and serializability or commitment order preservation also allows prerelease, overwriting, and aborting prerelease.
4.4 Cascadelessness
Cascadelessness (also known as avoiding cascading aborts or rollbacks—ACA, ACR) is a database consistency condition that is used to exclude scenarios where one aborting transaction \(T_i\) forces another transaction \(T_j\) to abort, because \(T_j\) read from \(T_i\) before \(T_i\) aborted. It is used to impose additional requirements on serializable executions. It is defined as follows (after [8]):
Definition 9
(Cascadelessness) History \(H\) is cascadeless iff for any \(T_i, T_j \in H\) s.t. \(i\ne j\) and \(T_j\) reads from \(T_i\), \(T_i\) commits before the read.
Cascadelessness restricts reading from live transactions. Therefore, cascadelessness clearly removes all the scenarios encompassed by Definition 2. Since this is the only provision of cascadelessness, the property forbids prerelease without giving any additional guarantees. Hence, it also does not support overwriting nor aborting prerelease.
Lemma 10
Cascadelessness does not support prerelease.
Proof
By contradiction let us assume that cascadelessness supports prerelease. Then, from Definition 3, there exists some cascadeless history \(H\), s.t. there exists some transaction \(T_i \in H\) that prereleases some variable \( x \) in \(H\). From Definition 2, this implies that there exists some prefix P of \(H\) s.t.
-
(a)
there is an operation execution \( op _i = w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) and \( op _i \in P|T_i\),
-
(b)
there exists a transaction \(T_j \in P\) (\(i\ne j\)) and an operation execution \( op _j = r _{j}({ x })\!\rightarrow \!{ v }\), s.t. \( op _j \in P|T_j\) and \( op _i\) precedes \( op _j\) in P,
-
(c)
\(T_i\) is live in P.
These imply that \( op _j\) follows \( op _i\) in P in such a way that there does not exist in P an operation \( op _c = tryC _i\rightarrow C _i\) in P s.t. \( op _c \prec _P op _j\). Therefore, such \( op _c\) does not exist in \(H\) either. This contradicts Definition 9, which dictates that \(T_i\) must commit before \(T_j\) reads from \(T_i\), so \(H\) is not cascadeless, which is a contradiction. \(\square \)
Since both Definitions 4 and 5 require prerelease support, then:
Corollary 1
Cascadelessness does not support overwriting.
Corollary 2
Cascadelessness does not support aborting prerelease.
4.5 Strictness
Strictness [8] is a strong database property that, given a write in one transaction, and some other following operation in another transaction, that second operation can only be executed if the transaction executing the write already committed or aborted. Formally:
Definition 10
(Strictness) History \(H\) is strict iff for any \(T_i, T_j \in H\) (\(i\ne j\)) and given any operation execution \( op _i = r _{i}^{}( x )\!\rightarrow \!{v}\) or \( op _i = w _{i}^{}({ x }){v'}\!\rightarrow \!{ ok _i}\) in \(H|T_i\), and any operation execution \( op _j = w _{j}^{}({ x }){v}\!\rightarrow \!{ ok _j}\) in \(H|T_j\), if \( op _i\) follows \( op _j\), then \(T_j\) commits or aborts before \( op _i\).
The definition unequivocally states that a transaction cannot read from another transaction, until the latter is committed or aborted. Thus, strictness precludes prerelease altogether.
Lemma 11
Strictness does not support prerelease.
Proof
By contradiction let us assume that strictness supports prerelease. Then, from Definition 3, there exists some history \(H\), s.t. \(H\) is strict and there exists some transaction \(T_i \in H\) that prereleases some variable \( x \) in \(H\). From Definition 2, this implies that there exists some prefix P of \(H\) s.t.
-
(a)
there is an operation execution \( op _i = w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) and \( op _i \in P|T_i\),
-
(b)
there exists a transaction \(T_j \in P\) (\(i\ne j\)) and an operation execution \( op _j = r _{j}({ x })\!\rightarrow \!{ v }\), s.t. \( op _j \in P|T_j\) and \( op _i\) precedes \( op _j\) in P,
-
(c)
\(T_i\) is live in P.
These imply that \( op _j\) follows \( op _i\) in P in such a way that there does not exist in P an operation \( op _c\) that returns either \( A _i\) or \( C _i\) and \( op _i \prec _P op _c \prec _P op _j\). Therefore, there does not exist an operation \( op _c\) in \(H\) that returns either \( A _i\) or \( C _i\) and \( op _i \prec _H op _c \prec _H op _j\). This contradicts Definition 10, so \(H\) is not strict, which is a contradiction. \(\square \)
Since both Definitions 4 and 5 require prerelease support, then:
Corollary 3
Strictness does not support overwriting.
Corollary 4
Strictness does not support aborting prerelease.
Note, that while strictness does not allow prerelease as defined by Definition 2, it allows for parallel execution of reads by live transactions which can be considered a limited form of prerelease (e.g. [21]).
4.6 Opacity
Opacity [16, 17] can be considered the standard TM safety property that guarantees serializability and preservation of real-time order, and prevents reading from live transactions. It is defined by the following two definitions. The first definition specifies final state opacity that ensures the appropriate guarantees for a complete transactional history. The second definition uses final state opacity to define a safety property that is prefix-closed. Both definitions follow those in [17].
Definition 11
(Final state opacity) A finite TM history \(H\) is final-state opaque if, and only if, there exists a sequential history S equivalent to any completion of \(H\) s.t.,
-
(a)
S preserves the real-time order of \(H\),
-
(b)
every transaction \(T_i\) in S is legal in S.
Definition 12
(Opacity) A TM history \(H\) is opaque if, and only if, every finite prefix of \(H\) is final-state opaque.
This definition of opacity forbids reading from live transactions, so it precludes any use of prerelease whatsoever.
Lemma 12
Opacity does not support prerelease.
Proof
By contradiction let us assume that opacity supports prerelease. Then, from Definition 3, there exists some history \(H\) (with unique writes), s.t. \(H\) is opaque and there exists some transaction \(T_i \in H\) that prereleases some variable \( x \) in \(H\).
From Definition 2, this implies that there exists some prefix P of \(H\) s.t.
-
(a)
there is an operation execution \( op _i = w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) and \( op _i \in P|T_i\),
-
(b)
there exists a transaction \(T_j \in P\) (\(i\ne j\)) and an operation execution \( op _j = r _{j}({ x })\!\rightarrow \!{ v }\), s.t. \( op _j \in P|T_j\) and \( op _i\) precedes \( op _j\) in P,
-
(c)
\(T_i\) is live in P.
Let \(P_c\) be any completion of P. Since \(T_i\) is live in P, by definition of completion, it is necessarily aborted in \(P_c\) (ie. \(A_i \in P_c|T_i\)). Given any sequential history \({\hat{P}}_c\) equivalent to \(P_c\), since \(T_i\) is aborted in \({\hat{P}}_c\) and \( Vis ({\hat{P}}_c, T_j)\) only contains operations of committed transactions, then \(P_c|T_i \nsubseteq Vis ({\hat{P}}_c, T_j)\). This means that \( op _j \in Vis ({\hat{P}}_c, T_j)\) but \( op _i \not \in Vis ({\hat{P}}_c, T_j)\), so \( Vis ({\hat{P}}_c, T_j) \nsubseteq Seq ( x )\) and therefore \( Vis ({\hat{P}}_c, T_j)\) is not legal.
On the other hand, Definition 12 implies that any prefix P of \(H\) is final state opaque, which, by Definition 11, implies that there exists some completion \(P_c\) of P for which there exists an equivalent sequential history \({\hat{P}}_c\) s.t., any \(T_j\) in \({\hat{P}}_c\) is legal in \({\hat{P}}_c\). Since any \(T_j\) is legal in \({\hat{P}}_c\) then for all \(T\), \( Vis ({\hat{P}}_c, T)\) is also legal. But this is a contradiction with the paragraph above. Thus, there cannot exist a history like \(H\) that is both opaque and contains a transaction that prereleases some variable. \(\square \)
Since both Definitions 4 and 5 require prerelease support, then:
Corollary 5
Opacity does not support overwriting.
Corollary 6
Opacity does not support aborting prerelease.
It is worth noting that opacity precludes reading from live transactions even if the read can be performed safely. For instance, a transaction that writes a value, does not overwrite it, and is guaranteed to eventually commit by the implementation, still cannot expose this value to other transactions before the writer transaction commits.
4.7 Markability
Markability [29] is a TM safety property equivalent to opacity (i.e. every opaque history is markable, and every markable history is opaque) introduced as a simpler way to prove opacity. Since every markable history is opaque, then it follows from Lemma 12, and Corollaries 5 and 6, that:
Corollary 7
Markability does not support prerelease.
Corollary 8
Markability does not support overwriting.
Corollary 9
Markability does not support aborting prerelease.
4.8 Rigorousness
Rigorousness is a strong database property which requires that given any two transactions executing operations on the same variable, the latter of them cannot execute any operations until the former commits or aborts. It is defined as a condition added onto strictness, as follows (following [10]):
Definition 13
(Rigorousness) History \(H\) is rigorous iff it is strict and for any \(T_i, T_j \in H\) (\(i\ne j\)) such that \(T_i\) writes to variable \( x \), i.e., \( op _i = w _{i}({ x }){v}\!\rightarrow \!{ ok _i} \in H|T_i\) after \(T_j\) reads \( x \), then \(T_j\) commits or aborts before \( op _i\).
Since in [5] the authors demonstrate that rigorous histories are opaque, and since we show in Lemma 12 and Corollaries 5 and 6 that opaque histories do not support prerelease, then neither does rigorousness.
Corollary 10
Rigorousness does not support overwriting.
Corollary 11
Rigorousness does not support overwriting.
Corollary 12
Rigorousness does not support aborting prerelease.
4.9 Transactional memory specification
In [13] the authors argue that some scenarios, such as sharing variables between transactional and non-transactional code, require additional safety properties. Thus, they propose and rigorously define two consistency conditions for TM: transactional memory specification 1 (TMS1) and transactional memory specification 2 (TMS2).
TMS1 follows a set of design principles including a requirement for observing consistent behavior that can be justified by some serialization. Among others, TMS1 also requires that partial effects of transactions are hidden from other transactions. These principles are reflected in the definition of the TMS1 automaton. We paraphrase only parts relevant to our further discussion, i.e. the condition for the correctness of an operation’s response in the following definitions (see the definitions of extConsPrefix and validResp for TMS1 in [13]).
Given history \(H\) and some response event r in H, let \(H\!\!\uparrow \!\!r\) denote a subhistory of \(H\), s.t. for every operation execution \( op \in H\), \( op \in H\!\!\uparrow \!\!r\) iff \( op \prec _H r\) and op is complete. This represents all operations executed “thus far,” when considering the legality of r.
Let \(\mathbb {T}^c_H\) be the set of all such transactions that \(T_k \in \mathbb {T}^c_H\) iff \(T_k \in H\) and \( inv _{k}^{}( tryC _k) \in H|T_k\) (or \( inv _{k}^{}( tryA _k) \in H|T_k\)). This set represent transactions which either committed or aborted (i.e., transactions that are not live). Given response event r, let \(\mathbb {T}^c_H\!\!\uparrow \!\!r\) be the set of all transactions in \(H\) s.t. \(T_k \in \mathbb {T}^c_H\!\!\uparrow \!\!r\) if \(T_k \in \mathbb {T}^c_H\) and \( inv _{k}^{}( tryC _k) \prec _{H} r\). This set represents all transactions that either committed or aborted before response event r.
Given some history \(H\), let \(\mathbb {T}_H'\) by any subset of transactions in \(H\). Let \(\sigma \) be a sequence of transactions. Let \(\textit{ser}(\mathbb {T}_H', \prec _{H})\) be a set of all sequences of transactions s.t. \(\sigma \in \textit{ser}(\mathbb {T}_H', \prec _{H})\) if \(\sigma \) contains every element of \(\mathbb {T}_H'\) exactly once, and, for any \(T_i, T_j \in \mathbb {T}_H'\), if \(T_i \prec _{H} T_j\) then \(T_i\) precedes \(T_j\) in \(\sigma \).
Given a history H and some response event r in H, let \(\textit{ops}(\sigma , r)\) be a sequence of operations s.t. if \(\sigma = [ T_1, T_2, \ldots , T_n]\) then \(\textit{ops}(\sigma , r) = H\!\!\uparrow \!\!r|T_1 \cdot H\!\!\uparrow \!\!r|T_2 \cdot \ldots \cdot H\!\!\uparrow \!\!r|T_n\). This represents the sequential history prior to response event r that respects a specific order of transactions defined by \(\sigma \).
The most relevant condition in TMS1 with respect to our further discussion is the validity condition of individual response operations. A prerequisite for checking validity is to check whether a response event can be justified by some externally consistent prefix. This prefix consists of operations from all transactions that precede the response event and whose effects are visible to other transactions. Specifically, if a transaction precedes another transaction in the real time order, then it must be both committed and included in the prefix, or both not committed and excluded from the prefix. However, if a transaction does not precede another transaction, it can be in the prefix regardless of whether it committed or aborted.
Definition 14
(Externally Consistent Prefix) Given a history \(H\) and a response event r, let the externally consistent prefix \(\mathbb {T}^r_H\) be any subset of all transactions in \(H\) s.t. for any \(T_i, T_j \in \mathbb {T}^r_H\), if \(T_i \prec _HT_j\) then \(T_i\) is in \(\mathbb {T}^r_H\) iff \( res _{i}^{}( C _i) \in H\!\!\uparrow \!\!r|T_i\).
TMS1 specifies that each response to an operation invocation in a safe history must be valid. Intuitively, a valid response event is one for which there exists a sequential prefix that is both legal and meets the conditions of an externally consistent prefix. More precisely, the following condition must be met:
Definition 15
(Valid Response) Given a transaction \(T_i\) in \(H\), we say the response r to some operation invocation e in \(H|T_i\) is valid if there exists set \(\mathbb {T}^r_H\subseteq \mathbb {T}^c_H\!\!\uparrow \!\!r\) and sequence \(\sigma \in \textit{ser}(\mathbb {T}^r_H, \prec _{H})\) s.t. \(\mathbb {T}^r_H\) satisfies Definition 14 and \(\textit{ops}(\sigma \cdot T_i, r) \cdot [e \rightarrow r]\) is legal.
Intuitively, TMS1 specifies that each response to an operation in a safe history must be valid (Definition 15), which means it is explained by a sequential prefix that is both legal and meets the conditions of an externally consistent prefix (Definition 14). Since the externally consistent prefix excludes live transactions, then TMS1 does not allow prerelease in general. More formally:
Lemma 13
TMS1 does not support prerelease.
Proof
Assume by contradiction that TMS1 supports prerelease. Then by Definition 3, there exists some TMS1 history \(H\) s.t. \(T_i,T_j \in H\) and there is a prefix P of \(H\) s.t. \( op _i = w _{i}({ x }){ v }\!\rightarrow \!{ ok _i} \in P|T_i\), \( op _j = r _{j}({ x })\!\rightarrow \!{ v } \in P|T_j\), and \(T_i\) is live in \(H\). This implies that \( inv _{i}^{}( tryC _i) \not \in P\!\!\uparrow \!\! res _{j}^{}( v )|T_i\). This means that \(T_i \not \in \mathbb {T}^c_H\) and therefore is not in any \(\mathbb {T}_{H}' \subseteq \mathbb {T}^c_H\) or, by extension, is not in any \(\sigma \in \textit{ser}(\mathbb {T}_{H}', \prec _{H})\). Therefore, there is no \( op _i\) in \(\textit{ops}(\sigma , res _{j}^{}( v ))\), so, assuming unique writes, \( op _j\) is not preceded by a write of \( v \) to \( x \) in \(\textit{ops}(\sigma \cdot T_j, res _{j}^{}( v )) \cdot [ r _{j}({ x })\!\rightarrow \!{ v } ]\). Therefore, \(\textit{ops}(\sigma \cdot T_j, res _{j}^{}( v )) \cdot [ r _{j}({ x })\!\rightarrow \!{ v } ]\) is not legal, which contradicts Definition 15. \(\square \)
Since both Definitions 4 and 5 require prerelease support, then:
Corollary 13
TMS1 does not support overwriting.
Corollary 14
TMS1 does not support aborting prerelease.
TMS2 is a stricter, but more intuitive version of TMS1. Since the authors show in [13] that TMS2 is strictly stronger than TMS1 (TMS2 implements TMS1), the conclusions above equally apply to TMS2. Hence, from Lemma 13:
Corollary 15
TMS2 does not support prerelease.
Corollary 16
TMS2 does not support overwriting.
Corollary 17
TMS2 does not support aborting prerelease.
4.10 Virtual world consistency
The requirements of opacity, while very important in the context of TM’s ability to execute any operation transactionally, can often be excessively stringent. On the other hand serializability is considered too weak for many TM applications. Thus, a weaker TM consistency condition called virtual world consistency (VWC) was introduced in [23, 24].
Let us first define a partial order \(\prec ^{\textit{PO}}_H\) on the set of all transactions in \(H\). Given two transactions \(T_i, T_j \in H\), \(T_i \prec ^{\textit{PO}}_HT_j\) if:
-
(a)
\(T_i\) and \(T_j\) are executed by the same process \(p_k\) and \( res _{i}^{k}( C _i) \prec _H inv _{j}^{k}( start _j)\), or
-
(b)
\(T_j\) reads from \(T_i\), or
-
(c)
there exists some \(T_l \in H\) such that \(T_i \prec ^{\textit{PO}}_HT_l\) and \(T_l \prec ^{\textit{PO}}_HT_j\).
The authors of the property remark further that there is no \(\prec ^{\textit{PO}}_H\) relation between \(T_i\) and \(T_j\) (\(T_i \prec ^{\textit{PO}}_HT_j\)) if \(T_i\) is aborted (where \(T_j\) can commit or abort). We say sequential history S is a linear extension of \(H\) if \(S \equiv H\) and the order of transactions in S preserves the partial order \(\prec ^{\textit{PO}}_H\), i.e., \(\prec ^{\textit{PO}}_H\subseteq \prec _S\). Then, the causal past \(C(H, T_i)\) of some transaction \(T_i\) in some history \(H\) is such a history that includes \(T_i\) (i.e. \(H|T_i \subseteq C(H, T_i)\) and includes every \(T_j\) (i.e. \(H|T_j \subseteq C(H, T_i)\) s.t. \(T_j \prec ^{\textit{PO}}_HT_i\).
Definition 16
(Virtual World Consistency) History \(H\) is virtual world consistent iff its subhistory containing all committed transactions is serializable and preserves real-time order, and for each aborted transaction \(T_i\) there exists a linear extension S of its causal past \(C(H, T_i)\) that is legal.
VWC allows limited support for prerelease as follows.
Lemma 14
VWC supports prerelease.
Proof
Let \(H\) be a transactional history as shown in Fig. 6. Here, \(T_i\) performs two operations on \( x \) and one on \( y \), while \(T_j\) reads \( x \). The sequential witness history of \(H\) is \(S = H|T_i \cdot H|T_j\) wherein both transactions are committed and trivially legal. Thus \(H\) is VWC. Since, by Definition 2, \(T_i\) prereleases a variable in \(H\), then, by Definition 3, VWC supports prerelease. \(\square \)
Lemma 15
VWC does not support overwriting.
Proof
Since VWC requires that aborting transactions view a legal causal past, then, if a transaction reading \( x \) is aborted, it must read a legal (i.e. “final”) value of \( x \). Thus, let us consider some history \(H\) (with unique writes) where some \(T_i\) writes value \( v \) to \( x \) and prereleases \( x \), and some \(T_j\) reads \( v \) from \( x \) (so \(T_j\) reads from \(T_i\)).
-
(a)
If \(T_i\) writes some value \( v '\) to \( x \) after releasing it, and \(T_j\) commits, then \(T_j\) is not legal in any sequential witness history \(\hat{S}_{H}\) of \(H\) because there is another write operation execution in \(\hat{S}_{H}\) writing \( v '\) to \( x \) between a write writing \( v \) to \( x \) and a read on \( x \) returning \( v \), and therefore \(H\) does not satisfy VWC.
-
(b)
If \(T_i\) writes some value \( v '\) to \( x \) after releasing it, and \(T_j\) aborts, then the causal past \(C(H,T_j)\) contains \(T_i\), and \(T_j\) is illegal in \(C(H,T_j)\), because there is another write operation execution writing \( v '\) to \( x \) between a write writing \( v \) to \( x \) and a read on \( x \) returning \( v \), so \(C(H,T_j)\) is not legal. Thus, \(H\) does not satisfy VWC.
Therefore, any history \(H\) containing \(T_i\), such that \(T_i\) prereleases \( x \) and modifies it after release does not satisfy VWC. Hence, by Definition 4, VWC does not support overwriting. \(\square \)
Lemma 16
VWC does not support aborting prerelease
Proof
Given a history \(H\) that satisfies VWC and a transaction \(T_i \in H\) that prereleases variable \( x \) in \(H\), let us assume for the sake of contradiction that \(T_i\) eventually aborts. By Definition 2, there is some \(T_j\) in \(H\) that reads from \(T_i\). If \(T_i\) eventually aborts, then \(T_j\) reads from an aborted transaction.
-
(a)
If \(T_j\) eventually aborts, then its causal past \(C(H, T_j)\) does not contain aborted transaction \(T_i\) and is, therefore, trivially illegal. Hence \(H\) does not satisfy VWC, which is a contradiction.
-
(b)
If \(T_j\) eventually commits, then the sequential witness history is also illegal. Hence \(H\) does not satisfy VWC, which is a contradiction.
Therefore, if \(T_i\) eventually aborts, \(H\) does not satisfy VWC, which is a contradiction. Thus, since a VWC history cannot contain an abortable transaction that prereleases a variable, by Definition 5, VWC does not support aborting prerelease. \(\square \)
While VWC supports prerelease, there are severe limitations to this capability. That is, VWC does not allow a transaction that prereleased variables to subsequently abort for any reason. In addition, VWC places a requirement on transactions to execute all read operations before executing any of its writes. This places severe practical limitations on how programmers write transactional code.
4.11 Live opacity
Live opacity was introduced in [14] as part of a set of consistency conditions and safety properties that were meant to regulate the ability of transactions to read from live transactions. The work analyzes a number of properties and for each one presents a commit oriented variant that forbids prerelease and a live variant that allows it. Here, we concentrate on live opacity, since it best fits alongside the other properties presented here, however our conclusions will apply to the remainder of live properties. Intuitively, live opacity works by removing all write operations and local read operations from uncommitted transactions in a history and checking if the resulting history is opaque.
Let \(H|(T_i, r)\) be the longest subsequence of \(H|T_i\) containing only read operation executions (possibly pending), with the exclusion of the last read operation if its response event is \( A _i\). Let \(H|(T_i, gr)\) be a subsequence of \(H|(T_i, r)\) that contains only non-local read operation executions. Let \(T_i^r\) be a transaction that invokes the same transactional operations as those invoked in \([ start _i\rightarrow ok _i] \cdot H|(T_i, r) \cdot [ inv _{i}^{}( tryC _i)]\) if \(H|(T_i, r) \ne \varnothing \), or \(\varnothing \) otherwise. Let \(T_i^{\textit{gr}}\) be a transaction that invokes the same transactional operations as those invoked in \([ start _i\rightarrow ok _i] \cdot H|(T_i, \textit{gr}) \cdot [ tryC _i \rightarrow C _i]\) if \(H|(T_i, \textit{gr}) \ne \varnothing \), or \(\varnothing \) otherwise.
Given a history \(H\), a transaction \(T_i \in H\), and a complete local operation execution \( op = r _{i}({ x })\!\rightarrow \!{ v }\), we say the latter’s response event \( res _{i}^{}( v )\) is legal if the last preceding write operation in \(H|T_i\) writes \( v \) to \( x \). We say sequential history S justifies the serializability of history \(H\) when there exists a history \(H'\) that is a subsequence of \(H\) s.t. \(H'\) only contains invocation and response events issued and received by transactions committed in \(H\), and S is a legal history equivalent to \(H'\).
Definition 17
(Live Opacity) A history \(H\) is live opaque iff, there exists a sequential history S that preserves the real time order of \(H\) and justifies that \(H\) is serializable and all of the following hold:
-
(a)
We can extend history S to get a sequential history \(S'\) such that:
-
for each transaction \(T_i \in H\) s.t. \(T_i \not \in S\), \(T_i^{\textit{gr}} \in S'\),
-
if < is a partial order induced by the real time order of S in such a way that for each transaction \(T_i \in H\) s.t. \(T_i \not \in S\) we replace each instance of \(T_i\) in the set of pairs that constitute the real time order relation of \(H\) with transaction \(T_i^{\textit{gr}}\), then \(S'\) respects <,
-
\(S'\) is legal.
-
-
(b)
For each transaction \(T_i \in H\) s.t. \(T_i \not \in S\) and for each operation \( op \) in \(T_i^{r}\) that is not in \(T_i^{\textit{gr}}\), the response for \( op \) is legal.
Live opacity is a variant of opacity specifically introduced to allow prerelease, but only for non-aborting transactions. We show this below.
Lemma 17
Live opacity supports prerelease.
Proof
Let history \(H\) be that represented in Fig. 7. Since there is a transaction \(T_i \in H\) that writes 1 to \( x \) and a transaction \(T_j\) that reads 1 from \( x \) before \(T_i\) commits, then there is a prefix P of \(H\) that meets Definition 2. Therefore \(T_i\) prereleases \( x \) in \(H\).
Let S be a sequential history s.t. \(S = H|T_i \cdot H|T_j\). Since the real-time order of H is \(\varnothing \), then, trivially, S preserves the real-time order of \(H\). Since \( Vis (S, T_i)\) contains only \(H|T_i\) and therefore only a single write operation execution and no reads, then it is legal and \(T_i\) in S is legal in S. Furthermore, \( Vis (S, T_j)\) is such that \( Vis (S, T_j) = H|T_i \cdot H|T_j\) and contains a read operation \( r _{j}({ x })\!\rightarrow \!{1}\) preceded by the only write operation \( w _{i}({ x }){1}\!\rightarrow \!{ ok _i}\), so \( Vis (S, T_j)\) is legal, and, consequently, \(T_j\) in S is legal in S. Thus, all transactions in S are legal in S, so \(H\) is serializable.
Let \(S'\) be a sequential history that extends S in accordance to Definition 17. Since there are no transactions in \(S'\) that are not in S, then \(S'=S\). Thus, since every transaction in S is legal in S, then every transaction in \(S'\) is legal in \(S'\). Trivially, \(S'\) also preserves the real time order of S. Therefore, the condition Definition 17a is met. Since there are no local read operations in S, then condition Definition 17b is trivially met as well. Therefore, \(H\) is live opaque.
Since \(H\) is both live opaque and contains a transaction that prereleases a variable, then the lemma holds. \(\square \)
Lemma 18
Live opacity does not support overwriting.
Proof
For the sake of contradiction, let us assume that there is a history (with unique writes) \(H\) that is live opaque and, from Definition 4, contains some transaction \(T_i\) that writes value \( v \) to some variable \( x \) and prereleases \( x \) and subsequently executes another write operation writing \( v '\) to \( x \) where the second write follows a read operation executed by transaction \(T_j\) reading \( v \) from \( x \).
Since \(H\) is live opaque there exists a sequential history S that justifies the serializability of \(H\). There cannot exist a sequential history S where \(T_j\) reads from \( x \) between two writes to \( x \) executed by \(T_i\), because there cannot exist a legal \( Vis (S, T_j)\), so \(T_j\) would not be legal in S. Therefore, \(T_j\) must be aborted in \(H\) and therefore \(T_j\) is not in any sequential history S that justifies the serializability of \(H\).
Since \(T_j\) is in \(H\) but not in S, then given any sequential extension \(S'\) of S in accordance to Definition 17, \(T_j\) is replaced in \(S'\) by \(T_j^{gr}\) which reads \( v \) from \( x \) and finally commits. However, since the write operation execution writing \( v \) to \( x \) in \(T_i\) is followed in \(S'|T_i\) by another write operation execution that writes \( v '\) to \( x \), then there cannot exist a \( Vis (S', T_j^{gr})\) that is legal. Thus \(T_j^{gr}\) in \(S'\) cannot be legal in \(S'\), which contradicts Definition 17a. Thus, \(H\) is not live opaque, which is a contradiction.
Therefore \(H\) cannot simultaneously be live opaque and contain a prereleasing transaction and overwriting. \(\square \)
Lemma 19
Live opacity does not support aborting prerelease.
Proof
For the sake of contradiction, let us assume that there is a history (with unique writes) \(H\) that is live opaque and, from Definition 5, contains some transaction \(T_i\) that writes value \( v \) to some variable \( x \) and releases \( x \) and subsequently aborts in \(H\).
Let S be any sequential history that justifies the serializability of \(H\), and let \(S'\) be any sequential extension of S in accordance to Definition 17. Since \(T_i\) aborts in \(H\), then it is not in S, and therefore it is replaced in \(S'\) by \(T_i^{gr}\). Since \(T_i^{gr}\) does not contain any write operation executions, there is no write operation execution writing \( v \) to \( x \) in \(S'\), by definition. Since \(T_i\) prereleased \( x \) in \(H\) there is a transaction \(T_j\) in \(H\) that executes a read operation reading \( v \) from \( x \) and the same read operation is in \(S'\). But since there is no write operation execution writing \( v \) to \( x \) in \(S'\), no transaction containing a read operation execution reading \( v \) from \( x \) can be legal in \(S'\). Thus, \(H\) is not live opaque, which is a contradiction.
Therefore \(H\) cannot be simultaneously live opaque and contain a transaction with prerelease that aborts. \(\square \)
In addition, note that, if some transaction \(T_i\) in some history \(H\) reads from a live transaction \(T_k\) and \(T_i\) is itself live, then, according to live opacity, there cannot be any transaction \(T_j\) that reads from \(T_i\). This is because if \(T_i\) is replaced in \(S'\) with \(T_i^{gr}\), then whatever value \(T_j\) reads from \(T_i\) will not be written by \(T_i^{gr}\), so the read in \(T_j\) (or \(T_j^{gr}\)) may not be legal. Transactions which prerelease are already not allowed to abort, so we consider this additional restriction to be overstrict. Transactions that read from live transactions will not experience inconsistent views regardless of whether that live transaction reads only from committed transactions or whether it reads from some yet another live transaction—all such live transactions must eventually commit. Therefore, it is not necessary for live opacity to preclude this scenario. Nevertheless, live opacity does preclude it.
4.12 Elastic opacity
Elastic opacity is a safety property based on opacity, that was introduced to describe the safety guarantees of elastic transactions [15]. The property allows to relax the atomicity requirement of transactions to allow each of them to execute as a series of smaller transactions.
An elastic transaction \(T_i\) is split into a sequence of subhistories called a cut denoted \(\mathcal {C}_{i}(H)\), where each subhistory represents a “subtransaction.” In brief, a cut that contains more than one operation execution is well-formed if all subhistories are longer than one operation execution, all the write operations within the same transaction are in the same subhistory, and the first operation execution on any variable in every subhistory is not a write operation, except possibly in the first subhistory. A well-formed cut of some transaction \(T_i\) is consistent in some history \(H\), if given any two operation executions \( op _i\) and \( op _i'\) on \( x \) in any subhistories of the cut, no transaction \(T_j\) (\(i\ne j\)) executes a write operation \( op _j\) on \( x \) s.t. \( op _i \prec _H op _j \prec _H op _i'\). In addition, given any two operation executions \( op _i\) and \( op _i'\) on \( x , y \) respectively, no two transactions \(T_k, T_l\) (\(l\ne i\), \(k\ne i\)) execute writes \( op _k\) on \( x \) and \( op _l\) on \( y \), s.t. \( op _i \prec _H op _k \prec _H op _i'\) and \( op _i \prec _H op _l \prec _H op _i'\). A cutting function \(f_\mathcal {C}\) takes a history \(H\) as an argument and produces a new history \(H_f\) where for each transaction \(T_i \in H\) declared as elastic, \(T_i\) is replaced in \(H_f\) with the transactions resulting from the cut \(\mathcal {C}_{i}(H)\) of \(T_i\). If some transaction is committed (aborted) in \(H\), then all transactions resulting from its cut are committed (aborted) in \(f_\mathcal {C}(H)\). Then, elastic opacity is defined as follows:
Definition 18
(Elastic Opacity) History \(H\) is elastic opaque iff there exists a cutting function \(f_\mathcal {C}\) that replaces each elastic transaction \(T_i\) in \(H\) with its consistent cut \(\mathcal {C}_{i}(H)\), such that history \(f_\mathcal {C}(H)\) is opaque.
Note that the authors demonstrate in [15] that if, for some initial history \(H\), the history \(f_\mathcal {C}(H)\) is opaque, then it does not necessarily mean that H is serializable. Thus, elastic opacity is not strictly stronger than serializability.
Elastic opacity (Definition 18) checks the validity of a history, not by validating the consistency of transactions, but of fragments of transactions. Hence, elastic opacity supports prerelease. A formal demonstration follows.
Lemma 20
Elastic opacity supports prerelease.
Proof
Let \(H\) be a transactional history with unique writes as shown in Fig. 8. Let \(T_i\) be an elastic transaction. Let \(\mathcal {C}_{i}(H)\) be a cut of subhistory \(H|T_i\), such that:
All subhistories of \(\mathcal {C}_{i}(H)\) are longer than one operation, all the writes are in the first subhistory, and no subhistory starts with a write, so \(\mathcal {C}_{i}(H)\) is well-formed. Since there are no write operations outside of \(T_i\), then it follows that \(\mathcal {C}_{i}(H)\) is a consistent cut in \(H\). Let \(f_\mathcal {C}\) be any cutting function such that it cuts \(T_i\) according to \(\mathcal {C}_{i}(H)\), in which case \(f_\mathcal {C}(H)\) is defined as in Fig. 9. Let S be a sequential history s.t. \(S = f_\mathcal {C}(H)|T_{i'} \cdot f_\mathcal {C}(H)|T_{j} \cdot f_\mathcal {C}(H)|T_{i''}\). Since \(T_{i'}\) precedes \(T_{i''}\) in S as well as in \(f_\mathcal {C}(H)\), and all other transactions are not real time ordered, S preserves the real time order of \(f_\mathcal {C}(H)\). Trivially, each transaction in S is legal in S. Thus, \(f_\mathcal {C}(H)\) is opaque by Definition 12, and in effect \(H\) is elastic opaque by Definition 18. Since in \(H\) transaction \(T_j\) reads \( x \) from \(T_i\) while \(T_i\) is live, then, by Definition 2, \(T_i\) prereleases \( x \) in \(H\). Hence, since \(H\) is elastic opaque, elastic opacity supports prerelease, by Definition 3. \(\square \)
Lemma 21
Elastic opacity does not support overwriting.
Proof
For the sake of contradiction, let us assume that there is an elastic opaque history \(H\), s.t. transaction \(T_i\) writes value \( v \) to some variable \( x \) and prereleases it in \(H\). Furthermore, let us assume that there is overwriting, so after some transaction \(T_j\) reads \( v \) from \( x \), \(T_i\) writes \( u \) to \( x \). Since only elastic transactions can prerelease in elastic opaque histories, and \(T_i\) prereleases a variable, \(T_i\) is necessarily elastic. Thus, in any \(f_\mathcal {C}(H)\) \(T_i\) is replaced by a cut \(\mathcal {C}_{i}(H)\).
The two writes on \( x \) in \(T_i\) are either a) in two different subhistories in \(\mathcal {C}_{i}(H)\), or b) in the same subhistory in \(\mathcal {C}_{i}(H)\). Since the definition of a consistent cut requires all writes on a single variable to be within one subhistory of the cut, then in case (a), \(\mathcal {C}_{i}(H)\) is inconsistent. Since by Definition 18 elastic opaque histories are created using consistent cuts, then \(H\) is not elastic opaque, which is a contradiction.
In the case of (b), let us say that both writes are in a subhistory that is converted into transaction \(T_{i'}\) in \(f_\mathcal {C}(H)\). Since \(T_i\) prereleases \( x \), then by Definition 2, there is a transaction \(T_{j'}\) in \(f_\mathcal {C}(H)\) which executes a read on \( x \) reading the value written by \(T_{i'}\) in \(f_\mathcal {C}(H)\). Since we assume overwriting, the read operation on \( x \) in \(T_{j'}\) reads the value written by the first of the two writes in \(T_{i'}\) and does so before the other write on \( x \) is performed within \(\mathcal {C}_{H}(i)\). Then, in any sequential history S equivalent to \(f_\mathcal {C}(H)\) either \(T_{j'} \prec _S T_{i'}\) or \(T_{i'} \prec _S T_{j'}\). In the former case \(T_{j'}\) in S is not legal in S, since the read on \( x \) that yields value \( v \) will not be preceded by any operation that writes \( v \) to \( x \) in any possible \( Vis (S, T_{j'})\). In the latter case \(T_{j'}\) in S is also not legal in S, since there will be a write operation writing \( u \) to \( x \) between the read on \( x \) that yields value \( v \) and any operation that writes \( v \) to \( x \) in \( Vis (S, T_{j'})\). Since \(T_{j'}\) in S is not legal in any S equivalent to \(f_\mathcal {C}(H)\), then, by Definition 11, \(f_\mathcal {C}(H)\) is not final-state opaque, and hence, by Definition 12, not opaque. In effect, by Definition 18, \(H\) is not opaque, which is a contradiction.
Thus, there cannot be an elastic opaque history \(H\) with overwriting. \(\square \)
Lemma 22
Elastic opacity does not support aborting prerelease.
Proof
For the sake of contradiction, let us assume that there is an elastic opaque history \(H\) s.t. transaction \(T_i\) prereleases some variable \( x \) in \(H\) and aborts. Since \(T_i\) prereleases a variable then it writes \( v \) to \( x \), and there is another \(T_j\) that executes a read on \( x \) that returns \( v \) before \(T_i\) aborts. Since only elastic transactions can prerelease in elastic opaque histories, and \(T_i\) prereleases a variable, \(T_i\) is necessarily elastic. If \(T_i\) aborts in \(H\), then all of the transactions resulting from its cut \(\mathcal {C}_{i}(H)\) in \(f_\mathcal {C}(H)\) also abort (by construction of \(f_\mathcal {C}(H)\)). Therefore, for any sequential history S equivalent to \(f_\mathcal {C}(H)\), there is no subhistory \(H' \in \mathcal {C}_{i}(H)\) s.t. \(H' \subseteq Vis (S, T_j)\), and in effect the read operation in \(T_j\) on \( x \) reading \( v \) is not preceded by a write operation writing \( v \) to \( x \). Therefore, \( Vis (S, T_j)\) is illegal, so \(T_j\) in S is not legal in S, and thus, by Definition 12\(f_\mathcal {C}(H)\) is not opaque. Since \(f_\mathcal {C}(H)\) is not opaque, then by Definition 18, \(H\) is not elastic opaque, which is a contradiction. \(\square \)
Elastic opacity supports prerelease, but, since it does not guarantee serializability (as shown in [15]), we consider it to be a relatively weak property. This is contrary to our premise of finding a property that allows prerelease and provides stronger guarantees than serializability. It also makes elastic opacity unintuitive to programmers, and therefore less than practical.
In addition, elastic transactions, i.e. transactions described by elastic opacity, were proposed as an alternative to traditional transactions for implementing search structures. However, we submit that the restrictions placed on the composition of elastic transactions and the need for transactions with prerelease to be non-aborting put an unnecessary burden on general-purpose TM. In particular, for a cut to be well-formed, it is necessary that all writes on the same variable are executed in the same subtransaction, and that no subtransaction starts with a write, which severely limits how prerelease can be used and precludes scenarios that are nevertheless intuitively correct.
4.13 Summary
In Table 1 we present a summary of the properties discussed in this section. The table informs whether a particular property is a database property or a TM property, and whether each of the properties satisfies the definitions for prerelease support, overwriting support, and aborting prerelease support. Finally, the last column informs whether each property is at least as strong as serializability.
The survey of properties shows that, while there are many safety properties for TM with a wide range of guarantees they provide, with respect to prerelease they fall into three basic groups.
The first group consists of properties that allow prerelease but do not prevent overwriting: serializability, commit order preservation, and recoverability. These properties do not regulate what can be seen by aborting transactions. In effect, they allow any dangerous scenario to occur with respect to prerelease, as long as the situation is resolved by aborting offending transactions. As argued in [17], this is insufficient for TM in general, because operating on inconsistent state may lead to uncontrollable errors, including crashing the process.
The second group consists of properties that preclude the dangerous situations allowed by the first group. This group includes cascadelessness, strictness, rigorousness, opacity, markability, TMS1, and TMS2. The properties in this group forbid prerelease altogether, thus solving all related consistency problems, but making them unusable in conjunction with the prerelease technique.
The third group allows prerelease but precludes overwriting and reading from aborting transactions. It includes live opacity, elastic opacity, and VWC. These properties seem to provide a reasonable middle ground between allowing prerelease and eliminating inconsistent views. However, these properties forbid transactions to prerelease and abort. As such they can be useful only for TM operating in the commit-only model, or in TM systems where transactions that prerelease become irrevocable.
On the other hand the commit-only model limits the applicability of such TMs in certain contexts, since arbitrary aborts can be a necessary prerequisite for some applications. For instance, aborts are a necessary part of recovery mechanisms that bring the TM system to a consistent state as a result of a partial failure. Another example is a deadlock recovery system, which aborts transactions to eliminate wait dependency cycles. Furthermore, TM systems that provide the programmer access to arbitrary aborts are more expressive. That is, there are situations where the programmer may want to withdraw any changes made by a transaction mid-execution. Reverting changes ad hoc detracts from the readability of the code, and it is usually less efficient. The problem becomes magnified in distributed TM, where performing an ad hoc abort and compensation remotely usually comes at a price of extra network communication overhead. Thus, for DTM and TM systems in the arbitrary abort model, live opacity and VWC are not useful.
On the other hand, if transactions are allowed to abort in general, but not in the case of ones that prerelease variables, then this results in additional complexity to a TM (see e.g., [27, 45]). Moreover, in applications like distributed computing, transaction aborts may be induced by external stimuli, so it can be completely impossible to prevent transactions from aborting [41].
In addition, some of those properties also have specific problems that make them difficult to apply widely in practice. For instance, elastic opacity introduces unnecessary restrictions on the order of operations within a transaction, while simultaneously diverging from the minimal standard set by serializability. Meanwhile, live opacity arbitrarily precludes transactions that read prereleased variables from prereleasing themselves.
In summary, properties from the first group are not adequate for any TM and those from the second group do not allow any form of prerelease. The third group imposes an overstrict requirement that transactions which prerelease be irrevocable. None of the properties provide a satisfactory, strong safety property that could be used for a TM with prerelease in general. Thus, guarantees given by a TM where prerelease is a necessary component, but where transactions cannot be prevented from aborting, cannot be adequately expressed with the existing properties.
5 Last-use opacity
We present last-use opacity, a new TM safety property that provides strong consistency guarantees and allows prerelease without compromising on the ability of transactions to abort. We present an intuition behind the basic concepts and the property itself first, followed by formal definitions. We then give examples of histories that fulfill or fail to fulfill the property and finally discuss the guarantees the property gives.
5.1 Intuitions and definitions
The idea of last-use opacity hinges on two basic concepts: enforcing transactional restraint and on identifying the closing write operation execution on a given variable within the code of individual transactions.
5.1.1 Restraint
Informally, restraint specifies what actions a transaction is allowed to take after it becomes clear that it has viewed inconsistent data. A transaction that reads from a live transaction is, after all, doomed to abort as soon as that other transaction aborts. A transaction that views the state of an aborted transaction clearly should not be able to commit, but should it be allowed to write or read before it eventually aborts? While in theory some systems may allow reading or writing within such doomed transactions, the authors are not aware of any systems that do so in practice. This is because any action undertaken after the transaction becomes doomed is at best unnecessary (destined to be rolled back) and at worst have a detrimental or unexpected effect on the execution of the program. Restraint excludes such effects by requiring that doomed transactions only perform operations that lead to an abort.
Formally, given a history \(H\) containing two transactions \(T_i, T_j \in H\), \(T_i\) depends on \(T_j\) iff \(T_i\) reads from \(T_j\) or there exists \(T_k \in H\) such that \(T_k\) reads from \(T_j\) and \(T_i\) depends on \(T_k\).
Given history \(H\), a transaction \(T_i \in H\), and an event \(e \in H\), let \(\textit{after}_{H}(T_i,e)\) be the longest subsequence of \(H|T_i\) containing only such events that follow e in \(H\).
Definition 19
(Restraint) History \(H\) is restrained if given any two transactions \(T_i, T_j \in H\) s.t. \(T_i\) depends on \(T_j\), if \(T_j\) aborts (ie. \( res _{j}^{}( A ) \in H|T_j\)) then \(\textit{after}_{H}(T_i, res _{j}^{}( A ))\) is either:
-
(a)
an empty sequence,
-
(b)
a sequence containing only \( res _{i}^{}( A )\),
-
(c)
a sequence containing only a single invocation,
-
(d)
a sequence containing only a single invocation followed by \( res _{i}^{}( A )\).
In itself, restraint does not defend a transaction against executing local, non-transactional operations using data originating from inconsistent views, which may potentially lead to unanticipated operations such as going into infinite loops and dividing by zero (we will discuss this issue in Sect. 5.4). Since these operations typically cannot be controlled by the TM system, it would be impractical to have them restricted. Instead, we introduce another concept called closing writes that ensures the data leaking via inconsistent view is safe to use in local operations.
5.1.2 Closing writes
Informally, a closing write describes a point in time after which a transaction has “settled” on the state of some variable. The biggest component of this consideration is whether the variable will be modified further between a write operation and the eventual commit attempt. So, in essence, a closing write on some variable is such, that the transaction which executed it will not subsequently execute another write operation on the same variable in any possible extension of the history. What is possible is determined by the program that is being evaluated to create that history. Knowing the program, it is possible to infer (to an extent) what operations a particular transaction will execute. Hence, knowing the program, we can determine whether a particular operation on some variable is the last possible such operation on that variable within a given transaction. Thus, we can determine whether a given operation is the closing write operation in a transaction.
In addition, in a system containing invariants, some variables must be considered in groups, rather than individually. When several variables are involved in an invariant, we cannot say that the value of one of them is “settled” until all of them are. Thus, a closing write on any variable which tangled an invariant is the latest write in a given transaction on any of the variables involved in that invariant.
Take, for instance, the program in Fig. 10, where subprogram \(\mathcal {P}_1\) spawns transaction \(T_1\), and \(\mathcal {P}_2\) spawns \(T_2\). Let us assume that initially \( x \) and \( y \) are set to 0. Depending on the semantics of the TM, as these subprograms interweave during the execution, a number of histories can be produced. We can divide all of among them into two cases. In the first case \(T_2\) writes 1 to \( y \) in line 11 (in \(\mathcal {P}_2\)) and this value is then read by \(T_1\) in line 4 (in \(\mathcal {P}_1\)). As a consequence, \(T_1\) will execute the write operation in line 5. The second case assumes that \(T_1\) reads 0 in line 4 (e.g., because \(T_2\) executed line 11 much later). In this case, \(T_1\) will not execute the write operation in line 5. We can see, however, that in either of the above cases, once \(T_1\) executes the write to \( x \) in line 5, then no further writes to \( x \) will follow in \(T_1\) in any conceivable history. Thus, the write operation execution generated by line 5 is the closing write on \( x \) in \(T_1\). On the other hand, the write operation execution generated by line 3 of \(\mathcal {P}_1\) is never the closing write on \( x \) in \(T_1\), because there exists a conceivable history where another write operation execution will appear (i.e., once line 5 is evaluated). This is true even in the second of the cases, because line 5 can be executed in potentia, even if it is not executed de facto.
Given program \(\mathbb {P}\) and a set of processes \(\varPi \) executing \(\mathbb {P}\), since different interleavings of \(\varPi \) cause an execution \(\mathcal {E}({\mathbb {P}},{\varPi })\) to produce different histories, then let \(\mathbb {H}^{{\mathbb {P}},{\varPi }}\) be the set of all possible histories that can be produced by \(\mathcal {E}({\mathbb {P}},{\varPi })\), i.e., \(\mathbb {H}^{{\mathbb {P}},{\varPi }}\) is the largest possible set s.t. \(\mathbb {H}^{{\mathbb {P}},{\varPi }} = \{ H\mid H\models \mathcal {E}({\mathbb {P}},{\varPi }) \}\).
Definition 20
(Closing Write Invocation) Given a program \(\mathbb {P}\), a set of invariants  , a set of processes \(\varPi \) executing \(\mathbb {P}\), and a history \(H\) s.t. \(H\models \mathcal {E}({\mathbb {P}},{\varPi })\), an invocation \( inv _{i}^{}( w ^{}({ y }){ v })\) on some variable \( y \) by transaction \(T_i\) in \(H\) is the closing write invocation on some variable \( x \) by transaction \(T_i\) in \(H\), if \( y \in \mathbb {I}^{ x }_{i}\) and for any history \(H' \in \mathbb {H}^{{\mathbb {P}},{\varPi }}\) for which \(H\) and \(H'\) have a common prefix P ending with \( inv _{i}^{}( w ^{}({ y }){ v })\) i.e., \(P = P' \cdot [ inv _{i}^{}( w ^{}({ y }){ v }) ]\), \(H= P \cdot R\), and \(H' = P \cdot R'\), there is no write operation invocation \(\textit{inv}'= inv _{i}^{}( w ^{}({ z }){ u })\) for any variable \( z \in \mathbb {I}^{ x }_{i}\), s.t. \( inv _{i}^{}( w ^{}({ y }){ v })\) precedes \(\textit{inv}'\) in \(H'|T_i\).
, a set of processes \(\varPi \) executing \(\mathbb {P}\), and a history \(H\) s.t. \(H\models \mathcal {E}({\mathbb {P}},{\varPi })\), an invocation \( inv _{i}^{}( w ^{}({ y }){ v })\) on some variable \( y \) by transaction \(T_i\) in \(H\) is the closing write invocation on some variable \( x \) by transaction \(T_i\) in \(H\), if \( y \in \mathbb {I}^{ x }_{i}\) and for any history \(H' \in \mathbb {H}^{{\mathbb {P}},{\varPi }}\) for which \(H\) and \(H'\) have a common prefix P ending with \( inv _{i}^{}( w ^{}({ y }){ v })\) i.e., \(P = P' \cdot [ inv _{i}^{}( w ^{}({ y }){ v }) ]\), \(H= P \cdot R\), and \(H' = P \cdot R'\), there is no write operation invocation \(\textit{inv}'= inv _{i}^{}( w ^{}({ z }){ u })\) for any variable \( z \in \mathbb {I}^{ x }_{i}\), s.t. \( inv _{i}^{}( w ^{}({ y }){ v })\) precedes \(\textit{inv}'\) in \(H'|T_i\).
Definition 21
(Closing Write) Given a program \(\mathbb {P}\), a set of processes \(\varPi \) executing \(\mathbb {P}\) and a history \(H\) s.t. \(H\models \mathcal {E}({\mathbb {P}},{\varPi })\), an operation execution is the closing write on some variable \( x \) by transaction \(T_i\) in \(H\) if it comprises of an invocation and a response other than \( A _i\), and the invocation is the closing write invocation on \( x \) by \(T_i\) in \(H\).
We call a write invocation or operation that is not closing, a non-closing write invocation or operation, and so on for read invocations and operations. In transaction diagrams we mark a closing write operation execution in some history as  . Note that an operation can be the ultimate operation execution in some transaction, but still not fit the definition of a closing operation execution.
. Note that an operation can be the ultimate operation execution in some transaction, but still not fit the definition of a closing operation execution.
What is considered a closing write depends on invariants associated with a given system. It is worth exploring how specific examples of invariant sets impact the definition of closing write invocations. Let us first consider a system with an empty set of invariants  . If a system declares no invariants, then for any variable \( x \) and any transaction \(T_i\), the set \(\mathbb {I}^{x}_{i}\) contains only \( x \). The same is true if the system has only invariants whose domains are singletons
. If a system declares no invariants, then for any variable \( x \) and any transaction \(T_i\), the set \(\mathbb {I}^{x}_{i}\) contains only \( x \). The same is true if the system has only invariants whose domains are singletons  . In both cases the closing write invocation on a variable will simply be the last possible write invocation on that variable in a given transaction. Alternatively, in
. In both cases the closing write invocation on a variable will simply be the last possible write invocation on that variable in a given transaction. Alternatively, in  , where all variables are involved in an invariant in all transactions, \(\mathbb {I}^{x}_{i}\) is the set of all variables, so the closing write on all variables in a transaction will be any last possible write invocation on any variable in that transaction.
, where all variables are involved in an invariant in all transactions, \(\mathbb {I}^{x}_{i}\) is the set of all variables, so the closing write on all variables in a transaction will be any last possible write invocation on any variable in that transaction.
Note that once any transaction \(T_i\) completes executing its closing write on some variable \( x \), it is certain that no further modifications to that variable are intended by the programmer as part of \(T_i\). This means, from the perspective of \(T_i\) (and assuming no other transaction modifies \( x \)) the state of \( x \) would be the same at the time of the closing write as if the transaction attempted to commit. Hence, with respect to \( x \), we can treat \(T_i\) as if it had attempted to commit. Thus, if a transaction executes its closing write on some variable, we say that the transaction decided on \( x \).
Definition 22
(Transaction Decided on \( x \)) Given a program \(\mathbb {P}\), a set of processes \(\varPi \) and a history \(H\) s.t. \(H\models \mathcal {E}({\mathbb {P}},{\varPi })\), we say transaction \(T_i \in H\) decided on variable \( x \) in \(H\) iff \(H|T_i\) contains a complete write operation execution \( w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) that is the closing write on \( x \).
5.1.3 Last-use opacity
Last use opacity uses the concepts of restraint and closing writes to dictate when a transaction can read from another transaction.
Intuitively, given any two transactions, \(T_i\) and \(T_j\), last-use opacity allows \(T_i\) to read variable \( x \) from \(T_j\) if the latter is either committed or commit-pending, or, if \(T_j\) is live and it already executed its closing write on \( x \). This has the benefit of allowing prerelease while excluding overwriting completely.
Simultaneously all transactions must be restrained to avoid performing operations on data coming from inconsistent views. This approach prevents most inconsistent views. Inconsistent views can only occur when a transaction releases a variable after a closing write and subsequently aborts. Due to the prescribed finality of closing writes and due to the restriction on using inconsistent data imposed by the definition of restrain we consider this situation to be benign in practice. We discuss the details of this and other implications of last-use opacity after giving the formal definition. Specifically, we discuss the guarantees given by the property in full in Sect. 5.3 and the implications of inconsistent views in Sect. 5.5, as well as ways of mitigating them. We compare the strength of last-use opacity with other properties in Sect. 5.6.
Given some history \(H\), let \(\hat{\mathbb {T}}^{H}\) be a set of transactions s.t. \(T_i \in \hat{\mathbb {T}}^{H}\) iff there is some variable \( x \) s.t. \(T_i\) decided on \( x \) in \(H\). Given any \(T_i \in H\), a decided transaction subhistory, denoted \(H\hat{|}T_i\), is the longest subsequence of \(H|T_i\) s.t.:
-
(a)
\(H\hat{|}T_i\) contains \( start _i\rightarrow ok _i\), and
-
(b)
for any variable \( x \), if \(T_i\) decided on \( x \) in \(H\), then \(H\hat{|}T_i\) contains \((H|T_i)| x \).
In addition, a decided transaction subhistory completion, denoted \(H\breve{|}T_i\), is a sequence s.t. \(H\breve{|}T_i = H\hat{|}T_i \cdot \big [ tryC _i\rightarrow C _i\big ]\).
The definition of opacity includes a definition of \( Vis {}\), a subhistory visible to a specific transaction. Last-use Opacity includes a similar definition: \( LVis {}\). The definition of \( Vis {}\) specifies that a transaction may view the operations performed by itself or other committed transactions. \( LVis {}\) makes the same requirement of committed transactions, but uncommitted transactions have a choice to either view operations performed in some decided transaction subhistory, or not. This freedom assures that transactions are not forced to read from doomed or aborting transactions and it is further illustrated in Sect. 5.2.4. Formally, given a sequential history S s.t. \(S\equiv H\), \( LVis (S,T_i)\) is the longest subhistory of S, s.t. for each \(T_j \in S\):
-
(a)
if \(i=j\) or both \(T_j\) is committed in S and \(T_j \prec _S T_i\), then \(S|T_j \subseteq LVis (S,T_i)\),
-
(b)
if \(T_j\) is not committed in S but \(T_j \in \hat{\mathbb {T}}^{H}\) and \(T_j \prec _S T_i\), and it is not true that \(T_j \prec _HT_i\), then either \(S\breve{|}T_j \subseteq LVis (S,T_i)\) or not.
Given a sequential history S and a transaction \(T_i \in S\), we then say that transaction \(T_i\) is last-use legal in S if \( LVis (S,T_i)\) is legal. Note that if S is legal, then it is also last-use legal (see appendix for proof).
Definition 23
(Final-state Last-use Opacity) A finite history \(H\) is final-state last-use opaque if, and only if, there exists a sequential history S equivalent to \( Compl (H)\) s.t.,
-
(a)
S preserves the real-time order of \(H\),
-
(b)
every transaction in S that is committed in S is legal in S,
-
(c)
every transaction in S that is not committed in S is last-use legal in S,
-
(d)
\(H\) is restrained.
Definition 24
(Last-use Opacity) A history \(H\) is last-use opaque if, and only if, every finite prefix of \(H\) is final-state last-use opaque.
Theorem 1
Last-use opacity is a safety property.
Proof
By Definition 24, last-use opacity is trivially prefix-closed.
Given \(H_L\) that is an infinite limit of any sequence of finite histories \(H_0, H_1, \ldots \), s.t every \(H_h\) in the sequence is last-use–opaque and every \(H_h\) is a prefix of \(H_{h+1}\), since each prefix \(H_h\) of \(H_L\) is last-use–opaque, then, by extension, every prefix of \(H_L\) is also final-state last-use opaque, so, by Definition 24, \(H_L\) is last-use–opaque. Hence, last-use opacity is limit-closed.
Since last-use opacity is both prefix-closed and limit-closed, then, by Definition 1, it is a safety property. \(\square \)
5.2 Examples
In order to aid understanding of the property we present examples of last-use opaque histories. These are contrasted by examples of histories that are not last-use opaque. We discuss the examples below.
5.2.1 Prerelease on closing write
The example in Fig. 11 shows \(T_i\) executing a write on \( x \) once and prereleasing \( x \) to \(T_j\). We assume that the program generating the history is such, that the write operation executed by \(T_i\) is the closing write operation execution on \( x \). The history is intuitively correct, since both transactions commit, and \(T_j\) reads a value written by \(T_i\). On the formal side, since both transactions are committed in this history, the equivalent sequential history would consist of all the events in \(T_i\) followed by the events in \(T_j\) and both transactions would be legal, since \(T_i\) writes a legal value to \( x \) and \(T_j\) reads the last value written by \(T_i\) to \( x \). Thus, the history is final-state last-use opaque.
Since last-use opacity requires prefix closeness, then all prefixes of the history in Fig. 11 also need to be final-state last-use opaque. We present only two of the interesting prefixes, since the remainder are either similar or trivial. The first interesting prefix is created by removing the commit operation execution from \(T_j\), which means \(T_j\) is aborted in any completion of the history. We show such a completion in Fig. 12. Still, \(T_i\) writes a legal value to \( x \) and \(T_j\) reads the last value written by \(T_i\) to \( x \), so that prefix is also final-state last-use opaque. Another interesting prefix is created by removing the commit operation executions from both transactions. Then, in the completion of the history both transactions are aborted, as in Fig. 13. Then, in an equivalent sequential history \(T_j\) would read a value written by an aborted transaction. In order to show legality of a committed transaction, we use the subhistory denoted \( Vis \), which does not contain any transactions that were not committed in the history from which it was derived. Thus, if \(T_j\) were committed, it would not be legal, since its \( Vis \) would not contain a write operation execution writing the value the transaction actually read. However, since \(T_j\) is aborted, the definition of final-state last-use opacity only requires that \( LVis \) rather than \( Vis \) be legal, and \( LVis \) can contain operation executions on particular variables from an aborted transaction under the condition that the transaction already executed its closing write on the variables in question. Since, in the example \(T_i\) executed its closing write on \( x \), then this write will be included in \( LVis \) for \(T_j\), so \(T_j\) will be last-use legal. In consequence the prefix is also final-state last-use opaque. Indeed, all prefixes of example Fig. 11 are final-state last-use opaque, so the example is last-use opaque, and, by extension, so are the examples in Figs. 12 and 13.
5.2.2 Prerelease on non-closing write
Contrast the example in Fig. 11 with the one in Fig. 14. The histories presented in both are identical, with the exception that the write operation in Fig. 11 is considered to be the closing operation execution, while in Fig. 14 it is not. The difference would stem from differences in the programs that produced these histories. For instance, the program producing the history in Fig. 14 could conditionally execute another operation on \( x \), so, even though that condition was not met in this history, the potential of another write on \( x \) means that the existing write cannot be considered a closing write operation execution. The consequence of this is that while the example itself is final-state last-use opaque, one of its prefixes is not, so the history is not last-use opaque. We would reach the same conclusion if \(T_j\) would abort. The offending prefix is created by removing commit operations in both transactions, so both transactions would abort in any completion, as in Fig. 15. Here, since \(T_i\) does not execute the closing write operation on \( x \), then the write operation would not be included in \( LVis \) for \(T_j\), so the value read by \(T_j\) could not be justified. Thus, \(T_j\) is not legal in that history, and, therefore, the history in Fig. 15 is not final-state last-use opaque (so also not last-use opaque). Fig. 15 represents the completion of a prefix of the history in Fig. 14, so Fig. 15 not being final-state last-use opaque, means that Fig. 14 is not last-use opaque.
5.2.3 Recoverability
The examples in Figs. 16 and 17, show that recoverability is required, i.e., transactions must commit in order. Last-use opacity of the example in Fig. 16 is analogous to the one in Fig. 12, since their equivalent sequential histories are identical, as are the sequential histories equivalent to their prefixes. Furthermore, intuitively, if \(T_j\) reads a value of a variable prereleased by \(T_i\) and aborts before \(T_i\) commits, this is correct behavior. On the other hand, the history in Fig. 17 is not last-use opaque, even though it is final-state last-use opaque (by analogy to Fig. 11). More specifically, a prefix of the history where the commit operation execution is removed from \(T_i\) is not final-state last-use opaque. This is because a completion will require that \(T_i\) be aborted. By definition, operations from aborted operations cannot be included in \( Vis \), so operations executed by \(T_i\) are not going to be included in \( Vis \) for \(T_j\). Since \(T_j\) is committed, then its \( Vis \) must be legal, but it is not, because the read operation reading 1 will not be preceded by any writes in \( Vis \). Since the prefix contains an illegal transaction, then it is not final-state last-use opaque, and thus, the history in Fig. 17 is not last-use opaque.
On the other hand, the example in Fig. 18 shows that the commitment order is not required for all conflicting transactions, just those with a reads-from relation. Here, the example is analogous to Fig. 17, but \(T_j\) does not read from \(T_i\). This means that \(T_j\)’s \( LVis \) and \( Vis \) will be legal regardless of whether \(T_i\)’s operations are included or excluded. Then, given a sequential history equivalent to the example, where \(T_i\) precedes \(T_j\), both \(T_i\) and \(T_j\) in such a history will be legal. Hence the history is final-state last-use opaque. Then, in all prefixes of the history \(T_i\) is aborted in the completion, whereas \(T_j\) may be either committed or aborted. If \(T_j\) is committed, then \(T_i\) will not be included in \(T_j\)’s \( Vis \), but this does not make \( Vis \) illegal, as we pointed out earlier. Similarly, if \(T_j\) is aborted, then \(T_i\) may or may not be included in \(T_j\)’s \( LVis \), but this is immaterial with respect to \(T_j\)’s \( LVis \) being legal. Hence all the prefixes will be final-state last-use opaque as well, and, in effect, the example is last-use opaque.
5.2.4 Consistent values
The example in Fig. 19 shows that a transaction is allowed to read from a transaction that eventually aborts, or ignore that transaction, because of the freedom left within the definition of \( LVis \). I.e., transaction \(T_j\) is concurrent to \(T_i\), but \(T_k\) follows \(T_i\) in real time. \(T_i\) executes a closing write on \( x \), so \(T_j\) is allowed to include the write operation in its \( LVis \). Since \(T_j\) sees the value written to \( x \) by that write, \(T_j\) includes the write in \( LVis \). On the other hand, \(T_k\) cannot include \(T_i\)’s write in \( LVis \), since \(T_i\) aborted before \(T_k\) even started, so the write should not be visible to \(T_k\). On the other hand \(T_k\) is allowed to include \(T_j\) in its \( LVis \). \(T_k\) should not do so, however, since it ignores \(T_j\) as well as \(T_i\) (which makes sense as \(T_j\) is doomed to abort). Hence \(T_k\) reads the value of \( x \) to be 0. If \(T_j\) is included in \(T_k\)’s \( LVis \), reading 0 would be incorrect. Hence, the definition of \( LVis \) allows \(T_j\) to be arbitrarily excluded. In effect all three transactions are correct (so long as \(T_j\) does not eventually commit).
5.2.5 Overwriting
Figure 20 shows an example of overwriting, which is not last-use opaque, since there is no equivalent sequential history where the write operation in \(T_i\) writing 1 to \( x \) would precede the read operation in \(T_j\) reading 1 from \( x \) without the other write operation writing 2 to \( x \) also preceding the read. Thus, in all cases \(T_j\) is not legal, and the history is neither final-state last-use opaque, nor last-use opaque.
5.2.6 Dependency cycle
Finally, Fig. 21 shows an example of a cyclic dependency, where \(T_j\) reads \( x \) from \(T_i\), and subsequently \(T_i\) reads \( y \) from \(T_j\). Both writes in the history are closing writes. This example has unfinished transactions, which are thus aborted in any possible completion of this history. There are two possible sequential histories equivalent to that completion: one where \(T_i\) precedes \(T_j\) and one where \(T_j\) precedes \(T_i\). In the former case, \( LVis \) of \(T_i\) does not contain any operations from \(T_j\), because \(T_j\) follows \(T_i\). Thus, there is no write operation on \( y \) preceding a read on \( y \) returning 1 in \(T_i\)’s \( LVis \), which does not conform to the sequential specification, so \(T_i\)’s \( LVis \) is not legal. Hence, \(T_i\) is not legal in that scenario. The former case is analogous: \(T_j\)’s \( LVis \) will not contain a write operation from \(T_i\), because \(T_i\) follows \(T_j\). Therefore \(T_j\)’s \( LVis \) contains a read on \( x \) that returns 1, which is not preceded by any write on \( x \), which causes the sequence not to conform to the sequential specification and renders the transaction not legal. Since either case contains a transaction that is not legal, then that history is not final-state last-use opaque, and therefore not last-use opaque.
5.3 Guarantees
Last-use opacity gives the programmer the following guarantees.
5.3.1 Serializability
If a transaction commits, then the value it reads can be explained by operations executed by preceding or concurrent transactions. This guarantees that a transaction that views inconsistent state will not commit.
Lemma 23
(Serializability) Every last-use–opaque history is serializable.
Proof
For the sake of contradiction let us assume that \(H\) is last-use–opaque and not serializable. Since \(H\) is last-use–opaque, then from Definition 24\(H\) is also final-state last-use opaque. Then, from Definition 23 there exists a completion \(H_C= Compl (H)\) such that there is a sequential history \(\hat{S}_{H}\) s.t. \(\hat{S}_{H}\equiv H_C\), \(\hat{S}_{H}\) preserves the real-time order of \(H_C\), and any committed transaction in \(\hat{S}_{H}\) is legal in \(\hat{S}_{H}\). However, since \(H\) is not serializable, then from Definition 6 there does not exist a completion \(H_C= Compl (H)\) such that there is a sequential history \(\hat{S}_{H}\) s.t. \(\hat{S}_{H}\equiv H_C\), and any committed transaction in \(\hat{S}_{H}\) is legal in \(\hat{S}_{H}\). This contradicts the previous statement. \(\square \)
5.3.2 Real-time order
Successive transactions will not be rearranged to fit serializability, so a correct history will agree with an external clock, or an external order of events.
Lemma 24
(Real-time Order) Every last-use–opaque history preserves real-time order.
Proof
Trivially from Definitions 24 and 23a. \(\square \)
5.3.3 Recoverability
If one transaction reads from another transaction, the former will commit only after the latter commits. This guarantees that transactions commit in order.
Lemma 25
(Recoverability) Every last-use–opaque history is recoverable.
Proof
Let us assume that \(H\) is not recoverable. Then there must be some transactions \(T_i\) and \(T_j\) s.t. \(T_j\) reads from \(T_i\) and then \(T_j\) commits before \(T_i\). Such a history will contain a prefix P where any completion will contain an aborted \(T_i\) and a committed \(T_j\), so for any equivalent sequential history \(\hat{S}_{H}\) \( Vis (\hat{S}_{H}, T_j)\) will not contain \(\hat{S}_{H}|T_i\). Since \(T_j\) reads from \(T_i\) then such \( Vis (\hat{S}_{H}, T_j)\) will not be legal, so by Definition 23P is not last-use opaque and thus, by Definition 24, \(H\) is not last-use opaque, which is a contradiction. \(\square \)
Last-use opacity does not preserve commitment order as defined in Definition 7 (see e.g., Fig. 18), but we consider recoverability sufficient for TM. Note that strong properties like opacity also deal with commitment order only to the extent of recoverability.
5.3.4 Precluding overwriting
If transaction \(T_i\) reads the value of some variable written by transaction \(T_j\), then \(T_j\) will never subsequently modify that variable.
Lemma 26
(Precluding Overwriting) Last-use opacity does not support overwriting.
Proof
For the sake of contradiction let us assume that there exists \(H\) that is a last-use–opaque history with overwriting (and unique writes), i.e. (from Definition 4) there are transactions \(T_i\) and \(T_j\) s.t.:
-
(a)
\(T_i\) prereleases some variable \( x \),
-
(b)
\(H|T_i\) contains \( w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) and \( w _{i}({ x }){ v '}\!\rightarrow \!{ ok _i}\), s.t. the former precedes the latter in \(H|T_i\),
-
(c)
\(H|T_j\) contains \( r _{j}({ x })\!\rightarrow \!{ v }\) that precedes \( w _{i}({ x }){ v '}\!\rightarrow \!{ ok _i}\) in \(H.\)
Since \(H\) is opaque, then there is a completion \(C = Compl (H)\) and a sequential history S s.t. \(S \equiv Compl (H)\), S preserves the real-time order of \(H\), and both \(T_i\) and \(T_j\) in S are legal in S. In S, either \(T_i \prec _S T_j\) or \(T_j \prec _S T_i\). In either case, any \( Vis (S, T_j)\) or \( LVis (S,T_j)\) by their definitions will contain either the sequence of both \( w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) and \( w _{i}({ x }){ v '}\!\rightarrow \!{ ok _i}\) or neither of those write operation executions. In either case, \( r _{j}({ x })\!\rightarrow \!{ v }\) will not be directly preceded by \( w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) among operations on \( x \) in either \( Vis (S, T_j)\) or \( LVis (S,T_j)\). Therefore, \(T_j\) in S cannot be legal in S, which is a contradiction. \(\square \)
5.3.5 Aborting prerelease
A transaction can prerelease some variable and subsequently abort.
Lemma 27
(Aborting Prerelease) Last-use opacity supports aborting prerelease.
Proof
Let \(H\) be the history depicted in Fig. 13. Here, \(T_i\) prereleases \( x \) to \(T_j\) and subsequently aborts, which satisfies Definition 5. Since \(T_i\) and \(T_j\) are both aborted in \(H\), \(H\) has a completion \(C = Compl (H) = H\). Let S be a sequential history s.t. \(S=H|T_i \cdot H|T_j\). S vacuously preserves the real-time order of \(H\) and trivially \(S \equiv H\). Transaction \(T_i\) in S is last-use legal in S, because \( LVis (S,T_i) = S|T_i\)—whose operations on \( x \) are limited to a single write operation execution—is within the sequential specification of \( x \). Transaction \(T_j\) in S is also last-use legal in S, since \( LVis (S,T_j) = H\breve{|}T_i\,\cdot \,S|T_j\)—whose operations on \( x \) consist of \( w _{i}({ x }){ v }\!\rightarrow \!{ ok _i}\) followed by \( r _{j}({ x })\!\rightarrow \!{ v }\)—is also within the sequential specification of \( x \). Since both \(T_i\) and \(T_j\) in S are last-use legal in S, \(H\) is final-state last-use opaque. All prefixes of \(H\) are trivially also final-state last-use opaque (since either their completion is the same as \(H\)’s, they contain only a single write operation execution on \( x \), or contain no operation executions on variables), so \(H\) is last-use opaque. \(\square \)
5.4 Invariants
Invariants impact when a value can be read from a live transaction, so they define which inconsistent states are allowed to be seen outside of a running transaction while still satisfying last-use opacity. By default we assume there are no invariants ( ). This means that a variable written by some live transaction can be read as soon as it can be determined that a transaction will not perform any more writes on that exact variable. This allows for more parallel executions, but the resulting inconsistent states may result in harmful operations.
). This means that a variable written by some live transaction can be read as soon as it can be determined that a transaction will not perform any more writes on that exact variable. This allows for more parallel executions, but the resulting inconsistent states may result in harmful operations.
For example, take the program in Fig. 22. The programmer silently assumes that \( x \ne y \), but this assumption is not part of formal requirements (that is, we still assume  ). Nevertheless, any sequential execution of subprograms \(\mathcal {P}_5\) and \(\mathcal {P}_6\) will not yield errors, as the assumption is born out as postconditions of each transaction block.
). Nevertheless, any sequential execution of subprograms \(\mathcal {P}_5\) and \(\mathcal {P}_6\) will not yield errors, as the assumption is born out as postconditions of each transaction block.
However, an interleaved execution in Fig. 23 would produce an error. Here \(\mathcal {P}_5\) executes transaction \(T_i\) and \(\mathcal {P}_6\) executes \(T_j\). In this execution, the writer transaction \(T_i\) could be interleaved with the reader \(T_j\) in such a way that \(T_j\) reads the value of \( y \) from before \(T_i\) and the value of \( x \) written by \(T_i\). Since there is no other possible future write to \( x \) in \(T_i\), the read does not break last-use opacity. But it does crash the program: If the value of just \( x \) is read from \(T_i\), but not \( y \), the values may be equal, leading \(\mathcal {P}_6\) to end up dividing by zero.
On the other hand, if the set of invariants includes an invariant representing \( x \ne y \) applied to (at least) \(T_i\), then the write \( w _{i}({ x }){1}\!\rightarrow \!{ ok _i}\) is no longer closing. Instead, a write on \( y \) will be the closing write for both \( x \) and \( y \) in \(T_i\), which makes the history not last-use–opaque, and the crash is precluded. This is safer, but removes some ability to parallelize transactions wherever invariants come into effect.
Parameterizing a system with a set of explicit invariants may not always be practical. In that case, the designer may use  as the default assumption. This means that a transaction will never allow reading from a live transaction until it finishes all of its writes. This precludes harmful operations involving assumptions about relationships among shared variables. This also still allows live transactions to expose values they write before committing, allowing other transactions to parallelize with them for the duration of any local calculations or subsequent reads. However, the degree to which transactions are allowed to execute in parallel is much more limited than with an assumption of
as the default assumption. This means that a transaction will never allow reading from a live transaction until it finishes all of its writes. This precludes harmful operations involving assumptions about relationships among shared variables. This also still allows live transactions to expose values they write before committing, allowing other transactions to parallelize with them for the duration of any local calculations or subsequent reads. However, the degree to which transactions are allowed to execute in parallel is much more limited than with an assumption of  or a more tailored set of invariants.
or a more tailored set of invariants.
In any case, the inconsistent views seen by last-use–opaque transactions are limited to only to those, where each transaction only ever exposes values it wrote that it expected to commit with. But, in addition, if the assumptions about relationships between variables are comprehensively expressed as a set of invariants, for any variables entangled in such relationships, each transaction will only ever expose a variable if all related variables reach a state that the transaction planned to commit with. In this way, the exposed inconsistent views are prevented from causing harm.
5.5 Inconsistent views
Last-use opacity does not preclude transactions from aborting after prereleasing a variable. As a consequence there may be instances of cascading aborts, which have varying implications on consistency depending on whether the TM model allows transactions to abort programmatically. We distinguish three cases of models and discuss them below.
5.5.1 Commit-only model
Let us assume that transactions cannot arbitrarily abort, but only do so as a result of receiving an abort response to invoking a read or write operation, or while attempting to commit. In other words, there is no \( tryA \) operation in the transactional API, as per the commit-only transactional model. In that case, since overwriting is not allowed, the transaction never reveals intermediate values of variables to other transactions. This means that if a transaction prereleased a variable, then the programmer did not intend to change the value of that variable. Neither did she intend to change the values of any variables co-occurring with this one in an invariant. So, if the transaction eventually committed, the value of the variable would have been the same. Furthermore, if a variable is a part of an invariant, the transaction will not expose it, until all other variables involved in the invariant reach a fixed point within that transaction. So, if the transaction is eventually forced to abort rather than committing, the value of any variable prereleased would be the same regardless of whether the transaction committed or aborted. Therefore, we can consider the inconsistent state to be safe. In other words, if the variable caused an error to occur, the error would be caused regardless of whether the transaction finally aborts or commits. Thus, we can say that with this set of assumptions, the programmer is guaranteed that none of the inconsistent views will cause unexpected behavior, even if cascading aborts are possible. Note that the use of this model is not uncommon (see eg. [3, 4, 15]), and there are transactional systems that restrict the API even further by precluding aborts completely [1, 30].
5.5.2 Arbitrary abort model
Alternatively, let us assume that transactions can arbitrarily abort (in addition to forced aborts as described above) by executing the operation \( tryA \) as a result of some instruction in the program. In that case it is possible to imagine programs that use the abort instruction to cancel a transaction due to the “business logic” of the program. Therefore a programmer explicitly specifies that the value of a variable is different depending on whether the transaction finally commits or not. An example of such a program is given in Fig. 24 (subprogram \(\mathcal {P}_3\)). Here, the programmer enforced an invariant that the value of x should never be less than zero. If the invariant is not fulfilled, the transaction aborts. However, writing a value to x that breaks the invariant is the closing write operation execution for this program, so it is possible that another transaction reads the value of x before the transaction aborts. If the transaction that reads x is like the one in Fig. 24 (subprogram \(\mathcal {P}_4\)), where x is used to index an array via pointer arithmetic, a memory error is possible. Nevertheless, the history from Fig. 25 that corresponds to a problematic execution of these two transactions is clearly allowed by last-use opacity (assuming that the domain of x is \({\mathbb {Z}}\)). Thus, if the abort operation is available to the programmer the guarantee that inconsistent views will not lead to unexpected effects is lost. Note that this is the case no matter if the transaction that has read from the programmatically aborted transaction will eventually abort or commit. Therefore it is up to the programmer to use aborts wisely or to prevent inconsistent views from causing problems, by prechecking invariants at the outset of a transaction, or maintaining invariants also within a transaction (in a similar way as with monitor invariants). Alternatively, a mechanism can be built into the TM that prevents specific transactions at risk from reading variables that were prereleased, while other transactions are allowed to do so. However, if these workarounds are not satisfactory, we present a stronger variant of last-use opacity in Sect. 6 that deals specifically with this model and eliminates its inconsistent views.
5.5.3 Restricted abort model
We present a third alternative to aborts in transactions: a compromise between only forced aborts and programmer-initiated aborts. This option assumes that the \( tryA \) operation is not available to the programmer, so it cannot be used to implement business logic. However, we allow the TM system to somehow inject \( tryA \) operations in the code in response to external stimuli, such as crashes or exceptions and use aborts as a fault tolerance mechanism. However, since the programmer cannot use the operation, the programs must be coded as in the commit-only model, and therefore the same guarantees are given as in the commit-only model.
5.6 Strength
We compare the relative strength of last-use opacity with other properties from Sect. 4 and present the result of the comparison in Fig. 26. We provide the proofs for each comparison in the appendix.
5.7 Performance
In general, parallelizing transactions is an important component of TM performance and other research has shown that doing so by allowing reading from live transactions can be very beneficial [1, 35, 37]. More specifically, existing last-use–opaque implementations of pessimistic and distributed TM systems show that prerelease yields a performance benefit in terms of throughput in experimental scenarios with high contention [26, 40, 41]. In those cases transactions that prerelease variables can execute partially in parallel with other transactions that depend on the same variables. In contrast, counterpart opaque implementations are forced to essentially serialize such transactions. The effect is more pronounced in write-heavy workloads, since parallelizing writer transactions with one another involves some form of prerelease. The performance bump is also more apparent with longer transactions (both in terms of local operations and shared variable accesses), because the difference between reading a value at the time it is written vs waiting until the live transaction commits is greater. However, we also see that in low contention, last-use–opaque implementations do less well, since the locking and prerelease mechanisms are more costly than speculative execution. Practical applications could benefit from adaptively managing prerelease and the associated mechanisms by monitoring contention and enabling them only when contention is sufficiently high.
6 Strong last-use opacity
Even though last-use opacity prevents inconsistent views in the commit-only and restricted abort models, it does not prevent inconsistent views in the arbitrary aborts model. Hence, we present a stronger variant of last-use opacity. Strong last-use opacity extends the definition of a closing write operation to take \( tryA \) operations into account, as if it were an operation that modifies a given variable.
6.1 Intuition and definition
Strong last-use opacity is very similar to last-use opacity: it requires restraint and it prevents transactions from reading from other live transactions, unless the transaction is guaranteed not to further modify the variable in question and all required invariants are preserved. The difference between last-use opacity and strong last-use opacity is that the latter also considers aborts as operations that modify the variable, whereas last-use opacity only considers writes to be such operations. Thus, strong last-use opacity defines its own variant of a closing write to be any write operation execution that is not followed by another write on the variable, nor any voluntary abort. In this way, transactions that can start a cascading abort are prevented from prereleasing. This means that inconsistent views are excluded, while prereleasing transactions are prevented from aborting.
Below we define the concept of a strongly closing write to some variable by a particular transaction: we first define a strongly closing write operation invocation, and then extend the definition to complete operation executions.
Definition 25
(Strongly Closing Write Invocation) Given a program \(\mathbb {P}\), a set of invariants  , a set of processes \(\varPi \) executing \(\mathbb {P}\), and a history \(H\) s.t. \(H\models \mathcal {E}({\mathbb {P}},{\varPi })\), an invocation \( inv _{i}^{}( w ^{}({ y }){ v })\) on some variable \( y \) by transaction \(T_i\) in \(H\) is the strongly closing write invocation on some variable \( x \) by transaction \(T_i\) in \(H\), if \( y \in \mathbb {I}^{ x }_{i}\) and for any history \(H' \in \mathbb {H}^{{\mathbb {P}},{\varPi }}\) for which \(H\) and \(H'\) have a common prefix P ending with \( inv _{i}^{}( w ^{}({ y }){ v })\) i.e., \(P = P' \cdot [ inv _{i}^{}( w ^{}({ y }){ v }) ]\), \(H= P \cdot R\), and \(H' = P \cdot R'\), there is no operation invocation \(\textit{inv}'\) s.t. \( inv _{i}^{}( w ^{}({ y }){ v })\) precedes \(\textit{inv}'\) in \(H'|T_i\) and either (a) \(\textit{inv}' = inv _{i}^{}( w ^{}({ z }){ u })\) for any variable \( z \in \mathbb {I}^{ x }_{i}\), or (b) \(\textit{inv}' = inv _{i}^{}( tryA )\).
, a set of processes \(\varPi \) executing \(\mathbb {P}\), and a history \(H\) s.t. \(H\models \mathcal {E}({\mathbb {P}},{\varPi })\), an invocation \( inv _{i}^{}( w ^{}({ y }){ v })\) on some variable \( y \) by transaction \(T_i\) in \(H\) is the strongly closing write invocation on some variable \( x \) by transaction \(T_i\) in \(H\), if \( y \in \mathbb {I}^{ x }_{i}\) and for any history \(H' \in \mathbb {H}^{{\mathbb {P}},{\varPi }}\) for which \(H\) and \(H'\) have a common prefix P ending with \( inv _{i}^{}( w ^{}({ y }){ v })\) i.e., \(P = P' \cdot [ inv _{i}^{}( w ^{}({ y }){ v }) ]\), \(H= P \cdot R\), and \(H' = P \cdot R'\), there is no operation invocation \(\textit{inv}'\) s.t. \( inv _{i}^{}( w ^{}({ y }){ v })\) precedes \(\textit{inv}'\) in \(H'|T_i\) and either (a) \(\textit{inv}' = inv _{i}^{}( w ^{}({ z }){ u })\) for any variable \( z \in \mathbb {I}^{ x }_{i}\), or (b) \(\textit{inv}' = inv _{i}^{}( tryA )\).
The remainder of the definitions of strong last-use opacity are formed by analogy to their counterparts in last-use opacity. Note that these definitions do not preclude some other operation than \( tryA \) returning \( A _i\) after a strongly closing write.
The definition of a strongly closing write operation execution is analogous to that of closing write operation execution Definition 21. The strongly closing write is used instead of the closing write to define a transaction strongly decided on \( x \) in analogy to Definition 22. Then, that definition is used to define \(\underline{\hat{\mathbb {T}}}^{H}\), \(H\underline{\hat{|}}T_j\), and \(H\underline{\breve{|}}T_j\) by analogy to \(\hat{\mathbb {T}}^{H}\), \(H\hat{|}T_j\) and \(H\breve{|}T_j\). Next, those definitions are used to define \( SLVis \) by analogy to \( LVis \). Finally, we say a transaction \(T_i\) is strongly last-use legal in some sequential history S if \( SLVis (S,T_i)\) is legal. This allows us to define strong last-use opacity as follows.
Definition 26
(Final-state Strong Last-use Opacity) A finite history \(H\) is final-state strongly last-use opaque if, and only if, there exists a sequential history S equivalent to \( Compl (H)\) s.t.,
-
(a)
S preserves the real-time order of \(H\),
-
(b)
every transaction in S that is committed in S is legal in S,
-
(c)
every transaction in S that is not committed in S is strongly last-use legal in S,
-
(d)
\(H\) is restrained.
Definition 27
(Strong Last-use Opacity) A history \(H\) is strongly last-use opaque if, and only if, every finite prefix of \(H\) is final-state strongly last-use opaque.
Theorem 2
Strong last-use opacity is a safety property.
Proof
By Definition 27, strong last-use opacity is trivially prefix-closed.
Given \(H_L\) that is an infinite limit of any sequence of finite histories \(H_0, H_1, \ldots \), s.t every \(H_h\) in the sequence is strongly last-use opaque and every \(H_h\) is a prefix of \(H_{h+1}\), since each prefix \(H_h\) of \(H_L\) is strongly last-use opaque, then, by extension, every prefix of \(H_L\) is also final-state strongly last-use opaque, so, by Definition 27, \(H_L\) is strongly last-use opaque. Hence, strong last-use opacity is limit-closed.
Since strong last-use opacity is both prefix-closed and limit-closed, then, by Definition 1, it is a safety property. \(\square \)
6.2 Examples
In Table 2 we show whether the examples in Figs. 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 and 21 satisfy strong last-use opacity alongside last-use opacity. Note that the properties allow and exclude histories in the same way except for two: Figs. 13 and 19. In those histories an aborting transaction prereleases a variable, which means that each such transaction’s last write was not, in fact, strongly closing, even though it was closing. This means that the write cannot be included in \( SLVis \) of the other transaction that read from the aborting transaction. In effect, the reading transactions are not strongly legal, which causes the histories to fail to satisfy strong last-use opacity.
6.3 Guarantees
Strong last-use opacity gives most of the same guarantees as last-use opacity: serializability, real-time order, recoverability, precluding overwriting, and aborting prerelease (in the case of forced aborts). We forgo formal definitions and proofs of these, since they are analogous to those in Sect. 5.3.
6.4 Strength
We compare the relative strength of strong last-use opacity with last-use opacity and other properties from Sect. 4 and present the result of the comparison in Fig. 27. The proofs are analogous to those for last-use opacity. We also discuss how strong last-use opacity compares with last-use opacity in various abort models below.
In the commit-only model, the strong last-use opacity property is equivalent to last-use opacity. This is trivial, since if there are no \( tryA \) operations in any history, then the definition of a strong closing write invocation is identical to the definition of a closing write invocation.
In the arbitrary abort model, strong last-use opacity property is strictly stronger than last-use opacity, because the definition of strong closing writes excludes histories that last-use opacity allows, including those with cascading aborts initiated by a voluntary abort.
In the restricted abort model, strong last-use opacity property is also strictly stronger than last-use opacity, but it is too strong to be applicable to systems with prerelease. In the first place, even though the histories that are excluded by strong last-use opacity contain inconsistent views, these are harmless, because as we argue in Sect. 5.5, transactions always release variables with “final” values. Since the \( tryA \) operation is not available to the programmer, these final values cannot be reverted by a programmer-initiated abort, so if the programmer or TM algorithm sets up a closing write to a variable in a transaction, the value that was written was expected to both remain unchanged and be committed. Hence, it is acceptable for these values to be read by other transactions, even before the original transaction commits.
Finally, in both the restricted and the arbitrary abort models (but especially the former), we assume that a TM system can inject a \( tryA \) operation into the transactional code to respond to some outside stimuli, such as crashes. Such events are unpredictable, so it may be possible for any transaction to abort at any time. Hence, it is necessary to assume that a \( tryA \) operation can be produced as the next operation invocation in any transaction at any time. In effect, as the definition of strong last-use opacity does not allow a transaction to prerelease a variable if a \( tryA \) is possible in the future, strong last-use opacity may prevent prerelease altogether in the restricted abort model.
In summary, strong last-use opacity is a useful variant of last-use opacity to exclude inconsistent views in the arbitrary abort model (if workarounds suggested in Sect. 5.5 are insufficient solutions). However strong last-use opacity may be too strict for TMs operating in the restricted and arbitrary abort models, where it may prevents prerelease altogether, depending on whether the injection of a \( tryA \) invocation into a transaction’s code can be predicted or not. Certainly, in systems where aborts are used as a response to partial failures, strong last-use opacity prevents prerelease altogether.
6.5 Summary
In Table 3 we present a summary of the properties discussed in this section by analogy to the summary in Table 1. The table informs that a particular property is a TM safety property and whether it satisfies the definitions for prerelease support, overwriting support, and aborting prerelease support. Finally, the last column informs whether each property is at least as strong as serializability.
The table shows that both of the introduced properties allow prerelease without a requirement for transactions that prerelease not to abort. Nevertheless the properties are strong enough to prevent most inconsistent views and make others inconsequential. Specifically, neither property admits inconsistent views in the commit-only model and the compromise restricted abort model. Last-use opacity allows a narrow class of inconsistent views in the arbitrary abort model, which can be mitigated by the programmer. On the other hand, the strong last-use opacity variant eliminates inconsistent views in all models, although does so for the price of preventing prerelease in transactions that invoke the \( tryA \) operation. We consider strong last-use opacity and last-use opacity to be practical safety properties for TM systems that employ prerelease.
7 Related work
Ever since opacity [16, 17] was introduced, it seems, there were attempts to weaken its stringent requirements, while retaining some guarantees over what serializability [7, 33] provides. We explore the most pertinent examples in Sect. 4: TMS1, TMS2 [13], elastic opacity [15], live opacity [14], and VWC [23], as well as some apposite consistency criteria: recoverability [18], cascadelessness [8], strictness [8], commit ordering [44] and rigorousness [10]. Other attempts were more specialized and include virtual time opacity [23], where the real-time order condition is relaxed.
Similarly, the \(\diamond \) opacity family of properties [25] relax the time ordering requirements of opacity to provide properties applicable to deferred update replication. Another example is view transactions [2], where it is only required that a transaction commits on any snapshot, that can be different than the one the transaction viewed initially, provided that operating on either snapshot produced externally indistinguishable results. While these properties have specific applications, none weaken the consistency to allow variable access before commit.
Although algorithms and systems are not the focus of this paper, some systems research that explores relaxed consistency should be noted. Dynamic STM [21] can be credited with introducing the concept of early release in the TM context. Dynamic STM allows transactions that only perform read operations on particular variables to (manually) release them for use by other transactions. However, it left the assurance of safety to the programmer, and, as the authors state, even linearizability cannot be guaranteed by the system. The authors of [42] expanded on the work above and evaluated the concept of early release with respect to read-only variables on several concurrent data structures. The results showed that early release does not provide a significant advantage in most cases, although there are scenarios where it would be advantageous if it were automated. Prerelease expands this idea further by allowing writers to expose written values before attempting to commit.
In [1], the authors introduce a pessimistic lock elision algorithm (improving on pessimistic algorithms introduced in [30, 34]), where read/write transactions are serialized, while read-only transactions are wait-free. Write transactions write values directly into memory, but maintain a bounded log of overwritten values. The read transactions prevent conflicting with writers by accessing older but consistent values from the log, if a variable was overwritten. In effect, the algorithm allows multiple readers to operate in parallel showing a performance improvement. The parallelization is done without prerelease, although at the cost of serializing writers, logging values, and reading out of date values.
Twilight STM [9] relaxes isolation to allow transactions to read variables that are used by other transactions, and allow them to re-read their values as they change in order to maintain the correctness of the computation. If inconsistencies arise, a reconciliation is attempted on commit, and aborts are induced if this is impossible. Since it allows operating on variables that were prereleased, but potentially before a closing write, Twilight STM will not satisfy the consistency requirements of last-use opacity, but it is likely to guarantee serializability and recoverability.
DATM [35] is yet another noteworthy system with a prerelease mechanism. DATM is an optimistic multicore-oriented TM based on TL2 [12], augmented with prerelease support. It allows a transaction \(T_i\) to write to a variable that was accessed by some uncommitted transaction \(T_j\), as long as \(T_j\) commits before \(T_i\). DATM also allows transaction \(T_i\) to read a speculative value, one written by \(T_j\) and accessed by \(T_i\) before \(T_j\) commits. DATM detects if \(T_j\) overwrites the data or aborts, in which case \(T_i\) is forced to restart. DATM allows all schedules allowed by conflict-serializability. This means that DATM allows overwriting, as well as cascading aborts. It also means that it does not satisfy last-use opacity.
In [37], the authors proposed algorithms for processing transactions in a predefined order. The work associates each transaction with a unique age attribute that is known a priori and reprised for retries, and which is then used to direct concurrency control and ensure that transactions commit in the order of age (a property called Age-based Commit Order). The paper introduces an algorithm that allows reading from live transactions, Ordered Undo Log (OUL), and its variant with co-operative writers, OUL-stealing. These algorithms outperform other implementations in most benchmarks, showing a clean performance benefit to reading from live transactions. The paper shows that OUL and OUL-stealing are strictly serializable, but since they both allow overwriting, neither is last-use–opaque.
Finally, SVA is a distributed TM system introduced in [41] (building on an earlier non-distributed rollback-free variant from [46,47,48]). The main aspect of SVA is the ability to prerelease variables. The prerelease mechanism in SVA is based on a priori knowledge about the maximum number of accesses that a transaction can perform on particular variables. A transaction that knows it performed exactly as many operations on some variable as the upper bound allows may then release that variable. SVA does not require the upper bounds to be precise, and can handle situations when they are either too great (some variables are not prereleased) or too low (transactions are aborted). The resulting parallelization of transaction executions leads to improved performance [26, 41]. The algorithm was further extended to produce OptSVA [40], that uses buffering to expedite the execution of read-only transactions and defer writes in write-only ones and whose implementation outperforms its predecessor. Both OptSVA and SVA satisfy last-use opacity.
8 Conclusions
This paper explored the space of TM safety properties in terms of whether or not, and to what extent, they allow a transaction to prerelease a variable, or, in other words, for a transaction to read a value written by a live transaction. We showed that existing properties are either strong, but prevent prerelease altogether (opacity, TMS1 and TMS2), or pose impractical restrictions on the ability of transactions to abort (VWC and live opacity). The remainder of the properties are not strong enough for TM applications (serializability and recoverability) since they allow a large range of inconsistent views, including overwriting. Hence, we presented a new TM safety property called last-use opacity that strikes a reasonable compromise at the price of explicitly including reasoning about transactional code and invariants in safety considerations. It allows prerelease without a requirement for transactions that prerelease variables not to abort, but one that is nevertheless strong enough to prevent most inconsistent views and make others inconsequential. The resulting property may be a useful practical criterion for reasoning about TMs with prerelease support.
We discussed the histories that are allowed by last-use opacity and examined the guarantees the property gives to the programmer. Last-use opacity always allows for potential inconsistent views to occur due to cascading aborts. However, no other inconsistent views are allowed. The inconsistent views that can occur can be made harmless by taking away the programmer’s ability to execute arbitrary aborts by either removing that operation completely or by removing it from the programmer’s toolkit, but allowing it to be used by the TM system, e.g. for fault tolerance. Allowing the programmers to abort a transaction at will means that they will need to eliminate dangerous situations (possible division by zero, invalid memory accesses, etc.) on a case-by-case basis. Nevertheless, we predict that inconsistent views of this sort will be relatively rare in practical TM applications, and typically result from using the abort operation to program business logic. Alternatively, a variant of last-use opacity called strong last-use opacity can be used instead, which eliminates the inconsistent views by preventing prerelease in transactions where a programmatic abort is possible.
References
Afek, Y., Matveev, A., Shavit, N.: Pessimistic software lock-elision. In: Proceedings of DISC’12: The 26th International Symposium on Distributed Computing (2012)
Afek, Y., Morrison, A., Tzafrir, M.: Brief announcement: view transactions: transactional model with relaxed consistency checks. In: Proceedings of PODC’10: The 29th ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing (2010)
Attiya, H., Gotsman, A., Hans, S., Rinetzky, N.: A programming language perspective on transactional memory consistency. In: Proceedings of PODC’13: The 32nd ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing (2013)
Attiya, H., Gotsman, A., Hans, S., Rinetzky, N.: Safety of live transactions in transactional memory: TMS is necessary and sufficient. In: Proceedings of DISC’14: The 28th International Symposium on Distributed Computing (2014)
Attiya, H., Hans, S.: Transactions are back—but how different they are? In: Proceedings of TRANSACT’14: The 7th ACM SIGPLAN Workshop on Transactional Computing (2014)
Attiya, H., Hans, S., Kuznetsov, P., Ravi, S.: Safety of deferred update in transactional memory. In: Proceedings of ICDCS’13: The 33rd International Conference on Distributed Computing Systems (2013)
Bernstein, P., Shipman, D., Wong, W.: Formal aspects of serializability in database concurrency control. IEEE Trans. Softw. Eng. SE–5(3), 203–216 (1979)
Bernstein, P.A., Hadzilacos, V., Goodman, N.: Concurrency Control and Recovery in Database Systems. Addison-Wesley, Boston (1987)
Bieniusa, A., Middelkoop, A., Thiemann, P.: Brief announcement: actions in the twilight—concurrent irrevocable transactions and inconsistency repair. In: Proceedings of PODC’10: The 29th ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing (2010)
Breitbart, Y., Georgakopoulos, D., Rusinkiewicz, M., Silberschatz, A.: On rigorous transaction scheduling. IEEE Trans. Softw. Eng. 17(9), 954–960 (1991)
Dalessandro, L., Scott, M.L.: Sandboxing transactional memory. In: Proceedings of PACT’12: The 21st International Conference on Parallel Architectures and Compilation Techniques (2012)
Dice, D., Shalev, O., Shavit, N.: Transactional Locking II. In: Proceedings of DISC’06: The 20th International Symposium on Distributed Computing (2006)
Doherty, S., Groves, L., Luchangco, V., Moir, M.: Towards formally specifying and verifying transactional memory. Form. Asp. Comput. 25(5), 769–799 (2013)
Dziuma, D., Fatourou, P., Kanellou, E.: Consistency for transactional memory computing. Bull. EATCS 2(113), 3 (2014)
Felber, P., Gramoli, V., Guerraoui, R.: Elastic transactions. In: Proceedings of DISC’09: The 23rd International Symposium on Distributed Computing (2009)
Guerraoui, R., Kapałka, M.: On the correctness of transactional memory. In: Proceedings of PPoPP’08: The 13th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (2008)
Guerraoui, R., Kapałka, M.: Principles of Transactional Memory. Morgan & Claypool, San Rafael (2010)
Hadzilacos, V.: A theory of reliability in database systems. J. ACM 35(1), 121–145 (1988)
Harris, T., Fraser, K.: Language support for lightweight transactions. In: Proceedings of OOPSLA’03: The 18th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications (2003)
Harris, T., Marlow, S., Peyton Jones, S., Herlihy, M.: Composable memory transactions. In: Proceedings of PPoPP’05: The ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (2005)
Herlihy, M., Luchangco, V., Moir, M., Scherer, I.W.N.: Software transactional memory for dynamic-sized data structures. In: Proceedings of PODC’03: The 22nd ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing (2003)
Herlihy, M., Moss, J.E.B.: Transactional memory: architectural support for lock-free data structures. In: Proceedings of ISCA’93: The 20th International Symposium on Computer Architecture (1993)
Imbs, D., de Mendivil, J.R., Raynal, M.: On the consistency conditions or transactional memories. Tech. Rep. 1917, IRISA (2008)
Imbs, D., Raynal, M.: Virtual world consistency: a condition for STM systems (with a versatile protocol with invisible read operations). Theor. Comput. Sci. 444, 113–127 (2012)
Kobus, T., Kokociński, M., Wojciechowski, P.T.: Relaxing real-time order in opacity and linearizability. J. Parallel Distrib. Comput. 100, 57–70 (2017)
Kobyliński, P., Siek, K., Baranowski, J., Wojciechowski, P.T.: Helenos: a realistic benchmark for distributed transactional memory. J. Softw. Pract. Exp. 48(3), 528–549 (2018)
Kończak, J.Z., Wojciechowski, P.T., Guerraoui, R.: Operation-level wait-free transactional memory with support for irrevocable operations. IEEE Trans. Parallel Distrib. Syst. 28(12), 3570–3583 (2017)
Lamport, L.: Proving the correctness of multiprocess programs. IEEE Trans. Softw. Eng. SE–3(2), 125–143 (1977)
Lesani, M., Palsberg, J.: Decomposing opacity. In: Proceedings of DISC’14: The 28th International Symposium on Distributed Computing (2014)
Matveev, A., Shavit, N.: Towards a fully pessimistic STM model. In: Proceedings of TRANSACT ’12: The 7th ACM SIGPLAN Workshop on Transactional Computing (2012)
Ni, Y., Welc, A., Adl-Tabatabai, A.R., Bach, M., Berkowits, S., Cownie, J., Geva, R., Kozhukow, S., Narayanaswamy, R., Olivier, J., Preis, S., Saha, B., Tal, A., Tian, X.: Design and implementation of transactional constructs for C/C++. In: Proceedings of OOPSLA’08: The 23rd ACM SIGPLAN Conference on Object-oriented Programming, Systems Languages and Applications (2008)
Olszewski, M., Cutler, J., Steffan, J.G.: JudoSTM: a dynamic binary-rewriting approach to software transactional memory. In: Proceedings of PACT’07: The 16th International Conference on Parallel Architectures and Compilation Techniques (2007)
Papadimitrou, C.H.: The serializability of concurrent database updates. J. ACM 26(4), 631–653 (1979)
Perelman, D., Fan, R., Keidar, I.: On maintaining multiple versions in STM. In: Proceedings of PODC’10: The 29th ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing (2010)
Ramadan, H.E., Roy, I., Herlihy, M., Witchel, E.: Committing conflicting transactions in an STM. In: Proceedings of PPoPP’09: The 14th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (2009)
Ringenburg, M.F., Grossman, D.: AtomCaml: first-class atomicity via rollback. In: Proceedings of ICFP’05: The 10th ACM SIGPLAN International Conference on Functional Programming (2005)
Saad, M.M., Kishi, M.J., Jing, S., Hans, S., Palmieri, R.: Processing transactions in a predefined order. In: Proceedings of PPoPP’19: The 24th Symposium on Principles and Practice of Parallel Programming (2019)
Saha, B., Adl-Tabatabai, A., Hudson, R.L., Minh, C.C., Hertzberg, B.: McRT-STM: a high performance software transactional memory system for a multi-core runtime. In: Proceedings of PPoPP’06: The ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (2006)
Shavit, N., Touitou, D.: Software transactional memory. In: Proceedings of PODC’95: The 14th ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing (1995)
Siek, K., Wojciechowski, P.T.: Atomic RMI 2: highly parallel pessimistic distributed transactional memory. abs/1606.03928 (2016). arXiv:1606.03928
Siek, K., Wojciechowski, P.T.: Atomic RMI: a distributed transactional memory framework. Int. J. Parallel Program. 44(3), 598–619 (2016)
Skare, T., Kozyrakis, C.: Early release: friend or foe? In: Proceedings of WTW’06: The Workshop on Transactional Memory Workloads (2006)
Weihl, W.E.: Local atomicity properties: modular concurrency control for abstract data types. ACM Trans. Program. Lang. Syst. 11(2), 249–282 (1989)
Weikum, G., Vossen, G.: Transactional Information Systems: Theory, Algorithms, and the Practice of Concurrency Control and Recovery. Morgan Kaufmann Publishers, Burlington (2002)
Welc, A., Saha, B., Adl-Tabatabai, A.R.: Irrevocable transactions and their applications. In: Proceedings of SPAA’08: The 20th ACM Symposium on Parallelism in Algorithms and Architectures (2008)
Wojciechowski, P.T.: Isolation-only transactions by typing and versioning. In: Proceedings of PPDP’05: The 7th ACM SIGPLAN International Symposium on Principles and Practice of Declarative Programming (2005)
Wojciechowski, P.T.: Language Design for Atomicity, Declarative Synchronization, and Dynamic Update in Communicating Systems. Publishing House of Poznań University of Technology, Poznan (2007)
Wojciechowski, P.T., Rütti, O., Schiper, A.: SAMOA: a framework for a synchronisation-augmented microprotocol approach. In: Proceedings of IPDPS’04: The 18th IEEE International Parallel and Distributed Processing Symposium (2004)
Acknowledgements
We would like to thank the anonymous reviewers for their diligence and insight that led to substantial improvements to our work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research leading to these results received funding from Polish National Science Centre, under Grant Agreement No. DEC-2012/07/B/ST6/01230. The first author was also supported by the Czech Ministry of Education, Youth, and Sports from the Czech Operational Programme Research, Development, and Education, under Grant Agreement No. CZ.02.1.01/0.0/0.0/15_003/0000421.
Appendix A: Property strength
Appendix A: Property strength
1.1 A.1 Last-use opacity
Below we compare last-use opacity to other properties and consistency conditions to determine their relative strength.
1.1.1 A.1.1 Last-use opacity versus opacity
Opacity is (strictly) stronger than last-use opacity.
Lemma 28
For any history S and transaction \(T_i \in S\), if \( Vis (S, T_i)\) is legal, then \( LVis (S,T_i)\) is legal.
Proof
By definition of \( Vis (S, T_i)\), if operation \( op \in Vis (S, T_i)\), then \( op \in Vis (S, T_i)\) only if \( op \in H|T_j\) and either \(i=j\) or \(T_j \prec _S T_i\) and \(T_j\) is committed. By definition of \( LVis (S,T_i)\), given transactions \(T_i, T_j\) and operation \( op \in S|{T_j}\), if \(i=j\) or \(T_j \prec _S T_i\) and \(T_j\) is committed, then \(S|T_j \subseteq LVis (S,T_i)\). Therefore \( LVis (S,T_i) \equiv Vis (S, T_i)\). Since both \( Vis (S, T_i)\) and \( LVis (S,T_i)\) preserve the order of operations in S, then both \( LVis (S,T_i)\) and \( Vis (S, T_i)\) are the same. Hence, if \( Vis (S, T_i)\) is legal, then \( LVis (S,T_i)\) is legal. \(\square \)
Lemma 29
Every final-state opaque history is restrained.
Proof
From Definition 11, for any final-state opaque history \(H\), there is a sequential history \(S \equiv Compl (H)\) s.t. S preserves the real time order of \(H\) and every transaction \(T_i\) in S is legal in S. Thus, for every transaction \(T_i\) in S \( Vis (S, T_i)\) is legal. Let \(T_i, T_j\) be any two transactions in \(H\). If \(T_i\) depends on \(T_j\) then there is a non-local write in \(T_j\) writing some value \( v \) to some variable \( x \) that some other transaction \(T_k\) (possibly \(k = i\)) reads. Since \(T_k\) is legal, then \(S|T_j \in \textit{Vis}({S,T_k})\), which implies that \(T_j\) is not aborted. Then it is true that either \(T_i\) depends on \(T_j\) or that \(T_j\) aborts, but not both. Therefore, \(H\) is restrained. \(\square \)
Lemma 30
Every final-state opaque history is final-state last-use–opaque.
Proof
From Definition 11, for any final-state opaque history \(H\), there is a sequential history \(S \equiv Compl (H)\) s.t. S preserves the real time order of \(H\) and every transaction \(T_i\) in S is legal in S. Thus, for every transaction \(T_i\) in S \( Vis (S, T_i)\) is legal. From the definition of completion, any \(T_i\) is either committed or aborted in \( Compl (H)\) and therefore likewise completed or aborted in S. If \(T_i\) is committed in S, then it is legal in S, so \( Vis (S, T_i)\) is legal, and therefore \(T_i\) is last-use legal in S. If \(T_i\) is aborted in S, then it is legal in S, so \( Vis (S, T_i)\) is legal, and therefore, from Lemma 28, \( LVis (S,T_i)\) is also legal, so \(T_i\) is last-use legal in S. Given that all transactions in S are last-use legal in S, and, from Lemma 29, \(H\) is restrained, then, from Definition 23, \(H\) is final-state last-use opaque. \(\square \)
Lemma 31
Every opaque history \(H\) is last-use–opaque.
Proof
If \(H\) is opaque, then, from Definition 12, any prefix P of \(H\) is final-state opaque. Since any prefix P of \(H\) is final-state opaque, then, from Lemma 30, any P is also final-state last-use opaque. Then, by Definition 24\(H\) is last-use opaque. \(\square \)
1.1.2 A.1.2 Last-use opacity versus serializability
Last-use opacity is (strictly) stronger than serializability as shown in Lemma 23.
1.1.3 A.1.3 Last-use opacity versus virtual world consistency
VWC is incomparable to last-use opacity.
VWC history example [24]
TMS1 history example [13]
Lemma 32
There exists a last-use–opaque history \(H\) that is not virtual world consistent.
Proof
Since last-use opacity supports aborting prerelease (Lemma 27), then by Definition 3 and by Definition 5 there exists some last-use–opaque history where some transaction reads from a live transaction which subsequently aborts. Since, by Lemma 16, VWC does not support aborting releasing transactions, then, by the same definitions, such a history is not VWC. Hence a history with a transaction prereleasing may be last-use–opaque but not VWC. \(\square \)
Lemma 33
There exists a virtual world consistent history H that is not last-use–opaque.
Proof
Let history \(H\) be the history presented in Fig. 28. In [24] (Fig. 2 therein) the authors declare that the history satisfies VWC. The same history is not last-use opaque, because for any witness history S, \( LVis (S,T_l)\) must contain \(H|T_j \cdot H|T_k \cdot H|T_l\). Since \( r ^{}({ x }){1}\) is preceded in \( LVis (S,T_l)\) by \( w ^{}({ x }){2}\), then \( LVis (S,T_l)\) is not legal. Thus, \(H\) is not final-state last-use opaque, and so \(H\) is not last-use opaque. \(\square \)
1.1.4 A.1.4 Last-use opacity versus transactional memory specification
TMS1 is incomparable to last-use opacity.
Lemma 34
There exists a last-use–opaque history H that is not TMS1.
Proof
Since last-use opacity supports aborting prerelease (Lemma 27), then from Definition 5 it necessarily follows that it supports prerelease. In that case, if follows from Definition 3 that there exists some last-use–opaque history where some transaction reads from a live transaction which subsequently aborts. Since, by Lemma 13 TMS1, does not support prerelease, then, by the same definitions, histories containing prerelease are not TMS1. Hence a history with a transaction prereleasing may be last-use–opaque but not TMS1. \(\square \)
Lemma 35
There exists a TMS1 history \(H\) that is not last-use–opaque.
Proof
Let history \(H\) be the history presented in Fig. 29. In [13] (Fig. 6 therein) the authors show that the history satisfies TMS1. The same history is not last-use opaque. Note that if \( Vis (S, T_i)\) is to be legal, in any S equivalent to \(H\), \(T_i \prec _S T_j\), because \(T_i\) reads 0 from \( x \) and \(T_j\) writes 2 to \( x \) (and commits). In addition, \(T_j \prec _S T_l\), because \(T_l\) reads 2 from \( x \) and \(T_k \prec _S T_l\), because \(T_l\) reads \( z \) from \(T_k\). Then, by extension \(T_i \prec _S T_j \prec _S T_l\). However, note that in any S it must be that \(T_l \prec _S T_i\), because \(T_l\) reads 0 for \( y \), which is a contradiction. Thus, \(H\) is not last-use opaque. \(\square \)
TMS2 is (strictly) stronger than last-use opacity.
Proposition 1
All TMS2 histories are last-use–opaque.
Proof
The authors of [13] believe (but do not demonstrate) that every execution allowed by TMS2 also satisfies opacity (modulo cosmetic interface differences). If this is the case, then, since all opaque histories are last-use–opaque (Lemma 31), then it is true that all TMS2 histories satisfy last-use-opacity. Thus, we believe the proposition is true, pending a demonstration that all TMS2 histories satisfy opacity. \(\square \)
1.1.5 A.1.5 Last-use opacity versus cascadelessness
Cascadelessness is incomparable to last-use opacity.
Lemma 36
There exists a last-use–opaque history \(H\) that is not cascadeless.
Proof
Let \(H\) be the history in Fig. 11. Since \(T_j\) reads from \(T_i\) in \(H\) and \( r _{j}({ x })\!\rightarrow \!{1} \prec _{H} tryC _i\!\rightarrow \! C _i\) the history is not cascadeless, since it contradicts Definition 9. Let \(C= Compl (H)\) s.t. \(H=C\), and let \(\hat{S}_{H}\) be a sequential history s.t. \(\hat{S}_{H}= C|T_i \cdot C|T_j\). Then \( Vis (\hat{S}_{H}, T_i) = \hat{S}_{H}|T_i = [ w _{i}({ x }){1}\!\rightarrow \!{ ok _i}]\) and \( LVis (\hat{S}_{H},T_j)=\hat{S}_{H}|T_i \cdot \hat{S}_{H}|T_j = [ w _{i}({ x }){1}\!\rightarrow \!{ ok _i}, r _{j}({ x })\!\rightarrow \!{1}]\). Trivially, \( Vis (\hat{S}_{H}, T_i)\) and \( LVis (\hat{S}_{H},T_j)\) are both legal, so \(T_i\) is committed and legal, and \(T_j\) is last-use legal. Thus \(H\) is final-state last-use opaque. By analogy, all prefixes of \(H\) are also final-state last-use opaque, so \(H\) is last-use opaque. \(\square \)
Lemma 37
There exists a cascadeless history \(H\) that is not last-use–opaque.
Proof
The history in Fig. 30 is shown to be cascadeless (ACA) in [5]. However, note, that \( Compl (H) = H\), and given any sequential \(S \equiv Compl (H)\) \(T_k\) must follow both \(T_i\) and \(T_j\) in S because \(T_k\) reads from both transactions. Since \(T_i \prec _H T_j\) and \(T_i \prec _H T_k\), then \(T_i\) must precede both other transactions in S.
Hence, \(S = H|T_i \cdot H|T_j \cdot H|T_k\), so \( Vis (S, T_k) = S\) and therefore \( Vis (S, T_k)\) is illegal because \( r _{k}({ x })\!\rightarrow \!{1}\) is preceded in \( Vis (S, T_k)| x \) by \( w _{j}({ x }){2}\!\rightarrow \!{ok_j}\). \(\square \)
1.1.6 A.1.6 Last-use opacity versus elastic opacity
Last-use Opacity and elastic opacity are incomparable.
Lemma 38
There exists an elastic opaque history \(H\) that is not last-use–opaque.
Proof
Since elastic opaque histories may not be serializable [15], and since, as all last-use–opaque histories trivially require serializability then some elastic opaque histories are not last-use–opaque. \(\square \)
Lemma 39
There exists a last-use–opaque history \(H\) that is not elastic opaque.
Proof
Let history \(H\) be the history presented in Fig. 31. It should be straightforward to see that \(H\) is last-use–opaque for an equivalent sequential history \(S=H|T_i \cdot H|T_j\). Operations on \( z \) are always justified in any sequential equivalent history since they are all within \(T_i\) and their effects are not visible in \(T_j\). The read operation on \( y \) is expected to read 0 since it is not preceded in S by any write, and it does read 0. Thus operations on \( y \) and \( z \) will not break legality of either \(T_i\) or \(T_j\). With that in mind, the history can be shown to be last-use opaque by analogy to Lemma 36.
On the other hand, let \(T_i\) be an elastic transaction. The only possible well-formed cut of \(H|T_i\) is \(C_i = \{ [ r _{}({z})\!\rightarrow \!{0}, w _{}({x}){1}\!\rightarrow \!{ ok }, \) \( r _{}({y})\!\rightarrow \!{0}, w _{}({y}){1}\!\rightarrow \!{ ok } ] \}\). (In particular, the following cut is not well-formed, since \( w _{}({x}){1}\!\rightarrow \!{ ok }\) and \( w _{}({y}){0}\!\rightarrow \!{ ok }\) are in two different subhistories of the cut: \(C_i' = \{ [ r _{}({z})\!\rightarrow \!{0}, w _{}({x}){1}\!\rightarrow \!{ ok } ], [ r _{}({y})\!\rightarrow \!{0},\) \( w _{}({y}){1}\!\rightarrow \!{ ok } ] \}\)). Let \(f_C(H)\) be a cutting function that applies cut C. Then, since the cut contains only one subhistory, it should be straightforward to see that \(f_C(H) = H\). Then, we note that \(H\) contains an operation in \(H|T_j\) that reads the value of \( x \) from \(H|T_i\) and \(T_i\) is live. That means that in the prefix P of H s.t. \(H = P \cdot [ tryC _i\!\rightarrow \! C _i, tryC _j\!\rightarrow \! C _j]\) both transactions will be aborted in any completion of P, so for any sequential equivalent history S \( Vis (S, T_i)\) will not contain \(S|T_j\), since \(T_j\) is aborted in any S. Therefore \( Vis (S, T_i)\) will not justify reading 1 from \( x \) and will not be legal, causing P not to be final state opaque (Definition 11), which in turn means that \(H\) is not opaque (Definition 12). \(\square \)
1.1.7 A.1.7 Last-use opacity versus recoverability
Last-use opacity is (strictly) stronger than recoverability.
Lemma 40
Every last-use–opaque history H is recoverable.
Proof
From Lemma 25. \(\square \)
1.1.8 A.1.8 Last-use opacity versus strictness
Strictness and last-use opacity are also incomparable.
Lemma 41
There exists a last-use–opaque history H that is not strict.
Proof
Since any strict history is also ACA [5], and since Lemma 36 shows that not all last-use–opaque histories are ACA, then not all last-use–opaque histories are strict. \(\square \)
Lemma 42
There exists a strict history H that is not last-use–opaque.
Proof
The history in Fig. 30 is shown to be strict in [5].
However, as we show in Lemma 37, this history is not last-use–opaque. \(\square \)
1.1.9 A.1.9 Last-use opacity versus rigorousness
Rigorousness is (strictly) stronger than last-use opacity.
Lemma 43
Every rigorous history H is last-use–opaque.
Proof
Since [5] demonstrates that rigorous histories are opaque, and since we show in Lemma 31 that opaque histories are also last-use–opaque, then all rigorous histories are last-use–opaque. \(\square \)
1.1.10 A.1.10 Last-use opacity versus live opacity
Live opacity is (strictly) stronger than last-use opacity.
Lemma 44
Every live opaque history is restrained.
Proof
Let \(H\) be a live opaque history. Let S be any sequential history that justifies the serializability of \(H\), and let \(S'\) be any sequential extension of S in accordance to Definition 17. Let \(T_i, T_j\) be any two transactions in \(H\). If \(T_i\) depends on \(T_j\) then there is a non-local write in \(T_j\) writing some value \( v \) to some variable \( x \) that some other transaction \(T_k\) (possibly \(k = i\)) reads. Since S is legal, and since \(T_j^{gr}\) does not contain write operations, then it must be true that \(T_j \in S\) (as opposed to \(T_j^{gr} \in S\)). That means that \(T_j\) does not abort. Then it is true that either \(T_i\) depends on \(T_j\) or that \(T_j\) aborts, but not both. Therefore, \(H\) is restrained. \(\square \)
Lemma 45
Every live opaque history \(H\) is last-use–opaque.
Proof
Since \(H\) is live opaque there exists a sequential history S that justifies serializability of \(H\) and an extension \(S'\) of S where if transaction \(T_i\) is not in S then it is replaced in \(S'\) by \(T_i^{gr}\) containing only non-local reads. \(S'\) is legal and preserves the real-time order of \(H\) (accounting for replaced transactions). In addition, from Lemma 19, no transaction in \(H\) reads from a live transaction (in any prefix of \(H\)). Therefore, since \(S'\) is legal, any read operation \( op _i = r _{i}({ x })\!\rightarrow \!{ v }\) in \(H\) that is preceded by \( w _{j}({ x }){ v }\!\rightarrow \!{ u }\) in \(H\), \(T_j\) is committed in S and is included in \(S'\) in full.
Let \(S''\) be a sequential history constructed by replacing the operations removed to create \(S'\) where if \(T_i \in H\) and \(T_i \not \in S\) then \(T_i\) is aborted in \(S''\). \(S''\) preserves the real time order of \(H\) and \(S'' \equiv H\). Note that, since \(S'\) is legal, if some write \( op ^w\) is in \(S''\) and not in \(S'\), then there is no non-local read operation \( op ^r\) reading the value written by \( op ^w\). Hence any operation reading the value written by \( op ^w\) is local, and since all local reads in transactions that are replaced in \(S'\) read legal values (by Definition 17), then all reads reading from any \( op _w\) read legal values in \(S''\). Since \(S'\) is legal, then all reads reading from transactions that are in S read legal values in \(S'\). Since \(S'' \equiv H\), then these read and write operations also read legal values in \(S''\). Because of this, and since no transaction reads from another live transaction, \( Vis (S'', T_i)\) will be legal for any transaction in \(S''\). In addition, \( LVis (S'',T_i)\) will be legal for any aborted transaction in \(S''\). Therefore, and given that any live opaque \(H\) is restrained (Lemma 44), any live opaque \(H\) will be final state last-use opaque. Since any prefix of \(H\) is also live opaque, then any prefix will also be final-state last-use opaque, hence \(H\) is last-use opaque. \(\square \)
1.1.11 A.1.11 Last-use opacity versus markability
Lemma 46
Every markable history \(H\) is last-use–opaque.
Proof
Trivially from Lemma 31. \(\square \)
1.1.12 A.1.12 Last-use opacity versus commitment order preservation
CO and last-use opacity are incomparable.
Lemma 47
There exists a last-use–opaque history H that is not CO.
Proof
Let \(H\) be the history in Fig. 18. Since both \(H|T_i\) and \(H|T_j\) each contain a single write operation on \( x \), then for any equivalent sequential history \(\hat{S}_{H}\), all of \( Vis (\hat{S}_{H}, T_i)\), \( Vis (\hat{S}_{H}, T_j)\), \( LVis (\hat{S}_{H},T_i)\), and \( LVis (\hat{S}_{H},T_j)\) are always legal. Hence, \(H\) is final-state last-use opaque. Since the conclusion follows for any prefix of \(H\), then any prefix is final-state last-use opaque, and \(H\) is last-use opaque. However, since \(T_i\) and \(T_j\) conflict, and since \(T_i\) executes its write on \( x \) before \(T_j\), but \(T_j\) commits before \(T_i\), then \(H\) is not CO. \(\square \)
Lemma 48
There exists a CO history H that is not last-use opaque.
Proof
We show in Lemma 5 that CO supports overwriting, so by Definition 4, there exists some \(H\) that contains overwriting and satisfies CO. We show in Lemma 26 that last-use opacity precludes overwriting, so such \(H\) is not last-use opaque. \(\square \)
1.2 A.2 Strong last-use opacity
Strong last-use opacity is strictly stronger than last-use opacity.
Lemma 49
For any history S and transaction \(T_i \in S\), if \( SLVis (S,T_i)\) is legal, then \( LVis (S,T_i)\) is legal.
Proof
Given \( SLVis (S,T_i)\) and \( LVis (S,T_i)\) and some operation \( op \in H|T_j\), then from definitions of \( SLVis \) and \( LVis \):
-
(a)
\(i=j\) or both \(T_j\) is committed in S and \(T_j \prec _S T_i\) then \( op \in SLVis (S,T_i)\) and \( op \in LVis (S,T_i)\).
-
(b)
if \(T_j\) is not committed in S but \(T_j \in \hat{\mathbb {T}}^{H} \cap \underline{\hat{\mathbb {T}}}^{H}\) and \(T_j \prec _S T_i\), and it is not true that \(T_j \prec _HT_i\), then either both \( op \in SLVis (S,T_i)\) and \( op \in LVis (S,T_i)\) or both \( op \not \in SLVis (S,T_i)\) and \( op \not \in LVis (S,T_i)\).
Then \( op \in Vis (S, T_i)\) only if it is true that \( op \in H|T_j\) and in addition either \(i=j\) or both \(T_j \prec _S T_i\) and \(T_j\) is committed. By definition of \( SLVis (S,T_i)\), given transactions \(T_i, T_j\) and operation \( op \in S|{T_j}\), if \(i=j\) or \(T_j \prec _S T_i\) and \(T_j\) is committed, then \(S|T_j \subseteq SLVis (S,T_i)\). Therefore \( SLVis (S,T_i) \equiv Vis (S, T_i)\). Since \( Vis (S, T_i)\) and \( SLVis (S,T_i)\) preserve the order of operations in S, then \( SLVis (S,T_i) = Vis (S, T_i)\). Hence, if \( Vis (S, T_i)\) is legal, then \( SLVis (S,T_i)\) is legal. \(\square \)
Corollary 18
Any strongly last-use opaque history \(H\) is last-use–opaque.
The remaining proofs are by analogy to Sect. A. 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Siek, K., Wojciechowski, P.T. Last-use opacity: a strong safety property for transactional memory with prerelease support. Distrib. Comput. 35, 265–301 (2022). https://doi.org/10.1007/s00446-022-00420-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00446-022-00420-2







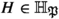 is also in
is also in  ,
, and
and  .
. :
: :
: :
:



























