1 Introduction

Many financial decision problems involve the forecasting of future liability cash flows. For insurance products, the planning horizon extends beyond a decade: for example, pension funds have a planning horizon of more than 30 years. So, for an insurance company operating in life business, it is essential to build a model to forecast the evolution of cash inflows and outflows over time. All the techniques and the models used by a company to address financial risk due to the mismatching between assets and liabilities portfolios are part of the Asset Liability Management (ALM). The traditional ALM programs focus on interest rate risk and liquidity risk, but, depending on the business model of the company, the specific definition of the underlying models for the assets and liabilities may vary.

Historically, the first ALM methods were developed starting from the milestone works by Macaulay (1938), Samuelson (1945), Redington (1952) and Fisher and Weil (2017), ordered according to the publication year. In these earlier models, the bond immunization, i.e., the matching between bond portfolio interest rate sensitivity and liability streams interest rate sensitivity, was the unique subject. These models are single stage models and do not take into account the stochastic evolution of interest rate since they use only the duration, or at most also the convexity, as risk measure. Nowadays, these techniques are unsuitable for an insurance company due to the complexity of both the asset portfolio and the liability portfolio. An insurance asset portfolio is not composed only of plain vanilla bonds and liquidity, but also of subordinated bonds which have embedded options (typically call options), structured bonds, no fixed income products, such as stocks, hedge funds, private equity and real asset products (see Zenios 1995). However, when dealing with ALM models, the real challenge lies in the liability side. Due to the presence of surrender options, death benefits and other random features, an ALM model has to capture the stochastic dynamics and the uncertain characteristics inherent with insurance policies. The presence of these options with early exercise and asymmetric distribution makes essential the development of a suitable valuation functionality, not only to evaluate the company’s balance sheet at current date, but also to simulate the firm’s position at future dates.

So, a company needs to develop an ALM tool able to forecast its balance sheet evolution over time predicting future cash inflows and outflows, in order to ensure the solvency of the company, i.e., its capability to meet all its financial obligations. A correct forecasting of the evolution of the balance sheet, including cash flow generation, and the calculation of duration and convexity mismatching allow to manage the risk of future unexpected cash flows that could compromise the business of the firm.

But the aim of an ALM tool does not end here, because the purpose of ALM is to satisfy the interests of shareholders, policyholders and regulators in a common framework. Therefore, an ALM tool includes the allocation of assets to increase the profit of the company. The insurer invests in a portfolio the return of which is consistent with the offering of competitive products, in the shareholders’ and policyholders’ interest, while satisfying the regulators. In this sense, ALM stands between risk management and strategic asset allocation, having the purpose of maximizing the investment returns, while minimizing the reinvestment risks. A complete guide on ALM models can be found in Zenios and Ziemba (2006) and Zenios and Ziemba (2007) and in the references therein.

It is clear that these models have a particular relevance in life insurance industry, even more after the introduction of the Solvency Capital Requirement computed under Solvency II Directive (see Sandström 2016; Wüthrich and Merz 2013), based on the computation of the 99.5% Value-at-Risk over one year of company’s own funds, so that a proper joint estimation of both assets and liabilities values becomes essential.

The literature of ALM models for life insurance companies is very wide. We refer to Ballotta et al. (2006), Bauer et al. (2006), Gerstner et al. (2008) and Møller and Steffensen (2007) and the references therein. In the life insurance sector, the presence of embedded options in policies makes very difficult to correctly forecast the cash outflows [the problem of the pricing of embedded options has been widely treated in literature, see, for example, Bacinello (2003a, 2003b, 2005), Grosen and Jørgensen (2000) and Milevsky and Salisbury (2006)]. The need of a more accurate approximation of the portfolio evolution over time, especially on liabilities side, jointly with the increase in computational power, makes feasible and suitable for an insurance firm the development of a stochastic scenario-based ALM model. In fact, significant resources have been invested into the development of such models, specially in insurance companies. Naturally, a trade off between complexity and practicality is always involved.

Starting from the seminal works by Bradley and Crane (1972) and by Lane and Hutchinson (1980), dynamic stochastic programming techniques have been applied to ALM models. In particular, Bradley and Crane were the first to use a dynamic recourse programming in a portfolio problem restricted to fixed interest securities. Stochastic programming in the form of a multistage recourse problem is a general formulation of a multistage ALM model in which the objective function is typically characterized in terms of the expected value of a linear or nonlinear utility function of wealth at the horizon (see Dempster 1980). This approach has become very popular in finance both among academics and practitioners. The literature on the application of stochastic programming with recourse to ALM models is very wide. An interested reader could find some of these applications in Cariño et al. (1994), Consigli and Dempster (1998), Dantzig and Infanger (1993), Dempster and Ireland (1991), Grebeck and Rachev (2005) and Zenios (1995). Recently, Fernández et al in Fernández et al. (2018) have presented an ALM model for a life insurance company together with its numerical simulations performed in a new high-performance computing architectures provided by GPUs technology. They consider a portfolio comprising with-profit life insurance policies with some innovations with respect to literature in the modeling of the surrenders of the policyholders. However, in the estimate of future supposed liabilities cash flows, they take into account neither possible future surrenders nor the so-called new production, i.e., the cash flows due to new policyholders which subscribe to the policy at future times.

In this paper, we build a two-stage stochastic ALM model for a life insurance company’s portfolio. First, we propose a multistep reinvestment strategy using a scenario-based approach in which the assets and the liabilities are jointly simulated using appropriated stochastic models. On the asset side, we consider a portfolio composed of bonds, divided in buckets of duration, stocks and cash. On the liability side, we consider a portfolio comprising with-profit life insurance policies, such that policyholders’ saving account earns a rate given by the maximum between a minimum guaranteed rate of return and a percentage, called participation rate, of the asset portfolio return. In order to keep track of the evolution of the liability portfolio, we take into account, in addition to the policyholders’ saving account model, the biometric model and the surrender model. Also, we consider cash flows due to new production. The question of the issue of new policies has been investigated in previous works (see, for example, Eckert et al. 2020; Hieber et al. 2019; Orozco-Garcia and Schmeiser 2019), but we propose, as far as we know, an innovative approach to this feature with respect to existing literature. At each time step k, we jointly simulate all the random variables of the model and, then, we compute asset duration and liability duration, estimating the projections of all future cash flows, made up of death, maturity and surrender payments, also related to new production. To the best of our knowledge, the fact that we consider also cash flows due to future surrenders and new production when computing balance sheet projections constitutes an innovation with respect to literature and allows to better forecast the evolution of the balance sheet of an insurance company, therefore to compute more reliable estimates of actuarial reserves and of probabilities of default. From the technical point of view, it leads to the need to estimate conditional expectations with respect to the information available at time step k, so that we employ a Least Squares Monte Carlo technique. At each time step k, after having computed the duration of asset portfolio and of liability portfolio, we perform a rebalancing of the asset portfolio by solving a nonlinearly constrained optimization problem in which we minimize the distance between the asset duration and the liability duration, subject to the achievement of a target return and other constraints that are typical for an asset allocation problem. Indeed, we consider real world constraints, such as the so-called budget constraint, constraints that do not allow short sales, constraints on the upper and on the lower bounds for the size of a single asset class weight or of a combination of asset classes weights, constraints on single (on one asset class) and on portfolio turnover. This dynamic portfolio rebalancing strategy allows to simultaneously satisfy the interest of shareholders and policyholders. Indeed, the minimization of the distance between asset duration and liability duration permits to guarantee the solvency of the company, whereas the achievement of a target return allows to build a competitive portfolio. Since the decision rules previously described do not build an optimal dynamic reinvestment strategy, we propose a second stage of portfolio optimization in order to maximize the expected value of a chosen utility function, using the results obtained from the previous rebalancing strategy as investment constraints. However, we focus our analysis on the first stage of portfolio rebalancing strategy and we do not perform any tests on the second stage of the portfolio optimization that requires standard stochastic programming techniques (see, for example, Dempster 1980), leaving the choice of a specific utility function and of the final wealth to the investment officer of the firm.

In order to test our ALM model, we firstly present our portfolio rebalancing strategy under certain market hypotheses and initial scenario assumptions. Moreover, we focus on the evolution over time of the number of alive policies that is affected by the mortality model as well as by the surrender and new production models. Finally, an analysis of the participation rate sensitivity is conducted by keeping track of the evolution over time of actuarial reserves, that is to say, the discounted value of all future cash flows on the liability side, and of own funds, and by investigating default probability.

The paper is organized as follows. In Sect. 2, we define our asset portfolio and liability portfolio, and we introduce the general features of our ALM model. In Sect. 3, we focus on the liability model and on the computation of liability duration that requires the estimation of future firm’s cash flows, consisting of maturity, death and surrender payments, also related to new production, and entails the definition of a mortality model as well as a surrender and new production model. Moreover, we introduce the interest rate model associated with the term structure of interest rates. In Sect. 4, we deal with the asset model, thus presenting bonds, equity and cash models. Then, in Sect. 5, we introduce the nonlinearly constrained rebalancing rules to solve in order to dynamically restructure the asset portfolio. We consider several real world constraints. In Sect. 6, we give an overview of the second stage of the portfolio optimization. In Sect. 7, we describe market data, and in Sect. 8 we present and analyze some numerical results. Finally, in Sect. 9, we point out the main conclusions.

2 The model

We build a stochastic ALM model with dynamic reinvestment strategy for a life insurance company’s portfolio. Therefore, we deal with both a liability portfolio and an asset portfolio, that is regularly rebalanced in order to not only obtain a certain portfolio return, but also to be able to meet future financial obligations. In order to properly rebalance the company’s portfolio, we need to forecast the balance sheet evolution over time, computing the joint projections of the future cash flows of both liabilities and assets portfolios.

Table 1 Simplified life insurance company’s balance sheet
Full size table

A simplified balance sheet for a life insurance company is summarized in Table 1. The last item, equity capital, consists of the surplus which is kept by the company’s shareholders and is defined by:

$$\begin{aligned} \text {Equity capital} = \text {Assets} - \text {Present value of life insurance policies}. \end{aligned}$$
(1)

On the asset side, we consider a portfolio composed of bonds, divided in buckets of duration, equity and cash. Bonds, equity and cash are simulated together over time according to stochastic models. The need of an insurance company to have a conservative investment strategy, as required by regulators (Braun et al. 2017), is reinforced in our model from the fact that in the case of with-profit life policies a more aggressive investment strategy would represent an advantage for policyholders, but an excessive risk of shareholders. In fact, policyholders would benefit from high returns and would not be hit by negative returns, since a minimum rate of return is guaranteed, while shareholders would be hit by negative returns and would barely benefit from positive returns, since only a small percentage of returns is kept by the company’s shareholders. Therefore, the company refrains from following a more aggressive investment strategy. For these reasons, we hold larger positions in fixed-income assets, and we allocate a smaller percentage of the total in stocks. Moreover, we consider some real investment policy constraints on portfolio asset classes weights and on particular combinations of them.

On the liabilities side, we consider a portfolio only comprising the so-called with-profit life policies, a type of products that is very popular in life insurance business. In these contracts, on the one hand, the policyholder pays a premium that can be either single, paid at the beginning of the contract, or periodic, paid with a certain frequency during the policy life. On the other hand, the insurer receives the premiums and invests this capital in the financial market. Moreover, the insurer pays both a periodic variable rate in a policyholder saving account and a benefit that is disbursed at policy maturity date, if the policyholder is still alive, or before policy maturity date, if the contract ends before policy expiration, because the policyholder dies or decides to exercise the surrender option, if the contract entitles to abandon the policy before maturity. Our ALM model includes the surrender option. Also, we consider the possibility that policyholders do not enter into the policy all together, say at time 0, but there is the chance that a policyholder signs the contract in the following years, thus creating the so-called new production. In summary, we consider the most important features of a with-profit life policy:

  • policyholders’ saving account grows at a rate given by the maximum between a minimum guaranteed rate of return and a fraction of the asset portfolio return;

  • a mortality model is taken into account to keep track of death occurrences;

  • policyholders are entitled to surrender the contract at any time before the maturity date;

  • cash flows due to the so-called new production are included.

In our model, the insurance company has to refund the beneficiaries of policies of policyholders that die before the maturity date, the policyholders that abandon the contract before policy expiration, as well as policyholders that are still alive when their policies expire. Except from the timing of payments due to the maturity of the policies, the timing of all the other payments is uncertain and depends on the market evolution and on the stochastic behavior of policyholders’ biometry. More precisely, the decision to abandon the contract before policy expiration and new production strongly depend on stochastic economic variables. Indeed, we infer the probability that a policyholder cancels the contract before maturity or that a new policyholder subscribes to the policy comparing the earnings offered by the policy with the earnings offered by competing products in the market, represented by the return of a suitable benchmark index chosen from the market. This issue is fully addressed in Sect. 3.1. In contrast with surrender events and new production, death occurrences are actuarial events, that are usually assumed independent of economic variables. Therefore, in order to infer the number of policyholders that die before policy expiration, we follow a biometric model, based on a life table in which the survival probability of a policyholder is only dependent on age and gender. More details about the mortality model are given in Sect. 3.2.

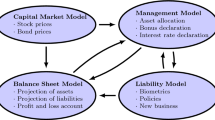
Our ALM model is summarized in Table 2.

Table 2 ALM model
Full size table

Since the set of contracts could be very copious and, also, each insurance contract could offer a different guaranteed rate of return, could be signed by policyholders of different ages and could expire at different dates, computing the joint projections of the future cash flows of both assets and liabilities portfolios for each contract can lead to a highly time-consuming task. In order to manage this issue, as in Fernández et al. (2018), we group policies with similar characteristics in buckets, called model points, thus reducing the computational cost of the calculus. More details on how to build the model points can be found in Jansen (2008), for instance. Thus, our liability portfolio is given by the set of model points, \(I = \{m_i/ m_i \text { is a model point}\}\), with cardinality \(N_M := \vert I\vert \), so that we will work on a representative set of contracts. More precisely, in order to handle the heterogeneity of the plethora of different contracts in the liabilities portfolio, we gather together policies with similar minimum guaranteed rate of return, similar age of the policyholder and same maturity date. For example, in Sect. 8, where some numerical results are shown, we suppose that all the policies in our liabilities portfolio expire in 10 years, and that some of these contracts offer a minimum guaranteed rate of return of 0%, others of 1% and still others of 2%. Moreover, contracts are signed by policyholders aged from 38 to 67. We split the contracts in model points as shown in Table 3.

Table 3 Example of representative contracts (model points) for different policyholders’ ages and different minimum guaranteed rates of return
Full size table

In conclusion of the general description of our ALM model, we introduce the possibility of default of the insurance company. Indeed, if a policyholder dies, abandons the contract or is still alive at policy maturity date, the company has to pay a refund based on the value of the policyholder’s saving account that, as said before, earns an interest rate given by the maximum between a minimum guaranteed rate of return and a percentage of the return on the insurer’s investment portfolio. Therefore, the company needs to use the capital that comes from new production if portfolio return is not sufficient to meet its liabilities, and, if there are not enough new policyholders, the company employs its own funds. If own funds become negative, the company is declared defaulted.

3 Liability model

In this section, we describe how we model the cash flows connected to policyholders’ benefits and premiums. Whereas some cash flows are scheduled, such as cash flows related to maturity payments, the timing of other cash flows is not known a priori and can depend either on the market situation, in the case of payments due to surrender option and in the case of cash inflows due to new production, or on actuarial events, in the case of payments due to death occurrences.

We consider a time discretization given by a mesh of equispaced time instants, \(0=t_0< t_1< \ldots < t_N=T\), and we define the period k as \([t_k,t_{k+1}]\), for \(k=0,\ldots ,T-1\). In each period, we assume that premiums are paid at the beginning while benefits are disbursed at the end. Administrative costs are included in the premium.

At each period, we need to keep track not only of the number of alive policyholders, but also of the number of policyholders that die or exercise the surrender option, of the number of policies that expire, as well as of the number of new policyholder that subscribe to a contract. Therefore, we introduce the following notations:

  • \({_s}n_{k,i}\) is the number of policyholders in the model point \(m_i \in I\) that entered into the contract at time s and are still alive at the end of period k;

  • \(n_{k,i}\) is the total number of alive policyholders in model point \(m_i \in I\) at the end of period k, independently from their starting times, so that

    $$\begin{aligned} n_{k,i} = \sum _{s=0}^{T-1} {_s}n_{k,i}; \end{aligned}$$

  • \({_s}n_{k,i}^D, {_s}n_{k,i}^S, {_s}n_{k,i}^M\) are the numbers of policyholders in model point \(m_i \in I\) that started the contract at time s and die, surrender or reach maturity at period k, respectively;

  • \(\varvec{n}_{k,i}^D, \varvec{n}_{k,i}^S\) and \(\varvec{n}_{k,i}^M\) are the vectors defined as:

    $$\begin{aligned} \varvec{n}_{k,i}^X = ({_0}n_{k,i}^X, {_1}n_{k,i}^X, \ldots , {_{k-1}}n_{k,i}^X),\ \ X=\{D,S,M\}; \end{aligned}$$
    (2)

  • \(n_{k,i}^P\) is the number of new policyholder in the ith model point that enters into the contract at period k.

In the biometric model used to determine the policyholders’ death rate, the distinction between men and women is taken into account. So, when the previous symbols present the superscript “\({\mathcal {M}}\)” or “\({\mathcal {F}}\),” they are referred only to the corresponding portion of male or female policyholders, respectively.

We denote by \({_s}l^D_{k,i}, {_s}l^S_{k,i}\) and \({_s}l^M_{k,i}\) the death, surrender and maturity benefits at period k for a policyholder in model point \(m_i\) that signed the contract at time s. They are the guaranteed payments in case of death of the policyholder, cancellation of the contract or policy expiration, respectively, and their sizes depend on policyholders’ saving account. The saving account of policyholders in model point \(m_i\) at period k grows at a rate given by \(\max (g_{k,i},\beta _{k,i} R^P_k)\), where \(g_{k,i}\) and \(\beta _{k,i}\) are the minimum guaranteed rate of return and the participation rate at period k for the model point \(m_i\), respectively, and \(R^P_k\) is the asset portfolio return at period k. Therefore, we assume death, surrender and maturity benefits at period k for a policyholder in model point \(m_i\) that entered into the contract at time s grow according to the recursive formula:

$$\begin{aligned} {\left\{ \begin{array}{ll} {_s}l^X_{s,i} = l^P_{s,i},\\ {_s}l^X_{k,i} = {_s}l^X_{k-1,i}\max (g_{k,i},\beta _{k,i} R^P_k) + l^{\Pi }_{k,i}, \ \ k > s, \end{array}\right. } \end{aligned}$$
(3)

where \(l^P_{s,i}\) is the payment made by the policyholder when entering into the contract at period s, and \(l^{\Pi }_{k,i}\) denotes the premium payment made by the policyholder at period k. In formula (3) X can be either D, S or M.

Note that we have made the assumption that the benefits in case of death, survival at maturity or surrender evolve over time according to the same recursive formula, but, in general, they may have different structures. For example, there can be some penalties in case of surrender and the minimum guaranteed rate and the participation rate can depend on X.

Finally, we denote by \(\varvec{l}^D_{k,i}, \varvec{l}^S_{k,i}\) and \(\varvec{l}^M_{k,i}\) the vectors given by:

$$\begin{aligned} \varvec{l}^X_{k,i} = ({_0}l^X_{k,i},{_1}l^X_{k,i},\ldots ,{_{k-1}}l^X_{k,i}), \ \ X = \{D,S,M\}. \end{aligned}$$
(4)

After having introduced the previous notations, we are able to list in the following the quantities we need to take into account to determine the cash flows at period k.

  • Premium payments, \(\Pi _k\). These are the payments made by policyholders at the beginning of period k, if still alive. At period k, premium payments related to model point \(m_i\) are given by:

    $$\begin{aligned} \Pi _{k,i} = n_{k-1,i} l^{\Pi }_{k,i}. \end{aligned}$$
    (5)

    Clearly, at period k the total amount of premium payments can be computed as follows:

    $$\begin{aligned} \Pi _k = \sum _{i=1}^{N_M} \Pi _{k,i}. \end{aligned}$$
    (6)

  • New production, \(P_k\). It consists of payments made by new policyholders at the beginning of period k. New production at period k for the model point \(m_i\) is defined as:

    $$\begin{aligned} P_{k,i} = n_{k,i}^P l^P_{k,i}, \end{aligned}$$
    (7)

    and the total amount of new production at period k is given by:

    $$\begin{aligned} P_k = \sum _{i=1}^{N_M} P_{k,i}. \end{aligned}$$
    (8)

  • Death payments, \(D_k\). These are the rewards that the company has to give to the beneficiaries of policies of policyholders that die before maturity at period k. Death payments related to model point \(m_i\) are given by:

    $$\begin{aligned} D_{k,i} = \varvec{n}_{k,i}^D \cdot \varvec{l}^D_{k,i}. \end{aligned}$$
    (9)

    Evidently, the total amount of death payments at period k is obtained as:

    $$\begin{aligned} D_k = \sum _{i=1}^{N_M} D_{k,i}. \end{aligned}$$
    (10)

  • Surrender payments, \(\Gamma _k\). They are made up of the refunds that the company has to give to policyholders that abandon the policy before its contractual expiration date at period k. For model point \(m_i\), we have:

    $$\begin{aligned} \Gamma _{k,i} = \varvec{n}_{k,i}^S \cdot \varvec{l}^S_{k,i}. \end{aligned}$$
    (11)

    The total amount of surrender payments at period k is given by:

    $$\begin{aligned} \Gamma _k = \sum _{i=1}^{N_M} \Gamma _{k,i}. \end{aligned}$$
    (12)

  • Maturity payments, \(M_k\). These are the payments that the company has to make due to policies in model point \(m_i\) that reach maturity at time k. Maturity payments at period k for model point \(m_i\) are defined as:

    $$\begin{aligned} M_{k,i} = \varvec{n}^M_{k,i} \cdot \varvec{l}^M_{k,i}, \end{aligned}$$
    (13)

    and the total amount of maturity payments at period k is obviously computed as:

    $$\begin{aligned} M_k = \sum _{i=1}^{N_M} M_{k,i}. \end{aligned}$$
    (14)

Liability value On the basis of previous definitions, we can write a formula to describe the evolution over time of the liability value. The value of liabilities related to model point \(m_i\) at time 0 is given by \(L_{0,i}=\Pi _{0,i}\), and, for \(k=1,\ldots ,T_i-1\), it evolves according to:

$$\begin{aligned} L_{k,i} = L_{k-1,i}(1 + \max (g_{k,i} ,\beta _{k,i} R^P_k)) + \Pi _{k,i} + P_{k,i} - D_{k,i} - \Gamma _{k,i}. \end{aligned}$$
(15)

Since \(T_i\) denotes the maturity date of policies in model point \(m_i, L_{k,i}=0\) for \(k\ge T_i\).

Cash flows We can write the total amount of cash flows at period k as:

$$\begin{aligned} cf_k = \displaystyle \sum _{i=1}^{N_M} cf_{k,i}. \end{aligned}$$
(16)

In the previous formula, \(cf_{k,i}\) denotes the size of cash flows at period k for model point \(m_i\), given by:

$$\begin{aligned} cf_{k,i} = \left\{ \begin{array}{ll} \Gamma _{k,i} + D_{k,i} &{} \text {if } t_k < T_i, \\ M_{k,i} + D_{k,i} &{} \text {if } t_k = T_i, \\ 0 &{} \text {otherwise}, \end{array}\right. \end{aligned}$$
(17)

where \(T_i\) denotes the maturity date of policies in the ith model point.

Liability duration In the literature of ALM models, the most commonly used risk measure is duration. In order to compute the duration of our liabilities, using the Macaulay duration formula, we have to estimate the so-called actuarial reserves that are the present value of the amount that the insurer needs at future periods to meet obligations associated with the policies. We denote by \(v_k\) the actuarial reserves at period k, and we have that:

$$\begin{aligned} v_{k} = \sum _{i=1}^{N_M} v_{k,i}, \end{aligned}$$
(18)

where \(v_{k,i}\) denotes the reserves at period k connected to the ith model point and is given by the sum of the discounted supposed cash flows at future periods \(j>k\), that is to say:

$$\begin{aligned} v_{k,i} = \sum _{j > k} d_{j|k} cf_{j,i|k}. \end{aligned}$$
(19)

In the previous formula, we have denoted by \(d_{j|k}\) and \(cf_{j,i|k}\) the discount factor at period j and the size of cash flows at period j for the model point \(m_i\) estimated at period k, respectively. More precisely, the discount factor \(d_{j|k}\) is the price at time k of a zero-coupon bond with tenor j and is computed after having defined a model for the term structure of interest rates. Our choice for the interest rate model is described in Sect. 3.4.

Once we have estimated the supposed liabilities cash flows, the liability duration at period \(k, L_k^D\), according to the Macaulay formula, is given by:

$$\begin{aligned} L^D_k = \frac{\displaystyle \sum _{j>k} j d_{j|k} cf_{j|k}}{\displaystyle \sum _{j>k} d_{j|k} cf_{j|k} }. \end{aligned}$$
(20)

3.1 The surrender and new production model

In order to determine the timing and the size of surrender payments, as well as new production cash flows, we need to build a model for the probability of surrender and for the probability of new production that is the probability that a contract is signed by a new client.

It makes sense that the exercise of surrender option is strongly dependent on market condition, since we can suppose that a policyholder abandons the policy if he finds in the market an analogous product which offers a higher rate of return with respect to the return rate offered by his policy at the same moment. Thus, following (Fernández et al. 2018), the surrender probability is parametrized on the basis of the spread between the earnings offered by the insurance company, depending on the insurer’s portfolio return, and the return offered by an analogous product in the market, represented by a benchmark index return. In this way, we can model the fact that if competing products return is greater than the rate of return offered by the policy, a policyholder is more motivated to surrender his investment.

In particular, for each period k and for each model point \(m_i \in I\), we introduce the quantity \(\delta r^S_{k,i}\) as:

$$\begin{aligned} \delta r^S_{k,i} = (R^I_k - \max (g_{k,i},\beta _{k,i} R^P_k))^+, \end{aligned}$$
(21)

where \(R^I_k\) is the benchmark index rate of return at period k. For the sake of brevity, we have used the notation \(x^+=\max (x,0)\). Note that \(\delta r^S_{k,i}\) does not depend on policyholder’s gender or age, but only on the minimum guaranteed rate of return offered by the contract.

Table 4 Surrender and new production probabilities
Full size table

In order to size \(\delta r^S_{k,i}\), we introduce the threshold intervals \(I^q\), for \(q=1,\ldots ,Q\). For example, in our numerical tests we choose \(Q=3\) and define \(I^1=[0,0.01], I^2=(0.01,0.03]\), and \(I^3=(0.03,+\infty )\). We infer the surrender probability at period k for the model point \(m_i, p_{k,i}^S\), from Table 4, where surrender probabilities, depending only on the threshold interval \(I^q\) and on the period k, are denoted by \(p_{q k}^S\), for \(q=1,2,3\) and \(k=0,\ldots ,T-1\). In particular, if \(\delta r^S_{k,i}\) falls in the interval \(I^q\), then \(p_{q k}^S\) gives the surrender probability at period k for policies in model point \(m_i\), i.e., \(p_{k,i}^S = p_{q k}^S\).

After having inferred the probability of surrender at each period and for each model point, we model the number of policyholders that entered into the contract at period s and cancel it at period k by a Binomial distribution:

$$\begin{aligned} {_s}n_{k,i}^S \sim Bin({_s}n_{k-1,i},p_{k,i}^S). \end{aligned}$$
(22)

Moreover, new production probability at period k for the model point \(m_i\), denoted by \(p_{k,i}^P\), is deduced in a similar way as the surrender probability, using Table 4, where new production probabilities, \(p_{q k}^P\), for \(q=1,2,3\) and \(k=0,\ldots ,T-1\), depend only on the threshold interval \(I^q\) and on the period k. More precisely, we introduce the quantity

$$\begin{aligned} \delta r^P_{k,i} = (\max (g_{k,i},\beta _{k,i} R^P_k) - R^I_k)^+ \end{aligned}$$
(23)

and assume that if \(\delta r^P_{k,i}\) lies in the interval \(I^q\), then new production probability at time k in the ith model point is given by \(p_{q k}^P\), i.e., \(p_{k,i}^P = p_{q k}^P\).

Note that \(p_{qk}^S\) and \(p_{qk}^P\) in Table 4 are chosen taking into account that surrender probability and new production probability increase with \(\delta ^S_{k,i}\) and \(\delta ^P_{k,i}\), respectively.

Once we have deduced the probability of new production from Table 4 at each time for each model point, we can model the number of policyholders in the ith model point that start the contract at time k, for \(k>0\), by a Binomial distribution:

$$\begin{aligned} n_{k,i}^P \sim Bin(n_{k-1,i}, p_{k,i}^P). \end{aligned}$$
(24)

We point out that the use of \(\delta r^S_{k,i}\) for surrender probability and \(\delta r^P_{k,i}\) for new production probability is due to the fact that it is reasonable to assume that only if competing products in the market, represented by the benchmark return \(R^I\), offer a rate of return greater than the rate of return offered by the insurance company, that is, \(\max (g_{k,i},\beta _{k,i} R^P_k)\), a private investor may be motivated to abandon the policy, so there may be surrenders, but there are not new policyholders signing the contract, vice versa, if \(\max (g_{k,i},\beta _{k,i} R^P_k)\) is greater than \(R^I_k\), new clients may be motivated to put his savings in the policy, but there are not policyholders that exercise the surrender option.

3.2 The mortality model

Since the payments due to deaths of policyholders before maturity are not dependent on market condition, we use a biometric model in which the death probability is provided by a specific life table (Table 5) depending on policyholders’ age and gender. More precisely, since in numerical examples considered in Sect. 8 we choose a time step of 1 year, that is to say, the distance between time k and time \(k+1\) is 1 year, in Table 5 we report the probabilities that individuals that have just had a birthday will not celebrate the next birthday.

Table 5 2019 period life table
Full size table

We denote by \(p_i^{D,{\mathcal {M}}}\) and \(p_i^{D,{\mathcal {F}}}\) the death probabilities for the model point \(m_i\) for male and female policyholders, respectively. In particular, we model the number of male and female policyholders in model point \(m_i\) that entered into the contract at time s and die at period k, \({_s}n_{k,i}^{D,{\mathcal {M}}}\) and \({_s}n_{k,i}^{D,{\mathcal {F}}}\), by a Binomial distribution, so that:

$$\begin{aligned} {_s}n_{k,i}^{D,X} \sim Bin({_s}n_{k-1,i}^X , p_i^{D,X}), \ \ X=\{{\mathcal {M}},{\mathcal {F}}\}. \end{aligned}$$
(25)

Obviously, the total number of deaths at period k for the model point \(m_i\), denoted by \(n_{k,i}^D\), is computed as:

$$\begin{aligned} n_{k,i}^D = \sum _{s=0}^{k-1} ({_s}n_{k,i}^{D,{\mathcal {M}}} + {_s}n_{k,i}^{D,{\mathcal {F}}}). \end{aligned}$$
(26)

3.3 Approximation of future cash flows

In this section, we deal with the estimation at period k of the projections of future cash flows, given by (16) and (17), at each period \(j>k\), needed to compute the liability duration, according to (20). More precisely, we have to estimate the timing and the size of future death, surrender and maturity payments, taking into account that new policyholders can subscribe to a policy at future periods.

Future value of death, surrender and maturity benefits The size of payments that the company has to make due to death of policyholders, abandons of the contract and policy contractual expiration depends on death, surrender and maturity benefits, that grow according to (3). Therefore, in order to measure the expected size of future payments at period k, we need to estimate:

$$\begin{aligned} {{\,\mathrm{E}\,}}[ \max ( g_{j,i}, \beta _{j,i} R_j^P ) | {\mathcal {F}}_k], \ \ \text { for } j>k, \end{aligned}$$
(27)

where \({{\,\mathrm{E}\,}}[\cdot | {\mathcal {F}}_k]\) denotes the expectation with respect to the information available at period k, denoted by \({\mathcal {F}}_k\).

In order to estimate (27), we employ the Least Squares Monte Carlo Method (Longstaff and Schwartz 2001). More precisely, we can write the conditional expectation in (27) as linear combination of W basis functions \(\{\psi ^w\}_{w=1,\dots ,W}\) as follows:

$$\begin{aligned} {{\,\mathrm{E}\,}}[ \max (g_{j,i},\beta _{j,i} R^P_j) | {\mathcal {F}}_k] \simeq \sum _{w=1}^{W} {\bar{b}}_{k,j,i}^w \psi ^w (R^P_k) = {\bar{b}}_{k,j,i}^T \psi (R^P_k). \end{aligned}$$
(28)

For example, we can choose the Laguerre polynomials as basis functions, being simple to implement, because they can be defined recursively:

$$\begin{aligned} {\left\{ \begin{array}{ll} L_0(x) = 1, \\ L_1(x) = 1 - x, \\ L_{k}(x) = \frac{1}{k} ( (2(k-1)+1-x)L_{k-1}(x) - (k-1) L_{k-2}(x) ), \ \ k\ge 2. \end{array}\right. } \end{aligned}$$
(29)

We search for the regression coefficients \({\bar{b}}_{k,j,i}\) that are solution of the following problem:

$$\begin{aligned} {\bar{b}}_{k,j,i}^* = \mathop {\hbox {argmin}}\limits _{{\bar{b}}_{k,j,i}} {{\,\mathrm{E}\,}}_k \Big [ \Big ( \psi (R^P_k)^T {\bar{b}}_{k,j,i} - {{\,\mathrm{E}\,}}_k[ \max (g_{j,i},\beta _{j,i} R^P_j) ] \Big )^2 \Big ], \end{aligned}$$

where we have used the notation \({{\,\mathrm{E}\,}}_k[\cdot ]={{\,\mathrm{E}\,}}[\cdot |{\mathcal {F}}_k]\).

We vanish the derivative with respect to \({\bar{b}}_{k,j,i}\) of the quantity to minimize, and we get:

$$\begin{aligned} {{\,\mathrm{E}\,}}_k \Big [ \psi (R^P_k) \psi (R^P_k)^T\Big ] {\bar{b}}^*_{k,j,i} = {{\,\mathrm{E}\,}}_k \Big [ \psi (R^P_k) \max (g_{j,i},\beta _{j,i} R^P_j) \Big ]. \end{aligned}$$

In order to compute the regression coefficients, we use Monte Carlo techniques. More precisely, we simulate \(N_P\) paths of \(R^P_k\), for \(k=1,\ldots ,T\), and we denote by \(R^{P,n}_k\) the value at time k in the nth simulation. After having defined \(\Psi _{k,i}\) as the \(W \times W\) matrix with coefficients:

$$\begin{aligned} (\Psi _{k,i})_{uv} = \frac{1}{N_P} \sum _{n=1}^{N_P} \psi ^u(R^{P,n}_k) \psi ^v(R^{P,n}_k), \end{aligned}$$

and \(d_{k,j,i}\) as the W-array with the vth element given by:

$$\begin{aligned} (d_{k,j,i})_v = \frac{1}{N_P} \sum _{n=1}^{N_P} \psi ^v(R^{P,n}_k) \max (g_{j,i},\beta _{j,i} R^{P,n}_j), \end{aligned}$$

we reduce the problem of regression coefficients computation to the problem of solving the system \(\Psi _{k,i} {\bar{b}}_{k,j,i} = d_{k,j,i}\).

Once we have obtained regression coefficients, we are able to compute \({{\,\mathrm{E}\,}}[ \max ( g_{j,i}, \beta _{j,i} R_j^P ) | {\mathcal {F}}_k]\), for \(j>k\), simply using (28). This means we need to simulate only the current value \(R^P_k\).

Future death payments Once we have estimated the value of the death benefit at future periods and predicted the number of policyholders who will die at each future period according to the biometric model described in Sect. 3.2, we can compute the size of death payments according to (9) and (10).

Future surrender payments In order to forecast the size and the timing of future surrender payments, we need to predict the number of policyholders that cancel the contract at each future period \(j>k\) and, so, the probability of surrender at each period \(j>k\). To do that, we compute:

$$\begin{aligned} \Delta R^S_i(j|k) = {{\,\mathrm{E}\,}}[\delta r^S_{j,i}| {\mathcal {F}}_k], \ \ \text {for } j>k. \end{aligned}$$
(30)

Indeed, the computation of (30) allows us to forecast the probability of surrender at future periods by using Table 4 and, then, the number of abandons at each future periods according to (22). After having estimated the number of surrenders at future periods, we can use the estimation of the surrender benefit to compute the amount the company is expected to pay due to surrenders according to (11) and (12).

From the definition of \(\delta r^S_{j,i}\) in (21), we get:

$$\begin{aligned} \Delta R^S_i(j|k) = {{\,\mathrm{E}\,}}_k[ (R^I_j - \max (g_{j,i},\beta _{j,i} R^P_j)^+], \ \ \text {for } j>k. \end{aligned}$$
(31)

Due to the nonlinearity of \(\delta r^S_{j,i}\), we estimate the conditional expectations in (30) with a Least Squares approach (Longstaff and Schwartz 2001); thus, following the same procedure we have used to forecast future returns. Therefore, we write \(\Delta R^S_i(j|k)\) as linear combination of basis functions \(\{\psi ^w\}_{w=1,\dots ,W}\):

$$\begin{aligned} \Delta R^S_i(j|k) \simeq \sum _{w=1}^{W} \bar{{\bar{b}}}_{k,j,i}^w \psi ^w({\hat{R}}^P_{k,i},R_k^I) = \bar{{\bar{b}}}_{k,j,i}^T \psi ({\hat{R}}^P_{k,i},R_k^I), \end{aligned}$$
(32)

where we have used the notation \({\hat{R}}^P_{k,i} = \max (g_{j,i},\beta _{j,i} R^P_j)\).

This time, the basis functions are bidimensional functions. For example, we can choose the bidimensional Laguerre polynomials, given by the product of couples of unidimensional Laguerre polynomials, defined above.

We look for the regression coefficients \(\bar{{\bar{b}}}_{k,j,i}^*\) such that:

$$\begin{aligned} \bar{{\bar{b}}}_{k,j,i}^* = \mathop {\hbox {argmin}}\limits _{\bar{{\bar{b}}}_{k,j,i}} {{\,\mathrm{E}\,}}_k \Big [ \Big ( \psi ({\hat{R}}^P_{k,i},R_k^I)^T \bar{{\bar{b}}}_{k,j,i} - {{\,\mathrm{E}\,}}_k[\delta r_{j,i}] \Big )^2 \Big ], \end{aligned}$$

that leads to:

$$\begin{aligned} {{\,\mathrm{E}\,}}_k \Big [ \psi ({\hat{R}}^P_{k,i},R_k^I) \psi ({\hat{R}}^P_{k,i},R_k^I)^T\Big ] \bar{{\bar{b}}}^*_{k,j,i} = {{\,\mathrm{E}\,}}_k \Big [ \psi ({\hat{R}}^P_{k,i},R_k^I) \delta r_{j,i} \Big ]. \end{aligned}$$

Again, we use Monte Carlo techniques to compute regression coefficients. More precisely, we simulate \(N_P\) paths of \({\hat{R}}^P_{k,i}\) and \({\hat{R}}^I_k\), for \(k=1,\ldots ,T\), and we denote by \({\hat{R}}_{k,i}^{P,n}, R_{k}^{I,n}\) their respective values at time k in the nth simulation. This time, we have to solve the system \(\Psi _{k,i} \bar{{\bar{b}}}_{k,j,i} = d_{k,j,i}\), where the \(W \times W\) matrix \(\Psi _{k,i}\) and the W-array \(d_{k,j,i}\) are such that:

$$\begin{aligned} \begin{aligned} (\Psi _{k,i})_{uv}&= \frac{1}{N_P} \sum _{n=1}^{N_P} \psi ^u({\hat{R}}_{k,i}^{P,n},R_{k,i}^{I,n}) \psi ^v({\hat{R}}_{k,i}^{P,n},R_{k,i}^{I,n}),\\ (d_{k,j,i})_v&= \frac{1}{N_P} \sum _{n=1}^{N_P} \psi ^v({\hat{R}}_{k,i}^{P,n},R_{k}^{I,n}) (R_{j}^{I,n}-{\hat{R}}_{j,i}^{P,n})^+. \end{aligned} \end{aligned}$$

After having computed regression coefficients, we obtain \(R^S_i(j|k)\), for \(j>k\), from (32), so that we need to simulate only the current values \({\hat{R}}^P_{k,i}\) and \({\hat{R}}^I_k\).

Future new production Following the same procedure used for \(\Delta R^S_i(j|k)\) in (30), we compute

$$\begin{aligned} \Delta R^P_i(j|k) = {{\,\mathrm{E}\,}}[\delta r^P_{j,i}| {\mathcal {F}}_k], \ \ \text {for } j>k, \end{aligned}$$
(33)

to predict the probability of new production at future periods by using Table 4 with the aim to forecast the number of new policyholders signing a contract at the each future periods according to (24). New production cash flows are computed by (7) and (8).

Future maturity payments As regard to maturity payments, they can be computed by (13) and (14), taking into account the estimation of maturity benefit and that the number of policyholders that are still alive at policy maturity date is given by the total number of policyholders that entered into the contract, at any time, minus the number of policyholders that died or surrendered the contract before policy expiration.

Benchmark index model In conclusion of the section, we point out that in order to compute (30) we need to define both the dynamics of the benchmark return and the dynamics of the asset classes in the portfolio, to deduce the portfolio return, also needed to compute (27). To end the section, we describe the model for the benchmark return, whereas the dynamics of portfolio asset classes are described in Sect. 4. We assume that the benchmark index price follows a geometric Brownian motion. Therefore, the price of the benchmark index, \(I_t\), is governed by:

$$\begin{aligned} d I_t = \mu ^I I_t dt + \sigma ^I I_t dW_t^I, \end{aligned}$$
(34)

where the constant parameters \(\mu _I \in {\mathbb {R}}\) and \(\sigma ^I > 0\) are the drift and the volatility of the process \(I_t\), respectively, and \(W_t^I\) is a Brownian motion. It is well known that the solution of Eq. (34) at time t conditional to \(F_s\), with \(s<t\), is given by

$$\begin{aligned} I_t = I_s \exp \left( \left( \mu ^I - \frac{(\sigma ^I)^2}{2}\right) (t-s) + \sigma ^I (W^I_t - W^I_s)\right) . \end{aligned}$$
(35)

3.4 Interest rate model associated with the term structure of interest rates

In order to compute the liability duration by using the Macaulay formula (20), we need to calculate the discount factors that are prices of zero-coupon bonds, so that we need to evolve the term structure of interest rates. For this reason, we introduce a short rate model. The convenience in the use of a short rate model is that the term structure of interest rates is an affine term structure in the sense that, at time t, the zero rate with maturity T is an affine function of the instantaneous short rate process at time t. In particular, we choose the one factor Hull & White model in the version referred in the literature as \(G1++\) model. For the equivalence between \(G1++\) model and the original one factor Hull & White model see Brigo and Mercurio (2007) and Hull and White (1990), for instance. The advantages in the use of the \(G1++\) model with respect to its classical counterpart are well known. For example, the generation of forward paths is numerically more stable and the analytical formula for bond prices is more tractable.

In the \(G1++\) model, the dynamics of the instantaneous short rate \(r_t\) under the risk neutral measure Q is given by

$$\begin{aligned} r_t = x_t + f_t, \end{aligned}$$
(36)

with initial value \(r_0\). We assume that the process \(x_t\) satisfies the following stochastic differential equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0 = 0, \\ x_t = -a^x x_t dt + \sigma ^x(t) d W^x_t, \end{array}\right. } \end{aligned}$$
(37)

where \(a^x\) is a positive constant, \(\sigma ^x(t)\) is a positive deterministic function and \(W_t^x\) is a standard Brownian motion. The function f is deterministic and is given by an exact fitting to the term structure of discount factors observed in the market. We choose to employ a piecewise constant functional specification for the volatility of the process \(x_t\). More precisely, the volatility \(\sigma ^x(t)\) is constant in the intervals [0, 1], (1, 3], \((3,+\infty )\), so that:

$$\begin{aligned} \sigma ^x(t) = {\left\{ \begin{array}{ll} \sigma ^1, \text { if } t \in [0,1], \\ \sigma ^2, \text { if } t \in (1,3], \\ \sigma ^3, \text { if } t \in (3,+\infty ). \end{array}\right. } \end{aligned}$$
(38)

The parameters \(a^x\) and \(\sigma ^1, \sigma ^2, \sigma ^3\) can be calibrated by using market swaption prices. In fact, Di Francesco (2012) and Schrager and Pelsser (2006), for example, present an approximated swaption pricing formula, effective in the setting of the \(G1++\) model, in the case that the strike is at the money:

$$\begin{aligned} ES(0,T,t_k,K,N) = N\frac{VOL}{\sqrt{2\pi }} \sum _{i=1}^{k} \tau _i P(0,t_i) \equiv N\frac{VOL}{\sqrt{2\pi }} P_{t_1}^{t_k}, \end{aligned}$$
(39)

where \(ES(0,T,t_k,K,N)\) is the price at time 0 of a European call swaption with maturity T, strike K and nominal value N, which gives the holder the right to enter at time \(T=t_0\) into a swap in which the holder pays the fixed rate K and receives the Libor rate at dates \(t_1,\ldots ,t_k\), with \(t_0<t_1<\ldots <t_k\). In (39), \(\tau _i\) denotes the year fraction from \(t_{i-1}\) and \(t_i, P(0,t_i)\) represents the price at time 0 of a zero-coupon bond with maturity \(t_i\) years, and

$$\begin{aligned} VOL = \sqrt{ \int _{0}^{T} (\sigma (u)^x)^2 A^2 e^{2 a^x u} du }, \end{aligned}$$

with

$$\begin{aligned} A = e^{-a^x T}\frac{P(0,T)}{a^x P_{t_1}^{t_k}} - e^{-a^x t_k}\frac{P(0,t_k)}{ a^x P_{t_1}^{t_k}} - \frac{K}{a^x} \sum _{i=1}^{k} e^{-a^x t_i} \tau _i \frac{P(0,t_i)}{P_{t_1}^{t_k}}. \end{aligned}$$

We have calibrated the \(G1++\) model using the swaption prices observed on September 30, 2020, and reported in Table 6, thus obtaining the following parameters values: \(a^x= 0.0048\), and \(\sigma ^1=0.0018\), \(\sigma ^2=0.0042, \sigma ^3=0.0065\).

Table 6 Swaption prices observed on September 30, 2020
Full size table

After having calibrated the parameters of the process \(x_t\), in order to simulate the process \(r_t\), we use its conditional distribution. More precisely, from (36) and (37), for \(s<t\), we have that \(r_t\), conditional to \({\mathcal {F}}_s\), is normally distributed with:

$$\begin{aligned} {{\,\mathrm{E}\,}}[r_t| {\mathcal {F}}_s] =&x_s e^{-a^x (t-s)} + f_t,\\ {{\,\mathrm{Var}\,}}[r_t| {\mathcal {F}}_s] =&(\sigma ^x(t))^{2}\frac{1-e^{-2a^x(t-s)}}{2a^x}, \end{aligned}$$

where \({{\,\mathrm{E}\,}}\) and \({{\,\mathrm{Var}\,}}\) denote the mean and the variance under the measure Q, respectively.

In the framework of the \(G1++\) model, the price of a zero coupon bond at time t with maturity at time T, P(t, T), can be computed using the following formula:

$$\begin{aligned} P(t,T)= A(t,T) e^{-B(t,T)x_t}, \end{aligned}$$
(40)

where

$$\begin{aligned} A(t,T)&= \frac{P^M(0,T)}{P^M(0,t)}e^{\frac{1}{2}[V(t,T) - V(0,T) + V(0,t) ]}, \end{aligned}$$
(41)
$$\begin{aligned} B(t,T)&= \frac{1 - e^{-a^x(T-t)}}{a^x}, \end{aligned}$$
(42)
$$\begin{aligned} V(t,T)&= \frac{(\sigma ^x(t))^2}{(a^x)^2}\left( T -t - 2\frac{1-e^{-a^x(T-t)}}{a^x} + \frac{1-e^{-2a^x(T-t)}}{2a^x} \right) . \end{aligned}$$
(43)

In (41) \(P^M(0,t)\) denotes the market price of a zero-coupon bond with maturity t years, observed at time 0, i.e., the initial term structure.

4 Asset model

Our asset portfolio is composed of bonds, equity and cash. We split the bonds into four classes with different maturities: a class for bonds with maturity less than 3 years; a class including all the bonds with maturity between 3 and 5 years; a class comprising bonds with maturity from 5 to 10 years; finally, a class consisting of bonds with maturity greater than 10 years.

Since an insurance company has a conservative investment strategy, the largest part of portfolio is composed of bonds. So, in our strategy, we consider a lower bound for the portion of portfolio invested in bonds. We also consider an upper bound for the part of portfolio invested in equity. The remaining part is invested in cash. Section 5 deals with the question of constraints on portfolio weights with more details, whereas in the following we describe the stochastic models used to simulate the returns of portfolio asset classes.

Bonds and equity models In order to simulate bonds and equity returns, we assume that the underlying indexes dynamics follow geometric Brownian motions. Therefore, denoting by \(S_t\) the price of equity index at time t and by \(B_t^\tau \) the price at time t of bond index with duration \(\tau \), we have:

$$\begin{aligned} dS_t =&\mu ^S S_t dt + \sigma ^S S_t dW_t^S, \end{aligned}$$
(44)
$$\begin{aligned} dB_t^\tau =&\mu ^{B^\tau } B_t^\tau dt + \sigma ^{B^\tau } B_t^\tau dW_t^{B^{\tau }}, \end{aligned}$$
(45)

where \(\mu ^S, \mu ^{B^\tau } \in {\mathbb {R}}\) are the drifts of the processes \(S_t\) and \(B_t^\tau \), respectively, and \(\sigma ^S\), \(\sigma ^{B^\tau }\) are strictly positive constant parameters representing their volatilities. Moreover, \(W^S_t\) and \(W_t^{B^\tau }\) are correlated Brownian motions and, obviously, they are both correlated with the other sources of randomness in the model, i.e., \(W_t^I\), that appears in (35), and \(W_t^x\), that is involved in (37). It is well known that the solutions of Eqs. (44) and (45) at time t conditional to \({\mathcal {F}}_s\), with \(s<t\), are, respectively, given by

$$\begin{aligned} S_t&= S_s \exp \left( \left( \mu ^S - \frac{(\sigma ^S)^2}{2}\right) (t-s) + \sigma ^S (W^S_t - W^S_s)\right) , \end{aligned}$$
(46)
$$\begin{aligned} B_t^\tau&= B_s^\tau \exp \left( \left( \mu ^{B^\tau } - \frac{(\sigma ^{B^\tau })^2}{2}\right) (t-s) + \sigma ^{B^\tau } (W^{B^{\tau }}_t - W_s^{B^{\tau }})\right) . \end{aligned}$$
(47)

We refer to the work by Doherty and Garven (1986) as an early paper where the Geometric Brownian Motion has been used in modeling Asset and Liabilities. In the paper, a discrete-time option pricing model is used to derive the “fair” rate of return of an insurance firm.

Cash model The evolution of the dynamics of cash in the asset portfolio is deduced from the short rate model described in Sect. 3, taking into account that (see Di Francesco 2012, for instance):

$$\begin{aligned} e^ {\int _{0}^{t} r(s)ds} = \frac{ e^{\int _{0}^{t} x(s)ds} }{ e^{-\int _{0}^{t} f(s)ds} } = \frac{ e^{\int _{0}^{t} x(s)ds} }{ P^M(0,t) e^{-\frac{1}{2} V(0,t)} }. \end{aligned}$$
(48)

Note that the dynamics of the process \(x_t\) is given in (37), \(P^M(0,t)\) denotes the market price of a zero-coupon bond with maturity t, and the value of V(0, t) can be computed by (43).

We would like to point out that all the processes in the model are simulated according to their dynamics in the real world measure, P, but cash is simulated from \(r_t\) whose dynamics is in the risk neutral measure, Q. Indeed, in the case of cash we can assume that the dynamics in P coincides with the dynamics in Q, being the risk premium null.

Asset value After having described the dynamics of portfolio asset classes, we are able to compute the asset portfolio return at each period \(k, R^P_k\), so that we can write a formula for the evolution of the asset value over time:

$$\begin{aligned} A_k = A_{k-1} (1 + R^P_k) + \Pi _k + P_k - D_k - \Gamma _k - M_k, \ \ k>0, \end{aligned}$$
(49)

where \(A_0\) is given by premiums collected from policyholders at period 0 plus the initial investment on the part of the company.

5 First stage of portfolio rebalancing

In our stochastic ALM model, we consider a dynamic reinvestment strategy in which the asset portfolio is restructured at each period k according to the evolution of the liabilities portfolio. We use a scenario-based simulation approach. For each scenario at each period k, the investment strategy decides which types of asset class must be sold or bought in order to guarantee that there is enough money to meet the obligations with policyholders and company’s shareholders. In particular, for each simulation at each period k, we compute the duration of liabilities, the duration of asset portfolio and the asset portfolio return. Then, we rebalance our asset portfolio with the aim to accomplish two goals:

  1. i.

    matching between assets duration and liabilities duration. More precisely, we aspire to minimize the positive part of the difference between assets duration and liabilities duration, since liquidity problems can arise when the assets have a longer duration than liabilities, but not vice versa;

  2. ii.

    achievement of a certain target return. In particular, we ask that the portfolio return is not too much distant from the benchmark return.

In order to rebalance our portfolio composition, for each simulation at each period k, we solve a nonlinearly constrained optimization problem subject to several real world constraints. In particular, we consider the so-called budget constraint and no short selling constraint, and for each asset class we set upper and lower bounds and we fix a maximum turnover. In addition, we set a maximum portfolio turnover, and we impose other linear constraints given by the investment policy. All these constraints are reasonable for an insurance company and we calibrate them on an EU-based life insurance company’s portfolio. We summarize all these constraints in Table 7, where we have denoted by \(\varvec{\alpha }_k = (\alpha ^{B1}_k,\alpha ^{B2}_k,\alpha ^{B3}_k,\alpha ^{B4}_k,\alpha ^{E}_k,\alpha ^{C}_k)\) the array of asset classes weights at period k. In particular, \(\alpha ^{Bn}_k, \alpha ^{E}_k, \alpha ^{C}_k\) are the weights in the portfolio composition at period k of the nth class of bonds, equity and cash, respectively. We denote by \(I_{\alpha }=\{B1,B2,B3,B4,E,C\}\). In Table 7, \(m^B\) denotes the lower bound for the sum of the bonds weights in portfolio composition, \(M^E\) the upper bound for weight of equity, and TO and \(TO^{tot}\) are, respectively, the maximum turnover on each asset class and the maximum portfolio turnover.

Table 7 Constraints imposed in the optimization problem
Full size table

At period k, the optimization problem consists of finding an optimal array of asset classes weights \(\varvec{\alpha }_k\) such that:

$$\begin{aligned} \begin{aligned}&\text {minimize} \ \ \ \ ( A^D(\varvec{\alpha }_k) - L^D_k )^+; \\&\text {subject to } \ \ {\left\{ \begin{array}{ll} \beta ^{L} R^I_{k+1} \le R^P_{k+1} \le \beta ^{U} R^I_{k+1}, \ \ \text {with constant }\beta ^L, \beta ^U, \\ \text {constraints in Table}~7. \end{array}\right. } \end{aligned} \end{aligned}$$
(50)

Note that assets duration, \(A^D\), is a combination of durations of bonds in the assets portfolio.

In a general framework, we can include transaction costs, that arise when rebalancing the assets portfolio. In the case of no null transaction costs, the portfolio return at period k is given by:

$$\begin{aligned} R^P_k = \varvec{\alpha }_k \cdot \varvec{R}_k - [ \varvec{c}^S \cdot (\varvec{\alpha }_{k-1}-\varvec{\alpha }_k)^+ + \varvec{c}^B \cdot (\varvec{\alpha }_k - \varvec{\alpha }_{k-1})^+ ], \end{aligned}$$
(51)

where \(\varvec{c}^S\) and \(\varvec{c}^B\) are the vectors of asset classes selling and buying costs, respectively, and \(\varvec{R}_k\) is the vector of asset classes returns at time k. In the numerical tests, we assume null transaction costs, because the introduction of transaction costs different from zero substantially increases the elapsed computational time, but does not affect results in a significant way, in the sense that results with transaction costs are comparable to results without them.

6 Second stage of portfolio optimization

In the previous section, we have chosen a portfolio rebalancing strategy that ensures the company will be solvable, and shareholders and policyholders will benefit from a competitive return. But the proposed strategy is not necessarily optimal. For this reason, we now introduce a second stage of portfolio optimization with the aim of maximizing the expected value of a chosen utility function, taking into account the results obtained from the first stage of portfolio rebalancing. Indeed, in the first step of portfolio rebalancing we consider only six asset classes, and in the second step for each bonds asset class and for equity asset class, taking into account several sub-sectors, we run a sectorial optimization problem that maximizes the expected utility function of terminal wealth over specified horizon (see Consigli and Dempster 1998). We suggest to solve sectorial optimization problems in the second stage to refrain from managing an excessive number of asset classes. For instance, for each bond asset class sub-sectors could be government core and government peripheral bonds, financial and corporate bonds, financial investment grade and financial sub-investment grade bonds, etc. For equity asset class sub-sectors could be energy, healthcare, utilities, information technology, etc.

More precisely, chosen a utility function U, at each time step k we solve five sectorial optimization problems, so that we search for the optimal weights vectors \(\varvec{\omega }^{i}_k = (\omega _k^{i,1},\ldots ,\omega _k^{i,N_i})\), for \(i \in I_{\alpha } \setminus \{C\}\), such that:

$$\begin{aligned} \begin{aligned}&\text {maximize} \ \ {{\,\mathrm{E}\,}}_k \left[ \max _{\varvec{{\bar{\omega }}^i_{k+1}}} {{\,\mathrm{E}\,}}_{k+1} \left[ \max _{\varvec{{\bar{\omega }}^i_{k+2}}} {{\,\mathrm{E}\,}}_{k+2} \left[ \ldots \max _{\varvec{{\bar{\omega }}^i_{T-1}}}{{\,\mathrm{E}\,}}_{T-1} \left[ U(\varvec{\omega }_{T-1}^{i} \cdot \varvec{R}^i_T ) \right] \ldots \right] \right] \right] ; \\&\text {subject to} \ \ \sum _{j=1}^{N_i} \omega _k^{i,j} = \alpha _k^i, \ \end{aligned} \end{aligned}$$
(52)

where \(\varvec{R}^i_l\) and \(N_i\) are the vector of sub-sectors returns at period I and the number of sub-sectors for asset class i, respectively. In this way, an optimal portfolio strategy is proposed (see Mossin 1968).

However, in numerical results presented in Sect. 8 we focus on the first step of the portfolio rebalancing strategy, because the second step can be performed by standard techniques of stochastic programming (see, for example, Dempster 1980).

7 Market data

In our portfolio optimization problem, we assume the insurance company can invest in six specific asset classes, summarized in Table 8. In order to simulate the dynamics of bonds and equity log-returns, respectively, deduced from (44) and (45), we use the historical estimations of annualized mean and standard deviation of representative indexes daily log-returns, computed considering an annualization factor of 252. We do the same for the dynamics of log-returns of the benchmark index, used in the surrender and new production models. The dynamics of the benchmark return is inferred from (34). Indexes and their log-returns statistics are listed in Table 8. We have considered daily observations from September 30, 2010 to September 30, 2020, for a total of 2614 observations. Data have been obtained from Bloomberg. Also, in Table 8, for each representative index of the asset classes of the investable portfolio we show the index duration, given by the average duration of the index components, weighted on the basis of their market prices. Finally, since cash log-returns are simulated by using the short rate model, in Table 8, we report the representative index for the short rate, used only as proxy to estimate correlation between the dynamics of cash and the dynamics of all the other stochastic variables. Indeed, all the sources of randomness in the model are correlated. When simulating, the historical correlation of indexes is used as correlation between the Brownian motions in the model, i.e., \(W^I\), involved in the dynamics of the benchmark index (34), \(W^x\), included in the dynamics of the short rate (37), \(W^S\), that is in the dynamics of equity (44), and \(W^{B^{\tau }}\), contained in the dynamics of bonds with duration \(\tau \) (45).

Table 8 Asset classes representative indexes, short rate representative index and benchmark index
Full size table

In Table 9, we report the historical correlations.

Table 9 Correlation matrix
Full size table

Since the aim of an insurance company is not only to meet its financial obligations, but also to obtain a profit, we are interested in the changes in own funds value. Therefore, we keep track of the evolution over time of the difference between asset and liability values, so that we need to make an assumption on the relation between them at the initial time, say at time 0. In particular, we set the level of liabilities at the initial time to 90% of the value of the assets at the same time, that is to say, the following relation is satisfied:

$$\begin{aligned} L_0 = 0.887 A_0. \end{aligned}$$
(53)

Another assumption we need to make concerns the initial portfolio composition, described in Table 10. Portfolio is periodically rebalanced observing constraints on asset classes weights, as fully discussed in Sect. 5. In particular, in Table 7 we choose \(m^B=0.70,M^E=0.20\), \(TO=0.05\) and \(TO^{tot}=30\).

Table 10 Initial portfolio composition
Full size table

8 Numerical results

In this section, some numerical results are presented. In particular, we deduce how the portfolio has to be rebalanced according to the strategy illustrated in Sect. 5. Also, we focus on the values of actuarial reserves and own funds. Moreover, we are interested in the study of the impact of mortality model and of surrender and new production models on how the number of alive policies changes over time.

We have used \(10^3\) simulations for the phase of regression coefficients computation in the Least Squares Monte Carlo method and we have generated \(10^4\) different scenarios for the phase of portfolio composition optimization. All tests have been performed by using MATLAB on an Intel(R) Core(TM) i7-8550U, 1.99 GHz, 16 GB (RAM), x64-based processor.

In the following, we make the assumptions listed below:

  • all contracts have the same value, say €10 000, in the moment they are signed;

  • all policies expire at the same future date, say at time \(T=10\) years;

  • the initial number of policyholders in each model point is reported in Table 11;

  • at the initial time policies are equally distributed between male and female policyholders (gender equality);

  • portfolio is rebalanced at each time step, that is one year;

  • policyholders pay a single premium at the beginning of the contract;

  • the participation rate \(\beta \) is the same for all model points and is set to 95%, constant over time, unless otherwise stated.

Table 11 Initial number of policyholders in each model point
Full size table

In Fig. 1, we exhibit how the portfolio composition is rebalanced every year following the strategy described in Sect. 5. In particular, we show the mean value of portfolio composition weights over all the scenarios. We infer that the weight of bonds with maturity less than 3 years has to increase significantly over time, while the weight of equity rises slightly. Moreover, the weights of cash and bonds with maturity between 3 and 5 years remain nearly constant over time, whereas we have to invest less and less in bonds with longer maturity. The portfolio composition evolution in Fig. 1 originates from the fact that all policies expire at time \(T=10\), so that liability duration approaches to zero with the passing of time. As a result, in order to match asset duration and liability duration, we need to invest more and more in asset classes with short duration, and less and less on asset classes with long duration.

Fig. 1
figure 1

Portfolio composition rebalancing

Full size image

In Fig. 2, we illustrate how much the liability value of each model point weighs on the total value of liabilities. We consider the interval [0, 9], because at maturity date, i.e., \(T=10\), all policyholders have been refunded and the total liability value is zero. We note that the weights of model points related to younger policyholders increase over time, while the weights of model points associated with policyholders aged 60 or more decrease. In fact, young policyholders are less likely to die with respect to older policyholders (see Table 5), so that death payments that the company has to make at each time are due especially to deaths of older policyholders. This means that the company has to refund before maturity more old policyholders than young policyholders, thus lightening the weight on the total value of liabilities of model points related to old policyholders.

Fig. 2
figure 2

Model points weights on liabilities value

Full size image

As regard to the number of alive contracts, it decreases over time, as shown in Fig. 3. Evidently, at each time step new production is not enough to counterbalance deaths and surrenders. However, the evolution of the number of alive policies may be different if other assumptions are made on the model or another set of parameters is chosen. It is even possible that the number of alive contracts increases over time, since the number of new investors may exceed the number of policyholders who die or exercise the surrender option. The right plot in Fig. 3 considers separately male and female policyholders, thus allowing us to evaluate the effect of mortality model on the changes of the alive policies number. In fact, since the surrender and the new production models do not depend on gender, the different rate of decrease for men and women is only due to the fact that women mortality rate is lower than men mortality rate (see Table 5).

Fig. 3
figure 3

Mean number of alive policies at each time. On the left the total number is plotted; on the right the distinction between males and females is taken into account

Full size image

In order to better analyze the issue of new production, in Fig. 4 we plot the mean number over all the scenarios of alive policyholders considering separately policies with different starting time. So, on the top we show the number of policies that started at time 0, on the bottom the numbers of policies that started after time 0. As expected, the major decrease can be observed in the population that entered into the contract at time 0, meaning that at each time it is more likely that a policyholder who started the contract at time 0 dies or abandons the policy rather than a policyholder who started the contract after time 0. In fact, the set of policyholders that entered at time 0 is more numerous.

Fig. 4
figure 4

Mean number of alive policies with different starting time. The plot on the top displays the evolution of the number of alive contracts that started at time zero; lines in the plot on the bottom show the evolution of the numbers of alive policies that started at time \(1,2,\ldots ,9\), respectively

Full size image

Participation rate sensitivity So far we have considered a fixed participation rate, but it is interesting to study how different values for \(\beta \) influence actuarial reserves and own funds, as well as the number of abandons and new production.

In Fig. 5, we plot actuarial reserves for different values of \(\beta \). As expected, if \(\beta \) grows, the payments that the company has to make due to policyholders who die, abandon the contract or reach maturity, are more consistent. Therefore, actuarial reserves, discounted expectation of future disbursements, increase. Note that we consider the time interval [0, 9], thus ignoring the maturity date, \(T=10\), when all policies have expired and actuarial reserves are zero, because the company has no more future payments to make.

In Fig. 6, we show the difference between asset value and liability value changing the participation rate. Evidently, the difference examined in the plot decreases when increasing the participation rate, in fact:

$$\begin{aligned} A_t - L_t = A_{t-1} (1 + R_t^P) - \sum _{i=1}^{N_M} L_{t-1,i} ( 1 + \max (g_i,\beta R_t^P) ), \end{aligned}$$
(54)

where the liability term increases if \(\beta \) becomes greater. However, in any case own funds rise over time.

Fig. 5
figure 5

Mean actuarial reserves for different values of the participation rate

Full size image
Fig. 6
figure 6

Mean difference between asset value and liability value for different values of the participation rate

Full size image
Fig. 7
figure 7

Mean number of alive policies at each time for different values of the participation rate

Full size image

In addition, Fig. 6 shows that at each time step the mean value of the difference between asset value and liability value is positive. However, in some scenarios own funds become negative and the company is declared defaulted. In Table 12, we report the probability of default, defined as the ratio between the number of scenarios in which the company defaults and the total number of scenarios (10000), for three different values of the participation rate \(\beta \). Obviously, probability of default rises by increasing \(\beta \).

Table 12 Probability of default for different values of the participation rate
Full size table

Finally, we analyze how the value of the participation rate affects the changes in the number of alive policies over time, as shown in Fig. 7. On the contrary of what happens in the right plot in Fig. 3, where the impact of the mortality model is presented, in Fig. 7 the effect of surrender and new production models can be observed. In fact, the mortality model does not depend on the participation rate, while surrender and new production models strongly depend on it (see Sect. 3.1). In particular, the earnings offered by the insurance company rise when increasing \(\beta \), so that less policyholders are motivated to abandon the contract, and more investors subscribe to the policy. As a result, the number of alive policies decreases more slowly in the case of larger values of the participation rate.

9 Conclusions

In this paper, we have built a two-stage ALM model for a life insurance company, including a policyholders’ saving account model, a mortality model and a surrender model, as well as a new production model, an innovative feature with respect to existing works in literature, as far as we know. In order to handle the large number of contracts, we have split them into model points, by grouping policies with similar age of the policyholder, same minimum guaranteed rate of return and same time-to-maturity. Since an insurance company has the purpose of both ensuring its solvency and obtaining a profit, firstly, we have built a strategy for the asset portfolio rebalancing that aims to match asset duration and liability duration and to achieve a target return. Also, we have considered several real world constraints on portfolio composition weights. From the technical point of view, the portfolio rebalancing strategy is the result of a nonlinearly constrained optimization problem that requires the computation of future cash flows projections. According to our knowledge, we have proposed an innovation with respect to literature: When computing balance sheets projections, we have considered, in addition to future death and maturity payments, also future surrender payments and future cash flows due to new production. Next, we have proposed a second stage of portfolio rebalancing that includes sectorial optimization problems with the aim to maximize the expected value of a chosen utility function. In this way, we have built an optimal portfolio rebalancing strategy based on risk-averse decisions.

On the side of numerical tests, we have focused on the first stage of portfolio rebalancing, and we have shown how the portfolio has to be dynamically rebalanced and how the liability value associated with each model point weighs on the total value of liabilities. We have pointed out the effect of the mortality model on the evolution over time of the number of alive policies by considering separately male policyholders and female policyholders. We have proposed an analysis of the participation rate sensitivity, taking account of the evolution of actuarial reserves and of own funds. As expected, actuarial reserves increase and own funds decrease by increasing the participation rate. Moreover, we have focused on the positive result that the mean value of own funds raises over time for any considered value of the participation rate. However, there is a small probability, depending on the participation rate, that in certain scenarios the company defaults, because own funds become negative. Finally, we have analyzed how the number of alive policies varies by changing the value of the participation rate, thus showing how it depends on surrender and new production models. Indeed, the participation rate does not affect policyholders’ mortality, so that the different rate of decrease in the number of alive policies with different values of the participation rate is due only to the different numbers of surrenders and of new policyholders.