Electrokinetic effect in porous rocks of the sea coast provided by long sea waves

Abstract

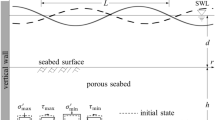
We analyze theoretically ultra-low frequency electromagnetic noise caused by deformations of seabed and porous coastal rocks subjected to incident long oceanic waves. A variable pressure on the seabed due to propagation of long gravity waves (LGWs) gives rise to variations in pore pressure gradient followed by groundwater filtration in pores and channels of porous rocks. These processes result in the generation of telluric electric currents in water-saturated porous rock of the seashore due to electrokinetic effect. In the model a displacement of the sea surface in LGWs is described in the "shallow water" approximation. A set of basic equations describing rock strain and electrokinetic effect is solved in quasi-static approximation. The telluric electric field in the porous rocks of coastal zone are found as a function of depth and distance to the coastline at different frequencies of LGWs. The theoretical analysis has shown that telluric electric noise produced by the LGW can exceed the level of natural electric noise during geomagnetically quiet period in a coastal strip about several tens of meters.

Appendix

Applying Fourier transform with respect to $x$ to Eqs. (6) and (7), we obtain a set of the ordinary differential equations

$$\begin{aligned} & \left( {1 - 2\nu } \right)w_{x}^{\prime \prime } + ikw_{z}^{\prime } - 2\left( {1 - \nu } \right)k^{2} w_{x} = 0, \\ & 2\left( {1 - \nu } \right)w_{z}^{\prime \prime } + ikw_{x}^{\prime } - \left( {1 - 2\nu } \right)k^{2} w_{z} = 0, \\ \end{aligned}$$

(17)

where $k$ is the parameter of the Fourier transform and the primes denote derivatives with respect to $z$. Here we made use the following abbreviations

$$w_{x,z} \left( {k,z} \right) = \int\limits_{ - \infty }^{\infty } {u_{x,z} \left( {x,z} \right)\exp \left( { - ikx} \right)dx} ,\quad p\left( k \right) = \int\limits_{ - \infty }^{\infty } {\delta P\left( x \right)\exp \left( { - ikx} \right)dx} .$$

(18)

The boundary conditions (7) at $z = 0$ are reduced to the form

$$\begin{aligned} & \left( {K_{p} + \frac{{4\mu_{p} }}{3}} \right)w_{z}^{\prime } + \left( {K_{p} - \frac{{2\mu_{p} }}{3}} \right)w_{x} = - p, \\ & w_{x}^{\prime } + ikw_{z} = 0. \\ \end{aligned}$$

(19)

Rearranging the equation set (17), yields

$$w_{x,z}^{{{\text{IV}}}} - 2w^{\prime\prime}_{x,z} + k^{4} w_{x,z} = 0.$$

(20)

The solution of Eq. (20) has to be finite when $z \to \infty$. Taking into account this condition, we obtain:

$$w_{x} = \left( {C_{1} + C_{2} z} \right)\exp \left( { - \left| k \right|z} \right),\quad w_{z} = \left( {C_{3} + C_{4} z} \right)\exp \left( { - \left| k \right|z} \right),$$

(21)

where $C_{1} - C_{4}$ are undetermined coefficients. Substituting solution (21) into Eq. (17) and boundary conditions (19), we arrive at the following set of algebraic equations for the undetermined coefficients. Solving this set, we obtain:

$$\begin{aligned} & w_{x} = \frac{{iC_{1} }}{{2\left( {1 - \nu } \right)}}\left( {1 - 2\nu - kz} \right)\exp \left( { - \left| k \right|z} \right),\quad C_{1} = \frac{{2p\left( k \right)\left( {1 - \nu } \right)}}{{\left( {K_{p} + {{2\mu_{p} } \mathord{\left/ {\vphantom {{2\mu_{p} } 3}} \right. \kern-\nulldelimiterspace} 3}} \right)\left( {1 - 2\nu } \right)}}, \\ & w_{z} = C_{1} \left( {1 + \frac{kz}{{2\left( {1 - \nu } \right)}}} \right)\exp \left( { - \left| k \right|z} \right). \\ \end{aligned}$$

(22)

Now one can find the Fourier transform of the volumetric strain:

$$\vartheta \left( {k,z} \right) = - \left( {ikw_{x} + w^{\prime}_{z} } \right) = \frac{2kp\left( k \right)}{{\left( {K_{p} + {{2\mu_{p} } \mathord{\left/ {\vphantom {{2\mu_{p} } 3}} \right. \kern-\nulldelimiterspace} 3}} \right)}}\exp \left( { - \left| k \right|z} \right).$$

(23)

In the spatial representation, the volumetric strain of the medium is given by:

$$\theta \left( {x,z} \right) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\vartheta \left( {k,z} \right)\exp \left( {ikx} \right)dk} = \frac{1}{{\pi \left( {K_{p} + {{2\mu_{p} } \mathord{\left/ {\vphantom {{2\mu_{p} } 3}} \right. \kern-\nulldelimiterspace} 3}} \right)}}\int\limits_{ - \infty }^{\infty } {kp\left( k \right)\exp \left( {ikx - \left| k \right|z} \right)dk} .$$

(24)

Using Eq. (3), we can find the Fourier transform of the pressure $p\left( k \right)$ produced by the LGW on the seabed:

$$\begin{aligned} p\left( k \right) = & \rho g\left\{ {A\int\limits_{0}^{{x_{0} }} {{\text J}_{0} \left( {2\left\{ {sx^{\prime}} \right\}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \right)\exp \left( { - ikx^{\prime}} \right)dx^{\prime}} } \right. \\ & \quad + \left. {\mathop {\lim }\limits_{\varepsilon \to 0 + } \int\limits_{{x_{0} }}^{\infty } {\left[ {\eta_{0} \exp \left( { - ik_{0} x^{\prime}} \right) + B\exp \left( {ik_{0} x^{\prime}} \right)} \right]\exp \left( { - ikx^{\prime} - \varepsilon x^{\prime}} \right)dx^{\prime}} } \right\}. \\ \end{aligned}$$

(25)

Let us now substitute Eq. (25) for $p\left( k \right)$ into Eq. (24) and then change the order of integration over $k$ and $x^{\prime}$. Performing the internal integration over $k$, yields:

$$\begin{aligned} \theta \left( {x,z} \right) = & - \frac{4i\rho gz}{{\pi \left( {K_{p} + {{2\mu_{p} } \mathord{\left/ {\vphantom {{2\mu_{p} } 3}} \right. \kern-\nulldelimiterspace} 3}} \right)}}\left\{ {A\int\limits_{0}^{{x_{0} }} {{\text J}_{0} \left( {2\left\{ {sx^{\prime}} \right\}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \right)\frac{{\left( {x + x^{\prime}} \right)dx^{\prime}}}{{\left[ {\left( {x + x^{\prime}} \right)^{2} + z^{2} } \right]^{2} }}} } \right. \\ & \quad + \left. {\int\limits_{{x_{0} }}^{\infty } {\left\{ {\eta_{0} \exp \left( { - ik_{0} x^{\prime}} \right) + B\exp \left( {ik_{0} x^{\prime}} \right)} \right\}\frac{{\left( {x + x^{\prime}} \right)dx^{\prime}}}{{\left[ {\left( {x + x^{\prime}} \right)^{2} + z^{2} } \right]^{2} }}} } \right\}. \\ \end{aligned}$$

(26)