Rumor Transmission in Online Social Networks Under Nash Equilibrium of a Psychological Decision Game

Abstract

This paper investigates rumor transmission over online social networks, such as those via Facebook or Twitter, where users liberally generate visible content to their followers, and the attractiveness of rumors varies over time and gives rise to opposition such as counter-rumors. All users in social media platforms are modeled as nodes in one of five compartments of a directed random graph: susceptible, hesitating, infected, mitigated, and recovered (SHIMR). The system is expressed with edge-based formulation and the transition dynamics are derived as a system of ordinary differential equations. We further allow individuals to decide whether to share, or disregard, or debunk the rumor so as to balance the potential gain and loss. This decision process is formulated as a game, and the condition to achieve mixed Nash equilibrium is derived. The system dynamics under equilibrium are solved and verified based on simulation results. A series of parametric analyses are conducted to investigate the factors that affect the transmission process. Insights are drawn from these results to help social media platforms design proper control strategies that can enhance the robustness of the online community against rumors.

1 Introduction

Over the past decade, rapid development of online social communities has made far and profound impacts on multiple aspects of the modern world. Unlike word-of-mouth communication networks or traditional news media (e.g., newspapers or television), online social networks (OSNs), such as those based on Facebook and Twitter, have changed the way how information is transmitted – users do not only behave as passive information receivers, but also have the liberty to generate or pass new content to others. Such an interactive mechanism makes information more accessible to all users, but at the same time also leads to difficulties in guaranteeing the reliability and truthfulness of transmitted contents. In certain cases, people with ignorance or foul intentions may even purposefully transmit rumors (i.e., unconfirmed elaboration or annotation of information that is of public interest (Wang et al. 2015)) to influence public opinions. For example, in January 2020, false information on possible ways to cure COVID-19, such as drinking detergent products, was widely transmitted in OSNs and resulted in hundreds of deaths (Islam et al. 2020). In recognition of the serious consequences that rumors may bring, the World Economic Forum listed “massive digital misinformation” as one of the top risks facing a modern society (Howell 2013).

Transmission of rumors and their negative social impacts can be largely attributed to the absence of administrative control over vicious and misleading information. Various methods that suggest optimal control exist in the literature. For example, a widely adopted control mechanism has been proposed for solving the Influence Maximization (IM) problem (Vega-Oliveros et al. 2020), where individuals that have a large impact on networks are identified. However, the effectiveness of these control methods crucially depends on the accuracy of the underlying mathematical model that describes the information diffusion process in OSNs. In fact, despite the abundance of data that most OSNs possess during their operation, there still lacks a method that generates accurate assessments of the status quo (especially for rumors that are still developing) that are necessary for efficient content screening strategies. In light of this need, quantitative models that describe rumor transmission mechanisms have become a popular interdisciplinary research topic, branching into studies of cloud-based multicasting mechanism (Wang et al. 2013), normative mechanism (Lee and Oh 2017), self-growth mechanism (Huo and Cheng 2019), etc. To the best of our knowledge, most of the previous efforts on this topic have not considered the decision-making processes of users with different psychological states and their influence on rumor transmission.

This paper aims to fill the above gaps by proposing a more comprehensive modeling framework for rumor transmission over OSNs.

• 1. We introduce a directed graph to represent an OSN, which can not only effectively describe the directional transmission of rumors, but also accurately capture a user’s follower and followee numbers.

• 2. We represent the mixed population with five compartments¹, namely the susceptible (S), the hesitating (H), the infected (I), the mitigated (M), and the recovered (R), and develop novel transmission rules to describe their transmission dynamics. Analytical formulas for the system dynamics equation, expressed in forms of a system of differential equations, as well as the effective reproduction number and the final compartment sizes, are derived.

• 3. We further propose a heterogeneous transmission game to describe the decision-making process of a user on whether or not to react to a topic. Each user is assumed to be risk-averse while weighing a trade-off between expected popularity among followers and possible penalty from the social media platform for spreading false information.

• 4. A series of numerical experiments, as well as parametric sensitivity analyses, are conducted to demonstrate the applicability of the proposed model, as well as to draw insights. Characteristics of the rumors and those of the users are examined to give a better understanding on their impacts on the rumor transmission process. Moreover, sensitivity analyses on various system parameters are also conducted; the findings can be used to design policies that can control rumor transmission toward certain objectives (e.g., containing the final influenced population, or limit the peak of transmission rate) under limited budget or resources.

The rest of this paper is organized as follows. s. Section 2 reviews the related work. Section 3 introduces the dynamics of an OSN system, with S, H, I, M, R compartments, and basic characteristics. Section 4 proposes a transmission game in which users interact with one another to reach an equilibrium condition. In Sect. 5, we verify the proposed model with simulations, and conduct a series of parametric sensitivity analyses. Lastly, we make final remarks in Sect. 6.

2 Related Work

In this section, we comment on the previous efforts that are related to the present article.

2.1 Rumor Transmission Model

Two widely adopted information diffusion models are the Linear Threshold Model (LTM)(Chen et al. 2010; Kempe et al. 2003) and the Independent Cascade Model (ICM)(Lu et al. 2017). The ICM is normally implemented in discrete time steps. Starting from an initial subset of nodes, the state of other nodes are changed by a cascade; i.e., an infected node will attempt to infect its susceptible neighbors and may succeed according to certain probability. Such a probability usually varies over edges to represent the relationship credulity. On the other hand, the LTM models this stochastic process in a slightly different manner. A node changes from susceptible state to infected state only when the frequency of receiving information from its neighbors is larger than a node-specific threshold(Zhu et al. 2014). Inspired by these basic models, while recognizing clear similarities between the transmission of rumors and infectious diseases (Gomez-Rodriguez et al. 2013), researches have been extensively exploring describing information diffusion via epidemiological models. In the 1920s, Kermack and McKendrick (1927) first modeled the infection dynamics of a disease, whereas the population is divided into three compartments: the susceptible, the infected and the recovered (SIR). The SIR model describes the state dynamics of nodes in a general system, and it sees adoption in a variety of application contexts, such as data transmissions in mobile Inter-vehicular communication networks (Mashwama et al. 2020), and dynamic emotion contagion in a crowd of evacuees (Xiang et al. 2018). After that, the development of various epidemiological models and mechanisms subsequently emerged, often assuming a well-mixed population that can be described by an SIR-type system dynamics (Daley and Kendall 1964; Maki and Thompson 1973; Sudbury 1985; Rey et al. 2016). Recently, Lu and Ouyang (2019) proposed a new epidemic dynamics model with a vaccination game to describe the influence of “vaccine-phobia” on the disease propagation process.

However, basic epidemiological models cannot fully represent the process of rumor transmission in OSNs due to different characteristics of the system (e.g., interaction mechanisms and graph structures) that drive more complex system dynamics. For example, information transmission in OSNs is typically directional, from leaders to followers, hence requiring descriptions based on directed graphs. In addition, rumor transmission depends on a much more subjective decision-making process that involves complex psychological factors of the participants; hence, the SIR-type dynamic system models need to be extended to capture the mental states (such as hesitation and reactions) of individuals.

These challenges were partially addressed in some of the studies on rumor transmission. On one hand, more complex population distributions, such as “scale-free networks” (Albert et al. 2000; Nekovee et al. 2007) and “small-world networks” (Zanette 2002; Lü et al. 2011), have been used to better describe the online community. These studies utilized the edge-based dynamics model proposed by Volz (2008) for random graphs (which was later simplified/extended by Miller (2011)). After that, many extended edge-based models were proposed to study the process of information transmission (Spencer and Srikant 2015; Xian et al. 2020), most of which nevertheless considered information transmission in undirected networks. On the other hand, dynamical systems with additional compartments (beyond S, I, and R), and those with multiple types of information, have also been developed to describe the diverse states and scenarios associated with participants in OSNs. Examples of the former include the Susceptible–Infected–Counterattack–Refractory model (SICR), which introduces the counter-rumor compartment and counterattack mechanism (Zan et al. 2014), and the Susceptible–Exposed–Infected–Recovered–Susceptible model (SEIRS-QV), with explicit consideration of vaccination and quarantine states (Hosseini and Azgomi 2018). Examples of the latter include the ignorant-spreader I-spreader II-stifler model ($IS_1S_2R$) model, with differentiation of information only in the propagation state (Zhuang et al. 2017), and the double SIR model (DSIR), where each type of information has its own complete dissemination process (Zan 2018). Muhlmeyer et al. (2020) summarized some previous dynamical systems and presented stochastic versions of these models.

2.2 Rumor Psychological Game

Efforts have also been made to address the psychological factors influencing rumor transmission in OSNs, mainly via the use of game theory that captures the decision-making process and interactions among different individuals. Zinoviev and Duong (2011) proposed a game-theoretic model for one-way information forwarding behavior in a star-shaped social network. Different participants, such as authorities (Zinoviev and Duong 2011) and rumor makers (Li and Liu 2016), were later added to the game to quantify their influence on rumor transmission. Etesami and Başar (2016) investigated a competitive transmission game for multi-information competition and communication over undirected networks. Recently, Huang et al. (2020) introduced a differential game-theoretic model by estimating the expected net utility of rumormongers and the expected loss of rumor victims. Moreover, it is typical to explicitly model people’s utility in order to understand the decision-making process under various human factors (such as cognitive behavior, psychology, neighbour influence) and popularity of information. These factors are further categorized as internal and external ones (Xiao et al. 2019). Internal factors include the number of followers (Wang et al. 2017), the emotional states (Li et al. 2020), the influence power of one individual (He et al. 2019) as well as the individual’s cognition, the self-interest in information and reputation (Qing and ZhengGong 2020). External factors often include herd psychology and herd pressure (Xiao et al. 2019; Yan and Jiang 2018).

Despite these efforts, two important aspects of the problem were missing in the literature. First, most of the proposed rumor transmission models are derived with undirected networks, implicitly assuming equal likelihood for either participant in a pair to influence each other. Such an assumption is not very realistic in modern OSNs; asymmetric information transmission in directed networks is much more realistic and generic, but has rarely been considered. Second, heterogeneous individuals’ rational decisions, and their collective potential to reach an equilibrium, have not yet been thoroughly considered. In particular, the number of followers is found to have a large impact on people’s transmission utilities, but to the best of the authors’ knowledge, such a mechanism has rarely been studied in the literature on rumor transmission.

3 SHIMR Model

This section introduces the proposed Susceptible-Hesitating-Infected-Mitigated-Recovered (SHIMR) model, a generalization of the classic SIR model (Kermack and McKendrick 1927) that explicitly considers human’s psychological behavior while facing rumors.

3.1 Model Formulation

In our model, we consider the joint transmission of a rumor and a counter rumor (i.e., opposite opinions or claims over an controversial topic), neither of which have evident support or authoritative endorsement. Online users are assumed ignorant (i.e., possessing no knowledge regarding the fact), have no inherent bias, and may possibly choose to believe and spread either opinion.

We consider a directed graph $G(\mathcal {N},\mathcal {E})$ representing a social media network, where $\mathcal {N}$ and $\mathcal {E}$ stand for the sets of account nodes and communications arcs, respectively, and $n = |\mathcal {N} |$. The network is simple (i.e., free of self-loops or multiple arcs between any pair of nodes, as explained in Newman et al. (2001)). The nodes in this graph are divided into five compartments:

• 1. Susceptible nodes (S): those who are not yet exposed to the rumor or counter-rumor so far;

• 2. Hesitating nodes (H): those who are aware of the controversial topic but have not decided whether to express an opinion;

• 3. Infected nodes (I): those who have decided to spread the rumor;

• 4. Mitigated nodes (M): those who have decided to spread the counter-rumor;

• 5. Recovered nodes (R): those who are aware of, but have eventually lost interest in, the controversial topic.

For simplicity, we hereon denote the fractions of nodes in all five compartments over the entire population by S, H, I, M, R, respectively. Clearly,

$$\begin{aligned} S(t) + H(t) + I(t) + M(t) + R(t) = 1, \forall t \ge 0. \end{aligned}$$

(1)

Although a few spreaders must exist to initiate the discussion, the size of their population is assumed negligible at time $t=0$, i.e., $\frac{I(0)}{S(0)}\rightarrow 0$. Moreover, for any compartment $A \in \{S, H, I, M, R\}$, we let $A_{jk}(t)$ be the fraction of nodes in that compartment that have in-degree $j\in \{1,...,J\}$ and out-degree $k \in \{1,...,K\}$ at time t. We also let $p_{jk}$ be the probability that an arbitrary node has degree-(j, k). Then, we have:

$$\begin{aligned}&A(t) = \sum _{j,\ k}A_{jk}(t), \forall j = 1, \cdots , J, \forall k = 1, \cdots , K, \end{aligned}$$

(2)

$$\begin{aligned}&p_{jk} = S_{jk}(t) + H_{jk}(t) + I_{jk}(t) + M_{jk}(t) + R_{jk}(t). \end{aligned}$$

(3)

According to Newman et al. (2001), the distribution of degrees in a random network follows a power law (Fu et al. 2008), which can be expressed in the form of a probability generating function, as follows:

$$\begin{aligned} F(x,y) = \sum _{j,\ k} p_{jk}x^jy^k. \end{aligned}$$

(4)

The average in-degree, $\langle j \rangle$, and out-degree, $\langle k\rangle$, are given as follows:

$$\begin{aligned} \langle j \rangle = \langle k\rangle = \frac{\partial F}{\partial x} \mid _{x=y=1}. \end{aligned}$$

(5)

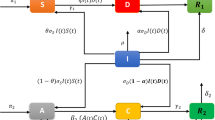
We assume that an $S_{jk}$-type node may receive the rumor (or counter-rumor) from one of its infected (or mitigated) neighbors according to a Poisson process with a constant rate $r_I$ (or $r_M$). Upon being exposed to the topic, this node will transition into the H compartment immediately. The amount of time needed for an $H_{jk}$-type node to react follows a negative exponential distribution with parameter $\beta$. This node decides to either transmit a pertinent opinion (rumor or counter-rumor), which occurs with probability $\gamma _{jk}$, or stay silent and ignore the topic, which occurs with probability $(1-\gamma _{jk})$. This decision on whether to stay silent will be the result of a Nash equilibrium, which will be discussed in Sect. 3. If the node decides to transmit an opinion, it will spread the rumor with conditional probability q(t), or counter-rumor with probability $(1-q(t))$. These sequence of decisions will determine how this H node will transition into the corresponding compartment (i.e., I, M, or R). Finally, an $I_{jk}$-type (or $M_{jk}$-type) node may lose interest in the topic completely and transition into the R compartment with rate $\mu _{I}$ (or $\mu _{M}$). All the abovementioned transition processes can be described as a decision tree, as illustrated in Fig. 1.

Fig. 1

Decision process of an individual regarding a rumor

To simplify the analyses, we further assume that the network degree distribution remains approximately stable during the spread of the rumor (i.e., based on the Barabási–Albert model (Albert and Barabási 2002)). For convenience, we say that a node is in a certain compartment if it belongs to the corresponding compartment. Let $\theta (t)$ be the probability that an arbitrary arc with an S-state successor has not transmitted an opinion by time t. Since transmissions on arcs occur independently according to a Poisson process, $\theta (t)$ can be alternatively interpreted as the fraction of in-degree-one susceptible nodes at time t. We further differentiate the arcs by the state of its predecessor, using $\theta _{S}$, $\theta _{H}$, $\theta _{I}$, $\theta _{M}$, $\theta _{R}$ to denote the corresponding probabilities. Obviously, we have

$$\begin{aligned} \theta (t) = \theta _{S}(t) + \theta _{H}(t) + \theta _{I}(t) + \theta _{M}(t) + \theta _{R}(t), \forall t \ge 0. \end{aligned}$$

(6)

Fig. 2

Compartment representation of the SHIMR system in terms of $\theta$

The transition process is illustrated in Fig. 2. An arc no longer satisfies the definition of $\theta (t)$ as soon as the predecessor was in I- or M-compartment but has just transmitted an opinion to the corresponding S-state successor. Therefore, the change of $\theta$ over time is captured as follows:

$$\begin{aligned} \dot{\theta }(t) = -(r_I\theta _{I}(t) + r_M\theta _{M}(t))\ . \end{aligned}$$

(7)

According to Volz (2008), the conditional probability for an arc to have an S-state successor and an I-state predecessor is $\eta _I(t) = {\theta _{I}(t)}/{\theta (t)}$. Consider an S node with degree-(j, k), the expected number of arcs connected to I-state predecessors is then given by $j \eta _I(t)$. We also define $\eta _M(t)$ in a similar fashion for compartment M. As shown in Volz (2008), the fraction of degree-(j, k) nodes that still remain in S-state at time t (i.e., no transmission has ever occurred), denoted by $u_{jk}(t)$, should satisfy the following differential equation:

$$\begin{aligned} \frac{\dot{u}_{jk}(t)}{u_{jk}(t)}= r_I j \eta _I(t) + r_M j \eta _M(t) \ , \end{aligned}$$

(8)

which directly yields the explicit solution

$$\begin{aligned} u_{jk}(t) = C_1 \cdot \Big (\exp \{-\int _{\tau = 0}^{t} [r_I\eta _I(\tau ) + r_M\eta _M(\tau ) ]\ d\tau \}\Big )^j . \end{aligned}$$

(9)

With our assumed initial condition, i.e., $u_{jk}(0)\rightarrow 1$, we can see that constant $C_1 \rightarrow 1$.

Recall that $\theta (t)$ is equal to $u_{1k}(t) = \exp \{-\int _{\tau = 0}^{t} [r_I\eta _I(\tau ) + r_M\eta _M(\tau )] \ d\tau \}$. Therefore, the fraction of S-nodes with degree-(j, k) at time t is:

$$\begin{aligned} S_{jk}(t) = p_{jk} \cdot u_{jk}(t) = p_{jk}[\theta (t)]^j . \end{aligned}$$

(10)

The dynamics of $\theta _{I}(t)$ and $\theta _{M}(t)$ are derived next. For an arbitrary target node, we use $\xi _{jk}^{in}$ to denote the probability that any of its in-degree neighbors has degree-(j, k). This probability has an alternative interpretation – for an arbitrary directed arc with the target node as the successor, the probability that the predecessor of this arc has degree-(j, k). The total number of nodes with degree-(j, k) is $p_{jk} \cdot n$, so the total number of out-going arcs from these nodes is $p_{jk} \cdot n \cdot k$. Then, the probability that the predecessor of an arbitrary node has degree-(j, k) gives $\xi _{jk}^{in}$, as follows:

$$\begin{aligned} \xi _{jk}^{in} = \frac{p_{jk} \cdot n \cdot k}{\langle k\rangle \cdot n} = \frac{kp_{jk}}{\langle k\rangle }. \end{aligned}$$

(11)

Clearly, by definition, $\theta _S(t)$ can be expressed as follows:

$$\begin{aligned} \theta _S(t) = \sum _{j,\ k}u_{jk}(t) \cdot \xi _{jk}^{in} = \sum _{j,\ k} \frac{k}{\langle k \rangle }{S}_{jk}(t) \ . \end{aligned}$$

(12)

Note from Eq. (12) that $\theta _S(t)$ = $[\sum _{j,\ k}kn{S}_{jk}(t)]$ $/ [{\sum _{j,\ k}\langle k \rangle }n]$, i.e., the ratio of the total out-degrees from all $S_{jk}$-type nodes to the total out-degrees from all nodes in the network. We can derive $\theta _{H}(t)$, $\theta _{I}(t)$ and $\theta _{M}(t)$ in a similar fashion as follows:

$$\begin{aligned} \begin{aligned}&\theta _H(t) = \sum _{j,\ k} \frac{k}{\langle k \rangle }H_{jk}(t) , \\&\theta _I(t) = \sum _{j,\ k} \frac{k}{\langle k \rangle }I_{jk}(t) , \\&\theta _M(t) = \sum _{j,\ k} \frac{k}{\langle k \rangle }M_{jk}(t) . \end{aligned} \end{aligned}$$

(13)

Using the aforementioned transmission rules, the dynamics of $\theta _{I}$ consists of two parts: a positive term capturing a fraction of H-state nodes newly deciding to transmit the rumor, and a negative term indicating (a) a fraction of I-state nodes becoming stiflers and (b) successfully infecting an S-state node.

$$\begin{aligned} \dot{\theta }_I&= \sum _{j,\ k} \frac{k}{\langle k \rangle }\beta \gamma _{jk} q H_{jk} - (r_I + \mu _{I})\theta _I. \end{aligned}$$

(14)

The dynamics of $\theta _{M}$ can be derived similarly:

$$\begin{aligned} \dot{\theta }_M&= \sum _{j,\ k} \frac{k}{\langle k \rangle }\beta \gamma _{jk} (1 - q) H_{jk} - (r_M + \mu _{M})\theta _M . \end{aligned}$$

(15)

According to Knapp (1944), the probability of transmitting rumor is roughly in inverse proportion to the credibility of counter-rumor. Hence, we define the attractiveness difference between the rumor and the counter-rumor. To stay focused, we assume that the latter is closer to the fact, but the former is more appealing at its debut (especially when it is intentionally fabricated to be persuasive). As the public gradually reveals the truth, the rumor loses its attractiveness. Therefore, we assume the attractiveness difference of the rumor over counter-rumor, denoted $\pi (t)$, gradually decreases over time from a large value of $\pi _0$ until becoming completely stale with a small (or even negative) value of $\pi _\infty$. We modify the functional form suggested in Zhang et al. (2018) and assume the following:

$$\begin{aligned} \pi (t) = \frac{\pi _0- \pi _\infty }{\lg (10 + vt)} + \pi _\infty , \end{aligned}$$

(16)

where v is the variation speed, and clearly $\pi (0) =\pi _0$ and $\pi (\infty ) = \pi _\infty$. We further assume the probability that node i chooses to spread the rumor, q(t), is related to $\pi$ per the Fermi–Dirac statistics (McDougall and Stoner 1938) as follows:

$$\begin{aligned} q(t) = \{1 + \exp (- \pi (t))\}^{-1} . \end{aligned}$$

(17)

Now, we are ready to summarize the dynamics of a degree-(j, k) node in all compartments, including Eqs. (7)-(10),(12)-(15) and the following:

$$\begin{aligned} \begin{aligned}&\dot{S}_{jk} = \dot{\theta }p_{jk}j\theta ^{j-1} = j\frac{\dot{\theta }}{\theta }S_{jk} = -j(r_I\frac{\theta _I}{\theta } + r_M\frac{\theta _M}{\theta })S_{jk} , \\&\dot{H}_{jk} = -\dot{S}_{jk} - \beta H_{jk} , \\&\dot{I}_{jk} = \beta \gamma _{jk} q H_{jk} - \mu _{I}I_{jk} , \\&\dot{M}_{jk} = \beta \gamma _{jk} (1 - q) H_{jk} - \mu _{M}M_{jk} , \\&\dot{R}_{jk} = \beta (1 - \gamma _{jk}) H_{jk} + \mu _{I}I_{jk} + \mu _{M}M_{jk} , \\&\dot{\theta }_S = \sum _{j,\ k} \frac{k}{\langle k \rangle }\dot{S}_{jk}, \\&\dot{\theta }_H = \sum _{j,\ k} \frac{k}{\langle k \rangle } \dot{H}_{jk}, \\&\dot{\theta }_R = \dot{\theta }- \dot{\theta }_S - \dot{\theta }_H - \dot{\theta }_I - \dot{\theta }_M .\\ \end{aligned} \end{aligned}$$

(18)

3.2 Effective Reproduction Number

The effective reproduction number of an arbitrary test node at time t, denoted $R_e(t)$, indicates the expected number of “infections” it can directly generate (Delamater et al. 2019). In our context, this quantity measures the transmission potential of a rumor topic and gives a necessary condition for a mass discussion “outbreak” to happen; i.e., if $R_e(t) < 1$, the topic is expected to naturally die out without spreading to the entire population, and the opposite also holds. We follow the process proposed by Diekmann et al. (1990) to compute $R_e(t)$. The detailed derivation in the appendix shows that an expression is given by

$$\begin{aligned} R_e(t) = \frac{1}{\langle k \rangle } \sum _{j,\ k} jkp_{jk} \theta (t)^{j - 1} \gamma _{jk} \cdot \Big (\frac{r_I q(t)}{\mu _{I} + r_I} + \frac{r_M (1 - q(t))}{\mu _{M} + r_M} \Big ) . \end{aligned}$$

(19)

In particular, its value at $t=0$, $R_e(0)$, is also known as the basic reproduction number (Diekmann et al. 1990), which predicts the system’s vulnerability to a topic. Such vulnerability value serves as an effective check on the potential necessity for rumor control and intervention.

3.3 Final Compartment Sizes

At time $t=\infty$, the value of $A_{jk}(\infty )$ is the final fraction of degree-(j, k) nodes in compartment $A \in \{S, H, I, M, R\}$. In particular, $1 - S(\infty )$ measures the final size of the population influenced by the rumor or counter-rumor. Following Miller (2011), we show below how to derive formulas for these values when the probability of users receiving or discarding either opinion (rumor or counter-rumor) is equal, i.e. $r_I = r_M = r$, and $\mu _I = \mu _M = \mu$.²

To this end, we define the “transmissibility” T as the probability that, conditional on the successor of an edge being in S-state and the predecessor in I or M-state, this edge successfully transmitted a pertinent opinion before its predecessor turns into state R. The transmissibility is given by $T = \frac{r}{r + \mu }$. Further, we define $\phi$ to be the probability that the predecessor of an arbitrary node has been in either I or M state. Recall from Eq. (11) that the probability for a predecessor of an arbitrary node to have degree-(j, k) is $\frac{kp_{jk}}{\langle k \rangle }$, and the probabilities for this degree-(j, k) predecessor to ever be in the H state and to transmit an opinion, are $(1 - \theta (\infty ))^j$ and $\gamma _{jk}$, respectively. Hence $\phi$ is given by summing up the product of all these terms across for degree types; i.e.,

$$\begin{aligned} \phi = \sum _{j,\ k} \frac{kp_{jk}}{\langle k \rangle }(1 - \theta (\infty )^j) \gamma _{jk}. \end{aligned}$$

(20)

Clearly, the probability that an arbitrary edge with an S-predecessor has successfully transmitted opinion is given by $T \cdot \phi$. Since every edge initially has an S-predecessor, this probability equivalently gives the fraction of the edges whose successors have been converted into the H state. By definition of $\theta (\infty )$, we give the following expression

$$\begin{aligned} \theta (\infty ) = 1 - \frac{r}{r + \mu } \cdot \sum _{j,\ k} \frac{kp_{jk}}{\langle k \rangle }(1 - \theta (\infty )^j) \gamma _{jk},\ \end{aligned}$$

(21)

which is in the form of a fixed point if we define the right-hand-side as a function $h(\theta (\infty ))$.

Hence, the fraction of nodes in different compartments at infinity time can be represented as follows:

$$\begin{aligned} \begin{aligned}&S_{jk}(\infty ) = p_{jk} \cdot \theta (\infty )^{j}, \\&H_{jk}(\infty ) = I_{jk}(\infty ) = M_{jk}(\infty ) = 0, \\&R_{jk}(\infty ) = 1 - S_{jk}(\infty ). \end{aligned} \end{aligned}$$

(22)

4 Transmission Game in the H Compartment

In this section, we consider that a hesitating individual i in the H compartment with degree-(j, k) rationally makes decisions about whether to react to a topic. We assume all participants in the H compartment try to maximize their own utilities, and their willingness to transmit a rumor (or a counter-rumor) only depends on the benefits and penalties that result from the collective decisions of all OSN users. As we have many individuals of the same type, and they repeatedly deal with rumors, the decision-making strategy of each individual is specified by a Bernoulli probability distribution over the binary actions, with probability $\gamma _{jk}^{i}$ for transmitting opinions.

Social media users mainly aim to gain popularity by increasing fan number, so that the users can enjoy public attention (Knapp 1944) or receive monetary reward through advertisement (Khamis et al. 2017). Generally, users realize this purpose by regularly making posts to appeal to their fans. Moreover, in order to quickly win fame or attention, some users decide to transmit controversial opinions. However, this risky action is a double-edged sword. Transmitting controversial opinions can also lead to the loss of fans. To reflect this phenomenon, we here define the utility as the public influence gained by posting controversial opinions. The utility consists of two parts:

In the first part, we define $f_1(k, \gamma _{jk}^{i})$ as the expected popularity affected by fan numbers, which has a positive correlation with $\gamma _{jk}^{i}$. Users with a small out-degree k are relatively more prone to transmitting controversial opinions in order to increase popularity. They are less risk averse. In contrast, those already popular (with a large out-degree k) are likely to be more conservative and risk averse. Hence, we assume that all users in the online social media follow risk averse behavior, which is represented by an increasing utility function with respect to $\gamma _{jk}^{i}$. This function is also characterized by the coefficient $\frac{k}{\alpha _1}$ to represent the degree of risk aversion, as follows (Guzavicius et al. 2014) :

$$\begin{aligned} f_1(k, \gamma _{jk}^{i}) = {\left\{ \begin{array}{ll} \frac{(\gamma _{jk}^{i} + 1)^{1 - \frac{k}{\alpha _1}} - 1}{1-\frac{k}{\alpha _1}} , k \ne \alpha _1 \\ \ln (\gamma _{jk}^{i} + 1) , k = \alpha _1 \ \end{array}\right. } \ . \end{aligned}$$

(23)

Clearly when $k\rightarrow \infty$ the utility function approaches zero.

Second, social media platforms may take the initiative to stop an opinion from transmitting in order to avoid offending certain user groups. This is commonly done by penalizing super-spreaders with account suspension or warning labels, often after the rumor propagation has ended. The severity of the expected penalty is assumed to be proportional to the impact of the topic, e.g., the final size of the influenced population $R(\infty \mid \ \varvec{\gamma })$, where $\varvec{\gamma } =\{\gamma _{jk}^{i}\}_{\forall i,j,k}$ denotes the decisions from the entire population. Moreover, the platform is assumed to be absolute risk-averse, and hence would naturally focus on penalizing popular accounts that spread the rumor. We assume that the coefficient of the penalty is monotonically increasing with the out-degree k as well as $\gamma _{jk}^{i}$. When the platform is absolute risk-averse, the coefficient has a constant ratio of the second order derivative to the first-order derivative (with respect to $\gamma _{jk}^{i}$ and k); a common choice would be taking an exponential form Pratt (1978). As such, we assume the coefficient satisfies the following $e^{\ln \alpha _3 + \gamma _{jk}^{i}\frac{k}{\alpha _2}}$, where $\alpha _2, \alpha _3$ capture the impacts of the platform’s penalty on the user’s utility. Further, in the derivation of Eq. (20) we see that the probability for a node to receive the penalty is $\gamma _{jk}^{i}(1 - \theta (\infty \mid \ \varvec{\gamma })^j)$. Hence, the expected penalty of the $i^{th}$ individual can be written as:

$$\begin{aligned} f_2(k, \gamma _{jk}^{i} \mid \ \varvec{\gamma }) = R(\infty \mid \ \varvec{\gamma }) e^{\ln \alpha _3 + \gamma _{jk}^{i}\frac{k}{\alpha _2}} \gamma _{jk}^{i} (1 - \theta (\infty \mid \ \varvec{\gamma })^j). \end{aligned}$$

(24)

Putting Eqs. (23) and (24) together, the expected utility function for the $i^{th}$ individual $U_{jk}^i$ is as follows:

$$\begin{aligned} U_{jk}^{i}(\gamma _{jk}^{i} \mid \ \varvec{\gamma })= f_1(k, \gamma _{jk}^{i}) - f_2(k, \gamma _{jk}^{i} \mid \ \varvec{\gamma }) . \end{aligned}$$

(25)

Note that $U_{jk}^{i}(\gamma _{jk}^{i} \mid \ \varvec{\gamma })$ takes the same form and parameters for all the probabilistically identical users in a group with degree-(j, k). Intuitively, the strategy taken at equilibrium should thus be identical among each group, i.e., $\gamma _{jk}^{i*} = \gamma _{jk}^{*}, \forall i$. Therefore, we can drop the superscript i in Eq. (25), and equivalently state the mixed Nash equilibrium conditions.

$$\begin{aligned} \begin{aligned} \{\gamma _{jk}^{*}\}_{\forall j,k}&= \mathop {\arg \max }_{\{\gamma _{jk}\}_{\forall j,k}}U_{jk}(\gamma _{jk} \mid \ \varvec{\gamma }) \ , \forall j,k \\ \text {s.t.}&\ 0 \le \gamma _{jk} \le 1 \ . \end{aligned} \end{aligned}$$

(26)

We are then ready to give the following statement on the existence and uniqueness of mixed Nash equilibrium.

Proposition 1

Consider the utility function given Eq. (25). A unique mixed Nash equilibrium is achieved when $\{\gamma _{jk}^{*}\}_{\forall j,k}$ satisfies Eq. (26).

Proof

The existence of equilibrium is easy to see. Since $\gamma _{jk}$ takes value from a closed domain [0, 1], and the objective function in Eq. (26) is continuous and bounded, there must exist a global maximum.

We then prove the uniqueness. For all $k \ge 1$, it is easy to verify that the first order derivatives of Eq. (23) is positive and monotonically decreasing with respect to $\gamma _{jk}$. Similarly, the first order derivative of Eq. (24) is also monotonically increasing with $\gamma _{jk}$. Therefore, we see that the derivative of the utility function $\frac{\partial }{\partial \gamma _{jk}} U_{jk}$ is monotonically decreasing with $\gamma _{jk}$. It is also easy to verify that this derivative is positive at $\gamma _{jk}=0$. Thus, there can be either one root $\gamma _{jk}^{*} \in [0,1], \forall j,k$, where the utility function has a stationary point, or none, where $\gamma ^{*}_{jk}=1, \forall j,k$ is the global maximizer. The latter case may happen if the topic is highly unlikely to spread out and have an impact (i.e., small $R(\infty \mid \ \varvec{\gamma })$), or if the platform lacks the credibility (i.e., small $\alpha _3$). In this case the transmitter bears little loss of its popularity from the penalty, thus would incline to transmit.$\square$

We are then ready to propose an algorithm to solve for this equilibrium, i.e., $\varvec{\gamma }$ and $\theta (\infty \mid \ \varvec{\gamma })$ (embedded in the computation of $S_{jk}$) satisfying Eqs. (26) and (21) simultaneously. Note that Eq. (21) defines $\theta (\infty \mid \ \varvec{\gamma })$ in the form of a fixed-point $\theta (\infty \mid \ \varvec{\gamma }) = h(\theta (\infty \mid \ \varvec{\gamma }))$, it is then natural to solve it through fixed-point iteration per Proposition 2 below.

Proposition 2

Eq. (21) is contract on $[0,\tilde{\theta }(\infty \mid \ \varvec{\gamma })]$. Further, the fixed-point $\theta ^*(\infty \mid \ \varvec{\gamma })$ can be found by the fixed-point iteration with an initial guess $\theta _0(\infty \mid \ \varvec{\gamma }) \in [0,\tilde{\theta }(\infty \mid \ \varvec{\gamma })]$.

Proof

According to Hale et al. (2008), evaluating Eq. (21) at $\theta (\infty \mid \ \varvec{\gamma }) = 0$ and 1 gives $h(1)=1$ and $h(0)\in (0,1]$. In addition, $h(\theta (\infty \mid \ \varvec{\gamma }))$ is monotonically increasing and convex. There thus exists two fixed points $\theta ^*(\infty \mid \ \varvec{\gamma })$ and 1, with $0< \theta ^*(\infty \mid \ \varvec{\gamma }) < 1$. Using the mean value theorem, there must exist a point $\tilde{\theta }(\infty \mid \ \varvec{\gamma }) \in [\theta ^*(\infty \mid \ \varvec{\gamma }),1]$ such that

$$\begin{aligned} h'(\tilde{\theta }(\infty \mid \ \varvec{\gamma })) = \frac{h(1)-h(\theta (\infty \mid \ \varvec{\gamma }))}{1-\theta (\infty \mid \ \varvec{\gamma })} = 1. \end{aligned}$$

It then directly follows that $h'(\theta (\infty \mid \ \varvec{\gamma })) < h'(\tilde{\theta }(\infty \mid \ \varvec{\gamma }))=1 , \forall \ \theta (\infty \mid \ \varvec{\gamma }) \in [0,\tilde{\theta }(\infty \mid \ \varvec{\gamma }))$. According to the Banach fixed-point theorem, starting from an initial guess $\theta _0(\infty \mid \ \varvec{\gamma }) \in [0,\tilde{\theta }(\infty \mid \ \varvec{\gamma })]$, fixed point $\theta ^*(\infty \mid \ \varvec{\gamma })$ can be found through iterations. The proof is complete.$\square$  

Given an initial solution $\varvec{\gamma }$, the algorithm proceeds by iteratively solving for $\theta (\infty \mid \ \varvec{\gamma })$ using a fixed-point method, and $\varvec{\gamma }$ using a bi-section method. Each element of the initial $\varvec{\gamma }$ can be arbitrarily selected in [0, 1]. The integrated algorithm proceeds by solving for $\gamma$ and $\theta _\infty$ iteratively. The algorithm is described as follows:

5 Numerical Simulation and Discussions

5.1 Validation of Analytical Model

We consider a social network with heterogeneous users in an instance of wide-spreading topic (e.g., COVID-19). We conduct a series of simulations and use the results to verify the SHIMR model by predicting the evolution of the system during the transmission. The simulation assumes a power-law degree distribution for the number of fans of each individual (Huang and Su 2013). The maximum value of in- and out-degrees is set to $J = K = 1000$.

The following parameters are used for the system: $r = 0.03$, $\mu = 0.01$, $\beta = 0.01$, $\alpha _1 = 12$, $\alpha _2 = 8$, $\alpha _3 = 0.01$, $v=2, \pi _0= 61, \pi _\infty = -39$. Moreover, the initial condition at time $t = 0$ is set as $S(0) = 0.999$ and $I(0) = 0.001$. We then conduct Monte Carlo simulations over random instances of a network with 10000 total nodes, which are generated using the Molloy–Reed algorithm (Molloy and Reed 1995). A total of 100 simulations are conducted, with 20 random runs over each of 5 generated networks. We randomly assign 10 rumor-spreaders at time $t = 0$ to activate the transmission, and null initialization for other states, i.e., $I(0) = 10$, $S (0) = 9990$, $H(0) = 0$, $M(0) = 0$, $R(0) = 0$.

Fig. 3

Comparison between simulations and the SHIMR model

The comparison of the model prediction the simulated benchmark is shown in Fig. 3. The solid lines show the predicted evolution of the compartments in the SHIMR model. The dashed lines and the shadow areas describe the corresponding means and $95\%$ confidence intervals from 100 simulations. As shown, the model prediction of each compartment is in good accordance with the simulation result. The final epidemic size $R_\infty$ computed from system dynamic model is 0.9903 and that from simulation is 0.9804, yielding a 1.01% relative difference. The peak values of predicted I and M compartments are 0.1977 and 0.1540 while the simulated peaks are 0.2023 and 0.1492, and the relative differences are 2.27% and 3.22%, respectively. These results demonstrate the fidelity of the formulas from the SHIMR model.

5.2 Sensitivity Analyses on Decision Game

To further observe the equilibrium of the decision game, we examine the stationary solution for each user group. While $\{\gamma _{jk}^{*}\}_{\forall j,k}$ is numerically solved, we note from Eq. (26) that the individual decision at equilibrium should depend on the connectivity of this node. We plot the distribution of probability $\gamma _{jk}$ in Fig. 4(a) over the in- and out-degrees. The value clearly decreases rapidly with respect to the out-degrees because popular users put more values on their popularity. Particularly, there is an abrupt change of $\gamma _{jk}$ value between $10-100$ out-degrees. The marginal impacts of additional out-degrees diminishes beyond that change.

In contrast, the trend over in-degrees is not so obvious, partially due to the setup of our utility functions. This is also due to the small value of $\alpha _3$, which corresponds to the case that social media platform has little influence on suppress rumor spreading. Now, we select a larger $\alpha _3$ and plot the zoomed-in view in Fig. 4(b). In this figure, $\gamma _{jk}$ decreases with the in-degree slowly. Users that tend to transmit opinions are clustered, all with small out-degrees (which also consist of the majority of the population according to the power-law distribution). Therefore, if the social media platform wish to discourage users from participating in the mass discussion, it shall pay attention to those users with small out-degrees.

Fig. 4

The influence of in- and out-degree on the decision of dissemination information

It is necessary to understand how the system will behave from a macroscopic perspective. We observe how the effective production number $R_e(0)$ changes with respect to parameters $\alpha _1,\alpha _2,\alpha _3$, as shown in Fig. 5. With larger $\alpha _3$, the initial momentum of transmitting the topic in this social media platform is reduced. In both figures, $\alpha _2$ has more influence than $\alpha _1$. The results suggest that it is better to strengthen the influence of the platforms than to rely on the rationality of individuals on popularity. Additionally, the gradient is steeper at small $\alpha _2$. Since $\alpha _2$ indicates the inclusiveness of an enforcement (e.g., the minimum threshold of followers to be inspected for foul posts), we see that penalty-based controls are more effective when imposed on small and scattered accounts.

Fig. 5

The influence of $\alpha _1, \alpha _2, \alpha _3$ on the effective reproduction number $R_e(0)$

5.3 Sensitivity Analyses on Human Factors

To have a more in-depth understanding of the overall transmission process, we further investigate some hyper-parameters. We are interested in characteristics of human behavior (r, $\mu$, $\beta$) and the credibility of the social media platform ($\alpha _3$). Figure 6 shows the peak magnitude of I compartment ($I_{max}$) and the time reaching the peak ($t_{I_{max}}$) when r, $\beta$, $\mu$ and $\alpha _3$ range from 0.01 to 0.3. For simplicity, we only show simulation results here.

Fig. 6

Peak “infected” population and time reaching the peak

Higher values of r and $\beta$ both foster wide transmitting of a rumor in a similar fashion, as the corresponding peaks of “infected” population increase and are reached earlier. Therefore, to alleviate the surges of the infection, it is beneficial to consider (1) reducing $\beta$ by enhancing general education on internet moral and safety (which reduces emotional and blind decision-making), and (2) reducing r through browser censoring or lowering recommendation rate of disputable posts. However, note that the curves for these parameters are steeper at small values, indicating a large marginal gain only when these measures are taken to an extreme extent or the population is already very well educated.

On the other hand, the peak size of I compartment diminishes rapidly with $\mu$ due to its significant role in removing I-state nodes. Thus it is effective to timely broadcast authorized alarm or clarification so that the public tends to be vigilant and willing to avoid discussing the topic. The curve is most steep when $\mu$ takes value between 0.01 and 0.05, suggesting significant effectiveness in that range. The impact of $\alpha _3$ is almost linear. This can be considered by the social media platform to achieve penalty effectiveness by strengthening its impact.

Similarly, the final influenced compartment size $R(\infty )$, as well as those who have believed in the rumor and transmitted it (denoted $R_I(\infty )$) are shown in Fig. 7.

Fig. 7

Final influenced and accumulative “infected” population

If containing the size of $R_I(\infty )$ is the objective, the policymaker can reduce r and $\beta$. This may be an effective option when the system currently falls in the steep region, although the overall difference is not significant. Alternatively, the policymaker can consider increasing $\mu$ or $\alpha _3$ which yields a linear marginal gain. It is noteworthy that $\mu$ is the only parameter that has a significant impact, while other parameters have relatively negligible impacts. Recall the discussion over Fig. 6. It appears that prospectively educating the online community (i.e., reducing r and $\beta$) is less effective than post-reaction (e.g., by debunking rumor and punishing spreaders).

6 Conclusion

In this paper, we propose an SHIMR model to predict rumor transmission in a modern social network. The social network is represented by a random directed graph where each node indicates a user, and the in- and out-degrees follow a power-law distribution. The population is categorized, according to the stage of experiencing a rumor, into five compartments (i.e., S, H, I, M, R). The system dynamics is expressed, based on an edge-based formulation, as a set of ordinary differential equations. Furthermore, the effective reproduction number and the final compartment size are derived in closed form to capture the rumor’s tendency to propagate and its ultimate influence. A decision game is designed to describe how users rationally decide either to react to or disregard the ongoing rumor, whereas potential benefits and risks in transmitting an opinion are considered in the utility function. Then, the paper discusses conditions under which a Nash equilibrium can be reached among the OSN users, its uniqueness, and how to efficiently solve it via a fixed-point iteration and bisection search. The derived formulas and equilibrium solutions are validated with simulations. It is shown that the proposed SHIMR transmission model successfully predicts the rumor and counter-rumor transmission process. A series of experiments are conducted to illustrate the effects of various system parameters on the overall rumor transmission process. The result provides insights that could aid the design of policies and control strategies to achieve certain objectives, such as confining peak “infection” rate or final influenced population.

This paper paves the way for many future research directions. First, this study uses Monte Carlo simulations (as the ground truth) to verify the system dynamics predicted by our model. In future research, real-world data from social networks (e.g., traces of an opinion in Twitter or Weibo) should be used for model calibration and validation. Second, the model provides predictive power on rumor propagation, which can serve as a building block to design optimal control strategies that can resist turmoils. Dynamic and adaptive control laws may be established for timely interventions, especially in early stages of rumor development. Third, findings from this research could also be combined with efforts on improving compartment observability in real time, such as classifying the content of user posts through machine learning for statistical inference. Fourth, in this work, only one type of rumor is considered. Another direction of research, therefore, could look into extending the model towards more complex and realistic instances, where multiple interrelated rumors may emerge and transmit simultaneously, through one or multiple OSN platforms. The proposed modeling framework (and conclusions) may even be applied to systems in other application contexts, as long as they involve interdependent decision makers with dynamically changing states, such as those related to traffic congestion and equilibrium in a transportation network.

Appendix A. Derivation of \(R_e\)

We follow the idea mentioned in Diekmann et al. (1990) to derive $R_e(t)$ which the definition can be found in Sect. 3.2. The computation of $R_e(t)$ requires information only on compartments $H_{jk}(t)$, $I_{jk}(t)$ and $M_{jk}(t)$. For simplicity, we hereon omit the time argument for all variables in this appendix.

Based on Eq. (18), for all $j \in \{1, ...,J\}, k \in \{1, ...,K\}$, we have

$$\begin{aligned} \begin{aligned}&\dot{H}_{jk} = j(r_I\frac{\theta _I}{\theta } + r_M\frac{\theta _M}{\theta })S_{jk} - \beta H_{jk}, \\&\dot{I}_{jk} = \beta \gamma _{jk} q H_{jk} - \mu _{I}I_{jk} , \\&\dot{M}_{jk} = \beta \gamma _{jk} (1 - q) H_{jk} - \mu _{M}M_{jk}. \end{aligned} \end{aligned}$$

This can be written in the following vector form

$$\begin{aligned}{}[ \dot{H}_{11}, \cdots , \dot{H}_{JK}, \dot{I}_{11}, \cdots , \dot{I}_{JK}, \dot{M}_{11}, \cdots , \dot{M}_{JK}]^T = \mathcal {F} - \mathcal {V}, \end{aligned}$$

(28)

where $\mathcal {F} = [1 \cdot (r_I \frac{\theta _I}{\theta } + r_M \frac{\theta _M}{\theta })S_{11}, \cdots , J(r_I\frac{\theta _I}{\theta } + r_M\frac{\theta _M}{\theta })S_{JK}, \mathbf {0}_{1 \times JK}, \mathbf {0}_{1 \times JK}]^T$ represents the increment of hesitating users from all other compartments, while $\begin{aligned}&\mathcal {V} = [\beta H_{11}, \cdots , \beta H_{JK}, \mu _{I}I_{11}-\beta \gamma _{11} q H_{11}, \cdots , \mu _{I}I_{JK}-\beta \gamma _{JK}qH_{JK}, \mu _{M}M_{11}-\beta \gamma _{11}(1 - q)H_{11}, \cdots , \mu _{M}M_{JK}-\beta \gamma _{JK}(1 - q)H_{JK}]^T\end{aligned}$ represents the transmission of hesitating users into other compartments. Here $\mathbf {0}$ represents a zero vector/matrix. The Jacobian matrices of $\mathcal {F}$ and $\mathcal {V}$, denoted as F and V, can be computed respectively as follows:

$$\begin{aligned} {F} = \begin{bmatrix} \varvec{0}_{JK \times JK} &{} B \\ \varvec{0}_{2JK \times JK} &{} \varvec{0}_{2JK \times 2JK} \end{bmatrix}, \ {V} = \begin{bmatrix} D &{} \varvec{0}_{JK \times 2JK} \\ P &{} Q \end{bmatrix}, \end{aligned}$$

(29)

where

$$\begin{aligned} \begin{aligned}&B = \\&{\left[ \begin{array}{ccccc} 1 \cdot \frac{1 \cdot r_I}{\theta \langle k \rangle }S_{11} &{} \cdots &{} 1 \cdot \frac{1 \cdot r_M}{\theta \langle k \rangle }S_{11} &{} \cdots &{} 1 \cdot \frac{K \cdot r_M}{\theta \langle k \rangle }S_{11}\\ \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots \\ 1 \cdot \frac{1 \cdot r_I}{\theta \langle k \rangle }S_{1K} &{} \cdots &{} 1 \cdot \frac{1 \cdot r_M}{\theta \langle k \rangle }S_{1K} &{} \cdots &{} 1 \cdot \frac{K \cdot r_M}{\theta \langle k \rangle }S_{1K} \\ \vdots &{} \ddots &{} \vdots &{} \ddots &{} \vdots \\ j \cdot \frac{1 \cdot r_I}{\theta \langle k \rangle }S_{JK} &{} \cdots &{} j \cdot \frac{1 \cdot r_M}{\theta \langle k \rangle }S_{JK} &{} \cdots &{} j \cdot \frac{K \cdot r_M}{\theta \langle k \rangle }S_{JK} \end{array} \right] } , \end{aligned} \end{aligned}$$

$$\begin{aligned} D = \beta \cdot E_{J \times K} , Q = {\left[ \begin{array}{cc} \mu _I \cdot E_{J \times K} &{} \mathbf {0}_{JK \times JK} \\ \mathbf {0}_{JK \times JK} &{} \mu _M \cdot E_{J \times K} \end{array} \right] } , \end{aligned}$$

$$\begin{aligned} P = {\left[ \begin{array}{ccc} -\beta \gamma _{11}q &{} \cdots &{} 0 \\ 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} -\beta \gamma _{JK}q \\ -\beta \gamma _{11}(1-q) &{} \cdots &{} 0 \\ 0 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} -\beta \gamma _{JK}(1-q) \end{array} \right] } . \end{aligned}$$

In the above, E represents the identity matrix. Following Diekmann et al. (1990), we call $FV^{-1}$ the next generation matrix for the model, and it can be calculated as:

$$\begin{aligned} FV^{-1} = {\left[ \begin{array}{cc} -BQ^{-1}PD^{-1} &{} BQ^{-1} \\ \mathbf {0}_{2JK \times JK} &{} \mathbf {0}_{2JK \times 2JK} \end{array} \right] } . \end{aligned}$$

(30)

It is well known from Lyapunov stability theorem that the effective reproduction number $R_e$ is the spectral radius of matrix $FV^{-1}$; i.e.:

$$\begin{aligned} R_e = \rho (FV^{-1}). \end{aligned}$$

(31)

From Eq. (29), $FV^{-1}$ is an upper triangular block matrix, whose eigenvalues are given by those of its only nonzero diagonal block submatrix $-BQ^{-1}PD^{-1}$. Note that

$$\begin{aligned} -BQ^{-1}PD^{-1} = \frac{1}{\langle k \rangle }{\left[ \begin{array}{ccc}1 \cdot p_{11}\theta ^0 \\ \vdots \\ 1 \cdot p_{1K}\theta ^0 \\ 2 \cdot p_{21}\theta ^1 \\ \vdots \\ J \cdot p_{JK}\theta ^{J-1} \end{array} \right] } \cdot \ {\left[ \begin{array}{ccc} 1 \cdot \gamma _{11}(\frac{r_Iq}{\mu _{I}} + \frac{r_M(1 - q)}{\mu _{M}}) \\ \vdots \\ K \cdot \gamma _{1K}(\frac{r_Iq}{\mu _{I}} + \frac{r_M(1 - q)}{\mu _{M}}) \\ 1 \cdot \gamma _{21}(\frac{r_Iq}{\mu _{I}} + \frac{r_M(1 - q)}{\mu _{M}}) \\ \vdots \\ K \cdot \gamma _{JK}(\frac{r_Iq}{\mu _{I}} + \frac{r_M(1 - q)}{\mu _{M}}) \end{array} \right] }^T . \end{aligned}$$

(32)

Clearly, rank ($-BQ^{-1}PD^{-1}$) = 1. Hence,

$$\begin{aligned} R_e = {\mathrm {tr}(-BQ^{-1}PD^{-1})} = \frac{1}{\langle k \rangle } \sum _{j,\ k} jkp_{jk} \theta ^{j - 1} \gamma _{jk} \cdot (\frac{r_I q}{\mu _{I}} + \frac{r_M (1 - q)}{\mu _{M}}). \end{aligned}$$

(33)