Abstract
In this study, we analyze the performance of stochastic coverage controllers inspired by the chemotaxis of bacteria. The control algorithm of bacteria to generate the chemotaxis switches between forward movement and random rotation based on the difference between the current and previous concentration of a chemical. The considered coverage controllers mimic this algorithm, where bacteria and the chemical concentration are regarded as agents and the achieved degree of coverage, respectively. Because the coverage controllers operate similar to the control algorithm of bacteria, they are potentially suitable for molecular robots. Molecular robots, which consist of biomolecules, are recognized as a key component in the development of future medical systems based on micro-robots working inside the human body. However, the performance of the controllers has not yet been analyzed, and no theoretical guarantee of coverage completion has been provided. We address this problem by determining whether a performance index that quantifies the achieved degree of coverage increases over time for the feedback system. We first show that the performance index is characterized by the distance between agents under certain conditions. Using this result, we prove that the performance index increases with probability 1 under some conditions although the controllers are stochastic. This provides partial evidence for coverage completion, which makes the controllers more reliable. The analysis result is validated by numerical experiments.
Similar content being viewed by others
1 Introduction
Coverage by multi-agent systems, where agents cover a given space in some sense via a distributed algorithm, has become a popular research topic in the area of multi-agent control. The reason for this popularity lies in its wide range of applications, including the exploration of hazardous environments using vehicles and environmental monitoring for pollution detection using a mobile sensor network.
To date, many researchers have studied control for coverage. Cortes et al. [5] considered a coverage control problem and presented a solution based on the Voronoi partition. This work was extended to agents described as hybrid systems [9], agents with constant speeds [11], and dynamic unicycle-type agents [17]. Moreover, Oyekan et al. [14] developed bio-inspired coverage controllers to achieve a desired distribution of agents. Atınç et al. [2] proposed a swarm-based approach to dynamic coverage control. Gao and Kan [6] considered a coverage control problem for heterogeneous driftless control affine systems. In other related studies, algorithms to generate the flocking behavior of agents were developed. Virágh et al. [16] proposed a flocking algorithm for flying agents inspired by animal collective motion. Yang et al. [18] proposed an algorithm to achieve V-shape formations inspired by the swarm behavior of birds. Liu et al. [10] addressed the problem of finite-time flocking and collision avoidance for second-order multi-agent systems.
In [8], our group presented coverage controllers based on biomimetics, i.e., inspired by the chemotaxis [1, 3, 15] of bacteria. Chemotaxis is a biological phenomenon wherein each organism moves to the highest (or lowest) concentration point of a chemical in an environment by sensing the concentration, as illustrated in Fig. 1. If the chemical is an attractant such as food, each organism aims to reach the highest concentration point; if the chemical is a repellent such as a toxin, it aims to reach the lowest concentration point. In [8], we regarded each agent as a bacterium in chemotaxis and the achieved degree of coverage as the concentration of an attractant. Subsequently, using a controller for chemotaxis to maximize the achieved degree, we obtained chemotaxis-inspired controllers for coverage.
Our coverage controllers have two potential applications that are different from those of artificial coverage controllers [5, 6, 9, 11, 17]. One application is cost reduction in the production of swarm robotic systems. As will be explained later, the controllers provide only two movement commands for agents, i.e., forward movement and random rotation. Fewer movement commands reduce the required resolution of signals and actuators. Therefore, the controllers are suitable for low-cost robots with limited computational power and mobility. Reducing the cost of each robot in the production of swarm robotic systems leads to substantial cost reduction. The other application is to generate the coordinated behavior of molecular robots [13] comprising biomolecules. Molecular robots are a key component in the development of future medical systems based on micro-robots working inside the human body. However, because the components of molecular robots are biomolecules, traditional controllers, which assume implementation as computer programs, are not directly applicable. Our controllers have the potential for solving this problem. The controllers mimic a control algorithm of bacteria, i.e., living things; therefore, they can be implemented in biomolecular devices.
In [8], we demonstrated the effectiveness of our coverage controllers through simulation and experiment but provided no theoretical guarantee of coverage completion. Providing such a guarantee makes the controllers more reliable, which further motivates their usage. This is especially important for our controllers because they are stochastic controllers whose outputs are randomly determined under some conditions owing to the random rotation command described above. Stochastic controllers make the behavior of the resulting feedback systems uncertain. Although bio-inspired stochastic controllers for coverage were reported in [14], the theoretical analysis of their stochastic properties was not performed.
Thus, the aim of this paper is to analyze the performance of the coverage controllers presented in [8] in a theoretical manner. To this end, we investigate the time evolution of a performance index that quantifies the achieved degree of coverage for the feedback system. The performance index is described using integrals over sets and its direct calculation is difficult, which makes the analysis difficult. However, we reveal that the performance index is characterized by the distance between agents under certain conditions, from which we show an increase in the performance index with probability 1 and conditions for it. This clarifies some properties of the controllers on coverage completion. The analysis result is verified through numerical experiments.
This paper is an extension of the conference version [7]. The conference version is a one-page abstract that briefly describes the purpose of the study. By contrast, this paper presents a complete explanation, including problem formulation, the main result and its proof, and the results of numerical experiments.
2 Preliminary
This section summarizes the basic notation and formula used in this paper.
Let \(\mathbb {R}\) and \(\mathbb {R}_{+}\) denote the real number field and the set of positive real numbers, respectively. Both the zero scalar and the zero vector are represented by 0. For the vector x, we denote by \(x^\top\) and \(\Vert x\Vert\) its transpose and Euclidean norm, respectively. The cardinality of the set \(\mathbb {S}\) is represented by \(|\mathbb {S}|\). Let \(\mathbb {B}(c,r)\) denote a closed disk in \(\mathbb {R}^2\) with the center c and the radius r, i.e., \(\mathbb {B}(c,r):=\{x\in \mathbb {R}^2\,|\,\Vert x-c\Vert \le r\}\). For the vectors \(x_1,x_2,\ldots ,x_n \in \mathbb {R}^2\) and the set \(\mathbb {I}:=\{ i_{1},i_{2},\ldots ,i_{m}\}\subseteq \{ 1,2,\ldots ,n\}\), we define \([x_i ]_{i\in \mathbb {I}}:=[x_{i_1}^\top ~x_{i_2}^\top ~\cdots ~x_{i_m}^\top ]^\top \in \mathbb {R}^{2m}\). For instance, \(x_1,x_2,\ldots ,x_6\) and \(\mathbb {I}:=\{ 2,3,6\}\) yield \([x_i ]_{i\in \mathbb {I}}:=[x_{2}^\top ~x_{3}^\top ~x_6^\top ]^\top\). For the vector x that contains the vector \(x_i\) as its element, \(\overline{x}(i,z)\) represents the vector obtained by replacing \(x_i\) with z. Examples for this are \(\overline{x}(2,z):=[x_{1}^\top ~z^\top ~x_3^\top ]^\top\) for \(x:=[x_{1}^\top ~x_2^\top ~x_3^\top ]^\top\) and \(\overline{[x_i ]}_{i\in \mathbb {I}}(4,z):=[x_{2}^\top ~z^\top ]^\top\) for \(x_1,x_2,\ldots ,x_5\) and \(\mathbb {I}:=\{ 2,4\}\).
In addition, the following property of trigonometric functions is used in this paper:
where \(a,b,\theta \in \mathbb {R}\) and \(\varphi\) is the angle satisfying
3 Chemotaxis-inspired coverage control
This section briefly introduces the chemotaxis-inspired coverage controllers presented in [8]. We first introduce the problem addressed in [8], the coverage controllers to solve it, and an existing result regarding the controllers. Based on these, we point out that some questions remain unaddressed.
3.1 Problem formulation
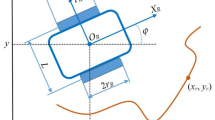
Consider the multi-agent system depicted in Fig. 2. This system is composed of n agents, and each agent incorporates a controller.
Agent i is expressed as a discrete-time model of a two-wheeled mobile robot, i.e.,
where \(i\in \{1,2,\ldots ,n\}\), \([x_{i1}(t)\ x_{i2}(t)]^\top \in \mathbb {R}^2\) (denoted by \(x_i(t)\)) is the position, \(\theta _i(t)\in \mathbb {R}\) is the orientation, and \(u_{i1}(t),u_{i2}(t)\in \mathbb {R}\) are the control inputs to determine the translational and rotational velocities, respectively. Note that \(x_i(t)\) is a vector but \(x_{i1}(t)\) and \(x_{i2}(t)\) are scalar.
The controller of each agent i is of the form
where \(\xi _i(t)\in \mathbb {R}^m\) is the state, \([x_j(t)]_{j\in \mathbb {N}_i(t)}\in \mathbb {R}^{2|\mathbb {N}_i(t)|}\) is the input, \(u_{i}(t)\in \mathbb {R}^2\) is the output, that is, \(u_i(t):=[u_{i1}(t)\ \, u_{i2}(t)]^\top\), and \(f_1:\mathbb {R}^m\times \mathbb {R}^{2|\mathbb {N}_i(t)|}\rightarrow \mathbb {R}^m\) and \(f_2:\mathbb {R}^m\times \mathbb {R}^{2|\mathbb {N}_i(t)|}\rightarrow \mathbb {R}^2\) are functions specifying the behavior of the controller. The set \(\mathbb {N}_i(t)\subseteq \{1,2,\ldots ,n\}\) is the index set of the neighboring agents, i.e., the agents whose positions can be observed by agent i. The controller \(K_i\) is distributed in the sense that its input is restricted to \([x_j(t)]_{j\in \mathbb {N}_i(t)}\). We assume that the functions \(f_1\) and \(f_2\) and the initial state \(\xi _i(0)\) are the same for every \(i\in \{1,2,\ldots ,n\}\). This implies that no agent is distinguishable from the others, ensuring the scalability of the entire system. We further assume \(\xi _i(0):=0\) to simplify the discussion.
The agents are supposed to be connected through an r-disk proximity network [4]; that is, each agent can obtain the positional information of itself and the agents within the radius r. In this case, the neighbor set \(\mathbb {N}_i(t)\) is given by
Next, we explain the coverage problem. Coverage is to spread agents in a given space for purposes such as exploring and monitoring environments. To this end, we consider the following performance index [12]:
where \(x:=[x_{1}^\top ~x_{2}^\top ~\cdots ~x_{n}^\top ]^\top\), \(q\in \mathbb {R}^2\) is the integration variable, and \(\mathbb {Q}\subset \mathbb {R}^2\) is a space that n agents cover. We suppose that the boundary of \(\mathbb {Q}\) is indicated by, for example, lines, and there are no walls around the agents. The performance index J represents the area of the union of the disks \(\mathbb {B}(x_i,r/2)\) with \(i=1,2,\ldots ,n\) in the space \(\mathbb {Q}\). Hence, by maximizing J, we can achieve coverage in the sense that the distance between every pair of agents is larger than a certain value, as illustrated in Fig. 3. With this notation, our problem is stated as follows:
Problem 1
For the multi-agent system depicted in Fig. 2, suppose that a coverage space \(\mathbb {Q}\subset \mathbb {R}^2\) is given. Find controllers \(K_1,K_2,\ldots ,K_n\) (i.e., functions \(f_1\) and \(f_2\)) satisfying
for every initial state \((x_i(0),\theta _i(0))\in \mathbb {Q}\times \mathbb {R}\) with \(i=1,2,\ldots ,n\).
Remark 1
The reason for considering the disk \(\mathbb {B}(x_i,r/2)\) of the radius r/2 in J in (6) is that the system is with the r-disk proximity network. In this setting, each agent cannot observe the positions of other agents at distances larger than r. Therefore, a possible configuration of the agents for coverage is that each agent is located at distances larger than r from the others, as shown in Fig. 3. To achieve such a configuration, we introduce the disk \(\mathbb {B}(x_i,r/2)\) of the radius r/2 and maximize J.
Remark 2
As can be seen from Fig. 3, the configuration of the agents maximizing J in (6) is not necessarily unique. Hence, better configurations may exist depending on the mission of the agents even if J is maximized.
Remark 3
Problem 1 can be solved using the gradient-based approach [12]. However, we focus on the chemotaxis-inspired solution because of its potential applications explained in Sect. 1. In addition, the flocking algorithms developed in [10, 16, 18] cannot be directly applied to Problem 1. This is because they are aimed at forming a swarm of agents in some sense and do not consider the coverage space \(\mathbb {Q}\).
Coverage. The left and right figures display the initial and final configurations of the agents, respectively, where each gray area indicates \(\mathbb {B}(x_i,r/2)\) for each agent i. In this case, the maximization of J in (6) implies that the gray areas do not overlap with each other as in the final configuration. This corresponds to the situation that each agent is located at distances larger than r from the others
3.2 Stochastic coverage controllers inspired by chemotaxis
Izumi et al. [8] proposed the following solution to Problem 1:
where \(\xi _i(t)\) is scalar (i.e., \(m:=1\)), \(v\in \mathbb {R}_+\) is a constant, and \(w_i(t)\in \{-1,1\}\) is a Bernoulli random variable that takes \(-1\) or 1 with equal probability. The function \(J_i\) is the local performance index defined as
where \(i\in \{1,2,\ldots ,n\}\). By the definition (5) of the neighbor set \(\mathbb {N}_i(t)\), \(J_i\) represents the area of the region that only agent i covers. Because \(J_i\) is a function of \([x_j]_{j\in \mathbb {N}_i}\) as shown in (10), the resulting controller \(K_i\) is distributed.
The controller \(K_i\) constructed by (4) and (8)–(10) operates as follows. It follows from (4) and (8) that the state \(\xi _i(t)\) memorizes the previous value of the local performance index as \(\xi _i(t)=J_i([x_j(t-1)]_{j\in \mathbb {N}_i(t-1)})\). Therefore, \(\xi _i(t)\le J_i([x_j(t)]_{j\in \mathbb {N}_i(t)})\) implies that the current position of agent i is better than or equal to the previous one in the sense of \(J_i\). In this case, \(K_i\) drives agent i straight because the current movement direction might be favorable. Conversely, \(\xi _i(t)> J_i([x_j(t)]_{j\in \mathbb {N}_i(t)})\) implies that the current position of agent i is worse than the previous one in the sense of \(J_i\). In this case, \(K_i\) drives agent i in another direction by commanding a rotation of \(2\pi /3\) radians and a straight movement because the current movement direction might be unfavorable. The direction of the rotation is randomly determined by \(w_i(t)\). This controller was inspired by a controller for the chemotaxis of bacteria, as described in Sect. 1, where agent i and \(J_i\) correspond to each bacterium and the concentration of an attractant in the environment, respectively, and agent i moves to a location with a higher value of \(J_i\) via the controller.
Regarding this controller, Izumi et al. [8] obtained the following result:
Lemma 1
The performance index J defined by (6) and the local performance index \(J_i\) defined by (10) satisfy
for every \(i\in \{1,2,\ldots ,n\}\), where \(\overline{x}(i,z)\in \mathbb {R}^{2n}\) and \(\overline{[x_j]}_{j\in \mathbb {N}_i}(i,z)\in \mathbb {R}^{2|\mathbb {N}_i|}\) are as defined in Sect. 2.
Lemma 1 indicates that, when only agent i moves, the magnitude of the change in the performance index J is the same as that in the local performance index \(J_i\). In this sense, the increase in \(J_i\) corresponds to that in J, and thus we would achieve coverage by increasing each \(J_i\) via the aforementioned controller. The reason for using not J but \(J_i\) in (8) and (9) is that the resulting controller \(K_i\) must be distributed as in (4). The direct application of J yields a centralized \(K_i\) because J depends on the positions of all the agents from (6).
Lemma 1 only states the relation between J and \(J_i\), and the controller \(K_i\) constructed by (4) and (8)–(10) was not theoretically analyzed in [8]. As a result, the following two questions remain open:
-
(a)
Can we theoretically guarantee that \(K_i\) operates to increase \(J_i\)?
-
(b)
If (a) is possible, what are the conditions under which \(J_i\) increases?
The answer to question (a) provides partial evidence for the completion of coverage by the controllers \(K_i\) with \(i=1,2,\ldots ,n\) from the above discussion on Lemma 1. This makes the controllers more reliable, which further motivates their usage. The answer to question (b) reveals the conditions under which the controllers work well. Knowing these conditions is important for the safe and efficient operation of the resulting feedback system.
4 Performance analysis
In this section, we analyze the performance of the coverage controllers described in Sect. 3.2 to answer questions (a) and (b). We first explain the analysis problem addressed here. Subsequently, we show a solution to the problem and the results of numerical experiments to validate the solution.
4.1 Analysis problem
Consider the feedback system given by (3), (4), and (8)–(10). For this system, the following assumption is imposed:
Assumption 1
At a time t, there exists an agent i satisfying the following two conditions:
-
(C1) The neighbor of agent i is only agent k, and it is more than \(r+v\) away from the agents other than agent k.
-
(C2) Agent i is more than \(r/2+v\) away from the boundary of the coverage space \(\mathbb {Q}\).
Assumption 1 implies that at a time t, there exists an agent such that the number of its neighbors is one and its distance from the boundary of \(\mathbb {Q}\) is large, as depicted in Fig. 4, where v in (9) is added to allow the agent to take one action. This situation appears when the number n of agents and the range r of the connection are not too large for the size of \(\mathbb {Q}\). We focus on this simple situation as the first step of the study and address the following problem:
Problem 2
For the feedback system given by (3), (4), and (8)–(10), assume that Assumption 1 holds and the state \(\xi _i(t)\) is given. Then, check whether \(J_i(\overline{[x_j(t)]}_{j\in \mathbb {N}_i(t)}(i,x_i(t+1)))>J_i([x_j(t)]_{j\in \mathbb {N}_i(t)})\) holds or not.
In Problem 2, \(J_i(\overline{[x_j(t)]}_{j\in \mathbb {N}_i(t)}(i,x_i(t+1)))>J_i([x_j(t)]_{j\in \mathbb {N}_i(t)})\) indicates that the local performance index \(J_i\) increases when only agent i moves at time t. Hence, if \(J_i(\overline{[x_j(t)]}_{j\in \mathbb {N}_i(t)}(i,x_i(t+1)))>J_i([x_j(t)]_{j\in \mathbb {N}_i(t)})\) holds for the feedback system given by (3), (4), and (8)–(10), we can conclude that the incorporated controller \(K_i\) operates to increase \(J_i\) in the same situation as that considered in Lemma 1. Meanwhile, \(K_i\) is stochastic owing to the random variable \(w_i(t)\) in (9); therefore, the agent position \(x_i(t+1)\) under consideration is a random variable. In addition, \(J_i\) is composed of two integrals over sets, as shown in (10), and its direct calculation is difficult. These factors make the problem difficult.
Situation considered in Assumption 1. The black dots and rectangle and the gray circle indicate agents, \(\mathbb {Q}\), and \(\mathbb {B}(x_i,r)\), respectively. There exists an agent i such that its neighbor is only agent k and the distances from the agents other than agent k and that from the boundary of \(\mathbb {Q}\) are large
4.2 Main result
To solve Problem 2, we present the following result:
Lemma 2
For an agent i satisfying (C1) and (C2) in Assumption 1, the following statements hold:
-
(i)
The following equality holds:
$$\begin{aligned} J_i([x_j]_{j\in \mathbb {N}_i}) = \dfrac{\pi r^2}{4}-\dfrac{r^2}{2}\cos ^{-1}\left( \dfrac{\Vert x_i-x_k\Vert }{r}\right) +\dfrac{\Vert x_i-x_k\Vert }{2}\sqrt{r^2-\Vert x_i-x_k\Vert ^2}. \end{aligned}$$(12) -
(ii)
The function \(J_i([x_j]_{j\in \mathbb {N}_i})\) is monotonically increasing with respect to \(\Vert x_i-x_k\Vert <r\) and takes the maximum value when \(\Vert x_i-x_k\Vert \ge r\).
Proof
-
(i)
From (10), (C1), and (C2), we only need to consider the positions \(x_i\) and \(x_k\) of agents i and k to prove the statement. Fig. 5 illustrates the relationship between \(x_i\) and \(x_k\). Let \(a_s,a_t\in \mathbb {R}_+\cup \{0\}\) denote the areas of the gray sector and the triangle with the vertices \(x_i\), \(p_1\), and \(p_2\) in Fig. 5, respectively. Then, geometric computation provides
$$\begin{aligned}&a_{s}=\dfrac{r^2}{4}\cos ^{-1}\left( \dfrac{\Vert x_i-x_k\Vert }{r}\right) , \end{aligned}$$(13)$$\begin{aligned}&a_{t}=\dfrac{\Vert x_i-x_k\Vert }{2}\sqrt{\left( \dfrac{r}{2}\right) ^2-\left( \dfrac{\Vert x_i-x_k\Vert }{2}\right) ^2}, \end{aligned}$$(14)where we use the fact that Fig. 5 is symmetric with respect to the line with \(p_1\) and \(p_2\) because r is the same for agents i and k. The definition of \(J_i\) and Fig. 5 imply
$$\begin{aligned} J_i([x_j]_{j\in \mathbb {N}_i})=\dfrac{\pi r^2}{4}-2(a_s-a_{t}). \end{aligned}$$(15)Substituting (13) and (14) into (15) gives (12), which proves the statement.
-
(ii)
This is a straightforward consequence of the definition of \(J_i\) and Fig. 5.
\(\square\)
Lemma 2 implies that for an agent i satisfying (C1) and (C2), the local performance index \(J_i\) is characterized by the distance \(\Vert x_i-x_k\Vert\). In particular, statement (ii) means that an increase or decrease in \(J_i\) corresponds to that in \(\Vert x_i-x_k\Vert\) subject to \(\Vert x_i-x_k\Vert <r\). Therefore, we investigate whether \(\Vert x_i-x_k\Vert\) increases via the controller \(K_i\) given by (4) and (8)–(10) or not.
Based on this idea, we obtain the following theorem:
Theorem 1
For the feedback system given by (3), (4), and (8)–(10), assume that Assumption 1 holds and the state \(\xi _i(t)\) is given. Then,
holds with probability 1 if either of the following two conditions holds:
where \(\phi _s,\phi _c:\mathbb {R}^{2}\times \mathbb {R}^{2}\times \mathbb {R}\rightarrow \mathbb {R}\) are the functions defined by
for the angle \(\alpha (x_i(t),x_k(t))\in (-\pi ,\pi ]\) satisfying
Proof
From Lemma 2, we can prove (16) by showing that \(\Vert x_i(t)-x_k(t)\Vert\) increases when only agent i moves, i.e., \(\Vert x_i(t+1)-x_k(t)\Vert >\Vert x_i(t)-x_k(t)\Vert\). In the following, we assume \(x_k(t)=0\) without loss of generality and show \(\Vert x_i(t+1)\Vert >\Vert x_i(t)\Vert\).
First, we consider the condition (17). From (4) and (9), the inequality \(\xi _i(t)\le J_i([x_j(t)]_{j\in \mathbb {N}_i(t)})\) indicates that \(u_i(t)=[v\ \ 0]^\top\) holds. This and (3) yield
Thus, \(\Vert x_i(t+1)\Vert >\Vert x_i(t)\Vert\) holds if
Applying (1) and \(v>0\) to (23) yields
Hence, \(\Vert x_i(t+1)\Vert >\Vert x_i(t)\Vert\) holds under \(\xi _i(t)\le J_i([x_j(t)]_{j\in \mathbb {N}_i(t)})\) and (24). By considering the case of \(x_k(t)\ne 0\) and replacing \(\Vert x_i(t)\Vert\) and \(\alpha (x_i(t),0)\) in (24) with \(\Vert x_i(t)-x_k(t)\Vert\) and \(\alpha (x_i(t),x_k(t))\), respectively, we can derive \(\phi _s(x_i(t),x_k(t),\theta _i(t))>-v/2\), where \(\phi _s(x_i(t),x_k(t),\theta _i(t))\) is defined in (19). This and the discussion at the beginning of the proof indicate that (16) holds under (17).
Next, we consider the condition (18). Equations (4) and (9) imply that \(u_i(t)=[v\ \ 2\pi /3]^\top\) or \([v\ -2\pi /3]^\top\) holds when \(\xi _i(t)> J_i([x_j(t)]_{j\in \mathbb {N}_i(t)})\). In the case of \(u_i(t)=[v\ \ 2\pi /3]^\top\), a calculation similar to the above yields
which indicates that \(\Vert x_i(t+1)\Vert >\Vert x_i(t)\Vert\) holds if
Using (1) and \(v>0\) for (26), we obtain
From the formula for trigonometric addition, (27) is calculated as
Hence, \(\Vert x_i(t+1)\Vert >\Vert x_i(t)\Vert\) holds under \(\xi _i(t)> J_i([x_k(t)]_{k\in \mathbb {N}_i(t)})\) and (28). By considering the case of \(x_k(t)\ne 0\) and replacing \(\Vert x_i(t)\Vert\) and \(\alpha (x_i(t),0)\) in (28) with \(\Vert x_i(t)-x_k(t)\Vert\) and \(\alpha (x_i(t),x_k(t))\), respectively, we obtain
where \(\phi _c(x_i(t),x_k(t),\theta _i(t))\) is defined in (20). Similarly, in the case of \(u_i(t)=[v\ -2\pi /3]^\top\), a condition corresponding to (29) is derived as
Combining (29) and (30) yields the second inequality in (18). Consequently, from the discussion at the beginning of the proof, (16) holds in both cases of \(u_i(t)=[v\ \ 2\pi /3]^\top\) and \([v\ -2\pi /3]^\top\), i.e., \(w_i(t)=1\) and \(-1\), under (18). This completes the proof. \(\square\)
Theorem 1 indicates that under Assumption 1 and (17) or (18), the local performance index \(J_i\) increases with probability 1 when only agent i moves, although the controller \(K_i\) given by (4) and (8)–(10) is stochastic. This result provides answers to questions (a) and (b) in Sect. 3.2.
In addition, the following corollary is directly obtained from Lemma 1 and Theorem 1.
Corollary 1
In the same situation as that of Theorem 1,
holds with probability 1 if either (17) or (18) holds.
This result extends Theorem 1 to the performance index J. Namely, in the same situation as that of Theorem 1, J increases with probability 1 when only agent i moves.
Remark 4
The above results do not guarantee that the agents always spread via the controllers given by (4) and (8)–(10). However, Corollary 1 indicates that the performance index J increases under certain conditions, which provides partial evidence for the spread of the agents in the sense of the increase in J. Such theoretical evidence was not provided in the previous study [8].
Examples for Theorem 1. a Position \(x_1(t)\) of agent 1 (corresponding to agent i) at a time t such that (C1) and (C2) in Assumption 1 and either (17) or (18) in Theorem 1 are satisfied, where \(\theta _1(t)=\pi /4\) and the position \(x_2(t)\) of agent 2 (corresponding to agent k) is set as \(x_2(t)=[1\ \, 1]^\top\). The black and gray dots indicate \(x_1(t)\) such that (17) and (18) are satisfied, respectively. The blue triangle represents \(x_2(t)\), and the black circle represents \(\mathbb {B}(x_2(t),r)\). The state \(\xi _1(t)\) is determined by calculating the previous positions \(x_1(t-1)\) and \(x_2(t-1)\) from (3) and \(u_{\ell 1}(t-1)=v\) for every \(\ell \in \{1,2\}\) and using \(\xi _1(t)=J_1([x_j(t-1)]_{j\in \mathbb {N}_1(t-1)})\), where \(\theta _2(t)=\pi /2\). b Possible \(x_1(t+1)\) resulting from the controller \(K_1\). The black and gray dots correspond to those in (a). Agent 1 moves away from agent 2
Time series of the agent positions for coverage. The numbers 1–7 denote the agent indices, the small circles and the line segments represent the translational and rotational positions of the agents, respectively, and the large circles represent \(\mathbb {B}(x_\ell (t),r/2)\) for \(\ell =1,2,\ldots ,7\). The agents move so that the large circles do not overlap with each other
4.3 Numerical experiments
Consider the multi-agent system with \(n:=2\) and \(r:=0.5\). The coverage space is chosen as \(\mathbb {Q}:=[0,2]^2\). We employ the controllers \(K_1\) and \(K_2\) given by (4) and (8)–(10) with \(v:=0.1\).
Fig. 6 (a) shows the position \(x_1(t)\) of agent 1 (corresponding to agent i) at a time t such that (C1) and (C2) in Assumption 1 and either (17) or (18) in Theorem 1 are satisfied. We observe that there exist regions where the conditions for increasing \(J_1\) are satisfied. In addition, Fig. 6 (b) shows the possible \(x_1(t+1)\) resulting from the controller \(K_1\). It turns out that agent 1 moves away from agent 2. For all of the positions shown in Fig. 6 (a) and (b), we can numerically confirm that \(J_1(\overline{[x_j(t)]}_{j\in \mathbb {N}_1(t)}(1,x_1(t+1)))>J_1([x_j(t)]_{j\in \mathbb {N}_1(t)})\) holds, which validates Theorem 1.
Next, we present an example for coverageFootnote 1. Consider the case of \(n:=7\) and \(r:=0.65\). The coverage space \(\mathbb {Q}\) and the controllers \(K_\ell\) with \(\ell =1,2,\ldots ,7\) are the same as above, except for \(v:=0.04\). Fig. 7 displays snapshots of the agent positions at several time steps. Fig. 8 illustrates the change in the performance index J(x(t)) over time. These results demonstrate that coverage is achieved. We further show in Fig. 9 the change in the local performance indices \(J_\ell ([x_j(t)]_{j\in \mathbb {N}_\ell (t)})\) with \(\ell =1,2,\ldots ,7\) over time. We can confirm that each controller \(K_\ell\) steers agent \(\ell\) so that \(J_\ell\) increases.
5 Conclusion
In this study, we theoretically analyzed the performance of stochastic coverage controllers inspired by bacterial chemotaxis. More precisely, we addressed the problem of determining whether a performance index quantifying the achieved degree of coverage increases over time for the feedback system. For this problem, we showed that the performance index increases with probability 1 under certain conditions by focusing on the distance between agents.
The results of this study partially indicate that the controllers mimicking a control algorithm of bacteria achieve coverage from a theoretical point of view. The major difference between the controllers and the original bacteria algorithm is that, in the controllers, the concentration of a chemical attractant is replaced by the value of the local performance index. Hence, we can expect the application of the controllers to coverage by molecular robots if each robot can obtain information corresponding to the local performance index.
Finally, we discuss the future work. Because this study focused on the case of two agents for the simplicity of the analysis, we should consider the case of more agents in the future. In addition, our chemotaxis-inspired controllers can handle other tasks (e.g., rendezvous) [8], and thus we plan to extend the results of this study to such tasks.
Notes
Although similar results can be found in [8], we present this different example to ensure that the paper is self-contained.
References
Adler, J.: Chemotaxis in bacteria. Science 153(3737), 708–716 (1966)
Atınç, G.M., Stipanović, D.M., Voulgaris, P.G.: A swarm-based approach to dynamic coverage control of multi-agent systems. Automatica 112, 108637 (2020)
Berg, H.C., Brown, D.A.: Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature 239(5374), 500–504 (1972)
Bullo, F., Cortés, J., Martínez, S.: Distributed control of robotic networks. Princeton University Press (2009)
Cortes, J., Martinez, S., Karatas, T., Bullo, F.: Coverage control for mobile sensing networks. IEEE Transactions on Robotics and Automation 20(2), 243–255 (2004)
Gao, S., Kan, Z.: Effective dynamic coverage control for heterogeneous driftless control affine systems. IEEE Control Systems Letters 5(6), 2018–2023 (2021)
Izumi, S.: Performance analysis of chemotaxis-inspired coverage controllers for multi-agent systems. In: Program Booklet of 4th International Symposium on Swarm Behavior and Bio-Inspired Robotics, p. 125 (2021)
Izumi, S., Azuma, S., Sugie, T.: Multi-robot control inspired by bacterial chemotaxis: Coverage and rendezvous via networking of chemotaxis controllers. IEEE Access 8, 124172–124184 (2020)
Kwok, A., Martìnez, S.: Unicycle coverage control via hybrid modeling. IEEE Transactions on Automatic Control 55(2), 528–532 (2010)
Liu, H., Wang, X., Li, X., Liu, Y.: Finite-time flocking and collision avoidance for second-order multi-agent systems. International Journal of Systems Science 51(1), 102–115 (2020)
Liu, Q., Ye, M., Sun, Z., Qin, J., Yu, C.: Coverage control of unicycle agents under constant speed constraints. IFAC-PapersOnLine 50(1), 2471–2476 (2017)
Martinez, S., Cortes, J., Bullo, F.: Motion coordination with distributed information. IEEE Control Systems Magazine 27(4), 75–88 (2007)
Murata, S., Konagaya, A., Kobayashi, S., Saito, H., Hagiya, M.: Molecular robotics: A new paradigm for artifacts. New Generation Computing 31(1), 27–45 (2013)
Oyekan, J., Hu, H., Gu, D.: A novel bio-inspired distributed coverage controller for pollution monitoring. In: Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, pp. 1651–1656 (2011)
Tso, W., Adler, J.: Negative chemotaxis in Escherichia coli. Journal of Bacteriology 118(2), 560–576 (1974)
Virágh, C., Vásárhelyi, G., Tarcai, N., Szörényi, T., Somorjai, G., Nepusz, T., Vicsek, T.: Flocking algorithm for autonomous flying robots. Bioinspiration & Biomimetics 9(2), 025012 (2014)
Yan, M., Guo, Y., Zuo, L., Yang, P.: Information-based optimal deployment for a group of dynamic unicycles. International Journal of Control, Automation and Systems 16(4), 1824–1832 (2018)
Yang, J., Wang, X., Bauer, P.: V-shaped formation control for robotic swarms constrained by field of view. Applied Sciences 8(11), 2120 (2018)
Funding
This work was supported in part by JSPS KAKENHI under Grant 19K15016.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Izumi, S. Performance Analysis of Chemotaxis-Inspired Stochastic Controllers for Multi-Agent Coverage. New Gener. Comput. 40, 871–887 (2022). https://doi.org/10.1007/s00354-022-00189-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00354-022-00189-9