Abstract
This paper introduces two methods for the fully discrete time-dependent Bingham problem in a three-dimensional domain and for the flow in a pipe also named after Mosolov. The first time discretisation is a generalised midpoint rule and the second time discretisation is a discontinuous Galerkin scheme. The space discretisation in both cases employs the non-conforming first-order finite elements of Crouzeix and Raviart. The a priori error analyses for both schemes yield certain convergence rates in time and optimal convergence rates in space. It guarantees convergence of the fully-discrete scheme with a discontinuous Galerkin time-discretisation for consistent initial conditions and a source term \(f\in H^1(0,T;L^2(\Omega ))\).
Similar content being viewed by others
1 Introduction
The mathematical model The parabolic variational inequality of this paper describes the flow of a Bingham fluid, which behaves as a rigid material, if the stress is below a certain threshold. If the flow is sufficiently slow (i.e., if the convective term can be omitted for small Reynolds numbers), the inertial terms can be neglected, and, in the case of a uni-directional flow, i.e., the flow in a pipe of cross-section \(\Omega \subset {\mathbb {R}}^2\), the problem reads as follows. Given a viscosity \(\mu >0\), a yield limit \(g\ge 0\), some right-hand side \(f\in L^2(0,T;L^2(\Omega ))\) and initial data \(u_0\in L^2(\Omega )\) in a bounded polygonal Lipschitz domain \(\Omega \subset {\mathbb {R}}^2\), the time-dependent Mosolov or Bingham problem for the flow in a pipe seeks \(u\in L^2(0,T;H^1_0(\Omega ))\) with a time derivative \({\dot{u}}\in L^2(0,T;H^{-1}(\Omega ))\) such that \(u(0)=u_0\) and, at a.e. \(t\in [0,T]\), any \(v\in H^1_0(\Omega )\) satisfies
Here and throughout the paper, \(\nabla \) denotes the gradient with respect to the space variable, \({\dot{v}}=(d/dt) v\) denotes the time-derivative of a function \(v:[0,T]\rightarrow X\), and \(\langle a,b\rangle _{H^{-1}(\Omega )\times H^1_0(\Omega )}\) denotes the dual pairing of \(a\in H^{-1}(\Omega )\) and \(b\in H^1_0(\Omega )\). Although this paper mainly considers uni-directional flows, all of the results are also valid for the general flow in a three-dimensional domain as outlined in Sect. 5.
Discretisations in space Conforming finite element methods (FEM) for the discretisation in space suffer from the non-differentiable \(L^1\) norm, which results in a suboptimal predicted convergence \(O(h^{1/2})\) for general smooth solutions and in a convergence \(O(h\sqrt{\log (1/h)})\) for a particular prototype example of a circular domain [16]. The traditional analysis for linear problems via the Strang-Fix lemma for non-conforming schemes relies qualitatively on the smoothness of the exact solution. This has been overcome recently by a medius analysis, which employs techniques from a posteriori analysis to prove a priori results [7, 9, 12, 18]. Quasi-optimal error estimates for the stationary Bingham problem were proved for a non-conforming FEM [11] based on the finite element space of Crouzeix and Raviart [10] whenever a stress-like variable belongs to \(H^1(\Omega )\). This results in the optimal convergence O(h), whenever the solution and a corresponding stress-like variable are smooth. The only other discretisations in space with proved optimal convergence rates were those of [14] (which is equivalent to the discretisation of [11]) and the mixed discretisations of the very recent paper [15]. The generalisation to the three-dimensional case is still open [15] and the combination of it with a time-discretisation is left for future research.
Time discretisation This paper combines the discretisation of [11] in space with two time-discretisations of (tB): A generalised midpoint rule and a discontinuous Galerkin discretisation.
The mathematical analysis of this paper is twofold: The dG(0) scheme is studied under the relatively weak assumption of consistent initial data and a source term \(f\in H^1(0,T;L^2(\Omega ))\) that guarantees a weak solution \(u\in H^1(0,T;L^2(\Omega ))\cap L^2(0,T;H^1_0(\Omega ))\). This results in a discrete approximation \(u_\textrm{DG}\in P_0({\mathcal {K}};\textrm{CR}^1_0({\mathcal {T}}))\) that is piecewise constant in time with minimal time-step \({\underline{k}}\) and maximal time-step k and a Crouzeix-Raviart function in space based on a shape-regular triangulation \({\mathcal {T}}\) with maximal mesh-size h with the plain convergence
under the (mild) constraint \(h\lesssim \sqrt{{\underline{k}}}\). In fact, according to the best knowledge of the authors (and seemingly that of our anonymous referees) this is the first paper that proves convergence under realistic regularity assumptions on the weak solution. In the absence of further regularity of the weak solution u, any convergence rate in (1.1) remains unclear. This paper identifies certain best-approximation terms of \(\nabla u\) and a stress-type variable \(\sigma \in \partial W(\nabla u)\) (derived in Theorem 2.3) plus data oscillation terms of f as an upper bound for the errors in (1.1). The backward Euler scheme is a modified dG(0) scheme with a slightly different treatment of the source term. In this low regularity regime, there are no other convergence results for the generalised midpoint scheme. In all numerical examples below f is piecewise constant and so \(u_\textrm{DG}=u_h\) (for \(\theta _\ell =1\) in the generalised mid-point rule with \(\tau _\ell =t_\ell \) for the backward Euler scheme). The second look at the class of time-discretisations hence solely concerns the generalised mid-point rules under the (possibly) unrealistic regularity assumptions \(u\in W^{m,1}(0,T;L^2(\Omega )) \cap C(0,T;H^1_0(\Omega ))\) and \(\sigma \in C(0,T;L^2(\Omega ;{\mathbb {R}}^2))\) that allow for a pointwise evaluation of the variational inequality at the prescribed times \(\tau _\ell \) for \(m=2,3\). In the second analysis for smooth solutions, the convergence rates are \(O(h+k)\) and for a uniform mid-point rule \(O(h+k^2)\). This improves the known result for a conforming FEM of [21].
Although discontinuous Galerkin methods for parabolic equations are already included in textbooks [19], to the best of the authors knowledge only [2, 8] define a discontinuous Galerkin FEM for a time-dependent variational inequality.
An overview over some time-stepping schemes for problem (tB) can be found in [13, 17]; see also the references therein. However, proofs of convergence rates are rare and only concern the combination of continuous linear finite elements in space with backward differences in time, which result in a convergence \(O(h^{1/2}+k)\) in [21] under the much stronger regularity assumptions \(u\in L^\infty (0,T;H^2(\Omega ))\), \({\dot{u}}\in L^2(0,T;H^1(\Omega ))\cap L^\infty (0,T;L^2(\Omega ))\), and \(\ddot{u}\in L^2(0,T;H^{-1}(\Omega ))\). This suboptimal convergence in space should be contrasted with the optimal convergence rate obtained in this paper, which is a consequence of the non-conforming discretisation in space.
Structure of the paper The paper is organised as follows. Section 2 specifies notation and states the main results in Sect. 2.4. The proofs of the error estimates for the generalised midpoint rule follow in Sect. 3, while the error estimate for the discontinuous Galerkin FEM is proved in Sect. 4. Section 5 generalises the results to the Bingham flow in a three-dimensional domain. Section 6 concludes the paper with numerical experiments.
General notation Standard notation on Lebesgue and Sobolev spaces applies throughout the paper and the space of \(L^2\) functions with values in \({\mathbb {R}}^m\) reads \(L^2(\Omega ;{\mathbb {R}}^m)\) and \(\int _\Omega \bullet \,dx\) denotes an integral over a domain \(\Omega \subset {\mathbb {R}}^2\) in space, while \(\int _{\widetilde{Q}} \bullet \,dQ\) denotes an integral over a domain \(\widetilde{Q}=(t_1,t_2)\times \Omega \) in space and time and \(\left\| \bullet \right\| _{L^2(\Omega )}\) and \(\left\| \bullet \right\| _{L^2(\widetilde{Q})}\) denote the respective \(L^2\) norms. The notation \(\bullet \) abbreviates the identity mapping. The space \(L^2(t_0,t_1;X)\) denotes the space of \(L^2\) functions \(v:[t_0,t_1]\rightarrow X\) for any linear space X, the space \(W^{m,p}(t_0,t_1;X)\) denotes the space of m-times (weakly) differentiable \(L^p(t_0,t_1;X)\) functions, whose derivatives belong to \(L^p(t_0,t_1;X)\), while \(C(t_0,t_1;X)\) denotes the space of continuous functions from \([t_0,t_1]\) to X. We abbreviate \(\Vert \bullet \Vert _{L^p(L^q)}:=\Vert \bullet \Vert _{L^p(0,T;L^q(\Omega ))}\). The formula \(A\lesssim B\) abbreviates that there exists a positive generic mesh-size independent constant \(C>0\) such that \(A\le C B\), \(A\approx B\) abbreviates \(A\lesssim B\lesssim A\).
2 Notation and main results
This section defines some notation in Sect. 2.1 and recalls two operators for the \(P_1\) non-conforming finite element space in Sect. 2.2, before it defines the discrete problems in Sect. 2.3 and states the main results in Sect. 2.4.
2.1 Notation
A shape-regular triangulation \({\mathcal {T}}\) of a polygonal bounded Lipschitz domain \(\Omega \subset {\mathbb {R}}^n\) is a set of simplices such that \({\overline{\Omega }}=\bigcup {\mathcal {T}}\) and any two distinct simplices are either disjoint or share exactly one common face, edge or vertex. Let \({\mathcal {E}}\) denote the set of sides in \({\mathcal {T}}\) and \({\mathcal {N}}\) the set of vertices. Let \(P_p(K;{\mathbb {R}}^m)\) denote the set of polynomials on K of total degree \(\le p\) and \(P_p({\mathcal {T}};{\mathbb {R}}^m)\) the set of piecewise polynomials, i.e.,
and let \(P_p({\mathcal {T}}):=P_p({\mathcal {T}};{\mathbb {R}})\). Define the space of continuous piecewise affine functions with homogeneous boundary conditions by
where \(C_0(\Omega )\) denotes the space of continuous functions with homogeneous boundary conditions on \(\partial \Omega \).
For an edge \(E\in {\mathcal {E}}\), \(\textrm{mid}(E)\) denotes the midpoint of E. The integral mean over a domain \(\omega \subseteq \Omega \) or \(\omega \subseteq [0,T]\) is defined as 
, where \(|\omega |\) denotes the volume of \(\omega \) or the length of \(\omega \), if it is an edge or an interval. The \(L^2\)-projection onto \({\mathcal {T}}\)-piecewise constant functions or vectors \({\Pi _0:L^2(\Omega ;{\mathbb {R}}^m)\rightarrow P_0({\mathcal {T}};{\mathbb {R}}^m)}\) is defined by 
for all \(K\in {\mathcal {T}}\) with area \(\vert K\vert \) and all \(f\in L^2(\Omega ;{\mathbb {R}}^m)\). Let \(h_{\mathcal {T}}\in P_0({\mathcal {T}})\) denote the piecewise constant mesh-size with \(h_{\mathcal {T}}\vert _K:={\textrm{diam}}(K)\) for all \(K\in {\mathcal {T}}\). The square of the oscillations of a function \(f\in L^2(\Omega )\) is defined by \(\textrm{osc}^2(f,{\mathcal {T}}):=\Vert h_{\mathcal {T}}(f-\Pi _0 f)\Vert _{L^2(\Omega )}^2\). For piecewise affine functions \(v_h\in P_1({\mathcal {T}})\) the \({\mathcal {T}}\)-piecewise gradient \(\nabla _{\textrm{NC}}v_h\) with \((\nabla _{\textrm{NC}}v_h)\vert _K=\nabla (v_h\vert _K)\) for all \(K\in {\mathcal {T}}\) exists and \(\nabla _{\textrm{NC}}v_h\in P_0({\mathcal {T}};{\mathbb {R}}^{n})\).
The \(P_1\) non-conforming finite element space [10], sometimes named after Crouzeix and Raviart, reads
2.2 Interpolation and companion operators
This subsection recalls the non-conforming interpolation operator and a companion operator for Crouzeix-Raviart functions in 2D.
Non-conforming interpolation operator The non-conforming interpolation operator \(I_{\textrm{NC}}:H^1_0(\Omega )\rightarrow \textrm{CR}^1_0({\mathcal {T}})\) is defined by
and satisfies the integral mean property
and the approximation and stability estimates
with constant \(C_{\textrm{NC}}=0.4396\) [5, Theorem 2.1].
Companion operators The design of three conforming companions to any \(v_h\in \textrm{CR}^1_0({\mathcal {T}})\) begins with the map \(J_1: \textrm{CR}^1_0({\mathcal {T}})\rightarrow S^1_0({\mathcal {T}})\). Given a vertex \(z\in {\mathcal {N}}\), let \({\mathcal {T}}(z):=\{T\in {\mathcal {T}}\mid z\in {\mathcal {T}}\}\) denote the set of triangles that contain z. Then \(J_1\) is defined by
with the conforming nodal basis function \(\varphi _z\in S^1_0({\mathcal {T}})\). This operator is also known as enriching operator in the context of fast solvers [3]. For a given edge \(E:={\textrm{conv}}\{a,b\}\in {\mathcal {E}}\) let \(b_E:=6\varphi _a\varphi _b\) denote the edge bubble function. Then the operator \(J_2:\textrm{CR}^1_0({\mathcal {T}})\rightarrow P_2({\mathcal {T}})\cap C_0(\Omega )\) is given by
For any triangle \(T\in {\mathcal {T}}\) with \(T={\textrm{conv}}\{a,b,c\}\) define the element bubble function \(b_T:=60\varphi _a\varphi _b\varphi _c\). The operator \(J_3:\textrm{CR}^1_0({\mathcal {T}})\rightarrow P_3({\mathcal {T}})\cap C_0(\Omega )\) is given by
Lemma 2.1
( [6]) The operators \(J_m:\textrm{CR}^1_0({\mathcal {T}})\rightarrow (P_m({\mathcal {T}})\cap C_0(\Omega ))\), \(m=1,2,3\), defined above satisfy the approximation and stability properties
and the conservation properties
2.3 Problem formulation
Given a yield limit \(g>0\) and \(f\in L^2(0,T;L^2(\Omega ))\), define the functionals
Then j is convex and lower semi continuous.
The following problem admits a unique solution [17, Chapter III, Theorem 6.1].
Definition 2.2
(Problem (tB)) Given initial data \(u_0\in L^2(\Omega )\), the time-dependent Mosolov problem in two dimensions seeks \(u\in L^2(0,T;H^1_0(\Omega ))\cap H^{1}(0,T;H^{-1}(\Omega ))\) such that \(u(0) = u_0\) and, for a.e. \(t\in (0,T)\) and all \(v\in H^1_0(\Omega )\), it holds that
The following theorem proves the existence of some stress-like variable \(\sigma \). Furthermore, it proves regularity of the solution u of (tB) under smoothness assumptions on f and \(u_0\). In the stationary case, the existence of the stress-like variable \(\sigma \) is proved in [17, Chapter II, Theorem 6.3].
Theorem 2.3
(Regularity result) There exists a stress-like variable \(\sigma \in L^2(0,T;\) \(L^2(\Omega ;{\mathbb {R}}^2))\) that, at a.e. \(t\in (0,T)\), satisfies
where \(W(A):=(\mu /2)|A|^2 + g |A|\) for all \(A\in {\mathbb {R}}^2\).
Suppose \(f\in H^1(0,T;L^2(\Omega ))\) and consistent initial values in the sense that \(u_0\in H^1_0(\Omega )\) and there exists some \(w\in L^2(\Omega )\) such that, for all \(v\in H^1_0(\Omega )\),
Then the solution u to (tB) satisfies \(u\in H^1(0,T;L^2(\Omega ))\).
Proof
The proof of the existence of the stress-like variable \(\sigma \) follows similar to the stationary case with a regularisation argument as in [17, Chapter II, Theorem 6.3]: The regularisation
of W leads to a stress \(\sigma _\varepsilon :=D W_\varepsilon (\nabla u_\varepsilon )\in L^2(0,T;L^2(\Omega ))\) with the solution \(u_\varepsilon \in L^2(0,T;H^1_0(\Omega ))\) of (tB) with \(j(\nabla v) - j(\nabla u(t))\) replaced by
Since \(|\sigma _\varepsilon (t) - \mu \nabla u_\varepsilon (t)|\le 1\) for a.e. \(t\in (0,T)\) almost everywhere in \(\Omega \), there exists a weak limit \(\sigma \in L^2(0,T;L^2(\Omega ))\) of a subsequence. The claimed properties of \(\sigma \) then follow as in the proof of [17, Chapter II, Theorem 6.3].
The proof of the second part follows from [20, Proposition 55.5] with \(V=H^1_0(\Omega )\), \(H=L^2(\Omega )\), \(a(\bullet ,\bullet )=\mu \int _\Omega \nabla \bullet \cdot \nabla \bullet \,dx\), \(\varphi =j\) and \(b=f\). \(\square \)
For the discretisation in time, consider the partition \({\mathcal {K}}=(t_0,\dots ,t_N)\) of the time-interval (0, T) with subordinated evaluation points \(\tau _1,\dots ,\tau _N\) for the generalised midpoint rule with
Let \(k_\ell :=t_\ell -t_{\ell -1}\) for all \(\ell =1,\dots ,N\) and \(0<\theta _\ell \le 1\) such that \(\tau _\ell =\theta _\ell t_\ell +(1-\theta _\ell )t_{\ell -1}\). For \(0\le s_0< s_1\le T\), let \(P_p(s_0,s_1;X)\) denote the space of polynomials from the interval \([s_0,s_1]\) with values in X of degree \(\le p\) and define the discrete spaces
Let \(U_0\in \textrm{CR}^1_0({\mathcal {T}})\) be an approximation to \(u_0\).
Definition 2.4
(Generalised midpoint rule) The generalised midpoint rule seeks \(u_h\in S^1({\mathcal {K}};\textrm{CR}^1_0({\mathcal {T}}))\) such that \(u_h(0)=U_0\) and, for all \(\ell =1,\dots ,N\) and for all \(v_h\in \textrm{CR}^1_0({\mathcal {T}})\), it holds
The generalised midpoint rule requires the evaluation of the right-hand side \(F(\tau _\ell ,\bullet )\) at \(\tau _\ell \) and, hence, it requires \(f\in C(0,T;L^2(\Omega ))\), while the subsequent discontinuous Galerkin discretisation merely involves an integrability \(f\in L^2(0,T;L^2(\Omega ))\). For a piecewise smooth (in time) function \(v_\textrm{DG}\), define the left and right limit and the jump at \(t_\ell \) by
Furthermore, define the time-space cylinders \(Q_\ell :=I_\ell \times \Omega \), where \(I_\ell :=(t_{\ell -1},t_\ell )\).
Definition 2.5
(dG(0) FEM) The dG(0) FEM seeks \(u_\textrm{DG}\in P_0({\mathcal {K}};\textrm{CR}^1_0({\mathcal {T}}))\) such that \(u_\textrm{DG}(0)=U_0\) and, for all \(\ell =1,\dots , N\) and for all \(v_\textrm{DG}\in P_0({\mathcal {K}};\textrm{CR}^1_0({\mathcal {T}}))\), it holds
Proposition 2.6
There exist unique solutions to problems (tB\(_h\)) and (dG(0)).
Proof
The existence of solutions to problems (tB\(_h\)) and (dG(0)) follows in every time step from the equivalence to the minimization problems
with discrete energies
where 
. The uniqueness follows from the strong convexity of the energies. \(\square \)
2.4 Main results
This section states the error estimates for the generalised midpoint rule and the discontinuous Galerkin scheme. The proofs follow in Sects. 3–4.
The first two theorems state error estimates for the generalised midpoint rule (tB\(_h\)). The first theorem proves an error estimate for the case that \(\theta _\ell >1/2\) for all \(\ell =1,\dots ,N\). Let \(e_\ell :=u(t_\ell )-u_h(t_\ell )\) and \(e(\tau _\ell ):=u(\tau _\ell )-u_h(\tau _\ell )\) and recall the definition of \(\sigma \) from Theorem 2.3.
Theorem 2.7
Assume that \(f\in C(0,T;L^2(\Omega ))\), \(u_0\in H^1(\Omega )\), \(u\in W^{2,1}(0,T;\) \(L^2(\Omega ))\cap C(0,T;H^1_0(\Omega ))\), and \(\sigma \in C(0,T;L^2(\Omega ;{\mathbb {R}}^2))\) and define \(\sigma _\ell :=\sigma (\tau _\ell )\). Suppose that there exists \(\alpha \le 1\) and \(\beta <1\) with \((1-\theta _{\ell -1}) k_{\ell -1}\le \alpha \theta _\ell k_\ell \) and \((1-\theta _\ell )\le \beta \theta _\ell \) (i.e., \(\theta _\ell >1/2\)), and let \(\delta :=(2-\alpha -\beta )/2>0\). Then it holds that
The following theorem asserts quadratic convergence in time for the uniform midpoint rule.
Theorem 2.8
(Error estimate for uniform midpoint rule) Assume that \(f\in C(0,T;L^2(\Omega ))\), \(u\in W^{3,1}(0,T;L^2(\Omega ))\cap C(0,T;H^1_0(\Omega ))\) and \(\sigma \in C(0,T;L^2(\Omega ;{\mathbb {R}}^2))\) and define \(\sigma _\ell :=\sigma (\tau _\ell )\). Suppose \(\theta =\theta _\ell =1/2\) and \(k_\ell =k=T/N\) and \(\Vert h_{\mathcal {T}}\Vert _{L^\infty (\Omega )}< k\sqrt{\mu }/(8\sqrt{T} C_{\textrm{NC}})\) with \(C_{\textrm{NC}}=0.4396\) from (2.1). Then it holds
The following theorem states an error estimate for the discontinuous Galerkin scheme. Let \(e:=u-u_\textrm{DG}\in L^2(0,T;L^2(\Omega ))\) and let \(e(t_\ell ^-):=\lim _{s\nearrow t_\ell } e(s)\) denote the right limit of e in \(t_\ell \) and \(u(t_{\ell -1}^+)\) and \(u(t_\ell ^-)\) denote the left and right limits of u in \(t_{\ell -1}\) and \(t_\ell \). Recall the non-conforming interpolation operator \(I_{\textrm{NC}}\) from Sect. 2.2.
Theorem 2.9
(Error estimate for dG(0)) Assume that \(u\in C(0,T;L^2(\Omega ))\) and let \({\overline{f}}\in L^2(0,T;L^2(\Omega ))\) and \({\overline{u}}\in L^2(0,T;L^2(\Omega ))\) be defined by
It holds for any \(\ell =1,\dots ,N\)
Remark 2.10
A piecewise Poincaré-Friedrichs inequality [4] proves, that \(\left\| \nabla _{\textrm{NC}}\bullet \right\| _{L^2(Q_\ell )}\) defines in fact a norm on \(L^2([t_{\ell -1},t_\ell ];H^1_0(\Omega )+\textrm{CR}^1_0({\mathcal {T}}))\).
The following lemma proves a trace inequality with respect to a time interval. This is employed in Corollary 2.12 below, which states a convergence rate for dG(0).
Lemma 2.11
(Trace inequality) Let X be a normed linear space. Any \(w\in H^{1}(a,b;X)\) satisfies
Proof
The fundamental theorem of calculus implies for a.e. \(s\in [a,b]\)
An integration over \(s\in [a,b]\), a triangle inequality and two Hölder inequalities lead to
This eventually proves
\(\square \)
Corollary 2.12
(Convergence of dG(0)) Let the conditions of Theorem 2.3 be fulfilled, i.e., let \(f\in H^1(0,T;L^2(\Omega ))\) and \(u_0\in H^1_0(\Omega )\) satisfy (2.7). Let \(h:=\Vert h_{\mathcal {T}}\Vert _{L^\infty (\Omega )}\) and \(k:=\max \{k_\ell \vert \ell =1,\dots ,N\}\) and \(\Vert u_0-U_0\Vert _{L^2(\Omega )}\rightarrow 0\) for \(h\rightarrow 0\). If \(h^2/\min \{k_\ell \vert \ell =1,\dots ,N\}\le C\) for some constant \(C<\infty \), then
If furthermore \(\Vert u_0-U_0\Vert _{L^2(\Omega )}=O(h)\), \(\sigma \in L^2(0,T;H^1(\Omega ))\), and \(u\in L^2(0,T;H^2(\Omega ))\), then \(\left\| \nabla _{\textrm{NC}}(u-u_\textrm{DG})\right\| _{L^2(0,T;L^2(\Omega ))}=O(h+k^{1/2})\) as \((h,k)\rightarrow 0\).
Proof
A summation over \(\ell =1,\dots ,N\) in (2.8) together with two applications of Young’s inequality shows for \(Q=(0,T)\times \Omega \)
By assumption \(\Vert u_0-U_0\Vert _{L^2(\Omega )}\rightarrow 0\) and, since \(f\in H^1(0,T;L^2(\Omega ))\),
Theorem 2.3 guarantees \(\sigma \in L^2(0,T;L^2(\Omega ;{\mathbb {R}}^2))\) and \(u\in H^1(0,T;L^2(\Omega ))\), and the assumption \(h^2/\min \{k_\ell \vert \ell =1,\dots ,N\}\le C\) proves convergence to zero of
Moreover, \(\Vert \sigma -\Pi _0\sigma \Vert _{L^2(Q)}\rightarrow 0\) and the trace inequality of Lemma 2.11 and a Poincaré inequality imply
The \(L^2\) projection of \({\dot{u}}\) onto piecewise constants (in time),
satisfies
This leads to plain convergence of dG(0).
Under the additional assumptions \(\sigma \in L^2(0,T;H^1(\Omega ))\), \(u\in L^2(0,T;H^2(\Omega ))\), and \(\Vert u_0-U_0\Vert _{L^2(\Omega )}=O(h)\), the convergence rate \(O(h+k^{1/2})\) follows from the above estimates. \(\square \)
Remark 2.13
(comparison of midpoint rule and dG(0)) The convergence \(h+k^{1/2}\) for dG(0) (by Corollary 2.12) is suboptimal in comparison to the generalised midpoint rule (for a smooth solution u). But the convergence of dG(0) is guaranteed for more general and realistic regularity of the solution \(u\in H^1(0,T;L^2(\Omega ))\cap L^2(0,T;H^1(\Omega ))\) and \(\sigma \in L^2(0,T;L^2(\Omega ;{\mathbb {R}}^2))\).
3 Proofs of theorems 2.7–2.8
This section starts with a stability result for the generalised midpoint rule for the two cases \(\theta _\ell >1/2\) as well as \(\theta _\ell =1/2\) for all \(\ell =1,\dots ,n\). Sect. 3.2 proves the error estimates from Theorems 2.7 and 2.8.
3.1 Stability
The stability of the generalised midpoint rule will be employed in the error estimate of Theorem 2.7. The stability of the uniform midpoint rule with \(\theta =\theta _\ell =1/2\), will not enter the proof of the error estimate of Theorem 2.8 below, and is merely given for completeness.
Theorem 3.1
(Stability) Assume that \(f\in C(0,T;L^2(\Omega ))\) and let \(n\in \{1,\dots ,N\}\). If \(\theta =\theta _\ell =1/2\) and \(k=k_\ell \) for all \(\ell =1,\dots ,n\), then
If \(\theta _\ell >1/2\), assume that there exists \(\alpha \le 1\) and \(\beta <1\) with \((1-\theta _{\ell -1}) k_{\ell -1}\le \alpha \theta _\ell k_\ell \) and \((1-\theta _\ell )\le \beta \theta _\ell \) (i.e., \(\theta _\ell >1/2\)) for all \(\ell =1,\dots ,n\). Then \(\delta :=(2-\alpha -\beta )/2>0\) satisfies
Proof
Let \(\ell \in \{1,\dots ,n\}\) and choose \(v_h=u_h(\tau _{\ell -1})\) in (tB\(_h\)) (with \(\tau _0:=t_0=0\)) to conclude that
Since \({\dot{u}}_h\) is piecewise constant with respect to the time-intervals, it follows
Therefore, the left-hand side of (3.1) reads with \(\theta _0:=k_0:=0\) and \({\dot{u}}_h(0):=0\) as
The identity \(u_h(\tau _\ell )=(u_h(\tau _\ell )-u_h(\tau _{\ell -1}))/2 + (u_h(\tau _\ell )+u_h(\tau _{\ell -1}))/2\) reveals
The combination of the previous inequalities with the sum of (3.1) over \(\ell =1,\dots ,n\) reads
Case 1 (Uniform midpoint rule): \(\theta =\theta _\ell =1/2\) and \(k=k_\ell \).
The Cauchy inequality and the Young inequality with weight 1/2 for each time step lead to
The combination with (3.3) results in
Case 2: There exists \(\alpha \le 1\) with \(\theta _\ell > 1/2\) and \((1-\theta _{\ell -1}) k_{\ell -1}\le \alpha \theta _\ell k_\ell \).
Let \(\beta <1\) such that \((1-\theta _\ell )\le \beta \theta _\ell \) for all \(\ell =1,\dots ,n\) and set \(\delta :=(2-\alpha -\beta )/2>0\). This implies
The combination with (3.3) leads to
The identities of (3.2) plus Cauchy and Young inequalities with weight \(\gamma >0\) imply
Since \((1-\theta _\ell )\le \beta \theta _\ell \) for all \(\ell =1,\dots ,n\) and \({\dot{u}}_h(0)=0\) by definition, it follows
Therefore, \((1-\theta _{\ell -1})k_{\ell -1}\le \alpha \theta _\ell k_\ell \) implies
For \(\gamma =\delta /(1+\beta )\), this and the combination with (3.4) lead to
This concludes the proof. \(\square \)
3.2 Error estimates
The following theorem controls the error in space for a fixed time \(\tau _\ell \). The proof follows the arguments of [11] and considers \(\sigma _\ell :=\sigma (\tau _\ell )\) with \(\sigma \) from (2.6). Recall the constants \(C_\textrm{comp}\) and \(C_{\textrm{NC}}\) from Sect. 2.2.
Theorem 3.2
(Error estimate in space) Assume that \(f\in C(0,T;L^2(\Omega ))\), \(\sigma \in C(0,T;L^2(\Omega ;{\mathbb {R}}^2))\) and \({\dot{u}}\in C(0,T;L^2(\Omega ))\). The error \(e(\tau _\ell ):=u(\tau _\ell )-u_h(\tau _\ell )\) satisfies
Proof
Theorem 3.2 of [11] proves the existence of \(\sigma _{h,\ell }\in P_0({\mathcal {T}};{\mathbb {R}}^2)\cap \partial W(\nabla _{\textrm{NC}}u_h(\tau _\ell ))\) with W as in Theorem 2.3 such that for all \(v_h\in \textrm{CR}^1_0({\mathcal {T}})\)
The definition of the subgradients \(\sigma _{h,\ell }\in \partial W(\nabla _{\textrm{NC}}u_h(\tau _\ell ))\) and \(\sigma _\ell \in \partial W(\nabla u(\tau _\ell ))\) results in
Since \(\nabla _{\textrm{NC}}I_{\textrm{NC}}u(\tau _\ell )=\Pi _0\nabla u(\tau _\ell )\), Jensen’s inequality proves
This, \(F(\tau _\ell ,\bullet )-{\dot{u}}(\tau _\ell ) + {\text {div}}\sigma _\ell = 0\) in \(H^{-1}(\Omega )\), and its discrete analogue (3.5) lead to
The integral mean property of \(I_{\textrm{NC}}\) implies that the last term vanishes. The conservation property (2.4) and the stability property (2.3) prove
The conservation property (2.5) and the approximation property (2.3) imply
The integral mean property and the approximation property of \(I_{\textrm{NC}}\) yield
A calculation reveals
The combination of the previously displayed formulas with two applications of Young’s inequality with weight \(2/\mu \) lead to
The approximation properties of \(J_3\) and \(I_{\textrm{NC}}\), two applications of the Cauchy inequality, and two applications of a weighted Young’s inequality with weight \(4/\mu \) lead to
The combination of the two previously displayed inequalities concludes the proof. \(\square \)
The following theorem proves a first error estimate for the discretisation (tB\(_h\)).
Theorem 3.3
(A priori error estimate for the full discretisation) Assume that \(f\in C(0,T;L^2(\Omega ))\), \(u\in W^{2,1}(0,T;L^2(\Omega ))\cap C(0,T;H^1_0(\Omega ))\) and \(\sigma \in C(0,T;L^2(\Omega ;{\mathbb {R}}^2))\). If \(\theta _\ell > 1/2\), then it holds
If \(k=k_\ell =T/N\), \(\theta =\theta _\ell =1/2\), and, in addition to the above regularity assumptions \(u\in W^{3,1}(0,T;L^2(\Omega ))\), then
Proof
The error analysis with respect to the time discretisation follows as in [1, Proposition 5.1] for elastoplasticity with \(|||\bullet |||\) replaced by the \(L^2\) norm \(\Vert \bullet \Vert _{L^2(\Omega )}\) and the scalar product \(a(\bullet ,\bullet )\) replaced by the \(L^2\) scalar product. Those arguments lead to
for the generalised midpoint rule with \(\theta >1/2\) and
for the uniform midpoint rule. The combination with the error estimate in space of \(\int _\Omega {\dot{e}}(\tau _\ell ) e(\tau _\ell )\,dx\) from Theorem 3.2 then proves the assertion. \(\square \)
Proof of Theorem 2.7
The combination of Theorem 3.3 with the estimation of \(\Vert h_{\mathcal {T}}{\dot{u}}_h(\tau _\ell )\Vert _{L^2(\Omega )}^2\) from Theorem 3.1 leads to Theorem 2.7. \(\square \)
Proof of Theorem 2.8
For \(\theta =1/2\), a Young inequality implies
with \(\widetilde{e}:=\widetilde{u} -u_h\) for the nodal interpolation \(\widetilde{u}=I_h u\in S^1({\mathcal {K}};H^1_0(\Omega ))\) of u in time with \(I_h u(t_\ell )=u(t_\ell )\) for all \(\ell =0,\dots ,N\). Recall \(Q_\ell =[t_{\ell -1},t_\ell ]\times \Omega \). Since 
, the second term on the right-hand side in (3.7) is bounded by
Let \(H:=\Vert h_{\mathcal {T}}\Vert _{L^\infty (\Omega )}\) abbreviate the maximal (spatial) mesh-size. Since \(\widetilde{u}(t_\ell )=u(t_\ell )\) by the definition of \(\widetilde{u}\), it holds \(\widetilde{e}(t_\ell )=e_\ell \). For the first term on the right-hand side of (3.7), the representation
and a triangle inequality lead to
If \(H< k\sqrt{\mu }/(8\sqrt{T}C_{\textrm{NC}})\), then \(N=T/k\) leads to
Eventually, the right-hand side of (3.8) can be absorbed on the right-hand side of (3.6). The combination of this with Theorem 3.3 concludes the proof of Theorem 2.8. \(\square \)
4 Proof of theorem 2.9
This section proves the error estimate for the discontinuous Galerkin discretisation (dG(0)) from Theorem 2.9.
4.1 Error estimate in space
Since \(\sigma (t)\in \partial W(\nabla u(t))\) for a.e. \(t\in [0,T]\), the sum rule of the subderivative implies \(\sigma (t)-\mu \nabla u(t)\in \partial j(\nabla u(t))\). The definition of the subderivative implies for all \(q\in L^2(\Omega ;{\mathbb {R}}^2)\)
Since \(\Pi _0 \nabla J_3 u_\textrm{DG}(t) = \nabla _{\textrm{NC}}u_\textrm{DG}(t)\), for \(q=\nabla _{\textrm{NC}}u_\textrm{DG}(t)\) and \(e:=u-u_\textrm{DG}\) the left-hand side reads
The application of \(-{\text {div}}\sigma (t) = (f(t)-{\dot{u}}(t))\in H^{-1}(\Omega )\) leads for the second term to
The integral mean property of \(J_3\) from (2.5) and the combination of (4.1)–(4.2) with an integration over \(t\in I_j\) results in
4.2 Combination of variational inequalities
The sum of (dG(0)) with the new notation \(v_\textrm{DG}=u_\textrm{DG}^\star \) (to highlight that this will be chosen below to approximate the exact solution) and (4.3) provides
Since \((d/dt) J_3 u_\textrm{DG}=0\) in \(I_\ell \), the fourth term on the right-hand side of (4.4) reads
Since \(u_\textrm{DG}\) is constant on \(I_\ell \), the binomial formulas show
The approximation properties (2.3) of \(J_3\) and a Cauchy inequality imply
Since by assumption \(u\in C(0,T;L^2(\Omega ))\) is continuous, and \(e=u-u_\textrm{DG}\), the fifth term on the right-hand side of (4.4) reads
The definition of the average \(\langle v \rangle _{\ell -1}=(v(t_{\ell -1}^+) + v(t_{\ell -1}^-))/2\) implies \((e)_{\ell -1}^+ = \langle e \rangle _{\ell -1} + [e]_{\ell -1}/2\). Consequently,
The product rule \([ab]_{\ell -1}=[a]_{\ell -1}\langle b\rangle _{\ell -1}+\langle a\rangle _{\ell -1}[b]_{\ell -1}\) for any piecewise continuous a, b implies
Therefore, (4.7) results in
The approximation and stability properties (2.3) of \(J_{3}\) prove
Since \(\Vert \nabla _{\textrm{NC}}e\Vert _{L^2(Q_\ell )}\) can be absorbed, the combination of (4.4) with (4.5)–(4.6), (4.8)–(4.9) and
leads to
4.3 Choosing \(u_\textrm{DG}^\star \)
Define \({\overline{u}}\in L^2(\Omega )\) by 
for a.e. \(x\in \Omega \). Note that \({\overline{u}}\in H^1_0(\Omega )\) and 
(from Fubini’s theorem). Define \(u_\textrm{DG}^\star \vert _{I_\ell }:=I_{\textrm{NC}}{\overline{u}}\). The integral mean property \(\nabla _{\textrm{NC}}I_{\textrm{NC}}\bullet =\Pi _0\nabla \bullet \) implies 
. This and \(\nabla _{\textrm{NC}}u_\textrm{DG}\in P_0(Q_\ell ;{\mathbb {R}}^2)\) lead to
Jensen’s inequality yields
It remains to estimate (4.10) and (4.11). Define
\({\overline{f}}\in L^2(\Omega )\) by 
for a.e. \(x\in \Omega \). Then
A Cauchy inequality implies for the first term
The definition of \( u_\textrm{DG}^\star = I_{\textrm{NC}}{\overline{u}}\) and the approximation property of \(I_{\textrm{NC}}\) imply
Since 
and 
, it follows 
for a.e. \(x\in \Omega \). Hence, Jensen’s inequality proves
The combination of the previous inequalities leads to
Since u is continuous,
Since \(u_\textrm{DG}^\star = I_{\textrm{NC}}{\overline{u}}\) and \({\overline{u}}\vert _{I_\ell }\in H^1(\Omega )\), (2.1) implies
Altogether,
This concludes the proof of Theorem 2.9.
5 Generalization to 3D
In this section, let \(\Omega \subseteq {\mathbb {R}}^3\) be a three-dimensional bounded polyhedral Lipschitz domain. Define the vector-valued spaces
and let \(H^{-1}(\Omega ;{\mathbb {R}}^3)\) denote the dual space of \(H^1_0(\Omega ;{\mathbb {R}}^3)\). Furthermore, the linearised Green strain tensor \(\varepsilon (u)=(\nabla u+\nabla u^\top )/2\) denotes the symmetric part of the gradient of a velocity function \(u\in H^1_0(\Omega ;{\mathbb {R}}^3)\) and : denotes the scalar product between two matrices \(A,B\in {\mathbb {R}}^{3\times 3}\), i.e., \(A:B:=\sum _{\ell =1}^3 \sum _{m=1}^3 A_{\ell m}B_{\ell m}\).
Given \(f\in L^2(0,T;L^2(\Omega ;{\mathbb {R}}^3))\) and initial data \(u_0\in H({\text {div}},\Omega )\) with \({\text {div}}u_0=0\), the time-dependent Bingham flow problem in 3D seeks \(u\in L^2(0,T;Z)\) with \({\dot{u}}\in L^2(0,T;H^{-1}(\Omega ;{\mathbb {R}}^3))\) such that \(u(0)=u_0\) and, at a.e. \(t\in [0,T]\), any \(v\in Z\) satisfies
A direct discretisation of the variational inequality with \(P_1\) non-conforming finite elements is not possible, since \(\int _\Omega \varepsilon _{\textrm{NC}}(\bullet ):\varepsilon _{\textrm{NC}}(\bullet )\,dx\) is not positive definite on the \(P_1\) non-conforming finite element space: Korn’s inequality fails for \(\textrm{CR}^1_0({\mathcal {T}};{\mathbb {R}}^3)\) in general. However, for homogeneous Dirichlet boundary conditions, a straightforward calculation reveals, for all \(v,w\in H^1_0(\Omega ;{\mathbb {R}}^3)\), that
Since \(u(t)\in Z\), the following problem is equivalent to (5.1): Seek \(u\in L^2(0,T;Z)\) with time derivative \({\dot{u}}\in L^2(0,T;H^{-1}(\Omega ;{\mathbb {R}}^3))\) such that \(u(0)=u_0\) and, at a.e. \(t\in [0,T]\), any \(v\in Z\) satisfies
The \(P_1\) non-conforming finite element space in this three-dimensional context consists of piecewise affine functions, which are continuous in the midpoints of interior faces and vanish in midpoints of boundary faces. Let \({\text {div}}_{\textrm{NC}}\) and \(\varepsilon _{\textrm{NC}}\) denote the piecewise versions of \({\text {div}}\) and \(\varepsilon \) and define the vector-valued spaces
Let \(U_0\in \textrm{CR}^1_0({\mathcal {T}};{\mathbb {R}}^3)\) be some approximation of \(u_0\). With the notation for the partition of the time interval \({\mathcal {K}}\) from Sect. 2, the generalised midpoint rule seeks \(u_h\in S^1({\mathcal {K}};Z_\textrm{CR})\) such that \(u_h(0)=U_0\) and, for all \(\ell =1,\dots ,N\) and for all \(v_h\in Z_\textrm{CR}\), it holds
Recall the notation of the jump \([\bullet ]_\ell \) and the left limit \((\bullet )^+_\ell \) from Sect. 2. The discontinuous Galerkin FEM in 3D seeks \(u_\textrm{DG}\in P_0({\mathcal {K}};Z_\textrm{CR})\) such that, for all \(\ell =1,\dots , N\) and for all \(v_\textrm{DG}\in P_0({\mathcal {K}};Z_\textrm{CR})\), it holds
The divergence-free condition \(u_h(t)\in Z_\textrm{CR}\) and \(u_\textrm{DG}\vert _{I_\ell }\in Z_\textrm{CR}\) can be implemented using a piecewise constant Lagrange multiplier as it is common for the Stokes equations. Define
Let \(t\in [0,T]\) be arbitrary such that (5.2) holds and \(f(t)-{\dot{u}}(t)\in H^{-1}(\Omega )\) and \(u(t)\in H^1_0(\Omega )\). Define \(W_{3D}(A):=(\mu /4) |A|^2 + g|{\textrm{sym}} A|\). The Euler-Lagrange equations of [11, Theorem 5.1] prove the existence of \(\sigma (t)\in H({\text {div}},\Omega ;{\mathbb {R}}^{3\times 3})\) and \(\xi (t)\in L^2_0(\Omega )\) with
With this \(\sigma \), the error estimates of Theorems 2.7–2.9 equally hold in this three-dimensional situation. The proof follows as in Sects. 3–4, see also [11, Theorem 5.2] for the analysis of the error estimate in space. We want to highlight that it is essential for the proof that the functions in \(Z_\textrm{CR}\) are pointwise divergence-free.
6 Numerical experiments
This section is devoted to two numerical experiments for the two discretisations (tB\(_h\)) and (dG(0)) in Sects. 6.2–6.3. Sect. 6.1 describes how the solution to the discrete nonlinear problems are approximated, while Sect. 6.4 draws some conclusions of the numerical experiments.
6.1 Numerical realisation
The discrete solutions of (tB\(_h\)) and (dG(0)) are approximated by the following Uzawa algorithm from [13]. It is recalled here for the sake of completeness.
The numerical experiments in Subsects. 6.2–6.3 employ \(\rho =\mu /g^2\approx 44.4\) and \(\texttt {tol}=10^{-6}\) for the discrete solutions (resp. \(\texttt {tol}=10^{-6}\) for the computation of the reference solutions) and we neglect the influence of the error in the Usawa algorithm in the discussion.
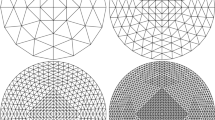
Initial triangulations for the numerical examples from Sect. 6
Red-refined triangle
Plot of rigid regions of \(u_{\textrm{DG},m,j}\) at times 0.0333, 0.1 and 0.2 for different values of m and j for the numerical experiment from Sect. 6.2
Plot of rigid regions of \(u_{0.5,m,j}\) at times 0.0333, 0.1 and 0.2 for different values of m and j for the numerical experiment from Sect. 6.2
6.2 Numerical experiment on the square
This example approximates the solution to (tB) on the unit square \(\Omega =(0,1)^2\) and the time intervall [0, T] with \(T=0.2\) and initial value \(u(0)=0\), right-hand side \(f=5\), viscosity \(\mu =1\), and yield limit \(g=0.15\). The initial triangulation \({\mathcal {T}}_0\) is depicted in Fig. 1a. The approximations \(u_{\textrm{DG},m,j}\) defined by (dG(0)) and \(u_{\theta ,m,j}\) defined by (tB\(_h\)) for \(\theta =\theta _\ell =0.5\) and \(\theta =\theta _\ell =1\) for all time steps \(\ell \) are computed on a sequence \(({\mathcal {T}}_m)_{m=0,\dots ,5}\) of red-refined triangulations (see Fig. 2 for a red-refined triangle). The time step sizes are chosen as \(3^{-j}T/2\) for \(j=0,1,\dots ,4\) and the parameter \(\texttt {tol}\) in the Uzawa algorithm as \(10^{-6}\). A discrete rigid region of \(u_{\theta ,m,j}\) or \(u_{\textrm{DG},m,j}\) at some time t is defined as the union of all triangles where the norm of its (spatial) gradient is less than 1
of the maximal norm of the gradient at that time. These rigid regions are plotted in Fig. 3 (resp. Fig. 4) for \(u_{\textrm{DG},m,j}\) (resp. \(u_{\theta ,m,j}\)) for three different times and for different mesh-sizes and time-step sizes to illustrate the behaviour of the discrete solutions. A reference solution \(u_\textrm{ref}\) is computed on the triangulation \({\mathcal {T}}_6\) with time step size \(3^{-5}T/2\) and \(\texttt {tol}=10^{-7}\). Note that the refinement in time is chosen in such a way that the evaluation points \(\tau _\ell \) with respect to a coarse time step are also evaluation points on a finer time step. The errors \(e_{\theta ,m,j}\) (resp. \(e_{\textrm{DG},m,j}\)) read
for \(u_h=u_{\textrm{DG},m,j}\) (resp. \(u_h=u_{\theta ,m,j}\)) and are plotted in Fig. 5 against the numbers of degrees of freedom (ndof) in \({\mathcal {T}}_m\), while the errors
for the number of time steps N are plotted in Fig. 6.
For a time step size of \(k=3^{-5}T/2\), the errors from (6.1) and (6.2) for all three methods show a convergence rate of \(\texttt {ndof}^{-1/2} = O(h)\). For \(\theta =0.5\) this convergence rate is also achieved for a time step size of \(k=3^{-4}T/2\). In Figs. 7 and 8, the same errors are plotted against the number of time steps. The errors (6.1) show a convergence rate of O(k) on the finest triangulation \({\mathcal {T}}_5\) for all considered methods for the first time steps. In particular, the observed convergence rate is O(k) instead of the predicted \(O(k^{1/2})\) for the discretisation (dG(0)). For larger time steps, the error in space already seems to dominate the error, so that the convergence is diminished. The errors (6.2) converge with rate between O(k) and \(O(k^{1/2})\) for \(\theta =1\) on \({\mathcal {T}}_5\) for the first time steps. This is a slower convergence compared to the predicted convergence rate of Theorem 2.7 and it seems that preasymptotic effects diminish the convergence rate. For \(\theta =0.5\), the convergence between O(k) and the predicted \(O(k^2)\) is visible. It seems that preasymptotic effects or the error in space slow down the convergence.
Plot of rigid regions of \(u_{\textrm{DG},m,j}\) at times 0.0333, 0.1 and 0.2 for different values of m and j for the numerical experiment from Sect. 6.3
Plot of rigid regions of \(u_{0.5,m,j}\) at times 0.0333, 0.1 and 0.2 for different values of m and j for the numerical experiment from Sect. 6.3
6.3 Numerical experiment on the L-shaped domain
This example approximates the solution of (tB) on the L-shaped domain \(\Omega =(-1,1)^2\setminus ([0,1]\times [0,1])\) and the time interval [0, T] with \(T=0.2\) and with initial value \(u(0)=0\), right-hand side \(f=5\), viscosity \(\mu =1\), and yield limit \(g=0.15\). As in Sect. 6.2, the approximations \(u_{\textrm{DG},m,j}\) defined by (dG(0)) and \(u_{\theta ,m,j}\) defined by (tB\(_h\)) for \(\theta =\theta _\ell =0.5\) and \(\theta =\theta _\ell =1\) for all time steps \(\ell \) are computed on a sequence \(({\mathcal {T}}_m)_{m=0,\dots ,5}\) of red-refined triangulations (see Fig. 2 for a red-refined triangle). The initial triangulation \({\mathcal {T}}_0\) is depicted in Fig. 1b. The time step sizes are chosen as \(3^{-j}T/2\) for \(j=0,1,\dots ,4\) and the parameter \(\texttt {tol}\) in the Uzawa algorithm as \(10^{-6}\). As in Sect. 6.2, the rigid regions are plotted in Fig. 9 (resp. Fig. 10) for \(u_{\textrm{DG},m,j}\) (resp. \(u_{\theta ,m,j}\)) for three different times and for different mesh-sizes and time-step sizes to illustrate the behaviour of the discrete solutions.
A reference solution \(u_\textrm{ref}\) is computed on the triangulation \({\mathcal {T}}_6\) with time step size \(3^{-5}T/2\) and \(\texttt {tol}=10^{-7}\). The errors from (6.1) are plotted in Fig. 11 against the number of degrees of freedom (ndof) in \({\mathcal {T}}_m\), while Fig. 12 displays the errors from (6.2). For coarse time steps, the convergence is limited by the error in time, while for small time steps, the errors for all methods show a convergence rate slightly smaller than O(h). In the stationary case, the experiments of [11] show a convergence rate slightly larger than \(O(h^{2/3})\) due to the re-entrant corner and the resulting singularity of the solution on an L-shaped domain. However, for the time-dependent situation considered here, it seems that (at least preasymptotic) the singularity has merely a marginal influence. Figures 13 and 14 display the same errors plotted against the number of time steps. The observed convergence rates are O(k) for the first refinement in time on the fines triangulation for all three methods and the two errors. The predicted convergence rate of \(O(k^2)\) for the uniform midpoint rule cannot be observed. The error in space seems to dominate the approximation error as in Sect. 6.2 on coarser triangulations.
6.4 Conclusions
Section 2.4 states error estimates for the discretisations (tB\(_h\)) and (dG(0)). The numerical experiments of this section illustrate those results. Moreover, they indicate the following results beyond the theoretical statements from Sect. 2.4.
-
The convergence history plots show no preasymptotic effect with respect to h.
-
The empirical convergence for the discontinuous Galerkin discretisation is O(k) rather than \(O(k^{1/2})\) as \(k\rightarrow 0\) predicted by Theorem 2.9.
-
The factor \(h^2/k^{1/2}\) in the upper bound for the error of the discontinuous Galerkin discretisation cannot be seen in the numerical experiments, i.e., the error do not increase, when k becomes small for large h.
-
The condition \(\Vert h_{\mathcal {T}}\Vert _{L^\infty (\Omega )}<k\sqrt{\mu }/(8\sqrt{T}C_{\textrm{NC}})\) that was needed in the error estimate for the uniform midpoint rule in Theorem 2.8 is satisfied only for the pairs \((m,j)\in \{(3,0),(4,0),(5,0),(5,1)\}\) for both experiments in Subsects. 6.2–6.3. Although Theorem 2.8 only proves a parameter conditional convergence, the numerical experiments indicate that the convergence is independent of that parameter.
References
Alberty, J., Carstensen, C.: Numerical analysis of time-depending primal elastoplasticity with hardening. SIAM J. Numer. Anal. 37(4), 1271–1294 (2000)
Alberty, J., Carstensen, C.: Discontinuous Galerkin time discretization in elastoplasticity: motivation, numerical algorithms, and applications. Comput. Methods Appl. Mech. Eng. 191(43), 4949–4968 (2002)
Brenner, S.C.: Two-level additive Schwarz preconditioners for nonconforming finite element methods. Math. Comp. 65(215), 897–921 (1996)
Brenner, S.C.: Poincaré-Friedrichs inequalities for piecewise \(H^{1}\) functions. SIAM J. Numer. Anal. 41(1), 306–324 (2003)
Carstensen, C., Gedicke, J.: Guaranteed lower bounds for eigenvalues. Math. Comp. 83(290), 2605–2629 (2014)
Carstensen, C., Gallistl, D., Schedensack, M.: Adaptive nonconforming Crouzeix-Raviart FEM for eigenvalue problems. Math. Comp. 84(293), 1061–1087 (2015)
Carstensen, C., Gallistl, D., Schedensack, M.: \(L^2\) best-approximation of the elastic stress in the Arnold-Winther FEM. IMA J. Numer. Anal. 36(3), 1096–1119 (2016)
Carstensen, C., Liu, D., Alberty, J.: Convergence of \(\rm dG (1)\) in elastoplastic evolution. Numer. Math. 141(3), 715–742 (2019)
Carstensen, C., Peterseim, D., Schedensack, M.: Comparison results of finite element methods for the Poisson model problem. SIAM J. Numer. Anal. 50(6), 2803–2823 (2012)
Crouzeix, M., Raviart, P.-A.: Conforming and nonconforming finite element methods for solving the stationary Stokes equations. I. Rev. Française Automat. Informat. Recherche Opérationnelle Sér. Rouge, 7(R-3):33–75, (1973)
Carstensen, C., Reddy, B.D., Schedensack, M.: A natural nonconforming FEM for the Bingham flow problem is quasi-optimal. Numer. Math. 133(1), 37–66 (2016)
Carstensen, C., Schedensack, M.: Medius analysis and comparison results for first-order finite element methods in linear elasticity. IMA J. Numer. Anal. 35(4), 1591–1621 (2015)
Dean, E.J., Glowinski, R., Guidoboni, G.: On the numerical simulation of Bingham visco-plastic flow: Old and new results. J. Non-Newtonian Fluid Mech. 142, 36–62 (2007)
Falk, R.S., Mercier, B.: Error estimates for elastic-plastic problems. RAIRO, Anal. Numér., 11:135–144, (1977)
Gustafsson, T., Lederer, P.L.: Mixed finite elements for Bingham flow in a pipe. Numer. Math. 152(4), 819–840 (2022)
Glowinski, R.: Sur l’approximation d’une inéquation variationnelle elliptique de type Bingham. RAIRO Analyse Numérique, 10(R-3):13–30, 1976
Glowinski, R.: Numerical methods for nonlinear variational problems. Scientific Computation. Springer-Verlag, Berlin, 2008. Reprint of the 1984 original
Gudi, T.: A new error analysis for discontinuous finite element methods for linear elliptic problems. Math. Comp. 79(272), 2169–2189 (2010)
Thomée, V.: Galerkin finite element methods for parabolic problems. Springer Series in Computational Mathematics, vol. 25. Springer-Verlag, Berlin (1997)
Zeidler, E., Nonlinear functional analysis and its applications. III. Springer-Verlag, New York,: Variational methods and optimization. Translated from the German by Leo F, Boron (1985)
Zhang, Y.: Error estimates for the numerical approximation of time-dependent flow of Bingham fluid in cylindrical pipes by the regularization method. Numer. Math. 96(1), 153–184 (2003)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work of the authors was supported by the Deutsche Forschungsgemeinschaft(DFG) in the Priority Program 1748 “Reliable simulation techniques in solid mechanics: Development of non-standard discretization methods, mechanical and mathematical analysis,” under the projects CA 151/22 and SCHE1885/1-1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carstensen, C., Schedensack, M. Two discretisations of the time-dependent Bingham problem. Numer. Math. 153, 411–450 (2023). https://doi.org/10.1007/s00211-022-01338-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-022-01338-4