Non-integrability of the planar elliptic restricted three-body problem

Abstract

We present the non-integrability proof for the planar elliptic restricted three-body problem. Two versions of this problem are considered: the classical one when only gravitational interactions are taken into account, and the photo-gravitational version where radiation pressure from the primaries is also included. Our result is valid for nonzero eccentricity and arbitrary mass ratio of the primaries. In the proof, we apply the differential Galois approach to study the integrability.

1 Introduction

One of the fundamental model systems of celestial mechanics which has a plenty of applications is the restricted three-body problem. In this model, we assume that a point with a negligible mass moves in the gravity field of two other point masses called the primaries with masses $m_1$ and $m_2$. They move in elliptic Keplerian orbits around their common mass centre. In the special case when ellipses become circles, we speak about the circular restricted three-body problem. As examples of the restricted three-body problem, we mention the Sun-Jupiter-asteroid or Sun-planet-object systems. In the case when an infinitesimal mass particle moves in the same plane as the orbits of the primaries, the problem is called planar elliptic restricted three-body problem, otherwise is called spatial one. We introduce the mass parameter $\mu =\tfrac{m_2}{m_1+m_2}$, $m_2\le m_1$, $\mu \in (0, 1/2]$ and we assume that $m_1+m_2=1$. Then the primaries have the following masses: the heavier one $m_1=1-\mu$ and the lighter one $m_2=\mu$, respectively. The circular restricted three-body problem with $\mu =\tfrac{1}{2}$ is called the Copenhagen Problem after the series of papers published by Strömgren and colleagues in the Copenhagen Observatory Publication, see Szebehely and Nacozy (1967), Danby (1967) and references therein.

The problem of the integrability of the circular problem was investigated by many authors using different techniques starting from the famous memoir of Poincaré (1890) in which he proved the non-existence of an additional first integral which is analytic in coordinates, momenta and parameter $\mu$ for small $\mu$. The dynamical reason of the non-integrability is the existence of periodic solutions with nonzero characteristic exponents, which originate from the breaking of periodic invariant tori of the integrable approximations. Poincaré improved and extended his result in Poincaré (1892, Chap. 5) where he started from the restricted planar circular problem, then passed to the unrestricted planar problem, and finally to the unrestricted spatial problem. Ideas and methods presented in these works were interpreted, extended and generalized by many authors. Using the Melnikov method Xia (1992) showed that for small enough $\mu$, there exist transversal homoclinic orbits and this implies the non-existence of any real analytic integral for all but possibly finite number of values of $\mu$. This result was generalized in Guardia et al. (2016) where the occurrence of transverse intersection between the stable and unstable manifolds of the infinity (the notion introduced by authors) for any $\mu \in (0,1)$ was shown. Recently, the non-integrability of this problem was also proved by means of differential Galois approach in Yagasaki (2021).

We know only few papers devoted to study the same question for the elliptic problem. The Arnold diffusion in the circular problem is prevented by KAM tori, but it is possible in the elliptic case, see Féjoz et al. (2016). For example, Xia (1993) proved the presence of the Arnold diffusion. His proof is based on the fact that the transversal homoclinic orbits in the circular restricted three-body problem exist. Capiński et al. (2016) used another approach based on shadowing of pseudo-orbits generated by two dynamics: an ‘outer dynamics’, given by homoclinic trajectories to a normally hyperbolic invariant manifold, and an ‘inner dynamics’, given by the restriction to that manifold. Other diffusive orbits in elliptic restricted three-body problem are described in Bolotin (2006). Along these orbits, the angular momentum changes in a bounded interval while trajectories come close to collisions. In Delshams et al. (2019), authors proved the existence of orbits whose angular momentum performs arbitrary excursions in a large region leading to global instability. In Guardia et al. (2017), Delshams et al. (2019), the existence of oscillatory orbits for the elliptic case and in Llibre and Simó (1980); Guardia et al. (2016) for the circular case, was proved. A trajectory is called oscillatory if it leaves every bounded region but returns infinitely often to some fixed bounded region.

The phenomena mentioned above show that the dynamics of the elliptic restricted three-body system is complex and in fact it is not integrable. All these results have been shown with applications of highly advanced analytical methods.

Our aim is to give a proof of the non-integrability of the planar elliptic restricted three-body problem. We consider two versions of this problem. In the classical version of the problem, only the gravitational interactions are taken into account, while in the photo-gravitational problem also the radiation pressure forces are included. We use methods which till now were not applied to study the integrability of the elliptic restricted problem.

2 Equations of motion

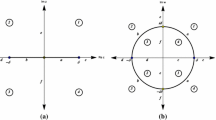
We assume that the considered three masses move in a plane. The primaries with masses $m_1$ and $m_2$ move in Keplerian elliptic orbits around their common mass centre, which is taken as the origin of the inertial barycentric and the rotating reference frames. The x-axis of the rotating frame is directed from the more to the less massive primary. The coordinates are rescaled by the distance between the primaries. In this rotating and pulsating frame, the primaries are located at $P_1=(-\mu , 0)$ and $P_2=(1-\mu , 0)$, respectively, see Fig. 1.

Fig. 1

Geometry of the restricted three-body problem in the rotating and pulsating frame

The motion of the third body with an infinitesimal mass is described by the following equations

$$\begin{aligned} \frac{\textrm{d}^2 q_1}{\textrm{d}\nu ^2}-2\frac{\textrm{d}q_2}{\textrm{d}\nu } = f(e,\nu )\frac{\partial U}{\partial q_1},\qquad \frac{\textrm{d}^2 q_2}{\textrm{d}\nu ^2}+2\frac{\textrm{d}q_1}{\textrm{d}\nu } = f(e,\nu )\frac{\partial U}{\partial q_2}, \end{aligned}$$

(1)

where

$$\begin{aligned} f(e,\nu )=\frac{1}{1+e\cos \nu }, \end{aligned}$$

and the effective potential is

$$\begin{aligned} U=\frac{1}{2}(q_1^2+q_2^2)+\frac{1-\mu }{r_1}+\frac{\mu }{r_2},\quad r_1=\sqrt{(q_1+\mu )^2+q_2^2},\quad r_2=\sqrt{(q_1-1+\mu )^2+q_2^2}. \end{aligned}$$

The independent variable in these equations is the true anomaly $\nu$. For details, see, Szebehely (1967, Sect. 10.3), Gawlik et al. (2009). We fix the units in such a way that $m_1+m_2=1$, the gravitational constant $G=1$, the semi-major axis of the relative orbit of the primaries $a=1$.

As it is well known, the system has five equilibria, called the Lagrange points. In our considerations, we will use only triangular libration point $L_4=\left( \tfrac{1}{2}-\mu ,\tfrac{\sqrt{3}}{2}\right)$. In the inertial frame, this is just an elliptic orbit and its eccentricity and the semi-major axis are the same as the relative orbit of the primaries.

The photo-gravitational elliptic restricted three-body problem is a generalization of the above described system when an infinitesimal mass is affected not only by gravitation but also by radiation pressure from the primaries. We assume that both the primaries are stars radiating a constant amount of the light and the infinitesimal mass is a spherical particle with a uniform albedo. Since the radiation pressure force $F_\textrm{r}$ changes with the distance according to the same inverse square law as the gravity force $F_\textrm{g}$ but with opposite sign, the total force exerted by a primary is $F=F_\textrm{g}-F_\textrm{r}=F_\textrm{g}\left( 1-\beta \right)$, where $\beta = F_\textrm{r}/F_\textrm{g}$ and the effect of the radiation pressure is the same as that of reducing the stellar mass by a term $\beta$, see e.g. Chernikov (1970), Todoran and Roman (1993). The tidal and rotational distortions of the radiating primaries are here neglected. If we introduce $\sigma _i^3=1-\beta _i$, $i=1,2$ for the respective primaries, then the equations of motion of the infinitesimal mass particle are the following

$$\begin{aligned} \begin{aligned}&\frac{\textrm{d}^2 q_1}{\textrm{d}\nu ^2}-2\frac{\textrm{d}q_2}{\textrm{d}\nu } = f(e,\nu )\frac{\partial W}{\partial q_1}, \quad \frac{d^2 q_2}{\textrm{d}\nu ^2}+2\frac{\textrm{d}q_1}{\textrm{d}\nu } = f(e,\nu )\frac{\partial W}{\partial q_2},\\&W=\frac{1}{2}(q_1^2+q_2^2)+\frac{\sigma _1^3(1-\mu )}{r_1}+\frac{\sigma _2^3\mu }{r_2}. \end{aligned} \end{aligned}$$

(2)

The constants are $\sigma _i\in [0,1]$, where $\sigma _i=1$ corresponds the previously described case without radiation, while $\sigma _i=0$ corresponds to the situation when radiation pressure force balances the gravitational force. Also the photo-gravitational problems with only one radiating body are considered as it was in the first article concerning the photo-gravitation restricted three-body problem of Radzievskii (1950), whereas the primaries were considered: the Sun and a planet, and a dust particle as an infinitesimal mass. For a discussion of different versions of this problem see Kunitsyn and Polyakhova (1995).

If $\sigma _1+\sigma _2\ge 1$, then there exist triangular libration points, and, in this case $L_4=(q_1^{0},q_2^{0})$, where

$$\begin{aligned} q_1^{0}=\tfrac{1}{2}\left( 1-2\mu +\sigma _1^{2}- \sigma _2^{2} \right) ,\qquad q_2^{0}=\tfrac{1}{2}\sqrt{4\sigma _1^{2}- \left( 1+\sigma _1^{2}-\sigma _2^{2}\right) ^2}. \end{aligned}$$

Thus, the distances between the primaries and the libration point are

$$\begin{aligned} r_1^0 = \sigma _1, \qquad r_1^0 = \sigma _2, \end{aligned}$$

(3)

so, assumption $\sigma _1+\sigma _2\ge 1$ is just the triangle inequality because the distance between the primaries is 1.

Let us notice that the equations of motion (2) as well as its particular case (1) are Hamiltonian. In fact, they are equivalent to the canonical equations generated by the following Hamiltonian function

$$\begin{aligned} {\mathscr {H}}(\varvec{q},\varvec{p},\nu )=\frac{1}{2} (p_1^2+p_2^2)+p_1q_2 - p_2q_1 + f(e,\nu )\left[ \frac{e}{2}\cos (\nu )(q_1^2+q_2^2) +V(q_1,q_2)\right] , \end{aligned}$$

(4)

where

$$\begin{aligned} V(q_1,q_2) = - \frac{\sigma _1^3(1-\mu )}{r_1}-\frac{\sigma _2^3\mu }{r_2}. \end{aligned}$$

(5)

Let us notice that Hamilton equations governed by (4) have an additional first integral $L=p_1q_2 - p_2q_1$ in the following cases: when either $\mu =0$ or $\mu =1$, i.e. one of the primaries vanish, or when $\sigma _1=\sigma _2=0$, i.e. when radiation pressure forces of both the primaries balance their gravitational interactions. The Hamiltonian system generated by (4) is not autonomous ($\nu$ is the independent variable); however, it is $2\pi$ periodic.

3 Non-integrability theorem

Our aim is to study the integrability of the Hamiltonian system given by (4). At first, we recall some basic facts about the integrability.

An autonomous Hamiltonian system with n degrees of freedom is given by its Hamiltonian function $H(\varvec{q},\varvec{p})$, where $\varvec{q}=(q_1, \ldots , q_n)$ and $\varvec{p}=(p_1, \ldots , p_n)$ are the canonical coordinates and momenta, respectively. A function $F(\varvec{q},\varvec{p})$ is a first integral of this system if it is constant along all solutions of the Hamilton equations

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\varvec{q}= \dfrac{\partial H }{\partial \varvec{p}}(\varvec{q},\varvec{p}), \qquad \frac{\textrm{d}}{\textrm{d}t}\varvec{p}= -\dfrac{\partial H }{\partial \varvec{q}}(\varvec{q},\varvec{p}), \end{aligned}$$

(6)

or equivalently, if $\{H,F\}=0$, where

$$\begin{aligned} \{H,F \}=\sum _{i=1}^{n} \left( \dfrac{\partial H }{\partial q_i}\dfrac{\partial F }{\partial p_i} - \dfrac{\partial H }{\partial p_i}\dfrac{\partial F }{\partial q_i} \right) , \end{aligned}$$

(7)

denotes the Poisson bracket. We say that the system is integrable in the Liouville sense, or that it is completely integrable if it admits n functionally independent first integrals $F_1, \ldots ,F_n$ which pairwise commute, that is, $\{F_i,F_j\}=0$, for $i,j=1,\ldots ,n$. The integrability of the system implies that it is solvable by quadratures. For a detailed exposition, see, Arnold (1989), Arnold et al. (1988).

If the Hamiltonian of the system depends explicitly on time $H=H(\varvec{q},\varvec{p},t)$, then we can introduce an additional canonical pair of variables $(q_{n+1},p_{n+1})$ and Hamiltonian function $K=H(\varvec{q},\varvec{p},p_{n+1}) -q_{n+1}$. Then, the last pair of equations of motion reads,

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}q_{n+1}= \dfrac{\partial H }{\partial t}(\varvec{q},\varvec{p},p_{n+1}), \qquad \frac{\textrm{d}}{\textrm{d}t}p_{n+1}= 1. \end{aligned}$$

(8)

Hence, $p_{n+1}$ is the time. We say that the non-autonomous Hamiltonian system given by Hamiltonian $H(\varvec{q},\varvec{p},t)$ is completely integrable, if the system with $(n+1)$ degrees of freedom given by Hamiltonian $K=H(\varvec{q},\varvec{p},p_{n+1}) -q_{n+1}$ is completely integrable. For a detailed explanation, we refer here to the paper of Kozlov (1983).

In our investigation of the integrability of the elliptic restricted problem, we apply a method which is based on the study of the variational equations of the considered system along a particular solution. The variational equations are Hamiltonian and if the original system is integrable, then the variational system is also integrable. The variational equations are linear, and their integrability puts strong restrictions on the properties of the monodromy and the differential Galois groups which are attached to them. These arguments are just a starting point for the Ziglin and the Morales–Ramis theories, see Morales Ruiz (1999). The fundamental result of this approach is the Morales–Ramis theorem.

Theorem 1

Assume that a complex Hamiltonian system with n degrees of freedom is integrable with complex meromorphic first integrals in the Liouville sense in a neighbourhood of a phase curve $\Gamma$. Then, the identity component of the differential Galois group of the variational equations along $\Gamma$ is Abelian.

For details, see the paper of Morales Ruiz (1999). Although this theorem is based on involved mathematical theory, it appears that it can be effectively applied to study the integrability of a wide variety of systems from dynamical astronomy, physics and other branches of applied sciences. It is enough to mention here the problem of the integrability of the three-body problem which was solved thanks to the application of this theory, see articles Boucher and Weil (2003), Maciejewski and Przybylska (2011), and also Tsygvintsev (2000), Tsygvintsev (2001) where the monodromy group that is a subgroup of the differential Galois group was used. Moreover, it appears that for application of this theorem, there are algorithms accessible for a wide audience. A practical introduction to the subject and numerous applications of the above theorem can be found in Morales-Ruiz and Ramis (2010).

In the above theorem, it is assumed that the Hamiltonian as well as the first integrals which guarantee the integrability are complex meromorphic functions. In the considered case, Hamiltonian (4) is not a meromorphic function because it contains terms with radicals. However, as it was explained in Combot (2013), Maciejewski and Przybylska (2016), still one can apply the Morales–Ramis theory for systems with algebraic potentials.

We formulate our main result in the following two theorems. The first one concerns the classical restricted problem.

Theorem 2

If $\mu \in \left( 0,\tfrac{1}{2}\right]$, and $e\in (0,1)$, then the system given by Hamiltonian (4) with $\sigma _1=\sigma _2=1$, is not completely integrable with first integrals which are meromorphic functions of variables $(q_1,q_2,p_1,p_2,r_1,r_2,\cos (\nu ), \sin (\nu ))$.

The second theorem concerns the photo-gravitational problem.

Theorem 3

If $\mu \in \left( 0,\tfrac{1}{2}\right]$, $e\in (0,1)$, and

$$\begin{aligned} \sigma _1 + \sigma _2>1, \end{aligned}$$

(9)

then the system given by Hamiltonian (4) is not completely integrable with first integrals which are meromorphic functions of the variables $(q_1,q_2,p_1,p_2,r_1,r_2,\cos (\nu ), \sin (\nu ))$.

Notice that in the above theorem, we assume the strict inequality (9), although the triangular libration point $L_4$ exists when $\sigma _1 + \sigma _2=1$. We did not exclude this case accidentally. The reason is that, as we demonstrate it later, for this particular case the necessary conditions are fulfilled. An investigation of the integrability in this case needs stronger tools. Here, we remark only that in the case $\sigma _1 + \sigma _2=1$, the triangular point is, in fact, a collinear one.

The above theorems also prove the non-integrability of the spatial version of the restricted problem as the former is an invariant subsystem of the latter.

In the proof of this theorem, we will use the Morales–Ramis Theorem 1. As a particular solution, we take the triangular libration point $L_4$. This is why, we need the assumption (9).

4 Variational equations

We consider our problem in the extended phase space with coordinates $(q_1,q_2,q_3)$ and the conjugated momenta $(p_1,p_2,p_3)$. We set $\varvec{z}=(\varvec{q},\varvec{p},q_3,p_3)$, where $\varvec{q}=(q_1,q_2)$ and $\varvec{p}=(p_1,p_2)$. In this space, equations of motion of the system are generated by Hamiltonian

$$\begin{aligned} {\mathscr {K}}(\varvec{z})={\mathscr {H}}(\varvec{q},\varvec{p},p_3) - q_3. \end{aligned}$$

(10)

They have the following form

$$\begin{aligned} \begin{aligned} \dot{q}_1&= p_1 + q_2, \qquad \dot{p}_1 = p_2 - f(p_3,e) \left( e q_1 \cos (p_3) +\dfrac{\partial V }{\partial q_1}(q_1,q_2) \right) , \\ \dot{q}_2&= p_2 -q_1, \qquad \dot{p}_2= -p_1 - f(p_3,e) \left( e q_2 \cos (p_3) +\dfrac{\partial V }{\partial q_2}(q_1,q_2) \right) , \\ \dot{q}_3&=-\frac{e}{2}f(p_3,e)^2\sin (\nu ) \left( q_1^2 +q_2^2- 2V(q_1,q_2) \right) , \qquad \dot{p}_3 =1. \end{aligned} \end{aligned}$$

(11)

These equations admit the particular solution

$$\begin{aligned} q_1(\nu )= & {} q_1^0, \quad q_2(\nu )=q_2^0, \quad p_1(\nu ) =-q_2^0, \quad p_2(\nu )=q_1^0, \end{aligned}$$

(12)

$$\begin{aligned} q_3(\nu )= & {} - \frac{1}{2}f(\nu ,e) \left[ (q_1^0)^2 + (q_2^0)^2- 2V(q_1^0,q_2^0) \right] , \quad p_3(\nu )=\nu . \end{aligned}$$

(13)

The variational equations along this solution have the form

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}\nu }\varvec{Z}= \varvec{A}(\nu )\varvec{Z}, \end{aligned}$$

(14)

where

$$\begin{aligned} \varvec{A}(\nu )= & {} \begin{bmatrix} \varvec{J}&{} \varvec{I}&{} \varvec{0}\\ -f(\nu ,e)\left[ e \cos (\nu )\varvec{I}+\varvec{V}\right] &{} \varvec{J}&{} \varvec{0}\\ \varvec{0}&{} \varvec{0}&{} \varvec{D}(\nu ) \end{bmatrix}, \end{aligned}$$

(15)

$$\begin{aligned} \varvec{I}= & {} \begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \end{bmatrix} , \quad \varvec{J}= \begin{bmatrix} 0 &{} 1 \\ -1 &{} 0 \end{bmatrix} , \quad \varvec{D}(\nu )= \begin{bmatrix} 0 &{} d(\nu ) \\ 0 &{} 0 \end{bmatrix} ,\quad \varvec{V}=V''(q_1^0,q_2^0), \end{aligned}$$

(16)

and

$$\begin{aligned} d(\nu )= \frac{e}{4}f(\nu ,e)^3 \Big (-2 \cos (\nu ) + e(\cos (2\nu )-3)\Big ) \Big [ (q_1^0)^2 + (q_2^0)^2- 2V(q_1^0,q_2^0) \Big ] . \end{aligned}$$

(17)

As it is clearly visible, the system (14) splits into two subsystems. The first one, called the normal variational equation, corresponds to the first $4\times 4$ block, the second one, called the tangential equation, is given by the $2\times 2$ block. In our study of the integrability, it is enough to investigate the normal variational equation, that is

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}\nu }\varvec{z}=\varvec{A}_{\textrm{N}}(\nu ) \varvec{z}, \qquad \varvec{A}_{\textrm{N}}(\nu ) = \begin{bmatrix} \varvec{J}&{} \varvec{I}\\ - f(\nu ,e)[e \cos (\nu )\varvec{I}+\varvec{V}] &{} \varvec{J}\end{bmatrix}, \end{aligned}$$

(18)

where $\varvec{z}=[z_1,z_2,z_3,z_4]^T$.

We perform a further simplification of this equation. To this end, we first make a transformation with constant coefficients. Namely, we put $\varvec{x}= \varvec{C}\varvec{z}$, where $\varvec{z}=[z_1,z_2,z_3,z_4]^T$ denotes the original variables, and

$$\begin{aligned} \varvec{C}= \begin{bmatrix} \varvec{R}(\varphi ) &{} \varvec{0}\\ \varvec{R}(\varphi )\varvec{J}&{} \varvec{R}(\varphi ) \end{bmatrix} , \qquad \varvec{R}(\varphi )= \begin{bmatrix} \cos \varphi &{} -\sin \varphi \\ \sin \varphi &{} \cos \varphi \end{bmatrix}, \end{aligned}$$

(19)

where $\varphi$ is a parameter which we will fix later. As a result, we obtain

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}\nu }\varvec{x}=\varvec{B}_{\textrm{N}}(\nu ) \varvec{x}, \quad \varvec{B}_{\textrm{N}}(\nu ) = \varvec{C}\varvec{A}_{\textrm{N}}(\nu )\varvec{C}^{-1} = \begin{bmatrix} \varvec{0}&{} \varvec{I}\\ f(\nu ,e)[\varvec{I}-\widetilde{\varvec{V}}] &{} 2\varvec{J}\end{bmatrix}, \end{aligned}$$

(20)

where $\widetilde{\varvec{V}}= \varvec{R}(\varphi )\varvec{V}\varvec{R}(\varphi )^{-1}$. Because the Hessian matrix $\varvec{V}$ is real and symmetric, one can find a rotation matrix $\varvec{R}(\varphi )$ which transforms it to the diagonal form. Thus, we can assume that the matrix $\varvec{I}-\widetilde{\varvec{V}}$ is diagonal. Direct calculations give

$$\begin{aligned} \varvec{I}-\widetilde{\varvec{V}}={\text {diag}}(c_{+},c_{-}), \qquad c_{\pm }= \frac{3}{2} \left( 1 \pm \delta \right) , \end{aligned}$$

(21)

where

$$\begin{aligned} \delta =\sqrt{1-g}, \quad g=\mu (1-\mu )\left( 4-\tfrac{(\sigma _1^{2}+ \sigma _2^{2}-1)^2}{\sigma _1^{2}\sigma _2^{2}}\right) , \quad \delta \in [0, \infty ). \end{aligned}$$

(22)

For the classical purely gravitational problem, the parameter $\delta$ simplifies to

$$\begin{aligned} \delta =\sqrt{1-3\mu (1-\mu )}, \qquad \delta \in (1/2,1). \end{aligned}$$

(23)

Notice that the case $\delta =0$ is impossible in the purely gravitational problem, and in the photo-gravitational problem, it occurs when $\mu =1/2$ and $\sigma _1^{2}+ \sigma _2^{2}=1$.

In the lemmas below, the value $\delta =1$ is excluded. Again, this case is impossible in the purely gravitational problem. It occurs only when $g=0$. As by assumption $\mu (1-\mu )\ne 0$, according to (22) we have

$$\begin{aligned} 0=\left( 4-\tfrac{(\sigma _1^{2}+\sigma _2^{2}-1)^2}{\sigma _1^{2}\sigma _2^{2}}\right) =\frac{1}{\sigma _1^{2}\sigma _2^{2}} \left( \sigma _1-\sigma _2-1\right) \left( \sigma _1-\sigma _2+1\right) \left( \sigma _1+\sigma _2-1\right) \left( \sigma _1+\sigma _2+1\right) . \end{aligned}$$

Thus, one factor in the above formula vanishes. However, as $\sigma _1,\sigma _2\in (0,1]$, there is only one possibility, namely $\sigma _1+\sigma _2=1$. In this case, $L_4$ coincides with a collinear libration point $L_1$.

The above simplification of the variational equation for the triangular libration points in the elliptic restricted three-body problem is well known, see for example Szebehely (1967, Sect. 10.3) or Grebenikov (1964). For the triangular libration points of the photo-gravitational elliptic restricted three-body problem, it can be found in Markellos et al. (1992).

If we introduce the entries of the Hessian matrix

$$\begin{aligned} \begin{aligned}&\varvec{V}=V''(q_1^0,q_2^0)=\begin{pmatrix} \alpha &{}\beta \\ \beta &{}\gamma \end{pmatrix},\\&\alpha =\tfrac{(1-\mu )\sigma _1^3 \left( (q^0_2)^2 - 2 (q^0_1 + \mu )^2\right) }{(r^0_1)^5}+ \tfrac{\mu \sigma _2^3\left( (q^0_2)^2 - 2 (\mu -1 + q^0_1)^2\right) }{(r^0_2)^5},\quad \beta =\tfrac{3 (\mu -1)\sigma _1^3q^0_2 (q^0_1 + \mu )}{(r^0_1)^5}-\tfrac{3\mu \sigma _2^3 q^0_2 (\mu -1 + q^0_1)}{(r^0_2)^5},\\&\gamma =\tfrac{(\mu -1)\sigma _1^3 (2 (q^0_2)^2 - (q^0_1 + \mu )^2) }{(r^0_1)^5} +\tfrac{\mu \sigma _2^3\left( (q^0_1)^2 - 2 (q^0_2)^2 + 2 q^0_1 (\mu -1) + (\mu -1)^2\right) }{(r^0_2)^5}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} r^0_1=\sqrt{(q^0_1+\mu )^2+(q^0_2)^2},\quad r^0_2=\sqrt{(q^0_1-1+\mu )^2+(q^0_2)^2}, \end{aligned}$$

then the parameter $\varphi$ determining the orthogonal transformation $\varvec{R}(\varphi )$ diagonalizing $\varvec{V}$ can be obtained from the vanishing of off-diagonal elements of the transformed matrix $\widetilde{\varvec{V}}= \varvec{R}(\varphi )\varvec{V}\varvec{R}(\varphi )^{-1}$ which gives

$$\begin{aligned} \varphi =\frac{1}{2}\arctan \left( \frac{2\beta }{\gamma -\alpha }\right) . \end{aligned}$$

(24)

The transformed normal variational equation depends only on two parameters: $e\in (0,1)$ and $\delta \in [0,\infty )$. However, planning an application of the Morales–Ramis theory we need to our disposal tools which allow determining the monodromy and the differential Galois group of this parameter-dependent equations. Unfortunately, for systems of four equations, there are no sufficiently strong results. This is why we will continue a simplification of the equation.

In the sixties of the previous century, the analysis of the stability of libration points was a popular subject, see Danby (1964), Grebenikov (1964), Bennett (1965), Alfriend and Rand (1969), Tschauner (1971), Meire (1981). Just for the needs of these investigations, Tschauner (1971) found a time dependent transformation which splits the systems of four coupled equations into two uncoupled second-order equations. Later Meire (1981), Matas (1982), Matas (1973) continued the study of this problem in more details. All of these results concerns only the classical elliptic restricted problem. At first, we assume that $\delta \ne 0$, and let us introduce the following quantities

$$\begin{aligned} Q(e,\delta )= 9 \delta ^4-8 \delta ^2+e^4+2 \delta ^2 e^2,\qquad \Delta =\sqrt{Q(e,\delta )}, \end{aligned}$$

(25)

and matrices

$$\begin{aligned} \varvec{B}_{\pm }(\nu )= \varvec{B}_0(\nu ) \pm \frac{\Delta }{4\delta }f(\nu ,e)\varvec{J}, \end{aligned}$$

(26)

where

$$\begin{aligned} \small { \varvec{B}_0(\nu ) = \tfrac{f(\nu ,e)}{4\delta } \begin{bmatrix} -2 e \sin (\nu ) (\delta -e \cos (\nu )) &{} -3\delta ^2 +e^2 \cos (2\nu ) \\ -3\delta ^2 +e^2 \cos (2\nu ) &{} -2 e \sin (\nu ) (\delta +e \cos (\nu )) \end{bmatrix} +\varvec{J}. } \end{aligned}$$

(27)

Now, the transformation given by

$$\begin{aligned} \varvec{x}=\varvec{T}(\nu )\varvec{y}, \qquad \varvec{T}(\nu )= \begin{bmatrix} \varvec{I}&{} \varvec{I}\\ \varvec{B}_{+}(\nu ) &{} \varvec{B}_{-}(\nu ) \end{bmatrix}, \end{aligned}$$

(28)

is non-singular if $Q(e,\delta )\ne 0$. In fact,

$$\begin{aligned} \det \varvec{T}(\nu ) =\left[ \frac{f(\nu ,e)}{2\delta }\right] ^2 Q(e,\delta ). \end{aligned}$$

(29)

Using this transformation, we obtain

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}\nu }\varvec{y}=\varvec{B}(\nu )\varvec{y}, \end{aligned}$$

(30)

where

$$\begin{aligned} \varvec{B}(\nu )= \varvec{T}(\nu )^{-1} \left( \varvec{B}_\textrm{N}(\nu ) \varvec{T}(\nu ) - \varvec{T}'(\nu ) \right) = \begin{bmatrix} \varvec{B}_{+}(\nu ) &{} \varvec{0}\\ \varvec{0}&{} \varvec{B}_{-}(\nu ) \end{bmatrix}. \end{aligned}$$

(31)

The above transformation is just a simple generalization of the transformation given by Tschauner (1971), see also Markellos et al. (1993).

Fig. 2

Curve $Q(e,\delta )=0$ (solid line) and curve $\eta _-(e,\delta )=0$ (dashed line) with crossing points denoted by dots

The values of the parameters that lie on the curve $Q(e,\delta )=0$, see solid line curve in Fig. 2, are excluded in the above considerations. However, we cannot exclude them from the study of the integrability. We did not find any investigation of this particular case. The question if the variational equations split in these cases was unknown. This is why we decided to investigate it with the help of differential algebra tools, see Compoint and Weil (2004). Omitting the details, the result is the following.

Assume that $Q(e,\delta )=0$, and set

$$\begin{aligned} \varvec{S}(\nu ) = \begin{bmatrix} \varvec{0}&{} \dfrac{1}{2 \delta (1 + 3 e \cos \nu )}\varvec{U}(\nu ) \\ \frac{1}{2}f(\nu ,e)\varvec{J}&{} \varvec{I}\end{bmatrix}, \end{aligned}$$

(32)

where

$$\begin{aligned} \varvec{U}(\nu ) = \begin{bmatrix} -2 e \sin (\nu ) (\delta +e \cos (\nu )) &{} \delta (3 \delta -4 e \cos (\nu )-4)-e^2 \cos (2 \nu ) \\ \delta (3 \delta +4 e \cos (\nu )+4)-e^2 \cos (2 \nu ) &{} 2 e \sin (\nu ) (e \cos (\nu )-\delta ) \end{bmatrix}.\nonumber \\ \end{aligned}$$

(33)

The matrix $\varvec{S}(\nu )$ is invertible because

$$\begin{aligned} \det \varvec{S}(\nu )= \frac{1}{2 +2e\cos \nu (4+3e\cos \nu )}. \end{aligned}$$

Then, the change of variables $\varvec{y}=\varvec{S}(\nu )\varvec{x}$ transforms equation (20) to equation (30) with a block triangular form of the matrix $\varvec{B}(\nu )$

$$\begin{aligned} \varvec{B}(\nu )= \varvec{S}(\nu )^{-1}(\varvec{B}_\textrm{N}\varvec{S}(\nu )-\varvec{S}'(\nu ))= \begin{bmatrix} \varvec{B}_0 (\nu ) &{} \varvec{0}\\ \varvec{B}_{21}(\nu ) &{} \varvec{B}_{22}(\nu ) \end{bmatrix}, \end{aligned}$$

(34)

where $\varvec{B}_0 (\nu )$ is given by (27) and the explicit forms of the matrices $\varvec{B}_{21}(\nu )$ and $\varvec{B}_{22}(\nu )$ will not be used later. Notice that if $Q(e,\delta )=0$, then $\varvec{B}_0(\nu )=\varvec{B}_+ (\nu )= \varvec{B}_- (\nu )$.

Finally, we consider the particular case when $\delta =0$, or equivalently, case $g=1$, see (22). The maximal value of the function, $g=g(\mu ,\sigma _1, \sigma _2)$ in the considered domain of parameters, is one. Clearly, it is achieved for $\mu =1/2$, as the first term $\mu (1-\mu )$ of g is positive and has the maximum 1/4 at $\mu =1/2$. As it is easy to verify, the second term $\widetilde{g}=4-\tfrac{(\sigma _1^{2}+ \sigma _2^{2}-1)^2}{\sigma _1^{2}\sigma _2^{2}}$ of g, see (22), achieves its maximum value 4 along the curve $\sigma _1^{2}+\sigma _2^{2}-1=0$. This curve is contained in the domain where the libration point $L_4$ exists denoted by a grey region, see Fig. 3.

Fig. 3

The curve of admissible values of $\sigma _1$ and $\sigma _2$ denoted by a thick line corresponding to $\delta =0$

For this particular case, matrix $\varvec{V}$ is diagonal and the matrix of normal variational equations given in (20) simplifies to

$$\begin{aligned} \varvec{B}_{\textrm{N}}(\nu )=\begin{bmatrix} 0 &{} 1 &{} 1 &{} 0 \\ -1 &{} 0 &{} 0 &{} 1 \\ \frac{3}{2+2 e \cos \nu }-1 &{} 0 &{} 0 &{} 1 \\ 0 &{} \frac{3}{2+2 e \cos \nu }-1 &{} -1 &{} 0 \end{bmatrix}. \end{aligned}$$

(35)

Now, the change of variables $\varvec{y}=\varvec{T}(\nu )\varvec{x}$ with the constant matrix

$$\begin{aligned} \varvec{T}(\nu )=\begin{bmatrix} 0 &{} 0 &{} -1 &{} \textrm{i}\\ \textrm{i}&{} 1 &{} 0 &{} 0 \\ \textrm{i}&{} -1 &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} -\textrm{i}\end{bmatrix}, \end{aligned}$$

(36)

transforms the system (20) into (30) where the block diagonal matrix $\varvec{B}(\nu )$ given by (31) has the following blocks

$$\begin{aligned} \varvec{B}_{+}(\nu )=\begin{bmatrix} \textrm{i}&{} \tfrac{3 i}{2+2 e \cos \nu }-\textrm{i}\\ -\textrm{i}&{} \textrm{i}\end{bmatrix},\,\, \varvec{B}_{-}(\nu )=\begin{bmatrix} -\textrm{i}&{} -\textrm{i}\\ \tfrac{3 i}{2+2 e \cos \nu }- \textrm{i}&{}-\textrm{i}\end{bmatrix}. \end{aligned}$$

(37)

5 Non-integrability

In this section, we outline the proof of Theorem 3. By Theorem 1, if the system is integrable, then the identity component of the differential Galois group of variational equations (14) is commutative. We also say that the differential Galois group is virtually commutative.

Anyway, our plan is to show that this group is not virtually commutative. The important fact is that if the differential Galois group of a system is virtually commutative, then the differential Galois group of each of its subsystem is also virtually commutative. From this fact, it follows that it is enough to investigate the normal variational equation (18) which after simple change of variable has a particularly simple form (20).

As we showed in the previous section, a further simplification is possible. Namely, after transformation (28), the system has a block diagonal form (30). Hence, it is enough to investigate a subsystem corresponding to one of these blocks. We choose

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}\nu }\varvec{y}= \varvec{B}_+(\nu )\varvec{y}, \qquad \varvec{y}=[y_1,y_2]^T. \end{aligned}$$

(38)

Elements of matrix $\varvec{B}_+(\nu )$ are periodic functions of $\nu$. Algorithms which we are going to apply assume that the coefficients of the considered system are rational functions of the independent variable. This is why we introduce the new independent variable $z=\textrm{e}^{\textrm{i}\nu }$. After this transformation, we obtain

$$\begin{aligned} \frac{\textrm{d}}{ \textrm{d}z}\varvec{y}= \varvec{C}_+(z)\varvec{y}, \qquad \varvec{C}_+(z)=-\textrm{i}z \varvec{B}_+(-\textrm{i}\ln z). \end{aligned}$$

(39)

As

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}\nu }= \textrm{i}z\frac{\textrm{d}}{ \textrm{d}z}, \qquad \sin \nu =\frac{1}{2\textrm{i}} \left( z -\frac{1}{z}\right) , \qquad \cos \nu =\frac{1}{2} \left( z +\frac{1}{z}\right) , \end{aligned}$$

(40)

matrix $\varvec{C}_+(z)$ is rational as required. Now we can claim the following.

Lemma 4

If $e\in (0,1)$, $\delta \in (0,\infty )\setminus \{1\}$ and $Q(e,\delta )\ne 0$, then the differential Galois group of equation (39) is not virtually commutative.

The proof of this lemma is given in “Appendix A”. In this way, we proved our Theorem 3 except the cases when $Q(e,\delta )= 0$.

Let us assume now that $Q(e,\delta )= 0$. Then, as we have shown in the previous section, the variational equations can be transformed to the block-triangular form (34). Hence, for further considerations, we take the subsystem corresponding to the block $\varvec{B}_0(\nu )$, see (27), and we make the same change of independent variable as in the previous case. In effect, we obtain the following system

$$\begin{aligned} \frac{\textrm{d}}{ \textrm{d}z}\varvec{y}= \varvec{C}_0(z)\varvec{y}, \qquad \varvec{C}_0(z)=-\textrm{i}z \varvec{B}_0(-\textrm{i}\ln z). \end{aligned}$$

(41)

Elements of the matrix $\varvec{C}_0(z)$ are rational functions of z. The final step of our reasoning is the following lemma.

Lemma 5

If $e\in (0,1)$, $\delta \in (0,\infty )\setminus \{1\}$ and $Q(e,\delta )=0$, then the differential Galois group of equation (39) is not virtually commutative.

We prove this lemma in “Appendix A”.

Finally, we consider the particular case excluded in the previous lemmas when $\delta =0$. Then, the variational equations can be also transformed to the block-triangular form (34) with blocks $\varvec{B}_+,\varvec{B}_-$ given in (37). In the next step, we rationalize the subsystem corresponding to $\varvec{B}_+$ defining matrix of linear system with rational coefficients $\varvec{C}_+(z)$ according to (39). Analysis of the differential Galois group of these linear differential equations gives the last lemma.

Lemma 6

If $e\in (0,1)$ and $\delta =0$, then the differential Galois group of equation (39) is not virtually commutative.

The proof of this lemma is also contained in “Appendix A”.

In effect, we have shown that for all assumed values of the parameters the differential Galois group of a subsystem of the variational equations is not virtually commutative, so the differential Galois group of the variational equations is not virtually commutative. Hence, by the Morales–Ramis Theorem 1, the system is not integrable.

6 Conclusions

In this paper, we have presented the non-integrability proof of the elliptic restricted three-body problem for arbitrary nonzero eccentricity $e\in (0,1)$ and arbitrary ratio of masses of the primaries $\mu \in \left( 0,\tfrac{1}{2}\right]$. Analysis was made for the classical case when only gravitational influence of the primaries on the test particle is considered and also for the photo-gravitational version when also the radiation pressure from the primaries is included. This generalization introduces two additional parameters which measure the strength of the radiation forces from two primaries. We prove the non-integrability of this problem for all allowable values of parameters such that the triangular libration point exists.

The proof uses properties of the differential Galois group of four dimensional variational equations along a particular solution determined by the triangular libration point $L_4$. When checking the differential Galois group of variational equations, their factorization into two 2D subsystems turned out to be very useful.

The fact that we succeeded to prove the non-integrability of the photo-gravitational problem for a whole domain of four parameters is in some sense exceptional. Typically, for certain values of parameters, the necessary conditions are fulfilled. We showed that the variational equations for both, classical and photo-gravitational problem, depend only on two parameters e and $\delta$, and this is why the complete integrability analysis was performed for both versions simultaneously.

We show that the method used for proving the non-integrability when applied to study the considered system reduces to a quite simple algorithm which can be applied for other problems.

Appendices

Appendix A: Proofs

Here, we present the proofs of Lemmas 4, 5 and 6 . All of them are just direct applications of Lemma 7 which we formulated in “Appendix B”. This Lemma, follows from the Kovacic algorithm (Kovacic 1986). It is described in many places, see, for example Morales-Ruiz (1989), Duval and Loday-Richaud (1989). So here we only recall that this algorithm gives definitive answer when a second-order differential equation with rational coefficient

$$\begin{aligned} w''+p(z)w'(z)+q(z)w=0, \qquad p(z), q(z)\in \mathbb {C}(z), \end{aligned}$$

(A.1)

is solvable in terms of Liouvillian functions. If it gives the negative answer, then the differential Galois group of this equation is not virtually commutative. This is why it is used frequently in cases when for the integrability studies of a system the Morales–Ramis Theorem 1 is applied.

Before we pass to the proofs, we recall that a system of two linear equations

$$\begin{aligned} y_1'= a_{11}(z) y_1 + a_{12}(z) y_2, \qquad y_2'= a_{21}(z) y_1 + a_{22}(z) y_2, \end{aligned}$$

(A.2)

can be transformed into a second-order differential equation of the form (A.1). This transformation is not unique. In general, we take a linear combination $w = \alpha _1 y_1 + \alpha _2 y_2$ with constant coefficients $\alpha _1$ and $\alpha _1$. Then, we calculate $w'$, and using it together with (A.2) we can express $w''$ in terms of w and $w'$. This procedure works for a ‘generic’ choice of $(\alpha _1,\alpha _2)$ and different choices of these constants give different coefficients p(z) and q(z).

1.1 A.1. Proof of Lemmas 4 and 5

First, we transform system (39) to the second-order equation. We put $w = y_1 + \textrm{i}y_2$. Using the above described procedure, we obtain an equation of the form (A.1) with

$$\begin{aligned} \begin{aligned} p(z)&=\frac{1}{z}\left( 1 + \frac{2 e^2}{e^2 -3 \delta ^2 z^2}\right) , \\ q(x)&= 3\frac{e^2+\delta ^2 e z \left( z^2+3\right) +\delta z^2 (\delta +\Delta )}{z \left( e z^2+e+2 z\right) \left( e^2 -3 \delta ^2 z^2\right) }. \end{aligned} \end{aligned}$$

(A.3)

In order to apply Lemma 7, we transform this equation to the reduced form

$$\begin{aligned} v'' = r(z) v, \qquad r(z) =\frac{1}{2}p'(z) + \frac{1}{4}p(z)^2 -q(z), \end{aligned}$$

(A.4)

by setting

$$\begin{aligned} w = v \exp \left[ -\frac{1}{2} \int ^z_{z_0} p(s)\, ds \right] . \end{aligned}$$

(A.5)

Rational function r(z) reads

$$\begin{aligned} r(z)=\frac{3}{4}\frac{ P(z)}{z^2\left( e z^2+e+2 z\right) \left( e^2 -3 \delta ^2 z^2\right) ^2}, \end{aligned}$$

(A.6)

where P(z) is a polynomial of degree six

$$\begin{aligned} P(z)= & {} \sum _{i=0}^6 a_i z^i, \,\,\, a_0=e^5,\,\, a_1=-2 e^4, \,\, a_2=e^3 \left( e^2-2 \delta ^2\right) , \end{aligned}$$

(A.7)

$$\begin{aligned} a_3= & {} 4 \delta e^2 (7 \delta -\Delta ),\quad a_4=3 \delta ^2 e \left( 11 \delta ^2+2 e^2\right) ,\quad a_5=6 \delta ^3 (\delta +2 \Delta ), \quad a_6=9 \delta ^4 e. \nonumber \\ \end{aligned}$$

(A.8)

Singular points of equation (A.6) are zeros of the denominator of the function r(z) and the infinity. Thus, the equation has six singular points

$$\begin{aligned} z_0= 0, \quad z_{1,2}=\pm \frac{e}{\sqrt{3}\delta }, \quad z_{3,4}=-\frac{1}{e} \left( 1\pm \sqrt{1-e^2}\right) , \quad z_{\infty }=\infty . \end{aligned}$$

(A.9)

At first, we assume that they are pairwise different. That is, that the discriminant $\textrm{disc}(d(z))$ of the polynomial

$$\begin{aligned} d(z)=z\left( e z^2+e+2 z\right) \left( e^2 -3 \delta ^2 z^2\right) , \end{aligned}$$

does not vanish. Direct calculations give

$$\begin{aligned} \textrm{disc}(d(z))=-48 \delta ^2 e^6 \left( e^2-1\right) \left( 9 \delta ^4-12 \delta ^2+e^4+6 \delta ^2 e^2\right) ^2. \end{aligned}$$

As $e, \delta \in (0,1)$, this discriminant vanishes if the polynomial

$$\begin{aligned} \eta (e,\delta )=\left( e^2 +3\delta ^2\right) ^2 - 12 \delta ^2 \end{aligned}$$

(A.10)

vanishes. Hence, at first we assume that $\eta (e,\delta )\ne 0$. Even under this assumption, it can happen that for certain values of parameters, the numerator and the denominator of r(z) are not relatively prime. Then, the order of singular points can depend on parameters. To check this, we have to calculate the resultant of the numerator and denominator of r(z). If they have a common factor, then the resultant vanishes. It appears that for the assumed values of the parameters, it vanishes only along the curve $\eta (e,\delta )=0$. A justification of this fact is direct, but rather long, so we omit it.

The function r(z) has the following expansion at singular points

$$\begin{aligned} r(z) = \frac{\alpha _i}{ (z -z_i)^2 } + {\mathscr {O}}((z-z_i)^{-1}), \end{aligned}$$

(A.11)

where

$$\begin{aligned} \alpha _0=\alpha _1=\alpha _2=\frac{3}{4},\qquad \alpha _3=\alpha _4=0. \end{aligned}$$

Moreover, its expansion at infinity reads

$$\begin{aligned} r(z) = \frac{3}{4z^2} +{\mathscr {O}}(z^{-3}). \end{aligned}$$

Hence, all singularities of equation (A.6) are regular. The differences of exponents $\Delta _i$ at the respective singularities are

$$\begin{aligned} \Delta _0=\Delta _1=\Delta _2=\Delta _{\infty }=2,\quad \Delta _3=\Delta _4=1. \end{aligned}$$

Thus, it is possible that the logarithmic terms are present in local solutions near a singularity, see explanations above equation (B.7) in “Appendix B”. In fact, such a term can be found for a solution near $z=0$. One local solution corresponding to the exponent $\rho ^+=3/2$ has the form

$$\begin{aligned} w_{+}(z)=z^{3/2}f(z),\qquad f(z)=1+\sum _{i=1}^{\infty }f_i^{+} z^i. \end{aligned}$$

(A.12)

One can find easily that

$$\begin{aligned} f_1^+= -\frac{1}{e} , \qquad f_2^+ = 3\frac{\delta ^2+3}{8e^2}, \end{aligned}$$

so, according to formula (B.8), the coefficient $g_2$ multiplying the logarithmic term in local solution is

$$\begin{aligned} g_2 = -3\frac{\delta ^2-1}{4e^2}. \end{aligned}$$

As $\delta \in (0,\infty )\setminus \{1\}$, $g_2\ne 0$ and the logarithmic term is always present.

Now, we show that equation (A.4) does not admit a nonzero hyperexponential solution. For the definition of this notion and its calculations, see “Appendix B” starting from the paragraph above Lemma 7. According to equation (B.9), we have to select all possible choices of exponents $\varvec{\varepsilon }=(\varepsilon _0, \ldots ,\varepsilon _4,\varepsilon _\infty )$ such that

$$\begin{aligned} n= \varepsilon _\infty - (\varepsilon _0+ \varepsilon _1+\varepsilon _2+\varepsilon _3+\varepsilon _4) \end{aligned}$$

is a non-negative integer. Because $z_3$ and $z_4$ are poles of the first order, then $\varepsilon _3=\varepsilon _4=1$, see “Appendix B”. For the remaining singular points we have

$$\begin{aligned} \varepsilon _0, \varepsilon _1,\varepsilon _2,\varepsilon _\infty \in \left\{ -\frac{1}{2}, \frac{3}{2}\right\} . \end{aligned}$$

In effect there is only one choice

$$\begin{aligned} \varvec{\varepsilon }= \left( -\frac{1}{2}, -\frac{1}{2}, -\frac{1}{2}, 1,1, \frac{3}{2} \right) , \end{aligned}$$

(A.13)

which gives $n=1$, and the corresponding function $\omega (z)$ defined in (B.9) is

$$\begin{aligned} \omega (z)=-\frac{1}{2} \left( \frac{1}{z} + \frac{1}{z-z_1}+ \frac{1}{z-z_2}\right) +\frac{1}{z-z_3}+\frac{1}{z-z_4}. \end{aligned}$$

Inserting the polynomial $P(z)=z +p_0$ into equation (B.11), we obtain a system of three algebraic equations for $(p_0,e, \delta )$ which has a solution only when either $e=0$ or $\delta =\pm 1$. These values of parameters are excluded, thus there is no polynomial P(z) of degree one which satisfies equation (B.11). In effect, Eq. (A.4) does not admit a hyperexponential solution, and its differential Galois group is not virtually commutative.

The above conclusion is valid under the assumptions that $\eta (e,\delta )\ne 0$, see (A.10). Polynomial $\eta (e,\delta )$ factorizes as

$$\begin{aligned} \eta (e, \delta )=\eta _+(e,\delta )\eta _-(e,\delta ), \qquad \eta _\pm (e, \delta )= e^2 +3\delta ^2 \pm 2\sqrt{3}\delta . \end{aligned}$$

(A.14)

The curve $\eta _+(e,\delta )=0$ does not have a real component, so it is enough to investigate the curve $\eta _-(e,\delta )=0$, see dashed curve in Fig. 2. This curve admits the following rational parametrization

$$\begin{aligned} e = \frac{2s}{1+s^2}, \qquad \delta = \frac{2\sqrt{3}s^2}{3(1+s^2)}. \end{aligned}$$

As we restricted values of $\delta$ to interval $(0,\infty )\setminus \{1\}$, the range of s is $(0,\infty )\setminus \left\{ \sqrt{3 +2\sqrt{3}}\right\}$. With this parametrization the differential equation (A.4) has five singular points

$$\begin{aligned} z_0=0, \qquad z_{1}=- \frac{1}{s}, \qquad z_{2}=+ \frac{1}{s}, \qquad z_3= -s, \qquad z_\infty =\infty . \end{aligned}$$

(A.15)

At point $z=z_3$ the function r(z) has a pole of order one. The differences of exponents $\Delta _i$ at the respective singularities are

$$\begin{aligned} \Delta _0=\Delta _2=\Delta _{\infty }=2,\qquad \Delta _1= \sqrt{2(1 +\textrm{sign}(s^2-1))}, \qquad \Delta _3=1. \end{aligned}$$

(A.16)

If $s<1$, then $\Delta _1=0$, and the logarithmic term always appears in local solutions near $z=z_1$. We show that such term appear for $s>1$ in local solutions near $z=0$. One local solution near this point is

$$\begin{aligned} w_+(z)= z^{3/2} \left( 1 +f_1^+z + f_2^+z^2+\cdots \right) , \end{aligned}$$

(A.17)

where

$$\begin{aligned} f_1^+=-\frac{1}{2}\left( s+\frac{1}{s}\right) , \qquad f_2^+= \frac{13 s^{4}+18 s^{2}+9}{32 s^{2}}. \end{aligned}$$

(A.18)

Hence, by formulae (B.8), we get

$$\begin{aligned} g_2= \frac{-s^{4}+6 s^{2}+3}{16 s^{2}}. \end{aligned}$$

(A.19)

Equation $g_2=0$ has only one positive root $s=\sqrt{3+2\sqrt{3}}$ corresponding to the excluded value $\delta =1$. Thus, $g_2\ne 0$ for $s\in (0,\infty )\setminus \left\{ \sqrt{3 +2\sqrt{3}}\right\}$, and the logarithmic term in the local solutions is present.

Let $s<1$. We show that Eq. (A.4) does not admit a hyperexponential solution. There are four choices of exponents

$$\begin{aligned} \varvec{\varepsilon }= (\varepsilon _0,\varepsilon _1, \varepsilon _2, \varepsilon _3,\varepsilon _\infty ) =\left( -\frac{1}{2}, +\frac{1}{2}, -\frac{1}{2}, 1, \frac{3}{2} \right) \end{aligned}$$

such that

$$\begin{aligned} n=\varepsilon _\infty -(\varepsilon _0+\varepsilon _1+\varepsilon _2, +\varepsilon _3), \end{aligned}$$

is a non-negative integer, and here $n=1$. The function $\omega (z)$ now is

$$\begin{aligned} \omega (z) = -\frac{1}{2} \left( \frac{1}{z} - \frac{1}{z-z_1} +\frac{1}{z-z_2}\right) +\frac{1}{z-z_3}. \end{aligned}$$

With this $\omega (z)$, the polynomial $P(z)=z+p_0$ is not a solution of Eq. (B.11) with $s\in \left( 0,\sqrt{3+2\sqrt{3}}\right)$ for any $p_0$.

If $s>1$, then there are four choices of the exponents

$$\begin{aligned} \begin{aligned}&\varvec{\varepsilon }^{(1)}= (\varepsilon _0,\varepsilon _1, \varepsilon _2, ,\varepsilon _3,\varepsilon _\infty ) =\left( -\frac{1}{2}, -\frac{1}{2}, -\frac{1}{2}, 1, \frac{3}{2}, \right) ,\\&\varvec{\varepsilon }^{(2)}= (\varepsilon _0,\varepsilon _1, \varepsilon _2, ,\varepsilon _3,\varepsilon _\infty ) =\left( \frac{3}{2}, -\frac{1}{2}, -\frac{1}{2}, 1, \frac{3}{2}, \right) ,\\&\varvec{\varepsilon }^{(3)}= (\varepsilon _0,\varepsilon _1, \varepsilon _2, ,\varepsilon _3,\varepsilon _\infty ) =\left( -\frac{1}{2}, \frac{3}{2}, -\frac{1}{2}, 1, \frac{3}{2}, \right) ,\\&\varvec{\varepsilon }^{(4)}= (\varepsilon _0,\varepsilon _1, \varepsilon _2, ,\varepsilon _3,\varepsilon _\infty ) =\left( -\frac{1}{2}, -\frac{1}{2}, \frac{3}{2}, 1, \frac{3}{2}, \right) , \end{aligned} \end{aligned}$$

for that Eq. (A.4) can have a hyperexponential solution. For the first choice $n=2$ as the degree of polynomial P(z). Function $\omega (z)$ is now

$$\begin{aligned} \omega ^{(1)}(z) = -\frac{1}{2} \left( \frac{1}{z} + \frac{1}{z-z_1} + \frac{1}{z-z_2}\right) +\frac{1}{z-z_3}. \end{aligned}$$

Inserting now $P(z)=z^2 + p_1 z + p_0$ into Eq. (B.11), we obtain a system of five polynomial equations in $(p_0,p_1,s)$ which does not have any solution.

The remaining three choices correspond to $n=0$ and without loss of the generality one can take $P(z)=1$ and the corresponding functions $\omega (z)$ are

$$\begin{aligned} \begin{aligned}&\omega ^{(2)}(z) = \frac{3}{2z} -\frac{1}{2} \left( \frac{1}{z-z_1} +\frac{1}{z-z_2}\right) +\frac{1}{z-z_3},\\&\omega ^{(3)}(z) = \frac{3}{2}\frac{1}{z-z_1} -\frac{1}{2} \left( \frac{1}{z} +\frac{1}{z-z_2}\right) +\frac{1}{z-z_3},\\&\omega ^{(4)}(z) = \frac{3}{2}\frac{1}{z-z_2} -\frac{1}{2} \left( \frac{1}{z} +\frac{1}{z-z_1}\right) +\frac{1}{z-z_3}. \end{aligned} \end{aligned}$$

In all these cases, substitution to Eq. (B.11) gives an overdetermined system for s which does not have a solution. So, in this case the equation does not admit hyperexponential solution, and the differential Galois group of the equation is not virtually commutative. This ends the proof of Lemma 4.

Let us note that in the above proof, we did not use the assumption that $Q(e,\delta )\ne 0$. The only unchecked possibility is that curves $Q(e,\delta )= 0$ and $\eta (e,\delta )= 0$ intersect. But if it is so, then also $\eta (e,\delta )-Q(e,\delta )=4\delta ^2(e^2-1)=0$ and this holds only for $\delta =0$ or $e=1$. However, these values are excluded by assumption. In effect, the Lemma 5 is also proved.

Figure 2 shows the curve $Q(e,\delta )= 0$ plotted with solid line and the curve $\eta _{-}(e,\delta )=0$ represented by a dashed line. These curves intersect only at two points $(e,\delta )=(0,0)$ and $(e,\delta )=\left( 1,\tfrac{\sqrt{3}}{3}\right)$ excluded by assumptions from this analysis.

1.2 A.2. Proof of Lemma 6

Finally, we consider the case when $\delta =0$, thus we consider the variational equations (39) defined by the matrix $\varvec{B}_{+}(\nu )$ given in (37). Then, the second-order equation for the variable $w = y_2$ takes the form (A.1) with rational coefficients

$$\begin{aligned} p(z)=-\frac{1}{z},\quad q(z)=\frac{3}{z(e z^2+2 z+e)} \end{aligned}$$

(A.20)

and the reduced form (A.4) of this equation has coefficient

$$\begin{aligned} r(z)=\frac{3}{4 z^2}-\frac{3}{z (e z^2 + 2 z+e)}. \end{aligned}$$

(A.21)

The condition for coalescence of singularities is $e(e^2-1)=0$, thus by assumptions we always have four singularities: one pole of the second-order $z_0=0$, two poles of the first-order $z_{1,2}=\tfrac{-1\pm \sqrt{1-e^2}}{e}$ and the infinity $z_{\infty }=\infty$ with the local expansion of r(z)

$$\begin{aligned} r(z) = \frac{3}{4z^2} +{\mathscr {O}}(z^{-3}). \end{aligned}$$

(A.22)

Taking into account (A.21) and (A.22), the coefficients $\alpha _i$ of the expansions of r(z) at singularities defined in (A.11) and differences of exponents are respectively

$$\begin{aligned} \begin{aligned}&\alpha _0=\alpha _{\infty }=\frac{3}{4},\qquad \alpha _1=\alpha _2=0,\\&\Delta _0=\Delta _{\infty }=2,\qquad \Delta _1=\Delta _2=1. \end{aligned} \end{aligned}$$

Then, we check whether in local solutions near $z_0$ which have the form (A.12), the logarithmic terms are present. Coefficients $f_1^+$ and $f_2^+$ are

$$\begin{aligned} f_1^+= -\frac{1}{e} , \qquad f_2^+ = \frac{9}{8e^2}, \end{aligned}$$

and according to formula (B.8), the multiplier $g_2$ of the logarithmic term in the local solution is

$$\begin{aligned} g_2 = \frac{3}{4e^2}. \end{aligned}$$

It means that $g_2\ne 0$ and the logarithmic term in the local solutions is always present. Now we check whether equation (A.4) admits a nonzero hyperexponential solution. We have only one choice of $\varvec{\varepsilon }=(\varepsilon _0, \varepsilon _1 ,\varepsilon _2,\varepsilon _\infty )$ such that

$$\begin{aligned} n= \varepsilon _\infty - (\varepsilon _0+ \varepsilon _1+\varepsilon _2), \end{aligned}$$

is a non-negative integer. For poles of the first-order, $\varepsilon _1= \varepsilon _2=1$ and the remaining exponents belong to the set

$$\begin{aligned} \varepsilon _0,\varepsilon _\infty \in \left\{ -\frac{1}{2}, \frac{3}{2}\right\} . \end{aligned}$$

This gives only one choice

$$\begin{aligned} \varvec{\varepsilon }= \left( -\frac{1}{2}, 1,1, \frac{3}{2} \right) , \end{aligned}$$

with $n=0$ and

$$\begin{aligned} \omega (z)=-\frac{1}{2z}+ \frac{1}{z-z_1}+ \frac{1}{z-z_2}. \end{aligned}$$

Without loss of generality, we can take $P(z)=1$ and substitution into Eq. (B.11) gives contradiction $1\ne 0$. Thus, also in this case, a subset of normal variational equations does not have a hyperexponential solution and its differential Galois group is full $\textrm{SL}(2,\mathbb {C})$ which gives the statement of Lemma 6.

Appendix B: Second-order differential equations

We recall basic notions and facts concerning linear second-order differential equations limited to the needs of this paper. This topic is clearly presented in concise Chapter X of book (Whittaker and Watson 1935).

Consider the second-order linear differential equation in reduced form with rational coefficient

$$\begin{aligned} w'' =r(z)w,\qquad r(z)\in \mathbb {C}(z). \end{aligned}$$

(B.1)

A point $z=c\in \mathbb {C}$ is a singular point of this equation if it is a pole of r(z). It is a regular singular point if it is a pole of order not higher than two. The infinity is a regular singular point if function $z^{-2}r(z^{-1})$ has a pole $z=0$ of order not higher than two. We assume that all singularities of the considered equation are regular. Such an equation is called Fuchsian.

Then, the function r(z) has the following expansions: at a singular point $c\in \mathbb {C}$

$$\begin{aligned} r(z)=\frac{\alpha _c}{(z-c)^2} + {\mathscr {O}}\left( (z-c)^{-1}\right) , \end{aligned}$$

(B.2)

and in infinity

$$\begin{aligned} r(z)=\frac{\alpha _\infty }{z^2} + {\mathscr {O}}\left( z^{-3}\right) . \end{aligned}$$

(B.3)

Near each singular point c Eq. (B.1) has two linearly independent solutions of the form

$$\begin{aligned} w_{\pm }(z)=(z-c)^{\rho _\pm }f(z),\qquad f(z)=1+\sum _{i=1}^{\infty }f_i^{\pm } (z-c)^i, \end{aligned}$$

(B.4)

where $\rho _\pm$ are solutions of the so-called indicial equation

$$\begin{aligned} \rho (\rho -1) -\alpha _c = 0, \end{aligned}$$

(B.5)

that is

$$\begin{aligned} \rho _\pm =\frac{1}{2}\left( 1 \pm \sqrt{1+4\alpha _c}\right) . \end{aligned}$$

(B.6)

They are called exponents of Eq. (B.1) at singularity c. Then, substituting expansion (B.4) into Eq. (B.1), we can successively determine coefficients $f_i^{\pm }$ for $i=1,2, \dots$.

This statement is valid under the assumption that the difference of exponents $\Delta _c=\rho _+-\rho _-= \sqrt{1+4\alpha _c}$ is not an integer. If $s=\Delta _c$ is a non-negative integer, then the solution $w_+(z)$ has the prescribed form (B.4). But the second solution $w_-(z)$ has to be determined by the variation of constants method. It has the form

$$\begin{aligned} w(z)= g_s w_+(z)\ln (z-c)+(z-c)^{\rho _-} h(z), \end{aligned}$$

(B.7)

where function h(z) is holomorphic at $z=c$. Constant coefficient $g_s$ can be determined using the method described in Whittaker and Watson (1935) and the explicit formula is given in Maciejewski et al. (2013). For small s, they are

$$\begin{aligned} g_0=1, \qquad g_1= 2f_1^+, \qquad g_2= -2f_2^+ + 3(f_1^+)^2. \end{aligned}$$

(B.8)

If for a given singularity logarithmic terms are present in a local solution, then we say that this singularity is logarithmic.

Differential Galois group of Eq. (B.1) is a subgroup of $\textrm{SL}(2,\mathbb {C})$, see, for example, Kovacic (1986), Morales Ruiz (1999). For testing the integrability, we need to decide if it is a proper subgroup of $\textrm{SL}(2,\mathbb {C})$. The presence of a logarithmic singularity allows to formulate a simple and effective criterion. Before its formulation, we recall that the function w(z) is called hyperexponential if $w'(z)/w(z)$ is a rational function. In other words, it is of the form $w(z)=\exp [\int a(z) \textrm{d}z]$, where a(z) is a rational function.

Lemma 7

Assume that the differential equation (B.1) has a logarithmic singularity, and it has no nonzero hyperexponential solution, then its differential Galois group is $\textrm{SL}(2,\mathbb {C})$.

Let us describe shortly the algorithm which allows to find the hyperexponential solution of Fuchsian equation (B.1), if it exists. In fact, it is the first case of the Kovacic algorithm (Kovacic 1986).

The hyperexponential solution that we look for has the following form

$$\begin{aligned} w(z) = P(z)\exp \left[ \int \omega (z) \textrm{d}z\right] ,\qquad \omega (z)=\sum _{i=1}^M \frac{\varepsilon _i}{z-z_i}, \end{aligned}$$

(B.9)

where P(z) is a polynomial, $z_i$ are poles of r(z) of the first or the second order, and $\varepsilon _i$ is an exponent corresponding to this singularity. For each second order pole we have two choices for $\varepsilon$ given by equation (B.6), and for each first order pole there is only one choice $\varepsilon =1$. Polynomial P(z) is of degree n, where

$$\begin{aligned} n = \varepsilon _\infty -\sum _{i=1}^M \varepsilon _i, \end{aligned}$$

(B.10)

and $\varepsilon _\infty$ is the exponent at infinity. Here, the sum is taken over all poles of r(z). Moreover, the polynomial P(z) has to be the solution of the following equation

$$\begin{aligned} P'' +2 \omega (z) P' + (\omega '(z) + \omega (z)^2 - r(z)) P = 0. \end{aligned}$$

(B.11)

In practice as a candidate for P(z) we take a polynomial of degree n with indefinite coefficients and insert it into the above equation. Then, the problem reduces to finding solutions of linear equations for these coefficients. For an equation with m singular points, we have $2^{m+1}$ possible choices of elements $(\varepsilon _1,\ldots ,\varepsilon _m, \varepsilon _\infty )$, so we have at most such number of possibilities for choice of n and $\omega (z)$.

For the proof of the above Lemma and its numerous applications, we refer the reader to Morales Ruiz (1999).