(p,q)-biclique counting and enumeration for large sparse bipartite graphs

Abstract

In this paper, we study the problem of ($p$, $q$)-biclique counting and enumeration for large sparse bipartite graphs. Given a bipartite graph $G=(U,V,E)$ and two integer parameters p and q, we aim to efficiently count and enumerate all ($p$, $q$)-bicliques in G, where a ($p$, $q$)-biclique B(L, R) is a complete subgraph of G with $L \subseteq U$, $R \subseteq V$, $|L|=p$, and $|R|=q$. The problem of ($p$, $q$)-biclique counting and enumeration has many applications, such as graph neural network information aggregation, densest subgraph detection, and cohesive subgroup analysis. Despite the wide range of applications, to the best of our knowledge, we note that there is no efficient and scalable solution to this problem in the literature . This problem is computationally challenging, due to the worst-case exponential number of ($p$, $q$)-bicliques. In this paper, we propose a competitive branch-and-bound baseline method, namely BCList, which explores the search space in a depth-first manner, together with a variety of pruning techniques. Although BCList offers a useful computation framework to our problem, its worst-case time complexity is exponential to $p+q$. To alleviate this, we propose an advanced approach, called BCList++. Particularly, BCList++ applies a layer-based exploring strategy to enumerate ($p$, $q$)-bicliques by anchoring the search on either U or V only, which has a worst-case time complexity exponential to either p or q only. Consequently, a vital task is to choose a layer with the least computation cost. To this end, we develop a cost model, which is built upon an unbiased estimator for the density of 2-hop graph induced by U or V. To improve computation efficiency, BCList++ exploits pre-allocated arrays and vertex labeling techniques such that the frequent subgraph creating operations can be substituted by array element switching operations. We conduct extensive experiments on 16 real-life datasets, and the experimental results demonstrate that BCList++ significantly outperforms the baseline methods by up to 3 orders of magnitude. We show via a case study that ($p$, $q$)-bicliques optimizes the efficiency of graph neural networks. In this paper, we extend our techniques to count and enumerate ($p$, $q$)-bicliques on uncertain bipartite graphs. An efficient method IUBCList is developed on the top of BCList++, together with a couple of pruning techniques, including common neighbor refinement and search branch early termination, to discard unpromising uncertain ($p$, $q$)-bicliques early. The experimental results demonstrate that IUBCList significantly outperforms the baseline method by up to 2 orders of magnitude.

1 Introduction

As a natural data structure to model relationships between two different types of entities [8, 26], bipartite graph has been used in many real-world applications, such as online customer-product networks [50], gene co-expression networks [56], author-paper networks [15], graph neural networks [21], etc. Formally, a bipartite graph $G=(U, V, E)$ consists of two disjoint vertex sets U and V, where an edge $e \in E$ connects a vertex in U and another in V. An example bipartite graph is shown in Fig. 1. Recently, a lot of research efforts have been devoted to many fundamental problems in analyzing bipartite graphs, such as $(\alpha , \beta )$-core query [16, 30], maximal biclique enumeration [2, 31, 56], butterfly counting [40, 51, 52], fraud detection [22, 50], to name just a few.

In this paper, we introduce the concept of ($p$, $q$)-biclique. Given a bipartite graph $G=(U, V, E)$, a biclique B(L, R) is a complete subgraph of G, where $L \subseteq U$, $R \subseteq V$, that is $\forall (u,v) \in L\times R$, $(u,v) \in E(G)$, and B(L, R) is called a ($p$, $q$)-biclique if $|L|=p$ and $|R|=q$. We study the problem of ($p$, $q$)-biclique counting and enumeration for large sparse bipartite graphs, given two integer parameters p and q.

Fig. 1

An example bipartite graph G

Motivations. Many real-world bipartite graphs are very large and sparse, such as those listed in Table 3. A special case of ($p$, $q$)-biclique (where $p=2$ and $q=2$) called butterfly [40, 51, 52] has demonstrated great importance in defining basic metrics such as the clustering coefficient in a bipartite graph [29, 37]. However, in many graph-based tasks, ($p$, $q$)-biclique s, where p and q are not fixed to 2, are needed. Below are a small list of examples.

• (1) GNN Information Aggregation. Graph neural network (GNN) has received much research interests in recent years [21, 49, 55] and has numerous applications. A pivotal operation in a GNN is to recursively aggregate information from vertices’ neighbors in graph. A naive method simply propagates information on each pair of vertices separately, which leads to redundant computations, since vertices in a graph may often share many neighbors. Interestingly, we remark that ($p$, $q$)-biclique enumeration can optimize the task of GNN information aggregation. Our case study results in Sect. 7.4 report that our ($p$, $q$)-biclique-based method achieves the most efficient when (p, q) settings are (5, 10) and (4, 10) on two datasets IMDB and PPI, respectively, which are employed to evaluate the state-of-the-art algorithm HAG [25]. The results show that our method achieves near an order of magnitude of performance improvement over existing methods. Details about how to apply ($p$, $q$)-bicliques to GNN information aggregation are illustrated in our case study in Sect. 7.4.

• (2) Densest Subgraph Detection. Recently, Mitzenmacher et al.[35] formulate the concept of ($p$, $q$)-biclique density. For a subgraph S in a bipartite graph, its ($p$, $q$)-biclique density is defined as the ratio between the number of ($p$, $q$)-bicliques in S and the size of S. Based on the ($p$, $q$)-biclique density, they study the problem of finding the ($p$, $q$)-biclique densest subgraph in a bipartite graph. They point out that ($p$, $q$)-biclique enumeration is a required procedure in their methods.

• (3) Cohesive Subgroup Analysis. Borgatti et al. [8] study the problem of identifying cohesive subgroups in bipartite graphs. They consider using ($p$, $q$)-biclique to identify cohesive subgroups in a bipartite graph, where p and q are greater than or equal to 3. For example, in a social event bipartite graph with 18 guests and 14 events, (3, 3)-bicliques can reveal two basic groups together with some outsiders, which matches the ground truth well.

To the best of our knowledge, the problem of ($p$, $q$)-biclique counting and enumeration on large sparse bipartite graphs has not been thoroughly investigated. The closest related work is the work of finding ($p$, $q$)-biclique densest subgraph [35], where ($p$, $q$)-biclique enumeration is a necessary step. The performance of their solution is not yet satisfactory, since it is developed on top of costly maximal biclique enumeration. (2, 2)-biclique- and (3, 3)-biclique-based densities are adopted to make their solution more practical. However, even under the setting $p=q=3$, their solution cannot finish in 10 hours on a medium-sized bipartite graph (with 18k vertices and 92k edges).

Challenges. The problem of ($p$, $q$)-biclique counting and enumeration is computationally challenging. Given a bipartite graph $G=(U, V, E)$, a straightforward solution is to enumerate all ${|U| \atopwithdelims ()p} {|V| \atopwithdelims ()q}$ combinations of vertex sets and verify whether each of them is a biclique. However, this approach is obviously cost-prohibitive, because the number of ($p$, $q$)-bicliques in a bipartite graph can be much larger than the size of the bipartite graph. Assuming $|U| = |V| = n$, then the number of ($p$, $q$)-bicliques could be up to $O({|U| \atopwithdelims ()p} {|V| \atopwithdelims ()q}) \approx O(n^{p+q})$. This shows that our problem is more difficult than other related counting problems, such as butterfly counting [40, 52] and bi-triangle counting [54]. For example, the dataset Twitter contains $2.06 \times 10^{8}$ butterflies and $1.61 \times 10^{12}$ bi-triangles, but $1.45 \times 10^{19}$ (6, 2)-bicliques.

Besides, we aim to support queries with arbitrary p and q values, which makes our problem even harder. For problems such as butterfly counting and bi-triangle counting, where the answers are small and fixed patterns, one may build many intermediate structures (e.g., wedges) to facilitate query processing. This is infeasible to our problem since the intermediate result size would be extremely huge even for slightly larger p and q values. Last but not least, we aim to support both counting and enumerating ($p$, $q$)-bicliques, which is generally more difficult than counting only.

Contributions. To tackle the computation challenges, we propose efficient query processing techniques. In the database research community, algorithms that combine backtracking with branch-and-bound techniques are widely adopted to deal with graph-based problems, such as maximal biclique enumeration [2, 56]. Inspired by these, we propose a competitive branch-and-bound baseline method, namely BCList, which explores the search space in a depth-first manner. Specifically, BCList maintains a partial biclique and recursively adds the candidate vertices into the partial biclique to generate ($p$, $q$)-bicliques. To improve the performance of BCList, we propose new efficient pruning techniques, such as 2-hop neighbors to reduce candidate size, size pruning to terminate search branch early, and vertex ordering to avoid redundant computation.

BCList provides a promising computation framework to solve our problem. However, observe that BCList utilizes a vertex-based exploring strategy, which has a time complexity of $O((|U| + |V|)(d_{\max } + d_{2 \max })^{p+q-2})$, where $d_{\max }$ and $d_{2\max }$ are the maximum degree and 2-hop degree of a vertex in G, respectively. It is still time costly for BCList to handle queries when p and q are large.

To alleviate these issues, we propose an advanced approach, called BCList++. In particular, BCList++ applies a layer-based exploring strategy to enumerate ($p$, $q$)-bicliques by anchoring the search on either U or V only. This exploring strategy leads to a time complexity of $O(a(H)^{p-2}|E(H)|d_{\max } +\bigtriangleup )$ if the left layer U is selected, where H is the 2-hop graph constructed on U, E(H) is the edges in H, a(H) is the arboricity of H [12], $d_{\max }$ is the maximum degree of a vertex in U, and $\bigtriangleup$ is the result size. Compared to BCList, BCList++ is more efficient w.r.t the values of p and q. It should also be remarked that many real bipartite graphs are unbalanced in practice (e.g., Edit-en and Edit-fr in Table 3), and the values of p and q may be quite different as well. Hence, the performance of BCList++ could be significantly influenced by the choice of the search layer (i.e., U or V). Consequently, a vital task is to choose a layer with the least computation cost. To this end, we develop a new cost model, built upon an unbiased estimator for the density of 2-hop graph H, to efficiently estimate the computation cost. We theoretically analyze the effectiveness of the cost model.

We use pre-allocated arrays and vertex labelling techniques to implement BCList++ such that the frequent subgraph creating operations can be substituted by array element switching operations. To further accelerate the computation, we introduce useful graph reduction techniques and extend our approach to a parallel environment, where multiple threading is available. Empirical study shows that BCList++ can significantly outperform the baseline method BCList and other competitors by up to 3 orders of magnitude. The cost model is clearly effective. A case study about our techniques for optimizing the efficiency of GNN information aggregation is presented.

In some applications, edges in the graph may exist with a probability. For instance, in a gene co-expression networks [56], the edge existential probability is the score of co-expression level between genes and conditions. In a recommendation user-item network, the edge existential probability is the likelihood that a user would enjoy or purchase an item [58]. A network with uncertain edges is called uncertain (bipartite) graph, which has also been studied among many related problems, such as cohesive subgraph decomposition [7, 24, 59], maximal clique enumeration [4, 5, 13], and motif counting [23, 32, 47, 58]. In this paper, we also study the problem of ($p$, $q$)-biclique counting and enumeration on uncertain bipartite graphs. Below are a couple of concrete examples.

• (1) Biclustering of Gene Expression Data Given a gene co-expression network consisting of genes and conditions, an important task is to find groups of co-regulated genes. As one of the main techniques to deal with this task, biclustering considers to find the clusterings of genes and conditions simultaneously [11, 33, 36]. We observe that our uncertain ($p$, $q$)-biclique model offers a possible solution for this task. First, in an uncertain ($p$, $q$)-biclique, any pair of gene and condition are connected, which implies that the genes co-express under each condition. Second, the probability guarantees the expression confidence level. By setting different size values and probability threshold, we are able to find different biclustering results for the co-expression data, which provide hints for further exploring of the data. We present a case study about COVID-19 blood samples gene expression data in Sect. 7.6.

• (2) Item Recommendation On a movie rating platform such as Netflix, the rating score denotes how much a user enjoys a movie. By normalizing the rating scores into region [0, 1],we can model the rating platform as an uncertain bipartite graph, in which the edge probability denotes how much a user enjoys a movie. By analyzing a ($p$, $q$)-biclique with high probability, we can find a group of users U that are likely to be interested in a set of movies. Suppose there is a new movie v that is watched and given high probabilities by all users in U but u. Then, we can recommend movie v to user u, because u is likely to be interested in v.

In Sect. 6, we first formally introduce and formulate the problem of ($p$, $q$)-biclique counting and enumeration on uncertain bipartite graphs. Then, we develop a baseline method, namely UBCList, which is built on top of BCList++, considering its superior performance on deterministic graphs. Observe that the UBCList needs to enumerate and verify all ($p$, $q$)-bicliques on the backbone graph, which is inefficient when a lot of them do not meet the uncertainty threshold. To improve the computation performance, we propose an improved method, namely IUBCList, which is equipped with a couple of pruning techniques, including common neighbor refinement and search branch early termination. Thanks to these pruning techniques, we are able to discard some unpromising ($p$, $q$)-bicliques earlier before enumerating them completely. The performance studies suggest that IUBCList can significantly outperform UBCList by up to 2 orders of magnitude.

The preliminary version is published in [53]. The main contributions of this work are summarized as follows.

• This is the first work to systematically study the problem of ($p$, $q$)-biclique counting and enumeration for large sparse bipartite graphs. We propose BCList which combines backtracking with branch-and-bound techniques, together with a variety of pruning techniques.

• We propose a layer-based approach BCList++, where a cost model is used to guide the selection of the layer with the least computation cost. To improve efficiency further, we implement BCList++ using pre-allocated arrays and vertex labelling techniques such that the frequent subgraph creating operations can be substituted by array element switching operations.

• We extend our techniques to deal with the problem of ($p$, $q$)-biclique counting and enumeration for uncertain bipartite graphs. To resolve this problem efficiently, we propose a method IUBCList, which can discard unpromising ($p$, $q$)-bicliques early by using a couple of pruning techniques.

• The comprehensive performance evaluation on real data demonstrates the efficiency of our new techniques proposed in this paper.

Roadmap. The rest of this paper is organized as follows: In Sect. 2, we introduce basic concepts and problem definition. In Sect. 3, we propose a baseline method. In Sect. 4, we propose an advanced approach. Two optimizations are proposed in Sect. 5. In Sect. 6, we extend our techniques to handle the problem on uncertain bipartite graphs. We conduct extensive experiments in Sect. 7. Section 8 reviews the related work and Sect. 9 concludes the paper.

2 Preliminaries

Table 1 Frequently used notations

In this section, we introduce basic concepts and definitions used in this paper. Table 1 summarizes some notations frequently used throughout this paper. We consider an unweighted and undirected bipartite graph $G=(U, V, E)$, where U(G) and V(G) denote two disjoint vertex sets, i.e., $U(G) \cap V(G) = \emptyset$, and $E(G) \subseteq U(G) \times V(G)$ denotes the edge set of G. An edge in G is denoted by either (u, v) or (v, u). For each vertex $u \in U(G)$, the neighbors of u is denoted as $N(u, G)=\{ v | (u, v) \in E(G)\}$. The degree of u, denoted as d(u, G), is the number of neighbors of u, i.e., $d(u, G) = |N(u, G)|$. We have symmetrical definitions for vertices in V(G). For presentation simplicity, in the rest of the paper, we omit G in the notations when the context is self-evident.

Definition 1

(Biclique) Given a bipartite graph $G=(U,V, E)$, a biclique B(L, R) is a complete subgraph of G, where $L \subseteq U(G)$ and $R \subseteq V(G)$, i.e., $\forall (u, v) \in L \times R, (u, v) \in E(G)$.

In this paper, we call L and R the left and right side (or layer) of vertices in a biclique B(L, R), respectively.

Definition 2

((p, q)-Biclique) Given a bipartite graph G, and two integer parameters p and q, a ($p$, $q$)-biclique B(L, R) is a biclique of G with $|L|=p$ and $|R|=q$.

Problem statement. Given a bipartite graph $G=(U, V, E)$, and two integer parameters p and q, we study the problem of counting and enumerating ($p$, $q$)-bicliques in G.

Example 1

Consider the bipartite graph in Fig. 1. Assuming $p=2$ and $q=3$, there are two ($p$, $q$)-bicliques. They are $(\{u_1, u_2\}, \{v_1, v_2, v_3\})$ and $(\{u_2, u_3\}, \{v_2, v_3, v_4\})$.

In the rest of the paper, we focus on the enumeration problem and we show how to extend our techniques to the counting problem.

3 The baseline solution

A brute-force solution for our problem is to enumerate all ${|U| \atopwithdelims ()p} {|V| \atopwithdelims ()q}$ combinations of vertex sets and verify whether each of them is a biclique, which is cost-prohibitive. In the database research community, algorithms that combine backtracking with branch-and-bound techniques are widely adopted to deal with graph-based problems, such as maximal biclique enumeration [2, 56]. Inspired by these, in this section, we propose a competitive branch-and-bound baseline method, called BCList. In the following, we first give the main idea of BCList together with some important pruning techniques and then present the overall algorithm.

3.1 Solution overview

We begin with the concept of partial biclique.

Definition 3

(Partial Biclique) Given a pair of integers p and q, a partial biclique B(L, R) is biclique with $|L| \le p$ and $|R| < q$, or $|L| < p$ and $|R| \le q$.

Main idea. In a nutshell, BCList maintains a partial biclique and recursively adds the candidate vertices into the partial biclique to generate full bicliques, i.e., ($p$, $q$)-bicliques. More specifically, BCList operates on the following four dynamically changing vertex sets: (i) L, a subset of U containing the left side of vertices in a partial biclique; (ii) R, a subset of V containing the right side of vertices in a partial biclique; (iii) $C_L$, a subset of U containing the candidate vertices that may be added to L; (iv) $C_R$, a subset of V containing the candidate vertices that may be added to R. In each iteration, BCList chooses one vertex from $C_L$ or $C_R$ to expand the partial biclique. The four vertex sets are utilized and maintained in a depth-first traversal of a recursion search tree to generate ($p$, $q$)-bicliques.

Clearly, to improve the computation efficiency, the key is to reduce the search space, i.e., the size of recursion search tree. In the following, we aim to develop efficient pruning and query processing techniques.

3.2 Pruning techniques

Lemma 1

Given a partial biclique B(L, R), the candidate sets $C_L$ and $C_R$ only contain the vertices that are common neighbors of vertices in R and L, respectively.

• (1) If $u \in C_L$, then $\forall v \in R: (u, v) \in E$; and

• (2) If $v \in C_R$, then $\forall u \in L: (u, v) \in E$.

Proof

The lemma is immediate. $\square$

Based on Lemma 1, we can substantially reduce the number of candidate vertices by only considering the common neighbors. In particular, when the partial bicliques are expanded, $C_L$ and $C_R$ are contracted. We have the following corollary based on Lemma 1.

Corollary 1

Given a partial biclique B(L, R), and the corresponding candidate sets $C_L$ and $C_R$,

• (1) if $|L| = p$ and $|R| + |C_R| \ge q$, then L forms a ($p$, $q$)-biclique with each q-sized subset of $R \cup C_R$; and

• (2) if $|R| = q$ and $|L| + |C_L| \ge p$, then R forms a ($p$, $q$)-biclique with each p-sized subset of $L \cup C_L$.

Lemma 1 provides an efficient way to reduce the number of candidate vertices on the opposite side when a new vertex is added into the partial biclique. Next, we explore to reduce the number of candidate vertices on the same side as well. Before that, we introduce the important concept of 2-hop neighbor.

Definition 4

($\tau$-strength 2-Hop Neighbor) Given a bipartite graph $G=(U, V, E)$ and an integer $\tau$, for a vertex w in G, the $\tau$-strength 2-hop neighbors of w, denoted as $N_2^{\tau }(w, G)$, contains all vertices in G, each of them has at least $\tau$ common neighbors with w, i.e., $N_2^{\tau }(w, G) = \{w' | w' \in U \cup V$ and $|N(w, G) \cap N(w', G)| \ge \tau \}$.

For presentation convenience, given a bipartite graph $G=(U, V, E)$, and two integers p and q, for each $u \in U$, we define the 2-hop neighbors of u, denoted as $N_2(u, G)$, to be the q-strength 2-hop neighbors of u, i.e., $N_2(u, G) = N_2^q(u, G)$. Similarly, for each $v \in V$, $N_2(v, G) = N_2^p(v, G)$.

Example 2

Consider $u_3$ in the bipartite graph in Fig. 1 again. We assume $p=2$ and $q=3$. Since $u_2$ is the only 3-strength 2-hop neighbor of $u_3$ with common neighbors $v_2$, $v_3$, and $v_4$, we have $N_2(u_3, G) = \{u_2\}$.

Lemma 2

Given a partial biclique B(L, R), the candidate sets $C_L$ and $C_R$ only contain the vertices that are common 2-hop neighbors of L and R, respectively.

• (1) If $u \in C_L$, then $\forall w \in L$: $u \in N_2(w, G)$; and

• (2) If $v \in C_R$, then $\forall w \in R$: $v \in N_2(w, G)$.

Proof

We only prove (1), as we can prove (2) similarly. Given a certain vertex $u \in C_L$, we prove that $\forall w \in L$: $u \in N_2(w, G)$ by contradiction. Suppose that $\exists w \in L$ s.t. $u \not \in N_2(w, G)$, which implies that $|N(w, G) \cap N(u, G)| < q$. This contradicts with the fact that any two vertices in left side of a ($p$, $q$)-biclique must have at least q common neighbors, i.e., $|N(w, G) \cap N(u, G)| \ge q$. Therefore, the lemma holds. $\square$

Example 3

Following Example 2, suppose $L=\{u_3\}$. Based on Lemma 2, we have that the candidate set $C_L \subseteq N_2(u_3, G)$, which implies that we only need to consider $u_2$ as the candidate vertex to expand L, rather than all vertices in $\{u_0, u_1, u_2, u_4\}$.

Collecting 2-hop neighbors. Algorithm 1 illustrates the details of collecting the 2-hop neighbors of vertices in a bipartite graph. For each vertex u in G, we use a hashmap C to keep the 2-hop neighbors of u along with the number of common neighbors (Line 2). In the algorithm, we first search the neighbors of u (Line 3), and then search the 2-hop neighbors (Line 4). If the possible 2-hop neighbor is a vertex rather than u itself, we increase the entry in C by 1 (Lines 5–6). After processing all neighbors of u, we check the candidate 2-hop neighbors and only keep the q-strength (resp. p-strength) 2-hop neighbors if $u \in U$ (resp. $u \in V$) (Lines 7–9).

Theorem 1

The time complexity of Algorithm 1 is $O(\sum _{u \in U}d(u,G)^2 + \sum _{v \in V}d(v,G)^2)$.

Proof

The time complexity is clearly dominated by Lines 1–6. Consider the fact that each middle vertex v is searched by each of its neighbors (Lines 1–3) and also searched all its neighbors (Line 4). This theorem is then immediate. $\square$

Size pruning. During the search processing, when the size of vertex set is relatively small, we may stop exploiting the current branch without missing any results.

Lemma 3

Given a partial biclique B(L, R), and the candidate sets $C_L$ and $C_R$, if $|L| + |C_L| < p$ or $|R| + |C_R| < q$, the four sets L, R, $C_L$, and $C_R$ cannot generate any ($p$, $q$)-bicliques.

Proof

The lemma is immediate since a ($p$, $q$)-biclique contains p vertices in the left side and q vertices in the right. $\square$

Vertex ordering. As a frequently considered factor to improve the efficiency of many graph search algorithms [12, 14, 52], vertex ordering can be utilized to avoid generating duplicate results and thus save computation cost. In the literature, the degree ordering [12, 52] and core ordering [14] are two widely adopted vertex ordering strategies. Our experimental studies in Sect. 7 show that the two orderings achieve comparable performance. Next, we introduce the degree ordering since it is more computationally efficient.

Definition 5

(Vertex Rank) Given a bipartite graph $G=(U, V, E)$, for a vertex u in G, the vertex rank r(u) is an integer where $r(u) \in [1, |U \cup V|]$. For two vertices $u, v \in U \cup V$, $r(u) > r(v)$ if

• $d(u) > d(v)$, or

• $d(u) = d(v)$ and $u.id < v.id$.¹

Table 2 The neighbor and 2-hop neighbor structure

Graph transformation. Given a bipartite graph G, let $\eta$ be a degree ordering on G. We say the directed bipartite graph $\overrightarrow{G}$ is induced by the ordering $\eta$, if $U(\overrightarrow{G}):= U(G)$, $V(\overrightarrow{G}):= V(G)$, and there is an edge $u \rightarrow v$ in $\overrightarrow{G}$ if $r(u) > r(v)$ and $(u,v) \in E(G)$.

In the rest of the paper, we slightly abuse the notation of G to denote its induced directed graph $\overrightarrow{G}$, unless otherwise specified. For a vertex u in G, N(u, G) only keeps the neighbors of u with a lower vertex rank than u. We have similar changes for d(u, G) and $N_2(u, G)$. Besides, we sort vertices in U(G), V(G), N(u, G), and $N_2(u, G)$ in descending order of their ranks by preprocessing.

Example 4

Following the example in Fig. 1. Assume $p=2$ and $q=3$. The sorted vertex order is as follows: $u_2$, $u_3$, $v_2$, $u_1$, $v_3$, $v_4$, $u_4$, $v_1$, $v_5$, $u_0$, $v_0$. Table 2 shows the neighbor and 2-hop neighbor structure of each vertex after graph transformation. Take $u_1$ as example. Although it has 3 neighbors, namely $v_1$, $v_2$, and $v_3$, we only keep $v_3$ and $v_1$ in $N(u_1, G)$. This is because $v_2$ has a higher rank than $u_1$. Note that vertices in N(u, G) and $N_2(u, G)$ are sorted in descending order of their ranks.

3.3 The overall algorithm of BClist

Fig. 2

(Partial) Recursion tree of the running example of BCList in Fig. 1 ($p=2$ and $q=3$)

Based on the above observations, we are ready to present BCList (Algorithm 2). We first collect the 2-hop neighbors for vertices in G (Line 1), which is described in Algorithm 1. Then, we compute the vertex rank for each vertex in the graph (Line 2) and construct the induced directed graph (Line 3). Finally, we enumerate all ($p$, $q$)-bicliques using the procedure VertexBasedListing (Line 4).

In the procedure VertexBasedListing, we maintain four vertex sets, i.e., L, R, $C_L$, and $C_R$, which are initialized as $\emptyset$, $\emptyset$, U(G), and V(G), respectively. During the processing of VertexBasedListing, we first check if the current branch can generate answers based on Corollary 1 (Line 7). For example, if $|L| \ge p$ and $|R| + |C_R| \ge q$, we can collect ($p$, $q$)-bicliques from L and each q-sized subset S of $R \cup C_R$ (Lines 8–10). Similarly, we might also obtain ($p$, $q$)-bicliques in Lines 11–13. Otherwise, we check if the current branch can be pruned by applying Lemma 3 (Line 14). Lastly, we search the sub-spaces (Lines 16–34).

More specifically, we iteratively select the vertices in $C_L$ and $C_R$ to expand the partial biclique, i.e., L and R (Lines 19–34). At each step, we choose from $C_L$ and $C_R$ the vertex with the highest rank (Line 20). Say u (i.e., $C_L[i]$) has a higher rank than v (i.e., $C_R[j]$) (Lines 21–27). Then, $L'$ is updated by adding u to L (Line 22). Based on Lemma 2, $C_L'$ is updated by computing the intersection of $C_L$ and $N_2(u, G)$. Note here that we need only to consider the last $|C_L|-i$ vertices in $C_L$ since the first i vertices have already been checked in previous iterations (Line 23). Meanwhile, based on Lemma 1, we can update $C_R'$ (Line 24). After that, we enter the new search space formed by the vertex sets $L'$, $R'$, $C_L'$, and $C_R'$ (Line 25). After finishing the new search space, we should remove u from $L'$ before going to next iteration (Line 26). Lines 28–34 describe the symmetrical case where $r(C_L[i] ) \le r(C_R[j])$.

Example 5

Following Example 4, we illustrate the overall running process of BCList. Figure 2 depicts the recursion tree of the entire search space. Note that a recursion tree contains three types of tree nodes: (i) open node marked by a dashed rectangle, which we have to explore further, e.g., $s_0$, $s_1$, $s_3$, and $s_8$; (ii) answer node marked by a green solid rectangle, where we find ($p$, $q$)-bicliques, e.g., $s_2$ and $s_4$; (iii) closed node marked by a red solid rectangle, which can be pruned safely, e.g., $s_5$, $s_6$, $s_7$, and $s_9$. Clearly, both answer and closed nodes are leaf nodes, while open node is an inner node.

We start from the root node $s_0$ and iteratively search the sub-spaces in a depth-first manner by selecting vertices from the candidate sets following the vertex rank order. By selecting $u_2$, we enter node $s_1$, where the candidate vertex sets are updated accordingly. In particular, we have $C_L = C_L \cap N_2(u_2, G) = \{u_3, u_1\}$ and $C_R = C_R \cap N(u_2, G) = \{v_2, v_3, v_4, v_1, v_0\}$ based on Lemma 2 and Lemma 1, respectively. Clearly, we cannot prune $s_1$ by Lemma 3 or generate answers by Corollary 1. Therefore, we expand node $s_1$, and enter the child node $s_2$, where a ($p$, $q$)-biclique is found according to Corollary 1, i.e., $(\{u_2, u_3\}, \{v_2, v_3, v_4\})$. Continuing this processing, we can find another result node $s_4$ with a ($p$, $q$)-biclique $(\{u_1, u_2\}, \{v_1, v_2, v_3\})$, while all closed nodes can be pruned by Lemma 3.

3.3.1 Analysis of BCList

Below we first show the correctness of BCList and then analyze the time and space complexity of BCList.

Theorem 2

BCList enumerates ($p$, $q$)-bicliques correctly.

Proof

We prove the correctness of BCList according to the following three aspects, namely soundness, completeness, and no duplication. Soundness BCList only collects answers in Line 10 and Line 13, where the soundness is guaranteed by Corollary 1. Completeness Consider an arbitrary ($p$, $q$)-biclique B(L, R) in G. We prove that B(L, R) is contained in an answer node s in the recursion tree. Let u and v be the last vertex in L and R, respectively. Let $s' = (L', R', C_L', C_R')$ be a tree node with $L' = L - \{u\}$ and $R' = R - \{v\}$. As long as $s'$ is in the recursion tree, s must be in the tree. This is because B(L, R) is a biclique and we have $u \in C_L'$ and $v \in C_R'$, and therefore, s must be expanded from $s'$ by selecting any of the two vertices u and v. Now, we repeat this process until reaching the root node $(\emptyset , \emptyset , U(G), V(G))$. Thus, B(L, R) must be returned by BCList. No duplication Consider an arbitrary ($p$, $q$)-biclique B(L, R) in G. Let s be the node in the recursion tree containing B(L, R). Since we generate the ($p$, $q$)-bicliques on the induced directed graph, where neighbors and 2-hop neighbors are only kept on the vertices with higher ranks, it is immediate that s is expanded from the root node $(\emptyset , \emptyset , U(G), V(G))$ following a unique path in the recursion tree. Therefore, B(L, R) is enumerated only once. $\square$

Next we focus on the recursion procedure VertexBasedListing when analyzing the time complexity of BCList. Note that the time complexity to preprocess the graph for collecting 2-hop neighbor is shown in Theorem 1.

Theorem 3

The time complexity of BCList is $O((|U(G)| + |V(G)|)(d_{\max } + d_{2\max })^{p+q-2})$, where $d_{\max }$ and $d_{2\max }$ are the maximum degree and 2-hop degree of a vertex in G, respectively.

Proof

The time complexity of BCList is clearly determined by the number of tree nodes in the recursion tree. For an open node $s=(L, R, C_L, C_R)$, the number of child nodes is $|C_L| + |C_R|$. We observe that $|C_L| = |U(G)|$ and $|C_R| = |V(G)|$ if s is root, otherwise, $|C_L|$ and $|C_R|$ are bounded by $d_{2\max }$ and $d_{\max }$, respectively. Besides, the depth of the recursion tree is bounded by $p+q-1$ since we expand the partial biclique with one vertex each time. By ignoring the pruning, we have that the total time complexity is $O((|U(G)| + |V(G)|)(d_{\max } + d_{2\max })^{p+q-2})$. $\square$

Theorem 4

The space complexity of BCList is $O(|E(G)| + |U(G)|^2 + |V(G)|^2)$.

Proof

The space to store adjacent lists is O(|E(G)|). In the worst case, for a vertex $u \in U(G)$, any other vertices in U(G) may be a 2-hop neighbor u. Thus, the overall worst-case space complexity is $O(|E(G)| + |U(G)|^2 + |V(G)|^2)$.

$\square$

3.4 Discussion for counting problem

To solve the counting problem, we only need to do minor changes for BCList. Specifically, in Lines 9–10 and Lines 12–13 of Algorithm 2, we count the number of results by using ${|S| \atopwithdelims ()q}$ and ${|S| \atopwithdelims ()p}$, respectively, rather than enumerating each subset of S.

4 An advanced approach

In this section, we propose an advanced approach, namely BCList++, to solve the problem of ($p$, $q$)-biclique counting and enumeration.

4.1 Motivation

Although BCList offers a useful computation framework to our problem, our empirical study suggests that it still has the following two drawbacks.

$\bullet$ Drawback 1: Large Search Space The recursion procedure VertexBasedListing in BCList utilizes a vertex ordering-based strategy to expand the search space, which may lead to a large search space in terms of both depth and width of the recursion tree when the value of $p+q$ is large. As a result, it can be inefficient since the time complexity of BCList is exponential to $p+q$ (see Theorem 3 for detials).

$\bullet$ Drawback 2: Inefficient Direct Implementation The direct implementation of BCList does not yield an efficient algorithm because it has to produce and store a large number of intermediate subgraphs. That is, we have to produce new L, R, $C_L$, and $C_R$ for each node in the recursion tree. It is costly to frequently create such data structures.

The advanced approach – BCList++. Based on the above analysis, we consider the following two aspects to alleviate the drawbacks of BCList.

$\bullet$ To resolve Drawback 1, we apply a layer-based exploring strategy to enumeration ($p$, $q$)-bicliques by anchoring the search on either U or V only. This exploring strategy leads to a time complexity exponential to either p or q (see Theorem 6). To deal with the unbalanced bipartite graphs and queries with different p and q, we develop an efficient and effective cost model to choose a layer with the least computation cost.

$\bullet$ To tackle Drawback 2, we implement BCList++ using pre-allocated arrays and vertex labelling techniques such that the frequent subgraph creating operations can be substituted by array element switching operations. By using these data structures and operations, we only need to create them once during the entire processing of the algorithm.

4.2 BCList++ algorithm

We begin with the important concept of 2-hop graph.

Definition 6

(2-Hop Graph) Given a bipartite graph $G=(U, V, E)$ and a pair of parameters p and q, the 2-hop graph $H = (U, E)$ of G is a graph induced by G with the following properties²:

• (1) $U(H):= U(G)$; and

• (2) $\forall u, v \in U(H)$, $(u, v) \in E(H)$ if u and v are 2-hop neighbors in G.

Fig. 3

2-hop graph H and vertex neighbor structures

Given a bipartite graph G and its induced 2-hop graph H, for each $u \in U(H)$, the neighbors of u in H are denoted as $N(u, H) = \{v | (u, v) \in E(H)\}$, while N(u, G) is reserved to keep neighbors of u in G. Note that, we transform H into a directed acyclic graph (DAG) and sort vertices in U(H) and N(u, H) in descending order of their ranks as well.

Example 6

Continuing our running example, Fig. 3a shows the induced 2-hop graph H of G, which contains two edges, i.e., $u_2 \rightarrow u_1$ and $u_2 \rightarrow u_3$. This is because there are only two pairs of 2-hop neighbors (i.e., $\langle u_1, u_2\rangle$ and $\langle u_2, u_3\rangle$) among vertices in U(H), Fig. 3b presents the neighbor structures of vertices in H. Note that, for each vertex $u \in U(H)$, N(u, G) contains all neighbors of u in G.

Moreover, given a 2-hop graph H, a clique c is a complete subgraph of H by ignoring the edge direction. We say a clique c is a p-clique if the number of vertices in c is p. For example, $(u_1, u_2)$ is a 2-clique in Fig. 3a.

The details of BCList++. Algorithm 3 illustrates the details of our advanced method BCList++. We first choose the layer with least cost as anchor layer, i.e., U(G), by using a cost model (Lines 1–3), which is introduced in detail in Sect. 4.3. Then, we collect the 2-hop neighbors for each vertex in U(G) (Line 4) and compute the vertex ranks according to the 2-hop degree of a vertex (Line 5). Next, we construct the 2-hop graph H based on vertices in U(G) (Line 6). In Line 7, we initialize a set of p empty arrays to store the common neighbors in G for vertices in U(H). Finally, we enumerate all ($p$, $q$)-bicliques using LayerBasedListing (Line 8).

Generally, in LayerBasedListing, we recursively enumerate p-cliques on H and simultaneously collect their common neighbors in G using vectors S. By combining the two parts together, we retrieve the ($p$, $q$)-bicliques.

Specifically, we use L to store the clique in H and start from depth 0 (i.e., $l=0$). During the processing of LayerBasedListing, we first check if $l=p$ (Line 11), which implies that we have traversed p steps and a p-clique is found. We simply collect ($p$, $q$)-bicliques from L and each q-sized subset R of $S[l-1]$ (Lines 12–13). Otherwise, we iteratively select vertex $u \in U(H)$ to expand the clique L (Lines 14–22). We start by computing the common neighbors of u and previous vertices in L using S[l]. Particularly, if $l=0$, we simply add all vertices in N(u, G) to S[l] (Line 16). Otherwise, S[l] is computed by the intersection between $S[l-1]$ and N(u, G) since $S[l-1]$ stores the common neighbors of existing vertices in L (Line 18). After that, we may be able to skip the current branch if the number of common neighbors is less than q (i.e., $|S[l]| < q$), or there is not enough vertices to expand L (i.e., $|N(u, H)| < p-l-1$). Last, we construct subgraph $H'$ of H induced by N(u, H) and enter the sub-space by expanding L with u (Lines 21–22).

Example 7

Continuing Example 6, we illustrate the overall running processing of BCList++. Since the vertices in U(H) are $u_2, u_1, u_3, u_0, u_4$, we start from $u_2$. Thus, we have $S[0] = N(u_2, G) = \{v_0, v_1, v_2, v_3, v_4\}$, and the induced subgraph $H'$ contains two isolated vertices $u_1$ and $u_3$ since $N(u_2, H) = \{u_1, u_3\}$ (see Fig. 3). We search the sub-space by adding $u_2$ to L. Next, we consider $u_1$ and have that $S[1] = \{v_1, v_2, v_3\}$ by computing the intersection between S[0] and $N(u_1, G)$. Meanwhile, $H'$ is empty due to the fact that $N(u_1, H)$ is empty. After adding $u_1$ to L, we enter the new search space. Since we have $l=p=2$ at this point, we begin to enumerate ($p$, $q$)-bicliques by L and S[1], where $(\{u_1, u_2\}, \{v_1, v_2, v_3\})$ is found. Continuing this processing, we can find another ($p$, $q$)-biclique $(\{u_2, u_3\}, \{v_2, v_3, v_4\})$.

Theorem 5

BCList++ enumerates ($p$, $q$)-bicliques correctly.

Proof

We prove the correctness of BCList++ according to the following three aspects, namely soundness, completeness, and no duplication. Soundness Consider an answer B(L, R) returned in Line 13. We first prove that $|L| = p$. Since $H'$ is always constructed by the out-neighbors of u and H is a DAG, we have that L is a vertex set expanded p times with different vertices. Thus, $|L|=p$. Together with the fact that R is a q-sized subset of common neighbors of vertices in L, we have that B(L, R) is a ($p$, $q$)-biclique. Completeness Consider an arbitrary ($p$, $q$)-biclique B(L, R) in G. We prove B(L, R) must be returned in Line 13. To this end, we only need to prove that L is processed in Line 13 since vertices in R are common neighbors of L. Since L is contained in a ($p$, $q$)-biclique, we have that, for any two vertices $u, v \in L$, u and v are 2-hop neighbors. Therefore, L is a p-clique in H and must be processed in Line 13. No duplication Since H is a DAG, it is easy to see that LayerBasedListing enumerates p-cliques without duplications. Therefore, it follows that the ($p$, $q$)-bicliques returned in Line 13 do not contain duplicates. $\square$

Efficient implementation. BCList++ can be implemented efficiently using the following data structures and operations which are an adaption of the ones used in [12, 14] for listing cliques in generic graphs. Note that the only frequently constructed object is the DAG H in Line 6 and Line 21. This is because L in LayerBasedListing can be represented as an array of size p and S are a set of p arrays.

For each vertex $u \in U(H)$, we use an adjacency list N(u, H) to store its out-neighbors. No other adjacency lists will be created during the processing BCList++. Specifically, given the current 2-hop graph H in the recursion, we make sure that the out-neighbors of any vertex in H always appear first in N(u, H). Given H and a vertex u, the subgraph $H'$ induced by N(u, H) is built as follows.

• Assign each vertex a label initially set to 0.

• For each $v \in N(u, H)$, set its label to $l+1$ if its current label is equal to l. It ensures that v is in the new DAG $H'$ induced by N(u, H).

• For each $v \in N(u, H)$, move all the neighbors in N(v, H) with label equal to $l+1$ in the first part of N(v, H) (by swapping vertices) and compute the out-degree of vertex v in the new DAG $H'$ to update d(v). The first d(v) vertices in N(v, H) are thus the out-neighbors of v in $H'$.

• For each $v \in N(u, H)$, set its label back to l after finishing a recursion search branch.

4.3 Cost analysis

In this section, we first analyze the time and space complexity of BCList++ and then introduce the cost model used by BCList++.

4.3.1 Time and space complexity analysis

We focus on analyzing the time complexity of the main recursion procedure LayerBasedListing. To this end, we follow the methodology used in [12], which studies the parameterized complexity. Particularly, we use the concept of arboricity a(H), which is defined as the minimum number of edge-disjoint spanning forests into which H can be decomposed.

Theorem 6

The time complexity of BCList++ is $O(a(H)^{p-2} |E(H)|d_{\max } +\bigtriangleup )$ where $d_{\max }$ is the maximum degree of a vertex in U and $\bigtriangleup$ is the result size.

Proof

The time cost of LayerBasedListing can be divided into three parts, including (i) Lines 11–13, (ii) Lines 15–18, and (iii) Line 21. Since Lines 11–13 simply return the answers, it is immediate that the time cost of (i) is $O(\bigtriangleup )$. Since LayerBasedListing essentially enumerates all p-cliques on H, where the specific implementation follows that in [12], we have that the time cost of (iii) is $O(a(H)^{p-2}|E(H)|)$ as shown in [12]. Now, since the number of executions for (ii) can be bounded by $O(a(H)^{p-2}|E(H)|)$ and the time for each execution is $O(d_{\max })$, the time cost of (ii) is at most $O(a(H)^{p-2}|E(H)|d_{\max })$. Therefore, the overall time complexity is $O(a(H)^{p-2}|E(H)|d_{\max } +\bigtriangleup )$.

$\square$

Theorem 7

The space complexity of BCList++ is $O(|E(G)|+|E(H)|)$.

Proof

Apart from the bipartite graph G and its 2-hop graph H, the only information we need to store is the p vectors (i.e., S in Line 7) to collect the common neighbors of vertices in p-cliques on H. The space for this part is clearly bounded by graph size (i.e., |E(G)|). Thus, the theorem is immediate. $\square$

4.3.2 Cost model analysis

In BCList++, the first step is to choose the layer with the least computation cost to construct the 2-hop graph H (Lines 1–3 in Algorithms 3). Theorem 6 implies that we need to compute the arboricity a(H) of H, which is suggested as an open problem [20]. Harold [19] proposes a parametric flow-based method to compute the arboricity of an undirected graph $G=(V,E)$ with a time complexity of $O(|V||E|\log (|V|^2/|E|))$, which is, however, computationally costly for large graphs.

In practice, we observe that the average degree is a good substitution for the arboricity, since both of them are used to measure the “density” of a graph. Therefore, we use average degree to estimate the computation cost of BCList++ due to its high computation efficiency. A straightforward way is to directly compute the 2-hop neighbors for vertices in both layers using Algorithm 1. However, Theorem 1 shows that it is expensive to compute the exact 2-hop degree for all vertices in G.

In the following, we resort to a random sampling method to approximate the total 2-hop degree D for a given layer, say U(G). The intuition is to use the 2-hop degree of a sampled vertex to estimate the total 2-hop degree of vertices in U(G). Since the sampled local subgraph is typically much smaller than the original graph G, it is cost-saving to compute the 2-hop degree of sampled vertex instead.

Degree estimation Algorithm 4 illustrates the details of our degree estimation method. Note that we only introduce the computation for layer U(G), and computation for V(G) is similar. In each sampling, we choose a vertex u from U(G) uniformly at random (Line 1). We then compute the 2-hop degree $D_u$ of u using procedure TwoHopDegree (Line 2). Here, we skip introducing the details since it is basically a subroutine of Algorithm 1. Last, we return $n \cdot D_u$ as an estimation for the total 2-hop degree of vertices in U(G), where $n = |U(G)|$ (Line 3). It is easy to verify that the time complexity of DegreeEstimator is $O(d(u)d_{\max })$, where $d_{\max }$ is the maximum degree of vertices in V(G).

Next, we show that Algorithm 4 yields an unbiased estimation for the total degree of H. Let Y denote the value returned by Algorithm 4. Let D denote the true value of total degree of H. Let $p_s$ denote the number of degree pairs that attaching the same vertex. We have the following lemma.

Lemma 4

${\textbf{E}}[Y] = D$, and $\textbf{Var}[Y] \le n(D+p_s) - {D \atopwithdelims ()2}$.

Proof

Let $X=D_u$, the degree of the uniformly sampled vertex u. Consider that the degree in H is numbered from 1 to D. For $i=1,...,D$, let $X_i$ be an indicator random variable equal to 1 if the $i^{th}$ degree is attaching the vertex u. We have $X=\sum _{i=1}^{D}X_i$. Since each degree must come from a single vertex, we have that ${\textbf{E}}[X_i] = \textbf{Pr}[X_i = 1]=\dfrac{1}{n}$. Thus, ${\textbf{E}}[X] = {\textbf{E}}[\sum _{i=1}^{D}X_i] = \sum _{i=1}^{D}{\textbf{E}}[X_i] = \dfrac{D}{n}$. Since $Y=n\cdot X$, we have that ${\textbf{E}}[Y] = n\cdot {\textbf{E}}[X] = D$.

Next, we discuss the variance of Y.

$$\begin{aligned} \textbf{Var}[Y]&= \textbf{Var}[n\sum _{i=1}^{D}X_i] = n^2\textbf{Var}[\sum _{i=1}^DX_i] \\&=n^2(\sum _{i=1}^D\textbf{Var}[X_i] + \sum _{i \ne j}\textbf{Cov}(X_i,X_j)) \\&=n^2(\sum _{i=1}^D({\textbf{E}}[X_i^2]-({\textbf{E}}[X_i])^2) \\&+ \sum _{i \ne j}({\textbf{E}}[X_iX_j] -{\textbf{E}}[X_i]{\textbf{E}}[X_j])) \end{aligned}$$

To calculate the covariance of two random variables $X_i$ and $X_j$, we evaluate the joint probability of different degrees being sampled together. Clearly, the set of all degree pairs can be divided into two categories, namely attaching the same vertex and attaching different vertices.

For these attaching different vertices, there is zero probability that two degrees are sampled together since we only draw a single vertex each time. Hence, ${\textbf{E}}[X_iX_j] = 0$ and $\textbf{Cov}(X_i,X_j)=-\dfrac{1}{n^2}$.

For these attaching the same vertex, ${\textbf{E}}[X_iX_j] = \textbf{Pr}[X_i=1,X_j=1] = \textbf{Pr}[X_i=1]\textbf{Pr}[X_j=1|X_i=1] = \dfrac{1}{n}\cdot 1 =\dfrac{1}{n}$. Thus, $\textbf{Cov}(X_i,X_j)=\dfrac{1}{n} - \dfrac{1}{n^2}$.

Recall that $p_s$ denote the number of degree pairs attaching the same vertex. Further, by $p_d$, we denote the number of degree pairs attaching different vertices. Since the total degree is D, we have that $p_d + p_s = {D \atopwithdelims ()2}$.

Therefore, we have that $\textbf{Var}[Y] = n^2(D(\dfrac{1}{n} - \dfrac{1}{n^2}) + p_d (-\dfrac{1}{n^2}) + p_s (\dfrac{1}{n} - \dfrac{1}{n^2})) = D(n-1) + np_s - p_d - p_s =$ $D(n-1) - {D \atopwithdelims ()2} + np_s \le n(D+p_s) - {D \atopwithdelims ()2}$. $\square$

Let Z be the average of r independent instances of Y. According to the fact that $\textbf{Var}[Z] = \textbf{Var}[Y]/r$ and Chebyshev’s inequality, we have $\textbf{Pr}[|Z - D| \ge \epsilon D] \le \dfrac{\textbf{Var}[Z]}{\epsilon ^2 D^2} = \dfrac{\textbf{Var}[Y]}{r\epsilon ^2 D^2}$. Next, we show that by running Algorithm 4 multiple independent instances, we can obtain an $(\epsilon , \delta )$-estimator using standard method.

Lemma 5

There is an algorithm that runs $r=\dfrac{n}{\epsilon ^2 \delta }(\dfrac{1}{D}+\dfrac{p_s}{D^2}) - \dfrac{1}{2\epsilon ^2 \delta }$ independent times of Algorithm 4 and provides an $(\epsilon , \delta )$-estimator of D.

Proof

Since $\textbf{Pr}[|Z - D| \ge \epsilon D] \le \dfrac{\textbf{Var}[Y]}{r\epsilon ^2 D^2}$, let $\delta = \dfrac{\textbf{Var}[Y]}{r\epsilon ^2 D^2}$. It is easy to obtain that $r=\dfrac{n}{\epsilon ^2 \delta }(\dfrac{1}{D}+\dfrac{p_s}{D^2}) - \dfrac{1}{2\epsilon ^2 \delta }$. $\square$

Overall cost model We now proceed to estimate the overall computational cost of LayerBasedListing. According to Theorem 6, for layer U(G), we have

$$\begin{aligned} \textsf{Cost}(U(G), p) = (D/|U(G)|)^{p-2}Dd_{\max } \end{aligned}$$

(1)

where D is estimated by Algorithm 4, and $d_{\max }$ is the maximum degree of vertices in U(G). The cost on V(G) can be computed similarly. We omit $\bigtriangleup$ for both $\textsf{Cost}(U(G),p)$ and $\textsf{Cost}(V(G),q)$.

5 Optimizations

In this section, we develop optimizations to further boost the performance of our proposals.

5.1 Graph reduction

We proceed to show how to reduce the bipartite graph by exploiting some properties of our problem.

Core reduction. To reduce the size of the bipartite graph, a promising way is to remove vertices having degrees that are small enough. This is because a vertex u contributing a ($p$, $q$)-biclique must have degree at least q if $u \in U(G)$, otherwise p. We can repeat this operation until all remaining vertices satisfy this condition. Particularly, the remaining subgraph can be formally formulated by the so-called $(\alpha , \beta )$-core, which is defined as below [16, 30].

Definition 7

($(\alpha , \beta )$-core) Given a bipartite graph $G=(U, V, E)$, and two integers $\alpha$ and $\beta$, the $(\alpha , \beta )$-core of G, denoted by $C_{\alpha , \beta }(G)$, is a maximal subgraph of G induced by two vertex sets $U_C \subseteq U$ and $V_C \subseteq V$, in which all vertices in $U_C$ have degree at least $\alpha$ and all vertices in $V_C$ have degree at least $\beta$, i.e., $\forall u \in U_C, d(u) \ge \alpha \wedge \forall v \in V_C, d(v) \ge \beta$.

Given a bipartite graph G, the state-of-the-art algorithm computes its $(\alpha , \beta )$-core in linear time (i.e., O(|E(G)|)) [16]. Intuitively, it computes $(\alpha , \beta )$-core by iteratively removing vertices in U(G) with degree smaller than $\alpha$ and vertices in V(G) with degree smaller than $\beta$ until no more vertices can be removed. Based on the $(\alpha , \beta )$-core, we derive the following lemma.

Lemma 6

Given a bipartite graph $G=(U, V, E)$ and two integers p and q, let C be the (q, p)-core of G. Then, for any ($p$, $q$)-biclique B(L, R) exists in G, B must be in C, i.e., $\forall B(L, R) \subseteq G$, we have $B \subseteq C$.

Proof

We prove by contradiction. Suppose B(L, R) exists in G while not in C. Then, there must be at least one vertex in B(L, R) not existing in C, say $u \in L$. According to Definition 7, we have that $d(u, G) < q$, which is contradicted to the fact that $d(u, G) \ge q$ must hold since u is in a ($p$, $q$)-biclique. Thus, the lemma is complete. $\square$

Based on Lemma 6, we can safely reduce the size of the bipartite graph without missing results, which can be applied to both BCList and BCList++.

Example 8

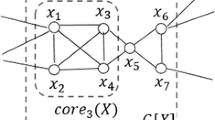
Continuing our running example in Fig. 1 with $p=2$ and $q=3$, we compute (3, 2)-core as follows. We first remove $u_0$ and $v_0$. Then, we remove $u_4$ since $d(u_4)=2$ which is smaller than $q=3$. After that, $v_5$ can be removed since currently $d(u_5)=1$. At this point, no more vertex can be further removed, and the remaining subgraph is a (3, 2)-core. The number of vertices in the graph is reduced from 11 to 7.

5.2 Parallelization

One appealing property of BCList is that it can enumerate ($p$, $q$)-bicliques in parallel when multiple threading is available. That is because the entire search space of ($p$, $q$)-bicliques is materialized by a recursion tree, in which the answers fall only in the leaf nodes. BCList can use a thread to process a subtree of the recursion tree to enumerate a sub-space independently.

Our empirical studies show that BCList++ is much more efficient and scalable on large datasets. Therefore, in this paper, we focus on parallelizing BCList++. Particularly, we initiate a thread for each subgraph $H'$ of the 2-hop graph H induced by each vertex $u \in U(H)$. Algorithm 5 illustrates the details of parallel version of BCList++. Specifically, we only need to replace Line 8 of Algorithm 3 with Lines 2–4 of Algorithm 5.

6 Handling uncertain graphs

In this section, we extend our techniques to handle uncertain bipartite graphs. We first give the problem definition in Sect. 6.1. We then introduce a baseline method in Sect. 6.2, followed by an improved method in Sect. 6.3.

Fig. 4

An example uncertain bipartite graph ${\mathcal {G}}$

6.1 Problem definition

Definition 8

(Uncertain Bipartite Graph) An uncertain bipartite graph is a pair ${\mathcal {G}} = (G, P)$, where $G = (U,V,E)$ is a deterministic bipartite graph, and $P:E\rightarrow (0, 1]$ is a mapping function assigned to each edge $e \in E$ a nonzero existential probability $Pr(e) \in (0, 1]$.

Given an uncertain bipartite graph ${\mathcal {G}} = (G, P)$, we also say G is the backbone of ${\mathcal {G}}$. An example uncertain bipartite graph is shown in Fig. 4. In this paper, we follow the conventional Possible World Semantics [3, 24, 32, 58]. More specifically, we assume the existential probability of each edge in ${\mathcal {G}}$ is independent of each other, and ${\mathcal {G}}$ can be interpreted by a set of $2^{|E|}$ possible worlds $\{G_0,..., G_{2^{|E|-1}}\}$, where each possible world $G_i$ represents one possible outcome by randomly determining if each edge $e \in E$ exists in $G_i$ based on Pr(e). The existential probability of each possible world $G_i \in {\mathcal {G}}$ can be computed as follows.

$$\begin{aligned} Pr(G_i) = \prod _{e \in E(G_i)}Pr(e) \prod _{e \in E \setminus E(G_i)} (1-Pr(e)). \end{aligned}$$

(2)

Based on the above uncertain bipartite graph model, we have the following lemma which is the foundation of the methodology presented in this section.

Lemma 7

Given an uncertain bipartite graph ${\mathcal {G}} = (G, P)$, for any substructure $g \subseteq G$, the existential probability of g can be calculated by $Pr(g) = \prod _{e \in E(g)}Pr(e)$.

Proof

According to the possible world semantics, the existential probability of g is the total sum of existential probabilities for all possible worlds containing g. We divide the edges in G into two groups, including E(g) and $E(G){\setminus } E(g)$. Clearly, each existence status for edges in $E(G) \setminus E(g)$ defines a unique possible world that contains g. By $\tilde{{\mathcal {G}}}$, we denote these $2^{|E(G)\setminus E(g)|}$ possible worlds. Then, we have:

$$\begin{aligned} Pr(g)&= Pr(\tilde{{\mathcal {G}}}) = \sum _{G_i \in \tilde{{\mathcal {G}}}}Pr(G_i) \\&= \sum _{G_i \in \tilde{{\mathcal {G}}}}\prod _{e\in E(g)}Pr(e) \\&\cdot \prod _{e\in E(G_i)\setminus E(g)}Pr(e) \prod _{e\in E\setminus E(G_i)}(1-Pr(e)) \\&= \prod _{e\in E(g)}Pr(e) \\&\cdot \sum _{G_i \in \tilde{{\mathcal {G}}}} \prod _{e\in E(G_i)\setminus E(g)}Pr(e) \prod _{e\in E\setminus E(G_i)}(1-Pr(e)) \\&= \prod _{e\in E(g)}Pr(e), \end{aligned}$$

where the last step is based on Law of Total Probability. $\square$

Next, we introduce the concept of uncertain ($p$, $q$)-biclique, followed by its counting and enumeration problem.

Definition 9

(Uncertain (p, q)-biclique) Given an uncertain bipartite graph ${\mathcal {G}} = (G, P)$, and two integer parameters p and q, an uncertain ($p$, $q$)-biclique is topologically a ($p$, $q$)-biclique in the backbone graph G.

Based on Lemma 7, the existential probability of an uncertain ($p$, $q$)-biclique B can be calculated by $Pr(B)=\prod _{e \in E(B)}Pr(e)$. For instance, the existential probability of the (2, 2)-biclique $(\{u_0, u_1\}, \{v_1,v_2\})$ in Fig. 4 is $0.6 \times 0.5 \times 0.7 \times 0.8 = 0.168$.

Problem statement. Given an uncertain bipartite graph ${\mathcal {G}} = (G, P)$, two integers p and q, and an existential probability threshold t, we study the problem of counting and enumerating uncertain ($p$, $q$)-bicliques in ${\mathcal {G}}$ whose existential probability are greater than or equal to t.

Example 9

Consider the uncertain bipartite graph in Fig. 4. Assuming that $p=q=2$ and $t=0.1$, there is only one uncertain ($p$, $q$)-biclique, i.e., $(\{u_0, u_1\}, \{v_1,v_2\})$. Note that, although $(\{u_2, u_3\}, \{v_3, v_4\})$ is also a (2, 2)-biclique, it is not a final result because its existential probability is $0.06 < t$.

6.2 A baseline method

In this section, we develop a baseline method to the uncertain ($p$, $q$)-biclique counting and enumeration problem.

A promising baseline method is to extend the algorithms for the deterministic variation of our problem, such as BCList and BCList++ proposed in previous sections. Here, we focus on extending BCList++ due to its superior performance improvement over BCList as suggested in our experimental studies in Sect. 7. The main idea of our baseline method is to enumerate ($p$, $q$)-bicliques on the backbone graph and return these satisfying the existential probability threshold. To accelerate the computation, we can reduce the uncertain bipartite graph by discarding edges with existential probability lower than the probability threshold. It is worth mentioning that all the graph reduction techniques in Sect. 5.1 are also applicable to the methods developed in this section.

Lemma 8

Given an edge e and the existential probability threshold t, if $Pr(e) < t$, then e cannot be a part of any uncertain ($p$, $q$)-bicliques.

Proof

Since all probabilities must not be larger than 1, this lemma can be proved trivially. $\square$

Algorithm details. Algorithm 6 illustrates the details of the baseline algorithm UBCList. We first reduce the graph by discarding edges with existential probability lower than the threshold t (Line 1). Then, we extract the backbone graph G of the uncertain bipartite graph ${\mathcal {G}}$ (Line 2). Last, we utilize the same strategy of BCList++ to enumerate the ($p$, $q$)-bicliques on the backbone graph G (Line 3). The only difference is the result verification where we only keep ($p$, $q$)-bicliques with existential probability no less than t (Line 8–9). The correctness of UBCList is immediate since it explicitly examines all ($p$, $q$)-bicliques on the backbone graph. The time and space complexity of UBCList are the same as BCList++.

6.3 An improved method

In the baseline method, we need to enumerate all ($p$, $q$)-bicliques in the backbone bipartite graph and then discard those with existential probability lower than the threshold. One may ask the following question. Can we discard some unpromising ($p$, $q$)-bicliques earlier before enumerating them completely? We answer this question positively. In this section, we develop efficient pruning techniques to boost the computation performance.

Early candidate discarding. Recall that, Lemma 8 states that we can safely reduce the size of the uncertain graph by removing edges with probability lower than the probability threshold. In fact, we can generalize this logic to any other graphlet structures of a ($p$, $q$)-biclique. By taking the existential probability into consideration, we can further refine the common neighbor set or even terminate the current search branch early. Next, we start with the concept of k-star.

Definition 10

(k-Star) Given an uncertain bipartite graph ${\mathcal {G}} = (G, P)$, a k-star of ${\mathcal {G}}$ is a subgraph of ${\mathcal {G}}$ induced by a vertex in ${\mathcal {G}}$ and its k neighbors.

We say a k-star, denoted by $s_v$, is anchored on vertex v if v is the center vertex; that is $s_v$ is induced by v and its k neighbors. Clear, a k-star s consists of k edges with a common end vertex, and the existential probability of s is calculated by $Pr(s) = \prod _{e \in E(s)} Pr(e)$ according to Lemma 7.

Common neighbors refinement. Recall that, in BCList++, we generate ($p$, $q$)-bicliques by recursively enumerating p-cliques on the 2-hop graph H, and simultaneously collecting their common neighbors in G. Specifically, in Lines 3-3 of Algorithm 3, we collect the common neighbors of vertices in the partial clique. In the following discussion, we focus on a specific search state of BCList++, which is represented by $\Omega (L, C)$, where L is a k-clique in H with $1 \le k \le p$, and C is a set of common neighbors of L in G. The following lemma states that we can refine the common neighbors C by removing vertices with k-star probability lower than the existential probability threshold.

Fig. 5

An example of intermediate search state

Lemma 9

Given a search state $\Omega (L, C)$ and the existential probability threshold t, let v be a vertex in C and $s_v$ be the k-star induced by v and the k vertices in L. Then, v can be removed from C if $Pr(s_v) < t$.

Proof

Since L is the partial clique, for any vertex $v \in C$, v must be connecting to all k vertices in L. Due to the fact all probabilities must be lower than 1, the k-star $s_v$ cannot be a part of any ($p$, $q$)-biclique if $Pr(s_v) < t$. Therefore, v can be removed from C. $\square$

Example 10

Consider the example in Fig. 5, where we assume $p=3$, $q=2$, and $t=0.4$. In the current search state, we have $L=\{u_0, u_1\}$ and $C=\{v_0,v_1,v_2,v_3\}$. Based on Lemma 9, we can remove $v_3$ from C since its corresponding 2-star existential probability is $0.3 < t$.

Branch early termination. During the search processing, if the existential probability of the k-star of vertices in C is small enough, we may stop exploiting the current branch without missing any results.

Lemma 10

Given a search state $\Omega (L, C)$ and the existential probability threshold t, let $\Psi$ be the q vertices in C with the largest k-star existential probability. Then, we can stop exploiting the current branch if $\Pi _{v \in \Psi }Pr(s_v) < t$.

Proof

Given any uncertain biclique B generated under the current search branch, B must contain q vertices in C, which we denote by $\Psi '$. Then, we have $Pr(B) \le \Pi _{v \in \Psi '}Pr(s_v) \le \Pi _{v \in \Psi }Pr(s_v) < t$, where the first inequality follows the facts that a biclique must contain all stars of the q vertices in $\Psi '$ and all probabilities must be lower than 1. $\square$

Example 11

Continuing the example in Fig. 5, we have that $\Psi = \{v_0, v_1\}$ because they have the largest 2-star existential probability. Now, since $Pr(s_{v_0})Pr(s_{v_1}) = 0.9\times 0.7\times 0.8\times 0.7=0.3528$ which is smaller than the probability threshold $t=0.4$, we can stop exploiting the current search branch.

Corollary 2

Given a search state $\Omega (L, C)$ and the existential probability threshold t, let $\Psi$ be the $q-1$ vertices in C with the largest k-star existential probability. Then, for any vertex $w \in C-\Psi$, it can be removed from C if $Pr(s_w)\Pi _{v \in \Psi }Pr(s_v) < t$.

Clearly, Corollary 2 is a generic case of Lemma 10, which can be employed to further refine the common neighbors of vertices in the partial clique.

6.3.1 IUBCList algorithm

Algorithm 7 illustrates the details of our improved method IUBCList. In general, it adopts the same computation paradigm as the baseline method as shown in Lines 1–3. The improvement is achieved in the recursive searching step by making use of the k-star structure.

In specific, when collecting the common neighbors of the vertex u and previous vertices in L, we also calculate the k-star existential probability and only keep these with existential probability no smaller than t (Lines 16–20). After that, we may be able to skip the current branch if the number of common neighbors is less than q (i.e., $|S[l]| < q$), or there is not enough vertices to expand L (i.e., $|N(u, H)| < p-l-1$). We may also be able to skip the current branch if the k-star probabilities are small enough based on Lemma 10 (Lines 23–25). Besides, we may further refine the common neighbors of vertices in L according to Corollary 2 (Lines 26–29).

Theorem 8

IUBCList enumerates uncertain ($p$, $q$)-bicliques correctly.

Proof

On the one hand, it is clear that IUBCList is built upon BCList++, which implies that the uncertain ($p$, $q$)-bicliques enumerated by IUBCList are topologically correct. On the other hand, the correctness of existential probability-based pruning rules is guaranteed by Lemma 9, Lemma 10, and Corollary 2 together. Thus, the theorem holds. $\square$

Theorem 9

IUBCList has the same time and space complexities as BCList++.

Proof

Time complexity Compared to BCList++, one extra task is to find q vertices with the largest k-star existential probability (Lines 23–29). Since the number of common neighbors is bounded by $O(d_{\max })$, the time for each execution of this task is $O(d_{\max })$ by using Bin sort, which is the same as common neighbor collecting in BCList++. Space complexity Compared to BCList++, the only extra information we need to keep is the existential probabilities for k-stars. Since we only record a single probability value for each common neighbor, it is immediate the space complexity of IUBCList is the same as BCList++. $\square$

6.4 Discussion for counting problem

It is easy to see that the counting problem of our uncertain ($p$, $q$)-bicliques is basically the same as enumeration problem. This is because, in both UBCList and IUBCList, we need to verify the existential probability for each enumerated ($p$, $q$)-biclique.

7 Experimental study

Table 3 Some characteristics of datasets

In this section, we empirically evaluate the performance of the proposed techniques. All experiments are conducted on PCs with Intel Xeon 2 $\times$ 2.4GHz CPU containing 40 cores and 128GB RAM running Ubuntu 20.04.2 LTS. Unless otherwise specified, we run algorithms against a single core. We terminate an algorithm if the running time is more than 10 hours which is denoted as INF.

7.1 Experimental setup

Algorithms. In the experiments, we evaluate the following algorithms for counting by default.

• BClist The baseline method proposed in Sect. 3.

• BClist++ The advanced approach devised in Sect. 4.

• PMBE Adapted algorithm from the state of the art for maximal biclique enumeration proposed in [2].

• BFC-VP$^{++}$ The state-of-the-art butterfly counting algorithm proposed in [52].

• BFC Butterfly counting algorithm proposed in [40].

• UBCList The baseline method for uncertain ($p$, $q$)-biclique counting and enumeration proposed in 6.2.

• IUBCList The improved method for uncertain ($p$, $q$)-biclique counting and enumeration proposed in 6.3.

It is easy to verify that a ($p$, $q$)-biclique must be contained by maximal bicliques with at least p and q vertices in the left and right side, respectively. With this property, we can immediately come up with another baseline method as follows. First, applying the off-the-shelf maximal biclique enumeration algorithms to list all maximal bicliques with size constraint and then enumerating all ($p$, $q$)-bicliques from the obtained maximal bicliques and removing the duplicates. The state-of-the-art algorithm, called PMBE [2], offers a threshold-based solution for maximal biclique enumeration, which is much more efficient than the version without threshold. For presentation convenience, we use the name of PMBE to denote the adapted algorithm for our problem. We obtain the source codes of PMBE from the authors of [2]. To ensure the fairness, in our experiments, we only record the time cost of PMBE for enumerating maximal bicliques, while ignoring the time for enumerating ($p$, $q$)-bicliques and remvoing duplicates. For BFC-VP $^{++}$ and BFC, we obtain the source code from the authors of [52] and [40], respectively. All algorithms are implemented in standard C++ with STL library support and compiled with GNU GCC, except PMBE, which is implemented in Java and the JVM maximum heap size is set to large enough for all datasets.

Fig. 6

Effect of vertex orderings ($p=4$ and $q=4$)

Datasets. We use 18 real datasets selected from different domains with various data properties. All datasets are obtained from KONECT,³ some of which are used to evaluate the algorithms for related problems [31, 40, 52, 54]. The detailed characteristics of the 16 datasets are shown in Table 3. We choose 4 representative datasets from Table 3 as default datasets, including Youtube, Stackoverflow, Twitter, and Edit-id, which cover different types of datasets, and various graph scales. To evaluate the uncertain problem, we employ both real-life probabilistic graphs and simulated graphs. Specifically, COVID-19 [1] and Human [11] are two gene expression datasets, where the edge probability value is a normalized gene expression level, and Bookcrossing and Amazon are rating graphs, where the edge probability are is a normalized rating score. We use the value normalization strategy adopted by [57]. For the remaining datasets, we randomly assign a synthetic probability to each edge by following a specific distribution. In this paper, we choose uniform and normal distribution, where the parameters for normal distribution vary between datasets to add variety to each individual graph. For example, on Record, the mean and standard deviation are 0.6 and 0.2, respectively.

Fig. 7

Effect of cost model

Queries. To better evaluate our proposals, we generate multiple (p, q) settings by fixing the value of $p+q=8$ and varying values of p and q from 2 to 6 by default. Unless otherwise specified, experiments are conducted with $p=4$ and $q=4$ by default.

7.2 Performance tuning

Exp-1: Effect of vertex ordering. We start by evaluating the effect of vertex ordering. We evaluate three vertex orderings, including degree, core, and random. Note that, we use the combination of algorithm name and order name. For example, BCList(Degree) stands for BCList using degree ordering. Figure 6a shows the results for BCList. Generally, both BCList(Degree) and BCList(Core) run quite stably compared with BCList(Random), and BCList(Degree) is slightly faster than BCList(Core). Figure 6b reports the results for BCList++. On one hand, we observe that BCList++(Degree) achieves the best performance under most datasets. On the other hand, the performance gap between BCList++(Degree) and others is very marginal. This implies that the performance improvement brought by vertex ordering is limited. In the following experiments, we use degree vertex order for both BCList and BCList++.

Exp-2: Effect of cost model. We evaluate the effectiveness of the cost model, which is proposed in Sect. 4.3. By BCList++(NM), we denote BCList++ without the cost model. The number of sampling iterations is set to $0.01\times |U(H)|$, where U(H) is the vertex set in the selected layer. Figure 7 reports the experiment results. Not surprisingly, the cost model has a huge impact on the performance of BCList++. For example, BCList++(NM) cannot even handle the smallest dataset Youtube when $p=6$ and $q=2$, while BCList++ can finish in less than one second. It is generally observed that BCList++ can achieve at least one order of magnitude performance improvement by using the cost model. Besides, the performance improvement enlarges quickly as the difference between p and q increases. This is because the time complexity of BCList++ is exponential to the value of p or q. Overall, our cost model can judiciously choose the layer with the least cost by taking both the graph size and values of p and q into consideration.

Exp-3: Evaluating graph reduction. Figure 8 evaluates the effectiveness of the graph reduction techniques proposed in Sect. 5.1. In particular, Fig. 8a reports the experimental results for BCList, where BCList(NR) stands for BCList without graph reduction techniques. We observe that, by using graph reduction, BCList can achieve roughly $10\%$ of performance improvement on Stackoverflow and Twitter. Figure 8b reports the experimental results for BCList++. It is observed that BCList++ runs 4 times faster on Stackoverflow than BCList++(NR). However, the benefit brought by graph reduction seems limited for both BCList and BCList++ on Youtube and Edit-id. The reason is that the most time-consuming part is the recursion search for enumerating ($p$, $q$)-bicliques.

Fig. 8

Evaluating graph reduction ($p=4$ and $q=4$)

Fig. 9

Evaluation over all datasets ($p=4$ and $q=4$)

7.3 Performance evaluation

Exp-4: Experiments over all datasets. We now proceed to compare BCList++ with the two baseline algorithms BCList and PMBE on all 16 datasets in terms of both processing time and memory usage. Processing time It is reported in Fig. 9a that BCList++ significantly outperforms the competitors on most datasets regarding processing time. Among the two baseline methods, BCList runs much faster than PMBE does on most datasets. For example, it is at least 2 orders of magnitude faster than PMBE on Actor-movie, IMDB, or DBLP. We observe that BCList is beaten by PMBE on two datasets Edit-en and Edit-fr. The reason is that these datasets are rather unbalanced, and the number of 2-hop neighbors of vertices on the “heavy” layer is quite large. Generally, PMBE can only process relatively small datasets, e.g., Record, Youtube, and CiteSeer, while neither of the two baseline methods can handle large datasets, e.g., Edit-id, Edit-fa, and Edit-ar. PMBE even runs into INF on Github, which only contains 440 thousands of edges. From the results shown in Fig. 9a, we notice that BCList++ is much more efficient and scalable than its compititors, and outperforms the competitors by more than one order of magnitude on datasets such as Youtube, Github, Stackoverflow, and Twitter. This is because BCList++ adopts an efficient layer-based search strategy equipped with a highly effective cost model as shown in Fig. 7. Memory usage Fig. 9b reports the memory usage of the three algorithms. Note that we do not show the memory usage for an algorithm if its running time is INF on the corresponding dataset. In general, BCList consumes the least amount of memory, and BCList++ consumes a bit more memory than BCList. This is because we implement BCList++ with extra arrays to avoid creating the subgraphs frequently. The memory usage of PMBE is much larger than that of our algorithms. For example, PMBE could consume up to an order of magnitude more memory on datasets such as Youtube and CiteSeer. The reason is that PMBE needs to build a heavy index structure to facilitate the enumeration. The only exceptions occur on Edit-en and Edit-fr where BCList consumes the most amount of memory. This is still because the amount of 2-hop neighbors of vertices on the “heavy” layer of such unbalanced bipartite graphs is large, which however can be avoided by BCList++ by selecting the other layer using the cost model.

Fig. 10

Varying values of p and q

Fig. 11

Varying graph scale ($p=4$ and $q=4$)

Fig. 12

Evaluating the parallelization ($p=4$ and $q=4$)

Exp-5: Varying values of p and q. To evaluate the effect of p and q values, we conduct experiments on the default (p, q) settings where $p+q = 8$, and p and q vary from 2 to 6. Figure 10 reports the experiment results. It is reported that, compared to the baseline methods, BCList++ is much more friendly to queries when the difference between p and q is large. For example, on Twitter shown in Fig. 10c, when $p=2$ and $q=6$, BCList runs into INF and PMBE spends near 10 hours, while it only takes less than 7 seconds for BCList++ to finish. This is because BCList++ is equipped with a cost model, which can judiciously select the layer with the least computation cost as our search layer by considering the values of p and q. Even under queries with the same values of p and q (i.e., $p=q=4$), BCList++ is still more than one order of magnitude faster than its competitors on all datasets. To better evaluate the effect of p and q values, we conduct experiments on extra (p, q) settings. More specifically, we fix the ratio p/q or q/p as 2 and increase the value of $p+q$ from 6 to 12. The experimental results are shown in Fig. 10e–h. Overall, BCList++ is at least two orders of magnitude faster than the baseline methods under all query settings. Interestingly, the running time of BCList++ grows steadily as $p+q$ increases, while that of PMBE declines contrarily. This is because PMBE is a threshold-based method. Since the number of maximal bicliques decreases as the size constraints (i.e., values of p and q) increase, PMBE runs more efficiently.

Exp-6: Varying graph scale. In this experiment, we test the effect of graph size. For each dataset, we randomly sample $20\%$, $40\%$, $60\%$, $80\%$, and $100\%$ edges from the original dataset, and conduct experiment on each sampled dataset. Figure 11 reports that the running time of the algorithms grows as the size increases on all datasets, and the performance ranks of the algorithms remain the same under most of the settings. It is also observed that our algorithms BCList and BCList++ perform more steadily than PMBE, and BCList++ is much more scalable than others.

Fig. 13

Evaluating butterfly counting

Fig. 14

Information aggregation in GNN

Fig. 15

Evaluating GNN information aggregation

Exp-7: Evaluating the parallelization. To better evaluate the parallel performance of BCList++, we choose 4 most time-consuming datasets for BCList++, i.e., Github, Edit-id, Edit-fa, and Edit-ar, as shown in Fig. 9a. Figure 12 reports the experiment results where the thread number varies from 1 to 16. we observe that the running time of BCList++ decreases almost linearly as the thread number increases on all datasets, which implies that BCList++ is very parallel-friendly.

Exp-8: Evaluating butterfly counting. In this experiment, we evaluate the performance of algorithms for butterfly counting (i.e., $p=2$ and $q=2$). PMBE is excluded from the evaluation because it failed to give response within 10 hours on most of datasets. Figure 13 shows the experiment results. Interestingly, we observe that although BCList++ is not particularly designed for butterfly counting, it is still quite competitive compared with the state-of-the-art butterfly counting algorithms, such as BFC-VP $^{++}$ and BFC. As we can see, BCList++ even ranks the first on dataset Youtube and Twitter. BCList++ is relatively slow on Edit-id. This reason is that Edit-id is a large graph, and BCList++ needs to execute the step of cost estimation, which deteriorates the performance of BCList++.

7.4 Case study for deterministic graph

($p$, $q$)-biclique can be used to optimize the efficiency of Graph Neural Network (GNN) which has been one of the most successful and extensively studied research topics in recent years [21, 49, 55]. A pivotal operation in a GNN is to recursively aggregate information from vertices’ neighbors in graph. A naive method simply propagates information on each pair of vertices separately. Observing that vertices in a graph usually share many neighbors, this naive method leads to redundant computations. To improve the computation efficiency, Jia et al. [25] propose a new GNN representation technique called hierarchically aggregated computation graphs (HAGs) aiming at reducing the number of sum operations. Interestingly, we observe that ($p$, $q$)-biclique enumeration can be applied on the task of GNN information aggregation.

Fig. 16

Varying values of uncertainty threshold t ($p=4$ and $q=4$)

Example 12

A running example for information aggregation in a GNN under different methods is shown in Fig. 14, where Fig. 14a shows the input graph. Figure 14b shows just a single layer of the GNN-graph of the input graph in Fig. 14a. For instance, for vertex A, its new activation $h_A^k$ at layer k is computed by aggregating its neighbors’ activations $h_A^{k-1}$, $h_B^{k-1}$, and $h_C^{k-1}$ at layer $k-1$. Note that we consider aggregating vertex’s own activation as well. Thus, 2 sum operations occur on A. The new activations of other vertices can be computed similarly. Clearly, the naive method generates 8 sum operations in total. In Fig. 14c, HAG considers merging the common neighbors of A and C, including A, B, and C, where 2 sum operations are needed for merging them to $a_1$. Similarly, we have that 1 and 2 sum operations occur on $a_2$ and B, respectively. Therefore, the total number of sum operations for HAG is 5. Last, in our ($p$, $q$)-biclique-based method, the two sides of vertices of the aggregation layer are naturally considered as a bipartite graph (Fig. 14d), where both sides contain exactly the same number of vertices as input graph. In the (3, 3)-biclique (marked by dashed rectangle), 2 sum operations are required, that is merging $A_{k-1}$, $B_{k-1}$, and $C_{k-1}$ together. Besides, both $B_k$ and $D_k$ need an extra sum operation. Thus, our ($p$, $q$)-biclique-based method needs the least amount of 4 sum operations.

We conduct experiments on two datasets, namely IMDB (with 19, 502 vertices and 197, 806 edges) and PPI (with 56, 944 vertices and 1, 612, 348 edges), both of which are employed to evaluate the performance of HAG [25]. The experiment results shown in Fig. 15 report that our ($p$, $q$)-biclique-based method achieves the best performance when (p, q) are (5, 10) and (4, 10) on IMDB and PPI, respectively, and outperforms the competitors by near an order of magnitude for GNN information aggregation.

Algorithm applying details. According to Example 12, to reduce the number of activation propagations, a promising way is to extract bicliques (not necessarily ($p$, $q$)-bicliques) as much and large as possible. To this end, we need to consider two things as follows. (i) The number of edges covered by bicliques should be large and the number of bicliques should be small; (ii) There is no overlapping between the bicliques that we feed to GNN information aggregation. To realize these two things, we perform the following 3 steps. First, after retrieving ($p$, $q$)-bicliques by algorithms such as BCList++, we merge them together as much as possible. That is, for two bicliques $B_1(L_1, R_1)$ and $B_2(L_2, R_2)$, we merge them together to form a larger biclique if $L_1 = L_2$ or $R_1 = R_2$. Second, we apply a greedy method to iteratively choose the bicliques. In specific, at each step, we choose the largest biclique which does not contain any edge that is covered by previously chosen bicliques. We repeat this step until there is no such bicliques. Last, We feed these selected bicliques to GNN information aggregation.

Fig. 17

Evaluating uncertain algorithms over all datasets ($p=4$, $q=4$ and $t=0.01$)

One may ask that maximal biclique-based method might be also applicable to this task. However, our preliminary experimental results show that maximal biclique enumerating itself is time-consuming. For example, on both IMDB and PPI, the state-of-the-art maximal biclique enumerating method [2] failed to return answers within 10 hours, while our ($p$, $q$)-biclique-based method can finish in one minute.

7.5 Evaluations on uncertain graphs

Exp-9: Varying values of threshold t. To evaluate the effect of the uncertainty threshold t, we conduct experiments on the 4 default datasets by varying t from 0.00001 to 0.1. The experiment results are shown in Fig. 16. In specific, Fig. 16a–d reports the running time for the two uncertain algorithms. It is observed that IUBCList runs much faster than UBCList under all settings. Especially, the performance gap enlarges dramatically as the uncertainty threshold increases. For example, on Twitter, IUBCList can finish in 49 seconds, while UBCList needs 18814 seconds when $t=0.01$. This is because the common neighbor refinement and branch early termination techniques can substantially reduce the search space when t increases. To better understand the experimental results, we also report the result size in Fig. 16e–h, where #Results(Uncertain) and #Results(Deterministic) denote the number of results in the uncertain graph and its deterministic graph (i.e., backbone graph), respectively. As we can see, the result size decreases as t increases. Note that both IUBCList and UBCList run into INF on Edit-id when $t \le 0.0001$, as shown in Fig. 16d. This reason is that the result size is extremely large under these settings since the result size on backbone graphs is over $10^{18}$. Thus, it takes a large amount of time for IUBCList to verify the existential probability.

Exp-10: Experiments over all datasets. In the last experiment, we evaluate the uncertain algorithms over all datasets. Figure 17 reports the experiment results. We observe from Fig. 17a that IUBCList significantly outperforms UBCList on difficult datasets, such as, Twitter, Edit-en, Edit-fr, etc. This is because IUBCList is equipped with efficient search space pruning techniques. It is also observed that UBCList cannot even handle two relatively small datasets COVID-19 and Human. The reason is that COVID-19 and Human are two dense gene expression graphs with average degrees 119.38 and 175.22, respectively. Thus, there are a huge amount of ($p$, $q$)-bicliques to verify for UBCList. The memory consumption is rather similar for IUBCList and UBCList as shown in Fig. 17b. The reason is that both of the two algorithms are developed on top of BCList++, and the only extra information we need to store is the edge probability.

Fig. 18

Results on COVID-19 with $p=5$, $q=5$ and $t=0.68$

7.6 Case study for uncertain graph

We focus on a gene expression dataset called COVID-19 which is collected from [1]. As shown in Table 3, COVID-19 contains 293 whole blood samples from COVID-19 convalescent donors and healthy donors. These samples are conducted experiments against 75 mRNAs. Thus, the samples and mRNAs are naturally modeled as an uncertain bipartite graph, where the edge probability values reflect the expression level, which is obtained by NanoString Technologies. We first conduct experiments with $p=5$, $q=5$ and $t=0.68$. Figure 18 reports a resulting ($p$, $q$)-biclique, where we depict the edge probabilities that are less than 1. In this biclique, GSM6469396 is a healthy donor and the others are convalescent donors. As we can see, the 5 mRNAs all shown high level of expression on the 5 samples, doctors could focus on these mRNAs to explore the key to dealing with COVID-19. For example, the 5 mRNAs may work together to protect the body against COVID-19 virus. By inspecting such mRNA and sample groups, a professional doctor/researcher might be able to acquire some hints for further analysing this virus.

8 Related work

Motif counting in bipartite graphs. As a special case of our problem, butterfly counting has attracted many research efforts recently. Wang et al. [51] for the first time present exact algorithm for butterfly (rectangle) counting in a bipartite graph, which avoids enumerating all the butterflies. First, a layer is selected at random. Then, for each vertex u in the selected layer, they compute its 2-hop neighbors, and for each 2-hop neighbor w, they count the number of common neighbors between u and w denoted as $n_{uw}$. The number of butterflies starting from u is simply ${n_{uw} \atopwithdelims ()2}$. Finally, they add all the counts together, and the added counts divided by two is the total number of butterflies. Under the same computation paradigm, Sanei-Mehri et al. [40] propose a layer-based method to improve the efficiency of [51] by selecting the layer with the least computation cost. Later, Wang et al. [52] propose a vertex priority-based method to further accelerate the computation. Apart from these exact algorithms, research efforts have also been devoted to approximate approaches [28, 40, 44]. Recently, Yang et al. [54] investigate the problem of bi-triangle counting in bipartite graphs, where a bi-triangle is defined as a 6-cycle. It is worth mentioning that although our method BCList++ utilizes a layer-based strategy as well, the cost models of BCList++ and BFC [40] are different. This is because we have to consider both the graph unbalance and values of p and q. Besides, our methods also support enumeration problem. Those together make our cost model much more sophisticated than that of BFC.

Maximal biclique enumeration in bipartite graphs. A closely related problem is maximal biclique enumeration in bipartite graphs. A biclique is said to be maximal if it is not contained in any larger bicliques. David Eppstein [17] provides a linear algorithm to list maximal bicliques in any graph of bounded arboricity (i.e., $a(G)=O(1)$). In [39], maximal bicliques are enumerated by exhaustively enumerating subsets of vertices in one layer, obtaining the vertices in other layer as their common neighbors, and then checking the maximality of the obtained bicliques. Li et al. [27] enumerate the maximal bicliques by using efficient algorithms for mining closed patterns, which have been extensively studied in the data mining field. Inspired by the classical BK algorithm [9], Zhang et al. [56] propose algorithm iMBEA, which combines backtracking with branch-and-bound framework, where useful pruning techniques are employed to filter out the branches that cannot lead to maximal bicliques. The state-of-the-art approach [2] utilizes pivot pruning to improve the efficiency of maximal biclique enumeration. A variant problem is maximum biclique search, which has also been extensively studied recently [10, 18, 31, 42, 43]. It is worth mentioning that although our approaches for ($p$, $q$)-biclique enumeration also adopt the branch-and-bound framework, the specific pruning and searching strategies are different. For example, maximal biclique enumeration algorithms utilize the important non-maximality pruning technique, which is, however, invalid for our problem.

Listing k-cliques in unipartite graphs. The problem of listing k-cliques in unipartite graphs has a long research history and a wide range of applications [6, 38, 41]. The seminal work is the algorithm of Chiba and Nishizeki [12], which provides an efficient implementation of a branch-and-bound approach. Under the same framework, recently, Danisch et al. [14] propose a core ordering-based method to resolve this problem. The advantages of their proposal are demonstrated by both theoretical and empirical analyses. Other algorithms initially devised for counting and listing maximal cliques can also be adapted to deal with k-clique listing [34, 46]. Recently, the problem of k-clique densest subgraph search has received increasing attention [35, 41, 45, 48].

Motif counting in uncertain graphs. The problem of motif counting in uncertain graphs has also been studied in the literature. A popular analytic model is Possible World Semantics [3]. Based on this model, Huang et al.[23] calculate the mean value for a given motif. Later, apart from mean, Todor et al. [47] also evaluate the variance. More recently, Ma et al. [32] develop more efficient and scalable algorithms for evaluating the occurrence statistics of a given motif, including pmf (short for probability mass function), mean, variance. Very recently, Zhou et al. [58] study the problem of butterfly counting on uncertain bipartite graphs, which is the closest related work to our problem. In particular, the authors develop efficient algorithms based on the state-of-the-art butterfly counting algorithm for deterministic bipartite graphs [52]. Similar to its variation on deterministic graph, uncertain butterfly counting is also a special case of our uncertain ($p$, $q$)-biclique counting.

9 Conclusion

In this paper, we study the problem of ($p$, $q$)-biclique counting and enumeration for large sparse bipartite graphs. To efficiently solve this problem, we propose a competitive branch-and-bound baseline method, called BCList, which offers a useful computation framework to the problem. To improve the computation efficiency, we propose an advanced approach, namely BCList++, by anchoring the search on a single layer of the bipartite graph. Effective cost model and optimization techniques are proposed to enhance the performance of BCList++. We also extend our techniques to resolve the problem of ($p$, $q$)-biclique counting and enumeration on uncertain bipartite graphs. To resolve this problem, we develop an efficient method IUBCList, which is equipped with a couple of pruning techniques. Extensive experiments on 16 real datasets demonstrate the efficiency of our new techniques proposed in this paper.