1 Introduction

Since uncertainty theory was founded by Liu (2007) and perfected by Liu (2009), it has been widely applied into many fields, such as physics, engineering and finance. As an important part of uncertainty theory, uncertain differential equation driven by Liu process was introduced by Liu (2008). After that, uncertain differential equation quickly became a good tool to describe uncertain dynamic systems.

With a lot of good properties, uncertain differential equations attracted the attentions of many researchers. In 2010, a sufficient condition for the existence and uniqueness of the solution of an uncertain differential equation was proposed by Chen and Liu (2010). After that, a crucial Yao-Chen formula was proposed by Yao and Chen (2013) to connect uncertain differential equations with ordinary differential equations. Since the analytic solutions of uncertain differential equations may usually be unavailable, based on Yao-Chen formula, many numerical methods for uncertain differential equations were proposed, such as Euler method (Yao, 2013) and Runge–Kutta method (Yang and Shen, 2015). Uncertain differential equations had been widely applied to many fields, such as financial markets (Liu, 2009) and optimal control (Zhu, 2010, 2019).

As mentioned above, uncertain differential equations may properly describe uncertain dynamic systems. In applications, we usually construct a model based on uncertain differential equation to fit the corresponding uncertain dynamic system. Thus, it is crucial to work on the parameter estimation of uncertain differential equations. On that purpose, moment estimation (Yao and Liu, 2020), least squares estimation (Sheng et al., 2020), generalized moment estimation (Liu, 2021), maximum likelihood estimation (Liu and Liu, 2022a) and the method of moments with the help of residuals (Liu and Liu, 2022b) were proposed. In 2022, Ye and Liu (2022a) proposed the concept of uncertain hypothesis test and then applied it to uncertain differential equations (Ye and Liu 2022b). In recent years, parameter estimation in uncertain differential equations made a contribution to the epidemic model of COVID-19 (Chen et al., 2021; Jia and Chen, 2021; Lio and Liu, 2021). Moreover, for the sake of coping with uncertain dynamic systems with memory characteristic, Zhu (2015) gave the definition of uncertain fractional differential equation. Then, He et al. (2022) introduced an algorithm of parameter estimation for uncertain fractional differential equations based on method of moments.

Actually, many uncertain dynamic systems in our lives are autonomous, whose states at the next time are only related to the previous states. To cope with this kind of autonomous uncertain dynamic systems, we propose the definition of autonomous uncertain differential equation. For some cases, the information of an autonomous uncertain dynamic system is not enough to construct a parametric model. In this situation, only a nonparametric model is available. To solve the problem of nonparametric estimation, we need to obtain a parametric model as the approximation of the nonparametric model. Legendre polynomials have many outstanding properties such as orthogonality, symmetry and recursiveness. In 2020, Gu et al. (2020) proposed a Legendre polynomials based numerical method for the solutions of optimal control problems, which suggested that the Legendre polynomials have good property of arbitrary approximation for continuous functions. Thus, we may utilize the Legendre polynomials sequence to approximate the nonparametric functions in uncertain differential equations. In this paper, we discuss the method of nonparametric estimation for autonomous uncertain differential equations.

The rest of this paper is organized as follows. In Sect. 2, we introduce some definitions and properties of Legendre polynomials, uncertainty differential equations and uncertain hypothesis tests. Then, a method of nonparametric estimation for uncertain differential equations is proposed in Sect. 3. In Sect. 4, we give three numerical examples to show the effectiveness of our method. Finally in Sect. 5, we apply the nonparametric estimation into the atmospheric carbon dioxide model.

2 Preliminaries

Let \(C_t\) be a Liu process. Suppose that \(f,g:[0,+\infty )\times \mathbb {R}\rightarrow \mathbb {R}\) are two functions. Uncertain differential equation

$$\begin{aligned} dX_t=f(t,X_t)dt+g(t,X_t)dC_t,\; t\in [0,T] \end{aligned}$$
(1)

may be used to describe uncertain dynamic systems. If functions f and g are parametric forms, then there are many researches for the estimations of unknown parameters. However, in some cases, we may only construct the nonparametric models. To cope with these models, we consider to utilize an orthogonal function sequence with unknown weights to approximate the nonparametric functions f and g in (1). Then, the method of parameter estimation may be used to estimate the weights.

In this paper, with many outstanding properties, the Legendre polynomials are used for the approximation of nonparametric function. For \(x\in \mathbb {R}\), the Legendre polynomials \(p_n(x)\) are the polynomial solutions to Legendre’s differential equation

$$\begin{aligned} \frac{d}{dx}\left( \left( 1-x^2 \right) \frac{d}{dx}p_n(x) \right) +n(n+1)p_n(x)=0,\; n=0,1,2,\ldots \end{aligned}$$

Thus, Legendre polynomials are given in the following form

$$\begin{aligned} p_0(x)=1,\; p_n(x)=\frac{1}{2^nn!}\frac{d^n}{dx^n}\left( x^2-1 \right) ^n,\; n=1,2,\ldots \end{aligned}$$
(2)

Based on Eq. (2), we have

$$\begin{aligned}{} & {} p_1(x)=\frac{1}{2}\frac{d}{dx}\left( x^2-1 \right) =x,\\{} & {} p_2(x)=\frac{1}{2^2\times 2!}\frac{d^2}{dx^2}\left( x^2-1 \right) ^2=\frac{1}{2}\left( 3x^2-1 \right) ,\\{} & {} p_3(x)=\frac{1}{2^3\times 3!}\frac{d^3}{dx^3}\left( x^2-1 \right) ^3=\frac{1}{2}\left( 5x^3-3x \right) ,\\{} & {} \cdots \end{aligned}$$

The following three properties of Legendre polynomials are useful.

Property 1

[Orthogonality (Kashin and Saakian, 1984)] Legendre polynomials are orthogonal polynomials with respect to the \(L^2\) on the interval \([-1,1]\), i.e.,

$$\begin{aligned} \int ^1_{-1}p_m(x)p_n(x)dx=\frac{2}{2n+1}\delta _{mn}, \end{aligned}$$

where \(\delta _{mn}\) denotes the Kronecker symbol

$$\begin{aligned} \delta _{mn}= {\left\{ \begin{array}{ll} 1,\quad m=n,\\ 0,\quad m\ne n. \end{array}\right. } \end{aligned}$$

Property 2

[Symmetric and antisymmetric (Kashin and Saakian, 1984)] Each Legendre polynomial is symmetric or antisymmetric on the interval \([-1,1]\), i.e.,

$$\begin{aligned} {\left\{ \begin{array}{ll} p_n(-x)=-p_n(x),\;n\text { is odd},\\ p_n(-x)=p_n(x),\;n\text { is even}. \end{array}\right. } \end{aligned}$$

Property 3

[Recursiveness (Kashin and Saakian, 1984)] On the interval \([-1,1]\), the Legendre polynomials follow the three-term recurrence relation, which is known as Bonnets recursion formula

$$\begin{aligned} (n+1)p_{n+1}(x)=(2n+1)xp_n(x)-np_{n-1}(x) \end{aligned}$$

and

$$\begin{aligned} \frac{x^2-1}{n}\frac{d}{dx}p_n(x)=xp_n(x)-p_{n-1}(x). \end{aligned}$$

A continuous function \(\varphi (x)\) \((x\in [-1,1])\) may be expressed in terms of Legendre series as

$$\begin{aligned} \varphi (x)=\sum ^{\infty }_{i=0}c_ip_i(x), \end{aligned}$$

where \(c_i\in \mathbb {R}\) for \(i=0,1,2,\ldots \) In calculation, \(\varphi (x)\) is approximated by the partial sum of Legendre series. Then, we have

$$\begin{aligned} \varphi (x)\approx \sum ^{K}_{i=0}c_ip_i(x), \end{aligned}$$
(3)

where \(c_i\in \mathbb {R}\) for \(i=0,1,2,\ldots ,K\) and K is an appropriate positive integer.

For some uncertain dynamic systems, the variations of the current states are only directly affected by the states of themselves, such as the stock price and the atmospheric greenhouse gas. The uncertain dynamic systems with this phenomenon are called autonomous uncertain dynamic systems. To cope with this kind of systems, we give the definition of autonomous uncertain differential equation.

Definition 1

Let \(C_t\) be a Liu process. Suppose that \(f,g:\mathbb {R}\rightarrow \mathbb {R}\) are two functions. Then

$$\begin{aligned} dX_t=f(X_t)dt+g(X_t)dC_t \end{aligned}$$
(4)

is called an autonomous uncertain differential equation. A solution of (4) is an uncertain process \(X_t\) such that

$$\begin{aligned} X_t=X_0+\int ^{t}_{0}f(X_s)ds+\int ^{t}_{0}g(X_s)dC_s \end{aligned}$$

holds almost surely.

With the help of the Legendre polynomials, we may obtain an approximation of the autonomous uncertain differential Eq. (4) with weights. Then, the unknown weights in the approximation may be estimated by the method of parameter estimation. Ye and Liu (2022b) discussed uncertain hypothesis test for uncertain differential equations, which proposed a standard to test whether the estimated parameters are acceptable.

Theorem 1

(Ye and Liu, 2022b) Let \(\xi \) be a population with regular uncertainty distribution \(\mathcal {L}(a,b)\) with unknown parameters a and b. Then the test for the hypotheses

$$\begin{aligned} H_0:a=a_0\text { and }b=b_0\text { versus }H_1:a\ne a_0\text { or }b\ne b_0 \end{aligned}$$

at significance level \(\beta \) is

$$\begin{aligned} W=\Bigg \{ (z_1,z_2,\ldots ,z_n):\text { there are at least }\lfloor \beta n\rfloor +1\text { of indexes }i\text {'s with } \\ 1\le i\le n\text { such that }z_i<\Phi ^{-1}_{0}\left( \frac{\beta }{2} \right) \text { or }z_i>\Phi ^{-1}_{0}\left( 1-\frac{\beta }{2} \right) \Bigg \}. \end{aligned}$$

where \(\Phi ^{-1}_0(\beta )\) is the inverse uncertainty distribution of \(\mathcal {L}(a_0,b_0)\), i.e.,

$$\begin{aligned} \Phi ^{-1}_0(\beta )=(1-\beta )a_0+\beta b_0. \end{aligned}$$

Remark 1

For uncertain differential Eq. (1) with observations \(x_{t_1},x_{t_2},\ldots ,x_{t_n}\) of \(X_t\) at \(t_1,t_2,\ldots ,t_n\), respectively, residuals of the estimation of (1) should be obtained as \(\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _n\) with the help of Liu and Liu (2022b). According to Liu and Liu (2022b), the residual \(\varepsilon _i\) may be regraded as a sample of the linear uncertainty distribution \(\mathcal {L}(0,1)\) if estimated uncertain differential equation is appropriate.

Based on the conception of uncertain hypothesis test for uncertain differential equations proposed by Ye and Liu (2022b), to test whether the estimation may properly fit the observations \(x_{t_1}\), \(x_{t_2}\), \(\ldots \), \(x_{t_n}\), the test at a given significance level \(\beta =0.05\) is

$$\begin{aligned} H_0:a=0\text { and }b=1\text { versus }H_1:a\ne 0\text { or }b\ne 1 \end{aligned}$$

and the reject set is

$$\begin{aligned} W=\Bigg \{ (\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{n}):\text { there are at least }\lfloor 0.05 (n-1)\rfloor +1\text { of indexes }i\text {'s} \\ \text {with }2\le i\le n\text { such that }\varepsilon _i<0.025\text { or }\varepsilon _i>0.975 \Bigg \}. \end{aligned}$$

If the vector of the \(n-1\) residuals belongs to the test W, i.e.,

$$\begin{aligned} \left( \varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{n} \right) \in W, \end{aligned}$$

then the estimation of uncertain differential Eq. (1) is not a good fit to the observed data \(x_{t_1},x_{t_2},\ldots ,x_{t_n}\). If

$$\begin{aligned} \left( \varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{n} \right) \notin W, \end{aligned}$$

then the estimation of uncertain differential Eq. (1) is an applicable fit to the observed data \(x_{t_1},x_{t_2},\ldots ,x_{t_n}\).

3 Nonparametric estimation

Consider an autonomous uncertain differential equation in the following form

$$\begin{aligned} dX_t=f(X_t)dt+\sigma g(X_t)dC_t,\; t\in [0,T], \end{aligned}$$
(5)

where \(f: \mathbb {R}\rightarrow \mathbb {R}\) is an unknown continuous function, \(g: \mathbb {R}\rightarrow \mathbb {R}\) is a known continuous function and \(\sigma \) is an unknown parameter. Let \(0<t_1<t_2<\dots <t_n=T\). Assume that there are n observations \(x_{t_1}, x_{t_2},\ldots ,x_{t_n}\) of solution \(X_t\) at the times \(t_1,t_2,\ldots ,t_n\), respectively.

According to Eq. (3), for a fixed \(K\in \mathbb {N}\), we have

$$\begin{aligned} f(X_t)\approx \sum ^{K}_{i=0}c_ip_i(X_t), \end{aligned}$$
(6)

where \(c_i\in \mathbb {R}\) for \(i=0,1,2,\ldots ,K\). According to (6), the approximation of model (5) may be obtained in the following form

$$\begin{aligned} \displaystyle dX_t=\sum ^{K}_{i=0}c_ip_i(X_t)dt+\sigma g(X_t)dC_t,\; t\in [0,T]. \end{aligned}$$
(7)

As suggested by Yao and Liu (2020), for \(j=1,2,\ldots ,n-1\), we have

$$\begin{aligned} \frac{X_{t_{j+1}}-X_{t_j}-\left( \sum ^{K}_{i=0}c_ip_i(X_{t_j}) \right) \left( t_{j+1}-t_j \right) }{ g(X_{t_j})(t_{j+1}-t_j)}=\sigma \frac{C_{t_{j+1}}-C_{t_j}}{t_{j+1}-t_j}, \end{aligned}$$

i.e.,

$$\begin{aligned} \frac{X_{t_{j+1}}-X_{t_j}}{ g(X_{t_j})(t_{j+1}-t_j)}=\sum ^{K}_{i=0}\frac{c_ip_i(X_{t_j})}{ g(X_{t_j})}+\sigma \frac{C_{t_{j+1}}-C_{t_j}}{t_{j+1}-t_j}. \end{aligned}$$
(8)

According to the definition of Liu process \(C_t\),

$$\begin{aligned} \frac{C_{t_{j+1}}-C_{t_j}}{t_{j+1}-t_j}\sim \mathcal {N}(0,1),\quad j=1,2,\ldots ,n-1 \end{aligned}$$

are independent identically distributed. Thus, we denote that

$$\begin{aligned} \epsilon _0=\sigma \frac{C_{t_{j+1}}-C_{t_j}}{t_{j+1}-t_j}\sim \mathcal {N}(0,\sigma ) \end{aligned}$$

is the noise. Denote that \({\varvec{c}}_K=(c_0,c_1,\ldots ,c_K)\). We consider the following uncertain linear regression model

$$\begin{aligned} y={\varvec{c}}_K{\varvec{\eta }}^\text {T}+\epsilon _0, \end{aligned}$$
(9)

where \({\varvec{\eta }}=\left( \eta _0,\eta _1,\ldots ,\eta _K \right) \) is a vector of explanatory variables and y is a response variable. According to Eq. (8), we may assume that the observations of \({\varvec{\eta }}\) and y are

$$\begin{aligned} {\varvec{\eta }}_j=\left( \frac{p_0(x_{t_j})}{g(x_{t_j})},\frac{p_1(x_{t_j})}{g(x_{t_j})},\ldots ,\frac{p_K(x_{t_j})}{g(x_{t_j})} \right) , \quad j=1,2,\ldots ,n-1 \end{aligned}$$
(10)

and

$$\begin{aligned} y_j=\frac{x_{t_{j+1}}-x_{t_j}}{g(x_{t_j})(t_{j+1}-t_j)}, \quad j=1,2,\ldots ,n-1, \end{aligned}$$
(11)

respectively. Apparently, the regression model (9) is equivalent to Eq. (8). Suppose that \(\tilde{\varvec{c}}_K=\left( c_{0}^*,c_{1}^*,c_{2}^*,\ldots ,c_{K}^* \right) \) is the estimation of \({\varvec{c}}_K\) and \(\sigma ^*\) is the estimation of \(\sigma \). Based on the method of uncertain maximum likelihood estimation proposed by Lio and Liu (2020), \(\tilde{\varvec{c}}_K\) solves the minimization problem

$$\begin{aligned} \min _{\varvec{c}_K} \bigvee _{j=1}^{n-1}|y_j-{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} |\end{aligned}$$
(12)

and \(\sigma ^*\) solves the maximization problem

$$\begin{aligned} \max _{\sigma >0}\frac{\displaystyle \frac{\pi }{\sqrt{3}\sigma }\exp \left( \frac{\pi }{\sqrt{3}\sigma }\bigvee _{j=1}^{n-1} |y_j-\tilde{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} |\right) }{\displaystyle \left( 1+\exp \left( \frac{\pi }{\sqrt{3}\sigma }\bigvee _{j=1}^{n-1} |y_j-\tilde{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} |\right) \right) ^2}. \end{aligned}$$

According to Liu and Liu (2022a), we have

$$\begin{aligned} \sigma ^*=\frac{\pi }{\sqrt{3}\lambda }\bigvee _{j=1}^{n-1} |y_j-\tilde{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} |, \end{aligned}$$
(13)

where \(\lambda \) is the root of equation

$$\begin{aligned} 1+x+\exp (x)-x\exp (x)=0 \end{aligned}$$

and may be taken as 1.5434 approximately in numerical solution.

It is important to first find an appropriate estimation of K (denoted as \(K^*\)). Based on the property of Legendre polynomial approximation, the right side of (6) would converge to the left side of (6) with \(K\rightarrow +\infty \), i.e., for \(j=1,2,\ldots ,n-1\), we have

$$\begin{aligned} \lim _{K\rightarrow +\infty }\left|f(x_{t_j})-{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} \right|=0. \end{aligned}$$

Since

$$\begin{aligned} \left|y_j-{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} \right|\le \left|\big ( y_j-f(x_{t_j}) \big ) \right|+ \left|\big ( f(x_{t_j})-{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} \big ) \right|\end{aligned}$$

and

$$\begin{aligned} \left|y_j-{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} \right|\ge \left|\big ( y_j-f(x_{t_j}) \big ) \right|- \left|\big ( f(x_{t_j})-{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} \big ) \right|, \end{aligned}$$

based on the Squeeze theorem, we have

$$\begin{aligned} \lim _{K\rightarrow +\infty }\left|y_j-{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} \right|=\left|y_j-f(x_{t_j}) \right|. \end{aligned}$$

Thus, we have

$$\begin{aligned} \lim _{K\rightarrow +\infty } \bigvee _{j=1}^{n-1}|y_j-{\varvec{c}}_K{\varvec{\eta }}_j^\text {T} |= \bigvee _{j=1}^{n-1}\left|y_j-f(x_{t_j}) \right|. \end{aligned}$$

According to the objective function of optimization problem (12), we denote that

$$\begin{aligned} \phi (K)=\bigvee _{j=1}^{n-1}\left|\frac{x_{t_{j+1}}-x_{t_j}}{g(x_{t_j})(t_{j+1}-t_j)}-\sum ^{K}_{i=0}\frac{c_i^*p_i(x_{t_j})}{ g(x_{t_j})} \right|,\; K\in \mathbb {N}. \end{aligned}$$

In order to avoid too much computation, we suppose that \(\Delta \) is the acceptable error and the smallest K that satisfies

$$\begin{aligned} \big |\phi (K)-\phi (K-1) \big |<\Delta \end{aligned}$$

is the value of \(K^*\). Then the value of \(\tilde{\varvec{c}}_{K^*}\) may be obtained. Now we give the Algorithm 1 to calculate the values of \(\tilde{\varvec{c}}_{K^*}\) and \(K^*\).

figure a

Remark 2

For uncertain differential Eq. (5), if \(g: \mathbb {R}\rightarrow \mathbb {R}\) is also an unknown continuous function, with the help of Legendre polynomials, similar to (7), we have the approximation of (5) in the following form

$$\begin{aligned} \displaystyle dX_t=\sum ^{K_1}_{i=0}c_ip_i(X_t)dt+\sum ^{K_2}_{i=0}d_ip_i(X_t)(X_t)dC_t,\; t\in [0,T], \end{aligned}$$
(14)

where \(c_0,c_1,\ldots ,c_{K_1},d_0,d_1,\ldots ,d_{K_2}\in \mathbb {R}\). Then we have

$$\begin{aligned} \frac{X_{t_{j+1}}-X_{t_j}}{\left( \sum ^{K_2}_{i=0}d_ip_i(X_{t_j}) \right) (t_{j+1}-t_j)}-\frac{\sum ^{K_1}_{i=0}c_ip_i(X_{t_j})}{\sum ^{K_2}_{i=0}d_ip_i(X_{t_j})}=\frac{C_{t_{j+1}}-C_{t_j}}{t_{j+1}-t_j}\sim \mathcal {N}(0,1). \end{aligned}$$
(15)

Based on the method of maximum likelihood estimation, the estimations of \(c_0\), \(c_1\), \(\ldots \), \(c_{K_1}\), \(d_0\), \(d_1\), \(\ldots \), \(d_{K_2}\) are the solutions of the following optimization problem

$$\begin{aligned} \min _{c_{0},\ldots ,c_{K_1},d_{0},\ldots ,d_{K_2}}\bigvee _{j=1}^{n-1}\left|\frac{x_{t_{j+1}}-x_{t_j}}{\left( \sum ^{K_2}_{i=0}d_ip_i(x_{t_j}) \right) (t_{j+1}-t_j)}-\frac{\sum ^{K_1}_{i=0}c_ip_i(x_{t_j})}{\sum ^{K_2}_{i=0}d_ip_i(x_{t_j})} \right|. \end{aligned}$$
(16)

Apparently, the absolute values of \(d_0,d_1,\ldots ,d_{K_2}\) in the solutions of optimization problem (16) will be very large. Since the aim of nonparametric estimation is to find a properly estimated uncertain differential Eq. (14) as the estimation of uncertain differential Eq. (5), estimations of \(d_0,d_1,\ldots ,d_{K_2}\) with large absolute values will give the solution of (14) a strong disturbance, which is obviously unsatisfactory.

In fact, we may easily obtain the estimation of f in a uncertain differential Eq. (5), which is the most important thing in nonparametric estimation if g is already known. Thus, in application, we tend to define g in a known and acceptable form for observations. Then Algorithm 1 may be employed for the estimation of this uncertain differential equation.

4 Numerical experiments

Example 1

Consider uncertain differential equation

$$\begin{aligned} dX_t=f(X_t)dt+\sigma dC_t \end{aligned}$$
(17)

with some observations of \(X_t\) which are shown in Table 1.

Table 1 Observed data in Example 1
Full size table

Utilizing (6), we have the approximation of uncertain differential Eq. (17) in the following form

$$\begin{aligned} \displaystyle dX_t=\sum ^{K}_{i=0}c_ip_i(X_t)dt+\sigma dC_t. \end{aligned}$$

With the help of Algorithm 1 (where \(\Delta = 10^{-4}\)), we have \(K^*=2\) and

$$\begin{aligned} c_0^*=-0.1073,\quad c_1^*=1.7032,\quad c_2^*=-1.8488,\quad \sigma ^*=0.6787. \end{aligned}$$

Thus the estimated uncertain differential equation of (17) is

$$\begin{aligned} dX_t=\,\left( -0.1073p_0(X_t)+1.7032p_1(X_t)-1.8488p_2(X_t) \right) dt+0.6787dC_t. \end{aligned}$$
(18)

According to Liu and Liu (2022b), the residuals of uncertain differential Eq. (18) may be obtained and given in Table 2. If uncertain differential Eq. (18) does fit the observed data in Table 1 well, then the residuals in Table 2 should follow the linear uncertainty distribution \(\mathcal {L}(0,1)\), i.e.,

$$\begin{aligned} \varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{25}\sim \mathcal {L}(0,1). \end{aligned}$$

Apparently, all the residuals are included in [0.025, 0.975], we have

$$\begin{aligned} \left( \varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _{25} \right) \notin W. \end{aligned}$$

It follows from Remark 1 that the uncertain differential Eq. (18) is an applicable fit to the observed data in Table 1.

Table 2 Residuals of uncertain differential Eq. (18)
Full size table

Example 2

Consider uncertain differential equation

$$\begin{aligned} dX_t=f(X_t)dt+\sigma X_tdC_t \end{aligned}$$
(19)

with some observations of \(X_t\) which are shown in Table 3.

Table 3 Observed data in Example 2
Full size table

Similarly to Example 1, we have the estimation of uncertain differential Eq. (19) in the following form

$$\begin{aligned} dX_t=&\left( -3.8379p_0(X_t)+10.2704p_1(X_t)-6.7872p_2(X_t) \right. \nonumber \\&\left. +3.7387p_3(X_t)+0.3933p_4(X_t) \right) dt+1.0668X_tdC_t. \end{aligned}$$
(20)

The residuals of uncertain differential Eq. (20) may be obtained and given in Table 4. Since all the residuals are included in [0.025, 0.975], it follows from Remark 1 that the uncertain differential Eq. (20) is an applicable fit to the observed data in Table 3.

Table 4 Residuals of uncertain differential Eq. (20)
Full size table

Example 3

Consider the uncertain differential equation with initial value

$$\begin{aligned} {\left\{ \begin{array}{ll} dX_t=f(X_t)dt+\sigma X_tdC_t,\; t\in [0,1],\\ X_0=0. \end{array}\right. } \end{aligned}$$
(21)

Let us give the function f(x) by

$$\begin{aligned} f(x)=2\sin 5x+\cos 2x. \end{aligned}$$

and the true value of \(\sigma \) by \(\sigma =1\). Then the corresponding \(\alpha \)-path \(X_t^{\alpha }\) of (21) satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} dX_t^\alpha =(2\sin 5X_t^\alpha +\cos 2X_t^\alpha )dt+\frac{\sqrt{3}}{\pi }X_t^\alpha \ln \frac{\alpha }{1-\alpha }dt,\; t\in [0,1],\\ X_0^\alpha =0. \end{array}\right. } \end{aligned}$$
(22)

Note that the inverse uncertainty distribution of solution \(X_t\) to (21) is solution \(X_t^\alpha \) to (22). That is, for \(\alpha \in (0,1)\), \(X_t^\alpha \) is a sample point of \(X_t\) at time t. Observed data in Table 5 are produced by solving (22) for arbitrary \(\alpha \in (0,1)\) at time \(t_i\).

Table 5 Observed data in Example 3
Full size table

Based on the observed data, similarly to Example 1, we have the estimation of uncertain differential Eq. (21) in the following form

$$\begin{aligned} {\left\{ \begin{array}{ll} dX_t\,=\,\left( 44.5335p_0(X_t)-111.0393p_1(X_t)+120.2136p_2(X_t)-95.3485p_3(X_t) \right. \\ \left. \quad \quad \quad +44.9572p_4(X_t)-12.4951p_5(X_t) \right) dt+1.3989X_tdC_t,\; t\in [0,1],\\ X_0=0. \end{array}\right. } \end{aligned}$$
(23)

The residuals of uncertain differential Eq. (23) may be obtained and given in Table 6. Since all the residuals are included in [0.025, 0.975], it follows from Remark 1 that the uncertain differential Eq. (23) is an applicable fit to the observed data in Table 5.

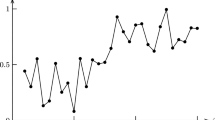
Table 6 Residuals of uncertain differential Eq. (23)
Full size table

As may be seen in (23), the estimated function of f(x) is

$$\begin{aligned} f^*(x)=&44.5335p_0(x)-111.0393p_1(x)+120.2136p_2(x)\\&-95.3485p_3(x)+44.9572p_4(x)-12.4951p_5(x). \end{aligned}$$

Since all the observations of \(X_t\) are located in interval [0, 0.8], in Fig. 1, we give the image of true function f(x) and its estimation \(f^*(x)\) in \(x\in [0,0.8]\). Obviously, \(f^*(x)\) may properly approximate f(x).

Fig. 1
figure 1

Image of true function f(x) and the estimation \(f^*(x)\)

Full size image

All these three numerical examples suggest that the estimated uncertain differential equations may fit the corresponding observations well.

5 Application to atmospheric carbon dioxide problem

In this section, we apply the method of nonparametric estimation into the modeling of the atmospheric carbon dioxide problem. The data of monthly mean atmospheric carbon dioxide measured at Mauna Loa Observatory (Hawaii) from February 2018 to September 2022 are shown in Table 7. (All the data may be found at https://www.co2.earth/. The unit of these data is parts per million)

Table 7 Data of atmospheric carbon dioxide
Full size table

5.1 Modeling of atmospheric carbon dioxide problem

Denote that the observed times are \(t_1=0.1,t_2=0.2,\ldots ,t_{56}=5.6\). Assume that \({\varvec{z}}\) is the vector consisting of all values in Table 7. Since the Legendre polynomials may only approximate the continuous functions in domain \([-1,1]\), we multiply all values by \(\frac{0.8}{\max {\varvec{z}}}\), i.e., 0.0019. Then the processed data are denoted as the observed data \(x_{t_1},x_{t_2},\ldots ,x_{t_{56}}\) at times \(t_1,t_2,\ldots ,t_{56}\) and given in Table 8.

Table 8 Processed data
Full size table

Now we construct the following atmospheric carbon dioxide model based on the processed data in Table 8.

$$\begin{aligned} dX_t=f(X_t)dt+\sigma X_tdC_t, \end{aligned}$$
(24)

where \(f: \mathbb {R}\rightarrow \mathbb {R}\) is an unknown continuous function and \(\sigma >0\) is an unknown parameter. Approximating the uncertain differential Eq. (24) by the following form

$$\begin{aligned} \displaystyle dX_t=\sum ^{K}_{i=0}c_ip_i(X_t)dt+\sigma X_tdC_t. \end{aligned}$$

Then, Algorithm 1 may be used to obtain \(K^*=2\) and

$$\begin{aligned} c_0^*=-19.0413,\quad c_1^*=31.6427,\quad c_2^*=-13.6719,\quad \sigma ^*=0.0577. \end{aligned}$$

Thus the estimated uncertain differential equation of (24) is

$$\begin{aligned} dX_t=\left( -19.0413p_0(X_t)+31.6427p_1(X_t)-13.6719p_2(X_t)\right) dt+0.0577X_tdC_t. \end{aligned}$$
(25)
Table 9 Residuals of uncertain differential Eq. (25)
Full size table

The residuals of the uncertain differential Eq. (25) may be obtained and given in Table 9. Since all the residuals are included in [0.025, 0.975], the uncertain differential Eq. (25) is an applicable fit to the observed data in Table 8. Therefore, we say that the dynamic process of atmospheric carbon dioxide measured at Mauna Loa Observatory from February 2018 to September 2022 follows the uncertain differential Eq. (25).

5.2 Completion of lost data

Due to the unexpected accidents, some data may be lost in management or storage. Let us take this atmospheric carbon dioxide problem for example. Referring to Table 7, we assume that the data in March 2018, June 2019 are lost. That is, the proceed data at \(j=2\) and \(j=17\) in Table 8 are lost. For the parametric form

$$\begin{aligned} \displaystyle dX_t=\sum ^{K}_{i=0}c_ip_i(X_t)dt+\sigma X_tdC_t, \end{aligned}$$

similarly to Sect. 5.1, the estimated values may be obtained as \(K^*=2\) and

$$\begin{aligned} c_0^*=-17.8493,\quad c_1^*=29.6757,\quad c_2^*=-12.8425,\quad \sigma ^*=0.0576. \end{aligned}$$

Then the estimation of model (24) is

$$\begin{aligned} dX_t=\left( -17.8493p_0(X_t)+29.6757p_1(X_t)-12.8425p_2(X_t)\right) +0.0576X_tdC_t. \end{aligned}$$
(26)

The residuals of uncertain differential Eq. (26) may be obtained and given in Table 10. Since all the residuals are included in [0.025, 0.975], uncertain differential Eq. (26) is an applicable fit to the existing observed data in Table 8.

Table 10 Residuals of uncertain differential Eq. (26)
Full size table

According to the definitions of forecast value and confidence interval given by Lio and Liu (2018), we may obtain the forecast value of y in uncertain regression model (9) as

$$\begin{aligned} \hat{y}=\tilde{\varvec{c}}_{K^*}\;{\varvec{\eta }}^\text {T}=\sum ^{K^*}_{i=0}{c_i^*}\eta _i \end{aligned}$$
(27)

and \(\gamma \)-confidence interval (e.g., \(\gamma =0.95\)) of y as

$$\begin{aligned} \left[ \hat{y}-\frac{\sigma ^*\sqrt{3}}{\pi }\ln \frac{1+\gamma }{1-\gamma },\hat{y}+\frac{\sigma ^*\sqrt{3}}{\pi }\ln \frac{1+\gamma }{1-\gamma } \right] . \end{aligned}$$
(28)

For a fixed j, we suppose that the observed value of \(X_{t_{j+1}}\) is missing. Thus, we denote the forecast value of \(X_{t_{j+1}}\) as \(\hat{X}_{t_{j+1}}\). According to (10) and (11), we may obtain the j-th observations of \({\varvec{\eta }}\) as

$$\begin{aligned} {\varvec{\eta }}_j=\left( \frac{p_0(x_{t_j})}{x_{t_j}},\frac{p_1(x_{t_j})}{x_{t_j}},\ldots ,\frac{p_K(x_{t_j})}{x_{t_j}} \right) \end{aligned}$$

and the j-th observations of y as

$$\begin{aligned} y_j=\frac{\hat{X}_{t_{j+1}}-x_{t_j}}{x_{t_j}(t_{j+1}-t_j)}. \end{aligned}$$

Substituting \({\varvec{\eta }}={\varvec{\eta }}_j\) and \(\hat{y}=y_j\) into (27), we have the forecast value of \(X_{t_{j+1}}\) as

$$\begin{aligned} \hat{X}_{t_{j+1}}=x_{t_j}+\left( \sum ^{K^*}_{i=0}{c_i^*}p_i(x_{t_j}) \right) (t_{j+1}-t_j). \end{aligned}$$
(29)

Substituting \({\varvec{\eta }}={\varvec{\eta }}_j\) and \(\hat{y}=y_j\) into (28), we have the \(\gamma \)-confidence interval of \(X_{t_{j+1}}\) as

$$\begin{aligned} \left[ \hat{X}_{t_{j+1}}-x_{t_j}(t_{j+1}-t_j)\frac{\sigma ^*\sqrt{3}}{\pi }\ln \frac{1+\gamma }{1-\gamma },\hat{X}_{t_{j+1}}+x_{t_j}(t_{j+1}-t_j)\frac{\sigma ^*\sqrt{3}}{\pi }\ln \frac{1+\gamma }{1-\gamma } \right] . \end{aligned}$$
(30)

With (29), we have the forecast values of \(X_{t_2}\) and \(X_{t_{17}}\) as \(\hat{X}_{t_2}=0.7763\) and \(\hat{X}_{t_{17}}=0.7878\), respectively. Then with (30), we have the \(95\%\)-confidence interval of \(X_{t_2}\) and \(X_{t_{17}}\) as [0.7673, 0.7853] and [0.7786, 0.7970], respectively.

Restoring the processed data to the original data, we have the forecast value of the lost data in March 2018 as 408.52 with \(95\%\)-confidence interval [403.77, 413.27] and the forecast value of the lost data in June 2019 as 414.57 with \(95\%\)-confidence interval [409.74, 419.39]. Referring to Table 7, we may clearly see that the actual value in March 2018 is 409.59 which is in the interval [403.77, 413.27] and the actual value in June 2019 is 414.16 which is in the interval [409.74, 419.39]. Thus we claim that model (26) may complete the lost data well.

In general, the estimated model obtained by nonparametric estimation may properly fit the observations and complete the lost data. Thus we claim that our method of nonparametric estimation is effective for this atmospheric carbon dioxide model.

6 Conclusion

In this paper, we proposed a method of nonparametric estimation for autonomous uncertain differential equations. An algorithm was introduced and illustrated with three numerical examples. With the help of residuals and uncertain hypothesis test, we proved that the estimated uncertain differential equations may fit their observations well. Finally, we applied the nonparametric estimation into the atmospheric carbon dioxide problem. With the data of monthly mean atmospheric carbon dioxide from February 2018 to September 2022, we obtained an uncertain differential equation based model by using the method of nonparametric estimation. Then, the model was proved to be an applicable fit to the observations and an effective tool to complete the lost data. In the future, we will further research on the method of nonparametric estimation for nonautonomous uncertain differential equations whose variations of the current states are directly affected by both the states and the time.