Quantities vs. prices: monopoly regulation without transfer under asymmetric demand information

Abstract

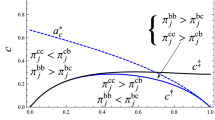
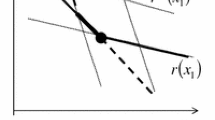
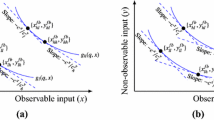
This paper examines the optimal monopoly regulation without transfer based on Basso, Figueroa and Vásquez (Rand J Econ 48(3):557–578, 2017), which compare the quantity-based and price-based instruments to regulate a monopoly that has better information concerning its market demand than the regulator. The optimal screening mechanisms, which offer multiple menus of contracts for the regulated firm to select, and pooling mechanisms, which only provide a uniform contract, are characterized for each instrument. Furthermore, the corresponding performances of the regulator’s social welfare are ranked. Results show that, with non-increasing marginal costs of the regulated firm, the screening price mechanism would strictly dominate the screening quantity mechanism. The pooling price mechanism is always preferred to the pooling quantity mechanism when the slope of marginal costs is negative or slightly positive. Otherwise, the pooling quantity mechanism may be superior depending on the relative magnitude of the slope of marginal costs and demand function.

Appendices

Appendix

Proof of Lemma 1

Under the quantity-floor allocation, the regulator’s welfare objective can be written as

$$\begin{aligned} E_{\theta } w(\theta_{c} ) = & \int_{{\underline {\theta } }}^{{\theta_{c} }} {[\int_{0}^{{q^{f} (\theta_{c} )}} {(P(\tilde{q}) + \theta )} d\tilde{q} - (P(q^{f} (\theta_{c} )) + \theta )q^{f} (\theta_{c} ) + \alpha (P(q^{f} (\theta_{c} )) + \theta - c_{0} - {{c_{1} q^{f} (\theta_{c} )} \mathord{\left/ {\vphantom {{c_{1} q^{f} (\theta_{c} )} 2}} \right. \kern-0pt} 2})q^{f} (\theta_{c} )]} dF(\theta ) \\ & + \int_{{\theta_{c} }}^{{\overline{\theta }}} {[\int_{0}^{{q^{f} (\theta )}} {(P(\tilde{q}) + \theta )} d\tilde{q} - (P(q^{f} (\theta )) + \theta )q^{f} (\theta ) + \alpha (P(q^{f} (\theta )) + \theta - c_{0} - {{c_{1} q^{f} (\theta )} \mathord{\left/ {\vphantom {{c_{1} q^{f} (\theta )} 2}} \right. \kern-0pt} 2})q^{f} (\theta )]} dF(\theta ). \\ \end{aligned}$$

With the respect of $\theta_{c}$, the first-order condition of this function can be obtained as

$$q^{{f^{{\prime }} }} \left( {\theta _{c} } \right)\int_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } }}^{{\theta _{c} }} {\left[ { - (1 - \alpha )P^{{\prime }} (q^{f} (\theta _{c} ))q^{f} (\theta _{c} ) + \alpha (P(q^{f} (\theta _{c} )) + \theta - c_{0} - c_{1} q^{f} \left( {\theta _{c} } \right)/2} \right]} dF\left( \theta \right) = 0,$$

where $q^{{f^{{\prime }} }} \left( {\theta _{c} } \right) = - 1/u_{{qq}} \left( {q^{f} (\theta _{c} ),\theta _{c} } \right) > 0$. Thus, we can obtain $\int_{{\underline {\theta } }}^{{\theta_{c} }} {w_{q} (q^{f} (\theta_{c} ),\theta )} {\text{d}}F(\theta ) = 0$ as requested by Lemma 1.

Proof of Lemma 2

Notice that $w_{q\theta } (q^{f} (\theta_{c} ),\theta ) = \alpha > 0$ and thus,

$$w_{q} (q^{f} (\theta_{c} ),\underline {\theta } ) = - (1 - \alpha )P^{\prime } (q^{f} (\theta_{c} ))q^{f} (\theta_{c} ) + \alpha (P(q^{f} (\theta_{c} )) + \underline {\theta } - c_{0} - c_{1} q) < 0.$$

We can conclude

$$u(q^{f} (\theta _{c} ),\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) = (P(q^{f} (\theta _{c} )) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } - c_{0} - c_{1} q/2)q^{f} (\theta _{c} ) < \left[ {\left( {1/\alpha - 1} \right)P^{{\prime }} (q^{f} (\theta _{c} )) + c_{1} /2} \right]q^{{f2}} (\theta _{c} ) < 0.$$

Proof of Proposition 2

First, by expressing the IC constraint in usual integral form plus a monotonicity requirement, the regulator’s problem can be rewritten as:

$$\mathop {\max }\limits_{q} \int_{{\underline {\theta } }}^{{\overline{\theta }}} {w(q(\theta ),\theta )} dF(\theta )$$

subject to:

$$(P(q(\theta )) + \theta - c_{0} )q(\theta ) = \int_{{\underline {\theta } }}^{\theta } {q(\tilde{\theta })d} \tilde{\theta } + \underline {U} ,{\text{for}}\;{\text{all}}\;\theta \in \Theta\\$$

$$q(\theta )\,\,{\text{non-decreasing}}, \,{\text {for all}}\,\, \theta \in \Theta$$

$$(P(q(\theta )) + \theta - c_{0} )q(\theta ) \ge 0,\;{\text{for}}\;{\text{all}}\;\theta \in \Theta$$

(A1)

where $\underline {U} = (P(q(\underline {\theta } )) + \underline {\theta } - c_{0} )q(\underline {\theta } ).$ Following Amador and Bagwell (2013), the incentive compatible constraints can be re-stated as a monotonicity requirement and two inequalities which can be shown below:

$$\int_{{\underline {\theta } }}^{\theta } {q(\tilde{\theta })d} \tilde{\theta } + \underline {U} - (P(q(\theta )) + \theta - c_{0} )q(\theta ) \le 0\;{\text{for all}}\;\theta \in \Theta, $$

(A2)

$$- \int_{{\underline {\theta } }}^{\theta } {q(\tilde{\theta })d} \tilde{\theta } - \underline {U} + (P(q(\theta )) + \theta - c_{0} )q(\theta ) \le 0\;{\text{for}}\;{\text{all}}\;\theta \in \Theta .$$

(A3)

By assigning two non-decreasing cumulative Lagrange multiplier functions $\lambda_{1} (\theta )$ and $\lambda_{2} (\theta )$ associated with the two inequalities (A2) and (A3), and denoting a non-decreasing multiplier function $\mu (\theta )$ of the participation constraint that satisfy complementary slackness, the Lagrangian for the problem writes as:

$$\begin{aligned} L = & \int_{{\underline {\theta } }}^{{\overline{\theta }}} {w(q(\theta ),\theta )} dF(\theta ) - \int_{{\underline {\theta } }}^{{\overline{\theta }}} {\left[ {\int_{{\underline {\theta } }}^{\theta } {q(\tilde{\theta })d} \tilde{\theta } + \underline {U} - (P(q(\theta )) + \theta - c_{0} )q(\theta )} \right]} d(\lambda_{1} (\theta ) - \lambda_{2} (\theta )) \\ & + \int_{{\underline {\theta } }}^{{\overline{\theta }}} {(P(q(\theta )) + \theta - c_{0} )q(\theta )} d\mu (\theta ). \\ \end{aligned}$$

Let us propose some non-decreasing multiplier functions to satisfy

$$\lambda (\theta ) = \lambda_{1} (\theta ) - \lambda_{2} (\theta ) = \left\{ \begin{gathered} 0 \hfill \\ - w_{q} (q^{f} (\theta ),\theta )f(\theta ) \hfill \\ - \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta }) - \kappa F(\theta ) \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} ; \\ ; \\ ; \\ \end{array} \begin{array}{*{20}c} {\theta = \overline{\theta },} \\ {\theta \in (\theta_{r} ,\overline{\theta }),} \\ {\theta \in [\underline {\theta } ,\theta_{r} ],} \\ \end{array}$$

and $\mu (\theta ) = \left\{ \begin{gathered} 0 \hfill \\ - \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta }) \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} ; \\ ; \\ \end{array} \begin{array}{*{20}c} {\theta \in (\underline {\theta } ,\overline{\theta }]} \\ {\theta = \underline {\theta } } \\ \end{array} ,$ where $\kappa$ is the relative concavity parameter. The proposition 2 ensures that $\kappa F(\theta ) + \lambda (\theta )$ is non-decreasing. We can propose $\lambda_{1} (\theta ) = \kappa F(\theta ) + \lambda (\theta )$ and $\lambda_{2} (\theta ) = \kappa F(\theta ).$ To satisfy $\mu (\theta )$ is non-decreasing, we require $\frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta }) \ge 0.$

To check whether the proposed allocation maximizes the resulting Lagrangian with proposed Lagrange multipliers, it is particularly useful to verify that the resulting Lagrangian is concave in $q$ and the first-order conditions are satisfied. First, we now check the concavity of the Lagrangian. Using these proposed multiplier functions and integrating by parts the Lagrangian, we can obtain

$$\begin{aligned} L = & \int_{{\underline {\theta } }}^{{\overline{\theta }}} {w(q(\theta ),\theta )} dF(\theta ) - \int_{{\underline {\theta } }}^{{\overline{\theta }}} {\left[ {\int_{{\underline {\theta } }}^{\theta } {q(\tilde{\theta })d} \tilde{\theta } + \underline {U} - (P(q(\theta )) + \theta - c_{0} )q(\theta )} \right]} d\lambda (\theta ) \\ & + \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta })(P(q(\underline {\theta } )) + \underline {\theta } - c_{0} )q(\underline {\theta } ){\kern 1pt} . \\ \end{aligned}$$

Using $\underline {U} = (P(q(\underline {\theta } )) + \underline {\theta } - c_{0} )q(\underline {\theta } ),\;\lambda (\underline {\theta } ) = - \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} {\text{d}}F(\tilde{\theta })\;{\text{and}}\;\lambda (\overline{\theta }) = 0,$ the Lagrangian can be written as

$$L = \int_{{\underline {\theta } }}^{{\overline{\theta }}} {w(q(\theta ),\theta )} dF(\theta ) - \int_{{\underline {\theta } }}^{{\overline{\theta }}} {\left[ {\int_{{\underline {\theta } }}^{\theta } {q(\tilde{\theta })d} \tilde{\theta } - (P(q(\theta )) + \theta - c_{0} )q(\theta )} \right]} d\lambda (\theta ).$$

Integrating by parts, it can be rewritten as

$$L = \int_{{\underline {\theta } }}^{{\overline{\theta }}} {(w(q(\theta ),\theta )} f(\theta ) + \lambda (\theta )q(\theta ))d\theta + \int_{{\underline {\theta } }}^{{\overline{\theta }}} {P(q(\theta )) + \theta - c_{0} )q(\theta )} d\lambda (\theta ).$$

Adding and deducting $\kappa (P(q(\theta )) + \theta - c_{0} )q(\theta )]f(\theta ),$ we get.

$L = \int_{{\underline {\theta } }}^{{\overline{\theta }}} {\{ [w(q(\theta ),\theta )} - \kappa (P(q(\theta )) + \theta - c_{0} )q(\theta )]f(\theta ) + \lambda (\theta )q(\theta )\} d\theta + \int_{{\underline {\theta } }}^{{\overline{\theta }}} {(P(q(\theta )) + \theta - c_{0} )q(\theta )} d(\kappa F(\theta ) + \lambda (\theta )).$ Recalling the relative concavity parameter, we get $w_{qq} (q,\theta ) - \kappa u_{qq} (q,\theta ) \le 0$. Therefore, the Lagrangian is concave in $q(\theta )\;{\text{if}}\;\kappa F(\theta ) + \lambda (\theta )$ is non-decreasing for all $\theta \in \Theta$. The conditions in Proposition 2 show that $\kappa F(\theta ) - w_{q} (q^{f} (\theta ),\theta )f(\theta )$ is non-decreasing for all $\theta \in (\theta_{r} ,\overline{\theta }]$. Thus, we only need to check that the jumps at $\overline{\theta }$ and $\theta_{r}$ are nonnegative. The jumps are

$- w_{q} (q^{f} (\overline{\theta }),\overline{\theta })f(\overline{\theta }) \le 0$,$\kappa F(\theta_{r} ) - w_{q} (q^{f} (\theta_{r} ),\theta_{r} )f(\theta_{r} ) \ge - \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta }).$

The former is satisfied by the utility’s direction of bias, and the latter is satisfied by the condition (ii) in Proposition 2. Therefore, the Lagrangian is concave at the proposed multiplier functions.

We now proceed to show the quantity IR-floor allocation maximizes the Lagrangian. Following Amador and Bagwell (2013), the entire positive ray of the real line for concave function $w$ and $u$ and a convex cone of choice set $\Omega = \{ \left. q \right|q:\Theta \to \Re_{ + } {\kern 1pt} {\kern 1pt} {\text{and}}{\kern 1pt} {\kern 1pt} q{\kern 1pt} {\kern 1pt} {\text{nondecreasing}}\}$ are extended. Maximizing the concave functions on a convex cone needs the Lagrangian is a concave functional and the following first-order conditions are satisfied in terms of Gateaux differentials:

$$\partial L(q^{r} ,q^{r} ) = 0$$

$$\partial L(q^{r} ,x) \le 0\,{\text{for}}\;{\text{all}}\;x \in \Omega .$$

Taking Gateaux differential in direction $x$, using $(P^{\prime } (q^{f} (\theta ) + \theta - c_{0} )q^{f} (\theta ) + P(q^{f} (\theta )) = 0$ and the constructed multiplier functions, we have

$\partial L(q^{r} ,x) = \int_{{\underline {\theta } }}^{{\theta_{r} }} {[w_{q} (q^{f} (\theta_{r} ),\theta )} f(\theta ) - \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta }) - \kappa F(\theta ) + \kappa (\theta_{r} - \theta )f(\theta )]x(\theta )d\theta$ which can be rewritten through integrating by parts as

$$\begin{aligned} \partial L(q^{r} ,x) = & \int_{{\underline {\theta } }}^{{\theta_{r} }} {[w_{q} (q^{f} (\theta_{r} ),\theta )} f(\theta ) - \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta }) - \kappa F(\theta ) + \kappa (\theta_{r} - \theta )f(\theta )]d\theta x(\underline {\theta } ) \\ & + \int_{{\underline {\theta } }}^{{\theta_{r} }} {\{ \int_{\theta }^{{\theta_{r} }} {[w_{q} (q^{f} (\theta_{r} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } ) - \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta }) - \kappa F(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } ) + \kappa (\theta_{r} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )]d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } } } \} dx(\theta ). \\ \end{aligned}$$

By $\partial L(q^{r} ,q^{r} ) = 0,$ we have

$$\int_{{\underline {\theta } }}^{{\theta_{r} }} {[w_{q} (q^{f} (\theta_{r} ),\theta )} f(\theta ) - \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta }) - \kappa F(\theta ) + \kappa (\theta_{r} - \theta )f(\theta )]d\theta x(\underline {\theta } ) = 0.$$

So, we need to satisfy the following inequality

$$\int_{{\underline {\theta } }}^{{\theta_{r} }} {\left\{ {\int_{\theta }^{{\theta_{r} }} {\left[ {w_{q} (q^{f} (\theta_{r} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } ) - \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })} dF(\tilde{\theta }) - \kappa F(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } ) + \kappa (\theta_{r} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )} \right]d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } } } \right\}} dx(\theta ) \le {\kern 1pt} 0.$$

Integrating by parts, we can get the following inequality holds under the condition (ii) in Proposition 2:

$\int_{\theta }^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } - \frac{{\theta_{r} - \theta }}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })f(\tilde{\theta })d\tilde{\theta }} } - \kappa (\theta_{r} - \theta )F(\theta ) \le 0.$ And the condition (i) and (iii) are needed to satisfy the non-decreasing property of the proposed multiplier functions.

We now complete the proof to apply the modified version of Luenberger’s Sufficiency Theorem (1969) in Amador and Bagwell (2013). Setting

• (1) $x_{0} = q^{r} ;$

• (2) $X = \{ \left. q \right|q:\Theta \to {\kern 1pt} {\kern 1pt} {\rm O}\} ;$

• (3) $\Omega = \{ \left. q \right|q:\Theta \to \Re_{ + } {\kern 1pt} {\kern 1pt} {\text{and}}{\kern 1pt} {\kern 1pt} q{\kern 1pt} {\kern 1pt} {\text{nondecreasing}}\};$

• (4) $f,$ as a real valued functional of $q \in X,$ is the negative of the objective function $Ew(q(\theta ),\theta );$

• (5) $Z = \{ \left. {(z_{1,} z_{2} ,z_{3} )} \right|z_{1} :\Theta \to \Re {\kern 1pt} ,z_{2} :\Theta \to \Re {\kern 1pt} ,z_{3} :\Theta \to \Re \} ;$

• (6) $P = \left\{ {\left. {(z_{1,} z_{2} ,z_{3} )} \right|(z_{1,} z_{2} ,z_{3} ) \in Z\;{\text{such}}\;{\text{that}}\;z_{1} (\theta ) \ge 0,z_{2} (\theta ) \ge 0,z_{3} (\theta ) \ge 0\;{\text{for}}\;{\text{all}}\;\theta \in \Theta } \right\};$

• (7) The mapping $G$ from $\Omega$ to $Z$ is given by the left sides of inequalities (A1), (A2) and (A3);

• (8) The linear mapping $T$ is given by $T((z_{1} ,z_{2} ,z_{3} )) = \int_{{\underline {\theta } }}^{{\overline{\theta }}} {z_{1} d\lambda_{1} (\theta )} + \int_{{\underline {\theta } }}^{{\overline{\theta }}} {z_{2} d\lambda_{1} (\theta )} + \int_{{\underline {\theta } }}^{{\overline{\theta }}} {z_{3} } d\mu (\theta ),$

where non-decreasing multiplier functions $\lambda_{1} (\theta ),\;\lambda_{2} (\theta )\;{\text{and}}\;\mu (\theta ),$ and $\mu (\theta )$ imply $T(z) \ge 0$ for $z \in P$. When (A1), (A2) and (A3) bind under the $q^{r}$ allocation and the proposed multiplier $\mu (\theta )$ is considered, we get

$$T(G(x_{0} )) = \int_{{\underline {\theta } }}^{{\overline{\theta }}} {\left[ {\int_{{\underline {\theta } }}^{\theta } {q^{r} (\tilde{\theta })d} \tilde{\theta } + \underline {U} - (P(q^{r} (\theta )) + \theta - c_{0} )q^{r} (\theta )} \right]} d(\lambda_{1} (\theta ) - \lambda_{2} (\theta )) = 0.$$

Therefore, we have found the conditions in Proposition 2 under which the proposed the $q^{r}$ allocation solves the minimization problem of $f(x)$ for $x \in \Omega$ subject to $- G(x) \in P.$

Proof of Corollary 1

First, we define $T(\theta ) = \frac{1}{{\theta_{r} - \theta }}\int_{\theta }^{{\theta_{r} }} {w_{q} (q^{f}_{f} (\theta_{r} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )f(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } )d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } } - \kappa F(\theta )\;\;$ for all $\theta \in [\underline {\theta } ,\theta_{r} ]$ and $T(\underline {\theta } ) = \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {w_{q} (q^{f} (\theta_{r} ),\tilde{\theta })f(\tilde{\theta })d\tilde{\theta }} .$

Considering that $w_{q} (q(\theta ),\theta ) = - (1 - \alpha )P^{ {\prime }} (q(\theta ))q(\theta ) + \alpha (P(q(\theta )) + \theta - c_{0} ),$ we have

$$\begin{gathered} T(\theta ) = \frac{1}{{\theta_{r} - \theta }}\int_{\theta }^{{\theta_{r} }} {[ - (1 - \alpha )P^{\prime}(q^{f} (\theta_{r} ))q^{f} (\theta_{r} ) + \alpha (P(q^{f} (\theta_{r} )) + \tilde{\theta } - c_{0} )]f(\tilde{\theta })d\tilde{\theta } - } \kappa F(\theta ) \hfill \\ = \frac{1}{{\theta_{r} - \theta }}\int_{\theta }^{{\theta_{r} }} {\alpha (\tilde{\theta } - \underline {\theta } )f(\tilde{\theta })d\tilde{\theta } - } \kappa F(\theta ) - (1 - \alpha )P^{\prime}(q^{f} (\theta_{r} ))q^{f} (\theta_{r} )\frac{{F(\theta_{r} ) - F(\theta )}}{{\theta_{r} - \theta }}{\kern 1pt} {\kern 1pt} . \hfill \\ \end{gathered}$$

First, we find that the condition (i) in Proposition 2 can be automatically satisfied, as following

$$T(\underline {\theta } ) = \frac{1}{{\theta_{r} - \underline {\theta } }}\int_{{\underline {\theta } }}^{{\theta_{r} }} {\alpha (\tilde{\theta } - \underline {\theta } )f(\tilde{\theta })d\tilde{\theta }} + (\alpha - 1)P^{\prime } (q^{f} (\theta_{r} ))q^{f} (\theta_{r} )\frac{{F(\theta_{r} )}}{{\theta_{r} - \underline {\theta } }} \ge 0.$$

Second, for the condition (ii) in Proposition 2, we get

$$G^{ {\prime }} (\theta ) = \frac{1}{{(\theta_{r} - \theta )^{2} }}\int_{\theta }^{{\theta_{r} }} {\alpha (\tilde{\theta } - \underline {\theta } )f(\tilde{\theta })d\tilde{\theta } - } \alpha \frac{{\theta - \underline {\theta } }}{{\theta_{r} - \theta }}f(\theta ) - \kappa f(\theta ) - \frac{{(1 - \alpha )P^{ {\prime }} (q^{f} (\theta_{r} ))q^{f} (\theta_{r} )}}{{\theta_{r} - \theta }}\left( {\frac{{F(\theta_{r} ) - F(\theta )}}{{\theta_{r} - \theta }} - f(\theta )} \right).$$

If $f^{\prime } (\theta ) \le 0$ and $\kappa \ge \frac{1}{2}\alpha ,$ we have

$$G^{\prime } (\theta ) \le \frac{1}{{(\theta_{r} - \theta )^{2} }}\int_{\theta }^{{\theta_{r} }} {\alpha (\tilde{\theta } - \underline {\theta } )f(\theta )d\tilde{\theta } - } \alpha \frac{{\theta - \underline {\theta } }}{{\theta_{r} - \theta }}f(\theta ) - \kappa f(\theta ) = f(\theta )\left( {\frac{1}{2}\alpha - \kappa } \right) \le 0.$$

Then, $T(\theta ) \le T(\underline {\theta } )$ and the condition (ii) is satisfied.

Finally, for the condition (iii) in Proposition 2, we define $R(\theta ) = \kappa F(\theta ) - w_{q} (q^{f} (\theta ),\theta )f(\theta ) = \kappa F(\theta ) + P^{ {\prime }} (q^{f} (\theta ))q^{f} (\theta )f(\theta ).$ Taking the derivation with the respect of $\theta$, we have $R(\theta ) = \kappa F(\theta ) - w_{q} (q^{f} (\theta ),\theta )f(\theta ) = \kappa F(\theta ) + P^{{\prime }} (q^{f} (\theta ))q^{f} (\theta )f(\theta ).$ Considering $\kappa = \mathop {\min }\limits_{{\theta ,q}} \left\{ {\frac{{w_{{qq}} (q,\theta )}}{{u_{{qq}} (q,\theta )}}} \right\} \le \frac{{ - (1 - \alpha )P^{{\prime \prime }} (q)q + (2\alpha - 1)P^{\prime } (q)}}{{P^{\prime\prime}(q)q + 2P^{\prime } (q)}} = \alpha - \frac{{P^{{\prime \prime }} (q)q + P^{\prime } (q)}}{{P^{{{\prime \prime }}} (q)q + 2P^{\prime } (q)}},$ we obtain $P^{\prime \prime } (q)q + P^{\prime } (q) \ge - (\kappa - \alpha )(P^{\prime \prime } (q)q + 2P^{\prime } (q)).$ Thus, if $f^{\prime } (\theta ) \le 0$ and $\kappa \ge \frac{1}{2}\alpha ,$ the condition (iii) will hold as following

$$R^{\prime } (\theta ) \ge \kappa f(\theta ) - (\kappa - \alpha )(P^{{\prime \prime }} (q^{f} (\theta ))q^{f} (\theta ) + 2P^{\prime } (q^{{f^{{\prime }} }} (\theta )))q^{f} (\theta )f(\theta ) + P^{\prime } (q^{f} (\theta ))q^{f} (\theta )f^{\prime } (\theta ) = (2\kappa - \alpha )f(\theta ) + P^{\prime } (q^{f} (\theta ))q^{f} (\theta )f^{\prime } (\theta ) \ge 0$$

in which $q^{{f^{{\prime }} }} (\theta ) = - \frac{1}{{u_{{qq}} (q^{f} (\theta ),\theta )}} = - \frac{1}{{P^{{\prime \prime }} (q^{f} (\theta ))q^{f} (\theta ) + 2P^{\prime } (q^{f} (\theta ))}}.$

Proof of Proposition 3

With decreasing marginal cost, the regulator’s problem is to choose one unique $p$ to maximize $E_{\theta } w(p,\theta )$ subject to the IR constraint $u(p,\theta ) \ge 0$. Characterizing the optimal pooling price $p^{s}$ when the IR constraint is ignored, we can obtain the price $p^{s}$ will violates the firm’s IR constraint if

$$p^{s} - c_{0} - \frac{1}{2}c_{1} Q(p^{s} ,\theta ) = \left( {1 - \frac{1}{2}c_{1} Q_{p} (p^{s} ,E(\theta )) - \frac{1}{\alpha }} \right)\frac{{Q(p^{s} ,E(\theta ))}}{{ - Q_{p} (p^{s} ,E(\theta ))}} - \frac{1}{2}c_{1} Q_{p} (p^{s} ,E(\theta ))(E(\theta ) - \theta ) < 0{\kern 1pt} .$$

When $c_{1} < 0$, the IR constraint will be violated, since $p^{s} - c_{0} - \frac{1}{2}c_{1} Q(p^{s} ,\theta ) < 0.$ The IR constraint can be written as

$u(p,\theta ) = (p - c_{0} - c_{1} Q(p,\theta ))Q(p,\theta ) + \frac{1}{2}c_{1} Q^{2} (p,\theta ) \ge 0.$ Thus, we can obtain

$u_{\theta } (p,\theta ) = (p - c_{0} - c_{1} Q(p,\theta ))Q_{\theta } (p,\theta ) \ge 0,$ since $c_{1} < 0,\;Q_{\theta } (p,\theta ) > 0.$ Therefore, the optimal price is determined when the IR constraint binds for lowest type, as $u(p^{u} ,\underline {\theta } ) = p^{u} Q(p^{u} ,\underline {\theta } ) - c_{0} Q(p^{u} ,\underline {\theta } ) - \frac{1}{2}c_{1} Q^{2} (p^{u} ,\underline {\theta } ) = 0.$

Proof of Proposition 4

From the first-order condition and the assumed linear demand function, we can obtain

$$q^{s} = \frac{{\alpha (P(0) + E(\theta ) - c_{0} )}}{{ - (2\alpha - 1)P^{\prime } (q^{s} ) + \alpha c_{1} }}.$$

Defining $A = \left[ {\frac{1}{2}c_{1} - \left( {1 - \frac{1}{\alpha }} \right)P^{\prime } (q^{s} )} \right]q^{s} - (E(\theta ) - \underline {\theta } )$ and substituting $q^{s}$, we can have

$$A = \left[ {\frac{1}{2}c_{1} - \left( {1 - \frac{1}{\alpha }} \right)P^{\prime } (q^{s} )} \right]\frac{{\alpha (P(0) + E(\theta ) - c_{0} )}}{{ - (2\alpha - 1)P^{\prime}(q^{s} ) + \alpha c_{1} }} - (E(\theta ) - \underline {\theta } ).$$

Assumed that $P(0) + E(\theta ) - c_{0} > 4(E(\theta ) - \underline {\theta } ),$ it shows if $c_{1} \ge 2\left( {1 - \frac{1}{\alpha } - \frac{{E(\theta ) - \underline {\theta } }}{{\alpha [P(0) + E(\theta ) - c_{0} - 2(E(\theta ) - \underline {\theta } )]}}} \right)P^{\prime } (q^{s} ) > 0,\;A > 0,$ and thus, the optimal quantity $q^{s}$ satisfies the IR constraint. Otherwise, $A < 0$ and $q^{s}$ violates the IR constraint and the IR constraint binds for $\underline {\theta }$ if

$$2P^{\prime } (q^{s} ) < c_{1} < 2\left( {1 - \frac{1}{\alpha } - \frac{{E(\theta ) - \underline {\theta } }}{{\alpha [P(0) + E(\theta ) - c_{0} - 2(E(\theta ) - \underline {\theta } )]}}} \right)P^{\prime } (q^{s} ).$$

Proof of Proposition 5

When $c_{1} < 0$, the IR constraint will be violated, since $p^{s} - c_{0} - \frac{1}{2}c_{1} Q(p^{s} ,\theta ) < 0.$ The IR constraint can be written as $u(p,\theta ) = (p - c_{0} - c_{1} Q(p,\theta ))Q(p,\theta ) + \frac{1}{2}c_{1} Q^{2} (p,\theta ) \ge 0.$ Thus, we can obtain $u_{\theta } (p,\theta ) = (p - c_{0} - c_{1} Q(p,\theta ))Q_{\theta } (p,\theta ) \ge 0,$ since $c_{1} < 0,\;Q_{\theta } (p,\theta ) > 0.$ Therefore, the optimal price is determined when the IR constraint binds for lowest type, as $u(p^{u} ,\underline {\theta } ) = p^{u} Q(p^{u} ,\underline {\theta } ) - c_{0} Q(p^{u} ,\underline {\theta } ) - \frac{1}{2}c_{1} Q^{2} (p^{u} ,\underline {\theta } ) = 0.$

When $c_{1} \ge 0$, we define

$B = \left( {1 - \frac{1}{2}c_{1} Q_{p} (p^{s} ,E(\theta )) - \frac{1}{\alpha }} \right)\frac{{Q(p^{s} ,E(\theta ))}}{{ - Q_{p} (p^{s} ,E(\theta ))}} - \frac{1}{2}c_{1} Q_{p} (p^{s} ,E(\theta ))(E(\theta ) - \theta ).$

Considering the linear demand and $\alpha = 1,\;B = \frac{1}{2}c_{1} Q(p^{s} ,2E(\theta ) - \theta ) > 0.$ Therefore, the optimal price $p^{s}$ satisfies the IR constraint.

Proof of Corollary 3

Consider $P(q) = P(0) + P^{\prime } (q)q$ and $Q(p,\theta ) = \frac{P(0) + \theta - p}{{ - P^{ {\prime }} (q)}}.$

Part 1. $c_{1} < 0$. We can obtain $q^{u} = \frac{{2\left( {P(0) + \underline {\theta } - c_{0} } \right)}}{{c_{1} - 2P^{\prime } (q)}}$ and $p^{u} = \frac{{2P^{\prime } (q)c_{0} - c_{1} (P(0) + \underline {\theta } )}}{{2P^{\prime } (q) - c_{1} }},$ that are independent with the weight $\alpha$. Thus, the social welfare of the two regulatory mechanism is linear and increasing with the weight $\alpha$.

When $\alpha = 0$, the difference of the regulator’s welfare is

$$\ \Delta = E_{\theta } (w(q^{u} ,\theta )) - E_{\theta } (w(p^{u} ,\theta )) = E_{\theta } [\int_{0}^{{q^{u} }} {(P(\tilde{q}) + \theta )} d\tilde{q} - (P(q^{u} ) + \theta )q^{u} - E_{\theta } [\int_{0}^{{Q(p^{u} ,\theta )}} {(P(\tilde{q}) + \theta )} d\tilde{q} - (P(Q(p^{u} ,\theta )) + \theta )Q(p^{u} ,\theta ) = - \frac{{P^{\prime } (q)}}{2}(q^{{u^{2} }} - E_{\theta } Q^{2} (p^{u} ,\theta )).{\text{ }}$$

Considering that $E_{\theta } Q^{2} (p^{u} ,\theta ) > Q^{2} (p^{u} ,E(\theta ))$ through Jensen’s Inequality, we get $\Delta < - \frac{{P^{\prime } (q)}}{2}(q^{{u2}} - Q^{2} (p^{u} ,E(\theta ))) \le 0,$ since $q^{u} - Q(p^{u} ,E(\theta )) = \frac{{E(\theta ) - \underline {\theta } }}{{P^{\prime}(q)}} \le 0.$

When $\alpha = 1,$$\Delta = \int_{0}^{{q^{u} }} {(P(\tilde{q}) + E(\theta ))} d\tilde{q} - \left( {c_{0} + \frac{1}{2}c_{1} q^{u} } \right)q^{u} - E_{\theta } \left[ {\int_{0}^{{Q(p^{u} ,\theta )}} {(P(\tilde{q}) + \theta )} d\tilde{q} - (c_{0} + \frac{1}{2}c_{1} Q(p^{u} ,\theta ))Q(p^{u} ,\theta )} \right].$

Note that $w_{\theta \theta } (p^{u} ,\theta ) = - c_{1} Q_{\theta }^{2} (p^{u} ,\theta ) > 0.$ Thus, $E_{\theta } (w(p^{u} ,\theta )) > w(p^{u} ,E(\theta ))$ by Jensen’s Inequality. We have $\Delta < \int_{0}^{{q^{u} }} {(P(\tilde{q}) + E(\theta ))} d\tilde{q} - \left( {c_{0} + \frac{1}{2}c_{1} q^{u} } \right)q^{u} - \left[ {\int_{0}^{{Q(p^{u} ,\theta )}} {(P(\tilde{q}) + E(\theta ))} d\tilde{q} - (c_{0} + \frac{1}{2}c_{1} Q(p^{u} ,E(\theta )))Q(p^{u} ,E(\theta ))} \right]$ . Considering $w_{q} (q,E(\theta )) = P(q) + E(\theta ) - c_{0} - c_{1} q = P(q) + \underline {\theta } - c_{0} - \frac{1}{2}c_{1} q + E(\theta ) - \underline {\theta } - \frac{1}{2}c_{1} q > 0$ where $P(q) + \underline {\theta } - c_{0} - \frac{1}{2}c_{1} q \ge 0$ by IR constraint, it shows $\Delta < 0.$ Consequently, $E_{\theta } (w(q^{u} ,\theta )) < E_{\theta } (w(p^{u} ,\theta ))$ for all $\alpha \in [0,1].$

Part 2. $0 \le c_{1} < c_{1}^{q}$ in which $c_{1}^{q} = - \frac{{2(E(\theta ) - \underline {\theta } )}}{{P(0) + E(\theta ) - c_{0} - 2(E(\theta ) - \underline {\theta } )}}P^{\prime } (q)$ when $\alpha = 1.$ Now, we have

$$\Delta = E_{\theta } [\int_{0}^{{q^{u} }} {(P(\tilde{q}) + \theta )} d\tilde{q} - (c_{0} + \frac{1}{2}c_{1} q^{u} )q^{u} ] - E_{\theta } [\int_{0}^{{Q(p^{u} ,\theta )}} {(P(\tilde{q}) + \theta )} d\tilde{q} - (c_{0} + \frac{1}{2}c_{1} Q(p^{u} ,\theta ))Q(p^{u} ,\theta )]{\kern 1pt} {\kern 1pt} .$$

Considering $w(p^{u} ,\theta ) = \int_{0}^{{q^{u} }} {(P(\tilde{q}) + \theta )} d\tilde{q} - (c_{0} + \frac{1}{2}c_{1} q^{u} )q^{u} + (P(q^{u} ) + \theta - c_{0} - c_{1} q^{u} )(Q(p^{u} ,\theta ) - q^{u} ) + \frac{1}{2}(P^{\prime}(q^{u} ) - c_{1} )(Q(p^{u} ,\theta ) - q^{u} )^{2} ,$ we have

$$\Delta = E_{\theta } \left[ {(P(q^{u} ) + \theta - c_{0} - c_{1} q^{u} )(q^{u} - Q(p^{u} ,\theta )) + \frac{1}{2}(c_{1} - P^{{ {\prime \prime }}} (q))(q^{u} - Q(p^{u} ,\theta ))^{2} } \right].$$

Noting $q^{u} = \frac{{2(P(0) + \underline {\theta } - c_{0} )}}{{c_{1} - 2P^{\prime } (q)}}$ and $Q(p^{u} ,\theta ) = \frac{{P(0) + E(\theta ) - c_{0} + \left( {1 + \frac{{c_{1} }}{{ - P^{\prime } (q)}}} \right)(\theta - E(\theta ))}}{{c_{1} - P^{\prime } (q)}},$ we get $\Delta = \frac{{ - c_{1}^{2} }}{{2(c_{1} - P^{ {\prime }} (q))(c_{1} - 2P^{ {\prime }} (q))^{2} }}E_{\theta } K(\theta ),$ where $K(\theta ) = m(\theta )n(\theta )$ such that $m(\theta ) = P(0) - c_{0} + \underline {\theta } + \frac{{(2P^{\prime } (q) - c_{1} )(P^{\prime } (q) + c_{1} )}}{{c_{1} P^{\prime}(q)}}(\theta - \underline {\theta } ) + \left( {\frac{{c_{1} }}{{P^{\prime}(q)}} - 2} \right)(E(\theta ) - \underline {\theta } )$ and $n(\theta ) = P(0) - c_{0} + \underline {\theta } + \left( {2 - \frac{{c_{1} }}{{P^{ {\prime }} (q)}}} \right)(E(\theta ) - \underline {\theta } ) + \frac{{(2P^{ {\prime }} (q) - c_{1} )(P^{ {\prime }} (q) - c_{1} )}}{{c_{1} P^{\prime}(q)}}(\theta - \underline {\theta } ).$

From $c_{1}^{q} = - \frac{{2(E(\theta ) - \underline {\theta } )}}{{P(0) + E(\theta ) - c_{0} - 2(E(\theta ) - \underline {\theta } )}}P^{ {\prime }} (q),$ it shows

$P(0) + \underline {\theta } - c_{0} = E(\theta ) - \underline {\theta } - \frac{{2(E(\theta ) - \underline {\theta } )}}{{c_{1}^{q} }}P^{ {\prime }} (q).$ Substituting it to $m(\theta )$ and $n(\theta )$, we have $m(\theta ) = - 2P^{ {\prime }} (q)\left( {\frac{1}{{c_{1} }} - \frac{1}{{c_{1}^{q} }}} \right)(E(\theta ) - \underline {\theta } ) + \frac{{(2P^{ {\prime }} (q) - c_{1} )(P^{ {\prime }} (q) + c_{1} )}}{{c_{1} P^{ {\prime }} (q)}}(\theta - E(\theta ))$ and $n(\theta ) = - 2P^{ {\prime }} (q)\left( {\frac{1}{{c_{1} }} - \frac{1}{{c_{1}^{q} }}} \right)(E(\theta ) - \underline {\theta } ) + \frac{{(2P^{ {\prime }} (q) - c_{1} )(P^{ {\prime }} (q) - c_{1} )}}{{c_{1} P^{ {\prime }} (q)}}(\theta - E(\theta )),$where $P^{ {\prime }} (q) + c_{1} < P^{ {\prime }} (q) + c_{1}^{q} < 0$ under the assumption of $P(0) + E(\theta ) - c_{0} > 4(E(\theta ) - \underline {\theta } ).$

Note that $K^{{ {\prime \prime }}} (\theta ) = \frac{{(2P^{ {\prime }} (q) - c_{1} )^{2} (P^{{ {\prime }2}} (q) - c_{1}^{2} )}}{{2c_{1}^{2} P^{{ {\prime }2}} (q)}} > 0,$ and thus $E_{\theta } K(\theta ) > K(E(\theta )) = 4P^{\prime 2} (q)\left( {\frac{1}{{c_{1} }} - \frac{1}{{c_{1}^{q} }}} \right)^{2} (E(\theta ) - \underline {\theta } )^{2} \ge 0,$ by Jensen’s Inequality. Therefore, it shows $\Delta < 0.$

Part 3. $c_{1} \ge c_{1}^{q}$. We get $q^{u} = \frac{{P(0) + E(\theta ) - c_{0} }}{{c_{1} - P^{\prime}(q)}}$, $p^{u} = \frac{{c_{1} (P(0) + E(\theta )) - c_{0} P^{\prime } (q)}}{{c_{1} - P^{\prime } (q)}}.$

Similar to Part 2, we have

$$\Delta = E_{\theta } \left[ {(P(q^{u} ) + \theta - c_{0} - c_{1} q^{u} )(q^{u} - Q(p^{u} ,\theta )) + \frac{1}{2}(c_{1} - P^{\prime } (q))(q^{u} - Q(p^{u} ,\theta ))^{2} } \right].$$

Considering $P(q^{u} ) + \theta - c_{0} - c_{1} q^{u} = \theta - E(\theta ),\;q^{u} - Q(p^{u} ,\theta ) = \frac{E(\theta ) - \theta }{{ - P^{\prime } (q)}},$ we obtain $\Delta = E_{\theta } \left[ {\frac{1}{2}(c_{1} + P^{\prime } (q))\frac{{(E(\theta ) - \theta )^{2} }}{{P^{\prime 2} (q)}}} \right].$ Therefore, $\Delta > 0$ only if $c_{1} < - P^{\prime } (q).$ Note that $c_{1}^{q} < - P^{\prime } (q)$ under the assumption of $P(0) + E(\theta ) - c_{0} > 4(E(\theta ) - \underline {\theta } )$. To ensure $Q(p^{u} ,\theta )$ is not negative, we assume that $c_{1} \le - P^{\prime } (q)\left( {\frac{{P(0) + E(\theta ) - c_{0} }}{{E(\theta ) - \underline {\theta } }} - 1} \right).$