1 Introduction

In the field of epidemiology, understanding the natural history of a chronic disease, which refers to the clinical course of a disease progress, is important for formulating prevention and control strategies for the disease. In dementia studies, the cognitive function of a senior is assessed periodically and summarized roughly as intact cognition, mild cognitive impairment (MCI), or dementia. The transitions among these states describe the natural history of the disease. An example is the Nun Study of aging and Alzheimer’s disease (Nun Study), which monitored nuns aged 75 years or older at entry for future disease progression with approximately annual examination up to 10 years. In this study cohort, some individuals were already found to be in the dementia state in their screening tests, yielding two sub-cohorts: the incident cohort of subjects without dementia at entry and followed for the potential diagnosis of dementia and death, and the prevalent cohort of subjects who were diagnosed with dementia at entry and followed up to death.

Of particular interest is the study of risk factors for cognitive decline and the duration from dementia onset to death. In the analyses using incident cohort data from the Nun Study, Tyas et al. (2007) concluded that the presence of apolipoprotein E4 allele (ApoE4) and low education increased the risk of transition to MCI but not the risk of the transition from MCI to dementia or death. Meanwhile, Wei et al. (2014) showed that both risk factors were positively associated with the transitions to MCI and dementia. Although the incident cohort is the collection of random samples from the target population, it is possibly limited in its ability to observe sufficient events of death. This factor can be mitigated by including the prevalent cohort with more failure events. Analyzing the combined data from the incident and prevalent cohorts leads to more efficiency in estimating baseline intensity functions and evaluating risk factors. In this paper, we revisit the association of risk factors with the transitions to MCI, dementia, and death by using both incident and prevalent cohorts from the Nun Study.

Analyzing the combined incident and prevalent cohort data is complex, owing to some unique and challenging data features. First, cognitive functioning is often assessed by intermittent visits, resulting in interval censored times for transitions. Second, since reverting from MCI back to intact cognition is fairly common in the natural history of dementia, the exact disease trajectory for a subject is difficult to ascertain. Third, the patients sampled in the midst of dementia usually cannot provide the exact starting date of the dementia. Only the remaining period of the progression from dementia to death, the time from study enrollment to death or loss to follow-up, is observed from the prevalent cohort. Lastly, the subjects from the prevalent cohort are likely to have longer durations from dementia to death compared to the dementia patients in the incidence cohort, which causes selection bias, i.e., the left-truncation problem. Failure to address these theoretical challenges when combining incident and prevalent cohorts may result in biased inference on the natural history of the disease and its association with risk factors.

With a single survival endpoint of interest, a few works from the literature have shown the benefits of combining both incident and prevalent cohorts. For example, Lee et al. (2019) proposed an efficient estimation procedure that uses both the incident and prevalent cohorts under a proportional mean residual life model with right-censored data. In other areas, Wolfson et al. (2019) suggested approaches for estimating the non-parametric estimators of the survival function with the combined data in myotonic dystrophy by assuming that the disease onset of a prevalent case was known to be within an interval. McVittie et al. (2020) constructed the parametric likelihood of the combined data to estimate hospital stay durations, subject to right-censoring and the assumption of stationarity. Although important, their methods are not applicable to describe the natural history of disease that is represented with transitions between multiple states and often observed with data subject to selection bias. Joint modeling of the combined data with multiple transitions has been proposed in the literature. For example, Kulathinal et al. (2020) showed a gain in efficiency by combining both the incident and prevalent cohorts under the multistate model framework. They postulated that the incidence of the event of interest could be retrospectively observed in the prevalent cohort. On the other hand, Saarela et al. (2009) and Gorfine et al. (2021) proposed estimation procedures to jointly model both prevalent and incident cases subject to right censoring when important information from the prevalent cases is uncertain. To the best of our knowledge, there is no prior work that addresses the topic of modeling interval-censored natural history data obtained from a combination of incident and prevalent cohorts, particularly when the onset of prevalent disease cannot be observed retrospectively.

We propose a multistate approach for analyzing interval-censored event history data that are observed from both incident and prevalent cohorts to examine the association of risk factors with the transitions that are involved in the natural history of the disease. The modelling of cognitive changes and death in dementia is illustrated with a nonhomogeneous multistate Markov model, allowing for the reversible transition between intact cognition and MCI and the transition from any cognitive state to death. Within a multistate modeling framework, we derive the distribution of dementia onset using event-history observations, and we use this to model the observable residual periods of prevalent samples in a general truncation structure. We present a likelihood-based estimation procedure for jointly modelling the combined data from incident and prevalent cohorts in Sect. 2. In Sect. 3, intensive simulation studies are conducted to investigate the finite sample performance of the estimation procedure and to show the efficiency gains of the estimators compared to those that are obtained using the incident cohort only. We use the proposed method to analyze the Nun Study in Sect. 4. Section 5 contains some concluding remarks.

2 Statistical methodologies

2.1 Notations and model

Fig. 1
figure 1

Transition diagram with four states for dementia: state 0 for intact cognition, state 1 for mild cognitive impairment (MCI), state 2 for dementia and state 3 for death

Full size image

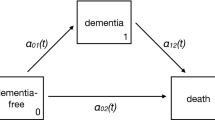
We denote the participant’s health status at a given time t \((t\ge 0)\) by a multistate process X(t) that takes a finite number of the values for the states representing discrete clinical conditions or death. In dementia studies, the multistate processes are typically characterized with four states, namely \(X(t)\in \{0, 1, 2, 3\}\), where 0 denotes cognitively intact for age, 1 denotes cognitive impairment, 2 denotes clinical dementia, and 3 denotes death. The biologically plausible transitions between the four states are depicted in Fig. 1, where the transition between state 0 and state 1 is potentially reversible, the transition from state 0 to 2 is assumed to proceed through MCI, and state 3 is the absorbing state that can be reached from all other states.

Assume that X(t) follows a conditional Markov multistate model with four states, characterized by the conditional transition probabilities,

$$\begin{aligned} p_{kl} (t_1, t_2|{\textbf{Z}}) = P\lbrace X(t_2) = l|X(t_1) = k, {\textbf{Z}}\rbrace , \end{aligned}$$

where \(k, l \in \{0, 1, 2, 3\}\), \(t_1 \le t_2\) and \({\textbf{Z}}\) is a vector of risk factors. Then, the conditional transition intensity from k to l, \(q_{kl}(t|{\textbf{Z}})\), is

$$\begin{aligned} q_{kl}(t|{\textbf{Z}}) = \lim _{\Delta t\rightarrow 0^+}\frac{P(X(t^-+\Delta t)=l|X(t^-)=k,{\textbf{Z}})}{\Delta t}, \end{aligned}$$

for \(k \ne l\) and \(q_{kk}(t|{\textbf{Z}}) = - \sum _{l\ne k} q_{kl}(t|{\textbf{Z}})\) (Cox and Miller 1965). Let \({\textbf{P}}(t_1, t_2)\) denote the transition probability matrix whose (k, l) entry is \(p_{kl} (t_1, t_2|{\textbf{Z}})\) and \({\textbf{Q}}(t)\) denote the transition intensity matrix whose (k, l) entry is \(q_{kl}(t|{\textbf{Z}})\) and \(k, l \in \{0, 1, 2, 3\}\). With the possible transitions shown in Fig. 1,

$$\begin{aligned}{\textbf{P}}(t_1, t_2)= &\left( \begin{array}{cccc} p_{00} (t_1, t_2|{\textbf{Z}}) &{} p_{01} (t_1, t_2|{\textbf{Z}}) &{} p_{02} (t_1, t_2|{\textbf{Z}}) &{} p_{03} (t_1, t_2|{\textbf{Z}}) \\ p_{10} (t_1, t_2|{\textbf{Z}}) &{} p_{11} (t_1, t_2|{\textbf{Z}}) &{} p_{12} (t_1, t_2|{\textbf{Z}}) &{} p_{13} (t_1, t_2|{\textbf{Z}}) \\ 0 &{} 0 &{} p_{22} (t_1, t_2|{\textbf{Z}}) &{} p_{23} (t_1, t_2|{\textbf{Z}})\\ 0 &{} 0 &{} 0 &{} 1 \\ \end{array}\right) \text{ and } \\{\textbf{Q}}(t)=& \left( \begin{array}{cccc} q_{00}(t|{\textbf{Z}}) &{} q_{01}(t|{\textbf{Z}}) &{} 0 &{} q_{03}(t|{\textbf{Z}})\\ q_{10}(t|{\textbf{Z}}) &{} q_{11}(t|{\textbf{Z}}) &{} q_{12}(t|{\textbf{Z}}) &{} q_{13}(t|{\textbf{Z}}) \\ 0 &{} 0 &{} q_{22}(t|{\textbf{Z}}) &{} q_{23}(t|{\textbf{Z}}) \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array}\right) . \end{aligned}$$

The transition probabilities for a continuous-time Markov process can be obtained by solving the following Kolmogorov forward equation,

$$\begin{aligned} \frac{d{\textbf{P}}(t_0, t)}{dt} = {\textbf{P}}(t_0, t) {\textbf{Q}}(t), \end{aligned}$$
(1)

where \({\textbf{P}}(t_0, t_0) ={\textbf{I}}\) is the identity matrix. For a nonhomogeneous Markov model, however, the solution to equation (1) is intractable with non-trivial forms of \({\textbf{Q}}(t)\), and it is computationally intensive to get the solution with covariates (Titman 2011). In some situations, an analytic solution to equation (1) is available; the first example is a progressive process with a small number of states (Pak et al. 2017, 2019), and the second example is a time transformation model that assumes the transition intensity matrix is a form of \({\textbf{Q}}(t) = {\textbf{Q}}_0dh(t)/dt\) with the operation time h(t), where \({\textbf{Q}}_0\) is the transition intensity matrix for a homogeneous Markov process and h(t) is a nonnegative function (Kalbfleisch and Lawless 1985; Omar et al. 1995; Hubbard et al. 2008). We adapt the time transformation model when constructing the likelihood function for event-history data.

We assume the multiplicative intensity model for each transition that is

$$\begin{aligned} q_{kl}(t|{\textbf{Z}}) = q^{(0)}_{kl}(t)\exp ({\textbf{Z}}^\prime {\varvec{\beta }}_{kl}), \ \ k \ne l \end{aligned}$$
(2)

where \(q^{(0)}_{kl}(t)\) is the k-to-l baseline transition intensity and \({\varvec{\beta }}_{kl}\) is the regression coefficient vector for the transition from state k to state l. We use the Weibull distribution to model the baseline transition intensities under the assumption of the same time dependency across transitions, namely, \(q^{(0)}_{kl}(t) = \lambda _{kl} \gamma t^{\gamma - 1}\) with unknown positive parameters, \(\lambda _{kl}\) and \(\gamma \). Then, the transition intensity matrix \({\textbf{Q}}(t)\) can be expressed as \({\textbf{Q}}_0dh(t)/dt\), where \({\textbf{Q}}_0\) is the transition intensity matrix whose (k, l) entry is \(\lambda _{kl}\exp \left( {\textbf{Z}}^\prime {\varvec{\beta }}_{kl}\right) \) and \(dh(t)/dt = \gamma t^{\gamma -1}\). This implies that there exists a new time scale, h(t), which leads to the homogeneous process with the transition intensity matrix \({\textbf{Q}}_0\) (Hubbard et al. 2008). Thus, we have \({\textbf{P}}(t_1, t_2) = \exp \left[ {\textbf{Q}}_0 \{h(t_2) - h(t_1)\}\right] \), where \(h(t) = \int _0^t \gamma s^{\gamma -1}ds\).

Fig. 2
figure 2

The diagram for left truncation in a prevalent cohort study: Case (1) is for a subject sampled in the cohort, and Case (2) is for a subject not sampled in the cohort

Full size image

We introduce additional notation to model the prevalent samples. The prevalent cohort includes participants who are alive but with dementia at the time of recruitment. Let U denote individual’s age at study enrollment. Further, we let \(A^o\) be the age of onset for clinical dementia and \(A^d\) be the age at death. Then, the prevalent cohort is formed by the individuals whose age at enrollment U is between \(A^o\) and \(A^d\). Let \(\widetilde{W} = U - A^o\) denote the time from dementia onset to study enrollment and \(\widetilde{T} = A^d - A^o\) denote the time from dementia onset to death within a prevalent population of patients with dementia. Let (W, T) be a pair of \((\widetilde{W}, \widetilde{T})\) for the observed samples in the prevalent cohort among those who are eligible to be sampled at the time of recruitment (i.e., \(\widetilde{T} > \widetilde{W}\)). Note that (W, T) is not exactly observed. This is because the exact age at dementia onset is generally unavailable from the prevalent cohort. We let \(T = W + V\), where V is the observed time from study recruitment to death and C denote a residual censoring time from study recruitment to loss of follow-up. The diagram in Fig. 2 depicts these notations for the prevalent sampling.

2.2 Likelihood and estimation

Consider a random sample of m independent subjects that are combined from both the incident and prevalent cohorts with respective sample sizes of \(m_1\) and \(m_2\), where \(m = m_1 + m_2\). Suppose that those in the incident cohort are labeled \(1, \cdots , m_1, m_1 < m\). Let \(X_i(t)\) be the state of the health condition at time t for the i-th subject (\(i = 1, \cdots , m\)). For the i-th subject, we let \({\varvec{s}}_{i} = (s_{i1}, \cdots , s_{in_i})^\prime \) denote the states, consecutively observed by \(n_i\) observations with the corresponding time points \({\varvec{t}}_{i} = (t_{i1}, \cdots , t_{in_i})^\prime \), and \({\textbf{z}}_{i}\) denote a vector of baseline risk factors. In the Nun Study, the time to death was observed exactly when a subject died during the study. Let \(\delta _i = 1\) if the i-th subject died before the end of study and \(\delta _i = 0\) otherwise. Then, \(s_{in_i}=3\) for \(\delta _i = 1\) and \(s_{in_i}\in (0, 1, 2)\) for \(\delta _i = 0\).

The observed event history data from the incident cohort consist of \(\mathcal {O}^{(inc)} \equiv (\mathcal {O}^{(inc)}_1, \cdots , \mathcal {O}^{(inc)}_{m_1})\), where \(\mathcal {O}^{(inc)}_i = ({\varvec{t}}_{i}, {\varvec{s}}_{i}, \delta _i, {\textbf{z}}_i)\) and \(i = 1\cdots , m_1\). We assume that the disease progression is a Markov process and \(\mathcal {O}^{(inc)}_i\) is independent across subjects. Denote the vector of all model parameters by \({\varvec{\theta }}\). The likelihood for the incident cohort of the i-th subject who was alive at the end of the study, denoted by \(\mathcal {L}^{(inc)}_i({\varvec{\theta }};\,{\varvec{t}}_{i}, {\varvec{s}}_{i}, \delta _i = 0, {\textbf{z}}_i)\), can be expressed as the product of the transition probabilities, which is

$$\begin{aligned} \mathcal {L}^{(inc)}_i({\varvec{\theta }};\, {\varvec{t}}_{i}, {\varvec{s}}_{i}, \delta _i = 0, {\textbf{z}}_i) = P\{X(t_{i1}) = s_{i1}|{\textbf{z}}_{i}\} \left\{ \prod _{r=2}^{n_i} p_{s_{i(r-1)} s_{ir}} (t_{i(r-1)}, t_{ir}|{\textbf{z}}_{i}) \right\} , \end{aligned}$$
(3)

where \(P\{X(t_{i1}) = s_{i1}|{\textbf{z}}_{i}\}\) can be approximated by \(p_{0s_{i1}} (t_{0}, t_{i1}|{\textbf{z}}_{i})\) with a possible time point \(t_0\) of being in intact cognition, such as the age at which the disease initiated.

In the Nun Study, a subject’s cognitive state at the moment of death was unknown unless they were diagnosed with dementia before death. Multiple possible risks of death may exist after the last cognitive assessment of the subject. For example, if the last assessment of a subject was the MCI state, there were three possible risks of death: (1) cognitive function was improved and she died in the cognitive intact state, (2) dementia was not developed before death and she died in the MCI state, and (3) dementia was developed and she died in the dementia state. The likelihood for the i-th subject of the incident cohort who died during the study (i.e., the subject with \(s_{n_i} = 3\) for \(i = 1, \cdots , m_1\)) is then

$$\begin{aligned} \mathcal {L}^{(inc)}_i({\varvec{\theta }};\,{\varvec{t}}_{i}, {\varvec{s}}_{i}, \delta _i = 1, {\textbf{z}}_i) =&P\{X(t_{i1}) = s_{i1}|{\textbf{z}}_{i}\} \left\{ \prod _{r=2}^{n_i - 1} p_{s_{i(r-1)} s_{ir}} (t_{i(r-1)}, t_{ir}|{\textbf{z}}_{i}) \right\} \nonumber \\&\times \sum _{k\ne 3}p_{s_{i(n_i-1)} k}(t_{i(n_i-1)}, t_{in_i}^-|{\textbf{z}}_{i})q_{k3}(t_{in_i}|{\textbf{z}}_i). \end{aligned}$$
(4)

Therefore, the likelihood of the incident cohort data, \(\mathcal {L}^{(inc)}\), is

$$\begin{aligned} \mathcal {L}^{(inc)}({\varvec{\theta }}; \mathcal {O}^{(inc)}) = \prod _{i = 1}^{m_1} \mathcal {L}^{(inc)}_{i}({\varvec{\theta }};\,{\varvec{t}}_{i}, {\varvec{s}}_{i}, \delta _i, {\textbf{z}}_i). \end{aligned}$$
(5)

Next, we construct the likelihood for the prevalent cohort after adjusting for left-truncation. Based on our multistate model, the probability density function of the age of dementia onset \(A^o\) given the covariates \({\textbf{Z}}= {\textbf{z}}\), denoted by \(f_{A^o}(a|{\textbf{z}})\), is

$$\begin{aligned} f_{A^{o}}(a|{\textbf{z}}) = \frac{p_{01}(0, a|{\textbf{z}}) q_{12}(a|{\textbf{z}})}{\int _0^\infty p_{01}(0, u|{\textbf{z}}) q_{12}(u|{\textbf{z}})du}. \end{aligned}$$
(6)

Then, the conditional density function of \(\widetilde{T}\) given \(A^o = a\) follows:

$$\begin{aligned} f_{\widetilde{T}|A^o}(t|a, {\textbf{z}}) = \frac{f_{23}(a + t|{\textbf{z}})}{S_{23}(a|{\textbf{z}})}, \end{aligned}$$
(7)

where \(f_{23}\) and \(S_{23}\) are, respectively, the density function and the survival function for \(A^d\) given \({\textbf{Z}}= {\textbf{z}}\).

We assume that \(\widetilde{T}\) is independent of \(\widetilde{W}\) given \(A^o\) and \({\textbf{Z}}= {\textbf{z}}\). Note that the subjects from the prevalent cohort of the Nun Study are among those who have \(\widetilde{T} > \widetilde{W}\) due to the prevalent sampling, and T is dependent of (W, V) due to their relationship in \(T = W + V\). If a subject from the prevalent cohort dies during the study, the age of study enrollment U and the residual survival time V are observable. With (6) and (7), the joint density of (U, V) given \({\textbf{Z}}= {\textbf{z}}\) and the sampling constraint, denoted by \(f(u, v|{\textbf{z}})\), follows:

$$\begin{aligned} f(u, v|{\textbf{z}})&= P(U = u, V = v|\widetilde{T}> \widetilde{W},{\textbf{Z}}={\textbf{z}})\\&=\frac{\int _0^{u} P(\widetilde{T} = u + v - a, \widetilde{W} = {u}-a|A^o = a, {\textbf{Z}}={\textbf{z}}) f_{A^{o}}(a|{\textbf{z}})da}{P(\widetilde{T}> \widetilde{W}|{\textbf{Z}}={\textbf{z}})}\\&=\frac{\int _0^{u} f_{\widetilde{T}|A^o}(u + v - a|{\textbf{z}})g(u - a|{\textbf{z}})f_{A^{o}}(a|{\textbf{z}})da}{P(\widetilde{T} > \widetilde{W}| {\textbf{Z}}={\textbf{z}})}, \end{aligned}$$

where \(g(w|{\textbf{z}})\) is the probability density function for \(\widetilde{W}\) given \({\textbf{Z}}= {\textbf{z}}\), and

$$\begin{aligned} P(\widetilde{T}> \widetilde{W}|{\textbf{Z}}={\textbf{z}})&= \int _0^\infty P(\widetilde{T}> \widetilde{W}, A^{o} = a|{\textbf{Z}}={\textbf{z}}) da\\&= \int _0^\infty \int _0^\infty P(\widetilde{T} > \widetilde{W}, \widetilde{W} = w|A^{o} = a, {\textbf{Z}}={\textbf{z}}) f_{A^{o}}(a|{\textbf{z}})dadw \\&= \int _0^\infty \int _0^\infty S_{\widetilde{T}|A^o}(w|{\textbf{z}}) g(w|{\textbf{z}})f_{A^{o}}(a|{\textbf{z}})dadw. \end{aligned}$$

A parametric family of distribution can be used for \(g(w|{\textbf{z}})\). Length-biased sampling can also be assumed by letting \(g(w|{\textbf{z}})\) be a uniform distribution over \((0, \tau )\), where \(\tau \) is a constant that makes the probability mass \(P(T = t|T > A) \to 0\) for \(t > \tau \) (Shen et al. 2009).

Since the transition that is possible for a subject with dementia is the transition toward death, the information on study enrollment and last assessment suffices to describe the prevalent cohort data. Let \(u_i\) be the age at study enrollment and \(y_i\) be the observed time from study entry to the last assessment for the i-th subject. Then, the observed data for the i-th subject consist of \(u_i\), \(y_i = \min (V_i, C_i)\), \(\delta _i = I(V_i < C_i)\), and \({\textbf{z}}_i\). We denote the prevalent cohort data as \(\mathcal {O}^{(pre)} \equiv (\mathcal {O}^{(pre)}_{m_1 + 1}, \cdots , \mathcal {O}^{(pre)}_{m})\), where \(\mathcal {O}^{(pre)}_i = (u_i, y_i, \delta _i, {\textbf{z}}_i)\) and \(i = m_1 + 1,\cdots , m\).

Assume that C is independent of \((\widetilde{T}, \widetilde{W}, V)\) given \({\textbf{Z}}={\textbf{z}}\). Then, the likelihood for the prevalent cohort is proportional to

$$\begin{aligned} \mathcal {L}^{(pre)}({\varvec{\theta }}, {\varvec{\xi }}; \mathcal {O}^{(pre)}) \propto \prod _{i = m_1 + 1}^{m_2}f(u_i, y_i|{\textbf{z}}_i)^{\delta _i} S(u_i, y_i|{\textbf{z}}_i)^{1 - \delta _i}, \end{aligned}$$
(8)

where \(S(u, y|{\textbf{z}}) = \int _{y}^\infty f(u, r|{\textbf{z}})dr\), \({\varvec{\theta }}\) is a vector of the same model parameters for the target population of the incident cohort, and \({\varvec{\xi }}\) is a vector of the parameters in \(g(w|{\textbf{z}})\).

Table 1 Simulation results for estimating \({\varvec{\beta }}\) with incident cohort data only \((m_1 = 300)\) or with the combined cohort (\(m_1 = 300\) and \(m_2 = 300\)) under different censoring rates for the prevalent cohort. The coefficient vector for k-l transition is denoted by \({\varvec{\beta }}_{kl} = (\beta _{kl}^{(1)}, \beta _{kl}^{(2)})^\prime \), where \(\beta _{kl}^{(1)}\) for \(Z_1\) and \(\beta _{kl}^{(1)}\) for \(Z_2\)
Full size table

The likelihood function for combined data from incident and prevalent cohorts can be expressed as the product of the likelihoods given in (5) and (8),

$$\begin{aligned} \mathcal {L}({\varvec{\theta }}, {\varvec{\xi }}; \mathcal {O}^{(inc)}, \mathcal {O}^{(pre)}) \propto \mathcal {L}^{(inc)}({\varvec{\theta }}; \mathcal {O}^{(inc)}) \times \mathcal {L}^{(pre)}({\varvec{\theta }}, {\varvec{\xi }}; \mathcal {O}^{(pre)}). \end{aligned}$$
(9)

We can estimate \({\varvec{\theta }}\) and \({\varvec{\xi }}\) by maximizing the logarithm of the likelihood in (9).

The likelihood function can readily be extended to handle the event history data with interval-censored events in the prevalent cohort. Assume that the residual period of a prevalent subject is only known to be within a specific interval, i.e., \(V \in [L, R)\), where \(L \ge U \) and \(R = \infty \) for right-censoring. The likelihood for the prevalent cohort can be generalized to

$$\begin{aligned} \mathcal {L}^{(pre)}({\varvec{\theta }}, {\varvec{\xi }}; \mathcal {O}^{(pre)}) \propto \prod _{i = m_1 + 1}^{m_2}&\left\{ f(u_i, y_i|{\textbf{z}}_i)^{\delta _i} S(u_i, y_i|{\textbf{z}}_i)^{1 - \delta _i}\right\} ^{1 - \delta _{Ii}} \nonumber \\&\times \left\{ S(u_i, l_i|{\textbf{z}}_i) - S(u_i, r_i|{\textbf{z}}_i)\right\} ^{\delta _{Ii}}, \end{aligned}$$
(10)

where \((l_i, r_i)\) is the interval of (L, R) for the i-th subject, and \(\delta _{Ii} = I(R_i < \infty )\). Thus, the likelihood function for the combined data with interval-censored prevalent samples is proportional to the product of the likelihoods given in (5) and (10).

The maximum likelihood implementation requires calculating integrals over finite or infinite intervals, which may not have analytic solutions. In such a case, we obtain a numerical integral value by using the Gauss-Jacobi quadrature after transforming an integral over the unit interval (0, 1). The statistical inference about \({\varvec{\eta }}\equiv ({\varvec{\theta }}^\prime , {\varvec{\xi }}^\prime )^\prime \) can be performed with the asymptotic distribution of \(\hat{{\varvec{\eta }}}\), which we approximate by \(N(\hat{{\varvec{\eta }}}, I^{-1}_{obs}(\hat{{\varvec{\eta }}}))\), where \(I_{obs}\) is the observed information matrix.

3 Simulation studies

We conducted a series of simulation studies to assess finite sample properties of the proposed likelihood-based approach. Two different sets of sample sizes for the incident cohort and the prevalent cohort were considered: (a) \(m = 600\) (\(m_1 = 300\) and \(m_2 = 300\)) and (b) \(m = 1200\) (\(m_1 = 600\) and \(m_2 = 600\)). We generated two independent covariates from \(Z_1 \sim \text{ Bernoulli }(0.4)\) and \(Z_2 \sim \text{ Uniform }(0, 1)\), i.e., \({\textbf{Z}}= (Z_1, Z_2)^\prime \). In data generation of the life-history process for a subject, the Weibull baseline transition intensities were used with the set of parameters: \(\lambda _{01} = 0.5\), \(\lambda _{03} = 0.2\), \(\lambda _{10} = 0.4\), \(\lambda _{12} = 0.3\), \(\lambda _{13} = 0.4\), \(\lambda _{23} = 0.3\), and \(\gamma = 1.5\). The coefficients of \({\textbf{Z}}\) for transitions, denoted by \({\varvec{\beta }}= ({\varvec{\beta }}_{01}^\prime , {\varvec{\beta }}_{03}^\prime , {\varvec{\beta }}_{10}^\prime , {\varvec{\beta }}_{12}^\prime , {\varvec{\beta }}_{23}^\prime )^\prime \), were chosen to be \({\varvec{\beta }}_{01}^\prime = (0.2, -0.2)\), \({\varvec{\beta }}_{03}^\prime = (0.1, -0.2)\), \({\varvec{\beta }}_{10}^\prime = (-0.2, 0.2)\), \({\varvec{\beta }}_{12}^\prime = (0.2, -0.3)\), \({\varvec{\beta }}_{13}^\prime = (0.2, 0.2)\), and \({\varvec{\beta }}_{23}^\prime = (0.3, -0.2)\). Ten cognitive assessment times for each subject were simulated to generate interval censored data, which were set to \(t_1 = 0.2 + \text{ Uniform }(0, 0.4)\) and \(t_j = t_{j-1} + \text{ Uniform }(0.2, 0.4)\) for \(j = 2, \cdots , 10\). With these assessment rules, about \(50\%\) of subjects were still alive at the last assessment. For the prevalent cohort, the distribution of \(\widetilde{W}\) was assumed to follow the Weibull distribution that is \(g(w) = 0.6 w^{0.2}\exp (-0.5 w^{1.2})\), and the residual censoring time C was generated from \(\text{ Uniform }(0, c)\), where c was set to achieve two censoring percentages, \(15\%\) and \(30\%\). Lastly, 1000 replicates were generated in each set of sample sizes for Monte Carlo simulations.

Table 2 Simulation results for estimating \({\varvec{\beta }}\) with incident cohort data only \((m_1 = 600)\) or with the combined cohort (\(m_1 = 600\) and \(m_2 = 600\)) under different censoring rates for the prevalent cohort. The coefficient vector for k-l transition is denoted by \({\varvec{\beta }}_{kl} = (\beta _{kl}^{(1)}, \beta _{kl}^{(2)})^\prime \), where \(\beta _{kl}^{(1)}\) for \(Z_1\) and \(\beta _{kl}^{(1)}\) for \(Z_2\)
Full size table

Tables 1 and 2 show the simulation results for estimating \({\varvec{\beta }}\) from the combined cohort data with the different censoring rates of a prevalent cohort, along with the results of fitting a multistate model to the incident cohort data only. The mean estimates from all simulated cohort data are close to the true parameter values. The empirical standard errors of the estimates are almost the same as the mean of the estimated asymptotic standard errors, and they decrease by almost \(\sqrt{2}\) when the sample size doubles. The coverage probability for every estimator is also close to the nominal level. We further calculated the relative efficiency (RE) of the two approaches, defined as the ratio of the mean square error of the estimator from the combined cohort to that from the incident cohort. As expected, the approach using the combined cohort data has the highest efficiency gain in estimating \({\varvec{\beta }}_{23}\) with the range of REs being about from 7.4 to 11.7 across all scenarios. The censoring rate of the prevalent samples is negatively related to the RE of \({\varvec{\beta }}_{23}\). The efficiency gains in estimating the baseline intensity for the 2-to-3 transition are also depicted in Fig. 3; the 95% pointwise confidence intervals of the baseline intensities from the combined cohort data are narrower than those of the incident cohort data. Although the prevalent samples provide the information on the 2-to-3 transition only, REs of the parameters for other transitions also tend to be over one. This implies that combining the incident and prevalent cohorts affects the estimation of overall transition probabilities.

The results for the baseline intensity parameters and the parameters in g(w) are relegated to the Supplementary Information. They show similar trends to the regression parameters. The RE of \(\lambda _{23}\) ranges from 5.2 to 6.7 across all scenarios. A slight improvement in efficiency also was shown in the estimation of other baseline intensity parameters, especially for \(\gamma \), as their REs were greater than one. The parameters in g(w) also were reasonably close to the true values with the coverage probabilities close to the nominal level.

We also performed a sensitivity analysis when the density of \(\widetilde{W}\) was incorrectly specified under the current simulation settings (see Table S3 of the Supplementary Information). We considered two misspecified cases: \(\widetilde{W}\) is assumed to follow (1) the exponential distribution and (2) the uniform distribution (i.e., the length-biased sampling). In summary, the parameter estimates from the proposed method were found to be reasonably robust against the misspecification of the form for g(w).

Fig. 3
figure 3

The average of the estimated baseline intensities with the pointwise 95% confidence intervals, obtained from the combined cohort data (red) and the incident cohort only (blue) under the scenario with \(m_1 = 300\), \(m_2 = 300\), and 30% censoring rate for the prevalent cohort (Color figure online)

Full size image

4 Application

The Nun Study is a longitudinal study of aging and dementia with a cohort of 678 participants who were born before 1917 and recruited among members of the School Sisters of Notre Dame congregation in the United States. The cognitive status of each participant was assessed annually for close to a decade and their awareness of deficits were classified into four stages according to severity: cognitively intact for age, cognitive deficit not affecting activities of daily living, cognitive deficit affecting one or more activities of daily living, and clinical dementia. Ages at their assessments and deaths were also recorded during the follow-up, along with two important covariates, the presence of at least one apolipoprotein E4 allele (APOE4) and their level of education (EDUCAT). To reduce dimensionality, we grouped the participants’ status into four states and recorded them as follows: 0 for intact cognition, 1 for MCI, 2 for dementia, and 3 for death.

We applied the proposed approach to data from 501 subjects with complete baseline information. Among them, 424 were in the intact cognition or MCI state (i.e., incidence cases), while 77 were diagnosed with clinical dementia (i.e., prevalent cases) at their study recruitment. In the incident cohort, about 36% progressed to dementia and only 29% died with dementia during the follow-up. In the prevalent cohort, about 97% died during the follow-up. The flow chart for the samples of the incident cohort and the prevalent cohort from the Nun Study is available in the Supplementary Information. The average age at the first assessment was 82.53 years for the incident cohort and 85.89 years for the prevalent cohort. Table 3 shows the distribution of risk factors by cohort. The combined cohorts consist of more dementia cases in each group compared to the incident cohort. In the analysis, 75 years old, which is the earliest age at the intact cognition state in the incident cohort, is set as the initial time point of disease progression. The exponential distribution is used for the density of \(\widetilde{W}\), which implies that the period between dementia onset and study entry does not depend on the dementia onset itself.

Table 3 Distribution of risk factors by cohort with the number of patients who experienced dementia before death during the study and the number of death at last follow-up
Full size table

The resulting parameter estimates and their standard errors, respectively obtained by analyzing the combined cohorts data and the incident cohort data only, are shown in Table 4. In model estimation, the proposed method was refitted to the data sets without the regression coefficients for the 0-to-3 transition because their estimates were close to zero. The results with both incident and prevalent cohorts of the Nun Study show that ApoE4 promotes the cognitive decline of a subject, in that an ApoE4 carrier is expected to have a relatively longer time of the transition from MCI back to intact cognition (p value = 0.011); a higher risk of being in MCI, which is marginally significant (p value = 0.054); and a shorter time of the transition from MCI to dementia (p value = 0.032), compared to a non-carrier. The education level of a subject is found to be significantly associated with the 0-to-1 and 2-to-3 transitions; the higher level of education (12 years or more) is found to decrease the risk of progression from intact cognition to MCI (p value = 0.003) and increase the risk of death with dementia (p value = 0.049). The results of incident cohort data show similar results with those of the combined cohort data except that education level was not significantly related to the 2-to-3 transition. The positive association between higher education and mortality with dementia also has been reported in other studies (Stern et al. 1995; Contador et al. 2017).

Table 4 Results of the parameter estimation in each transition using the combined cohorts and the incident cohort from the Nun Study
Full size table

Figure 4 shows the estimated baseline intensity for the 2-to-3 transition with pointwise 95% confidence intervals. The analysis results of the combined data from the incident and prevalent cohorts show narrower 95% pointwise confidence intervals than those of the incident cohort data only. The estimated density of the dementia onset in the prevalent population is presented in Fig. 5 as a byproduct of the analysis of the combined data. The median onset age of dementia was 86.43 (95% CI: \(84.85 - 88.01\)) for an ApoE4 carrier with low education and 87.66 (95% CI: \(86.57 - 88.76\)) for a non-carrier with low education. The estimated median survival after the onset of dementia was 3.13 years (95% CI: \(2.27 - 4.00\)) for a patient with ApoE4 and a higher level of educational attained from the combined cohort data, while it was 3.04 years (95% CI: \(1.97 - 4.11\)) from the incident cohort data.

Fig. 4
figure 4

The estimated baseline survival functions with the pointwise 95% confidence intervals, obtained from the combined cohort (red) and the incident cohort (blue) of the Nun Study

Full size image
Fig. 5
figure 5

The density of the dementia onset in the prevalent population by the presence of the apolipoprotein E4 allele and the level of education

Full size image

5 Discussion

In this paper, we propose a multistate approach based on the likelihood-based inference to assess the effects of risk factors on the transitions that are related to the natural history of disease by using event history data that consists of both incident and prevalent samples. In the observational studies that are designed to follow the life course of a disease, prevalent samples are commonly available because patients receiving routine care in healthcare facilities are often within a study population. In the analysis with the prevalent samples, identifying the age of disease onset is essential because it plays a key role in addressing sampling bias induced by the prevalent sampling scheme. However, it is often difficult to retrospectively identify age of onset for many chronic diseases. The proposed method overcomes this challenge by using the complementary information that both incident cohort and prevalent cohort provide to each other, while accounting for interval censored observations of transition times between disease states.

The approach was illustrated by incorporating parametric transition intensities into a multistate model; however, it can be easily modified with other flexible forms such as a locally weighted smoother (Hubbard et al. 2008) and linear splines (Pak et al. 2019), although a substantial increase in the number of parameters to estimate is inevitable with many cases of possible transitions. By utilizing the commonly used temporal homogeneity model for transition intensity, we have a parsimonious model to capture the potential reversible transition between intact cognition and MCI in dementia progression. Alternatively, one could employ piecewise constant models to accommodate the more flexible temporal trend of the disease process, though it will require more transition events being observed to obtain stable estimates (Pérez-Ocón et al. 2001; Titman 2011).

As with other prevalent-data settings, it would be a challenge to incorporate time-dependent covariates into the analysis of combined data. If the time-dependent covariates are specified differently relative to each transition, one must know which transitions a prevalent individual went through before the development of dementia. Nevertheless, with extra information for the prevalent samples or modeling assumptions, one may incorporate time-dependent covariates when combining the incident and prevalent cohorts, which merits future research.

The key benefit of the analysis of the event history data is that one can simultaneously assess the effects of risk factors on every transition that represents the natural history of the disease. The proposed method can be applied to event history data from other disease studies. An example is with studies on the natural history of the coronavirus disease (COVID-19), where the information from travelers who are found to be infected upon arrival (i.e., prevalent samples) can be a complement to the study on the endpoints of death or recovery in periods of quarantine.