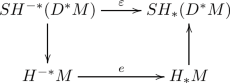Loop coproduct in Morse and Floer homology

Abstract

By a well-known theorem of Viterbo, the symplectic homology of the cotangent bundle of a closed manifold is isomorphic to the homology of its loop space. In this paper, we extend the scope of this isomorphism in several directions. First, we give a direct definition of Rabinowitz loop homology in terms of Morse theory on the loop space and prove that its product agrees with the pair-of-pants product on Rabinowitz Floer homology. The proof uses compactified moduli spaces of punctured annuli. Second, we prove that, when restricted to positive Floer homology, resp. loop space homology relative to the constant loops, the Viterbo isomorphism intertwines various constructions of secondary pair-of-pants coproducts with the loop homology coproduct. Third, we introduce reduced loop homology, which is a common domain of definition for a canonical reduction of the loop product and for extensions of the loop homology coproduct which together define the structure of a commutative cocommutative unital infinitesimal anti-symmetric bialgebra. Along the way, we show that the Abbondandolo–Schwarz quasi-isomorphism going from the Floer complex of quadratic Hamiltonians to the Morse complex of the energy functional can be turned into a filtered chain isomorphism using linear Hamiltonians and the square root of the energy functional.

1 Introduction

For a closed manifold M, there are canonical isomorphisms

$$\begin{aligned} H_*(\Lambda ,\Lambda _0;\eta ) \cong FH_*^{>0}(T^*M) \cong SH_*^{>0}(D^*M) \cong SH^{1-*}_{<0}(S^*M). \end{aligned}$$

(1)

Here, we use coefficients in any commutative ring R, twisted in the first group by a suitable local system $\eta$ which restricts to the orientation local system on the space $\Lambda _0\subset \Lambda$ of constant loops (see Appendix A). The groups in the above chain of isomorphisms are as follows: $H_*(\Lambda ,\Lambda _0)$ denotes the homology of the free loop space $\Lambda =C^\infty (S^1,M)$ relative to $\Lambda _0$; $FH_*^{>0}(T^*M)$ the positive action part of the Floer homology of a fibrewise quadratic Hamiltonian on the cotangent bundle; $SH_*^{>0}(D^*M)$ the positive symplectic homology of the unit cotangent bundle $D^*M$; and $SH^{1-*}_{<0}(S^*M)$ the negative symplectic cohomology of the trivial Liouville cobordism $W=[1,2]\times S^*M$ over the unit cotangent bundle $S^*M$. The first isomorphism is the result of work of many people starting with Viterbo (see [1, 3, 5, 7, 17, 30, 34, 35, 39]); the second one is obvious; and the third one is a restriction of the Poincaré duality isomorphism from [22].

Restricting to field coefficients, all the groups in (1) carry natural coproducts of degree $1-n$:

• the loop homology coproduct (in the sequel simply called loop coproduct) $\lambda$ on $H_*(\Lambda ,\Lambda _0;\eta )$ defined by Sullivan [36] and further studied by Goresky and the second author in [27], see also [29];

• the (secondary) pair-or-pants coproduct $\lambda ^{AS}$ on $FH_*^{>0}(T^*M)$ defined by Abbondandolo and Schwarz [4];

• the varying weights coproduct $\lambda ^w$ on $SH_*^{>0}(D^*M)$ first described by Seidel and further explored in [26];

• the continuation coproduct $\lambda ^F$ on $SH_*^{>0}(D^*M)$ described in [20];

• the Poincaré duality coproduct $\lambda ^{PD}$ on $SH^{1-*}_{<0}(S^*M)$ dual to the pair-of-pants product on $SH_{1-*}^{<0}(S^*M)$, described in [16].

The first result of this paper is

Theorem 1.1

With field coefficients, all the above coproducts are equivalent under the isomorphisms in (1).

Remark 1.2

(Coproducts and field coefficients) There is a formal algebraic reason why we need to restrict to field coefficients when speaking about homology coproducts. Given a chain complex $C=C_*$ and a chain map $C\rightarrow C\otimes C$, we obtain a map $H_*(C) \rightarrow H_*(C\otimes C)$. However, the latter factors through $H_*(C)\otimes H_*(C)$ only if the Künneth isomorphism $H_*(C)\otimes H_*(C){\mathop {\rightarrow }\limits ^{\simeq }}H_*(C\otimes C)$ holds, which is the case with field coefficients. All our coproducts are defined at chain level with arbitrary coefficients, and we would not need to restrict to field coefficients if we carried the discussion at chain level.

Remark 1.3

(Coefficients twisted by local systems) The chain of isomorphisms (1) also holds if one further twists each of the factors by an additional local system. If the latter is compatible with products in the sense of Appendix A.5, then all groups still carry natural coproducts of degree $1-n$ and Theorem 1.1 continues to hold. This is particularly relevant when M is orientable: the constant local system on $\Lambda$ is indeed of the form $\sigma ^{-1}\otimes \eta$, where $\sigma$ is the transgression of the second Stiefel–Whitney class, so that $H_*(\Lambda ,\Lambda _0)\simeq SH_*^{>0}(D^*M;\sigma ^{-1})$. See Appendix A.9.

Remark 1.4

All our statements have counterparts for open strings, in which the free loop space is replaced by the based loop space and symplectic homology of $T^*M$ is replaced by wrapped Floer homology of the cotangent fibre $T^*_qM$. See [16]. We do not spell out these results and focus on closed strings in this paper.

The first two isomorphisms in (1) are obtained by dividing out the constant loops, resp. the action zero part in the chain of isomorphisms

$$\begin{aligned} H_*(\Lambda ;\eta ) \cong FH_*(T^*M) \cong SH_*(D^*M). \end{aligned}$$

(2)

According to Abbondandolo and Schwarz [3], these isomorphisms intertwine the Chas–Sullivan loop product [13] on the first group with the pair-of-pants products on the other two groups. On the other hand, according to [16, 21], the product on $SH_*(D^*M)$ and the coproduct on $SH_*^{>0}(D^*M)$ are related to the pair-of-pants product and coproduct on $SH_*(S^*M)$ by the “almost split” exact sequence

(3)

where the maps have the following properties.

• The map $\iota$ intertwines the pair-of-pants products, and the map $\pi$ intertwines the pair-of-pants coproducts.

• The “almost splitting” i satisfies $\pi \circ i = j$ and intertwines the product dual to $\lambda ^F$ on $SH^{1-*}_{>0}(D^*M)$ with the pair-of-pants product on $SH_*(S^*M)$.

• The “almost splitting” p satisfies $p\circ \iota = q$ and intertwines the coproduct on $SH_*(S^*M)$ with the continuation coproduct $\lambda ^F$ on $SH_*^{>0}(D^*M)$.

• The map ${\varepsilon }$ lives only in degree 0 and factors through the constant loops as the connecting map in the Gysin sequence for the cohomology $H^{n-*}(S^*M)$

  

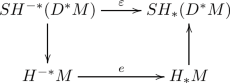  (4)

Here, the map e is multiplication with the Euler characteristic of M in degree 0. From this perspective, and up to some discrepancy at the constant loops, both the pair-of-pants product on $SH_*(D^*M)$ and the product dual to $\lambda ^F$ on $SH^{1-*}_{>0}(D^*M)$ appear as “components” of the pair-of-pants product on $SH_*(S^*M)$. See [21, §7].

Our second goal is to define a topological counterpart of $SH_*(S^*M)$.¹ The starting point is the topological counterpart of diagram (4):

(5)

Here, the map ${\varepsilon }$ is induced by a chain map on the Morse complex (with respect to the energy functional)

$$\begin{aligned} c:MC^{-*}(\Lambda )\rightarrow MC^{-*}(M)\rightarrow MC_*(M)\rightarrow MC_*(\Lambda ), \end{aligned}$$

where the exterior maps are induced by the inclusion of constant loops, and the middle map lives in degree zero and is given by multiplication with the Euler characteristic of M. We define the Rabinowitz loop homology as the homology of the cone of c,

$$\begin{aligned} \widehat{H}_*\Lambda {:}{=} H_*(Cone(c)). \end{aligned}$$

By general properties of the cone construction (see e.g. [22]), this fits into a long exact sequence

(6)

Our second result is

Theorem 1.5

The Rabinowitz loop homology $\widehat{H}_*\Lambda$ carries a natural product of degree $-n$ such that the map $\iota$ in (6) is a ring homomorphism. Moreover, for $n\ne 2$, there exists an isomorphism of rings $SH_*(S^*M)\cong \widehat{H}_*\Lambda$ such that the following diagram commutes:

Remark 1.6

(a) In [16] we defined $\widehat{H}_*\Lambda$ as $SH_*(S^*M)$, and with this definition Theorem 1.5 is a tautology. The point of the present paper is to define $\widehat{H}_*\Lambda$ in purely topological terms as above, in which case Theorem 1.5 becomes an actual theorem. It can be seen as an upgrade of Viterbo’s isomorphism [39] from symplectic homology to Rabinowitz Floer homology.

(b) The hypothesis $n\ne 2$ is only an artefact of our proof and can be removed by upgrading the theory of $A_2^+$-structures in [20] to a theory of $A_3^+$-structures, which would take into account arity 3 operations.

One difficulty with the proof of Theorem 1.5 is the lack of an obvious chain map inducing the isomorphism $SH_*(S^*M)\cong \widehat{H}_*\Lambda$, due to the fact that the natural chain maps inducing Viterbo’s isomorphisms on homology and cohomology go in opposite directions. We overcome this difficulty using the theory of $A_2^+$-structures from [20]. We will prove that the Abbondandolo–Schwarz map on chain level yields a quasi-isomorphism of $A_2^+$-structures, and then appeal to algebraic results from [20] concerning such structures and their associated cones.

Starting from the exact sequence (6), we define in this paper reduced loop homology and cohomology

$$\begin{aligned} \overline{H}_*\Lambda = \textrm{ coker }\,{\varepsilon }, \qquad \overline{H}^*\Lambda = \ker {\varepsilon }. \end{aligned}$$

Theorem 1.7

([21]) The loop product on $H_*\Lambda$ descends to $\overline{H}_*\Lambda$ and the loop coproduct on $H_*(\Lambda ,\Lambda _0)$ extends to $\overline{H}_*\Lambda$ (canonically if we have $H_1M=0$). Each such extension $\lambda$ defines together with the loop product $\mu$ the structure of a commutative cocommutative unital infinitesimal anti-symmetric bialgebra on $\overline{{\mathbb {H}}}_*\Lambda =\overline{H}_{*+n}\Lambda$. In particular, the following relation holds:

where we denote the identity map and 1 the unit for the product $\mu$.

We refer to [19, 21] for the definition of a commutative cocommutative unital infinitesimal anti-symmetric bialgebra. The extensions of the coproduct depend on the choice of auxiliary data consisting of a Morse function on M with a unique maximum, a Morse–Smale gradient vector field, and a vector field with nondegenerate zeroes located away from the $(n-1)$-skeleton. We discuss this dependence in Sect. 4. The coproduct is independent of all choices when $H_1M=0$ (Proposition 4.7), and in that case it also vanishes on the unit 1 (Corollary 4.9), so that the above relation becomes the unital infinitesimal relation

Structure of the paper. In Sect. 2, we define the notion of a special $A_2^+$-structure and prove that the Morse complex of the energy functional on loop space carries such a structure. In particular, this includes a Morse theoretic definition of the loop coproduct.

In Sect. 3 we construct a special $A_2^+$-structure on the chain complexes underlying symplectic homology of $D^*M$.

In Sect. 4, we discuss extensions of the loop coproduct to reduced homology, and also the dependence of these extensions on choices.

In Sect. 5, we revisit the Viterbo isomorphism between symplectic homology of the cotangent bundle and loop space homology. We show that the Abbondandolo–Schwarz map

$$\begin{aligned} \Psi :SH_*(D^*M){\mathop {\rightarrow }\limits ^{\simeq }}H_*(\Lambda ;\eta ), \end{aligned}$$

which was originally constructed using asymptotically quadratic Hamiltonians and as such did not preserve the natural filtrations (at the source by the non-Hamiltonian action, and at the target by the square root of the energy), can be made to preserve these filtrations when implemented for the linear Hamiltonians used in the definition of symplectic homology. As such, $\Psi$ becomes an isomorphism at chain level. This uses a length vs. action estimate inspired by [17].

In Sect. 6, we prove that the isomorphism $\Psi$ intertwines the special $A_2^+$-structures of Sect. 2 and Sect. 3, which together with algebraic results from [20] yields Theorem 1.5. Our proof uses homotopies in certain compactified moduli spaces of punctured annuli. In Remark 6.2, we discuss some related open questions involving the two chain-level isomorphisms between Morse and Floer complexes constructed by Abbondandolo–Schwarz in [1, 6].

In Sect. 7, we restrict to positive symplectic homology on the symplectic side, respectively, to loop homology rel constant loops on the topological side. We relate there the coproduct $\lambda ^F$ resulting from Sect. 3 to the other secondary coproducts mentioned above, thus proving Theorem 1.1. In particular, this implies that the secondary coproduct defined by Abbondandolo and Schwarz in [4] corresponds under the isomorphism $\Psi$ (restricted to the positive range) to the loop coproduct. For completeness, we also give a direct proof of this last fact in Sect. 7.4.

In Sect. 8, we compute the extended coproducts on reduced loop homology of odd-dimensional spheres $S^n$. For $n\ge 3$, these coproducts are canonical, but for $n=1$ one sees explicitly the dependence on the choice of auxiliary data discussed in Sect. 4.

The Appendix contains a complete discussion of local systems on free loop spaces and their behaviour with respect to the loop product and coproduct. Local systems are unavoidable in the context of manifolds which are not orientable [7, 31], and also in the context of the correspondence between symplectic homology of $D^*M$ and loop space homology of M [5, 7, 30]. They also proved useful in applications [9].

2 $A_2^+$-structure for loop space homology

2.1 $A_2^+$-algebras

In this subsection, we recall from [20] the definition and basic properties of $A_2^+$-algebras. We will restrict to the case of special $A_2^+$-algebras which suffices for our purposes.

Let R be a commutative ring with unit, and $(\mathcal {A},{\partial })$ a differential graded R-module. Let $\mathcal {A}^\vee _*=\textrm{Hom}_R(\mathcal {A}_{-*},R)$ be its graded dual, and $\textrm{ev}:\mathcal {A}^\vee \otimes \mathcal {A}\rightarrow R$ the canonical evaluation map. We denote

$$\begin{aligned} \tau :\mathcal {A}\otimes \mathcal {A}\rightarrow \mathcal {A}\otimes \mathcal {A},\qquad a\otimes b\mapsto (-1)^{\deg a\deg b}b\otimes a. \end{aligned}$$

Definition 2.1

A special $A_2^+$-structure on $(\mathcal {A},{\partial })$ consists of the following R-linear maps:

• the continuation quadratic vector $c_0:R\rightarrow \mathcal {A}\otimes \mathcal {A}$, of degree 0;

• the secondary continuation quadratic vector $Q_0:R\rightarrow \mathcal {A}\otimes \mathcal {A}$, of degree 1;

• the product $\mu :\mathcal {A}\otimes \mathcal {A}\rightarrow \mathcal {A}$, of degree 0;

• the secondary coproduct $\lambda :\mathcal {A}\rightarrow \mathcal {A}\otimes \mathcal {A}$, of degree 1.

The continuation quadratic vector $c_0$ gives rise to the continuation map

$$\begin{aligned} c{:}{=}(\textrm{ev}\otimes 1)(1\otimes c_0):\mathcal {A}^\vee \rightarrow \mathcal {A}. \end{aligned}$$

These maps are subject to the following conditions:

• 1. $c_0$ is a cycle;

• 2. $c_0$ is symmetric up to a homotopy given by $Q_0$, i.e.

  $$\begin{aligned} \tau c_0-c_0=[{\partial },Q_0]; \end{aligned}$$

• 3. $\mu$ is a chain map;

• 4. $\lambda$ satisfies the relation

  $$\begin{aligned}{}[{\partial }, \lambda ]=(\mu \otimes 1)(1\otimes c_0) - (1\otimes \mu )(\tau c_0\otimes 1); \end{aligned}$$

• 5. Denoting $\lambda =\lambda _{c_0,c_0}$ and

  $$\begin{aligned} \lambda _{\tau c_0,\tau c_0}&= \lambda _{c_0,c_0} + (\mu \otimes 1)(1\otimes Q_0) - (1\otimes \mu )(\tau Q_0\otimes 1),\\ \lambda _{c_0,\tau c_0}&= \lambda _{c_0,c_0} + (\mu \otimes 1)(1\otimes Q_0),\\ \lambda _{\tau c_0,c_0}&= \lambda _{c_0,c_0} - (1\otimes \mu )(\tau Q_0\otimes 1), \end{aligned}$$

  we require that

  $$\begin{aligned} (\lambda _{c_0,\tau c_0} \otimes 1) \tau c_0 = (\lambda _{\tau c_0,c_0}\otimes 1)\tau c_0=(\lambda _{\tau c_0,\tau c_0}\otimes 1) c_0 =0. \end{aligned}$$

We call the tuple $(\mathcal {A},{\partial },c_0,Q_0,\mu ,\lambda )$ a special $A_2^+$-algebra.

Proposition 2.2

([20]) Let $(\mathcal {A},{\partial },c_0,Q_0,\mu ,\lambda )$ be a special $A_2^+$-algebra. Then, the cone Cone(c) carries a canonical product $\varvec{\mu }$ which commutes with the boundary operator and thus descends to homology. Moreover, in the long exact sequence

the map $\iota$ is a ring map with respect to $\mu$ and $\varvec{\mu }$.

Next, we discuss morphisms (again only a special case).

Definition 2.3

A special morphism of special $A_2^+$-algebras $(\Psi ,\Gamma ,\Theta ):\mathcal {A}\rightarrow \mathcal {A}'$ consists of the following R-linear maps:

• (i) a degree 0 chain map $\Psi :\mathcal {A}\rightarrow \mathcal {A}'$ satisfying

  $$\begin{aligned} c_0'=(\Psi \otimes \Psi )c_0,\qquad Q'_0=(\Psi \otimes \Psi )Q_0; \end{aligned}$$

• (ii) a degree 1 bilinear map $\Gamma :\mathcal {A}\otimes \mathcal {A}\rightarrow \mathcal {A}'$ satisfying

  $$\begin{aligned}{}[{\partial },\Gamma ] = \mu '(\Psi \otimes \Psi )-\Psi \mu ; \end{aligned}$$

• (iii) a degree 2 bilinear map $\Theta :\mathcal {A}\rightarrow \mathcal {A}'\otimes \mathcal {A}'$ satisfying $\Theta c=0$ and

  $$\begin{aligned}{}[{\partial },\Theta ] = \lambda '\Psi -(\Psi \otimes \Psi )\lambda - (\Gamma \otimes \Psi )(1\otimes c_0) + (\Psi \otimes \Gamma )(\tau c_0\otimes 1). \end{aligned}$$

Proposition 2.4

([20]) Let $(\Psi ,\Gamma ,\Theta ):\mathcal {A}\rightarrow \mathcal {A}'$ be a special morphism of special $A_2^+$-algebras such that the induced map $\Psi _*:H_*(\mathcal {A})\rightarrow H_*(\mathcal {A}')$ is an isomorphism. Then, there exists a canonical ring isomorphism $H_*(Cone(c))\cong H_*(Cone(c'))$ such that the following diagram commutes:

Remark 2.5

The word “special” refers to the conditions (5) in Definition 2.1 and $\Theta c=0$ in Definition 2.3. These conditions are imposed in order to simplify the algebra in [20]. These conditions, as well as the hypothesis $n\ne 2$ from Theorems 1.5 and 6.1, can be removed by upgrading the theory of $A_2^+$-structure to a theory of $A_3^+$-structures, which would include arity 3 operations.

Remark 2.6

(a) The conditions in Definition 2.1 imply (Proposition 2.2) that $\mu$ and $\lambda$ induce a product $\varvec{\mu }$ on $H_*(Cone(c))$. Associativity of $\varvec{\mu }$ requires further compatibilities between $\mu$ and $\lambda$, one of them being the “unital infinitesimal relation” [16, 20, 21].

(b) The conditions in Definition 2.1 imply that $\lambda$ descends to the “reduced homology” $H_*(\mathcal {A}/\textrm{im}\,c)$ and the map $\pi$ in (6) intertwines it with a naturally defined coproduct $\varvec{\lambda }$ on the cone; see [21] for further details.

2.2 $A_2^+$-structure on the Morse complex of the loop space

Let now M be a closed connected manifold of dimension n. For simplicity, we assume that M is oriented and we use untwisted coefficients in a commutative ring R; the necessary adjustments with twisted coefficients are explained in Appendix A. We denote

$$\begin{aligned} S^1{:}{=}{\mathbb {R}}/{\mathbb {Z}}\quad \text {and}\quad \Lambda {:}{=}W^{1,2}(S^1,M). \end{aligned}$$

Our goal in this subsection is to construct an $A_2^+$-structure on the Morse complex of $\Lambda$. The analysis underlying the Morse complex is identical to the one in [1, 24] and we refer to there for details.

The Morse complex. Consider a smooth Lagrangian $L:S^1\times TM\rightarrow {\mathbb {R}}$ which outside a compact set has the form $L(t,q,v)=\frac{1}{2}|v|^2-V_\infty (t,q)$ for a smooth potential $V_\infty :S^1\times M\rightarrow {\mathbb {R}}$. It induces an action functional

$$\begin{aligned} S_L:\Lambda \rightarrow {\mathbb {R}},\qquad q\mapsto \int _0^1L(t,q,\dot{q})\textrm{d}t, \end{aligned}$$

which we can assume to be a Morse function. This functional is continuously differentiable and twice Gâteaux-differentiable on the space of loops of class $W^{1,2}$, but in general it is not smooth (unless L is everywhere quadratic) [2]. Abbondandolo and Schwarz proved in [2] that it admits a negative pseudo-gradient vector field which is smooth and Morse–Smale. The latter condition means that for all $a,b\in \textrm{Crit}(S_L)$ the unstable manifold $W^-(a)$ and the stable manifold $W^+(b)$ with respect to the negative pseudo-gradient intersect transversely in a manifold of dimension $\textrm{ind}(a)-\textrm{ind}(b)$, where $\textrm{ind}(a)$ denotes the Morse index with respect to $S_L$.

Let $(MC_*,{\partial })$ be the Morse complex of $S_L$ with R-coefficients. It is graded by the Morse index and the differential is given by

$$\begin{aligned} {\partial }:MC_*\rightarrow MC_{*-1},\qquad a\mapsto \sum _{\textrm{ind}(b)=\textrm{ind}(a)-1}\#\mathcal {M}(a;b)\,b, \end{aligned}$$

where $\#\mathcal {M}(a;b)$ denotes the signed count of points in the oriented 0-dimensional manifold

$$\begin{aligned} \mathcal {M}(a;b) {:}{=} \bigl (W^-(a)\cap W^+(b)\bigr )/{\mathbb {R}}. \end{aligned}$$

Then, ${\partial }\circ {\partial }=0$ and its homology $MH_*$ is isomorphic to the singular homology $H_*\Lambda$. We will assume in addition that near the zero section $L(t,q,v)=\frac{1}{2}|v|^2-V(q)$ for a time-independent Morse function $V:M\rightarrow {\mathbb {R}}$ such that all nonconstant critical points of $S_L$ have action larger than $-\min V$. Then, the constant critical points define a subcomplex $MC_*^{=0}$ of $MC_*$ which agrees with the Morse cochain complex of V on M, with degrees of $q\in \textrm{Crit}(V)$ related by $\textrm{ind}(q)=n-\textrm{ind}_V(q)$.

We assume that $L|_M$ has a unique minimum $q_0$ and a unique maximum $q_\textrm{Max}$. We denote by $\chi =\chi (M)$ the Euler characteristic of M and define the R-linear map $c_0:R\rightarrow MC_0\otimes MC_0$ by

$$\begin{aligned} c_0(1) {:}{=} \chi \,q_0\otimes q_0. \end{aligned}$$

The element $c_0$ is clearly a cycle and we actually have $\tau c_0=c_0$. Note, however, that the secondary continuation element $Q_0$ that we construct in the sequel may be nonzero. See also Sect. 4.

Remark 2.7

The operation $c_0$ can also be defined by a count of pairs of semi-infinite gradient lines with common starting point.

The product $\mu$. For a path $\alpha :[0,1]\rightarrow M$ and $\tau \in [0,1]$, we define the restrictions $\alpha |_{[0,\tau ]},\,\alpha |_{[\tau ,1]}:[0,1]\rightarrow M$ by

$$\begin{aligned} \alpha |_{[0,\tau ]}(t) {:}{=} \alpha (\tau t),\qquad \alpha |_{[\tau ,1]}(t) {:}{=} \alpha \bigl (\tau +(1-\tau )t\bigr ). \end{aligned}$$

(7)

For paths $\alpha ,\beta :[0,1]\rightarrow M$ with $\alpha (1)=\beta (0)$, we define their concatenation $\alpha \#\beta :[0,1]\rightarrow M$ by

$$\begin{aligned} \alpha \#\beta (t) {:}{=} {\left\{ \begin{array}{ll} \alpha (2t) &{}\quad t\leqslant 1/2, \\ \beta (2t-1) &{}\quad t\geqslant 1/2. \end{array}\right. } \end{aligned}$$

For $a,b,c\in \textrm{Crit}(S_L)$ set

$$\begin{aligned} \mathcal {M}(a,b;c) {:}{=} \bigl \{(\alpha ,\beta ,\gamma )\in W^-(a)\times W^-(b)\times W^+(c)\mid \gamma =\alpha \#\beta \bigr \}, \end{aligned}$$

which is a transversely cut out manifold of dimension

$$\begin{aligned} \dim \mathcal {M}(a,b;c) = \textrm{ind}(a)+\textrm{ind}(b)-\textrm{ind}(c)-n. \end{aligned}$$

If its dimension equals zero this manifold is compact and defines a map

$$\begin{aligned} \mu :(MC\otimes MC)_*\rightarrow MC_{*-n},\qquad a\otimes b\mapsto \sum _{c}\#\mathcal {M}(a,b;c)\,c. \end{aligned}$$

If the dimension equals 1 it can be compactified to a compact 1-dimensional manifold with boundary

$$\begin{aligned} {\partial }\mathcal {M}(a,b;c)&= \coprod _{\textrm{ind}(a')=\textrm{ind}(a)-1}\mathcal {M}(a;a')\times \mathcal {M}(a',b;c) \\&\amalg \coprod _{\textrm{ind}(b')=\textrm{ind}(b)-1}\mathcal {M}(b;b')\times \mathcal {M}(a,b';c) \\&\amalg \coprod _{\textrm{ind}(c')=\textrm{ind}(c)+1}\mathcal {M}(a,b;c')\times \mathcal {M}(c';c). \end{aligned}$$

corresponding to broken pseudo-gradient lines. Therefore, we have

$$\begin{aligned} \mu ({\partial }\otimes \textrm{ id}+\textrm{ id}\otimes {\partial }) - {\partial }\mu = 0, \end{aligned}$$

(8)

i.e. $\mu$ satisfies condition (3) in Definition 2.1. The induced map on homology

$$\begin{aligned} \mu _*:(MH\otimes MH)_*\rightarrow MH_{*-n} \end{aligned}$$

agrees with the loop product under the canonical isomorphism $MH_*\cong H_*\Lambda$. The loop product is associative, and this is reflected at chain level by the fact that $\mu$ is associative up to chain homotopy.

The critical point $q_\textrm{Max}$ is a cycle which is a two-sided unit for $\mu$ up to homotopy. Moreover, the subcomplex of constant loops $MC_*^{=0}\subset MC_*$ is stable under $\mu$ and we can choose the Morse data such that $q_\textrm{Max}$ is a strict unit for the restriction of $\mu$ to $MC_*^{=0}$.

The coproduct $\lambda$. We fix a small vector field v on M with nondegenerate zeroes such that the only periodic orbits of v with period $\leqslant 1$ are its zeroes. (The last property can be arranged, e.g. by choosing v gradient-like near its critical points; then the periods of nonconstant periodic orbits are uniformly bounded from below by a constant $c>0$, so v/2c has the desired property.) Denote by

$$\begin{aligned} f_t:M{\mathop {\longrightarrow }\limits ^{\cong }}M, \qquad t\in {\mathbb {R}}\end{aligned}$$

the flow of v, i.e. the solution of the ordinary differential equation $\frac{\textrm{d}}{\textrm{d}t}f_t=v\circ f_t$. It follows that the only fixed points of $f=f_1$ are the zeroes of v, each zero q is nondegenerate as a fixed point, and

$$\begin{aligned} \textrm{ sign }\det (T_qf-\textrm{ id}) = \textrm{ind}_v(q), \end{aligned}$$

where $\textrm{ind}_v(q)$ is the index of q as a zero of v. The map

$$\begin{aligned} f\times \textrm{ id}:M\rightarrow M\times M,\qquad q\mapsto \bigl (f(q),q\bigr ) \end{aligned}$$

is transverse to the diagonal $\Delta \subset M\times M$ and

$$\begin{aligned} (f\times \textrm{ id})^{-1}(\Delta ) = \{q\in M\mid f(q)=q\} = \textrm{Fix}(f). \end{aligned}$$

Since for $q\in \textrm{Fix}(f)$ the map $T_qM\rightarrow T_qM\times T_qM$, $w\mapsto \bigl ((T_qf-\textrm{ id})w,0\bigr )$ fills up the complement to $T_{(q,q)}\Delta$, the induced orientation on $\textrm{Fix}(f)=(f\times \textrm{ id})^{-1}(\Delta )$ endows q with the sign $\textrm{ind}_v(q)$.

Remark 2.8

Alternatively, we could use the exponential map of some Riemannian metric to define a map $M\rightarrow M$ by $q\mapsto \exp _qtv(q)$. Although this map differs from $f_t$ above, for v sufficiently small it shares its preceding properties and could be used in place of $f_t$.

Consider now a generic family of vector fields $v^\tau$, $\tau \in [0,1]$ which interpolates between $v^0=v$ and $v^1=-v$. We denote $f_t^\tau$, $t\in {\mathbb {R}}$ the flow of $v^\tau$ and $f^\tau =f_1^\tau$. Note that, while v and $-v$ have nondegenerate zeroes, this condition cannot be guaranteed for $v^\tau$. Genericity of the family means that the maps $f^0\times 1:M\rightarrow M\times M$, $f^1\times 1:M\rightarrow M\times M$, and $[0,1]\times M\rightarrow M\times M$, $(\tau ,p)\mapsto (f^\tau (p),p)$, are transverse to the diagonal.

For each $q\in M$ and $\tau \in [0,1]$, we denote the induced path from q to $f^\tau (q)$ by

$$\begin{aligned} \pi _q^\tau :[0,1]\rightarrow M,\qquad \pi _q^\tau (t){:}{=}f_t^\tau (q), \end{aligned}$$

and the inverse path by

$$\begin{aligned} (\pi _q^\tau )^{-1}:[0,1]\rightarrow M,\qquad (\pi _q^\tau )^{-1}(t){:}{=}f_{1-t}^\tau (q). \end{aligned}$$

Recall from above the restriction and concatenation of paths. Now, for $a,b,c\in \textrm{Crit}(S_L)$, we set

$$\begin{aligned} \mathcal {M}^1(a;b,c) {:}{=} \bigl \{&(\tau ,\alpha ,\beta ,\gamma )\in [0,1]\times W^-(a)\times W^+(b)\times W^+(c)\mid \\ {}&\beta = \alpha ^\tau _1,\ \gamma = \alpha ^\tau _2\bigr \} \end{aligned}$$

with

$$\begin{aligned} \alpha ^\tau _1(t)&{:}{=} \alpha |_{[0,\tau ]}\#(\pi _{\alpha (0)}^\tau )^{-1} = {\left\{ \begin{array}{ll} \alpha (2\tau t) &{}\quad t\leqslant 1/2, \\ f_{2-2t}^\tau \bigl (\alpha (0)\bigr ) &{}\quad t\geqslant 1/2, \end{array}\right. } \\ \alpha ^\tau _2(t)&{:}{=} \pi _{\alpha (0)}^\tau \#\alpha |_{[\tau ,1]} = {\left\{ \begin{array}{ll} f_{2t}^\tau \bigl (\alpha (0)\bigr ) &{}\quad t\leqslant 1/2, \\ \alpha \bigl (2\tau -1+(2-2\tau )t\bigr ) &{}\quad t\geqslant 1/2. \end{array}\right. } \end{aligned}$$

See Fig. 1.

Fig. 1

Matching conditions for the definition of the loop coproduct via Morse chains

Note that the matching conditions imply $\alpha (\tau )=f^\tau \circ \alpha (0)$. This is a codimension n condition and, as the family $v^\tau$ is generic, $\mathcal {M}^1(a;b,c)$ is a transversely cut out manifold of dimension

$$\begin{aligned} \dim \mathcal {M}^1(a;b,c) = \textrm{ind}(a)-\textrm{ind}(b)-\textrm{ind}(c)+1-n. \end{aligned}$$

If its dimension equals zero this manifold is compact and defines a map

$$\begin{aligned} \lambda :MC_*\rightarrow (MC\otimes MC)_{*+1-n},\qquad a\mapsto \sum _{b,c}\#\mathcal {M}^1(a;b,c)\,b\otimes c. \end{aligned}$$

If the dimension equals 1 it can be compactified to a compact 1-dimensional manifold with boundary

$$\begin{aligned} {\partial }\mathcal {M}^1(a;b,c)&= \coprod _{\textrm{ind}(a')=\textrm{ind}(a)-1}\mathcal {M}(a;a')\times \mathcal {M}^1(a';b,c) \\&\amalg \coprod _{\textrm{ind}(b')=\textrm{ind}(b)+1}\mathcal {M}^1(a;b',c)\times \mathcal {M}(b';b) \\&\amalg \coprod _{\textrm{ind}(c')=\textrm{ind}(c)+1}\mathcal {M}^1(a;b,c')\times \mathcal {M}(c';c) \\&\amalg \mathcal {M}^1_{\tau =1}(a;b,c) \amalg \mathcal {M}^1_{\tau =0}(a;b,c). \end{aligned}$$

Here, the first three terms correspond to broken pseudo-gradient lines and the last two terms to the intersection of $\mathcal {M}^1(a;b,c)$ with the sets $\{\tau =1\}$ and $\{\tau =0\}$, respectively. Therefore, we have

$$\begin{aligned} ({\partial }\otimes \textrm{ id}+\textrm{ id}\otimes {\partial })\lambda + \lambda {\partial }= \lambda _1-\lambda _0, \end{aligned}$$

(9)

where for $i=0,1$, we set

$$\begin{aligned} \lambda _i:MC_*\rightarrow (MC\otimes MC)_{*-n},\qquad a\mapsto \sum _{b,c}\#\mathcal {M}^1_{\tau =i}(a;b,c)\,b\otimes c. \end{aligned}$$

Let us look more closely at the map $\lambda _1$. For $\tau =1$ the matching conditions in $\mathcal {M}^1(a;b,c)$ imply that $\alpha (0)=q$ is a fixed point of $f^1$, the time-one flow of $-v$, and $\gamma =q$ is the constant loop at q. Assuming that $L|_M$ has a unique minimum $q_0$ and the fixed points of $f^1$ are in general position with respect to the stable and unstable manifolds of $L|_M$, the condition $q\in W^+(c)$ is only satisfied for $c=q_0$. Thus, $\mathcal {M}^1_{\tau =1}(a;b,c)$ is empty if $c\ne q_0$ and

$$\begin{aligned} \mathcal {M}^1_{\tau =1}(a;b,q_0) \cong \coprod _{q\in \textrm{Fix}(f^1)}\bigl \{(\alpha ,\beta )\in W^-(a)\times W^+(b)\mid \beta = \alpha \# q\bigr \}. \end{aligned}$$

Choosing all fixed points of $f^1$ closely together, we can achieve that the terms on the right hand side corresponding to different $q\in \textrm{Fix}(f^1)$ are in canonical bijection to each other. By the discussion before Remark 2.8, the terms corresponding to a fixed point q come with the sign $\textrm{ind}_{-v}(q)$. Since $\sum _q \textrm{ind}_{-v}(q) = \chi$ and $W^-(q_0)=\{q_0\}$, we obtain

$$\begin{aligned} \#\mathcal {M}^1_{\tau =1}&(a;b,q_0) \\ {}&= \sum _{q\in \textrm{Fix}(f^1)}\#\bigl \{(\alpha ,\beta )\in W^-(a)\times W^+(b)\mid \beta = \alpha \# q\bigr \} \\ {}&= \sum _{q\in \textrm{Fix}(f^1)}(-1)^{\textrm{ind}_{-v}(q)}\#\bigl \{(\alpha ,\beta )\in W^-(a)\times W^+(b)\mid \beta = \alpha \# q_0\bigr \} \\ {}&= \chi \,\#\bigl \{(\alpha ,\gamma ,\beta )\in W^-(a)\times W^-(q_0)\times W^+(b)\mid \beta = \alpha \# \gamma \bigr \} \\ {}&= \chi \,\#\mathcal {M}(a,q_0;b). \end{aligned}$$

Since the last moduli space is the one in the definition of $\mu$, we conclude

$$\begin{aligned} \lambda _1(a)=\chi \,\mu (a\otimes q_0)\otimes q_0, \end{aligned}$$

or equivalently

$$\begin{aligned} \lambda _1=(\mu \otimes 1)(1\otimes c_0). \end{aligned}$$

Similarly, we have

$$\begin{aligned} \lambda _0(a)=\chi q_0\otimes \mu (q_0\otimes a), \end{aligned}$$

or equivalently

$$\begin{aligned} \lambda _0=(1\otimes \mu )(c_0\otimes 1) =(1\otimes \mu )(\tau c_0\otimes 1). \end{aligned}$$

In conclusion, we obtain condition (4) in Definition 2.1,

$$\begin{aligned}{}[{\partial },\lambda ]= (\mu \otimes 1)(1\otimes c_0) - (1\otimes \mu )(\tau c_0\otimes 1). \end{aligned}$$

We define the secondary continuation quadratic vector $Q_0$ by

$$\begin{aligned} Q_0=-\lambda (q_\textrm{Max}). \end{aligned}$$

Condition (2), i.e. $\tau c_0-c_0=[{\partial },Q_0]$, follows by inserting $q_\textrm{Max}$ into the relation for $[{\partial },\lambda ]$ and using that $q_\textrm{Max}$ is a strict two-sided unit for $\mu$ on $MC_*^{=0}$. This is an instance of unital $A_2^+$-structure [20]. Note that $Q_0\in MC_*^{=0}\otimes MC_*^{=0}$ for energy reasons.

We now prove condition (5) in Definition 2.1. For $n=1$ it holds because $\chi =0$, hence $c=0$. We, therefore, assume w.l.o.g. $n\ge 2$ and give the proof in two steps.

• 1. We first prove $\lambda c=0$. This follows from $\lambda (q_0)=0$, which is seen as follows. The coefficient $\langle \lambda (q_0),x\otimes y\rangle$ can only be nonzero if x, y are critical points of K. Since $\lambda$ has degree $1-n$, we must have $1-n = \textrm{ind}(x)+\textrm{ind}(y)-\textrm{ind}(q_0) = n-\textrm{ind}_V(x)-\textrm{ind}_V(y)+\textrm{ind}_V(q_0)$, hence $\textrm{ind}_V(x)+\textrm{ind}_V(y)=\textrm{ind}_V(q_0)+2n-1=3n-1$. Since $\textrm{ind}_V(x)+\textrm{ind}_V(y)\leqslant 2n$, this is impossible for $n\ge 2$.

• 2. We now show that $(1\otimes \mu \otimes 1)({\varvec{a}}\otimes {\varvec{b}})=0$, where $({\varvec{a}},{\varvec{b}})=(\tau Q_0,c_0), (\tau c_0,Q_0), (\tau Q_0,\tau c_0), (c_0,\tau Q_0)$. We identify $MC_*^{=0}(L)$ with the Morse cochain complex $MC^{n-*}(V)$. The cohomological index of $Q_0$ is $2n-1$, so its components must have degrees $n-1$ and n. If $n\ge 2$ these degrees are both positive, and therefore any component of $Q_0$ is killed by multiplication with $q_0$ because the latter has cohomological index n.

In summary, we have shown

Proposition 2.9

Each vector field v on M satisfying the preceding conditions gives rise to a special $A_2^+$-structure $(c_0,Q_0,\mu ,\lambda )$ on the Morse complex $MC_*$ of the functional $S_L:\Lambda \rightarrow {\mathbb {R}}$.

Remark 2.10

In the previous construction, we used an interpolating family of vector fields $v^\tau$ such that $v^1=-v^0$. This choice is important because it ensures that the product on the Rabinowitz loop homology obtained from the $A_2^+$-structure via the cone construction is associative, and much more: in view of the isomorphism with the $A_2^+$-structure on symplectic homology proved in Sect. 6 and in view of [16, 20], the resulting product fits into a graded Frobenius algebra structure on $\widehat{H}_*\Lambda$.

While the construction of an $A_2^+$-structure would have worked with any choice of nondegenerate vector fields $v^0$ and $v^1$ at the endpoints of the parametrising interval, the necessity of the condition $v^1=-v^0$, which ensures these fine properties of the product, would become visible at chain level within a theory of $A_3^+$-structures. The development of such a theory is a matter for further study.

Remark 2.11

The description of $\mathcal {M}^1_{\tau =1}(a;b,q_0)$ and $\mathcal {M}^1_{\tau =0}(a;q_0,c)$ above implies that $\lambda _1,\lambda _0:MC_*\rightarrow (MC\otimes MC)_{*-n}$ are chain maps. By Eq. (9) they are chain homotopic, hence they induce the same “primary” coproduct

$$\begin{aligned}{}[\lambda _0]=[\lambda _1]:MH_*\rightarrow (MH\otimes MH)_{*-n} \end{aligned}$$

and the preceding discussion recovers [4, Lemma 5.1].

Remark 2.12

Alternatively, we could define the loop coproduct using the spaces

$$\begin{aligned} {\widetilde{\mathcal {M}}}^1(a;b,c)&{:}{=} \bigl \{(\tau ,\alpha ,\beta ,\gamma )\in [0,1]\times W^-(a)\times W^+(b)\times W^+(c)\mid \\ \beta (t)&= (f_t^\tau )^{-1}\circ \alpha (\tau t),\\ \gamma (t)&= (f_{1-t}^\tau )^{-1}\circ \alpha (\tau +(1-\tau )t)\bigr \}. \end{aligned}$$

Again the matching conditions imply $\alpha (\tau )=f^\tau \circ \alpha (0)$, and ${\widetilde{\mathcal {M}}}^1(a;b,c)$ is a transversely cut out manifold of dimension $\textrm{ind}(a)-\textrm{ind}(b)-\textrm{ind}(c)+1-n$ whose rigid counts define a map

$$\begin{aligned} {\widetilde{\lambda }}:MC_*\rightarrow (MC\otimes MC)_{*+1-n},\qquad a\mapsto \sum _{b,c}\#{\widetilde{\mathcal {M}}}^1(a;b,c)\,b\otimes c. \end{aligned}$$

A discussion analogous to that for $\lambda$ shows that Proposition 2.9 also holds with ${\widetilde{\lambda }}$ in place of $\lambda$. The obvious homotopies between the loops $\alpha _1^\tau$ and $\alpha _2^\tau$ in the definition of $\lambda$ and the loops $t\mapsto (f_t^\tau )^{-1}\circ \alpha (\tau t)$ and $t\mapsto (f_{1-t}^\tau )^{-1}\circ \alpha (\tau +(1-\tau )t)$ in the definition of ${\widetilde{\lambda }}$ provide a special morphism between $(c_0,Q_0,\mu ,\lambda )$ and $(c_0,{\widetilde{Q}}_0,\mu ,{\widetilde{\lambda }})$, where ${\widetilde{Q}}_0=-{\widetilde{\lambda }} (q_\textrm{Max})$. We will use the restriction of the map ${\widetilde{\lambda }}$ to Morse chains modulo constants in the proof of Proposition 7.4.

3 $A_2^+$-structure for symplectic homology

As in the previous section, let M be a closed oriented manifold. We pick a Riemannian metric on M and denote by $S^*M\subset D^*M\subset T^*M$ its unit sphere resp. unit disc cotangent bundle. The latter is a Liouville domain whose completion is $T^*M$. Its symplectic homology $SH_*(D^*M)$ is defined as the direct limit of the Floer homologies $FH_*(K)$ over Hamiltonians $K:S^1\times T^*M\rightarrow {\mathbb {R}}$ that are negative on $D^*M$ and linear outside a compact see; see [22] for general background on symplectic homology. The goal of this section is to construct a special $A_2^+$-structure on the chain complex underlying symplectic homology.

3.1 The continuation map $c^F$

Recall from [22] that for Hamiltonians $H\leqslant K$, we have a continuation map $c_{H,K}:FC_*(H)\rightarrow FC_*(K)$, defined by counting Floer cylinders for an s-dependent Hamiltonian $\widehat{H}(s,\cdot )$ which agrees with K for small s, with H for large s, and which satisfies ${\partial }_s\widehat{H}\leqslant 0$. In this subsection, we will describe the continuation map

$$\begin{aligned} c^F=c_{-K,K}:FC_*(-K)\rightarrow FC_*(K) \end{aligned}$$

for a smooth Hamiltonian $K:T^*M\rightarrow {\mathbb {R}}$ of the form

$$\begin{aligned} K(q,p) = k(|p|) + V(q) \end{aligned}$$

for a convex function k with $k(0)=0$ and $k(r)=\mu r$ for large r, with $\mu >0$ not in the length spectrum, and a potential $V:M\rightarrow {\mathbb {R}}$ which has a unique maximum $q_0$ and a unique minimum $q_\textrm{Max}$. For 1-periodic orbits x of $-K$ and y of K, the coefficient $\langle c^Fx,y\rangle$ is given by the count of solutions $u:{\mathbb {R}}\times S^1\rightarrow T^*M$ of the Floer equation

$$\begin{aligned} {\partial }_su+J(u)\bigl ({\partial }_tu-\phi (s)X_K(u)\bigr )=0 \end{aligned}$$

(10)

converging to x as $s\rightarrow +\infty$ and to y as $s\rightarrow -\infty$. Here, $\phi :{\mathbb {R}}\rightarrow [-1,1]$ is a nonincreasing smooth function which equals 1 for small s and $-1$ for large s. For action reasons the coefficient can only be nonzero if x, y are constant solutions corresponding to critical points of V on the zero section $M\subset T^*M$, in which case the solutions u are t-independent and the Floer equation becomes the Morse equation

$$\begin{aligned} {\partial }_su+\phi (s)\nabla K(u)=0. \end{aligned}$$

(11)

The Fredholm index of this problem is

$$\begin{aligned} \textrm{CZ}_{-K}(x)-\textrm{CZ}_K(y) = -\textrm{CZ}_K(x)-\textrm{CZ}_K(y) = \textrm{ind}_V(x)+\textrm{ind}_V(y)-2n\leqslant 0, \end{aligned}$$

with equality iff $x=y=q_0$ for the maximum $q_0\in M$ of V. On the other hand, solutions u of (11) are in one-to-one correspondence to points $u(0)\in W_x^-\cap W_y^-$, where $W_x^-$ denotes the stable manifold of x with respect to $\nabla V$. This shows that the Fredholm problem given by (10) resp. (11) is degenerate.

To perturb it, we denote by $\textrm{Skel}_k(V)\subset M$ the k-skeleton, i.e. the union of the descending manifolds $W_x^-$ of critical points of index $\leqslant k$. We pick a 1-form $\eta$ on M satisfying the following condition:

$$\begin{aligned} \text {All zeroes of }\eta \text { are nondegenerate and lie in }M\setminus \textrm{Skel}_{n-1}(V). \end{aligned}$$

(12)

It gives rise to the flow

$$\begin{aligned} F^\eta _t:T^*M\rightarrow T^*M,\qquad F^\eta _t(q,p){:}{=}\bigl (q,p+t\eta (q)\bigr ) \end{aligned}$$

generated by the vector field $\widehat{\eta }$ on $T^*M$,

$$\begin{aligned} \widehat{\eta }(q,p) {:}{=} \frac{\textrm{d}}{\textrm{d}t}\Bigl |_{t=0}F_t^\eta (q,p). \end{aligned}$$

We pick a compactly supported function $\rho :{\mathbb {R}}\rightarrow [0,\infty )$ with $\int _{\mathbb {R}}\rho =1$ and perturb Eqs. (10) and (11) to

$$\begin{aligned} {\partial }_su+J(u)\bigl ({\partial }_tu-\phi (s)X_K(u)\bigr ) = \rho (s)\widehat{\eta }(u). \end{aligned}$$

(13)

and

$$\begin{aligned} {\partial }_su+\phi (s)\nabla K(u) = \rho (s)\widehat{\eta }(u). \end{aligned}$$

(14)

To understand solutions of the perturbed Morse equation, we choose $\phi ,\rho$ such that $\phi \equiv 0$ on $[-1,1]$ and $\textrm{ supp}(\rho )\subset [-1,1]$. Then, solutions u of (14) are in one-to-one correspondence to points

$$\begin{aligned} u(1)\in W_x^-\cap F^\eta _1(W_y^-), \end{aligned}$$

where the intersection is taken in $T^*M$. By condition (12) this intersection is empty unless $x=y=q_0$, in which case intersection points correspond to zeroes of $\eta$ and their signed count equals the Euler characteristic $\chi$ of M. This shows that the only nontrivial term in the continuation map $c^F:FC_*(-K)\rightarrow FC_*(K)$ is

$$\begin{aligned} c^F q_0=\chi q_0 \end{aligned}$$

and the corresponding quadratic vector $c_0^F$ is given by

$$\begin{aligned} c_0^F(1) = \chi q_0\otimes q_0. \end{aligned}$$

In particular, $c_0^F$ satisfies the closedness condition in Definition 2.1, and it is also symmetric $\tau c_0^F=c_0^F$. Note that this holds without any symmetry assumptions on the data such as $\phi (-s)=-\phi (s)$ or $\rho (-s)=\rho (s)$. Note also that, although the definition of $c_0^F$ on the chain level requires the choice of a pair $(V,\eta )$ consisting of a Morse function $V:M\rightarrow {\mathbb {R}}$ and a 1-form $\eta$ on M subject to condition (12), the result does not depend on this choice. In contrast, the secondary continuation quadratic vector $Q_0^F$ which we construct below may depend on this choice. See also Sect. 4.

3.2 The product $\mu ^F$ and coproduct $\lambda ^F$

The pair-of-pants product $\mu ^F:FC_*(K)\otimes FC_*(K)\rightarrow FC_*(2K)$ (of degree $-n$) counts maps from a pair-of-pants satisfying a Floer equation with weights 1 at the two positive punctures and weight 2 at the negative puncture. The definition is entirely analogous to the one for the coproduct $\lambda ^F$ given below, without the additional parameter $\tau$. It is well-known that $\mu ^F$ is a chain map which is associative and graded commutative up to chain homotopy (see e.g. [3]), so condition (2) in Definition 2.1 holds.

The critical point $q_\textrm{Max}$ is a constant orbit and is a cycle which is a two-sided unit for $\mu ^F$ up to homotopy. The subcomplex $FC_*^{=0}(K)\subset FC_*(K)$ generated by small action orbits is stable under $\mu ^F$ and we can choose the auxiliary data such that $q_\textrm{Max}$ is a strict unit for the restriction of $\mu ^F$ to $FC_*^{=0}(K)$.

In [21], a secondary coproduct $\lambda$ is defined in terms of continuation maps on the reduced symplectic homology of a large class of Weinstein domains which includes cotangent bundles. See also [16, 20]. In this subsection, we recall its definition for $D^*M$; we will call it the continuation coproduct and denote it by $\lambda ^F$.

The definition in [16, 20] is described in terms of real parameters $\lambda _1,\lambda _2<0<\mu _1,\mu _2,\mu$ satisfying $\mu \leqslant \min (\lambda _1+\mu _2,\mu _1+\lambda _2)$. For simplicity, we choose the parameters as $\lambda _1=\lambda _2=-\mu$ and $\mu _1=\mu _2=2\mu$ for some $\mu >0$. We assume that $\mu$ and $2\mu$ do not belong to the action spectrum of $S^*M$.

As before, we denote by $r=|p|$ the radial coordinate on $T^*M$. Let $K=K_\mu$ be a convex smoothing of the Hamiltonian which is zero on $D^*M$ and equals $r\mapsto \mu r$ outside $D^*M$. Then, $2K=K_{2\mu }$ and $-K=K_{-\mu }$ are the corresponding Hamiltonians of slopes $2\mu$ and $-\mu$, respectively.

Let $\Sigma$ be the 3-punctured Riemann sphere, where we view one puncture as positive (input) and the other two as negative (outputs). We fix cylindrical coordinates $(s,t)\in [0,\infty )\times S^1$ near the positive puncture and $(s,t)\in (-\infty ,0]\times S^1$ near the negative punctures. Consider a 1-form $\beta$ on $\Sigma$ which equals $B\,\textrm{d}t$ near the positive puncture and $A_i \textrm{d}t$ near the i-th negative puncture $(i=1,2$) for some $A_i,B\in {\mathbb {R}}$. We say that $\beta$ has weights $B,A_1,A_2$. We, moreover, require $\textrm{d}\beta \leqslant 0$, which is possible iff

$$\begin{aligned} A_1+A_2\geqslant B. \end{aligned}$$

We consider maps $u:\Sigma \rightarrow T^*M$ satisfying the perturbed Cauchy–Riemann equation

$$\begin{aligned} (\textrm{d}u-X_K\otimes \beta )^{0,1}=0. \end{aligned}$$

Near the punctures this becomes the Floer equation for the Hamiltonians BK and $A_iK$, respectively, and the algebraic count of such maps defines a (primary) coproduct

$$\begin{aligned} FC_*(BK)\rightarrow FC_*(A_1K)\otimes FC_*(A_2K) \end{aligned}$$

which has degree $-n$ and decreases the Hamiltonian action.

To define the secondary coproduct $\lambda ^F$, we choose a 1-parameter family of 1-forms $\beta _\tau$, $\tau \in (0,1)$, with the following properties (see Fig. 2):

• $\textrm{d}\beta _\tau \leqslant 0$ for all $\tau$;

• $\beta _\tau$ equals $\textrm{d}t$ near the positive puncture and $+2\textrm{d}t$ near each negative puncture, i.e. $\beta _\tau$ has weights 1, 2, 2;

• as $\tau \rightarrow 0$, $\beta _\tau$ equals $-\textrm{d}t$ on cylinders near the first negative puncture whose length tends to $\infty$, so that $\beta _0$ consists of a 1-form on $\Sigma$ with weights $1,-1,2$ and a 1-form with weights $-1,2$ on an infinite cylinder attached at the first negative puncture;

• as $\tau \rightarrow 1$, $\beta _\tau$ equals $-\textrm{d}t$ on cylinders near the second negative puncture whose length tends to $\infty$, so that $\beta _1$ consists of a 1-form on $\Sigma$ with weights $1,2,-1$ and a 1-form with weights $-1,2$ on an infinite cylinder attached at the second negative puncture.

Fig. 2

The continuation coproduct $\lambda ^F$

Now, we consider pairs $(\tau ,u)$ where $\tau \in [0,1]$ and $u:\Sigma \rightarrow T^*M$ satisfies the perturbed Cauchy–Riemann equation

$$\begin{aligned} (\textrm{d}u-X_K\otimes \beta _\tau )^{0,1}=0. \end{aligned}$$

The algebraic count of such pairs defines a (secondary) coproduct

$$\begin{aligned} \lambda ^F:FC_*(K)\rightarrow FC_*(2K)\otimes FC_*(2K) \end{aligned}$$

which has degree $1-n$ and decreases the Hamiltonian action.

Let us analyse the contributions from $\tau =0,1$. The algebraic count of cylinders with weights $-1,2$ defines the continuation map (of degree 0)

$$\begin{aligned} c^F=c_{-K,2K}:FC_*(-K)\rightarrow FC_*(2K). \end{aligned}$$

As explained in the previous subsection, to define $c^F$, we perturb K by a Morse function $V:M\rightarrow {\mathbb {R}}$ with a unique maximum at $q_0$ and a unique minimum at $q_\textrm{Max}$. Moreover, we choose a family of 1-forms $\eta _\tau$ on M such that $\eta _0=\eta _1$ satisfies condition (12) (for all practical purposes one can think of $\eta _\tau$ as being constant). Finally, we choose a family of compactly supported 1-forms $\alpha _\tau$ on $\Sigma$ which for $\tau =0,1$ agree with $\rho (s)ds$ supported in the split off cylinder, for a function $\rho :{\mathbb {R}}\rightarrow [0,\infty )$ satisfying $\int _{\mathbb {R}}\rho =1$. For example, we can take $\alpha _\tau =(1-\tau )\alpha _0+\tau \alpha _1$ where $\alpha _0=\rho (s)ds$ supported on the first negative end, and $\alpha _1=\rho (s)ds$ supported on the second negative end (below the level where the splitting happens at $\tau =0,1$). With $\widehat{\eta }_\tau$ the vector field on $T^*M$ corresponding to $\eta _\tau$, we replace the Cauchy–Riemann equation in the definition of $\lambda ^F$ by

$$\begin{aligned} (\textrm{d}u-X_K\otimes \beta _\tau )^{0,1}=(\widehat{\eta }_\tau \otimes \alpha _\tau )^{0,1}. \end{aligned}$$

(15)

With these choices, it follows from the discussion in the previous subsection that the only nontrivial terms in the continuation maps at $\tau =0,1$ are $c^Fq_0=\chi q_0$, where $\chi$ is the Euler characteristic of M.

As shown in Fig. 2, the contribution at $\tau =0$ consists of a pair-of-pants with one positive puncture of weight 1 and two negative punctures of weights $-1$ and 2, with a cylinder of weights $-1$ and 2 attached at the first negative puncture. We reinterpret this as a pair-of-pants with two positive punctures of weights 1 and one negative puncture of weight 2, with a cylinder with two negative punctures of weights 2 and 1 attached at the first positive puncture. The preceding discussion shows that the count of these configurations corresponds to the composition $(1\otimes \mu ^F)(\tau c_0^F\otimes 1)$. A similar discussion at $\tau =1$ establishes that $\lambda ^F$ satisfies condition (4) in Definition 2.1.

We define the secondary continuation quadratic vector $Q_0^F$ by

$$\begin{aligned} Q_0^F=-\lambda ^F(q_\textrm{Max}). \end{aligned}$$

Condition (2), i.e. $\tau c_0^F-c_0^F=[{\partial },Q_0^F]$, follows by inserting $q_\textrm{Max}$ into the relation for $[{\partial },\lambda ^F]$ and using that $q_\textrm{Max}$ is a strict two-sided unit for $\mu$ on $FC_*^{=0}(K)$. This is an instance of unital $A_2^+$-structure [20]. Note that $Q_0^F\in FC_*^{=0}(K)\otimes FC_*^{=0}(K)$ for energy reasons. An inspection of the definition shows that $Q_0^F$ coincides with the secondary continuation element defined in Sect. 4.2 by interpolating between the perturbing 1-form $\eta$ and its opposite $-\eta$. See also [21].

It remains to prove condition (5) in Definition 2.1. For $n=1$ it holds because $\chi =0$, so that $c_0^F=0$. We, therefore, assume w.l.o.g. $n\ge 2$ and, as in the Morse case, we prove condition (5) in two steps.

• 1. We first prove $\lambda ^Fc^F=0$. This follows from $\lambda ^F(q_0)=0$, which is seen as follows. For action reasons, the coefficient $\langle \lambda ^F(q_0),x\otimes y\rangle$ can only be nonzero if x, y are critical points of K. Since $\lambda ^F$ has degree $1-n$, we must have $1-n = \textrm{CZ}(x)+\textrm{CZ}(y)-\textrm{CZ}(q_0) = n-\textrm{ind}_V(x)-\textrm{ind}_V(y)+\textrm{ind}_V(q_0)$, hence $\textrm{ind}_V(x)+\textrm{ind}_V(y)=\textrm{ind}_V(q_0)+2n-1=3n-1$. Since $\textrm{ind}_V(x)+\textrm{ind}_V(y)\leqslant 2n$, this is impossible for $n\ge 2$.

• 2. We are left to show that $(1\otimes \mu ^F\otimes 1)({\varvec{a}}\otimes {\varvec{b}})=0$, where $({\varvec{a}},{\varvec{b}})=(\tau Q_0^F,c_0^F), (\tau c_0^F,Q_0^F), (\tau Q_0^F,\tau c_0^F), (c_0^F,\tau Q_0^F)$. We identify the Floer subcomplex $FC_*^{=0}(K)$ generated by orbits of small action with the Morse cochain complex $MC^{n-*}(V)$. The cohomological index of $Q_0^F$ is $2n-1$, so its components must have degrees $n-1$ and n. If $n\ge 2$ these degrees are both positive, and therefore any component of $Q_0$ is killed by multiplication with $q_0$ because the latter has cohomological index n.

In summary, we have shown

Proposition 3.1

The operations $c_0^F,Q_0^F,\mu ^F,\lambda ^F$ on the Floer chain complexes $FC_*(K)$ resp. $FC_*(2K)$ satisfy the relations of a special $A_2^+$-structure.

The operations $c_0^F,Q_0^F\mu ^F,\lambda ^F$ are compatible with Floer continuation maps between different Hamiltonians $H\leqslant K$. We will refer to this structure as being the special $A_2^+$-structure for symplectic homology $SH_*(D^*M)$.

Remark 3.2

In the previous construction, we imposed the condition $\eta _0=\eta _1$ at the endpoints of the family of 1-forms $\eta _\tau$ for the same reason why we imposed $v^1=-v^0$ in the Morse case: this ensures that the product on Rabinowitz Floer homology obtained from the $A_2^+$-structure via the cone construction coincides with the product from [16] and fits into a graded Frobenius algebra structure on $S{\mathbb {H}}_*(S^*M)$.

The construction of an $A_2^+$-structure would have worked with any choice of interpolating family $\eta _\tau$ such that $\eta _0$ and $\eta _1$ satisfy (12). The necessity of the condition $\eta _1=\eta _0$ for this fine behaviour of the product would become visible at chain level within a theory of $A_3^+$-structures.

4 Reduced loop homology

This section expands material from [21, §4] in the particular case of cotangent bundles. We assume that M is connected and orientable, and we work either with constant coefficients on the loop space, or with local coefficients $\eta$ obtained by transgressing the 2nd Stiefel–Whitney class. In each of these two cases we have a commutative diagram

where the vertical maps are restriction to, resp. inclusion of constant loops, and ${\varepsilon }_0$ is induced by multiplication with the Euler characteristic $\chi$. From now on, we omit from the notation the local system $\eta$.

Definition 4.1

We define reduced loop homology, resp. cohomology,

$$\begin{aligned} \overline{H}_*(\Lambda )=\textrm{ coker }\, {\varepsilon },\qquad \overline{H}^*(\Lambda )=\ker {\varepsilon }. \end{aligned}$$

In the sequel, we restrict the discussion to reduced homology. Reduced cohomology features similar properties, with the roles of the product and coproduct being exchanged (as yet another instantiation of Poincaré duality for loop spaces [16]).

The behaviour of reduced homology with respect to the product is very robust. The image of ${\varepsilon }$ is an ideal in $H_*(\Lambda )$ (see for example [38] or [16]), and therefore the loop product canonically descends to reduced homology $\overline{H}_*(\Lambda )$.

In contrast, the behaviour of reduced homology with respect to the coproduct is very subtle. To describe it, the following variant of reduced loop homology arises naturally.

Definition 4.2

We define loop homology relative to $\chi \cdot$ point as

$$\begin{aligned} H_*(\Lambda ,\chi \cdot \textrm{point}) = H_*(C_*(\Lambda )/\chi C_*(\textrm{point})). \end{aligned}$$

A straightforward calculation shows that we have a canonical isomorphism

$$\begin{aligned} \overline{H}_*(\Lambda )\simeq H_*(\Lambda ,\chi \cdot \text {point}) \end{aligned}$$

whenever the map $\chi H_0(\text {point})\rightarrow H_0(\Lambda )$ is injective, see Appendix A.8. This is the case if M is orientable and if we use a local system that is constant on the component of contractible loops, or if $\chi =0$, or if R is 2-torsion. We place ourselves from now on in this setup, so that we do not need to distinguish between $\overline{H}_*(\Lambda )$ and $H_*(\Lambda ,\chi \cdot \text {point})$.

The loop coproduct is canonically defined on $H_*(\Lambda ,\Lambda _0)$. We now explain that it always extends to $H_*(\Lambda ,\chi \cdot \text {point})$ (and hence to $\overline{H}_*(\Lambda )$ under our assumptions). However, this extension is not canonical. The extension depends on a choice of vector field with nondegenerate zeroes and on the choice of a Morse function on M. We will completely describe the dependence of the extension on the choice of vector field, and give sufficient conditions for independence of the extension on the choice of Morse function.

4.1 Reduced symplectic homology

We work with symplectic homology of $D^*M$, our favourite model for loop space homology. Recalling notation from Sect. 3.1, we fix the following continuation data:

• a Morse function $V:M\rightarrow {\mathbb {R}}$ with a unique maximum $q_0$.

• a 1-form $\eta$ on M which satisfies condition (12), i.e. the zeroes of $\eta$ are nondegenerate and lie outside of $\text {Skel}_{n-1}(V)$ (this is equivalent to a vector field v on M whose zeroes have the same property).

We consider Hamiltonians $K:T^*M\rightarrow {\mathbb {R}}$ of the form $K(q,p)=k(|p|)+V(q)$, where $k(0)=0$ and $k=k(r)$ is a linear function of r outside a compact set, of positive slope not belonging to the length spectrum. This data determines via Eq. (13) the Floer continuation map

$$\begin{aligned} c^F:FC_*(-K)\rightarrow FC_*(K), \end{aligned}$$

which has the property that the only generator on which it may be nonzero is $q_0$. Moreover, we have computed in  Sect. 3.1 that

$$\begin{aligned} c^F(q_0)=\chi q_0. \end{aligned}$$

The continuation map can be equivalently interpreted as a quadratic vector

$$\begin{aligned} c_0^F(1)=\chi q_0\otimes q_0\in FC_*(K)\otimes FC_*(K). \end{aligned}$$

We emphasise that the chain-level expression of the continuation map is the same for any choice of continuation data $(V,\eta )$.

Definition 4.3

The reduced Floer complex of K is

$$\begin{aligned} \overline{FC}_*(K)=FC_*(K)/\textrm{im}\,c^F. \end{aligned}$$

Its homology is the reduced Floer homology of K, denoted $\overline{FH}_*(K)$.

The reduced symplectic homology $\overline{SH}_*(D^*M)$ is the direct limit of reduced Floer homologies $\overline{FH}_*(K)$ over Hamiltonians K which vanish on $D^*M$ and are linear outside a compact set, perturbed to have the form $k(|p|)+V(q)$ near the zero section as above.²

The relation

$$\begin{aligned}{}[{\partial },\lambda ^F] = (\mu ^F\otimes 1)(1\otimes c_0^F) - (1\otimes \mu ^F)(\tau c_0^F\otimes 1) \end{aligned}$$

proved in Sect. 3.2, together with $\tau c_0^F=c_0^F$, shows that $\lambda ^F$ descends to a chain map $\overline{FC}_*(K)\rightarrow \overline{FC}_*(2K)\otimes \overline{FC}_*(2K)$. These maps are compatible with the continuation maps obtained by increasing the slope of K, giving rise in the limit (with field coefficients) to a well-defined coproduct of degree $-n+1$, denoted

$$\begin{aligned} \lambda ^F:\overline{SH}_*(D^*M)\rightarrow \overline{SH}_*(D^*M)\otimes \overline{SH}_*(D^*M). \end{aligned}$$

A straightforward enhancement of the Viterbo–Abbondandolo–Schwarz isomorphism shows that the map $\Psi$ induces an isomorphism between reduced homologies

$$\begin{aligned} \Psi _*:\overline{SH}_*(D^*M){\mathop {\longrightarrow }\limits ^{\simeq }}\overline{H}_*(\Lambda ). \end{aligned}$$

In particular, associated to a choice of continuation data $(V,\eta )$ is a coproduct on $\overline{H}_*(\Lambda )$. The key to understanding the dependence of the coproduct on the choice of continuation data $(V,\eta )$ is the secondary continuation map, which we describe next.

4.2 The secondary continuation map

Homotopies between different choices of pairs $(V,\eta )$ give rise to secondary operations which we describe in this subsection.

Consider two pairs $(V_i,\eta _i)$, $i=0,1$, satisfying the conditions of the previous subsection, i.e. $V_i:M\rightarrow {\mathbb {R}}$ is a Morse function with a unique maximum $q_i$ and $\eta _i$ a 1-form on M such that condition (12) holds. For $i=0,1$ let $K_i:T^*M\rightarrow {\mathbb {R}}$ be associated Hamiltonians as in the previous subsection. After shifting $V_0,V_1$ by constants we may assume without loss of generality that $-K_0\leqslant -K_1\leqslant K_1\leqslant K_0$.

As in the previous subsection, we pick a function $\phi :{\mathbb {R}}\rightarrow [-1,1]$ which equals 1 for $s\leqslant -1$ and $-1$ for $s\geqslant 1$. Let $H_\sigma :{\mathbb {R}}\times T^*M\rightarrow {\mathbb {R}}$, $\sigma \in [0,\infty )$, be a smooth family of s-dependent Hamiltonians with the following properties:

• ${\partial }_sH_\sigma (s,x)\leqslant 0$ for all $\sigma ,s,x$;

• $H_0(s,x)=\phi (s)K_0(x)$;

• $H_\sigma (s,x)$ equals $K_0(x)$ for $s\leqslant -\sigma -1$ and $-K_0(x)$ for $s\geqslant \sigma +1$;

• $H_\sigma (s,x)=\phi (s)K_1(x)$ for $|s|\leqslant \sigma$ and $\sigma \geqslant 1$.

Let $\eta _\sigma$, $\sigma \in [0,\infty )$, be a smooth family of 1-forms with $\eta _\sigma =\eta _1$ for all $\sigma \geqslant 1$. We consider pairs $(\sigma ,u)$ with $\sigma \in [0,\infty )$ and $u:{\mathbb {R}}\times S^1\rightarrow T^*M$ solving the Floer equation

$$\begin{aligned} {\partial }_su+J(u)\bigl ({\partial }_tu-X_{H_\sigma }(s,u)\bigr )=0 \end{aligned}$$

and converging to 1-periodic orbits of ${\mp } K_0$ as $s\rightarrow \pm \infty$. Their algebraic count gives rise to a degree 1 map

$$\begin{aligned} \textbf{Q}:FC_*(-K_0) \rightarrow FC_{*+1}(K_0) \end{aligned}$$

satisfying

$$\begin{aligned} {\partial }_{K_0}\textbf{Q} + \textbf{Q}{\partial }_{-K_0} = c_{10}c_1c_{01} - c_0, \end{aligned}$$

(16)

with the Floer continuation maps $c_i:FC_*(-K_i)\rightarrow FC_*(K_i)$ for $i=0,1$, $c_{01}:FC_*(-K_0)\rightarrow FC_*(-K_1)$, and $c_{10}:FC_*(K_1)\rightarrow FC_*(K_0)$. The map $\textbf{Q}$ factors through the action zero part which we will denote by $\textbf{Q}^{=0}$. Since the $V_i$ have unique maxima $q_i$, it follows from the previous subsection that the only nontrivial contribution to $c_0$ is $c_0(q_0)=\chi q_0$. Similarly, the only nontrivial contribution to the composition $c_{10}c_1c_{01}$ sends $q_0\mapsto q_1\mapsto \chi q_1\mapsto \chi q_0$. This shows that the right hand side of Eq. (16) vanishes, and therefore $\textbf{Q}$ descends to a map on homology

$$\begin{aligned} \textbf{Q}:FH_*(-K_0) \rightarrow FH_{*+1}(K_0) \end{aligned}$$

which factors through the action zero part

$$\begin{aligned} \textbf{Q}^{=0}:FH_*^{=0}(-K_0)\cong H_{n+*}(M) \rightarrow FH_{*+1}^{=0}(K_0)\cong H^{n-*-1}(M). \end{aligned}$$

For degree reasons nontrivial contributions can only occur for $*=0$ and $*=-1$ and give maps

$$\begin{aligned} H_n(M)\rightarrow H^{n-1}(M)\quad \text {resp.}\quad H_{n-1}(M)\rightarrow H^n(M). \end{aligned}$$

In particular, we have shown

Proposition 4.4

If $H_1(M)=0$, then the secondary continuation map $\textbf{Q}:FH_*(-K_0) \rightarrow FH_{*+1}(K_0)$ associated to any interpolation between pairs $(V_i,\eta _i)$, $i=0,1$, of continuation data vanishes. $\square$

4.3 Dependence of the continuation coproduct on choices

In this subsection, we discuss the dependence of the continuation coproduct $\lambda ^F$ on the data $(V,\eta )$ of a Morse function and a 1-form on M.

We consider the setup of the previous subsection and retain the terminology from there. Thus, we are given two pairs $(V_i,\eta _i)$, $i=0,1$, with associated Hamiltonians $K_i:T^*M\rightarrow {\mathbb {R}}$ satisfying $-K_0\leqslant -K_1\leqslant K_1\leqslant K_0$. They give rise to Floer continuation maps $c_i:FC_*(-K_i)\rightarrow FC_*(K_i)$, $c_{01}:FC_*(-K_0)\rightarrow FC_*(-K_1)$, and $c_{10}:FC_*(K_1)\rightarrow FC_*(K_0)$, and to a degree 1 map $\textbf{Q}:FC_*(-K_0) \rightarrow FC_{*+1}(K_0)$ satisfying Eq. (16).

We denote by $\lambda ^F_i:FC_*(K_i)\rightarrow FC_*(2K_i)\otimes FC_*(2K_i)$ the continuation coproducts (of degree $1-n$) defined with the data $(V_i,\eta _i)$ and families $\eta _{i,\tau }$, $\tau \in [0,1]$ such that $\eta _{i,0}=\eta _{i,1}=\eta _i$ as in Sect. 3.2. Let

$$\begin{aligned} P:FC_*(K_1)\rightarrow FC_*(2K_0)\otimes FC_*(2K_0) \end{aligned}$$

be the degree $2-n$ map defined by the 2-parametric family of Floer problems depicted in Fig. 3.

Fig. 3

The operation P

These Floer problems are defined in terms of a 2-parametric family of Hamiltonian valued 1-forms on the 3-punctured sphere with asymptotics and degenerations as in the figure, and a 2-parametric family of 1-forms on M which agree with $\eta _{1,\tau }$, $\tau \in [0,1]$ on the top side, with $\eta _1$ on the two top slanted sides, and with $\eta _{0,\tau }$, $\tau \in [0,1]$ on the bottom side of the hexagon.

On the reduced Floer chain complex the compositions along the top vertical sides vanish because they factor through the continuation map $c_1:FC_*(-K_1)\rightarrow FC_*(K_1)$, so we obtain the relation

$$\begin{aligned}{}[{\partial },P] = \lambda ^F_0 c_{10} - (c_{10}\otimes c_{10})\lambda ^F_1 + (1\otimes \textbf{Q})\lambda ^F_{01}c_{10} - (\textbf{Q}\otimes 1)\lambda ^F_{00}c_{10}. \end{aligned}$$

Here, $\lambda ^F_{00}:FC_*(K_0)\rightarrow FC_*(-K_0)\otimes FC_*(2K_0)$ and $\lambda ^F_{01}:FC_*(K_0)\rightarrow FC_*(2K_0)\otimes FC_*(-K_0)$ are the degree $-n$ operations appearing at the ends of the continuation coproduct $\lambda ^F_0$ as in Fig. 2.

All the maps appearing on the right hand side of the last displayed equation are chain maps, so they descend to maps on reduced Floer homology (denoted by the same letters) satisfying

$$\begin{aligned} (c_{10}\otimes c_{10})\lambda ^F_1 - \lambda ^F_0 c_{10} = (1\otimes \textbf{Q})\lambda ^F_{01}c_{10} - (\textbf{Q}\otimes 1)\lambda ^F_{00}c_{10}. \end{aligned}$$

Passing to the direct limit over Hamiltonians $K_0,K_1$ as above, we have therefore shown

Proposition 4.5

The continuation coproducts $\lambda _i^F$ on $\overline{SH}_*(D^*M)$ defined with continuation data $(V_i,\eta _i)$, $i=0,1$, satisfy the relation

$$\begin{aligned} \lambda ^F_1 - \lambda ^F_0 = (1\otimes \textbf{Q})\lambda ^F_{01} - (\textbf{Q}\otimes 1)\lambda ^F_{00}, \end{aligned}$$

where $\textbf{Q}$ is the secondary continuation map of the previous subsection and $\lambda ^F_{00}$, $\lambda ^F_{01}$ are induced by the maps defined above. $\square$

Remark 4.6

The right hand side of the previous equation can be rephrased in terms of the secondary continuation map and the product $\mu ^F$. We refer to [21, §4.3] for further details.

Proposition 4.5 shows that in general the continuation coproduct may depend on the data $(V,\eta )$. If $H_1(M)=0$, however, the secondary coproduct $\textbf{Q}$ vanishes by Proposition 4.4 and we obtain

Proposition 4.7

If $H_1(M)=0$, then the continuation coproduct on reduced symplectic homology $\overline{SH}(D^*M)$ is independent of the choice of continuation data $(V,\eta )$. $\square$

Remark 4.8

In Sect. 3.2, we defined the coproduct $\lambda _F$ using a family $\eta _\tau$, $\tau \in [0,1]$ with equal endpoints $\eta _0=\eta _1=\eta$. The proof of Proposition 4.5 shows that, under the assumption $H_1(M)=0$, the coproduct can be defined using families $\eta _\tau$ with arbitrary endpoints satisfying condition (12) (in particular, we can take $\eta _1=-\eta _0$). This observation simplifies the computations in Sect. 8 for spheres of dimension $>1$ by allowing the use of constant families of vector fields $v^\tau \equiv v$ for the topological definition of the coproduct.

Corollary 4.9

If $H_1(M)=0$ then, denoting $1\in \overline{SH}_*(D^*M)$ the unit and $\lambda _F$ the canonical coproduct, we have $\lambda _F(1)=0$.

A proof of this result in a more general setting is given in [21, §4], based on the vanishing of the secondary continuation map. We give here a topological proof, see also Sect. 8.2 for the case of spheres of odd dimension $\ge 3$.

Proof

We work on the topological side $\overline{H}_*\Lambda$ and compute, as in Sect. 8.2, the image of the fundamental class 1 by representing it by constant loops and using a constant vector field $v^\tau \equiv v$ with isolated nondegenerate zeroes. If v has no zeroes then its image under the coproduct is zero because it is represented by the empty chain. In the general case, the image is a degenerate 1-chain, hence vanishes in homology. $\square$

5 Viterbo’s isomorphism revisited

As before, in this section, M is a closed oriented manifold, $T^*M$ its cotangent bundle with the Liouville form $\lambda =p\,\textrm{d}q$, and $D^*M\subset T^*M$ its unit disc cotangent bundle viewed as a Liouville domain. The symplectic homology $SH_*(D^*M;\sigma )$ is isomorphic to the Floer homology $FH_*(H;\sigma )$ of a fibrewise quadratic Hamiltonian $H:S^1\times T^*M\rightarrow {\mathbb {R}}$. On the other hand, $FH_*(H;\sigma )$ is isomorphic to the loop homology $H_*(\Lambda )$ (Viterbo [39], Abbondandolo–Schwarz [1, 5], Salamon–Weber [35], Abouzaid [7]). Here, we use coefficients twisted by the local system $\sigma$ defined by transgressing the second Stiefel–Whitney class, cf. Appendix A. We drop the local system $\sigma$ from the notation in the rest of this section.

The construction most relevant for our purposes is the chain map

$$\begin{aligned} \Psi :FC_*(H)\rightarrow MC_*(S) \end{aligned}$$

from the Floer complex of a Hamiltonian $H:S^1\times T^*M\rightarrow {\mathbb {R}}$ to the Morse complex of an action functional $S:\Lambda \rightarrow {\mathbb {R}}$ on the loop space defined in [4]. When applied to a fibrewise quadratic Hamiltonian H and the action functional $S_L$ associated to its Legendre transform L, it induces an isomorphism on homology

$$\begin{aligned} \Psi _*:SH_*(D^*M)\cong FH_*(H)\rightarrow MH_*(S_L)\cong H_*\Lambda \end{aligned}$$

intertwining the pair-of-pants product with the loop product [4].

One annoying feature of the map $\Psi$ has been that, in contrast to its chain homotopy inverse $\Phi :MC_*(S_L)\rightarrow FC_*(H)$, it does not preserve the action filtrations. This would make it unsuitable for some of our applications in [16] such as those concerned with critical values. Using an estimate inspired by [17], we show in this section that $\Psi$ does preserve suitable action filtrations when applied to fibrewise linear Hamiltonians rather than fibrewise quadratic ones.

5.1 Floer homology

Consider a smooth time-periodic Hamiltonian $H:S^1\times T^*M\rightarrow {\mathbb {R}}$ which outside a compact set is either fibrewise quadratic, or linear with slope not in the action spectrum. It induces a smooth Hamiltonian action functional

$$\begin{aligned} A_H:C^\infty (S^1,T^*M)\rightarrow {\mathbb {R}},\qquad x\mapsto \int _0^1\bigl (x^*\lambda -H(t,x)\textrm{d}t\bigr ). \end{aligned}$$

Its critical points are 1-periodic orbits x, which we can assume to be nondegenerate with Conley–Zehnder index $\textrm{CZ}(x)$. Let J be a compatible almost complex structure on $T^*M$ and denote the Cauchy–Riemann operator with Hamiltonian perturbation on $u:{\mathbb {R}}\times S^1\rightarrow T^*M$ by

$$\begin{aligned} \overline{\partial }_Hu {:}{=} {\partial }_su+J(u)\bigl ({\partial }_tu-X_H(t,u)\bigr ). \end{aligned}$$

Let $FC_*(H)$ be the free R-module generated by $\textrm{Crit}(A_H)$ and graded by the Conley–Zehnder index. The Floer differential is given by

$$\begin{aligned} {\partial }^F:FC_*(H)\rightarrow FC_{*-1}(H),\qquad x\mapsto \sum _{\textrm{CZ}(y)=\textrm{CZ}(x)-1}\#\mathcal {M}(x;y)\,y, \end{aligned}$$

where $\#\mathcal {M}(x;y)$ denotes the signed count of points in the oriented 0-dimensional manifold

$$\begin{aligned} \mathcal {M}(x;y)&{:}{=} \{ u:{\mathbb {R}}\times S^1\rightarrow T^*M\mid \, \, \overline{\partial }_Hu=0, \\ u(+\infty )&=x,\ u(-\infty )=y\}/{\mathbb {R}}. \end{aligned}$$

Then, ${\partial }^F\circ {\partial }^F=0$ and its homology $FH_*(H)$ is isomorphic to the symplectic homology $SH_*(T^*M)$ if H is quadratic. If H is linear, we obtain an isomorphism to $SH_*(T^*M)$ in the direct limit as the slope goes to infinity.

5.2 The isomorphism $\Phi$

Suppose now that H is fibrewise convex with fibrewise Legendre transform $L:S^1\times TM\rightarrow {\mathbb {R}}$. As in Sect. 2.2, we consider the Morse complex $(MC_*,{\partial })$ of the action functional

$$\begin{aligned} S_L:\Lambda \rightarrow {\mathbb {R}},\qquad S_L(q)=\int _0^1L(t,q,\dot{q})\textrm{d}t. \end{aligned}$$

Following [1], for $a\in \textrm{Crit}(S_L)$ and $x\in \textrm{Crit}(A_H)$, we consider the space

$$\begin{aligned} \mathcal {M}(a;x)&{:}{=} \{u:(-\infty ,0]\times S^1\rightarrow T^*M\mid \overline{\partial }_H(u)=0,\ u(-\infty )=x, \\ {}&\quad \pi \circ u(0,\cdot )\in W^-(a)\}, \end{aligned}$$

where $W^-(a)$ denotes the stable manifold for the pseudo-gradient flow of $S_L$ and $\pi :T^*M\rightarrow M$ is the projection. (It is sometimes useful to view $W^-(a)$ as the unstable manifold for the negative pseudo-gradient flow of $S_L$.) For generic H this is a manifold of dimension

$$\begin{aligned} \dim \mathcal {M}(a;x) = \textrm{ind}(a)-\textrm{CZ}(x). \end{aligned}$$

The signed count of 0-dimensional spaces $\mathcal {M}(a;x)$ defines a chain map

$$\begin{aligned} \Phi :MC_*(S_L)\rightarrow FC_*(H),\qquad a\mapsto \sum _{\textrm{CZ}(x)=\textrm{ind}(a)}\#\mathcal {M}(a;x)\,x. \end{aligned}$$

(17)

It was shown in [1] that the induced map on homology is an isomorphism

$$\begin{aligned} \Phi _*:MH_*(S_L){\mathop {\longrightarrow }\limits ^{\cong }}FH_*(H). \end{aligned}$$

For $u\in \mathcal {M}(a;x)$ consider the loop $(q,p)=u(0,\cdot ):S^1\rightarrow T^*M$ at $s=0$. The definition of the Legendre transform yields the estimate

$$\begin{aligned} A_H(q,p) = \int _0^1\Bigl (\langle p,\dot{q}\rangle -H(t,q,p)\Bigr )\textrm{d}t \ \leqslant \int _0^1L(t,q,\dot{q})\textrm{d}t = S_L(q). \end{aligned}$$

It follows that

$$\begin{aligned} A_H(x)\leqslant A_H\bigl (u(0,\cdot )\bigr )\leqslant S_L(q)\leqslant S_L(a) \end{aligned}$$

whenever $\mathcal {M}(a;x)$ is nonempty, so $\Phi$ decreases action.

5.3 The isomorphism $\Psi$

Consider once again a fibrewise quadratic Hamiltonian $H:S^1\times T^*M\rightarrow {\mathbb {R}}$ as in Sect. 5.2 with Legendre transform L. Following [4, 17], for $x\in \textrm{Crit}(A_H)$ and $a\in \textrm{Crit}(S_L)$, we define

$$\begin{aligned} \mathcal {M}(x)&{:}{=} \{u:[0,\infty )\times S^1\rightarrow T^*M \mid \,\, \overline{\partial }_Hu=0,\\&\quad u(+\infty ,\cdot )=x,\ u(0,\cdot )\subset M\} \end{aligned}$$

and

$$\begin{aligned} \mathcal {M}(x;a) {:}{=} \{u\in \mathcal {M}(x)\mid u(0,\cdot )\in W^+(a)\}, \end{aligned}$$

where $W^+(a)$ is the stable manifold of a for the negative pseudo-gradient flow of $S_L$, see Fig. 4.

Fig. 4

Moduli spaces for the map $\Psi$

For generic H, these are manifolds of dimensions

$$\begin{aligned} \dim \mathcal {M}(x) = \textrm{CZ}(x),\qquad \dim \mathcal {M}(x;a) = \textrm{CZ}(x)-\textrm{ind}(a). \end{aligned}$$

The signed count of 0-dimensional spaces $\mathcal {M}(x;a)$ defines a chain map

$$\begin{aligned} \Psi :FC_*(H)\rightarrow MC_*(S_L),\qquad x\mapsto \sum _{\textrm{ind}(a)=\textrm{CZ}(x)}\#\mathcal {M}(x;a)\,a. \end{aligned}$$

The induced map on homology is an isomorphism

$$\begin{aligned} \Psi _*=\Phi _*^{-1}:FH_*(H){\mathop {\longrightarrow }\limits ^{\cong }}MH_*(S_L)\cong H_*\Lambda , \end{aligned}$$

which is the inverse of $\Phi _*$ and intertwines the pair-of-pants product with the loop product. This was shown by Abbondandolo and Schwarz [4] with ${\mathbb {Z}}/2$-coefficients, and by Abouzaid [7] (following work of Kragh [30], see also Abbondandolo–Schwarz [5]) with general coefficients, twisted on $H_*\Lambda$ by a suitable local system, see Appendix A. Moreover, Abouzaid proved that $\Psi _*$ is an isomorphism of twisted BV algebras.

Unfortunately, the map $\Psi$ does not preserve the action filtrations. This already happens for a classical Hamiltonian $H(q,p)=\frac{1}{2}|p|^2+V(q)$: For $u\in \mathcal {M}(x;a)$ the loop $q=u(0,\cdot ):S^1\rightarrow M$ satisfies

$$\begin{aligned} A_H(x)&\geqslant A_H\bigl (u(0,\cdot )\bigr ) = -\int _0^1V(q)\textrm{d}t \\ {}&\leqslant \int _0^1\Bigl (\frac{1}{2}|\dot{q}|^2-V(q)\Bigr )\textrm{d}t = S_L(q)\geqslant S_L(a), \end{aligned}$$

so the middle inequality goes in the wrong direction (even if $V=0$).

5.4 An action estimate for Floer half-cylinders

Now, we will replace the quadratic Hamiltonians from the previous subsections by Hamiltonians of the shape used in the definition of symplectic homology. For Floer half-cylinders of such Hamiltonians, we will estimate the length of their boundary loop on the zero section by the Hamiltonian action at $+\infty$.

We equip M with a Riemannian metric and choose the following data.

The Riemannian metric on M induces a canonical almost complex structure $J_\textrm{st}$ on $T^*M$ compatible with the symplectic form ${\omega }_\textrm{st}=\textrm{d}p\wedge \textrm{d}q$ (Nagano [32], Tachibana–Okumura [37], see also [11, Ch. 9]). In geodesic normal coordinates $q_i$ at a point q and dual coordinates $p_i$ it is given by

$$\begin{aligned} J_\textrm{st}:\frac{{\partial }}{{\partial }q_i}\mapsto -\frac{{\partial }}{{\partial }p_i},\qquad \frac{{\partial }}{{\partial }p_i}\mapsto \frac{{\partial }}{{\partial }q_i}. \end{aligned}$$

We pick a nondecreasing smooth function $\rho :[0,\infty )\rightarrow (0,\infty )$ with $\rho (r)\equiv 1$ near $r=0$ and $\rho (r)=r$ for large r. Then,

$$\begin{aligned} J:\frac{{\partial }}{{\partial }q_i}\mapsto -\rho (|p|)\frac{{\partial }}{{\partial }p_i},\qquad \rho (|p|)\frac{{\partial }}{{\partial }p_i}\mapsto \frac{{\partial }}{{\partial }q_i} \end{aligned}$$

(in geodesic normal coordinates) defines a compatible almost complex structure on $T^*M$ which agrees with $J_\textrm{st}$ near the zero section and is cylindrical outside the unit cotangent bundle.

We view $r(q,p)=|p|$ as a function on $T^*M$. Then, on $T^*M{\setminus } M$, we have

$$\begin{aligned} \lambda =r\alpha ,\qquad \alpha {:}{=}\frac{p\,\textrm{d}q}{|p|}. \end{aligned}$$

Consider a Hamiltonian of the form $H=h\circ r:T^*M\rightarrow {\mathbb {R}}$ for a smooth function $h:[0,\infty )\rightarrow [0,\infty )$ vanishing near $r=0$. Then, its Hamiltonian vector field equals $X_H=h'(r)R$, where R is the Reeb vector field of $(S^*M,\alpha )$. The symplectic and Hamiltonian actions of a nonconstant 1-periodic Hamiltonian orbit $x:S^1\rightarrow T^*M$ are given by

$$\begin{aligned} \int _x\alpha = h'(r),\qquad A_H(x) = rh'(r)-h(r). \end{aligned}$$

Given a slope $\mu >0$ which is not in the action spectrum of $(S^*M,\alpha )$ and any ${\varepsilon }>0$, we can pick h with the following properties:

• $h(r)\equiv 0$ for $r\leqslant 1$ and $h'(r)\equiv \mu$ for $r\geqslant 1+\delta$, with some $\delta >0$;

• $h''(r)>0$ and $rh'(r)-h(r)-{\varepsilon }\leqslant h'(r)\leqslant rh'(r)-h(r)$ for $r\in (1,1+\delta )$.

Specifically, we choose $0<\delta \le {\varepsilon }/\mu$, we consider a smooth function $\beta :[0,\infty )\rightarrow [0,1]$ such that $\beta =0$ on [0, 1], $\beta =1$ on $[1+\delta ,\infty )$ and $\beta$ is strictly increasing on $(1,1+\delta )$, and we define $h:[0,\infty )\rightarrow [0,\infty )$ by

$$\begin{aligned} h(r)=\mu \int _1^r \beta (\rho ) \, \textrm{d}\rho . \end{aligned}$$

We have $rh'-h-h'=\mu \left( (r-1)\beta - \int _1^r\beta \right)$. This expression differentiates to $\mu (r-1)\beta '\ge 0$ and vanishes on [0, 1], hence it is nonnegative for $r\ge 0$. On the other hand, we have an upper bound $\mu \left( (r-1)\beta - \int _1^r\beta \right) \le \mu \delta$ for $r\in (1,1+\delta )$, and indeed for $r\ge 0$. Given our choice $\delta \le {\varepsilon }/\mu$, this establishes the inequalities $rh'(r)-h(r)-{\varepsilon }\leqslant h'(r)\leqslant rh'(r)-h(r)$ for all $r\ge 0$.

These inequalities imply that for each nonconstant 1-periodic Hamiltonian orbit x, we have

$$\begin{aligned} A_H(x)-{\varepsilon }\leqslant \int _x\alpha \leqslant A_H(x). \end{aligned}$$

(18)

With this choice of J and H, consider now as in the previous subsection a map $u:[0,\infty )\times S^1\rightarrow T^*M$ satisfying

$$\begin{aligned} \overline{\partial }_Hu=0,\ u(+\infty ,\cdot )=x,\ u(0,\cdot )\subset M. \end{aligned}$$

Set $q(t){:}{=}u(0,t)$ and denote its length by

$$\begin{aligned} \ell (q) {:}{=} \int _0^1|\dot{q}|\textrm{d}t. \end{aligned}$$

The following proposition is a special case of [17, Lemma 7.2]. Since the proof was only sketched there, we give a detailed proof below.

Proposition 5.1

Let H, J, u be as above with $q=u(0,\cdot )$ and a nonconstant orbit $x=u(+\infty ,\cdot )$. Then,

$$\begin{aligned} \ell (q)\leqslant \int _x\alpha \leqslant A_H(x). \end{aligned}$$

The first inequality is an equality if and only if u is contained in the half-cylinder over a closed geodesic q, in particular x is the lift of the geodesic q.

The idea of the proof is to show that

$$\begin{aligned} 0\leqslant \int _{(0,\infty )\times S^1}u^*\textrm{d}\alpha = \int _x\alpha -\ell (q). \end{aligned}$$

Since the image $u\bigl ((0,\infty )\times S^1\bigr )$ can hit the zero section M where $\alpha$ is undefined, the quantity $\int _{(0,\infty )\times S^1}u^*\textrm{d}\alpha$ has to be interpreted as an improper integral as follows. Given ${\varepsilon }>0$, let $\tau =\tau _{\varepsilon }:[0,\infty ) \rightarrow [0,\infty )$ be a smooth function with $\tau '(r)\geqslant 0$ for all r, $\tau (r)=0$ near $r=0$, and $\tau (r)=1$ for $r\geqslant {\varepsilon }$, and consider the globally defined 1-form on $T^*M$ given by

$$\begin{aligned} \alpha _{\varepsilon }{:}{=} \frac{\tau (|p|) p\,\textrm{d}q}{|p|}. \end{aligned}$$

We now define

$$\begin{aligned} \int _{(0,\infty )\times S^1}u^*\textrm{d}\alpha = \lim \limits _{\sigma \searrow 0}\lim \limits _{{\varepsilon }\searrow 0}\int _{[\sigma ,\infty )\times S^1}u^*\textrm{d}\alpha _{\varepsilon }. \end{aligned}$$

(19)

The proof of Proposition 5.1 is based on the following lemma.

Lemma 5.2

For any $v\in T_{(q,p)}T^*Q$, we have

$$\begin{aligned} \textrm{d}\alpha _{\varepsilon }(v,Jv)\geqslant 0. \end{aligned}$$

At points where $\tau '(|p|)>0$, equality only holds for $v=0$, whereas at points where $\tau '=0$ and $\tau \ne 0$ equality holds if and only if v is a linear combination of $p{\partial }_p$ and $p{\partial }_q$.

Proof

In geodesic normal coordinates, we compute

$$\begin{aligned} \textrm{d}\alpha _{\varepsilon }&= d\left( \sum _i\frac{\tau (|p|)p_i\textrm{d}q_i}{|p|}\right) \\&= \sum _i\frac{\tau (|p|)\textrm{d}p_i\wedge \textrm{d}q_i}{|p|} + \sum _{i,j}\frac{(\tau '(|p|)|p|-\tau (|p|))p_ip_j\textrm{d}p_i\wedge \textrm{d}q_j}{|p|^3}. \end{aligned}$$

For a vector of the form $v=\sum _ia_i\rho (|p|){\partial }_{p_i}$, we obtain $J_\rho v=\sum _ia_i{\partial }_{q_i}$ and hence by the Cauchy–Schwarz inequality

$$\begin{aligned} \textrm{d}\alpha _{\varepsilon }(v,Jv)&= \sum _i\frac{\tau (|p|)\rho (|p|)a_i^2}{|p|} + \sum _{i,j}\frac{(\tau '(|p|)|p|-\tau (|p|))\rho (|p|)p_ip_ja_ia_j}{|p|^3} \\ {}&= \frac{\tau (|p|)\rho (|p|)}{|p|^3}(|a|^2|p|^2-\langle a,p\rangle ^2) + \frac{\tau '(|p|)\rho (|p|)}{|p|^2}\langle a,p\rangle ^2 \\ {}&\geqslant 0. \end{aligned}$$

At points where $\tau '>0$, equality only holds for $a=0$, and at points where $\tau '=0$ and $\tau >0$ equality holds iff a is a multiple of p. Similarly, for a general vector $v=\sum _ia_i\rho (|p|){\partial }_{p_i} - \sum _ib_i{\partial }_{q_i}$, we get $\textrm{d}\alpha _{\varepsilon }(v,Jv)\geqslant 0$, with equality iff either $a=b=0$ or $\tau '=0$ and both a and b are multiples of p. $\square$

Proof of Proposition 5.1

The proof consists in 3 steps.

Step 1. We prove that $\int _{(0,\infty )\times S^1} u^*\textrm{d}\alpha \ge 0$.

In view of Definition (19), it is enough to show that $u^*\textrm{d}\alpha _{\varepsilon }\geqslant 0$ on all of $(0,\infty )\times S^1$. To see this, recall that u satisfies the equation ${\partial }_su+J(u)\bigl ({\partial }_tu-X_H(u)\bigr )=0$, so that

$$\begin{aligned} u^*\textrm{d}\alpha _{\varepsilon }= \textrm{d}\alpha _{\varepsilon }({\partial }_su,{\partial }_tu)ds\wedge \textrm{d}t = \textrm{d}\alpha _{\varepsilon }\bigl ({\partial }_su,J(u){\partial }_su+X_H(u)\bigr )ds\wedge \textrm{d}t. \end{aligned}$$

Now, at points in $D^*M$ the Hamiltonian vector field $X_H$ vanishes. At points outside $D^*M$, we have $X_H=h'(r)R$ and $\alpha _{\varepsilon }=\alpha$ (we can assume w.l.o.g. ${\varepsilon }\le 1$), so that $i_{X_H}\textrm{d}\alpha _{\varepsilon }=h'(r)i_R\textrm{d}\alpha =0$. In either case, we have

$$\begin{aligned} u^*\textrm{d}\alpha _{\varepsilon }= \textrm{d}\alpha _{\varepsilon }({\partial }_su,J(u){\partial }_su)ds\wedge \textrm{d}t, \end{aligned}$$

which is nonnegative by Lemma 5.2.

Step 2. Denote $u_\sigma =u(\sigma ,\cdot )$ for $\sigma >0$. We have

$$\begin{aligned} \lim \limits _{\sigma \searrow 0}\lim \limits _{{\varepsilon }\searrow 0}\int _{S^1}u_\sigma ^*\alpha _{\varepsilon }= \ell (q). \end{aligned}$$

To see this, we consider the map

$$\begin{aligned} {\tilde{q}}:[0,\infty )\times S^1\rightarrow T^*M,\qquad {\tilde{q}}(s,t){:}{=}\bigl (q(t),s\dot{q}(t)\bigr ), \end{aligned}$$

and denote as above ${\tilde{q}}_\sigma ={\tilde{q}}(\sigma ,\cdot )$ for $\sigma >0$. Since $J=J_\textrm{st}$ near the zero section, the maps u and ${\tilde{q}}$ agree with their first derivatives along the boundary loop q at $s=0$, hence $u_\sigma$ and ${\tilde{q}}_\sigma$ are $C^1$-close for $\sigma$ close to 0. On the other hand $\alpha _{\varepsilon }$ is $C^0$-bounded near the zero section uniformly with respect to ${\varepsilon }\rightarrow 0$. These two facts imply that the integrals $\int _{S^1}u_\sigma ^*\alpha _{\varepsilon }$ and $\int _{S^1} {\tilde{q}}_\sigma ^*\alpha _{\varepsilon }$ are $C^0$-close for $\sigma$ close to 0, uniformly with respect to ${\varepsilon }\rightarrow 0$, and therefore

$$\begin{aligned} \lim \limits _{\sigma \searrow 0}\lim \limits _{{\varepsilon }\searrow 0}\int _{S^1}u_\sigma ^*\alpha _{\varepsilon }= \lim \limits _{\sigma \searrow 0}\lim \limits _{{\varepsilon }\searrow 0}\int _{S^1}{\tilde{q}}_\sigma ^*\alpha _{\varepsilon }. \end{aligned}$$

We now prove that

$$\begin{aligned} \lim \limits _{{\varepsilon }\searrow 0}\int _{S^1}{\tilde{q}}_\sigma ^* \alpha _{\varepsilon }= \ell (q) \end{aligned}$$

(20)

for all $\sigma >0$, which implies the desired conclusion. Fix therefore $\sigma >0$. Let $I_{\varepsilon }=\{t\in S^1\,: \, |\sigma \dot{q}(t)|\le {\varepsilon }\}$, so that $I_{\varepsilon }\subset I_{{\varepsilon }'}$ for ${\varepsilon }\le {\varepsilon }'$ and $\int _{{\varepsilon }>0} I_{\varepsilon }= I_0 = \{t\,: \, \dot{q}(t)=0\}$. On the one hand, we have

$$\begin{aligned} \int _{S^1\setminus I_{\varepsilon }}{\tilde{q}}_\sigma ^*\alpha _{\varepsilon }&= \int _{S^1\setminus I_{\varepsilon }}{\tilde{q}}_\sigma ^*\alpha = \int _{S^1\setminus I_{\varepsilon }}\alpha _{(q(t),\sigma \dot{q}(t))}\cdot \dot{{\tilde{q}}}(t) \\&= \int _{S^1\setminus I_{\varepsilon }} \frac{\sigma |\dot{q}(t)|^2}{|\sigma \dot{q}(t)|}\textrm{d}t = \int _{S^1\setminus I_{\varepsilon }} |\dot{q}(t)|\textrm{d}t = \ell (q|_{S^1\setminus I_{\varepsilon }}). \end{aligned}$$

We can, therefore, estimate

$$\begin{aligned} \left| \int _{S^1} {\tilde{q}}_\sigma ^*\alpha _{\varepsilon }- \ell (q|_{S^1\setminus I_{\varepsilon }})\right|&= \left| \int _{I_{\varepsilon }} {\tilde{q}}_\sigma ^*\alpha _{\varepsilon }\right| = \left| \int _{I_{\varepsilon }}\alpha _{\varepsilon }({\tilde{q}}_\sigma (t))\cdot \dot{{\tilde{q}}}_\sigma (t) \textrm{d}t\right| \\&\le C \cdot \frac{{\varepsilon }}{\sigma }\cdot m(I_{\varepsilon }) \rightarrow 0 \quad \text {for } {\varepsilon }\rightarrow 0. \end{aligned}$$

Here, $m(I_{\varepsilon })$ is the measure of $I_{\varepsilon }$, uniformly bounded by the length of the circle, $C>0$ is a $C^0$-bound on $\alpha _{\varepsilon }$ near the 0-section, uniform with respect to ${\varepsilon }\rightarrow 0$, and ${\varepsilon }/\sigma$ is by definition the bound on $|\dot{q}(t)|$ on $I_{\varepsilon }$. The estimate follows from $\dot{{\tilde{q}}}_\sigma = (\dot{q},\sigma \ddot{q})$ and the fact that the 1-form $\alpha _{\varepsilon }$ only acts on the first component of the vector $\dot{{\tilde{q}}}_\sigma$.

Since $\lim \limits _{{\varepsilon }\searrow 0}\ell (q|_{S^1{\setminus } I_{\varepsilon }}) = \ell (q|_{S^1{\setminus } I_0}) =\ell (q)$, equality (20) follows.

Step 3. We prove

$$\begin{aligned} \int _{(0,\infty )\times S^1}u^*\textrm{d}\alpha = \int _x \alpha -\ell (q). \end{aligned}$$

Indeed, for $\sigma ,{\varepsilon }>0$ Stokes’ theorem gives

$$\begin{aligned} \int _{[\sigma ,\infty )\times S^1}u^*\textrm{d}\alpha _{\varepsilon }= \int _x\alpha - \int _{u_\sigma }\alpha _{\varepsilon }. \end{aligned}$$

(The 1-form $\alpha _{\varepsilon }$ is equal to $\alpha$ near the orbit x.) The desired equality follows from the definition of $\int _{(0,\infty )\times S^1}u^*\textrm{d}\alpha$ and Step 2.

Conclusion. Combining Step 3 with Step 1, we obtain the first inequality $\ell (q)\leqslant \int _x\alpha$ in Proposition 5.1. Moreover, Lemma 5.2 (in the limit ${\varepsilon }\rightarrow 0$) shows that this inequality is an equality if and only if u is contained in the half-cylinder over a closed geodesic.

The second inequality $\int _x\alpha \leqslant A_H(x)$ follows from (18). $\square$

5.5 The isomorphism $\Psi$ from symplectic to loop homology

Now, we adjust the definition of $\Psi$ to symplectic homology. For J, H as in the previous subsection and $x\in \textrm{Crit}(A_H)$, we define as before

$$\begin{aligned} \mathcal {M}(x)&{:}{=} \{u:[0,\infty )\times S^1\rightarrow T^*M \mid \, \, \overline{\partial }_Hu=0,\\&\quad u(+\infty ,\cdot )=x,\ u(0,\cdot )\subset M\}. \end{aligned}$$

By Proposition 5.1, the loop $q=u(0,\cdot )$ satisfies $\ell (q)\leqslant A_H(x)$. Moreover, the loop q is smooth and in particular has Sobolev class $H^1$, hence following Anosov [10] it has a unique $H^1$-reparametrisation $\overline{q}:S^1\rightarrow M$, with $|\dot{\overline{q}}|\equiv \textrm{const}$ and $\overline{q}(0)=q(0)$ (we say that $\overline{q}$ is parametrized proportionally to arclength, or PPAL). We have

$$\begin{aligned} \ell (q) = \ell (\overline{q}) = \int _0^1|\dot{\overline{q}}|\textrm{d}t = \Bigl (\int _0^1|\dot{\overline{q}}|^2\textrm{d}t\Bigr )^{1/2} = E(\overline{q})^{1/2} \end{aligned}$$

with the energy

$$\begin{aligned} E:\Lambda \rightarrow {\mathbb {R}},\qquad E(q) {:}{=} \int _0^1|\dot{q}|^2\textrm{d}t. \end{aligned}$$

The energy defines a smooth Morse–Bott function on the loop space whose critical points are constant loops and geodesics parametrized proportionally to arclength. We denote by $W^\pm (a)$ the unstable/stable manifolds of $a\in \textrm{Crit}(E)$ with respect to $\nabla E$. Now, for $x\in \textrm{Crit}(A_H)$ and $a\in \textrm{Crit}(E)$, we define

$$\begin{aligned} \mathcal {M}(x;a) {:}{=} \{u\in \mathcal {M}(x)\mid \overline{u(0,\cdot )}\in W^+(a)\}. \end{aligned}$$

An element u in this moduli space still looks as in Fig. 4, where now the loop $q=u(0,\cdot )$ is reparametrized proportionally to arclength and then flown into a using the flow of $-\nabla E$. By Proposition 5.1, for $u\in \mathcal {M}(x;a)$, we have the estimate

$$\begin{aligned} A_H(x) \geqslant \ell (q) = E(\overline{q})^{1/2} \geqslant E(a)^{1/2}. \end{aligned}$$

(21)

To define the map $\Psi$, we now perturb H and E by small Morse functions near the constant loops on M and the closed geodesics, and we generically perturb the almost complex structure J from the previous subsection. For generic such perturbations, each $\mathcal {M}(x;a)$ is a manifold of dimension

$$\begin{aligned} \dim \mathcal {M}(x;a) = \textrm{CZ}(x)-\textrm{ind}(a). \end{aligned}$$

The signed count of 0-dimensional spaces $\mathcal {M}(x;a)$ defines a chain map

$$\begin{aligned} \Psi :FC_*(H)\rightarrow MC_*(E^{1/2}),\qquad x\mapsto \sum _{\textrm{ind}(a)=\textrm{CZ}(x)}\#\mathcal {M}(x;a)\,a. \end{aligned}$$

Here, $MC_*(E^{1/2})$ denotes the Morse chain complex of $E:\Lambda \rightarrow {\mathbb {R}}$, graded by the Morse indices of E, but filtered by the square root $E^{1/2}$ (which is decreasing under the negative gradient flow of E). The action estimate (21) continues to hold for the perturbed data up to an arbitrarily small error, which we can make smaller than the smallest difference between lengths of geodesics below a given length $\mu$. Thus, $\Psi$ preserves the filtrations

$$\begin{aligned} \Psi :FC_*^{<b}(H)\rightarrow MC^{<b}_*(E^{1/2}). \end{aligned}$$

The induced maps on filtered Floer homology

$$\begin{aligned} \Psi _*:FH_*^{(a,b)}(H)\rightarrow MH_*^{(a,b)}(E^{1/2})\cong H_*^{(a,b)}\Lambda \end{aligned}$$

have upper triangular form with respect to the filtrations with $\pm 1$ on the diagonal (given by the half-cylinders over closed geodesics in Proposition 5.1), so they are isomorphisms. It follows from [4, 7] that $\Psi _*$ intertwines the pair-of-pants product with the loop product, as well as the corresponding BV operators. Passing to the direct limit over Hamiltonians H, we have thus proved

Theorem 5.3

The map $\Psi$ induces isomorphisms on filtered symplectic homology

$$\begin{aligned} \Psi _*:SH_*^{(a,b)}(D^*M){\mathop {\longrightarrow }\limits ^{\cong }}MH_*^{(a,b)}(E^{1/2})\cong H_*^{(a,b)}\Lambda , \end{aligned}$$

where the left hand side is filtered by non-Hamiltonian action and the right hand side by the square root of the energy. These isomorphisms intertwine the pair-of-pants product with the Chas–Sullivan loop product, as well as the corresponding BV operators. $\square$

6 Viterbo’s isomorphism intertwines $A_2^+$-structures

We keep the setup from the previous section, so M is a closed oriented Riemannian manifold and $D^*M\subset T^*M$ its unit disc cotangent bundle. In this section, we prove Theorem 1.5, which will be an immediate consequence of earlier results and the following theorem.

Theorem 6.1

The chain maps underlying the isomorphism

$$\begin{aligned} \Psi _*:SH_*(D^*M){\mathop {\longrightarrow }\limits ^{\cong }}H_*\Lambda \end{aligned}$$

from Theorem 5.3 are morphisms of special $A_2^+$-algebras. For $n\ne 2$ these morphisms are special.

Proof of Theorem 1.5

The first assertion follows from Proposition 2.9 and Proposition 2.2. The second assertion follows from Theorem 6.1 and Proposition 2.4. $\square$

Remark 6.2

(open questions about the various identifications between Morse and Floer complexes for cotangent bundles) We have already discussed in Sect. 5.2 the action-preserving chain-level isomorphism $\Phi :MC_*(S_L)\rightarrow FC_*(H)$ of Abbondandolo–Schwarz [1], defined for an asymptotically quadratic Hamiltonian H. It would be interesting to clarify whether $\Phi$ also defines a morphism of special $A_2^+$-algebras.

Abbondandolo–Schwarz constructed in [6] an action-preserving chain-level isomorphism $\Psi _{AS}:FC_*(H)\rightarrow MC_*(S_L)$ which is a chain homotopy inverse of $\Phi$. They also argued that, from the perspective of the Legendre transform, the moduli spaces that define $\Psi _{AS}$ arise naturally from the moduli spaces for $\Phi$. We expect that $\Psi _{AS}$ and our morphism $\Psi$ can be connected by a suitable chain homotopy (we know that they induce the same map $\Phi ^{-1}_*$ in homology). It would also be interesting to clarify whether $\Psi _{AS}$ is a morphism of special $A_2^+$-algebras. We expect this to hold or fail for both $\Psi _{AS}$ and $\Phi$ simultaneously.

One can further ask whether $\Psi _{AS}$ and $\Psi$ are homotopic as morphisms of $A_2^+$-structures. This would require in particular to develop the discussion of $A_2^+$-structures from [20] by defining such a notion of homotopy.

To prove Theorem 6.1, we need to verify the conditions in Definition 2.3 for each chain map $\Psi :FC_*(K)\rightarrow MC_*(E^{1/2})$ associated to a Hamiltonian $K=K_\mu$ as in the previous subsection. The first part of condition (i) holds because $\Psi q_0=q_0$, which follows directly from the definition of $\Psi$. Moreover, seen through the canonical identifications $FC_*^{=0}(K)\equiv MC_*^{=0}(E^{1/2})\equiv MC^{n-*}(V)$, the restriction of $\Psi$ to the energy zero Floer subcomplex acts as the identity. This shows that the second part of condition (i) is also satisfied.

The map $\Gamma :FC_*(K)\otimes FC_*(K)\rightarrow MC_*(E^{1/2})$ in condition (ii) is defined by the count of elements in 0-dimensional moduli spaces of solutions to a 1-parametric mixed Floer–Morse problem which we describe below. Inspection of the boundary of the 1-dimensional moduli spaces of solutions shows that $\Gamma$ satisfies condition (ii). This fact was previously proved in [4], which contains the description of an essentially equivalent map $\Gamma$.

The 1-parametric Floer–Morse problem is a count of Floer discs in $T^*M$ with two positive punctures and boundary on the zero section, followed by a Morse pseudo-gradient line in the loop space of M. It is obtained as a concatenation of 3 distinct 1-parametric Floer–Morse problems described by Fig. 5. On the first interval of parametrisation the underlying moduli space of curves is that of discs with 2 interior punctures and one boundary marked point, where the punctures and the marked point are requested to be aligned. At the negative end of the interval the 2 interior punctures collide and form a sphere bubble (this gives rise to the term $-\Psi \mu ^F$ in the expression of $[{\partial },\Gamma ]$), whereas at the positive end of the interval the second puncture collides with the marked point and gives rise to a disc bubble containing the marked point. In this configuration the interior punctures, the node and the marked point are all aligned. On the second interval of parametrisation, we allow the marked point to move clockwise towards the node. At the positive end of this interval the marked point collides with the node and forms a disc bubble. However, this disc bubble is constant because the 0-section is an exact Lagrangian, so that we directly replace the configuration by one where the marked point lies at the node. On the third and last interval of parametrisation, we insert length $T>0$ pseudo-gradient lines before imposing the incidence condition at the marked point. The positive end of this interval of parametrisation corresponds to $T=\infty$ and gives rise to the term $\mu (\Psi \otimes \Psi )$ in the expression of $[{\partial },\Gamma ]$.

In Fig. 5, the dashed lines represent pseudo-gradient flow lines for the energy functional on loop space. We only represent them in the last two configurations depicted in Fig. 5 in order not to burden excessively the drawing. However, the reader should be aware that such pseudo-gradient lines are also present in the first five configurations from Fig. 5.

For further reference, it is convenient to write

$$\begin{aligned} \Gamma =\Gamma _1+\Gamma _2+\Gamma _3, \end{aligned}$$

(22)

where $\Gamma _i$, $i=1,2,3$ corresponds to the count of elements in the 0-dimensional moduli spaces of solutions to the Floer–Morse problem restricted to the i-th interval of parametrisation for $\Gamma$.

Fig. 5

The map $\Gamma$

The remainder of this section is devoted to the proof of condition (iii). For this, we need to construct a chain homotopy

$$\begin{aligned} \Theta : FC_*(K) \rightarrow MC_*(E^{1/2})\otimes MC_*(E^{1/2}) \end{aligned}$$

satisfying $\Theta c^F=0$ and

$$\begin{aligned}{}[{\partial },\Theta ] = \lambda \Psi - (\Psi \otimes \Psi )\lambda ^F - (\Gamma \otimes \Psi )(1\otimes c_0^F) + (\Psi \otimes \Gamma )(\tau c_0^F\otimes 1). \end{aligned}$$

(23)

The map $\Theta$ will be defined by a count of Floer maps to $T^*M$ defined over a 2-parametric family of punctured annuli. In the first subsection, we describe the underlying moduli space of conformal annuli.

6.1 Conformal annuli

A (conformal) annulus is a compact genus zero Riemann surface with two boundary components. By the uniformisation theorem (see for example [12]), each annulus is biholomorphic to $[0,R]\times {\mathbb {R}}/{\mathbb {Z}}$ with its standard complex structure for a unique $R>0$ called its (conformal) modulus. The exponential map $s+it\mapsto e^{2\pi (s+it)}$ sends the standard annulus onto the annulus

$$\begin{aligned} A_R=\{z\in {\mathbb {C}}\mid 1\leqslant |z|\leqslant e^{2\pi R}\}\subset {\mathbb {C}}. \end{aligned}$$

It will be useful to consider slightly more general annuli in the Riemann sphere $S^2={\mathbb {C}}\cup \{\infty \}$. A circle in $S^2$ is the transverse intersection of $S^2\subset {\mathbb {R}}^3$ with a plane. We will call a disc in $S^2$ an open domain $D\subset S^2$ bounded by a circle, and an annulus in $S^2$ a set $\overline{D}\setminus D'$ for two discs $D,D'\subset S^2$ satisfying $\overline{D'}\subset D$ (with the induced complex structure).

Lemma 6.3

Every annulus A in $S^2$ of conformal modulus R can be mapped by a Möbius transformation onto the standard annulus $A_R\subset {\mathbb {C}}\subset S^2$ above.

Proof

Write $A=\overline{D}\setminus D'$ for discs $D,D'\subset S^2$. After applying a Möbius transformation, we may assume that D is the disc $\{z\in {\mathbb {C}}\mid |z|<e^{2\pi R}\}$. Let $D_1\subset D$ be the unit disc. There exists a Möbius transformation $\phi$ of D sending a point $z'\in {\partial }D'$ to a point $z_1\in {\partial }D_1$ and the positive tangent direction to ${\partial }D'$ at $z'$ to the positive tangent direction to ${\partial }D_1$ at $z_1$. Thus, $\phi$ sends ${\partial }D'$ to a circle tangent to ${\partial }D_1$ at $z_1$, and since the annuli $\overline{D}{\setminus } D'$ and $\overline{D}{\setminus } D_1$ both have modulus R, we must have $\phi ({\partial }D')={\partial }D_1$, hence $\phi (D')=D_1$. $\square$

For each R, the standard annulus $[0,R]\times {\mathbb {R}}/{\mathbb {Z}}$ carries two canonical foliations: one by the line segments $[0,R]\times \textrm{pt}$ and one by the circles $\textrm{pt}\times {\mathbb {R}}/{\mathbb {Z}}$. Moreover, these two foliations are invariant under the automorphism group of the annulus. Hence, by Lemma 6.3 each annulus in $S^2$ also carries two canonical foliations, one by circle segments connecting the two boundary components and one by circles, such that the foliations are orthogonal and the second one contains the two boundary loops. These two foliations can be intrinsically described as follows: the automorphism group of an annulus A is $\textrm{ Aut}(A)\simeq S^1$. The second foliation consists of the orbits of the $S^1$-action. The first foliation is the unique foliation orthogonal to the first one. Its leaves connect the two boundary components because this is the case for a standard annulus.

Figure 6 shows a 1-parametric family of annuli in ${\mathbb {C}}$ whose conformal moduli tend to 0 together with their canonical foliations. The domain at modulus 0 is the difference of two discs touching at one point, the node. Putting the node at the origin, the inversion $z\mapsto 1/z$ maps this domain onto a horizontal strip in ${\mathbb {C}}$ (with the node at $\infty$) with its standard foliations by straight line segments and lines. Opening up the node, we can conformally map it onto the standard disc with two boundary points corresponding to the node (since the map is not a Möbius transformation, the two foliations will not be by circle segments).

Fig. 6

Conformal annuli and their canonical foliations

Annuli with aligned marked points. The relevant domains for our purposes are annuli with 3 marked points, one interior and one on each boundary component. We require that the 3 points are aligned, by which we mean that they lie on the same leaf of the canonical foliation connecting the two boundary components. (In the next subsection, the interior marked point will correspond to the input from the Floer complex and the boundary marked points will be the initial points of the boundary loops on the zero section.)

Figure 7 shows the moduli space of such annuli with fixed finite conformal modulus. It is an interval over which the interior marked point moves from one boundary component to the other. Each end of the interval corresponds to a rigid nodal curve consisting of an annulus with one boundary marked point and a disc with an interior and a boundary marked point, where the marked point and the node are aligned in the annulus, and the two marked points and the node are aligned in the disc (i.e. they lie on a circle segment perpendicular to the boundary).

Fig. 7

Annuli with aligned marked points and fixed modulus

Figure 8 shows the moduli space of such annuli with varying conformal modulus. It is a pentagon in which we will view the two lower sides as being “horizontal” (although they meet at an actual corner). Then, in the vertical direction the conformal modulus increases from 0 (on the top side) to $\infty$ (on the two lower sides), while in the horizontal direction the interior marked point moves from one boundary component to the other. In all configurations the marked points and nodes are aligned. The interior nodes occurring along the bottom sides carry asymptotic markers (depicted as arrows) that are aligned with the boundary marked points. In particular, each interior node comes with an orientation reversing isomorphism between the tangent circles matching the asymptotic markers (this is the “decorated compactification”).

Fig. 8

Annuli with aligned marked points and varying modulus

6.2 Floer annuli

Now, we define a moduli space of Floer maps into $T^*M$ over the moduli space $\mathcal {P}$ of annuli in Fig. 8. For this, we choose a family of 1-forms $\beta _\tau$, $\tau \in \mathcal {P}$, with the following properties (see Fig. 9):

• $\textrm{d}\beta _\tau \leqslant 0$ for all $\tau$;

• $\beta _\tau$ equals $\textrm{d}t$ near the (positive) interior puncture, and $2\,\textrm{d}t$ in coordinates $(s,t)\in [0,{\varepsilon })\times {\mathbb {R}}/{\mathbb {Z}}$ near each (negative) boundary component, i.e. it has weights 1, 2, 2;

• on annuli of infinite modulus, $\beta _\tau$ has weights at the punctures (positive or negative) as shown in the figure.

Fig. 9

The hexagon of Floer annuli

In the figure, the (black) bottom circles are boundary components, (blue) intermediate circles are interior punctures (viewed as positive or negative when going upwards or downwards), and (red) numbers denote the weights. Such a family $\beta _\tau$ exists because on each component of each broken curve the sum of negative weights is greater or equal to the sum of positive weights.

The annuli carry two marked points on their boundary circles (depicted as black dashes) which are aligned with the interior puncture. Again, all interior punctures carry asymptotic markers (not drawn) that are aligned with the boundary marked points, also over broken curves and are matching across each pair of positive/negative punctures.

Note that the bottom corner of the pentagon in Fig. 8 has been replaced by a new side over which the underlying stable domain is fixed, but the weights at the positive/negative puncture vary as depicted with $a\in [-1,2]$. Thus, the conformal modulus is 0 along the top side, and $\infty$ along the three bottom sides.

We fix a nonnegative Hamiltonian $K:T^*M\rightarrow {\mathbb {R}}$ as in Sect. 3.2. For $\tau \in \mathcal {P}$, we denote by $\Sigma _\tau$ the corresponding (possibly broken) annulus with one positive interior puncture $z_+$ and two numbered boundary marked points $z_1,z_2$ on the boundary components $C_1,C_2$, equipped with the 1-form $\beta _\tau$. Given $x\in FC_*(K)$, we define the moduli space

$$\begin{aligned} \mathcal {P}(x) {:}{=} \{&(\tau ,u)\mid \tau \in \mathcal {P},\; u:\Sigma _\tau \rightarrow T^*M,\;(\textrm{d}u-X_K\otimes \beta _\tau )^{0,1}=0,\\ {}&u(z_+)=x,\;u(C_i)\subset M \text { for }i=1,2\}, \end{aligned}$$

where the condition $u(z_+)=x$ is understood as being $C^\infty$-convergence $u(s,\cdot )\rightarrow x$ as $s\rightarrow \infty$ in cylindrical coordinates $(s,t)\in [0,\infty )\times S^1$ near the positive puncture $z_+$. By Anosov [10], the restriction $u|_{C_i}$ can be uniquely parametrized over [0, 1] as an $H^1$-curve proportionally to arclength such that time 0 corresponds to the marked point $z_i$, $i=1,2$. Viewing $u|_{C_i}$ with these parametrisations thus yields a boundary evaluation map

$$\begin{aligned} \textrm{ev}_{\partial }:\mathcal {P}(x)\rightarrow \Lambda \times \Lambda ,\qquad (\tau ,u)\mapsto (u|_{C_1},u|_{C_2}). \end{aligned}$$

Note that this map is also canonically defined over the boundary of $\mathcal {P}$. Indeed, this is clear everywhere except possibly over the two vertical sides where one boundary loop is split into two. There one component of $\Sigma _\tau$ is an annulus without interior puncture, on which the map u is therefore constant (see the next subsection). Hence, in the split boundary loop, one component is constant, and we map it simply to the other component parametrized proportionally to arclength.

The expected dimension of $\mathcal {P}(x)$ is

$$\begin{aligned} \dim \mathcal {P}(x) = n\chi (\Sigma _\tau ) + \textrm{CZ}(x) + \dim \mathcal {P}= \textrm{CZ}(x) + 2 - n, \end{aligned}$$

where $\chi (\Sigma _\tau )=-1$ is the Euler characteristic of the punctured annulus. However, the moduli space $\mathcal {P}(x)$ is not transversely cut out over the vertical sides of $\mathcal {P}$. Indeed, the moduli space of non-punctured annuli appearing there has Fredholm index $n\chi (A) + 1=1$, where $\chi (A)=0$ is the Euler characteristic of the annulus A and the $+1$ corresponds to the varying conformal modulus. But the actual dimension of this space is $n+1$, where n is the dimension of the space of constant maps $A\rightarrow M$. In the following subsections, we explain how to achieve transversality by perturbing the Floer equation by a section in the obstruction bundle.

6.3 Moduli problems and obstruction bundles

To facilitate the discussion in the next subsection, we introduce in this subsection a general setup for moduli problems and obstruction bundles. Our notion of a moduli problem will be a slight generalisation of that of a G-moduli problem in [18] for the case of the trivial group G, which allows us to work with integer rather than rational coefficients.

A moduli problem is a quadruple $(\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$ with the following properties:

• $p:\mathcal {F}\rightarrow \mathcal {B}$ is a Banach fibre bundle over a Banach manifold;

• $\mathcal {Z}\subset \mathcal {F}$ is a Banach submanifold transverse to the fibres³;

• $\mathcal {S}:\mathcal {B}\rightarrow \mathcal {F}$ is a smooth section such that the solution set

  $$\begin{aligned} \mathcal {M}{:}{=} \mathcal {S}^{-1}(\mathcal {Z})\subset \mathcal {B}\end{aligned}$$

  is compact and for each $b\in \mathcal {M}$ the composed operator

  $$\begin{aligned} D_b\mathcal {S}:T_b\mathcal {B}{\mathop {\longrightarrow }\limits ^{T_b\mathcal {S}}}T_{\mathcal {S}(b)}\mathcal {F}\longrightarrow T_{\mathcal {S}(b)}\mathcal {F}/T_{\mathcal {S}(b)}\mathcal {Z}\end{aligned}$$

  is Fredholm with constant index $\textrm{ind}(\mathcal {S})=\textrm{ind}(D_b\mathcal {S})$, and its determinant bundle

  $$\begin{aligned} \det (\mathcal {S}) = \Lambda ^{\textrm{top}}\ker (D\mathcal {S})\otimes \Lambda ^\textrm{top}\textrm{ coker }(D\mathcal {S})^* \rightarrow \mathcal {M}\end{aligned}$$

  is oriented.

A morphism between moduli problems $(\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$ and $(\mathcal {B}',\mathcal {F}',\mathcal {S}',\mathcal {Z}')$ is a pair $(\psi ,\Psi )$ with the following properties:

• $\psi :\mathcal {B}\hookrightarrow \mathcal {B}'$ is a smooth embedding;

• $\Psi :\mathcal {F}\rightarrow \mathcal {F}'$ is a smooth injective bundle map covering $\psi$ such that

  $$\begin{aligned} \mathcal {S}'\circ \psi =\Psi \circ \mathcal {S},\qquad \mathcal {M}'=\psi (\mathcal {M}),\qquad \mathcal {Z}'=\Psi (\mathcal {Z}). \end{aligned}$$

  Moreover, the linear operators $T_b\psi :T_b\mathcal {B}\rightarrow T_{\psi (b)}\mathcal {B}'$ and $D_z\Psi :T_z\mathcal {F}/T_z\mathcal {Z}\rightarrow T_{\Psi (z)}\mathcal {F}/T_{\Psi (z)}\mathcal {Z}$ induce for each $b\in \mathcal {M}$ isomorphisms

  $$\begin{aligned} T_b\psi :\ker D_b\mathcal {S}\rightarrow \ker D_{\psi (b)}\mathcal {S}',\quad D_{\mathcal {S}(b)}\Psi :\textrm{ coker }D_b\mathcal {S}\rightarrow \textrm{ coker }D_{\psi (b)}\mathcal {S}' \end{aligned}$$

  such that the resulting isomorphism from $\det (\mathcal {S})$ to $\det (\mathcal {S}')$ is orientation preserving.

Proposition 6.4

Each moduli problem $(\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$ has a canonical Euler class

$$\begin{aligned} \chi (\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})\in H_{\textrm{ind}(\mathcal {S})}(\mathcal {B};{\mathbb {Z}}). \end{aligned}$$

Moreover, if $(\psi ,\Psi )$ is a morphism between moduli problems $(\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$ and $(\mathcal {B}',\mathcal {F}',\mathcal {S}',\mathcal {Z}')$, then $\textrm{ind}(\mathcal {S})=\textrm{ind}(\mathcal {S}')$ and

$$\begin{aligned} \psi _*\bigl (\chi (\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})\bigr )=\chi (\mathcal {B}',\mathcal {F}',\mathcal {S}',\mathcal {Z}')\in H_{\textrm{ind}(\mathcal {S})}(\mathcal {B}';{\mathbb {Z}}). \end{aligned}$$

Proof

This follows directly from the corresponding results in [18]. To construct the Euler class, we compactly perturb $\mathcal {S}$ to a section ${\widetilde{\mathcal {S}}}$ which is transverse to $\mathcal {Z}$; then ${\widetilde{\mathcal {M}}}={\widetilde{\mathcal {S}}}^{-1}(\mathcal {Z})$ is a compact manifold of dimension $d=\textrm{ind}(\mathcal {S})$ which inherits a canonical orientation and thus represents a class in $H_d(\mathcal {B};{\mathbb {Z}})$, and it is easy to see that this class is independent of the choice of perturbation. The assertion about morphisms is obvious. $\square$

A special case of a moduli problem arises if $\mathcal {F}=\mathcal {E}\rightarrow \mathcal {B}$ is a Banach vector bundle and $\mathcal {Z}=\mathcal {Z}_\mathcal {E}$ is the zero section in $\mathcal {E}$. In this case $D_b\mathcal {S}$ is the vertical differential of $\mathcal {S}$ at $b\in \mathcal {M}=\mathcal {S}^{-1}(0)$ and we arrive at the usual notion of a Fredholm section. This is the setup considered in [18]; the general case can be reduced to this one (via a morphism of moduli problems) by passing to the normal bundle of $\mathcal {Z}$.

Consider now a moduli problem $(\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$ such that

• (i) $\mathcal {M}=\mathcal {S}^{-1}(\mathcal {Z})\subset \mathcal {B}$ is a smooth submanifold, and

• (ii) $\ker (D_b\mathcal {S})=T_b\mathcal {M}$ for each $b\in \mathcal {M}$.

Then, the cokernels $\textrm{ coker }(D_b\mathcal {S})$ fit together into the smooth obstruction bundle

$$\begin{aligned} \mathcal {O}{:}{=} \textrm{ coker }(D\mathcal {S})\rightarrow \mathcal {M}\end{aligned}$$

whose rank is related to the Fredholm index of $\mathcal {S}$ by

$$\begin{aligned} \dim \mathcal {M}= \textrm{ind}(\mathcal {S}) + \textrm{rk}\,\mathcal {O}. \end{aligned}$$

We thus obtain a finite-dimensional moduli problem $(\mathcal {M},\mathcal {O},0,\mathcal {Z}_\mathcal {O})$, where $0:\mathcal {M}\rightarrow \mathcal {O}$ denotes the zero section and $\mathcal {Z}_\mathcal {O}\subset \mathcal {O}$ its graph.

Lemma 6.5

In the preceding situation, there exists a canonical morphism of moduli problems

$$\begin{aligned} (\iota ,\exp ):(\mathcal {M},\mathcal {O},0,\mathcal {Z}_\mathcal {O})\rightarrow (\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z}), \end{aligned}$$

where $\psi =\iota :\mathcal {M}\hookrightarrow \mathcal {B}$ is the inclusion and $\exp :\mathcal {O}\hookrightarrow \mathcal {F}$ is a fibrewise exponential map.

Proof

Choose $\mathcal {N}\rightarrow \mathcal {Z}$ a smooth Banach vector bundle such that for each $z\in \mathcal {Z}$,

$$\begin{aligned} \mathcal {N}_z\subset T_z\mathcal {F}_{p(z)}\quad \text {and}\quad T_z\mathcal {F}=T_z\mathcal {Z}\oplus \mathcal {N}_z. \end{aligned}$$

Since $\mathcal {N}$ represents the normal bundle to $\mathcal {Z}$ in $\mathcal {F}$, we can assume that $D\mathcal {S}$ takes values in $\mathcal {N}$ and $\mathcal {O}$ is a subbundle of $\mathcal {N}$ complementary to $\textrm{im}\,D\mathcal {S}$. Pick a fibrewise Riemannian metric on $\mathcal {F}$ whose exponential map restricts to a fibre preserving embedding

$$\begin{aligned} \exp :\mathcal {O}\hookrightarrow \mathcal {F},\qquad \mathcal {O}_z\hookrightarrow \mathcal {F}_{p(z)}. \end{aligned}$$

Now, it is easy to check that $(\iota ,\exp )$ with the inclusion $\iota :\mathcal {M}\hookrightarrow \mathcal {B}$ defines a morphism $(\mathcal {M},\mathcal {O},0,\mathcal {Z}_\mathcal {O})\rightarrow (\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$. $\square$

In the situation of Lemma 6.5, the Euler class of $(\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$ is therefore represented by the zero set $\eta ^{-1}(0)$ of a section $\eta :\mathcal {M}\rightarrow \mathcal {O}$ in the obstruction bundle which is transverse to the zero section. Concretely, keeping the notation from the proof, $\exp \circ \eta$ defines a section of the fibre bundle $\mathcal {F}|_\mathcal {M}\rightarrow \mathcal {M}$. We extend the bundle $\mathcal {O}\rightarrow \mathcal {M}$ to a bundle ${\widetilde{\mathcal {O}}}\rightarrow {\widetilde{\mathcal {B}}}$ on a neighbourhood ${\widetilde{\mathcal {B}}}\subset \mathcal {B}$ of $\mathcal {M}$ and $\eta$ to a section ${\widetilde{\eta }}$ of the bundle ${\widetilde{\mathcal {O}}}\rightarrow {\widetilde{\mathcal {B}}}$ vanishing near the boundary of ${\widetilde{\mathcal {B}}}$. Then, the perturbed section ${\widetilde{\mathcal {S}}}=\mathcal {S}+\exp \circ {\widetilde{\eta }}$ of $\mathcal {F}\rightarrow \mathcal {B}$ is transverse to $\mathcal {Z}$ and its solution set ${\widetilde{\mathcal {S}}}^{-1}(\mathcal {Z})$ represents the Euler class of $(\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$.

Remark 6.6

(orientations) In the situation of Lemma 6.5, we are given an orientation of

$$\begin{aligned} \det (\mathcal {S}) = \Lambda ^{\textrm{top}}T\mathcal {M}\otimes \Lambda ^\textrm{top}\mathcal {O}^*. \end{aligned}$$

(24)

Let now $\eta :\mathcal {M}\rightarrow \mathcal {O}$ be a section transverse to the zero section. Its zero set $\mathcal {A}{:}{=}\eta ^{-1}(0)\subset \mathcal {M}$ is a submanifold and at each $b\in \mathcal {A}$ the linearisation $D_b\eta :T_b\mathcal {M}\rightarrow \mathcal {O}_b$ is surjective with kernel $\ker D_b\eta =T_b\mathcal {A}$, so we get a canonical isomorphism of line bundles

$$\begin{aligned} \Lambda ^{\textrm{top}}T\mathcal {M}|_\mathcal {A}\cong \Lambda ^{\textrm{top}}T\mathcal {A}\otimes \Lambda ^\textrm{top}\mathcal {O}|_\mathcal {A}\rightarrow \mathcal {A}. \end{aligned}$$

Combined with (24) this yields a canonical isomorphism

$$\begin{aligned} \Lambda ^{\textrm{top}}T\mathcal {A}\cong \det (\mathcal {S})|_\mathcal {A}, \end{aligned}$$

so an orientation of $\det (\mathcal {S})$ induces an orientation of $\mathcal {A}$. In the case $\textrm{ind}(\mathcal {S})=0$ this can be made more explicit as follows. Then, $\textrm{rk}\,\mathcal {O}=\dim \mathcal {M}$ and an orientation of $\det (\mathcal {S})$ induces an isomorphism

$$\begin{aligned} \Lambda ^{\textrm{top}}T\mathcal {M}\cong \Lambda ^{\textrm{top}}\mathcal {O}. \end{aligned}$$

For $b\in \eta ^{-1}(0)$, we define the sign $\sigma (b)$ to be $+1$ if the isomorphism $D_b\eta :T_b\mathcal {M}{\mathop {\longrightarrow }\limits ^{\cong }}\mathcal {O}_b$ preserves orientations, and $-1$ otherwise. Then, the signed count

$$\begin{aligned} \chi (\mathcal {O}) = \sum _{b\in \eta ^{-1}(0)}\sigma (b) \end{aligned}$$

is the Euler number of the obstruction bundle $\mathcal {O}\rightarrow \mathcal {M}$.

Finally, consider a moduli problem $(\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$ which splits as follows:

• $p=(p_0,p_1):\mathcal {F}=\mathcal {F}_0\times _{\mathcal {B}}\mathcal {F}_1\rightarrow \mathcal {B}$;

• $\mathcal {Z}=\mathcal {Z}_0\times _{\mathcal {B}}\mathcal {Z}_1$;

• $\mathcal {S}=\mathcal {S}_0\times \mathcal {S}_1$ for sections $\mathcal {S}_i:\mathcal {B}\rightarrow \mathcal {F}_i$ such that $\mathcal {S}_1$ is transverse to $\mathcal {Z}_1$.

Lemma 6.7

In the situation above, there exists a reduced moduli problem

$$\begin{aligned} (\overline{\mathcal {B}},\overline{\mathcal {F}},\overline{\mathcal {S}},\overline{\mathcal {Z}})=\bigl (\mathcal {S}_1^{-1}(\mathcal {Z}_1),\mathcal {F}_0|_{\overline{\mathcal {B}}},\mathcal {S}_0|_{\overline{\mathcal {B}}}, \mathcal {Z}_0|_{\overline{\mathcal {B}}}\bigr ) \end{aligned}$$

and a morphism $(\psi ,\Psi )$ of moduli problems from $(\overline{\mathcal {B}},\overline{\mathcal {F}},\overline{\mathcal {S}},\overline{\mathcal {Z}})$ to $(\mathcal {B},\mathcal {F},\mathcal {S},\mathcal {Z})$, with $\psi :\overline{\mathcal {B}}\hookrightarrow \mathcal {B}$ the inclusion and $\Psi (f_0)=\bigl (f_0,S_1\circ p_0(f_0)\bigr )$.

Proof

Since $\mathcal {S}_1$ is transverse to $\mathcal {Z}_1$, it follows that $\overline{\mathcal {B}}\subset \mathcal {B}$ is a submanifold and $(\overline{\mathcal {B}},\overline{\mathcal {F}},\overline{\mathcal {S}},\overline{\mathcal {Z}})$ defines a moduli problem. Now, it follows directly from the definitions that $(\psi ,\Psi )$ as in the lemma induces for $b\in \overline{\mathcal {B}}$ the canonical identities

$$\begin{aligned} T_b\psi :\ker D_b\overline{\mathcal {S}}= \ker D_b\mathcal {S}_0\cap \ker D_b\mathcal {S}_1 = \ker D_{\psi (b)}\mathcal {S},\\ D_{\overline{\mathcal {S}}(b)}\Psi :\textrm{ coker }D_b\overline{\mathcal {S}}= \textrm{ coker }(D_b\mathcal {S}_0|_{\ker D_b\mathcal {S}_1}) = \textrm{ coker }D_{\psi (b)}\mathcal {S}, \end{aligned}$$

hence it defines a morphism of moduli problems. $\square$

6.4 Constant Floer annuli

In this subsection, we apply the results of the previous subsection to moduli spaces of annuli. We begin with a rather general setup. Let $(\Sigma ,j)$ be a compact Riemann surface with boundary, and (V, J) be an almost complex manifold with a half-dimensional totally real submanifold $L\subset V$. For $m\in {\mathbb {N}}$ and $p\in {\mathbb {R}}$ with $mp>2$, we consider the Banach manifold

$$\begin{aligned} \mathcal {B}= W^{m,p}\bigl ((\Sigma ,{\partial }\Sigma ),(V,L)\bigr ) \end{aligned}$$

and the Banach space bundle $\mathcal {E}\rightarrow \mathcal {B}$ whose fibre over $u\in \mathcal {B}$ is

$$\begin{aligned} \mathcal {E}_u = W^{m-1,p}\bigl (\Sigma ,\textrm{Hom}^{0,1}(T\Sigma ,u^*TV)\bigr ). \end{aligned}$$

Denote $\mathcal {Z}_\mathcal {E}$ the zero section. The Cauchy–Riemann operator

$$\begin{aligned} \overline{\partial }u = (\textrm{d}u)^{0,1} = \frac{1}{2}\bigl (\textrm{d}u+J(u)\circ \textrm{d}u\circ j\bigr ) \end{aligned}$$

defines a Fredholm section $\overline{\partial }:\mathcal {B}\rightarrow \mathcal {E}$. Assuming a setup in which the space of solutions $\overline{\partial }^{-1}(\mathcal {Z}_\mathcal {E})$ is compact (e.g. if J is tamed by an exact symplectic structure on V, the totally real submanifold L is exact Lagrangian, and $\Sigma$ has a compact group of automorphisms), we obtain a moduli problem $(\mathcal {B},\mathcal {E},{\bar{\partial }},\mathcal {Z}_\mathcal {E})$.

Constant annuli of positive modulus. Now, we apply the preceding discussion to the moduli space of constant annuli appearing in the previous subsection. Consider a fixed annulus $(\Sigma ,j)$ of finite conformal modulus $R>0$, equipped with a 1-form $\beta$ as above satisfying $\textrm{d}\beta \leqslant 0$ and $\beta =2\textrm{d}t$ in cylindrical coordinates near the two (negative) boundary loops. Let K be the nonnegative Hamiltonian from Sect. 3.2. Then, the Floer operator $\overline{\partial }_Ku{:}{=}(\textrm{d}u-X_K\otimes \beta )^{0,1}$ defines a Fredholm section in the appropriate bundle $\mathcal {E}\rightarrow \mathcal {B}$ over the Banach manifold

$$\begin{aligned} \mathcal {B}= W^{m,p}\bigl ((\Sigma ,{\partial }\Sigma ),(T^*M,M)\bigr ). \end{aligned}$$

We denote its zero set by $\mathcal {M}{:}{=}\overline{\partial }_K^{-1}(0)$. For $u\in \mathcal {M}$ the usual energy estimate (see e.g. [34]) gives

$$\begin{aligned} E(u) = \frac{1}{2}\int _\Sigma |\textrm{d}u-X_K(u)\otimes \beta |^2\textrm{vol}_\Sigma \leqslant - A_{2K}(u|_{{\partial }\Sigma }) = 0, \end{aligned}$$

where the Hamiltonian action of $u|_{{\partial }\Sigma }$ vanishes because both the Liouville form and the Hamiltonian K vanish on the zero section M. This implies that $\textrm{d}u-X_K(u)\otimes \beta \equiv 0$. Since $X_K$ vanishes near the zero section, it follows that $\textrm{d}u\equiv 0$ near ${\partial }\Sigma$ and therefore, by unique continuation, u is constant equal to a point in M. Hence, the moduli space

$$\begin{aligned} \mathcal {M}= M \end{aligned}$$

consists of points in M, viewed as constant maps $\Sigma \rightarrow M$. Since $X_K$ vanishes near the zero section, the Floer operator $\overline{\partial }_K$ agrees with the Cauchy–Riemann operator $\overline{\partial }$ near $\mathcal {M}$, so we can and will replace $\overline{\partial }_K$ by $\overline{\partial }$ in the following discussion of obstruction bundles.

We identify $\Sigma$ with the standard annulus $[0,R]\times {\mathbb {R}}/{\mathbb {Z}}$ and its trivial tangent bundle $T\Sigma = \Sigma \times {\mathbb {C}}$. Consider a point $u\in M$, viewed as a constant map $u:\Sigma \rightarrow M$. We identify

$$\begin{aligned} T_u^*M= {\mathbb {R}}^n,\qquad T_uM=i{\mathbb {R}}^n,\qquad T_u(T^*M)={\mathbb {C}}^n. \end{aligned}$$

Then, we have

$$\begin{aligned} T_u\mathcal {B}&= W^{m,p}\bigl ((\Sigma ,{\partial }\Sigma ),({\mathbb {C}}^n,i{\mathbb {R}}^n)\bigr ), \\ \mathcal {E}_u&= W^{m-1,p}\bigl (\Sigma ,\textrm{Hom}^{0,1}({\mathbb {C}},{\mathbb {C}}^n)\bigr ) = W^{m-1,p}(\Sigma ,{\mathbb {C}}^n), \end{aligned}$$

where for the last equality, we use the canonical isomorphism

$$\begin{aligned} \textrm{Hom}^{0,1}({\mathbb {C}},{\mathbb {C}}^n){\mathop {\longrightarrow }\limits ^{\cong }}{\mathbb {C}}^n,\qquad \eta \mapsto \eta ({\partial }_s). \end{aligned}$$

With these identifications, the linearized Cauchy–Riemann operator reads

$$\begin{aligned} D_u\overline{\partial }:W^{m,p}\bigl ((\Sigma ,{\partial }\Sigma ),({\mathbb {C}}^n,i{\mathbb {R}}^n)\bigr ) \rightarrow W^{m-1,p}(\Sigma ,{\mathbb {C}}^n),\qquad \xi \mapsto {\partial }_s\xi +i{\partial }_t\xi . \end{aligned}$$

An easy computation using Fourier series (see [14]) shows that

$$\begin{aligned} \ker (D_u\overline{\partial })=i{\mathbb {R}}^n=T_uM,\qquad \textrm{ coker }(D_u\overline{\partial })={\mathbb {R}}^n=T_u^*M. \end{aligned}$$

Therefore, the Cauchy–Riemann operator, and thus the Floer operator, satisfies conditions (i) and (ii) in the previous subsection with the obstruction bundle

$$\begin{aligned} \mathcal {O}=\textrm{ coker }(D\overline{\partial }_K)\cong T^*M\rightarrow M=\mathcal {M}, \end{aligned}$$

and Lemma 6.5 implies

Corollary 6.8

In the preceding situation, there exists a canonical morphism of moduli problems

$$\begin{aligned} (\iota ,I):(M,T^*M,0,\mathcal {Z}_{T^*M})\rightarrow (\mathcal {B},\mathcal {E},\overline{\partial },\mathcal {Z}_{\mathcal {E}}), \end{aligned}$$

where $\iota :M\hookrightarrow \mathcal {B}$ is the inclusion as constant maps and I converts a cotangent vector into a constant (0, 1)-form. $\square$

Note in particular that $\overline{\partial }_K$ has index zero. A section in the obstruction bundle transverse to the zero section corresponds under the isomorphism $\mathcal {O}\cong T^*M$ to a 1-form $\eta$ on M with nondegenerate zeroes $p_1,\dots ,p_k$, and the zero set of the perturbed Floer operator $\overline{\partial }_K+{\widetilde{\eta }}$ consists of $p_1,\dots p_k$ viewed as constant maps $\Sigma \rightarrow M$. Having chosen the orientation of $\det ({\bar{\partial }})$ to be induced by the canonical isomorphism $TM\cong T^*M$, we obtain that the signed count

$$\begin{aligned} \sum _{i=1}^k\sigma (p_i) = \chi (T^*M) \end{aligned}$$

agrees with the Euler number of $T^*M$. Note that the Euler number of $T^*M$ equals the Euler characteristic of M (this follows from the canonical isomorphism $T^*M\cong TM$ and the Poincaré–Hopf theorem).

Constant annuli of modulus zero. Annuli of conformal modulus zero can be viewed as moduli problems in two equivalent ways. For the first view, we take as domain the compact region $A\subset {\mathbb {C}}$ bounded by two circles touching at one point, the node. Given (V, J) and $L\subset V$ as above, we, therefore, obtain a moduli problem $(\mathcal {B}^A,\mathcal {E}^A,\mathcal {S}^A,\mathcal {Z}_{\mathcal {E}^A})$ with

$$\begin{aligned} \mathcal {B}^A = W^{m,p}\bigl ((A,{\partial }A),(V,L)\bigr ),\quad \mathcal {E}^A_u = W^{m-1,p}\bigl (A,\textrm{Hom}^{0,1}(TA,u^*TV)\bigr ), \end{aligned}$$

the Cauchy–Riemann operator $\mathcal {S}^A=\overline{\partial }^A$, and the zero section $\mathcal {Z}_{\mathcal {E}^A}\subset \mathcal {E}^A$.

For the second view, we take as domain the closed unit disc $D\subset {\mathbb {C}}$ with $\pm i$ viewed as nodal points which are identified. This gives rise to a moduli problem $(\mathcal {B}^D,\mathcal {F}^D,\mathcal {S}^D,\mathcal {Z}^D)$ with

$$\begin{aligned} \mathcal {B}^D&= W^{m,p}\bigl ((D,{\partial }D),(V,L)\bigr ),\\ \mathcal {F}^D&= \mathcal {E}^D\times (L\times L),\qquad \mathcal {E}^D_u = W^{m-1,p}\bigl (D,\textrm{Hom}^{0,1}(TD,u^*TV)\bigr ),\\ \mathcal {S}^D&= \overline{\partial }^D\times \textrm{ev}:\mathcal {B}^D\rightarrow \mathcal {E}^D\times (L\times L),\qquad \textrm{ev}(u)=\bigl (u(i),u(-i)\bigr ),\\ \mathcal {Z}^D&= \mathcal {Z}_{\mathcal {E}^D}\times \Delta ,\qquad \Delta =\{(q,q)\mid q\in L\}\subset L\times L. \end{aligned}$$

Note that the indices of the two moduli problems agree,

$$\begin{aligned} \textrm{ind}(\mathcal {S}^D) = \textrm{ind}(\overline{\partial }^D)-n = \textrm{ind}(\mathcal {S}^A). \end{aligned}$$

Let $\phi :D\rightarrow A$ be a continuous map which maps $\pm i$ onto the nodal point and is otherwise one-to-one, and which is biholomorphic in the interior.⁴ Then, composition with $\phi$ defines a diffeomorphism

$$\begin{aligned} \mathcal {B}^D\supset \textrm{ev}^{-1}(\Delta )\cong \mathcal {B}^A \end{aligned}$$

(where we use as area form on A the pullback under $\phi$ of an area form on D). Since $\textrm{ev}:\mathcal {B}^D\rightarrow L\times L$ is transverse to the diagonal $\Delta$, we are in the situation of Lemma 6.7. We conclude that there exists a morphism of moduli problems

$$\begin{aligned} (\psi ,\Psi ):(\mathcal {B}^A,\mathcal {E}^A,\mathcal {S}^A,\mathcal {Z}_{\mathcal {E}^A})\rightarrow (\mathcal {B}^D,\mathcal {F}^D,\mathcal {S}^D,\mathcal {Z}^D), \end{aligned}$$

where $\psi :\mathcal {B}^A=\textrm{ev}^{-1}(\Delta )\hookrightarrow \mathcal {B}^D$ is the inclusion and $\Psi (u;\eta )=\bigl (u;\eta ,\textrm{ev}(u)\bigr )$.

Now, we specialise to the case $(V,L) = (T^*M,M)$ with its canonical almost complex structure J. Then, both solution spaces $\mathcal {M}^A=(\overline{\partial }^A)^{-1}(0)$ and $\mathcal {M}^D=(\mathcal {S}^D)^{-1}(\mathcal {Z}^D)=(\overline{\partial }^D)^{-1}(0)=M$ consist of constant maps to M. Moreover, in view of the preceding discussion and the fact that the Cauchy–Riemann operator $\overline{\partial }^D:\mathcal {B}^D\rightarrow \mathcal {E}^D$ over the disc is transverse to the zero section, they both satisfy the hypotheses (i) and (ii) of Lemma 6.5, so combined with the preceding discussion, we obtain

Corollary 6.9

There exists a commuting diagram of morphisms of moduli problems

where $\iota ^A:M\hookrightarrow \mathcal {B}^A$ and $\iota ^D:M\hookrightarrow \mathcal {B}^D$ are the inclusions as constant maps, the bundle $M\times M\rightarrow M$ is given by projection onto the first factor, and $\exp :T^*M\rightarrow M\times M$ is the composition of the isomorphism $T^*M\cong TM$ induced by a metric on M with the exponential map $TM\rightarrow M\times M$. Thus, the Euler class of each of these moduli problems is represented by the nondegenerate zeroes $p_1,\dots ,p_k$ of a 1-form $\eta$ on M (or equivalently, of a vector field v on M), with signs that add up (up to a global sign) to the Euler characteristic $\chi$ of M. $\square$

6.5 Proof of Theorem 6.1

Now, we can conclude the proof of Theorem 6.1.

For $x\in FC_*(K)$ consider the moduli space $\mathcal {P}(x)$ of Floer annuli described in Sect. 6.2 with its boundary evaluation map $\textrm{ev}_{\partial }:\mathcal {P}(x)\rightarrow \Lambda \times \Lambda$. Pick a 1-form $\eta$ on M with nondegenerate zeroes $p_1,\dots ,p_k$. As in Sect. 6.4, we view $\eta$ as a section of the obstruction bundle over the vertical sides of the hexagon in Fig. 9. We extend this section by a cutoff function to a section ${\widetilde{\eta }}$ over the whole hexagon and add it as a right hand side to the Floer equation. We choose the data such that the moduli space $\mathcal {P}(x)$ is transversely cut out, and thus defines a compact manifold with corners of dimension $\textrm{CZ}(x)+2-n$.

We may assume without loss of generality that M is connected. We pick a $C^2$-small Morse function $V:M\rightarrow {\mathbb {R}}$ with a unique maximum at $q_0\in M$ such that $p_1,\dots ,p_k$ flow to $q_0$ under the positive gradient flow of V. Let $MC_*(S)$ denote the Morse complex of the perturbed energy functional

$$\begin{aligned} S:\Lambda \rightarrow {\mathbb {R}},\qquad S(q){:}{=}\int _0^1\bigl (|\dot{q}|^2-V(q)\bigr )\textrm{d}t \end{aligned}$$

(note that there is no factor 1/2 in front of $|\dot{q}|^2$). For $x\in FC_*(K)$ and $a,b\in MC_*(S)$, we define

$$\begin{aligned} \mathcal {P}(x;a,b) {:}{=} \{(\tau ,u)\in \mathcal {P}(x)\mid \textrm{ev}_{\partial }(u)\in W^+(a)\times W^+(b)\}, \end{aligned}$$

where $W^+(a)$ is the stable manifold of a with respect to the negative pseudo-gradient flow of S. Recall that the boundary evaluation map involves reparametrisation of the boundary loops proportionally to arclength. For generic choices, these are manifolds of dimension

$$\begin{aligned} \dim \mathcal {P}(x;a,b) = \textrm{CZ}(x)-\textrm{ind}(a)-\textrm{ind}(b)+2-n. \end{aligned}$$

If the dimension is 0 these spaces are compact and their signed counts

$$\begin{aligned} \Theta _1(x) {:}{=} \sum _{a,b}\#\mathcal {P}_{\dim =0}(x;a,b)\,a\otimes b \end{aligned}$$

define a degree $2-n$ map

$$\begin{aligned} \Theta _1: FC_*(K)\rightarrow MC_*(S)\otimes MC_*(S). \end{aligned}$$

Next, we consider a 1-dimensional moduli space $\mathcal {P}_{\dim =1}(x;a,b)$ and compute its boundary. Besides splitting off index 1 Floer cylinders and negative pseudo-gradient flow lines, which give rise to the term $[{\partial },\Theta _1]$, there are contributions from the sides of the hexagon in Fig. 9 which we analyse separately. Note that the indices now satisfy

$$\begin{aligned} \textrm{CZ}(x)-\textrm{ind}(a)-\textrm{ind}(b)=n-1. \end{aligned}$$

Vertical left side: Here, the broken curves consist of a half-cylinder attached at a boundary node to an annulus without interior puncture, where the two boundary loops flow into a, b under the negative pseudo-gradient flow of S. By the discussion in Sect. 6.4 the moduli space of annuli is $[0,\infty ]\times \eta ^{-1}(0)$, where $[0,\infty ]$ encodes the conformal modulus and $\eta ^{-1}(0)$ consists of the points $p_1,\dots ,p_k$ (with signs $\sigma (p_i)$). In particular, we must have $b=q_0$ and therefore $\textrm{ind}(b)=\textrm{ind}(q_0)=0$. The half-cylinders belong to the moduli space

$$\begin{aligned} \mathcal {M}(x;a) = \{&u:[0,\infty )\times S^1\rightarrow T^*M\mid (\textrm{d}u-X_K\otimes \beta )^{0,1}={\widetilde{\eta }},\\ {}&u(\infty ,\cdot )=x,\ u(0,\cdot )\in W^+(a)\}. \end{aligned}$$

They carry a boundary nodal point which is aligned with the boundary marked point (0, 0) and the puncture at $\infty$, and is therefore given by (0, 1/2). The evaluation at the nodal point defines an evaluation map

$$\begin{aligned} \textrm{ev}_{1/2}:\mathcal {M}(x;a)\rightarrow M,\qquad u\mapsto u(0,1/2). \end{aligned}$$

For the broken curve to exist this evaluation map must meet one of the constant annuli, i.e. one of the points $p_1,\dots ,p_k\in M$, which generically does not happen because

$$\begin{aligned} \dim \mathcal {M}(x;a) = \textrm{CZ}(x)-\textrm{ind}(a) = n-1. \end{aligned}$$

Hence, the vertical left side gives no contribution to the boundary.

Vertical right side: Similarly, the vertical right side gives no contribution to the boundary.

Lower left side: Here, the broken curves consist of a disc with two interior punctures, one positive and one negative, attached at its negative puncture to the positive puncture of a half-cylinder along an orbit in $FC_*(-K)$, where the two boundary loops flow into a, b under the negative pseudo-gradient flow of S. By choosing the 1-form $\beta$ equal to $\textrm{d}t$ on a long cylindrical piece of the half-cylinder, we can achieve that these half-cylinders are in one-to-one correspondence with broken curves consisting of a cylinder with weights $(-1,1)$ and a half-cylinder with weights (1, 2), as shown in the middle of Fig. 10. Reinterpreting these curves as on the right of that figure, we see that their count corresponds to the composition $-(\Gamma _1\otimes \Psi )(1\otimes c_0^F)$, where we recall that $\Gamma _1$ denotes the first term in the expression $\Gamma =\Gamma _1+\Gamma _2+\Gamma _3$ from (22).

Fig. 10

Degenerating the half-cylinders

Lower right side: Similarly, the contribution from the lower right side corresponds to the composition $(\Psi \otimes \Gamma _1)(c_0^F\otimes 1)$.

The discussion so far shows that

$$\begin{aligned}{}[{\partial },\Theta _1] = (\Psi \otimes \Gamma _1)(\tau c_0^F\otimes 1) -(\Gamma _1\otimes \Psi )(1\otimes c_0^F) + \Theta ^{\textrm{top}} + \Theta ^{\textrm{bottom}}, \end{aligned}$$

(25)

where $\Theta ^{\textrm{top}}$ and $\Theta ^{\textrm{bottom}}$ are the degree $1-n$ maps arising from the contributions of the top and bottom sides of the hexagon to the boundary of $\mathcal {P}_{\dim =1}(x;a,b)$ which we discuss next.

Bottom side: The family of broken curves on the bottom side can be deformed in an obvious way to the family of broken curves shown in Fig. 11. Since the half-cylinders with weights (2, 2) define the map $\Psi$ and the family of 3-punctured spheres above them defines the continuation coproduct $\lambda ^F$ from Sect. 3.2, this shows that $\Theta ^{\textrm{bottom}}$ is equal to $-(\Psi \otimes \Psi )\lambda ^F$.

Fig. 11

Degenerating the curves on the bottom side

Top side: The family on the top side of the hexagon consists of punctured annuli of modulus 0, i.e. punctured discs with two nodal points on the boundary that are identified to a node. Moreover, the boundary carries two marked points that are separated by the nodal points and aligned with the interior puncture. We wish to relate this family to the loop coproduct, but for this we face two problems: First, the boundary loops carry two marked points whereas the loops for the loop coproduct carry only one (the initial time $t=0$); and second, the self-intersection of the boundary loop occurs at the nodal points and not at one of the marked points.

Both problems are resolved simultaneously as follows. We enlarge this 1-parametric family to a 2-parametric family in which we keep the two boundary marked points aligned, but drop the condition that the interior puncture is aligned with them. The 2-parametric family forms the hexagon shown in Fig. 12. Here, the interior puncture is depicted as a cross, the aligned boundary marked points as endpoints of a dashed line, and the nodal points as thick dots. The bottom side of the hexagon (drawn in black) corresponds to the 1-parametric family on the top side of Fig. 9. Note that here we made a choice by letting the interior puncture move freely above the dashed line connecting the two boundary marked points; we could equally well have taken the mirror hexagon where the interior puncture moves below the dashed line.

Fig. 12

Floer annuli of modulus zero

The hexagon in Fig. 12 defines a deformation from the bottom (black) side to the top side (drawn in red). The configurations in this figure are to be interpreted as follows.

$\bullet$ Each configuration has two boundary loops obtained by going around in the counterclockwise direction: the first loop from the bottom to the top nodal point, and the second one from the top to the bottom nodal point. Each boundary loop carries a marked point. As before, each boundary loop of the zero section is reparametrized proportionally to arclength and then flown into a critical point on $\Lambda$ under the negative pseudo-gradient flow of the functional $S:\Lambda \rightarrow {\mathbb {R}}$.

$\bullet$ In each configuration, the unique component carrying the interior puncture (which may be nonconstant) is drawn as a large disc, so the small discs are all constant. In particular, each small disc carrying the two nodal points is a constant annulus of modulus zero. Under the perturbation of the Cauchy–Riemann equation described in Corollary 6.9, such a component lands on the transverse zeroes $p_1,\dots ,p_k$ of a 1-form $\eta$ and further flows into the basepoint $q_0$. In particular, since the signs add up to $\chi$ we have that all configurations on the upper and lower left sides land in $R\chi q_0\otimes MC_*(S)$, while those on the upper and lower right sides land in $MC_*(S)\otimes R\chi q_0$. The upper and lower left sides therefore compute $-(\Gamma _2\otimes \Psi )(1\otimes c_0^F)$, whereas the lower and upper right sides compute $(\Psi \otimes \Gamma _2)(\tau c_0^F\otimes 1)$, with $\Gamma _2$ being the second term in (22).

Thus, the hexagon in Fig. 12 provides a chain homotopy $\Theta _2$ from $\Theta ^{\textrm{top}}$ (defined by the bottom side) to the operation ${\widetilde{\Theta }}^{\textrm{top}} + (\Psi \otimes \Gamma _2)(\tau c_0^F\otimes 1) -(\Gamma _2\otimes \Psi )(1\otimes c_0^F)$, where ${\widetilde{\Theta }}^{\textrm{top}}$ is defined by the top side, i.e.

$$\begin{aligned}{}[{\partial },\Theta _2]= {\widetilde{\Theta }}^{\textrm{top}} + (\Psi \otimes \Gamma _2)(\tau c_0^F\otimes 1) -(\Gamma _2\otimes \Psi )(1\otimes c_0^F) - \Theta ^{\textrm{top}}. \end{aligned}$$

(26)

$\bullet$ Consider now the top side. Since both marked points and the black nodal point lie on the same constant component, we can remove this component and replace the three points by one nodal/marked point as shown in Fig. 13.

Fig. 13

Interpreting the curves on the top side

The boundary of these configurations consists of loops $q:[0,1]\rightarrow M$ with one (black) marked/nodal point at time 0 and an additional (red) nodal point at time s which moves from 0 to 1 as we traverse the side from left to right. In view of Corollary 6.9 and Remark 6.6, the map ${\widetilde{\Theta }}^{\textrm{top}}:FC_*(K)\rightarrow MC_*(S)\otimes MC_*(S)$ is defined by counting isolated configurations consisting of punctured discs as in the definition of the moduli spaces $\mathcal {M}(x)$ from Sect. 5.5, additionally decorated with two marked points, with an incidence condition at the marked points, followed by semi-infinite negative pseudo-gradient lines of S starting at the de-concatenated loops. Now, we deform ${\widetilde{\Theta }}^{\textrm{top}}$ once more by inserting a negative pseudo-gradient trajectory of S of finite length $T\ge 0$ between the boundary loop of the disc and the loop on which we impose the incidence condition at the marked points. As $T\rightarrow \infty$ this becomes the chain map $\Psi :FC_*(K)\rightarrow MC_*(S)$ followed by the Morse theoretic coproduct $\lambda$, whereas on the boundary of the top side we see appear the terms $(\Psi \otimes \Gamma _3)(\tau c_0^F\otimes 1) -(\Gamma _3\otimes \Psi )(1\otimes c_0^F)$, with $\Gamma _3$ being the third term from (22). We obtain therefore a homotopy $\Theta _3$ between the operation ${\widetilde{\Theta }}^{\textrm{top}}$ defined by the top side and $\lambda \Psi +(\Psi \otimes \Gamma _3)(\tau c_0^F\otimes 1) -(\Gamma _3\otimes \Psi )(1\otimes c_0^F)$, i.e.

$$\begin{aligned}{}[{\partial },\Theta _3]= \lambda \Psi +(\Psi \otimes \Gamma _3)(\tau c_0^F\otimes 1) -(\Gamma _3\otimes \Psi )(1\otimes c_0^F) - {\widetilde{\Theta }}^{\textrm{top}}. \end{aligned}$$

(27)

Summing together Eqs. (25), (26) and (27), and recalling that $\Gamma =\Gamma _1+\Gamma _2+\Gamma _3$, we obtain the desired relation (23).

For $n\ne 2$, the condition $\Theta c^F=0$ follows by an index argument analogous to the proof of the relation $\lambda ^Fc^F=0$ in Proposition 3.1. Together with the discussion at the beginning of this section, this concludes the proof of Theorem 6.1. $\square$

Remark 6.10

(Perturbation by 1-form/vector field) Let us analyse how the perturbation by a 1-form $\eta$ with transverse zeroes propagates to the diagrams in the preceding proof. Along the left hand sides of the hexagon in Fig. 9, we perturb the Floer operator by ${\widetilde{\eta }}$ at the second output. This continues along the left hand sides of the hexagon in Fig. 12 as the perturbation of the constant modulus zero annuli by the vector field v corresponding to $\eta$ at the second output. As a result, the left hand configuration in Fig. 13 is perturbed by applying the time-one-map f of v as we go counterclockwise from the black to the red dot. This means for $s\geqslant 0$ close to 0 the evaluations of the corresponding loops $q:[0,1]\rightarrow M$ at time 0 (the black dot) and s (the red dot) are related by $q(s)=f(q(0))$.

Along the right hand sides of the hexagon in Fig. 9, we perturb the Floer operator by ${\widetilde{\eta }}$ at the first output. As a result, the right hand configuration in Fig. 13 is perturbed by applying the time-one-map f of v as we go clockwise from the black to the red dot. This means that for $s\leqslant 1$ close to 1 the evaluations of the corresponding loops $q:[0,1]\rightarrow M$ at time 0 (the black dot) and s (the red dot) are related by $q(0)=f(q(s))$, or equivalently, $q(s)=f^{-1}(q(0))$.

Therefore, the perturbation by the 1-form $\eta$ on the Floer side translates on the loop side into the perturbation by an s-dependent vector field which agrees with v near $s=0$ and with $-v$ near $s=1$.

7 Relation to other Floer-type coproducts

The continuation coproduct $\lambda ^F$ discussed in the previous sections descends to positive action symplectic homology $SH_*^{>0}(D^*M)$ (since the action inequality implies that if the input orbit is constant, then so must be the output orbits). In this section we relate $\lambda ^F$ to other coproducts on $SH_*^{>0}(D^*M)$ that have appeared in the literature, thus proving Theorem 1.1 from the Sect. 1.

In particular, we will prove that $\lambda ^F$ agrees with the Abbondandolo–Schwarz coproduct $\lambda ^{AS}$ defined in [4]. Abbondandolo and Schwarz defined in [4] the ring isomorphism $\Psi _*:SH_*(D^*M){\mathop {\longrightarrow }\limits ^{\cong }}H_*\Lambda$ and they asserted [4, Theorem 1.4] that its reduction modulo constant loops $\Psi _*^{>0}:SH_*^{>0}(D^*M){\mathop {\longrightarrow }\limits ^{\cong }}H_*(\Lambda ,\Lambda _0)$ intertwines the coproduct $\lambda ^{AS}$ with the loop coproduct $\lambda$. However, to our knowledge no proof of this result has appeared. We will actually give two proofs in this section: the first one uses Theorem 6.1 and the identification $\lambda ^F=\lambda ^{AS}$, the second one uses a direct argument and suitable interpolating moduli spaces.

This section is structured as follows. In Sect. 7.1, we recall from [20] the definition of the varying weights coproduct $\lambda ^w$, which coincides with $\lambda ^F$ by [20, Lemma 7.2] and which can be more easily related to $\lambda ^{AS}$. In Sect. 7.2, we recall from [4] the definition of the Abbondandolo–Schwarz coproduct $\lambda ^{AS}$. In Sect. 7.3, we show that $\lambda ^{AS}$ is equal to $\lambda ^w$. In Sect. 7.4, we prove directly that $\lambda ^{AS}$ corresponds to the loop coproduct $\lambda$ under the isomorphism $SH_*^{>0}(D^*M)\cong H_*(\Lambda ,\Lambda _0)$.

The situation is summarised in the following diagram.

(28)

The whole discussion concerns the free loop space, but it carries over verbatim to the based loop space.

For simplicity, we assume throughout this section that M is oriented and we use untwisted coefficients in a commutative ring R; the necessary adjustments in the nonorientable case and with twisted coefficients are explained in Appendix A. We denote

$$\begin{aligned} S^1{:}{=}{\mathbb {R}}/{\mathbb {Z}}\quad \text {and}\quad \Lambda {:}{=}W^{1,2}(S^1,M). \end{aligned}$$

7.1 Varying weights coproduct

We recall the definition of the varying weights coproduct $\lambda ^w$ on $SH_*^{>0}(V)$ from [20, §7.1]. Since there we actually describe the algebraically dual product on $SH_*^{<0}(V,{\partial }V)$, we will recap in some detail the necessary notation and arguments. The construction goes back to Seidel, see also [26]. We work with a Liouville domain V of dimension 2n, the symplectic completion is denoted $\widehat{V}=V\cup [1,\infty )\times {\partial }V$ and the radial coordinate in the positive symplectisation $[1,\infty )\times {\partial }V$ is denoted r.

Let $\Sigma$ be the genus zero Riemann surface with three punctures, one of them labelled as positive $\chi _+$ and the other two labelled as negative $\upsilon _-$, $\zeta _-$, endowed with cylindrical ends $[0,\infty )\times S^1$ at the positive puncture and $(-\infty , 0]\times S^1$ at the negative punctures. Denote (s, t), $t\in S^1$ the induced cylindrical coordinates at each of the punctures. Consider a smooth family of 1-forms $\beta _\tau \in \Omega ^1(\Sigma )$, $\tau \in (0,1)$ satisfying the following conditions:

• (nonpositive) $\textrm{d}\beta _\tau \le 0$;

• (weights) $\beta _\tau =\textrm{d}t$ near each of the punctures;

• (interpolation) we have $\beta _\tau =\tau \textrm{d}t$ on $[-R(\tau ),0]\times S^1$ in the cylindrical end near $\upsilon _-$, and $\beta _\tau =(1-\tau ) \textrm{d}t$ on $[-R(1-\tau ),0]\times S^1$ in the cylindrical end near $\zeta _-$, for some smooth function $R:(0,1)\rightarrow {\mathbb {R}}_{>0}$. In other words, the family $\{\beta _\tau \}$ interpolates between a 1-form which varies a lot near $\upsilon _-$ and very little near $\zeta _-$, and a 1-form which varies a lot near $\zeta _-$ and very little near $\upsilon _-$;

• (neck stretching) we have $R(\tau )\rightarrow +\infty$ as $\tau \rightarrow 0$.

We can assume without loss of generality that for $\tau$ close to 0 we have $\beta _\tau =f_\tau (s)\textrm{d}t$ in the cylindrical end at the negative puncture $\upsilon _-$, with $f'_\tau \le 0$, $f_\tau =1$ near $-\infty$, and $f_\tau =\tau$ on $[-R(\tau ),0]$, and similarly for $\tau$ close to 1 in the cylindrical end at the negative puncture $\zeta _-$.

Let $H:\widehat{V}\rightarrow {\mathbb {R}}$ be a convex smoothing localised near ${\partial }V$ of a Hamiltonian which is zero on V and linear with respect to r with positive slope on $[1,\infty )\times {\partial }V$. The Hamiltonian H further includes a small time-dependent perturbation localised near ${\partial }V$, so that all 1-periodic orbits are nondegenerate. Assume the slope is not equal to the period of a closed Reeb orbit. Denote $\mathcal {P}(H)$ the set of 1-periodic orbits of H. The elements of $\mathcal {P}(H)$ are contained in a compact set close to V.

Let $J=(J_\tau ^\zeta )$, $\zeta \in \Sigma$, $\tau \in (0,1)$ be a generic family of compatible almost complex structures, independent of $\tau$ and s near the punctures, cylindrical and independent of $\tau$ and $\zeta$ in the symplectisation $[1,\infty )\times {\partial }V$. For $x,y,z\in \mathcal {P}(H)$ denote

$$\begin{aligned}&\mathcal {M}^1(x;y,z) {:}{=} \bigl \{(\tau ,u)\;\bigl |\; \tau \in (0,1),\ u:\Sigma \rightarrow \widehat{V}, \\ {}&(\textrm{d}u-X_H\otimes \beta _\tau )^{0,1}=0, \\ {}&\lim _{{\mathop {\zeta =(s,t)\rightarrow \chi _+}\limits ^{s\rightarrow +\infty }}}u(\zeta )=x(t),\\ {}&\lim _{{\mathop {\zeta =(s,t)\rightarrow \upsilon _-}\limits ^{s\rightarrow -\infty }}} u(\zeta )=y(t),\quad \lim _{{\mathop {\zeta =(s,t)\rightarrow \zeta _-}\limits ^{s\rightarrow -\infty }}} u(\zeta )=z(t) \bigr \}. \end{aligned}$$

In the symplectisation $[1,\infty )\times {\partial }V$, we have $H\ge 0$ and therefore $d(H\beta )\le 0$, so that elements of the above moduli space are contained in a compact set. The dimension of the moduli space is

$$\begin{aligned} \dim \, \mathcal {M}^1(x;y,z) = \textrm{CZ}(x)-\textrm{CZ}(y)-\textrm{CZ}(z)-n+1. \end{aligned}$$

When it has dimension zero the moduli space $\mathcal {M}^1_{\dim =0}(x;y,z)$ is compact. When it has dimension 1 the moduli space $\mathcal {M}^1_{\dim =1}(x;y,z)$ admits a natural compactification into a manifold with boundary

$$\begin{aligned} {\partial }\mathcal {M}^1_{\dim =1}(x;y,z)&= \coprod _{\textrm{CZ}(x')=\textrm{CZ}(x)-1}\mathcal {M}(x;x')\times \mathcal {M}^1_{\dim =0}(x';y,z) \\&\amalg \coprod _{\textrm{CZ}(y')=\textrm{CZ}(y)+1}\mathcal {M}^1_{\dim =0}(x;y',z)\times \mathcal {M}(y';y) \\&\amalg \coprod _{\textrm{CZ}(z')=\textrm{CZ}(z)+1}\mathcal {M}^1_{\dim =0}(x;y,z')\times \mathcal {M}(z';z) \\ {}&\amalg \mathcal {M}^1_{\tau =1}(x;y,z) \amalg \mathcal {M}^1_{\tau =0}(x;y,z). \end{aligned}$$

Here, $\mathcal {M}^1_{\tau =1}(x;y,z)$ and $\mathcal {M}^1_{\tau =0}(x;y,z)$ denote the fibres of the first projection $\mathcal {M}^1_{\dim =1}(x;y,z)\rightarrow (0,1)$, $(\tau ,u)\mapsto \tau$ near 1, respectively near 0. (By a standard glueing argument the projection is a trivial fibration with finite fibre near the endpoints of the interval (0, 1).)

Consider the degree $-n+1$ operation

$$\begin{aligned} \lambda ^w:FC_*(H)\rightarrow FC_*(H)\otimes FC_*(H) \end{aligned}$$

defined on generators by

$$\begin{aligned} \lambda ^w(x)=\sum _{\textrm{CZ}(y)+\textrm{CZ}(z)=\textrm{CZ}(x)-n+1} \# \mathcal {M}^1_{\dim =0}(x;y,z) y\otimes z, \end{aligned}$$

where $\# \mathcal {M}^1_{\dim =0}(x;y,z)$ denotes the signed count of elements in the 0-dimensional moduli space $\mathcal {M}^1_{\dim =0}(x;y,z)$. Consider also the degree $-n$ operations

$$\begin{aligned} \lambda ^w_i:FC_*(H)\rightarrow FC_*(H)\otimes FC_*(H), \qquad i=0,1 \end{aligned}$$

defined on generators by

$$\begin{aligned} \lambda ^w_i(x)=\sum _{\textrm{CZ}(y)+\textrm{CZ}(z)=\textrm{CZ}(x)-n} \# \mathcal {M}^1_{\tau =i}(x;y,z) y\otimes z, \end{aligned}$$

where $\# \mathcal {M}^1_{\tau =i}(x;y,z)$ denotes the signed count of elements in the 0-dimensional moduli space $\mathcal {M}^1_{\tau =i}(x;y,z)$.

Denote by ${\partial }^F$ the Floer differential on the Floer complex of H. The formula for ${\partial }\mathcal {M}^1_{\dim =1}(x;y,z)$ translates into the algebraic relation

$$\begin{aligned} {\partial }^F \lambda ^w + \lambda ^w({\partial }^F\otimes \textrm{id}+ \textrm{id}\otimes {\partial }^F)=\lambda ^w_1-\lambda ^w_0. \end{aligned}$$

(29)

We now claim that

$$\begin{aligned} \textrm{Im}(\lambda ^w_0)\subset FC_*^{=0}(H)\otimes FC_*(H),\quad \textrm{Im}(\lambda ^w_1)\subset FC_*(H)\otimes FC_*^{=0}(H). \end{aligned}$$

To prove the claim for $\lambda ^w_0$, note that this map can be expressed as a composition $(c\otimes \textrm{id})\circ \lambda _0$, where $\lambda _0:FC_*(H)\rightarrow FC_*(\tau H)\otimes FC_*(H)$ is a pair-of-pants coproduct with $\tau >0$ small, and $c:FC_*(\tau H)\rightarrow FC_*(H)$ is a continuation map. Taking into account that $\tau H$ has no nontrivial 1-periodic orbits for $\tau$ small, and because the action decreases along continuation maps, we obtain $c(FC_*(\tau H))\subset FC_*^{=0}(H)$, which proves the claim. The argument for $\lambda ^w_1$ is similar.

It follows that $\lambda ^w$ induces a degree $-n+1$ chain map

$$\begin{aligned} \lambda ^w:FC_*^{>0}(H)\rightarrow FC_*^{>0}(H)\otimes FC_*^{>0}(H). \end{aligned}$$

(30)

Passing to the limit as the slope of H goes to $+\infty$, we obtain the degree $-n+1$ varying weights coproduct $\lambda ^w$ on $SH_*^{>0}(V)$.

Proposition 7.1

([20, Lemma 7.2]) The continuation coproduct and the varying weights coproduct coincide on $SH_*^{>0}(V)$:

$$\begin{aligned} \lambda ^F=\lambda ^w. \end{aligned}$$

$\square$

7.2 Abbondandolo–Schwarz coproduct

In this subsection, we recall from [4] the definition of a secondary pair-of-pants product on Floer homology of a cotangent bundle, which we will refer to as the Abbondandolo–Schwarz coproduct $\lambda ^{AS}$. We recall the notation and conventions from Sect. 5.1 regarding the Floer complex. In particular near the zero section $H(q,p)=\varepsilon |p|^2 + V(q)$ for a small $\varepsilon >0$ and a Morse function $V:M\rightarrow {\mathbb {R}}$ such that all nonconstant critical points of $A_H$ have action larger than $\min \, V$.

For $x,y,z\in \textrm{Crit}(A_H)$, set (see Fig. 14)

$$\begin{aligned} \mathcal {M}^{1,AS}&(x;y,z) \\&{:}{=} \bigl \{ (\tau ,u,v,w)\;\bigl |\; \tau \in [0,1],\ u:[0,\infty )\times S^1\rightarrow T^*M \\ {}&\qquad \, v,w: (-\infty ,0]\times S^1\rightarrow T^*M,\ \overline{\partial }_Hu=\overline{\partial }_Hv=\overline{\partial }_Hw=0, \\ {}&\qquad \, u(+\infty ,\cdot )=x,\ v(-\infty ,\cdot )=y,\ w(-\infty ,\cdot )=z,\\&\qquad \, v(0,t) = u(0,\tau t),\ w(0,t)=u(0,\tau +(1-\tau )t)\bigr \}. \end{aligned}$$

Note that the matching conditions imply $u(0,\tau )=u(0,0)$.

Fig. 14

The moduli spaces $\mathcal {M}^{1,AS}(x;y,z)$

Lemma 7.2

([4, §5]) For generic choices of Hamiltonian and almost complex structure the space $\mathcal {M}^{1,AS}(x;y,z)$ is a transversely cut out manifold of dimension

$$\begin{aligned} \dim \mathcal {M}^{1,AS}(x;y,z) = \textrm{CZ}(x)-\textrm{CZ}(y)-\textrm{CZ}(z)-n+1. \end{aligned}$$

$\square$

The dimension of $\mathcal {M}^{1,AS}(x;y,z)$ is calculated in [4] using an equivalent description of the moduli space as follows. Define ${\widetilde{v}},{\widetilde{w}}: (-\infty ,0]\times [0,1]\rightarrow T^*M$ by ${\widetilde{v}}(s,t) = v(s,t)$ and ${\widetilde{w}}(s,t) = w(s,t)$, and also ${\widetilde{y}}, {\widetilde{z}}:[0,1]\rightarrow T^*M$ by ${\widetilde{y}}(t) = y(t)$ and ${\widetilde{z}}(t) = z(t)$. Then, there is a canonical identification between elements of $\mathcal {M}^{1,AS}(x;y,z)$ and elements of

$$\begin{aligned} \widetilde{\mathcal {M}}^{1,AS}&(x;{\widetilde{y}},{\widetilde{z}}) \\&{:}{=} \bigl \{(\tau ,u,{\widetilde{v}},{\widetilde{w}})\;\bigl |\; \tau \in [0,1],\ u:[0,\infty )\times S^1\rightarrow T^*M \\ {}&\qquad \, {\widetilde{v}},{\widetilde{w}}: (-\infty ,0]\times [0,1]\rightarrow T^*M,\\ {}&\qquad \, \overline{\partial }_Hu=\overline{\partial }_H{\widetilde{v}}=\overline{\partial }_H{\widetilde{w}}=0, \\ {}&\qquad \, u(+\infty ,\cdot )=x,\ {\widetilde{v}}(-\infty ,\cdot )={\widetilde{y}},\ {\widetilde{w}}(-\infty ,\cdot )={\widetilde{z}},\\ {}&\qquad \, \bigl ({\widetilde{v}}(s,0),\textbf{C}{\widetilde{v}}(s,1)\bigr )\in N^*\Delta ,\ \bigl ({\widetilde{w}}(s,0),\textbf{C}{\widetilde{w}}(s,1)\bigr )\in N^*\Delta , \\ {}&\qquad \, {\widetilde{v}}(0,t) = u(0,\tau t),\ {\widetilde{w}}(0,t)=u(0,\tau +(1-\tau )t)\bigr \}. \end{aligned}$$

Here, $\textbf{C}:T^*M\rightarrow T^*M$ is the antisymplectic involution $(q,p)\mapsto (q,-p)$, $\Delta \subset M\times M$ is the diagonal, and $N^*\Delta \subset T^*(M\times M)$ its conormal bundle. The space ${\widetilde{\mathcal {M}}}^{1,AS}(x;{\widetilde{y}},{\widetilde{z}})$ is a moduli space with jumping Lagrangian boundary conditions as in [3], so for generic H and J it is a transversely cut out manifold. Its dimension is given by the Fredholm index of the linearised problem [4, (37)].

If $\mathcal {M}^{1,AS}(x;y,z)$ has dimension zero it is compact and defines a map

$$\begin{aligned} \lambda ^{AS}:FC_*\rightarrow (FC\otimes FC)_{*-n+1},\qquad x\mapsto \sum _{y,z}\#\mathcal {M}^{1,AS}_{\dim =0}(x;y,z)\,y\otimes z. \end{aligned}$$

If it has dimension 1, it can be compactified to a compact 1-dimensional manifold with boundary

$$\begin{aligned} {\partial }\mathcal {M}^{1,AS}_{\dim =1}(x;y,z)&= \coprod _{\textrm{CZ}(x')=\textrm{CZ}(x)-1}\mathcal {M}(x;x')\times \mathcal {M}^{1,AS}_{\dim =0}(x';y,z) \\&\amalg \coprod _{\textrm{CZ}(y')=\textrm{CZ}(y)+1}\mathcal {M}^{1,AS}_{\dim =0}(x;y',z)\times \mathcal {M}(y';y) \\&\amalg \coprod _{\textrm{CZ}(z')=\textrm{CZ}(z)+1}\mathcal {M}^{1,AS}_{\dim =0}(x;y,z')\times \mathcal {M}(z';z) \\ {}&\amalg \mathcal {M}^{1,AS}_{\tau =1}(x;y,z) \amalg \mathcal {M}^{1,AS}_{\tau =0}(x;y,z). \end{aligned}$$

Here, the first three terms correspond to broken Floer cylinders and the last two terms to the intersection of $\mathcal {M}^{1,AS}(x;y,z)$ with the sets $\{\tau =1\}$ and $\{\tau =0\}$, respectively. Therefore, we have

$$\begin{aligned} ({\partial }^F\otimes \textrm{ id}+\textrm{ id}\otimes {\partial }^F)\lambda ^{AS} + \lambda ^{AS}{\partial }^F = \lambda ^{AS}_1-\lambda ^{AS}_0, \end{aligned}$$

(31)

where for $i=0,1$, we set

$$\begin{aligned} \lambda ^{AS}_i:FC_*\rightarrow (FC\otimes FC)_{*-n},\qquad x\mapsto \sum _{y,z}\#\mathcal {M}^{1,AS}_{\tau =i}(x;y,z)\,y\otimes z. \end{aligned}$$

Let us look more closely at the map $\lambda ^{AS}_1$. For $\tau =1$ the matching conditions in $\mathcal {M}^{1,AS}(x;y,z)$ imply that $w(0,t)=u(0,0)$ is a constant loop. For action reasons z must then be a critical point, so that $\textrm{Im}(\lambda ^{AS}_1)\subset FC_*(H)\otimes FC_*^{=0}(H)$. Similarly, we have $\textrm{Im}(\lambda ^{AS}_0)\subset FC_*^{=0}(H)\otimes FC_*(H)$, and therefore $\lambda ^{AS}$ descends to a chain map

$$\begin{aligned} \lambda ^{AS}:FH_*^{>0}\rightarrow (FH^{>0}\otimes FH^{>0})_{*-n+1} \end{aligned}$$

(32)

with $FC_*^{>0}=FC_*(H)/FC_*^{=0}(H)$. Note that we have $FH_*^{>0}(H)\cong SH_*^{>0}(D^*M)$ for the quadratic Hamiltonians considered in this section.

7.3 The varying weights coproduct equals the Abbondandolo–Schwarz coproduct

Proposition 7.3

Let M be a closed connected oriented manifold. The secondary coproducts $\lambda ^w$ defined via (30) and $\lambda ^{AS}$ defined via (32) agree on $SH_*^{>0}(D^*M)$.

Proof

We assume without loss of generality that the Hamiltonian used in the definition of the coproduct $\lambda ^{AS}$ is the same as the one used in the definition of the coproduct $\lambda ^w$, i.e. a convex smoothing of a Hamiltonian which vanishes on $D^*M$ and is linear with respect to the radial coordinate $r=|p|$ outside of $D^*M$. The point of the proof is to exhibit the Floer problem defining the moduli spaces $\mathcal {M}^{1,AS}(x;y,z)$ for $\lambda ^{AS}$ as a limiting case of the Floer problem defining the moduli spaces $\mathcal {M}^1(x;y,z)$ for $\lambda ^w$.

Note first that for 0-dimensional moduli spaces $\mathcal {M}^{1,AS}_{\dim =0}(x;y,z)$, we can restrict $\tau$ to (0, 1). Given $\tau \in (0,1)$ a triple (u, v, w) as in the definition of $\mathcal {M}^{1,AS}(x;y,z)$ can be interpreted as a single map ${\tilde{u}}:\Sigma \rightarrow T^*M$ satisfying $(d{\tilde{u}}-X_H\otimes \beta _\tau )^{0,1}=0$, where $\Sigma$ is a Riemann surface and $\beta _\tau$ is a 1-form explicitly described as follows. The Riemann surface is

$$\begin{aligned} \Sigma ={\mathbb {R}}\times [-\tau ,0]\, \amalg \, {\mathbb {R}}\times [0,1-\tau ]\, / \sim \end{aligned}$$

with

$$\begin{aligned}{} & {} (s,-\tau )\sim (s,1-\tau ), \quad (s,0^-)\sim (s,0^+) \quad \text{ for } s\ge 0, \\{} & {} (s,-\tau )\sim (s,0^-), \quad (s,0^+)\sim (s,1-\tau ) \quad \text{ for } s\le 0. \end{aligned}$$

(We use the notation $(s,0^-)$ for points in ${\mathbb {R}}\times \{0\}\subset {\partial }({\mathbb {R}}\times [-\tau ,0])$, and $(s,0^+)$ for points in ${\mathbb {R}}\times \{0\}\subset {\partial }({\mathbb {R}}\times [0,1-\tau ])$.) This is a smooth Riemann surface with canonical cylindrical ends $[0,\infty )\times S^1$ at the positive puncture and $(-\infty ,0]\times {\mathbb {R}}/\tau {\mathbb {Z}}$ and $(-\infty ,0]\times {\mathbb {R}}/(1-\tau ){\mathbb {Z}}$ at the negative punctures. See Fig. 15.

Fig. 15

A pair-of-pants $\Sigma$ with large cylindrical ends

A conformal parametrisation of $\Sigma$ near the point (0, 0) is induced from the map ${\mathbb {C}}\rightarrow {\mathbb {C}}$, $z\mapsto z^2$.⁵ The Riemann surface $\Sigma$ carries a canonical smooth closed 1-form $\textrm{d}t$.⁶ Upon identifying the cylindrical ends at the negative punctures with $(-\infty ,0]\times S^1$, this canonical 1-form becomes equal to $\tau \textrm{d}t$, respectively $(1-\tau )\textrm{d}t$ at those punctures. The 1-form $\beta _\tau$ is defined to be the discontinuous 1-form equal to $\textrm{d}t$ on the cylindrical end $[0,\infty )\times S^1$ at the positive puncture, equal to $\frac{1}{\tau }\textrm{d}t$ on the cylindrical end $(-\infty ,0]\times {\mathbb {R}}/\tau {\mathbb {Z}}$ at the first negative puncture, and equal to $\frac{1}{1-\tau } \textrm{d}t$ on the cylindrical end $(-\infty ,0]\times {\mathbb {R}}/(1-\tau ){\mathbb {Z}}$ at the second negative puncture. Equivalently, upon normalising the cylindrical ends at the negative punctures into $(-\infty ,0]\times S^1$, the 1-form $\beta _\tau$ is simply $\textrm{d}t$. This discontinuous 1-form $\beta _\tau$ can be interpreted as a limit of 1-forms which are obtained by interpolating from $\tau \,\textrm{d}t$ and $(1-\tau )\textrm{d}t$ (near 0) towards $\textrm{d}t$ (near $-\infty$) in the normalised cylindrical ends at the negative punctures, where the interpolation region shrinks and approaches $s=0$. It was noted in Sect. 7.2 that the limit case defines a Fredholm problem $\widetilde{\mathcal {M}}^{1,AS}(x;{\widetilde{y}},{\widetilde{z}})$ with jumping Lagrangian boundary conditions. The Fredholm problem before the limit is naturally phrased in terms of the Riemann surface $\Sigma$ without boundary, but it can be reinterpreted as a problem with Lagrangian boundary conditions by cutting $\Sigma$ open along $\{s=0\}$. As such, it converges in the limit to the Fredholm problem with jumping Lagrangian boundary conditions described above. By regularity and compactness, the two Fredholm problems are equivalent near the limit, and the corresponding counts of elements in 0-dimensional moduli spaces are the same. $\square$

7.4 Abbondandolo–Schwarz coproduct equals loop coproduct

Recall the Hamiltonian $H:S^1\times T^*M\rightarrow {\mathbb {R}}$ from Sect. 7.2 and its fibrewise Legendre transform $L:S^1\times TM\rightarrow {\mathbb {R}}$ from Sect. 2.2. Also recall from Sect. 2.2 the notations concerning the Morse complex $MC_*$ of the action functional $S_L$ which we will use freely. In particular, ${\partial }$ denotes the Morse boundary operator and ${\widetilde{\lambda }}$ the coproduct from Remark 2.12.

We assume that M is oriented and we use the Morse complex twisted by the local system $\sigma$ obtained by transgressing the second Stiefel–Whitney class.

Following [4], for $x\in \textrm{Crit}(A_H)$ and $a\in \textrm{Crit}(S_L)$, we define

$$\begin{aligned} \mathcal {M}(x)&{:}{=} \{u:[0,\infty )\times S^1\rightarrow T^*M\mid \ \overline{\partial }_Hu=0,\\&\quad u(+\infty ,\cdot )=x,\ u(0,\cdot )\subset M\} \end{aligned}$$

and

$$\begin{aligned} \mathcal {M}(x;a) {:}{=} \{u\in \mathcal {M}(x)\mid u(0,\cdot )\in W^+(a)\}, \end{aligned}$$

(33)

where $W^+(a)$ is the stable manifold of a for the negative pseudo-gradient flow of $S_L$. See Fig. 4.

For generic H these are manifolds of dimensions

$$\begin{aligned} \dim \mathcal {M}(x) = \textrm{CZ}(x),\qquad \dim \mathcal {M}(x;a) = \textrm{CZ}(x)-\textrm{ind}(a). \end{aligned}$$

The signed count of 0-dimensional spaces $\mathcal {M}(x;a)$ defines a chain map

$$\begin{aligned} \Psi :FC_*\rightarrow MC_*,\qquad a\mapsto \sum _{\textrm{ind}(a)=\textrm{CZ}(a)}\#\mathcal {M}(x;a)\,a. \end{aligned}$$

The induced map on homology is an isomorphism

$$\begin{aligned} \Psi _*:FH_*{\mathop {\longrightarrow }\limits ^{\cong }}MH_*\cong H_*(\Lambda ;\sigma ) \end{aligned}$$

intertwining the pair-of-pants product with the loop product.

Proposition 7.4

The map $\Psi$ descends to an isomorphism on homology modulo the constant loops

$$\begin{aligned} \Psi _*:FH_*^{>0}{\mathop {\longrightarrow }\limits ^{\cong }}MH_*^{>0}\cong H_*(\Lambda ,\Lambda _0;\sigma ) \end{aligned}$$

which intertwines the Abbondandolo–Schwarz coproduct $\lambda ^{AS}$ with the loop coproduct $\lambda$.

Proof

For $x\in \textrm{Crit}(A_H)$ and $b,c\in \textrm{Crit}(S_L)$ define

$$\begin{aligned} \mathcal {M}^+(x) {:}{=} \bigl \{&(\sigma ,\tau ,u,v,w)\;\bigl |\; \sigma \in [0,\infty ),\ \tau \in [0,1],\\ {}&u:[\sigma ,\infty )\times S^1\rightarrow T^*M, v,w: [0,\sigma ]\times S^1\rightarrow T^*M, \\ {}&\ \overline{\partial }_Hu=\overline{\partial }_Hv=\overline{\partial }_Hw=0, \\ {}&u(+\infty ,\cdot )=x,\ v(0,t)\in M,\ w(0,t)\in M,\\ {}&v(\sigma ,t) = u(\sigma ,\tau t),\ w(\sigma ,t)= u(\sigma ,\tau +(1-\tau )t)\bigr \}, \\ \mathcal {M}^+(x;b,c) {:}{=} \{&(\sigma ,\tau ,u,v,w)\in \mathcal {M}^+(x)\mid \\ {}&v(0,\cdot )\in W^+(b),\ w(0,\cdot )\in W^+(c)\}, \\ \mathcal {M}^-(x;b,c) {:}{=} \bigl \{&(\sigma ,\tau ,u,\alpha ,\beta ,\gamma )\;\bigl |\; \sigma \in (-\infty ,0],\ \tau \in [0,1],\ u\in \mathcal {M}(x), \\ {}&\alpha =\phi _{-\sigma }(u(0,\cdot )),\ \beta \in W^+(b),\ \gamma \in W^+(c), \\ {}&\beta (t) = \alpha (\tau t),\ \gamma (t)=\alpha (\tau +(1-\tau )t) \bigr \}, \end{aligned}$$

where $\mathcal {M}(x)$ was defined above and $\phi _s:\Lambda \rightarrow \Lambda$ for $s\geqslant 0$ denotes the flow of the negative pseudo-gradient of $S_L$. Note that $\alpha ,\beta ,\gamma$ in the definition of $\mathcal {M}^-(x;b,c)$ are actually redundant and just included to make the definition more transparent. As above it follows that for generic H these spaces are transversely cut out manifolds of dimensions $\dim \mathcal {M}^+(x)=\textrm{CZ}(x)-n+2$ and

$$\begin{aligned} \dim \mathcal {M}^+(x;b,c) = \dim \mathcal {M}^-(x;b,c) = \textrm{CZ}(x)-\textrm{ind}(b)-\textrm{ind}(c)-n+2. \end{aligned}$$

We set

$$\begin{aligned} \mathcal {M}^2(x;b,c) {:}{=} \mathcal {M}^+(x;b,c) \amalg \mathcal {M}^-(x;b,c). \end{aligned}$$

If this space has dimension zero it is compact and defines a map

$$\begin{aligned} \Theta :FC_*\rightarrow (MC\otimes MC)_{*-n+2},\qquad x\mapsto \sum _{b,c}\#\mathcal {M}^2_{\dim =0}(x;b,c)\,b\otimes c. \end{aligned}$$

If it has dimension 1 it can be compactified to a compact 1-dimensional manifold with boundary

$$\begin{aligned} {\partial }\mathcal {M}^2_{\dim =1}(x;b,c)&= \coprod _{\textrm{CZ}(x')=\textrm{CZ}(x)-1}\mathcal {M}(x;x')\times \mathcal {M}^2_{\dim =0}(x';b,c) \\&\amalg \, \coprod _{\textrm{ind}(b')=\textrm{ind}(b)+1}\mathcal {M}^2_{\dim =0}(x;b',c)\times \mathcal {M}(b';b) \\ {}&\amalg \, \coprod _{\textrm{ind}(c')=\textrm{ind}(c)+1}\mathcal {M}^2_{\dim =0}(x;b,c')\times \mathcal {M}(c';c) \\ {}&\amalg \, \coprod _{y,z}\mathcal {M}^1_{\dim =0}(x;y,z)\times \mathcal {M}(y;b)\times \mathcal {M}(z;c) \\&\amalg \, \coprod _a\mathcal {M}(x;a)\times {\widetilde{\mathcal {M}}}^1_{\dim =0}(a;b,c) \\&\amalg \mathcal {M}^2_{\tau =1}(x;b,c) \amalg \mathcal {M}^2_{\tau =0}(x;b,c), \end{aligned}$$

where ${\widetilde{\mathcal {M}}}^1(a;b,c)$ are the moduli spaces in Remark 2.12 defining the coproduct ${\widetilde{\lambda }}$ with $f_t=\textrm{id}$. Here, the first term corresponds to splitting off of Floer cylinders, the second and third ones to splitting off of Morse pseudo-gradient lines, the fourth one to $\sigma =+\infty$, the fifth one to $\sigma =-\infty$, and the last two terms to the intersection of $\mathcal {M}^2(x;b,c)$ with the sets $\{\tau =1\}$ and $\{\tau =0\}$, respectively. The intersections of $\mathcal {M}^\pm (x;b,c)$ with the set $\{\sigma =0\}$ are equal with opposite orientations and thus cancel out. Therefore, we have

$$\begin{aligned} ({\partial }\otimes \textrm{ id}+\textrm{ id}\otimes {\partial })\Theta + \Theta {\partial }^F = (\Psi \otimes \Psi )\lambda ^{AS} - {\widetilde{\lambda }}\Psi + \Theta _1-\Theta _0, \end{aligned}$$

(34)

where for $i=0,1$, we set

$$\begin{aligned} \Theta _i:FC_*\rightarrow (MC\otimes MC)_{*-n+1},\qquad x\mapsto \sum _{b,c}\#\mathcal {M}^2_{\tau =i}(x;b,c)\,b\otimes c. \end{aligned}$$

Arguing as in the previous subsection, we see that the $\Theta _0$ has image in $MC_*^{=0}\otimes MC_*$, and $\Theta _1$ has image in $MC_*\otimes MC_*^{=0}$. Together with Eq. (34) this shows that $\Theta$ descends to a map

$$\begin{aligned} \Theta :FC_*^{>0}\rightarrow (MC^{>0}\otimes MC^{>0})_{*-n+2} \end{aligned}$$

between the positive chain complexes which is a chain homotopy between $(\Psi \otimes \Psi )\lambda ^{AS}$ and ${\widetilde{\lambda }}\Psi$, which concludes the proof. $\square$

8 Loop coproduct for odd-dimensional spheres

In this section, we compute the loop coproduct on reduced loop homology $\overline{H}_*(\Lambda S^n)=H_*(\Lambda S^n)$ of odd-dimensional spheres $S^n$. For its definition, we use a Morse function $S^n\rightarrow {\mathbb {R}}$ with only two critical points, the minimum and the maximum, and a vector field v (or equivalently a 1-form $\eta$) which is nowhere vanishing. By Proposition 4.7, the coproduct does not depend on these choices if $n\geqslant 2$. For the same reason, in the definition of the loop coproduct, we can use a constant family $v^\tau \equiv v$ instead of the family $v^\tau$ interpolating between $v^0=v$ and $v^1=-v$ from Sect. 2.2 (see Remark 4.8). In the case $n=1$, we will see that the loop coproduct actually depends on the choice of v.

For our computation, we first give a third definition of the loop coproduct on reduced loop homology in terms of singular homology.

8.1 Topological description of the loop coproduct

We define the loop coproduct on singular loop homology relative to $\chi \cdot$point. It is induced by a densely defined operation

$$\begin{aligned} \lambda : C_*(\Lambda )\rightarrow C_{*+1-n}(\Lambda \times \Lambda ) \end{aligned}$$

on singular chains constructed as follows. The beginning of the construction is like in Sect. 2.2. We fix a small vector field v on M with nondegenerate zeroes such that the only periodic orbits of v with period $\leqslant 1$ are its zeroes, and we consider a generic family of vector fields $v^\tau$, $\tau \in [0,1]$ which interpolates between $v^0=v$ and $v^1=-v$. We denote $f_t^\tau :M{\mathop {\longrightarrow }\limits ^{\cong }}M$, $t\in {\mathbb {R}}$ the flow of $v^\tau$, and $f^\tau =f_1^\tau$. For each $q\in M$, we denote as in Sect. 2.2 the induced path from q to $f^\tau (q)$ by $\pi _q^\tau :[0,1]\rightarrow M$, $\pi _q^\tau (t){:}{=}f_t^\tau (q)$, and the inverse path by $(\pi _q^\tau )^{-1}$.

In the spirit of [13], let $a:K_a\rightarrow \Lambda$ be a chain such that the map

$$\begin{aligned} \textrm{ev}_a:K_a\times [0,1]\rightarrow M\times M,\qquad (x,\tau )\mapsto \Bigl (f^\tau \bigl (a(x)(0)\bigr ),a(x)(\tau )\Bigr ) \end{aligned}$$

is transverse to the diagonal $\Delta \subset M\times M$. Then,

$$\begin{aligned} K_{\lambda (a)} {:}{=} \textrm{ev}_a^{-1}(\Delta ) = \{(x,\tau )\in K_a\times [0,1]\mid a(x)(\tau ) = f^\tau \bigl (a(x)(0)\bigr )\} \end{aligned}$$

is a compact manifold with corners and we define

$$\begin{aligned} \lambda (a): K_{\lambda (a)}\rightarrow \Lambda \times \Lambda \end{aligned}$$

by

$$\begin{aligned} \lambda (a)(x,\tau ) {:}{=} \Bigl (a(x)|_{[0,\tau ]}\#(\pi _{a(x)(0)}^\tau )^{-1},\, \pi _{a(x)(0)}^\tau \#a(x)|_{[\tau ,1]}\Bigr ). \end{aligned}$$

See Fig. 1 where $\alpha =a(x)$. At $\tau =0$ and $\tau =1$ the condition in $K_{\lambda (a)}$ becomes $a(x)(0)=q\in \textrm{Fix}(f^0)$, respectively $a(x)(1)=q\in \textrm{Fix}(f^1)$, and denoting the constant loop at q by the same letter we find

$$\begin{aligned} \lambda (a)(x,1) = \bigl (a(x)\#q,q\bigr ),\qquad \lambda (a)(x,0) = \bigl (q,q\#a(x)\bigr ). \end{aligned}$$

It follows that

$$\begin{aligned} {\partial }\lambda (a) \pm \lambda ({\partial }a) = \sum _{q\in \textrm{Fix}(f^1)}\textrm{ind}_{-v}(q)(a\bullet q)\times q - \sum _{q\in \textrm{Fix}(f^0)}\textrm{ind}_v(q)q\times (q\bullet a), \end{aligned}$$

where q is viewed as a 0-chain and the loop products with the constant loop q are given by

$$\begin{aligned} a\bullet q&: K_{a\bullet q}=\{x\in K_a\mid a(x)(0)=q\}\rightarrow \Lambda ,\qquad x\mapsto a(x)\#q, \\ q\bullet a&: K_{q\bullet a}=\{x\in K_a\mid q=a(x)(0)\}\rightarrow \Lambda ,\qquad x\mapsto q\#a(x). \end{aligned}$$

Here, the signs $\textrm{ind}_{\pm v}(q)$ arise from the discussion before Remark 2.8, noting that the restriction of $\textrm{ev}_a$ to $\tau =0$ or $\tau =1$ is the composition of the evaluation $K_a\rightarrow M$, $x\mapsto a(x)(0)$ and the map $M\rightarrow M\times M$, $q\mapsto \bigl (f^0(q),q\bigr )$, respectively $q\mapsto \bigl (f^1(q),q\bigr )$.

Let us now fix a basepoint $q_0\in M$ and consider a such that the map

$$\begin{aligned} \textrm{ev}_{a,0}:K_a\rightarrow M,\qquad x\mapsto a(x)(0) \end{aligned}$$

is transverse to $q_0$. We choose all zeroes of v (i.e. fixed points of $f^0$ and $f^1$) so close to $q_0$ that $\textrm{ev}_{a,0}$ is transverse to each of them. Then, after identifying the domains $K_{q\bullet a}$ with $K_{q_0\bullet a}$ and transferring loops at q to loops at $q_0$, we have

$$\begin{aligned} {\partial }\lambda (a) \pm \lambda ({\partial }a) = \chi \Bigl ((a\bullet q_0)\times q_0 - q_0\times (q_0\bullet a)\Bigr ), \end{aligned}$$

(35)

where $\chi =\sum _{q\in \textrm{Fix}(f^1)}\textrm{ind}_{-v}(q)=\sum _{q\in \textrm{Fix}(f^0)}\textrm{ind}_{v}(q)$ is the Euler characteristic of M. Recalling the notation $C_*(\Lambda ,\chi \text {pt}){:}{=}C_*(\Lambda )/\chi R q_0$ for the chains relative to $\chi \cdot$point, we see that $\lambda$ induces a chain map $C_*\Lambda \rightarrow (C(\Lambda ,\chi \text {pt})\otimes C(\Lambda ,\chi \text {pt}))_{*+1-n}$. Moreover, this factors through $C_*(\Lambda ,\chi \text {pt})$: if $n\ge 2$ this holds for degree reasons, and if $n=1$ this holds tautologically because the Euler characteristic is zero. The outcome is a coproduct $H_*(\Lambda ,\chi \text {pt})\rightarrow (H(\Lambda ,\chi \text {pt})\otimes H(\Lambda ,\chi \text {pt}))_{*+1-n}$ on the homology relative to $\chi \cdot$point. Under our standing assumption of orientability on M, this is the same as a coproduct on reduced loop homology $\overline{H}_*\Lambda \rightarrow (\overline{H}\Lambda \otimes \overline{H}\Lambda )_{*+1-n}$.

8.2 Loop coproduct for spheres of odd dimension $n\geqslant 3$

In this subsection, we use ${\mathbb {Z}}$-coefficients and assume $n\geqslant 3$ is odd. Recall from [23] that the degree shifted homology of the free loop space of $S^n$ is the free graded commutative algebra

$$\begin{aligned} {\mathbb {H}}_*(\Lambda S^n)=H_{*+n}(\Lambda S^n) \cong \Lambda [A,U],\qquad |A|=-n,\quad |U|=n-1, \end{aligned}$$

where the shifted degree |a| is related to the geometric degree by $|a|=\deg a-n$. Here, A is the class of a point (of geometric degree 0) and U is represented by the descending manifold of the Bott family of simple great circles tangent at their basepoint to a given non-vanishing vector field on the sphere (of geometric degree $2n-1$). Since $\chi (S^n)=0$, the coproduct $\lambda$ is defined on ${\mathbb {H}}_*(\Lambda S^n)$ and has shifted degree $1-2n$ (and geometric degree $1-n$). The unit 1 is represented by the fundamental chain of all constant loops (of geometric degree n).

We begin with some explicit computations of coproducts, to be compared to [29].

Lemma 8.1

For $n\ge 3$ odd, the loop coproduct on ${\mathbb {H}}_*(\Lambda S^n)$ satisfies

• (a) $\lambda (A)=\lambda (1)=0$,

• (b) $\lambda (AU) = A\otimes A$,

• (c) $\lambda (AU^2) = A\otimes AU+AU\otimes A$,

• (d) $\lambda (U) = A\otimes 1-1\otimes A$.

Proof

We will actually prove these relations in $H_*(\Lambda S^n)$, in which case (a-c) remain unchanged, but (d) becomes $\lambda (U)=A\otimes 1 + 1 \otimes A$ (the sign change comes from the odd degree shift by n).

We recall the observation made at the beginning of this section that in the definition of the loop coproduct, we can use a constant family of vector fields $v^\tau \equiv v$. We fix such a choice in the sequel, with v small and nowhere vanishing. We denote $f^\tau _t=f_t$ the flow of $v^\tau =v$, and we denote $f^\tau =f$ the time-one flow.

(a) To prove $\lambda (A)=0$, we represent A by the constant loop at $q_0$. Then, $f^\tau (q_0)\ne q_0$ for all values of $\tau \in [0,1]$ and therefore $\lambda (A)$ is supported by the empty set. To prove $\lambda (1)=0$, we represent 1 by the $S^n$-family of constant loops and note that $f^\tau (q)\ne q$ for all $q\in S^n$. Thus, $\lambda (1)$ is supported by the empty set.

(b) We fix a unit tangent vector $v_0$ at $q_0$ and we represent AU by the $(n-1)$-chain $a:K^{n-1} \rightarrow \Lambda S^n$ of all circles with fixed initial point $q_0$ and initial direction $v_0$. ($K^{n-1}$ is the $(n-1)$-disc of all 2-planes in ${\mathbb {R}}^{n+1}$ through $q_0$ containing the vector $v_0$, whose boundary is mapped to $q_0$.) Then, $a(k)(0)=q_0$ for all $k\in K^{n-1}$. Since the evaluation map $(k,\tau )\mapsto a(k)(\tau )$ covers $S^n$ once, there exists a unique $(k,\tau )$ for which $a(k)(\tau )=f^\tau (q_0)=f(q_0)$. Therefore, $\lambda (a)$ is homologous to the 0-cycle $A\otimes A$.

(c) We represent $AU^2$ by the $(2n-2)$-chain $a:K^{2n-2} \rightarrow \Lambda S^n$ of all circles with fixed initial point $q_0$. ($K^{2n-2}$ is a fibre bundle $K^{n-1}\rightarrow K^{2n-2}\rightarrow S^{n-1}$, where $S^{n-1}$ is the $(n-1)$-sphere of all initial directions at $q_0$ and $K^{n-1}$ is the $(n-1)$-disc from (b) of all circles through $q_0$ in a given initial direction.) Then, $a(k)(0)=q_0$ for all $k\in K^{2n-2}$. Recall that $f(q_0)\ne q_0$ is a point close to $q_0$. Let us fix some initial direction $v_0$ at $q_0$. For every sufficiently large circle (whose diameter is bigger than the distance from $q_0$ to $f(q_0)$) with initial point $q_0$ and initial direction $v_0$ there exist precisely two rotations of the initial direction such that the rotated circles pass through $f(q_0)$. One of these rotated circles passes though $f(q_0)$ near $\tau =0$ and the other one near $\tau =1$. As the circle varies over the $(n-1)$-chain $K^{n-1}$ of all circles with initial point $q_0$ and initial direction $v_0$ (and we let $f(q_0)$ move to $q_0$), these two families of rotated circles give rise to cycles representing the classes $A\otimes AU$ and $AU\otimes A$, respectively.

(d) We represent U by the $(2n-1)$-chain $a:K^{2n-1}\rightarrow \Lambda S^n$ of all circles starting at their basepoint $q\in S^n$ in direction v(q). ($K^{2n-1}$ is a fibre bundle $K^{n-1}\rightarrow K^{2n-1}\rightarrow S^n$, where $S^n$ corresponds to the initial points and $K^{n-1}$ is the $(n-1)$-disc from (b).) For every q, there exists a unique circle $a(x_q)$ starting at q in direction v(q) and passing through f(q). Since all the circles constituting the chain a are simple, there is a unique $\tau _q$ such that $a(x_q)(\tau _q)=f(q)=f^{\tau _q}(a(x_q)(0))$. By splitting each $a(x_q)$ at the parameter value $\tau _q$ using the path $\pi _q(t)=f_t(q)$, we obtain a cycle $s:S^n\rightarrow \Lambda \times \Lambda$ that represents $\lambda (a)$. This cycle has degree n, it sits over the diagonal $\Delta \subset S^n\times S^n$ as an element of the fibration $(\textrm{ev},\textrm{ev}):\Lambda \times \Lambda \rightarrow S^n\times S^n$, and denoting $\pi :\Lambda \times _{S^n} \Lambda \rightarrow S^n$ the restriction of this fibration to the diagonal, we have $\pi \circ s=\textrm{Id}_{S^n}$. On the other hand, $H_n(\Lambda \times _{S^n} \Lambda )$ has rank 1, generated by the class of the diagonal: that the rank is at most 1 follows by inspection of the spectral sequence of the fibration $\Omega S^n\times \Omega S^n\hookrightarrow \Lambda \times _{S^n}\Lambda \rightarrow S^n$, using the fact that $H_*({\Omega }S^n)$ is a polynomial ring on one generator in degree $n-1$, and that it is at least one follows from the fact that the diagonal is a section. This implies that the cycle s is homologous to the diagonal $\Delta \subset S^n\times S^n$ in $\Lambda \times _{S^n}\Lambda$, hence also in $\Lambda \times \Lambda$, and we conclude $\lambda (U)=[\Delta ]=[pt]\otimes [S^n] + [S^n]\otimes [pt] = A\otimes 1 + 1 \otimes A$ in $H_*(\Lambda )\otimes H_*(\Lambda )$.

The previous proof uses an algebraic argument related to the diagonal. An alternative, entirely geometric proof can be given in case the sphere $S^n$ admits two orthogonal non-vanishing vector fields. (By Adams’ theorem [8], this is the case if and only $n+1$ is divisible by 4.) We pick v to be one of these and denote w the other one. We represent U by the $(2n-1)$-chain $a:K^{2n-1} \rightarrow \Lambda S^n$ of all circles starting at their basepoint $q\in S^n$ in direction w(q). Thus, for every $q\in S^n$, there exists a unique circle $a(x_q)$ starting at q in direction w(q) and passing through f(q), and since all the circles constituting the chain a are simple there is a unique $\tau _q$ such that $a(x_q)(\tau _q)=f(q)=f^{\tau _q}(a(x_q)(0))$. Since v is orthogonal to w, each circle $a(x_q)$ is small and the resulting cycle $\lambda (a)$ can be deformed in $\Lambda \times \Lambda$ to the diagonal $\Delta \subset \Lambda _0\times \Lambda _0$. In turn, this is represented in $H_*(\Lambda _0)\otimes H_*(\Lambda _0)$ by $[q_0]\otimes [\Lambda _0]+[\Lambda _0]\otimes [q_0]$, i.e. $A\otimes 1 + 1 \otimes A$. $\square$

Note that Lemma 8.1 is compatible with graded cocommutativity of $\lambda$ on ${\mathbb {H}}_*\Lambda$, i.e. $\tau \lambda =-\lambda$. To compute the full expression of the coproduct, we use the following structural result from [21].

Theorem 8.2

([21, Theorem 6.4]) Let M be a closed manifold of dimension $n\ge 2$. Then, the loop homology ${\mathbb {H}}_*(\Lambda M)$ endowed with the loop product $\mu$ and the loop coproduct $\lambda$ is a commutative and cocommutative unital infinitesimal anti-symmetric bialgebra. In particular, the following “unital infinitesimal relation” holds:

where we denote the identity map and 1 the unit for the product. $\square$

For $M=S^n$ with $n\geqslant 3$ odd, we proved in Lemma 8.1 that $\lambda 1=0$, so the unital infinitesimal relation reduces to the so-called “infinitesimal relation”, or “Sullivan relation”

Such a relation was conjectured in [36]. Note that Sullivan’s relation is not satisfied by the “extension by 0” loop coproduct from [29].

Proposition 8.3

For $n\geqslant 3$ odd, the loop coproduct on ${\mathbb {H}}_*(\Lambda S^n)$ satisfies for all $k\geqslant 0$

$$\begin{aligned} \lambda (U^k)&= \sum _{i,j\geqslant 0,\ i+j=k-1}\bigl (AU^i\otimes U^j - U^i\otimes AU^j\bigr ), \\ \lambda (AU^k)&= \sum _{i,j\geqslant 0,\ i+j=k-1}AU^i\otimes AU^j. \end{aligned}$$

Proof

The proof is a straightforward induction on k using knowledge of $\mu$, Sullivan’s relation, and the values $\lambda (A)=0$ and $\lambda (U)=A\otimes 1-1\otimes A$ from Lemma 8.1. As an example, the values of $\lambda (AU)$ and $\lambda (AU^2)$ from Lemma 8.1 can be recovered as follows. For the computation, recall that the shifted degrees of A, AU, $\lambda$ are odd, the shifted degree of U is even, and $A^2=0$.

$\square$

Remark 8.4

We note in particular that this extended coproduct on reduced homology has contributions from the constant loops, unlike the one from [29]. These contributions from the constant loops play an essential role for the unital infinitesimal algebra structure.

The previous computation allows us to recover the Sullivan–Goresky–Hingston coproduct on ${\mathbb {H}}_*(\Lambda S^n,\Lambda _0)=H_{*+n}(\Lambda S^n,\Lambda _0)$ [27, 29]. Our method ultimately relies on the infinitesimal relation and involves a minimal geometric input in the form of Lemma 8.1 (a) and (d). In comparison, the computation from [29] of the coproduct on $H_*(\Lambda S^n,\Lambda _0)$ relies on geometric input which is quite involved. In a sense, the “algebra” of the infinitesimal relation replaces the “geometry” of spaces of circles from [29].

Corollary 8.5

For $n\ge 3$ odd, the Sullivan–Goresky–Hingston coproduct on ${\mathbb {H}}_*(\Lambda S^n,\Lambda _0)$ is given by

$$\begin{aligned} \lambda (U^k)&= \sum _{i,j\geqslant 1,\ i+j=k-1}\bigl (AU^i\otimes U^j - U^i\otimes AU^j\bigr ), \\ \lambda (AU^k)&= \sum _{i,j\geqslant 1,\ i+j=k-1}AU^i\otimes AU^j. \end{aligned}$$

Proof

It is enough to discard the terms involving constant loops from the formulas of Proposition 8.3. $\square$

8.3 Loop coproduct for $S^1$

In this section, we study the loop coproduct on the loop space of $S^1={\mathbb {R}}/{\mathbb {Z}}$. The degree shifted loop homology with R-coefficients is as a ring with respect to the loop product given by

$$\begin{aligned} {\mathbb {H}}_*(\Lambda S^1) = H_{*+1}(\Lambda S^1) = \Lambda [A,U,U^{-1}],\qquad |U|=0,\,|A|=-1, \end{aligned}$$

where the classes $AU^k$ and $U^k$ are represented by the cycles

$$\begin{aligned} AU^k(t) = kt,\qquad U^k(r,t) = r+kt,\qquad r,t\in S^1,\ k\in {\mathbb {Z}}. \end{aligned}$$

To define the loop coproduct $\lambda$ (of shifted degree $-1$), we need to pick a nowhere vanishing vector field on $S^1$. Up to homotopy there are two choices of non-vanishing vector fields on $S^1$,

$$\begin{aligned} v_\pm (x) = \pm {\varepsilon }, \end{aligned}$$

for some fixed small ${\varepsilon }>0$. We associate to $v_\pm$ the $\tau$-dependent vector fields

$$\begin{aligned} v_\pm ^\tau (x) = \pm (1-2\tau ){\varepsilon },\qquad \tau \in [0,1] \end{aligned}$$

which agree with $v_\pm$ at $\tau =0$ and with $-v_\pm$ at $\tau =1$. Their time-one maps are

$$\begin{aligned} f_\pm ^\tau (x) = x\pm (1-2\tau ){\varepsilon }. \end{aligned}$$

In the next Proposition, we compute the coproducts $\lambda _\pm$ associated to this choice of $\tau$-dependent vector fields.

Proposition 8.6

The loop coproducts $\lambda _\pm$ on ${\mathbb {H}}_*(\Lambda S^1)$ defined with the $\tau$-dependent vector fields $v_\pm ^\tau$ are given for $k\in {\mathbb {Z}}$ by

$$\begin{aligned} \lambda _+(AU^k)&= {\left\{ \begin{array}{ll} \quad \sum _{i=0}^{k}AU^i\otimes AU^{k-i}, &{}\quad k\geqslant 0, \\ -\sum _{i=k+1}^{-1}AU^i\otimes AU^{k-i}, &{}\quad k<0, \end{array}\right. } \\ \lambda _+(U^k)&= {\left\{ \begin{array}{ll} \quad \sum _{i=0}^{k}(AU^i\otimes U^{k-i} - U^i\otimes AU^{k-i}), &{}\quad k\geqslant 0, \\ -\sum _{i=k+1}^{-1}(AU^i\otimes U^{k-i} - U^i\otimes AU^{k-i}), &{}\quad k<0, \end{array}\right. }\\ \lambda _-(AU^k)&= {\left\{ \begin{array}{ll} \quad \sum _{i=1}^{k-1}AU^i\otimes AU^{k-i}, &{} \quad k> 0, \\ -\sum _{i=k}^{0}AU^i\otimes AU^{k-i}, &{}\quad k\leqslant 0, \end{array}\right. } \\ \lambda _-(U^k)&= {\left\{ \begin{array}{ll} \quad \sum _{i=1}^{k-1}(AU^i\otimes U^{k-i} - U^i\otimes AU^{k-i}), &{}\quad k> 0, \\ -\sum _{i=k}^{0}(AU^i\otimes U^{k-i} - U^i\otimes AU^{k-i}), &{}\quad k\leqslant 0. \end{array}\right. } \end{aligned}$$

Proof

Let us compute $\lambda _\pm (AU^k)$. By definition, we need to determine the times $\tau \in (0,1)$ such that

$$\begin{aligned} AU^k(\tau ) = k\tau = f_\pm ^\tau (AU^k(0)) = \pm (1-2\tau ){\varepsilon }\mod {\mathbb {Z}}, \end{aligned}$$

i.e. $k\tau = i\pm (1-2\tau ){\varepsilon }$ with $i\in {\mathbb {Z}}$. In other words, we are looking for the $i\in {\mathbb {Z}}$ such that

$$\begin{aligned} \tau = \frac{i\pm {\varepsilon }}{k\pm 2{\varepsilon }} \in (0,1). \end{aligned}$$

For $\lambda _+$, we obtain

$$\begin{aligned} \tau = \frac{i+{\varepsilon }}{k+2{\varepsilon }} \in (0,1) \Longleftrightarrow {\left\{ \begin{array}{ll} i=0,\dots ,k, &{}\quad k\geqslant 0, \\ i=k+1,\dots ,-1, &{}\quad k<0, \end{array}\right. } \end{aligned}$$

while for $\lambda _-$, we get

$$\begin{aligned} \tau = \frac{i-{\varepsilon }}{k-2{\varepsilon }} \in (0,1) \Longleftrightarrow {\left\{ \begin{array}{ll} i=1,\dots ,k-1, &{}\quad k > 0, \\ i=k,\dots ,0, &{}\quad k\leqslant 0. \end{array}\right. } \end{aligned}$$

This yields the expressions for $\lambda _\pm (AU^k)$, and $\lambda _\pm (U^k)$ is computed similarly. $\square$

Proposition 8.6 shows that for $M=S^1$ the coproduct on reduced loop homology does depend on the choice of a nowhere vanishing vector field. One can verify that both coproducts $\lambda _\pm$ define together with the loop product a commutative cocommutative infinitesimal anti-symmetric bialgebra in the sense of [21] with

$$\begin{aligned} \lambda _\pm (1) = \pm (A\otimes 1-1\otimes A). \end{aligned}$$

The unital infinitesimal relation reads now

Remark 8.7

Just like in the case of higher dimensional spheres, the expressions of the coproducts $\lambda _\pm$ on ${\mathbb {H}}_*(\Lambda S^1)$ can be derived from the unital infinitesimal relation combined with knowledge of the product $\mu$ and of the values

$$\begin{aligned} \lambda _\pm (1)&=\pm (A\otimes 1-1\otimes A),\\ \lambda _\pm (A)&=\pm A\otimes A,\\ \lambda _+(U)&=(A\otimes U - U\otimes A) + (AU\otimes 1 - 1\otimes AU),\\ \lambda _-(U)&=0. \end{aligned}$$

For example, to compute $\lambda _\pm (U^{-1})$ one applies the unital infinitesimal relation to $U\otimes U^{-1}$, to compute $\lambda _\pm (AU^{-1})$ one applies the unital infinitesimal relation to $A\otimes U^{-1}$ (or to $AU^{-1}\otimes U$) etc.

Remark 8.8

The example of the circle is very rich in that it also shows that the condition $v^1=-v^0$ for the family of vector fields $v^\tau$ is necessary in order for the coproducts to have a good algebraic behaviour. For example, with a constant family $v^\tau \equiv v_+$, we find an operation $\lambda _{v_+,v_+}$ given by

$$\begin{aligned} \lambda _{v_+,v_+}(AU^k)&= {\left\{ \begin{array}{ll} \quad \sum _{i=0}^{k-1}AU^i\otimes AU^{k-i}, &{}\quad k\geqslant 0, \\ -\sum _{i=k}^{-1}AU^i\otimes AU^{k-i}, &{}\quad k<0, \end{array}\right. } \\ \lambda _{v_+,v_+}(U^k)&= {\left\{ \begin{array}{ll} \quad \sum _{i=0}^{k-1}(AU^i\otimes U^{k-i} - U^i\otimes AU^{k-i}), &{}\quad k\geqslant 0, \\ -\sum _{i=k}^{-1}(AU^i\otimes U^{k-i} - U^i\otimes AU^{k-i}), &{}\quad k<0. \end{array}\right. } \end{aligned}$$

A direct check shows that this operation is neither coassociative, nor cocommutative, though it satisfies the unital infinitesimal relation with $\lambda _{v_+,v_+}(1)=0$, i.e. Sullivan’s relation. Similarly, with the constant family $v^\tau \equiv v_-$, we find an operation $\lambda _{v_-,v_-}$ given by

$$\begin{aligned} \lambda _{v_-,v_-}(AU^k)&= {\left\{ \begin{array}{ll} \quad \sum _{i=1}^{k}AU^i\otimes AU^{k-i}, &{}\quad k> 0, \\ -\sum _{i=k+1}^{0}AU^i\otimes AU^{k-i}, &{}\quad k\leqslant 0, \end{array}\right. } \\ \lambda _{v_-,v_-}(U^k)&= {\left\{ \begin{array}{ll} \quad \sum _{i=1}^{k}(AU^i\otimes U^{k-i} - U^i\otimes AU^{k-i}), &{}\quad k> 0, \\ -\sum _{i=k+1}^{0}(AU^i\otimes U^{k-i} - U^i\otimes AU^{k-i}), &{}\quad k\leqslant 0. \end{array}\right. } \end{aligned}$$

Again, this is neither coassociative, nor cocommutative, though it satisfies Sullivan’s relation.

Appendix A: Local systems

We describe in this section the loop product and the loop coproduct with general twisted coefficients. This allows us in particular to dispose of the usual orientability assumption for the underlying manifold. To the best of our knowledge, the Chas–Sullivan product on loop space homology was constructed for the first time on nonorientable manifolds by Laudenbach [31], and the BV algebra structure by Abouzaid [7]. In this appendix, we extend the definitions to more general local systems, we take into account the coproduct, and we discuss the adaptations to reduced homology and cohomology groups $\overline{H}_*\Lambda$ and $\overline{H}^*\Lambda$. We also discuss the formulation and properties of the isomorphism between symplectic homology and loop homology with twisted coefficients.

1.1 A.1. Conventions

We use the following conventions from [7, §9.7]. Given a finite-dimensional real vector space V, its determinant line is the 1-dimensional real vector space $\det V=\Lambda ^{\max } V$. We view it as being a ${\mathbb {Z}}$-graded real vector space supported in degree $\dim _{\mathbb {R}}V$. To any 1-dimensional graded real vector space L, we associate an orientation line |L|, which is the rank 1 graded free abelian group generated by the two possible orientations of L, modulo the relation that their sum vanishes. The orientation line |L| is by definition supported in the same degree as L. When $L=\det V$, we denote its orientation line |V|.

Given a ${\mathbb {Z}}$-graded line $\ell$ (rank 1 free abelian group), its dual line $\ell ^{-1}=\textrm{Hom}_{\mathbb {Z}}(\ell ,{\mathbb {Z}})$ is by definition supported in opposite degree as $\ell$. There is a canonical isomorphism $\ell ^{-1}\otimes \ell \cong {\mathbb {Z}}$ induced by evaluation.

Given a ${\mathbb {Z}}$-graded object F, we denote F[k] the ${\mathbb {Z}}$-graded object obtained by shifting the degree down by $k\in {\mathbb {Z}}$, i.e. $F[k]_n=F_{n+k}$. For example, the shifted orientation line $|V|[\dim \, V]$ is supported in degree 0. A linear map $f:E\rightarrow F$ between ${\mathbb {Z}}$-graded vector spaces or free abelian groups has degree d if $f(E_n)\subset F_{n+d}$ for all n. In an equivalent formulation, the induced map $f[d]:E\rightarrow F[d]$ has degree 0. For example, the dual of a vector space or free abelian group supported in degree k is supported in degree $-k$. This is compatible with the grading convention for duals of ${\mathbb {Z}}$-graded orientation lines. Given a ${\mathbb {Z}}$-graded rank 1 free abelian group $\ell$, we denote $\underline{\ell }$ the same abelian group with degree set to 0. For example $\underline{|V|}=|V|[\dim \, V]$.

Given two oriented real vector spaces U and W, we induce an orientation on their direct sum $U\oplus W$ by defining a positive basis to consist of a positive basis for U followed by a positive basis for W. This defines a canonical isomorphism at the level of orientation lines

$$\begin{aligned} |U|\otimes |W|\cong |U\oplus W|. \end{aligned}$$

Given an exact sequence of vector spaces

$$\begin{aligned} 0\rightarrow U \rightarrow V\rightarrow W\rightarrow 0, \end{aligned}$$

we induce an orientation on V out of orientations of U and W by defining a positive basis to consist of a positive basis for U followed by the lift of a positive basis for W. This defines a canonical isomorphism

$$\begin{aligned} |U|\otimes |W|\cong |V|. \end{aligned}$$

The following example will play a key role in the sequel.

Example A.1

(normal bundle to the diagonal) Let M be a manifold of dimension n. Consider the diagonal $\Delta \subset M\times M$ and denote $\nu \Delta$ its normal bundle. Let $p_{1,2}:M\times M\rightarrow M$ be the projections on the two factors, so that we have a canonical isomorphism $T(M\times M)\cong p_1^*TM \oplus p_2^*TM$. When restricted to $\Delta$ the projections coincide with the canonical diffeomorphism $p:\Delta {\mathop {\longrightarrow }\limits ^{\simeq }}M$. We obtain an exact sequence of bundles

$$\begin{aligned} 0\rightarrow T\Delta \rightarrow p^*TM\oplus p^*TM \rightarrow \nu \Delta \rightarrow 0. \end{aligned}$$

This gives rise to a canonical isomorphism $|\Delta |\otimes |\nu \Delta |\cong p^*|M|\otimes p^*|M|$ and, because $p^*|M|\otimes p^*|M|$ is canonically trivial, we obtain a canonical isomorphism

$$\begin{aligned} |\Delta |\cong |\nu \Delta |. \end{aligned}$$

Explicitly, this isomorphism associates to the equivalence class of a basis $((v_1,v_1),\dots , (v_n,v_n))$, $v_i\in T_qM$ of $T_{(q,q)}\Delta$ the equivalence class of the basis $([(0,v_1)],\dots ,[(0,v_n)])$ of $\nu _{(q,q)}\Delta$.

1.2 A.2. Homology with local systems

By local system, we mean a local system of ${\mathbb {Z}}$-graded rank 1 free ${\mathbb {Z}}$-modules. On each path-connected component of the underlying space, we think of such a local system in one of the following three equivalent ways: either as the data of the parallel transport representation of the fundamental groupoid, or as the data of the monodromy representation from the fundamental group $\pi$ to the multiplicative group $\{\pm 1\}$ together with the data of an integer (the degree), or as the data of a ${\mathbb {Z}}$-graded ${\mathbb {Z}}[\pi ]$-module which is free and of rank 1 as a ${\mathbb {Z}}$-module. Isomorphism classes of local systems on a path-connected space X are thus in bijective correspondence with $H^1(X;{\mathbb {Z}}/2)\times {\mathbb {Z}}$, where the first factor corresponds to the monodromy representation and the second factor to the grading. Here, and in the sequel, we identify the multiplicative group $\{\pm 1\}$ with the additive group ${\mathbb {Z}}/2$. We refer to [9] for a comprehensive discussion with emphasis on local systems on free loop spaces. One other point of view on local systems describes these as locally constant sheaves, but we will only marginally touch upon it in §A.3.

Given a local system $\nu$, we can change the coefficients to any commutative ring R by considering $\nu _R=\nu \otimes _{\mathbb {Z}}R$. The monodromy of such a local system still takes values in $\{\pm 1\}$, and this property characterises local systems of rank 1 free R-modules which are obtained from local systems of rank 1 free ${\mathbb {Z}}$-modules by tensoring with R.

Let X be a path-connected space admitting a universal cover ${\tilde{X}}$. Denote its fundamental group at some fixed basepoint $\pi =\pi _1(X)$. Interpreting a local system $\nu$ on X as a ${\mathbb {Z}}[\pi ]$-module, one defines singular homology/cohomology with coefficients in $\nu$ in terms of singular chains on ${\tilde{X}}$ as

$$\begin{aligned} H_*(X;\nu )= & {} H_*(C_*({\tilde{X}};{\mathbb {Z}})\otimes _{{\mathbb {Z}}[\pi ]}\nu ), \\ H^*(X;\nu )= & {} H_*(\textrm{Hom}_{{\mathbb {Z}}[\pi ]}(C_*({\tilde{X}};{\mathbb {Z}}),\nu )). \end{aligned}$$

The homology/cohomology with local coefficients extended to a commutative ring R are the R-modules

$$\begin{aligned} H_*(X;\nu _R)= & {} H_*(C_*({\tilde{X}};{\mathbb {Z}})\otimes _{{\mathbb {Z}}[\pi ]}\nu _R), \\ H^*(X;\nu _R)= & {} H_*\bigl (\textrm{Hom}_{{\mathbb {Z}}[\pi ]}(C_*({\tilde{X}};{\mathbb {Z}}),\nu _R)\bigr ). \end{aligned}$$

In our grading convention, the cohomology with constant coefficients is supported in nonpositive degrees and equals the usual cohomology in the opposite degree. The induced differential on the dual group $\textrm{Hom}_{{\mathbb {Z}}[\pi ]}(C_*({\tilde{X}};{\mathbb {Z}}),\nu _R)$ has degree $-1$.

The tensor product $\nu _1\otimes \nu _2$ of two local systems is again a local system. Its ${\mathbb {Z}}[\pi ]$-module structure is the diagonal one and its degree is the sum of the degrees of the factors. Note that viewing $\nu _1,\nu _2$ as elements in $H^1(X;{\mathbb {Z}}/2)\times {\mathbb {Z}}$, their tensor product is given by their sum $\nu _1+\nu _2$. Operations like cap or cup product naturally land in homology/cohomology with coefficients in the tensor product of the coefficients of the factors.

Homology/cohomology with local coefficients behave functorially in the following sense. Given a continuous map $f:X\rightarrow Y$ and a local system $\nu$ on Y described as a ${\mathbb {Z}}[\pi _1(Y)]$-module, the pullback local system $f^*\nu$ on X is defined by inducing a ${\mathbb {Z}}[\pi _1(X)]$-module structure via $f_*$. We then have canonical maps

$$\begin{aligned} f_*:H_*(X;f^*\nu )\rightarrow H_*(Y;\nu ),\qquad f^*:H^*(Y;\nu )\rightarrow H^*(X;f^*\nu ). \end{aligned}$$

The algebraic duality isomorphism with coefficients in a field $\mathbb {K}$ takes the form

$$\begin{aligned} H^{-k}(X;\nu _\mathbb {K}^{-1}){\mathop {\longrightarrow }\limits ^{\cong }}H_k(X; \nu _\mathbb {K})^\vee , \qquad k\in {\mathbb {Z}}. \end{aligned}$$

The map is induced by the canonical evaluation of cochains on chains. We check that degrees fit in the case of graded local systems: given a local system $\nu _\mathbb {K}$ of degree d, and recalling our notation $\underline{\nu _\mathbb {K}}=\nu _\mathbb {K}[d]$ and $\underline{\nu _\mathbb {K}^{-1}}= \nu _\mathbb {K}^{-1}[-d]$, we have

$$\begin{aligned} H_k(X;\nu _\mathbb {K}) = H_{k-d}(X;\underline{\nu _\mathbb {K}}),\qquad H^{-k}(X;\nu _\mathbb {K}^{-1})=H^{-k+d}(X;\underline{\nu _\mathbb {K}^{-1}}), \end{aligned}$$

so $H_k(X;\nu _\mathbb {K})^\vee$ and $H^{-k}(X;\nu _\mathbb {K}^{-1})$ both live in degree $d-k$.

1.3 A.3. Poincaré duality

Consider a manifold M of dimension n. We denote by |M| the local system on M whose fibre at any point $q\in M$ is the orientation line $|T_qM|$, supported by definition in degree n. We refer to |M| as the orientation local system of M. The monodromy along a loop $\gamma$ is $+1$ if the loop preserves the orientation (i.e. the pullback bundle $\gamma ^*TM$ is orientable), and $-1$ if the loop reverses it. The local system |M| is trivial if and only if the manifold M is orientable. A choice of orientation is equivalent to the choice of one of the two possible isomorphisms $\underline{|M|}\simeq {\mathbb {Z}}$. The local system $|M|\otimes {\mathbb {Z}}/2$ is trivial, and this reflects the fact that any manifold is ${\mathbb {Z}}/2$-orientable.

Suppose now that M is closed. Then, it carries a fundamental class $[M]\in H_n(M;\underline{|M|})=H_0(M;|M|^{-1})$.

For any local system $\nu$ on M, the cap product with a fundamental class defines a Poincaré duality isomorphism

$$\begin{aligned} H^*(M;\nu ) {\mathop {\longrightarrow }\limits ^{\cong }}H_*(M;\nu \otimes |M|^{-1}),\qquad \alpha \mapsto [M]\cap \alpha . \end{aligned}$$

Remark A.2

Here is a description of the fundamental class using the interpretation of local systems as locally constant sheaves (see for example [28], Lemma 3.27 and Example 3 H.3). Let $M'{\mathop {\rightarrow }\limits ^{p}}M$ be the orientation double cover. Given the constant local system ${\mathbb {Z}}$ on $M'$, the pushforward $p_*{\mathbb {Z}}$ to M has rank 2 and can be decomposed as $\underline{|M|}\oplus {\mathbb {Z}}$ (the map ${\mathbb {Z}}\oplus {\mathbb {Z}}\rightarrow {\mathbb {Z}}\oplus {\mathbb {Z}}$, $(x,y)\mapsto (y,x)$ fixes the diagonal and acts by $-\textrm{Id}$ on the anti-diagonal). The composition $H_*(M';{\mathbb {Z}}){\mathop {\rightarrow }\limits ^{p_*}}H_*(M;p_*{\mathbb {Z}}){\mathop {\rightarrow }\limits ^{\simeq }}H_*(M;\underline{|M|})\oplus H_*(M;{\mathbb {Z}})$ is an isomorphism because $p_*$ is an isomorphism. Since $H_n(M;{\mathbb {Z}})=0$ if M is nonorientable, we obtain that $H_n(M;\underline{|M|})$ has rank 1. A generator is the image of a generator in $H_n(M';{\mathbb {Z}})$ via the above composition.

1.4 A.4. Thom isomorphism and Gysin sequence

Let $E{\mathop {\longrightarrow }\limits ^{p}}X$ be a real vector bundle of rank r, and denote $\dot{E}$ the complement of the zero section. Let |E| be the local system on X whose fibre at a point $x\in X$ is the orientation line $|E_x|$ of the fibre of E at x. The local system |E| is called the orientation local system of E and is supported in degree r. The Thom class is a generator

$$\begin{aligned} \tau \in H^{-r}(E,\dot{E};\underline{p^*|E|})=H^0(E,\dot{E};p^*|E|). \end{aligned}$$

The Thom isomorphism takes the form

$$\begin{aligned} H_k(E,\dot{E}){\mathop {\longrightarrow }\limits ^{\simeq }}H_{k-r}(X;\underline{|E|})=H_k(X;|E|), \qquad k\in {\mathbb {Z}}\end{aligned}$$

(cap product with $\tau$), respectively

$$\begin{aligned} H^k(X;|E|^{-1})=H^{k+r}(X;\underline{|E|^{-1}}){\mathop {\longrightarrow }\limits ^{\simeq }}H^k(E,\dot{E}), \qquad k\in {\mathbb {Z}}\end{aligned}$$

(cup product with $\tau$). More generally, for any local system $\nu$ on X, we have isomorphisms

$$\begin{aligned}{} & {} H_k(E,\dot{E};p^*\nu ) {\mathop {\longrightarrow }\limits ^{\simeq }}H_{k-r}(X;\nu \otimes \underline{|E|})=H_k(X;\nu \otimes |E|), \\{} & {} H^k(X;\nu \otimes |E|^{-1}) = H^{k+r}(X;\nu \otimes \underline{|E|^{-1}}){\mathop {\longrightarrow }\limits ^{\simeq }}H^k(E,\dot{E};p^*\nu ). \end{aligned}$$

Pulling back the Thom class under the inclusion $i:X\rightarrow E$ of the zero section yields the Euler class

$$\begin{aligned} e = i^*\tau \in H^{-r}(X;\underline{|E|})=H^0(X;|E|). \end{aligned}$$

Denote by $S\subset \dot{E}$ the sphere bundle with projection $\pi =p|_S:S\rightarrow X$. Then, the long exact sequence of the pair $(E,\dot{E})$ fits into the commuting diagram

where the lower sequence is the Gysin sequence. More generally, for each local system $\nu$ on X, we get a Gysin sequence

$$\begin{aligned} \cdots \, H^k(X;\nu \otimes |E|^{-1})&{\mathop {\longrightarrow }\limits ^{\cup e}}H^k(X;\nu ) \\&\qquad {\mathop {\longrightarrow }\limits ^{\pi ^*}}H^k(S;\pi ^*\nu ) {\mathop {\longrightarrow }\limits ^{\pi _*}}H^{k-1}(X;\nu \otimes |E|^{-1})\, \cdots \end{aligned}$$

1.5 A.5. Spaces of loops with self-intersection

Let M be a manifold of dimension n, $\Lambda =\Lambda M$ its space of free loops of Sobolev class $W^{1,2}$, and $\textrm{ev}_s:\Lambda \rightarrow M$ the evaluation of loops at time s. We define

$$\begin{aligned} \mathcal {F}=\{(\gamma ,\delta )\in \Lambda \times \Lambda \mid \gamma (0)=\delta (0)\}\subset \Lambda \times \Lambda \end{aligned}$$

(pairs of loops with the same basepoint), and

$$\begin{aligned} \mathcal {F}_s = \{\gamma \in \Lambda \mid \gamma (s)=\gamma (0)\}\subset \Lambda , \qquad s\in (0,1) \end{aligned}$$

(loops with a self-intersection at time s). Denoting $f:\Lambda \times \Lambda \rightarrow M\times M$, $f=\textrm{ev}_0\times \textrm{ev}_0$ and $f_s:\Lambda \rightarrow M\times M$, $f_s=(\textrm{ev}_0,\textrm{ev}_s)$, we can equivalently write

$$\begin{aligned} \mathcal {F}=f^{-1}(\Delta ),\qquad \mathcal {F}_s=f_s^{-1}(\Delta ). \end{aligned}$$

The maps f and $f_s$ are smooth and transverse to the diagonal $\Delta$, so that $\mathcal {F}$ and $\mathcal {F}_s$ are Hilbert submanifolds of codimension n. Denoting $\nu \mathcal {F}$ and $\nu \mathcal {F}_s$ their normal bundles, we obtain canonical isomorphisms

$$\begin{aligned} \nu \mathcal {F}\cong f^*\nu \Delta ,\qquad \nu \mathcal {F}_s\cong f_s^*\nu \Delta . \end{aligned}$$

In view of Example A.1, we infer canonical isomorphisms

$$\begin{aligned} |\nu \mathcal {F}|\cong f^*|\Delta |\cong \textrm{ev}_0^*|M|,\qquad |\nu \mathcal {F}_s|\cong f_s^*|\Delta |\cong \textrm{ev}_0^*|M|, \end{aligned}$$

(36)

where, in the first formula, $\textrm{ev}_0:\mathcal {F}\rightarrow M$ is the evaluation of pairs of loops at their common origin.

Denote $i:\mathcal {F}\hookrightarrow \Lambda \times \Lambda$ and $i_s:\mathcal {F}_s\hookrightarrow \Lambda$ the inclusions. Recall the restriction maps (7). Define the cutting map at time s

$$\begin{aligned} c_s: \mathcal {F}_s\rightarrow \mathcal {F},\qquad c_s(\gamma )=(\gamma |_{[0,s]},\gamma |_{[s,1]}) \end{aligned}$$

and the concatenation map at time s

$$\begin{aligned} g_s:\mathcal {F}\rightarrow \mathcal {F}_s, \qquad g_s(\gamma _1,\gamma _2)(t)=\left\{ \begin{array}{ll}\gamma _1(\frac{t}{s}), &{}\quad t\in [0,s],\\ \gamma _2(\frac{t-s}{1-s}), &{}\quad t\in [s,1].\end{array}\right. \end{aligned}$$

The maps $c_s$ and $g_s$ are smooth diffeomorphisms inverse to each other. The situation is summarised in the diagram

Lemma A.3

Let $\nu$ be a local system (of rank 1 free abelian groups) on $\Lambda$ supported in degree 0. Denote $p_{1,2}:\Lambda \times \Lambda \rightarrow \Lambda$ the projections on the two factors. The following two conditions are equivalent:

$$\begin{aligned} c_s^*(p_1^*\nu \otimes p_2^*\nu )|_\mathcal {F}\simeq \nu |_{\mathcal {F}_s}, \end{aligned}$$

(37)

and

$$\begin{aligned} (p_1^*\nu \otimes p_2^*\nu )|_\mathcal {F}\simeq g_s^*(\nu |_{\mathcal {F}_s}). \end{aligned}$$

(38)

Proof

The first condition is $c_s^*i^*(p_1^*\nu \otimes p_2^*\nu )\simeq i_s^*\nu$. Since $g_s$ is a homeomorphism, this is equivalent to

$$\begin{aligned} g_s^*c_s^*i^*(p_1^*\nu \otimes p_2^*\nu )\simeq g_s^*i_s^*\nu . \end{aligned}$$

In view of $c_sg_s=\textrm{Id}_{\mathcal {F}_s}$, this is the same as the second condition. $\square$

Definition A.4

A degree 0 local system $\nu$ on $\Lambda$ is compatible with products if it satisfies the equivalent conditions of Lemma A.3.

A local system $\nu$ which is compatible with products must necessarily have degree 0 (and rank 1). Also, $\nu |_M$ must be trivial: restricting both sides of (37) or (38) to the constant loops yields $\nu |_M\otimes \nu |_M\simeq \nu |_M$.

Remark A.5

Local systems which are compatible with products play a key role in the sequel definition of the loop product and loop coproduct with local coefficients. Condition (37) is the one that ensures the coproduct is defined with coefficients twisted by $\nu$, whereas condition (38) is the one that ensures the product is defined with coefficients twisted by $\nu$. That the two conditions are equivalent can be seen as yet another instance of Poincaré duality for free loops.

We refer to Remark A.11 for an additional condition on the isomorphisms (38) which is needed for the associativity of the product and coassociativity of the coproduct.

Example A.6

(Transgressive local systems) Let $\Lambda =\sqcup _\alpha \Lambda _\alpha M$ be the decomposition of the free loop space into connected components, indexed by conjugacy classes $\alpha$ in the fundamental group. We view loops $\gamma :S^1\rightarrow \Lambda$ as maps $\gamma \times S^1:S^1\times S^1\rightarrow M$, $(u,t)\mapsto \gamma (u)(t)$. This induces a map $\pi _1(\Lambda _\alpha M)\rightarrow H_1(\Lambda _\alpha M;{\mathbb {Z}})\rightarrow H_2(M;{\mathbb {Z}})$, $[\gamma ]\mapsto [\gamma \times S^1]$. Dually, and specialising to ${\mathbb {Z}}/2$-coefficients, any cohomology class $c\in H^2(M;{\mathbb {Z}}/2)$ determines a cohomology class $\tau _c\in H^1(\Lambda ;{\mathbb {Z}}/2)=\prod _\alpha \textrm{Hom}(\pi _1(\Lambda _\alpha M);{\mathbb {Z}}/2)$ via

$$\begin{aligned} \langle \tau _c,[\gamma ]\rangle = \langle c,[\gamma \times S^1]\rangle . \end{aligned}$$

We denote the corresponding local system on $\Lambda$ also by $\tau _c$. Degree 0 local systems obtained in this way are called transgressive [7].

Transgressive local systems are compatible with products. Indeed, the identity (38) is a direct consequence of the equality $[g_s(\gamma _1,\gamma _2) \times S^1]=[\gamma _1\times S^1]+[\gamma _2\times S^1]$, which holds in $H_2(M;{\mathbb {Z}})$ for all $(\gamma _1,\gamma _2):S^1\rightarrow \mathcal {F}$.

The transgressive local system

$$\begin{aligned} \sigma =\tau _{w_2} \end{aligned}$$

(39)

defined by the second Stiefel–Whitney class $w_2\in H^2(M;{\mathbb {Z}}/2)$ will play a special role in the sequel.

Example A.7

Following Abouzaid [7], define for each loop $\gamma \in \Lambda$ the shift

$$\begin{aligned} w(\gamma )=\left\{ \begin{array}{ll}0, &{}\quad \text{ if } \gamma \text{ preserves } \text{ the } \text{ orientation }, \\ -1, &{}\quad \text{ if } \gamma \text{ reverses } \text{ the } \text{ orientation }. \end{array}\right. \end{aligned}$$

Define the local system

$$\begin{aligned} {\tilde{o}}=\textrm{ev}_0^*\underline{|M|}^{-w} \end{aligned}$$

(40)

to be trivial on the components where $\gamma$ preserves the orientation, and equal to $\textrm{ev}_0^*\underline{|M|}$ on components where $\gamma$ reverses the orientation.

The local system ${\tilde{o}}$ is compatible with products: the equality $w(\gamma _1)+w(\gamma _2)=w(g_s(\gamma _1,\gamma _2))$ holds in ${\mathbb {Z}}/2$ for all $(\gamma _1,\gamma _2)\in \mathcal {F}$. Note that the local system ${\tilde{o}}$ is not transgressive and, in case M is nonorientable, it is nontrivial on all connected components $\Lambda _\alpha M$ whose elements reverse orientation.

Question A.8

Characterise in cohomological terms the local systems on $\Lambda$ which are compatible with products. For example, it follows from [9, Lemma 1] that, on a simply connected manifold, a local system $\nu$ is compatible with products if and only if $\nu |_M$ is trivial. A mild generalisation is given by [9, Proposition 10].

1.6 A.6. Loop product with local coefficients

Following [27], we view the loop product as being defined by going from left to right in the diagram

$$\begin{aligned} \Lambda \times \Lambda \hookleftarrow \mathcal {F}{\mathop {\longrightarrow }\limits ^{g}}\Lambda , \end{aligned}$$

where $g=i_sg_s$ for some fixed $s\in (0,1)$. More precisely, the loop product with integer coefficients is defined as the composition

$$\begin{aligned} H_i (\Lambda ;{\mathbb {Z}}) \otimes H_j (\Lambda ;{\mathbb {Z}})&{\mathop {\longrightarrow }\limits ^{\epsilon \times }} H_{i+j}(\Lambda \times \Lambda ;{\mathbb {Z}}) \\&\longrightarrow H_{i+j}(\nu \mathcal {F},{\dot{\nu }}\mathcal {F};{\mathbb {Z}}) \\&{\mathop {\longrightarrow }\limits ^{\simeq }} H_{i+j}(\mathcal {F};\textrm{ev}_0^*{|M|}) \\&{\mathop {\longrightarrow }\limits ^{g_*}} H_{i+j}(\Lambda ;\textrm{ev}_0^*{|M|}). \end{aligned}$$

The first map is the homology cross-product corrected by a sign $\epsilon =(-1)^{n(i+n)}$ ([29, Appendix B]), the second map is the composition of the map induced by inclusion $\Lambda \times \Lambda \hookrightarrow (\Lambda \times \Lambda ,\Lambda \times \Lambda {\setminus } \mathcal {F})$ with excision and the tubular neighbourhood isomorphism, and the third map is the Thom isomorphism. In case M is not orientable the loop product does not land in homology with integer coefficients and thus fails to define an algebra structure on $H_*(\Lambda ;{\mathbb {Z}})$. This can be corrected by using at the source homology with local coefficients.

Definition A.9

Define on $\Lambda$ the local system

$$\begin{aligned} \mu {:}{=} \textrm{ev}_0^*|M|^{-1}. \end{aligned}$$

The archetypal loop product is the bilinear map

$$\begin{aligned} \bullet : H_i(\Lambda ;\mu ) \otimes H_j(\Lambda ;\mu ) \rightarrow H_{i+j}(\Lambda ;\mu ) \end{aligned}$$

defined as the composition

$$\begin{aligned} H_i (\Lambda ;\mu ) \otimes H_j (\Lambda ;\mu )&{\mathop {\longrightarrow }\limits ^{\epsilon \times }} H_{i+j}(\Lambda \times \Lambda ;p_1^*\mu \otimes p_2^*\mu ) \\&\longrightarrow H_{i+j}(\nu \mathcal {F},{\dot{\nu }}\mathcal {F};p_1^*\mu \otimes p_2^*\mu |_{\nu \mathcal {F}}) \\&{\mathop {\longrightarrow }\limits ^{\simeq }} H_{i+j}(\mathcal {F};(p_1^*\mu \otimes p_2^*\mu )|_\mathcal {F}\otimes \textrm{ev}_0^*|M|) \\&{\mathop {\longrightarrow }\limits ^{g_*}} H_{i+j}(\Lambda ;\mu ). \end{aligned}$$

The description of the maps is the same as above, with $\epsilon =(-1)^{ni}$ because of the shift $H_i(\Lambda ;\mu )=H_{i+n}(\Lambda ;\underline{\mu })$. However, one still needs to check that the local systems of coefficients are indeed as written. For the first, second and third map the behaviour of the coefficients follows general patterns. For the last map, we use that

$$\begin{aligned} (p_1^*\mu \otimes p_2^*\mu )|_\mathcal {F}\otimes \textrm{ev}_0^*|M|\simeq g^*\mu , \end{aligned}$$

which is true for our specific $\mu =\textrm{ev}_0^*|M|^{-1}$.

The archetypal loop product is associative, graded commutative, and it has a unit represented by the fundamental class

$$\begin{aligned}{}[M]\in H_0(M;|M|^{-1})=H_n(M;\underline{|M|}) \end{aligned}$$

from §A.3. With our grading conventions, the archetypal loop product has degree 0 and the local system $\mu$ is supported in degree $-n$. In the case where M is oriented, we recover the usual loop product.

More generally, the loop product can be defined with further twisted coefficients.

Definition A.10

Let $\nu$ be a degree 0 local system (of rank 1 free ${\mathbb {Z}}$-modules) on $\Lambda$ which is compatible with products. The loop product with coefficients twisted by $\nu$ is the bilinear map

$$\begin{aligned} \bullet : H_i(\Lambda ;\nu \otimes \mu ) \otimes H_j(\Lambda ;\nu \otimes \mu ) \rightarrow H_{i+j}(\Lambda ;\nu \otimes \mu ) \end{aligned}$$

(with $\mu =\textrm{ev}_0^*|M|^{-1}$ as above) defined as the composition

$$\begin{aligned} H_i (\Lambda ;\nu \otimes \mu )&\otimes H_j (\Lambda ;\nu \otimes \mu ) \\&{\mathop {\longrightarrow }\limits ^{\epsilon \times }} H_{i+j}(\Lambda \times \Lambda ;(p_1^*\nu \otimes p_2^*\nu ) \otimes (p_1^*\mu \otimes p_2^*\mu )) \\&\longrightarrow H_{i+j}(\nu \mathcal {F},{\dot{\nu }}\mathcal {F};(p_1^*\nu \otimes p_2^*\nu ) \otimes (p_1^*\mu \otimes p_2^*\mu )|_{\nu \mathcal {F}}) \\&{\mathop {\longrightarrow }\limits ^{\simeq }} H_{i+j}(\mathcal {F};(p_1^*\nu \otimes p_2^*\nu ) \otimes (p_1^*\mu \otimes p_2^*\mu )|_\mathcal {F}\otimes \textrm{ev}_0^*|M|) \\&{\mathop {\longrightarrow }\limits ^{g_*}} H_{i+j}(\Lambda ;\nu \otimes \mu ). \end{aligned}$$

As before, we have $\epsilon =ni$. For the last map, we use the isomorphism $(p_1^*\mu \otimes p_2^*\mu )|_\mathcal {F}\otimes \textrm{ev}_0^*|M|\simeq g^*\mu$, and the isomorphism $(p_1^*\nu \otimes p_2^*\nu )|_\mathcal {F}\simeq g^*\nu$ which expresses the compatibility with products for $\nu$.

The loop product with twisted coefficients is graded commutative and unital. Recalling that the compatibility with products for $\nu$ forces its restriction to M to be trivial, the unit is again represented by the fundamental class

$$\begin{aligned}{}[M]\in H_0(M;\nu |_M\otimes |M|^{-1})=H_0(M;|M|^{-1})=H_n(M;\underline{|M|}). \end{aligned}$$

Remark A.11

Associativity of the loop product with twisted coefficients depends on the following associativity condition on the isomorphisms (37) and (38). Given $s,s'\in (0,1)$ denote $s''=(s'-ss')/(1-ss')$, so that $g_{s'}\circ (g_s\times \textrm{id})=g_{ss'}\circ (\textrm{id}\times g_{s''})$. Denoting $\Phi _s:(p_1^*\nu \otimes p_2^*\nu )|_\mathcal {F}{\mathop {\rightarrow }\limits ^{\simeq }}g_s^*\nu |_{\mathcal {F}_s}$ the isomorphism from (38), we require the associativity condition

$$\begin{aligned} \Phi _{ss'}\circ (\textrm{Id}\otimes \Phi _{s''})=\Phi _{s'}\circ (\Phi _s\otimes \textrm{Id}). \end{aligned}$$

This holds for the transgressive local systems from Example A.6 and for the local system in Example A.7.

Also, because (37) and (38) are equivalent, this condition on (38) will guarantee coassociativity of the coproduct, see below.

1.7 A.7. Loop coproduct with coefficients

Again following [27], we view the primary coproduct on loop homology as being defined by going from left to right in the diagram

$$\begin{aligned} \Lambda \hookleftarrow \mathcal {F}_s {\mathop {\longrightarrow }\limits ^{c_s}}\Lambda \times \Lambda \end{aligned}$$

for some fixed $s\in (0,1)$, where $c_s$ stands for $ic_s$ in the notation of §A.5. We restrict in this section to coefficients in a field $\mathbb {K}$ and all local systems are accordingly understood in this category. The reason for this restriction is explained below. The primary coproduct with constant coefficients is defined as the composition

The first map is the composition of the map induced by inclusion $\Lambda \rightarrow (\Lambda ,\Lambda \setminus \mathcal {F}_s)$ with the excision isomorphism towards the homology rel boundary of a tubular neighbourhood of $\mathcal {F}_s$. The second map is the Thom isomorphism. For the third map, we use that $c_s^*p_1^*\textrm{ev}_0^*=\textrm{ev}_0^*$. The fourth map is the Alexander–Whitney diagonal map followed by the Künneth isomorphism.⁷ Just like for the loop product, we see that if M is nonorientable the primary coproduct fails to define a coalgebra structure on $H_*(\Lambda ;\mathbb {K})$. This is corrected using homology with local coefficients as follows.

Definition A.12

Define on $\Lambda$ the local system

$$\begin{aligned} o {:}{=} \textrm{ev}_0^*|M| = \mu ^{-1}. \end{aligned}$$

The archetypal primary coproduct is the bilinear map

$$\begin{aligned} \vee _s: H_k(\Lambda ;o) \rightarrow \bigoplus _{i+j=k}H_i(\Lambda ;o) \otimes H_j(\Lambda ;o) \end{aligned}$$

(for some fixed $s\in [0,1]$) defined as the composition

$$\begin{aligned} H_k (\Lambda ;o)&\longrightarrow H_k(\nu \mathcal {F}_s,{\dot{\nu }}\mathcal {F}_s;o|_{\nu \mathcal {F}_s}) \\&{\mathop {\longleftarrow }\limits ^{\simeq }} H_k(\mathcal {F}_s;o\otimes \textrm{ev}_0^*|M|) \\&{\mathop {\longrightarrow }\limits ^{c_{s*}}} H_k(\Lambda \times \Lambda ;p_1^*o\otimes p_2^*o) \\&{\mathop {\longrightarrow }\limits ^{AW}} \bigoplus _{i+j=k}H_i(\Lambda ;o)\otimes H_j(\Lambda ;o). \end{aligned}$$

With our grading conventions, this coproduct has degree 0. Taking into account that $o=\textrm{ev}_0^*|M|$ is supported in degree n, this results in the coproduct having the usual degree $-n$ in ungraded notation. In the orientable case it recovers the usual primary coproduct.

Just like the product, the primary coproduct can be defined with further twisted coefficients.

Definition A.13

Let $\nu$ be a degree 0 local system (of rank one $\mathbb {K}$-vector spaces) on $\Lambda$ which is compatible with products. The primary coproduct with twisted coefficients is the bilinear map

$$\begin{aligned} \vee _s: H_k(\Lambda ;\nu \otimes o) \rightarrow \bigoplus _{i+j=k}H_i(\Lambda ;\nu \otimes o) \otimes H_j(\Lambda ;\nu \otimes o) \end{aligned}$$

(with $o=\textrm{ev}_0^*|M|$ as above and some fixed $s\in [0,1]$) defined as the composition

$$\begin{aligned} H_k (\Lambda ;\nu \otimes o)&\longrightarrow H_k(\nu \mathcal {F}_s,{\dot{\nu }}\mathcal {F}_s;\nu \otimes o|_{\nu \mathcal {F}_s}) \\&{\mathop {\longleftarrow }\limits ^{\simeq }} H_k(\mathcal {F}_s;\nu \otimes o^{\otimes 2}) \\&{\mathop {\longrightarrow }\limits ^{c_{s*}}} H_k(\Lambda \times \Lambda ;p_1^*(\nu \otimes o)\otimes p_2^*(\nu \otimes o)) \\&{\mathop {\longrightarrow }\limits ^{AW}} \bigoplus _{i+j=k}H_i(\Lambda ;\nu \otimes o)\otimes H_j(\Lambda ;\nu \otimes o). \end{aligned}$$

In the definition, we use $c_s^*(p_1^*o\otimes p_2^*o)\simeq o\otimes o$, and the condition $c_s^*(p_1^*\nu \otimes p_2^*\nu )\simeq \nu |_{\mathcal {F}_s}$ which is part of the condition of being compatible with products for $\nu$.

The arguments of Goresky–Hingston [27, §8] which show that, in the orientable case, there is a secondary coproduct of degree $-n+1$ defined on relative homology $H_*(\Lambda ,\Lambda _0;\mathbb {K})$, apply verbatim in the current setup involving local coefficients. As an outcome, we obtain the following.

Definition-Proposition A.14

For any degree 0 local system $\nu$ of rank one $\mathbb {K}$-vector spaces on $\Lambda$ which is compatible with products, there is a well-defined (secondary) loop coproduct with twisted coefficients (abbreviate $o=\textrm{ev}_0^*|M|$)

$$\begin{aligned} \vee : H_k(\Lambda ,\Lambda _0;\nu \otimes o) \rightarrow \bigoplus _{i+j=k+1}H_i(\Lambda ,\Lambda _0;\nu \otimes o) \otimes H_j(\Lambda ,\Lambda _0;\nu \otimes o). \end{aligned}$$

$\square$

As explained in [29], in order for this secondary coproduct to be coassociative in the case of a constant local system $\nu$, we need to correct the ij-component of the secondary product induced by the previously defined primary product by a sign $\epsilon =(-1)^{(n-1)(j-n)}$ (see [29, Definition 1.7] and note the shift in grading $H_j(\Lambda ,\Lambda _0;\nu \otimes o)=H_{j-n}(\Lambda ,\Lambda _0;\nu \otimes \underline{o})$). With this correction, the coproduct with constant local system $\nu$ is also graded cocommutative if gradings are shifted so that it has degree 0. However, it has no counit (this would contradict the infinite dimensionality of the homology of $\Lambda$).

In the case of coefficients twisted by a local system $\nu$ which is nonconstant, coassociativity further requires that the isomorphisms $\Phi _s$ expressing compatibility with products for $\nu$ satisfy the condition from Remark A.11. The coproduct is then also cocommutative.

One obtains dually a cohomology product [27, 29]. Note that, in contrast to the loop coproduct, the dual loop cohomology product is defined with arbitrary coefficients because its definition does not require the Künneth isomorphism.

Definition-Proposition A.15

For any degree 0 local system $\nu$ of rank 1 free abelian groups on $\Lambda$ which is compatible with products, there is a well-defined cohomology product with twisted coefficients (abbreviate $\mu =\textrm{ev}_0^*|M|^{-1}$)

$$\begin{aligned} \circledast : H^i(\Lambda ,\Lambda _0;\nu \otimes \mu ) \otimes H^j(\Lambda ,\Lambda _0;\nu \otimes \mu ) \rightarrow H^{i+j-1}(\Lambda ,\Lambda _0;\nu \otimes \mu ). \end{aligned}$$

$\square$

The cohomology product with twisted coefficients is associative. It is also graded commutative when viewing it as a degree 0 product on $H^{*-1}(\Lambda ,\Lambda _0;\nu \otimes \mu )$.

1.8 A.8. Reduced- vs. loop homology relative to $\chi \cdot$point

We explain in this section the interplay between reduced loop homology and loop homology relative to $\chi \cdot$point in the presence of local coefficients.

Recall the previous notation $o=\textrm{ev}_0^*|M|=\mu ^{-1}$, and let $\nu$ be a local system compatible with products. The arguments of Sect. 2.2 carry over verbatim to give a description of the loop product and coproduct in Morse homology with local coefficients in $\nu \otimes \mu$, respectively $\nu \otimes o$. For a definition of Morse homology with local coefficients, we refer to [7, §11.3] or [33, §7.2].

The reduced loop (co)homology groups $\overline{MH}_*$ and $\overline{MH}^*$ are defined with local coefficients as follows. Recall that $\nu |_M$ is trivial. We consider the map ${\varepsilon }$ given as the composition

where the vertical maps are restriction to, respectively inclusion of constant loops, and ${\varepsilon }_0$ is induced by multiplication with the Euler characteristic. We then define

$$\begin{aligned} \overline{MH}^*(\Lambda ;\nu \otimes \underline{\mu })=\ker {\varepsilon },\qquad \overline{MH}_*(\Lambda ;\nu \otimes \underline{\mu })=\textrm{ coker }\, {\varepsilon }. \end{aligned}$$

Thus, $\overline{MH}_*(\Lambda ;\nu \otimes \mu )=\overline{MH}_{*-n}(\Lambda ;\nu \otimes \underline{\mu })$ and $\overline{MH}_*(\Lambda ;\nu \otimes o)=\overline{MH}_{*+n}(\Lambda ;\nu \otimes \underline{\mu })$. Similarly to Sect. 2.2, the loop product descends to $\overline{MH}_*(\Lambda ;\nu \otimes \underline{\mu })$ because $\textrm{im}\,{\varepsilon }\subset H_*(\Lambda ;\nu \otimes \underline{\mu })$ is an ideal.

The loop (co)homology groups relative to $\chi \cdot$point are defined with local coefficients as follows. Recall again that $\nu |_M$ is trivial. Consider the embedding $\chi R q_0 \rightarrow MC_*(\Lambda ;\nu \otimes \underline{o})$ given by the inclusion $\chi R\hookrightarrow R$ and define the Morse chains relative to $\chi \cdot$point as $MC_*(\Lambda ,\chi \text {pt};\nu \otimes \underline{o})=MC_*(\Lambda ;\nu \otimes \underline{o})/\chi R q_0$. Similarly consider the projection $\pi :MC^*(\Lambda ;\nu \otimes \underline{\mu })\rightarrow R q_0$ and define the Morse cochains relative to $\chi \cdot$point to be $MC^*(\Lambda ,\chi \text {pt};\nu \otimes \underline{\mu })=\pi ^{-1} \ker (R{\mathop {\longrightarrow }\limits ^{\cdot \chi }}R)$. The loop (co)homology groups relative to $\chi \cdot$point are

$$\begin{aligned}{} & {} MH_*(\Lambda ,\chi \text {pt};\nu \otimes \underline{o}) = H_*(MC_*(\Lambda ,\chi \text {pt};\nu \otimes \underline{o})), \\{} & {} MH^*(\Lambda ,\chi \text {pt};\nu \otimes \underline{\mu }) = H^*(MC^*(\Lambda ,\chi \text {pt};\nu \otimes \underline{\mu })). \end{aligned}$$

The arguments of Sect. 2.2 carry over verbatim in order to show that the loop coproduct extends to $MH_*(\Lambda ,\chi \text {pt};\nu \otimes \underline{o})$ (for algebraic reasons, we need to use field coefficients as in §A.7). Interpreted dually as a product on cohomology, this is defined with arbitrary coefficients on $MH^*(\Lambda ,\chi \text {pt};\nu \otimes \underline{\mu })$.

The comparison between reduced loop homology and loop homology relative to a point goes as follows. Recalling that $\underline{\mu }=\underline{o}$, we have a commutative diagram

which induces

We thus get a canonical map

$$\begin{aligned} \overline{MH}_*(\Lambda ;\nu \otimes \underline{\mu })\longrightarrow MH_*(\Lambda ,\chi \text {pt};\nu \otimes \underline{o}) \end{aligned}$$

(41)

which is an isomorphism if and only if the map $\chi R \rightarrow MH_0(\Lambda ;\nu \otimes \underline{o})$ is injective. To study its injectivity, we can restrict without loss of generality to the component of contractible loops, in which case the target of this map is R if $\nu \otimes \underline{o}$ is trivial and R/2R if $\nu \otimes \underline{o}$ is nontrivial on that component. We thus obtain injectivity of this map, and an isomorphism in (41), under any of the following conditions:

• (i) $\nu \otimes \underline{o}$ is trivial on the component of contractible loops.

• (ii) $\chi =0$.

• (iii) R is 2-torsion.

1.9 A.9. Isomorphism between symplectic homology and loop homology

We spell out in this section the isomorphism between the symplectic homology of the cotangent bundle and the homology of the free loop space with twisted coefficients.

For the next definition, recall the local systems

$$\begin{aligned} \sigma = \tau _{w_2},\qquad {\tilde{o}} = \textrm{ev}_0^*\underline{|M|}^{-w} \end{aligned}$$

from (39) and (40), as well as the orientation local systems

$$\begin{aligned} \mu =\textrm{ev}_0^*|M|^{-1}=o^{-1}. \end{aligned}$$

Definition A.16

(Abouzaid [7]) The fundamental local system for symplectic homology of the cotangent bundle is the local system on $\Lambda$ given by

$$\begin{aligned} \eta = \sigma \otimes \mu \otimes {\tilde{o}}. \end{aligned}$$

The fundamental local system $\eta$ is supported in degree $-n$. Our previous discussion shows that the loop product is defined and has degree 0 on $H_*(\Lambda ;\eta )$, and the loop coproduct is defined and has degree $+1$ on $H_*(\Lambda ,\Lambda _0;\eta ^{-1})$. We can view the loop product as being defined on $H_*(\Lambda ;\underline{\eta })$, where it has degree $-n$, and the loop coproduct as being defined (with field coefficients) on $H_*(\Lambda ,\Lambda _0;\underline{\eta })$, where it has degree $1-n$. This point of view is useful when considering $\overline{H}_*(\Lambda ;\underline{\eta })$, which is a common space of definition (to which the product descends and the coproduct extends).

As proved in [5, 7], the chain map $\Psi =\Psi ^{\text {quadratic}}$ discussed in Sect. 5.3 associated to a quadratic Hamiltonian acts as

$$\begin{aligned} \Psi :FC_*(H)\rightarrow MC_*(S_L;\underline{\eta }) \end{aligned}$$

and induces an isomorphism $SH_*(D^*M){\mathop {\longrightarrow }\limits ^{\simeq }}H_*(\Lambda ;\underline{\eta })$. Given any local system $\nu$, the same map acts as $\Psi :FC_*(H;\nu )\rightarrow MC_*(S_L;\nu \otimes \underline{\eta })$ and induces an isomorphism $SH_*(D^*M;\nu ){\mathop {\longrightarrow }\limits ^{\simeq }}H_*(\Lambda ;\nu \otimes \underline{\eta })$.

Our filtered chain map $\Psi =\Psi ^{\text {linear}}$ from Sect. 5.5 associated to a linear Hamiltonian is a chain isomorphism $FC_*(H){\mathop {\longrightarrow }\limits ^{\simeq }}MC_*^{\le \mu }(E^{1/2};\underline{\eta })$, with $\mu$ the slope of the Hamiltonian. Given any local system $\nu$, we obtain a filtered chain isomorphism $FC_*(H;\nu ){\mathop {\longrightarrow }\limits ^{\simeq }}MC_*^{\le \mu }(E^{1/2};\nu \otimes \underline{\eta })$.

In case the local system $\nu$ is compatible with products, the arguments of [1, 3, 7] adapt in order to show that the map $\Psi$ intertwines the pair-of-pants product on the symplectic homology side with the homology product on the Morse side. The arguments of Theorem 6.1 adapt in order to show that the map $\Psi$ descends on homology relative to the constant loops, where it intertwines the continuation coproduct with the loop coproduct (with field coefficients).

Theorem A.17

([1, 3, 5, 7], Theorem 5.3, Theorem 6.1) Given any local system $\nu$ compatible with products, the filtered chain level map $\Psi$ induces filtered isomorphisms

$$\begin{aligned}{} & {} \Psi _*:SH_*(D^*M;\nu ){\mathop {\longrightarrow }\limits ^{\simeq }}H_*(\Lambda ;\nu \otimes \underline{\eta }),\\{} & {} \Psi _*^{>0}:SH_*^{>0}(D^*M;\nu ){\mathop {\longrightarrow }\limits ^{\simeq }}H_*(\Lambda ,\Lambda _0;\nu \otimes \underline{\eta }). \end{aligned}$$

Moreover,

• $\Psi _*$ intertwines the pair-of-pants product with the Chas–Sullivan loop product,

• $\Psi _*^{>0}$ intertwines the continuation coproduct with the loop coproduct (with field coefficients).

$\square$

There are also reduced versions of the map $\Psi$ which intertwine the product, and which also intertwine the coproducts provided both are defined using the same continuation data at the endpoints. The statements for the coproducts can, moreover, be interpreted as dual statements about products in cohomology.