Holt–Winters method for run-off triangles in claims reserving

Abstract

Run-off triangles present usual instruments for claims reserve predictions. The paper suggests a relatively simple method of such predictions based on the Holt–Winters recursive formulas modified for missing data. The technique explicitly calculates the corresponding prediction error grounded in the state space modeling and evaluates the claims reserving risk in this way. Empirical data examples enable us to compare the suggested approach with results published by other authors.

1 Introduction

Various methods of claims reserve prediction in general insurance have been developed by actuaries over several last decades, see [8]. Even though a substantial part of them are stochastic ones based on stochastic models, only a limited number of them are declared explicitly as time series models. Refer to the discussion in [5, 6] or consult the concept of the time series model as a particular case of chain-ladder models in [31, p. 49]. This is a surprising fact since claims data are usually a sequence of discrete time data showing trend and seasonal features, see Fig. 1. In particular, the time series approach consisting in state space modeling (closely related to the Kalman filter methodology) seems to be suitable in this context, see [1, 12, 14, 20,21,22, 24, 28,29,30, 33] and others. Moreover, one can use diagonal-ordering following the classical calendar time ordering, see [11], or row-ordering applied in our work, see [2] and [10]. The latter reference even shows how the tail effect can be treated in this context.

Fig. 1

Row-wise ordering with missing observations of run-off triangle for AFG claims data (solid line) and predictions of missing observations by additive HW (dashed line)

The usual organization of claims reserve data consists in the so-called run-off triangles in the double-index format, see Table 1. The rows of such a triangle represent the accident (or origin) years, and its columns the development years. Notably, the value C_md (m = 1, …, s, d = 0, 1, …, s − m) denotes the (incremental) payment for loss events that occurred at time m and were reported at time t = m + d. One observes payments until the current time t = s and should predict all future payments in the missing positions below the diagonal of the given triangle. Then the total sum of these predicted values represents the total claims reserve of the type IBNR (Incurred But Not Reported) necessary at time s. Some reserving methods transfer the incremental data to the cumulative form D_ij = C_i0 + … + C_ij or the logarithmic form Y_ij = log C_ij assuming implicitly that C_ij > 0, see [31].

Table 1 Run-off triangle for incremental claim amounts C_md (m = 1, …, s, d = 0, 1, …, s − m)

The approach applied in this paper is based on a row-wise ordering of the original double-index format to the single-index format of a time series with missing observations, see Table 2. Due to the claims process behavior (mainly a strong seasonality), the corresponding time series {y_t} can be modeled using the state space modeling approach, where the (unobserved) state variables are level, trend (slope), and seasonal components. In the context of run-off triangles, the level and trend components respond to long-term movements along particular rows of the run-off triangle (jumps in the level, changes in the slope), and the seasonal (periodic) component captures the column effect (covering the dynamic character of seasonality). Using the loss reserving terminology, according to Table 1, one can imagine that the level component L_t and the trend (or slope) component T_t represent the development over development years d of an accident (or origin) year m. Similarly, the seasonal component I_t with seasonality s refers to claim volume changes over accident years m corresponding to a development year d.

Table 2 Row-wise ordering of a run-off triangle to time series with missing observations

The state space modeling published so far in the loss reserving context is based on the (linear) structural models which make use of Kalman filtering methodology, refer to [2, 5, 6, 18]. The applications of the (linear) structural models in the general framework of time series analysis can be found in [13, 16, 17, 26], and others. In this paper, we apply the so-called ETS models (Error, Trend, Seasonal) by Hyndman et al. [19]. These (additive or multiplicative) models present a single source of error alternative to structural models (SSOE or innovations state space models, see Appendix A5). The ETS models have several advantages. They mainly provide simple algorithms for signal smoothing and prediction, including calculating prediction errors. In the most usual cases, the corresponding algorithms have the form of exponential smoothing. For instance, if seasonality is present, the related procedures are called the (additive or multiplicative) Holt–Winters (HW) method. The exponential smoothing procedures are prevalent in practical time series analysis due to their simplicity. Still, in the context of run-off triangles, they must be modified to cover the case of missing observations, seesumming over all gaps of missing observations Sect. 2. In addition, one completes the application of HW by the formulas for the corresponding claims reserve prediction errors (see RMSE in (A13) and (A19)) to evaluate the claims (or loss) reserving risk.

The paper is organized as follows: Sect. 2 reviews the additive and multiplicative HW for time series with missing data and brings additional formulas for calculating the root mean squared error of the claims reserve prediction. Section 3 deals with the technicalities of HW (initial values, choice of smoothing constants). In Sect. 4, one applies the suggested methods for empirical run-off data used as a benchmark in the actuarial literature to compare the proposed approach with results published by other authors. The numerical ETS models corresponding to this data set are verified utilizing residual analysis. The derivations of formulas used in the paper are deferred to the Appendix.

2 Holt–Winters method with missing observations

To remind the principle of exponential smoothing, which plays a crucial role in the HW methods, let us consider the simplest case (the so-called simple exponential smoothing) for time series {y_t} with a local level L_t only. Then the k-step-ahead prediction of value y_t+k constructed at time t using information y_t, y_t−1, y_t−2 … (for k = 0 one speaks on “smoothed” value of the given time series at time t) by minimizing the following sum of exponentially weighted squares

$$\sum\limits_{\tau = 0}^\infty {{{(1 - \alpha )}^\tau }{{({y_{t - \tau }} - {L_t})}^2}}$$

across real L_t using a fixed smoothing constant α (0 < α < 1) which assigns the highest weights to the most actual observations concerning time t. It should be pointed out that the sum in the expression above is infinite, even though we know only a finite number of values y₁, …, y_t at time t. However, the hypothetical extension of time series to the (infinite) past significantly simplifies the corresponding formulas due to limit transition. Hence one obtains

$$\hat{y}_{t} = \hat{y}_{t + k} (t) = L_{t} = \alpha \sum\limits_{\tau = 0}^{\infty } {(1 - \alpha )^{\tau } y_{t - \tau } } = \alpha y_{t} + (1 - \alpha )L_{t - 1} ,$$

where the smoothing constant α is chosen in advance in a recommended way, see [3]. The HW methodology used in this paper generalizes the simple exponential smoothing in several aspects, namely (i) it completes the level L_t by the trend component (slope) T_t and the seasonal component (index) I_t when distinguishing the additive and multiplicative case; (ii) it admits missing observations in the time series {y_t}; (iii) it derives the ETS models corresponding to the ad hoc recursive formulas including the calculation of prediction errors (such a sequence proceeding from ad hoc calculation formulas to theoretical models is typical in this context, see [19]).

2.1 Additive case

Let us consider observations $y_{{t_{1} }} ,\;y_{{t_{2} }} ,\; \ldots ,\;y_{{t_{n} }}$ recorded at irregularly spaced times t₁ < t₂ < … < t_n. If the symbols L_t, T_t, and I_t denote the estimated level, trend, and seasonal index at time t, respectively, then the corresponding recursive additive HW formulas are (see [9]):

$$L_{{t_{i} }} = a_{{t_{i} }} (y_{{t_{i} }} - I_{{t_{i}^{ * } }} ) + (1 - a_{{t_{i} }} )[L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} ],$$

(1)

$$T_{{t_{i} }} = c_{{t_{i} }} \frac{{L_{{t_{i} }} - L_{{t_{i - 1} }} }}{{t{}_{i} - t{}_{i - 1}}} + (1 - c_{{t_{i} }} )T_{{t_{i - 1} }} ,$$

(2)

$$I_{{t_{i} }} = d_{{t_{i} }} (y_{{t_{i} }} - L_{{t_{i} }} ) + (1 - d_{{t_{i} }} )I_{{t_{i}^{ * } }} ,$$

(3)

where t_i^* denotes the largest value among t_i−1, t_i−2, … such that t_i^* corresponds to the same seasonal period as the time t_i. The dynamic smoothing constants a, b, and c are calculated recursively using the original static smoothing constants α, γ and δ (0 < α, γ, δ < 1):

$$a_{{t_{i} }} = \frac{{a_{{t_{i - 1} }} }}{{(1 - \alpha )^{{t_{i} - t_{i - 1} }} + a_{{t_{i - 1} }} }},\;\;c_{{t_{i} }} = \frac{{c_{{t_{i - 1} }} }}{{(1 - \gamma )^{{t_{i} - t_{i - 1} }} + c_{{t_{i - 1} }} }},\;\;d_{{t_{i} }} = \frac{{d_{{t_{i - 1} }} }}{{(1 - \delta )^{{t_{i} - t_{i - 1} }} + d_{{t_{i - 1} }} }}.$$

(4)

Then the observations missing in the gap between times t_i and t_i+1 can be estimated as the following predictions:

$$\hat{y}_{{t_{i} + k}} = \hat{y}_{{t_{i} + k}} (t_{i} ) = L_{{t_{i} }} + k \cdot \;T_{{t_{i} }} + I_{{(t_{i} + k)^{ * } }} \;\;{\rm for}\;0 < k < t_{i + 1} - t_{i} .$$

(5)

It is possible to demonstrate this approach using the simple exponential smoothing. For our data published at irregularly spaced times, one can write

$$\hat{y}_{{t_{i} }} = L_{{t_{i} }} = a_{{t_{i} }} \sum\limits_{j = 1}^{i} {(1 - \alpha )^{{t_{i} - t_{j} }} y_{{t_{j} }} } \;\;{\rm for}\;\;a_{{t_{i} }} = \frac{1}{{\sum\limits_{j = 1}^{i} {(1 - \alpha )^{{t_{i} - t_{j} }} } }} = \frac{{a_{{t_{i - 1} }} }}{{(1 - \alpha )^{{t_{i} - t_{i - 1} }} + a_{{t_{i - 1} }} }}.$$

In particular, Cipra et al. [9] suggested a suitable choice of initial values for (1)–(4), including the optimal choice of α, γ and δ (see Sect. 3).

Applying the described HW method for run-off data, one obtains the claims reserve predictions (i.e., the predicted outstanding payments in the run-off triangle) by summing partial sums

$$\sum\limits_{k = 1}^{{t_{i + 1} - t_{i} - 1}} {\hat{y}_{{t_{i} + k}} (t_{i} )}$$

(6)

over all gaps of missing observations in the time series corresponding to the given triangle. It is important to stress that the HW method (both additive and multiplicative) adjusted for run-off data can be understood as a purely algorithmic method to set claims reserves, i.e., a mechanical technique to predict future liability. However, this understanding generally does not allow quantifying the uncertainties in these predictions. Such uncertainties (including reserve prediction errors) can be determined only if one randomizes the HW method by choice of an underlying stochastic model on which the reserving algorithm can be grounded. Refer also to discussion in [31, p. 15]. Here a suitable selection of appropriate stochastic models seems to be just the ETS models.

The claims reserve prediction errors can be evaluated using a stochastic model framework relevant to the ad hoc recursive formulas (1)–(4). The state space modeling based on the ETS models from Sect. 1 (ETS with additive error, additive trend, and additive seasonality, see [19]), which is adapted for the case of missing observations, seems to be proper in this context:

$$y_{{t_{i} }} = L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} + I_{{t_{i}^{ * } }} + e_{{t_{i} }} ,$$

(7)

$$L_{{t_{i} }} = L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} + a_{{t_{i} }} e_{{t_{i} }} ,$$

(8)

$$T_{{t_{i} }} = T_{{t_{i - 1} }} + \frac{{a_{{t_{i} }} c_{{t_{i} }} }}{{t{}_{i} - t{}_{i - 1}}}e_{{t_{i} }} ,$$

(9)

$$I_{{t_{i} }} = I_{{t_{i}^{ * } }} + d_{{t_{i} }} (1 - a_{{t_{i} }} )e_{{t_{i} }} ,$$

(10)

where $e_{{t_{i} }}$ are iid innovations with zero mean value and variance σ_e² (the derivation of this ETS model representation can be found in Appendix A1). In particular, when applying this model scheme, then RMSE (root mean squared error) of the claims reserve prediction in the given run-off triangle can be expressed analytically as

$${\text{RMSE}} = \left[ {\sum\limits_{i = 1}^{n - 1} {\;\sum\limits_{k = 1}^{{t_{i + 1} - t_{i} - 1}} {\left( {\sum\nolimits_{j = 0}^{k - 1} {v_{j} } } \right)^{2} } } } \right]^{1/2} \cdot \sigma_{e} ,$$

(11)

where

$$v_{j} = \left\{ \begin{gathered} 1\;\;\;\;\;\;\;\;\;\;\;\;\;,\;j = 0 \hfill \\ \alpha + j\alpha \gamma \;\;\;,\;j = \;1,\;...,\;s - 1 \hfill \\ \end{gathered} \right.,$$

(12)

summing over all gaps of missing observations in the corresponding time series (see Appendix A3 for derivation). One should remind that the mean squared error represents the conditional process variance describing the variation within the applied stochastic model, see [31].

2.2 Multiplicative case

In the multiplicative case, the recursive HW formulas with the multiplicative seasonal factors (see [9]) are

$$L_{{t_{i} }} = a_{{t_{i} }} \frac{{y_{{t_{i} }} }}{{I_{{t_{i}^{ * } }} }} + (1 - a_{{t_{i} }} )[L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} ],$$

(13)

$$T_{{t_{i} }} = c_{{t_{i} }} \frac{{L_{{t_{i} }} - L_{{t_{i - 1} }} }}{{t{}_{i} - t{}_{i - 1}}} + (1 - c_{{t_{i} }} )T_{{t_{i - 1} }} ,$$

(14)

$$I_{{t_{i} }} = d_{{t_{i} }} \frac{{y_{{t_{i} }} }}{{L_{{t_{i} }} }} + (1 - d_{{t_{i} }} )I_{{t_{i}^{ * } }}$$

(15)

(see the comments to (1)–(4)). The observations missing in the gap between times t_i and t_i+1 can be estimated as predictions:

$$\hat{y}_{{t_{i} + k}} = \hat{y}_{{t_{i} + k}} (t_{i} ) = (L_{{t_{i} }} + k \cdot \;T_{{t_{i} }} )I_{{(t_{i} + k)^{ * } }} \;\;{\rm for}\;0 < k < t_{i + 1} - t_{i} .$$

(16)

In [9], one can find recommendations of a suitable choice of initial values for (4) and (13)–(15), including the optimal choice of α, γ and δ again (see Sect. 3).

The estimated claims reserve can be constructed analogously as in (6). The ETS model (with additive error, additive trend, and multiplicative seasonality, see [19]) necessary for the calculation of claims reserve error in the multiplicative case has the following form:

$$y_{{t_{i} }} = [L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} ]\;I_{{t_{i}^{ * } }} + e_{{t_{i} }} ,$$

(17)

$$L_{{t_{i} }} = L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} + a_{{t_{i} }} e_{{t_{i} }} /I_{{t_{i}^{ * } }} ,$$

(18)

$$T_{{t_{i} }} = T_{{t_{i - 1} }} + \frac{{a_{{t_{i} }} c_{{t_{i} }} }}{{t{}_{i} - t{}_{i - 1}}}e_{{t_{i} }} /I_{{t_{i}^{ * } }} ,$$

(19)

$$I_{{t_{i} }} = I_{{t_{i}^{ * } }} + d_{{t_{i} }} (1 - a_{{t_{i} }} )e_{{t_{i} }} /L_{{t_{i} }} ,$$

(20)

where $e_{t_{i}}$ are iid innovations with zero mean value and variance σ_e² (see the derivation given in Appendix A2).

The root mean squared error of the claims reserve prediction (6) can be expressed analytically as

$$RMSE = \left[ {\sum\limits_{i = 1}^{n - 1} {\;\sum\limits_{k = 1}^{{t_{i + 1} - t_{i} - 1}} {\left( {\sum\nolimits_{j = 0}^{k - 1} {v_{j} (I_{{(t_{i + 1} - k + j)^{ * } }} /I_{{(t_{i + 1} - k)^{ * } }} )} } \right)}^{2} } } \right]^{1/2} \cdot \sigma_{e} ,$$

(21)

summing again over all gaps of missing observations (v_j are the same as in (12), see Appendix A4 for derivation).

3 Technicalities of HW

Cipra et al. [9] recommended a suitable choice of initial values and smoothing constants necessary for the additive or multiplicative HW methods with missing observations. In the context of run-off triangle data, the initial values for the additive recursive formulas (1)–(4) can be simplified to the form

$$L_{0} = \overline{y}_{1} - \;\frac{s + 1}{2}\;T_{0} ,$$

(22)

$$T_{0} = \frac{{\overline{y}_{2} - \overline{y}_{1} }}{s},$$

(23)

$$I_{ - s + 1} = y_{1} - \left[ {\overline{y}_{1} - \frac{s - 1}{2}T_{0} } \right],\;\;I_{ - s + 2} = y_{2} - \left[ {\overline{y}_{1} - \frac{s - 3}{2}T_{0} } \right],\;\;...,\;\;I_{0} = y_{s} - \left[ {\overline{y}_{1} + \frac{s - 1}{2}T_{0} } \right],$$

(24)

$$a_{0} = \alpha ,\;\;c_{0} = \gamma ,\;\;d_{0} = \delta,$$

(25)

where $\overline{y}_{m}$ is the arithmetic average of observations over the m-th season (i.e., m-th accident year).

For the multiplicative recursive formulas (4) and (13)–(15), it is sufficient to replace only the initial values (24) by

$$I_{ - s + 1} = \frac{{y_{1} }}{{\overline{y}_{1} - \frac{s - 1}{2}T_{0} }},\;\;I_{ - s + 2} = \frac{{y_{2} }}{{\overline{y}_{1} - \frac{s - 3}{2}T_{0} }},\;\;...,\;\;I_{0} = \frac{{y_{s} }}{{\overline{y}_{1} + \frac{s - 1}{2}T_{0} }}.$$

(26)

Concerning the smoothing constants, a recommended approach selects the smoothing constants employing the (quasi) maximum likelihood procedure derived for the general ETS model (with an additive error). The parameters α, γ and δ are constrained to the interval (0, 1).

Finally, the residual analysis should verify the choice of a proper model (an additive or multiplicative one, a model with original data, or after removing outliers, etc.). Only when a model fits the observed data properly according to such an analysis, then the minimal RMSE (see (A13)) can be used as a criterion for comparing various models (see Sect. 4).

As a matter of fact, the structural model in [2] uses only the level and seasonal components considering the trend component to be redundant (indeed, in both numerical examples in the following Sect. 4, the optimal trend smoothing constant γ comes out negligible). Despite the preference for simplicity in practice, we present the HW methodology in its general form (i.e., including the trend component T_t) since it includes the mentioned simplification as a particular case.

4 Numerical study

4.1 AFG data

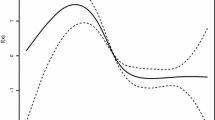
The suggested HW methods are studied for the empirical run-off data from Table 3 regarded as a benchmark in the actuarial literature to compare various run-off methods, see [2, 14]. These incremental claims data are usually called the AFG data since they relate to the Automatic Facultative General Liability (excluding Asbestos and Environmental) and have been published in Historical Loss Development Study [25]. They show considerable variability among accident years (notice also the negative value in this run-off triangle, which can be treated like other positive incremental values). The graph of the corresponding time series (with missing observations) is plotted by the solid line in Fig. 1.

Table 3 Run-off triangle for AFG claims data

To estimate the corresponding claims reserve, one has applied the HW method described in Sect. 3 (both in the additive and multiplicative versions). One has calculated the predicted values $\hat{y}_{{t_{i} + k}}$ of missing observations representing the estimated claims reserves (see the formula (5) in the additive case and (16) in the multiplicative case). For instance, the dashed line in Fig. 1 plots the predictions of missing observations for AFG data applying the additive HW.

The technical details of particular recursive algorithms are as follows:

• The initial values are set up according to (22)–(26).

• The smoothing constants are chosen by maximizing the (quasi) likelihood function (see the recommendation in Sect. 3 and optimal values of constants α, γ, and δ in Table 4).

• The claims reserve estimate is constructed by summing (6) over all gaps of missing observations, and its error (i.e., the reserving risk) is evaluated as the coefficient of variation CV (in %) relating the estimated RMSE in (11) or (21) to the estimated claims reserve. The standard deviation σ_e in RMSE is estimated as the sample standard deviation of prediction errors e_t (t − 1) over the observed values in the given run-off triangle using the one-step-ahead predictions constructed by the corresponding HW method.

Table 4 Estimated claims reserves and their errors CV (reserving risk) for AFG loss data

Table 4 summarizes the main outputs of the example with AFG data, namely the claims reserves estimated by HW methods suggested in Sect. 3, including the errors (risks CV) of these estimates. Moreover, comparisons with other approaches are also presented in Table 4 for AFG data, namely (i) the stochastic Chain Ladder model by Mack [23] (see [2 or 14]), (ii) the bootstrap Chain Ladder model calculation (see [15]), (iii) the Poisson model by England and Verrall [14] (see also [2]), (iv) the state space model by Atherino et al. [2] with two variants of interventions for modeling outliers.

The results of the additive and multiplicative HW methods are relevant only when a suitable residual analysis (for residuals standardized by their standard deviations) verifies that the corresponding models fit the data adequately. Some outputs of residual analysis will be shown only for the additive HW method since the outcomes of the multiplicative HW method are similar.

Figure 2 displays the row-wise ordered standardized residuals, which are further analyzed by selected statistical tests. Their results are reported herein utilizing the corresponding p-values. For instance, one verified: (i) the independence of standardized residuals by the classical Ljung–Box test (p = 0.228), by the median test (p = 0.094), and by the difference sign test (p = 0.815), (ii) the elimination of heteroscedasticity by the F-test based on the squared standardized residuals (p = 0.434), (iii) the elimination of conditional heteroscedasticity by the Ljung–Box test based on the squared standardized residuals (p = 0.543). Further, one tested the standardized residual normality by the Shapiro–Wilk test (p = 0.187), Q–Q and P–P plots (see Fig. 3), and Cullen and Frey graph (see Fig. 4). The outputs of all tests are positive with high levels of significance. The outcomes indicate no evidence in the data against the model’s basic assumptions, even with a significance level of 10%. Therefore, Fig. 3 can serve as a (graphical) residual diagnosis.

Fig. 2

Row-wise ordered standardized residuals estimated by the additive HW method

Fig. 3

Q-Q plot and P-P plot of standardized residuals estimated by the additive HW method for AFG claims data

Fig. 4

Cullen and Frey graph of standardized residuals estimated by the additive HW method for AFG claims data

Figure 5 plots the standardized residuals ordered according to the accident and development years.

Fig. 5

Standardized residuals estimated by the additive HW method and ordered according to the accident and development years for AFG claims data

Due to the positive results of residual analysis for all HW methods, the outputs of the numerical study summarized in Table 4 are relevant. It enables us to compare various approaches to claims reserving in this benchmark example:

• (1) The claims reserve estimates based on the HW approach (primarily the additive one) are comparable with the classical methods (Stochastic Chain Ladder, Bootstrapping Chain Ladder, Poisson). Still, they seem to be nearly double accurate.

• (2) The reserves estimated by Atherino et al. [2] are based on row-wise ordering and state space modeling, similar to the HW approach. These claims reserves are significantly higher with lower CV than the HW reserves. However, the approach in [2] is very sophisticated, looking subjectively for outliers and modeling them as interventions.

Table 5 contains in-sample and out-of-sample measures (MSE, MAPE), which compare the proposed HW methods with the classic chain ladder techniques for incremental AFG data. Note that the out-of-sample measurement is performed by reestimating the run-off triangle without using the diagonal elements. Subsequently, excluded data are compared employing the same performance measures (MSE, MAPE). The HW methods outperform the classic chain ladder techniques regarding these goodness-of-fit metrics.

Table 5 In-sample and out-of-sample measures for incremental AFG loss data

4.2 Belgian data

The second example exploits Belgian insurance claims data in Table 6 (see also Fig. 6, including the predictions of missing observations by multiplicative HW).

Table 6 Run-off triangle for Belgian insurance claims data

Fig. 6

Row-wise ordering with missing observations of run-off triangle for Belgian insurance claims data (solid line) and predictions of missing observations by multiplicative HW (dashed line)

Table 7 summarizes the main outputs of this example for Belgian insurance data, similar to Table 4 for AFG data. The residual analysis results are not presented here since they are even better than the previous example due to the regular decomposition shape of the time series corresponding to the Belgian insurance data.

Table 7 Estimated claims reserves and their errors CV for Belgian insurance claims data

One can conclude that the results for Belgian data (claims reserves and reserving risks) based on the HW approach are comparable to those provided by the classical methods (Stochastic Chain Ladder and Bootstrapping Chain Ladder).

Table 8 contains in-sample and out-of-sample measures (MSE, MAPE), which compare the proposed HW methods with the classic chain ladder techniques for incremental Belgian insurance data. Note that the out-of-sample measurement is performed by reestimating the run-off triangle without using the diagonal elements. Subsequently, excluded data are again compared through the same performance measures (MSE, MAPE). For Belgian data, the HW methods are (slightly) outperformed by the classic chain ladder techniques in terms of these goodness-of-fit metrics.

Table 8 In-sample and out-of-sample measures for incremental Belgian insurance claims data

4.3 Technical aspects of implementation

The Holt–Winters methods described in Sects.  2 and 3 and applied in Sects.  4.1 and 4.2 were carried out in the statistical software R (ver. 4.1.2, https://cloud.r-project.org/src/base/). The key recursive formulas (7)–(10) and (17)–(20), together with the initialization described in Sect. 3, were implemented as the authors’ procedures. Maximum likelihood estimation employed the L-BFGS-B optimizer (limited-memory modification of the BFGS quasi-Newton method) with the starting values set as α = 0.05, γ = 0.05, δ = 0.30. The time needed for estimation was in units of seconds (depending on computational hardware). No numerical difficulty was observed. Point out that the recursive character and the relative simplicity of the proposed HW methods should be seen as their advantage since their implementation is very straightforward and can be performed in a wide variety of software.

5 Conclusions

The paper offers an alternative to state space models used for the claims reserve predicting in the row-wise ordered run-off triangles. The Holt–Winters methodology modified for time series with missing observations predicts the gaps representing the loss reserve just to be forecasted in the run-off context. Moreover, one derives simple analytical formulas for the conditional process variance describing the variation within stochastic models corresponding to the additive and multiplicative HW methods.

The numerical complexity of the suggested loss reserving methodology is relatively low (even though some technicalities must be solved during the calculations). Moreover, in the case of regular decomposition shapes of time series based on the row-wise ordering of original run-off data, the claims reserves based on the HW approach seem more accurate (i.e., less risky) than the reserves provided by classical methods. As the case of data with irregular decomposition shapes is concerned, one should eliminate at first the influence of outliers similarly as in [2].

Some suggestions call for further investigation:

• One can use the HW methodology in an interpolation way for particular missing gaps in time series, properly combining forward predictions in time using observations before the gap and backward predictions in time using observations after the gap.

• One can robustify the HW methodology to eliminate the influence of outliers similarly to some exponential smoothing procedures, see [7].

One can combine the HW methodology with a bootstrap algorithm to predict the probability distribution of corresponding loss reserves in run-off triangles, see [31].

Appendix

1.1 A1 Derivation of additive ETS representation

Consider the additive ETS model (7)–(10). Then it is easy to show that its level, trend, and seasonal components can be calculated recursively according to (1)–(3):

$${L_{{t_i}}} = {L_{{t_{i - 1}}}} + (t{}_i - t{}_{i - 1}){T_{{t_{i - 1}}}} + {a_{{t_i}}}{e_{{t_i}}} = {L_{{t_{i - 1}}}} + (t{}_i - t{}_{i - 1}){T_{{t_{i - 1}}}} + {a_{{t_i}}}\{{y_{{t_i}}} - [{L_{{t_{i - 1}}}} + (t{}_i - t{}_{i - 1}){T_{{t_{i - 1}}}} + \;{I_{t_i^ * }}]\}$$

$$= a_{{t_{i} }} (y_{{t_{i} }} - I_{{t_{i}^{ * } }} ) + (1 - a_{{t_{i} }} )[L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} ];$$

(A1)

$${T_{{t_i}}} = {T_{{t_{i - 1}}}} + \frac{{{a_{{t_i}}}{c_{{t_i}}}}}{{t{}_i - t{}_{i - 1}}}{e_{{t_i}}} = {T_{{t_{i - 1}}}} + \frac{{{c_{{t_i}}}}}{{t{}_i - t{}_{i - 1}}}[{L_{{t_i}}} - {L_{{t_{i - 1}}}} - (t{}_i - t{}_{i - 1}){T_{{t_{i - 1}}}}]$$

$$= c_{{t_{i} }} \frac{{L_{{t_{i} }} - L_{{t_{i - 1} }} }}{{t{}_{i} - t{}_{i - 1}}} + (1 - c_{{t_{i} }} )T_{{t_{i - 1} }} ;$$

(A2)

$${I_{{t_i}}} = {I_{t_i^ * }} + {d_{{t_i}}}(1 - {a_{{t_i}}}){e_{{t_i}}}$$

$$= I_{{t_{i}^{ * } }} + d_{{t_{i} }} \{y_{{t_{i} }} - [L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} \; + I_{{t_{i}^{ * } }} ]\} - d_{{t_{i} }} \{L_{{t_{i} }} - [L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} ]\}$$

$$= d_{{t_{i} }} (y_{{t_{i} }} - L_{{t_{i} }} ) + (1 - d_{{t_{i} }} )I_{{t_{i}^{ * } }} .$$

(A3)

1.2 A2 Derivation of multiplicative ETS representation

Consider the multiplicative ETS model (17)–(20). Then similarly to the additive case, one can derive the recursive formulas (13)–(15):

$${L_{{t_i}}} = {L_{{t_{i - 1}}}} + (t{}_i - t{}_{i - 1}){T_{{t_{i - 1}}}} + {a_{{t_i}}}{e_{{t_i}}}/{I_{t_i^ * }} = {L_{{t_{i - 1}}}} + (t{}_i - t{}_{i - 1}){T_{{t_{i - 1}}}} + {a_{{t_i}}}\{{y_{{t_i}}} - [{L_{{t_{i - 1}}}} + (t{}_i - t{}_{i - 1}){T_{{t_{i - 1}}}}]\;{I_{t_i^ * }}\}/{I_{t_i^ * }}$$

$$= a_{{t_{i} }} \frac{{y_{{t_{i} }} }}{{I_{{t_{i}^{ * } }} }} + (1 - a_{{t_{i} }} )[L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} ];$$

(A4)

$${T_{{t_i}}} = {T_{{t_{i - 1}}}} + \frac{{{a_{{t_i}}}{c_{{t_i}}}}}{{t{}_i - t{}_{i - 1}}}{e_{{t_i}}}/{I_{t_i^ * }} = {T_{{t_{i - 1}}}} + \frac{{{c_{{t_i}}}}}{{t{}_i - t{}_{i - 1}}}[{L_{{t_i}}} - {L_{{t_{i - 1}}}} - (t{}_i - t{}_{i - 1}){T_{{t_{i - 1}}}}]$$

$$= c_{{t_{i} }} \frac{{L_{{t_{i} }} - L_{{t_{i - 1} }} }}{{t{}_{i} - t{}_{i - 1}}} + (1 - c_{{t_{i} }} )T_{{t_{i - 1} }} ;$$

(A5)

$${I_{{t_i}}} = {I_{t_i^ * }} + {d_{{t_i}}}(1 - {a_{{t_i}}}){e_{{t_i}}}/{L_{{t_i}}}$$

$$= I_{{t_{i}^{ * } }} + d_{{t_{i} }} \{{y_{{t_{i} }} - [L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} ]\;I_{{t_{i}^{ * } }} { }}\}/L_{{t_{i} }} - d_{{t_{i} }} \{{L_{{t_{i} }} - [L_{{t_{i - 1} }} + (t{}_{i} - t{}_{i - 1})T_{{t_{i - 1} }} ]\}\;{ }}I_{{t_{i}^{ * } }} /L_{{t_{i} }}$$

(A6)

$= d_{{t_{i} }} \frac{{y_{{t_{i} }} }}{{L_{{t_{i} }} }} + (1 - d_{{t_{i} }} )I_{{t_{i}^{ * } }} .$

1.3 A3 Derivation of claims reserve error in additive case

Since one deals with prediction errors in (6), it is necessary to supplement (7)–(10) by the ETS equations concerning the values $y_{t}^{ * }$ missing in the gaps of corresponding time series, namely

$$y_{{t_{i} + k}}^{ * } = L_{{t_{i} + k - 1}} + T_{{t_{i} + k - 1}} + I_{{(t_{i} + k)^{ * } }} + e_{{t_{i} + k}} ,$$

(A7)

$$L_{{t_{i} + k}} = L_{{t_{i} + k - 1}} + T_{{t_{i} + k - 1}} + \alpha e_{{t_{i} + k}} ,$$

(A8)

$$T_{{t_{i} + k}} = T_{{t_{i} + k - 1}} + \alpha \gamma e_{{t_{i} + k}} ,$$

(A9)

$$I_{{t_{i} + k}} = I_{{(t_{i} + k)^{ * } }} + \delta (1 - \alpha )e_{{t_{i} + k}}$$

(A10)

for 0 < k < t_i+1 − t_i. Moreover, e_t are iid innovations with zero mean value and variance σ_e².

Let us denote the error of prediction $\hat{y}_{{t_{i} + k}} (t_{i} )$ as $e_{{t_{i} + k}} (t_{i} ) = y_{{t_{i} + k}}^{ * } - \hat{y}_{{t_{i} + k}} (t_{i} ).$ Then it holds

$$e_{{t_{i} + k}} (t_{i} ) = \sum\limits_{j = 0}^{k - 1} {v_{j} e_{{t_{i} + k - j}} } ,\;\;0 < k < s,$$

(A11)

where v_j are given by (12) (compare with [32]). The mathematical induction proofs (A11). For k = 1, it is really

$$e_{{t_{i} + 1}} (t_{i} ) = e_{{t_{i} + 1}} = v_{0} e_{{t_{i} + 1}} .$$

Let (A11) hold for k − 1. It will be shown that then (A11) holds also for k (1 < k < s). One can write using equations (A7)–(A9)

$$e_{{t_{i} + k}} (t_{i} ) = y_{{t_{i} + k}}^{ * } - \hat{y}_{{t_{i} + k}} (t_{i} ) = y_{{t_{i} + k}}^{ * } - \hat{y}_{{t_{i} + k}} (t_{i} + 1) + \hat{y}_{{t_{i} + k}} (t_{i} + 1) - \hat{y}_{{t_{i} + k}} (t_{i} )$$

$$= e_{{t_{i} + k}} (t_{i} + 1) + [L_{{t_{i} + 1}} + (k - 1) \cdot T_{{t_{i} + 1}} + I_{{(t_{i} + k)^{ * } }} ] - [L_{{t_{i} }} + k \cdot T_{{t_{i} }} + I_{{(t_{i} + k)^{ * } }}]$$

$$= e_{{t_{i} + k}} (t_{i} + 1) + L_{{t_{i} + 1}} - L_{{t_{i} }} - T_{{t_{i} }} + (k - 1) \cdot (T_{{t_{i} + 1}} - T_{{t_{i} }} ) = e_{{t_{i} + k}} (t_{i} + 1) + \alpha e_{{t_{i} + 1}} + (k - 1)\alpha \gamma e_{{t_{i} + 1}}$$

$$= \sum\limits_{j = 0}^{k - 2} {v_{j} e_{{t_{i} + k - j}} } + [\alpha + (k - 1)\alpha \gamma ]e_{{t_{i} + 1}} = \sum\limits_{j = 0}^{k - 1} {v_{j} e_{{t_{i} + k - j}} } ,$$

which accomplishes the proof.

Though it is not necessary in the case of run-off data, one can extend the proof of (A11) to all k > 0, but after supplement

$${v_j} = \left\{ \begin{array}{ll} \;1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,\;j = 0\\ \;\alpha + j\alpha \gamma \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,\;\j \ne 0\;mod\;\;s\;\\ \;\alpha + j\alpha \gamma + \delta (1 - \alpha )\;\;,\;j = s,\;2s,\;3s,\;... \end{array} \right.$$

(A12)

Since the innovations are iid with variance σ_e², one finally obtains the root mean squared error of the claims reserve prediction (6) as

$$RMSE = \left[ {\sum\limits_{i = 1}^{n - 1} {{\text{var}} \left\{ {\sum\limits_{k = 1}^{{t_{i + 1} - t_{i} - 1}} {e_{{t_{i} + k}} (t_{i} )} } \right\}} } \right]^{1/2} = \left[ {\sum\limits_{i = 1}^{n - 1} {\;\sum\limits_{k = 1}^{{t_{i + 1} - t_{i} - 1}} {\left( {\sum\limits_{j = 0}^{k - 1} {v_{j} } } \right)}^{2} } } \right]^{1/2} \cdot \sigma_{e},$$

(A13)

summing over all gaps of missing observations (see (11)).

1.4 A4 Derivation of claims reserve error in multiplicative case

The derivation is similar to the additive case. The ETS equation supplementing (17)-(20) for the values y_t^⃰ missing in the gaps of the corresponding time series are

$$y_{{t_{i} + k}}^{ * } = (L_{{t_{i} + k - 1}} + T_{{t_{i} + k - 1}} )I_{{(t_{i} + k)^{ * } }} + e_{{t_{i} + k}} ,$$

(A14)

$$L_{{t_{i} + k}} = L_{{t_{i} + k - 1}} + T_{{t_{i} + k - 1}} + \alpha e_{{t_{i} + k}} /I_{{(t_{i} + k)^{ * } }} ,$$

(A15)

$$T_{{t_{i} + k}} = T_{{t_{i} + k - 1}} + \alpha \gamma e_{{t_{i} + k}} /I_{{(t_{i} + k)^{ * } }} ,$$

(A16)

$$I_{{t_{i} + k}} = I_{{(t_{i} + k)^{ * } }} + \delta (1 - \alpha )e_{{t_{i} + k}} /L_{{t_{i} + k}}$$

(A17)

for 0 < k < t_i+1 − t_i. Moreover, e_t are iid innovations with zero mean value and variance σ_e².

If one denotes the error of prediction $\hat{y}_{{t_{i} + k}} (t_{i} )$ again as $e_{{t_{i} + k}} (t_{i} ) = y_{{t_{i} + k}}^{ * } - \hat{y}_{{t_{i} + k}} (t_{i} )$, then it holds

$$e_{{t_{i} + k}} (t_{i} ) = \sum\limits_{j = 0}^{k - 1} {v_{j} (I_{{(t_{i} + k)^{ * } }} /I_{{(t_{i} + k - j)^{ * } }} )e_{{t_{i} + k - j}} } ,\;\;0 < k < s,$$

(A18)

where v_j are given by (12) (compare with [4]). The mathematical induction proofs (A18). For k = 1, it is really $e_{{t_{i} + 1}} (t_{i} ) = e_{{t_{i} + 1}} = v_{0} (I_{{(t_{i} + 1)^{ * } }} /I_{{(t_{i} + 1)^{ * } }} )e_{{t_{i} + 1}}$.

Let (A18) hold for k − 1. It will be shown that then (A18) holds also for k (1 < k < s). One can write using equations (A14)–(A17)

$$e_{{t_{i} + k}} (t_{i} ) = y_{{t_{i} + k}}^{ * } - \hat{y}_{{t_{i} + k}} (t_{i} ) = y_{{t_{i} + k}}^{ * } - \hat{y}_{{t_{i} + k}} (t_{i} + 1) + \hat{y}_{{t_{i} + k}} (t_{i} + 1) - \hat{y}_{{t_{i} + k}} (t_{i} )$$

$$= e_{{t_{i} + k}} (t_{i} + 1) + [L_{{t_{i} + 1}} + (k - 1) \cdot T_{{t_{i} + 1}} ]I_{{(t_{i} + k)^{ * } }} - [L_{{t_{i} }} + k \cdot T_{{t_{i} }} ]I_{{(t_{i} + k)^{ * } }}$$

$$= e_{{t_{i} + k}} (t_{i} + 1) + [\alpha e_{{t_{i} + 1}} /I_{{(t_{i} + 1)^{ * } }} ]I_{{(t_{i} + k)^{ * } }} + [(k - 1)\alpha \gamma e_{{t_{i} + 1}} /I_{{(t_{i} + 1)^{ * } }} ]I_{{(t_{i} + k)^{ * } }}$$

$$= \sum\limits_{j = 0}^{k - 2} {v_{j} (I_{{(t_{i} + k)^{ * } }} /I_{{(t_{i} + k - j)^{ * } }} )e_{{t_{i} + k - j}} } + [\alpha + (k - 1)\alpha \gamma ](I_{{(t_{i} + k)^{ * } }} /I_{{(t_{i} + 1)^{ * } }} )e_{{t_{i} + 1}}$$

$$= \sum\limits_{j = 0}^{k - 1} {v_{j} (I_{{(t_{i} + k)^{ * } }} /I_{{(t_{i} + k - j)^{ * } }} )e_{{t_{i} + k - j}} },$$

which accomplishes the proof (again, one can extend (A18) to all k > 0 with v_j defined in (A12), but then some approximations are necessary in the multiplicative case).

Finally, the root mean squared error of the claims reserve prediction (21) can be derived as

$$RMSE = \left[ {\sum\limits_{i = 1}^{n - 1} {{\text{var}} \left\{ {\sum\limits_{k = 1}^{{t_{i + 1} - t_{i} - 1}} {e_{{t_{i} + k}} (t_{i} )} } \right\}} } \right]^{1/2} = \left[ {\sum\limits_{i = 1}^{n - 1} {\;\sum\limits_{k = 1}^{{t_{i + 1} - t_{i} - 1}} {\left( {\sum\nolimits_{j = 1}^{k - 1} {v_{j} (I_{{(t_{i + 1} - k + j)^{ * } }} /I_{{(t_{i + 1} - k)^{ * } }} )} } \right)^{2} } } } \right]^{1/2} \cdot \sigma_{e} ,$$

(A19)

summing again over all gaps of missing observations.

1.5 A5 Innovation state space models ETS supporting Holt–Winters methods

For simplicity, only the basic form for time series without missing observations {y_t} is considered according to [19] denoting the level component by L_t, the trend (or slope) component by T_t, and the seasonal component by I_t with seasonality s. Then the additive HW method predicts as

$$\hat{y}_{t + k} = \hat{y}_{t + k} (t) = L_{t} + k \cdot \;T_{t} + I_{t + k - s} \;\;{\rm for}\;0 < k \le s$$

(A20)

and with components calculated recursively as

$$L_{t} = \alpha (y_{t} - I_{t - s} ) + (1 - \alpha )[L_{t - 1} + T_{t - 1} ],$$

(A21)

$$T_{t} = \gamma (L_{t} - L_{t - 1} ) + (1 - \gamma )T_{t - 1} ,$$

(A22)

$$I_{t} = \delta (y_{t} - L_{t} ) + (1 - \delta )I_{t - s}$$

(A23)

is supported by the following ETS model

$$y_{t} = L_{t - 1} + T_{t - 1} + I_{t - s} + e_{t} ,$$

(A24)

$$L_{t} = L_{t - 1} + T_{t - 1} + \alpha e_{t} ,$$

(A25)

$$T_{t} = T_{t - 1} + \alpha \gamma e_{t} ,$$

(A26)

$$I_{t} = I_{t - s} + \delta (1 - \alpha )e_{t} ,$$

(A27)

where α, γ and δ are smoothing constants (0 < α, γ, δ < 1) and e_t are iid innovations with zero mean value and variance σ_e². Obviously, (A24) is the measurement equation of this state space model with the state vector (L_t, T_t, I_t, I_t−1, …, I_t−s+1)´. (A25)-(A27) are its state (or transition) equations (in contrast to the classical dynamic linear model supporting Kalman filtering, these state equations contain only a single source of error e_t now).

Similarly, the multiplicative HW method predicts as

$$\hat{y}_{t + k} = \hat{y}_{t + k} (t) = (L_{t} + k \cdot \;T_{t} )I_{t + k - s} \;\;{\rm for}\;0 < k \le s$$

(A28)

and with components calculated recursively as

$$L_{t} = \alpha y_{t} /I_{t - s} + (1 - \alpha )(L_{t - 1} + T_{t - 1} ),$$

(A29)

$$T_{t} = \gamma (L_{t} - L_{t - 1} ) + (1 - \gamma )T_{t - 1} ,$$

(A30)

$$I_{t} = \delta y_{t} /L_{t} + (1 - \delta )I_{t - s}$$

(A31)

is supported by the following ETS model

$$y_{t} = (L_{t - 1} + T_{t - 1} )I_{t - s} + e_{t} ,$$

(A32)

$$L_{t} = L_{t - 1} + T_{t - 1} + \alpha e_{t} /I_{t - s} ,$$

(A33)

$$T_{t} = T_{t - 1} + \alpha \gamma e_{t} /I_{t - s} ,$$

(A34)

$$I_{t} = I_{t - s} + \delta (1 - \alpha )e_{t} /L_{t} ,$$

(A35)

where once again α, γ and δ are smoothing constants (0 < α, γ, δ < 1) and e_t are iid innovations with zero mean value and variance σ_e². The system (A32)–(A35) can be again formulated in terms of the state space model, which is now nonlinear, see [19].