Three-fold Fay–Herriot model for small area estimation and its diagnostics

Abstract

This paper introduces a three-fold Fay–Herriot model with random effects at three hierarchical levels. Small area best linear unbiased predictors of linear indicators are derived from the new model and the corresponding mean squared errors are approximated and estimated analytically and by parametric bootstrap. The problem of influence analysis and model diagnostics is addressed by introducing measures adapted to small area estimation. Simulation experiments empirically investigate the behavior of the predictors and mean squared error estimators. The new statistical methodology is applied to Spanish living conditions survey of 2004–2008. The target is the estimation of proportions of women and men under the poverty line by province and year.

1 Introduction

Fay and Herriot (1979) introduced an area-level linear mixed model (LMM) that improves the accuracy of direct estimators by incorporating auxiliary information. In small area estimation (SAE), the advantage of using procedures based on area-level models lies in the greater facility to incorporate explanatory variables of quality in the inferential process, with respect to other approaches based on individual models. See, e.g. Chapter 16 of Morales et al. (2021).

Direct estimators only use the data for the variable of interest in the estimation domain. In those domains with small sample sizes, the direct estimators will have large variances and therefore will not be very precise. An alternative estimation procedure consists of introducing auxiliary information by means of a statistical model. Area-level linear mixed models do this and can take into account hierarchical, spatial or temporal correlation of the data.

The surveys or administrative records from previous time periods and the hierarchical structure of the data provide important sources of information that can be used to improve the efficiency of small area estimators. Some papers have generalized the Fay–Herriot model to borrow strength from time. They have considered correlated structures for sampling errors or random effects, time-varying random slopes, and state-space models. Without claiming to be exhaustive, we can cite the contributions of Pfeffermann and Burck (1990), Rao and Yu (1994), Ghosh et al. (1996), Datta et al. (1999, 2002), You and Rao (2000), Singh et al. (2005), González-Manteiga et al. (2010). Esteban et al. (2012), Marhuenda et al. (2013), Morales et al. (2015), Benavent and Morales (2021).

Another possible generalization of the Fay–Herriot model is to take advantage of the territorial and demographic structure of the population. Rao and Yu (1994) introduced an area-level LMM with two levels of hierarchy. However, its basic model has not been extended to three levels in order to jointly model data from domains, subdomains, and time periods or subsubdomains. Torabi and Rao (2014) studied an extension of the Fay–Herriot area-level model to sub-area level, to obtain estimators for sub-areas nested within areas. Cai and Rao (2022) extended the transformation method of Cai et al. (2020) for variable selection to a three-fold linking model. They proposed two transformation-based methods for variable selection: one is parameter free and the other is parameter-dependent. However, they didn’t report EBLUP estimation for the three-fold proposed model. While Krenzke et al. (2020) developed an area-level univariate and bivariate Hierarchical Bayes linear three-fold model for proportions and averages.

The scarce research on hierarchical temporal models may be due to the fact that the usual periodicity of surveys in public statistics (quarterly or annual) does not allow cross-section data obtained with the same methodology over long periods of time. For these reasons, it is difficult to fit models with complex correlation structures to data, when the number of consecutive surveys available is not large enough. This paper covers in part this gap by introducing, for the first time in the statistical literature, a three-fold Fay–Herriot model, but having in mind a real data problem of poverty estimation and mapping.

The new model is an area-level LMM with known error variances. This fact prevents, for example, the application of functions of the R packages lme4 or nlme for fitting LMMs. This is why we derive and implement a Fisher-scoring algorithm to estimate the model parameters by the residual maximum likelihood (REML) method. Based on the model, the empirical best linear unbiased predictors (EBLUP) of linear indicators are derived and the corresponding mean squared errors (MSE) are approximated. Two MSE estimators are considered. The first one is based on the analytical MSE approximation and the second one is based on parametric bootstrap. In the first case, we follow (Prasad and Rao 1990) and (Datta and Lahiri 2000). In the second case, we follow (Hall and Maiti 2006) and (González-Manteiga et al. 2008).

Influence and diagnostics analysis are tools to validate a model and to get valuable information to interpret underlying data relationships. The aim is to investigate if there are unfavorable cases by some established tolerance limits. Generally, exceeding those thresholds of attention may give an idea about the potential lack of fit of the model adopted. Some statistics in the literature are traditionally employed for detecting several aspects of these warnings, and then for assessing their theoretical and empirical implications. We follow (Demidenko and Stukel 2005; Zewotir and Galpin 2007; Christensen et al. 1992; Calvin and Sedransk 1991) to introduce leverages, Cook’s distances, Covratio statistics, and residuals.

Nevertheless, when LMMs are applied to SAE problems, the influence and diagnostic tools should also take into account the impact of deleting a domain in the EBLUPs and in the estimators of the corresponding MSEs. As far as we know, this SAE-specific influence analysis has not been yet investigated. This paper introduces new tools to analyze the influence of domain deletion in the SAE results. Further, it also gives measures of model efficiency by taking into account the correlations between residuals and perturbations and the variability of the variance component estimators. The new diagnostic tools are applied to the three-fold Fay–Herriot model selected to analyze poverty data.

The eradication of poverty is a priority in 21st-century societies. This has led to the emergence of many studies to investigate statistical methodology that allows poverty to be mapped at different levels of territorial aggregation. Regarding estimation techniques in small areas, we can cite some works. Molina and Rao (2010) proposed empirical best predictors (EBPs) based on a nested error regression model. Hobza and Morales (2016), Hobza et al. (2018) fitted a logit mixed model to unit-level poverty data and derived EBPs for poverty proportions. Tzavidis et al. (2008), Marchetti et al. (2012) introduced robust estimators of poverty indicators by using a quantile regression approach. Marchetti and Secondi (2017), Giusti et al. (2017), Tzavidis et al. (2015) gave interesting contributions to mapping poverty and health using Italian data while Tonutti et al. (2022) assessed anti-poverty policy at the Italian local level, and Guadarrama et al. (2022) based their poverty predictions on temporal linear mixed models. In the case of area-level models, Esteban et al. (2012), Marhuenda et al. (2013), Morales et al. (2015). However, Boubeta et al. (2016, 2017), López-Vizcaíno et al. (2013, 2015), Chandra et al. (2017) employed generalized linear mixed models, with Poisson or multinomial distributions. The books edited by Pratesi (2016), Betti and Lemmi (2013) give more contributions to the small area estimation of poverty indicators.

This paper introduces new statistical methodology for poverty mapping and presents an application to data from the Spanish living condition survey (SLCS). This survey is designed to obtain reliable direct estimators in NUTS 2 type regions (autonomous communities), but the sample sizes are quite small in NUTS 3 type territories (provinces), according to the current NUTS classification of EUROSTAT 2016. The aim of the study is to estimate the proportions of poverty by sex in the Spanish provinces during the years 2004–2008. For this reason, this paper introduces an area-level LMM with random effects in the province, in the province crossed with sex and in the crosses of province, sex and year. A three-fold Fay–Herriot model with time correlated AR(1) random effect is fitted for the application to SLCS data, but the results suggest to prefer a simpler model without complex temporal correlation structure, since we only have data for 5 periods (years).

The paper is organized as follows. Section 2 introduces the new three-fold Fay–Herriot model, the fitting algorithm to calculate the REML estimators of the model parameters, the specific influence and diagnostic tools, the EBLUPs of domain linear indicators and the analytic and bootstrap estimators of the corresponding MSEs. Section 3 presents some simulation experiments to investigate the performance of the fitting algorithm, the predictors, and the estimators of MSEs. In addition, the BLUPs and EBLUPs based on of the one-fold, two-fold and three-fold Fay–Herriot models are investigated. Section 4 deals with the application to real data and the mapping of poverty proportions. Section 5 gives some conclusions. The paper contains three appendixes. Appendix A derives the final expression of the analytic estimator of the MSEs. Appendix B defines the three-fold Fay–Herriot model, in case of AR(1) time effects, and presents the REML procedure for the estimation of the variance component parameters. Appendix C gives the list of Spanish provinces with the corresponding acronyms.

2 The three-fold Fay–Herriot model

2.1 The model

Let us consider the three-fold Fay–Herriot model

$$\begin{aligned} y_{drt}=\varvec{x}_{drt}\varvec{\beta }+u_{1,d}+u_{2,dr}+u_{3,drt}+e_{drt},\quad d=1,\ldots ,D,\,\,r=1,\ldots ,R,\,\,t=1,\ldots ,T, \end{aligned}$$

(2.1)

where $y_{drt}$ is a direct estimator of the characteristic of interest and $\varvec{x}_{drt}$ is a row vector containing the aggregated population values of p auxiliary variables. The subscripts d, r and t represent domains, subdomains, and subsubdomains respectively. For example, d, r and t may represent area (province), category (sex group), and time period (year) respectively. We assume that $u_{1,d}\sim N(0,\sigma _1^2)$, $u_{2,dr}\sim N(0,\sigma _2^2)$, $u_{3,drt}\sim N(0,\sigma _3^2)$, $e_{drt}\sim N(0,\sigma _{drt}^2)$, with $\sigma _{drt}^2>0$ known, $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, are mutually independent. The variance of $y_{drt}$ is $\text{ var }(y_{drt})=\sigma _1^2+\sigma _2^2+\sigma _3^2+\sigma _{drt}^2$, $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$. Model (2.1) generalizes the two-fold Fay–Herriot model described in Section 17.2 of Morales et al. (2021).

At the domain level d and subdomain level r, we define the matrices and vectors

$$\begin{aligned}{} & {} \varvec{X}_{dr}=\underset{1\le t \le T}{\hbox {col}}(\varvec{x}_{drt}),\, \varvec{Z}_{1,dr}=\varvec{Z}_{2,dr}=\varvec{1}_T,\, \varvec{Z}_{3,dr}=\varvec{I}_{T},\, \varvec{V}_{3,dr}=\sigma _3^2\varvec{I}_{T},\, \varvec{V}_{e,dr}\\{} & {} \quad =\underset{1\le t \le T}{\hbox {diag}}(\sigma ^2_{drt}), \\{} & {} \varvec{y}_{dr}=\underset{1\le t \le T}{\hbox {col}}(y_{drt}),\,\, \varvec{u}_{3,dr}=\underset{1\le t \le T}{\hbox {col}}(u_{3,drt})\sim N_T(\varvec{0}, \varvec{V}_{3,dr}),\,\, \varvec{e}_{dr}\\{} & {} \quad =\underset{1\le t \le T}{\hbox {col}}(e_{drt})\sim N_T(\varvec{0}, \varvec{V}_{e,dr}), \end{aligned}$$

where $\varvec{1}_T$ denotes the $T\times 1$ vector of ones, $\varvec{I}_T$ is the $T\times T$ identity matrix and col and diag are the columns and diagonal matrix operators respectively.

We can write model (2.1) in the subdomain form

$$\begin{aligned} \varvec{y}_{dr}=\varvec{X}_{dr}\varvec{\beta }+\varvec{Z}_{1,dr}u_{1,d}+\varvec{Z}_{2,dr}u_{2,dr}+\varvec{Z}_{3,dr}\varvec{u}_{3,dr}+\varvec{e}_{dr},\quad d=1,\ldots ,D,\,\,r=1,\ldots ,R. \end{aligned}$$

The variance matrix of $\varvec{y}_{dr}$ is

$$\begin{aligned} \varvec{V}_{dr}=\text{ var }(\varvec{y}_{dr})=\sigma _1^2\varvec{1}_T\varvec{1}_T^\prime +\sigma _2^2\varvec{1}_T\varvec{1}_T^\prime +\sigma _3^2\varvec{I}_{T}+\varvec{V}_{e,dr},\quad d=1,\ldots ,D,\, r=1,\ldots ,R. \end{aligned}$$

At the domain level d, we define the vectors and matrices

$$\begin{aligned}{} & {} \varvec{y}_{d}=\underset{1\le r \le R}{\hbox {col}}(\varvec{y}_{dr}),\, \varvec{X}_{d}=\underset{1\le r \le R}{\hbox {col}}(\varvec{X}_{dr}),\, \varvec{Z}_{1,d}=\varvec{1}_{RT},\, \varvec{Z}_{2,d}=\underset{1\le r \le R}{\hbox {diag}}(\varvec{Z}_{2,dr}),\, \varvec{Z}_{3,d}=\varvec{I}_{RT},\, \\{} & {} \varvec{V}_{2,d}=\sigma _2^2\varvec{I}_{R},\, \varvec{V}_{3,d}=\sigma _3^2\varvec{I}_{RT},\, \varvec{V}_{e,d}=\underset{1\le r \le R}{\hbox {diag}}(\varvec{V}_{e,dr}),\, \varvec{u}_{2,d}=\underset{1\le r \le R}{\hbox {col}}(u_{2,dr})\sim N_{R}(\varvec{0}, \varvec{V}_{2,d}), \\{} & {} \varvec{u}_{3,d}=\underset{1\le r \le R}{\hbox {col}}(\varvec{u}_{3,dr})\sim N_{RT}(\varvec{0}, \varvec{V}_{3,d}),\,\, \varvec{e}_{d}=\underset{1\le r \le R}{\hbox {col}}(\varvec{e}_{dr})\sim N_{RT}(\varvec{0}, \varvec{V}_{e,d}). \end{aligned}$$

We can write model (2.1) in the domain form

$$\begin{aligned} \varvec{y}_{d}=\varvec{X}_{d}\varvec{\beta }+\varvec{Z}_{1,d}u_{1,d}+\varvec{Z}_{2,d}\varvec{u}_{2,d}+\varvec{Z}_{3,d}\varvec{u}_{3,d}+\varvec{e}_{d},\quad d=1,\ldots ,D. \end{aligned}$$

(2.2)

Let us define the $RT\times (1+R+RT)$ matrix $\varvec{Z}_d=(\varvec{Z}_{1,d}\varvec{Z}_{2,d},\varvec{Z}_{3,d})$ and the $(1+R+RT)\times 1$ vector $\varvec{u}_d=(\varvec{u}_{1,d}^\prime ,\varvec{u}_{2,d}^\prime ,\varvec{u}_{3,d}^\prime )^\prime$, with $\varvec{V}_{ud}=\text{ var }(\varvec{u}_d)=\text{ diag }(\sigma _1^2,\varvec{V}_{2,d},\varvec{V}_{3,d})$. We can write model (2.2) in the linear mixed model form

$$\begin{aligned} \varvec{y}_{d}=\varvec{X}_{d}\varvec{\beta }+\varvec{Z}_{d}\varvec{u}_{d}+\varvec{e}_{d},\quad d=1,\ldots ,D. \end{aligned}$$

The variance matrix of $\varvec{y}_{d}$ is

$$\begin{aligned} \varvec{V}_d=\text{ var }(\varvec{y}_{d})=\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_T\varvec{1}_T^\prime ) +\sigma _3^2\varvec{I}_{RT}+\varvec{V}_{e,d},\quad d=1,\ldots ,D. \end{aligned}$$

At the population level, we define the vectors and matrices

$$\begin{aligned}{} & {} \varvec{y}=\underset{1\le d \le D}{\hbox {col}}(\varvec{y}_{d}),\, \varvec{X}=\underset{1\le d \le D}{\hbox {col}}(\varvec{X}_{d}),\, \varvec{Z}_{1}=\underset{1\le d \le D}{\hbox {diag}}(\varvec{Z}_{1,d}),\, \varvec{Z}_{2}=\underset{1\le d \le D}{\hbox {diag}}(\varvec{Z}_{2,d}),\, \varvec{Z}_{3}=\varvec{I}_{DRT},\, \\{} & {} \varvec{V}_{1}=\sigma _1^2\varvec{I}_{D},\, \varvec{V}_{2}=\sigma _2^2\varvec{I}_{DR},\, \varvec{V}_{3}=\sigma _3^2\varvec{I}_{DRT},\, \varvec{V}_{e}=\underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_{e,d}),\, \\{} & {} \varvec{u}_{1}=\underset{1\le d \le D}{\hbox {col}}(\varvec{u}_{1,d})\sim N_{D}(\varvec{0}, \varvec{V}_{1}),\,\, \varvec{u}_{2}=\underset{1\le d \le D}{\hbox {col}}(\varvec{u}_{2,d})\sim N_{DR}(\varvec{0}, \varvec{V}_{2}), \\{} & {} \varvec{u}_{3}=\underset{1\le d \le D}{\hbox {col}}(\varvec{u}_{3,d})\sim N_{DRT}(\varvec{0}, \varvec{V}_{3}),\,\, \varvec{e}=\underset{1\le d \le D}{\hbox {col}}(\varvec{e}_{d})\sim N_{RT}(\varvec{0}, \varvec{V}_{e}). \end{aligned}$$

We can write model (2.1) in the population form

$$\begin{aligned} \varvec{y}=\varvec{X}\varvec{\beta }+\varvec{Z}_{1}\varvec{u}_{1}+\varvec{Z}_{2}\varvec{u}_{2}+\varvec{Z}_{3}\varvec{u}_{3}+\varvec{e}, \end{aligned}$$

(2.3)

where the vectors $\varvec{u}_1$, $\varvec{u}_2$, $\varvec{u}_3$ and $\varvec{e}$ are mutually independent. The variance matrix of $\varvec{y}$ is

$$\begin{aligned}{} & {} \varvec{V}=\text{ var }(\varvec{y})=\underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_d)= \sigma _1^2\underset{1\le d \le D}{\hbox {diag}}(\varvec{1}_{RT}\varvec{1}_{RT}^\prime ) +\sigma _2^2\underset{1\le d \le D}{\hbox {diag}}\big (\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_T\varvec{1}_T^\prime )\big ) \\{} & {} \quad +\sigma _3^2\varvec{I}_{DRT}+\varvec{V}_{e}. \end{aligned}$$

Let us define the $DRT\times (D+DR+DRT)$ matrix $\varvec{Z}=(\varvec{Z}_1,\varvec{Z}_2,\varvec{Z}_3)$ and the $(D+DR+DRT)\times 1$ vector $\varvec{u}=(\varvec{u}_1^\prime ,\varvec{u}_2^\prime ,\varvec{u}_3^\prime )^\prime$, with $\varvec{V}_u=\text{ var }(\varvec{u})=\text{ diag }(\varvec{V}_{1},\varvec{V}_{2},\varvec{V}_{3})$. We can write model (2.3) in the linear mixed model form

$$\begin{aligned} \varvec{y}=\varvec{X}\varvec{\beta }+\varvec{Z}\varvec{u}+\varvec{e}, \end{aligned}$$

If we assume that $\sigma _1^2>0$, $\sigma _2^2>0$, and $\sigma _3^2>0$ are known, then the best linear unbiased estimator (BLUE) of $\varvec{\beta }$ and the best linear unbiased predictor (BLUP) of $\varvec{u}$ are

$$\begin{aligned} {\tilde{\varvec{\beta }}}= & {} (\varvec{X}^\prime \varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^\prime \varvec{V}^{-1}\varvec{y}=\bigg (\sum _{d=1}^D\varvec{X}_d^{\prime }\varvec{V}_d^{-1}\varvec{X}_d\bigg )^{-1} \bigg (\sum _{d=1}^D\varvec{X}_d^{\prime }\varvec{V}_d^{-1}\varvec{y}_d\bigg ), \\ \nonumber {\tilde{\varvec{u}}}= & {} \varvec{V}_u\varvec{Z}^\prime \varvec{V}^{-1}(\varvec{y}-\varvec{X}{\tilde{\varvec{\beta }}}) \\ \nonumber= & {} \left( \begin{array}{ccc}\sigma _1^2\varvec{I}_{D}&{} \varvec{0}&{}\varvec{0}\\ \varvec{0}&{} \sigma _2^2\varvec{I}_{DR}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\sigma _3^2\varvec{I}_{DRT}\end{array}\right) \left( \begin{array}{c} \underset{1\le d \le D}{\hbox {diag}}(\varvec{1}_{RT}^{\prime }) \\ \underset{1\le d \le D}{\hbox {diag}}(\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime }))\\ \varvec{I}_{DRT} \end{array}\right) \underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_{d}^{-1}) \underset{1\le d \le D}{\hbox {col}}(\varvec{y}_d-\varvec{X}_d{\tilde{\varvec{\beta }}}) \\ \nonumber= & {} \left( \begin{array}{c} \sigma _1^2\underset{1\le d \le D}{\hbox {col}}\big (\varvec{1}_{RT}^\prime \varvec{V}_d^{-1}(\varvec{y}_d-\varvec{X}_d{\tilde{\varvec{\beta }}})\big )\\ \sigma _2^2\underset{1\le d \le D}{\hbox {col}}\big (\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime })\varvec{V}_d^{-1}(\varvec{y}_d-\varvec{X}_d{\tilde{\varvec{\beta }}})\big )\\ \sigma _3^2\underset{1\le d \le D}{\hbox {col}}\big (\varvec{V}_d^{-1}(\varvec{y}_d-\varvec{X}_d{\tilde{\varvec{\beta }}})\big ) \end{array}\right) . \end{aligned}$$

(2.4)

The empirical versions, EBLUE of $\varvec{\beta }$ and EBLUP of $\varvec{u}$, are obtained by plugging estimators ${\hat{\sigma }}_1^2$, ${\hat{\sigma }}_2^2$ and ${\hat{\sigma }}_3^2$ in the place of $\sigma _1^2$, $\sigma _2^2$ and $\sigma _3^2$, i.e.

$$\begin{aligned} {{\hat{\varvec{\beta }}}}=(\varvec{X}^{\prime }{{\hat{\varvec{V}}}}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }{{\hat{\varvec{V}}}}^{-1}\varvec{y},\quad {{\hat{\varvec{u}}}}={{\hat{\varvec{V}}}}_{u}\varvec{Z}^{\prime }{{\hat{\varvec{V}}}}^{-1}\left( \varvec{y}-\varvec{X}{{\hat{\varvec{\beta }}}}\right) , \end{aligned}$$

(2.5)

where

$$\begin{aligned} {{\hat{\varvec{V}}}}_{u}= & {} \underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_{ud})=\text{ diag }({{\hat{\sigma }}}_1^2\varvec{I}_D,{{\hat{\sigma }}}_ 2^2\varvec{I}_{DR},{{\hat{\sigma }}}_3^2\varvec{I}_{DRT}), \\ {{\hat{\varvec{V}}}}= & {} \underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_{d})= {{\hat{\sigma }}}_1^2\underset{1\le d \le D}{\hbox {diag}}(\varvec{1}_{RT}\varvec{1}_{RT}^\prime ) +{{\hat{\sigma }}}_2^2\underset{1\le d \le D}{\hbox {diag}}\big (\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_T\varvec{1}_T^\prime )\big ) +{{\hat{\sigma }}}_3^2\varvec{I}_{DRT}+\varvec{V}_{e}. \end{aligned}$$

We are interested in predicting the linear combination of fixed and random effects $\mu _{drt}=\varvec{x}_{drt}\varvec{\beta }+u_{1,d}+u_{2,dr}+ u_{3,drt}$. If the vector of variance components $\varvec{\theta }=(\sigma _1^2, \sigma _2^2, \sigma _3^2)$ is known, the BLUP of $\mu _{drt}$ is ${{\tilde{\mu }}}_{drt}=\varvec{x}_{drt}{{\tilde{\varvec{\beta }}}}+{\tilde{u}}_{1,d}+ {\tilde{u}}_{2,dr}+ {\tilde{u}}_{3,drt}$. The corresponding EBLUP of $\mu _{drt}$ is obtained by substituting $\varvec{\theta }$ by an estimator ${{\hat{\varvec{\theta }}}}=({{\hat{\sigma }}}_1^2, {{\hat{\sigma }}}_2^2, {{\hat{\sigma }}}_3^2)$, and it has the form

$$\begin{aligned} {{\hat{\mu }}}_{drt}=\varvec{x}_{drt}{{\hat{\varvec{\beta }}}}+{\hat{u}}_{1,d}+{\hat{u}}_{2,dr}+{\hat{u}}_{3,drt}, \end{aligned}$$

where ${{\hat{\varvec{\beta }}}}$ and ${{\hat{\varvec{u}}}}$ are given in (2.5). The EBLUP of ${\mu }_{drt}$ is the predictor of the population mean $\overline{Y}_{drt}$, i.e. $\hat{\overline{Y}}_{drt}^{eblup}={\hat{\mu }}_{drt}$. The synthetic estimator, ${\hat{\mu }}_{drt}^{syn}=\varvec{x}_{drt}{\hat{\beta }}$, can be employed for out-of sample domains. The BLUP and EBLUP vectors are

$$\begin{aligned}{} & {} {{\tilde{\varvec{\mu }}}}_{dr}=\underset{1\le t \le T}{\hbox {col}}({{\tilde{\mu }}}_{drt}),\,\, {{\tilde{\varvec{\mu }}}}_{d}=\underset{1\le r \le R}{\hbox {col}}({{\tilde{\varvec{\mu }}}}_{dr}),\,\,\, {{\tilde{\varvec{\mu }}}}=\underset{1\le d \le D}{\hbox {col}}({{\tilde{\varvec{\mu }}}}_{d}), \\{} & {} {{\hat{\varvec{\mu }}}}_{dr}=\underset{1\le t \le T}{\hbox {col}}({{\hat{\mu }}}_{drt}),\,\, {\hat{\varvec{\mu }}}_{d}=\underset{1\le r \le R}{\hbox {col}}({\hat{\varvec{\mu }}}_{dr}),\,\,\, {\hat{\varvec{\mu }}}=\underset{1\le d \le D}{\hbox {col}}({{\hat{\varvec{\mu }}}}_{d}). \end{aligned}$$

Let us define $\varvec{Q}=(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}$, $\varvec{R}=\varvec{X}\varvec{Q}\varvec{X}^{\prime }\varvec{V}^{-1}$, $\varvec{I}=\varvec{I}_{DRT}$ and $\varvec{P}=\varvec{V}^{-1}(\varvec{I}-\varvec{R})=\varvec{V}^{-1}-\varvec{V}^{-1}\varvec{X}\varvec{Q}\varvec{X}^{\prime }\varvec{V}^{-1}$, and note that $\varvec{Z}\varvec{V}_u\varvec{Z}^\prime =\varvec{V}-\varvec{V}_e$. Then, $\varvec{X}{\tilde{\varvec{\beta }}}=\varvec{R}\varvec{y}$, $\varvec{y}-\varvec{X}{\tilde{\varvec{\beta }}}=(\varvec{I}-\varvec{R})\varvec{y}$ and the BLUP of $\varvec{\mu }$ can be written in the form

$$\begin{aligned} {\tilde{\varvec{\mu }}}= & {} \varvec{X}{\tilde{\varvec{\beta }}}+\varvec{Z}{\tilde{\varvec{u}}}=\varvec{R}\varvec{y}+\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{V}^{-1}(\varvec{y}-\varvec{X}{\tilde{\varvec{\beta }}}) =\varvec{R}\varvec{y}+(\varvec{V}-\varvec{V}_e)\varvec{V}^{-1}(\varvec{I}-\varvec{R})\varvec{y}\\= & {} \varvec{R}\varvec{y}+(\varvec{I}-\varvec{R})\varvec{y}-\varvec{V}_e\varvec{V}^{-1}(\varvec{I}-\varvec{R})\varvec{y}=\varvec{y}-\varvec{V}_{e}\varvec{P}\varvec{y}. \end{aligned}$$

2.2 Estimation of variance component parameters

This Section gives a Fisher-scoring algorithm to calculate the REML estimators of $\sigma _1^2$, $\sigma _2^2$ and $\sigma _3^2$. The REML log-likelihood is

$$\begin{aligned}{} & {} {l}_{reml}(\sigma _1^2,\sigma _2^2,\sigma _3^2)=-\frac{DRT-p}{2}\log 2\pi +\frac{1}{2}\log |\varvec{X}^{\prime }\varvec{X}|-\frac{1}{2}\log |\varvec{V}| \\{} & {} \quad - \frac{1}{2}\log |\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X}| -\frac{1}{2}\,\varvec{y}^{\prime }\varvec{P}\varvec{y}. \end{aligned}$$

Let us define $\varvec{\theta }=(\theta _1,\theta _2,\theta _3)=(\sigma _1^2,\sigma _2^2,\sigma _3^2)$. It holds that

$$\begin{aligned} \varvec{V}_1= & {} \frac{\partial \varvec{V}}{\partial \theta _1}=\underset{1\le d \le D}{\hbox {diag}}(\varvec{1}_{RT}\varvec{1}_{RT}^\prime ),\,\,\, \varvec{V}_2=\frac{\partial \varvec{V}}{\partial \theta _2}=\underset{1\le d \le D}{\hbox {diag}}\big ( \underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^{\prime })\big ),\,\,\, \varvec{V}_3=\frac{\partial \varvec{V}}{\partial \theta _3}=\varvec{I}_{DRT}, \\ \varvec{P}_a= & {} \frac{\partial \varvec{P}}{\partial \theta _a}=-\varvec{P}\frac{\partial \varvec{V}}{\partial \theta _a}\varvec{P}=-\varvec{P}\varvec{V}_a\varvec{P},\quad a=1,2,3. \end{aligned}$$

By taking derivatives of ${l}_{reml}$ with respect to $\theta _a$, we have the elements of the score vector $\varvec{S}=\varvec{S}(\varvec{\theta })= (S_1,S_2,S_3)^\prime$, i.e.

$$\begin{aligned} S_a=\frac{\partial {l}_{reml}}{\partial \theta _a}=-\frac{1}{2}\hbox {tr}(\varvec{P}\varvec{V}_a)+\frac{1}{2}\varvec{y}^{\prime }\varvec{P}\varvec{V}_a\varvec{P}\varvec{y},\quad a=1,2,3. \end{aligned}$$

By taking second derivatives with respect to $\theta _a$ and $\theta _b$, taking expectations and changing the sign, we obtain the components of the Fisher information matrix $\varvec{F}= \varvec{F}(\varvec{\theta }) = \left( F_{ab}\right) _{a,b=1,2,3}$, where

$$\begin{aligned} F_{ab}=\frac{1}{2}\hbox {tr}(\varvec{P}\varvec{V}_a\varvec{P}\varvec{V}_b),\quad a,b=1,2,3. \end{aligned}$$

The updating formula of the Fisher-scoring algorithm is

$$\begin{aligned} \varvec{\theta }^{(k+1)}=\varvec{\theta }^{(k)}+\varvec{F}^{-1}(\varvec{\theta }^{(k)})\varvec{S}(\varvec{\theta }^{(k)}). \end{aligned}$$

As algorithm seeds, we may take $\theta _1^{(0)}=\theta _2^{(0)}=\theta _3^{(0)}=S^2/3$, where $S^2=\frac{1}{DRT-p}(\varvec{y}-\varvec{X}\check{\varvec{\beta }})^{\prime }\varvec{V}_e^{-1}(\varvec{y}-\varvec{X}\check{\varvec{\beta }})$ and $\check{\varvec{\beta }}=(\varvec{X}^{\prime }\varvec{V}_e^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}_e^{-1}\varvec{y}$. The REML estimator of $\varvec{\beta }$ is

$$\begin{aligned} \hat{{\varvec{\beta }}}=({\varvec{X}}^{\prime }{\hat{\varvec{V}}}^{-1}{\varvec{X}})^{-1}{\varvec{X}}^{\prime }{\hat{\varvec{V}}}^{-1}{\varvec{y}}, \end{aligned}$$

where ${\hat{\varvec{V}}}=\varvec{V}({{\hat{\varvec{\theta }}}})$ was defined above. Under regularity assumptions, the asymptotic distributions of ${{\hat{\varvec{\theta }}}}$ and ${{\hat{\varvec{\beta }}}}$ are

$$\begin{aligned} {\hat{\varvec{\theta }}}\sim N_3(\varvec{\theta }, \varvec{F}^{-1}(\varvec{\theta })),\quad {\hat{\varvec{\beta }}}\sim N_p(\varvec{\beta }, (\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}). \end{aligned}$$

Asymptotic confidence intervals, at the level $1-\alpha$, for $\theta _a$ and $\beta _j$ are

$$\begin{aligned} {\hat{\theta }}_a\pm z_{\alpha /2}\,\nu _{aa}^{1/2},\,\, a=1,2,3,\quad {\hat{\beta }}_{j}\pm z_{\alpha /2}\,q_{jj}^{1/2},\,\, j=1,\ldots ,p, \end{aligned}$$

where $\varvec{F}^{-1}({{\hat{\varvec{\theta }}}})=(\nu _{ab})_{a,b=1,2,3}$, $(\varvec{X}^{\prime }\varvec{V}^{-1}({{\hat{\varvec{\theta }}}})\varvec{X})^{-1}=(q_{ij})_{i,j=1,\ldots ,p}$ and $z_{\alpha }$ is the $\alpha$-quantile of the standard normal distribution. If ${\hat{\beta }}_j=\beta _0$, then the p-value for testing $H_0:\,\beta _j=0$ is

$$\begin{aligned} p=2P_{H_0}({\hat{\beta }}_j>|\beta _0|)=2P(N(0,1)> |\beta _0|/\sqrt{q_{jj}}\,). \end{aligned}$$

2.3 Influence analysis and model diagnostics

Influence and diagnostics analysis are tools to validate a model, but also to get valuable information to interpret underlying data relationships. This section assumes that model parameters are estimated by the REML method. The aim is to investigate if there are unfavorable cases by some established tolerance limits. Generally, exceeding those thresholds of attention may give an idea about the potential lack of fit of the model adopted. Some statistics in the literature are traditionally employed for detecting several aspects of these warnings, and then for assessing their theoretical and empirical implications. We focused on some diagnostic measures, like the leverage points, the impact of domain deletion on fixed effects, the Cook’s distances, and the residual analysis. We present some additional valuations, given by some peculiarity of the area-level LMMs for SAE. In these types of models, like in the Fay–Herriot model or in the model (2.3), the variance of the regression error is given, instead of the case of the standard LMM. This fact has some interesting consequences, in terms of the measure of the general efficiency of the model. This section presents some influence and diagnostics tools adapted to the model (2.3). In particular, Sect. 2.3.4 introduces new influence statistics derived from the estimators of the MSEs of the EBLUPs, as the model efficiency and the mse-ratio.

2.3.1 Leverages

By following Demidenko and Stukel (2005), Zewotir and Galpin (2007), the leverage matrix of domain d is

$$\begin{aligned} \varvec{L}_d=\varvec{L}_{d}({{\hat{\varvec{\theta }}}})=\frac{\partial {\hat{\varvec{\mu }}}_{d}}{\partial \varvec{y}_{d}} =\frac{\partial \varvec{X}_{d}{\hat{\varvec{\beta }}}}{\partial \varvec{y}_{d}}+\frac{\partial {{\hat{\varvec{u}}}}_{d}}{\partial \varvec{y}_{d}} \triangleq \varvec{L}_{f,d}+\varvec{L}_{r,d}, \end{aligned}$$

where $\varvec{L}_{f,d}$ and $\varvec{L}_{r,d}$ correspond to fixed and random part of the model. They are

$$\begin{aligned} \varvec{L}_{f,d}=\varvec{X}_{d}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}_{d}^{\prime }\varvec{V}_{d}^{-1},\quad \varvec{L}_{r,d}=\varvec{Z}_{d}\varvec{V}_{ud}\varvec{Z}_{d}^{\prime }\varvec{V}_{d}^{-1}(\varvec{I}-\varvec{L}_{f,d}). \end{aligned}$$

We define the fixed-effects and random-effects leverages of domain d by averaging the diagonal elements of the corresponding leverage matrix, i.e.

$$\begin{aligned} L_{f,d}=\frac{1}{RT}\text{ tr }(\varvec{L}_{f,d}),\quad L_{r,d}=\frac{1}{RT}\text{ tr }(\varvec{L}_{r,d}), \end{aligned}$$

(2.6)

where $\text{ tr }(\varvec{A})$ indicates the trace of the square matrix $\varvec{A}$. As $\text{ tr }\big (\sum _{d=1}^{D}\varvec{L}_{f,d}\big )=\text{ rank }(\varvec{X}_d)$, a domain $d_0$ is first-level or second-level influential in the model fit if its fixed-effects or random-effects leverages fulfill

$$\begin{aligned} \text{ tr }(\varvec{L}_{f,d_0})> \frac{2}{D}\sum _{d=1}^{D}\text{ tr }(\varvec{L}_{f,d}),\quad \text{ or }\quad \text{ tr }(\varvec{L}_{r,d_0})> \frac{2}{D}\sum _{d=1}^{D}\text{ tr }(\varvec{L}_{r,d}), \end{aligned}$$

see (Demidenko and Stukel 2005). In particular, if the row-vectors $\varvec{x}_{drt}^{\prime }\sim N(\mathbf {\mu }_{x}, \mathbf {\Sigma }_{x})$ of the matrix $\varvec{X}_{d}$ follow a multinormal distribution, so that $\overline{\varvec{x}}_{d}^{\prime }=(1,\frac{1}{RT} \Sigma _{r=1}^{R}\Sigma _{t=1}^{T}\varvec{x}_{1,drt},...,\frac{1}{RT}\Sigma _{r=1}^{R}\Sigma _{t=1}^{T}\varvec{x}_{p,drt})$, with $\overline{\varvec{x}} _{d}^{\prime }\sim N(\mathbf {\mu }_{x},\mathbf {\Sigma }_{\overline{x}})$, then ( Belsley et al. (1980)):

$$\begin{aligned} \frac{(D-p)(\varvec{L}_{f,d}-\frac{1}{D})}{(p-1)(1-\varvec{L}_{f,d})}\sim F_{p,D-p}. \end{aligned}$$

(2.7)

With $D>50$, and $p>10$, the $95\%$ value of the F distribution is less than 2 (Bollen and Jackman 1990). It is easy to see that equation 2.7 gives 1 when $\varvec{L}_{f,d}=$ $\frac{1}{D}\Sigma _{d=1}^{D}tr(\varvec{L}_{f,d})=\frac{p}{D}$. Then the cut-off value for the leverage of fixed effects seems fairly defined by twice the average $\frac{1}{D}\Sigma _{d=1}^{D}\varvec{L}_{f,d}=$ $\frac{1}{D}\Sigma _{d=1}^{D}\frac{1}{RT}tr(\varvec{L}_{f,d})=\frac{p}{D}$, as happens for the linear regression model.

Those domains with leverages greater than the cut-off points reveal a potentially significant influence of the direct estimator on the value of the EBLUP vector ${{\hat{\varvec{\mu }}}}_d$.

2.3.2 Domain deletion

Domain deletion diagnostics allow knowing relevant shifts in the estimators of regression parameters. Let ${{\hat{\varvec{\beta }}}}_{(d)}$ be the estimator of $\varvec{\beta }$ calculated without using the data from domain d and let $\varvec{r}_{d}^{m}=\varvec{y}_{d}-\varvec{X}_{d}{\hat{\varvec{\beta }}}$ the vector of marginal residuals of domain d. It holds that

$$\begin{aligned} {\hat{\varvec{\beta }}}-{\hat{\varvec{\beta }}}_{(d)} =(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}_{d}^{\prime }\varvec{V}_{d}^{-1}(\varvec{I}-\varvec{L}_{f,d})^{-1}\varvec{r}_{d}^{m}. \end{aligned}$$

(2.8)

The Cook’s distance,

$$\begin{aligned} \Delta _{d}=\frac{1}{\text{ rank }(\varvec{X})}(\varvec{r}_{d}^{m})^{\prime }(\varvec{I}-\varvec{L}_{f,d})^{-1}\varvec{V}_{d}^{-1}\varvec{X}_{d}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}_{d}^{\prime }\varvec{V}_{d}^{-1}(\varvec{I}-\varvec{L}_{f,d})^{-1}\varvec{r}_{d}^{m}, \end{aligned}$$

(2.9)

studies the influence of the domain d, based jointly on marginal residuals and leverages, traditionally with a critical value 4/D.

In the linear regression with a sample of n observations, $i=1,...,n$, there are some accepted critical values for the Cook’s distance $\Delta _{i}$, when the observation i is deleted. One of this is $\Delta _{i}>1$, that corresponds to “distances”between $\widehat{\varvec{\beta }}$ and $\widehat{\varvec{\beta }}_{(i)}$ that lie beyond a $50\%$ confidence region, considered as too large. The most used cutoff values are $\Delta _{i}>\frac{4}{n}$, or $\Delta _{i}>\frac{4}{n-p}$. These values are derived starting from the alternative formula $\Delta _{i}=\frac{t_{i}^{2}}{p}\frac{\varvec{L}_{i}}{1-\varvec{L}_{i}}$, with $\varvec{L}_{i}$ the diagonal element of the leverage matrix, and $t_{i}$ the i-th studentized residual. Substituting the $\varvec{L}_{i}$ with the mean leverage $\varvec{L}_{i}=\frac{p}{n}$, the last critical value gives $\Delta _{i}=\frac{t_{i}^{2}}{p+1}\frac{\varvec{L}_{i}}{1-\varvec{L}_{i}}=\frac{t_{i}^{2}}{p}\frac{p}{n-p}=\frac{4}{n-p}$, when the regression studentized residuals exceed the usual critical value $t_{i}=2$. Using the formulation of Banerjee and Frees (1997) of the confidence ellipsoid at ($1-\alpha )100\%$ for the $\widehat{\varvec{\beta }}$’s, i.e. $(\varvec{\beta }-\widehat{\varvec{\beta }})^{\prime }(\varvec{X}^{\prime } \varvec{V}^{-1}\varvec{X})^{-1}(\varvec{\beta }-\widehat{\varvec{\beta }} )\le pF_{1-\alpha }$, for a linear mixed effects model we get the following critical region for $\Delta _{d}$:

$$\begin{aligned} \Delta _{d}=\frac{1}{rank(\varvec{X})}(\varvec{r}_{d}^{m})^{\prime }(\varvec{I}-\varvec{L}_{f,d})^{-1}\varvec{V}_{d}^{-1}\varvec{X}_{d}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}_{d}^{\prime }\varvec{V}_{d}^{-1}(\varvec{I}-\varvec{L}_{f,d})^{-1}\varvec{r}_{d}^{m}>F_{1-\alpha }. \end{aligned}$$

This critical value corresponds to the similar formula of the threshold defined in Cook (1977) for the linear regression model.

Christensen et al. (1992) introduced the Covratio statistics

$$\begin{aligned} \gamma ({\hat{\varvec{\theta }}}_{(d)})=\left| \frac{\det [\varvec{F}({\hat{\varvec{\theta }}}_{(d)})]}{\det [\varvec{F}({\hat{\varvec{\theta }}})]}-1\right| . \end{aligned}$$

(2.10)

where ${{\hat{\varvec{\theta }}}}$ and ${\hat{\varvec{\theta }}}_{(d)}$ are the REML estimators of $\varvec{\theta }$ calculated with and without the data of domain d and $\varvec{F}$ is the REML Fisher information matrix. A value of $\gamma ({\hat{\varvec{\theta }}}_{(d)})$ close to zero indicates that the influence of domain d on the estimation of the variance parameters $\varvec{\theta }$ is negligible. We are thus interested in detecting domains d with large departures of $\gamma ({\hat{\varvec{\theta }}}_{(d)})$ from zero.

With regards to SAE, it is interesting to evaluate the effect of domain deletion in the MSE of the EBLUP. For this sake, we calculate the MSE estimators with and without domain d and we evaluate and compare the following two different averages of MSE estimators

$$\begin{aligned} \overline{mse}({\hat{\varvec{\theta }}})= & {} \frac{1}{DRT}\sum _{\ell =1}^D\sum _{r=1}^{R}\sum _{t=1}^T mse\big ({\hat{\mu }}_{\ell rt}({\hat{\varvec{\theta }}})\big ), \nonumber \\ \overline{mse}({\hat{\varvec{\theta }}}_{(d)})= & {} \frac{1}{(D-1)RT}\sum _{\ell =1, \ell \ne d}^D\sum _{r=1}^{R}\sum _{t=1}^T mse\big ({\hat{\mu }}_{\ell rt}({\hat{\varvec{\theta }}}_{(d)})\big ). \end{aligned}$$

(2.11)

2.3.3 Residuals

We use the approach of Calvin and Sedransk (1991) to analyze the model residuals. The three-fold Fay–Herriot model is a block-diagonal LMM with correlated observations, by their nested hierarchical structure. The method employs the analysis of the model-scaled residuals, after using the Cholesky root of the covariance matrix of the vector of target variables. Then, the new model has a uniform dispersion matrix. Given the block-diagonal covariance matrix ${{\hat{\varvec{V}}}}=\varvec{V}({\hat{\varvec{\theta }}})$ and the correspondent Cholesky root ${{\hat{\varvec{V}}}}={\hat{\varvec{C}}}^{\prime }{\hat{\varvec{C}}}$, the transformed model is

$$\begin{aligned} \varvec{y}_{ch}={\hat{\varvec{C}}}^{\prime }{}^{-1}\varvec{y}=\overline{\varvec{X}}{\varvec{\beta }_{ch}}+\varvec{\epsilon }. \end{aligned}$$

(2.12)

where $\overline{\varvec{X}}={\hat{\varvec{C}}}^{\prime }{}^{-1}\varvec{X}$, $\varvec{\beta }_{ch}={\hat{\varvec{C}}}^{\prime }{}^{-1}\varvec{\beta }$, $\varvec{\epsilon }={\hat{\varvec{C}}}^{\prime }{}^{-1}(\varvec{Z}\varvec{u}+\varvec{e})$. The residuals of model (2.12) are

$$\begin{aligned} r_{ch,drt}^{m}={\hat{\varvec{C}}}^{\prime }{}^{-1}r_{drt}^{m}={\hat{\varvec{C}}}^{\prime }{}^{-1}(y_{drt}-\varvec{x}_{drt}^{\prime }{\hat{\varvec{\beta }}}), \end{aligned}$$

and the externally studentized residuals ${\tilde{\varvec{r}}}_{ch,drt}^{m}$ are

$$\begin{aligned} \tilde{r}_{ch,drt}^{m}=\frac{r_{ch,drt}^{m}}{\sqrt{v_{drt}}} =\frac{{\hat{\varvec{C}}}^{\prime }{}^{-1}(y_{drt}-\varvec{x}_{drt}^{\prime }{\hat{\varvec{\beta }}})}{\sqrt{v_{drt}}}\,, \end{aligned}$$

(2.13)

where $v_{drt}$ is the diagonal element of the matrix ${\hat{\sigma }}_{\varvec{\epsilon }_{(drt)}}^{2}\big (\varvec{I}-\overline{\varvec{X}}(\overline{\varvec{X}}^{\prime }\overline{\varvec{X}})^{-1}\overline{\varvec{X}}^{\prime }\big )$, and ${\hat{\sigma }}_{\varvec{\epsilon }_{(drt)}}^{2}$ is the estimated variance of the regression model (2.12), treated as a fixed effect linear model, with the data $(y_{drt},\varvec{x}_{drt})$ omitted. Furthermore, the asymptotic distribution of $\tilde{r}_{ch,drt}^{m}$ is Student’s t with $DRT-p-1$ degrees of freedom.

2.3.4 MSEs and correlations

The efficiency of the EBLUP in the small area estimation is usually evaluated by comparing the average MSE’s of the different models under investigation, given some application data. When theoretical studies or simulations are available, it is possible to compare the effectiveness of a model with respect to the population parameters given by a data generating process. Nevertheless, due to the circumstance that employing the BLUP approach is justified by the presence of large sampling variances in the small areas, one may study the behavior of the EBLUP in terms of the reduction of the estimated variability of the direct estimator, towards the prediction of the MSE of the EBLUP. Then, a normalized measure of the overall reduction of the sampling variances by the MSE’s may be quite useful, when assessing the efficiency of the linear predictor of a small area estimation model.

Let us consider the conditional residuals $\varvec{r}^{c}=\varvec{y}-{\tilde{\varvec{\mu }}}$, so that

$$\begin{aligned} {\tilde{\varvec{\mu }}}=\varvec{y}-\varvec{V}_{e}\varvec{P}\varvec{y}, \,\,\, \varvec{r}^{c}=\varvec{y}-{\tilde{\varvec{\mu }}}=\varvec{V}_{e}\varvec{P}\varvec{y},\,\,\, \text{ var }(\varvec{r}^{c})=\text{ var }(\varvec{y}-{\tilde{\varvec{\mu }}})=\varvec{V}_{e}\varvec{P}\varvec{V}\varvec{P}\varvec{V}_{e}=\varvec{V}_{e}\varvec{P}\varvec{V}_{e}. \end{aligned}$$

Appendix A calculates the MSE of the BLUP ${\tilde{\varvec{\mu }}}$ and obtains the formula (A.1), i.e. $MSE({\tilde{\varvec{\mu }}})=\varvec{V}_{e}-\varvec{V}_{e}\varvec{P}\varvec{V}_{e}$. Therefore, it holds that

$$\begin{aligned} \text{ cov }(\varvec{r}^{c},\varvec{e})= & {} \text{ cov }(\varvec{V}_{e}\varvec{P}\varvec{y},\varvec{e})=\varvec{V}_{e}\varvec{P}\text{ cov }(\varvec{y},\varvec{e}) =\varvec{V}_{e}\varvec{P}\varvec{V}_{e}=\varvec{V}_{e}-MSE({\tilde{\varvec{\mu }}}) =\text{ var }(\varvec{r}^{c}), \\ \text{ var }(\varvec{r}^{c}-\varvec{e})= & {} \text{ var }(\varvec{r}^{c})+\text{ var }(\varvec{e})-\text{ cov }(\varvec{r}^{c},\varvec{e})-\text{ cov }(\varvec{e},\varvec{r}^{c}) =\varvec{V}_{e}-\varvec{V}_{e}\varvec{P}\varvec{V}_{e}=MSE({\tilde{\varvec{\mu }}}). \end{aligned}$$

For ease of exposition, we write $i=1,\ldots ,DRT$, instead of $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$. For $i,j=1,\ldots ,DRT$, let $c_{ij}$ be the elements of matrix $\varvec{C}=\text{ cov }(\varvec{r}^{c},\varvec{e})$. By using the alternative formula $MSE({\tilde{\mu }}_{drt})=g_{1,drt}(\varvec{\theta })+g_{2,drt}(\varvec{\theta })$, with $g_{1,drt}(\varvec{\theta })$ and $g_{2,drt}(\varvec{\theta })$ given in (2.16), we have $c_{ii}=\sigma _{i}^{2}-g_{1,i}(\varvec{\theta })-g_{2,i}(\varvec{\theta })$ and

$$\begin{aligned} {\text{corr }}(r_{i}^{c} ,e_{j} ) = & \frac{{{\text{ cov }}(r_{i}^{c} ,e_{j} )}}{{\sqrt {{\text{ var }}(r_{i}^{c} ){\text{ var }}(e_{j} )} }} = \frac{{c_{{ij}} }}{{\sqrt {c_{{ii}} \sigma _{j}^{2} } }}, \\ {\text{ corr }}(r_{i}^{c} ,e_{i} ) = & \frac{{{\text{ cov }}(r_{i}^{c} ,e_{i} )}}{{\sqrt {{\text{ var }}(r_{i}^{c} ){\text{ var }}(e_{i} )} }} = \frac{{c_{{ii}} }}{{\sqrt {c_{{ii}} \sigma _{i}^{2} } }} = \sqrt {\frac{{c_{{ii}} }}{{\sigma _{i}^{2} }}} . \\ \end{aligned}$$

Moreover, $\varvec{r}^{c}=\varvec{V}_{e}\varvec{P}\varvec{y}\sim N(\textbf{0},\varvec{V}_{e}\varvec{P}\varvec{V}_{e})$, and $\left| corr(r_{i}^{c},e_{i})\right| \le 1$ implies $0\le c_{ii}\le \sigma _{i}^{2}$, with $c_{ii}$ the i-th diagonal element of the matrix $\varvec{V}_{e}\varvec{P}\varvec{V}_{e}$. If $corr(r_{i}^{c},e_{i})$ approaches 1, this suggests that the correspondent conditional residual $r_{i}^{c}$ can be considered a worthy replacement of the sampling error $e_{i}$. Given $0\le \frac{c_{ii}}{\sigma _{i}^{2}}\le 1$, it is clear that $\frac{ c_{ii}}{\sigma _{i}^{2}}\longrightarrow 0$ means that $c_{ii}\longrightarrow 0$, and $\frac{c_{ii}}{\sigma _{i}^{2}}\longrightarrow 1$ when $c_{ii}\longrightarrow \sigma _{i}^{2}$. Defining $c_{ii}^{*}$ as the i -th diagonal element of the matrix $\varvec{P}$, thus $c_{ii}=\sigma _{i}^{4}c_{ii}^{*}$, and $corr(r_{i}^{c},e_{i})=\sqrt{\frac{c_{ii}}{ \sigma _{i}^{2}}}=\sigma _{i}\sqrt{c_{ii}^{*}}$. Further, $c_{ii}\longrightarrow 0$ when $c_{ii}^{*}\longrightarrow 0$, and $c_{ii}\longrightarrow \sigma _{i}^{2}$ when $c_{ii}^{*}\longrightarrow \sigma _{i}^{-2}$. The range of $c_{ii}^{*}$ is then $0\le c_{ii}^{*}\le \sigma _{i}^{-2}$. The residuals $r_{i}^{c}$ can be written as $r_{i}^{c}=\sigma _{i}^{2}(c_{ii}^{*}y_{i}+\Sigma _{j\ne i}^{N}c_{ij}^{*}y_{j})$, if $N=DRT$. Following Zewotir and Galpin (2007) in the framework of mixed models, here we observe that if $c_{ii}^{*}\longrightarrow 0$ or $\sigma _{i}^{2}c_{ii}^{*}\longrightarrow 1$ (i.e. $c_{ii}^{*}\longrightarrow \sigma _{i}^{-2}$), then also $c_{ij}^{*}\longrightarrow 0$, for $i\ne j$. This means that small areas with small $c_{ij}^{*}$ give small residuals, and then they represent high leverage values. When $c_{ii}^{*}\longrightarrow 0$ the correspondent small areas make little contributions to $\varepsilon$, and the predicted MSE tends to equal the estimated sampling variance. Conversely, with $c_{ii}^{*}\longrightarrow \sigma _{i}^{-2}$, we have $corr(r_{i}^{c},e_{i})\longrightarrow 1$, and the conditional residuals as $r_{i}^{c}=y_{i}+\sigma _{i}^{2}\Sigma _{i\ne j}^{N}c_{ij}^{*}y_{j}\longrightarrow y_{i}$. This condition gives the major possible contribution of the i-th small area to the value of the index $\varepsilon$, and the best performance of the model in terms of the reduction of the expected MSE of the EBLUP.

A measure of the model efficiency, say $\varepsilon$, is then based on $\text{ tr }\big (\text{ corr }(\varvec{r}^{c},\varvec{e})\big )$, i.e.

$$\begin{aligned} \varepsilon =\frac{1}{DRT}\sum _{i=1}^{DRT}[\text{ corr }(\varvec{r}^{c},\varvec{e})]_{ii} =\frac{1}{DRT}\sum _{i=1}^{DRT}\sqrt{\frac{c_{ii}}{\sigma _{i}^{2}}} =\frac{1}{DRT}\sum _{i=1}^{DRT}\varepsilon _i,\quad -1\le \varepsilon \le 1, \end{aligned}$$

(2.14)

where the last sum in i can be calculated by adding the diagonal elements of the square matrix

$$\begin{aligned} \varvec{V}_{r}^{-\frac{1}{2}}\text{ cov }(\varvec{r}^{c},\varvec{e})\varvec{V}_{e}^{-\frac{1}{2}},\quad \varvec{V}_{r}=\text{ diag }\big (\text{ var }(r_{1}^{c}),...,\text{ var }(r_{DRT}^{c})\big ). \end{aligned}$$

Taking the MSE estimator $mse({\hat{\mu }}_{i})=mse({\tilde{\mu }}_i)+2g_{3,i}({\hat{\varvec{\theta }}})$ from Sect. 2.4, we define the mse-ratio

$$\begin{aligned} \pi _i =\frac{mse({\hat{\mu }}_{i})}{mse({\tilde{\mu }}_i)}-1 = \frac{2g_{3,i}({\hat{\varvec{\theta }}})}{mse({\tilde{\mu }}_i)},\quad i=1,\ldots ,DRT. \end{aligned}$$

(2.15)

A dispersion graph plotting $(\pi _i,\varepsilon _i)$ indicates jointly the efficiency of the model and the contribution of the variability of the variance component estimators to the estimation of the MSEs of the EBLUPs ${\hat{\mu }}_{i}$, $i=1,\ldots ,DRT$.

2.4 Estimation of mean squared errors

This Section considers the problem of estimating the MSE of the EBLUP of ${\hat{\mu }}_{drt}=\varvec{x}_{drt}{\hat{\varvec{\beta }}}+\hat{u}_{1,d}+\hat{u}_{2,dr}+\hat{u}_{3,drt}$ of $\mu _{drt}=\varvec{x}_{drt}\varvec{\beta }+u_{1,d}+u_{2,dr}+ u_{3,drt}$, $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, where ${\hat{\varvec{\beta }}}$ and ${{\hat{\varvec{u}}}}$ are given in (2.5). In matrix form, we have $\mu _{drt}=\varvec{a}^{\prime } \left( \varvec{X}\varvec{\beta }+ \varvec{Z}\varvec{u}\right)$, where $\varvec{a}=\varvec{a}_{drt}=\underset{1\le \ell \le D}{\hbox {col}}(\underset{1\le s \le R}{\hbox {col}}(\underset{1\le h \le T}{\hbox {col}}(\delta _{d\ell }\delta _{rs}\delta _{th})))$ is a vector having a one in the cell $t+(r-1)T+(d-1)RT$ and having zeros in the remaining cells. The symbol $\delta _{d\ell }$ denotes the Kronecker’s delta, i.e. $\delta _{d\ell }=1$ if $d=\ell$ and $\delta _{d\ell }=0$ otherwise. We give an analytic and a bootstrap MSE estimator.

2.4.1 Analytic estimator

For approximating the MSE of ${\hat{\mu }}_{drt}$, we follow Section 17.2.3 of Morales et al. (2021). We obtain the formulas

$$\begin{aligned} MSE({\hat{\mu }}_{drt})= & {} g_{1drt}(\varvec{\theta })+g_{2drt}(\varvec{\theta })+g_{3drt}(\varvec{\theta }), \\ \nonumber g_{1drt}(\varvec{\theta })= & {} \varvec{a}^{\prime }\big (\varvec{V}_e-\varvec{V}_e\varvec{V}^{-1}\varvec{V}_e\big )\varvec{a}=\varvec{a}^{\prime }\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\varvec{a}, \\ \nonumber g_{2drt}(\varvec{\theta })= & {} \varvec{a}^{\prime }\varvec{V}_e\varvec{V}^{-1}\varvec{X}\varvec{Q}\varvec{X}^\prime \varvec{V}_e\varvec{a}=\big (\varvec{a}^{\prime }\varvec{X}-\varvec{a}^{\prime }\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\varvec{V}_e^{-1}\varvec{X}\big ) \varvec{Q}\big (\varvec{X}^{\prime }\varvec{a}- \varvec{X}^{\prime }\varvec{V}_e^{-1}\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\varvec{a}\big ), \\ \nonumber g_{3drt}(\varvec{\theta })\approx & {} \text{ tr }\left\{ (\nabla \varvec{b}^{\prime })\varvec{V}(\nabla \varvec{b}^{\prime })^{\prime } E\left[ ({\hat{\varvec{\theta }}}-\varvec{\theta })({\hat{\varvec{\theta }}}-\varvec{\theta })^{\prime }\right] \right\} , \end{aligned}$$

(2.16)

where $\varvec{T}=\varvec{V}_u-\varvec{V}_u\varvec{Z}^{\prime }\varvec{V}^{-1}\varvec{Z}\varvec{V}_u$ and $\varvec{b}^{\prime }=\varvec{a}^{\prime }\varvec{Z}\varvec{V}_u\varvec{Z}^{\prime }\varvec{V}^{-1}$. An analytic estimator of the MSE of ${\hat{\mu }}_{drt}$ is

$$\begin{aligned} mse({\hat{\mu }}_{drt})=g_{1drt}({\hat{\varvec{\theta }}})+g_{2drt}({\hat{\varvec{\theta }}})+2g_{3drt}({\hat{\varvec{\theta }}}), \end{aligned}$$

where ${{\hat{\varvec{\theta }}}}$ is the REML estimator. Appendix A gives the calculations of $g_{1drt}$, $g_{2drt}$ and $g_{3drt}$. Alternatively, we introduce a parametric bootstrap procedure for estimating the $MSE({\hat{\mu }}_{drt})$.

2.4.2 Parametric bootstrap estimator

The parametric bootstrap procedure for estimating the MSE of ${\hat{\mu }}_{drt}$ has the following steps.

• 1. Calculate the REML estimators ${{\hat{\varvec{\theta }}}} = ({\hat{\sigma }}_1^2, {\hat{\sigma }}_2^2, {\hat{\sigma }}_3^2)$ and ${\hat{\varvec{\beta }}}$.

• 2. Repeat B times ($b=1,\ldots , B$):

  • (a) For $d=1,\ldots ,D$, generate $u_{1,d}^{*(b)}$ i.i.d. $N(0,{\hat{\sigma }}_1^2)$. Construct the vector $\varvec{u}_1^{*(b)}=\underset{1\le d \le D}{\hbox {col}}( u^{*(b)}_{1,d})$.

  • (b) For $d=1,\ldots ,D$, $r=1,\ldots ,R$, generate $u_{2,dr}^{*(b)}$ i.i.d. $N(0,{\hat{\sigma }}_2^2)$. Construct the vector $\varvec{u}_2^{*(b)}=\underset{1\le d \le D}{\hbox {col}}( \underset{1\le r \le R}{\hbox {col}}(u^{*(b)}_{2,dr}))$.

  • (c) For $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, generate $u_{3,drt}^{*(b)}$ i.i.d. $N(0,{\hat{\sigma }}_3^2)$. Construct the vector $\varvec{u}_3^{*(b)}=\underset{1\le d \le D}{\hbox {col}}(\underset{1\le r \le R}{\hbox {col}}(\underset{1\le t \le T}{\hbox {col}}(u^{*(b)}_{3,drt})))$.

  • (d) For $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$ generate independent variables $e^{*(b)}_{drt}\sim N(0,\sigma _{drt}^2)$. Construct the vector $\varvec{e}^{*(b)}=\underset{1\le d \le D}{\hbox {col}}(\underset{1\le r \le R}{\hbox {col}}(\underset{1\le t \le T}{\hbox {col}}(e^{*(b)}_{drt}))$.

  • (e) Calculate the bootstrap vector

    $$\begin{aligned} \varvec{y}^{*(b)}=\varvec{X}{{\hat{\varvec{\beta }}}}+\varvec{Z}_1\varvec{u}_1^{*(b)}+\varvec{Z}_2\varvec{u}_2^{*(b)}+\varvec{Z}_3\varvec{u}_3^{*(b)}+\varvec{e}^{*(b)}. \end{aligned}$$

    (2.17)

  • (f) Fit the assumed model to the bootstrap vector $\varvec{y}^{*(b)}$, calculate the estimators ${\hat{\varvec{\theta }}}^{*(b)}$, ${{\hat{\varvec{\beta }}}}^{*(b)}$ of the model parameters, the true value of the mixed parameter $\varvec{\mu }^{*(b)} = \varvec{X}{{\hat{\varvec{\beta }}}}+\varvec{Z}_1\varvec{u}_1^{*(b)}+\varvec{Z}_2\varvec{u}_2^{*(b)}+\varvec{Z}_3\varvec{u}_3^{*(b)}$ and the EBLUP ${{\hat{\varvec{\mu }}}}^{*(b)}$ with components $\mu _{drt}^{*(b)}$ and ${{\hat{\mu }}}_{drt}^{*(b)}$, respectively.

• 3. Output: for $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, calculate

  $$\begin{aligned} mse^*({\hat{\mu }}_{drt})=\frac{1}{B}\sum _{b=1}^B\left( {{\hat{\mu }}}_{drt}^{*(b)}-\mu _{drt}^{*(b)}\right) ^2. \end{aligned}$$

3 Simulations

Three simulation experiments are carried out under the three-fold Fay–Herriot model. The data generation process is inspired by the simulation experiments presented in Chapter 17 of Morales et al. (2021) for the FH2 model. The simulations investigate the behavior of the REML estimators of model parameters, the EBLUPs of domain means, and the bootstrap MSE estimators. The data generation process is

For $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, the explanatory and dependent variables are

$$\begin{aligned} x_{drt}= & {} \frac{1}{5}(b_{drt}-a_{drt})U_{drt}+a_{drt},\,\, U_{drt}=\frac{t}{T+1},\,\, a_{drt}=1,\,\, \\ b_{drt}= & {} 1+\frac{1}{DR}\big ((d-1)RT+(r-1)T+t\big ), \\ y_{drt}= & {} \beta _1+\beta _2x_{drt}+u_{1,d}+u_{2,dr}+u_{3,drt}+e_{drt},\,\,\beta _1=1,\,\beta _2=1,\, \end{aligned}$$

where $u_{1,d}\sim N(0,\sigma _1^2)$ with $\sigma _1^2=0.1$, $u_{2,dr}\sim N(0,\sigma _2^2)$ with $\sigma _2^2=0.1$, $u_{3,drt}\sim N(0,\sigma _2^2)$ with $\sigma _3^2=0.1$, $e_{drt}\sim N(0,\sigma _{drt}^2)$ and

$$\begin{aligned} \sigma _{drt}^2=\frac{2}{25}\frac{(d-1)RT+(r-1)T+t-1}{DRT-1}+0.8. \end{aligned}$$

3.1 Simulations

Simulation 1 investigates the bias and the MSE of the REML estimators of the model parameters and of the EBLUPs. The simulation steps are

• 1. Repeat $I=10^3$ times ($i=1,\ldots ,I$)

  • 1.1. Generate a sample of size DRT and calculate $\mu _{drt}^{(i)}=\beta _{1}+\beta _{2} x_{drt}+u_{1,d}^{(i)}+u_{2,dr}^{(i)}+u_{3,drt}^{(i)}$.

  • 1.2. Calculate the REML estimator ${\hat{\tau }}^{(i)}\in \{{\hat{\beta }}_{1}^{(i)},{\hat{\beta }}_{2}^{(i)},{\hat{\sigma }}_1^{2(i)},{\hat{\sigma }}_2^{2(i)},{\hat{\sigma }}_3^{2(i)}\}$ and the EBLUP ${\hat{\mu }}_{drt}^{(i)}$.

• 2. For ${\tau }\in \{\beta _1,\beta _2,\sigma _1^2,\sigma _2^2,\sigma _3^2\}$ and ${\mu }_{drt}$, $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, calculate

  $$\begin{aligned}{} & {} BIAS({\hat{\tau }})=\frac{1}{I}\sum _{i=1}^{I}({\hat{\tau }}^{(i)}-\tau ),\quad RMSE({\hat{\tau }})=\bigg (\frac{1}{I}\sum _{i=1}^{I}({\hat{\tau }}^{(i)}-\tau )^2\bigg )^{1/2}. \\{} & {} BIAS_{drt}=\frac{1}{I}\sum _{i=1}^{I}({\hat{\mu }}_{drt}^{(i)}-\mu _{drt}^{(i)}),\quad RMSE_{drt}=\bigg (\frac{1}{I}\sum _{i=1}^{I}({\hat{\mu }}_{drt}^{(i)}-\mu _{drt}^{(i)})^2\bigg )^{1/2}, \\{} & {} ABIAS=\frac{1}{DRT}\sum _{d=1}^{D}\sum _{r=1}^{R}\sum _{t=1}^{T}|BIAS_{drt}|,\quad RMSE=\frac{1}{DRT}\sum _{d=1}^{D}\sum _{r=1}^{R}\sum _{t=1}^{T}RMSE_{drt}. \end{aligned}$$

• 3. Calculate also the corresponding relative performance measures in %. The relative bias (RBIAS), the relative root-MSE (RRMSE), the average absolute relative bias (ARBIAS), and the average relative root-MSE (ARRMSE) are

  $$\begin{aligned} RBIAS_{{drt}} = & \frac{{100BIAS_{{drt}} }}{{\left( {\frac{1}{I}\sum\limits_{{i = 1}}^{I} {\mu _{{drt}}^{{(i)}} } } \right)}},{\mkern 1mu} {\mkern 1mu} RRMSE_{{drt}} = \frac{{100RMSE_{{drt}} }}{{\left( {\frac{1}{I}\sum\limits_{{i = 1}}^{I} {\mu _{{drt}}^{{(i)}} } } \right)}}, \\ ARBIAS = & \frac{1}{{DRT}}\sum\limits_{{d = 1}}^{D} {\sum\limits_{{r = 1}}^{R} {\sum\limits_{{t = 1}}^{T} | } } RBIAS_{{drt}} |,{\mkern 1mu} \\ ARRMSE = & \frac{1}{{DRT}}\sum\limits_{{d = 1}}^{D} {\sum\limits_{{r = 1}}^{R} {\sum\limits_{{t = 1}}^{T} R } } RMSE_{{drt}} . \\ \end{aligned}$$

Table 1 presents the results of Simulation 1 for $R=T=10$. It shows that the bias is always close to zero and that the MSE decreases when the number of domains D increases, so the REML estimators seem to be consistent. From the last line, one can observe that the MSE of the EBLUP is almost constant with increasing D. This behavior is expected since as the number of small areas increases, the number of terms that we have to predict also increases. So that the ratio of what we have to predict to sample size is constant.

Table 1 Results of Simulation 1 for $T=R=10$

3.2 Simulation 1a

Simulation 1a compares the BLUPs and EBLUPs based on of the one-fold, two-fold and three-fold Fay–Herriot models. We generate the data in the same way as in Simulation 1. This is to say, the data generating model is the FH3 model

$$\begin{aligned}{} & {} y_{drt}=\beta _1+\beta _2x_{drt}+u_{1,d}+u_{2,dr}+u_{3,drt}\\{} & {} \quad +e_{drt}\quad d=1,\ldots ,D,\, r=1,\ldots ,R,\, t=1,\ldots ,T. \end{aligned}$$

The one-fold Fay–Herriot model (FH1) is

$$\begin{aligned} y_{drt}=\beta _1+\beta _2x_{drt}+u_{3,drt}+e_{drt},\quad d=1,\ldots ,D,\, r=1,\ldots ,R,\, t=1,\ldots ,T. \end{aligned}$$

If we define the new index $i=(d,r,t)$, then we can write

$$\begin{aligned} y_{i}=\beta _1+\beta _2x_{i}+u_{3,i}+e_{i},\quad i=1,\ldots ,DRT. \end{aligned}$$

The two-fold Fay–Herriot model (FH2) is

$$\begin{aligned} y_{drt}=\beta _1+\beta _2x_{drt}+u_{2,dr}+u_{3,drt}+e_{drt},\quad d=1,\ldots ,D,\, r=1,\ldots ,R,\, t=1,\ldots ,T. \end{aligned}$$

If we define the new indexes $i=(d,r)$ and $j=t$, then we can write

$$\begin{aligned} y_{ij}=\beta _1+\beta _2x_{ij}+u_{2,i}+u_{3,ij}+e_{ij},\quad i=1,\ldots ,DR,\,j=1,\ldots ,T. \end{aligned}$$

We take $D=50$, $T=R=10$, $\beta _1=1$, $\beta _2=1$, $\sigma _2^2=\sigma _3^2=0.1$ and $\sigma _1^2=0.1, 0.5, 1, 1.5, 2$. Tables 2 presents the simulation results of absolute (top left) and relative (top right) Bias and root-MSE (bottom left) and relative root-MSE (bottom right) for BLUPs. As $\sigma ^2_1$ increases both FH1 and FH2 increase in Bias and MSE, instead FH3 model always remains stable. Table 3 presents the simulation results of absolute (top left) and relative (top right) Bias and root-MSE (bottom left) and relative root-MSE (bottom right) for EBLUPs. Compared to the BLUPs the results for the EBLUPs are mitigated although the same trend remains for FH1, FH2 and FH3.

Table 2 Bias (top) and RMSE (bottom) results of BLUPs

Table 3 Bias (top) and RMSE (bottom) results of EBLUPs

3.3 Simulation 2

Simulation 2 studies the behavior of the estimators of the MSE of the EBLUP, introduced in Sect. 2.4. Both the analytic and the parametric bootstrap estimators are investigated. More concretely, we investigate the behavior of the estimators $mse({\hat{\mu }}_{drt})$ and $mse^*({\hat{\mu }}_{drt})$. To do this, such estimators are compared with the empirical MSE of ${\hat{\mu }}_{drt}$ obtained at the output of Simulation 1. The procedure is as follows.

• 1. For $D=50, 100, 200, 300$, take the values of $MSE_{drt}$ from the output of Simulation 1.

• 2. Repeat $I=200$ times ($i=1,\ldots ,I$)

  • 2.1. Generate a sample $(y_{drt}^{(i)},x_{drt})$, $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$.

  • 2.2. Calculate the estimators ${\hat{\beta }}_{1}^{(i)}$, ${\hat{\beta }}_{2}^{(i)}$, ${\hat{\sigma }}_1^{2(i)}$, ${\hat{\sigma }}_2^{2(i)}$, ${\hat{\sigma }}_3^{2(i)}$.

  • 2.3. For $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, calculate $mse_{drt}^{0(i)}=mse({\hat{\mu }}^{(i)}_{drt})$ from (2.16).

  • 2.4. Repeat B times $(b=1,\ldots ,B)$

  • 2.4.1. Generate $u_{1,d}^{*(ib)}$, $u_{2,dr}^{*(ib)}$, $u_{3,drt}^{*(ib)}$, $e_{drt}^{*(ib)}$, $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, by using ${\hat{\sigma }}_1^{2(i)}$, ${\hat{\sigma }}_2^{2(i)}$, ${\hat{\sigma }}_3^{2(i)}$ instead of $\sigma _1^{2}$, $\sigma _2^{2}$, $\sigma _3^{2}$.

  • 2.4.2. Generate a bootstrap sample $\{y_{drt}^{*(ib)}; d=1,\ldots ,D, r=1,\ldots ,R, t=1,\ldots ,T\}$ from the model

    $$\begin{aligned} y_{drt}^{*(ib)}={\hat{\beta }}_{1}^{(i)}+{\hat{\beta }}_{2}^{(i)}x_{drt}+u_{1,d}^{*(ib)}+u_{2,dr}^{*(ib)}+u_{3,drt}^{*(ib)}+e_{drt}^{*(ib)}. \end{aligned}$$

  • 2.4.3. Calculate $\mu _{drt}^{*(ib)}={\hat{\beta }}_{1}^{(i)}+{\hat{\beta }}_{2}^{(i)}x_{drt}+u_{1,d}^{*(ib)}+u_{2,dr}^{*(ib)}+u_{3,drt}^{*(ib)}$.

  • 2.4.4. Calculate the estimators of the parameters of the bootstrap model, ${\hat{\beta }}_{1}^{*(ib)}$, ${\hat{\beta }}_{2}^{*(ib)}$, ${\hat{\sigma }}_1^{2*(ib)}$, ${\hat{\sigma }}_2^{2*(ib)}$, ${\hat{\sigma }}_3^{2*(ib)}$.

  • 2.4.5. For $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, calculate the EBLUP ${\hat{\mu }}_{drt}^{*(ib)}={\hat{\beta }}_{1}^{*(ib)}+{\hat{\beta }}_{2}^{*(ib)}x_{drt} +\hat{u}_{1,d}^{*(ib)}+\hat{u}_{2,dr}^{*(ib)}+\hat{u}_{3,drt}^{*(ib)}$.

  • 2.5 For $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, calculate

    $$\begin{aligned} mse_{drt}^{1(i)}=\frac{1}{B}\sum _{b=1}^B\left( {\hat{\mu }}_{drt}^{*(ib)}-\mu _{drt}^{*(ib)}\right) ^2. \end{aligned}$$

• 3. Output: for $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, calculate the performance measures. The bias (BIAS), the root mean squared error (RE), the average absolute bias (AAB), the average root mean squared error (ARE), the relative bias (RB), the relative root mean squared error (RRE), the average absolute relative bias (AARB) and the average relative root mean squared error (ARRE) are

  $$\begin{aligned}{} & {} BIAS_{drt}^{a}=\frac{1}{I}\sum _{i=1}^{I}\left( mse_{drt}^{a(i)}-MSE_{drt}\right),\,\, RE_{drt}^{a}=\bigg (\frac{1}{I}\sum _{i=1}^{I}\left( mse_{drt}^{a(i)}-MSE_{drt}\right) ^2\bigg )^{1/2},\, a=0,1, \\{} & {} AAB^{a}=\frac{1}{DRT}\sum _{d=1}^{D}\sum _{r=1}^{R}\sum _{t=1}^{T}|BIAS_{drt}^{a}|,\,\, ARE^{a}=\frac{1}{DRT}\sum _{d=1}^{D}\sum _{r=1}^{R}\sum _{t=1}^{T}RE_{drt}^{a},\,\,\, a=0,1, \end{aligned}$$

• 4. Output: for $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, calculate the relative performance measures in %

  $$\begin{aligned}{} & {} RB^{a}_{drt}=\frac{100 BIAS_{drt}^{a}}{\left( \frac{1}{I}\sum _{i=1}^{I}MSE_{drt}\right) }, \,\, RRE^{a}_{drt}=\frac{100 RE_{drt}^{a}}{\left( \frac{1}{I}\sum _{i=1}^{I}MSE_{drt}\right) }, \,\, a=0,1, \\{} & {} AARB^{a}=\frac{1}{DRT}\sum _{d=1}^{D}\sum _{r=1}^{R}\sum _{t=1}^{T}|RB_{drt}^{a}|,\,\, ARRE^{a}=\frac{1}{DRT}\sum _{d=1}^{D}\sum _{r=1}^{R}\sum _{t=1}^{T}RRE_{drt}^{a},\,\, a=0,1. \end{aligned}$$

Figure 1 plots the boxplots with the DRT values of $RB_{drt}^{1}$ (left) and $RRE_{drt}^{1}$ (right), with $D=50$ and $R=T=10$ for $B=100,200,300,400$. We observe that the parametric bootstrap method presents a small relative bias around zero and a relative root MSE which mean decreases from 0.73% to 0.54% as B increases. We recommend applying this method with at least $B=300$ replications, even if the calculation times can be heavy.

Fig. 1

Boxplots of $RB^{1}_{drt}$ (left) and ${RRE}^{1}_{drt}$ (right) with $D=50$ and $R=T=10$

Table 4 presents the results of the performance measures of Simulation 2 for $R=T=10$, $B=300$ and several values of D. It shows that $AAB^{a}$ and $ARE^{a}$, $a=0,1$, tend to zero as D grows. The analytical estimator $mse_{drt}^0$ has a very good behavior. It is basically unbiased and its average quadratic error is smaller than that of the basic bootstrap estimator $mse_{drt}^{1}$.

Table 4 $AAB^{a}$, $AARB^{a}$, $ARE^{a}$ and $ARRE^{a}$, $a=0,1$, with $R=T=10$ and $B=300$

4 The application

4.1 Model and poverty predictions

This Section presents an application to real data with the main goal to estimate the poverty incidence (proportion of individuals under poverty line) in Spanish domains under an area-level three-fold Fay–Herriot model. We use data from the SLCS corresponding to the years 2004–2008, with $D=52$ domains (provinces), $R=2$ subdomains (sexes) and $T=5$ time periods (years). The target variable $y_{drt}$ is de Hájeck direct estimator of the poverty proportion and the error variance $\sigma _{drt}^2$ is the estimate of the design-based variance of the direct estimator, as described in Section 2.5 of Morales et al. (2021).

As usually done in SAE, the auxiliary variables are related to demographic characteristics, socioeconomic status, education, and immigration status which are relevant for government policymaking and program planning, also at smaller geographical levels. It is essential to take into account the interpretation of the relationship between auxiliary and dependent variables, and the fact that it could vary with the level of aggregation.

We take the auxiliary variables from the Spanish Labour Force Survey (SLFS). The SLFS is published quarterly, includes nearly 65,000 dwellings, equivalent to approximately 160,000 people. Each quarterly SLFS sample size is larger than the size of an annual SLCS sample. Further, to increase the precision of the estimates, we jointly use the data from the four trimesters of years 2004–2008 to calculate the auxiliary variables by using the formula of the Hájek direct estimator of a domain mean. The constructed auxiliary variables are the domain proportions of people in the categories of the following factors:

• citizenship: with 2 categories denoted by cit1 for Spanish and cit2 for Not Spanish.

• labor: labor situation with 4 categories taking the values lab0 for Below 16 years, lab1 for Employed, lab2 for Unemployed and lab3 for Inactive.

In the strict sense, the explanatory variables have measurement errors independent of sampling errors. It would therefore be necessary to generalize to the FH3 model, the approaches of Ybarra and Lohr (2008), Burgard et al. (2020, 2022). This task exceeds the objectives of the current research. In this sense, this section presents an illustrative application of the statistical methodology introduced in Sect. 2.

Based on the preliminary exploratory analysis, the only significant covariates of the selected model were the ones included in Table 5. The model has two statistically significant variables that have a relevant meaning in the socio-economic sense. These variables are $cit2$ (not Spanish citizens) and $lab2$ (unemployed). Table 5 presents the regression parameters $\beta$ and their corresponding p-values. By observing the signs of the regression parameters we interpret that there is an inverse relationship between poverty proportion and the category $cit2$ of the explanatory variable. That is, poverty incidence tends to be smaller in those domains with a larger proportion of population in the subset defined by citizenship not Spanish. On the other hand, poverty incidence tends to be larger in those domains with a larger proportion of population in the subset defined by $lab2$, i.e. in the category of unemployed people. All the p-values are lower than 0.05 for all the considered auxiliary variables.

Table 5 $\beta$-parameters and p-values

Table 5 also gives the asymptotic confidence intervals (CIs) for the regression parameters at the 95% confidence level. The rows with labels INF and SUP contain the lower and upper limits respectively. By observing these confidence intervals, we conclude that all the regression parameters are significantly different from zero.

Table 6 presents the CIs for the variance parameters at the 95% confidence level. The columns with labels INF and SUP contain the lower and upper limits respectively. The column with label $0\in$CI contains T (true) if 0 belongs to the CI and F (false) otherwise. We observe that the CIs for all the variances do not contain the origin 0 in any case, so the variances are significantly positive. Table 6 also gives the CIs for the difference of variances $\sigma ^2_1-\sigma ^2_2$, $\sigma ^2_1-\sigma ^2_3$ and $\sigma ^2_2-\sigma ^2_3$. The three variances can be considered two by two as different at the 95% confidence level is significantly greater than zero. Therefore, we can recommend this model for deriving predictors of poverty indicators.

Table 6 95$\%$ CIs for variances

Figure 2 plots the direct and EBLUP poverty proportion estimates for all domains (province $\times$ sex $\times$ year). Concerning root-MSEs, the figure shows that the EBLUPs have lower MSEs than the direct estimators. Therefore it is worthwhile using model-based predictors instead of direct estimators.

Fig. 2

Estimates of poverty proportions (left) and root-MSEs (right) by province, sex, and year

Figure 3 plots the direct and EBLUP poverty proportion estimates for men (left) and women (right) in the year 2008. This figure shows that they follow a similar (parallel) pattern.

Fig. 3

Direct and EBLUP poverty estimates for men (left) and women (right) in 2008

Figure 4 plots the RMSEs of the direct estimators and the EBLUPs of poverty proportions for men (left) and women (right) in the year 2008. This figure shows that the model-based predictors have lower root-MSEs than the direct estimators.

Fig. 4

RMSEs of EBLUPS and direct estimators for men (left) and women (right) in 2008

Figure 5 plots the Spanish provinces in 4 colored categories depending on the values of the EBLUPs (in $\%$) of the poverty proportions. We observe that the Spanish regions where the proportion of the population under the poverty line is smallest are those situated in the north and east, like Cataluña, Navarra and Basque country. On the other hand, the Spanish regions with higher poverty proportions are those situated in the center-south, like Andalucía and Extremadura. In an intermediate position, we can find regions that are in the center-north of Spain, like Castilla León, Cantabria or Asturias.

Fig. 5

Map of poverty proportion for men (top) and women (bottom), year 2008

We also fitted the SLCS data to a simpler two-fold Fay–Herriot model as a competitor. On the basis of the likelihood-ratio test (LRT), at $95\%$ we rejected the null hypothesis that the simpler model is consistent with the data, and therefore we selected the three-fold Fay–Herriot model. The Akaike information criterion (AIC) is 1329.43 for the FH2 model versus 1331.673 for the FH3 model. We additionally calculated the Schwarz’s Bayesian information criterion (SBC) which result 1318.928 for the FH2 model versus 1315.92 for the FH3 model. From the results of the test LRT and the SBC measure we can consider the more complex three-fold Fay–Herriot model as the best model for the fitting. In order to check if used data from the SLCS can be modelled with a time correlated effect, we fitted them on a three-fold Fay–Herriot model with AR(1) time effects. Details on model definition, REML algorithm for variance components estimation and confidence intervals are given in Appendix B. Table 7 presents the regression parameters $\beta$ and their corresponding p-values. It shows that estimated regression coefficients are quite similar to the ones obtained fitting the model with independent time effects as shown in Table 5. Table 8 report the $95\%$ confidence intervals for the variance parameters of the random effects. The results show that fitting the three-fold Fay–Herriot model with correlated time effects leads to a lost in the significance for the variance of the second random effect $u_2$. Moreover, even if it is significant, the correlation parameter $\rho$ is close to zero. Figure 6 shows the comparison between the raw residuals $(y_{drt} - {\hat{\mu }}_{drt})$ of model with independent time effects and the raw residuals of model with AR(1) correlated time effects. The evidence from this figure is that there is no difference in the distribution of the residuals from the two models. So, for the parsimony principle we prefer the simpler model with independent time effects over the more complex model with time correlation parameter $\rho$.

Table 7 $\beta$-parameters and p-values of model with AR(1) correlated time effects

Table 8 95$\%$ CIs for variances and $\rho$ of model with AR(1) correlated time effects

Fig. 6

Comparing raw residuals of model with independent time effects and raw residuals of model with AR(1) correlated time effects

Finally, for being more confident about the selected model with independent time effects as a true generating model, we will give suitable diagnostics.

4.2 Model diagnostics

The employment of small area estimation models suggests investigating how the model diagnostics can be addressed to analyze some special questions that may be of interest to survey practitioners, that are typical of this field of investigation. For instance, traditional mixed model diagnostics methods can be supplied by the measures of the efficiency of the small area estimation model applied, or indexes that highlight the influence of data on the estimation of the mean squared error of the Eblup. The evaluation of the data structure, concerning their impact on the estimation of fixed and random-area effects, as well as on the covariance parameters estimates, are some of these diagnostic measures. For example, the evaluation of the influence of the data on the covariance parameters estimates may be relevant, in terms of the evaluation of the weight of the regression-synthetic estimation part of the model. In the sequel, we are interested in purely exploring the impact of observations on the fitting and the evaluation of the model, rather than remove permanently particular domains from the estimation process.

Figure 7 (left) plots the raw residuals of the fitted three-fold Fay–Herriot model against the direct estimates $y_{drt}$. Figure 7 (right) shows the raw residuals sorted (in ascending order) by the variances of the direct estimator. It shows that the greater the variances of the direct estimators are, the higher the residuals of the model are.

Fig. 7

Raw residuals versus direct estimates (left) sorted by the direct estimator variances (right)

Figure 8 plots the raw residuals for men (left) and women (right) at the year 2008. This figure shows that the model smooths the predictions. Positive men residuals indicates that the EBLUPs tend to be lower than the corresponding direct estimates. Analogously, negative women residuals indicates that the EBLUPs tend to be greater than the corresponding direct estimates.

Fig. 8

Residuals for men (left) and women (right) for the years 2008

Figure 9 (left) plots the fixed-effects and the random-effects average leverages points $\varvec{L}_{f,d}$ and $\varvec{L}_{r,d}$, defined in (2.6), of the domains (provinces), with the corresponding thresholds. Table 9 of Appendix C gives the acronyms of the Spanish provinces. After averaging by sub-domains, Almería (AL) is the most influential on fixed-effects because exceeds the second cut-off value $2\times \text{ rank }(\varvec{X})/DRT$ (see subsection 2.3.1). Barcelona (B) is on the border of the second-level threshold as leverage point for the random-effects. Nobre and Singer (2007) suggest evaluating the product $\Gamma =\varvec{Z}_{d}\varvec{G}_{d}\varvec{Z}_{d}^{\prime }\varvec{V}_{d}^{-1}=\varvec{L}_{r,d}+\varvec{Z}_{d}\varvec{G}_{d}\varvec{Z}_{d}^{\prime }\varvec{V}_{d}^{-1}\varvec{L}_{f,d}$, in order to measure leverages of the random effects. This means that, in the present application, a small average contribution in a specific domain, given the sampling variance of the direct estimator, can lead to relevant random-effects leverage values. Barcelona reports simultaneously low-level of sampling variances and moderate fixed-effects leverages, which is enough to justify the result reported.

Fig. 9

Fixed-effects and random-effects average leverages points $L_{f,d}$ and $L_{r,d}$ of the major domain (left), and joint variation by the covariates in the model, by plotting ${\hat{\varvec{\beta }}}_{(d)}-{\hat{\varvec{\beta }}}$ (right), with province abbreviations

Figure 9 (right) shows the joint variation by the covariates in the model, by plotting ${\hat{\varvec{\beta }}}_{(d)}-{\hat{\varvec{\beta }}}$, defined in (2.8). The “non Spanish citizenship”slope parameter estimate is close to $-0.27$, and the variation due to omitting Provinces has a moderate consequence on the fixed-effect estimation. The most explicit change is due to Burgos (BU) and Castellón (CS), which, when it is omitted, causes the major possible increase of the estimates of the fixed-effect parameter. The provinces of Madrid (M), Santa Cruz de Tenerife (TF) and Almería (AL), when omitted, cause the most important decrease of the corresponding fixed-effect estimate. This corresponds to improve the negative average impact on the model dependent variable, namely the poverty proportion direct estimate.

The variable “unemployed” (with an estimated slope parameter close to 0.44) has generally more impact on the estimates. Cáceres (CC) and Cádiz (CA) are the provinces that decrease the parameter estimate. This deals with the lowest possible value of the fixed-effect when a domain is deleted. When these provinces are omitted, the estimate of the coefficient estimate of the “Unemployed” variable undergoes the greatest decrease. Santa Cruz de Tenerife causes the major increase in the estimated parameter. When this province is deleted from the data, the impact of the “Unemployed” covariate on the dependent variable is very high.

Figure 10 shows the studentized residuals (2.13) with the confidence limits at $\pm 2$ (left) and a Normal Q-Q (quantile-quantile) plot of the studentized residuals (2.13) (right). Few labels are reported for some points to identify as outliers, which are coded as follows: the province abbreviation, letter ‘M’ for male or ‘F’ for female, the year from 2004 to 2008 for simplicity denoted from 1 to 5, separated with dots. From a graphical analysis of the figure we can conclude that the assumption of normality is reliable. The studentized residual quantiles present a linear trend in relation to the quantiles of the N(0, 1) distribution. Furthermore, with a confidence level of $95\%$ all points belong to the confidence region, with only two points falling outside, which are referred to Tenerife (TF) province.

Fig. 10

Studentized Residuals ${\tilde{\varvec{r}}}_{ch,drt}^{m}$ with confidence limits $\pm 2$ (left), and Normal Q-Q Plot of ${\tilde{\varvec{r}}}_{ch,drt}^{m}$ (right), with province abbreviations

Figure 11 (left) plots jointly the fixed-effects leverages of the model (2.12) and the residuals $\tilde{r}_{ch,drt}^{m}$, defined in (2.13), together with their cut-off thresholds. Again some labels are reported, which are coded as before: the province abbreviation, letter ‘M’ for male or ‘F’ for female, the year from 2004 to 2008 for simplicity denoted from 1 to 5, separated with dots. Leverage extreme points confirm that Almería (AL) as one of the most influential province, but the scaled residuals reveal that Málaga (MA), Coruña (C), and Valladolid (VA) (in some years), are quite very influential on the fixed effects estimates of the “reduced" model. In general, the residuals $\tilde{r}_{ch,drt}^{m}$ are averaged by the Cholesky decomposition, and then they can be masked by the correspondent smoothing effect (Calvin and Sedransk, 1991). This fact may not highlight some observations in the residual analysis. In the present case, we have evidence of provinces of Málaga, Coruña, and Valladolid in the residual plot of the $\tilde{r}_{ch,drt}^{m}$’s. This means that in the presence of two different smoothing given by averaging the fixed-effects leverages by the sub-domains and by the model variance decomposition, the first is the prevailing one.

Fig. 11

Fixed-effects leverages of the “reduced” model (2.12) and the residuals $\tilde{r}_{ch,drt}^{m}$, together with their cut-off thresholds (left), and Cook’s distances (right), with province abbreviations

Figure 11 (right) plots the Cook’s distances defined in (2.9), and highlights that the most influential provinces due to extreme residual points are Santa Cruz de Tenerife (TF), Castellón (CS), and Cáceres (CC). Due to very high fixed-effects leverage value, the most influential is Almería (AL).

Fig. 12

$\gamma ({\hat{\varvec{\theta }}}_{(d)})$ and the $\overline{mse}({\hat{\varvec{\theta }}}_{(d)})$ (left), and values of the ratio $\tau ({\hat{\varvec{\theta }}}_{(d)})$ considering a cut-off value $\tau =0$ (right) with province abbreviations

Figure 12 (left) shows values of $\gamma ({\hat{\varvec{\theta }}}_{(d)})$ and the $\overline{mse}({\hat{\varvec{\theta }}}_{(d)})$, introduced in (2.10) and (2.11) respectively, which points out that Barcelona (B), when pulled out of the data, causes the worst average loss in terms of efficiency of the model. Further, Santa Cruz de Tenerife (TF) when deleted produces the best gain in model efficiency. This fact causes simultaneously the maximum departure from the set of the covariance parameters estimates.

For the cut-off value $\tau =0$, Fig. 12 (right) reports the values of the ratio

$$\begin{aligned} \tau ({\hat{\varvec{\theta }}}_{(d)})=\frac{\overline{mse}({\hat{\varvec{\theta }}})-\overline{mse}(\hat{\varvec{\theta }}_{(d)})}{\overline{mse}({\hat{\varvec{\theta }}})}, \end{aligned}$$

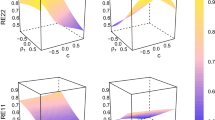
where $\overline{mse}({\hat{\varvec{\theta }}})$ was given by (2.11). Plotting $\gamma ({\hat{\varvec{\theta }}}_{(d)})$ defined in (2.10) and $\tau ({\hat{\varvec{\theta }}}_{(d)})$ indicates if varying (by deletion) the estimates ${\hat{\varvec{\theta }}}$, the model increases (decreases) the efficiency of the estimation. There are some important cases that reports highly negative $\tau ({\hat{\varvec{\theta }}}_{(d)})$’s, and this demonstrates again that Barcelona has the major negative relative impact on the average of the domain estimates of the prediction mean squared error, when deleted. The relative impact is positive when Soria (SO) is omitted.

Figure 13 plots the efficiencies $\varepsilon _i$ versus the mse-ratios $\pi _i$, defined in (2.14) and (2.15) respectively. This figure shows to which provinces the model attributes more efficiency $\varepsilon _i$ in the estimation. In our case study, we got $\varepsilon = 0.741251$, the vertical bar in the figure. In particular, provinces with the lowest values of $\varepsilon _{i}$ (here it is convenient to set $drt=i$) are those with smallest sampling variances (i.e., $\sigma _{i}^{2}$, see the subsection 2.3.4), and then this situation gives more weight to the first component (i.e., $g_{1,i}(\widehat{\mathbf {\theta }})$) of the estimated $MSE(\widetilde{\mathbf {\mu }})$, that is related to the variance of the direct estimator. The correspondent low values of $corr(r_{i}^{c},e_{i})=\varepsilon _{i}$ are justified by the fact that $MSE(\widetilde{\mathbf {\mu }})=g_{1,i}(\widehat{\mathbf {\theta }} )+g_{2,i}(\widehat{\mathbf {\theta }})$, almost approaching the sampling variance $\sigma _{i}^{2}$. Conversely, the highest values of $\varepsilon _{i}$ are provided by the provinces with $c_{i}=\sigma _{i}^{4}c_{ii}^{*}\simeq \sigma _{i}^{2}$, that implies $c_{ii}^{*}\simeq \sigma _{i}^{-2}$ (see again the subsection 2.3.4). Indeed, we observe that when $c_{ii}^{*}\longrightarrow \sigma _{i}^{-2}$ we get $c_{ij}^{*}\longrightarrow 0$ ($i\ne j$), and, consequently, $r_{i}^{c}=\sigma _{i}^{2}(c_{ii}^{*}y_{i}+\Sigma _{j\ne i}^{N}c_{ij}^{*}y_{i})=y_{i}+\sigma _{i}^{2}\Sigma _{i\ne j}^{N}c_{ij}^{*}y_{j}\longrightarrow y_{i}$. Finally, $(y_{i}-\widetilde{\mu }_{i})/y_{i}=r_{i}^{c}/y_{i}\longrightarrow 1$, and $corr(r_{i}^{c},e_{i}) \longrightarrow 1$. Ávila (AV), Cuenca (CU), Palencia (P), Segovia (SG), Soria (SO), and Zamora (ZA) are the most efficient in terms of $\varepsilon _i$ and a low value of the third component $2g_{3}$, i.e. in terms of the greatest relative difference between the sampling variance and the MSE, respect to the sampling variance itself (see the formula of $\varepsilon _i$ in 2.14). Moreover, provinces of Guipuzcoa (SS) and Cantabria (S) have some of the most relevant values in terms of the third component $2g_3$ of the MSE of the EBLUP (see $\pi$ in 2.15) Guipúzcoa (SS) and Gerona (GI) have some of the relevant values in terms of the third component of the MSE of the EBLUP.

Fig. 13

$\pi _i$ vs $\varepsilon _i$, with province abbreviations

5 Conclusions

This paper introduces the new three-fold Fay–Herriot model, which accounts for three levels of hierarchy to jointly model data from domains, subdomains, and time periods or subsubdomains. For calculating the REML estimators of the model parameters, a Fisher-scoring algorithm is implemented. Under the new model, the EBLUPs of linear indicators are derived and the corresponding MSEs are approximated. Two MSE estimators are proposed. The first one is analytic and based on the MSE approximation. The second one relies on parametric bootstrap. The simulation experiments empirically investigate the REML estimators, the EBLUPs and the MSE estimators. A three-fold Fay–Herriot model with AR(1) time effects is also introduced in Appendix B, but it is not finally selected in the application to real data.

Several measures of diagnostics are also proposed, not only to assess the general efficiency of the model but also to get valuable information to interpret underlying data relationships. Domain deletion diagnostics and Cook’s distance - both based on marginal residuals and leverages-allow to evaluate the influence of each domain on the estimates. The former through the shift in the estimators of regression parameters, the latter highlighting which area is the most influential in the analysis. Moreover, regarding the MSE of the EBLUPs, the average MSE estimators are computed iteratively removing one domain at a time, and then are combined in a ratio to assess the impact of each domain in the performance of the MSE estimates. The analysis of model residuals is achieved by employing the scaled residuals obtained through a Cholesky root of the covariance matrix of the original data, to appraise the connection of the selected covariates with the response variable. An efficiency measure of the model is instead proposed on the basis of the difference between the sampling variances and the $g_1$ and $g_2$ components of the mse and, finally, a mse-ratio is accomplished to fix the variability of the estimation of the variance components to the predicted MSE. The reported diagnostics are then combined together in nice graphical representations which give great support, especially in the interpretation of the results within the application to real data.

It is worth reflecting on some conclusions about the model diagnostics presented, and in particular, on the measures introduced. The model studied is an extension of the Fay–Herriot model, where are present areas in a three-fold matrix of random effects design. The model belongs to the class of LMMs with block-diagonal structure. We have two main features of this model, with relevant consequences in terms of evaluation of the results. The first is that the model has more than one observation unit per area, unlike the basic Fay–Herriot model. This is because of the presence of the variable of the gender, and also to repeated observations of the same area with respect to five-time instants. The second is that since we apply an area-level model to the data, the variance of the residual mixed model errors is given. Both these model characteristics are considered in the diagnostics and influence analysis reported. In particular, we analyze the model marginal residuals through their reduction to ordinary regression residuals, due to correlated observations. This procedure depicts the areas starting only from the fixed-effects matrix, and can play a significant role in the assessment of the connection of the selected covariates with the response variable. This allows also to study the model (2.12) as a theme-based model, through its scaled residuals $\varvec{r}_{ch}^{m}$, in addition to the considerations related to the model-based estimation. Anyway, in an effort to eliminate the instability induced by the sampling variances in the model estimation process, the linear relation at the basis of the study can be further assessed by the diagnostic properties of the model reduced by the Cholesky root. In particular, using the Cholesky decomposition for the residuals, make some information about the data (i.e. some influential provinces) visible that would otherwise remain masked.

A further and prominent aspect of small area estimation models is related to the best reduction of the MSE of the area level predictors. Following the usual linear mixed-model Covratio diagnostics, we introduced the use of some new plots, in order to rate possible favorable changes in the estimation of the model. This also with a joint evaluation of the level of the departure of the covariance parameters from the complete model and the change in the MSE. Finally, because in the area-level models the residual error variance is not to be estimated, model conditional residuals can be used to illustrate the level of efficiency of the model. The model efficiency index is then given by the joint consideration of conditional residuals and model errors, obtained by averaging their correlations.

The new small area model is applied to the Spanish living condition survey data of the periods 2004–2008. The target is to estimate poverty incidence by province, by sex and by year. Since the data were available for 5 periods, complex temporal correlation structures are not considered. The statistical inferences on the presented model show good results, both in the significance level of the estimated parameters and in the minimization of the MSEs of the EBLUP estimates. Then with a map is depicted the distribution of the EBLUP estimates for the proportion of poverty between the Spanish provinces. The model introduced retains its features in terms of assessment of the impact of the demographic and the economic predictors used on the poverty proportion. Being the observations of the Spanish Provinces, evaluated in domains of the sexes and repeated by time instants, the model offers the opportunity to read analytically the considerable differences that distinguish various territories of Spain. Finally, we remark that the simulations and the application of the model to the real data have been carried out with the programming language R. The developed software is available on request.

Appendices

A Appendix: MSE derivations

1.1 A.1 Basic calculations

The mean squared error matrix of ${\tilde{\varvec{\mu }}}$, with diagonal elements $MSE({\hat{\mu }}_{drt}^{blup})$, is

$$\begin{aligned} MSE({\tilde{\varvec{\mu }}})= & {} \text{ var }(\varvec{X}({\hat{\varvec{\beta }}}-\varvec{\beta })+\varvec{Z}({\tilde{\varvec{u}}}-\varvec{u})) \\= & {} \text{ var }(\varvec{X}{\hat{\varvec{\beta }}})+\text{ var }(\varvec{Z}({\tilde{\varvec{u}}}-\varvec{u}))+\text{ cov }(\varvec{X}{\hat{\varvec{\beta }}},\varvec{Z}({\tilde{\varvec{u}}}-\varvec{u}))+\text{ cov }(\varvec{Z}({\tilde{\varvec{u}}}-\varvec{u}),\varvec{X}{\hat{\varvec{\beta }}}). \end{aligned}$$

Let us define $\varvec{M}=(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}$, so that $\varvec{M}\varvec{V}\varvec{P}=\varvec{0}$. As $\text{ var }(\varvec{X}(\hat{\varvec{\beta }}-\varvec{\beta })+\varvec{Z}({\tilde{\varvec{u}}}-\varvec{u}))=\text{ var }(\varvec{X}{\hat{\varvec{\beta }}}+\varvec{Z}({\tilde{\varvec{u}}}-\varvec{u}))$, we have

$$\begin{aligned} \text{ var }({\tilde{\varvec{u}}}-\varvec{u})= & {} \text{ var }({\tilde{\varvec{u}}})+\text{ var }(\varvec{u})-\text{ cov }({\tilde{\varvec{u}}},\varvec{u})-\text{ cov }(\varvec{u},{\tilde{\varvec{u}}}) \\= & {} \varvec{V}_{u}\varvec{Z}^{\prime }\varvec{P}\varvec{Z}\varvec{V}_{u}+\text{ var }(\varvec{u})-\text{ var }({\tilde{\varvec{u}}})-\text{ var }({\tilde{\varvec{u}}}) =\varvec{V}_{u}-\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{P}\varvec{Z}\varvec{V}_{u}, \\ \text{ cov }({\hat{\varvec{\beta }}},{\tilde{\varvec{u}}}-\varvec{u})= & {} \varvec{M}[\text{ cov }(\varvec{y},{\tilde{\varvec{u}}})-\text{ cov }(\varvec{y},\varvec{u})] \\= & {} \varvec{M}[\text{ cov }(\varvec{y},\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{P}\varvec{y})-\varvec{Z}\varvec{V}_{u}]=\varvec{M}[\varvec{V}\varvec{P}\varvec{Z}\varvec{V}_{u}-\varvec{Z}\varvec{V}_{u}]=-\varvec{M}\varvec{Z}\varvec{V}_{u}, \\ \text{ cov }(\varvec{X}{\hat{\varvec{\beta }}},\varvec{Z}({\tilde{\varvec{u}}}-\varvec{u}))= & {} -\varvec{X}\varvec{M}\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\triangleq -\varvec{U}. \\ \text{ cov }({\tilde{\varvec{u}}},\varvec{u})= & {} \varvec{V}_{u}\varvec{Z}^{\prime }cov[\varvec{V}^{-1}(\varvec{y}-\varvec{X}{\hat{\varvec{\beta }}}),\varvec{u})]=\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{P}\varvec{Z}\varvec{V}_{u}=\text{ var }({\tilde{\varvec{u}}}), \\ \text{ var }(\varvec{X}{\hat{\varvec{\beta }}}+\varvec{Z}({\tilde{\varvec{u}}}-\varvec{u}))= & {} \varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }+\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime } -\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{P}\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime } \\- & {} \varvec{X}\varvec{M}\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }-\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{M}^{\prime }\varvec{X}^{\prime }. \end{aligned}$$

If we write $\varvec{P}=\varvec{V}^{-1}(\varvec{I}-\varvec{R})=\varvec{V}^{-1}-\varvec{V}^{-1}\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1} \varvec{X}^{\prime }\varvec{V}^{-1}=\varvec{V}^{-1}-\varvec{V}^{-1}\varvec{X}\varvec{M}$, we get $\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{P}\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }=\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{V}^{-1}\varvec{Z}\varvec{V}_{u} \varvec{Z}^{\prime }-\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{V}^{-1} \varvec{X}\varvec{M}\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }$, and:

$$\begin{aligned} g_{1}(\varvec{\theta })= & {} \varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }-\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{V}^{-1}\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }, \\ g_{2}(\varvec{\theta })= & {} \varvec{X}\varvec{M}\varvec{V}+\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{V}^{-1}\varvec{U}-\varvec{U}-\varvec{U}^{\prime }. \end{aligned}$$

Since $\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }=\varvec{V}-\varvec{V}_{e}$, $\varvec{U}=\varvec{X}\varvec{M}(\varvec{V}-\varvec{V}_{e})$, we observe that $\varvec{V}\varvec{M}^{\prime }\varvec{X}^{\prime }=\varvec{X}\varvec{M}\varvec{V}$, and $\varvec{V}_{e}\varvec{M}^{\prime }\varvec{X}^{\prime }=\varvec{V}_{e}\varvec{V}^{-1}\varvec{X}\varvec{M}\varvec{V}$. Therefore, we have

$$\begin{aligned} g_{1}(\varvec{\theta })= & {} (\varvec{V}-\varvec{V}_{e})-(\varvec{V}-\varvec{V}_{e})\varvec{V}^{-1}(\varvec{V}-\varvec{V}_{e}) \\= & {} (\varvec{V}-\varvec{V}_{e})-(\varvec{I}-\varvec{V}_{e}\varvec{V}^{-1})(\varvec{V}-\varvec{V}_{e})=\varvec{V}_{e}-\varvec{V}_{e}\varvec{V}^{-1}\varvec{V}_{e}=\varvec{Z}\varvec{T}\varvec{Z}^{\prime } \\ g_{2}(\varvec{\theta })= & {} \varvec{X}\varvec{M}\varvec{V}+[(\varvec{V}-\varvec{V}_{e})\varvec{V}^{-1}\varvec{X}\varvec{M}-\varvec{X}\varvec{M}](\varvec{V}-\varvec{V}_{e})-\varvec{V}\varvec{M}^{\prime }\varvec{X}^{\prime }+\varvec{V}_{e}\varvec{M}^{\prime }\varvec{X}^{\prime } \\= & {} -\varvec{V}_{e}\varvec{V}^{-1}\varvec{X}\varvec{M}(\varvec{V}-\varvec{V}_{e})+ \varvec{V}_{e}\varvec{M}^{\prime }\varvec{X}^{\prime }=\varvec{V}_{e}\varvec{V}^{-1}\varvec{X}\varvec{M}\varvec{V}_{e} \\= & {} \varvec{V}_{e}\varvec{V}^{-1}\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{V}_{e} =\big (\varvec{X}-\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\varvec{V}_e^{-1}\varvec{X}\big )\varvec{Q}\big (\varvec{X}^{\prime }-\varvec{X}^{\prime }\varvec{V}_e^{-1}\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\big ), \end{aligned}$$

where $\varvec{T}=\varvec{V}_u-\varvec{V}_u\varvec{Z}^{\prime }\varvec{V}^{-1}\varvec{Z}\varvec{V}_u$. Finally, we have

$$\begin{aligned} MSE({\tilde{\varvec{\mu }}})= & {} g_{1}(\varvec{\theta }) +g_{2}(\varvec{\theta }) \nonumber \\= & {} \varvec{V}_{e}-\varvec{V}_{e}\varvec{V}^{-1}\varvec{V}_{e}+\varvec{V}_{e}\varvec{V}^{-1}\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{V}_{e} \nonumber \\= & {} \varvec{V}_{e}-\varvec{V}_{e}\varvec{P}\varvec{V}_{e}. \end{aligned}$$

(A.1)

1.2 A.2 Calculation of $g_{1drt}(\varvec{\theta })$

It holds that $g_{1drt}(\varvec{\theta })=\varvec{a}^{\prime }\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\varvec{a}$, where $\varvec{T}=\varvec{V}_u-\varvec{V}_u\varvec{Z}^{\prime }\varvec{V}^{-1}\varvec{Z}\varvec{V}_u$. We have

$$\begin{aligned} \varvec{T}= & {} \left( \begin{array}{ccc}\sigma _1^2\varvec{I}_{D}&{} \varvec{0}&{}\varvec{0}\\ \varvec{0}&{} \sigma _2^2\varvec{I}_{DR}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\sigma _3^2\varvec{I}_{DRT}\end{array}\right) - \left( \begin{array}{ccc}\sigma _1^2\varvec{I}_{D}&{} \varvec{0}&{}\varvec{0}\\ \varvec{0}&{} \sigma _2^2\varvec{I}_{DR}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\sigma _3^2\varvec{I}_{DRT}\end{array}\right) \left( \begin{array}{c} \underset{1\le \ell \le D}{\hbox {diag}}(\varvec{1}_{RT}^{\prime }) \\ \underset{1\le \ell \le D}{\hbox {diag}}(\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime }))\\ \varvec{I}_{DRT} \end{array}\right) \\&\cdot\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{V}_{\ell }^{-1}) \Big (\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{1}_{RT}), \underset{1\le \ell \le D}{\hbox {diag}}(\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})), \varvec{I}_{DRT}\Big ) \left( \begin{array}{ccc}\sigma _1^2\varvec{I}_{D}&{} \varvec{0}&{}\varvec{0}\\ \varvec{0}&{} \sigma _2^2\varvec{I}_{DR}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\sigma _3^2\varvec{I}_{DRT}\end{array}\right) \\= & {} \left( \begin{array}{ccc}\varvec{T}_{11}&{} \varvec{T}_{12}&{} \varvec{T}_{13} \\ \varvec{T}_{21}&{} \varvec{T}_{22} &{} \varvec{T}_{23} \\ \varvec{T}_{31}&{} \varvec{T}_{32} &{} \varvec{T}_{33} \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} \varvec{T}_{11}= & {} \sigma _1^2\varvec{I}_D-\sigma _1^4\underset{1\le \ell \le D}{\hbox {diag}}\big (\varvec{1}_{RT}^{\prime }\varvec{V}_{\ell }^{-1}\varvec{1}_{RT}\big ) =\underset{1\le \ell \le D}{\hbox {diag}}(T_{11\ell }), \\ \varvec{T}_{12}= & {} -\sigma _1^2\sigma _2^2\underset{1\le \ell \le D}{\hbox {diag}}\Big (\varvec{1}_{RT}^{\prime }\varvec{V}_{\ell }^{-1} \underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\Big ) =\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{T}_{12\ell })=\varvec{T}_{21}^\prime , \\ \varvec{T}_{13}= & {} -\sigma _1^2\sigma _3^2\underset{1\le \ell \le D}{\hbox {diag}}\big (\varvec{1}_{RT}^{\prime }\varvec{V}_{\ell }^{-1}\big ) =\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{T}_{13\ell })=\varvec{T}_{31}^\prime , \\ \varvec{T}_{22}= & {} \sigma _2^2\varvec{I}_{DR} -\sigma _2^4\underset{1\le \ell \le D}{\hbox {diag}}\Big (\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime }) \varvec{V}_{\ell }^{-1} \underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\Big ) =\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{T}_{22\ell }), \\ \varvec{T}_{23}= & {} -\sigma _2^2\sigma _3^2\underset{1\le \ell \le D}{\hbox {diag}}\Big (\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime }) \varvec{V}_{\ell }^{-1}\Big ) =\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{T}_{23\ell })=\varvec{T}_{32}^\prime . \\ \varvec{T}_{33}= & {} \sigma _3^2\varvec{I}_{DRT} -\sigma _3^4\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{V}_{\ell }^{-1}) =\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{T}_{33\ell }). \end{aligned}$$

Note that $\varvec{a}=\underset{1\le \ell \le D}{\hbox {col}}(\delta _{d\ell }\varvec{a}_{rt})$, where $\varvec{a}_{rt}=\underset{1\le s \le S}{\hbox {col}}(\underset{1\le k \le T}{\hbox {col}}(\delta _{rs}\delta _{tk}))$. Then,we have

$$\begin{aligned} g_1= & {} g_{1drt}(\varvec{\theta })=\varvec{a}^{\prime }\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\varvec{a}\\= & {} \varvec{a}^{\prime } \Big (\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{1}_{RT}), \underset{1\le \ell \le D}{\hbox {diag}}(\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})), \varvec{I}_{DRT}\Big ) \left( \begin{array}{ccc}\varvec{T}_{11}&{} \varvec{T}_{12}&{} \varvec{T}_{13} \\ \varvec{T}_{21}&{} \varvec{T}_{22} &{} \varvec{T}_{23} \\ \varvec{T}_{31}&{} \varvec{T}_{32} &{} \varvec{T}_{33} \end{array}\right) \left( \begin{array}{c} \underset{1\le \ell \le D}{\hbox {diag}}(\varvec{1}_{RT}^{\prime }) \\ \underset{1\le \ell \le D}{\hbox {diag}}(\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime }))\\ \varvec{I}_{DRT} \end{array}\right) \varvec{a}\\= & {} \varvec{a}^{\prime }\underset{1\le \ell \le D}{\hbox {diag}}\Big ( \varvec{1}_{RT}T_{11\ell }\varvec{1}_{RT}^\prime +\varvec{1}_{T}\varvec{T}_{12\ell }\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^\prime ) +\varvec{1}_{RT}\varvec{T}_{13\ell } +\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\varvec{T}_{21\ell }\varvec{1}_{RT}^\prime \\+ & {} \underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\varvec{T}_{22\ell }\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^\prime ) +\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\varvec{T}_{23\ell } + \varvec{T}_{31\ell }\varvec{1}_{RT}^\prime +\varvec{T}_{32\ell }\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}) +\varvec{T}_{33\ell } \Big )\varvec{a}\\= & {} \varvec{a}^{\prime }_{rt}\Big ( \varvec{1}_{RT}T_{11d}\varvec{1}_{RT}^\prime +\varvec{1}_{RT}\varvec{T}_{12d}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^\prime ) +\varvec{1}_{RT}\varvec{T}_{13d} +\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\varvec{T}_{21d}\varvec{1}_{RT}^\prime \\+ & {} \underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\varvec{T}_{22d}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^\prime ) +\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\varvec{T}_{23d} + \varvec{T}_{31d}\varvec{1}_{RT}^\prime +\varvec{T}_{32d}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^\prime ) +\varvec{T}_{33d} \Big )\varvec{a}_{rt}. \end{aligned}$$

1.3 A.3 Calculation of $g_{2drt}(\varvec{\theta })$

It holds that

$$\begin{aligned} g_{2drt}(\varvec{\theta })= \big (\varvec{a}^{\prime }\varvec{X}-\varvec{a}^{\prime }\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\varvec{V}_e^{-1}\varvec{X}\big )\varvec{Q}\big (\varvec{X}^{\prime }\varvec{a}-\varvec{X}^{\prime }\varvec{V}_e^{-1}\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\varvec{a}\big ) =(\varvec{a}_1^{\prime }-\varvec{a}_2^{\prime })\varvec{Q}(\varvec{a}_1-\varvec{a}_2), \end{aligned}$$

where $\varvec{a}_1^{\prime }=\varvec{a}^{\prime }\varvec{X}=\varvec{a}_{rt}^{\prime }\varvec{X}_d=\varvec{x}_{drt}$ and

$$\begin{aligned} \varvec{a}_2^{\prime }= & {} \varvec{a}^{\prime }\varvec{Z}\varvec{T}\varvec{Z}^{\prime }\varvec{V}_e^{-1}\varvec{X}\\= & {} \varvec{a}^{\prime }\Big (\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{1}_{RT}), \underset{1\le \ell \le D}{\hbox {diag}}(\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})), \varvec{I}_{DRT}\Big ) \left( \begin{array}{ccc}\varvec{T}_{11}&{} \varvec{T}_{12}&{} \varvec{T}_{13} \\ \varvec{T}_{21}&{} \varvec{T}_{22} &{} \varvec{T}_{23} \\ \varvec{T}_{31}&{} \varvec{T}_{32} &{} \varvec{T}_{33} \end{array}\right) \left( \begin{array}{c} \underset{1\le \ell \le D}{\hbox {diag}}(\varvec{1}_{RT}^{\prime }) \\ \underset{1\le \ell \le D}{\hbox {diag}}(\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime }))\\ \varvec{I}_{DRT} \end{array}\right) \\ & \cdot \underset{1\le \ell \le D}{\hbox {diag}}(\varvec{V}_{e\ell }^{-1}) \underset{1\le \ell \le D}{\hbox {col}}(\varvec{X}_\ell ) \\ = & {} \varvec{a}_{rt}^{\prime }\Big ( \varvec{1}_{RT}T_{11d}\varvec{1}_{RT}^\prime +\varvec{1}_{RT}\varvec{T}_{12d}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^\prime ) +\varvec{1}_{RT}\varvec{T}_{13d} +\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\varvec{T}_{21d}\varvec{1}_{RT}^\prime \\+ & {} \underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\varvec{T}_{22d}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^\prime ) +\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})\varvec{T}_{23d} + \varvec{T}_{31d}\varvec{1}_{RT}^\prime + \varvec{T}_{32d}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^\prime ) +\varvec{T}_{33d} \Big ) \varvec{V}_{ed}^{-1}\varvec{X}_d. \end{aligned}$$

1.4 A.4 Calculation of $g_{3drt}(\varvec{\theta })$

It holds that

$$\begin{aligned} g_{3drt}(\varvec{\theta })\approx \text{ tr }\left\{ (\nabla \varvec{b}^{\prime })\varvec{V}(\nabla \varvec{b}^{\prime })^{\prime } E\left[ ({\hat{\varvec{\theta }}}-\varvec{\theta })({\hat{\varvec{\theta }}}-\varvec{\theta })^{\prime }\right] \right\} , \end{aligned}$$

where

$$\begin{aligned}{} & {} \varvec{b}^{\prime }=\varvec{a}^{\prime }\varvec{Z}\varvec{V}_u\varvec{Z}^{\prime }\varvec{V}^{-1} \\{} & {} \quad = \varvec{a}^{\prime } \Big (\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{1}_{RT}), \underset{1\le \ell \le D}{\hbox {diag}}(\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T})), \varvec{I}_{DRT}\Big ) \\{} & {} \quad \left( \begin{array}{ccc}\sigma _1^2\varvec{I}_{D}&{} \varvec{0}&{}\varvec{0}\\ \varvec{0}&{} \sigma _2^2\varvec{I}_{DR}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\sigma _3^2\varvec{I}_{DRT}\end{array}\right) \left( \begin{array}{c} \underset{1\le \ell \le D}{\hbox {diag}}(\varvec{1}_{RT}^{\prime }) \\ \underset{1\le \ell \le D}{\hbox {diag}}(\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime }))\\ \varvec{I}_{DRT} \end{array}\right) \\{} & {} \quad \cdot \underset{1\le \ell \le D}{\hbox {diag}}(\varvec{V}_{\ell }^{-1}) \\{} & {} \quad = \varvec{a}^{\prime }\underset{1\le \ell \le D}{\hbox {diag}}\Big (\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime ) +\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_\ell ^{-1}\Big ). \end{aligned}$$

The derivatives of $\varvec{b}^{\prime }$ are

$$\begin{aligned} \frac{\partial \varvec{b}^{\prime }}{\partial \sigma _1^2}= & {} \underset{1\le \ell \le D}{\hbox {col}^{\prime }}\Big (\delta _{d\ell }\varvec{a}_{rt}^{\prime }\varvec{1}_{RT}\varvec{1}_{RT}^\prime \varvec{V}_\ell ^{-1}\Big ) \\- & {} \underset{1\le \ell \le D}{\hbox {col}^{\prime }}\Big (\delta _{d\ell }\varvec{a}_{rt}^{\prime } \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime ) +\sigma _3^2\varvec{I}_{RT}\big )\varvec{V}_\ell ^{-1}\varvec{V}_{\ell 1}\varvec{V}_\ell ^{-1}\big ), \\ \frac{\partial \varvec{b}^{\prime }}{\partial \sigma _2^2}= & {} \underset{1\le \ell \le D}{\hbox {col}^{\prime }}\Big (\delta _{d\ell }\varvec{a}_{rt}^{\prime }\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_\ell ^{-1}\Big ) \\- & {} \underset{1\le \ell \le D}{\hbox {col}^{\prime }}\Big (\delta _{d\ell }\varvec{a}_{rt}^{\prime } \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime ) +\sigma _3^2\varvec{I}_{RT}\big )\varvec{V}_\ell ^{-1}\varvec{V}_{\ell 2}\varvec{V}_\ell ^{-1}\Big ), \\ \frac{\partial \varvec{b}^{\prime }}{\partial \sigma _3^2}= & {} \underset{1\le \ell \le D}{\hbox {col}^{\prime }}\Big (\delta _{d\ell }\varvec{a}_{rt}^{\prime }\varvec{I}_{RT}\varvec{V}_\ell ^{-1}\Big ) \\- & {} \underset{1\le \ell \le D}{\hbox {col}^{\prime }}\Big (\delta _{d\ell }\varvec{a}_{rt}^{\prime } \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_\ell ^{-1}\varvec{V}_{\ell 3}\varvec{V}_\ell ^{-1}\Big ), \end{aligned}$$

where $\varvec{V}_{\ell 1}=\frac{\partial \varvec{V}_\ell }{\partial \sigma _1^2}=\varvec{1}_{RT}\varvec{1}_{RT}^\prime$, $\varvec{V}_{\ell 2}=\frac{\partial \varvec{V}_\ell }{\partial \sigma _2^2}=\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )$, $\varvec{V}_{\ell 3}=\frac{\partial \varvec{V}_\ell }{\partial \sigma _3^2}=\varvec{I}_{RT}$. Let us define

$$\begin{aligned} \frac{\partial \varvec{b}_d^{\prime }}{\partial \sigma _1^2}= & {} \varvec{a}_{rt}^{\prime }\varvec{1}_{RT}\varvec{1}_{RT}^\prime \varvec{V}_d^{-1}- \varvec{a}_{rt}^{\prime } \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1}, \\ \frac{\partial \varvec{b}_d^{\prime }}{\partial \sigma _2^2}= & {} \varvec{a}_{rt}^{\prime }\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1} -\varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1}, \\ \frac{\partial \varvec{b}_d^{\prime }}{\partial \sigma _3^2}= & {} \varvec{a}_{rt}^{\prime }\varvec{I}_{RT}\varvec{V}_d^{-1}- \varvec{a}_{rt}^{\prime } \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\varvec{I}_{RT}\varvec{V}_d^{-1}. \end{aligned}$$

The components of $(\nabla \varvec{b}^{\prime })\varvec{V}(\nabla \varvec{b}^{\prime })^{\prime }$ take the form

$$\begin{aligned} q_{ab}=\frac{\partial \varvec{b}^{\prime }}{\partial \sigma _a^2}\underset{1\le \ell \le D}{\hbox {diag}}(\varvec{V}_\ell ) \left( \frac{\partial \varvec{b}^{\prime }}{\partial \sigma _b^2}\right) ^{\prime } = \frac{\partial \varvec{b}_d^{\prime }}{\partial \sigma _a^2}\,\varvec{V}_{d} \left( \frac{\partial \varvec{b}_d^{\prime }}{\partial \sigma _b^2}\right) ^{\prime },\quad a,b=1,2,3. \end{aligned}$$

They are

$$\begin{aligned} q_{11}=\, & {} \varvec{a}_{rt}^{\prime }\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1}\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{a}_{rt} \\ & -{} 2\varvec{a}_{rt}^{\prime }\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1}\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1} \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt} \\ &+ {} \varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1} \\ &\cdot \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt}, \\ q_{12}=\, & {} \varvec{a}_{rt}^{\prime }\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{a}_{rt} \\ &- {} \varvec{a}_{rt}^{\prime }\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1} \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt} \\ &- {} \varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{a}_{rt} \\ &+ {} \varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1} \\&\cdot \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt} =\,q_{21}, \\ q_{13}=\, & {} \varvec{a}_{rt}^{\prime }\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1}\varvec{I}_{RT}\varvec{a}_{rt} \\ &- {} \varvec{a}_{rt}^{\prime }\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-2} \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt} \\&- {} \varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\varvec{1}_{RT}\varvec{1}_{RT}^{\prime }\varvec{V}_d^{-1}\varvec{I}_{RT}\varvec{a}_{rt} \\ &+ {} \varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\varvec{1}_{RT}\varvec{1}_{RT}^\prime \varvec{V}_d^{-2} \\&\cdot \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt} =\,q_{31}, \end{aligned}$$

$$\begin{aligned} q_{22}= & {} \varvec{a}_{rt}^{\prime }\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{a}_{rt} \\& - {} 2\varvec{a}_{rt}^{\prime }\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1} \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt} \\&+ {} \varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1} \\&\cdot \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt}, \\ q_{23}= & {} \varvec{a}_{rt}^{\prime }\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1}\varvec{I}_{RT}\varvec{a}_{rt} \\&- {} \varvec{a}_{rt}^{\prime }\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-2} \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt} \\&- {} \varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-1}\varvec{I}_{RT}\varvec{a}_{rt} \\&+ {} \varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-1}\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )\varvec{V}_d^{-2} \\&\cdot \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt} =q_{32}, \\ q_{33}= & {} \varvec{a}_{rt}^{\prime }\varvec{V}_d^{-1}\varvec{a}_{rt} - 2\varvec{a}_{rt}^{\prime }\varvec{I}_{RT}\varvec{V}_d^{-2} \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt} \\&+ {} \varvec{a}_{rt}^{\prime }\big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big ) \varvec{V}_d^{-3} \\&\cdot \big (\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le s \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^\prime )+\sigma _3^2\varvec{I}_{RT}\big )\varvec{a}_{rt}. \end{aligned}$$

Finally, we have

$$\begin{aligned} g_{3drt}(\varvec{\theta })\approx \hbox {tr}\left\{ \left( \begin{array}{ccc}q_{11}&{}q_{12}&{}q_{13}\\ q_{21}&{}q_{22}&{}q_{23}\\ q_{31}&{}q_{32}&{}q_{33}\end{array}\right) \left( \begin{array}{ccc}F_{11}&{}F_{12}&{}F_{13}\\ F_{21}&{}F_{22}&{}F_{23}\\ F_{31}&{}F_{32}&{}F_{33} \end{array}\right) ^{-1}\right\} , \end{aligned}$$

where $F_{ab}$ is the generic element of the REML Fisher information matrix that was calculated for deriving the updating formula of the Fisher-scoring algorithm.

B Appendix: Three-fold Fay–Herriot model with AR(1) time effects

1.1 B.1 The model

Let us consider the model

$$\begin{aligned} y_{drt}=\varvec{x}_{drt}\varvec{\beta }+u_{1,d}+u_{2,dr}+u_{3,drt}+e_{drt},\quad d=1,\ldots ,D,\,\,r=1,\ldots ,R,\,\,t=1,\ldots ,T, \end{aligned}$$

(B.1)

where $y_{drt}$ is a direct estimator of the characteristic of interest and $\varvec{x}_{drt}$ is a row vector containing the aggregated population values of p auxiliary variables. The subscripts d, r and t represent domains, subdomains and subsubdomains respectively. For example, d, r and t may represent area, category (for example, sex-age group) and time period respectively. We assume that $u_{1,d}\sim N(0,\sigma _1^2)$, $u_{2,dr}\sim N(0,\sigma _2^2)$, $\varvec{u}_{3,dr}=(u_{3,dr1},\ldots ,u_{2,drT})^\prime \sim N_T(\varvec{0},\sigma _3^2\Omega _{dr}(\rho ))$, $e_{drt}\sim N(0,\sigma _{drt}^2)$, $d=1,\ldots ,D$, $r=1,\ldots ,R$, $t=1,\ldots ,T$, are mutually independent, with $\sigma _{drt}^2>0$ known and

$$\begin{aligned} \Omega _{dr}=\Omega _{dr}(\rho )=\frac{1}{1-\rho ^2}\left( \begin{array}{ccccc} 1&{}\rho &{}\ldots &{}\rho ^{T-2}&{}\rho ^{T-1}\\ \rho &{}1&{}\ddots &{}&{}\rho ^{T-2}\\ \vdots &{}\ddots &{}\ddots &{}\ddots &{}\vdots \\ \rho ^{T-2}&{}&{}\ddots &{}1&{}\rho \\ \rho ^{T-1}&{}\rho ^{T-2}&{}\ldots &{}\rho &{}1 \end{array}\right) _{T\times T}. \end{aligned}$$

Model (B.1) is a generalization of the two-fold Fay–Herriot model with correlated time effects described in Section 17.3 of Morales et al. (2021).

At the domain level d and subdomain level r, we define the matrices and vectors

$$\begin{aligned}{} & {} \varvec{X}_{dr}=\underset{1\le t \le T}{\hbox {col}}(\varvec{x}_{drt}),\, \varvec{Z}_{1,dr}=\varvec{Z}_{2,dr}=\varvec{1}_T,\, \varvec{Z}_{3,dr}=\varvec{I}_{T},\, \varvec{V}_{3,dr}=\sigma _3^2\Omega _{dr}(\rho ),\, \varvec{V}_{e,dr}\\{} & {} \quad =\underset{1\le t \le T}{\hbox {diag}}(\sigma ^2_{drt}), \\{} & {} \varvec{y}_{dr}=\underset{1\le t \le T}{\hbox {col}}(y_{drt}),\,\, \varvec{u}_{3,dr}=\underset{1\le t \le T}{\hbox {col}}(u_{3,drt})\sim N_T(\varvec{0}, \varvec{V}_{3,dr}),\,\, \varvec{e}_{dr}\ \\{} & {} \quad =\underset{1\le t \le T}{\hbox {col}}(e_{drt})\sim N_T(\varvec{0}, \varvec{V}_{e,dr}), \end{aligned}$$

where $\varvec{1}_T$ denotes the $T\times 1$ vector of ones and $\varvec{I}_T$ is the $T\times T$ identity matrix. We can write model (B.1) in the subdomain form

$$\begin{aligned} \varvec{y}_{dr}=\varvec{X}_{dr}\varvec{\beta }+\varvec{Z}_{1,dr}u_{1,d}+\varvec{Z}_{2,dr}u_{2,dr}+\varvec{Z}_{3,dr}\varvec{u}_{3,dr}+\varvec{e}_{dr},\quad d=1,\ldots ,D,\,\,r=1,\ldots ,R. \end{aligned}$$

The variance matrix of $\varvec{y}_{dr}$ is

$$\begin{aligned} \varvec{V}_{dr}=\text{ var }(\varvec{y}_{dr})=\sigma _1^2\varvec{1}_T\varvec{1}_T^\prime +\sigma _2^2\varvec{1}_T\varvec{1}_T^\prime +\sigma _3^2\Omega _{dr}(\rho )+\varvec{V}_{e,dr},\quad d=1,\ldots ,D,\, r=1,\ldots ,R. \end{aligned}$$

At the domain level d, we define the vectors and matrices

$$\begin{aligned}{} & {} \varvec{y}_{d}=\underset{1\le r \le R}{\hbox {col}}(\varvec{y}_{dr}),\, \varvec{X}_{d}=\underset{1\le r \le R}{\hbox {col}}(\varvec{X}_{dr}),\, \varvec{Z}_{1,d}=\varvec{1}_{RT},\, \varvec{Z}_{2,d}\\{} & {} \quad =\underset{1\le r \le R}{\hbox {diag}}(\varvec{Z}_{2,dr}),\, \varvec{Z}_{3,d}=\varvec{I}_{RT},\, \varvec{V}_{2,d}=\sigma _2^2\varvec{I}_{R}, \\{} & {} \Omega _d(\rho )=\underset{1\le r \le R}{\hbox {diag}}(\Omega _{dr}(\rho )),\, \varvec{V}_{3,d}=\sigma _3^2\Omega _d(\rho ),\, \varvec{V}_{e,d}=\underset{1\le r \le R}{\hbox {diag}}(\varvec{V}_{e,dr}),\, \varvec{u}_{2,d}\\{} & {} \quad =\underset{1\le r \le R}{\hbox {col}}(u_{2,dr})\sim N_{R}(\varvec{0}, \varvec{V}_{2,d}), \\{} & {} \varvec{u}_{3,d}=\underset{1\le r \le R}{\hbox {col}}(\varvec{u}_{3,dr})\sim N_{RT}(\varvec{0}, \varvec{V}_{3,d}),\,\, \varvec{e}_{d}\\{} & {} \quad =\underset{1\le r \le R}{\hbox {col}}(\varvec{e}_{dr})\sim N_{RT}(\varvec{0}, \varvec{V}_{e,d}). \end{aligned}$$

We can write model (B.1) in the domain form

$$\begin{aligned} \varvec{y}_{d}=\varvec{X}_{d}\varvec{\beta }+\varvec{Z}_{1,d}u_{1,d}+\varvec{Z}_{2,d}\varvec{u}_{2,d}+\varvec{Z}_{3,d}\varvec{u}_{3,d}+\varvec{e}_{d},\quad d=1,\ldots ,D. \end{aligned}$$

(B.2)

Let us define the $RT\times (1+R+RT)$ matrix $\varvec{Z}_d=(\varvec{Z}_{1,d},\varvec{Z}_{2,d},\varvec{Z}_{3,d})$ and the $(1+R+RT)\times 1$ vector $\varvec{u}_d=(u_{1,d},\varvec{u}_{2,d}^\prime ,\varvec{u}_{3,d}^\prime )^\prime$, with $\varvec{V}_{ud}=\text{ var }(\varvec{u}_d)=\text{ diag }(\sigma _1^2,\varvec{V}_{2,d},\varvec{V}_{3,d})$. We can write model (B.2) in the linear mixed model form

$$\begin{aligned} \varvec{y}_{d}=\varvec{X}_{d}\varvec{\beta }+\varvec{Z}_{d}\varvec{u}_{d}+\varvec{e}_{d},\quad d=1,\ldots ,D. \end{aligned}$$

The variance matrix of $\varvec{y}_{d}$ is

$$\begin{aligned} \varvec{V}_d=\text{ var }(\varvec{y}_{d})=\sigma _1^2\varvec{1}_{RT}\varvec{1}_{RT}^\prime +\sigma _2^2\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_T\varvec{1}_T^\prime ) +\sigma _3^2\underset{1\le r \le R}{\hbox {diag}}(\Omega _{dr}(\rho ))+\varvec{V}_{e,d},\quad d=1,\ldots ,D. \end{aligned}$$

At the population level, we define the vectors and matrices

$$\begin{aligned}{} & {} \varvec{y}=\underset{1\le d \le D}{\hbox {col}}(\varvec{y}_{d}),\, \varvec{X}=\underset{1\le d \le D}{\hbox {col}}(\varvec{X}_{d}),\, \varvec{Z}_{1}=\underset{1\le d \le D}{\hbox {diag}}(\varvec{Z}_{1,d}),\, \varvec{Z}_{2}=\underset{1\le d \le D}{\hbox {diag}}(\varvec{Z}_{2,d}),\, \varvec{Z}_{3}=\varvec{I}_{DRT},\, \\{} & {} \Omega (\rho )=\underset{1\le d \le D}{\hbox {diag}}(\Omega _{d}(\rho )),\, \varvec{V}_{1}=\sigma _1^2\varvec{I}_{D},\, \varvec{V}_{2}=\sigma _2^2\varvec{I}_{DR},\, \varvec{V}_{3}=\sigma _3^2\Omega (\rho ),\, \varvec{V}_{e}=\underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_{e,d}),\, \\{} & {} \varvec{u}_{1}=\underset{1\le d \le D}{\hbox {col}}(u_{1,d})\sim N_{D}(\varvec{0}, \varvec{V}_{1}),\,\, \varvec{u}_{2}=\underset{1\le d \le D}{\hbox {col}}(\varvec{u}_{2,d})\sim N_{DR}(\varvec{0}, \varvec{V}_{2}), \\{} & {} \varvec{u}_{3}=\underset{1\le d \le D}{\hbox {col}}(\varvec{u}_{3,d})\sim N_{DRT}(\varvec{0}, \varvec{V}_{3}),\,\, \varvec{e}=\underset{1\le d \le D}{\hbox {col}}(\varvec{e}_{d})\sim N_{RT}(\varvec{0}, \varvec{V}_{e}). \end{aligned}$$

We can write model (B.1) in the population form

$$\begin{aligned} \varvec{y}=\varvec{X}\varvec{\beta }+\varvec{Z}_{1}\varvec{u}_{1}+\varvec{Z}_{2}\varvec{u}_{2}+\varvec{Z}_{3}\varvec{u}_{3}+\varvec{e}, \end{aligned}$$

(B.3)

where the vectors $\varvec{u}_1$, $\varvec{u}_2$, $\varvec{u}_3$ and $\varvec{e}$ are mutually independent. The variance matrix of $\varvec{y}$ is $\varvec{V}=\text{ var }(\varvec{y})=\underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_d)$, i.e.

$$\begin{aligned} \varvec{V}= \sigma _1^2\underset{1\le d \le D}{\hbox {diag}}(\varvec{1}_{RT}\varvec{1}_{RT}^\prime ) +\sigma _2^2\underset{1\le d \le D}{\hbox {diag}}\big (\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_T\varvec{1}_T^\prime )\big ) +\sigma _3^2\underset{1\le d \le D}{\hbox {diag}}\big (\underset{1\le r \le R}{\hbox {diag}}(\Omega _{dr}(\rho ))\big )+\varvec{V}_{e}. \end{aligned}$$

Let us define the $DRT\times (D+DR+DRT)$ matrix $\varvec{Z}=(\varvec{Z}_1,\varvec{Z}_2,\varvec{Z}_3)$ and the $(D+DR+DRT)\times 1$ vector $\varvec{u}=(\varvec{u}_1^\prime ,\varvec{u}_2^\prime ,\varvec{u}_3^\prime )^\prime$, with $\varvec{V}_u=\text{ var }(\varvec{u})=\text{ diag }(\varvec{V}_{1},\varvec{V}_{2},\varvec{V}_{3})$. We can write model (B.3) in the linear mixed model form

$$\begin{aligned} \varvec{y}=\varvec{X}\varvec{\beta }+\varvec{Z}\varvec{u}+\varvec{e}, \end{aligned}$$

If we assume that $\sigma _1^2>0$, $\sigma _2^2>0$, $\sigma _3^2>0$ and $\rho \ne 0$ are known, then the best linear unbiased estimator (BLUE) of $\varvec{\beta }$ and the best linear unbiased predictor (BLUP) of $\varvec{u}$ are

$$\begin{aligned} {\tilde{\varvec{\beta }}}= & {} \left( \sum _{d=1}^D\varvec{X}_d^{\prime }\varvec{V}_d^{-1}\varvec{X}_d\right) ^{-1}\left( \sum _{d=1}^D\varvec{X}_d^{\prime }\varvec{V}_d^{-1}\varvec{y}_d\right) , \\ \nonumber {\tilde{\varvec{u}}}= & {} \varvec{V}_u\varvec{Z}^\prime \varvec{V}^{-1}(\varvec{y}-\varvec{X}{\hat{\varvec{\beta }}}) \\ \nonumber= & {} \left( \begin{array}{ccc}\sigma _1^2\varvec{I}_{D}&{} \varvec{0}&{}\varvec{0}\\ \varvec{0}&{} \sigma _2^2\varvec{I}_{DR}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\sigma _3^2\Omega (\rho )\end{array}\right) \left( \begin{array}{c} \underset{1\le d \le D}{\hbox {diag}}(\varvec{1}_{RT}^{\prime }) \\ \underset{1\le d \le D}{\hbox {diag}}(\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime }))\\ \varvec{I}_{DRT} \end{array}\right) \underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_{d}^{-1}) \underset{1\le d \le D}{\hbox {col}}(\varvec{y}_d-\varvec{X}_d{\tilde{\varvec{\beta }}}) \\ \nonumber= & {} \left( \begin{array}{c} \sigma _1^2\underset{1\le d \le D}{\hbox {col}}\big (\varvec{1}_{RT}^\prime \varvec{V}_d^{-1}(\varvec{y}_d-\varvec{X}_d{\tilde{\varvec{\beta }}})\big )\\ \sigma _2^2\underset{1\le d \le D}{\hbox {col}}\big (\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_{T}^{\prime })\varvec{V}_d^{-1}(\varvec{y}_d-\varvec{X}_d{\tilde{\varvec{\beta }}})\big )\\ \sigma _3^2\underset{1\le d \le D}{\hbox {col}}\big (\Omega _d(\rho )\varvec{V}_d^{-1}(\varvec{y}_d-\varvec{X}_d{\tilde{\varvec{\beta }}})\big ) \end{array}\right) . \end{aligned}$$

(B.4)

The empirical versions, EBLUE of $\varvec{\beta }$ and EBLUP of $\varvec{u}$, are obtained by plugging estimators ${\hat{\sigma }}_1^2$, ${\hat{\sigma }}_2^2$, ${\hat{\sigma }}_3^2$ and ${\hat{\rho }}$ in the place of $\sigma _1^2$, $\sigma _2^2$, $\sigma _3^2$ and $\rho$, i.e.

$$\begin{aligned} {\hat{\varvec{\beta }}}=(\varvec{X}^{\prime }{\hat{\varvec{V}}}^{-1}\varvec{X})^{-1}\varvec{X}^\prime {\hat{\varvec{V}}}^{-1}\varvec{y},\quad {\hat{\varvec{u}}}={\hat{\varvec{V}}}_u\varvec{Z}^\prime {\hat{\varvec{V}}}^{-1}\left( \varvec{y}-\varvec{X}{\hat{\varvec{\beta }}}\right) , \end{aligned}$$

(B.5)

where

$$\begin{aligned} {\hat{\varvec{V}}}_u= & {} \underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_{ud})=\text{ diag }({\hat{\sigma }}_1^2\varvec{I}_D,{\hat{\sigma }}_2^2\varvec{I}_{DR},{\hat{\sigma }}_3^2\Omega (\rho )), \\ {\hat{\varvec{V}}}= & {} \underset{1\le d \le D}{\hbox {diag}}(\varvec{V}_{d})= {\hat{\sigma }}_1^2\underset{1\le d \le D}{\hbox {diag}}(\varvec{1}_{RT}\varvec{1}_{RT}^\prime ) +{\hat{\sigma }}_2^2\underset{1\le d \le D}{\hbox {diag}}\big (\underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_T\varvec{1}_T^\prime )\big ) +{\hat{\sigma }}_3^2\Omega (\rho )+\varvec{V}_{e}. \end{aligned}$$

We are interested in predicting the linear combination of fixed and random effects $\mu _{drt}=\varvec{x}_{drt}\varvec{\beta }+u_{1,d}+u_{2,dr}+ u_{3,drt}$. If the variance components are known, the BLUP of $\mu _{drt}$ is ${\tilde{\mu }}_{drt}=\varvec{x}_{drt}{\tilde{\varvec{\beta }}}+{\tilde{u}}_{1,d}+ {\tilde{u}}_{2,dr}+ {\tilde{u}}_{3,drt}$. The corresponding EBLUP of $\mu _{drt}$ is obtained by substituting the estimators of the variance components $\varvec{\theta }=(\sigma _1^2, \sigma _2^2, \sigma _3^2, \rho )$ and it has the form

$$\begin{aligned} {\hat{\mu }}_{drt}=\varvec{x}_{drt}{\hat{\varvec{\beta }}}+{\hat{u}}_{1,d}+{\hat{u}}_{2,dr}+{\hat{u}}_{3,drt}, \end{aligned}$$

where ${\hat{\varvec{\beta }}}$ and ${\hat{\varvec{u}}}$ are given in (B.5). Similarly as before, we define the BLUP and EBLUP vectors

$$\begin{aligned}{} & {} {\tilde{\varvec{\mu }}}_{dr}=\underset{1\le t \le T}{\hbox {col}}({\tilde{\mu }}_{drt}),\,\, {\tilde{\varvec{\mu }}}_{d}=\underset{1\le r \le R}{\hbox {col}}({\tilde{\varvec{\mu }}}_{dr}),\,\,\, {\tilde{\varvec{\mu }}}=\underset{1\le d \le D}{\hbox {col}}({\tilde{\varvec{\mu }}}_{d}). \\{} & {} {\hat{\varvec{\mu }}}_{dr}=\underset{1\le t \le T}{\hbox {col}}({\hat{\mu }}_{drt}),\,\, {\hat{\varvec{\mu }}}_{d}=\underset{1\le r \le R}{\hbox {col}}({\hat{\varvec{\mu }}}_{dr}),\,\,\, {\hat{\varvec{\mu }}}=\underset{1\le d \le D}{\hbox {col}}({\hat{\varvec{\mu }}}_{d}). \end{aligned}$$

Let $\varvec{P}_{\textsc {x}}=\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}$ be the projection matrix in the p-dimensional subspace given by the column vectors of $\varvec{X}$ in the metric of $\varvec{V}^{-1}$, and define $\varvec{P}=\varvec{V}^{-1}(\varvec{I}-\varvec{P}_{\textsc {x}})=\varvec{V}^{-1}-\varvec{V}^{-1}\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}$ as the projection matrix in the residuals complement subspace of $\varvec{y}$. Then, we may write the model BLUP of $\varvec{\mu }$ as

$$\begin{aligned} {\tilde{\varvec{\mu }}}= & {} \varvec{X}{\hat{\varvec{\beta }}}+\varvec{Z}{\tilde{\varvec{u}}}=\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{y}+\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{V}^{-1}(\varvec{y}-\varvec{X}{\hat{\varvec{\beta }}}) \\= & {} \left\{ \varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}+\varvec{Z}\varvec{V}_{u} \varvec{Z}^{\prime }\varvec{V}^{-1}[\varvec{I}-\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1} \varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}]\right\} \varvec{y}\\= & {} [\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1} \varvec{X}^{\prime }\varvec{V}^{-1}+\varvec{Z}\varvec{V}_{u}\varvec{Z}^{\prime }\varvec{V}^{-1}(\varvec{I}- \varvec{P}_{\textsc {x}})]\varvec{y}\\= & {} [\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}+(\varvec{V}-\varvec{V}_{e})\varvec{V}^{-1}(\varvec{I}-\varvec{P}_{\textsc {x}})]\varvec{y}\\= & {} \varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{y}+(\varvec{I}-\varvec{P}_{\textsc {x}})\varvec{y}-\varvec{V}_{e}\varvec{V}^{-1}(\varvec{I}-\varvec{P}_{\textsc {x}})\varvec{y}\\= & {} \varvec{P}_{\textsc {x}}\varvec{y}+(\varvec{I}-\varvec{P}_{\textsc {x}})\varvec{y}-\varvec{V}_{e}\varvec{V}^{-1}(\varvec{I}-\varvec{P}_{\textsc {x}})\varvec{y}=\varvec{y}-\varvec{V}_{e}\varvec{V}^{-1}(\varvec{I}-\varvec{P}_{\textsc {x}})\varvec{y}=\varvec{y}-\varvec{V}_{e}\varvec{P}\varvec{y}. \end{aligned}$$

1.2 B.2 Estimation of variance component parameters

This section gives a Fisher-scoring algorithm to calculate the residual maximum likelihood (REML) estimator of $\varvec{\theta }=(\theta _1,\theta _2,\theta _3,\theta _4)^\prime =(\sigma _1^2, \sigma _2^2, \sigma _3^2,\rho )^\prime$. The REML log-likelihood is

$$\begin{aligned} {l}_{reml}(\varvec{\theta })=-\frac{DRT-p}{2}\log 2\pi +\frac{1}{2}\log |\varvec{X}^{\prime }\varvec{X}|-\frac{1}{2}\log |\varvec{V}| - \frac{1}{2}\log |\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X}| -\frac{1}{2}\,\varvec{y}^{\prime }\varvec{P}\varvec{y}, \end{aligned}$$

$\varvec{P}=\varvec{V}^{-1}-\varvec{V}^{-1}\varvec{X}(\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}^{-1}$. It holds that

$$\begin{aligned} \varvec{V}_1= & {} \frac{\partial \varvec{V}}{\partial \theta _1}=\underset{1\le d \le D}{\hbox {diag}}(\varvec{1}_{RT}\varvec{1}_{RT}^\prime ),\,\,\, \varvec{V}_2=\frac{\partial \varvec{V}}{\partial \theta _2}=\underset{1\le d \le D}{\hbox {diag}}\big ( \underset{1\le r \le R}{\hbox {diag}}(\varvec{1}_{T}\varvec{1}_{T}^{\prime })\big ),\,\,\, \\ \varvec{V}_3= & {} \frac{\partial \varvec{V}}{\partial \sigma _3^2}=\underset{1\le d \le D}{\hbox {diag}}(\underset{1\le r \le R}{\hbox {diag}}(\Omega _{dr}(\rho )),\quad \varvec{V}_4=\frac{\partial \varvec{V}}{\partial \rho }=\sigma _3^2\underset{1\le d \le D}{\hbox {diag}}(\underset{1\le r \le R}{\hbox {diag}}(\dot{\Omega }_{dr}(\rho )), \end{aligned}$$

where the derivative of matrix $\Omega _d(\rho )$ with respect to $\rho$ is

$$\begin{aligned} \dot{\Omega }_{dr}(\rho )= & {} \frac{1}{1-\rho ^2}\left( \begin{array}{ccccc} 0&{}1&{}\ldots &{}\ldots &{}(T-1)\rho ^{T-2}\\ 1&{}0&{}\ddots &{}&{}(T-2)\rho ^{T-3}\\ \vdots &{}\ddots &{}\ddots &{}\ddots &{}\vdots \\ (T-2)\rho ^{T-3}&{}&{}\ddots &{}0&{}1\\ (T-1)\rho ^{T-2}&{}\ldots &{}\ldots &{}1&{}0 \end{array}\right) + \frac{2\rho \Omega _{dr}(\rho )}{1-\rho ^2}. \end{aligned}$$

Further, we have

$$\begin{aligned} \varvec{P}_a=\frac{\partial \varvec{P}}{\partial \theta _a}=-\varvec{P}\frac{\partial \varvec{V}}{\partial \theta _a}\varvec{P}=-\varvec{P}\varvec{V}_a\varvec{P},\quad a=1,2,3,4. \end{aligned}$$

By taking derivatives of ${l}_{reml}$ with respect to $\theta _a$, we have the elements of the score vector $\varvec{S}=\varvec{S}(\varvec{\theta })= (S_1,S_2,S_3,S_4)^\prime$, i.e.

$$\begin{aligned} S_a=\frac{\partial {l}_{reml}}{\partial \theta _a}=-\frac{1}{2}\hbox {tr}(\varvec{P}\varvec{V}_a)+\frac{1}{2}\varvec{y}^{\prime }\varvec{P}\varvec{V}_a\varvec{P}\varvec{y},\quad a=1,2,3,4. \end{aligned}$$

By taking second derivatives with respect to $\theta _a$ and $\theta _b$, taking expectations and changing the sign, we obtain the components of the Fisher information matrix $\varvec{F}= \varvec{F}(\varvec{\theta }) = \left( F_{ab}\right) _{a,b=1,2,3,4}$, where

$$\begin{aligned} F_{ab}=\frac{1}{2}\hbox {tr}(\varvec{P}\varvec{V}_a\varvec{P}\varvec{V}_b),\quad a,b=1,2,3,4. \end{aligned}$$

The updating formula of the Fisher-scoring algorithm is

$$\begin{aligned} \varvec{\theta }^{(k+1)}=\varvec{\theta }^{(k)}+\varvec{F}^{-1}(\varvec{\theta }^{(k)})\varvec{S}(\varvec{\theta }^{(k)}). \end{aligned}$$

As algorithm seeds, we may take $\theta _1^{(0)}=\theta _2^{(0)}=\theta _3^{(0)}=S^2/3$, where $S^2=\frac{1}{DRT-p}(\varvec{y}-\varvec{X}\check{\varvec{\beta }})^{\prime }\varvec{V}_e^{-1}(\varvec{y}-\varvec{X}\check{\varvec{\beta }})$ and $\check{\varvec{\beta }}=(\varvec{X}^{\prime }\varvec{V}_e^{-1}\varvec{X})^{-1}\varvec{X}^{\prime }\varvec{V}_e^{-1}\varvec{y}$ and $\theta _4^{(0)}=0$. The REML estimator of $\varvec{\beta }$ is

$$\begin{aligned} \hat{{\varvec{\beta }}}=({\varvec{X}}^{\prime }{\hat{\varvec{V}}}^{-1}{\varvec{X}})^{-1}{\varvec{X}}^{\prime }{\hat{\varvec{V}}}^{-1}{\varvec{y}}, \end{aligned}$$

where ${\hat{\varvec{V}}}=\varvec{V}({\hat{\varvec{\theta }}})$ was defined above. Under regularity assumptions, the asymptotic distributions of ${\hat{\varvec{\theta }}}$ and ${\hat{\varvec{\beta }}}$ are

$$\begin{aligned} {\hat{\varvec{\theta }}}\sim N_4(\varvec{\theta }, \varvec{F}^{-1}(\varvec{\theta })),\quad {\hat{\varvec{\beta }}}\sim N_p(\varvec{\beta }, (\varvec{X}^{\prime }\varvec{V}^{-1}\varvec{X})^{-1}). \end{aligned}$$

Asymptotic confidence intervals, at the level $1-\alpha$, for $\theta _a$ and $\beta _j$ are

$$\begin{aligned} {\hat{\theta }}_a\pm z_{\alpha /2}\,\nu _{aa}^{1/2},\,\, a=1,2,3,4,\quad {\hat{\beta }}_{j}\pm z_{\alpha /2}\,q_{jj}^{1/2},\,\, j=1,\ldots ,p, \end{aligned}$$

where $\varvec{F}^{-1}({\hat{\varvec{\theta }}})=(\nu _{ab})_{a,b=1,2,3,4}$, $(\varvec{X}^{\prime }\varvec{V}^{-1}({\hat{\varvec{\theta }}})\varvec{X})^{-1}=(q_{ij})_{i,j=1,\ldots ,p}$ and $z_{\alpha }$ is the $\alpha$-quantile of the standard normal distribution. If ${\hat{\beta }}_j=\beta _0$, then the p-value for testing $H_0:\,\beta _j=0$ is

$$\begin{aligned} p=2P_{H_0}({\hat{\beta }}_j>|\beta _0|)=2P(N(0,1)> |\beta _0|/\sqrt{q_{jj}}\,). \end{aligned}$$

C Appendix: Spanish provinces

Table 9 presents the list of Spanish Provinces with their corresponding acronyms.

Table 9 List of Spanish Provinces with corresponding acronyms