Hybrid twin of RTM process at the scarce data limit

Abstract

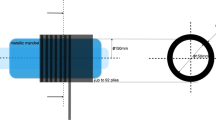
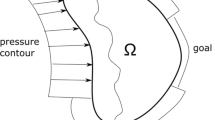
To ensure correct filling in the resin transfer molding (RTM) process, adequate numerical models have to be developed in order to correctly capture its physics, so that this model can be considered for process optimization. However, the complexity of the phenomenon often makes it impossible for numerical models to accurately predict its behavior, limiting its usage. To overcome this limitation, numerical models are enriched with measured data to ensure their correct predictability. Nevertheless, the data used is often limited due to practical constraints, such as a limited number of sensors or the high costs of experimental campaigns. In this context, the present paper demonstrates the implementation of a numerical model enriched with data, called Hybrid Twin applied to the RTM process when few sensors are considered in the mold to be injected. The performances of the developed hybrid twin are tested in a virtual test for the injection of a 2D mold, where the hybrid twin constructed using a simplified numerical model allows to accurately predict a complex model’s resin flow-front over its entire time history.

Appendix A: Approximation of sparse data; the sparse - PGD

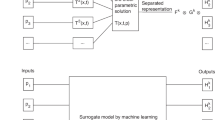
In real-life situations, having access to abundant and structured data is not always possible. In this situation a direct application of the PGD method is unfortunately not possible. To solve this limitation, in [33] an extension of the PGD method was proposed to deal with unstructured data and overcome in this sense the curse of dimensionality. This method is called sparse-PGD.

To illustrate the main ideas on how to determine the PGD decomposition for the case of sparse data, an approximation of a function $f(\nu _{1},\nu _{2}) \in \mathbb {R}^{2} \rightarrow \mathbb {R}$ is considered here, where its value is known over some P sampling points. In this case, the PGD decomposition is simply determined by solving the following minimization problem:

$$\begin{aligned} \text {min} \left\| { u_{m}(\nu _{1},\nu _{2}) - f(\nu _{1},\nu _{2}) }\right\| _{2}^{2} \end{aligned}$$

(A1)

with $\left\| {\bullet }\right\| _{2}^{2} = \int _{{\Omega }} (\bullet )^{2} \ d\nu _{1} d\nu _{2}$ and ${\Omega } = {\Omega }_{\nu _{1}} \times {\Omega }_{\nu _{2}}$. From the last expression, $u_{m}(\nu _{1},\nu _{2})$ corresponds to the PGD decomposition of $f(\nu _{1},\nu _{2})$, where m terms are considered, this is:

$$\begin{aligned} u_{m}(\nu _{1},\nu _{2}) = \sum \limits _{k=1}^{m} X_{1}^{k}(\nu _{1}) X_{2}^{k}(\nu _{2}) \end{aligned}$$

(A2)

with $X_{1}^{k}(\nu _{1})$ and $X_{2}^{k}(\nu _{2})$, $\forall k \in [1, ... , m]$ the separate variable functions to be determined. Here the PGD functions are not interpolated using, for example, the Finite Element Method (FEM) [3], in this case the functions used are globally defined over the whole interval considered for each variable. The functions that can be used could be for instance, Kriging interpolants functions [33] or radial basis functions [47], just to cite a few. In this context, the PGD functions for the 2D case are constructed as follows:

$$\begin{aligned} X_{1}^{k}(\nu _{1})= & {} \sum \limits _{j=1}^{n_{cp}} {N_{j}^{k}}(\nu _{1}) a_{\nu _{1},j}^{k} = ( \underline{\varvec{N}} _{\nu _{1}}^{k})^{T} \underline{\varvec{a}} _{\nu _{1}}^{k} \end{aligned}$$

(A3)

$$\begin{aligned} X_{2}^{k}(\nu _{2})= & {} \sum \limits _{j=1}^{n_{cp}} {N_{j}^{k}}(\nu _{2}) a_{\nu _{2},j}^{k} = ( \underline{\varvec{N}} _{\nu _{2}}^{k})^{T} \underline{\varvec{a}} _{\nu _{2}}^{k} \end{aligned}$$

(A4)

where ${N_{j}^{k}}(\nu _{i})$ and $a^{k}_{\nu _{i},j}$ denotes the shape functions and its respective nodal value for variable $\nu _{i}$ evaluated on the control point j at PGD mode k. If the shape functions are considered to be radial functions of multiquadric type [47], they are given as follows:

$$N_{j}(\nu _{i}) = \sqrt{ c^{2} \left[ (\nu _{i})_{j} - (\nu _{i}) \right] ^{2} + 1 } \ \ \text{for} \ \ j \in [1, ... , n_{cp}] \ \text {and} \ i \in [1,2] $$

(A5)

with $(\nu _{i})_{j}$ the coordinate of the control point associated to variable $\nu _{i}$ and c a parameter that drives the shape of the function, chosen such as it allows a non over-fitted PGD approximation. These PGD functions are classically determined one after the other in an incremental way, also denoted Greedy process. That is, one considers as known $m-1$ terms of the decomposition Eq. A2, and seeks the determination of the mode m, i.e., $u_{m}(\nu _{1},\nu _{2}) = u_{m-1}(\nu _{1},\nu _{2}) + X_{1}^{m}(\nu _{1}) X_{2}^{m}(\nu _{2})$. In this case one reformulates Eq. A1 as follows:

$$ \left\{ X_{1}^{m}(\nu _{1}) , X_{2}^{m}(\nu _{2}) \right\} = \underset{ \lbrace X_{1}^{m}(\nu _{1}) , X_{2}^{m}(\nu _{2}) \rbrace }{\text {arg min}} \Big \Vert X_{1}^{m}(\nu _{1}) X_{2}^{m}(\nu _{2}) - f_{\text {res}}(\nu _{1},\nu _{2}) \Big \Vert _{2}^{2} $$

(A6)

with $f_{\text {res}}(\nu _{1},\nu _{2}) = f(\nu _{1},\nu _{2}) - u_{m-1}(\nu _{1},\nu _{2})$. By minimizing the expression Eq. A6 yields:

$\forall {w}^{*}(\nu _{1},\nu _{2}),$

$$\begin{aligned} \int _{{\Omega }} {w}^{*}(\nu _{1},\nu _{2}) \left[ X_{1}^{m}(\nu _{1}) X_{2}^{m}(\nu _{2}) - f_{\text {res}}(\nu _{1},\nu _{2}) \right] d\nu _{1} d\nu _{2} = 0 \end{aligned}$$

(A7)

However since the information is just known at P sampling points $( (\nu _{1})_{i},(\nu _{2})_{i}), \forall i \in [1,...,P]$, the test function ${w}^{*}(\nu _{1},\nu _{2})$ is expressed as a set of Dirac delta functions collocated at these points, this is:

$$\begin{aligned}{} & {} {w}^{*}(\nu _{1},\nu _{2}) = {u}^{*}(\nu _{1},\nu _{2}) \sum \limits _{i=1}^{P} \delta ( (\nu _{1})_{i}, (\nu _{2})_{i} )\\= & {} \left[ {X_{1}}^{*}(\nu _{1}) X_{2}^{m}(\nu _{2}) + X_{1}^{m}(\nu _{1}) {X_{2}}^{*}(\nu _{2}) \right] \sum \limits _{i=1}^{P} \delta ((\nu _{1})_{i}, (\nu _{2})_{i})\nonumber \end{aligned}$$

(A8)

where $\delta ( (\nu _{1})_{i}, (\nu _{2})_{i} )$ here denotes the delta Dirac function evaluated at points $((\nu _{1})_{i}, (\nu _{2})_{i})$. By replacing ${w}^{*}(\nu _{1},\nu _{2})$ by its sparse version of Eqs. A8 into A7, and developing the expression yields the problems that must be solved to obtain the PGD functions:

Compute $X_{1}^{m}(\nu _{1})$ by solving:

$$ \int _{{\Omega }} X_{1}^{*}(\nu_1) \sum \limits _{i=1}^{P} \left[ X_{1}^{m}(\nu _{1}) X_{2}^{m}(\nu _{2})^{2} - X_{2}^{m}(\nu _{2}) f_{\text {res}}(\nu _{1},\nu _{2}) \right] \delta ( (\nu _{1})_{i},(\nu _{2})_{i} ) \ d\nu _{1} d\nu _{2} = 0 $$

(A9)

Compute $X_{2}^{m}(\nu _{2})$ by solving:

$$ \int _{{\Omega }} X_{2}^{*}(\nu_2) \sum \limits _{i=1}^{P} \left[ X_{2}^{m}(\nu _{2}) X_{1}^{m}(\nu _{1})^{2} - X_{1}^{m}(\nu _{1}) f_{\text {res}}(\nu _{1},\nu _{2}) \right] \delta ((\nu _{1})_{i},(\nu _{2})_{i} ) \ d\nu _{1} d\nu _{2} = 0 $$

(A10)

Equations A9 and A10 should be solved alternatively following a fixed-point strategy, where for the resolution of Eq. A9 one considers known the value of function $X_{2}^{m}(\nu _{2})$, and for the resolution of Eq. A10 one considers $X_{1}^{m}(\nu _{1})$ known. To illustrate this resolution, but only for the determination of $X_{1}^{m}(\nu _{1})$, lets define:

$$\begin{aligned} \underline{\underline{\varvec{A}}}^{kl}_{(\nu _{1})_{i}}= & {} \underline{\varvec{N}} _{\nu _{1}}^{k}((\nu _{1})_{i}) \otimes \underline{\varvec{N}} _{\nu _{1}}^{l}((\nu _{1})_{i}) \nonumber \\ \underline{\underline{\varvec{A}}}^{kl}_{(\nu _{2})_{i}}= & {} \underline{\varvec{N}} _{\nu _{2}}^{k}((\nu _{2})_{i}) \otimes \underline{\varvec{N}}_{\nu _{2}}^{l}((\nu _{2})_{i}) \end{aligned}$$

(A11)

where $\otimes$ denotes a Kronecker tensor product. By using the operators defined in Eq. A11 and approximations of Eq. A3 and A4, one obtains the following system of equations needed to be solved to compute the discretized DOFs related to $X_{1}^{m}(\nu _{1})$ ($\underline{\varvec{a}} ^{m}_{\nu _{1}}$).

$$\begin{aligned} \underline{\underline{\varvec{M}}}_{\nu _{1}} \underline{\varvec{a}} ^{m}_{\nu _{1}} = \underline{\varvec{f}} _{\nu _{1}} \end{aligned}$$

(A12)

where the matrix and vector are respectively given as:

$$\begin{aligned} \underline{\underline{\varvec{M}}}_{\nu _{1}}= & {} \sum _{i=1}^{P} \left[ ( \underline{\varvec{a}} ^{m}_{\nu _{2}})^{T} \underline{\underline{\varvec{A}}}^{m m}_{(\nu _{2})_{i}} \underline{\varvec{a}} ^{m}_{\nu _{2}} \right] \underline{\underline{\varvec{A}}}_{(\nu _{1})_{i}} \nonumber \\ \underline{\varvec{f}} _{\nu _{1}}= & {} \sum _{i=1}^{P} f_{\text {res}}((\nu _{1})_{i},(\nu _{2})_{i}) \underline{\varvec{N}} _{\nu _{1}}^{m}((\nu _{1})_{i}) \underline{\varvec{N}} _{\nu _{2}}^{m}((\nu _{2})_{i})^{T} \underline{\varvec{a}} ^{m}_{\nu _{2}} \end{aligned}$$

(A13)

The extension of the above method to the case of a multidimensional function is straightforward and follows the same methodology, for this case one has:

$$\begin{aligned} \text {min} \left\| { u_{m}(\nu _{1},\nu _{2}, ... \ , \nu _{n}) - f(\nu _{1},\nu _{2}, ... \ , \nu _{n}) }\right\| _{2}^{2} \end{aligned}$$

(A14)

where:

$$\begin{aligned} u_{m}(\nu _{1},\nu _{2}, ... \ , \nu _{n}) = \sum _{k=1}^{m} X_{1}^{k}(\nu _{1}) X_{2}^{k}(\nu _{2}) \ ... \ {X_{n}^{k}}(\nu _{n}) \end{aligned}$$

(A15)

with $\left\| {\bullet }\right\| _{2}^{2} = \int _{{\Omega }} (\bullet )^{2} \ d \nu _{1} d \nu _{2} \ ... \ d \nu _{n}$, where for this case ${\Omega } = {\Omega }_{\nu _{1}} \times {\Omega }_{\nu _{2}} \times ... \times {\Omega }_{\nu _{n}}$. For this case the same resolution procedure by the fixed-point technique must be applied. The determination of the nodal values of the m PGD function corresponding to parameter $\nu _{q}$ with $q \in [1, ... , n]$ is simply given as:

$$\begin{aligned} \underline{\underline{\varvec{M}}}_{\nu _{q}}\underline{\varvec{a}} _{\nu _{q}}^{m} = \underline{\varvec{f}} _{\nu _{q}} \end{aligned}$$

(A16)

where the respective matrix and vector are computed as follows:

$$\begin{aligned} \underline{\underline{\varvec{M}}}_{\nu _{q}}= & {} \sum \limits _{i=1}^{P} \underline{\underline{\varvec{A}}}^{m m}_{(\nu _{q})_{i}} \prod _{\forall j \ne q} \left[ ( \underline{\varvec{a}} _{\nu _{j}}^{m})^{T} \underline{\underline{\varvec{A}}}^{m m}_{(\nu _{j})_{i}} \underline{\varvec{a}} _{\nu _{j}}^{m} \right] \nonumber \\ \underline{\varvec{f}} _{\nu _{q}}= & {} \sum \limits _{i=1}^{P} f_{\text {res}}( \underline{{\nu }}_{i} ) \underline{\varvec{N}} _{\nu _{q}}^{m}((\nu _{q})_{i}) \prod _{\forall j \ne q} \underline{\varvec{N}} _{\nu _{j}}^{m}((\nu _{j})_{i})^{T} \underline{\varvec{a}} _{\nu _{j}}^{m} \end{aligned}$$

(A17)

with $f_{\text {res}}(\nu _{1},\nu _{2}, ... \ , \nu _{n}) = f(\nu _{1},\nu _{2}, ... \ , \nu _{n}) - u_{m-1}(\nu _{1},\nu _{2},$ $... \ , \nu _{n})$.