Skip to main content
SpringerLink
Log in

Further results on tensor nuclear norms

  • Published:
Calcolo Aims and scope Submit manuscript

Abstract

Several basic properties of tensor nuclear norms are established in [S. Friedland and L.-H. Lim, Math. Comp., 87 (2018), pp. 1255–1281]. In this work, we give further studies on tensor nuclear norms. We present some special cases of tensor nuclear decompositions. We list some examples to show basic relationships among tensor rank, orthogonal rank and nuclear rank. Spectral and nuclear norms of Hermitian tensors are studied. We show that spectral and nuclear norms of real Hermitian decomposable tensors do not depend on the choice of base field. At last, we extend matrix polar decompositions to the tensor case, which is the product of a Hermitian tensor and a tensor whose spectral norm equals one. That is, we establish a link between any tensor and a Hermitian tensor. Bounds of nuclear rank are given based on tensor polar decompositions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

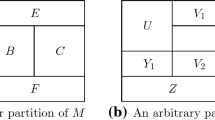
  1. Similarly, we can define the contraction between two tensors on any modes. In this paper, we only need the contraction on the first few modes. For convenience, we define \(\mathcal {A}(\mathcal {B})\) in this fashion.

References

  1. Adkins, W.A., Weintraub, S.H.: Algebra: An Approach via Module Theory, vol. 136. Springer, New York (2012)

    MATH  Google Scholar 

  2. Banach, S.: Über homogene Polynome in (L2). Stud. Math. 7(1), 36–44 (1938)

    Article  MATH  Google Scholar 

  3. Candès, E.J., Recht, B.: Exact matrix completion via convex optimization. Found. Comput. Math. 9(6), 717 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  4. Candès, E.J., Tao, T.: The power of convex relaxation: near-optimal matrix completion. IEEE Trans. Inf. Theory 56(5), 2053–2080 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  5. De Silva, V., Lim, L.-H.: Tensor rank and the ill-posedness of the best low-rank approximation problem. SIAM J. Matrix Anal. Appl. 30(3), 1084–1127 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  6. Derksen, H.: On the nuclear norm and the singular value decomposition of tensors. Found. Comput. Math. 16(3), 779–811 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  7. Derksen, H., Friedland, S., Lim, L.-H., Wang, L.: Theoretical and computational aspects of entanglement (2017). arXiv preprint arXiv:1705.07160

  8. Friedland, S.: Best rank one approximation of real symmetric tensors can be chosen symmetric. Front. Math. Chin. 8(1), 19–40 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  9. Friedland, S., Lim, L.-H.: Nuclear norm of higher-order tensors. Math. Comput. 87(311), 1255–1281 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  10. Horn, R.A., Johnson, C.R.: Matrix Analysis. Cambridge University Press, Cambridge (2012)

    Book  Google Scholar 

  11. Hu, S.: Relations of the nuclear norm of a tensor and its matrix flattenings. Linear Algebra Appl. 478, 188–199 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Jiang, B., Li, Z., Zhang, S.: Characterizing real-valued multivariate complex polynomials and their symmetric tensor representations. SIAM J. Matrix Anal. Appl. 37(1), 381–408 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kolda, T.G.: Orthogonal tensor decompositions. SIAM J. Matrix Anal. Appl. 23(1), 243–255 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  14. Krijnen, W.P., Dijkstra, T.K., Stegeman, A.: On the non-existence of optimal solutions and the occurrence of “degeneracy’’ in the CANDECOMP/PARAFAC model. Psychometrika 73(3), 431–439 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  15. Kruskal, J.B.: Three-way arrays: rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics. Linear Algebra Appl. 18(2), 95–138 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  16. Li, Z.: Bounds on the spectral norm and the nuclear norm of a tensor based on tensor partitions. SIAM J. Matrix Anal. Appl. 37(4), 1440–1452 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  17. Li, Z., Nakatsukasa, Y., Soma, T., Uschmajew, A.: On orthogonal tensors and best rank-one approximation ratio. SIAM J. Matrix Anal. Appl. 39(1), 400–425 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  18. Lim, L.-H.: Singular values and eigenvalues of tensors: a variational approach. In: 1st IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, pages 129–132. IEEE (2005)

  19. Lim, L.-H., Comon, P.: Blind multilinear identification. IEEE Trans. Inf. Theory 60(2), 1260–1280 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  20. Ni, G.: Hermitian tensor and quantum mixed state (2019). arXiv preprint arXiv:1902.02640

  21. Nie, J.: Symmetric tensor nuclear norms. SIAM J. Appl. Algebra Geom. 1(1), 599–625 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  22. Nie, J., Yang, Z.: Hermitian tensor decompositions. SIAM J. Matrix Anal. Appl. 41(3), 1115–1144 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  23. Qi, L.: The best rank-one approximation ratio of a tensor space. SIAM J. Matrix Anal. Appl. 32(2), 430–442 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  24. Recht, B., Fazel, M., Parrilo, P.A.: Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 52(3), 471–501 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  25. Sidiropoulos, N.D., Bro, R.: On the uniqueness of multilinear decomposition of N-way arrays. J. Chemometr.: A J. Chemometr. Soc. 14(3), 229–239 (2000)

    Article  Google Scholar 

  26. Taylor, A.E.: The norm of a real linear transformation in minkowski space. Enseign. Math. 2(4), 101–107 (1958)

    MathSciNet  MATH  Google Scholar 

  27. Vannieuwenhoven, N., Nicaise, J., Vandebril, R., Meerbergen, K.: On generic nonexistence of the Schmidt-Eckart-Young decomposition for complex tensors. SIAM J. Matrix Anal. Appl. 35(3), 886–903 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  28. Yuan, M., Zhang, C.-H.: On tensor completion via nuclear norm minimization. Found. Comput. Math. 16(4), 1031–1068 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  29. Zeng, C.: Rank properties and computational methods for orthogonal tensor decompositions. J. Sci. Comput. 94(1), 6 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  30. Zhang, T., Golub, G.H.: Rank-one approximation to high order tensors. SIAM J. Matrix Anal. Appl. 23(2), 534–550 (2001)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work was partially supported by the National Natural Science Foundation of China (12201319) and the Fundamental Research Funds for the Central Universities, Nankai University (63231142).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences and LPMC, Nankai University, Tianjin, China

    Chao Zeng

Authors
  1. Chao Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Chao Zeng is the single author of the manuscript and responsible for this work.

Corresponding author

Correspondence to Chao Zeng.

Ethics declarations

Conflict of interest

The author declares no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zeng, C. Further results on tensor nuclear norms. Calcolo 60, 34 (2023). https://doi.org/10.1007/s10092-023-00528-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10092-023-00528-2

Keywords

Mathematics Subject Classification

Search

Navigation