Public–Private Collusion

Abstract

We study collusion between a public firm and a private firm facing linear demand and quadratic costs. We characterize the collusive outcome that results from Nash bargaining and compare it to the non-cooperative outcome. If the public firm’s taste for consumer surplus is mild, both firms reduce output (as in a private duopoly). If it is intermediate, while the public firm reduces output, the private firm expands output to such an extent that total output increases. If it is strong, the private firm’s output expansion does not compensate for the public firm’s output contraction, and thus total output decreases. We also characterize collusion sustainability, and assess the impact of relative bargaining power, degree of cost convexity, public firm’s taste for total surplus, and cost asymmetry. We conclude that, by reducing the productive inefficiency that is caused by the public firm being more expansionary, collusion may lead to higher profits and consumer surplus.

1 Introduction

Agreements between competitors to suppress rivalry are generally unlawful, but there are two important exceptions in many countries: export cartels and agricultural cartels. These are frequently exempt (explicitly or implicitly) from antitrust laws due to their arguable benefits to society. In this paper, we examine a kind of cartel for which there are typically no explicit exemptions, although, in theory, they may benefit consumers and society as a whole: cartels that include a firm with a significant preference for consumer surplus. A prominent example is the case of a public firm that colludes with the objective of better serving consumers, directly through low prices or indirectly through high profits that revert to households. Philipson and Posner (2009) argued against antitrust exemptions in the not-for-profit sector; but our results suggest that case-by-case treatment of cartels that involve public and private firms may be considered.

There are numerous markets where public firms compete with private firms, giving rise to specific concerns and challenges to competition policy and cartel prosecution. Examples of cartel cases where state-owned firms were convicted are plenty and can be traced back to at least 1997 when the Spanish Competition Authority fined a price-fixing cartel in the dairy industry that was led by a state-owned firm.¹ Many cases have occurred in transportation industries;² but there were also cartel convictions that have involved state-owned enterprises in: banking in Tunisia and Portugal;³ cement⁴ and glucose in Egypt; jewelry stores in China; and waste management in Iceland (OECD, 2013, p. 81; Healey, 2020, pp. 8-9).

Despite this evidence of cartels involving public and private firms, the economic literature on this type of cooperation is lacking. We contribute to filling this gap by studying collusion between a public firm and a private firm in a Cournot duopoly with homogeneous goods, linear demand, and quadratic cost functions. The two firms are assumed to be symmetric in every respect except in their objectives: While the private firm maximizes its own profit, the public firm maximizes a weighted sum of its own profit and consumer surplus.

The collusive agreement, reached through Nash bargaining, qualitatively depends on whether the public firm’s preference for consumer surplus is mild, intermediate, or strong. If it is mild, both firms reduce output (as in a private duopoly). If it is intermediate, while the public firm reduces output, the private firm expands output to such an extent that total output increases. If it is strong, the output expansion by the private firm does not compensate for the output contraction by the public firm, and thus total output decreases.

Of course, both firms are better off under collusion than under competition (otherwise they would reject the agreement). This means that the private firm’s profit increases, while the public firm benefits from an increase in profit and/or an increase in consumer surplus. Since consumer surplus increases only if the public firm’s preference for consumer surplus is intermediate (consumer surplus increases if and only if total output increases), the public firm’s profit necessarily increases if its preference for consumer surplus is mild or strong. We also find that total surplus increases unless the public firm’s preference for consumer surplus is mild. The same applies to the sum of consumer surplus with the public firm’s profit, which should at least partially revert to households in the form of lower taxes.

In light of these results, competition authorities should be careful when analyzing cartel cases that involve public firms, since, depending on the public firm’s objective, collusion may increase or decrease both consumer surplus and total surplus.

1.1 Related Literature

Collusion between a public (welfare-maximizing) firm and a private (profit-maximizing) firm was first studied by Wen and Sasaki (2001), who concluded that the public firm contracts output (for collusion to benefit the private firm) while the private firm expands output (for collusion to benefit the public firm). They considered a Cournot supergame with homogeneous goods and constant marginal costs (symmetric across firms) with capacity constraints – which rule out productive inefficiency and imply that maximization of total surplus is equivalent to maximization of total output or consumer surplus. Hence, their assumption that the public firm maximizes total surplus guarantees that collusion not only increases total surplus (otherwise, the public firm would not be willing to collude) but also total output and consumer surplus. Wen and Sasaki (2001) characterized the socially optimal collusive agreement (among those that are sustainable), with exogenous and endogenous production capacities.

To the best of our knowledge, the only other paper on collusion between public and private firms is the recent contribution by Haraguchi and Matsumura (2018). They allow cost asymmetry and product differentiation (while maintaining the assumptions of linear demand, constant marginal cost, and total surplus maximization by the public firm). Haraguchi and Matsumura (2018) did not compute the collusive outcome, but were able to compare the Cournot and Bertrand supergames in terms of sustainability and welfare impact of collusion.

Our framework departs from that of Wen and Sasaki (2001) and Haraguchi and Matsumura (2018) in several aspects: First, while they focus on the collusive agreement that is preferred by the public firm (which, in their setting, is the agreement that maximizes total surplus), we describe the contract curve (a set of Pareto-optimal and individually rational outcomes) and focus on the collusive agreement that results from Nash bargaining between the public and the private firm when bargaining power is equally distributed.⁵ Second, while they assume constant marginal costs, we assume linearly increasing marginal costs (which captures constant marginal costs as a particular case) and briefly examine more general cost functions in an extension. Third, while they assume that the public firm maximizes total surplus, we assume that it maximizes a weighted sum of profit and consumer surplus.⁶ Finally, we abstract from product differentiation, and briefly examine the impact of cost asymmetry in an extension.⁷

Related research investigates the impact of coordination among symmetric firms that deviate from profit-maximizing behavior by valuing their own output or aggregate output, either due to delegation issues (Lambertini & Trombetta, 2002), labor-management (Delbono & Lambertini, 2014), not-for-profit motives (Philipson & Posner, 2009), or corporate social responsibility policies (Lambertini & Tampieri, 2012; Cunha & Mota, 2020). In these environments, symmetry among colluding firms makes the analysis technically close to the standard model of collusion in a private oligopoly. The same applies to the strand of literature that emerged from the pioneer contributions of Merrill and Schneider (1966) and Sertel (1988), which are dedicated to the study of collusion among private firms with public firms as outsiders.⁸

The difficulty of investigating collusion among heterogeneous firms is well known. Existing contributions address asymmetries in: costs (Donsimoni, 1985; Bae, 1987; Harrington, 1991; Verboven, 1997; Rothschild, 1999; Vasconcelos, 2005; Ganslandt et al., 2012; Correia-da-Silva & Pinho, 2016); production capacities (Compte et al., 2002; Bos & Harrington, 2010); or discount factors (Harrington, 1989). In our model, heterogeneity is in the objective functions.

The remainder of this paper is structured as follows: Sect. 2 presents the model; Sect. 3 characterizes the non-cooperative equilibrium; Sect. 4 characterizes the collusive outcome, with symmetric and asymmetric bargaining powers, and studies collusion sustainability; Sect. 5 investigates the impact of the public firm’s preference for total surplus, the degree of cost convexity, and cost asymmetry between firms; Sect. 6 concludes. Technical proofs are presented in the Appendix.

2 Model

Consider a market where one public firm, g, and one private firm, p, sell homogeneous goods. The two firms interact over an infinite number of periods. In each period, they simultaneously choose quantities: $q_g$ and $q_p$. Total (inverse) demand is linear and given by $P=1-Q$, where P is market price and $Q=q_{p}+q_{g}$ is total output. The total cost of producing q units is the same for both firms, and given by $C(q)=c_1q+\frac{c_2}{2}q^2$, with $c_1 \in \left[ 0,1\right]$ and $c_2 \ge 0$. Thus, the per-period profit of firm $i\in \{p,g\}$ is:

$$\begin{aligned} \pi _i(q_g,q_p)= (1-q_g-q_p)q_i-c_1q_i-\frac{c_2}{2}q_i^2. \end{aligned}$$

(1)

Firms are symmetric in every dimension except for their objective function. The private firm maximizes its own profit: $\pi _p$. The public firm maximizes a weighted sum of its own profit – $\pi _g$ – and consumer surplus – $C\!S(q_g,q_p)=\frac{(q_g+q_p)^2}{2}$:⁹

$$\begin{aligned} \Omega (q_g,q_p) \ = \ (1-\mu ) \pi _g(q_g,q_p) + \mu \,C\!S(q_g,q_p), \end{aligned}$$

(2)

where $\mu \ge 0$ is the weight attached to consumer surplus.¹⁰ If $\mu =0$, the public firm behaves like a private firm (maximizes its profit); while, if $\mu =\frac{1}{2}$, the public firm maximizes the sum of its profit and consumer surplus. The neglect of the private firm’s profit in the objective of the public firm is adequate for environments where the private firm distributes its profit among foreigners or a very small group of individuals, while the profit of the public firm is distributed among the general population in the form of lower taxes.¹¹ As $\mu$ increases, the public firm’s incentives to expand output become stronger. For sufficiently high values of $\mu$, the public firm produces so much that the private firm is driven out of the market. The following assumption ensures that the private firm is active in the non-cooperative equilibrium of the game:¹²

Assumption 1

$\mu < \frac{1+c_2}{2+c_2}$.

We allow the public firm to have negative profit. This is realistic in many industries, as government spending is frequently used to finance hospitals, schools, and urban transportation systems. Most of our results do not depend on this assumption. Except for very large values of $\mu$, the public firm has positive profit under duopolistic competition and under collusion.

3 Non-cooperative Equilibrium

In the absence of collusion, each firm chooses the output that maximizes its current-period payoff while taking the output of the rival as given (Cournot equilibrium).

The first-order condition (FOC) for profit-maximization by the private firm yields:

$$\begin{aligned} \frac{\partial {\pi _p}}{\partial {q_p}} = 0 \ \Leftrightarrow \ q_p = \frac{1-c_1-q_g}{2+c_2}. \end{aligned}$$

(3)

Thus, the higher is the public output, the lower is the private output (downward-sloping reaction function). The FOC for payoff-maximization by the public firm yields:

$$\begin{aligned} \frac{\partial \Omega }{\partial q_g} = 0 \ \Leftrightarrow \ q_g = \frac{(1-\mu )(1-c_1)-(1-2\mu )q_p}{2+c_2-\mu (3+c_2)}. \end{aligned}$$

(4)

If $\mu <\frac{1}{2}$, the greater is the private output, the lower is the public output: The model exhibits strategic substitutability (as is usual in quantity competition models). By contrast, if $\mu >\frac{1}{2}$, the higher is the private output, the greater is the public output. Hence, if the public firm weighs consumer surplus more than its profit, its reaction function is upward-sloping.

Combining (3) and (4), we obtain the non-cooperative equilibrium quantities:¹³

$$\begin{aligned} q_p^N= \frac{1-\mu \frac{2+c_2}{1+c_2}}{3+c_2-\mu (4+c_2)}(1-c_1), \quad q_g^N=\frac{1-\mu \frac{c_2}{1+c_2}}{3+c_2-\mu (4+c_2)}(1-c_1) \end{aligned}$$

(5)

and:

$$\begin{aligned} Q^N= \frac{2(1-\mu )}{3+c_2-\mu (4+c_2)}(1-c_1). \end{aligned}$$

(6)

If $\mu =0$, the two firms are symmetric and produce the same output level. If $\mu > 0$, the public firm produces more than the private firm. The more that the public firm weights consumer surplus (i.e., the higher is $\mu$), the higher is its output, and the lower is the output of the private firm. Total output is increasing in $\mu$ (see Fig. 1a), as the positive effect of $\mu$ on $q_g^N$ dominates the negative effect of $\mu$ on $q_p^N$. Since the two firms sell homogeneous goods, consumer surplus only depends on total output ($CS=\frac{Q^2}{2}$) and, therefore, is also increasing in $\mu$.

Replacing (5) in (1), we obtain the individual profits:

$$\begin{aligned} \pi _p^N =\frac{2+c_2}{2} (q_p^N)^2 \quad \text {and} \quad \pi _g^N = \pi _p^N + \frac{\frac{2 \mu (1-2\mu )}{1+c_2}}{[3+c_2-\mu (4+c_2)]^2}(1-c_1)^2. \end{aligned}$$

(7)

Replacing (5) in (2), we obtain the equilibrium payoff of the public firm:

$$\begin{aligned} \Omega ^N=(1-\mu ) \frac{1+c_2(1-2\mu )-\left( \frac{4}{2+c_2}-\frac{{c_2}^2}{1+c_2}\right) \mu ^2 }{2 (1+c_2) [3+c_2-(4+c_2) \mu ]^2} (2+c_2)(1-c_1)^2. \end{aligned}$$

(8)

The public firm has a higher profit than the private firm if and only if $\mu <\frac{1}{2}$. This result is reminiscent of the literature on strategic delegation, according to which it is profitable for a firm’s owner (unilaterally) to provide incentives for the manager to deviate from profit-maximization toward excessive output. Becoming a fiercer competitor may be profitable because it turns the rival into a milder competitor (Vickers, 1985; Fershtman & Judd, 1987; Sklivas, 1987) whenever the rival’s reaction function is downward sloping. In mixed oligopolies, similarly, valuing consumer surplus works as a kind of commitment device for the public firm to choose higher output, leading the private firm to choose lower output.

The following lemma relates the non-cooperative equilibrium outcome when $c_1=0$ and when $c_1 \ne 0$. It follows immediately from the inspection of expressions (5), (7), and (8) that the outcome when $c_1 \ne 0$ is qualitatively the same as when $c_1 = 0$.

Let $\mathring{x}$ denote the value of variable x in the model with $c_1=0$:

Lemma 1

For $i\in \{p,g\}$, we have:

$$\begin{aligned} q_i^N= (1-c_1)\,\mathring{q}_i^N, \quad \pi _i^N= (1-c_1)^2\,\mathring{\pi }_i^N \quad \text {and} \quad \Omega ^N= (1-c_1)^2\,\mathring{\Omega }^N. \end{aligned}$$

Under Assumption 1, the private firm has positive profit. If $\mu \le \frac{1}{2}$, since $\pi _g^N \ge \pi _p^N$, the public firm also has positive profit. However, this may not be true for higher values of $\mu$. Indeed, if $\mu > \frac{(1+c_2) (2+c_2)}{4+6c_2+{c_2}^2}$, the public firm has negative profit (see Figure 1b).

Furthermore, as $\frac{\partial \pi _p^N}{\partial \mu }=\frac{-4 \pi _p^N}{[1+c_2-\mu (2+c_2)][3+c_2-\mu (4+c_2)]}<0$, the profit of the private firm is decreasing in $\mu$. This is because the public firm competes more fiercely as $\mu$ increases. As $\frac{\partial \pi _g^N}{\partial \mu }=\frac{2 (1-c_1)^2[1+c_2-(2 {c_2}^2+7 c_2+4 ) \mu ]}{(1+c_2)^2 [3+c_2-\mu (4+c_2)]^3}$, we conclude that the profit of the public firm is increasing in $\mu$ only for sufficiently low values of $\mu$ (more precisely, if and only if $\mu <\frac{1+c_2}{4+7c_2+2{c_2}^2}$).¹⁴ On the one hand, a higher value of $\mu$ leads the private firm to contract output, which increases price and, therefore, the public firm’s revenues; on the other hand, a higher value of $\mu$ leads the public firm to deviate more from the profit-maximizing output (to increase consumer surplus). The second (negative) effect dominates the first (positive) effect if $\mu$ is sufficiently high.

Fig. 1

The effect of the public firm’s preference for CS on the non-cooperative outcome

4 Collusive Agreement

Let us now suppose that the two firms choose their output levels cooperatively. In the absence of side-payments, for the private firm to be willing to collude, the public firm must agree to decrease its output relative to the Cournot level. Otherwise, the private firm would be certainly worse off than under competition.¹⁵

If the public firm’s preference for consumer surplus is strong enough, in the Cournot equilibrium, the price is lower than the public firm’s marginal cost (but, of course, higher than the private firm’s marginal cost).¹⁶ In this case, the public firm is surely willing to contract output if the private firm expands its output by the same amount. This reallocation of output marginally is profitable for both firms and preserves consumer surplus. Note also that, with symmetric and strictly convex cost functions ($c_2>0$), productive efficiency is attained if and only if firms produce the same output. Since the public firm produces more than the private firm in the Cournot equilibrium, decreasing $q_g$ and increasing $q_p$ increases the size of the pie. This suggests a beneficial effect of collusion in our environment.

Since firms are asymmetric in their objectives, finding the natural collusive agreement is not straightforward.¹⁷ Following (Osborne & Pitchik, 1983; Schmalensee, 1987), and Harrington (1991), we assume that firms negotiate the collusive agreement in a way that leads to the Nash bargaining solution (Nash, 1950; Binmore et al., 1986). Firms select the agreement – $(q_g^C,q_p^C)$ – that maximizes the Nash product, $N\!P(q_g,q_p)\equiv \left[ \pi _p(q_g,q_p)-\pi _p^N\right] ^{\alpha }\left[ \Omega (q_g,q_p)-\Omega ^N\right] ^{1-\alpha }$. This is the geometric mean of their gains from collusion, weighted by their bargaining powers:

$$\begin{aligned} \max _{(q_g,q_p) \in \mathsf{I}\mathsf{R}^2_+} \left[ \pi _p(q_g,q_p)-\pi _p^N\right] ^{\alpha }\left[ \Omega (q_g,q_p)-\Omega ^N\right] ^{1-\alpha } \quad s.t. \quad \left\{ \begin{aligned}&\pi _p(q_g,q_p)\ge \pi _p^N\\&\Omega (q_g,q_p)\ge \Omega ^N,\\ \end{aligned}\right. \end{aligned}$$

(9)

where $\alpha \in [0,1]$ measures the relative bargaining power of the private firm vis-à-vis the public firm. In the extreme case where $\alpha =0$, the public firm has all the bargaining power and is thus able to make a take-it-or-leave-it offer to the private firm. By contrast, $\alpha =1$ corresponds to the opposite situation in which the private firm has all the bargaining power.

The first-order condition $\frac{\partial }{\partial q_g} N\!P(q_g,q_p) = 0$ yields:

$$\begin{aligned}&\alpha \left( \pi _p-\pi _p^N\right) ^{\alpha -1} \frac{\partial \pi _p}{\partial q_g}\left( \Omega -\Omega ^N\right) ^{1-\alpha }+(1-\alpha )\left( \pi _p-\pi _p^N\right) ^ {\alpha }\left( \Omega -\Omega ^N\right) ^{-\alpha }\frac{\partial \Omega }{\partial q_g} =0 \nonumber \\&\Leftrightarrow \ \frac{\alpha }{1-\alpha } \times \frac{\Omega -\Omega ^N}{\pi _p-\pi _p^N} =-\frac{\frac{\partial \Omega }{\partial q_g}}{\frac{\partial \pi _p}{\partial q_g}}. \end{aligned}$$

(10)

Similarly, the first-order condition $\frac{\partial }{\partial q_p} N\!P(q_g,q_p) = 0$ yields:

$$\begin{aligned} \frac{\alpha }{1-\alpha } \times \frac{\Omega -\Omega ^N}{\pi _p-\pi _p^N} =-\frac{\frac{\partial \Omega }{\partial q_p}}{\frac{\partial \pi _p}{\partial q_p}}. \end{aligned}$$

(11)

Equations (10)–(11) are quadratic in $q_p$ and $q_g$, and thus we are unable to find explicit analytic expressions for $q_g^C$ and $q_p^C$ for all values of $\alpha$ and $\mu$.

As in the case of Cournot equilibrium (see Lemma 1), the collusive outcome with $c_1 \ne 0$ can be obtained from that with $c_1 = 0$ by multiplying outputs by $(1-c_1)$ and payoffs by $(1-c_1)^2$:

Lemma 2

For $i\in \{p,g\}$, we have:

$$\begin{aligned} q_i^C= (1-c_1)\,\mathring{q}_i^C, \quad \pi _i^C= (1-c_1)^2\,\mathring{\pi }_i^C \quad \text {and} \quad \Omega ^C= (1-c_1)^2\,\mathring{\Omega }^C. \end{aligned}$$

Proof

See Appendix 1. $\square$

Note that Lemmas 1 and 2 allow us to set $c_1=0$ without loss of generality.

We proceed by analytically solving the case in which bargaining power is equally divided ($\alpha = \tfrac{1}{2}$) and the public firm maximizes the sum of its profit and consumer surplus ($\mu =\tfrac{1}{2}$). Afterward, we investigate numerically the impact of variations in $\mu$ and $\alpha$.

4.1 Symmetric Bargaining Powers

Suppose that firms have symmetric bargaining powers ($\alpha = \frac{1}{2}$), and the public firm maximizes the sum of individual profit and consumer surplus ($\mu =\tfrac{1}{2}$).

This behavior by the public firm maximizes the welfare of households in environments where the public firm’s profit (resp. loss) translates into a tax reduction (resp. increase) for households, while the private firm’s profit does not accrue to households.

Below, we also suppose that cost is convex ($c_2>0$). In the case of linear cost ($c_2=0$), output asymmetry does not entail productive inefficiency, and the impact of collusion is the traditional output contraction (illustrated in Figs. 2, 5, and 7).

Proposition 1

Let $c_2>0$. If firms have the same bargaining power ($\alpha =\frac{1}{2}$) and the public firm maximizes the sum of consumer surplus and own profit ($\mu =\frac{1}{2}$), collusion does not affect total output ($Q^C=Q^N$), but results in productive efficiency ($q_p^N<q_p^C=q_g^C<q_g^N$).

Proof

See Appendix 1. $\square$

With $\alpha =\frac{1}{2}$ and $\mu =\frac{1}{2}$, output levels and consumer surplus are given by:

$$\begin{aligned} q_p^C = q_g^C = \frac{1-c_1}{2+c_2}, \quad Q^C= \frac{2(1-c_1)}{2+c_2} \quad \text {and} \quad C\!S^C=\frac{2(1-c_1)^2}{(2+c_2)^2}, \end{aligned}$$

(12)

which leads to:

$$\begin{aligned} \pi _p^C - \pi _p^N = \pi _g^C - \pi _g^N = \frac{c_2(1-c_1)^2}{2 (1+c_2)^2(2+c_2)^2} \quad \text {and} \quad \Omega ^C - \Omega ^N = \frac{c_2(1-c_1)^2}{4 (1+c_2)^2(2+c_2)^2}. \end{aligned}$$

(13)

The profits of both firms increase under collusion, and consumer surplus is unaffected (because total output is the same in both regimes). Still, households should benefit from collusion through lower taxes (as the public firm’s profit increases).

Since we cannot find closed-form analytical expressions for $\mu \ne \frac{1}{2}$, we proceed with the analysis numerically. As shown previously, under competition, the private firm’s output is decreasing in $\mu$, while the public firm’s output and total output are increasing in $\mu$. Under collusion, both individual outputs are non-monotonic. Nevertheless, total output and consumer surplus remain increasing in $\mu$; see Figs. 2 and 3.

Fig. 2

Impact of collusion on output, with $\alpha =\frac{1}{2}$ and linear costs ($c_1=0$, $c_2=0$)

Fig. 3

Impact of collusion on output, with $\alpha =\frac{1}{2}$ and quadratic costs ($c_1=0$, $c_2=1$)

With linear costs, the impact of public-private collusion is akin to the impact of collusion among private firms: Firms reduce output to increase profits; see Figs. 2, 5, and 7. By contrast, with quadratic costs, if the public firms’ preference for consumer surplus is strong enough, the impact of public-private collusion is much different and deserves a careful discussion; see Figs. 3, 6, and 8.

Remark

With quadratic costs, there is a threshold for the public firm’s preference for consumer surplus, $\mu ^*$, above which the private firm expands output relative to the non-cooperative equilibrium. Notably, if $\mu \in \left( \mu ^* , \frac{1}{2}\right)$, collusion expands total output and consumer surplus.

Observe, in Fig. 3, the qualitative change of behavior at $\mu ^* \approx 0.388$. For $\mu < \mu ^*$, private output and public output are lower under collusion than under competition. Private output is decreasing in $\mu$, while public output is increasing in $\mu$. In this region, the effect of collusion between the public and the private firm appears to be a distorted version of the effect of collusion between two private firms: output contraction to increase price and profit.

At $\mu =\mu ^*$, private output and total output jump upward while public output jumps downward. For $\mu > \mu ^*$, collusion reduces public output ($q_g^C < q_g^N$) and increases private output ($q_p^C > q_p^N$). Importantly, collusion increases total output (and thus consumer surplus) for intermediate values of $\mu$: if and only if $\mu \in \left( \mu ^* , \frac{1}{2} \right)$.

The origin of the jump in collusive quantities at $\mu ^*$ is the convexity of the payoff of the public firm with respect to $q_p$ (consumer surplus is convex in $q_p$). The public firm prefers low $q_p$ (to enjoy higher profits) or high $q_p$ (to enjoy higher consumer surplus) rather than intermediate $q_p$. As a result, there is a critical value of $\mu$ at which the agreement that results from Nash bargaining jumps from low $q_p$ to high $q_p$, avoiding intermediate $q_p$; see Fig. 4.¹⁸

Fig. 4

Individually rational agreements, collusive outcome (black dot), and Cournot equilibrium (circle), with $\alpha =\frac{1}{2}$, $c_1=0$ and $c_2=1$

Under collusion, the public firm’s profit is positive for any value of $\mu$; see Fig. 5b. This is not true under competition, where its profit is negative for $\mu > \frac{(1+c_2) (2+c_2)}{4+6c_2+{c_2}^2}$. Notwithstanding, for intermediate levels of $\mu$, the public firm makes lower profits under collusion than under competition. For these values of $\mu$, the collusive gain for the public firm is coming from the increase in the consumer surplus (at the cost of a decrease in profit).

Fig. 5

Impact of collusion on payoffs, with linear costs ($\alpha =\frac{1}{2}$, $c_2=0$)

Fig. 6

Impact of collusion on surplus, with quadratic costs ($\alpha =\frac{1}{2}$, $c_2=1$)

Fig. 7

Impact of collusion on surplus, with linear costs ($\alpha =\frac{1}{2}$, $c_2=0$)

Fig. 8

Impact of collusion on surplus, with quadratic costs ($\alpha =\frac{1}{2}$, $c_2=1$)

Collusion increases total surplus if and only if $\mu > \mu ^*$. For low levels of $\mu$, the public firm is mostly concerned with its profit, and thus the traditional effect of collusion prevails: Both firms restrict output, which decreases total surplus; see Figure 6. For high levels of $\mu$, the public firm is highly concerned with consumer surplus, and thus agrees to contract output significantly in exchange for a significant output expansion by the private firm, which increases total surplus.

4.2 Asymmetric Bargaining Powers

Let us now allow asymmetric bargaining powers: $\alpha \ne \tfrac{1}{2}$.

If $\mu = \frac{1}{2}$, collusion strictly increases total surplus. This is an immediate consequence of individual rationality. Collusion increases the private firm’s profit (otherwise, the private firm would not accept the agreement), and increases the sum of the public firm’s profit and consumer surplus (otherwise, the public firm would not accept the agreement).

Proposition 2

If the public firm weights consumer surplus and own profit equally ($\mu =\frac{1}{2}$), and $(\pi _p^C,\Omega ^C)\ne (\pi _p^N,\Omega ^N)$, collusion strictly increases total surplus.

Proof

Individual rationality of collusion requires that $\pi _p^C \ge \pi _p^N$ and $\pi _g^C+C\!S^C \ge \pi _g^N+C\!S^N$. By assumption, one of the inequalities is strict. Therefore, $\pi _p^C+\pi _g^C+C\!S^C > \pi _p^N+\pi _g^N+C\!S^N$. $\square$

Combining the two first-order conditions for maximization of the Nash product – (10) and (11) – and replacing the expressions for the non-cooperative payoffs – (7) and (8) – we obtain the expression for the interior portion of the contract curve:¹⁹

$$\begin{aligned}{}[2+c_2-\mu (3+c_2)]q_g +(1-2 \mu ) q_p-(1-\mu )(1-c_1) = \frac{(1-2 \mu ) q_g q_p - \mu q_p^2}{(2+c_2) q_p+q_g-(1-c_1)}. \end{aligned}$$

(14)

As the relative bargaining power of the private firm increases from $\alpha =0$ to $\alpha =1$, the collusive agreement moves along the contract curve from the agreement that the public firm prefers (among those that are acceptable by the private firm) to the agreement that the private firm prefers (among those that are acceptable by the public firm).

The contract curve is plotted in Fig. 9 for several values of $\mu$. It is a relatively small subset of the set of Pareto-optimal outcomes with non-negative payoffs. Note that there is a jump in the best outcome for the public firm (which is unacceptable for the private firm, because $\pi _p=0<\pi ^N_p$) when $\mu$ increases from 0.35 to 0.4, from a public monopoly ($q_g \approx 0.406$ and $q_p=0$ in Fig. 9b) to a situation where total output is higher but mainly produced by the private firm ($q_g \approx 0.302$ and $q_p \approx 0.465$ in Fig. 9c).²⁰

Fig. 9

Pareto-optimal agreements with non-negative payoffs (solid line), contract curve (line segment between $\alpha =0$ and $\alpha =1$), and Cournot equilibrium (circle) for $c_1=0$ and $c_2=1$

Remark

There is a threshold for the public firm’s preference for consumer surplus above which the public monopoly is not Pareto-optimal. Both firms prefer a situation in which the private firm produces more than in the non-cooperative equilibrium.

The influence of the relative bargaining power on the impact of collusion on consumer surplus and total surplus is represented in Fig. 12a. Independently of the distribution of bargaining power, collusion increases total surplus if the public firm’s preference for consumer surplus is above a threshold ($\mu ^* \approx 0.388$), and collusion increases consumer surplus if $\mu \in \left( 0.388 , \mu ^{**} \right)$. However, $\mu ^{**}$ negatively depends on the bargaining power of the private firm.

4.3 Sustainability of Collusion

Firms may have incentives to deviate unilaterally from the collusive agreement: to produce the output that maximizes their individual payoff even though this triggers a punishment. For simplicity, assume that firms use grim trigger punishments: They permanently revert to the Cournot outcome after a deviation (Friedman, 1971).

If the private firm deviates, it chooses the output that solves $\max _{q_p} \left\{ \pi _p(q_g^C,q_p) \right\}$. If the public firm deviates, it chooses the output that solves $\max _{q_g} \left\{ \Omega (q_g,q_p^C) \right\}$.

The private firm is willing to comply with the collusive agreement if and only if the following incentive compatibility constraint (ICC) is satisfied:

$$\begin{aligned} \sum ^{\infty }_{s=t}\delta ^{s-t}\pi ^{C}_p\ge \pi ^{D}_p+\sum ^{\infty }_{s=t+1}\delta ^{s-t}\pi ^{N} _p \ \Leftrightarrow \ \delta \ge \frac{\pi ^{D}_p-\pi ^{C}_p}{\pi ^{D}_p-\pi ^{N}_p} \equiv \delta _p^{*}, \end{aligned}$$

where $\delta _p^{*}$ is the critical discount factor for the private firm. Likewise, the public firm will abide by the agreement if and only if:

$$\begin{aligned} \delta \ge \frac{\Omega ^{D}_g-\Omega ^{C}_g}{\Omega ^{D}_g-\Omega ^{N}_g} \equiv \delta _g^{*}, \end{aligned}$$

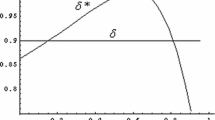
where $\delta _g^{*}$ is the critical discount factor for the public firm. The agreement is sustainable if no firm is better off deviating: if and only if $\delta \ge \delta ^*$, with $\delta ^*=\max \left\{ \delta _p^{*}, \delta _g^{*} \right\}$.²¹

Fig. 10

Outputs and critical discount factors with linear cost ($\alpha =\tfrac{1}{2}$, $c_2=0$)

Fig. 11

Outputs and critical discount factors with quadratic cost ($\alpha =\tfrac{1}{2}$, $c_2=1$)

Collusion is the easiest to sustain when the public firm maximizes profit disregarding consumer surplus; see Figs. 10 and 11.²² With quadratic costs, the incentives to collude are non-monotonic in the public firm’s preference for consumer surplus. For sufficiently high levels of $\mu$, the critical discount factor of the public firm is not only increasing in this parameter, but it is also binding: higher than the critical discount factor for the private firm. Note also that after the threshold $\mu ^* \approx 0.388$ is reached, while the public firm is tempted to deviate by expanding output, the private firm is tempted to deviate by reducing output.

5 Extensions

5.1 Public Firm Weights Private Firm Profit

Suppose now that the profit of the private firm also enters the public firm’s objective function. More precisely, suppose the public firm’s objective function is:

$$\begin{aligned} {\tilde{\Omega }}(q_g,q_p) \ = \ (1-\mu _c-\mu _p) \pi _g(q_g,q_p) + \mu _c\,C\!S(q_g,q_p) + \mu _p \pi _p(q_g,q_p), \end{aligned}$$

(15)

where $\mu _p \in \left[ 0,\mu _c\right]$ is the weight attached to the profit of the private firm.

This objective function incorporates biases (from profit-maximization) toward consumer surplus and toward total surplus.²³ The case where $\mu _p=0$ corresponds to our baseline case where the public firm is biased toward consumer surplus (neglects the profit of the private firm). The case where $\mu _c=\mu _p$ corresponds to the case where the public firm is biased toward total surplus (places equal weight on consumer surplus and on the profit of the private firm).

To compute the Cournot equilibrium, we follow the same steps as in Sect.3. The resulting expressions are presented in Appendix 1. To find the collusive outcome, we use numerical methods because closed-form analytical expressions are not available.

Figure 12b shows that the qualitative impact of collusion on consumer surplus and total surplus does not hinge on whether the public firm’s bias from profit-maximization is toward consumer surplus ($\mu _p=0$) or total surplus ($\mu _p=\mu _c$).

5.2 Impact of Cost Convexity

We now consider a more general marginal cost function. Instead of restricting to linearly increasing marginal cost, we allow marginal cost to be an arbitrary power function. More precisely, we set $C(q)=\frac{c}{\gamma } q^\gamma$, with $\gamma > 1$, implying $C'(q)= c\,q^{\gamma -1}$. These cost functions exhibit constant cost-output elasticity, since $\frac{dC/dq}{C/q} = \gamma$. Note that our baseline model (for any $c_2>0$) is captured by the particular case of $\gamma =2$.

Figure 12c suggests that the qualitative impact of collusion on consumer surplus and total surplus does not require a sufficient degree of cost convexity. As long as there is some convexity ($\gamma >1$), our qualitative results hold.

5.3 Impact of Cost Asymmetry

Finally, we analyze the case where the private firm has a cost advantage over the public firm. Precisely, while $C_p(q_p) = c_1 q_p-\frac{c_2}{2}q_p^2$, we assume that $C_g(q_g) = \lambda \left( c_1 q_g-\frac{c_2}{2}q_g^2 \right)$, with $\lambda \ge 1$.²⁴ Note that this cost advantage implies that the transference of output from the public to the private firm (which occurs under collusion) is even more beneficial in terms of productive efficiency. Hence, it should become more likely that collusion increases consumer surplus and total surplus. This intuition is corroborated by Fig. 12d.

Fig. 12

Impact of collusion on CS and TS, depending on: the public firm’s bargaining power ($\alpha$); the public firm’s preference for TS ($\mu _p$); the degree of cost convexity ($\gamma$); and the cost asymmetry ($\lambda$)

6 Conclusion

Motivated by numerous cartel cases that involve public and private firms, we investigated a model of collusion between a public and a private firm to contribute to the debate about whether antitrust policy should contemplate some kind of special treatment for cartels that involve public firms, and analyze such cases under the “rule of reason” rather than as per se antitrust violations.

Collusion is beneficial when the public firm’s taste for consumer surplus is sufficiently strong and costs are convex. One of the underlying reasons is that collusion reduces productive inefficiency. With symmetric and strictly increasing marginal costs, productive efficiency is attained when individual outputs are symmetric. However, in the non-cooperative equilibrium, the public firm produces more than does the private firm due to the public firm’s preference for consumer surplus. By colluding, the firms reduce that inefficiency because the public firm reduces its output (for collusion to benefit the private firm) while the private firm expands its output (for collusion to benefit the public firm). This result contrasts with the traditional idea that colluding firms restrict total output to increase market price.

The other benefit is more immediate: Suppose that the public firm maximizes the sum of profit and consumer surplus. For collusion to be advantageous for both firms, the private firm’s profit and the sum of the public firm’s profit with consumer surplus must increase. This implies that the total surplus necessarily increases.

With regard to collusion sustainability, it is interesting to note that, if the public firm’s preference for consumer surplus is sufficiently strong and costs are convex, while the public firm is tempted to deviate by increasing output (as usual), the private firm is tempted to deviate by restricting output. In any event, collusion is easiest to sustain when both firms maximize profits. This corroborates the conventional view that firm asymmetry hinders collusion sustainability.

The most important policy implication is that collusion may increase the total surplus and even also consumer surplus. Competition authorities should be aware of this when making decisions on cartel cases that involve public firms.

Our results should, however, be taken with a “grain of salt”: Opposite conclusions should be expected if the benevolent view with regard to the behavior of public firms that underlies our analysis is replaced with a dismal view where the public firm’s behavior is mostly driven by empire-building motives.

Appendices

Appendix 1 : Proofs

Proof of Lemma 2

Condition (10) holds, by assumption, for $c_1=0$:

$$\begin{aligned} \frac{\alpha }{1-\alpha } \times \frac{\mathring{\Omega }\left( \mathring{q}_g^C,\mathring{q}_p^C\right) -\mathring{\Omega }^N}{\mathring{\pi }_p\left( \mathring{q}_g^C,\mathring{q}_p^C\right) -\mathring{\pi }_p^N} =-\,\frac{\frac{\partial \mathring{\Omega }}{\partial q_i}\left( \mathring{q}_g^C,\mathring{q}_p^C\right) }{\frac{\partial \mathring{\pi }_p}{\partial q_i}\left( \mathring{q}_g^C,\mathring{q}_p^C\right) }, \quad \quad \text {for} \ i\in \{p,g\}. \end{aligned}$$

(16)

Our goal is to show that ${\hat{q}}_i=(1-c_1)\mathring{q}_i^C$ is the collusive quantity of firm $i\in \{p,g\}$ when $c_1\ne 0$. More precisely, we want to show that:

$$\begin{aligned} \frac{\alpha }{1-\alpha } \times \frac{\Omega \left( {\hat{q}}_g,{\hat{q}}_p\right) -\Omega ^N}{\pi _p\left( {\hat{q}}_g,{\hat{q}}_p\right) -\pi _p^N} =-\frac{\frac{\partial \Omega }{\partial q_i}\left( {\hat{q}}_g,{\hat{q}}_p\right) }{\frac{\partial \pi _p}{\partial q_i}\left( {\hat{q}}_g,{\hat{q}}_p\right) }, \quad \quad \text {for} \ i\in \{p,g\}. \end{aligned}$$

(17)

Using Lemma 1, we know that $\Omega ^N=(1-c_1)^2\,\mathring{\Omega }^N$ and $\pi _p^N=(1-c_1)^2\,\mathring{\pi }_p^N$.

Replacing ${\hat{q}}_i=(1-c_1)\,\mathring{q}_i^C$ in (1), we obtain:

$$\begin{aligned} \pi _i\left( {\hat{q}}_g,{\hat{q}}_p\right)&=\pi _i\Big ((1-c_1)\mathring{q}_g^C,(1-c_1)\mathring{q}_p^C\Big )\\&=(1-c_1)^2\left[ \left( 1-\mathring{q}_g^C-\mathring{q}_p^C\right) \mathring{q}_i^C-\frac{c_2}{2}\left( \mathring{q}_i^C\right) ^2\right] \\&=(1-c_1)^2\,\mathring{\pi }_i\left( \mathring{q}_g^C,\mathring{q}_p^C\right) . \end{aligned}$$

Doing the same exercise using expression (2), it follows that:

$$\begin{aligned} \Omega \left( {\hat{q}}_g,{\hat{q}}_p\right) =(1-c_1)^2\, \mathring{\Omega }\left( \mathring{q}_g^C,\mathring{q}_p^C\right) . \end{aligned}$$

Thus, we can rewrite (17) as follows:

$$\begin{aligned} \frac{\alpha }{1-\alpha } \times \frac{\mathring{\Omega }\left( \mathring{q}_g^C,\mathring{q}_p^C\right) -\mathring{\Omega }^N}{\mathring{\pi }_p\left( \mathring{q}_g^C,\mathring{q}_p^C\right) -\mathring{\pi }_p^N} =-\frac{\frac{\partial \Omega }{\partial q_i}\left( q_g^C,q_p^C\right) }{\frac{\partial \pi _p}{\partial q_i}\left( q_g^C,q_p^C\right) }. \end{aligned}$$

(18)

Differentiating (2) with respect to $q_p$ yields:

$$\begin{aligned} \frac{\partial \Omega }{\partial q_p}&=(1-\mu )\frac{\partial \pi _g}{\partial q_p}+\mu \frac{\partial CS}{\partial q_p} =(1-\mu )(-q_g)+\mu \left( q_p+q_g\right) =\mu q_p-(1-2\mu )q_g. \end{aligned}$$

Hence:

$$\begin{aligned} \frac{\partial \Omega }{\partial q_p} \left( {\hat{q}}_g,{\hat{q}}_p\right) =(1-c_1)\frac{\partial \mathring{\Omega }}{\partial q_p}\left( \mathring{q}_g^C,\mathring{q}_p^C\right) . \end{aligned}$$

(19)

Furthermore, since differentiating (1) with respect to $q_p$ yields:

$$\begin{aligned} \frac{\partial \pi _p}{\partial q_p}=1-c_1-q_g-(2-c_2)q_p, \end{aligned}$$

we also get that:

$$\begin{aligned} \frac{\partial \pi _p}{\partial q_p} \left( {\hat{q}}_g,{\hat{q}}_p\right) =(1-c_1)\frac{\partial \mathring{\pi }_p}{\partial q_p}\left( \mathring{q}_g^C,\mathring{q}_p^C\right) . \end{aligned}$$

(20)

Replacing (19) and (20) in (18), we obtain condition (16) for $i=p$, which holds by assumption.

To finish the proof, we need to show that the right-hand sides of (19) and (16) are also equal when $i=g$. Differentiating (2) with respect to $q_g$, we obtain:

$$\begin{aligned} \frac{\partial \Omega }{\partial q_g}&=(1-\mu )\frac{\partial \pi _g}{\partial q_g}+\mu \frac{\partial CS}{\partial q_g}=(1-\mu )(1-c_1-2q_g-q_p-c_2q_g)+\mu \left( q_p+q_g\right) . \end{aligned}$$

Thus:

$$\begin{aligned} \frac{\partial \Omega }{\partial q_g} \left( {\hat{q}}_g,{\hat{q}}_p\right) = (1-c_1)\frac{\partial \mathring{\Omega }}{\partial q_g}\left( \mathring{q}_g^C,\mathring{q}_p^C\right) . \end{aligned}$$

(21)

Finally, differentiating (1) with respect to $q_g$, we obtain:

$$\begin{aligned} \frac{\partial \pi _p}{\partial q_g}=-q_p, \end{aligned}$$

which means that:

$$\begin{aligned} \frac{\partial \pi _p}{\partial q_g} \left( {\hat{q}}_g,{\hat{q}}_p\right) = (1-c_1)\frac{\partial \mathring{\pi }_p}{\partial q_g}\left( \mathring{q}_g^C,\mathring{q}_p^C\right) . \end{aligned}$$

(22)

Replacing (21) and (22) in (18), we obtain condition (16) for $i=g$, which ends the proof. $\square$

Proof of Proposition 1

To solve the Nash bargaining problem (9), we start by solving a relaxed problem where side payments are feasible. Then, we show that the solution to the problem with side payments prescribes a null side payment and thus coincides with the solution of the problem without side payments (our original problem).

With side-payments, the Nash bargaining solution would be the triple $(q_g,q_p,S)$, where S denotes the side-payment from the public firm to the private firm (if $S<0$, the side-payment is in the opposite direction) that maximizes:²⁵

$$\begin{aligned} \tilde{N\!P} (q_g,q_p,S) = \left[ \pi _p+S-\pi _p^N\right] \left[ \tfrac{1}{2}C\!S+\tfrac{1}{2} (\pi _g-S) - \Omega ^N\right] , \end{aligned}$$

(23)

where $\pi _p^N=\frac{{c_2}^2}{2(1+c_2)^2(2+c_2)}(1-c_1)^2$ and $\Omega ^N=\frac{4+c_2(2+c_2)(4+c_2)}{4(1+c_2)^2 (2+c_2)^2}(1-c_1)^2$. Observe that:²⁶

$$\begin{aligned}&\max _{(q_p,q_g,S)} \tilde{N\!P} (q_g,q_p,S) = \max _{(q_p,q_g)} \Big \{ \max _S \ \tilde{N\!P} (q_g,q_p,S)\Big \} \nonumber \\&\quad = \tfrac{1}{2} \max _{(q_p,q_g)} \Big \{ \max _S \big (\pi _p-\pi _p^N+S\big ) \big (\pi _g+C\!S-2\Omega ^N-S\big ) \Big \} \nonumber \\&\quad = \tfrac{1}{8} \max _{(q_p,q_g)} \Big \{ \left( \pi _p-\pi _p^N+\pi _g +C\!S-2\Omega ^N\right) ^2 \Big \} \nonumber \\&\quad = \tfrac{1}{8} \Big [ \max _{(q_g,q_p)} \left\{ \pi _p+\pi _g+C\!S\right\} -\pi _p^N-2\Omega ^N\Big ]^2 \nonumber \\&\quad = \tfrac{1}{8} \bigg [ \max _{(Q,q_p)} \Big \{(1-Q)Q-c_1 Q-\tfrac{c_2}{2} q_p^2-\tfrac{c_2}{2}(Q-q_p)^2 + \tfrac{1}{2} Q^2 \Big \} -\pi _p^N-2\Omega ^N\bigg ]^2. \end{aligned}$$

(24)

The first-order condition (FOC) with respect to $q_p$ of the maximization problem in (24) yields $q_p=\frac{Q}{2}$. The FOC with respect to Q is:²⁷

$$\begin{aligned} 1-c_1-(1+c_2)Q+c_2q_p=0. \end{aligned}$$

Replacing $q_p=\frac{Q}{2}$ in the previous condition, we obtain:

$$\begin{aligned} Q^C=Q^N=\frac{2(1-c_1)}{2+c_2} \quad \Rightarrow \quad q_p^C=q_g^C=\frac{1-c_1}{2+c_2}. \end{aligned}$$

(25)

The resulting individual profits (before side payments) are:

$$\begin{aligned} \pi _g^C = \pi _p^C = \frac{c_2(1-c_1)^2}{2(2+c_2)^2}. \end{aligned}$$

Computing the optimal side-payment, we find that it is null:

$$\begin{aligned} S^*=\frac{1}{2} \left[ \pi _g^C+\frac{(q_g^C+q_p^C)^2}{2}-2\Omega ^N-\left( \pi _p^C-\pi _p^N\right) \right] =0. \end{aligned}$$

Thus, the quantities (25) also maximize the Nash product in the absence of side payments, given in (9). To finish the proof, note that the solution satisfies the constraints of the optimization problem: $q_p^C\ge 0$, $q_g^C\ge 0$, $\pi _p^C \ge \pi _p^N$ and $\Omega ^C \ge \Omega ^N$. $\square$

Appendix 2: Public Firm Weights Private Firm Profit

We impose a generalized version of Assumption 1 to ensure that the private firm is active.

Assumption 1’. $\mu _c<\frac{1+c_2}{2+c_2}(1-\mu _p)$.

Combining the first-order conditions of the individual maximization problems of the two firms, $\frac{\partial \pi _p}{\partial q_p}=0$ and $\frac{\partial {\tilde{\Omega }}}{\partial q_g}=0$, we obtain the Cournot equilibrium outputs:²⁸

$$\begin{aligned} {\tilde{q}}_p^N= & {} \frac{1-\mu _c\frac{2+c_2}{1+c_2}-\mu _p}{3+c_2-\mu _c(4+c_2)-\mu _p\frac{(2+c_2)^2}{1+c_2}}(1-c_1), \end{aligned}$$

(26)

$$\begin{aligned} {\tilde{q}}_g^N= & {} \frac{1-\mu _c\frac{c_2}{1+c_2}-\frac{2+c_2}{1+c_2}\mu _p}{3+c_2-\mu _c(4+c_2)-\mu _p\frac{(2+c_2)^2}{1+c_2}}(1-c_1) \end{aligned}$$

(27)

and

$$\begin{aligned} {\tilde{Q}}^N=\frac{2 (1-\mu _c)-\frac{3+2c_2}{1+c_2}\mu _p}{3+c_2-\mu _c(4+c_2)-\mu _p\frac{(2+c_2)^2}{1+c_2}}(1-c_1). \end{aligned}$$

Replacing (26)–(27) in the profit functions (1) and in the public firm’s objective (15), we obtain the non-cooperative equilibrium profits, ${\tilde{\pi }}_p^N$, ${\tilde{\pi }}_g^N$, and the public firm’s payoff, ${\tilde{\Omega }}^N$.