Introduction

The knowledge of discharge measurement in open channels is essential for the efficient management of water networks such as channel irrigation and drainage systems (Bos 1977). Measurement discharge devices for open channel flows are hydraulic structures requiring, for a free-flow condition, the measurement of the upstream water level h (Boiten 2000) and the availability of the stage-discharge relationship (i.e., a relationship between the discharge Q and h), which is strictly dependent on the shape and the sizes of the device (Nicosia and Ferro 2022).

Discharge in open channels can be measured by flumes, which should be designed to be mobile, to have a low cost and a good accuracy of the measured discharge (± 5%, according to Boiten (2000), p. 210). The design of flow-measuring flumes is based on the critical open-channel flow condition, which can be obtained by changing the channel size, e.g., using a side contraction or a bed level change (Bijankhan and Ferro 2017). Venturi was the first hydraulician to recognize the effect of a local contraction on both the pressure and the velocity distribution (Hager 1985). The well-known Venturi channel (Cone 1917) is a flat-bottom flume having a channel contraction obtained by a local thickening of the channel walls. Flumes with a local contraction of the channel width are widespread (Parshall 1926; Blaisdell 1994; Bijankhan and Ferro 2019), and in Europe, a throated flume characterized by a gradual width variation, named Khafagi flume, is widely used, whereas the Parshall flume is largely applied in Anglo-Saxon countries (Lotfi Kolavani et al. 2019).

As the cylinder is “the simplest body having a streamlined shape” (Hager 1985), Samani and Magallanez (2000) applied two semicylinders to the walls of a zero-sloping flume to obtain a width contraction from a channel width B to a throat width b. For this flume, Ferro (2002) proposed to describe the stage-discharge relationship by the following functional relationship:

$$f\left(Q,h,B,b,g,\mu \right)=0$$
(1)

in which f is a functional symbol, g is the acceleration due to gravity, and μ is water viscosity. For the SMBF flume, obtained by contracting a rectangular cross-section, having a width B, applying two semicylinders to the wall of a channel having a zero slope, Ferro (2002) proposed the following dimensionless functional stage-discharge relationship:

$$\phi \left(\frac{{Q}^{2/3}}{{g}^{1/3} {b}^{5/3}}, \frac{h}{b},r\right)=0$$
(2)

in which φ is a functional symbol, and r = b/B is the contraction ratio.

Baiamonte and Ferro (2007), using the incomplete self-similarity hypothesis (Barenblatt 1979, 1987; Ferro 1997), deduced the following stage-discharge equation:

$$\frac{{Q}^{2/3}}{{g}^{1/3} {b}^{5/3}}=a{\left( \frac{h}{b}\right)}^{n}$$
(3)

in which a and n are two coefficients that depend on the contraction ratio r. Baiamonte and Ferro (2007) determined a and n coefficients by the measurements carried out in a horizontal laboratory flume using six r values in the range 0.17–0.81. Carollo et al. (2016) tested the applicability of the theoretical stage-discharge (Eq. 3) using field measurements, carried out at the Sparacia experimental area, by a SMBF flume located in a horizontal channel and characterized by r = 0.5.

Recently, Achour and Amara (2022a) studied a flume in which the contraction is obtained by two prismatic elements (broad-crested lateral contraction) placed on each wall of the channel. The final flume configuration is that of a throat, having a length Lt, an opening width b, and a contraction ratio b/B, characterized by the following stage-discharge equation:

$$Q={C}_{d} b \sqrt{2g} {h}^{3/2}$$
(4)

where Cd is the discharge coefficient, for which Achour and Amara (2022a) deduced the following expression Cd,th:

$${C}_{d,th}= \frac{{\zeta }^{3/2}}{\sqrt{2}} {\left(\frac{1- {\xi }^{2}}{1-1.5 {\xi }^{2} }\right)}^{3/2}$$
(5)

in which ζ has to be calculated by the following approximate explicit relationship, which holds in the range 0.1 ≤ r ≤ 0.65:

$$\zeta =0.5789+ 0.103 r$$
(6)

and ξ is related to ζ by the following equation:

$$\xi =r {\zeta }^{3/2}$$
(7)

Equations (5), (6), and (7) demonstrate that the theoretical discharge coefficient is only dependent on the contraction ratio r. The analysis developed by Achour and Amara (2022a) demonstrated that the theoretical discharge coefficient overestimates the measured one as Cd = 0.9911 Cd,th.

Dividing both members of Eq. (4) by b3/2 and rearranging the following equation can be obtained:

$$\frac{{Q}^{2/3}}{{g}^{1/3} {b}^{5/3}}=\left({{C}_{d}}^{2/3} {2}^{1/3}\right) \frac{h}{b}$$
(8)

Equation (8) has the same mathematical shape of Eq. (3) with n = 1 and a = \({{C}_{d}}^{2/3} {2}^{1/3}\) depending only on the contraction ratio.

Achour and Amara (2022b) also studied a sharp-crested contraction obtained by introducing in a rectangular channel, B wide, two separate vertical thin plates forming a central opening with a width b < B. Their analysis demonstrated that Eq. (4) can be applied to express the stage-discharge relationship and the theoretical discharge coefficient Cd,th, which accounts for the effect of the approach flow velocity, is only dependent on the contraction ratio r according to the following equation:

$${C}_{d,th}= \frac{\sqrt{2}}{2} \left\{cos\left[\frac{1}{3} {cos}^{-1}\left(1-2 {r}^{2}\right)\right]+ \frac{1}{2}\right\}$$
(9)

The results by Achour and Amara (2022b) demonstrated that the theoretical discharge coefficient is very close to the measured one as Cd = 0.9998 Cd,th.

The U.S. Conservation Service (Brakensiek et al. 1979) proposed to measure flow discharge by H-flumes (Fig. 1) which are composed of a small inlet rectangular channel, having a depth D, and ending with a V-shaped opening. Three different versions (HS, H, and HL) of the flume are available and allow for measuring different ranges of discharge. For measuring discharge with the required accuracy, Brakensiek et al. (1979) recommended assembling the flume in strict accordance with the available drawings, in which dimensions of the H-flume components proportional to D are reported. The three versions have a different width B of the intel channel (1.05D for HS-flume, 1.9D for H, and 3.2D for HL) and a minimum recommended length of 2D. Bagarello and Ferro (2006), applying dimensional analysis and self-similarity theory, established that the stage-discharge relationship of each H-flume type can be expressed by the following equation:

$$\frac{{Q}^{2/3}}{{g}^{1/3} {B}^{2/3} D}=a{\left( \frac{h}{D}\right)}^{n}$$
(10)

in which h is the upstream water depth measured in the first cross-section of the end V opening, and the coefficients a and n, were determined by Bagarello and Ferro (2006) using the experimental measurements by Brakensiek et al. (1979).

Fig. 1
figure 1

Sketches (a) and view (b) of a H-flume

Full size image

Goel (2006) experimentally investigated a flume having a length 2b, consisting of an inlet reach, b long, in which the width linearly varies from the channel width B to b = B/2, and a throat reach, b long, having a constant width b. For the free-flow condition, a relationship between the discharge coefficient and the ratio h/B was established using measurements carried out in a laboratory flume (B = 0.4 m) and a field channel (B = 0.584 m).

Goel et al. (2015) carried out some experimental runs using a sharp-edged constricted flume having a plane transition, from the channel width B to the contracted width b, and four types of constrictions in the flow direction (2:1, 1.5:1, 1:1, and 90°). For the free-flow condition and each investigated flume, the discharge coefficient was related to the ratio b/h.

In this paper, the stage-discharge equation of a linear width contraction device was theoretically deduced by the π-Theorem of dimensional analysis and self-similarity condition. The coefficients of this new stage-discharge relationship were then estimated using the measurements by Goel et al. (2015). The proposed approach assured an accurate estimate of flow discharge. Moreover, the main novel element of this paper is to obtain a stage-discharge relationship giving an accurate estimate of discharge but, at the same time, having the advantage of working regardless of the discharge coefficient estimate.

Deducing the theoretical stage-discharge relationship of a linear width contraction device and a free-flow condition

For a linear width contraction device and a free-flow condition, the stage-discharge relationship is expressed by the following functional relationship:

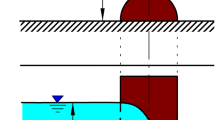
$$F\left(h, Q, g, \rho ,\mu , \sigma , B, b,\mathrm{sin}\alpha {, L}_{c}\right)=0$$
(11)

where F is a functional symbol, ρ is the water density, σ is the water surface tension, α is the angle of the device sides with the channel bank, and Lc is the length of the flume inlet reach (Fig. 2). The length of the flume throat Lt is not introduced into Eq. (11) as it is related to b, B, and α by the following equation:

$${L}_{t}=\frac{B-b}{2\,\mathrm{tan}\alpha }$$
(12)

As the functional relationship (Eq. 11) expresses a physical phenomenon that does not depend on the choice of measurement units, according to the π-theorem (Barenblatt 1979, 1987), Eq. (11) can be rewritten in the following dimensionless form:

$$\varphi \left({\Pi }_{1}, {\Pi }_{2}, {\Pi }_{3}, {\Pi }_{4}, {\Pi }_{5},{\Pi }_{6},{\Pi }_{7}\right)=0$$
(13)

where π1, π2, π3, π4, π5, π6 and π7 are dimensionless groups, and φ is a functional symbol.

Fig. 2
figure 2

Sketch of a linear width contraction device

Full size image

Using as dimensional independent variables B, g, and ρ, the following dimensionless groups are obtained (Nicosia and Ferro 2022; Nicosia et al. 2022a, b):

$${\Pi }_{1}= \frac{h}{B}$$
(14)
$${\Pi }_{2}= \frac{Q}{{B}^{5/2} {g}^{1/2}}$$
(15)
$${\Pi }_{3}= \frac{\mu }{{B}^{3/2} {g}^{1/2} \rho }$$
(16)
$${\Pi }_{4}=\frac{\sigma }{{B}^{2} g \rho }$$
(17)
$${\Pi }_{5}=\frac{b}{B}$$
(18)
$${\Pi }_{6}=\mathrm{sin}\alpha$$
(19)
$${\Pi }_{7}=\frac{{L}_{c}}{B}$$
(20)

Considering Eqs. (15) and (16), the following dimensionless group is obtained:

$${\Pi }_{\mathrm{3,2}}=\frac{{\Pi }_{2}}{{\Pi }_{3}}= \frac{Q}{{B}^{5/2} {g}^{1/2}} \frac{{B}^{3/2} {g}^{1/2} \rho }{\mu }= \frac{\rho Q}{\mu B}=Re$$
(21)

in which Re is the Reynolds number.

Considering Eqs. (14) and (17), the following dimensionless group is obtained:

$${\Pi }_{\mathrm{4,1}}=\frac{{\Pi }_{1}^{2}}{{\Pi }_{5}}= \frac{{h}^{2}}{{B}^{2}}\frac{{B}^{2} g \rho }{\sigma }= \frac{\varrho g {h}^{2}}{\sigma }=We$$
(22)

in which We is the Weber number.

Considering that some groups were rearranged to deduce dimensionless variables commonly used in hydraulics, the functional relationship (Eq. 13) can be rewritten as:

$${\varphi }_{2} \left({\Pi }_{1}, {\Pi }_{2}, {\Pi }_{\mathrm{3,2}}, {\Pi }_{\mathrm{4,1}}, {\Pi }_{5}, {\Pi }_{6},{\Pi }_{7}\right)=0$$
(23)

where φ2 is a functional symbol.

Considering the deduced dimensionless groups, the functional relationship (Eq. 23) can be rewritten as:

$${\varphi }_{2} \left(\frac{h}{B}, \frac{Q}{{B}^{5/2} {g}^{1/2}}, Re, We, \frac{b}{B},\mathrm{sin}\alpha , \frac{{L}_{c}}{B}\right)=0$$
(24)

Since for turbulent flows and water depth higher than 0.06 m the effects of the Reynolds number and the Weber number can be considered negligible (Sargison 1972; Ranga Raju and Asawa 1977; De Martino and Ragone 1984), Eq. (24) can be rewritten as follows:

$$\omega \left(\frac{h}{B}, \frac{Q}{{B}^{5/2} {g}^{1/2}}, \frac{b}{B},\mathrm{sin}\alpha , \frac{{L}_{c}}{B}\right)=0$$
(25)

where ω is a functional symbol.

For given values of the contraction ratio r = b/B, Lc/B, and the angle α, the functional relationship (Eq. 24) becomes:

$$\omega \left(\frac{h}{B}, \frac{Q}{{B}^{5/2} {g}^{1/2}}\right)=0$$
(26)

For determining the mathematical shape of the functional relationship (Eq. 26), the incomplete self-similarity condition (Barenblatt 1979, 1987) can be applied.

A phenomenon is defined as self-similar in a given dimensionless group πn when the functional relationship \({\Pi }_{1}={\varphi }_{3}\left({\Pi }_{2},{\Pi }_{3},\dots ..,{\Pi }_{n}\right)\), representing the physical phenomenon, is independent of πn. The self-similarity solutions of a problem are searched for boundary conditions, i.e., the behavior of φ3 is studied for \(\Pi_n \to 0\) or \(\Pi_n \to \infty\). When the function φ3 has a limit equal to 0 or ∞, the phenomenon is expressed by the following functional relationship:

$${\Pi }_{1}={\Pi }_{n}^{\varepsilon }{ \varphi }_{4}\left({\Pi }_{2},{\Pi }_{3},\dots ..,{\Pi }_{n-1}\right)$$
(27)

in which φ4 is a functional symbol, and ε is a numerical constant. This instance is named incomplete self-similarity (ISS) in the parameter πn (Barenblatt 1979; 1987).

When \(h/B\to 0\), then \(Q/{B}^{5/2} {g}^{1/2}\to 0\), and when \(h/B\to \infty\), then \(Q/{B}^{5/2} {g}^{1/2}\to \infty\), the ISS occurs. The functional relationship (Eq. 26) assumes the following mathematical shape (Barenblatt 1979, 1987):

$${\Pi }_{2}=\frac{Q}{{g}^{1/2} {B}^{5/2}}=a{\left( \frac{h}{B}\right)}^{n}$$
(28)

and the constants a and n have to be estimated by measurements.

Results and discussion

The theoretical stage-discharge relationship (Eq. 28) was calibrated using the measurements carried out by Goel et al. (2015) for a linear width contraction device. These authors carried out some experimental runs using a 12 m-long, 0.4 m-wide, and 0.6 m-deep horizontal rectangular flume. For these experimental runs, the device with different angles of its sides (sin α = 0.4472, 0.5547, 0.7071, and 1) was installed in a cross-section so that the upstream length of the channel, Lc, was sufficient for proper development of flow; i.e., the measurements by Goel et al. (2015) were carried out for a constant value of the ratio Lc/B. All the experiments by Goel et al. (2015) were performed using a single contraction ratio r of 0.5. Therefore, the measurements by Goel et al. (2015) allow for simply studying the variability of coefficients a and n of Eq. (28) with the angle α. The water depth upstream of the device was measured by a point gauge, and the flow discharge was measured by a flowmeter. Further details are reported in the paper by Goel et al. (2015).

The stage-discharge relationship (Eq. 28), corresponding to r = 0.5, was calibrated for each α value (Fig. 3) by the measured pairs (h, Q) obtained by Fig. 3 of the paper by Goel et al. (2015). For r = 0.5, the a and n coefficients of Eq. (28) are listed in Table 1.

Fig. 3
figure 3

Relationship between the stage-discharge equation (Eq. 28) and the experimental values h/B for α = 0.4472 (a), 0.5547 (b), 0.7071 (c), and 1 (d)

Full size image
Table 1 Values of the coefficients a and n of Eq. (28) for a linear width contraction device with r = 0.5
Full size table

The a and n values, listed in Table 1, point out that n varies in a narrow range (2.1452–2.1764), and consequently, a constant value corresponding to the mean n = 2.1653 can be applied.

In other words, the exponent n of the stage-discharge relationship (Eq. 28) can be assumed independent of the angle, and the stage-discharge relationship can assume the following form:

$$\frac{Q}{ {g}^{1/2}{B}^{5/2}}=a {\left(\frac{h}{B}\right)}^{2.1653}$$
(29)

The a values of Eq. (29), estimated by the least-square technique (Fig. 4), are listed in the last column of Table 1. These obtained values are related to sin α by the following equation (Fig. 5):

Fig. 4
figure 4

Relationship between the stage-discharge equation (Eq. 29) and the measurements for α = 0.4472 (a), 0.5547 (b), 0.7071 (c), and 1 (d)

Full size image
Fig. 5
figure 5

Relationship between sin α and the a values obtained for each angle value

Full size image
$$a=0.8935+0.4070 {\left(\mathrm{sin}\alpha \right)}^{2}-0.8115\mathrm{sin}\alpha$$
(30)

Figure 6 shows the comparison between measured discharge values Qm and those calculated by Eq. (29), with a estimated by Eq. (30), Qc. For the four investigated devices, the errors in the estimate of discharge E = 100 (Qc–Qm)/Qm for the stage-discharge relationship (Eq. 29), with a estimated by Eq. (30) range from − 3.84 to 1.9% (Fig. 7). The proposed stage-discharge equation is characterized by E values lower than or equal to ± 3% for 93.7% of cases and lower than or equal to ± 2% for 75.0% of cases. Therefore, the linear width contraction has a good accuracy of the measured discharge, less than the limit of ± 5% (Fig. 6) suggested in the literature (Boiten 2000). Figure 7 also demonstrates that the stage-discharge relationship is characterized by errors independent of the measured discharge Qm.

Fig. 6
figure 6

Comparison between measured discharge values Qm and those calculated by Eq. (29), with a estimated by Eq. (30), Qc

Full size image
Fig. 7
figure 7

Relationship between the errors in the estimate of discharge E = 100 (Qc–Qm)/Qm for the proposed stage-discharge relationship (Eq. 29), with a estimated by Eq. (30), and the measured flow discharge values Qm

Full size image

For each device, the discharge coefficient values, calculated by a power empirical relationship deduced by analyzing the pairs (b/h, Cd) measured by Goel et al. (2015), were introduced into Eq. (4) to evaluate if the proposed method (Eq. 29) guarantees an estimate of flow discharge as accurate as that obtained using Eq. (4). Using the estimated discharge coefficients and Eq. (4) gives E values lower than or equal to ± 2% for 78.0% of cases, highlighting a comparable accuracy in the discharge estimate. Nevertheless, the significant outcome of the developed analyses is a theoretical stage-discharge relationship which gives an accurate estimate of the flow discharge, but, at the same time, has the advantage of working regardless of the use of Eq. (4) and, consequently, the estimate of the discharge coefficient.

The limit of the proposed theoretical stage-discharge relationship depends on the available measurements to estimate the coefficients a and n of Eq. (28) as the experimental runs by Goel et al. (2015) were carried out for a known length of the inflow channel Lc (constant value of Lc/B), for a single contraction ratio r = 0.5 and four values of the angle α.

Further experiments are required to test the effect of the inflow channel length Lc on the stage-discharge relationship of a device, having given r and sen α values, and, possibly, state the minimum value of Lc useful to have a stable measurement of h. For given lengths of Lc and Lt, the measurement of pairs (h, Q), corresponding to devices with different r and α values, will allow for establishing the a and n coefficients of Eq. (28) for several geometrical configurations. This information will allow for determining the optimal dimensions (Lc/B, Lt/B) of the linear width contraction device and its stage-discharge relationship for different r and α values.

Conclusions

In this paper, the outflow process of a linear width contraction device for a free-flow condition is modeled using the dimensional analysis and the incomplete self-similarity condition.

This analysis allowed concluding that a power equation (Eq. 28) can be used for establishing the theoretical stage-discharge relationship of a device having given values of inflow channel length, contraction ratio, and angle of the device sides. The proposed flume is characterized by simple construction, easy installation, low cost, and a good accuracy of the measured discharge (ranging from -3.84 to 1.9%). The deduced stage-discharge equation is characterized by errors in the estimate of discharge lower than or equal to ± 3% for 93.7% of the investigated cases.

The linear width contraction has good accuracy, less than the limit of ± 5% suggested in the literature, in estimating the discharge. The main advantage of the proposed theoretical stage-discharge relationship is to join an accurate estimate of the flow discharge and working regardless of the discharge coefficient estimate.

Further investigations are required to test the effect of the flume geometrical characteristics (inflow channel length, contraction ratio, and angle of the device sides) on the stage-discharge relationship.