On Forced Periodicity of Perfect Colorings

Abstract

We study forced periodicity of two-dimensional configurations under certain constraints and use an algebraic approach to multidimensional symbolic dynamics in which d-dimensional configurations and finite patterns are presented as formal power series and Laurent polynomials, respectively, in d variables. We consider perfect colorings that are configurations such that the number of points of a given color in the neighborhood of any point depends only on the color of the point for some fixed relative neighborhood, and we show that by choosing the alphabet suitably any perfect coloring has a non-trivial annihilator, that is, there exists a Laurent polynomial whose formal product with the power series presenting the perfect coloring is zero. Using known results we obtain a sufficient condition for forced periodicity of two-dimensional perfect colorings. As corollaries of this result we get simple new proofs for known results of forced periodicity on the square and the triangular grids. Moreover, we obtain a new result concerning forced periodicity of perfect colorings in the king grid. We also consider perfect colorings of a particularly simple type: configurations that have low abelian complexity with respect to some shape, and we generalize a result that gives a sufficient condition for such configurations to be necessarily periodic. Also, some algorithmic aspects are considered.

1 Introduction

We say that a d-dimensional configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$, that is, a coloring of the d-dimensional integer grid $\mathbb {Z}^d$ using colors from a finite set $\mathcal {A}$ is a perfect coloring with respect to some finite relative neighborhood $D\subseteq \mathbb {Z}^d$ if the number of any given color of $\mathcal {A}$ in the pattern $c \vert _{\textbf{u} + D}$ depends only on the color $c(\textbf{u})$ for any $\textbf{u} \in \mathbb {Z}^d$. There is a similar version of this definition for general graphs: a vertex coloring $\varphi :V \rightarrow \mathcal {A}$ of a graph $G=(V,E)$ with a finite set $\mathcal {A}$ of colors is a perfect coloring of radius r if the number of any given color in the r-neighborhood of a vertex $u \in V$ depends only on the color $\varphi (u)$ of u [28, 29]. More generally, the definition of perfect colorings is a special case of the definition of equitable partitions [8].

If $\varphi :V \rightarrow \{0,1\}$ is a binary vertex coloring of a graph $G=(V,E)$ then we can define a subset $C \subseteq V$ of the vertex set – a code – such that it contains all the vertices with color 1. If $\varphi$ is a perfect coloring of radius r, then the code C has the property that the number of codewords of C in the r-neighborhood of a vertex $u \in V$ is a if $u \not \in C$ and b if $u \in C$ for some fixed non-negative integers a and b. This kind of code is called a perfect (r, b, a)-covering or simply just a perfect multiple covering [1, 5]. This definition is related to domination in graphs and covering codes [5, 11].

Let $D \subseteq \mathbb {Z}^d$ be a finite set and $\mathcal {A}$ a finite set of colors. Two finite patterns $p, q \in \mathcal {A}^D$ are abelian equivalent if the number of occurrences of each symbol in $\mathcal {A}$ is the same in them. The abelian complexity of a configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$ with respect to a finite shape D is the number of abelian equivalence classes of patterns of shape D in c [30]. We note that if $c \in \mathcal {A}^{\mathbb {Z}^d}$ is a perfect coloring with respect to D and $|\mathcal {A}| = n$, then the abelian complexity of c with respect to D is at most n. Abelian complexity is a widely studied concept in one-dimensional symbolic dynamics and combinatorics on words [22].

In this paper we study forced periodicity of two-dimensional perfect colorings, that is, we study conditions under which all the colorings are necessarily periodic. We give a general condition for forced periodicity. As corollaries of this result we get new proofs for known results [1, 28, 29] concerning forced periodicity of perfect colorings in the square and the triangular grid and a new result for forced periodicity of perfect colorings in the king grid. Moreover, we study two-dimensional configurations of low abelian complexity, that is, configurations that have abelian complexity 1 with respect to some shape: we generalize a statement of forced periodicity concerning this type of configurations. We use an algebraic approach [17] to multidimensional symbolic dynamics, i.e., we present configurations as formal power series and finite patterns as Laurent polynomials. This approach was developed to make progress in a famous open problem in symbolic dynamics – Nivat’s conjecture [27] – concerning forced periodicity of two-dimensional configurations that have a sufficiently low number of $m \times n$ rectangular patterns for some m, n. The Nivat’s conjecture thus claims a two-dimensional generalization of the Morse-Hedlund theorem [24].

This article is an extended version of the conference paper [12] where we considered forced periodicity of perfect coverings, that is, perfect colorings with only two colors.

1.1 The Structure of the Paper

We begin in Section 2 by introducing the basic concepts of symbolic dynamics, cellular automata and graphs, and defining perfect colorings formally. In Section 3 we present the relevant algebraic concepts and the algebraic approach to multidimensional symbolic dynamics, and in Section 4 we describe an algorithm to find the line polynomial factors of a given two-dimensional Laurent polynomial. In Section 5 we consider forced periodicity of perfect coverings, i.e., perfect colorings with only two colors and then in Section 6 we extend the results from the previous section to concern perfect colorings using arbitrarily large alphabets. After this we prove a statement concerning forced periodicity of two-dimensional configurations of low abelian complexity in Section 7. In Section 8 we consider some algorithmic questions concerning perfect colorings.

2 Preliminaries

2.1 Basics on symbolic dynamics

Let us review briefly some basic concepts of symbolic dynamics relevant to us. For a reference see e.g. [4, 19, 21]. Although our results concern mostly two-dimensional configurations, we state our definitions in an arbitrary dimension.

Let $\mathcal {A}$ be a finite set (the alphabet) and let d be a positive integer (the dimension). A d-dimensional configuration over $\mathcal {A}$ is a coloring of the infinite grid $\mathbb {Z}^d$ using colors from $\mathcal {A}$, that is, an element of $\mathcal {A}^{\mathbb {Z}^d}$ – the d-dimensional configuration space over the alphabet $\mathcal {A}$. which we call the d-dimensional configuration space. We denote by $c_{\textbf{u}} = c(\textbf{u})$ the symbol or color that a configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$ has in cell $\textbf{u}$. The translation $\tau ^{\textbf{t}}$ by a vector $\textbf{t} \in \mathbb {Z}^d$ shifts a configuration c such that $\tau ^{\textbf{t}}(c)_{\textbf{u}} = c_{\textbf{u} - \textbf{t}}$ for all $\textbf{u}\in \mathbb {Z}^d$. A configuration c is $\textbf{t}$-periodic if $\tau ^{\textbf{t}}(c) = c$, and it is periodic if it is $\textbf{t}$-periodic for some non-zero $\textbf{t} \in \mathbb {Z}^d$. Moreover, we say that a configuration is periodic in direction $\textbf{v} \in \mathbb {Q}^d\setminus \{\textbf{0}\}$ if it is $k \textbf{v}$-periodic for some $k \in \mathbb {Z}$. A d-dimensional configuration c is strongly periodic if it has d linearly independent vectors of periodicity. A strongly periodic configuration is periodic in every rational direction. Two-dimensional strongly periodic configurations are called two-periodic.

A finite pattern is an assignment of symbols on some finite shape $D \subseteq \mathbb {Z}^d$, that is, an element of $\mathcal {A}^D$. In particular, the finite patterns in $\mathcal {A}^D$ are called D-patterns. Let us denote by $\mathcal {A}^*$ the set of all finite patterns over $\mathcal {A}$ where the dimension d is known from the context. We say that a finite pattern $p \in \mathcal {A}^D$ appears in a configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$ or that c contains p if $\tau ^{\textbf{t}}(c) \vert _D = p$ for some $\textbf{t} \in \mathbb {Z}^d$. For a fixed shape D, the set of all D-patterns of c is the set $\mathcal {L}_{D}(c) = \{ \tau ^{\textbf{t}}(c) \vert _D \mid \textbf{t} \in \mathbb {Z}^d \}$ and the set of all finite patterns of c is denoted by $\mathcal {L}(c)$ which is called the language of c. For a set $\mathcal {S} \subseteq \mathcal {A}^{\mathbb {Z}^d}$ of configurations we define $\mathcal {L}_{D}(\mathcal {S})$ and $\mathcal {L}(\mathcal {S})$ as the unions of $\mathcal {L}_{D}(c)$ and $\mathcal {L}(c)$ over all $c\in \mathcal {S}$, respectively.

The pattern complexity P(c, D) of a configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$ with respect to a shape D is the number of distinct D-patterns that c contains. For any $a \in \mathcal {A}$ we denote by $\vert p \vert _a$ the number of occurrences of the color a in a finite pattern p. Two finite patterns $p,q \in \mathcal {A}^{D}$ are called abelian equivalent if $\vert p \vert _a = \vert q \vert _a$ for all $a \in \mathcal {A}$, that is, if the number of occurrences of each color is the same in both p and q. The abelian complexity A(c, D) of a configuration $c \in \mathcal {A}^{\mathbb {Z}^2}$ with respect to a finite shape D is the number of different D-patterns in c up to abelian equivalence [30]. Clearly $A(c,D) \le P(c,D)$. We say that c has low complexity with respect to D if

$$\begin{aligned} P(c,D) \le |D| \end{aligned}$$

and that c has low abelian complexity with respect to D if

$$\begin{aligned} A(c,D) = 1. \end{aligned}$$

The configuration space $\mathcal {A}^{\mathbb {Z}^d}$ can be made a compact topological space by endowing $\mathcal {A}$ with the discrete topology and considering the product topology it induces on $\mathcal {A}^{\mathbb {Z}^d}$ – the prodiscrete topology. This topology is induced by a metric where two configurations are close if they agree on a large area around the origin. So, $\mathcal {A}^{\mathbb {Z}^d}$ is a compact metric space.

A subset $\mathcal {S} \subseteq \mathcal {A}^{\mathbb {Z}^d}$ of the configuration space is a subshift if it is topologically closed and translation-invariant meaning that if $c \in \mathcal {S}$, then for all $\textbf{t} \in \mathbb {Z}^d$ also $\tau ^{\textbf{t}}(c) \in \mathcal {S}$. Equivalently, subshifts can be defined using forbidden patterns: Given a set $F \subseteq \mathcal {A}^*$ of forbidden finite patterns, the set

$$\begin{aligned} X_F=\{c \in \mathcal {A}^{\mathbb {Z}^d} \mid \mathcal {L}(c) \cap F = \emptyset \} \end{aligned}$$

of configurations that avoid all forbidden patterns is a subshift. Moreover, every subshift is obtained by forbidding some set of finite patterns. If $F \subseteq \mathcal {A}^*$ is finite, then we say that $X_F$ is a subshift of finite type (SFT).

The orbit of a configuration c is the set $\mathcal {O}(c) = \{ \tau ^{\textbf{t}}(c) \mid \textbf{t} \in \mathbb {Z}^d \}$ of its every translate. The orbit closure $\overline{\mathcal {O}(c)}$ is the topological closure of its orbit under the prodiscrete topology. The orbit closure of a configuration c is the smallest subshift that contains c. It consists of all configurations $c'$ such that $\mathcal {L}(c')\subseteq \mathcal {L}(c)$.

2.2 Cellular Automata

Let us describe briefly an old result of cellular automata theory that we use in Section 6. See [13] for a more thorough survey on the topic.

A d-dimensional cellular automaton or a CA for short over a finite alphabet $\mathcal {A}$ is a map $F :\mathcal {A}^{\mathbb {Z}^d} \longrightarrow \mathcal {A}^{\mathbb {Z}^d}$ determined by a neighborhood vector $N = (\textbf{t}_1, \ldots , \textbf{t}_n )$ and a local rule $f :\mathcal {A}^n \longrightarrow \mathcal {A}$ such that

$$\begin{aligned} F(c)(\textbf{u}) = f(c(\textbf{u} + \textbf{t}_1), \ldots , c(\textbf{u} + \textbf{t}_n)). \end{aligned}$$

A CA is additive or linear if its local rule is of the form

$$\begin{aligned} f(x_1,\ldots ,x_n) = a_1x_1 + \ldots + a_n x_n \end{aligned}$$

where $a_1,\ldots ,a_n \in R$ are elements of some finite ring R and $\mathcal {A}$ is an R-module.

In Section 6 we consider the surjectivity of cellular automata and use a classic result called the Garden-of-Eden theorem proved by Moore and Myhil that gives a characterization for surjectivity in terms of injectivity on “finite” configurations. Two configurations $c_1$ and $c_2$ are called asymptotic if the set $\text {diff}(c_1,c_2) = \{ \textbf{u} \mid c_1(\textbf{u}) \ne c_2(\textbf{u}) \}$ of cells where they differ is finite. A cellular automaton F is pre-injective if $F(c_1) \ne F(c_2)$ for any distinct asymptotic configurations $c_1$ and $c_2$. Clearly injective CA are pre-injective. The Garden-of-Eden theorem states that pre-injectivity of a CA is equivalent to surjectivity:

Theorem

(Garden-of-Eden theorem, [23, 25]) A CA is surjective if and only if it is pre-injective.

In the one-dimensional setting the Garden-of-Eden theorem yields the following corollary:

Corollary

For a one-dimensional surjective CA every configuration has only a finite number of pre-images.

2.3 Graphs

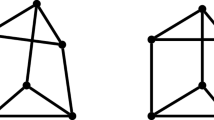
In this paper we consider graphs that are simple, undirected and connected. A graph G that has vertex set V and edge set E is denoted by $G=(V,E)$. The distance d(u, v) of two vertices $u\in V$ and $v\in V$ of a graph $G = (V,E)$ is the length of a shortest path between them in G. The r-neighborhood of $u \in V$ in a graph $G = (V,E)$ is the set $N_r(u) = \{ v \in V \mid d(v,u) \le r \}$. The graphs we consider has vertex set $V = \mathbb {Z}^2$ and a translation invariant edge set $E \subseteq \{ \{ \textbf{u}, \textbf{v} \} \mid \textbf{u}, \textbf{v} \in \mathbb {Z}^2, \textbf{u} \ne \textbf{v} \}$. This implies that for all r and for any two points $\textbf{u}\in \mathbb {Z}^2$ and $\textbf{v} \in \mathbb {Z}^2$ their r-neighborhoods are the same up to translation, that is, $N_r(\textbf{u}) =N_r(\textbf{v}) + \textbf{u} - \textbf{v}$. Moreover, we assume that all the vertices of G have only finitely many neighbors, i.e., we assume that the degree of G is finite. We call these graphs two-dimensional (infinite) grid graphs or just (infinite) grids. In a grid graph G, let us call the r-neighborhood of $\textbf{0}$ the relative r-neighborhood of G since it determines the r-neighborhood of any vertex in G. Indeed, for all $\textbf{u} \in \mathbb {Z}^2$ we have $N_r(\textbf{u}) = N_r + \textbf{u}$ where $N_r$ is the relative r-neighborhood of G. Given the edge set of a grid graph, the relative r-neighborhood is determined for every r. We specify three 2-dimensional infinite grid graphs:

• The square grid is the infinite grid graph $(\mathbb {Z}^2, E_{\mathcal {S}})$ with

  $$\begin{aligned} E_{\mathcal {S}} = \{ \{ \textbf{u} , \textbf{v} \} \mid \textbf{u} - \textbf{v} \in \{ (\pm 1,0), (0,\pm 1) \} \}. \end{aligned}$$

• The triangular grid is the infinite grid graph $(\mathbb {Z}^2, E_{\mathcal {T}})$ with

  $$\begin{aligned} E_{\mathcal {T}} = \{ \{ \textbf{u}, \textbf{v} \} \mid \textbf{u} - \textbf{v} \in \{ (\pm 1,0),(0,\pm 1),(1,1),(-1,-1) \} \}. \end{aligned}$$

• The king grid is the infinite grid graph $(\mathbb {Z}^2, E_{\mathcal {K}})$ with

  $$\begin{aligned} E_{\mathcal {K}} = \{ \{ \textbf{u}, \textbf{v} \} \mid \textbf{u} - \textbf{v} \in \{ (\pm 1,0),(0,\pm 1),(\pm 1,\pm 1) \} \}. \end{aligned}$$

The relative 2-neighborhoods of these grid graphs are pictured in Fig. 1.

Fig. 1

The relative 2-neighborhoods of the square grid, the triangular grid and the king grid, respectively

2.4 Perfect Colorings

Let $\mathcal {A}= \{a_1,\ldots ,a_n\}$ be a finite alphabet of n colors and let $D \subseteq \mathbb {Z}^d$ be a finite shape. A configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$ is a perfect coloring with respect to $D \subseteq \mathbb {Z}^d$ or a D-perfect coloring if for all $i,j \in \{1,\ldots , n\}$ there exist numbers $b_{ij}$ such that for all $\textbf{u} \in \mathbb {Z}^d$ with $c_{\textbf{u}} = a_j$ the number of occurrences of color $a_i$ in the D-neighborhood of $\textbf{u}$, i.e., in the pattern $c \vert _{\textbf{u} + D}$ is exactly $b_{ij}$. The matrix of a D-perfect coloring c is the matrix $\textbf{B} = (b_{ij})_{n \times n}$ where the numbers $b_{ij}$ are as above. A D-perfect coloring with matrix $\textbf{B}$ is called a (perfect) $(D,\textbf{B})$-coloring. Any D-perfect coloring is called simply a perfect coloring. In other words, a configuration is a perfect coloring if the number of cells of a given color in the given neighborhood of a vertex $\textbf{u}$ depends only on the color of $\textbf{u}$.

Perfect colorings are defined also for arbitrary graphs $G=(V,E)$. Again, let $\mathcal {A}= \{a_1, \ldots , a_n \}$ be a finite set of n colors. A vertex coloring $\varphi :V \rightarrow \mathcal {A}$ of G is an r-perfect coloring with matrix $\textbf{B} = (b_{ij})_{n \times n}$ if the number of vertices of color $a_i$ in the r-neighborhood of a vertex of color $a_j$ is exactly $b_{ij}$. Clearly if G is a translation invariant graph with vertex set $\mathbb {Z}^d$, then the r-perfect colorings of G are exactly the D-perfect colorings in $\mathcal {A}^{\mathbb {Z}^d}$ where D is the relative r-neighborhood of the graph G.

3 Algebraic Concepts

We review the basic concepts and some results relevant to us concerning an algebraic approach to multidimensional symbolic dynamics introduced and studied in [17]. See also [14] for a short survey of the topic.

Let $c \in \mathcal {A}^{\mathbb {Z}^d}$ be a d-dimensional configuration. The power series presenting c is the formal power series

$$\begin{aligned} c(X) = c(x_1,\ldots ,x_d) = \sum _{\textbf{u} = (u_1,\ldots ,u_d) \in \mathbb {Z}^d} c_{\textbf{u}} x_1^{u_1} \cdots x_d^{u_d} = \sum _{\textbf{u} \in \mathbb {Z}^d} c_{\textbf{u}} X^{\textbf{u}} \end{aligned}$$

in d variables $X = (x_1, \ldots , x_d)$. We denote the set of all formal power series in d variables $X = (x_1,\ldots ,x_d)$ over a domain M by $M[[X^{\pm 1}]] = M[[x_1^{\pm 1},\ldots ,x_d^{\pm 1}]]$. If $d=1$ or $d=2$, we denote $x=x_1$ and $y=x_2$. A power series is finitary if it has only finitely many distinct coefficients and integral if its coefficients are all integers, i.e., if it belongs to the set $\mathbb {Z}[[X^{\pm 1}]]$. A configuration is always presented by a finitary power series and a finitary power series always presents a configuration. So, from now on we may call any finitary power series a configuration.

We consider also Laurent polynomials which we may call simply just polynomials. We denote the set of Laurent polynomials in d variables $X=(x_1,\ldots ,x_d)$ over a ring R by $R[X^{\pm 1}] = R[x_1^{\pm 1}, \ldots , x_d^{\pm 1}]$. The term “proper” is used when we talk about proper (i.e., non-Laurent) polynomials and denote the proper polynomial ring over R by R[X] as usual.

We say that two Laurent polynomials have no common factors if all their common factors are units in the polynomial ring under consideration and that they have a common factor if they have a non–unit common factor. For example, in $\mathbb {C}[X^{\pm 1}]$ two polynomials have no common factors if all their common factors are constants or monomials, and two proper polynomials in $\mathbb {C}[X]$ have no common factors if all their common factors are constants. The support of a power series $c = c(X) = \sum _{\textbf{u} \in \mathbb {Z}^d} c_{\textbf{u}} X^{\textbf{u}}$ is the set $\text {supp}(c) = \{ \textbf{u} \in \mathbb {Z}^d \mid c_{\textbf{u}} \ne 0 \}$. Clearly a polynomial is a power series with a finite support. The kth dilation of a polynomial f(X) is the polynomial $f(X^k)$. See Fig. 2 for an illustration of dilations.

Fig. 2

The supports of the polynomial $f(X) = 1 + x^{-1}y^{-1} + x^{-1}y^{1} + x^{1}y^{-1} + x^{1}y^{1}$ and its dilations $f(X^2)$ and $f(X^3)$

The $x_i$-resultant $\text {Res}_{x_i}(f,g)$ of two proper polynomials $f,g \in R[x_1, \ldots , x_d]$ is the determinant of the Sylvester matrix of f and g with respect to variable $x_i$. We omit the details which the reader can check from [6], and instead we consider the resultant $\text {Res}_{x_i}(f,g) \in R[x_1,\ldots ,x_{i-1},x_{i+1},\ldots ,x_d]$ for every $i \in \{1,\ldots ,d\}$ as a certain proper polynomial that has the following two properties:

• $\text {Res}_{x_i}(f,g)$ is in the ideal generated by f and g, i.e., there exist proper polynomials h and l such that

  $$\begin{aligned} hf + lg = \text {Res}_{x_i}(f,g). \end{aligned}$$

• If two proper polynomials f and g have no common factors in $R[x_1, \ldots , x_d]$, then $\text {Res}_{x_i}(f,g) \ne 0$.

Let R be a ring and M a (left) R-module. The formal product of a polynomial $f=f(X) = \sum _{i=1}^m a_i X^{\textbf{u}_i} \in R[X^{\pm 1}]$ and a power series $c=c(X) = \sum _{\textbf{u} \in \mathbb {Z}^d} c_{\textbf{u}} X^{\textbf{u}} \in M[X^{\pm 1}]$ is well-defined as the formal power series

$$\begin{aligned} fc=f(X) c(X) = \sum _{\textbf{u} \in \mathbb {Z}^d} (fc)_{\textbf{u}} X^{\textbf{u}} \in M[X^{\pm 1}] \end{aligned}$$

where

$$\begin{aligned} (fc)_{\textbf{u}} = \sum _{i=1}^m a_i c_{\textbf{u} - \textbf{u}_i}. \end{aligned}$$

We say that a polynomial $f=f(X)$ annihilates (or is an annihilator of) a power series $c=c(X)$ if $fc=0$, that is, if their product is the zero power series.

In a typical setting, we assume that $\mathcal {A}\subseteq \mathbb {Z}$ and hence consider any configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$ as a finitary and integral power series c(X). Since multiplying c(X) by the monomial $X^{\textbf{u}}$ produces the power series presenting the translation $\tau ^{\textbf{u}}(c)$ of c by $\textbf{u}$, we have that c is $\textbf{u}$-periodic if and only if c(X) is annihilated by the difference polynomial $X^{\textbf{u}}-1$. (By a difference polynomial we mean a polynomial $X^{\textbf{u}}-1$ for any $\textbf{u}\ne 0$.) This means that it is natural to consider multiplication of c by polynomials in $\mathbb {C}[X^{\pm 1}]$. However, note that the product of c and a polynomial $f \in \mathbb {C}[X^{\pm 1}]$ may not be integral, but it is still finitary, hence a configuration.

We say that a polynomial f periodizes (or is a periodizer of) a configuration c if fc is strongly periodic, that is, periodic in d linearly independent directions. We denote the set of all periodizers with complex coefficients of a configuration c by $\text {Per}(c)$ which is an ideal of $\mathbb {C}[X^{\pm 1}]$ and hence we call it the periodizer ideal of c.

Note that annihilators are periodizers. Note also that if c has a periodizer f, then $(X^{\textbf{u}}-1)f$ is an annihilator of c for some $\textbf{u}$. Thus, c has a non-trivial (= non-zero) annihilator if and only if it has a non-trivial periodizer. The following theorem states that if a configuration has a non-trivial periodizer, then it has in fact an annihilator of a particular simple form – a product of difference polynomials.

Theorem 1

([17]) Let $c \in \mathbb {Z}[[X^{\pm 1}]]$ be a configuration in any dimension and assume that it has a non-trivial periodizer. Then there exist $m \ge 1$ and pairwise linearly independent vectors $\textbf{t}_1, \ldots ,\textbf{t}_m$ such that

$$\begin{aligned} (X^{\textbf{t}_1}-1) \cdots (X^{\textbf{t}_m}-1) \end{aligned}$$

annihilates c.

A line polynomial is a polynomial whose support contains at least two points and the points of the support lie on a unique line. In other words, a polynomial f is a line polynomial if it is not a monomial and there exist vectors $\textbf{u}, \textbf{v} \in \mathbb {Z}^d$ such that $\text {supp}(f) \subseteq \textbf{u} + \mathbb {Q}\textbf{v}$. In this case we say that f is a line polynomial in direction $\textbf{v}$. We say that non-zero vectors $\textbf{v},\textbf{v}'\in \mathbb {Z}^d$ are parallel if $\textbf{v}'\in \mathbb {Q}\textbf{v}$, and clearly then a line polynomial in direction $\textbf{v}$ is also a line polynomial in any parallel direction. A vector $\textbf{v}\in \mathbb {Z}^d$ is primitive if its components are pairwise relatively prime. If $\textbf{v}$ is primitive, then $\mathbb {Q}\textbf{v}\cap \mathbb {Z}^d = \mathbb {Z}\textbf{v}$. For any non-zero $\textbf{v}\in \mathbb {Z}^d$ there exists a parallel primitive vector $\textbf{v}'\in \mathbb {Z}^d$. Thus, we may assume the vector $\textbf{v}$ in the definition of a line polynomial f to be primitive so that $\text {supp}(f) \subseteq \textbf{u} + \mathbb {Z}\textbf{v}$. In the following our preferred presentations of directions are in terms of primitive vectors.

Any line polynomial $\phi$ in a (primitive) direction $\textbf{v}$ can be written uniquely in the form

$$\begin{aligned} \phi = X^{\textbf{u}}(a_0 + a_1 X^{\textbf{v}} + \ldots + a_n X^{n \textbf{v}}) = X^{\textbf{u}}(a_0 + a_1 t + \ldots + a_n t^n) \end{aligned}$$

where $\textbf{u} \in \mathbb {Z}^d, n \ge 1 , a_0 \ne 0 , a_n \ne 0$ and $t = X^{\textbf{v}}$. Let us call the single variable proper polynomial $a_0 + a_1 t + \ldots + a_n t^n \in \mathbb {C}[t]$ the normal form of $\phi$. Moreover, for a monomial $a X^{\textbf{u}}$ we define its normal form to be a. So, two line polynomials in the direction $\textbf{v}$ have the same normal form if and only if they are the same polynomial up to multiplication by $X^{\textbf{u}}$, for some $\textbf{u}\in \mathbb {Z}^d$.

Difference polynomials are line polynomials and hence the annihilator provided by Theorem 1 is a product of line polynomials. Annihilation by a difference polynomial means periodicity. More generally, annihilation of a configuration c by a line polynomial in a primitive direction $\textbf{v}$ can be understood as the annihilation of the one-dimensional $\textbf{v}$-fibers $\sum _{k \in \mathbb {Z}} c_{\textbf{u} + k \textbf{v}} X^{\textbf{u}+k\textbf{v}}$ of c in direction $\textbf{v}$, and since annihilation in the one-dimensional setting implies periodicity with a bounded period, we conclude that a configuration is periodic if and only if it is annihilated by a line polynomial. It is known that if c has a periodizer with line polynomial factors in at most one primitive direction, then c is periodic:

Theorem 2

([18]) Let $c \in \mathbb {Z}[[x^{\pm 1},y^{\pm 1}]]$ be a two-dimensional configuration and let f be a periodizer of c. Then the following conditions hold.

• If f does not have any line polynomial factors, then c is two-periodic.

• If all line polynomial factors of f are in the same primitive direction, then c is periodic in this direction.

Proof sketch. The periodizer ideal $\text {Per}(c) = \{ g \in \mathbb {C}[x^{\pm 1}, y^{\pm 1}] \mid gc \text { is two-periodic} \}$ of c is a principal ideal generated by a polynomial $g = \phi _1 \cdots \phi _m$ where $\phi _1, \ldots ,\phi _m$ are line polynomials in pairwise non-parallel directions [18]. Because $f\in \text {Per}(c)$, we know that g divides f. If f does not have any line polynomial factors, then $g = 1$ and hence $c = gc$ is two-periodic. If f has line polynomial factors, and they are in the same primitive direction $\textbf{v}$, then g is a line polynomial in this direction. Since gc is two-periodic, it is annihilated by $(X^{k \textbf{v}} - 1)$ for some $k \in \mathbb {Z}$. This implies that the configuration c is annihilated by the line polynomial $(X^{k \textbf{v}} - 1)g$ in direction $\textbf{v}$. We conclude that c is periodic in direction $\textbf{v}$. $\square$

The proof of the previous theorem sketched above relies heavily on the structure of the ideal $\text {Per}(c)$ developed in [17]. We give an alternative proof sketch that mimics the usage of resultants in [16]:

Second proof sketch of Theorem 2. The existence of a non-trivial periodizer f implies by Theorem 1 that c has a special annihilator $g=\phi _1 \cdots \phi _m$ that is a product of (difference) line polynomials $\phi _1, \ldots ,\phi _m$ in pairwise non-parallel directions. All irreducible factors of g are line polynomials. If f does not have any line polynomial factors, then the periodizers f and g do not have common factors. We can assume that both are proper polynomials as they can be multiplied by a suitable monomial if needed. Because $f,g\in \text {Per}(c)$, also their resultant $\text {Res}_x(f,g)\in \text {Per}(c)$, implying that c has a non-trivial annihilator containing only variable y since $\text {Res}_x(f,g) \ne 0$ because f and g have no common factors. This means that c is periodic in the vertical direction. Analogously, the y-resultant $\text {Res}_y(f,g)$ shows that c is horizontally periodic, and hence two-periodic.

The proof for the case that f has line polynomial factors only in one direction $\textbf{v}$ goes analogously by considering $\phi c$ instead of c, where $\phi$ is the greatest common line polynomial factor of f and g in the direction $\textbf{v}$. We get that $\phi c$ is two-periodic, implying that c is periodic in direction $\textbf{v}$. $\square$

In this paper we also consider configurations over alphabets $\mathcal {A}$ that are finite subsets of $\mathbb {Z}^{n}$, that is, the set of length n integer vectors, and hence study finitary formal power series from the set $\mathbb {Z}^n[[X^{\pm 1}]]$ for $n \ge 2$. In particular, we call this kind of configurations integral vector configurations. Also in this setting we consider multiplication of power series by polynomials. The coefficients of the polynomials are $n \times n$ integer matrices, i.e., elements of the ring $\mathbb {Z}^{n \times n}$. Since $\mathbb {Z}^n$ is a (left) $\mathbb {Z}^{n \times n}$-module where we consider the vectors of $\mathbb {Z}^n$ as column vectors, the product of a polynomial $f= f(X) \in \mathbb {Z}^{n\times n}[X^{\pm 1}]$ and a power series $c = c(X) \in \mathbb {Z}^n[[X^{\pm 1}]]$ is well-defined. Consequently, we say that $c(X) \in \mathbb {Z}^n[[X^{\pm 1}]]$ is $\textbf{t}$-periodic if it is annihilated by the polynomial $\textbf{I} X^{\textbf{t}} - \textbf{I}$ and that it is periodic if it is $\textbf{t}$-periodic for some non-zero $\textbf{t}$.

There is a natural way to present configurations over arbitrary alphabets as integral vector configurations. Let $\mathcal {A}= \{ a_1, \ldots , a_n \}$ be a finite alphabet with n elements. The vector presentation of a configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$ is the configuration $c' \in \{ \textbf{e}_1, \ldots , \textbf{e}_n \} ^{\mathbb {Z}^d}$ (or the power series $c'(X) \in \mathbb {Z}^n[[X^{\pm 1}]]$ presenting $c'$) defined such that $c'_{\textbf{u}} = \textbf{e}_i$ if and only if $c_{\textbf{u}} = a_i$. Here by $\textbf{e}_i \in \mathbb {Z}^n$ we denote the ith natural base vector, i.e., the vector whose ith component is 1 while all the other components are 0. Clearly c is $\textbf{t}$-periodic if and only if its vector presentation is $\textbf{t}$-periodic. Thus, to study the periodicity of a configuration it is sufficient to study the periodicity of its vector presentation.

The ith layer of $c = \sum \textbf{c}_{\textbf{u}} X^{\textbf{u}} \in \mathbb {Z}^n[[X^{\pm 1}]]$ is the power series

$$\begin{aligned} \text {layer}_i(c) = \sum c_{\textbf{u}}^{(i)} X^{\textbf{u}} \in \mathbb {Z}[[X^{\pm 1}]] \end{aligned}$$

where $c_{\textbf{u}}^{(i)}$ is the ith component of $\textbf{c}_{\textbf{u}}$. Clearly $c \in \mathbb {Z}^n[[X^{\pm 1}]]$ is periodic in direction $\textbf{v}$ if and only if for all $i \in \{1,\ldots ,n\}$ the ith layer of c is periodic in direction $\textbf{v}$.

Finally, let R be a finite ring and $\mathcal {A}$ a finite R-module. A polynomial $f(X) = \sum _{i=1}^n a_i X^{-\textbf{u}_i} \in R[x_1^{\pm 1}, \ldots , x_d^{\pm 1}]$ defines an additive CA that has neighborhood vector $(\textbf{u}_1,\ldots ,\textbf{u}_n)$ and local rule $f'(y_1,\ldots ,y_n) = a_1y_1 + \ldots + a_ny_n$. More precisely, the image of a configuration c under the CA determined by f is the configuration fc.

4 Finding the Line Polynomial Factors of a Given Two-Variate Laurent Polynomial

In this section we have $d=2$ and hence all our polynomials are in two variables x and y. The open and closed discrete half planes determined by a non-zero vector $\textbf{v} \in \mathbb {Z}^2$ are the sets $H_{\textbf{v}} = \{ \textbf{u} \in \mathbb {Z}^2 \mid \langle \textbf{u} , \textbf{v} ^{\perp } \rangle > 0 \}$ and $\overline{H}_{\textbf{v}} = \{ \textbf{u} \in \mathbb {Z}^2 \mid \langle \textbf{u} , \textbf{v} ^{\perp } \rangle \ge 0 \}$, respectively, where $\textbf{v}^{\perp } = (v_2,-v_1)$ is orthogonal to $\textbf{v} = (v_1,v_2)$. Let us also denote by $l_{\textbf{v}} = \overline{H}_{\textbf{v}} \setminus H_{\textbf{v}}$ the discrete line parallel to $\textbf{v}$ that goes through the origin. In other words, the half plane determined by $\textbf{v}$ is the half plane “to the right” of the line $l_{\textbf{v}}$ when moving along the line in the direction of $\textbf{v}$. We say that a finite set $D \subseteq \mathbb {Z}^2$ has an outer edge in direction $\textbf{v}$ if there exists a vector $\textbf{t} \in \mathbb {Z}^2$ such that $D \subseteq \overline{H}_{\textbf{v}} + \textbf{t}$ and $\vert D \cap (l_{\textbf{v}} + \textbf{t}) \vert \ge 2$. We call $D \cap (l_{\textbf{v}} + \textbf{t})$ the outer edge of D in direction $\textbf{v}$. An outer edge corresponding to $\textbf{v}$ means that the convex hull of D has an edge in direction $\textbf{v}$ in the clockwise orientation around D.

If a finite non-empty set D does not have an outer edge in direction $\textbf{v}$, then there exists a vector $\textbf{t} \in \mathbb {Z}^2$ such that $D \subseteq \overline{H}_{\textbf{v}} + \textbf{t}$ and $\vert D \cap (l_{\textbf{v}} + \textbf{t}) \vert = 1$, and then we say that D has a vertex in direction $\textbf{v}$. We call $D \cap (l_{\textbf{v}} + \textbf{t})$ the vertex of D in direction $\textbf{v}$. We say that a polynomial f has an outer edge or a vertex in direction $\textbf{v}$ if its support has an outer edge or a vertex in direction $\textbf{v}$, respectively. Note that every non-empty finite shape D has either an edge or a vertex in any non-zero direction. Note also that in this context directions $\textbf{v}$ and $-\textbf{v}$ are not the same: a shape may have an outer edge in direction $\textbf{v}$ but no outer edge in direction $-\textbf{v}$. The following lemma shows that a polynomial can have line polynomial factors only in the directions of its outer edges.

Lemma 3

([16]) Let f be a non-zero polynomial with a line polynomial factor in direction $\textbf{v}$. Then f has outer edges in directions $\textbf{v}$ and $-\textbf{v}$.

Let $\textbf{v} \in \mathbb {Z}^2 \setminus \{ \textbf{0} \}$ be a non-zero primitive vector and let $f = \sum f_{\textbf{u}} X^{\textbf{u}}$ be a polynomial. Recall that a $\textbf{v}$-fiber of f is a polynomial of the form

$$\sum _{k \in \mathbb {Z}} f_{\textbf{u} + k \textbf{v}} X^{\textbf{u} + k \textbf{v}}$$

for some $\textbf{u}\in \mathbb {Z}^2$. Thus, a non-zero $\textbf{v}$-fiber of a polynomial is either a line polynomial or a monomial. Let us denote by $\mathcal {F}_{\textbf{v}}(f)$ the set of different normal forms of all non-zero $\textbf{v}$-fibers of a polynomial f, which is hence a finite set of one-variate proper polynomials. The following simple example illustrates the concept of fibers and their normal forms.

Example 4

Let us determine the set $\mathcal {F}_{\textbf{v}}(f)$ for $f = f(X) = f(x,y) = 3x + y + xy^2 +xy + x^3y^3 + x^4y^4$ and $\textbf{v} = (1,1)$. By grouping the terms we can write

$$\begin{aligned} f = 3x + y(1 + xy) + xy(1 + x^2y^2 + x^3y^3) = X^{(1,0)} \cdot 3 + X^{(0,1)}(1 + t) + X^{(1,1)}(1 + t^2 + t^3) \end{aligned}$$

where $t = X^{(1,1)} = xy$. Hence, $\mathcal {F}_{\textbf{v}}(f) = \{ 3, 1 + t, 1 + t^2 + t^3 \}$. See Fig. 3 for a pictorial illustration.

Fig. 3

The support of $f = 3x + y + xy^2 +xy + x^3y^3 + x^4y^4$ and its different (1, 1)-fibers

As noticed in the example above, polynomials are linear combinations of their fibers: for any polynomial f and any non-zero primitive vector $\textbf{v}$ we can write

$$\begin{aligned} f = X^{\textbf{u}_1} \psi _1 + \ldots + X^{\textbf{u}_n} \psi _n \end{aligned}$$

for some $\textbf{u}_1, \ldots , \textbf{u}_n \in \mathbb {Z}^2$ where $\psi _1, \ldots , \psi _n\in \mathcal {F}_{\textbf{v}}(f)$. We use this in the proof of the next theorem.

Theorem 5

A polynomial f has a line polynomial factor in direction $\textbf{v}$ if and only if the polynomials in $\mathcal {F}_{\textbf{v}}(f)$ have a common factor.

Proof

For any line polynomial $\phi$ in direction $\textbf{v}$, and for any polynomial g, the $\textbf{v}$-fibers of the product $\phi g$ have a common factor $\phi$. In other words, if a polynomial f has a line polynomial factor $\phi$ in direction $\textbf{v}$, then the polynomials in $\mathcal {F}_{\textbf{v}}(f)$ have the normal form of $\phi$ as a common factor.

For the converse direction, assume that the polynomials in $\mathcal {F}_{\textbf{v}}(f)$ have a common factor $\phi$. Then there exist vectors $\textbf{u}_1, \ldots , \textbf{u}_n \in \mathbb {Z}^2$ and polynomials $\phi \psi _1, \ldots , \phi \psi _n \in \mathcal {F}_{\textbf{v}}(f)$ such that

$$\begin{aligned} f = X^{\textbf{u}_1} \phi \psi _1 + \ldots + X^{\textbf{u}_n} \phi \psi _n. \end{aligned}$$

Hence, $\phi$ is a line polynomial factor of f in direction $\textbf{v}$.$\square$

Note that Lemma 3 actually follows immediately from Theorem 5: A vertex instead of an outer edge in direction $\textbf{v}$ or $-\textbf{v}$ provides a non-zero monomial $\textbf{v}$-fiber, which implies that the polynomials in $\mathcal {F}_{\textbf{v}}(f)$ have no common factors.

So, to find out the line polynomial factors of f we first need to find out the possible directions of the line polynomials, that is, the directions of the (finitely many) outer edges of f, and then we need to check for which of these possible directions $\textbf{v}$ the polynomials in $\mathcal {F}_{\textbf{v}}(f)$ have a common factor. There are clearly algorithms to find the outer edges of a given polynomial and to determine whether finitely many line polynomials have a common factor. If such a factor exists, then by Theorem 5 the polynomial f has a line polynomial factor in this direction. We have proved the following theorem.

Theorem 6

There is an algorithm to find the line polynomial factors of a given (Laurent) polynomial in two variables.

5 Forced Periodicity of Perfect Colorings with Two Colors

In this section we consider forced periodicity of two-dimensional perfect colorings with only two colors. Without loss of generality we may assume that $\mathcal {A}= \{a_1, a_2 \} = \{ 0 , 1 \}$ ($a_1 =0,a_2=1$) and consider perfect colorings $c \in \mathcal {A}^{\mathbb {Z}^2}$ since the names of the colors do not matter in our considerations. So, let $c \in \{0,1\}^{\mathbb {Z}^2}$ be a perfect coloring with respect to $D \subseteq \mathbb {Z}^2$ and let $\textbf{B} = (b_{ij})_{2 \times 2}$ be the matrix of c. Let us define a set $C = \{ \textbf{u} \in \mathbb {Z}^2 \mid c_{\textbf{u}} = 1 \}$. This set has the property that the neighborhood $\textbf{u} + D$ of a point $\textbf{u}$ contains exactly $a = b_{21}$ points of color 1 if $\textbf{u} \not \in C$ and exactly $b = b_{22}$ points of color 1 if $\textbf{u} \in C$. In fact, C is a perfect (multiple) covering of the infinite grid G determined by the relative neighborhood D. More precisely, the set C is a (perfect) (D, b, a)-covering of G. This is a variant of the following definition: in any graph a subset C of its vertex set is an (r, b, a)-covering if the number of vertices of C in the r-neighborhood of a vertex u is a if $u \not \in C$ and b if $u \in C$. See [1] for a reference. Clearly in translation invariant graphs the (r, b, a)-coverings correspond to (D, b, a)-coverings where D is the relative r-neighborhood of the graph. Thus, it is natural to call any perfect coloring with only two colors a perfect covering. Note that a (D, b, a)-covering is a D-perfect coloring with the matrix

$$\begin{aligned} \textbf{B} = \begin{pmatrix} \vert D \vert - a &{} \vert D \vert - b \\ a &{} b \end{pmatrix}. \end{aligned}$$

The following theorem by Axenovich states that “almost every” (1, b, a)-covering in the square grid is two-periodic.

Theorem 7

([1]) If $b-a \ne 1$, then every (1, b, a)-covering in the square grid is two-periodic.

For a finite set $D \subseteq \mathbb {Z}^2$ we define its characteristic polynomial to be the polynomial $f_D(X) = \sum _{\textbf{u} \in D} X^{-\textbf{u}}$. We denote by $\mathbbm {1}(X)$ the constant power series $\sum _{\textbf{u} \in \mathbb {Z}^2} X^{\textbf{u}}$. If $c \in \{0,1\}^{\mathbb {Z}^2}$ is a (D, b, a)-covering, then from the definition we get that $f_D(X)c(X) = (b-a)c(X) + a \mathbbm {1}(X)$ which is equivalent to $\left( f_D(X) - (b-a) \right) c(X) = a \mathbbm {1}(X)$. Thus, if c is a (D, b, a)-covering, then $f_D(X) - (b-a)$ is a periodizer of c. Hence, by Theorem 2 the condition that the polynomial $f_D(X) - (b-a)$ has no line polynomial factors is a sufficient condition for forced periodicity of a (D, b, a)-covering. Hence, we have the following corollary of Theorem 2:

Corollary 8

Let $D \subseteq \mathbb {Z}^2$ be a finite shape and let b and a be non-negative integers. If $g=f_D - (b-a)$ has no line polynomial factors, then every (D, b, a)-covering is two-periodic.

Using our formulation and the algebraic approach we get a simple proof for Theorem 7:

Reformulation of Theorem 7 Let D be the relative 1-neighborhood of the square grid and assume that $b-a \ne 1$. Then every (D, b, a)-covering is two-periodic.

Proof

Let c be an arbitrary (D, b, a)-covering. The outer edges of $g = f_D - (b-a) = x^{-1} + y^{-1} + 1 - (b-a) + x + y$ are in directions $(1,1),(-1,-1),(1,-1)$ and $(-1,1)$ and hence by Lemma 3 any line polynomial factor of g is either in direction (1, 1) or $(1,-1)$. For $\textbf{v} \in \{(1,1),(1,-1)\}$ we have $\mathcal {F}_{\textbf{v}}(g) = \{ 1+t,1 -(b-a) \}$. See Fig. 4 for an illustration. Since $1 -(b-a)$ is a non-trivial monomial, by Theorem 5 the periodizer $g \in \text {Per}(c)$ has no line polynomial factors and hence the claim follows by corollary 8.$\square$

We also get a similar proof for the following known result concerning the forced periodicity of perfect coverings in the square grid with radius $r \ge 2$.

Theorem 9

([29]) Let $r \ge 2$ and let D be the relative r-neighborhood of the square grid. Then every (D, b, a)-covering is two-periodic. In other words, all (r, b, a)-coverings in the square grid are two-periodic for all $r \ge 2$.

Proof

Let c be an arbitrary (D, b, a)-covering. By Lemma 3 any line polynomial factor of $g = f_D -(b-a)$ has direction (1, 1) or $(1,-1)$. So, assume that $\textbf{v} \in \{ (1,1), (1,-1) \}$. We have $\phi _1=1+t+\ldots +t^r \in \mathcal {F}_{\textbf{v}}(g)$ and $\phi _2=1+t+\ldots +t^{r-1} \in \mathcal {F}_{\textbf{v}}(g)$. See Fig. 4 for an illustration in the case $r=2$. Since $\phi _1-\phi _2=t^r$, the polynomials $\phi _1$ and $\phi _2$ have no common factors, and hence by Theorem 5 the periodizer g has no line polynomial factors. Corollary 8 gives the claim.$\square$

Fig. 4

Pictorial illustrations for the proofs of Theorems 7, 9, 10, 11 and 12. The constellation on the left of the upper row illustrates the proof of Theorem 7. The constellation in the center of the upper row illustrates the proof of Theorem 9 with $r=2$. The constellation on the right of the upper row illustrates the proof of Theorem 12 with $r=2$. The constellation on the left of the lower row illustrates the proof of Theorem 10. The constellation on the right of the lower row illustrates the proof of Theorem 11 with $r=2$. In each of the constellations we have pointed out two normal forms with no common factors in $\mathcal {F}_{\textbf{v}}(g)$ from the points of $\text {supp}(g)$ for one of the outer edges $\textbf{v}$ of $\text {supp}(g)$

There are analogous results in the triangular grid, and we can prove them similarly using Corollary 8.

Theorem 10

([29]) Let D be the relative 1-neighborhood of the triangular grid and assume that $b - a \ne -1$. Then every (D, b, a)-covering in the triangular grid is two-periodic. In other words, all (1, b, a)-coverings in the triangular grid are two-periodic whenever $b-a \ne -1$.

Proof

Let c be an arbitrary (D, b, a)-covering. The outer edges of $g = f_D -(b-a) = x^{-1}y^{-1} + x^{-1} + y^{-1} + 1-(b-a) + x + y + xy$ have directions $(1,1),(-1,-1),(1,0),(-1,0)$, (0, 1) and $(0,-1)$ and hence by Lemma 3 any line polynomial factor of g has direction (1, 1), (1, 0) or (0, 1). So, let $\textbf{v} \in \{ (1,1), (1,0),(0,1) \}$. We have $\mathcal {F}_{\textbf{v}}(g) = \{ 1+t, 1+ (1 - (b-a))t + t^2 \}$. See Fig. 4 for an illustration. Polynomials $\phi _1=1+t$ and $\phi _2=1+ (1 - (b-a))t + t^2$ satisfy $\phi _1^2-\phi _2= (1+b-a)t$. Thus, they do not have any common factors if $b-a \ne -1$ and hence by Theorem 5 the polynomial g has no line polynomial factors. The claim follows by Corollary 8.$\square$

Theorem 11

([29]) Let $r \ge 2$ and let D be the relative r-neighborhood of the triangular grid. Then every (D, b, a)-covering is two-periodic. In other words, every (r, b, a)-covering in the triangular grid is two-periodic for all $r \ge 2$.

Proof

Let c be an arbitrary (D, b, a)-covering. The outer edges of $g = f_D -(b-a)$ have directions (1, 1), $(-1,-1)$, (1, 0), $(-1,0)$, (0, 1) and $(0,-1)$, and hence by Lemma 3 any line polynomial factor of g has direction (1, 1), (1, 0) or (0, 1). So, let $\textbf{v} \in \{ (1,1), (1,0),(0,1) \}$. There exists $n \ge 1$ such that $1+t+ \ldots + t^n \in \mathcal {F}_{\textbf{v}}(g)$ and $1+t+ \ldots + t^{n+1} \in \mathcal {F}_{\textbf{v}}(g)$. See Fig. 4 for an illustration with $r=2$. Since these two polynomials have no common factors, by Theorem 5 the polynomial g has no line polynomial factors. Again, Corollary 8 yields the claim.$\square$

If $a \ne b$, then for all $r \ge 1$ any (r, b, a)-covering in the king grid is two-periodic:

Theorem 12

Let $r \ge 1$ be arbitrary and let D be the relative r-neighborhood of the king grid and assume that $a \ne b$. Then any (D, b, a)-covering is two-periodic. In other words, all (r, b, a)-coverings in the king grid are two-periodic whenever $a \ne b$.

Proof

Let c be an arbitrary (D, b, a)-covering. The outer edges of $g = f_D -(b-a)$ are in directions $(1,0),(-1,0),(0,1)$ and $(0,-1)$. Hence, by Lemma 3 any line polynomial factor of g has direction (1, 0) or (0, 1). Let $\textbf{v} \in \{ (1,0),(0,1)\}$. We have $\phi _1 = 1+t+\ldots + t^{r-1} + (1-(b-a))t^r +t^{r+1} + \ldots + t^{2r} \in \mathcal {F}_{\textbf{v}}(g)$ and $\phi _2 = 1+t+ \ldots + t^{2r} \in \mathcal {F}_{\textbf{v}}(g)$. See Fig. 4 for an illustration in the case $r=2$. Since $\phi _2-\phi _1=(b-a)t^r$ is a non-trivial monomial, $\phi _1$ and $\phi _2$ have no common factors. Thus, by Theorem 5 the polynomial g has no line polynomial factors and the claim follows by Corollary 8.$\square$

In the above proofs we used the fact that two Laurent polynomials in one variable have no common factors if and only if they generate the entire ideal $\mathbb {C}[t^{\pm 1}]$, and they do this if and only if they generate a non-zero monomial. This is known as the weak Nullstellensatz [6].

A shape $D \subseteq \mathbb {Z}^2$ is convex if it is the intersection $D = \text {conv}(D) \cap \mathbb {Z}^2$ where $\text {conv}(D) \subseteq \mathbb {R}^2$ is the real convex hull of D. Above all our shapes were convex. Next we generalize the above theorems and give a sufficient condition for forced periodicity of (D, b, a)-coverings for convex D.

So, let $D \subseteq \mathbb {Z}^2$ be a finite convex shape. Any (D, b, a)-covering has a periodizer $g = f_D - (b-a)$. As earlier, we study whether g has any line polynomial factors since if it does not, then Corollary 8 guarantees forced periodicity. For any $\textbf{v} \ne \textbf{0}$ the set $\mathcal {F}_{\textbf{v}}(f_D)$ contains only polynomials $\phi _n = 1 + \ldots + t^{n-1}$ for different $n \ge 1$ since D is convex: if D contains two points, then D contains every point between them. Thus, $\mathcal {F}_{\textbf{v}}(g)$ contains only polynomials $\phi _n$ for different $n \ge 1$ and, if $b-a \ne 0$, it may also contain a polynomial $\phi _{n_0} - (b-a)t^{m_0}$ for some $n_0 \ge 1$ such that $\phi _{n_0} \in \mathcal {F}_{\textbf{v}}(f_D)$ and for some $m_0 \ge 0$. If $b-a=0$, then $g=f_D$ and thus $\mathcal {F}_{\textbf{v}}(g) = \mathcal {F}_{\textbf{v}}(f_D)$.

Two polynomials $\phi _m$ and $\phi _n$ have a common factor if and only if $\gcd (m,n) > 1$. More generally, the polynomials $\phi _{n_1}, \ldots , \phi _{n_r}$ have a common factor if and only if $d = \gcd (n_1,\ldots ,n_r) > 1$ and, in fact, their greatest common factor is the dth cyclotomic polynomial

$$\begin{aligned} \prod _{\begin{array}{c} 1 \le k \le d \\ \gcd (k,d) = 1 \end{array}}(t - e^{i \cdot \frac{2 \pi k}{d}}). \end{aligned}$$

Let us introduce the following notation. For any polynomial f, we denote by $\mathcal {F}'_{\textbf{v}}(f)$ the set of normal forms of the non-zero fibers $\sum _{k \in \mathbb {Z}} f_{\textbf{u} + k \textbf{v}} X^{\textbf{u} + k \textbf{v}}$ for all $\textbf{u}\not \in \mathbb {Z}\textbf{v}$. In other words, we exclude the fiber through the origin. Let us also denote $\text {fib}{\textbf{v}}{f}$ for the normal form of the fiber $\sum _{k \in \mathbb {Z}} f_{k \textbf{v}} X^{k \textbf{v}}$ through the origin. We have $\mathcal {F}_{\textbf{v}}(f)=\mathcal {F}'_{\textbf{v}}(f)\cup \{\text {fib}_{\textbf{v}}(f)\}$ if $\text {fib}_{\textbf{v}}(f) \ne 0$ and $\mathcal {F}_{\textbf{v}}(f)=\mathcal {F}'_{\textbf{v}}(f)$ if $\text {fib}_{\textbf{v}}(f) = 0$.

Applying Theorems 2 and 5 we have the following theorem that gives sufficient conditions for every (D, b, a)-covering to be periodic for a finite and convex D. This theorem generalizes the results proved above. In fact, they are corollaries of the theorem. The first part of the theorem was also mentioned in [7] in a slightly different context and in a more general form.

Theorem 13

Let D be a finite convex shape, $g = f_D - (b-a)$ and let E be the set of the primitive outer edge directions of g.

• Assume that $b-a = 0$. For any $\textbf{v} \in E$ denote $d_\textbf{v}=\gcd (n_1,\ldots ,n_r)$ where $\mathcal {F}_{\textbf{v}}(g) = \{ \phi _{n_1},\ldots ,\phi _{n_r}\}$. If $d_\textbf{v} = 1$ holds for all $\textbf{v} \in E$, then every (D, b, a)-covering is two-periodic. If $d_\textbf{v} = 1$ holds for all but some parallel $\textbf{v} \in E$, then every (D, b, a)-covering is periodic.

• Assume that $b-a \ne 0$. For any $\textbf{v} \in E$ denote $d_\textbf{v}=\gcd (n_1,\ldots ,n_r)$ where $\mathcal {F}'_{\textbf{v}}(g) = \{ \phi _{n_1},\ldots ,\phi _{n_r}\}$. If the $d_\textbf{v}$’th cyclotomic polynomial and $\text {fib}_{\textbf{v}}(g)$ have no common factors for any $\textbf{v} \in E$, then every (D, b, a)-covering is two-periodic. If the condition holds for all but some parallel $\textbf{v} \in E$, then every (D, b, a)-covering is periodic. (Note that the condition is satisfied, in particular, if $d_\textbf{v} = 1$.)

Proof

Assume first that $b-a=0$. If $d_{\textbf{v}}=1$ for all $\textbf{v} \in E$, then the $\textbf{v}$-fibers of g have no common factors and hence by Theorem 5 the polynomial g has no line polynomial factors. If $d_\textbf{v} = 1$ holds for all but some parallel $\textbf{v} \in E$, then all the line polynomial factors of g are in parallel directions. Thus, the claim follows by Theorem 2. Assume then that $b-a \ne 0$. If the $d_\textbf{v}$’th cyclotomic polynomial and $\text {fib}_{\textbf{v}}(g)$ have no common factors for all $\textbf{v} \in E$, then by Theorem 5 the polynomial g has no line polynomial factors. If the condition holds for all but some parallel $\textbf{v} \in E$, then all the line polynomial factors of g are in parallel directions. Thus, by Theorem 2 the claim holds also in this case.$\square$

6 Forced Periodicity of Perfect Colorings over Arbitrarily Large Alphabets

In this section we prove a theorem that gives a sufficient condition for forced periodicity of two-dimensional perfect colorings over an arbitrarily large alphabet. As corollaries of the theorem and theorems from the previous section we obtain conditions for forced periodicity of perfect colorings in two-dimensional infinite grid graphs.

We start by proving some lemmas that work in any dimension. We consider the vector presentations of perfect colorings because this way we get a non-trivial annihilator for any such vector presentation:

Lemma 14

Let c be the vector presentation of a D-perfect coloring over an alphabet of size n with matrix $\textbf{B} = (b_{ij})_{n \times n}$. Then c is annihilated by the polynomial

$$\begin{aligned} f(X) = \sum _{\textbf{u} \in D} \textbf{I} X^{-\textbf{u}} - \textbf{B}. \end{aligned}$$

Remark. Note the similarity of the above annihilator to the periodizer $\sum _{\textbf{u}\in D} X^{-\textbf{u}} - (b-a)$ of a (D, b, a)-covering.

Proof

Let $\textbf{v} \in \mathbb {Z}^d$ be arbitrary and assume that $c_{\textbf{v}} = \textbf{e}_j$. Then $(\textbf{B} c)_{\textbf{v}} = \textbf{B} \textbf{e}_j$ is the jth column of $\textbf{B}$. On the other hand, from the definition of $\textbf{B}$ we have $((\sum _{\textbf{u} \in D} \textbf{I} X^{-\textbf{u}}) c)_{\textbf{v}} = \sum _{\textbf{u} \in D} c_{\textbf{v} + \textbf{u}} = \sum _{i=1}^n b_{ij} \textbf{e}_i$ which is also the jth column of $\textbf{B}$. Thus, $(fc)_{\textbf{v}} = 0$ and hence $fc = 0$ since $\textbf{v}$ was arbitrary.$\square$

The following lemma shows that as in the case of integral configurations with non-trivial annihilators, also the vector presentation of a perfect coloring has a special annihilator which is a product of difference polynomials. By congruence of two polynomials with integer matrices as coefficients (mod p) we mean that their corresponding coefficients are congruent (mod p) and by congruence of two integer matrices (mod p) we mean that their corresponding components are congruent (mod p).

Lemma 15

Let c be the vector presentation of a D-perfect coloring over an alphabet of size n with matrix $\textbf{B} = (b_{ij})_{n \times n}$. Then c is annihilated by the polynomial

$$\begin{aligned} g(X) = (\textbf{I} X^{\textbf{v}_1} - \textbf{I}) \cdots (\textbf{I} X^{\textbf{v}_m} - \textbf{I}) \end{aligned}$$

for some vectors $\textbf{v}_1,\ldots ,\textbf{v}_m$.

Proof

By Lemma 14 the power series c is annihilated by $f(X) = \sum _{\textbf{u} \in D} \textbf{I} X^{-\textbf{u}} - \textbf{B}$. Let p be a prime larger than $n c_{\text {max}}$ where $c_{\text {max}}$ is the maximum absolute value of the components of the coefficients of c. Since the coefficients of f commute with each other, we have for any positive integer k using the binomial theorem that

$$\begin{aligned} f^{p^k} = f^{p^k}(X) \equiv \sum _{\textbf{u} \in D} \textbf{I} X^{-p^k \textbf{u}} - \textbf{B}^{p^k} \ \ (\text {mod } p). \end{aligned}$$

We have $f^{p^k}(X) c(X) \equiv 0 \ \ (\text {mod } p)$. There are only finitely many distinct matrices $\textbf{B}^{p^k} \ \ (\text {mod } p)$. So, let k and $k'$ be distinct and such that $\textbf{B}^{p^{k}} \equiv \textbf{B}^{p^{k'}} \ \ (\text {mod } p)$. Then the coefficients of $f' = f^{p^{k}} - f^{p^{k'}} \ \ (\text {mod } p)$ are among $\textbf{I}$ and $- \textbf{I}$. Since $f^{p^{k}} c \equiv 0 \ \ (\text {mod } p)$ and $f^{p^{k'}} c \equiv 0 \ \ (\text {mod } p)$, also

$$\begin{aligned} f^{\prime } c \equiv 0 \ \ (\text {mod } p). \end{aligned}$$

The components of the configuration $f' c$ are bounded in absolute value by $n c_{\text {max}}$. Since we chose p larger than $n c_{\text {max}}$, this implies that

$$\begin{aligned} f'c = 0. \end{aligned}$$

Because $f' = \sum _{\textbf{u} \in P_1} \textbf{I} X^{\textbf{u}} - \sum _{\textbf{u} \in P_2} \textbf{I} X^{\textbf{u}}$ for some finite subsets $P_1$ and $P_2$ of $\mathbb {Z}^d$, the annihilation of c by $f'$ is equivalent to the annihilation of every layer of c by $f'' = \sum _{\textbf{u} \in P_1} X^{\textbf{u}} - \sum _{\textbf{u} \in P_2} X^{\textbf{u}}$. Thus, every layer of c has a non-trivial annihilator and hence by Theorem 1 every layer of c has a special annihilator which is a product of difference polynomials. Let

$$\begin{aligned} g' = (X^{\textbf{v}_1}-1) \cdots (X^{\textbf{v}_m}-1) \end{aligned}$$

be the product of all these special annihilators. Since $g'$ annihilates every layer of c, the polynomial

$$\begin{aligned} g = (\textbf{I} X^{\textbf{v}_1} - \textbf{I}) \cdots (\textbf{I} X^{\textbf{v}_m} - \textbf{I}) \end{aligned}$$

annihilates c.$\square$

Lemma 16

Let p be a prime and let H be an additive CA over $\mathbb {Z}_p^n$ determined by a polynomial $h = \sum _{i=0}^k \textbf{A}_i X^{\textbf{u}_i} \in \mathbb {Z}_p^{n \times n}[X^{\pm 1}]$ whose coefficients $\textbf{A}_i$ commute with each other. Assume that there exist $M \in \mathbb {Z}_p \setminus \{0\}$ and matrices $\textbf{C}_0, \ldots , \textbf{C}_k$ that commute with each other and with every $\textbf{A}_i$ such that

$$\begin{aligned} \textbf{C}_0 \textbf{A}_0 + \ldots + \textbf{C}_k \textbf{A}_k = M \cdot \textbf{I} \end{aligned}$$

holds in $\mathbb {Z}_p^{k \times k}$. Then H is surjective.

Proof

Assume the contrary that H is not surjective. By the Garden-of-Eden theorem H is not pre-injective and hence there exist two distinct asymptotic configurations $c_1$ and $c_2$ such that $H(c_1) = H(c_2)$, that is, $h(X) c_1(X) = h(X) c_2(X)$. Thus, h is an annihilator of $e=c_1-c_2$. Without loss of generality we may assume that $c_1(\textbf{0}) \ne c_2(\textbf{0})$, i.e., that $e(\textbf{0}) = \textbf{v} \ne \textbf{0}$. Let l be such that the support $\text {supp}(e) = \{ \textbf{u} \in \mathbb {Z}^d \mid e(\textbf{u}) \ne \textbf{0} \}$ of e is contained in a d-dimensional $p^l \times \ldots \times p^l$ hypercube. Note that in $\mathbb {Z}_p^{k \times k}$ we have

$$\begin{aligned} f^{p^l} = \sum _{i=0}^k \textbf{A}_i^{p^l} X^{p^l \textbf{u}_i} \end{aligned}$$

which is also an annihilator of e. Hence, by the choice of l we have $\textbf{A}_i^{p^l} \textbf{v} = \textbf{0}$ for all $i \in \{ 1 , \ldots , k \}$. By raising the identity

$$\begin{aligned} \textbf{C}_0 \textbf{A}_0 + \ldots + \textbf{C}_k \textbf{A}_k = M \cdot \textbf{I} \end{aligned}$$

to power $p^l$ and multiplying the result by the vector $\textbf{v}$ from the right we get

$$\begin{aligned} M^{p^l} \cdot \textbf{v} = \textbf{C}_0^{p^l} \textbf{A}_0^{p^l} \textbf{v} + \ldots + \textbf{C}_k^{p^l} \textbf{A}_k^{p^l} \textbf{v} = \textbf{0} + \ldots + \textbf{0} = \textbf{0}. \end{aligned}$$

However, this is a contradiction because $M^{p^l} \textbf{v} \ne \textbf{0}$. Thus, H must be surjective as claimed.$\square$

Theorem 17

Let $D \subseteq \mathbb {Z}^2$ be a finite shape and assume that there exists an integer $t_0$ such that the polynomial $f_D - t = \sum _{\textbf{u} \in D} X^{-\textbf{u}} - t$ has no line polynomial factors whenever $t \ne t_0$. Then any D-perfect coloring with matrix $\textbf{B}$ is two-periodic whenever $\det (\textbf{B} - t_0 \textbf{I}) \ne 0$. If $f_D - t$ has no line polynomial factors for any t, then every D-perfect coloring is two-periodic.

Proof

Let c be the vector presentation of a D-perfect coloring with matrix $\textbf{B}$. By Lemmas 14 and 15 it has two distinct annihilators: $f= \sum _{\textbf{u} \in D} \textbf{I} X^{-\textbf{u}} - \textbf{B}$ and $g= (\textbf{I} X^{\textbf{v}_1} - \textbf{I}) \cdots (\textbf{I} X^{\textbf{v}_m} - \textbf{I})$. Let us replace $\textbf{I}$ by 1 and $\textbf{B}$ by a variable t and consider the corresponding integral polynomials $f' = \sum _{\textbf{u} \in D} X^{-\textbf{u}} - t = f_D - t$ and $g' = (X^{\textbf{v}_1} - 1) \cdots (X^{\textbf{v}_m} - 1)$ in $\mathbb {C}[x,y,t]$. Here $X=(x,y)$.

Without loss of generality we may assume that $f'$ and $g'$ are proper polynomials. Indeed, we can multiply $f'$ and $g'$ by monomials such that the obtained polynomials $f''$ and $g''$ are proper polynomials and that they have a common factor if and only if $f'$ and $g'$ have a common factor. So, we may consider $f''$ and $g''$ instead of $f'$ and $g'$ if they are not proper polynomials.

We consider the y-resultant $\text {Res}_y(f',g')$ of $f'$ and $g'$, and write

$$\begin{aligned} \text {Res}_y(f',g') = f_0(t) + f_1(t)x + \ldots + f_k(t) x^k. \end{aligned}$$

By the properties of resultants $\text {Res}_y(f',g')$ is in the ideal generated by $f'$ and $g'$, and it can be the zero polynomial only if $f'$ and $g'$ have a common factor. Since $g'$ is a product of line polynomials, any common factor of $f'$ and $g'$ is also a product of line polynomials. In particular, if $f'$ and $g'$ have a common factor, then they have a common line polynomial factor. However, by the assumption $f'$ has no line polynomial factors if $t \ne t_0$. Thus, $f'$ and $g'$ may have a common factor only if $t=t_0$ and hence $\text {Res}_y(f',g')$ can be zero only if $t = t_0$. On the other hand, $\text {Res}_y(f',g') = 0$ if and only if $f_0(t) = \ldots = f_k(t) = 0$. We conclude that $\gcd (f_0(t), \ldots , f_k(t)) = (t-t_0)^m$ for some $m \ge 0$. Thus,

$$\begin{aligned} \text {Res}_y(f',g') = (t-t_0)^m (f'_0(t) + f'_1(t)x + \ldots + f'_k(t) x^k) \end{aligned}$$

where the polynomials $f'_0(t), \ldots , f'_k(t)$ have no common factors.

By the Euclidean algorithm there are polynomials $a_0(t), \ldots , a_k(t)$ such that

$$\begin{aligned} a_0(t) f_0'(t) + \ldots + a_k(t) f_k'(t) = 1. \end{aligned}$$

(1)

Moreover, the coefficients of the polynomials $a_0(t), \ldots , a_k(t)$ are rational numbers because the polynomials $f'_0(t), \ldots , f'_k(t)$ are integral. Note that if $f'$ has no line polynomial factors for any t, then $m=0$ and hence $f_i'(t) = f_i(t)$ for every $i \in \{1,\ldots ,k\}$.

Let us now consider the polynomial

$$\begin{aligned} (\textbf{B}-t_0 \textbf{I})^m(f_0'(\textbf{B}) + f_1'(\textbf{B}) x + \ldots + f'_k(\textbf{B}) x^k) \end{aligned}$$

which is obtained from $\text {Res}_y(f',g')$ by plugging back $\textbf{I}$ and $\textbf{B}$ in the place of 1 and t, respectively. Since $\text {Res}_y(f',g')$ is in the ideal generated by $f'$ and $g'$, the above polynomial is in the ideal generated by f and g. Thus, it is an annihilator of c because both f and g are annihilators of c.

Assume that $\det (\textbf{B} - t_0 \textbf{I}) \ne 0$ or that $m=0$. Now also

$$\begin{aligned} h = f_0'(\textbf{B}) + f_1'(\textbf{B}) x + \ldots + f'_k(\textbf{B}) x^k \end{aligned}$$

is an annihilator of c. Since $f'_0(t), \ldots , f'_k(t)$ have no common factors, h is non-zero, because otherwise it would be $f_0'(\textbf{B}) = \ldots = f_k'(\textbf{B}) = 0$ and the minimal polynomial of $\textbf{B}$ would be a common factor of $f'_0(t), \ldots , f'_k(t)$, a contradiction.

Plugging $t = \textbf{B}$ to Equation 1 we get

$$\begin{aligned} a_0(\textbf{B}) f_0'(\textbf{B}) + \ldots + a_k(\textbf{B}) f_k'(\textbf{B}) = \textbf{I}. \end{aligned}$$

Let us multiply the above equation by a common multiple M of all the denominators of the rational numbers appearing in the equation and let us consider it (mod p) where p is a prime that does not divide M. We obtain the following identity

$$\begin{aligned} a_0'(\textbf{B}) f_0'(\textbf{B}) + \ldots + a_k'(\textbf{B}) f_k'(\textbf{B}) = M \cdot \textbf{I} \not \equiv 0 \ \ (\text {mod } p) \end{aligned}$$

where all the coefficients in the equation are integer matrices.

By Lemma 16 the additive CA determined by $h = \sum _{i=0}^k f_i'(\textbf{B})x^i$ is surjective. Since h is a polynomial in variable x only, it defines a 1-dimensional CA H which is surjective and which maps every horizontal fiber of c to 0. Hence, every horizontal fiber of c is a pre-image of 0. Let $c'$ be a horizontal fiber of c. The Garden-of-Eden theorem implies that 0 has finitely many, say N, pre-images under H. Since also every translation of $c'$ is a pre-image of 0, we conclude that $c' = \tau ^i(c')$ for some $i \in \{0, \ldots , N-1\}$. Thus, $(N-1)!$ is a common period of all the horizontal fibers of c and hence c is horizontally periodic.

Repeating the same argumentation for the x-resultant of $f'$ and $g'$ we can show that c is also vertically periodic. Thus, c is two-periodic.$\square$

As corollaries of the above theorem and theorems from the previous section, we obtain new proofs for forced periodicity of perfect colorings in the square and the triangular grids, and a new result for forced periodicity of perfect colorings in the king grid:

Corollary 18

([29]) Let D be the relative 1-neighborhood of the square grid. Then any D-perfect coloring with matrix $\textbf{B}$ is two-periodic whenever $\det (\textbf{B} - \textbf{I}) \ne 0$. In other words, any 1-perfect coloring with matrix $\textbf{B}$ in the square grid is two-periodic whenever $\det (\textbf{B} - \textbf{I}) \ne 0$.

Proof

In our proof of Theorem 7 it was shown that the polynomial $f_{D} - t$ has no line polynomial factors if $t \ne 1$. Thus, by Theorem 17 any $(D, \textbf{B})$-coloring is two-periodic whenever $\det (\textbf{B} - \textbf{I}) \ne 0$.$\square$

Corollary 19

([29]) Let D be the relative 1-neighborhood of the triangular grid. Then any D-perfect coloring with matrix $\textbf{B}$ is two-periodic whenever $\det (\textbf{B} + \textbf{I}) \ne 0$. In other words, any 1-perfect coloring with matrix $\textbf{B}$ in the triangular grid is two-periodic whenever $\det (\textbf{B} + \textbf{I}) \ne 0$.

Proof

In the proof of Theorem 10 it was shown that the polynomial $f_{D} - t$ has no line polynomial factors if $t \ne -1$. Thus, by Theorem 17 any $(D, \textbf{B})$-coloring is two-periodic whenever $\det (\textbf{B} + \textbf{I}) \ne 0$.$\square$

Corollary 20

([29]) Let $r \ge 2$ and let D be the relative r-neighborhood of the square grid. Then every D-perfect coloring is two-periodic. In other words, any r-perfect coloring in the square grid is two-periodic for all $r \ge 2$.

Proof

In the proof of Theorem 9 it was shown that the polynomial $f_D - t$ has no line polynomial factors for any t. Thus, by Theorem 17 every D-perfect coloring is two-periodic.$\square$

Corollary 21

([29]) Let $r \ge 2$ and let D be the relative r-neighborhood of the triangular grid. Then every D-perfect coloring is two-periodic. In other words, any r-perfect coloring in the triangular grid is two-periodic for all $r \ge 2$.

Proof

In the proof of Theorem 11 it was shown that the polynomial $f_D - t$ has no line polynomial factors for any t. Thus, by Theorem 17 every D-perfect coloring is two-periodic.$\square$

Corollary 22

Let $r \ge 1$ and let D be the relative r-neighborhood of the king grid. Then every D-perfect coloring with matrix $\textbf{B}$ is two-periodic whenever $\det (\textbf{B}) \ne 0$. In other words, every r-perfect coloring with matrix $\textbf{B}$ in the king grid is two-periodic whenever $\det (\textbf{B}) \ne 0$.

Proof

In the proof of Theorem 12 we showed that the polynomial $f_D - t$ has no line polynomial factors if $t \ne 0$. Thus, by Theorem 17 any $(D,\textbf{B})$-coloring is two-periodic whenever $\det (\textbf{B}) \ne 0$.$\square$

Remark. Note that the results in Corollaries 18, 19, 20 and 21 were stated and proved in [29] in a slightly more general form. Indeed, in [29] it was proved that if a configuration $c \in \mathcal {A}^{\mathbb {Z}^2}$ is annihilated by

$$\begin{aligned} \sum _{\textbf{u} \in D} \textbf{I} X^{-\textbf{u}} - \textbf{B} \end{aligned}$$

where $\textbf{B} \in \mathbb {Z}^{n \times n}$ is an arbitrary integer matrix whose determinant satisfies the conditions in the four corollaries and D is as in the corollaries, then c is necessarily periodic. This kind of configuration was called a generalized centered function. However, in Lemma 14 we proved that the vector presentation of any D-perfect coloring with matrix $\textbf{B}$ is annihilated by this polynomial, that is, we proved that the vector presentation of a perfect coloring is a generalized centered function. By analyzing the proof of Theorem 17 we see that the theorem holds also for generalized centered functions and hence the corollaries following it hold also for generalized centered functions, and thus we have the same results as in [29].

7 Forced Periodicity of Configurations of Low Abelian Complexity

In this section we prove a statement concerning forced periodicity of two-dimensional configurations of low abelian complexity which generalizes a result in [7]. In fact, as in [7] we generalize the definition of abelian complexity from finite patterns to polynomials and prove a statement of forced periodicity under this more general definition of abelian complexity.

Let $c \in \{\textbf{e}_1, \ldots , \textbf{e}_n \}^{\mathbb {Z}^d}$ and let $D \subseteq \mathbb {Z}^d$ be a finite shape. Consider the polynomial $f=\textbf{I} \cdot f_D(X) = \sum _{\textbf{u} \in D} \textbf{I} X^{-\textbf{u}} \in \mathbb {Z}^{n \times n}[X^{\pm 1}]$. The ith coefficient of $(fc)_{\textbf{v}} = \sum _{\textbf{u} \in D} \textbf{I} \cdot \mathbf {c_{\textbf{v}+\textbf{u}}}$ tells the number of cells of color $\textbf{e}_i$ in the D-neighborhood of $\textbf{v}$ in c and hence the abelian complexity of c with respect to D is exactly the number of distinct coefficients of fc.

More generally, we define the abelian complexity A(c, f) of an integral vector configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$ where $\mathcal {A}$ is finite set of integer vectors with respect to a polynomial $f \in \mathbb {Z}^{n \times n}[X^{\pm 1}]$ as

$$\begin{aligned} A(c,f) = \vert \{ (fc)_{\textbf{v}} \mid \textbf{v} \in \mathbb {Z}^d \} \vert . \end{aligned}$$

This definition can be extended to integral configurations and polynomials. Indeed, we define the abelian complexity A(c, f) of a configuration $c \in \mathcal {A}^{\mathbb {Z}^d}$ where $\mathcal {A}\subseteq \mathbb {Z}$ with respect to a polynomial $f = \sum f_i X^{\textbf{u}_i} \in \mathbb {Z}[X^{\pm 1}]$ to be the abelian complexity $A(c',f')$ of the vector presentation $c'$ of c with respect to the polynomial $f' = \textbf{I} \cdot f = \sum f_i \cdot \textbf{I} \cdot X^{\textbf{u}_i}$. Consequently, we say that c has low abelian complexity with respect to a polynomial f if $A(c,f) = 1$. Clearly this definition is consistent with the definition of low abelian complexity of a configuration with respect to a finite shape since if c is an integral configuration, then $A(c,D)=1$ if and only if $A(c,f_D)=1$, and if c is an integral vector configuration, then $A(c,D)=1$ if and only if $A(c,\textbf{I} \cdot f_D)=1$.

We study forced periodicity of two-dimensional configurations of low abelian complexity. Note that a configuration of low abelian complexity is not necessarily periodic. Indeed, in [30] it was shown that there exist non-periodic two-dimensional configurations that have abelian complexity $A(c,D) = 1$ for some finite shape D. However, in [7] it was shown that if $A(c,f) = 1$ and if the polynomial f has no line polynomial factors, then c is two-periodic assuming that the support of f is convex. The following theorem strengthens this result and shows that the convexity assumption of the support of the polynomial is not needed. We obtain this result as a corollary of Theorem 2.

Theorem 23

Let c be a two-dimensional integral configuration over an alphabet of size n and assume that it has low abelian complexity with respect to a polynomial $f \in \mathbb {Z}[x^{\pm 1}, y^{\pm 1}]$. If f has no line polynomial factors, then c is two-periodic. If f has line polynomial factors in a unique primitive direction $\textbf{v}$, then c is $\textbf{v}$-periodic. Thus, if $f_D$ has no line polynomial factors or its line polynomial factors are in a unique primitive direction, then any configuration that has low abelian complexity with respect to D is two-periodic or periodic, respectively.

Proof

By the assumption that $A(c,f)=1$ we have $f'c' = \textbf{c}_0 \mathbbm {1}$ for some $\textbf{c}_0 \in \mathbb {Z}^n$ where $c'$ is the vector presentation of c and $f' = \textbf{I} \cdot f$. Thus, f periodizes every layer of $c'$. If f has no line polynomial factors, then by Theorem 2 every layer of $c'$ is two-periodic and hence $c'$ is two-periodic. If f has line polynomial factors in a unique primitive direction $\textbf{v}$, then by Theorem 2 every layer of $c'$ is $\textbf{v}$-periodic and hence also $c'$ is $\textbf{v}$-periodic. Since c is periodic if and only if its vector presentation $c'$ is periodic, the claim follows.$\square$

Remark. In [7] a polynomial $f \in \mathbb {Z}[X^{\pm 1}]$ is called abelian rigid if an integral configuration c having low abelian complexity with respect to f implies that c is strongly periodic. In the above theorem we proved that if a polynomial $f \in \mathbb {Z}[x^{\pm 1},y^{\pm 1}]$ has no line polynomial factors then it is abelian rigid. Also, the converse holds as proved in [7], that is, if a polynomial $f \in \mathbb {Z}[x^{\pm 1},y^{\pm 1}]$ has a line polynomial factor then it is not abelian rigid. This means that if f has a line polynomial factor then there exists a configuration which is not two-periodic but has low abelian complexity with respect to f. In fact this direction holds for all d, not just for $d=2$ as reported in [7].

In the following example we introduce an open problem related to configurations of low abelian complexity.

Example 24

(Periodic tiling problem) This example concerns translational tilings by a single tile. In this context by a tile we mean any finite subset $F \subseteq \mathbb {Z}^d$ and by a tiling by the tile F we mean such subset $C \subseteq \mathbb {Z}^d$ that every point of the grid $\mathbb {Z}^d$ has a unique presentation as a sum of an element of F and an element of C. Presenting the tiling C as its indicator function we obtain a d-dimensional binary configuration $c \in \{0,1\}^{\mathbb {Z}^d}$ defined by

$$\begin{aligned} c_{\textbf{u}} = {\left\{ \begin{array}{ll} 1, \text { if } \textbf{u} \in C \\ 0, \text { if } \textbf{u} \not \in C \end{array}\right. }. \end{aligned}$$

The configuration c has exactly $\vert F \vert$ different patterns of shape $-F$, namely the patterns with exactly one symbol 1. In other words, it has low complexity with respect to $-F$. Let $f = f_F = \sum _{\textbf{u} \in F} X^{-\textbf{u}}$ be the characteristic polynomial of F. Since C is a tiling by F, we have $fc = \mathbbm {1}$. In fact, c has low abelian complexity with respect to f and $-F$. Thus, by Theorem 23 any tiling by $F \subseteq \mathbb {Z}^2$ is two-periodic if $f_F$ has no line polynomial factors.

The periodic tiling problem claims that if there exists a tiling by a tile $F \subseteq \mathbb {Z}^d$, then there exists also a periodic tiling by F [20, 31]. By a simple pigeonholing argument it can be seen that in dimension $d=1$ all translational tilings by a single tile are periodic and hence the periodic tiling problem holds in dimension 1 [26]. For $d \ge 2$ the conjecture is much trickier and only recently it was proved by Bhattacharya that it holds for $d=2$ [3]. In [9] it was presented a slightly different proof in the case $d=2$ with some generalizations. For $d \ge 3$ the conjecture is still partly open. However, very recently it has been proved that for some sufficiently large d the periodic tiling conjecture is false [10].

8 Algorithmic Aspects

All configurations in a subshift are periodic, in particular, if there are no configurations in the subshift at all! It is useful to be able to detect such trivial cases.

The set

$$\begin{aligned} \mathcal {S}(D,b,a) = \{ c \in \{0,1\}^{\mathbb {Z}^2} \mid (f_D - (b-a)) c = a \mathbbm {1}(X) \} \end{aligned}$$

of all (D, b, a)-coverings is an SFT for any given finite shape D and non-negative integers b and a. Hence, the question whether there exist any (D, b, a)-coverings for a given neighborhood D and covering constants b and a is equivalent to the question whether the SFT $\mathcal {S}(D,b,a)$ is non-empty. The question of emptiness of a given SFT is undecidable in general, but if the SFT is known to be not aperiodic, then the problem becomes decidable as a classic argumentation by Hao Wang shows:

Lemma 25

([32]) If an SFT is either the empty set or it contains a strongly periodic configuration, then its emptiness problem is decidable, that is, there is an algorithm to determine whether there exist any configurations in the SFT.

In particular, if $g = f_D - (b-a)$ has line polynomial factors in at most one direction, then the question whether there exist any (D, b, a)-coverings is decidable:

Theorem 26

Let a finite $D \subseteq \mathbb {Z}^2$ and non-negative integers b and a be given such that the polynomial $g=f_D - (b-a) \in \mathbb {Z}[x^{\pm 1},y^{\pm 1}]$ has line polynomial factors in at most one primitive direction. Then there exists an algorithm to determine whether there exist any (D, b, a)-coverings.

Proof

Let $\mathcal {S}=\mathcal {S}(D,b,a)$ be the SFT of all (D, b, a)-coverings. Since g has line polynomial factors in at most one primitive direction, by Theorem 2 every element of $\mathcal {S}$ is periodic. Any two-dimensional SFT that contains periodic configurations contains also two-periodic configurations. Thus, $\mathcal {S}$ is either empty or contains a two-periodic configuration and hence by Lemma 25 there is an algorithm to determine whether $\mathcal {S}$ is non-empty.$\square$

One may also want to design a perfect (D, b, a)-covering for given D, b and a. This can be effectively done under the assumptions of Theorem 26: As we have seen, if $\mathcal {S}=\mathcal {S}(D,b,a)$ is non-empty, it contains a two-periodic configuration. For any two-periodic configuration c it is easy to check if c contains a forbidden pattern. By enumerating two-periodic configurations one-by-one one is guaranteed to find eventually one that is in $\mathcal {S}$.

If the polynomial g has no line polynomial factors, then the following stronger result holds:

Theorem 27

If the polynomial $g=f_D - (b-a)$ has no line polynomial factors for given finite shape $D \subseteq \mathbb {Z}^2$ and non-negative integers b and a, then the SFT $\mathcal {S} = \mathcal {S}(D,b,a)$ is finite. One can then effectively construct all the finitely many elements of $\mathcal {S}$.

The proof of the first part of above theorem relies on the fact that a two-dimensional subshift is finite if and only if it contains only two-periodic configurations  [2]. If g has no line polynomial factors, then every configuration it periodizes (including every configuration in $\mathcal {S}$) is two-periodic by Theorem 2, and hence $\mathcal {S}$ is finite. The second part of the theorem, i.e., the fact that one can effectively produce all the finitely many elements of $\mathcal {S}$ holds generally for finite SFTs in any dimension:

Lemma 28

Given a finite $F \subseteq \mathcal {A}^*$ such that $X_F$ is finite, one can effectively construct the elements of $X_F$.

Proof

Given a finite $F \subseteq \mathcal {A}^*$ and a pattern $p\in \mathcal {A}^D$, assuming that strongly periodic configurations are dense in $X_F$, one can effectively check whether $p\in \mathcal {L}(X_F)$. Indeed, we have a semi-algorithm for the positive instances that guesses a strongly periodic configuration c and verifies that $c\in X_F$ and $p\in \mathcal {L}(c)$. A semi-algorithm for the negative instances exists for any SFT $X_F$ and is a standard compactness argument: guess a finite $E\subseteq \mathbb {Z}^d$ such that $D\subseteq E$ and verify that every $q\in \mathcal {A}^E$ such that $q \vert _D=p$ contains a forbidden subpattern.

Consequently, given finite $F,G \subseteq \mathcal {A}^*$, assuming that strongly periodic configurations are dense in $X_F$ and $X_G$, one can effectively determine whether $X_F=X_G$. Indeed, $X_F\subseteq X_G$ if and only if no $p\in G$ is in $\mathcal {L}(X_F)$, a condition that we have shown above to be decidable. Analogously we can test $X_G\subseteq X_F$.

Finally, let a finite $F \subseteq \mathcal {A}^*$ be given such that $X_F$ is known to be finite. All elements of $X_F$ are strongly periodic so that strongly periodic configurations are certainly dense in $X_F$. One can effectively enumerate all finite sets P of strongly periodic configurations. For each P that is translation invariant (and hence a finite SFT) one can construct a finite set $G\subseteq \mathcal {A}^*$ of forbidden patterns such that $X_G=P$. As shown above, there is an algorithm to test whether $X_F=X_G=P$. Since $X_F$ is finite, a set P is eventually found such that $X_F=P$.$\square$

Let us now turn to the more general question of existence of perfect colorings over alphabets of arbitrary size. Let $D \subseteq \mathbb {Z}^2$ be a finite shape and let $\textbf{B}$ be an $n \times n$ integer matrix. To determine whether there exist any $(D,\textbf{B})$-colorings is equivalent to asking whether the SFT

$$\begin{aligned} \mathcal {S}(D,\textbf{B}) = \{ c \in \{ \textbf{e}_1,\ldots ,\textbf{e}_n \}^{\mathbb {Z}^2} \mid g c = 0 \} \end{aligned}$$

is non-empty where $g = \sum _{\textbf{u} \in D} \textbf{I} X^{-\textbf{u}} - \textbf{B}$ since it is exactly the set of the vector presentations of all $(D,\textbf{B})$-colorings.

Theorem 29

Let a finite shape $D \subseteq \mathbb {Z}^2$, a non-negative integer matrix $\textbf{B}$ and an integer $t_0$ be given such that the polynomial $f_D(x,y) - t \in \mathbb {Z}[x^{\pm 1},y^{\pm 1}]$ has no line polynomial factors whenever $t \ne t_0$ and $\det (\textbf{B} - t_0 \textbf{I}) \ne 0$. Then there are only finitely many $(D,\textbf{B})$-colorings and one can effectively construct them. In particular, there is an algorithm to determine whether there exist any $(D,\textbf{B})$-colorings.

Proof

Let $\mathcal {S} = \mathcal {S}(D,\textbf{B})$ be the SFT of the vector presentations of all $(D, \textbf{B})$-colorings. By Theorem 17 all elements of $\mathcal {S}$ are two-periodic. Hence, $\mathcal {S}$ is finite, and the claim follows by Lemma 28.$\square$

Corollaries 18, 19, 20, 21 and 22 together with above theorem yield the following corollary.

Corollary 30

The following decision problems are decidable for a given matrix $\textbf{B}$ satisfying the given conditions.

• The existence of $(D,\textbf{B})$-colorings where D is the relative 1-neighborhood of the square grid and $\det (\textbf{B} - \textbf{I}) \ne 0$.

• The existence of $(D,\textbf{B})$-colorings where D is the relative 1-neighborhood of the triangular grid and $\det (\textbf{B} + \textbf{I}) \ne 0$.

• The existence of $(D,\textbf{B})$-colorings where D is the relative r-neighborhood of the square grid and $\textbf{B}$ is arbitrary.

• The existence of $(D,\textbf{B})$-colorings where D is the relative r-neighborhood of the triangular grid and $\textbf{B}$ is arbitrary.

• The existence of $(D,\textbf{B})$-colorings where D is the relative r-neighborhood of the king grid and $\det (\textbf{B}) \ne 0$.

Theorem 31

Given a polynomial f in two variables with line polynomial factors in at most one parallel direction there is an algorithm to determine whether there exist any two-dimensional configurations over an alphabet of size n that have low abelian complexity with respect to f. In fact, there are only finitely many such configurations and one can effectively construct all of them.

Proof

The set $\{ c \in \{ \textbf{e}_1 , \ldots , \textbf{e}_n \}^{\mathbb {Z}^2} \mid \textbf{I} f c = 0 \}$ of the vector presentations of all configurations over an alphabet of size n with low abelian complexity with respect to f is an SFT. By Theorem 23 it contains only two-periodic configurations and hence it is finite. Thus, by Lemma 28 we have the claim.$\square$

9 Conclusions

We studied two-dimensional perfect colorings and proved a general condition (Theorem 17) for their forced periodicity using an algebraic approach to multidimensional symbolic dynamics. As corollaries of this theorem we obtained new proofs for known results of forced periodicity in the square and the triangular grid and a new result in the king grid. Moreover, we generalized a statement of forced periodicity of two-dimensional configurations of low abelian complexity. Also, some observations of algorithmic decidability were made in the context of forced periodicity.

All our results of forced periodicity of perfect colorings used Theorem 2 and hence concerned only two-dimensional configurations. However, a d-dimensional version of Theorem 2 exists [15], and so we wonder whether an analogous result to Theorem 17 exists that would give a sufficient condition for forced periodicity of d-dimensional perfect colorings for arbitrary dimension d. Note that clearly every one-dimensional perfect coloring is necessarily periodic.