Beyond the Parallel Tangent Method to Predict the Composition of the First Nucleating Phase from Oversaturated Solutions

Abstract

The parallel tangent method widely applied to predict the composition and driving force to form a nucleus from an oversaturated solution is extended in this paper. The parallel tangent method is shown to (i) Over-estimates the composition difference between the first nucleus and the parent phase, (ii) Neglects the composition dependence of interfacial energies and (iii) Neglects the composition dependence of probability to form embryos prior to nucleation. New model equations are developed here for the composition dependence of the interfacial energies and probability to form the embryos as function of nucleus composition at given matrix composition. The most probable composition of the first nucleus is found at the maximum of the driving force of nucleation extended by the new model equations. The success of the extended method is demonstrated for an Al-Fe liquid alloy with 0.3 w% of Fe to predict the first nucleating intermetallic phases upon cooling after nucleation of the fcc phase. It is shown that although the prediction based on the parallel tangent method contradicts experimental observations, the prediction based on our extended method agrees with them.

Graphical Abstract

1 Introduction

Nucleation is an essential process in materials science and technologies as it determines the final microstructure and thus the final properties of solid materials.^{[1,2,3,4,5,6,7,8,9,10,11,12,13,14]} When a small nucleus precipitates from a large over-saturated solution, this process is usually accompanied by a composition change, i.e., the nucleus and the parent solution phase usually have different compositions. To find the composition of the nucleus as function of the composition of the parent solution phase the parallel tangent method is usually applied^{[15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]} (for its strict derivation, see^[26]). However, there are indications in the literature that the predictions of the parallel tangent method are not in good agreement with the experiments.^[23,27] Unfortunately, in these papers^[23,27] the extension of the parallel tangent method is not provided. Therefore, the goal here is to provide this extension in this paper. Let us make clear that this paper deals only with thermodynamics of nucleation (similarly as the parallel tangent method does); kinetic details are also important, but they are not considered here. This is because under identical transport conditions (viscosity, diffusion, etc) a higher driving force leads to faster nucleation, so the first task is to improve the current thermodynamic framework of nucleation.

For clarity let us mention that there are two “parallel tangent methods” in the literature: the second one (not discussed here) was developed to predict the equilibrium composition along the grain boundary (GB) and equilibrium GB energy as function of the solution phase surrounding the GB.^{[26,33,34,35,36,37,38,39,40]} Although this second parallel tangent method was already modified,^[41] this modification has been mostly neglected so far.^{[42,43,44,45]}

Now let us shortly remind here the well-known basic thermodynamic equations of homogeneous nucleation. The absolute Gibbs energy change accompanying nucleation of a solution phase β from a solution phase α (${\Delta }_{n}G$, J) is written for a spherical nucleus of radius r (m) as:

$$ \Delta_{n} G = \frac{4 \cdot \pi }{3} \cdot r^{3} \cdot \frac{{\Delta_{n} G_{m} }}{{V_{m,\beta } }} + 4 \cdot \pi \cdot r^{2} \cdot \sigma $$

(1a)

where $\Delta_{n} G_{m}$ (J/mol-atom) is the molar Gibbs energy change accompanying the nucleation of 1 mole of nucleus from an infinitely large parent phase, ${V}_{m,\beta }$ (m³/mol-atom) is the molar volume of the nucleus, $\sigma$ (J/m²) is the interfacial energy at the nucleus/parent phase interface of a positive value. The spontaneous formation and further growth of the nucleus is possible only if $\Delta_{n} G_{m} < 0$, that is why $- \Delta_{n} G_{m}$ is called here “the driving force of nucleation”. In case of $\Delta_{n} G_{m} < 0$ the function $\Delta_{n} G = f\left( r \right)$ goes through a maximum. The nucleus radius corresponding to this maximum is called the critical radius ($r_{cr}$, m) and its value is found from making the derivative of Eq 1a by r equal zero:

$$ r_{cr} = 2 \cdot V_{m,\beta } \cdot \left( {\frac{\sigma }{{ - \Delta_{n} G_{m} }}} \right) $$

(1b)

The first stage of nucleation, i.e., the increase of the nucleus radius from its atomic radius till the value of $r_{cr}$ is accompanied by a positive energy change and only its further growth is driven by the negative energy change. Therefore, nucleation will have a higher probability for those nuclei that have as small as possible value of ${r}_{cr}$, i.e., as small as possible value of $\sigma /(-{\Delta }_{n}{G}_{m})$. As the bulk value of ${-\Delta }_{n}{G}_{m}$ is known as function of nucleus composition with a much higher confidence compared to the interfacial energy value of $\sigma$ as function of the same,^{[46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]} usually the maximum of the bulk driving force $(-{\Delta }_{n}{G}_{m})$ is searched for and it is claimed that the composition of the first nucleus corresponds to this maximum. The parallel tangent method discussed here is a graphical way to find this maximum bulk driving force of nucleation. The effect of the composition dependence of ${V}_{m,\beta }$ is usually considered negligible. Although it is known that the effect of composition on $\sigma$ is not negligible, this effect is usually also neglected due to the lack of knowledge.

As follows from Eq 1a, in this paper only homogeneous nucleation is considered. In the future, this method can be extended to heterogeneous nucleation. It is obvious that the nature of the first nucleus will also depend on the nature of available nucleation sites.

2 Demonstration and Criticism of the Parallel Tangent Method

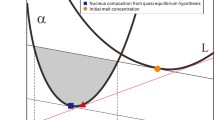
The parallel tangent method is demonstrated in Fig. 1. For this, the integral molar Gibbs energies of two solution phases ${G}_{\alpha }$ (J/mol-atom) and ${G}_{\beta }$ (J/mol-atom) are considered in a binary (A-B) system at constant pressure and temperature as function of composition, according to equations^{[26,30,62,63]}:

$$ G_{\alpha } = x \cdot G_{B\left( \alpha \right)}^{o} + R \cdot T \cdot \left[ {x \cdot lnx + \left( {1 - x} \right) \cdot {\text{ln}}\left( {1 - x} \right)} \right] $$

(2a)

$$ G_{\beta } = \left( {1 - x} \right) \cdot G_{A\left( \beta \right)}^{o} + R \cdot T \cdot \left[ {x \cdot lnx + \left( {1 - x} \right) \cdot {\text{ln}}\left( {1 - x} \right)} \right] $$

(2b)

where x (dimensionless) is the mole fraction of component B, $G_{B\left( \alpha \right)}^{o}$ = 8,000 J/mol-atom is the standard molar Gibbs energy of pure component B in phase alpha (note: $G_{A\left( \alpha \right)}^{o} \equiv$ 0 by definition), R = 8.3145 J/molK is the universal gas constant, T (K) is the absolute temperature, $G_{A\left( \beta \right)}^{o}$ = 5,000 J/mol-atom is the standard molar Gibbs energy of pure component A in phase beta (note: ${G}_{B\left(\beta \right)}^{o}\equiv$ 0 by definition). Eq 2a-b are written for ideal solutions for simplicity, but it does not pose any restriction to the parallel tangent method and its further modifications. Initially the system consists only of phase alpha. The “common tangent” line shown in Fig. 1 indicates the equilibrium values ${x}_{\alpha ,e}$ and ${x}_{\beta ,e}$ being the equilibrium molar ratios of component B in the two phases when they are in equilibrium with each other. When the initial composition of the parent phase is outside of this interval (${x}_{\alpha }{ \le x}_{\alpha ,e}$ or ${x}_{\alpha }{ \ge x}_{\beta ,e}$ in Fig. 1), then the bulk driving force of nucleation has a zero or negative value, and so nucleation of the beta phase from the alpha phase is not possible. Nucleation of the beta phase from the alpha phase is possible when the initial composition of the parent phase is between the two equilibrium values (${x}_{\alpha ,e}{<x}_{\alpha }<{x}_{\beta ,e}$), as in this case the bulk driving force of nucleation of the beta phase is positive in a finite composition interval. This situation is shown in Fig. 1 with ${x=x}_{\alpha }$ = 0.300 selected in the above interval.

Fig. 1

Demonstration of the parallel tangent method: concentration dependence of the molar integral Gibbs energies of two phases (phase alpha = initial parent phase, phase beta = nucleating phase) at fixed pressure of 1 bar and T = 1,000 K calculated by Eq 2a-b. The common tangent line touches the curves at the equilibrium values of ${x}_{\alpha ,e}$ = 0.219 and at ${x}_{\beta ,e}$ = 0.572. The leading tangent line is drawn to the alpha phase at ${x}_{\alpha }$ = 0.300 (this value is selected in the interval of the above equilibrium values). The secondary tangent line is parallel to the leading tangent line, and it is also a tangent line to the molar integral Gibbs energy curve of the beta phase; from their point of tangency the composition of the first beta nucleus is found as: ${x}_{\beta }$ = 0.672. The maximum driving force of nucleation ($-{\Delta }_{n}{G}_{m,min}$ = 1,297 J/mol-atom) is found as the vertical distance between the leading and the secondary tangent lines (see the longest and thickest vertical arrow). The driving force of nucleation is only positive in the interval of nucleus composition ${{x}_{\beta ,1}<x}_{\beta }<{x}_{\beta 2}$, wit ${x}_{\beta ,1}$ = 0.399, ${x}_{\beta ,2}$ = 0.909

As the parent phase is considered infinitely large compared to the nucleus phase, the composition of the parent phase remains constant during nucleation. That is why, the molar Gibbs energy curve of an equilibrium nucleus should be touching the “leading tangent line” drawn to the molar Gibbs energy curve of the parent phase at the selected value of ${x}_{\alpha }$ = 0.300. All other phases in the system can be divided into the following three groups:

• The curve for the molar integral Gibbs energy of a phase is positioned fully above the leading tangent line: those phases cannot form from this parent phase (not shown in Fig. 1),

• The curve for the molar integral Gibbs energy of a phase is positioned above the leading tangent line, but touches it at a single point: those phases are in equilibrium with this parent phase, but cannot nucleate from it as the driving force of nucleation is zero (not shown in Fig. 1),

• The curve for the molar integral Gibbs energy of a phase is positioned partly below the leading tangent line within a specific composition region (this phase is shown in Fig. 1 as “beta phase”); those phases can nucleate from the parent phase alpha within the specific concentration region with positive bulk driving force shown by vertical arrows in Fig. 1.

When the probability to form an embryo and the interfacial energy are independent of the composition of the nucleus, then the maximum bulk driving force of nucleation (${\Delta }_{n}{G}_{m,min}$) corresponds to the concentration of the first nucleus. This concentration is found by the parallel tangent method, when a “secondary tangent line” is drawn parallel to the “leading tangent line” in a way that it touches in a single point the curve of the integral molar Gibbs energy of phase beta. This point of tangency indicates the most probable composition of the first nucleus ${x}_{\beta }$ (see Fig. 1). Note that if the molar integral Gibbs energy of the nucleus is not differentiable, then the secondary tangent line is drawn to the lowest point of its molar integral Gibbs energy curve (not shown here).

The parallel tangent method demonstrated above contradicts experimental observations, as at ${{x}_{\beta ,e}>x}_{\alpha }>{x}_{\alpha ,e}$ this method predicts the composition of the first nucleus in the unexpected interval of ${x}_{\beta }>{x}_{\beta ,e}{>x}_{\alpha }$. In contrary, usually the composition of the first nucleus is observed experimentally in the interval of ${{x}_{\alpha }<x}_{\beta }<{x}_{\beta ,e}$.^[47] There are also two further theoretical reasons why the parallel tangent method should be improved. These are the two major over-simplified assumptions of the parallel tangent method:

• It is not true that the probability to form an embryo from a parent phase of given composition is independent of the composition of the embryo,

• It is also not true that the interfacial energy at the nucleus/parent phase interface is independent of the composition of the nucleus at fixed composition of the parent phase.

In this paper the parallel tangent method will be extended by considering the above two effects. Therefore, in the further theoretical treatment instead of the secondary tangent line only the vertical arrows are considered in Fig. 1. These arrows describe the negative driving force of nucleation of 1 mole-atom of the nucleus. This driving force (J/mol-atom of nucleus) is written by the following equation in agreement with Fig. 1, supposing the composition of the parent phase is not changed upon nucleation, as its amount is much larger compared to the amount of the nucleus:

$$ \Delta_{n} G_{m} = G_{m,\beta } \left( {x_{\beta } } \right) - G_{m,\alpha } \left( {x_{\alpha } } \right) - \left( {x_{\beta } - x_{\alpha } } \right) \cdot \left( {\frac{{dG_{m,\alpha } }}{dx}} \right)_{{x_{\alpha } }} $$

(2c)

where $G_{m,\beta } \left( {x_{\beta } } \right)$ (J/mol-atom) is the molar integral Gibbs energy of phase beta at $x = x_{\beta }$ (see Fig. 1), $G_{m,\alpha } \left( {x_{\alpha } } \right)$ (J/mol-atom) is the molar integral Gibbs energy of phase alpha at $x = x_{\alpha }$. Let us note that in the parallel tangent method the minimum of Eq 2c is found. Let us also note that Eq 2c provides negative values only in a limited interval $x_{\beta ,1} < x_{\beta } < x_{\beta 2}$. At $x_{\alpha }$ = 0.300 this interval is: $x_{\beta ,1}$ = 0.399, $x_{\beta ,2}$ = 0.909 (see Fig. 1).

3 On the Probability to Form an Embryo

Nucleation from an oversaturated solution phase alpha is usually explained in two steps: (i) step 1: the composition of the alpha phase fluctuates around its average composition ${x}_{\alpha }$, creating embryos of small volumes with local composition of ${x}_{\beta }$ but same structure as the parent phase, (ii) step 2: the embryo of local composition ${x}_{\beta }$ transforms into the beta phase of the same ${x}_{\beta }$ composition with its own structure being different from that of the alpha phase.

The parallel tangent method described above is in agreement with the above explanation except one detail: it is wrongly presumed that the probabilities to form different embryos with different ${x}_{\beta }$ values from the same parent solution of constant ${x}_{\alpha }$ values are identical; in fact such a claim is not made in the literature, it is just supposed so without claiming so, or in other words this detail was simply forgotten when the parallel tangent method was derived/introduced. However, it is obvious that increasing the composition difference between ${x}_{\beta }$ and ${x}_{\alpha }$ the probability to form an embryo will gradually decrease.^[23,27]

Now, let us model the probability that atoms B have the requested concentration needed for the embryo for phase beta: this probability is denoted here as $p_{B}$ (dimensionless). The probability of this fluctuation state is written after Boltzmann as:

$$ p_{B} = exp\left( { - \frac{{\Delta_{fl} G_{B} }}{R \cdot T}} \right) $$

(3a)

where $\Delta_{fl} G_{B}$ (J/mol-atom) is the molar Gibbs energy change accompanying the fluctuation of atoms B leading to the requested composition of the embryo for phase beta. First, let us consider the case with $x_{\beta } > x_{\alpha }$, in agreement with Fig. 1. Therefore, the fluctuation process should drive some B atoms from the alpha matrix phase of composition $x_{B\left( \alpha \right)}$ (= the initial state) into the embryo of composition $x_{B\left( \beta \right)}$ (= the final state). As only the configurational entropy term of the molar Gibbs energy of the parent solution phase relates to probability, only this term is considered when the molar Gibbs energy change accompanying this process is written as:

$$ \Delta_{fl} G_{B} = R \cdot T \cdot ln\frac{{x_{B\left( \beta \right)} }}{{x_{B\left( \alpha \right)} }} $$

(3b)

Applying Eq 3a, 3b follows as:

$$ p_{B} = \frac{{x_{{B\left( \alpha \right)}} }}{{x_{{B\left( \beta \right)}} }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x_{{B\left( \beta \right)}} > x_{{B\left( \alpha \right)}}$$

(3c)

As the condition $x_{B\left( \beta \right)} > x_{B\left( \alpha \right)}$ applies, $0 < p_{B} < 1$ follows from Eq 3c. Moreover, the larger the difference between the two compositions the lower is the probability that such an embryo can be formed by fluctuations. This agrees with our common-sense expectations. The same logic can be used to derive the equation for $x_{B\left( \beta \right)} < x_{B\left( \alpha \right)}$:

$$ p_{B} = \frac{{x_{B\left( \beta \right)} }}{{x_{B\left( \alpha \right)} }} \quad \quad \quad x_{B\left( \beta \right)} < x_{B\left( \alpha \right)} $$

(3d)

Similarly, to Eq 3c, Eq 3d also provides a probability value in the expected interval of $0 < p_{B} < 1$. However, it is not sufficient to adjust the composition of component B of the embryo for phase beta. In addition, the composition of the embryo should be also adjusted for all its components. The probability of fluctuations to adjust the composition of component A within the embryo is written with analogous equations to Eq 3c-d:

$$ p_{A} = \frac{{x_{A\left( \alpha \right)} }}{{x_{A\left( \beta \right)} }} \quad \quad \quad x_{A\left( \beta \right)} > x_{A\left( \alpha \right)} $$

(3e)

$$ p_{A} = \frac{{x_{A\left( \beta \right)} }}{{x_{A\left( \alpha \right)} }} \quad \quad \quad x_{A\left( \beta \right)} < x_{A\left( \alpha \right)} $$

(3f)

For a binary A-B system the complex probability to form an embryo for phase beta is written as the product of the partial probabilities:

$$ p_{\beta } = p_{A} \cdot p_{B} $$

(3g)

Substituting Eq 3c-f into Eq 3g for a binary solution alpha, the result is:

$$ p_{\beta } = \frac{{x_{\alpha } }}{{x_{\beta } }} \cdot \frac{{1 - x_{\beta } }}{{1 - x_{\alpha } }} \quad \quad \quad x_{\beta } \ge x_{\alpha } $$

(3h)

$$ p_{\beta } = \frac{{x_{\beta } }}{{x_{\alpha } }} \cdot \frac{{1 - x_{\alpha } }}{{1 - x_{\beta } }} \quad \quad \quad x_{\beta } \le x_{\alpha } $$

(3i)

Note that both terms of Eq 3h-i have positive values less than unity as expected for partial probability values. That is why also the complex probability has a positive value below unity, as expected. The concentration dependence of Eq 3h-i for $x_{\alpha }$ = 0.300 is shown in Fig. 2. As expected, it goes through a maximum point $p_{\beta }$ = 1 at the initial composition of the parent phase $x_{\beta } = x_{\alpha }$ = 0.300 and it tends towards zero as $x_{\beta }$ approaches zero or unity, i.e. at the compositions of any of the pure components.

Fig. 2

The dependence of the corrections calculated by different equations at the fixed composition of the parent phase (${x}_{\alpha }$ = 0.300) as function of the composition of the nucleus (k = 20 is applied in Eq 4j-k)

Let us note that the effect of embryo size is missing from the above equations. However, the larger the size of the embryo prior to nucleation, the smaller is the probability of its formation by compositional fluctuations given the same compositions of the initial matrix and the embryo. Therefore, Eq 3h-i should be multiplied by an additional term reflecting the size dependence of probability. In the first approximation, this size-dependent term will be not composition dependent, and that is why this new, size-dependent term of probability is eliminated when the composition of the first nucleus is calculated below. That is why this term is not discussed in this paper in more details.

Let us finally note that in the model equations for the rate of nucleation (not discussed here in details) the probability to form an embryo is usually not considered. Therefore, it is suggested here to multiply the current equations for the rate of nucleation by the value of ${p}_{\beta }$ defined by Eq 3h-i.

4 On the Concentration Dependence of the Interfacial Energy

In the parallel tangent method, the maximum value of $(-{\Delta }_{n}{G}_{m})$ is searched for, as the value of the interfacial energy in Eq 1b is supposed to be a constant, independent of the composition of the nucleus. However, this is a very crude approximation as the interfacial energy is known to be a strong function of composition difference of the two phases surrounding the interface.^[53,60] Naturally, the composition dependence of interfacial energy is specific for each system, thus an exact and generally valid equation cannot be found. Nevertheless, compared to the current practice of fully neglecting this effect even an approximated equation would serve better.

To find such an approximated relationship between the interfacial energy and the difference in compositions of the first nucleus and the parent phase let us apply our recently derived equation for the interfacial energy of semi-coherent interfaces ($\sigma$, J/m²)^[60]:

$$ \sigma = \sigma_{c} + \frac{{z_{V} }}{0.47} \cdot \left( {\sigma_{i} - \sigma_{c} } \right) $$

(4a)

where $\sigma_{c}$ (J/m²) is the interfacial energy along the coherent interface, $\sigma_{i}$ (J/m²) is the interfacial energy along the incoherent interface and $z_{V}$ is the volume misfit between the two phases defined as^[60]:

$$ z_{V} \equiv \left| {\frac{{V_{m,\alpha } }}{{V_{m,\beta } }} - 1} \right| $$

(4b)

where $V_{m,\alpha }$ (m³/mol) is the molar volume of the initial parent phase. In the first approximation the molar volume is a linear function of the molar ratio of component B (x, dimensionless):

$$ V_{m,\alpha } \cong V_{m,A}^{o} + \Delta V_{m}^{o} \cdot x_{\alpha } $$

(4c)

$$ V_{m,\beta } \cong V_{m,A}^{o} + \Delta V_{m}^{o} \cdot x_{\beta } $$

(4d)

where $V_{m,A}^{o}$ (m³/mol) is the standard molar volume of pure component A, $\Delta{V}_{m}^{o}$ (m³/mole) is the difference between the standard molar volumes of the two components, defined as:

$$ \Delta V_{m}^{o} \equiv V_{m,B}^{o} - V_{m,A}^{o} $$

(4e)

Now, let us substitute Eq 4c-d into Eq 4b; after some re-arrangements:

$$ z_{V} \cong \frac{{\left| {\Delta V_{m}^{o} } \right|}}{{V_{m,\beta } }} \cdot \left| {x_{\beta } - x_{\alpha } } \right| $$

(4f)

Now, let us substitute Eq 4f into Eq 4a:

$$ \sigma \cong \sigma_{c} \cdot \left( {1 + k \cdot \left| {x_{\beta } - x_{\alpha } } \right|} \right) $$

(4g)

where k (dimensionless) is a semi-empirical parameter defined as:

$$ k \equiv \frac{1}{0.47} \cdot \frac{{\left| {\Delta V_{m}^{o} } \right|}}{{V_{m,\beta } }} \cdot \left( {\frac{{\sigma_{i} }}{{\sigma_{c} }} - 1} \right) $$

(4h)

The characteristic values of parameters of Eq 4h are as follows: $\left| {\Delta V_{m}^{o} } \right|/V_{m,\beta } \cong 0.2...1.0$ and $\sigma_{i} /\sigma_{c} \cong 10 ... 50$.^[60] Substituting these values in Eq 4h: k = 4 … 100 with a characteristic value of $k \cong 20$ follows. Substituting Eq 4g into Eq 1b:

$$ r_{cr} = 2 \cdot V_{m,\beta } \cdot \sigma_{c} \cdot \left( {\frac{{1 + k \cdot \left| {x_{\beta } - x_{\alpha } } \right|}}{{ - \Delta_{n} G_{m} }}} \right) $$

(4i)

In the first approximation the composition dependence of $V_{m,\beta } \cdot \sigma_{c}$ is negligible, and so the critical size of the nucleus increases proportional to the composition difference $\left| {x_{\beta } - x_{\alpha } } \right|$ according to Eq 4i; however, increasing $\left| {x_{\beta } - x_{\alpha } } \right|$ also the value of $- \Delta G_{m}$ changes, see Eq 2c.

At this point let us make a disclaimer: if the actual composition dependence of the interfacial energy is known in the actual system, then that specific equation should be used instead of Eq 4g. Eq 4g can be used only in the first approximation in absence of information on the composition dependence of the interfacial energy in the actual system. Let us note that Eq 4g agrees well with experimental observations that during nucleation first usually transition phases are formed and later they gradually replace each other with the gradual increase of $\left|{x}_{\beta }-{x}_{\alpha }\right|$ values, the equilibrium phase being usually the last phase to form with its maximum value of $\left|{x}_{\beta }-{x}_{\alpha }\right|$.^[47] This is because the interface types of the transition phases usually gradually change from coherent through semi-coherent toward incoherent, in agreement with Eq 4a-h.^[60]

Finally, the complex correction due to the probability to form an embryo and due to the composition dependence of interfacial energy is written by combining Eq 3h-i, 4h:

$$ correction = \frac{{x_{\alpha } }}{{x_{\beta } }} \cdot \frac{{1 - x_{\beta } }}{{1 - x_{\alpha } }} \cdot \frac{1}{{1 + k \cdot \left( {x_{\beta } - x_{\alpha } } \right)}} \quad \quad \quad x_{\beta } \ge x_{\alpha } $$

(4j)

$$ correction = \frac{{x_{\beta } }}{{x_{\alpha } }} \cdot \frac{{1 - x_{\alpha } }}{{1 - x_{\beta } }} \cdot \frac{1}{{1 + k \cdot \left( {x_{\alpha } - x_{\beta } } \right)}} \quad \quad \quad x_{\beta } \le x_{\alpha } $$

(4k)

The complex corrections written by Eq 4j-k are shown as function of nucleus composition in Fig. 2 (calculated with k = 20). One can see that the corrections by Eq 3 h-i are enhanced by the complex corrections of Eq 4j-k.

5 The Combination of Different Parts of the New Model

Now, let us multiply Eq 4j-k by $\Delta_{n} G_{m}$ to define a new function F as:

$$ F \equiv \frac{{x_{\alpha } }}{{x_{\beta } }} \cdot \frac{{1 - x_{\beta } }}{{1 - x_{\alpha } }} \cdot \frac{{\Delta_{n} G_{m} }}{{1 + k \cdot \left( {x_{\beta } - x_{\alpha } } \right)}} \quad \quad \quad x_{\beta } \ge x_{\alpha } $$

(5a)

$$ F \equiv \frac{{x_{\beta } }}{{x_{\alpha } }} \cdot \frac{{1 - x_{\alpha } }}{{1 - x_{\beta } }} \cdot \frac{{\Delta_{n} G_{m} }}{{1 + k \cdot \left( {x_{\alpha } - x_{\beta } } \right)}} \quad \quad \quad x_{\beta } \le x_{\alpha } $$

(5b)

where $\Delta_{n} G_{m}$ is calculated by Eq 2c. The more negative the value of function F, the smaller is the critical radius of nucleation according to Eq 1b, 4i and the more probable is the formation of the nucleus according to Eq 3h-i. Therefore, the expected modified composition of the first nucleus is denoted here as $x_{\beta ,min,corr}$, which corresponds to the most negative (minimum) value of function F. In Fig. 3a-b ${\Delta }_{n}{G}_{m}$ calculated by Eq 2a-c is compared to F calculated by Eq 2a-c, 5a-b at k = 20 as function of the composition of the nucleus at fixed initial composition of the parent phase ${x}_{\alpha }$ = 0.400 and at fixed temperature T = 1,000 K. As follows from the comparison of Figs 3a-b, the minimum of function F is shifted considerably towards the composition of the parent phase (${x}_{\beta ,min,corr}$ = 0.450) compared to the value obtained by the parallel tangent method (${x}_{\beta ,min}$ = 0.761). Due to the shift in the composition of the first nucleus also the value of ${\Delta }_{n}{G}_{m,min}$ = − 2,653 J/mol-atom (Fig. 3a) is shifted to a less negative value of ${\Delta }_{n}{G}_{m,min,corr}$ = − 807.2 J/mol-atom, calculated by Eq 2a-c using the values of ${x}_{\alpha }$ = 0.400 and ${x}_{\beta ,min,corr}$ = 0.450. The same procedure as shown in Fig. 3a-b can be repeated at different values of the initial composition of the parent phase ${x}_{\alpha }$. The results are shown in Fig. 4 as function of initial composition of the parent phase.

Fig. 3

The molar Gibbs energy change accompanying nucleation of 1 mole of nucleus from infinite amount of the parent phase (Fig. 3a) calculated by Eq 2a-c and function F (Fig. 3b) calculated by Eq (2a-c, 5a-b) at k = 20 as functions of the composition of the nucleus at fixed composition of the parent phase ${x}_{\alpha }$b = 0.400 and at fixed temperature T = 1,000 K. The shift in the nucleus composition in Fig. 3b (${x}_{\beta ,min,corr}$ = 0.450) is shown relative to the value found in Fig. 3a (${x}_{\beta ,min}$ = 0.761) by horizontal arrow

Fig. 4

Dependence of the negative of the maximum driving force (Fig.4b) and the corresponding composition of the first nucleus (Fig. 4a) as function of the composition of the parent phase calculated by the “parallel tangent method” (see Fig. 1, 3a) and by the extended method (see Fig. 3b). The dotted lines are the equilibrium compositions of the two phases

As follows from Fig. 4a, the extended method provides the compositions of the first nucleus below its equilibrium value. In contrary, the parallel tangent method always predicts the composition of the first nucleus being higher than its equilibrium composition. In other words, the practical problem mentioned above in connection with the parallel tangent method and Fig. 1 is resolved: at ${{x}_{\beta ,e}>x}_{\alpha }>{x}_{\alpha ,e}$ the extended method correctly predicts ${{x}_{\alpha }<x}_{\beta ,min-corr}<{x}_{\beta ,e}$ (see Fig. 4a) in agreement with the experimental observations.^[47] In contrary, the parallel tangent method wrongly predicts ${x}_{\beta ,min}>{x}_{\beta ,e}{>x}_{\alpha }$ (see Fig. 1 and 4a) contradicting the experimental observations.^[47]

6 Extension of the Extended Method to Multi-component Systems

The method developed above is valid for binary systems. Now, let us extend it to a multicomponent solution phase alpha, from which a multi-component nucleus phase beta is precipitated. In this case the probability to form an embryo is calculated as the product obtained by the multiplication of the partial probabilities for all components of phase alpha:

$$ p_{\beta } = \mathop \prod \limits_{i} p_{i} $$

(6a)

where the partial probability to form an embryo for component i ($p_{i}$, dimensionless) is written in analogue with Eq 3h-i:

$$ p_{i} = \frac{{x_{i\left( \alpha \right)} }}{{x_{i\left( \beta \right)} }} \quad \quad \quad x_{i\left( \beta \right)} > x_{i\left( \alpha \right)} $$

(6b)

$$ p_{i} = \frac{{x_{i\left( \beta \right)} }}{{x_{i\left( \alpha \right)} }} \quad \quad \quad x_{i\left( \beta \right)} < x_{i\left( \alpha \right)} $$

(6c)

Eq 4h is extended to a C-component system by defining $\left| {x_{\beta } - x_{\alpha } } \right|$ as:

$$ \left| {x_{\beta } - x_{\alpha } } \right| = \sqrt {C^{ - 1} \cdot \mathop \sum \limits_{i} \left( {x_{i\left( \beta \right)} - x_{i\left( \alpha \right)} } \right)^{2} } $$

(6d)

Finally, Eq 5a-b are extended to a C-component systems as:

$$ F \equiv \mathop \prod \limits_{i} p_{i} \cdot \frac{{\Delta_{n} G_{m} }}{{1 + k \cdot \sqrt {C^{ - 1} \cdot \mathop \sum \nolimits_{i} \left( {x_{i\left( \beta \right)} - x_{i\left( \alpha \right)} } \right)^{2} } }} $$

(6e)

where the first term is calculated by Eq 6b-c and $\Delta_{n} G_{m}$ is calculated for the multi-component system using the Calphad method.^{[26,30,62,63]} Let us note that if the nucleating phase beta does not contain any of the components of the parent phase alpha, then this embryo will have zero formation probability.

7 Application to the Sequence of Nucleation from an Al-Fe Liquid Alloy

One of the important applications of the parallel tangent method is that (at least in principle) it allows to predict the most probable first nucleus when more than one phase can nucleate from the same over-saturated solution. One of such examples is presented by Malakhov et al.^[27] for the crystallization of liquid Al contaminated by a small amount of Fe. The driving forces calculated in^[27] using the parallel tangent method are shown in Fig. 5. They are calculated by Malakhov et al. by presuming that the formation of the Al-rich fcc solid solution takes place first from the slightly undercooled liquid solution and then the driving forces are calculated to nucleate different Al_nFe_m intermetallic compounds from the remaining liquid solution as function of temperature.^[27] As follows from Fig. 5, using the parallel tangent method it is predicted that the most probable first phase to be nucleated after the nucleation of the fcc phase is the Al₁₃Fe₄ phase. The same conclusion is found when the eutectic reaction is modelled by Thermo-Calc using the Scheil formalism.^[27] However, this phase is found experimentally only in the last solidifying portion of the casting, while the first-solidifying portion of the casting contains mostly the metastable Al₆Fe and Al₄Fe phases.^{[27,64,65,66,67,68,69,70,71,72]} This experimental finding contradicts the prediction of Fig. 5 made by the parallel tangent method. The reasons for this contradiction are explained by Malakhov et al.^[27] by the fact that the probability to form a nucleus is neglected by the parallel tangent method. This probability is worked out in this paper.

Fig. 5

The driving forces of nucleation of different Al_nFe_m intermetallic phases from the remaining liquid after the fcc phase is formed as function of temperature for the Al-0.3 w% Fe system calculated by the parallel tangent method by Malakhov et al. ^[27]. The stoichiometry numbers of Al_nFe_m phases are shown along the lines in the format “n/m”

Now, let us apply our corrected method developed in this paper to predict the sequence of phases that nucleate from the remaining of the Al-0.3w%Fe liquid solution upon cooling, after the precipitation of the fcc phase. For this purpose, the mole fraction of Fe of the remaining liquid phase is used, written by the following approximated equation, obtained after the numerical data by Malakhov et al.^[27] (T is given in °C):

$$ x_{L} \cong 0.215 + 2.20 \cdot 10^{ - 4} \cdot T - 8.07 \cdot 10^{ - 7} \cdot T^{2} $$

(7a)

The compositions of the nuclei (denoted as phase beta) are estimated from the stoichiometries of the compounds:

$$ x_{\beta } \cong \frac{m}{n + m} $$

(7b)

where n and m (both dimensionless) are the stoichiometry coefficients in Al_nFe_m intermetallic compounds. Now, let us re-write our Eq 5a-b for this case when the parent phase is a liquid phase (α = L):

$$ F \equiv \frac{{x_{L} }}{{x_{\beta } }} \cdot \frac{{1 - x_{\beta } }}{{1 - x_{L} }} \cdot \frac{{\Delta_{n} G_{m} }}{{1 + k \cdot \left( {x_{\beta } - x_{L} } \right)}} \quad \quad \quad x_{\beta } \ge x_{L} $$

(7c)

$$ F \equiv \frac{{x_{\beta } }}{{x_{L} }} \cdot \frac{{1 - x_{L} }}{{1 - x_{\beta } }} \cdot \frac{{\Delta_{n} G_{m} }}{{1 + k \cdot \left( {x_{L} - x_{\beta } } \right)}} \quad \quad \quad x_{\beta } \le x_{L} $$

(7d)

where $\Delta_{n} G_{m}$ (J/mol-atom) are the molar Gibbs energies of 1 mole of different phases accompanying nucleation taken from.^[27] The results of calculations by Eq 7a-d are shown in Fig. 6 using the same characteristic value k = 20 as was used above. As follows from Fig. 6, the first nucleus predicted by our extended method is the Al₆Fe phase, the second one is the Al₄Fe phase and the third one is the Al₁₃Fe₄ phase, in agreement with the experiments.^{[27,64,65,66,67,68,69,70,71,72]} This agreement proves the ability of our extended method presented above to correctly predict the correct sequence of nucleating phases.

Fig. 6

The corrected driving forces of different Al_nFe_m intermetallic phases from the remaining liquid after the fcc phase is formed as function of temperature for the Al-0.3 w% Fe system calculated by Eq 7a-d and k = 20. The stoichiometry numbers of Al_nFe_m phases are shown along the lines in the format “n/m”

8 Conclusions

• The “parallel tangent method” is analysed here and it is shown that (i) It over-estimates the composition difference between the first nucleus and the parent phase, (ii) It neglects the different probabilities to form embryos of different compositions prior to nucleation by compositional fluctuations of supersaturated solutions, (iii) It neglects the concentration dependence of the interfacial energy.

• An extended thermodynamic method is presented in this paper that takes the above two effects into account. It is found that the extended method does not over-estimate the composition of the first nucleus, or at least not in a principally wrong way.

• The new method is also extended to multicomponent systems.

• It is suggested here that the new equation for the probability to form the embryo should also be taken into account when the rate of nucleation is modelled.

• The new, extended method is tested against experimental data for the Al-Fe liquid alloy with 0.3 w% of Fe to predict the sequence of nucleation of intermetallic phases that nucleate after the fcc phase as function of temperature. It is found that the first nucleating phase should be Al₆Fe, the second one should be Al₄Fe and the third one should be Al₁₃Fe₄. This result is in agreement with experiments confirming the validity of the new method. Note: the classical parallel tangent method applied to the same system predicts wrongly that the first nucleating phase should be Al₁₃Fe₄ (see^[27]).