1 Introduction

In recent years, fractional differential equations have attracted much attention since they play an important role in widespread fields such as biochemistry, physics, biology, chemistry, and finance; please refer to [1–6]. The interest of the study of fractional differential equations lies in the fact that the fractional-order derivatives and integrals enable the description of memory and hereditary properties of various materials and processes [7]. Time-fractional diffusion equations, obtained from the standard diffusion equation by replacing the standard time derivative with a time-fractional derivative, have been studied with respect to their direct problems in different contexts, see [8–16] and references therein.

In some practical problems, we need to determine the diffusion coefficients, initial data or source term by additional measured data that will lead to some fractional diffusion inverse problems. Among them, the inverse source problems for the time-fractional diffusion equations have been widely studied. A large number of studies has been done to research the uniqueness [17–19], conditional stability [18–20], and numerical computations [18–25] of these problems. Many methods for solving these problems are based on the eigenfunction system of a corresponding differential operator [19–24]. This leads to a problem: only when the solution satisfies certain boundary conditions can the methods obtain better convergence results. Next, we illustrate this with the inverse source problem considered in this paper.

We consider the following unknown source problem in a time-fractional diffusion equation [20]:

$$ \textstyle\begin{cases} {}_{0}\partial _{t}^{\alpha}u-u_{xx}=f(x),&0< x< 1, 0< t< T, \\ u(0,t)=u(1,t)=0,&0\leq t\leq T, \\ u(x,0)=0,&0\leq x\leq 1, \\ u(x,T)=g(x),&0\leq x\leq 1, \end{cases} $$
(1)

where \({}_{0}\partial _{t}^{\alpha}u\) is the left-sided Caputo fractional derivative of order α defined by

$$ {}_{0}\partial _{t}^{\alpha}u= \frac{1}{\Gamma (1-\alpha )} \int _{0}^{t} \frac{\partial u(x,s)}{\partial s} \frac{ds}{(t-s)^{\alpha}},\quad 0< \alpha < 1, $$

where \(\Gamma (\cdot )\) is the Gamma function. Our goal is to recover the source term \(f(x)\) from the final data \(u(x,T)=g(x)\). Since the data \(g(x)\) is usually based on the observation, they must contain errors and we assume the noisy data \(g^{\delta}\) satisfies

$$ \bigl\Vert g^{\delta}-g \bigr\Vert \leq \delta . $$
(2)

To obtain the solution of problem (1), we solve the following Sturm–Liouville Problem (SLP)

$$ \textstyle\begin{cases} X''+\lambda X=0,\quad \text{in }(0,1), \\ X(0)=X(1)=0. \end{cases} $$
(3)

Its solution is

$$ \lambda _{\ell}=\ell ^{2}\pi ^{2},\qquad X_{\ell}= \sqrt{2}\sin \ell \pi x, \quad \ell =1,2,\ldots . $$

If we define the generalized Mittag–Leffler function as

$$ E_{\alpha ,\beta}(z)=\sum_{k=0}^{\infty} \frac{z^{k}}{\Gamma (\alpha k+\beta )}, $$
(4)

where \(\alpha >0\), \(\beta \in \mathcal{R}\), then it can be deduced that the solution of (1) has the form [20]:

$$ u(x,t)=\sum_{\ell =1}^{\infty} \frac{1-E_{\alpha ,1}(-\lambda _{\ell}t^{\alpha})}{\lambda _{\ell}}(f,X_{ \ell})X_{\ell}. $$

Hence, we can obtain

$$ g(x) = \sum_{\ell =1}^{\infty} \frac{1-E_{\alpha ,1}(-\ell ^{2}\pi ^{2}T^{\alpha})}{\ell ^{2}\pi ^{2}}(f,X_{ \ell})X_{\ell}. $$

Define operator \(K:f\rightarrow g\) as

$$ Kf(x)=\sum_{\ell =1}^{\infty} \frac{1-E_{\alpha ,1}(-\ell ^{2}\pi ^{2}T^{\alpha})}{\ell ^{2}\pi ^{2}}(f,X_{ \ell})X_{\ell}=g(x), $$
(5)

then a singular system \(\{\sigma _{\ell}, \phi _{\ell}, \varphi _{\ell}\}\) of K can be given as

$$ \sigma _{\ell}= \frac{1-E_{\alpha ,1}(-\lambda _{\ell}T^{\alpha})}{\lambda _{\ell}}, \qquad \phi _{\ell}= \varphi _{\ell}=X_{\ell}. $$
(6)

Hence, the inverse problem (1) can be transformed into solving the following compact operator equation

$$ Kf=g^{\delta}. $$
(7)

Based on the above singular system, we can obtain the stable solution of (7) by different regularization schemes and the complete process of the truncation method has been given in [20]. In this framework, the following source condition is needed to obtain the convergence rates of the regularization solution:

$$ \Biggl(\sum_{\ell =1}^{\infty} \lambda _{\ell}^{r} \bigl\vert \langle f,X_{\ell} \rangle \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} \leq E_{1},\quad r>0, $$
(8)

where \(E_{1}>0\) is a constant. In other words, the smoothness of the function is characterized by the decay rate of the expansion coefficient with respect to \(X_{\ell}\). However, it is well known that the Fourier-sine coefficients of a function can decay rapidly only if the function satisfies certain boundary conditions. Specifically, if boundary condition

$$ f(0)=f(1)=0 $$

does not hold, then even if the function is sufficiently smooth, the condition (8) holds only for \(r<1\). The fundamental reason for this situation is that the SLP in formula (3) is regular, i.e., a smooth function can be approximated by the eigenfunctions of (3) with spectral accuracy if and only if all its even derivatives vanish at the boundary [26].

Hence, in this paper we change the approach to approximate the source term f. A direct idea is that we can construct an approximation by Jacobi polynomials that are eigenfunctions of the singular SLPs. Jacobi polynomials as recommended basis functions have been used to solve some inverse problems [27–30]. In this paper, we will use the Jacobi polynomials instead of eigenfunctions \(\{X_{\ell}\}\). Moreover, we introduce a modified Tikhonov method to overcome the illposedness of the problem (7). The method has been used to solve a numerical differentiation problem in [30]. A discrepancy principle will be used to choose the regularization parameter and the new method can self-adaptively obtain the convergence rate without the limitation of boundary conditions.

The outline of the paper is as follows: we construct the regularization solution by a modified Tikhonov regularization method with Jacobi polynomials in Sect. 2. In Sect. 3, the detailed theoretical analysis of the method is carried out. Some numerical examples are given in Sect. 4 to confirm the effectiveness of the method. Finally, we end this paper with a brief conclusion in Sect. 5.

2 A modified Tikhonov regularization method based on Jacobi polynomials

The kth Jacobi polynomials are defined by [26]

$$ \begin{aligned} &{P}^{\alpha ,\beta}_{k}(x)=\frac{(-1)^{k}}{2^{k}k!} \frac{1}{(1-x)^{\alpha}(1+x)^{\beta}}\frac{d^{k}}{dx^{k}} \bigl[(1-x)^{k+ \alpha}(1+x)^{k+\beta} \bigr], \\ &\quad k=0,1,\ldots , \ \alpha , \beta >-1. \end{aligned} $$
(9)

They satisfy the orthogonality relations

$$ \int _{-1}^{1}\omega ^{\alpha ,\beta}(x){P}^{\alpha ,\beta}_{k}(x){P}^{ \alpha ,\beta}_{j}(x)\,dx = \gamma _{k}^{\alpha ,\beta}\delta _{k,j}, $$

where

$$ \gamma _{k}^{\alpha ,\beta}= \frac{2^{\alpha +\beta +1}\Gamma (k+\alpha +1)\Gamma (k+\beta +1)}{(2k+\alpha +\beta +1){k}!\Gamma (k+\alpha +\beta +1)}. $$

From [26], the following derivative relations hold

$$ \frac{d^{j}}{dx^{j}}P_{k}^{\alpha ,\beta}(x)=d_{k,j}^{\alpha ,\beta}P_{k-j}^{ \alpha +j,\beta +j}(x), \quad k\geq j, $$
(10)

where

$$ d_{k,j}^{\alpha ,\beta}= \frac{\Gamma (k+j+\alpha +\beta +1)}{2^{j}\Gamma (k+\alpha +\beta +1)}. $$

Since we consider the problem in the interval \(\Lambda =[0, 1]\), we introduce the functions \({L}_{k}(x)\), \(J_{k}(x)\) by coordinate transformation:

$$ \begin{aligned} & {L}_{k}(x) = \sqrt{2k+1} {P}^{0,0}_{k} (2x-1 ), \\ & J_{k}(x) =\frac{\sqrt{(2k+5)(k+3)(k+4)}}{4\sqrt{(k+1)(k+2)}}{P}_{k}^{2,2}(2x-1), \quad x\in [0,1]. \end{aligned} $$
(11)

The following related properties can be easily obtained:

$$ L_{k}(0)=(-1)^{k}\sqrt{2k+1},\qquad L_{k}(1)=\sqrt{2k+1}, \quad \text{and} \quad {L}''_{k}(x)=\eta _{k}J_{k-2}(x), $$
(12)

where

$$ \eta _{k}=\frac{\sqrt{(k-1)k{(k+1)(k+2)}}}{4}. $$

The orthogonality relations of \({L}_{k}\) and \(J_{k}\) can be given as:

$$\begin{aligned}& \int _{\Lambda}{L}_{k}(x){L}_{j}(x)\,dx = \delta _{k,j}{,}\\& \int _{\Lambda}{\omega}(x){J}_{k}(x){J}_{j}(x) \,dx =\delta _{k,j}, \end{aligned}$$

with

$$ \omega (x)=\omega ^{2,2}(2x-1)=\bigl(4x-4x^{2} \bigr)^{2}. $$

The weighted space \(L^{2}_{\omega}(\Lambda )\) is defined as

$$ L^{2}_{\omega}(\Lambda )= \biggl\{ f: \Vert f \Vert _{L^{2}_{\omega}}= \biggl( \int _{\Lambda} \omega (x)f^{2}(x)\,dx \biggr)^{1/2}< \infty \biggr\} . $$
(13)

For a function \(f\in L_{\omega}^{2}(\Lambda )\), we can obtain

$$ f(x)=\sum_{k=0}^{\infty} \hat{f}_{k}J_{k}(x), $$

with

$$ \hat{f}_{k}= \int _{\Lambda}\omega (x)f(x)\hat{J}_{k}(x)\,dx . $$

By the Parseval equality

$$ \Vert f \Vert _{L^{2}_{\omega}}^{2}=\sum ^{\infty}_{k=0}\hat{f}_{k}^{2}. $$

Let vector \(\vec{\mathbf{f}}=(\hat{f}_{0},\hat{f}_{1},\ldots \hat{f}_{n},\ldots )^{T}\) that contains all expansion coefficients of \(f\in L_{\omega}^{2}(\Lambda )\) with respect to \(J_{k}(x)\), and we define the operators

$$ \begin{aligned}& { ({\mathcal{J}}\vec{ \mathbf{f}} ) (x)=\sum_{k=0}^{ \infty } \hat{f}_{k}{J}_{k}(x)}, \\ & \mathcal{P}_{N} \vec{\mathbf{f}}=(\hat{f}_{0}, \hat{f}_{1},\ldots, \hat{f}_{N},0,0, \ldots )^{T}, \\ & \mathcal{R}\vec{\mathbf{{f}}}=\bigl( \hat{f}_{0}, e\hat{f}_{1}, \ldots , e^{n} \hat{f}_{n},\ldots \bigr)^{T}, \end{aligned} $$
(14)

where N is a nonnegative integer and e is the natural constant.

We introduce the following variable Hilbert scale spaces

$$ W_{2}^{\psi}:= \Biggl\{ f\in L_{\omega}^{2}(\Lambda ): \Vert f \Vert ^{2}_{\psi}:= \sum_{k=0}^{\infty} \psi ^{2}(k)\hat{f}_{k}^{2}< \infty \Biggr\} , $$
(15)

where \(\psi :[0,\infty )\rightarrow (0,\infty )\) is a nondecreasing function satisfying \(\lim_{x\rightarrow \infty}\psi (x)=\infty \). In this paper, we will consider the following two cases:

  1. 1.

    Finitely smoothing case:

    $$ \psi (x)=\phi _{r}(x)=\textstyle\begin{cases} 1,& x< 1, \\ x^{r},& x\geq 1,\end{cases}\displaystyle \quad r>1. $$
    (16)
  2. 2.

    Infinitely smoothing case:

    $$ \psi (x)=\varphi _{\lambda}(x)=e^{\lambda x},\quad \lambda >0. $$
    (17)

In both cases, the regularization solution of problem (1) is defined as the minimizer of the following Tikhonov functional:

$$ \bigl\Vert Kh-g^{\delta} \bigr\Vert ^{2}+\rho \Vert h \Vert ^{2}_{\varphi _{1}}{,} $$
(18)

where ρ is a regularization parameter and it will be chosen by the Morozov discrepancy principle: ρ is the solution of the equation

$$ \bigl\Vert Kh-g^{\delta} \bigr\Vert =C\delta , $$
(19)

with a given constant \(C>1\).

If we let \({A}=K\mathcal{J}\) and \(h=\mathcal{J}\vec{\mathbf{{h}}}\), then (18) becomes

$$ \bigl\Vert A\vec{\mathbf{{h}}}-g^{\delta} \bigr\Vert ^{2}+\rho \Vert \mathcal{R}\vec{\mathbf{{h}}} \Vert ^{2}_{ \ell ^{2}}, $$
(20)

hence, the minimizer of (18) can be given as

$$ h_{\rho}^{\delta}=\mathcal{J}\vec{ \mathbf{{h}}}_{\rho}^{\delta}, $$
(21)

where \(\vec{\mathbf{{h}}}_{\rho}^{\delta}\) is the solution of equation

$$ \bigl({A}^{*}{A}+\rho \mathcal{R}^{2} \bigr)\vec{\mathbf{{h}}}={A}^{*}g^{\delta}. $$
(22)

In this case, the equation (19) converts to

$$ \bigl\Vert A\vec{\mathbf{{h}}}^{\delta}_{\rho}-g^{\delta} \bigr\Vert =C\delta . $$
(23)

Lemma 1

[20] For \(0<\alpha <1\), \(E_{\alpha ,1}\) is a monotone decreasing function for \(t \geq 0\) and we have

$$ 1=E_{\alpha ,1}(0)>E_{\alpha ,1}(-t)>0,\quad t>0. $$
(24)

Lemma 2

[31] If we let \(\mathcal{B}=A\mathcal{R}^{-1}\), then by using functional calculus, we have

$$ \vec{\mathbf{{h}}}_{\rho}^{\delta}=\mathcal{R}^{-1}d_{\rho} \bigl(\mathcal{B}^{*} \mathcal{B}\bigr)\mathcal{B}^{*}g^{\delta} \quad \textit{with } d_{\rho}( \lambda )=\frac{1}{\lambda +\rho}. $$
(25)

The function \(d_{\rho}:(0,\|\mathcal{B}\|^{2}]\rightarrow (0,\infty )\) such that

$$ \sup_{\lambda >0}\lambda ^{1/2} \bigl\vert d_{\rho}(\lambda ) \bigr\vert \leq \frac{1}{2\sqrt{\rho}},\qquad \sup _{\lambda >0}\lambda \bigl\vert d_{\rho}( \lambda ) \bigr\vert \leq 1 $$
(26)

and

$$ \sup_{\lambda >0}\lambda ^{1/2} \bigl\vert 1-\lambda d_{\rho}(\lambda ) \bigr\vert \leq \frac{\sqrt{\rho}}{2},\qquad \sup _{\lambda >0} \bigl\vert 1-\lambda d_{\rho}( \lambda ) \bigr\vert \leq 1. $$
(27)

3 Convergence rates of the regularization solution

We will derive the error estimates of the method in this section. For any \(f\in W^{2}_{\psi}\), let \(\vec{\mathbf{{f}}}=(\hat{f}_{0},\hat{f}_{1},\ldots ,\hat{f}_{n},\ldots )^{T}\),

$$ \vec{\mathbf{{f}}}_{N}=\mathcal{P}_{N}\vec{ \mathbf{{f}}},\qquad f_{N}= \mathcal{J}(\mathcal{P}_{N} \vec{\mathbf{{f}}}) $$
(28)

and we define \(\vec{\mathbf{{f}}}_{\rho ,N}\) by

$$ \vec{\mathbf{{f}}}_{\rho ,N}=\mathcal{R}^{-1}d_{\rho} \bigl(\mathcal{B}^{*} \mathcal{B}\bigr)\mathcal{B}^{*}A \vec{\mathbf{{f}}}_{N}. $$
(29)

It should be noted that we only use the parameter N for theoretical derivation and it does not appear in practical computing. In the following different proof process, N has to be chosen properly. This approach is borrowed from [31].

It is easy to obtain that

$$ \begin{aligned} &A\bigl(\vec{\mathbf{{h}}}^{\delta}_{\rho}- \vec{\mathbf{{f}}}_{\rho ,N}\bigr)=\mathcal{B}d_{ \rho}\bigl( \mathcal{B}^{*}\mathcal{B}\bigr)\mathcal{B}^{*} \bigl(g^{\delta}-A \vec{\mathbf{{f}}}_{N}\bigr), \\ &A(\vec{\mathbf{{f}}}_{N}-\vec{\mathbf{{f}}}_{\rho ,N})= \mathcal{B}\bigl[I-d_{\rho}\bigl( \mathcal{B}^{*} \mathcal{B}\bigr)\mathcal{B}^{*}\mathcal{B}\bigr]\mathcal{R} \vec{ \mathbf{{f}}}_{N}, \\ &R\bigl(\vec{\mathbf{{h}}}^{\delta}_{\rho}-\vec{ \mathbf{{f}}}_{\rho ,N}\bigr)=d_{\rho}\bigl( \mathcal{B}^{*}\mathcal{B}\bigr)\mathcal{B}^{*} \bigl(g^{\delta}-A\vec{\mathbf{{f}}}_{N}\bigr), \\ &R(\vec{\mathbf{{f}}}_{N}-\vec{\mathbf{{f}}}_{\rho ,N})= \bigl[I-d_{\rho}\bigl(\mathcal{B}^{*} \mathcal{B}\bigr) \mathcal{B}^{*}\mathcal{B}\bigr]\mathcal{R}\vec{\mathbf{{f}}}_{N}. \end{aligned} $$
(30)

Lemma 3

If \(f\in W_{2}^{\psi}\), then we have

$$ \Vert \mathcal{R}\vec{\mathbf{{f}}}_{N} \Vert _{\ell ^{2}} \leq \biggl( \max_{0\leq k\leq N}\frac{e^{2k}}{\psi ^{2}(k)} \biggr)^{\frac{1}{2}} \Vert f \Vert _{\psi}. $$
(31)

Proof

From (14) and (15)

$$ \begin{aligned} \Vert \mathcal{R}\vec{\mathbf{{f}}}_{N} \Vert ^{2}_{\ell ^{2}}& =\sum _{k=0}^{N}e^{2k}\hat{f}_{k}^{2}= \sum_{k=0}^{N} \frac{e^{2k}}{\psi ^{2}(k)}\psi ^{2}(k)\hat{f}^{2}_{k} \\ & \leq \max_{0\leq k\leq N}\frac{e^{2k}}{\psi ^{2}(k)} \sum _{k=0}^{N}\psi ^{2}(k) \hat{f}^{2}_{k}\leq \max_{0\leq k\leq N} \frac{e^{2k}}{\psi ^{2}(k)} \Vert f \Vert _{\psi}. \end{aligned} $$

 □

Now, we define an operator K̂ as

$$ \hat{K}f = \sum_{\ell =1}^{\infty} \frac{1}{\ell ^{2}\pi ^{2}}(f,X_{ \ell})X_{\ell}. $$
(32)

Then, it is easily to see that

$$ \Vert Kf \Vert \leq \Vert \hat{K}f \Vert \leq \frac{1}{1-E_{\alpha ,1}(-\pi ^{2}T^{\alpha})} \Vert Kf \Vert . $$
(33)

Lemma 4

If \(f\in W_{2}^{\psi}\), then there exists a constant \(c_{1}>0\) such that

$$ \bigl\Vert A(I-P_{N})\vec{\mathbf{f}} \bigr\Vert \leq \frac{c_{1}}{N\psi (N)} \Vert f \Vert _{\psi}. $$
(34)

Proof

Let \(h_{1}=\mathcal{J}\vec{\mathbf{f}}\), \(h_{2}={\mathcal{J}}(\mathcal{P}_{N}\vec{\mathbf{f}})\) and \(q_{i}=\hat{K}h_{i}\), \(i=1,2\). Then, it can be deduced that \(q_{i}\) are the solutions of the following equations:

$$ \textstyle\begin{cases} -q^{\prime \prime }_{i}=h_{i}(x),\quad x\in (0,1), \\ q_{i}(0)=q_{i}(1)=0. \end{cases} $$

Then, from (12), we can obtain

$$ q_{1}(x)={-}\sum_{k=0}^{\infty} \frac{\hat{f}_{k}}{\eta _{k+2}}L_{k+2}(x)+ \Biggl(\sum _{k=0}^{\infty} \frac{[1+(-1)^{k+1}]\sqrt{2k+5}\hat{f}_{k}}{\eta _{k+2}}x +\sum _{k=0}^{ \infty}\frac{(-1)^{k}\sqrt{2k+5}\hat{f}_{k}}{\eta _{k+2}} \Biggr) $$
(35)

and

$$ q_{2}(x){=-}\sum_{k=0}^{N} \frac{\hat{f}_{k}}{\eta _{k+2}}L_{k+2}(x)+ \Biggl(\sum _{k=0}^{N} \frac{[1+(-1)^{k+1}]\sqrt{2k+5}\hat{f}_{k}}{\eta _{k+2}}x +\sum _{k=0}^{N} \frac{(-1)^{k}\sqrt{2k+5}\hat{f}_{k}}{\eta _{k+2}} \Biggr) .$$

By using the Cauchy inequality, we have

$$ \sum_{k=N+1}^{\infty} \frac{{\sqrt{2k+5}} \vert \hat{f}_{k} \vert }{\eta _{k+2}} \leq \Biggl( \sum_{k=N+1}^{\infty} \frac{2k+5}{\eta _{k+2}^{2}} \Biggr)^{ \frac{1}{2}} \Biggl(\sum ^{\infty}_{k=N+1}\hat{f}_{k}^{2} \Biggr)^{\frac{1}{2}}\leq \frac{2}{N\psi (N)} \Biggl(\sum _{k=N+1}^{ \infty}\psi ^{2}(k) \hat{f}_{k}^{2} \Biggr)^{\frac{1}{2}}. $$

Hence, we can obtain

$$ \begin{aligned} &\bigl\Vert A(I-P_{N})\vec{\mathbf{f}} \bigr\Vert \\ &\quad \leq \bigl\Vert \hat{K}\mathcal{J}(I-P_{N}) \vec{ \mathbf{f}} \bigr\Vert = \bigl\Vert q_{1}(x)-q_{2}(x) \bigr\Vert \\ &\quad = { \Biggl\Vert -\sum_{k=N+1}^{\infty} \frac{\hat{f}_{k}}{\eta _{k+2}}L_{k+2}(x)+ \Biggl(\sum ^{\infty}_{ k=N+1} \frac{[1+(-1)^{k+1}]\sqrt{2k+5}\hat{f}_{k}}{\eta _{k+2}}x + \sum _{k=N+1}^{ \infty}\frac{(-1)^{k}\sqrt{2k+5}\hat{f}_{k}}{\eta _{k+2}} \Biggr) \Biggr\Vert } \\ &\quad \leq { \Biggl\Vert \sum_{k=N+1}^{\infty} \frac{\hat{f}_{k}}{\eta _{k+2}}L_{k+2}(x) \Biggr\Vert +\sum _{k=N+1}^{ \infty}\frac{\sqrt{2k+5} \vert \hat{f}_{k} \vert }{\eta _{k+2}} \Vert x+1 \Vert } \\ &\quad \leq { \frac{2}{N^{2}\psi (N)} \Biggl(\sum _{k=N+1}^{ \infty}\psi ^{2}(k) \hat{f}_{k}^{2} \Biggr)^{\frac{1}{2}}+ \frac{2\sqrt{3}}{N\psi (N)} \Biggl(\sum_{k=N+1}^{\infty} \psi ^{2}(k) \hat{f}_{k}^{2} \Biggr)^{\frac{1}{2}}\leq \frac{c_{1}}{N\psi (N)} \Vert f \Vert _{\psi}.} \end{aligned} $$

 □

Lemma 5

If \(f\in W_{2}^{\psi}\), then we have

$$ \begin{aligned} &\bigl\Vert A\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert \leq {(C+1) \delta +\frac{c_{1}}{N\psi (N)} \Vert f \Vert _{\psi}}, \\ &\bigl\Vert \mathcal{R}\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert _{\ell ^{2}} \leq {\frac{1}{2\sqrt{\rho}} \biggl(\delta + \frac{c_{1}}{N\psi (N)} \Vert f \Vert _{\psi} \biggr)+ \biggl(\max_{0\leq k \leq N} \frac{e^{2k}}{\psi ^{2}(k)} \biggr)^{\frac{1}{2}} \Vert f \Vert _{\psi}}, \\ &\bigl\Vert A\vec{\mathbf{{h}}}_{\rho}^{\delta}-g^{\delta} \bigr\Vert \leq { \delta +\frac{c_{1}}{N\psi (N)} \Vert f \Vert _{\psi}+\frac{\sqrt{\rho}}{2} \biggl(\max_{0\leq k\leq N} \frac{e^{2k}}{\psi ^{2}(k)} \biggr)^{ \frac{1}{2}} \Vert f \Vert _{\psi}}. \end{aligned} $$

Proof

Using the triangle inequality, (2), (23), and Lemma 4, we obtain

$$ \begin{aligned} \bigl\Vert A\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert &\leq \bigl\Vert A \vec{ \mathbf{{h}}}_{\rho}^{\delta}-g^{\delta} \bigr\Vert + \bigl\Vert g^{\delta}-g \bigr\Vert + \bigl\Vert A(I- \mathcal{P}_{N})\vec{\mathbf{{f}}} \bigr\Vert \\ &\leq {(C+1)\delta +\frac{c_{1}}{N\psi (N)} \Vert f \Vert _{\psi}}. \end{aligned} $$

Due to the triangle inequality, (30), (2), and Lemmas 2–4

$$ \begin{aligned} \bigl\Vert \mathcal{R}\bigl(\vec{ \mathbf{{h}}}_{\rho}^{\delta}-\vec{\mathbf{{f}}}_{N} \bigr) \bigr\Vert _{\ell ^{2}}&\leq { \bigl\Vert \mathcal{R} \bigl( \vec{\mathbf{{h}}}_{\rho}^{\delta}-\vec{ \mathbf{{f}}}_{\rho ,N}\bigr) \bigr\Vert _{ \ell ^{2}}+ \bigl\Vert \mathcal{R}(\vec{\mathbf{{f}}}_{\rho ,N}-\vec{\mathbf{{f}}}_{N}) \bigr\Vert _{ \ell ^{2}}} \\ &\leq {\frac{1}{2\sqrt{\rho}} \bigl\Vert g^{\delta}-A \vec{ \mathbf{{f}}}_{N} \bigr\Vert + \Vert \mathcal{R}\vec{ \mathbf{{f}}}_{N} \Vert _{\ell ^{2}}} \\ &\leq {\frac{1}{2\sqrt{\rho}}\bigl( \bigl\Vert g^{\delta}-g \bigr\Vert + \bigl\Vert A(I- \mathcal{P}_{N})\vec{\mathbf{{f}}} \bigr\Vert \bigr)+ \biggl(\max_{0\leq k\leq N} \frac{e^{2k}}{\psi ^{2}(k)} \biggr)^{\frac{1}{2}} \Vert f \Vert _{\psi}} \\ &\leq {\frac{1}{2\sqrt{\rho}} \biggl(\delta + \frac{c_{1}}{N\psi (N)} \Vert f \Vert _{\psi} \biggr)+ \biggl(\max_{0\leq k \leq N} \frac{e^{2k}}{\psi ^{2}(k)} \biggr)^{\frac{1}{2}} \Vert f \Vert _{\psi}}. \end{aligned} $$

Let \(S_{\rho}=I-d_{\rho}(\mathcal{B}\mathcal{B}^{*})\mathcal{B} \mathcal{B}^{*}\), then we use the representation \(g^{\delta}-A\vec{\mathbf{{h}}}_{\rho}^{\delta}=S_{\rho}g^{ \delta}\) and obtain from the triangle inequality, (2), and Lemmas 2–4

$$ \begin{aligned} \bigl\Vert A\vec{\mathbf{{h}}}_{\rho}^{\delta}-g^{\delta} \bigr\Vert = \bigl\Vert S_{\rho}g^{ \delta} \bigr\Vert & \leq { \bigl\Vert S_{\rho}\bigl(g^{\delta}-g\bigr) \bigr\Vert + \bigl\Vert S_{\rho}(g-A \vec{\mathbf{{f}}}_{N}) \bigr\Vert + \Vert S_{\rho}A\vec{\mathbf{{f}}}_{N} \Vert } \\ &\leq {\delta + \bigl\Vert A(I-\mathcal{P}_{N}) \vec{\mathbf{{f}}} \bigr\Vert + \Vert S_{\rho}\mathcal{B} \Vert \cdot \Vert \mathcal{R} \vec{\mathbf{{f}}}_{N} \Vert _{\ell ^{2}}} \\ &\leq {\delta +\frac{c_{1}}{N\psi (N)} \Vert f \Vert _{\psi}+ \frac{\sqrt{\rho}}{2} \biggl(\max_{0\leq k\leq N} \frac{e^{2k}}{\psi ^{2}(k)} \biggr)^{\frac{1}{2}} \Vert f \Vert _{\psi}}. \end{aligned} $$

 □

3.1 Convergence rates for \(\psi (x)=\phi _{r}(x)\)

Lemma 6

If \(f\in W_{2}^{\psi}\) with \(\psi (x)=\phi _{r}(x)\) \((r>1)\), then there exists a constant \(c_{2}\) such that

$$ \Vert f \Vert _{L^{2}_{\omega}}\leq c_{2} \Vert {{K}}f \Vert ^{\frac{r}{r+2}} \Vert f \Vert _{\psi}^{ \frac{2}{r+2}}. $$
(36)

Proof

By using the Hölder inequality

$$ \begin{aligned} \Vert f \Vert _{L^{2}_{\omega}}^{2}&= {\sum _{k=0}^{\infty} \hat{f}_{k}^{2}= \sum_{k=0}^{\infty} \biggl( \frac{1}{\phi _{2}^{2}(k)} \hat{f}^{2}_{k} \biggr)^{\frac{r}{r+2}} \bigl(\phi _{r}^{2}(k) \hat{f}^{2}_{k} \bigr)^{\frac{2}{r+2}} } \\ &\leq { \Biggl(\sum_{k=0}^{\infty} \frac{1}{\phi _{2}^{2}(k)}\hat{f}^{2}_{k} \Biggr)^{\frac{r}{r+2}} \Biggl(\sum_{k=0}^{\infty} \phi _{r}^{2} (k)\hat{f}^{2}_{k} \Biggr)^{ \frac{2}{r+2}}.} \end{aligned} $$
(37)

From (35)

$$ \begin{aligned} &\Vert \hat{K}f \Vert \\ &\quad = { \Biggl\Vert {-}\sum_{k=0}^{ \infty} \frac{\hat{f}_{k}}{\eta _{k+2}}L_{k+2}(x)+ \Biggl(\sum _{k=0}^{ \infty}\frac{[1+(-1)^{k+1}]\sqrt{2k+5}\hat{f}_{k}}{\eta _{k+2}}x + \sum _{k=0}^{\infty} \frac{(-1)^{k}\sqrt{2k+5}\hat{f}_{k}}{\eta _{k+2}} \Biggr) \Biggr\Vert } \\ &\quad \geq { \Biggl\Vert \sum_{k=0}^{\infty} \frac{\hat{f}_{k}}{\eta _{k+2}}L_{k+2}(x) \Biggr\Vert }= { \Biggl( \sum_{k=0}^{\infty}\frac{\hat{f}^{2}_{k}}{\eta _{k+2}^{2}} \Biggr)^{\frac{1}{2}}}\geq {\frac{1}{\sqrt{6}} \Biggl( \sum _{k=0}^{\infty}\frac{1}{\phi _{2}^{2}(k)} \hat{f}^{2}_{k} \Biggr)^{ \frac{1}{2}}}. \end{aligned} $$
(38)

We can finish the proof by using (37), (38), and (33). □

Lemma 7

For the vector sequences \(\vec{\mathbf{{h}}}^{\delta}=(\hat{h}_{1}^{\delta},\hat{h}^{\delta}_{2}, \ldots ,\hat{h}^{\delta}_{n},\ldots )^{T}\), if

$$ \bigl\Vert A\vec{\mathbf{{h}}}^{\delta} \bigr\Vert \leq c_{3}\delta ,\qquad \bigl\Vert \mathcal{R} \vec{ \mathbf{{h}}}^{\delta} \bigr\Vert _{\ell ^{2}}\leq c_{4}e^{c_{5}\delta ^{- \frac{1}{r+1}}}\delta ^{\frac{r}{r+1}},\quad \textit{as } \delta \rightarrow 0 $$
(39)

hold with some nonnegative constants \(c_{3}\), \(c_{4}\), \(c_{5}\), then there exists a constant \(M_{1}\) such that

$$ \bigl\Vert \bigl(\mathcal{J}\vec{\mathbf{{h}}}^{\delta} \bigr) \bigr\Vert _{ \phi _{r-1}}\leq M_{1}. $$
(40)

Proof

Using the properties of the exponential function and the power function,

$$ e^{c_{5}\delta ^{-\frac{1}{r+1}}}>\frac{c_{5}^{r+1}}{\delta},\quad \forall \delta < \delta _{0} $$

holds for a constant \(\delta _{0}\). Now, we prove the lemma for \(\delta <\delta _{0}\), let

$$ N=c_{5}\delta ^{-\frac{1}{r+1}}, $$

then by using the triangle inequality

$$ \bigl\Vert \mathcal{J}\vec{\mathbf{{h}}}^{\delta} \bigr\Vert _{\phi _{r-1}}\leq \bigl\Vert \mathcal{J}\mathcal{P}_{N}\vec{ \mathbf{{h}}}^{\delta} \bigr\Vert _{ \phi _{r-1}}+ \bigl\Vert \mathcal{J}(I-\mathcal{P}_{N})\vec{\mathbf{{h}}}^{ \delta} \bigr\Vert _{\phi _{r-1}}=I_{1}+I_{2}. $$

For the first term \(I_{1}\),

$$ I_{1}^{2}= \bigl\Vert \mathcal{J} \mathcal{P}_{N}\vec{\mathbf{{h}}}^{\delta} \bigr\Vert ^{2}_{\phi _{r-1}}=\sum_{k=0}^{N} \phi ^{2}_{r-1}(k)\hat{f}_{k}^{2}= \sum_{k=0}^{N}\frac{\phi ^{2}_{r+1}(k)}{\phi _{2}^{2}(k)} \hat{f}_{k}^{2} \leq N^{2(r+1)}\sum _{k=0}^{N}\frac{1}{\phi _{2}^{2}(k)} \hat{f}_{k}^{2}. $$

For the second term \(I_{2}\),

$$ \begin{aligned} I_{2}^{2}&= \bigl\Vert \mathcal{J}(I-\mathcal{P}_{N})\vec{\mathbf{{f}}} \bigr\Vert ^{2}_{ \phi _{r-1}}= { \sum _{k=N+1}^{\infty}\phi ^{2}_{r-1}(k) \hat{f}_{k}^{2}=\sum_{k=N+1}^{\infty} \frac{\phi ^{2}_{r-1}(k)}{e^{2k}}{\bigl(e^{k}\hat{f}_{k} \bigr)^{2}}} \\ &\leq {\frac{N^{2r-2}}{e^{2N}} \bigl\Vert \mathcal{R}\vec{ \mathbf{{f}}}^{ \delta} \bigr\Vert ^{2}_{\ell ^{2}}} \rightarrow 0. \end{aligned} $$

This finishes the proof. □

Theorem 8

Suppose that \(f\in W_{2}^{\psi}\) with \(\psi (x)=\phi _{r}(x)\) (\(r>1\)) and the condition (2) holds. If the regularization solution \(h_{\rho}^{\delta}\) is defined by (21)–(23), then

$$ \bigl\Vert h_{\rho}^{\delta}-f \bigr\Vert _{L^{2}_{\omega}}=O \bigl(\delta ^{ \frac{r-1}{r+1}} \bigr). $$
(41)

Proof

From Lemma 5,

$$ \begin{aligned} &\bigl\Vert A\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert \leq {(C+1) \delta +\frac{c_{1}}{N^{r+1}} \Vert f \Vert _{\psi}}, \\ &\bigl\Vert \mathcal{R}\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert _{\ell ^{2}} \leq {\frac{1}{2\sqrt{\rho}} \biggl(\delta + \frac{c_{1}}{N^{r+1}} \Vert f \Vert _{\psi} \biggr)+\max \biggl(1, \frac{e^{N}}{N^{r}} \biggr) \Vert f \Vert _{\psi}}, \\ &C\delta = \bigl\Vert A\vec{\mathbf{{h}}}_{\rho}^{\delta}-g^{\delta} \bigr\Vert \leq {\delta +\frac{c_{1}}{N^{r+1}} \Vert f \Vert _{\psi}+ \frac{\sqrt{\rho}}{2}\max \biggl(1,\frac{e^{N}}{N^{r}} \biggr) \Vert f \Vert _{ \psi}.} \end{aligned} $$

Now, we choose N such that

$$ \frac{c_{1}}{N^{r+1}} \Vert f \Vert _{\psi}=\frac{C-1}{2} \delta , $$

then we can obtain that there exist constants \(C_{1}\), \(C_{2}\), \(C_{3}\) such that

$$ \begin{aligned} &\bigl\Vert A\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert \leq C_{1} \delta \\ &\bigl\Vert \mathcal{R}\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert _{\ell ^{2}} \leq {C_{2}e^{C_{3}\delta ^{-\frac{1}{r+1}}}\delta ^{ \frac{r}{r+1}}.} \end{aligned} $$

Hence, from Lemma 7, there exists a constant \(M_{2}\) such that

$$ \bigl\Vert \mathcal{J}\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert _{\phi _{r-1}}\leq M_{2}. $$

Hence, by using the triangle inequality

$$ \bigl\Vert h_{\rho}^{\delta}-f \bigr\Vert _{\phi _{r-1}}\leq \bigl\Vert \mathcal{J}\bigl( \vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert _{\phi _{r-1}}+ \Vert f-f_{N} \Vert _{\phi _{r-1}}\leq M_{2}+ \Vert f \Vert _{\psi}. $$
(42)

Moreover, from (2), (23), and the triangle inequality

$$ \bigl\Vert A\vec{\mathbf{{h}}}_{\rho}^{\delta}-g \bigr\Vert \leq \bigl\Vert A\vec{\mathbf{{h}}}_{\rho}^{ \delta}-g^{\delta} \bigr\Vert + \bigl\Vert g^{\delta}-g \bigr\Vert \leq (C+1)\delta . $$
(43)

It follows from Lemma 6 that the assertion of this theorem is true. □

3.2 Convergence rates for \(\psi (x)=\varphi _{\lambda}(x) (\lambda >0)\)

Lemma 9

If the functions sequences \(f^{\delta}\) satisfy

$$ \bigl\Vert Kf^{\delta} \bigr\Vert \leq c_{6}\delta , \qquad \bigl\Vert f^{\delta} \bigr\Vert _{\varphi _{ \lambda}}\leq c_{7},\quad \delta \rightarrow 0, $$
(44)

where \(c_{6}\), \(c_{7}\) are two fixed nonnegative constants, then we can obtain

$$ \bigl\Vert f^{\delta} \bigr\Vert _{L^{2}_{\omega}}=O \biggl(\delta \biggl(\log \biggl( \frac{1}{\delta} \biggr) \biggr)^{2} \biggr). $$
(45)

Proof

Let

$$ N=\frac{1}{\lambda} \biggl[\log \biggl(\frac{1}{\delta} \biggr)-\log \biggl(\log \biggl(\frac{1}{\delta} \biggr) \biggr)^{2} \biggr], $$

then we have

$$ \bigl\Vert \mathcal{P}_{N}f^{\delta} \bigr\Vert _{L^{2}_{\omega}}^{2}=\sum_{k=0}^{N} \bigl( \hat{f}^{\delta}_{k}\bigr)^{2}\leq \frac{1}{N^{4}}\sum_{k=0}^{N} \frac{1}{\phi _{2}^{2}(k)}\bigl(\hat{f}^{\delta}_{k} \bigr)^{2} $$

and

$$ \bigl\Vert (I-\mathcal{P}_{N})f^{\delta} \bigr\Vert _{L^{2}_{\omega}}^{2}=\sum_{k=N+1}^{ \infty} \bigl(\hat{f}^{\delta}_{k}\bigr)^{2}\leq \frac{1}{e^{2\lambda N}}\sum_{k=N+1}^{ \infty}e^{2\lambda k} \bigl(\hat{f}^{\delta}_{k}\bigr)^{2}. $$

 □

Theorem 10

Suppose that \(f\in W_{2}^{\psi}\) with \(\psi (x)=\varphi _{\lambda}(x)\) \((\lambda >0)\) and the condition (2) holds. If the regularization solution \(h_{\rho}^{\delta}\) is defined by (21)–(23), then

$$ \bigl\Vert {h}^{\delta}_{\rho}-f \bigr\Vert _{L^{2}_{\omega}}=O \biggl(\delta \biggl(\log \biggl(\frac{1}{\delta} \biggr) \biggr)^{2} \biggr). $$
(46)

Proof

From Lemma 5, for \(0<\lambda <1\),

$$ \begin{aligned} &\bigl\Vert A\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert \leq {(C+1) \delta +\frac{c_{1}}{Ne^{\lambda N}} \Vert f \Vert _{\psi}}, \\ &\bigl\Vert \mathcal{R}\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert _{\ell ^{2}} \leq {\frac{1}{2\sqrt{\rho}} \biggl(\delta + \frac{c_{1}}{Ne^{\lambda N}} \Vert f \Vert _{\psi} \biggr)+e^{(1-\lambda )N} \Vert f \Vert _{\psi}}, \\ &\bigl\Vert A\vec{\mathbf{{h}}}_{\rho}^{\delta}-g^{\delta} \bigr\Vert \leq { \delta +\frac{c_{1}}{Ne^{\lambda N}} \Vert f \Vert _{\psi}+ \frac{\sqrt{\rho}}{2}e^{(1-\lambda )N} \Vert f \Vert _{\psi}}. \end{aligned} $$

Now, we choose N such that

$$ \frac{c_{1}}{Ne^{\lambda N}} \Vert f \Vert _{\psi}=\frac{C-1}{2} \delta , $$

then

$$ \bigl\Vert A\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}-\vec{ \mathbf{{f}}}_{N}\bigr) \bigr\Vert \leq c_{4}\delta $$

and

$$ \bigl\Vert \mathcal{R}\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert _{\ell ^{2}} \leq c_{5}\delta ^{\frac{\lambda -1}{\lambda}} $$

hold with two constants \(c_{4}\) and \(c_{5}\). Hence, it is easy to obtain by the Hölder inequality that there exists a constant \(M_{3}\)

$$ \bigl\Vert \mathcal{J}\bigl(\vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert _{\varphi _{\lambda}}\leq M_{3}. $$
(47)

Hence, we can obtain

$$ \bigl\Vert h_{\rho}^{\delta}-f \bigr\Vert _{\varphi _{\lambda}}\leq \bigl\Vert \mathcal{J}\bigl( \vec{\mathbf{{h}}}_{\rho}^{\delta}- \vec{\mathbf{{f}}}_{N}\bigr) \bigr\Vert _{\varphi _{ \lambda}}+ \Vert f_{N}-f \Vert _{\varphi _{\lambda}}\leq M_{3}+ \Vert f \Vert _{\varphi _{ \lambda}}. $$
(48)

Secondly, for \(\lambda >1\), noting that \(\vec{\mathbf{{h}}}_{\rho}^{\delta}\) is the minimizer of (18), hence, we can obtain

$$ \bigl\Vert Kh^{\delta}_{\rho}-g^{\delta} \bigr\Vert ^{2}+\rho \bigl\Vert h^{\delta}_{\rho} \bigr\Vert ^{2}_{ \varphi _{1}}\leq \bigl\Vert Kf-g^{\delta} \bigr\Vert ^{2}+\rho \Vert f \Vert ^{2}_{\varphi _{1}}{ .} $$

Hence,

$$ \bigl\Vert h^{\delta}_{\rho} \bigr\Vert ^{2}_{\varphi _{1}}\leq \Vert f \Vert ^{2}_{\varphi _{1}}+ \frac{1}{\rho}\bigl( \bigl\Vert Kf-g^{\delta} \bigr\Vert ^{2}- \bigl\Vert Kh^{\delta}_{\rho}-g^{\delta} \bigr\Vert ^{2}\bigr)\leq \Vert f \Vert ^{2}_{\varphi _{1}}{.} $$

Therefore,

$$ \bigl\Vert h^{\delta}_{\rho}-f \bigr\Vert _{\varphi _{1}}\leq 2 \Vert f \Vert _{\varphi _{1}}. $$
(49)

Moreover, by the triangle inequality

$$ \bigl\Vert A\vec{\mathbf{{h}}}_{\rho}^{\delta}-g \bigr\Vert \leq \bigl\Vert A\vec{\mathbf{{h}}}_{\rho}^{ \delta}-g^{\delta} \bigr\Vert + \bigl\Vert g^{\delta}-g \bigr\Vert \leq (C+1)\delta . $$
(50)

It follows from Lemma 9 that the assertion of this theorem is true. □

4 Numerical experiments

In this section, we present several numerical results from our method. Let \(x_{i}=\frac{i}{M}\), \(i=0,1, \ldots , M\). For noisy data, we use

$$ g^{\delta} (x_{i} )=g (x_{i} ) (1+\epsilon _{i}), $$

where \(\{\epsilon _{i} \}_{i=1}^{N}\) are generated by Function \((2*\operatorname{rand}(N, 1)-1) * \delta _{1}\) in Matlab. Since the exact solution of the fractional diffusion equation is difficult to obtain, we generate the additional data \(g(x)\) by the method in [20].

We obtain \(\vec{\mathbf{{h}}}_{\rho}^{\delta}\) approximatively by solving the following equation:

$$ \bigl(\mathrm{A}^{*} \mathrm{A}+\mathrm{B} \bigr) \mathrm{h}= \mathrm{A} \mathbf{g}^{\delta}, $$

where

$$ \begin{aligned} \mathrm{A}&=\frac{2}{M} \begin{bmatrix} \sin \pi x_{1} & \sin 2\pi x_{1} & \ldots & \sin N\pi x_{1} \\ \sin \pi x_{2} & \sin 2\pi x_{2} & \ldots & \sin N\pi x_{2} \\ \vdots & \vdots & \vdots & \vdots \\ \sin \pi x_{M} & \sin 2\pi x_{M} & \ldots & \sin N\pi x_{M}\end{bmatrix} \\ &\quad {}\cdot \begin{bmatrix} a_{1}\sin \pi x_{1} & a_{1}\sin \pi x_{2} & \ldots & a_{1}\sin \pi x_{M} \\ \ a_{2}\sin 2\pi x_{1} & a_{2}\sin 2\pi x_{2} & \ldots & a_{2}\sin 2 \pi x_{M} \\ \vdots & \vdots & \vdots & \vdots \\ a_{N}\sin N\pi x_{1} & a_{N}\sin N\pi x_{2} & \ldots & a_{N}\sin N \pi x_{M}\end{bmatrix} \\ &\quad {} \cdot \begin{bmatrix} J_{0}(x_{0}) & J_{1}(x_{0}) & \ldots & J_{M}(x_{0}) \\ J_{0}(x_{1}) & J_{1}(x_{1}) & \ldots & J_{M}(x_{1}) \\ \vdots & \vdots & \vdots & \ldots \\ J_{0}(x_{M}) & J_{1}(x_{M}) & \ldots & J_{M}(x_{M})\end{bmatrix}, \end{aligned} $$

with \(a_{l}=\frac{1-E_{\alpha ,1}(-l^{2}\pi ^{2})}{l^{2}\pi ^{2}}\), \(l=0,1, \ldots , N\) and \(J_{k}(x)\), which is defined in (11), \(k=0,1, \ldots , M\) and \(\mathbf{g}^{\delta}= (g^{\delta}(x_{0}), g^{\delta}(x_{1}), \ldots , g^{\delta}(x_{M}) )^{T}\), B is a diagonal matrix with the elements of \((1, e^{2}, e^{4}, \ldots , e^{2 M} )^{T}\) on the main diagonal.

Then, the regularization parameter ρ is chosen by

$$ \bigl\Vert \mathrm{Ah}-\mathrm{g}^{\delta} \bigr\Vert _{l^{2}}=C \hat{\delta}, $$

with \(C=1.01\), where \(\hat{\delta}=\sqrt{M+1} \delta _{1}\).

Numerical tests for four examples are investigated as follows. We take \(T=1\) and \(M=N=256\) in all of the examples. The relative error of the numerical solution is measured by

$$ e_{r}(f)= \biggl( \frac{\sum_{i=0}^{M} ({h}_{\rho}^{\delta} (x_{i} )-f (x_{i} ) )^{2}}{\sum_{i=0}^{M} f (x_{i} )^{2}} \biggr)^{\frac{1}{2}}. $$

We also give the comparison of the numerical results between our method (M1) and the one in [20] (M2).

Example 1

Take

$$ f(x)=e^{x}, $$

then \(f(0)\neq 0\), \(f(1)\neq 0\) and \(f(x)\) is smooth.

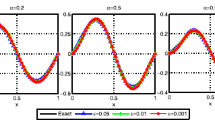
In Fig. 1(a), the comparisons between the exact solution and numerical approximations with \(\delta _{1}=1\text{e-2}\) are shown and we give the variation of \(e_{r}(f)\) with \(\delta _{1}\) in Fig. 1(b). Moreover, we present the relative errors for various α and \(\delta _{1}\) in Table 1. We can see that the results of M1 are much better than those of M2 when the boundary condition does not hold. For different α, there is little difference in the numerical results. Hence, in the following experiments we only give the results for \(\alpha =0.5\).

Figure 1
figure 1

Numerical results of Example 1 with \(\alpha =0.5\)

Full size image
Table 1 Relative errors of Example 1
Full size table

Example 2

[20] We take

$$ f(x)=x(x-0.1) (x-0.4) (x-0.6) (x-0.8) (x-1), $$

then \(f(0)=f(1)=0\) and \(f(x)\) is smooth.

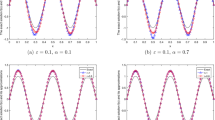
The relative error has been listed in Table 2. Figure 2(a) shows the comparisons between the exact solution and numerical solutions and Fig. 2(b) exhibits the changes of \(e_{r}(f)\) with \(\delta _{1}\). We can see that the results of M1 are still better than those of M2. The advantage of M1 becomes obvious as \(\delta _{1}\) decreases.

Figure 2
figure 2

Numerical results of Example 2 with \(\alpha =0.5\)

Full size image
Table 2 Relative errors of Example 2 with \(\alpha =0.5\)
Full size table

Next, we consider the case of piecewise-smooth functions. Example 3 does not satisfy the boundary condition but Example 4 does.

Example 3

Take

$$ f(x)=\textstyle\begin{cases} -2x+1,&0\leq x\leq 0.5, \\ 2x-1,&0.5< x\leq 1. \end{cases} $$

Example 4

Take

$$ f(x)=\textstyle\begin{cases} 2x,&0\leq x\leq 0.5, \\ -2x+2,&0.5< x\leq 1. \end{cases} $$

From the results of Figs. 3 and 4 and Tables 3 and 4, we can see that the results of the two examples using M1 are close. However, the results of Example 4 using M2 are obviously better than those of Example 3. The results of M1 in Example 3 are better than those of M2, but the results of M2 in Example 4 are slightly better than those of M1. These results are consistent with theoretical analysis.

Figure 3
figure 3

Numerical results of Example 3 with \(\alpha =0.5\)

Full size image
Figure 4
figure 4

Numerical results of Example 4 with \(\alpha =0.5\)

Full size image
Table 3 Relative errors of Example 3 with \(\alpha =0.5\)
Full size table
Table 4 Relative errors of Example 4 with \(\alpha =0.5\)
Full size table

5 Conclusion

To overcome the dependence of previous methods on boundary conditions, we present a modified Tikhonov method based on Jacobi polynomials to identify an unknown source in a time-fractional diffusion equation. The convergence results of the new method are no longer restricted by boundary conditions, and the method has obvious advantages when the solution has high smoothness.