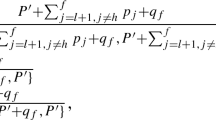An online joint replenishment problem combined with single machine scheduling

Abstract

This paper considers a combination of the joint replenishment problem with single machine scheduling. There is a single resource, which is required by all the unit-time jobs, and a job can be started at time point t on the machine if and only if the machine does not process another job at t, and the resource is replenished between its release date and t. Each replenishment has a cost, which is independent of the amount replenished. The objective is to minimize the total replenishment cost plus the maximum flow time of the jobs. We consider the online variant of the problem, where the jobs are released over time, and once a job is inserted into the schedule, its starting time cannot be changed. We propose a deterministic 2-competitive online algorithm for the general input. Moreover, we show that for a certain class of inputs (so-called p-bounded input), the competitive ratio of the algorithm tends to $\sqrt{2}$ as the number of jobs tends to infinity. We also derive several lower bounds for the best competitive ratio of any deterministic online algorithm under various assumptions.

1 Introduction

In this paper, we study a combination of the classical joint replenishment problem (JRP) with machine scheduling, proposed recently by Györgyi et al. (2023). The joint replenishment problem seeks an optimal replenishment policy of one or several items required to fulfill a sequence of demands over time. When combined with machine scheduling, a demand is fulfilled only after the required item is replenished, and, in addition, processed on a machine for a given amount of time. The machine processes the demands in some order that has to be determined. The cost to be minimized has two main components: one is related to the replenishment of the items, and another to the scheduling of the demands on the machine. An example for the former one is the fixed cost of replenishments due each time a subset of items is replenished, while a possible scheduling related cost is the maximum flow time, which is the maximum difference between the completion time of a demand on the machine and its arrival time. The processing of the demands on the machine adds an extra twist to the problem, and it may delay the fulfillment of the demands.

As a practical application, consider a paint-shop, where new items arrive regularly for painting. The paint operation takes the same amount of time for any item. The paints are ordered once the items are known, and we want to minimize the number of orders, while not delaying too much the painting of the items.

In the scheduling literature, a machine processes jobs, and we will identify the demands with jobs. Likewise, we will say that a job j has a release date $r_j$, which is the arrival time of the corresponding demand, and a processing time $p_j$, which equals the processing time of the demand on the machine. Preemption of processing is not allowed. A schedule S specifies a starting time $S_j$ for each job j. The completion time of job j in schedule S is $C_j = S_j + p_j$. It is required that $S_j \ge r_j$ for each job j, and distinct jobs be processed in non-overlapping time intervals, that is, for each pair of jobs $j \ne k$, either $C_j \ge C_k + p_j$ or $C_k \ge C_j + p_k$.

An online algorithm ALG for the above scheduling problem receives the jobs one-by-one over time, and decides about the replenishment times, and schedules the unscheduled jobs after the replenishments. The competitive ratio of ALG is

$$\begin{aligned} \rho = \textrm{sup}\{ ALG(I)/OPT(I)\,\ I \text { is a probem instance with at least 1 job } \}, \end{aligned}$$

where ALG(I) and OPT(I) denote the cost of the solution determined by ALG on input I, and the cost of an optimal solution on the same input, respectively.

In (Györgyi et al. 2023), a number of variants of the combined joint replenishment and machine scheduling problem are studied, which differ in the scheduling objective, and in the additional constraints on the processing times of the jobs, or in the frequency of the arrival of the jobs. In all variants, each time a subset X of items are replenished, the fixed cost of replenishment is $K_0 + \sum _{i\in X} K_i$, where $K_0$, and the $K_i$ are non-negative values. Optimal offline, and competitive online algorithms are proposed with various competitive ratios. In the online problems studied the scheduling objective was the total completion time, the total flow time, and the maximum flow time. However, in the variant with the maximum flow time objective, it was assumed that a job is released at every non-negative integer time point until no more jobs arrive, each job has a processing time of one time unit, and the only unknown parameter was when the last job arrives. For this online problem, a $\sqrt{2}$-competitive algorithm has been proposed.

In the present work we focus uniquely on the online problem with the maximum flow time scheduling objective. We consider only variants with a single resource required by every jobs. Each replenishment has the same cost, which is the most common assumption in case of one resource. Moreover, the processing time of each job is one time unit, i.e., $p_j=1$ for each job j. We propose a deterministic 2-competitive online algorithm for the input, where the jobs have unit processing time, and arrive at arbitrary distinct integer time points. Furthermore, we analyze the performance of the algorithm on restricted input, where the difference of the arrival time of any two consecutive jobs is bounded by some parameter p, so-called p-bounded input. In this setting, the competitive ratio of our algorithm tends to $\sqrt{2}$ as the number of jobs tends to infinity. We also provide some lower bounds for the best possible competitive ratio for any online algorithm for general as well as p-regular input, where a job arrives every p time units. According to our best knowledge, no paper has considered the combination of joint replenishment and machine scheduling problems apart from Györgyi et al. (2023). In that paper, every online algorithm with a fixed competitive ratio assumes $p_j=1$. In our paint-shop example, items may arrive regularly (p-regular input) or with bounded delays (p-bounded input), and the paint operation takes unit-time.

Notation. Throughout the paper, we will use the well-known $\alpha |\beta |\gamma$ notation introduced by Graham et al. (1979) for classifying scheduling problems, where the $\alpha$ field describes the processing environment, the $\beta$ field consists of the additional restrictions and extensions, while the $\gamma$ field provides the objective function. We consider single machine scheduling problems, which is denoted by 1 in the $\alpha$ field. In the $\beta$ field $r_j$ indicates that the jobs have release dates, while $p_j=1$ restricts the processing time of each job to be one time unit. In the $\gamma$ field, $c_{{\mathcal {Q}}}$ indicates the fixed cost of replenishments (it will be formally defined in Sect. 2), while $\sum w_j C_j$ is the total weighted completion time scheduling objective, where the $w_j$ are non-negative job weights, and $F_{\max }= \max _j F_j$ is the maximum flow time, where $F_j = C_j - r_j$. All these objectives are to be minimized in the respective machine scheduling problems. We will extended the $\beta$ field by jrp which indicates that we combine machine scheduling with joint replenishment, and $s=1$ means that there is only one item type required by all the jobs (demands). Moreover, $\textit{distinct } r_j$ stipulates that the jobs have distinct release dates, i.e., $r_j \ne r_k$ for each pair of distinct jobs j and k. So, $1|jrp, s=1, \textit{distinct } r_j|c_{\mathcal {Q}}+F_{\max }$ is a concise notation for the combined joint replenishment and scheduling problem on a single machine, where there is one item type, the jobs have distinct release dates, and the objective function is the maximum flow time plus the replenishment costs.

Related work. The joint replenishment problem has been studied for more than 50 years, see (Khouja and Goyal 2008) for an overview. In the simplest version of JRP, a demand is ready as soon as the required items are replenished. In other variants, such as JRP-D, the demands have deadlines, and the ordering cost is the only objective function. In this paper we deal with a variant, where the fulfillment of the demands may be delayed, and the objective is to minimize the total cost incurred by late delivery and by the replenishments. This is called JRP-W, and it is strongly NP-hard even in case of linear delay cost functions, which follows from the NP-hardness of another variant examined by Arkin et al. (1989) (called JRP-INV), by reversing the time line. Later, Nonner and Souza (2009) proved the NP-hardness of a more restricted variant, where each item admits only three distinct demands over the time horizon.

Arkin et al. (1989) proved the strong NP-hardness of JRP-INV, while Levi et al. (2006) gave a 2-approximation algorithm, which was improved to 1.8 by Levi and Sviridenko (2006). Several variants with monotonically increasing, submodular cost function was studied by Cheung et al. (2016). For JRP-W, Buchbinder et al. (2013) described a 3-competitive algorithm for the online problem with linear delay function, and they gave a lower bound of 2.64 for the best competitive ratio of any online algorithm. The latter was strengthened in Bienkowski et al. (2014) to 2.754, and the authors also proposed a 1.791-approximation algorithm for the offline problem.

Györgyi et al. (2023) analyzed the combination of the joint replenishment problem (JRP-W) and the single machine scheduling with different scheduling objective such as $\sum C_j, \sum w_jC_j, \sum F_j$ and $F_{\max }$. For the latter problem, the authors showed that if there are two resources, the problem is NP-hard even under very strong assumptions. For $1|jrp,s=1,r_j|c_{\mathcal {Q}}+F_{\max }$ and $1|jrp,s=const,p_j=p,r_j|c_{\mathcal {Q}}+ F_{\max }$, polynomial algorithms based on dynamic programming were proposed. The paper also considered some online variants of the problem with unit-time jobs and the $\sum w_j C_j$, $\sum F_j$, and $F_{\max }$ objectives. For the former two objectives, deterministic 2-competitive online algorithms were proposed, while for the $F_{\max }$ objective, only a special case was studied, where the input is regular, that is, a job arrives at every integer time point from time 0 on until some unknown time point when the sequence terminates. For this latter online problem, a deterministic $\sqrt{2}$-competitive algorithm was described, and it was shown that there is no deterministic $(4/3-\varepsilon )$-competitive algorithm for any $\varepsilon >0$. For the general input, it was shown that no deterministic online algorithm can achieve a competitive ratio better than $(\sqrt{5}+1)/2$.

Organization of the paper. We provide the problem formulation and an overview of our results in Sect. 2. In Sect. 3, we present some properties of the offline optimum for later use. In Sect. 4, we propose a deterministic 2-competitive online algorithm for the general input, and also prove that for p-bounded input, the competitive ratio of the same algorithm tends to $\sqrt{2}$. In Sect. 5 we present numerical results regarding the algorithm proposed in Sect. 4. In Sect. 6, we derive lower bounds for the best competitive ratio for the general and p-regular input, respectively. We conclude the paper in Sect. 7.

2 Problem formulation and overview of main results

There is a set of n jobs ${\mathcal {J}}$, one resource, and a single machine. Each job j has a processing time $p_j = 1$, and a release date $r_j$. The release dates are distinct, i.e., $r_j \ne r_k$ if $j \ne k$. A job can be processed on the machine from time t only if there is a replenishment from the resource in $[r_j,t]$. Each replenishment incurs a cost of K. All data is integral.

A solution of the problem is a pair $(S,{\mathcal {Q}})$, where $S = \{S_j, j \in {\mathcal {J}}\}$ is a schedule specifying the starting times of the jobs, and ${\mathcal {Q}}= \{\tau _i, 1\le i\le q\}$ is the set of replenishment times of the resource such that $\tau _i$ is the ith replenishment time, and $\tau _i < \tau _{i+1}$ for each $i=1,\ldots ,q-1$. The solution is feasible, if the jobs do not overlap in time, i.e. $S_j+1 \le S_k$ or $S_k+1 \le S_j$ holds for each $j \ne k$, and for each job $j \in {\mathcal {J}}$ there exists some $\tau _i \in {\mathcal {Q}}$ such that $\tau _i \in [r_j,S_j]$. The completion time of job j in schedule S is $C_j=S_j+1$, and its flow time is $F_j = C_j - r_j$. The replenishment cost of a solution is $c_{{\mathcal {Q}}}:= Kq$, while the maximum flow time is $F_{\max }=\max _{j\in {\mathcal {J}}} F_j$. The cost of a solution is $cost(S,{\mathcal {Q}}) = c_{{\mathcal {Q}}} + F_{\max }$. We seek a feasible solution of minimum cost.

In the online problem, the jobs arrive over time, and there is no information about them before their release date. The solution is constructed step-by-step, the starting time of a job and the replenishment times, once fixed, cannot be reversed. However, upon arrival of the last job, the scheduler is notified immediately that there will be no more jobs.

An input is called p-regular, if $r_j=(j-1)p$ for $j\ge 1$, for a given integer $p\ge 1$. It is regular if it is 1-regular. We will also consider p-bounded input, where the only known information about the input is that the difference of two consecutive release dates is upper bounded by some number p, i.e., $r_{j+1}-r_j \le p$ for $j \ge 1$.

The following example illustrates the problem and its possible solutions.

Example 1

Consider an input consisting of two jobs, with release dates $r_1=0$ and $r_2=t$ for some $t \ge 1$. If an algorithm makes two replenishments in $\tau _1 < t$ and $\tau _2 = t$, then the cost of this solution is $cost(S,{\mathcal {Q}}) = 2K + \tau _1+1$. However, if we postpone the replenishment and the starting time of the first job, then the objective is $cost(S', {\mathcal {Q}}') = K+t+1$. We have saved K at the replenishment cost, but the maximum flow time has increased by $t-\tau _1$. Depending on whether K or $t-\tau _1$ is bigger, the first or the second solution has a smaller cost. See Fig. 1 for an illustration. Of course, in an online setting we do not know when the second job is released, therefore, we have to make the decision about the first replenishment time $\tau _1$ before time t. $\square$

Fig. 1

Two feasible solutions. The arrows below the axis denote the replenishments

In this paper, we focus on the online problem $1|jrp,s=1, p_j=1, \textit{distinct } r_j|c_{\mathcal {Q}}+F_{\max }$. First, we present some new results regarding the offline optimal solutions in Sect. 3.

In Sect. 4, we devise a deterministic 2-competitive online algorithm for the problem $1|jrp,s=1,p_j=1,distinct \ r_j|c_{\mathcal {Q}}+ F_{\max }$. For the so-called sparse input, where the difference between two consecutive release dates $r_j$ and $r_{j+1}$ is lower bounded by Kj, this analysis is tight. On the other hand, we show that for the p-bounded input, the competitive ratio of the algorithm tends to $\sqrt{2}$ as the number of jobs tends to infinity. This result generalizes the one of Györgyi et al. (2023) for the regular input, and although it does not reach the $\sqrt{2}$-competitive ratio for short sequences of jobs, in the long run it gets arbitrarily close to it. We complement these worst-case guarantees by numerical tests in Sect. 5, which show how our algorithm performs in practice on inputs with different characteristics.

Lastly, we provide new lower bounds for the best competitive ratio in Sect. 6. For the general input, there is no online algorithm with competitive ratio of 3/2, even if there are only two jobs in the input. In the case of three jobs, this lower bound is 4/3. We also provide a lower bound for the best competitive ratio in the case of the p-regular input. For long sequences of jobs (i.e., where the last job arrives at some large time point $t > t_0$), there is no algorithm with a competitive ratio better than 1.015.

We mention that our online model is slightly different from that of Györgyi et al. (2023). While in this paper, upon the arrival of the last job we get the information that there will be no further jobs, in (Györgyi et al. 2023) this information is not available at once. Therefore, the presented lower bounds cannot be directly compared with each other. In fact, we derive a smaller lower bound for the general case (3/2 instead of $(\sqrt{5}+1)/2$).

We summarize our new results, along with some previous ones in Table 1.

Table 1 Old and new results for the online problem $1|jrp,s=1,p_j=1,\textit{distinct } r_j| c_{\mathcal {Q}}+F_{\max }$

3 Properties of the offline optimum

In this section we present some properties of the offline optimal solution on general, p-regular, and p-bounded input, respectively. Denote with OPT(I) the value of the offline optimum on input I. First, we make some easy observations:

Observation 1

(Györgyi et al. 2023) For any feasible solution $(S,{\mathcal {Q}})$ of $1|jrp, r_j|c_{{\mathcal {Q}}}+ F_{\max }$, there exists a feasible solution $(S',{\mathcal {Q}}')$ of at most the same objective function value such that the jobs are scheduled in non-decreasing release date order.

Observation 2

(Györgyi et al. 2023) For any feasible solution $(S,{\mathcal {Q}})$ of $1|jrp, r_j|c_{{\mathcal {Q}}}+ F_{\max }$, there exists a feasible solution $(S',{\mathcal {Q}}')$ of the same objective function value such that the resource is replenished only at some job release dates.

Observation 3

If $I' \subseteq I$, i.e., $I'$ consists of a subset of jobs of I, while the replenishment cost is the same, then $OPT(I') \le OPT(I)$.

We only consider inputs, where the release dates are distinct, and the jobs are of unit-time, i.e., we focus on the problem $1|jrp,s=1,p_j=1,distinct \ r_j| c_{\mathcal {Q}}+F_{\max }$. Note that without the restriction that the jobs have distinct release dates, we would face the more general problem, where the jobs have arbitrary processing times. Replacing each job j in the latter problem by $p_j$ unit-time jobs with release date of $r_j$, we get an instance of $1|jrp,s=1,p_j=1, \ r_j| c_{\mathcal {Q}}+F_{\max }$. Due to Observation 1, we can assume that the jobs created from j are scheduled consecutively in a fixed order in a feasible solution of $1|jrp,s=1,p_j=1, \ r_j| c_{\mathcal {Q}}+F_{\max }$. Hence, there is a bijection between these solutions and the solutions of the original problem with arbitrary job processing times: we can replace the $p_j$ unit-time jobs by the original job j and vice versa. Observe that the completion time of job j is the same as the that of the last unit-time job created from job j.

Observation 4

For any feasible schedule, consider any pair of two jobs, j and k (for which $r_j<r_k$), scheduled consecutively, i.e., $S_j+1 = S_k$, on the machine. Then $F_j \ge F_k$.

Following Observations 1 and 2, we only consider offline solutions, where the replenishments occur at the job release dates, and the jobs are scheduled in increasing release date order as soon as possible (i.e., after each of the earlier jobs are scheduled and after the first replenishment following their release date).

Next, we derive some properties of the p-regular input consisting of n jobs, which we denote by $R_n$.

Observation 5

Consider the p-regular input $R_n$.

• (i) If there is a replenishment which provides resource for at least $n'$ jobs in a feasible solution, then the maximum flow time is at least $(n'-1)p+1$.

• (ii) For any feasible solution with q replenishments, there exists a job which has a flow time of at least $(\lceil n/q\rceil -1)p+1$.

• (iii) The cost of any feasible solution with q replenishments is at least $qK+(\lceil n/q\rceil -1)p+1$.

Proof

Let $\tau$ be the time of the replenishment, and denote with f and $\ell$ the first and the last job in the schedule for which the replenishment is in $\tau$. Then, $\tau \ge r_{\ell } = r_f+(n'-1)p$, from which (i) follows.

If there are n jobs, then by the pigeonhole principle, there is a replenishment, which provides resources for at least $\lceil n/q\rceil$ jobs. Then, (ii) follows from (i).

Finally (iii) follows directly from (ii). $\square$

Proposition 1

For the p-regular input, the minimum cost of any solution with q replenishments is $qK+(\lceil n/q\rceil -1)p+1$.

Proof

We construct a feasible solution with q replenishments and total cost as claimed.

Let r be such that $n=q\lfloor n/q \rfloor + r$. Let

$$\begin{aligned} \tau _i:= {\left\{ \begin{array}{ll} -p, &{} \text { if } i=0,\\ i p\lceil n/q \rceil , &{} \text { if } i\in \{1,\ldots ,r\}, \\ i p\lfloor n/q \rfloor , &{} \text { if } i\in \{r+1,\ldots ,q\}, \end{array}\right. } \end{aligned}$$

and schedule the jobs in increasing release date order as soon as possible. Let j be the kth job ($k \ge 1$) arriving after $\tau _i$, but not later than $\tau _{i+1}$ for $i=0,\ldots ,q-1$. Then $\tau _i<r_j=\tau _i+kp\le \tau _{i+1}$, and $C_j=\tau _{i+1}+k$, thus $F_j=(\tau _{i+1}-\tau _i)+k(1-p)\le \lceil n/q\rceil p+k(1-p)$. By Observation 4, this expression is maximal if $k=1$. Therefore, $F_{\max }\le (\lceil n/q\rceil -1)p+1$ and the cost of this solution is at most $qK+(\lceil n/q\rceil -1)p+1$. Equality follows from Observation 5.$\square$

Now it follows immediately that

Lemma 1

For p-regular input, the offline optimum is

$$\begin{aligned} OPT(R_n) = \min _{q\in {\mathbb {Z}}_{\ge 1}} \left( Kq + (\lceil n/q \rceil -1)p + 1\right) . \end{aligned}$$

Let $q^\star$ determine the optimum value. Then there exists an optimal solution with $q^\star$ replenishments.

Next we derive lower and upper bounds on the optimum for p-regular input. To this end, we define the function f(q):

$$\begin{aligned} f(q) = Kq + (n/q -1)p+ 1. \end{aligned}$$

Note that f(q) is quite similar to the expression for $OPT(R_n)$ in Lemma 1.

Lemma 2

For p-regular input, $OPT(R_n) \ge \min _{q \in {\mathbb {R}}_{>0}} f(q) = 2\sqrt{npK}-p+1$.

Proof

By Lemma 1, we can derive

$$\begin{aligned} OPT(R_n) = Kq^{\star } + \left( \lceil {n}/{q^{\star }} \rceil -1 \right) p + 1 \ge f(q^\star ) \ge \min _{q \in {\mathbb {R}}_{>0}} f(q). \end{aligned}$$

This expression is minimal if $q=\sqrt{np/K}$, for which we obtain the minimum value of $2\sqrt{npK}-p+1$. $\square$

Lemma 3

For p-regular input, $OPT(R_n) \le 2\sqrt{npK} + K + 1$.

Proof

By Lemma 1, there exists some $q^* \in {\mathbb {Z}}_{\ge 1}$ such that

$$\begin{aligned} OPT(R_n) = Kq^{\star } + \left( \lceil {n}/{q^{\star }} \rceil -1 \right) p + 1. \end{aligned}$$

It is easy to see that $f(q^{\star }) \le OPT(R_n) \le f(q^{\star })+p$.

Let ${\hat{q}} = \sqrt{np/K}$ be the point minimizing f(q) on the positive orthant. Observe that f(q) is a convex function, hence $|{\hat{q}}-q^{\star }| < 1$ holds. We distinguish two cases.

First assume ${\hat{q}} \le q^{\star } < {\hat{q}}+1$. Then

$$\begin{aligned} f(q^{\star })= & {} Kq^{\star } + np/q^{\star } + 1 \le K({\hat{q}}+1) + np/{\hat{q}} + 1 \\= & {} f({\hat{q}})+K = 2 \sqrt{npK}-p+1 + K. \end{aligned}$$

Hence, $OPT(R_n)\le 2 \sqrt{npK}+K+1$.

Second, assume $q^{\star } < {\hat{q}} \le q^{\star }+1$, and we verify that

$$\begin{aligned} f({\hat{q}}) = 2 \sqrt{npK}-p+1 \ge OPT(R_n)-p-K, \end{aligned}$$

from which the statement follows. To see this, we compute

$$\begin{aligned} \begin{aligned} f({\hat{q}})&= K{\hat{q}}+ (n/{{\hat{q}}} -1)p + 1 \ge K q^{\star } + (n/{(q^{\star }+1)} -1)p+ 1 \\&\ge K (q^\star +1) + \left( \lceil n/(q^\star +1) \rceil -1 \right) p + 1 -p - K \ge OPT(R_n)-p-K, \end{aligned} \end{aligned}$$

where the first inequality follows from $q^\star < {\hat{q}} \le q^\star +1$ by assumption, the second from the properties of integer rounding, and the last from the definition of $q^\star$.$\square$

Let I be a p-bounded input, where the first job arrives in $t_{\min }$, and the last job arrives in $t_{\max }$. Consider the regular input and the p-regular input between $t_{\min }$ and $t_{\max }$ denoted by $D_I$ and $R_I$, respectively. See Fig. 2 for an illustration of these three different inputs in the case of $p=3$.

Fig. 2

The inputs I, $D_I$, and $R_I$ for $p=3$

Proposition 2

For a p-bounded input I, we have $OPT(D_I) \ge OPT(I) \ge OPT(R_I)-p$.

Proof

Consider an optimal solution for the input $D_I$. Since $I \subseteq D_I$, by removing the jobs in $D_I {\setminus } I$ from this optimal solution, we obtain a feasible solution for I. Therefore $OPT(D_I) \ge OPT(I)$.

Now consider an optimal solution $(S^\star ,{\mathcal {Q}}^\star )$ for the input I, and let $F_{\max }^\star$ be the maximum flow time of the jobs in schedule $S^\star$, and $\tau ^\star _1<\cdots < \tau ^\star _q$ the replenishments dates in ${\mathcal {Q}}^\star$. We transform this solution into a feasible solution $(S^R,{\mathcal {Q}}^R)$ for $R_I$ and follow how the objective function value changes.

Let $n = \lfloor (t_{\max }-t_{\min }+p-1)/p\rfloor$ be the number of jobs in $R_I$. These n jobs have release dates $t_{\min } + (i-1)p$ for $i=1,\ldots ,n$. Since I is p-bounded, we know that for each $i\in \{2,\ldots ,n\}$, I has a job $f_i$ with release date in the interval $[t_{\min } + (i-2)p+1, t_{\min }+(i-1)p]$. If there are more than one jobs with this property, then we pick one of them. We reset the release date of $f_i$ to $r'_{f_i}:=t_{\min }+(i-1)p$ for all $i=2,\ldots ,n$, and drop all other jobs. Observe that, we get $R_I$ by this modification.

Furthermore, we define a new replenishment structure ${\mathcal {Q}}^R$ using ${\mathcal {Q}}^\star$ as follows. Since we may assume that $\tau ^\star _q = t_{\max }$, we keep the last replenishment only if $t_{\min }+(n-1)p = \tau ^\star _q$, otherwise $t_{\min }+(n-1)p < \tau ^\star _q$ and we drop the last replenishment. For all other replenishments $\tau _\ell ^\star \in {\mathcal {Q}}^\star \setminus \{\tau ^\star _q\}$, we define a replenishment date $\tau _\ell$ such that $\tau _\ell = t_{\min }+ z\cdot p$ for some integer number $z\ge 0$ such that $t_{\min }+ (z-1)\cdot p <\tau ^\star _\ell \le t_{\min }+ z\cdot p$. Obviously, the replenishment cost cannot increase due to the above modification.

Let ${\mathcal {Q}}^R$ be the replenishment structure defined by the $\tau _\ell$ values and for $i=1,\ldots ,n$, denote $\tau ^\star _{\ell _i}$ the replenishment date of $f_i$ in $(S^\star , {\mathcal {Q}}^\star )$. We define $S^R$ as follows: schedule $f_1$ from $\tau _{\ell _1}$ and for $i=2,\ldots ,n$ schedule $f_i$ at time point $\max \{C_{f_{i-1}}, \tau _{\ell _i}\}$. $(S^R,{\mathcal {Q}}^R)$ is obviously a feasible solution for $R_I$ since $r'_{f_i}\le \tau _{\ell _i}$, and the jobs do not overlap. Let $F_{\max }$ be the flow time of this solution. Due to Observation 4, there is a job $f_i$ in $R_I$ such that its flow time is $F_{\max }$ and there is no job scheduled right before $f_i$ in $S^R$. Hence, $f_i$ starts at $\tau _{\ell _i}$ and

$$\begin{aligned} F_{\max }=\tau _{\ell _i}+1-r'_{f_i}\le \tau ^\star _{\ell _i}+p+1-r_{f_i}. \end{aligned}$$

Since $\tau ^\star _{\ell _i}$ is the replenishment date of $f_i$ in $(S^\star , {\mathcal {Q}}^\star )$, we have $F_{\max }^\star \ge \tau ^\star _{\ell _i}+1-r_{f_i}\ge F_{\max }-p$. The number of the replenishments in ${\mathcal {Q}}^R$ is at most that of in ${\mathcal {Q}}^\star$, hence, the proposition follows. $\square$

4 Online algorithm for the general input

In this section we propose an online algorithm for $1|jrp, s=1, p_j=1, \textit{distinct } r_j|c_{\mathcal {Q}}+ F_{\max }$ and analyze its performance on general as well as on p-bounded input.

Consider Algorithm 4. For any input I, denote ALG(I) the cost of the solution found by the algorithm, q the total number of replenishments, and $\tau _1<\cdots <\tau _q$ the q replenishment dates.

Observation 6

Let $f_i$ be the job scheduled at $\tau _i$ by the algorithm. Then $\tau _i = r_{f_i} + Ki -1$.

Observation 7

The number of jobs that get scheduled from $\tau _i$, i.e., the size of $B_{\tau _i}$, is at most Ki, and therefore, the jobs starting in $\tau _i$ are always finished before $\tau _{i+1}$.

Proposition 3

The cost of the algorithm at the ith replenishment is 2Ki, with maximum flow time of Ki for every $1 \le i \le q$.

Proof

We prove this by induction. At the first replenishment, the maximum flow time is K, hence the cost of the algorithm is 2K. Suppose that at $\tau _{i-1}$, the algorithm has a cost of $2K(i-1)$ with maximum flow time of $F_{\max }= K(i-1)$. The ith replenishment occurs when the maximum flow time of the jobs released after $\tau _{i-1}$ reaches $F_{\max }+ K = Ki$, while the total cost increases to 2Ki. $\square$

Proposition 4

$\tau _{i}-\tau _{i-1} \ge Ki$ for every $1 \le i \le q$.

Proof

If j is the first job released after the $(i-1)^{th}$ replenishment, then $r_j \ge \tau _{i-1}+1$. The maximum flow time at the ith replenishment is given by the flow time of j, which is Ki. Therefore, $Ki = F_j = \tau _i+1-r_j \le \tau _i-\tau _{i-1}$. $\square$

For the sake of analyzing the performance of Algorithm 4, we define a special class of inputs.

Definition 1

We call an input I sparse, if $r_{j+1}-r_j \ge Kj$ for all $1 \le j < n$, where n is the number of jobs in I.

Proposition 5

If I is a sparse input consisting of n jobs, then $OPT(I) = Kn+1$.

Proof

Let $(S,{\mathcal {Q}})$ be the feasible solution, where every job is replenished and scheduled at its release date (that is, $S_j=r_j$ for every $1 \le j \le n$, and $Q = \{r_1, \ldots , r_n\}$). We are going to show that $(S,{\mathcal {Q}})$ is optimal, from which the statement follows, since $cost(S,{\mathcal {Q}}) = Kn+1$.

By contradiction, assume that the solution $(S,{\mathcal {Q}})$ is not optimal. Consider an optimal solution $(S^\star , {\mathcal {Q}}^\star )$ consisting of $n-x$ replenishments, where $1 \le x < n$. This means that x replenishments are removed from ${\mathcal {Q}}$, and the jobs scheduled at these replenishment times in S are scheduled later in $S^\star$.

If for some $x < j \le n$, there is a job j such that $r_j \not \in {\mathcal {Q}}^\star$, then in $S^\star$, j starts not sooner than $r_{j+1}$. Hence, the flow time of j is not smaller than $r_{j+1}+1-r_j \ge Kj+1 > Kx+1$. Therefore, $cost(S^\star , {\mathcal {Q}}^\star ) > K(n-x)+Kx+1=Kn+1 = cost(S,{\mathcal {Q}})$, contradiction.

It follows that there is no such job j. Since there are $n-x$ replenishments and $r_{x+1}, \ldots , r_n \in {\mathcal {Q}}^\star$, then the first x replenishment times of $(S,{\mathcal {Q}})$ has to be all removed from $(S^\star , {\mathcal {Q}}^\star )$, and jobs $1, \ldots , x$ start from $r_{x+1}$. Then the flow time of the first job in $S^\star$ is $r_{x+1}+1-r_1 \ge Kx(x+1)/2 + 1$, and every other job has smaller flow time. Therefore, $cost(S^\star , {\mathcal {Q}}^\star ) \ge Kx(x+1)/2 + K(n-x)+1 > Kn+1 = cost(S,{\mathcal {Q}})$, contradiction.

Hence, the optimal solution is $(S,{\mathcal {Q}})$. $\square$

We can also make an observation regarding the behaviour of Algorithm 4 for the sparse input.

Proposition 6

If I is a sparse input consisting of n jobs, then Algorithm 4 replenishes n times. The cost of the solution is 2Kn.

Proof

We are going to show that each job is replenished individually from which the first statement follows. We proceed by induction on the job index. The first job is released at $r_1$, and Algorithm 4 replenishes and starts this job at time $\tau _1 = r_1+K-1$. Since $\tau _1 < r_2$, the second job gets a separate replenishment.

Suppose that the $(j-1)^{th}$ job is replenished at $\tau _{j-1} < r_j$, by that time there are $j-1$ replenishments, and the maximum flow time is $K(j-1)$ by Proposition 3. The next job is released at $r_j$, therefore, the algorithm is going to replenish and start this job when its flow time reaches Kj, i.e., $\tau _j= Kj + r_j - 1 \le r_{j+1}-1$, where the last inequality follows from the definition of the sparse input. By Proposition 3, the cost of the solution is 2Kn. $\square$

Theorem 1

Algorithm 4 is 2-competitive on general input.

Proof

Consider an input I for which Algorithm  4 makes q replenishments in time points $\tau _1, \ldots , \tau _q$. Then $ALG(I) = 2Kq$ by Proposition 3. For $1 \le i \le q$, denote with $f_{i}$ the job from I that starts at $\tau _{i}$. We define a new input with these q jobs, $I' = \{f_1, \ldots , f_q\}$, and job $f_i$ inherits the release date $r_{f_i}$ from input I. Since $r_{f_i} + K i-1 = \tau _i$ by Observation 6, and $r_{f_{i+1}} > \tau _i$ for $i=1,\ldots ,q-1$, we have $r_{f_{i+1}}-r_{f_i} \ge Ki$. Hence, $I'$ is a sparse input, and we have $OPT(I') = Kq + 1$ by Propositions 5. Moreover, $OPT(I) \ge OPT(I')$ by Observation 3. Therefore, we have

$$\begin{aligned} ALG(I)/OPT(I) \le ALG(I)/OPT(I') \le 2Kq/(Kq+1) \le 2. \end{aligned}$$

Finally, note that on any sparse input $I'$ with q jobs, we have

$$\begin{aligned} ALG(I') / OPT(I') = 2Kq / (Kq+1) \rightarrow 2 \end{aligned}$$

if q tends to $+\infty$, so the analysis is tight. $\square$

Theorem 2

On p-bounded input, the competitive ratio of Algorithm 4 tends to $\sqrt{2}$ as the number of jobs tends to infinity.

Proof

Consider a p-bounded input I consisting of n jobs, for which Algorithm 4 makes q replenishments in $\tau _1, \ldots , \tau _q$.

Let $n_i$ be the number of jobs released between $\tau _{i-1}+1$ and $\tau _i$ for $1 \le i \le q$. Since the input is p-bounded, we obtain that:

$$\begin{aligned} n_i \ge \lceil (\tau _i-\tau _{i-1})/p \rceil \ge \lceil Ki/p \rceil \ge Ki/p, \end{aligned}$$

where the second inequality follows by Proposition 4. Hence,

$$\begin{aligned} n = \sum _{i=1}^{q} n_i \ge \sum _{i=1}^{q} Ki/p = Kq(q+1)/2p \ge Kq^2/2p, \end{aligned}$$

from which $q \le \sqrt{2pn/K}$ follows. Therefore:

$$\begin{aligned} ALG(I) \le 2Kq \le 2K \sqrt{2np/K} = 2\sqrt{2npK}. \end{aligned}$$

On the other hand, by Lemma 2 and Proposition 2, we have

$$\begin{aligned} OPT(I) \ge 2\sqrt{npK}-2p+1. \end{aligned}$$

It follows that

$$\begin{aligned} \frac{ALG(I)}{OPT(I)} \le \frac{2\sqrt{2npK}}{2\sqrt{npK}-2p+1} = \frac{\sqrt{2npK}}{\sqrt{npK}-p+1/2} \rightarrow \sqrt{2}, \text { if } n \rightarrow \infty , \end{aligned}$$

hence, the statement is proved.

The analysis is tight: consider the p-regular input $R_n$, which is also p-bounded. By Lemma 3, $OPT(R_n) \le 2 \sqrt{npK}+K+1$. Therefore,

$$\begin{aligned} \frac{ALG(R_n)}{OPT(R_n)} \ge \frac{2\sqrt{2npK}}{2 \sqrt{npK}+K+1} = \frac{\sqrt{2npK}}{\sqrt{npK}+K/2+1/2} \rightarrow \sqrt{2} \text { if } n \rightarrow \infty . \end{aligned}$$

$\square$

5 Numerical results

In this section we analyse the competitive ratio proposed in Sect. 4. We proved that the algorithm has a competitive ratio of 2, which tends to $\sqrt{2}$ in the case of p-bounded inputs for some constant p. A question arises as to where does the competitive ratio lie if the difference of two consecutive release dates follows some probability distribution D.

Formally, we generate an input consisting of n jobs, where $r_j = X_1+\ldots +X_j$ for $1 \le j \le n$, and $X_j$ is a random variable chosen from a discrete distribution D, with possible values of 1, 2, 3 etc. Note that if the distribution D has a finite support, then it is straightforward that the competitive ratio of such inputs tend to $\sqrt{2}$ as n tends to infinity, since if D is upper bounded by some finite number p, then the inputs generated this way are p-bounded with probability 1. Hence, we assume that D has infinite support.

We chose D to be a geometric distribution with parameter $\beta$, supported on the set $\{1,2,3,\ldots \}$. That is, $P(X_j = k) = (1-\beta )^{k-1}\beta$ for every $1 \le j \le n$. We fixed the replenishment cost to $K=1$. We generated 1000 instances for different values of $\beta$ and n. For an input consisting of n jobs, we ran the offline algorithm and Algorithm 4, respectively, to obtain the competitive ratio. Figures 3, 4, 5 show the results of the experiments for $\beta \in \{0.01,0.001,0.0001\}$ and different values of n.

The smaller $\beta$ is, the closer the competitive ratio is to 2, since the input becomes sparse with high probability. On the other hand, by increasing the number of jobs, the competitive ratio is quickly decreasing, and it tends to the ratio $\sqrt{2}$ as in the case of a p-bounded input. This is due to the fact that the time between two consecutive release dates has an expected value of $1/\beta$, hence, if the number of jobs is sufficiently large, the input becomes $1/\beta$-bounded with high probability. If $\beta$ is relatively large, the competitive ratio is close to $\sqrt{2}$ even for small values of n, see Fig. 3. As the value of $\beta$ decreases, larger numbers of jobs are needed to approach the desired ratio of $\sqrt{2}$, see Figs. 4 and 5.

Fig. 3

Competitive ratios for $\beta = 0.01, n \in \{100,200,1000\}$

Fig. 4

Competitive ratios for $\beta = 0.001, n \in \{500,1000,5000\}$

Fig. 5

Competitive ratios for $\beta = 0.0001, n \in \{1000,5000,10000\}$

6 Lower bounds for the best competitive ratio

In this section, we provide several lower bounds for the best competitive ratio of an arbitrary online algorithm.

Theorem 3

On general input, if there are only two jobs released, there is no online algorithm with competitive ratio better than 3/2.

Proof

Consider an arbitrary online algorithm. Suppose that the first job is released at 0, and the algorithm replenishes and starts this job at t. Then, assume that the last job is released at $t+1$, therefore the algorithm schedules that job immediately, and then stops. Hence, $ALG = 2K+t+1$.

On the other hand, $OPT = \min \{2K+1,K+t+2\}$, because it either replenishes the resource once at $t+1$ or twice at 0 and at $t+1$. There are two cases to consider:

• 1. If $K \le t$, then $OPT = 2K+1$, and $ALG = 2K+t+1 \ge 3K+1$. Hence,

  $$\begin{aligned} \frac{ALG}{OPT} \ge \frac{3K+1}{2K+1} \rightarrow \frac{3}{2},\text { if } K \rightarrow \infty . \end{aligned}$$

• 2. If $K > t$, then $OPT = K+t+2$, therefore,

  $$\begin{aligned} \frac{ALG}{OPT} = \frac{2K+t+1}{K+t+2} {> \frac{3}{2}-\varepsilon , \text { for any } \varepsilon >0, \text { if } }K \rightarrow \infty . \end{aligned}$$

Therefore, no online algorithm can obtain a competitive ratio better than 3/2, even if there are only two jobs released. $\square$

Theorem 4

On general input, if there are at least three jobs released, there is no online algorithm with competitive ratio better than 4/3.

Proof

Consider an arbitrary online algorithm. Suppose that the first job is released at 0 and the algorithm replenishes and starts this job at $t_1$. Then, a second job is released at $t_1+1$, and the algorithm replenishes and starts this job at some $t_2\ge t_1$. Finally, the third and last job is released at $t_2+1$ which is replenished and started immediately.

We can assume that the flow time of the second job is at least the flow time of the first job, i.e. $t_1+1 \le t_2-t_1$, since replenishing and starting the second job sooner would not decrease the maximum flow time of the algorithm. Hence, $ALG = 3K+t_2-t_1$.

On the other hand, $OPT = \min \{K+t_2+2, 2K+t_1+1, 3K+1\}$, depending on the number of replenishments (one, two or three). We are going to distinguish three cases:

• 1. If $t_1 \le K-1$ and $t_2-t_1 \le K-1$, then, $ALG \ge 2K+t_2+1$, and $K+t_2+2 \le 2K+t_1+1 \le 3K$, from which $OPT = K+t_2+2$ follows. Therefore,

  $$\begin{aligned} \frac{ALG}{OPT} \ge \frac{2K+t_2+1}{K+t_2+2} = 1 + \frac{K-1}{K+t_2+2} \ge 1+\frac{K-1}{3K} \rightarrow \frac{4}{3},\text { if } K \rightarrow \infty . \end{aligned}$$

• 2. If $t_1 \le K-1$ and $t_2-t_1 \ge K$, then $ALG \ge 4K$, and $OPT = 2K+t_1+1$. Therefore:

  $$\begin{aligned} \frac{ALG}{OPT} \ge \frac{4K}{2K+t_1+1} \ge \frac{4K}{3K} = \frac{4}{3}. \end{aligned}$$

• 3. If $t_1 \ge K$ and $t_2-t_1 \ge K$, then $ALG \ge 4K$ and $OPT = 3K+1$. Therefore,

  $$\begin{aligned} \frac{ALG}{OPT} \ge \frac{4K}{3K+1} \rightarrow \frac{4}{3},\text { if } K \rightarrow \infty . \end{aligned}$$

It follows that no online algorithm can obtain a competitive ratio better than 4/3, if there are at least three jobs released. $\square$

Now we consider the p-regular input consisting of n jobs, denoted by $R_n$. That is, $r_j = (j-1)p$ for $1 \le j \le n$. In Sect. 4 we have presented a 2-competitive online algorithm whose competitive ratio tends to $\sqrt{2}$ as the number of jobs tends to infinity.

In this section we investigate the question whether the above limit of $\sqrt{2}$ could be decreased to $1+\varepsilon$ for an arbitrary small $\varepsilon > 0$. So, we will consider only long sequences of jobs, i.e., where the number of jobs is larger than some number $n_0$, which is independent of the input.

Lemma 4

On p-regular input, there exists $n_0 > 0$ such that for any $n \ge n_0$, the number of the replenishments in any c-approximate solution for $R_n$ is in

$$\begin{aligned} \left[ \frac{1}{2c+\varepsilon _n}\sqrt{\frac{np}{K}},c\left( 2\sqrt{\frac{np}{K}}+2\right) \right] , \end{aligned}$$

where $\varepsilon _n\rightarrow 0$ as $n\rightarrow +\infty$.

Proof

From Lemma 3, we have $OPT(R_n)\le 2\sqrt{npK}+K+1$. Hence, the objective function value in any c-approximate solution is at most $c(2\sqrt{npK}+K+1)$. Since $K\ge 1$, the upper bound on the number of the replenishments immediately follows.

On the other hand, we will prove that if the number of the replenishments is too small, then the flow time of the solution is larger than the upper bound for a c-approximate solution. Suppose for contradiction that we have $q<1/(2c+\varepsilon _n)\cdot \sqrt{np/K}$, where $\varepsilon _n \rightarrow 0$ as n tends to $+\infty$. After a small transformation, we get

$$\begin{aligned} \frac{np}{(2c+\varepsilon _n)\sqrt{npK}}> q, \end{aligned}$$

and then,

$$\begin{aligned} \frac{np}{c(2\sqrt{npK}+K+1)+p-1}> q, \end{aligned}$$

if $n \ge n_0$ for some $n_0 > 0$. We can reduce the denominator on the left-hand-side by using $OPT(R_n)\le 2\sqrt{npK}+K+1$ again to get

$$\begin{aligned} \frac{np}{c\cdot OPT(R_n)+p-1}> q. \end{aligned}$$

Rearranging terms gives

$$\begin{aligned} np/q-p+1> c\cdot OPT(R_n). \end{aligned}$$

Notice that the left hand side is smaller than $qK + \lceil n/q\rceil \cdot p-p+1$, which is the cost of a schedule with q replenishments by Observation  5. Therefore, q replenishments are not enough to obtain a c-approximate solution. $\square$

Lemma 5

On p-regular input, there exist a series $\varepsilon _n$ such that $\varepsilon _n\rightarrow 0$ as $n\rightarrow \infty$, and some integer $n_1 > 0$ such that for any $n \ge n_1$, the maximum flow time in any c-approximate solution for $R_n$ is in

$$\begin{aligned} \left[ \frac{K^{3/2}\sqrt{(n-1)p}}{(2+\varepsilon _n)c}-p+1,c\left( 2\sqrt{\frac{np}{K}}+K+1\right) \right] . \end{aligned}$$

Proof

The upper bound on the flow time follows immediately from the upper bound of Lemma 3 on $OPT(R_n)$.

We proceed with the lower bound. Let F be the maximum flow time of a solution with q replenishments. By Proposition 1, we have

$$\begin{aligned} Kq + F \ge Kq + \left( \lceil n/q \rceil -1 \right) p+1. \end{aligned}$$

After small transformations we get

$$\begin{aligned} (F+p-1)/p \ge \lceil n/q \rceil \ge n/q, \end{aligned}$$

from which it follows that the number of the replenishments q is at least $np/(F+p-1)$, thus the replenishment cost is at least $npK/(F+p-1)$.

Suppose the statement of the lemma does not hold, i.e., $F<(K^{3/2} \sqrt{(n-1)p})/((2+\varepsilon _n)c)-p+1$, for every $\varepsilon _n \rightarrow 0$ as $n \rightarrow \infty$. We will prove that then

$$\begin{aligned} npK/(F+p-1) > c(2\sqrt{np/K}+K+1), \end{aligned}$$

(1)

where the left hand side is a lower bound on the replenishment cost (see above), and the right hand side is an upper bound on the cost of a c-approximate solution (cf. Lemma 3), which is a contradiction, and the claimed lower bound on the maximum flow time follows. To this end, we rewrite our indirect assumption:

$$\begin{aligned} F + p -1 < \frac{(n-1)pK}{c(2+\varepsilon _n)\sqrt{(n-1)p/K}}. \end{aligned}$$

Observe that for $\varepsilon _n = (K+1) /\sqrt{np/K}$, we have $\varepsilon _n \rightarrow 0$ as $n\rightarrow \infty$, and

$$\begin{aligned} \frac{(n-1)pK}{c(2+\varepsilon _n)\sqrt{(n-1)p/K}}< \frac{npK}{c(2\sqrt{np/K}+K+1)}, \end{aligned}$$

which implies (1). $\square$

Theorem 5

For any $n_0> 0$, there is no deterministic online algorithm which is 1.015-competitive on any p-regular input $R_n$ with $n > n_0$ even if $K=1$.

Proof

Fix any $n_0 > 0$. Suppose there is a c-competitive deterministic online algorithm on p-regular input with $n \ge n_0$ jobs. For an arbitrary p-regular input $R_n$, let $(S(n), {\mathcal {Q}}(n))$ be the solution computed by the algorithm. Note that for any n, $R_n$ is unique, and thus $(S(n), {\mathcal {Q}}(n))$ is also uniquely defined, since the algorithm is deterministic.

Let $n_1>n_0$ be such that the algorithm replenishes the $2k^{th}$ time when the $n_1^{th}$ job is released at $(n_1-1)p$ for some integer $k>0$, independently whether the $n_1^{th}$ job is the last job released or not. Since the algorithm is deterministic on a p-regular input, $n_1$ is well-defined, and for any input where $n \ge n_1$, it produces the same schedule until $(n_1-1)p$. That is, $S(n_1)$ is a sub-schedule of S(n), and ${\mathcal {Q}}(n_1) \subseteq {\mathcal {Q}}(n)$ for any $n \ge n_1$.

From Lemma 5, we know that the maximum flow time in $(S(n_1),{\mathcal {Q}}(n_1))$ is at most $U(n_1) = c\left( 2\sqrt{n_1 p }+2\right)$, and the maximum flow time in $(S(n),{\mathcal {Q}}(n))$ is at least $L(n) = \sqrt{(n-1)p}/((2+\varepsilon _{n})c)-p+1$. We can choose n such that $L(n) \ge 2 U(n_1)$.

Now consider the following new feasible solution $(S'(n),{\mathcal {Q}}'(n))$ for $R_n$: starting with the first one, drop every second replenishment from ${\mathcal {Q}}(n)$ in $[0,(n_1-1)p]$. The flow time of the jobs arriving before $(n_1-1)p$ at most doubles (since $(n_1-1)p$ is the time of the $2k^{th}$ replenishment, it is not removed), and the flow time of the jobs released after $n_1$ does not change. Since $L(n) \ge 2 U(n_1)$, the maximum flow time of $(S'(n),{\mathcal {Q}}'(n))$ is not greater than of $(S(n),{\mathcal {Q}}(n))$.

The cost of the obtained solution is $cost(S'(n),{\mathcal {Q}}'(n)) \ge OPT(R_n)$. However, by Lemma 4, there are at least $\sqrt{n_1 p}/(2c+\varepsilon _{n_1})$ replenishments until $n_1$ in Q(n). Therefore $cost(S'(n), {\mathcal {Q}}'(n)) \le cost(S(n), {\mathcal {Q}}(n)) - \sqrt{n_1 p}/(4c+2\varepsilon _{n_1})$. Thus, $cost(S(n),{\mathcal {Q}}(n)) \ge OPT(R_n) + \sqrt{n_1 p}/(4c+2\varepsilon _{n_1})$.

Let $n_2:= 64(n_1-1)+1$. Then we have $OPT(R_{n_2})\le 2\sqrt{n_2 p}+2$ from Lemma 3, thus $OPT(R_{n_2})\le 16\sqrt{n_1 p}$. Let $(S(n_2),{\mathcal {Q}}(n_2))$ be the schedule and replenishment structure provided by a c-competitive algorithm, hence,

$$\begin{aligned} cost(S(n_2),{\mathcal {Q}}(n_2)) \le 16c\sqrt{n_1 p}. \end{aligned}$$

On the other hand, by Lemma 2,

$$\begin{aligned} OPT(R_{n_2}) \ge 2\sqrt{n_2 p} - p + 1 = 16\sqrt{(n_1-1)p+p/64} - p + 1. \end{aligned}$$

Therefore, $(S(n_2),{\mathcal {Q}}(n_2))$ can be a c-approximate solution only if

$$\begin{aligned} \left( 16+1/(4c+2\varepsilon _{n_1})\right) \sqrt{n_1 p}\le 16c\sqrt{n_1 p}. \end{aligned}$$

This inequality leads to a quadratic expression in c, and its solution yields that $(S(n_2),{\mathcal {Q}}(n_2))$ can be a c-approximate solution only if $c\ge (1+\sqrt{17/16})/2-\mu >1.015-\mu$, where $\mu \rightarrow 0$ as $n_1\rightarrow \infty$. $\square$

7 Conclusions

In this paper we have described a deterministic online 2-competitive algorithm for the online variant of the problem $1|jrp,s=1, p_j=1, distinct \ r_j | c_{\mathcal {Q}}+ F_{\max }$. The competitive ratio is even better for the case of p-regular input. Yet, there is a gap between the best upper and lower bounds. The natural question arises whether it is possible to provide an online algorithm with better competitive ratio, or to derive a stronger lower bound for the best competitive ratio. There are other open questions to consider: what can we say when the jobs can have arbitrarily big processing times, or if there are multiple types of resources. These problems can be intriguing for further research.