1 Introduction

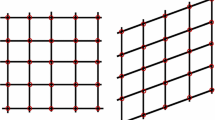
The emergence of 3D printing and related technologies has opened up a vast range of new possibilities for the design of architectured metamaterials having a variety of substructures. We are concerned in the present work with a particular substructure consisting of internal beams forming parallel planes that pivot about an orthogonal family of beams to form a three-dimensional pantographic block (Fig. 1).

Fig. 1
figure 1

Pantographic block consisting of orthogonal beams

Full size image

Drawing inspiration from standard theories of isolated beams, we propose a three-dimensional continuum theory of the block in which the beams are replaced by an initially orthogonal lattice. This may be interpreted as a coarse-grained version of a model of discrete beams in which the latter are represented by material lines forming the lattice of the continuum theory [1, 2]. However, here we do not investigate the homogenization of such a discrete model; rather, we propose the continuum model on its own merits. The elastic response of the individual beams and their mutual mechanical interactions are represented in the present model by a strain-energy function that depends on the first and second gradients of the deformation. These account for lattice flexure and certain additional non-standard effects.

From a modeling viewpoint, pantographic structures are noteworthy because they are one of the possible substructures characterizing a generalized continuum that can be described at a macroscopic level by a second-gradient model [3, 4]. Their mechanical performance is, on the other hand, beneficial for numerous applications in various fields. To name a few benefits, these materials can exhibit an advantageous weight–strength ratio, large deformations in the elastic range, toughness as well reliability, a “hierarchy of resistances” and their response to damage is easily quantified [5,6,7,8].

The basic kinematical structure of the theory is described in Sect. 2. The strain-energy function and associated response functions are discussed in Sect. 3, and the equilibrium theory is deduced in Sect. 4 on the basis of a virtual-power postulate. The paper concludes, in Sect. 5, with a number of numerical simulations of equilibrium deformations.

2 Fiber decompositions of the first and second deformation gradients

Consider a configuration in which the beams constituting the block are straight and mutually orthogonal, as in Fig. 1. We take this to be the reference configuration, denoted \(\kappa \), for the purposes of analysis. In the continuum theory, these beams are regarded as material fibers oriented by the fixed, right-handed orthonormal triad \(\{\textbf{L}_{i}\}\). This is used to write the three-dimensional referential identity as

$$\begin{aligned} \textbf{I}=\textbf{L}_{i}\otimes \textbf{L}_{i}. \end{aligned}$$
(1)

Let \(\textbf{X}\) be the position of a material point in \(\kappa \). Every such point is regarded as a point of intersection of three fibers, one from each family. A deformation \(\textbf{x}=\varvec{\chi } (\textbf{X})\) of the continuum is presumed to be twice differentiable, with first and second gradients

$$\begin{aligned} \textbf{F}=\nabla \varvec{\chi }{\quad and\quad }\textbf{G}=\nabla \textbf{F}=\nabla \nabla \varvec{\chi }, \end{aligned}$$
(2)

respectively, where \(\nabla \) is the gradient with respect to \(\textbf{X}\). In Cartesian index notation, we have \(\textbf{X}=X_{A}\textbf{E}_{A}\), \( \textbf{x}=x_{i}\textbf{e}_{i}\), \(\textbf{F}=F_{iA}\textbf{e}_{i}\otimes \textbf{E}_{A}\) and \(\textbf{G}=G_{iAB}\textbf{e}_{i}\otimes \textbf{E} _{A}\otimes \textbf{E}_{B},\) where \(\{\textbf{E}_{A}\}\) and \(\{\textbf{e} _{i}\}\) respectively are fixed right-handed bases associated with the referential and spatial Cartesian coordinates and where \(x_{i}=\chi _{i}(X_{A})\), \(F_{iA}=\chi _{i,A}\) and \(G_{iAB}=F_{iA,B}=\chi _{i,AB}\), in which commas followed by subscripts are used to denote partial derivatives with respect to the \(X^{\prime }s\), and the Einstein summation convention is also used. Moreover, small letters stand for indices in spatial representation, while capital letters are employed for the referential representation.

Using (1), we have the fiber decomposition of the deformation gradient:

$$\begin{aligned} \mathbf {F=FI}=\lambda _{1}\textbf{l}_{1}\otimes \textbf{L}_{1}+\lambda _{2} \textbf{l}_{2}\otimes \textbf{L}_{2}+\lambda _{3}\textbf{l}_{3}\otimes \textbf{L}_{3},\quad \text {where}\quad \lambda _{i}\textbf{l}_{i}=\textbf{FL} _{i}\quad \text {(no sum), }\lambda _{i}=\left| \textbf{FL} _{i}\right| \end{aligned}$$
(3)

are the fiber stretches, and \(\textbf{l}_{i}\) is the field of unit tangents to the \(i^{th}\) fiber family after deformation. Accordingly,

$$\begin{aligned} \det \textbf{F}=\lambda _{1}\lambda _{2}\lambda _{3}\textbf{l}_{1}\times \textbf{l}_{2}\cdot \textbf{l}_{3}. \end{aligned}$$
(4)

In terms of components, we have \(\textbf{l}_{j}=l_{i}^{(j)}\textbf{e}_{i},\) \(\textbf{L}_{j}=L_{A}^{(j)}\textbf{E}_{A}\) and

$$\begin{aligned} F_{iA}=\lambda _{1}l_{i}^{(1)}L_{A}^{(1)}+\lambda _{2}l_{i}^{(2)}L_{A}^{(2)}+\lambda _{3}l_{i}^{(3)}L_{A}^{(3)}. \end{aligned}$$
(5)

We seek a similar decomposition of the second gradient \(\textbf{G}\) that automatically satisfies the compatibility conditions \(G_{iAB}=G_{iBA}\), which follow from (2)\(_{2}\). To this end, we use (1) in the form

$$\begin{aligned} \delta _{AB}=L_{A}^{(1)}L_{B}^{(1)}+L_{A}^{(2)}L_{B}^{(2)}+L_{A}^{(3)}L_{B}^{(3)}, \end{aligned}$$
(6)

where \(\delta _{AB}\) is the Kronecker delta, together with

$$\begin{aligned} G_{iAB}=G_{i(CD)}\delta _{AC}\delta _{DB}=G_{iCD}\delta _{A(C}\delta _{D)B}= \tfrac{1}{2}G_{iCD}(\delta _{AC}\delta _{DB}+\delta _{AD}\delta _{CB}), \end{aligned}$$
(7)

where round braces are used to denote symmetrization, i.e., \(G_{i(CD)}= \tfrac{1}{2}(G_{iCD}+G_{iDC})\). We obtain

$$\begin{aligned} G_{iAB}= & {} g_{i}^{(1)}L_{A}^{(1)}L_{B}^{(1)}+g_{i}^{(2)}L_{A}^{(2)}L_{B}^{(2)}+g_{i}^{(3)}L_{A}^{(3)}L_{B}^{(3)} \nonumber \\{} & {} +\Gamma _{i}^{(1,2)}[L_{A}^{(1)}L_{B}^{(2)}+L_{A}^{(2)}L_{B}^{(1)}]+\Gamma _{i}^{(1,3)}[L_{A}^{(1)}L_{B}^{(3)}+L_{A}^{(3)}L_{B}^{(1)}]+\Gamma _{i}^{(2,3)}[L_{A}^{(2)}L_{B}^{(3)}+L_{A}^{(3)}L_{B}^{(2)}], \end{aligned}$$
(8)

where

$$\begin{aligned} g_{i}^{(1)}=G_{iCD}L_{C}^{(1)}L_{D}^{(1)}\quad \text {and }\Gamma _{i}^{(1,2)}=G_{iCD}L_{(C}^{(1)}L_{D)}^{(2)},\quad \text {etc.,} \end{aligned}$$
(9)

and thus arrive at the fiber decomposition

$$\begin{aligned} {\textbf {G}}= & {} {\textbf {g}}_{1}\otimes {\textbf {L}}_{1}\otimes {\textbf {L}}_{1}+ {\textbf {g}}_{2}\otimes {\textbf {L}}_{2}\otimes {\textbf {L}}_{2}+{\textbf {g}} _{3}\otimes {\textbf {L}}_{3}\otimes {\textbf {L}}_{3} \nonumber \\ {}{} & {} +\varvec{\Gamma }_{12}\otimes ({\textbf {L}}_{1}\otimes {\textbf {L}}_{2}+ {\textbf {L}}_{2}\otimes {\textbf {L}}_{1})\nonumber \\ {}{} & {} +\varvec{\Gamma }_{13}\otimes ({\textbf {L}}_{1}\otimes {\textbf {L}}_{3}+{\textbf {L}}_{3}\otimes {\textbf {L}}_{1})+\varvec{ \Gamma }_{23}\otimes ({\textbf {L}}_{2}\otimes {\textbf {L}}_{3}+{\textbf {L}} _{3}\otimes {\textbf {L}}_{2}), \end{aligned}$$
(10)

where \(\textbf{g}_{1}=\) \(g_{i}^{(1)}\textbf{e}_{i},\) \(\varvec{\Gamma } _{12}=\Gamma _{i}^{(1,2)}{} {\textbf {e}}_{i},\) etc.

We observe, from (2)\(_{2}\), (9) and the spatial uniformity of the lattice \(\{ \textbf{L}_{i}\}\), that

$$\begin{aligned} g_{i}^{(1)}=(F_{iC}L_{C}^{(1)})_{,D}L_{D}^{(1)}\quad \text {and }\Gamma _{i}^{(1,2)}=(F_{iC}L_{C}^{(1)})_{,D}L_{D}^{(2)}=(F_{iC}L_{C}^{(2)})_{,D}L_{D}^{(1)},\quad \text {etc.,} \end{aligned}$$
(11)

or, in direct notation,

$$\begin{aligned} \textbf{g}_{1}=[\nabla (\textbf{FL}_{1})]\textbf{L}_{1}\quad \text {and } \mathbf {\Gamma }_{12}=[\nabla (\textbf{FL}_{1})]\textbf{L}_{2}=[\nabla ( \textbf{FL}_{2})]\textbf{L}_{1}. \end{aligned}$$
(12)

Then, from (3) we have the orthogonal decompositions

$$\begin{aligned} {\textbf {g}}_{1}= & {} ({\textbf {L}}_{1}\cdot \nabla \lambda _{1}){\textbf {l}} _{1}+\lambda _{1}^{2}c _{1}{} {\textbf {n}}_{1}\quad \text{ and } \nonumber \\ \varvec{\Gamma }_{12}= & {} {} ({\textbf {L}}_{2}\cdot \nabla \lambda _{1}){\textbf {l}} _{1}+\lambda _{1}(\nabla {\textbf {l}}_{1}){\textbf {L}}_{2}=({\textbf {L}}_{1}\cdot \nabla \lambda _{2}){\textbf {l}}_{2}+\lambda _{2}(\nabla {\textbf {l}}_{2}) {\textbf {L}}_{1}, \end{aligned}$$
(13)

where \(c _{1}\) is the principal curvature of a deformed \(\textbf{l}_{1}\)-trajectory with principal unit normal \(\textbf{n}_{1}\). Thus, the \(\textbf{g} _{i}\) account for the tangential derivatives of the fiber stretches and for fiber bending, whereas the \(\varvec{\Gamma }_{ij}\) account for the cross derivatives of the fiber stretches and for fiber splay, that is, the rate of change of stretch and orientation, respectively, of a given fiber as one moves along a member of an orthogonal family.

3 Strain-energy and response functions

We take for granted the existence of a strain-energy density \(W(\textbf{F,G})\) such that the strain energy stored in the block is

$$\begin{aligned} E=\int _{\kappa }W\textrm{d}v. \end{aligned}$$
(14)

We suppose the material response to be uniform in the sense that W does not depend explicitly on \(\textbf{X}\). Further, we assume this function to be Galilean invariant and hence require that \(W(\textbf{F,G})=W(\textbf{QF,QG })\) for arbitrary spatially uniform rotations \(\textbf{Q}\), where \(\textbf{QF }\) is given by (3) but with \(\textbf{l}_{i}\) replaced by \(\textbf{Ql}_{i}\) and where \(\textbf{QG}\) is given by (10) but with \(\textbf{g}_{i}\) and \( \varvec{\Gamma }_{ij}\) replaced by \(\textbf{Qg}_{i}\) and \(\textbf{Q}\varvec{\Gamma } _{ij}\), respectively. In this work, we adopt the Galilean invariant function

$$\begin{aligned} W(\textbf{F,G})=W_{1}(\textbf{F})+W_{2}(\textbf{G}), \end{aligned}$$
(15)

with

$$\begin{aligned} W_{1}(\textbf{F})=\tfrac{1}{2}E_{1}\epsilon _{11}^{2}+\tfrac{1}{2} E_{2}\epsilon _{22}^{2}+\tfrac{1}{2}E_{3}\epsilon _{33}^{2}+G_{12}\epsilon _{12}^{2}+G_{13}\epsilon _{13}^{2}+G_{23}\epsilon _{23}^{2}, \end{aligned}$$
(16)

in which \(\epsilon _{ij}=\textbf{L}_{i}\otimes \textbf{L}_{j}\cdot \varvec{ \epsilon }\), \(\varvec{\epsilon }=\tfrac{1}{2}(\textbf{F}^{t}\mathbf {F-I})\) is the Lagrange strain, and \(E_{i}(>0)\) and \(G_{ij}(\ge 0)\) are material constants; and

$$\begin{aligned} W_{2}({\textbf {G}})=\tfrac{1}{2}(A_{1}\left| {\textbf {g}}_{1}\right| ^{2}+A_{2}\left| {\textbf {g}}_{2}\right| ^{2}+A_{3}\left| {\textbf {g }}_{3}\right| ^{2})+\tfrac{1}{2}(B_{12}\left| \varvec{\Gamma } _{12}\right| ^{2}+B_{13}\left| \varvec{\Gamma }_{13}\right| ^{2}+B_{23}\left| \varvec{\Gamma }_{23}\right| ^{2}), \end{aligned}$$
(17)

where \(A_{i}(>0)\) and \(B_{ij}(>0)\) are further material constants. These functions are such that W and its derivatives \(W_{\textbf{F}}\) and \(W_{ \textbf{G}}\) vanish when the body is undeformed, i.e., when \(\mathbf {F=I}\) and \(\mathbf {G=0.}\) Further, from (3) we have that the extensional and shear strains in the fiber axes are

$$\begin{aligned} \epsilon _{11}=\tfrac{1}{2}(\lambda _{1}^{2}-1)\quad \text {and} \quad \epsilon _{12}=\tfrac{1}{2}\lambda _{1}\lambda _{2}\textbf{l}_{1}\cdot \textbf{l}_{2},\quad \text {etc.} \end{aligned}$$
(18)

Evidently \(W_{2}(\textbf{G})\ge 0\) for all \(\textbf{G}\), with equality if and only if \(\textbf{g}_{i}\) and \(\varvec{\Gamma }_{ij}\) all vanish, i.e., if and only if \(\textbf{G}\) vanishes. Accordingly \(W(\textbf{F,G})\) is a homogeneous, positive definite, quadratic—and hence convex—function of \( \textbf{G}\). Granted further technical conditions, this guarantees the existence of energy minimizers in conservative boundary-value problems of the kind considered here. We refer to [9,10,11] for statements and proofs of the relevant theorems. With reference to (13)\(_{1}\), these statements remain valid if terms of the type \(A_{1}\left| \textbf{g}_{1}\right| ^{2}\) are replaced by \(A_{1}^{s}(\textbf{L}_{1}\cdot \nabla \lambda _{1})^{2}+A_{1}^{b}(\lambda _{1}^{2}c _{1})^{2}\), etc., where \( A_{1}^{s}(>0)\) is a stretch-gradient modulus and \(A_{1}^{b}(>0)\) is a bending modulus. We make such substitutions in the boundary-value problems discussed in Sect. 5. Similar statements apply to (13)\(_{2}\) and \( B_{12}\left| \varvec{\Gamma }_{12}\right| ^{2}\), etc. Moreover, W is a positive semi-definite—but not positive definite—function of the strain. Thus, if \(G_{12}=0\), for example, then \(\epsilon _{12} \) can be varied arbitrarily without affecting the energy, at least locally. In this case, all values of \(\textbf{l}_{1}\cdot \textbf{l}_{2}\) belonging to the interval \([-1,1]\) are energetically equivalent. We refer to this as a floppy mode. Fiber collapse is a special floppy mode in which \(\textbf{l}_{2}=\pm \textbf{l}_{1},\) yielding \(\det \textbf{F}=0\) (see (4)).

The choice of a quadratic form for \(W_{2}\) is appropriate if both the spacings of the actual fibers and their cross-sectional dimensions are much smaller than the length scale associated with the spatial variation of the deformation function \(\varvec{\chi }\). Taking l to the larger of these local material scales, we thus have that \(l\left| \nabla \nabla \varvec{ \chi }\right| \ll 1\) throughout the block. The leading-order dimensionless energy is then a homogeneous quadratic function of \(l\textbf{G }\). Naturally, this argument does not apply to \(W_{1}\) because \(\varvec{ \epsilon }\) is dimensionless. Instead, the quadratic dependence on \(\varvec{ \epsilon }\) is assumed here in anticipation of applications involving small strains and possibly large rotations. It is noteworthy that the assumed form of W does not fulfill the hypotheses of available existence theorems if \( W_{2}\) is suppressed, whereas unqualified existence is restored by the inclusion of \(W_{2}\).

We observe in passing that the energy (15) exhibits orthotropic symmetry in the sense that it remains invariant under the replacement \(\mathbf { F\rightarrow FR,}\) for

$$\begin{aligned} \textbf{R}\in \{\pm \textbf{L}_{1}\otimes \textbf{L}_{1}\pm \textbf{L} _{2}\otimes \textbf{L}_{2}\pm \textbf{L}_{3}\otimes \textbf{L}_{3}\}, \end{aligned}$$
(19)

(a subgroup of the orthogonal group) with any combination of signs. For example, \(\epsilon _{12}=\textbf{L}_{1}\cdot \varvec{\epsilon } \textbf{L} _{2}\rightarrow \textbf{L}_{1}\cdot \textbf{R}^{t}\varvec{\epsilon } \textbf{RL}_{2}= \textbf{RL}_{1}\cdot \varvec{\epsilon } \textbf{RL}_{2}=\pm \textbf{L}_{1}\cdot \varvec{\epsilon } \textbf{L}_{2}=\pm \epsilon _{12}\), so that \(\epsilon _{12}^{2}\) is invariant. Similarly, (12)\(_{2}\) yields that \(\varvec{\Gamma }_{12}=[\nabla ( {\textbf {FL}}_{1})]{\textbf {L}}_{2}\rightarrow [\nabla ({\textbf {FRL}}_{1})] {\textbf {L}}_{2}=\pm [\nabla ({\textbf {FL}}_{1})]{\textbf {L}}_{2}=\pm \varvec{\Gamma }_{12} \), and therefore that \(\varvec{\Gamma }_{12}\cdot \varvec{\Gamma }_{12}\) is invariant. This is an example of homogeneous symmetry in the general theory of second-grade elasticity [12, 13].

In view of (13) and (17), function (15) attributes elastic energy to various effects not accounted for in conventional elasticity theory. These include the cross derivatives of the fiber stretches and fiber splay, the latter featuring in theories of liquid crystals [14], and, as noted previously, also included are fiber bendings and tangential fiber stretch gradients, as in theories of rods [15] and fibers [16]. The influence of the cross derivatives of the stretches requires some explanation. Suppose, for example, that a fiber of the \(\textbf{L}_{1}\)-family is unstretched at a particular material point, i.e., \(\lambda _{1}=1\). A nonzero cross derivative \(\textbf{L}_{2}\cdot \nabla \lambda _{1}\) induces values of \( \lambda _{1}\) greater than, and less than, unity in adjacent fibers of the same family. The function W represents the average value of the associated energy over a small volume containing these fibers. Importantly, all of these effects must be taken into account to ensure the convexity of the energy with respect to \(\textbf{G}\). This situation also arises in two-dimensional versions of the theory considered here, intended for applications to the mechanics of thin sheets formed by two families of embedded fibers [17,18,19,20].

The basic response functions of the theory are the derivatives \(W_{\textbf{F} }\) and \(W_{\textbf{G}}\). To derive the latter, we evaluate the strain energy on a one-parameter family \(\varvec{\chi } (\textbf{X};\mu )\) of deformations and invoke the chain rule in the form

$$\begin{aligned} (\partial W/G_{iAB})\dot{G}_{iAB}=W_{{\textbf {G}}}\cdot \dot{{\textbf {G}}} =(W_{2})_{{\textbf {G}}}\cdot \dot{{\textbf {G}}}=A_{1}{} {\textbf {g}}_{1}\cdot \dot{ {\textbf {g}}}_{1}+ \cdots +B_{12}\varvec{\Gamma }_{12}\cdot \dot{\varvec{\Gamma }} _{12}+\cdots , \end{aligned}$$
(20)

where \(\dot{\textbf{G}}=\nabla \nabla \dot{\varvec{\chi }}\), the superposed dot is used to denote the derivative with respect to \(\mu \), and

$$\begin{aligned} {\textbf {g}}_{1}\cdot \dot{{\textbf {g}}}_{1}=g_{i}^{(1)}L_{A}^{(1)}L_{B}^{(1)} \dot{G}_{iAB} \text{ and } \varvec{\Gamma }_{12}\cdot \dot{\varvec{ \Gamma }}_{12}=\Gamma _{i}^{(1,2)}L_{(A}^{(1)}L_{B)}^{(2)}\dot{G}_{iAB},\quad \text{ etc. } \end{aligned}$$
(21)

Thus,

$$\begin{aligned} W_{{\textbf {G}}}= & {} {} A_{1}{} {\textbf {g}}_{1}\otimes {\textbf {L}}_{1}\otimes {\textbf {L}} _{1}+A_{2}{} {\textbf {g}}_{2}\otimes {\textbf {L}}_{2}\otimes {\textbf {L}}_{2}+A_{3} {\textbf {g}}_{3}\otimes {\textbf {L}}_{3}\otimes {\textbf {L}}_{3} \nonumber \\{}{} & {} {} +\tfrac{1}{2}B_{12}\varvec{\Gamma }_{12}\otimes ({\textbf {L}}_{1}\otimes {\textbf {L}}_{2}+{\textbf {L}}_{2}\otimes {\textbf {L}}_{1})+\tfrac{1}{2}B_{13} \varvec{\Gamma }_{13}\otimes ({\textbf {L}}_{1}\otimes {\textbf {L}}_{3}+{\textbf {L}} _{3}\otimes {\textbf {L}}_{1}) \nonumber \\{}{} & {} {} +\tfrac{1}{2}B_{23}\varvec{\Gamma }_{23}\otimes ({\textbf {L}}_{2}\otimes {\textbf {L}}_{3}+{\textbf {L}}_{3}\otimes {\textbf {L}}_{2}). \end{aligned}$$
(22)

We have incorporated the order-of-differentiation symmetry [21] \(\partial W/G_{iAB}=\partial W/G_{iBA},\) which follows from \((\partial W/G_{iAB})\dot{G }_{iAB}=(\partial W/G_{iAB})\dot{G}_{i(AB)}=(\partial W/G_{i(AB)})\dot{G} _{iAB}.\)

A similar calculation using \(\dot{\epsilon }_{ij}=Sym(\textbf{L}_{i}\otimes \textbf{L}_{j})\cdot \dot{\varvec{\epsilon }}\) yields

$$\begin{aligned} W_{\textbf{F}}=\textbf{F}(\tilde{W}_{1})_{\varvec{\epsilon }}, \end{aligned}$$
(23)

where \(W_{1}(\textbf{F})=\) \(\tilde{W}_{1}(\tfrac{1}{2}(\textbf{F}^{t}\mathbf { F-I}))\) and

$$\begin{aligned} (\tilde{W}_{1})_{\varvec{\epsilon }}= & {} E_{1}\epsilon _{11}\textbf{L} _{1}\otimes \textbf{L}_{1}+E_{2}\epsilon _{22}\textbf{L}_{2}\otimes \textbf{L }_{2}+E_{3}\epsilon _{33}\textbf{L}_{3}\otimes \textbf{L}_{3} \nonumber \\{} & {} +G_{12}\epsilon _{12}(\textbf{L}_{1}\otimes \textbf{L}_{2}+\textbf{L} _{2}\otimes \textbf{L}_{1})\nonumber \\{} & {} +G_{13}\epsilon _{13}(\textbf{L}_{1}\otimes \textbf{L}_{3}+\textbf{L}_{3}\otimes \textbf{L}_{1})+G_{23}\epsilon _{23}( \textbf{L}_{2}\otimes \textbf{L}_{3}+\textbf{L}_{3}\otimes \textbf{L}_{2}). \end{aligned}$$
(24)

4 Equilibrium conditions

4.1 Principle of virtual power

For the sake of completeness and to elucidate the structure of the model, in this section we use a virtual-power statement to derive the equilibrium equations and associated boundary conditions. However, our implementation of the model, using a routine available in the software package COMSOL, requires as input only the form (15)–(17) of the strain-energy function.

Thus, equilibria are identified with configurations that satisfy

$$\begin{aligned} \dot{E}=P, \end{aligned}$$
(25)

where E is the energy (14), the superposed dot is used to denote a variational derivative and P is the virtual power of the external actions, the form of which is made explicit below. Here,

$$\begin{aligned} \dot{E}=\int _{\kappa }\dot{W}\text {d}v, \end{aligned}$$
(26)

where, in index notation,

$$\begin{aligned} \dot{W}=P_{iA}u_{i,A}+(M_{iAB}u_{i,A})_{,B}, \end{aligned}$$
(27)

where \(u_{i}=\dot{\chi }_{i}\) is the virtual velocity,

$$\begin{aligned} M_{iAB}=\partial W/\partial G_{iAB} \end{aligned}$$
(28)

is given by (22), and

$$\begin{aligned} P_{iA}=\partial W/\partial F_{iA}-M_{iAB,B} \end{aligned}$$
(29)

is the Piola stress in which \(\partial W/\partial F_{iA}\) is given by (23) and (24).

Integration by parts yields

$$\begin{aligned} \dot{E}=\int _{\partial \kappa }(\textbf{P}\varvec{\nu }\cdot \mathbf {u+S}\cdot \nabla \textbf{u})\text {d}a-\int _{\kappa }\textbf{u}\cdot \text {Div}\textbf{P}\text {d}v, \end{aligned}$$
(30)

where \(\varvec{\nu }=\nu _{A}\textbf{E}_{A}\) is the exterior unit normal field on \(\partial \kappa \), \(\textbf{u}=u_{i}\textbf{e}_{i}\), \(\textbf{P} =P_{iA}\textbf{e}_{i}\otimes \textbf{E}_{A}\), \(\text {Div}\textbf{P}=P_{iA,A}\textbf{ e}_{i}\) and

$$\begin{aligned} \textbf{S}=S_{iA}\textbf{e}_{i}\otimes \textbf{E}_{A},\quad \text {where }S_{iA}=M_{iAB}\nu _{B}. \end{aligned}$$
(31)

To reduce the term involving \(\nabla \textbf{u}_{\mid \partial \kappa }\), we invoke the normal-tangential decomposition of the gradient in terms of the surface parametrization \(\textbf{X}(\theta ^{\beta })\) of \(\partial \kappa \), where \(\theta ^{\beta }\) \((\beta =1,2)\) is a system of convected surface coordinates. This induces the tangent basis \(\textbf{A}_{\alpha }=\textbf{X} _{,\alpha }\) and dual tangent basis \(\textbf{A}^{\alpha }\), which we use to write

$$\begin{aligned} \nabla \textbf{u}=\textbf{u}_{\nu }\otimes \varvec{\nu }+\textbf{u}_{,\alpha }\otimes \textbf{A}^{\alpha }, \end{aligned}$$
(32)

where \(\textbf{u}_{\nu }=(\nabla \mathbf {u)}\varvec{\nu }\) is the normal derivative of \(\textbf{u}\) and \(\textbf{u}_{,\alpha }=\partial \mathbf {u(X}(\theta ^{\beta }))/\partial \theta ^{\alpha }=(\nabla \mathbf {u)A}_{\alpha }\) are tangential derivatives. Thus,

$$\begin{aligned} \textbf{S}\cdot \nabla \textbf{u}=\textbf{S}\varvec{\nu } \cdot \textbf{u}_{\nu }+\textbf{S} ^{\alpha }\cdot \textbf{u}_{,\alpha },\quad \text {where} \quad \textbf{S} ^{\alpha }=\textbf{SA}^{\alpha }. \end{aligned}$$
(33)

Here, \(\partial \kappa \) is the union of a finite number of smooth subsurfaces \(\omega _{i}\) that intersect at edges \(e_{i}\) (Fig. 1). Applying Stokes’ theorem to each of these, we obtain

$$\begin{aligned} \int _{\partial \kappa }\textbf{S}^{\alpha }\cdot \textbf{u}_{,\alpha }\,\text {d}a=\sum \int _{\partial \omega _{i}}\textbf{S}^{\alpha }\xi _{(i)\alpha }\cdot \textbf{u}\,\text {d}s-\int _{\partial \kappa }\textbf{S}_{\mid \alpha }^{\alpha }\cdot \textbf{u}\,\text {d}a, \end{aligned}$$
(34)

where \(\varvec{\xi }_{i}=\xi _{(i)\alpha }\textbf{A}^{\alpha }\) is the unit normal to the curve \(\partial \omega _{i}\), oriented such that \(\{\varvec{ \nu }_{i},\varvec{\xi }_{i},\varvec{\tau }_{i}\}\) forms a right-handed orthonormal triad, where \(\varvec{\tau }_{i}\) is the unit tangent to \( \partial \omega _{i}\), s measures arclength in the direction of \(\varvec{ \tau }_{i}\), and where \(\textbf{S}_{\mid \alpha }^{\alpha }=(\sqrt{A})^{-1}( \sqrt{A}\textbf{S}^{\alpha })_{,\alpha }\) is the surface divergence, with \( A=\det (\textbf{A}_{\alpha }\cdot \textbf{A}_{\beta }).\) Here, it is understood that each curve \(\partial \omega _{i}\) is viewed from the side of \(\omega _{i}\) into which its normal \(\varvec{\nu }_{i}\) is directed.

Altogether, we then have

$$\begin{aligned} \dot{E}=\int _{\partial \kappa }[(\textbf{P}\varvec{\nu } -\textbf{S}_{\mid \alpha }^{\alpha })\cdot \mathbf {u+S}\varvec{\nu }\cdot \textbf{u}_{\nu }]\,\text {d}a+\sum \int _{\partial \omega _{i}}\textbf{S}\varvec{\xi }_{i}\cdot \textbf{u}\,\text {d}s-\int _{\kappa }\textbf{u} \cdot \text {Div}\textbf{P}\,\text {d}v. \end{aligned}$$
(35)

In a typical boundary-value problem, we fix \(\varvec{\chi }\) and its normal derivative \(\varvec{\chi }_{\nu }\) on parts \(\partial \kappa {\setminus } \partial \kappa _{p}\) and \(\partial \kappa {\setminus } \partial \kappa _{s}\) of \(\partial \kappa \), respectively, and also fix \(\varvec{\chi }\) on certain edges \(f_{i}\) of \(\partial \kappa \). Accordingly, \(\textbf{u}\) vanishes on \(\partial \kappa {\setminus } \partial \kappa _{p}\) and \(f_{i}\), and \(\textbf{u}_{\nu }\) vanishes on \(\partial \kappa {\setminus } \partial \kappa _{s}.\) Because \(\textbf{u}\) and \(\textbf{u}_{\nu }\) can be specified independently on \(\partial \kappa ,\) the virtual-power statement implies that

$$\begin{aligned} P=\int _{\partial \kappa _{p}}\mathbf {p\cdot u}\,\text {d}a+\int _{\partial \kappa _{s}} \mathbf {s\cdot u}_{\nu }\,\text {d}a+\sum \int _{e_{i}}\textbf{f}_{i}\cdot \textbf{u} \,\text {d}s+\int _{\kappa }\mathbf {g\cdot u}\,\text {d}v, \end{aligned}$$
(36)

where

$$\begin{aligned} \textbf{p}=\textbf{P}\varvec{\nu } -\textbf{S}_{\mid \alpha }^{\alpha } \end{aligned}$$
(37)

is the Piola traction on \(\partial \kappa _{p}\),

$$\begin{aligned} \mathbf {s=S}\varvec{\nu } \end{aligned}$$
(38)

is the double force density on \(\partial \kappa _{s}\),

$$\begin{aligned} \textbf{g}=-\text {Div}\textbf{P} \end{aligned}$$
(39)

is the body force density in \(\kappa \), and \(\textbf{f}_{i}\) is the edge force density on the \(i^{th}\) edge \(e_{i}\), where \(\{e_{i}\}\cup \{f_{i}\}\) is the set of all edges of \(\partial \kappa .\) Concerning the latter, we observe that an edge \(e\in \{e_{i}\}\) is the intersection of two subsurfaces \(\omega _{+}\) and \(\omega _{-}\), say. Accordingly, in (36) e is traversed twice: once in the sense of \(\mathbf {\tau }_{+}\) and once in the sense of \( \mathbf {\tau }_{-}=-\mathbf {\tau }_{+}\). With (37)–(39) in force, (25) then furnishes the edge force density

$$\begin{aligned} \textbf{f}=[\textbf{S}\varvec{\xi } ]\quad \text {on }e, \end{aligned}$$
(40)

where \([\cdot ]\) is the difference of the limits of the enclosed quantity on e when approached from \(\omega _{+}\) and \(\omega _{-}\), i.e., \([\cdot ]=(\cdot )_{+}-(\cdot )_{-}\).

4.2 Rigid-body variations

If \(\partial \kappa _{p}\) and \(\partial \kappa _{s}\) coincide with \(\partial \kappa \), and if \(\{f_{i}\}\) is empty, then rigid-body variations

$$\begin{aligned} \varvec{\chi } (\textbf{X};\mu )=\textbf{Q}(\mu )\mathbf {x+\textbf{d}(}\mu \mathbf {)} \end{aligned}$$
(41)

are admissible, where \(\textbf{x}=\varvec{\chi } (\textbf{X})\) is an equilibrium deformation field, \(\textbf{Q}(\mu )\) is a one-parameter family of rotations with \( \textbf{Q}(0)=\textbf{I}\), and \(\textbf{d}(\mu )\) is a family of vectors with \(\textbf{d}(0)=\textbf{0}\). Using superposed dots to denote derivatives with respect to \(\mu \), evaluated at \(\mu =0\), we compute the virtual velocity field \(\mathbf {u(X)}=\varvec{\omega } \times \textbf{x}+\dot{\textbf{d}}\), where \(\varvec{ \omega }\) is the axial vector of \(\dot{\textbf{Q}}\).

Because \(\dot{W}\) vanishes for such variations, the virtual-power statement (25) reduces to \(P=0\), which is satisfied for all rigid-body variations if and only if

$$\begin{aligned} \int _{\partial \kappa }\textbf{p}\,\text {d}a+\int _{\kappa }\textbf{g}\,\text {d}v+\sum \int _{e_{i}}\textbf{f}_{i}\,\text {d}s=\textbf{0} \end{aligned}$$
(42)

and

$$\begin{aligned} \int _{\partial \kappa }(\mathbf {x\times p+c)}\,\text {d}a+\int _{\kappa }\mathbf { x\times g}\,\text {d}v+\sum \int _{e_{i}}\mathbf {x\times f}_{i}\,\text {d}s=\textbf{0}, \end{aligned}$$
(43)

where

$$\begin{aligned} \mathbf {c=x}_{\nu }\times \textbf{s} \end{aligned}$$
(44)

and

$$\begin{aligned} \textbf{x}_{\nu }=(\nabla \varvec{\chi } )\varvec{\nu } \end{aligned}$$
(45)

is the normal derivative of the equilibrium deformation on \(\partial \kappa \).

These are respectively the force and torque balances for the body, the latter implying that \(\textbf{c}\) is a density of torques acting on the boundary. Because these conditions were derived using a special form of \( \textbf{u}\), they are necessary for equilibrium. Indeed, it may be shown that they follow from (37)–(39). However, they are not sufficient for equilibrium because (38) involves the full double force vector on \(\partial \kappa \), whereas (44) involves only that part which is perpendicular to \( \textbf{x}_{\nu }\). There is no one-to-one relation between \(\textbf{s}\) and \(\textbf{c}\), and it is accordingly not appropriate to assign the torque density \(\textbf{c}\) in a boundary-value problem.

In the present work, we confine attention to problems in which position is assigned on a pair of opposing faces of the block depicted in Fig. 1. These faces comprise \(\partial \kappa {\setminus } \partial \kappa _{p}\). We assign zero traction on the remaining part \(\partial \kappa _{p}\) of the boundary, zero double force on the entire boundary \(\partial \kappa (=\partial \kappa _{s})\), zero body force in \(\kappa \) and zero edge forces on the long edges \(e_{i}\) of the block. Thus, the equilibrium statement reduces simply to

$$\begin{aligned} \dot{E}=0. \end{aligned}$$
(46)

5 Some examples of exotic equilibrium configurations for pantographic lattices

We discuss several examples in which the pantographic lattice is specified by

$$\begin{aligned} \textbf{L}_{1}=\tfrac{\sqrt{2}}{2}(\textbf{E}_{1}+\textbf{E}_{2}),\quad \textbf{L}_{2}=\tfrac{\sqrt{2}}{2}(-\textbf{E}_{1}+\textbf{E}_{2})\quad \text {and }\textbf{L}_{3}=\textbf{E}_{3}, \end{aligned}$$
(47)

where \(\{\textbf{E}_{A}\}\) are aligned with the edges of the block (Fig. 1).

To set the material parameters for the numerical simulations, we observe that with reference to (16), the coefficients \(E_i\) and \(G_{ij}\) can be interpreted respectively as stiffnesses related to the resistance to stretching and shearing of the beams of the lattice. Accordingly, some formulae borrowed from the beam theory can be used to give a first estimate of their values (see, for more details, [22,23,24,25,26,27,28]); of course, the hypotheses underlying their deduction in Saint-Venant theory are not verified and therefore one must expect that correction coefficients will be needed when trying to predict experimental evidence (more details are given in [29,30,31,32]). Herein, for the sake of definiteness and tractability, we set the \(E_i\) coefficients to be equal, assuming that the fibers have the same cross-sectional area and density per unit volume.

Regarding the second-gradient moduli appearing in (17), we have separated out the effects of tangential stretch gradient, geodesic curvature and the normal curvature of the lattice fibers and assigned different elastic moduli to each contribution. In particular, the representation for the vectors \(\textbf{g}_i\) may be specialized as

$$\begin{aligned}&\textbf{g}_{1} = (\textbf{L}_{1}\cdot \nabla \lambda _{1})\textbf{l}_{1}+\lambda _{1}^{2}\,\eta _{1}(\textbf{n}_{12}\times \textbf{l}_{1})+\lambda _{1}^{2}\,\kappa _{1}\textbf{n}_{12} \quad \text {with} \quad \textbf{n}_{12}=\textbf{l}_{1}\times \textbf{l}_{2}\nonumber \\&\textbf{g}_{2} = (\textbf{L}_{2}\cdot \nabla \lambda _{2})\textbf{l}_{2}+\lambda _{2}^{2}\,\eta _{2}(\textbf{n}_{12}\times \textbf{l}_{2})+\lambda _{2}^{2}\,\kappa _{2}\textbf{n}_{12}\\&\textbf{g}_{3} = (\textbf{L}_{3}\cdot \nabla \lambda _{3})\textbf{l}_{3}+\lambda _{3}^{2}\,\kappa _{3}\textbf{n} \quad \text {with} \quad \textbf{l}_{3}\cdot \textbf{n} = 0 \nonumber \end{aligned}$$
(48)

in which for the pantographic plane \(X_1-X_2\) the three contributions mentioned above appear as addends in (48)\(_{1-2}\). The coefficients \(\eta _1\) and \(\eta _2\) are the geodesic curvatures of the deformed fibers, while \(\kappa _{1}\) and \(\kappa _{2}\) are their normal curvatures. In this way, the current directions \(\textbf{n}_{12}\times \textbf{l}_{1}\) and \(\textbf{n}_{12}\) (as well as \(\textbf{n}_{12}\times \textbf{l}_{2}\) and \(\textbf{n}_{12}\) for the other family of fibers) can be regarded as the principal directions of the cross section of the beams and, thus, the corresponding moduli related to the bending of the beams around them can be used. We note that the principal curvature \(c_1\) introduced in (13) is related to the curvatures in (48) by the relationship \((c_1)^2 = (\eta _1)^2 + (\kappa _1)^2\). Specifically, we introduce, for the beams along \(\textbf{L}_1\) in the reference configuration, \(A_1^s\), \(A_1^g\), \(A_1^n\) for the moduli relative to the tangential stretch gradient, geodesic curvature, and normal curvature, respectively. Similarly, \(A_2^s\), \(A_2^g\), \(A_2^n\) for the beams in \(\textbf{L}_2\)-direction. Regarding the \(\textbf{L}_3\)-direction, we limit our attention to the case when the beams interconnecting pantographic planes have circular cross sections. Therefore, one can avoid distinguishing between two different bending directions, and we introduce only the moduli related to tangential stretch gradient, \(A_3^s\), and to bending \(A_3^b\) associated with the curvature \(\kappa _{3}\).

The mechanical responses of the pantographic block are evaluated using the finite element software COMSOL Multiphysics, which allows for the straightforward implementation of the energy contributions (16) and (17). The finite element discretization employs Hermite elements of the third order since the continuum model considered is a second-gradient elastic one. Indeed, it requires, at least, a set of interpolating functions suited to span the Sobolev space \(H^2\). They preserve continuity across element boundaries as well as continuity with respect to the first spatial derivative. Equivalently, the same equilibrium shapes might be obtained more efficiently with an ad hoc code using isogeometric formulation [33,34,35,36,37], discrete Hencky models based on the geometry of the microstructure of the fibers in the three considered directions, as done in [38,39,40,41], or as recently proposed, based on swarm robotics [42, 43].

To characterize the peculiar behavior of pantographic metamaterials, two twisting tests with different material parameters are performed. The dimensions of the specimen are \(26\times 56.8\times 210\) mm. The boundary conditions are assigned displacements on the bases parallel to the planes \(X_2-X_3\) (Fig. 1). Particularly, a rigid rotation around the \(X_1\)-axis is imposed on one base through the displacement

$$\begin{aligned} \textbf{d}=(\textbf{R}_{X_1}(\vartheta )-\textbf{I})\,\textbf{X} \end{aligned}$$
(49)

where \(\textbf{R}_{X_1}(\vartheta )\) is the elemental rotation of an anti-clockwise angle \(\vartheta \), namely

$$\begin{aligned} d_1&= 0 \nonumber \\ d_2&= X_2\, [\cos (\vartheta )-1] - X_3 \sin (\vartheta )\nonumber \\ d_3&= X_2\sin (\vartheta )+ X_3\, [\cos (\vartheta )-1] \end{aligned}$$
(50)

The other base is completely fixed (\(d_1=d_2=d_3=0\)).

Fig. 2
figure 2

Pantographic block under twisting test: \(G_{12}=10\) MPa, \(\vartheta =59\) degrees. The displacement component \(d_3\), orthogonal to the pantographic plane, is indicated by colors

Full size image

The first-gradient moduli are set to be:

$$\begin{aligned} E_1=E_2=E_3=600\text { MPa}\quad G_{13}=G_{23}=214.3\text { MPa} \end{aligned}$$
(51)

while the modulus \(G_{12}\) related to the shear stiffness in the pantographic plane \(X_1-X_2\) is specified in two different instances.

The second-gradient moduli are set to be:

$$\begin{aligned}&A_1^s=A_2^s=1.9\text { N}\quad A_1^g=A_2^g=38.09\text { N} \quad A_{1}^{n}=A_{2}^{n}=9.52\text { N} \nonumber \\&A_3^s=0.020 \quad A_{3}^b=0.39\text { N} \nonumber \\&B_{12}=0.41\text { N}\quad B_{13}= B_{23}=1.31\text { N} \end{aligned}$$
(52)

In the first example, we set \(G_{12}=10\) MPa. The response for the twisting test is shown in Fig. 2. In \(\textbf{L}_{1}\)-direction, the fibers belonging to the pantographic plane are compressed beyond a certain threshold, and an in-plane fiber undulation occurs in that direction.

By setting the shear modulus to a much smaller value, namely, \(G_{12}=0.1\) MPa, instead, we find a dramatically different buckling mode with the necking behavior shown in Fig. 3.

Next, two compression tests are performed. In this kind of test, the dimensions of the specimen are \(43.77\times 40.2\times 112\) mm. A negative longitudinal displacement in \(X_1\)-direction is imposed on one face parallel to \(X_2-X_3\) plane and the other opposite face is held fixed.

Fig. 3
figure 3

Pantographic block under twisting test: \(G_{12}=0.1\) MPa, \(\vartheta =21\) degrees. The displacement component \(d_2\) is indicated by colors

Full size image
Fig. 4
figure 4

Pantographic block under compression with \(G_{12}=10\) Pa: a perspective view; b top view. Imposed displacement \(d_1=-20\) mm. The colors indicate the displacement \(d_2\) in \(X_2\)-direction

Full size image

The second-gradient moduli are set to be:

$$\begin{aligned}&A_1^s=A_2^s=3.67\text { N}\quad A_1^g=A_2^g=73.43\text { N} \quad A_{1}^{n}=A_{2}^{n}=26.43\text { N}\nonumber \\&A_3^s=0.030 \quad A_{3}^b=0.59\text { N} \nonumber \\&B_{12}=0.86\text { N}\quad B_{13}= B_{23}=0.86\text { N} \end{aligned}$$
(53)

All the other parameters are kept the same unless otherwise specified.

These simulations also exhibit strong sensitivity to \(G_{12}\). Relatively small values, for example, 10 Pa, result in a deformed shape with only one bulging “wave” along the long lateral faces (see Fig. 4).

Fig. 5
figure 5

Pantographic block under compression with \(G_{12}=100\) MPa: a perspective view; b top view. Imposed displacement \(d_1=-20\) mm. The colors indicate the displacement \(d_2\) in \(X_2\)-direction

Full size image

By increasing \(G_{12}\) up to 100 MPa, we obtain a two-wave bulging shape in the compression test (Fig. 5). Clearly, here the ratio between the geodesic bending and shear moduli determines this different behavior inducing either the spread of the deformation or the localization of it.

Fig. 6
figure 6

Three-point bending test: load application parallel to the pantographic plane. The colors are the displacement \(d_2\) in \(X_2\)-direction

Full size image
Fig. 7
figure 7

Three-point bending test: load application orthogonal to the pantographic plane: a perspective view; b top view. The colors are the displacement \(d_2\) in \(X_2\)-direction

Full size image

Finally, two three-point bending tests are performed in two orthogonal directions to illustrate the behavior of the pantographic plane with different boundary conditions (see Figs. 6 and 7). In these tests, the dimensions of the specimen are \(56.8\times 40\times 121.8\) mm.

The second-gradient moduli are set to be:

$$\begin{aligned}&A_1^s=A_2^s=1.94\text { N}\quad A_1^g=A_2^g=38.09\text { N} \quad A_{1}^{n}=A_{2}^{n}=9.52\text { N}\nonumber \\&A_3^s=0.019 \quad A_{3}^b=0.39\text { N} \\&B_{12}=2.04\text { N}\quad B_{13}= B_{23}=1.31\text { N} \nonumber \end{aligned}$$
(54)

All the other parameters are kept the same, while \(G_{12}=0.1\) MPa.

These last two tests are the only ones in which we do not impose displacements, but the effects of the edges upon which the block rests in the tests are simulated with an elastic barrier of potential that prevents the sample from overlapping with them. In these tests, the two supports beneath the sample are kept fixed, while the central edge on the top can have a displacement along \(X_2\)-direction or \(X_3\)-direction. Specifically, Figs. 6 and 7 show the deformation for a given displacement of the edge of \(d_2=-25\) mm and \(d_3=-15\) mm, respectively. When the direction of load application lies in the pantographic plane, as shown in Fig. 6, the deformation due to the blade is absorbed almost entirely on the same side of the load. In contrast, the opposite face remains quasi-plane, and the sample undergoes a significant elongation in the \(X_1\)-direction. This kind of response is remarkable in applications where a specific load must be shielded, hence, used to design specific metamaterials [44, 45]. By changing the direction for the application of the load, we observe a remarkable macroscopic Poisson effect amplified by the pantographic substructure lying in the \(X_1-X_2\) plane, as shown in Fig. 7. In Fig. 7, the pantographic layers are characterized by an anticlastic deformation mode. Specifically, they present an anticlastic curvature, i.e., a type of surface curvature where the surface bends in opposite directions along two orthogonal axes. Thus, the surface has a saddle-like shape, with one axis curving up and the other curving down. This specific phenomenon of anticlastic curvature arises from Poisson effects observable at the macroscopic level. The interaction between different pantographic layers is mainly characterized by a common first-gradient energy contribution; therefore, a standard kind of deformation is observed.

The numerical simulations which we have shown are intended to aid in the design of an experimental program using 3D-printed specimens both in polyamide and metal alloys. Indeed, experimental tests are needed to corroborate the proposed model, and we intend to conduct them in our future research. However, some measurements are already performed on this kind of material, which appear to confirm the predictive potential of the present model (see [46, 47]).