1 Introduction

In rail transit, the track is the key infrastructure for train operations [1,2,3]. Track irregularity reflects the macroscopic geometrical state of the track and is an important embodiment of track performance [4,5,6]. As a major excitation of the wheel–rail system, track irregularity plays a crucial role in the stability, comfort, and safety of the train operation, as well as in the service lives of vehicle and track components [7, 8]. In the literature, studies on track irregularity include track inspection, condition assessment, and prediction. First, static [9, 10] and dynamic [11,12,13] inspections are popular ways to collect data and to check the track condition in practice. Based on the collected data, the track conditions are assessed by evaluation methods such as scoring methods [14, 15], track quality index methods [16], and track spectrum methods [17]. The methods for track inspection and condition assessment mainly complete the data collection and condition evaluation of the track but do not pay attention to the evolution of the track condition and thus fail to predict its future conditions.

To fill this gap, many studies have been carried out on this topic in recent years, which can be divided into data-driven methods and physics-based methods. Among them, the former are mainly composed of statistical learning and machine learning methods. To predict the track condition, the commonly used statistical learning models include the stochastic process model [18] and the regression model [19, 20]. For example, Mercier et al. [18] established the prediction model for the deterioration of track irregularity based on the binary gamma process. The model parameters were estimated using the maximum likelihood estimation and expectation–maximization algorithm, and the track irregularity index was predicted after fitting the gamma process to the actual data. The effectiveness of the proposed model was validated by comparing the predictions of the gamma distribution model with those of the single–parameter model. Khouzani et al. [19] established the linear relationship between the track irregularity indices such as left and right track alignment, triangular pit, and track quality index and the influence factors such as total weight, track bed type, and weather conditions, and then optimized the tamping maintenance decision using an inheritance algorithm based on the built model. Finally, the model was verified by using the actual production data of a 39-km line in the Iranian railway. Methods based on machine learning usually include deep neural networks, a support vector machine, and so on to predict track conditions. Lasisi et al. [21] determined three principal components that have the highest impact on the track quality index through principal component analysis of track irregularity indices, such as height, level, gauge, triangle pit, and so on, and then predicted the overall track irregularity of American Class I railway based on machine learning methods such as random forest, linear discriminant analysis, and support vector machine. Falamarzi et al. [22] used an artificial neural network and a support vector machine to predict the deterioration values of the gauge deviation of the straight line and the curved line in the Melbourne tram. The results showed that the performance of the artificial neural network was slightly better than that of the support vector machine in predicting the gauge deviation of the straight line. On the contrary, the performance of the support vector machine was slightly better than that of the artificial neural network in predicting the gauge deviation of the curved line.

Although the data-driven method has promising results, it often requires a lot of historical data on the track condition evolution, and lacks explanations on the evolution mechanism of the track irregularity. In the case that the track state evolution data are insufficient or even difficult to obtain, the data-driven method may not be applicable. Therefore, many scholars have studied prediction methods based on the evolution mechanism of track irregularity. In physics, track irregularity is generally considered to be influenced by factors such as the train cyclic loads and geological conditions. At present, many researchers consider the influence of train cyclic loads on track irregularity and predict track irregularity through the characterization of the interaction between the vehicle load and the track line. In railway, Suarez et al. [23] studied the influence of factors such as track irregularity and rail-rolling contact fatigue on the accuracy of the dynamic rail–vehicle model through numerical simulations. On this basis, they accurately predicted the track irregularity and rail rolling contact fatigue. Gao [24] built a dynamic prediction model for track irregularity based on the track dynamics theory. He used numerical simulations to study the law of the vertical track displacement and track irregularity under the impact of the train loads and then predicted the trend of the track irregularity. The effectiveness of the simulation model was verified based on the actual track data. In subway, Meng et al. [25] analyzed the track dynamic response under multilevel track irregularity and rail roughness on the basis of building the vehicle–track coupling model.

The above studies place a greater emphasis on the influence of train cyclic loads on track irregularity but ignore the factors outside the rail transit system, such as the change of geological conditions, mainly referred to as the change of foundation morphology caused by some external forces. For such topics, some existing studies focus on the settlement of existing structures caused by the soil disturbance during the construction process. For example, Peck [26] put forward that the surface settlement curve can be approximated by a probability normal distribution curve, and believed that the surface settlement during construction was mainly caused by ground loss, and the volume of the surface settlement should be equal to the volume of ground loss. Yang et al. [27] proposed a simplified formula to calculate the surface deformation based on the random medium theory. Except for the shallow tunnel, the results calculated by the simplified formula were basically consistent with those of the original formula. Chakeri et al. [28] used the finite difference method to simulate the process of a tunnel crossing the mixed stratum and fault zone. The results showed that the maximum surface settlement and the shape of the horizontal settlement groove were closely related to the mixed stratum in front of the tunnel face and the thickness of the fault zone in the excavation direction. The above literature predicted the soil displacement caused by the construction disturbance using an empirical formula, theoretical analysis, and numerical simulation but failed to discuss the influence on the deformation of existing structures and the auxiliary tracks. Furthermore, Kui [29] studied the deformation of the existing station when a new tunnel passes through based on the numerical method; then the influence of track irregularity on wheel–rail interaction force and the safety of train operations was analyzed, which provided support for the risk control of the existing subway during the construction of new tunnels.

However, the track deformation induced during the construction has not been discussed. To this end, this paper proposes a unified three-stage method to predict the track irregularity for the scenario of shield tunnel crossing through the existing tunnel. Firstly, by considering the ground loss and construction load during tunneling, a three-dimensional model is built to estimate the ground displacement induced by the shield construction; Secondly, by considering the existing tunnel as a Timoshenko beam, the soil–tunnel interaction model is established to predict the deformation of the existing tunnel caused by the soil displacement. Finally, based on the description of tunnel–rail interaction, the track displacement is estimated for the calculation of track irregularity.

The rest of this article is organized as follows. In Sect. 2, we elaborate on the proposed three-stage method. First, the framework of the proposed method is presented. Then, the shield–soil influence, soil–tunnel interaction. and track displacement prediction are modeled. In Sect. 3, a series of experiments based on a real engineering case and finite element simulations are conducted to evaluate the performance of the proposed method for estimating track irregularity. Section 4 concludes the article.

2 Methodology

In this section, we first present the framework to estimate the track irregularity of the existing tunnel under-crossed by a shield tunnel. Secondly, we describe each model of the three-stage framework in detail, and then show how to calculate the track irregularity from the estimation of the track displacement.

2.1 Overview

As shown in Fig. 1, the proposed three-stage framework includes the following: (i) Shield–soil influence (SSI) model: SSI aims to estimate the displacement of the surrounding soil caused by new tunnel excavation; the construction parameters of shield tunneling inducing the soil displacement mainly include ground loss, support pressure of shield machine, frictions between the shield machine’s shell and the ground, and the grouting force at the tail of the shield machine. (ii) Soil–tunnel interaction (STI) model: after obtaining the soil displacement caused by the new tunnel excavation, establishing the SSI model is the key to estimate the deformation of the existing tunnel. (iii) Track displacement prediction (TDP) model: given the estimated tunnel deformation, we establish the tunnel–rail interaction model to estimate the track displacement. Then, based on vertical and horizontal track displacements, the track irregularity is calculated.

Fig. 1
figure 1

The three-stage framework

Full size image

By following the existing literature and considering engineering practice, in this article we assume the following:

  1. 1.

    The existing tunnel and the new tunnel are embedded in homogeneous soil

  2. 2.

    The existing tunnel is always in contact with the soil.

  3. 3.

    We modeled the existing tunnel as a Timoshenko beam.

  4. 4.

    The fixation between the track bed and the tunnel is assumed to be rigid.

  5. 5.

    The track bed and the rail are connected by elastic fasteners.

Notably, assumptions 1~3 are common in the modeling of the tunnel construction [30, 31] and assumption 5 appears frequently in the existing literature on rail modeling, such as [32, 33]. Assumption 4 is reasonable since the track bed is generally monolithic and fixed at the bottom of the tunnel.

2.2 Estimation of the ground displacement induced by new tunneling

The main factors inducing the ground displacement due to shield tunneling are the ground loss and the construction loads. Among them, the construction loads include the support pressure of the tunnel face, the frictional resistance between the shield shell and soil, and the grouting pressure at the shield tail [31, 34, 35]. In this section, the superposition principle is applied to estimate the total soil displacement caused by the shield construction. Firstly, the mechanism of soil displacement induced by ground loss is described. Secondly, the ground displacement caused by shield construction load is detailed. On this basis, we superpose the components of the soil displacements caused by each factor to obtain the total induced displacement. First, we model the soil displacement induced by the ground loss.

2.2.1 Soil displacement induced by the ground loss

To describe the soil disturbance induced by the ground loss at the shield tail, we first calculate the volume of ground loss during construction. For shield tunneling, the ground loss is defined as the difference between the excavated volume of the soil and the completed volume of the final tunnel (also known as the theoretical excavation volume, including the volume of grouting fluid wrapped around the tunnel) [36]. Thus, the ground loss \({V}_{\rm loss}\) for each length of tunnel segment can be estimated using the following formula,

$${V}_{\rm loss}={V}_{e}-{V}_{s}-{V}_{g},$$
(1)

where \({V}_{e}\) is the excavated volume of soil during shield tunneling, \({V}_{s}\) represents the volume around the tunnel formed by segments, \({V}_{g}\) is the volume of grouting fluid, \({V}_{e}\) and \({V}_{s}\) can be calculated from the tunnel design, while \({V}_{g}\) and \({V}_{c}\) are measured during tunneling. In the existing literature, most studies calculate the volume of the excavated soil by considering a straight tunneling segment, such that the estimated volume is more conservative than the actual volume of the excavated soil. To tackle this issue, we propose a new method to calculate the soil volume excavated in a curved segment during the shield construction.

2.2.1.1 The calculation of \({V}_{{\varvec{e}}}\)

During shield tunneling, the volume of the excavated soil is influenced by two factors, i.e., the excavation distance \(d\varepsilon\) and the angle \(\theta\), where \(\theta\) is defined as the included angle between the center lines of the shield machine before and after tunneling. According to the value of \(\theta\), the excavation process can be divided into two cases: straight excavation (\(\theta =0\)) and curved excavation (\(\theta >0\)). For straight excavation, the volume of the excavated soil for a distance \(d\varepsilon\) is calculated as

$${V}_{{\varvec{e}}}\left(d\varepsilon ,\theta \right)=\pi {\left({r}_{h}\right)}^{2}d\varepsilon ,$$
(2)

where \({r}_{h}\) is the radius of the shield machine face.

For curved excavation, as shown in Fig. 2, we observe that the volume of the excavated soil is represented by the volume of the shaded region. Based on the formula of ring volume, the volume of the excavated soil for a distance \(d\varepsilon\) is calculated as follows:

$${V}_{e}\left(d\varepsilon ,\theta \right)=\frac{\pi {l}_{s}}{2{R}_{T}}\left({R}_{\rm out}+{R}_{\rm in}\right){\left(\frac{{R}_{\rm out}-{R}_{\rm in}}{2}\right)}^{2},$$
(3)

where \({R}_{T}\) is the radius of the tunnel curvature, \({R}_{\rm in}={R}_{T}-{r}_{h}\), \({R}_{\rm out}=\sqrt{{\left({R}_{T}+{r}_{h}\right)}^{2}+{\left(\frac{S}{2}\right)}^{2}}\), and \(S\) is the length of the shield machine.

Fig. 2
figure 2

Calculation of the ground loss volume excavated in a curved segment

Full size image
2.2.1.2 Calculation of \({V}_{s}\)

For a straight segment, the tunnel volume enclosed when each ring segment is installed can be calculated as

$${V}_{s}=\pi {\left({r}_{s}\right)}^{2}{l}_{s},$$
(4)

where \({l}_{s}\) is the length of the centerline of one segment, and \({r}_{s}\) is the radius of the outer surface of the segment.

For curved segments, according to the formula of the ring volume, the tunnel volume enclosed when each ring segment is installed can be calculated as

$${V}_{s}=\frac{{l}_{s}}{2\pi {R}_{T}}*V=\frac{{l}_{s}}{2\pi {R}_{T}}*2{\pi }^{2}*{\left({r}_{s}\right)}^{2}*{R}_{T}=\pi {\left({r}_{s}\right)}^{2}{l}_{s},$$
(5)

where \({R}_{T}\) is the radius of the curved tunnel. Since \({V}_{g}\) and \({V}_{c}\) are recorded during the tunneling process, the ground loss volume \({V}_{e}\) is thus estimated.

2.2.1.3 Model for estimating soil displacement induced by ground loss

The ground loss caused by tunnel excavation is the key factor causing soil displacement. In this work, we follow the cavity expansion theory [37] to approximate the ground loss as the concentrated ground loss acting on the tunnel centerline. The relationship between a unit volume loss and the surrounding ground displacement field [31] is established as follows:

$$\left\{\begin{array}{l}{f}_{s}\left(x,y,z\right)=\frac{x}{4\pi }\left\{\frac{1}{{R}_{1}^{3}}+\frac{3-4v}{{R}_{2}^{3}}-\frac{6z\left(z+h\right)}{{R}_{2}^{5}}\right\}\\ {g}_{s}\left(x,y,z\right)=\frac{y}{4\pi }\left\{\frac{1}{{R}_{1}^{3}}+\frac{3-4v}{{R}_{2}^{3}}-\frac{6z\left(z+h\right)}{{R}_{2}^{5}}\right\}\\ {h}_{s}\left(x,y,z\right)=\frac{1}{4\pi }\left\{\frac{z-h}{{R}_{1}^{3}}+\frac{4v\left(z+h\right)-z-3h}{{R}_{2}^{3}}-\frac{6z{\left(z+h\right)}^{2}}{{R}_{2}^{5}}\right\}\end{array},\right.$$
(6)

As shown in Fig. 3, suppose that the extension path of the excavated tunnel is \(L\left(x,y\right)=0, y\in \left(-\infty ,0\right]\), let the equivalent ground loss function of any point \(\left(\eta ,\xi \right)\) in this path be \(V\left(\eta ,\xi \right)=\beta {V}_{\rm loss}\left(\eta ,\xi \right)\), where \(\beta\) is the equivalent coefficient. Then, through the integral along the curve \(L\), we obtain the ground loss-induced displacement for any point \(\left(x,y,z\right)\) underground:

Fig. 3
figure 3

Soil displacement induced by the ground loss during tunneling in a curved line

Full size image
$$\left\{\begin{array}{l}{u}_{x}^{V}={\int}_{L}{f}_{s}\left(x-\eta ,y-\xi ,z\right)dV={\int}_{L}{f}_{s}\left(x-\eta ,y-\xi ,z\right)\left({V}_{x}\left(\eta ,\xi \right)d\eta +{V}_{y}\left(\eta ,\xi \right)d\xi \right)\\ {u}_{y}^{V}={\int}_{L}{g}_{s}\left(x-\eta ,y-\xi ,z\right)dV={\int}_{L}{g}_{s}\left(x-\eta ,y-\xi ,z\right)\left({V}_{x}\left(\eta ,\xi \right)d\eta +{V}_{y}\left(\eta ,\xi \right)d\xi \right)\\ {u}_{y}^{V}={\int}_{L}{h}_{s}\left(x-\eta ,y-\xi ,z\right)dV={\int}_{L}{h}_{s}\left(x-\eta ,y-\xi ,z\right)\left({V}_{x}\left(\eta ,\xi \right)d\eta +{V}_{y}\left(\eta ,\xi \right)d\xi \right)\end{array}\right.,$$
(7)

In practice, the above formula can be approximated according to the discrete characteristics of the segment ring. Specifically, it is assumed that the center point of each ring segment in the shield tunnel is \(\left({\eta }_{k},{\xi }_{k}\right), k=\mathrm{0,1},2,\dots\)

$$\left\{ {\begin{array}{*{20}c} {u_{x}^{V} = \mathop \sum \limits_{{k = 0}}^{\infty } f_{s} \left( {x - \eta _{k} ,y - \xi _{k} ,z} \right)V\left( {\eta _{k} ,\xi _{k} } \right)} \\ {u_{y}^{V} = \mathop \sum \limits_{{k = 0}}^{\infty } g_{s} \left( {x - \eta _{k} ,y - \xi _{k} ,z} \right)V\left( {\eta _{k} ,\xi _{k} } \right)} \\ {u_{z}^{V} = \mathop \sum \limits_{{k = 0}}^{\infty } h_{s} \left( {x - \eta _{k} ,y - \xi _{k} ,z} \right)V\left( {\eta _{k} ,\xi _{k} } \right)} \\ \end{array} } \right.,$$
(8)

where \({r}_{1}=\sqrt{{x}^{2}+{\left(z-h\right)}^{2}}, {r}_{2}=\sqrt{{x}^{2}+{\left(z+h\right)}^{2}}\), \({R}_{1}=\sqrt{{x}^{2}+{y}^{2}+{\left(z-h\right)}^{2}}, {R}_{2}=\sqrt{{x}^{2}+{y}^{2}+{\left(z+h\right)}^{2}}\). \(v\) is Poisson’s ratio, \(h\) is the cover depth of the existing tunnel centerline, and\({r}_{0}\) is the radius of the existing tunnel.

2.2.2 Soil displacement induced by other parameters

The load of the shield construction will also cause soil displacement, so this subsection attempts to characterize how these loads, including the support pressure of the tunnel face, the frictional resistance of the shield shell, and the grouting pressure at the shield tail, will cause soil displacement. Among them, the support pressure of the tunnel face and the friction resistance of the shield shell are horizontal forces, while the grouting pressure of the shield tail is considered as vertical forces. Based on Mindlin’s solution [38], we obtain the soil displacements induced by these tunneling loads. Specifically, by applying a unit horizontal force at the depth of \(h\), the displacement of the soil at any point \((x, y, z)\) is calculated as

$$\left\{\begin{array}{l}{g}_{h}=\frac{xy}{16\pi G\left(1-v\right)}\left[\frac{1}{{R}_{1}^{3}}+\frac{3-4v}{{R}_{2}^{3}}-\frac{6hz}{{R}_{2}^{5}}-\frac{4\left(1-v\right)\left(1-2v\right)}{{R}_{2}{\left({R}_{2}+z+h\right)}^{2}}\right]\\ {h}_{h}=\frac{1}{16\pi G\left(1-v\right)}\left[\begin{array}{l}\frac{3-4v}{{R}_{1}}+\frac{1}{{R}_{2}}+\frac{{y}^{2}}{{R}_{1}^{3}}+\frac{\left(3-4v\right){y}^{2}}{{R}_{2}^{3}}+ \frac{2hz}{{R}_{2}^{3}}\left(1-\frac{3{y}^{2}}{{R}_{2}^{2}}\right)+\frac{4\left(1-v\right)\left(1-2v\right)}{{R}_{2}+z+h}\left(1-\frac{{y}^{2}}{{R}_{2}\left({R}_{2}+z+h\right)}\right)\end{array}\right]\\ {\varphi }_{h}=\frac{y}{16\pi G\left(1-v\right)}\left[\frac{z-h}{{R}_{1}^{3}}+\frac{\left(3-4v\right)\left(z-h\right)}{{R}_{2}^{3}}-\frac{6hz\left(z+h\right)}{{R}_{2}^{5}}+\frac{4\left(1-v\right)\left(1-2v\right)}{{R}_{2}\left({R}_{2}+z+h\right)}\right]\end{array}\right.,$$
(9)

where \(G\) is the shear modulus of the soil, \(a\) is the radius of the spherical cavity, and \(h\) is the cover depth of the tunnel centerline. By applying a unit vertical force at the depth of \(h\), the displacement of the soil at any point \((x, y, z)\) is calculated as

$$\left\{\begin{array}{l}{g}_{v}={\varphi }_{h}\frac{x}{y}\\ {h}_{v}={\varphi }_{h}\\ {\varphi }_{v}=\frac{1}{16\pi G\left(1-v\right)}\left[\begin{array}{l}\frac{3-4v}{{R}_{1}}+\frac{8{\left(1-v\right)}^{2}-\left(3-4v\right)}{{R}_{2}}+\frac{{\left(z-h\right)}^{2}}{{R}_{1}^{3}}+ \frac{\left(3-4v\right){\left(z+h\right)}^{2}-2hz}{{R}_{2}^{3}}+\frac{6hz\left(z+h\right)}{{R}_{2}^{5}}\end{array}\right]\end{array},\right.$$
(10)

For the ground displacement caused by the additional support pressure \(p\) of the shield, the ground displacement is obtained by integrating Green’s function on the working surface,

$$\left\{\begin{array}{l}{u}_{x}^{p}={\int}_{0}^{{r}_{h}}{\int}_{0}^{2\pi }p{g}_{h}\left(x-r\mathrm{cos}\theta ,y, z-r\mathrm{sin}\theta \right)d\theta d\xi \\ {u}_{y}^{p}={\int}_{0}^{{r}_{h}}{\int}_{0}^{2\pi }p{h}_{h}\left(x-r\mathrm{cos}\theta ,y, z-r\mathrm{sin}\theta \right)d\theta d\xi \\ {u}_{z}^{p}={\int}_{0}^{{r}_{h}}{\int}_{0}^{2\pi }p{\varphi }_{h}\left(x-r\mathrm{cos}\theta ,y, z-r\mathrm{sin}\theta \right)d\theta d\xi \end{array}\right. ,$$
(11)

where \({r}_{h}\) is the radius of the head of the shield machine. For the ground displacement caused by the shield shell friction \(f\), which is uniformly distributed, according to the geometry of the shield shell, the ground displacement is obtained as

$$\left\{\begin{array}{l}{u}_{x}^{f}={\int}_{0}^{S}{\int}_{0}^{2\pi }f{g}_{h}\left(x-{r}_{h}\mathrm{cos}\theta ,y-\xi , z-{r}_{h}\mathrm{sin}\theta \right)d\theta d\xi \\ {u}_{y}^{f}={\int}_{0}^{S}{\int}_{0}^{2\pi }f{h}_{h}\left(x-{r}_{h}\mathrm{cos}\theta ,y-\xi , z-{r}_{h}\mathrm{sin}\theta \right)d\theta d\xi \\ {u}_{z}^{f}={\int}_{0}^{S}{\int}_{0}^{2\pi }f{\varphi }_{h}\left(x-{r}_{h}\mathrm{cos}\theta ,y-\xi , z-{r}_{h}\mathrm{sin}\theta \right)d\theta d\xi \end{array}\right.,$$
(12)

where \(S\) is the length of the shield machine. For the ground displacement caused by grouting pressure \(q\), it can be obtained by integral according to the segment geometry,

$$\left\{\begin{array}{l}{u}_{x}^{\rm gr}={\int}_{0}^{{l}_{s}}{\int}_{0}^{2\pi }q{g}_{h}\left(x-{r}_{s}\mathrm{cos}\theta ,y-\xi , z-{r}_{s}\mathrm{sin}\theta \right)d\theta d\xi \\ {u}_{y}^{\rm gr}={\int}_{0}^{{l}_{s}}{\int}_{0}^{2\pi }q{h}_{h}\left(x-{r}_{s}\mathrm{cos}\theta ,y-\xi , z-{r}_{s}\mathrm{sin}\theta \right)d\theta d\xi \\ {u}_{z}^{\rm gr}={\int}_{0}^{{l}_{s}}{\int}_{0}^{2\pi }q{\varphi }_{h}\left(x-{r}_{s}\mathrm{cos}\theta ,y-\xi , z-{r}_{s}\mathrm{sin}\theta \right)d\theta d\xi \end{array}\right.,$$
(13)

where \({l}_{s}\) is the width of the segments.

Using the superposition principle, the soil displacements caused by ground loss and tunneling loads are added to obtain the total ground displacement \({\mathbf{U}}^{g}={\left[{u}_{x}^{g},{u}_{y}^{g},{u}_{z}^{g}\right]}^{\mathrm{T}}\),

$$\left\{\begin{array}{l}{u}_{x}^{g}={u}_{x}^{p}+{u}_{x}^{f}+{u}_{x}^{\rm gr}+{u}_{x}^{V}\\ {u}_{y}^{g}={u}_{y}^{p}+{u}_{y}^{f}+{u}_{y}^{\rm gr}+{u}_{y}^{V}\\ {u}_{z}^{g}={u}_{z}^{p}+{u}_{z}^{f}+{u}_{z}^{\rm gr}+{u}_{z}^{V}\end{array}\right.,$$
(14)

2.3 Tunnel displacement estimation based on soil–tunnel interaction

After the estimation of the soil deformation around the existing tunnel based on the SSI model, we attempt to establish the STI model to estimate the deformation of the existing tunnel. The existing tunnel is modeled as a Timoshenko beam. A barrel load around the existing tunnel is assumed.

Following [30, 39], we divide the soil displacement around the existing tunnel into the displacement induced by the interaction between the soil and the existing tunnel, as well as the displacement resulting from the evacuation of the new tunnel. In this way, the displacement of the existing tunnel \({\mathbf{u}}_{{\varvec{t}}}\) is represented by the greenfield soil displacement \({\mathbf{u}}_{s}\) (the displacement of soil induced only by the tunnel evacuation without other influencing factors) as follows:

$${\mathbf{u}}_{{\varvec{t}}}={\left(\mathbf{K}+{\mathbf{K}}_{s}+{\mathbf{K}}_{s}{\mathbf{G}}_{{\varvec{o}}}\mathbf{K}\right)}^{-1}{\mathbf{K}}_{{\varvec{s}}}{\mathbf{u}}_{s},$$
(15)

where \(\mathbf{K}\) is the stiffness matrix of the existing tunnel, \({\mathbf{K}}_{s}\) is the local stiffness matrix of the soil, \({\mathbf{K}}_{s}={\left[\begin{array}{cccc}{g}_{11}& 0& \dots & 0\\ 0& {g}_{22}& \dots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0& 0& \dots & {g}_{nn}\end{array}\right]}^{-1}\) and \({\mathbf{G}}_{{\varvec{o}}}=\left[\begin{array}{cccc}0& {g}_{12}& \dots & {g}_{1n}\\ {g}_{21}& 0& \dots & {g}_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ {g}_{n1}& {g}_{11}& \dots & 0\end{array}\right]\) are obtained from the soil flexibility matrix \(\mathbf{G}=\left[\begin{array}{cccc}{g}_{11}& {g}_{12}& \dots & {g}_{1n}\\ {g}_{21}& {g}_{22}& \dots & {g}_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ {g}_{n1}& {g}_{11}& \dots & {g}_{nn}\end{array}\right]\), where \({g}_{ij}\) represents the soil displacement at node \(i\) induced by the unit load at node \(j\). The soil flexibility matrix \(\mathbf{G}\) is derived as follows:

$${g}_{ij}=\left\{\begin{array}{l}2\Delta u\left({l}_{ij},h\right),i=j\\ \Delta u\left({l}_{ij},h\right)-\Delta u\left({\widetilde{l}}_{ij},h\right),i\ne j\end{array}\right.,$$
(16)

where \(\Delta u\left(\bullet ,\bullet \right)\) is the displacement of a given node, \(h\) is the distance of the tunnel centerline from the ground surface, \({l}_{ij}=\left(\left|i-j\right|+0.5\right)l\), \({\widetilde{l}}_{ij}=\left(\left|i-j\right|+0.5\right)l\), \(l\) is the distance between node \(i\) and node \(j\) along the centerline of the existing tunnel.

2.4 Track displacement prediction

The track bed in the tunnel is usually paved with reinforced concrete monolithic [33]; hence, it is reasonable to assume that the deformation between the tunnel and the track bed located above is consistent. In this subsection, we employ the direct stiffness method to estimate the track displacement through building a finite element model of the track bed, rail, and the connecting parts, as shown in Fig. 4. Here, we model the fasteners that possess the stiffness along \(z-\) and \(y-\) directions.

Fig. 4
figure 4

Model to estimate the track displacement

Full size image

From the above subsection, we obtain the tunnel displacements \({\mathbf{u}}_{k}=\left[{u}_{k,1},{u}_{k,2},\dots {u}_{k,q}\right], k=\mathrm{I},\mathrm{II},\mathrm{ III},\dots\). Since these nodes \(\mathrm{I},\mathrm{II},\mathrm{ III}\) generated by the previous procedures are not guaranteed to be consistent with the locations of fasteners, i.e., nodes \(\mathrm{i},\mathrm{ii},\mathrm{ iii},\dots\), the displacements at these nodes \({\widetilde{\mathbf{u}}}_{k}=\left[{\widetilde{u}}_{k,1},{\widetilde{u}}_{k,2},\dots {\widetilde{u}}_{k,q}\right], k=\mathrm{i},\mathrm{ii},\mathrm{ iii},\dots\) are unknown, but are necessary for the estimation of the track displacement. From assumption (iv), we know that the track-bed displacements are the same as the tunnel displacement. Hence, we use cubic splines to interpolate the displacement values of the existing tunnel over the \(xOy\) plane. In particular, by using cubic splines, the displacement function of the existing tunnel is represented as follows:

$$u\left(y\right)={\sum }_{j=1}^{M+K}{\beta }_{j}{h}_{j}\left(y\right),$$
(17)

where \({h}_{j}={y}^{j-1},j=1,\dots ,M\), \({h}_{M+l}\left(y\right)={\left(y-{\xi }_{l}\right)}_{+}^{M-1},l=1,\dots ,K\). \(M-1\) is the order of piecewise polynomials, and \(K\) is the number of knots. \({\left(y-{\xi }_{l}\right)}_{+}=\left\{\begin{array}{l}0, y<{\xi }_{l}\\ y-{\xi }_{l},y\ge {\xi }_{l}\end{array}\right.\). Here, we use the least squares method to estimate the coefficients and obtain the closed-form solution,

$$\widehat{{\varvec{\upbeta}}}={\left({\mathbf{H}}^{\mathrm{T}}\mathbf{H}\right)}^{-1}{\mathbf{H}}^{\mathrm{T}}y,$$
(18)

\(\mathbf{H}=\left[{\mathbf{h}}_{1}\left(\mathbf{y}\right),{\mathbf{h}}_{2}\left(\mathbf{y}\right),\dots ,{h}_{M+K}\left(\mathbf{y}\right)\right]\), \(\mathbf{y}=\left[{y}_{\mathrm{I}},{y}_{\mathrm{II}},\dots ,{y}_{n/2}\right]\) is the \(n/2\) training samples that associate with the nodes of the tunnel displacement. With the estimated \(\widehat{{\varvec{\upbeta}}}\), we can infer the displacement at the locations of the fasteners \(\mathop {\mathbf{\check{u}}}_{k} =\left[{u}_{1}\left({y}_{k}\right),\dots ,{u}_{q}\left({y}_{k}\right)\right], k=\mathrm{i},\mathrm{ii},\mathrm{iii},\dots\), \(q\) is the nodal degree of freedom.

On this basis, we regard the tunnel deformations \(\mathop {\mathbf{\check{u}}}_{k} , k=\mathrm{i},\mathrm{ii},\mathrm{iii},\dots\) at the locations of the fasteners as displacement boundary conditions, which are applied in such systems. Then, the track displacements \(\widetilde{\mathbf{u}}\) at the locations of the fasteners are estimated based on Hooke's law,

$${\mathbf{K}}_{R}\widetilde{\mathbf{u}}=\mathbf{f},$$
(19)

where \({\mathbf{K}}_{R}\in {\mathbb{R}}^{m\times m}\) is the stiffness matrix of this system, and \(\mathbf{f}\) is the force vector, which are applied to the rails. The master stiffness matrix \({\mathbf{K}}_{R}\) is originally assembled from the element stiffness matrices, \({\mathbf{K}}_{R}=\left[\begin{array}{ccccc}{k}_{11}& {k}_{12}& {k}_{13}& \dots & {k}_{1N}\\ {k}_{21}& {k}_{22}& {k}_{23}& \dots & {k}_{2N}\\ {k}_{31}& {k}_{32}& {k}_{33}& \dots & {k}_{3N}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {k}_{N1}& {k}_{N2}& {k}_{N3}& \dots & {k}_{NN}\end{array}\right]\). Specifically, the vertical \(\mathbf{f}\) is composed of gravity. The gravity is uniformly distributed on the rails. The displacements of the fastener’s nodes that connect with the track bed (i.e., node i, ii, iii, …) are regarded as the displacement boundary conditions and can be applied in the built system, as described in Proposition 1.

Proposition 1. For the estimation of track displacement, suppose the displacement \({\overline{u} }_{t}\) of node \(t\) is given. To impose such a displacement boundary condition, we only need to set \({k}_{it}=0\) for \(i=\mathrm{1,2},\dots ,N\) and \(i\ne t\), and correspondingly set \({f}_{t}={k}_{22}{\overline{u} }_{2}\). For example, if \(t=2\), the master stiffness matrix and the force vector are modified as follows:

$${\mathbf{K}}_{R} = \left[ {\begin{array}{*{20}c} {k_{11} } & 0 & {k_{13} } & \ldots & {k_{1N} } \\ 0 & {k_{22} } & 0 & \ldots & 0 \\ {k_{31} } & 0 & {k_{33} } & \ldots & {k_{3N} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {k_{N1} } & 0 & {k_{N3} } & \ldots & {k_{NN} } \\ \end{array} } \right]\,{\text{and}}\,{\overline{\mathbf{f}}} = \left[ {\begin{array}{*{20}c} {f_{1} - k_{12} \overline{u}_{2} } \\ {k_{22} \overline{u}_{2} } \\ {f_{3} - k_{32} \overline{u}_{2} } \\ \vdots \\ {f_{N} - k_{N2} \overline{u}_{2} } \\ \end{array} } \right]$$
(20)

Based on the modified master stiffness matrix and the modified force vector, Equation (19) can be solved reliably by any existing linear equation solver, and the track displacement is derived. Specifically, after the tunnel deformations \(\mathop {\mathbf{\check{u}}}_{k} , k=\mathrm{i},\mathrm{ii},\mathrm{iii},\dots\) at the locations of the fasteners are estimated using cubic splines, according to the modified master stiffness matrix and the modified force vector, we solve track displacements \(\widetilde{\mathbf{u}}\) at the locations of the fasteners as \(\widetilde{\mathbf{u}}={\left({\mathbf{K}}_{R}\right)}^{-1}\overline{\mathbf{f} }\).

Given the obtained track displacements \(\widetilde{\mathbf{u}}\), we may estimate two main types of track displacements, i.e., vertical displacements and lateral displacements, as shown in Fig. 5. Notably, the lateral track displacement refers to the horizontal displacement (i.e., along the \(y\)-axis) that is perpendicular to the track direction, while the vertical track displacement refers to the vertical displacement (i.e., along the \(z\)-axis) that is perpendicular to the track direction. The irregularity of the considered range \(\left[1,m\right]\) along the track are defined as the maximal track deviation in such a range, which can be mathematically formulated [40] by

$$\left\{\begin{array}{l}{y}_{i}={\widetilde{u}}_{i}-\frac{\left[i{\widetilde{u}}_{m}+\left(n-i\right){\widetilde{u}}_{1}\right]}{n}\\ {y}_{1\sim m}=\mathrm{max}\left({y}_{i}\right)\end{array}\right.,$$
(21)

where \(1\) and \(m\) are the locations of the considered range along the track, \({y}_{i}\) and \({\widetilde{u}}_{i}\) are the relative deviation of the track and the vertical (or lateral) displacements of rails at location \(i\), and \({y}_{1\sim m}\) represents the estimated track irregularity.

Fig. 5
figure 5

Illustration of track displacements induced by the tunnel displacement

Full size image

3 Experiment: engineering case and simulations

In this section, we attempt to evaluate the performance of the proposed three-stage method using a real engineering case and a simulation experiment. First, the project of Beijing Subway Line 16 under-crossing the existing Subway Line 7 is taken as an example, and the construction parameters and the monitoring data of the settlement of the existing tunnel are used to evaluate the performance of the proposed SSI-STI method in estimating the displacement of the existing tunnel induced by the crossing of the shield tunnel. Furthermore, finite element analysis is employed to model the rail–fastener system to verify the proposed TDP method. Finally, the track irregularity of Beijing Subway Line 7 in the real project is analyzed.

3.1 Evaluation of SSI-STI method for the estimation of the tunnel displacement

In order to verify the proposed SSI-STI method, we first introduce the real engineering of Beijing Line 16 undercrossing Subway Line 7. On this basis, we analyze the ground loss and the soil displacement estimated by the proposed method. Then, the effectiveness of the proposed method in estimating the displacement of the existing tunnel is verified by comparison with the monitored settlement data. Finally, the difference in ground loss estimated by the conventional method and the proposed method (considering the effect of the curved segment) are compared.

3.1.1 Project overview

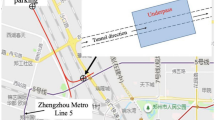
Figure 5 shows the engineering case in the Daguanying–Honglian South Section of Beijing Subway Line 16, where a tunnel at a depth of 20.1~31.3 m was constructed with an earth pressure balance shield. The outer and inner diameters of the shield tunnel are 6.4 m and 5.8 m, respectively as shown in Fig. 6a. The shield tunnel is 3.93 m below the existing tunnel. The diameter of the shield machine is 6.65 m with a length of 10.0 m. Geologically, the crossing section is mainly composed of a gravel layer, conglomerate layer, and mudstone layer, where large boulders are unevenly and randomly distributed in the gravel layer. See Table 1 for more details.

Fig. 6
figure 6

Structural layout of the considered project

Full size image
Table 1 Structural and geometric parameters of the project.
Full size table

3.1.2 Soil deformation estimated by SSI method

First, we analyze the ground movements estimated using the SSI method during shield tunneling, where the parameters are taken from the aforementioned project of interest. The ground displacements induced by the main factors are shown in Fig. 7, where three directions represent the horizontal, shield advancing, and vertical directions, respectively. The ground loss causes a settlement trough extending behind the shield machine, while the other factors generally produce spatial protrusions, as shown in Fig. 7b–d. From the results, we observe that the maximum displacements caused by the ground loss, face support pressure, shell friction, and grouting pressure are 1.2 mm, 0.006 mm, 0.06 mm, and 0.13 mm, respectively. Compared with other factors, the ground loss and grouting force are significant in inducing larger ground movements.

Fig. 7
figure 7

Vertical ground displacement induced by four factors

Full size image

Further, Fig. 8 shows the ground displacement induced by the major factors, i.e., ground loss and grouting pressure.

Fig. 8
figure 8

Horizontal ground displacements induced by a ground loss and b grouting pressure

Full size image

From Fig. 8a, it can be seen that the soil displacement along the y-direction caused by ground loss decreases with the increase in the distance from the tunnel centerline in the vertical direction, and the peak value appears near the centerline, which is consistent with the practice. Figure 8b shows the soil displacement along the y-direction caused by the grounding pressure. The soil displacement decreases with the increase in the distance from the centerline in both vertical and horizontal directions.

3.1.3 Result comparison and analysis

In order to verify the effectiveness of the proposed SSI-STI method, the tunnel settlement estimated by SSI-STI method is compared with the in situ settlement monitored during the construction of Beijing Metro Line 16. First of all, we describe the experimental procedure in detail. Then, the effectiveness of the method is verified by comparing the predicted tunnel settlement with the actual settlement of the track bed. Furthermore, we compare the prediction errors of the tunnel settlements estimated by the conventional method and the proposed method. Firstly, we introduce the procedure to predict the settlement of the existing tunnel during shield construction using the SSI-STI method, as follows:

  1. i.

    Establish the coordinate system for the case of interest, where the origin is selected as the point on the ground surface that corresponds to the endpoint of the new tunnel centerline, as shown in Fig. 9.

  2. ii.

    Coordinate representation of the tunnel centerline of the existing tunnel and the selected points on the tunnel surface.

  3. iii.

    With the process of shield tunneling, employ the SSI method to estimate the soil displacement of the selected points of the existing tunnel surface, i.e., the greenfield displacement.

  4. iv.

    Based on the STI method, predict the displacement of the existing tunnel.

Fig. 9
figure 9

Coordinate system for the scenario of a shield tunnel passing through the existing tunnel

Full size image

Before crossing the area of the existing tunnel, a 100 m testing region was scheduled to determine reasonable construction parameters, which are shown in Table 2. At the same time, some sensors are deployed at locations of \({\mathbf{x}}_{m}=\left(-18.25, -9.8, -1.35, 5.3\right)\) to measure the settlements of the existing tunnel every 0.5h.

Table 2 Key parameters of the shield machine during tunneling
Full size table

With these parameters, the proposed SSI-STI method is applied to predict the settlement of the existing tunnel at measurement points, and the predicted results are compared with the in situ measurements, as shown in Fig. 10. Figure 10a, b shows the comparisons from different views. In the two graphs, the curved surfaces represent the prediction of the tunnel settlements at different points, and the scatters represent the actual measurements of the settlements. The results show that the model can reasonably predict the settlement of the existing tunnel. The maximum settlement of the tunnel is 1.135, appearing at \(\widehat{x}=2.405\), which is close to the actual maximum settlement of 1.044 at \(x=1.69\). Among the results, the predictions of tunnel settlements at locations \(x<0\) are closer to the actual measurements than those at locations \(x>0\). This is because the right side of the tunnel is connected to the station, where the estimation may be affected by different structures.

Fig. 10
figure 10

Comparison between the predictions by the proposed method and the actual measurements during the process of shield tunneling. Among them, a and b are comparisons under different views

Full size image

In order to show the superiority of the proposed method during shield tunneling over curved segments, we take the conventional method that only considers shield tunneling in straight segments as the benchmark method and then compare the prediction errors of the proposed and benchmark methods. Here, the friction coefficient between the shield and the soil is related to the soil parameters. Since the crossing section of shield tunneling consists of sandy soil and gravels, we take the frictional coefficient between the shield and soil as 0.3. Specifically, the benchmark method employs an equivalent ground loss parameter (EGLP), which has been discussed in [41]. In this method, EGLP is defined using an empirical formula as follows:

$$u_{\varepsilon } \left( {x,z} \right) = \frac{{4gR + g^{2} }}{{4R^{2} }}\exp \left( { - \frac{{1.38x^{2} }}{{\left( {H + R} \right)}} - \frac{{0.69z^{2} }}{{H^{2} }}} \right),\,V = \frac{{4gR + g^{2} }}{{4R^{2} }}$$
(22)

where \(R\) is the radius of the new tunnel, \(g\) is the gap parameter, \(H\) is the cover depth of the shield tunnel, and \(V\) is the equivalent ground loss ratio (EGLP). Based on EGLP, the induced displacement at the location \(\left(x,y,z\right)\) in the space is given by

$$\left\{\begin{array}{l}{u}_{x}^{V}={\int}_{-\infty}^{0}2\pi R{u}_{\varepsilon }\left(x,z\right){f}_{s}\left(x-\eta ,y-\xi ,z\right)d\xi \\ {u}_{y}^{V}={\int}_{-\infty}^{0}2\pi R{u}_{\varepsilon }\left(x,z\right){g}_{s}\left(x-\eta ,y-\xi ,z\right)d\xi \\ {u}_{y}^{V}={\int}_{-\infty}^{0}2\pi R{u}_{\varepsilon }\left(x,z\right){h}_{s}\left(x-\eta ,y-\xi ,z\right)d\xi \end{array}\right.,$$
(23)

In this experiment, the parameter \(V\) takes the value of 1.3%, which is recommended by [41]. Other basic parameters used in the benchmark method are the same as in the proposed method, such as the diameter of the shield face, radius of the shield tunnel, Poisson’s ratio, and so on, as shown in Tables 1 and 2. The results of the proposed method and the benchmark method are shown in Fig. 11. From the results, we observe that our proposed method outperforms the benchmark method in terms of estimation error under the curved segments with a 400 m radius. For example, in such a scenario, the estimation errors resulting from the proposed method are distributed with a mean of \(-0.0687\), a medium of \(-0.0386\), and a standard deviation of \(0.1361\), while those resulting from the benchmark method are distributed with a mean of \(-0.0978\), a medium of \(-0.0527\), and a standard deviation of \(0.1570\). This is because the proposed model that considers the curved scenario may calculate the ground loss more accurately, which then facilitates the estimation of soil displacement, and thus predicts the settlements of the existing tunnel more accurately.

Fig. 11
figure 11

Comparison of the prediction errors on the tunnel settlements resulting from the benchmark and proposed methods

Full size image

3.2 Evaluation of the proposed TDP method based on FEM

In order to verify the effectiveness of the proposed TDP method, we build a finite element model (FEM) of the rail–fastener system, and then compare the track displacement predicted by the TDP method with that of FEM. Specifically, the rail of length 30 m is first modeled using the finite element method. The weight, density, Poisson’s ratio and elastic modulus of the rail are 60 kg/m, 7860 kg/\({\mathrm{m}}^{3}\), 0.25, and 2 × 105 MPa, respectively. By considering the characteristics of the rail and the lateral force of the fasteners, we model the rail as a constant cross-section cantilever beam and the fastener as a spring with one end constrained. The area and inertia moment of the cross-section are 8918 \({\mathrm{mm}}^{2}\) and 7562863 \({\mathrm{mm}}^{4}\). We also build springs every 0.6 m to model the fasteners that connect the rails with the track bed. We mesh the rail with 100 mm grids, resulting in 301 nodes that associate with the rail. Each node has six degrees of freedom including the x-, y- and z-directions and the rotation directions \({\theta }_{x}\) , \({\theta }_{y}\), \({\theta }_{z}\). The built model is shown in Fig. 12. Tunnel deformations are simulated by applying fixed constraints at the ends of the rail and displacement boundary conditions at the ends of some fastener springs. Figure 13 shows the deformation cloud of one special case.

Fig. 12
figure 12

Finite element model of the rail–fastener system

Full size image
Fig. 13
figure 13

Track displacement under a randomly specified DBC

Full size image

To evaluate the effectiveness of the proposed method, we apply the same boundary conditions and then compare the track displacement estimated by the proposed method with that output by FEM. In this study, in order to examine the performance of the proposed method along both the horizontal and vertical directions, we conduct two independent experiments by applying different displacement boundary conditions, respectively: (a) DBC 1: 1 mm displacement along the y-direction at node 310 and 3 mm displacement along the y-direction at node 330; (b) DBC 2: −3 mm displacement along the z-direction at node 310 and –1 mm displacement along the z-direction at node 330. Figure 14 shows the track displacements derived under these two DBC scenarios. We observe that the proposed method estimates the track displacements well, which provide a reliable basis for the calculation of track irregularity.

Fig. 14
figure 14

Estimation errors of TDP compared with that of FEM

Full size image

To further validate the superiority of the proposed method, we then compare the performance of our proposed method with the linear regression (LR) model. To train the LR model, we first generate the experimental data based on the FEM of the rail. Specifically, we randomly produce samples of the tunnel deformation \(\mathop {\mathbf{\check{u}}}^{(i)} \in {\mathbb{R}}^{{q \times K}} _{k}\) at the locations of the fasteners based on Latin hypercube sampling, where \(q\) is the nodal degree of freedom and \(K\) is the number of fasteners in the considered model. To reduce the complexity of the regression model, here we take \(q=1\) and \(K=4\). For each \(\mathop {\mathbf{u}}\limits^{{\vee }(i)}\), we run the built FEM to produce the track displacements \({\widetilde{\mathbf{u}}}^{\left(i\right)}\in {\mathbb{R}}^{m}\), such that the complete samples \(\left( {\mathbf{\check{u}}}^{(i)} ,{\mathbf{\tilde{u}}}^{{\left( i \right)}} \right)\) are obtained. Then, we divide the obtained samples into the training set \({\mathcal{D}}^{\rm tr}\) and the testing set \({\mathcal{D}}^{\rm ts}\). Based on the training set, we train the linear model \({\mathbf{\tilde{u}}} = f_{\rm {LR}} \left( {\mathop {\mathbf{u}}\limits^{ \vee } ;{\mathbf{B}}} \right)\) and then estimate the track displacements of each sample in \({\mathcal{D}}^{\rm ts}\), obtaining \(\mathop {\mathbf{\check{u}}}^{(i)}_{\rm {LR}}\). Since the proposed method is free of training, we apply the TDP to directly estimate the track displacements of each sample in \({\mathcal{D}}^{\rm ts}\), obtaining \(\mathop {\mathbf{\check{u}}}^{(i)}_{\rm {RPD}}\). Finally, we calculate the estimation errors of each method based on the mean absolute error (MAE), recorded as \({\varepsilon }_{s}^{\left(i\right)}, j=1,\dots ,\left|{\mathcal{D}}^{\rm ts}\right|, s\in \left\{LR,RPD\right\}\). Then, the mean \({\mu }_{\rm MAE}\) and standard deviation \({\sigma }_{\rm MAE}\) of the estimation errors for each method are derived. Based on this procedure, we conduct experiments for each \(m\in \left\{\mathrm{4,8},\mathrm{10,12}\right\}\) and the results are presented in Table 3. From the results, we observe that the proposed method achieves smaller errors under every setting than the linear model, which validates the superiority of the proposed RPD in estimating the track displacements.

Table 3 Comparison of the estimation errors of the track displacements estimated by each method (\({\mu }_{\rm MAE}\pm {\sigma }_{\rm MAE}\)).
Full size table

3.3 Track irregularity analysis for the considered real case

In this subsection, we estimate and analyze the track displacements for the case of Beijing Line 16. First, we evaluate the interpolation performance of cubic splines. Assuming the measurements at monitoring points are given, we use cubic splines to interpolate the values of unknown points, and the results for both vertical and horizontal displacements are shown in Fig. 15. From the results, we observe that although only limited measurements are available, cubic splines perform quite well in interpolating the displacement at most regions.

Fig. 15
figure 15

Performance of cubic splines for the interpolation of the tunnel displacement

Full size image

After the unknown displacements are interpolated, we then obtain the tunnel displacement (i.e., the displacement of the track bed) at the locations of the fasteners. On this basis, we apply these DBCs on the built rail–fastener system. Here, the weight, density, Poisson’s ratio, and elastic modulus of the switch rails are 60 kg/m, 7860 kg/\({\mathrm{m}}^{3}\), 0.25, and 2 × 105MPa, respectively. The inertia moment of the rail at any cross-section is 756.3 \(c{m}^{4}\). The stiffness of the fastener is \(7.5\times {10}^{6}\). The track displacement is solved based on the direct stiffness method, and the results are shown in Fig. 16. We observe that the track displacement is slightly smaller than that of the tunnel. The maximums of vertical and horizontal track displacements are 1.0928 mm and 0.2495mm, respectively which indicates that the track irregularity is slight.

Fig. 16
figure 16

Track displacements estimated based on the proposed method.

Full size image

4 Conclusion

In this article, we consider the estimation of the track displacement during the shield tunnel crossing through the existing tunnel as three subproblems: the estimation of soil displacement during the shield tunneling, the estimation of tunnel deformation induced by the soil displacement, and the estimation of the track displacement caused by the tunnel deformation. Thereafter, a three-stage method for the estimation of the track displacement is proposed. Then, we establish the SSI model during the curved shield tunneling, STI model, and tunnel–rail interaction model. Finally, based on the estimated track displacements, the track irregularity is calculated. The main contributions of this work lie in the following:

  1. (i)

    Integrated model for predicting track irregularity during shield construction: By analyzing the response of shield tunneling, we consider the track response during construction as a three-stage process among four elements, i.e., shield machine—soil—existing tunnel—rail. On this basis, three stages are modeled separately, which ultimately provides an accurate prediction for the track displacement.

  2. (ii)

    Estimation of ground loss and ground displacement during curved shield tunneling: Most conventional methods only consider the estimation of ground displacement under the scenario of shield tunneling over a straight segment, which may not be accurate when applied to the scenario of curved tunneling. Hence, we propose a novel method for the estimation of ground loss and ground displacement during curved shield tunning, which improves the accuracy of the ground loss estimation in the curved scenario and then improves the prediction performance of the ground displacement and the deformation of the existing tunnel.

  3. (iii)

    Model for the estimation of track displacement and track irregularity: Due to the unknown displacements of the tunnel at the locations of fasteners, the displacement boundary conditions (DBCs) cannot be applied directly. To tackle this issue, cubic splines are employed to interpolate the unknown displacements of the existing tunnel. On this basis, the track bed–rail interaction is modeled using the direct stiffness method, and the track displacement as well as the track irregularity are further estimated.

Based on the settlement data collected in a real engineering project, the effectiveness of the proposed SSI-STI method in estimating the tunnel displacement is verified. Then, with the finite element simulation, we verify the accuracy of the proposed TDP method in estimating the track displacement. The experimental results show that the proposed three-stage method provides a feasible solution for the estimation of track irregularity during shield tunneling.

An interesting future topic is to consider the effects of train loads since soil compaction will be the main factor inducing ground displacement after the shield tunnel crosses the existing tunnel, where the dynamic train track–soil interaction model is the key task to be studied.