1 Introduction

It is well known that the mechanical properties of nanosized structures differ significantly from those of macroscopic ones [1,2,3]. In order to properly simulate the mechanical response of the nanomaterials and small-scale structures, generalized (extended) theories have been developed [4]. Mathematical theories of non-classical mechanics can be regarded as one of two kinds, i.e., either the higher-order or the higher-grade continua. Within the framework of the higher-order continua, the number of degrees of freedom is extended which is the case for the micropolar [5,6,7] and micromorphic [8,9,10] continua. Within the framework of the higher-grade continua, the degrees of freedom are kept identical but the higher-order gradients of some physical quantities (e.g., the displacement vector or the strain tensor, the electric field vector or the polarization vector) are involved into the space of internal energy density function. Mindlin’s strain gradient theory [11, 12] belongs to this group. This theory includes the higher-order gradients of the displacement vector into the space of constitutive parameters. Note that the response of electric polarization to non-uniform mechanical deformation (i.e., the strain gradient) is referred to as the flexoelectric effect [13]. Therefore, the mathematical models of dielectrics that consider the effect of strain gradients on electric polarization can be regarded as theories with flexoelectricity [13,14,15].

Another higher-grade theory of dielectrics incorporates the gradients of electrical variables into the space of constitutive parameters. This theory can also be subdivided into two frameworks: polarization gradient theories [16] and electric field gradient theories [17]. Kafadar [18] suggested the advanced theory of dielectrics with electric quadrupoles. Since the electric field gradients are conjugated with electric quadrupoles, theories with electric field gradients sometimes are referred to as theories with electric quadrupoles. Besides the classical constants, the mentioned non-classical theories include additional parameters related to the material microstructure, thus having a length dimension (i.e., the length-scale parameters).

Eringen developed the extended continuum mechanics by introducing the additional structural length-scale parameter which verbalizes the long-range forces between atoms. This group of theories rests upon the non-local (functional-type) constitutive equations and can be referred to as non-local models of media with spatial dispersion. The non-local field theory has been developed in [19,20,21]. Hence, much investigation effort is directed toward the elaboration of non-classical theories of mechanics. More detail can be found in [7, 20, 22,23,24,25,26,27,28].

Recent studies [29, 30] confirmed the possibility of developing well-posed size-dependent models by considering the effect of local mass displacement (LMD) and its coupling with mechanical deformation, electric polarization, and heat conduction. The LMD is concerned with the changes in material microstructure described by the mass flux of non-diffusive and non-convective origin. For the first time, such mass flux was introduced by Burak [31] for thermo-elastic solids. The advanced theories of continuum mechanics concerning the effect of LMS on material behavior are referred to as the local gradient theories [28]. Recent investigations showed that the local gradient models can provide another effective way to study the coupled fields and processes in nanomechanics [29, 30, 32,33,34,35].

Micro/nano-electro-mechanical structures are widely used in modern engineering applications [36, 37]. Piezoelectric and flexoelectric material properties are crucial for the overall performance of such structures [23, 24]. In the flexoelectric effect, the following phenomena can be observed: the static and dynamic bulk flexoelectric effects, the surface flexoelectric effect, and surface piezoelectricity [23, 38]. The dynamic flexoelectric effect is associated with the polarization response to the accelerated motion of a medium [23]. The phenomenological theory of the dynamic flexoelectric effect was developed by Tagantsev [39, 40] and Kvasov and Tagantsev [38].

The literature survey reveals that large numbers of investigations are mainly focused on studies of static flexoelectricity, surface flexoelectric, and piezoelectric effects [25, 41,42,43]. However, the influence of the flexodynamic effect and polarization inertia on the size-dependent behavior of polarized structures is not sufficiently analyzed. To the best of our knowledge, there are a small number of works where the electromechanical coupling response of piezoelectric nanostructures with the static and dynamic flexoelectric effects was investigated [44,45,46,47,48,49,50,51]. These studies showed that the dynamic flexoelectric effect is size-dependent and more pronounced for the higher vibration modes. It was also proved that the accelerated motion of a linear dielectric causes its polarization. In wave problems, it is important to consider the effect of polarization inertia [52]. However, the analysis of the polarization inertia effect on coupled fields in dielectrics is still scarce [46, 49, 52,53,54]. This fact was the main motivation for the current study which is focused on the role of both flexodynamic and polarization inertia effects in dielectrics. Thereby, the objective of the present work is to develop the local gradient theory of polarized media. In this study, to further shed light on the electro-thermo-mechanical coupling at the nanoscale, a complete size-dependent model of polarized non-ferromagnetic media is formulated with the consideration of the LMD, non-local heat conduction, polarization inertia, and flexodynamic effect.

The structure of the paper is as follows. In Sect. 2, the entropy balance, induced mass balance, and Maxwell equations are formulated for a local gradient electro-elastic continuum. Making use of the axiom of objectivity, the mass conservation law and the generalized balance of linear momentum are rigorously derived from the total energy balance law. The gradient-type constitutive equations, non-local kinematic expressions for heat flux, and an additional differential equation linking the polarization, displacement, and local and macroscopic electric fields are derived in Sect. 3. In Sect. 4, the linear constitutive equations and governing equations are specified for centrosymmetric isotropic local gradient electro-elastic media incorporating non-classical Fourier law, polarization inertia, and flexodynamic effect. In Sect. 5, the plane wave propagation in unbounded polarized media is discussed. Concluding remarks are addressed in the final section of the paper.

2 Balance equations

Herein, we formulate a higher-grade continuum model of dielectrics that accounts for microstructural effects by means of non-convective and non-diffusive mass flux. We shall work out a mathematical model which considers the interaction between the process of deformation of the body described by the displacement vector and the stress field, the thermal process described by the temperature field, the electromagnetic processes characterized by the electromagnetic field vectors, and the process of microstructure changes characterized by non-diffusive and non-convective mass flux. The local gradient theory of dielectrics will be generalized to include the non-local heat conduction law, flexodynamic, and polarization inertia effects. In this section, on the basis of non-equilibrium thermodynamics and the Maxwell equations, the balance laws for the electro-thermo-elastic non-ferromagnetic continuum will be presented.

Consider a deformable polarized body that occupies a domain \(\left( {{V}'} \right) \) bounded by a smooth surface \(\left( {{\Sigma }'} \right) \). The body is thermo-elastic and subjected to mechanical, electromagnetic, and thermal impacts. In response to external loads, the body can deform, transfer heat, and polarize. The changes in the material microstructure as well as their influence on the coupled fields in the solid are also addressed in the mathematical model. We relate these changes with the LMD. The mechanical motion, heat conduction, the changes in the material microstructure, and electric charges are regarded as the reason for all the objective physical phenomena in the solid. All the fields characterizing these phenomena are to comply with the fundamental laws of continuum physics, including the basic laws of electrodynamics and the first and second laws of thermodynamics.

2.1 Entropy balance equation

The process of heat conduction is characterized by absolute temperature T, entropy S, heat flux \({{\textbf {J}}}^{q}=\left\{ {J_{i}^{q} } \right\} \), entropy flux \({{\textbf {J}}}^{s}=\left\{ {J_{i}^{s} } \right\} \), and higher-grade flux \({{\textbf {Q}}}=\left\{ {Q_{ij} } \right\} \) (the flux of the heat flux). Here, indices i and j span the range {1, 2, 3}. Different generalizations of the heat conduction equation have been studied in the literature [55,56,57]. The generalized fractional-order thermo-elastic models are developed in [58, 59]. The various formats of the heat conduction laws were discussed in [60]. Herein, the following phenomenological expression

$$\begin{aligned} J_{i}^{s} =\frac{1}{T}J_{i}^{q} +J_{j}^{q} Q_{ij} \end{aligned}$$
(1)

is adopted for the entropy flux [56]. Here, the repeated indices within the term denote summation from 1 to 3. In [55], the second-order symmetric tensor \({{\textbf {Q}}}\) is interpreted as an internal variable because it is not directly measurable quantity.

In body \(\left( {V_{*} } \right) \), consider an arbitrary volume \(\left( V \right) \) bounded by the closed surface \(\left( \Sigma \right) \). For volume \(\left( V \right) \), the general form of the entropy balance equation reads as [61]:

(2)

Here, t denotes the time variable, \({{\textbf {v}}}=\{v_{i} \}\) is a velocity vector, \(\upsigma _{s} \) denotes the entropy production, \(\uprho \) is the mass density, \(\Re \) denotes the distributed thermal sources, and \({{\textbf {n}}}=\{n_{i} \}\) is the unit normal vector for surface \((\Sigma )\).

By using the divergence theorem to transform the surface integral into the volumetric one, Eq. (2) yields

$$\begin{aligned} \frac{d}{dt}\int \limits _{(V)} {S\,dV} =\int \limits _{(V)} {\left[ {-\nabla _{i} \left( {J_{i}^{s} +Sv_{i} } \right) +\upsigma _{s} +\uprho \frac{\Re }{T}} \right] dV}, \end{aligned}$$
(3)

where \({\nabla } =\left\{ {\nabla _{i} } \right\} \) is the differential nabla operator. Since \(\left( V \right) \) is an arbitrary volume, the latter formula yields the following local form of the entropy balance equation:

$$\begin{aligned} \frac{\partial S}{\partial t}=-\nabla _{i} J_{i}^{s} -\nabla _{i} \left( {Sv_{i} } \right) +\upsigma _{s} +\uprho \frac{\Re }{T}. \end{aligned}$$

This equation can be rewritten as:

$$\begin{aligned} \frac{dS}{dt}=-S\nabla _{i} v_{i} -\nabla _{i} J_{i}^{s} +\upsigma _{s} +\uprho \frac{\Re }{T}, \end{aligned}$$
(4)

where \({d...}/{d\,t}={\partial ...}/{\partial t\,}+v_{i} \nabla _{i}...\) denotes the substantive derivative. Phenomenological expression (1) and balance equation (4) allow us to represent the entropy balance equation (4) in the form as follows:

$$\begin{aligned} \frac{dS}{dt}=-S\nabla _{i} v_{i} -\frac{1}{T}\nabla _{i} J_{i}^{q} -\nabla _{i} \left( {\frac{1}{T}} \right) J_{i}^{q} -\nabla _{j} \left( {J_{i}^{q} } \right) Q_{ij} -J_{i}^{q} \left( {\nabla _{j} Q_{ji} } \right) +\upsigma _{s} +\frac{\uprho }{T}\Re . \end{aligned}$$
(5)

2.2 Electromagnetic field equations

The basic laws of electrodynamics (Maxwell equations) in a differential form can be written as [20, 62]:

$$\begin{aligned}{} & {} \hbox {Gauss--Coulomb law:} \qquad \qquad \qquad \qquad \nabla _{i} D_{i} =\uprho _{e}, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \hbox {Gauss--Faraday law:} \qquad \qquad \qquad \qquad \nabla _{i} B_{i} =0, \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \hbox {Faraday law:} \qquad \qquad \qquad \qquad \qquad e_{ijk} \nabla _{j} E_{k} =-\frac{\partial B_{i} }{\partial t}, \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \hbox {Maxwell--Amp}\grave{e}\hbox {re law:} \qquad \qquad \qquad \qquad e_{ijk} \nabla _{j} H_{k} =J_{i}^{e} +\upvarepsilon _{0} \frac{\partial E_{i} }{\partial t}+\frac{\partial \Pi _{i}^{e}}{\partial t}. \end{aligned}$$
(9)

Here, \({{\textbf {E}}}=\{E_{i} \}\) and \({{\textbf {H}}}=\{H_{i} \}\) are the electric and the magnetic fields vectors, \({{\textbf {D}}}=\{D_{i} \}\) and \({{\textbf {B}}}=\left\{ {B_{i} } \right\} \) are the electric and magnetic induction vectors, \(\varvec{\Pi }^{e}=\{{\Pi } _{i}^{e} \}\) is the polarization vector (i.e., the local displacement of electric charges), \({{\textbf {J}}}^{e}=\{J_{i}^{e} \}\) denotes the density of the electric current, related to the displacement of free charges (the conduction and convection currents), \(\uprho _{e} \) is a density of free electric charge, \(\upvarepsilon _{0} \) denotes the electric constant (\(\upvarepsilon _{0} =8.85\times 10^{-12\,}\,\text{ F/m})\), and \(e_{ijk} \) is the permutation symbol, which is zero when two indices are equal; otherwise, it possesses the properties: \(e_{123} =e_{231} =e_{312} =1\) and \(e_{132} =e_{213} =e_{321} =-1\). Here, the indices i, j and k span the range {1, 2, 3}, while superscript ‘e’ means ‘electric.’

Consider non-ferromagnetic perfect dielectric materials for which free electric charges, electric current, and magnetization are absent. In such materials, the constitutive relations for magnetic and electric inductions are the following [62]:

$$\begin{aligned} B_{i} =\upmu _{0} H_{i}, D_{i} =\upvarepsilon _{0} E_{i} +\Pi _{i}^{e}, \end{aligned}$$
(10)

where \(\upmu _{0} \) is the magnetic constant. A law of the conservation of energy of an electromagnetic field can be derived from Maxwell’s equations (6)–(9) [28]. The conservation law of electromagnetic field energy is given as [28]:

$$\begin{aligned} \frac{\partial U_{e} }{\partial t}+\nabla _{i} S_{i}^{e} +\frac{\partial \Pi _{i}^{e} }{\partial t}E_{i} =0. \end{aligned}$$
(11)

Here, \(U_{e} ={\left( {\upvarepsilon _{0} E_{i}^{2} +\upmu _{0} H_{i}^{2} } \right) } / 2\) is the electromagnetic energy density [63], \({{\textbf {S}}}^{e}={{\textbf {E}}}\times {{\textbf {H}}}\), \({{\textbf {S}}}^{e}=\left\{ {S_{i}^{e} } \right\} \) is the energy flux of an electromagnetic field (i.e., the Poynting vector) [63], and ‘\(\times \)’ stands for the vector product.

The last term in Eq. (11) describes the influence of the electromagnetic field on a substance, which together with the field present a single material system. We rewrite this term in such a way that it contains the electric field vector \({{\textbf {E}}}^{*}\) and polarization \(\varvec{\Pi }^{e*}\) in the reference frame of the center of mass moving with the velocity \({{\textbf {v}}}\) relatively to the laboratory reference frame. In this co-moving frame, the mentioned vectors are transformed according to the relations: \({{\textbf {E}}}^{*}={{\textbf {E}}}+{{\textbf {v}}}\times {{\textbf {B}}}\), \(\varvec{\Pi }^{e*}=\varvec{\Pi }^{e}\) [20, 62, 63]. Using these formulae and the identity: \({{\textbf {a}}}\cdot ({{\textbf {b}}}\times {{\textbf {c}}})={{\textbf {b}}}\cdot ({{\textbf {c}}}\times {{\textbf {a}}})={{\textbf {c}}}\cdot ({{\textbf {a}}}\times {{\textbf {b}}})\), the balance law (11) can be rewritten as follows:

$$\begin{aligned} \frac{\partial U_{e} }{\partial t}+\nabla _{i} S_{i}^{e} +\frac{\partial \left( {\uprho \uppi _{i}^{e} } \right) }{\partial t}E_{i}^{*} +e_{ijk} v_{i} \frac{\partial \left( {\uprho \uppi _{j}^{e} } \right) }{\partial t}B_{k} =0, \end{aligned}$$
(12)

where \(\uppi _{i}^{e} =\Pi _{i}^{e} /\uprho \).

2.3 Local displacement of mass

In continuum mechanics, a material body is modeled as a continuum comprised of an infinite number of small material particles (representative elements). Within the framework of the classical theories, each material particle is considered as a geometric point (mass center of the element), which can only undergo the translation motion, i.e., convective displacement of the mass center. The representative element (material point) is characterized by geometric properties (location and translation motion) and some physical characteristics (mass density, electric charge density, etc.). Thus, classical theories fail to capture the effect of microstructure on the behavior of elastic solids.

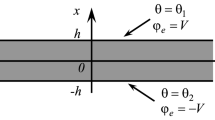
The considered here mathematical model takes into account the internal motion within the interior of a representative element of the body and describes the above changes in material microstructure by a non-convective and non-diffusive mass flux \({{\textbf {J}}}^{ms}\). To take into account the effect of the material microstructure, we assume that the displacement of the mass center of a representative element \(\left( V \right) \) may be induced not only by a convective displacement of this element as a rigid entity but also by the changes of the relative positions of microparticles within this element. Such displacement is referred to as a local displacement of mass. Note that the changes in material structure can be observed, for instance, in the body near-surface/interface regions (see Fig. 1). Due to violation of the atom force balance, the particles located on the body surface are in different conditions than their bulk counterparts. This results in distinct properties of the solid near-surface/interface and bulk regions. The non-convective and non-diffusive mass flux \({{\textbf {J}}}^{ms}\) characterizes the mentioned changes in microstructure [31]. We link this mass flux with the process of the LMD [29].

The physical quantities associated with the LMD have been introduced in [29]. The vector of the local displacement of mass \(\varvec{\Pi }^{m}=\{{\Pi } _{i}^{m} \}\) and vector of mass flux \({{\textbf {J}}}^{ms}=\{J_{i}^{ms} \}\) caused by the changing in material structure are related by the expression:

$$\begin{aligned} J_{i}^{ms} =\frac{\partial \Pi _{i}^{m} }{\partial t}. \end{aligned}$$
(13)
Fig. 1
figure 1

A sketch of the cross section of a free infinite layer that shows the different material properties close to the body surface and bulk regions. The change of the mass center of a representative element close to the surface is described with the non-diffusive and non-convective mass flux \(\varvec{{\uppi }}_{m}\) due to material microstructure changes in the vicinity of the body surface

Full size image

Here, \(i\in \left\{ {1,2,3} \right\} \), and superscripts ‘ms’ and ‘m’ mean ‘material structure’ and ‘mass.’ Via the integral expression

$$\begin{aligned} \int \limits _{(V)} {\varvec{{\Pi }}^{m}dV=\int \limits _{(V)} {\uprho _{m\pi } \,{{{\textbf {r}}}}} } \,dV, \end{aligned}$$
(14)

the scalar quantity \(\uprho _{m\uppi } \) (with a dimension of mass density) was introduced [29]. In Eq. (14), r is the position vector of a material point. By analogy with the electrodynamics, where the density of induced electric charge \(\uprho _{e\uppi } \) was introduced by a similar relationship (see, for example, [63]), the scalar quantity \(\uprho _{m\uppi } \) was referred to as the density of induced mass. From integral relation (14), the expression

$$\begin{aligned} \uprho _{m\uppi } =-\nabla _{i} \Pi _{i}^{m} \end{aligned}$$
(15)

can be obtained [28]. By differentiating Eq. (15) with respect to time and taking formula (13) into account, one can obtain the differential equation which has the form of the conservation law of the induced mass:

$$\begin{aligned} \frac{\partial \uprho _{m\uppi } }{\partial t}+\nabla _{i} J_{i}^{ms} =0. \end{aligned}$$
(16)

2.4 Conservation of energy for a system ‘material body—electromagnetic field’

The polarized elastic body is embedded into an ambient electromagnetic field. The total energy \(\mathscr {E}\) of the system ‘solid–electromagnetic field’ is the sum of the internal energy, the kinetic energy, and the energy of the electromagnetic field: \(\mathscr {E}=\uprho u+U_{e} +K\). Following [23], assume that besides the classical inertia terms, the expression for the density of kinetic energy Kincludes the terms, proportional to \(\frac{d{\mathbf{{\varvec{\uppi }}}}^{e}}{dt}\otimes \frac{d\mathbf{{{\varvec{\uppi }}}}^{e}}{dt}\) and \({{{\textbf {v}}}}\otimes \frac{d\mathbf{{{\varvec{\uppi }}}}^{e}}{dt}\) (\(\otimes \) is the dyadic product), i.e.:

$$\begin{aligned} K=\uprho \left( {\frac{1}{2}v_{i}^{2} +\frac{1}{2}\upgamma _{ij} \frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}+M_{ij} v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) . \end{aligned}$$
(17)

Here, \(\upgamma _{ij} \) are the phenomenological coefficients controlling the dynamics of polarization and \(M_{ij} \) are the components of the flexodynamic tensor [38]. In (17), the second term represents the polarization kinetic energy, while the mixed term \(\uprho M_{ij} v_{i} \frac{d\uppi ^{e}_{j} }{dt}\) is related to the dynamic flexoelectric effect. Hence, for an arbitrary moment of time, the total energy \(\mathscr {E}\) can be given as:

$$\begin{aligned} \mathscr {E}=\uprho u+U_{e} +\frac{1}{2}\uprho v_{k}^{2} +\frac{1}{2}\uprho \upgamma _{ij} \frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}+\uprho M_{ij} v_{i} \frac{d\uppi _{j}^{e} }{dt}. \end{aligned}$$

The change in the total energy \(\mathscr {E}\) over a certain body volume \(\left( V \right) \) can be caused by two types of factors, i.e., the sources produced within the considered body volume, and the energy transfer across the boundaries of this domain [61]. Within the considered mathematical model of dielectrics, the change in the total energy may be caused by the following factors: (i)  the convective energy transport \((\uprho u+K)v_{i} \) through the surface \(\left( \Sigma \right) \), (ii) the energy flux due to the mechanical work of the surface forces, i.e., \(\upsigma _{ki} v_{i} \), (iii) the heat flux \(J_{i}^{q} \), (iv) the electromagnetic energy flux \(S_{i}^{e} \), (v) the energy flux \(\upmu _{c} J_{i}^{m} \) linked with the mass transport relative to the mass center of the representative volume, (vi) the energy flux \(\upmu _{\uppi } J_{i}^{ms} \) due to changing in the material microstructure of representative element (caused by the LMD), and (vii) the action of mechanical mass forces \({{\textbf {F}}}=\{F_{i} \}\) and distributed thermal sources \(\Re \). Hence, according to the first principle of thermodynamics, for the considered arbitrary volume \(\left( V \right) \) bounded by a surface \(\left( \Sigma \right) \) the total energy balance equation can be written as:

$$\begin{aligned} \frac{d}{dt}\int \limits _{\left( V \right) } {\mathscr {E}} dV\,= & {} -\,\oint \limits _{\left( \Sigma \right) } {\,\left[ {\uprho v_{k} \left( {u+\frac{1}{2}v_{i}^{2} +\frac{1}{2}\upgamma _{ij} \frac{d{\uppi }_{i}^{e} }{dt}\frac{d{\uppi }_{j}^{e} }{dt}+M_{ij} v_{i} \frac{d{\uppi }_{j}^{e} }{dt}} \right) \,-\,}\right. } \upsigma _{ki} v_{i}\nonumber \\{} & {} \left. {+S_{k}^{e} +J_{k}^{q} +\upmu _{c} J_{k}^{m} \,+\upmu _{\uppi } J_{k}^{ms} \,} \right] n_{k} \,d\Sigma \,+\int \limits _{\left( V \right) } {\uprho \left( {v_{i} F_{i} \,+\,\Re } \right) \,dV} . \end{aligned}$$
(18)

Here, \(\varvec{\upsigma } =\{{\upsigma } _{ij} \}\) is the Cauchy stress tensor, \(\upmu _{c} \) represents the chemical potential, \(\upmu _{\uppi } \) is the energy measure of the influence of the LMD on the internal energy of the body [28, 29], \({{\textbf {J}}}^{m}=\uprho ({{\textbf {v}}}_{*} -{{\textbf {v}}})\), \({{\textbf {J}}}^{m}=\{J_{i}^{m} \}\) denotes the convective mass flux, \({{\textbf {v}}}=\{v_{i} \}\) is the velocity vector of the center of mass, and \({{\textbf {v}}}_{*} =\{v_{*i} \}\) is the velocity of convective displacement of the representative element. Vectors \({{\textbf {v}}}\) and \({{\textbf {v}}}_{*} \) are related through the formula: \({{\textbf {v}}}={{\textbf {v}}}_{*} +\uprho ^{-1}{{\textbf {J}}}^{ms}\) [29]. This means that: \({{\textbf {J}}}^{ms}=-{{\textbf {J}}}^{m}\) [28]. Thus, the component of the mass flux \({{\textbf {J}}}^{m}\) can be defined as:

$$\begin{aligned} J_{i}^{m} =-\frac{\partial \Pi _{i}^{m} }{\partial t}. \end{aligned}$$
(19)

Using the divergence theorem and formulae (13) and (19), we can transform the surface integral into a volume integral and rewrite Eq. (18) in the local form as follows:

$$\begin{aligned}{} & {} \frac{\partial }{\partial t}\left( {\uprho u+U_{e} +\frac{1}{2}\uprho v_{k}^{2} +\frac{1}{2}\uprho \upgamma _{ij} \frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}+\uprho M_{ij} v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) =\uprho F_{i} v_{i} +\uprho \Re \nonumber \\{} & {} \quad -\nabla _{k} \left[ {\uprho v_{k} \left( {u+\frac{1}{2}v_{i}^{2} +\frac{1}{2}\upgamma _{ij} \frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}+M_{ij} v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) -\upsigma _{ki} v_{i} +S_{k}^{e} +J_{k}^{q} +{\upmu }'_{\uppi } \frac{\partial \Pi _{k}^{m} }{\partial t}} \right] . \end{aligned}$$
(20)

Here, \({\upmu }'_{\uppi } =\upmu _{\uppi } -\upmu _{c} \). After some algebra, the latter expression can be written as:

$$\begin{aligned}{} & {} \left[ {\frac{\partial \uprho }{\partial t}+\nabla _{k} \left( {\uprho v_{k} } \right) } \right] \left( {u+\frac{1}{2}v_{i}^{2} +\frac{1}{2}\upgamma _{ij} \frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}+M_{ij} v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) \\{} & {} \quad \quad +\uprho \frac{du}{dt}+\frac{1}{2}\uprho \upgamma _{ij} \frac{d}{dt}\left( {\frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}} \right) +\uprho M_{ij} \frac{d}{dt}\left( {v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) +\frac{\partial U_{e} }{\partial t}+\nabla _{i} S_{i}^{e}\\{} & {} \quad =v_{i} \left( {\nabla _{j} \upsigma _{ji} +\uprho F_{i} -\uprho \frac{dv_{i} }{dt}} \right) +\upsigma _{ji} \nabla _{j} v_{i} -\nabla _{i} J_{i}^{q} -\nabla _{i} {\upmu }'_{\uppi } \frac{\partial \Pi _{i}^{m} }{\partial t}-{\upmu }'_{\uppi } \frac{\partial \nabla _{i} \Pi _{i}^{m} }{\partial t}+\uprho \Re . \end{aligned}$$

Making use of the entropy balance equation (5), the energy conservation law for electromagnetic field (12), and formula (2), the latter expression yields:

$$\begin{aligned} \uprho \frac{du}{dt}= & {} \upsigma _{ki} \nabla _{k} v_{i} +T\frac{dS}{dt}+\frac{\partial \left( {\uprho \uppi _{i}^{e} } \right) }{\partial t}E_{i}^{*} +{\upmu }'_{\uppi } \frac{\partial \uprho _{m\uppi } }{\partial t}-\nabla _{i} {\upmu }'_{\uppi } \frac{\partial \Pi _{i}^{m} }{\partial t}\nonumber \\{} & {} -\left[ {\frac{\partial \uprho }{\partial t}+\nabla _{k} \left( {\uprho v_{k} } \right) } \right] \left( {u+\frac{1}{2}v_{i}^{2} +\frac{1}{2}\upgamma _{ij} \frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}+M_{ij} v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) +TS\nabla _{i} v_{i}\nonumber \\{} & {} +v_{i} \left( {\nabla _{j} \upsigma _{ji} +\uprho F_{i} +e_{ijk} \frac{\partial \left( {\uprho \uppi _{j}^{e} } \right) }{\partial t}B_{k} -\uprho \frac{dv_{i} }{dt}} \right) -\frac{1}{2}\uprho \upgamma _{ij} \frac{d}{dt}\left( {\frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}} \right) -\uprho M_{ij} \frac{d}{dt}\left( {v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) \nonumber \\{} & {} +T\left\{ {\left[ {\nabla _{i} \left( {\frac{1}{T}} \right) +\left( {\nabla _{j} Q_{ji} } \right) } \right] J_{i}^{q} +\nabla _{j} \left( {J_{i}^{q} } \right) Q_{ij} -\upsigma _{s} } \right\} . \end{aligned}$$
(21)

Using the specific quantities \(s=S/\uprho \), \(\uprho _{m} =\uprho _{m\uppi } /\uprho \), \(\uppi _{i}^{m} =\Pi _{i}^{m} /\uprho \) and substantive time derivatives, the relation (21) can be given in the form as follows:

$$\begin{aligned} \uprho \frac{du}{dt}= & {} \upsigma _{ji}^{*} \frac{d\left( {\nabla _{j} u_{i} } \right) }{dt}+\uprho T\frac{ds}{dt}+\uprho E_{i}^{*} \frac{d\uppi _{i}^{e} }{dt}+\uprho {\upmu }'_{\uppi } \frac{d\uprho _{m} }{dt}-\uprho \nabla _{i} {\upmu }'_{\uppi } \frac{d\uppi _{i}^{m} }{dt}\nonumber \\{} & {} -\left[ {\frac{\partial \uprho }{\partial t}+\nabla _{k} \left( {\uprho v_{k} } \right) } \right] \left( {u-Ts-\uppi _{i}^{e} E_{i}^{*} -{\upmu }'_{\uppi } \uprho _{m} +\uppi _{i}^{m} \nabla _{i} {\upmu }'_{\uppi } +\frac{1}{2}v_{i}^{2} +\frac{1}{2}\upgamma _{ij} \frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}+M_{ij} v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) \nonumber \\{} & {} +v_{i} \left[ {\nabla _{j} \upsigma _{ji}^{*} +\uprho F_{i}^{*} +F_{i}^{e} -\uprho \frac{dv_{i} }{dt}} \right] -\frac{1}{2}\uprho \upgamma _{ij} \frac{d}{dt}\left( {\frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}} \right) -\uprho M_{ij} \frac{d}{dt}\left( {v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) \nonumber \\{} & {} +T\left\{ {\left[ {\nabla _{i} \left( {\frac{1}{T}} \right) +\left( {\nabla _{j} Q_{ji} } \right) } \right] J_{i}^{q} +\nabla _{j} \left( {J_{i}^{q} } \right) Q_{ij} -\upsigma _{s} } \right\} . \end{aligned}$$
(22)

Here,

$$\begin{aligned} \upsigma _{ij}^{*} =\upsigma _{ij} -\uprho \left( {\uppi _{k}^{e} E_{k}^{*} +\uprho _{m} {\upmu }'_{\uppi } -\uppi _{k}^{m} \nabla _{k} {\upmu }'_{\uppi } } \right) \updelta _{ij} \end{aligned}$$
(23)

is the modified stress tensor (\(\updelta _{ij} \) is the Kronecker delta),

$$\begin{aligned} F_{i}^{*} =F_{i} +\uprho _{m} \nabla _{i} {\upmu }'_{\uppi } -\uppi _{j}^{m} \nabla _{i} \nabla _{j} {\upmu }'_{\uppi } \end{aligned}$$
(24)

is the additional mass force which appears in the equation of motion for elastic dielectrics, and

$$\begin{aligned} F_{i}^{e} =e_{ijk} \frac{\partial \left( {\uprho \uppi _{j}^{e} } \right) }{\partial t}B_{k} +\uprho \uppi _{j}^{e} \nabla _{i} E_{j}^{*} \end{aligned}$$
(25)

is the classical ponderomotive force [54].

Note that \(\uprho _{m} \) is a dimensionless quantity, whereas vector \(\varvec{\uppi }^{m}\) has the length dimension, [m].

The classical theory of dielectrics considers macroscopic electric field. Toupin [64, 65] assumed the field of each particle of dielectric bodies to be influenced not only by the mean macroscopic field, but also by the fields of its neighboring particles. Consequently, the macroscopic electric field and the local field in dielectric media exhibit some difference. After Toupin [64, 65], we take into account the difference between the local electric and macroscopic electric fields. Thus, we assume that the local thermodynamic state of the dielectric body is determined not by the macroscopic field \({{\textbf {E}}}^{*}\), but rather by the local value \({{\textbf {E}}}^{L}=\left\{ {E_{i}^{L} } \right\} \). Therefore, we rewrite the balance equation (22) as follows:

$$\begin{aligned} \uprho \frac{du}{dt}= & {} \uprho T\frac{ds}{dt}+\upsigma _{ij}^{*} \frac{d\left( {\nabla _{i} u_{j} } \right) }{dt}+\uprho E_{i}^{L} \frac{d\uppi _{i}^{e} }{dt}+\uprho {\upmu }'_{\uppi } \frac{d\uprho _{m} }{dt}-\uprho \nabla _{i} {\upmu }'_{\uppi } \frac{d\uppi _{i}^{m} }{dt}\nonumber \\{} & {} +\uprho \left[ {E_{i}^{*} -E_{i}^{L} -\frac{1}{2}\left( {\upgamma _{ji} +\upgamma _{ij} } \right) \frac{d^{2}\uppi _{j}^{e} }{dt^{2}}-M_{ji} \frac{d^{2}u_{j} }{dt^{2}}} \right] \frac{d\uppi _{i}^{e} }{dt}\nonumber \\{} & {} -\left[ {\frac{\partial \uprho }{\partial t}+\nabla _{k} \left( {\uprho v_{k} } \right) } \right] \left( {u-Ts-\uppi _{i}^{e} E_{i}^{*} -{\upmu }'_{\uppi } \uprho _{m} +\uppi _{i}^{m} \nabla _{i} {\upmu }'_{\uppi } +\frac{1}{2}v_{i}^{2} +\frac{1}{2}\upgamma _{ij} \frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}+M_{ij} v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) \nonumber \\{} & {} +v_{i} \left[ {\nabla _{j} \upsigma _{ji}^{*} +\uprho F_{i}^{*} +F_{i}^{e} -\uprho \frac{d^{2}u_{i} }{dt^{2}}-\uprho M_{ij} \frac{d^{2}\uppi _{j}^{e} }{dt^{2}}} \right] \nonumber \\ {}{} & {} +T\left\{ {\left[ {\nabla _{i} \left( {\frac{1}{T}} \right) +\nabla _{j} Q_{ji} } \right] J_{i}^{q} +\nabla _{j} \left( {J_{i}^{q} } \right) Q_{ij} -\upsigma _{s} } \right\} . \end{aligned}$$
(26)

Note that in the above equation, the following formulae are taken into account:

$$\begin{aligned} \frac{1}{2}\uprho \upgamma _{ij} \frac{d}{dt}\left( {\frac{d\uppi _{i}^{e} }{dt}\frac{d\uppi _{j}^{e} }{dt}} \right) =\frac{1}{2}\uprho \left( {\upgamma _{ji} +\upgamma _{ij} } \right) \frac{d^{2}\uppi _{j}^{e} }{dt^{2}}\frac{d\uppi _{i}^{e} }{dt}, \uprho M_{ij} \frac{d}{dt}\left( {v_{i} \frac{d\uppi _{j}^{e} }{dt}} \right) =\uprho M_{ji} \frac{d^{2}u_{j} }{dt^{2}}\frac{d\uppi _{i}^{e} }{dt}+\uprho M_{ij} v_{i} \frac{d^{2}\uppi _{j}^{e} }{dt^{2}}. \end{aligned}$$

Equation (26) should satisfy the principle of frame indifference in a rigid translation [20]. Therefore, we assume the energy balance equation (26) to be valid under superimposed rigid body translation, when \({{\textbf {v}}}\rightarrow {{\textbf {v}}}+{{\textbf {a}}}\) [66]. Here, \({{\textbf {a}}}\) is an arbitrary constant vector. Then, from Eq. (26), we can get the balance equation of linear momentum:

$$\begin{aligned} \nabla _{j} \upsigma _{ji}^{*} +\uprho F_{i}^{*} +F_{i}^{e} =\uprho \frac{d^{2}u_{i} }{dt^{2}}+\uprho M_{ij} \frac{d^{2}\uppi _{j}^{e} }{dt^{2}}, \end{aligned}$$
(27)

the mass balance equation (i.e., the continuity equation) [61]:

$$\begin{aligned} \frac{\partial \uprho }{\partial t}+\nabla _{i} \left( {\uprho v_{i} } \right) =0, \end{aligned}$$
(28)

and the following internal energy balance equation:

$$\begin{aligned} \uprho \frac{du}{dt}= & {} \uprho T\frac{ds}{dt}+\upsigma _{ij}^{*} \frac{d\left( {\nabla _{i} u_{j} } \right) }{dt}+\uprho E_{i}^{L} \frac{d\uppi _{i}^{e} }{dt}+\uprho {\upmu }'_{\uppi } \frac{d\uprho _{m} }{dt}-\uprho \nabla _{i} {\upmu }'_{\uppi } \frac{d\uppi _{i}^{m} }{dt}\nonumber \\{} & {} +\uprho \left[ {E_{i}^{*} -E_{i}^{L} -\frac{1}{2}\left( {\upgamma _{ji} +\upgamma _{ij} } \right) \frac{d^{2}\uppi _{j}^{e} }{dt^{2}}-M_{ji} \frac{d^{2}u_{j} }{dt^{2}}} \right] \frac{d\uppi _{i}^{e} }{dt}\nonumber \\{} & {} +T\left\{ {\left[ {\nabla _{i} \left( {\frac{1}{T}} \right) +\nabla _{j} Q_{ji} } \right] J_{i}^{q} +\nabla _{j} \left( {J_{i}^{q} } \right) Q_{ij} -\upsigma _{s} } \right\} . \end{aligned}$$
(29)

The balance of momentum is formulated for the modified stress tensor \({{\varvec{\upsigma }}}^{*}=\{{{\upsigma }}_{ij}^{*} \}\) because the LMD induces additional spherical stresses \({{\upsigma }}_{ij}^{m} =\uprho \left( {\uppi _{k}^{m} \nabla _{k} {\upmu }'_{\uppi } -\uprho _{m} {\upmu }'_{\uppi } } \right) \updelta _{ij} \) within the body (see Eq. (3)). Note that \(\varvec{\upsigma }^{*}\) is a symmetric tensor and for linear approximation it can be replaced with the ordinary Cauchy stress tensor \(\varvec{\upsigma }=\{{\upsigma }_{ij} \}\). From (27), we can conclude that accounting LMD leads to the appearance of an additional nonlinear mass force \({{\textbf {F}}}^{*}=\{F_{i}^{*} \}\) in the equation of motion (see formula (4)). Also, in the right-hand side of Eq. (27), an additional term with the second time derivative of the polarization vector appears in comparison with the classical theory. This term controls the influence of the dynamic flexoelectric effect on the mechanical motion of dielectric solids. If \(M_{ij} =\) 0, \(F_{i}^{*} =\) 0, \(\upsigma _{ij}^{m} =\) 0, then Eq. (27) reduces to the classical balance equation of linear momentum.

Let us represent \(\nabla _{j} u_{i} \) via expression \(\nabla _{j} u_{i} ={\varvec{\upvarepsilon }}_{ij} +\upomega _{ij} \), where the symmetric strain tensor \(\varvec{\upvarepsilon }=\{{\upvarepsilon }_{ij} \}\) and antisymmetric tensor of rotation \({{\varvec{\upomega }}} =\{{{\upomega }}_{ij} \}\) are defined as usual:

$$\begin{aligned} {{\upvarepsilon }}_{ij} =\frac{1}{2}\left( {\nabla _{j} u_{i} +\nabla _{i} u_{j} } \right) , \upomega _{ij} =\frac{1}{2}\left( {\nabla _{j} u_{i} -\nabla _{i} u_{j} } \right) . \end{aligned}$$
(30)

Since tensor \(\mathbf {{\varvec{\upsigma }}}^{*}\) is symmetric and a convolution of symmetric and antisymmetric tensors is equal to zero, thus we can write:

$$\begin{aligned} \upsigma _{ij}^{*} \frac{d(\nabla _{i} u_{j} )}{dt}=\upsigma _{ij}^{*} \frac{d\upvarepsilon _{ij} }{dt}. \end{aligned}$$
(31)

By using the expression \(f=u-Ts-E_{i}^{L} \uppi _{i}^{e} -{\upmu }'_{\uppi } \uprho _{m} +\uppi _{i}^{m} \nabla _{i} {\upmu }'_{\uppi } \), we introduce the generalized Helmholtz free energy. From (29) within the context of the foregoing definition of the free energy function and formula (31), we can derive the following free energy balance equation:

$$\begin{aligned} \uprho \frac{df}{dt}= & {} \upsigma _{ij}^{*} \frac{d\upvarepsilon _{ij} }{dt}-\uprho s\frac{dT}{dt}-\uprho \uppi _{i}^{e} \frac{dE_{i}^{L} }{dt}-\uprho \uprho _{m} \frac{d{\upmu }'_{\uppi } }{dt}+\uprho \uppi _{i}^{m} \frac{d\nabla _{i} {\upmu }'_{\uppi } }{dt}\nonumber \\{} & {} +\uprho \left[ {E_{i}^{*} -E_{i}^{L} -\frac{1}{2}(\upgamma _{ji} +\upgamma _{ij} )\frac{d^{2}\uppi _{j}^{e} }{dt^{2}}-M_{ji} \frac{d^{2}u_{j} }{dt^{2}}} \right] \frac{d\uppi _{i}^{e} }{dt}\nonumber \\{} & {} +T\left\{ {\left[ {\nabla _{i} \left( {\frac{1}{T}} \right) +\nabla _{j} Q_{ji} } \right] J_{i}^{q} +\nabla _{j} \left( {J_{i}^{q} } \right) Q_{ij} -\upsigma _{s} } \right\} . \end{aligned}$$
(32)

Since the summands in the second and third lines of Eq. (32) do not depend on the ratios

$$\begin{aligned} \frac{d\upvarepsilon _{ij} }{dt}, \frac{dT}{dt}, \frac{dE_{i}^{L} }{dt}, \frac{d\uprho _{m} }{dt}\hbox { and }\frac{d\nabla _{i} {\upmu }'_{\uppi } }{dt}, \end{aligned}$$

we can get the generalized Gibbs equation

$$\begin{aligned} df=\frac{1}{\uprho }\upsigma _{ij}^{*} d\upvarepsilon _{ij} -sdT-\uppi _{i}^{e} dE_{i}^{L} -\uprho _{m} d{\upmu }'_{\uppi } +\uppi _{i}^{m} d\left( {\nabla _{i} {\upmu }'_{\uppi } } \right) , \end{aligned}$$
(33)

the relation for the entropy production

$$\begin{aligned} \upsigma _{s} =\left[ {\nabla _{i} \left( {\frac{1}{T}} \right) +\left( {\nabla _{j} Q_{ji} } \right) } \right] J_{i}^{q} +\nabla _{j} \left( {J_{i}^{q} } \right) Q_{ij}, \end{aligned}$$
(34)

and differential equation

$$\begin{aligned} E_{i}^{*} =E_{i}^{L} +\frac{1}{2}(\upgamma _{ji} +\upgamma _{ij} )\frac{d^{2}\uppi _{j}^{e} }{dt^{2}}+M_{ji} \frac{d^{2}u_{j} }{dt^{2}}, \end{aligned}$$
(35)

linking the polarization \(\uppi _{j}^{e} \), displacement \(u_{j} \), local electric field \(E_{i}^{L} \), and the macroscopic electric field.

From Eq. (33), it can be concluded that the strain tensor, the temperature, the local electric field, the modified chemical potential, and its gradient do contribute to the free energy density \(f=f\left( {\upvarepsilon _{ij},T,E_{i}^{L},{\upmu }'_{\uppi },\nabla _{i} {\upmu }'_{\uppi } } \right) \). Also, within the framework of the considered theory, a more general expression (34) for entropy production is derived. Equations (33)–(35) are fundamental to the development of the constitutive and kinematic equations.

Note that Eqs. (27) and (35) comply with the results obtained by Awad et al. [49], who studied the dynamic flexoelectric effect based on strain gradient elasticity. Note also that setting \(M_{ji} =0\) in (35), we can get the so-called intramolecular force balance law obtained by Maugin [54, 67], who took the polarization inertia into account. Thus, Eq. (35) can be regarded as a generalization of Maugin’s intramolecular force balance equation for the case of elastic dielectrics by accounting for the polarization inertia and dynamic flexoelectric effect. Also, if material constants \(\upgamma _{ji} \) are omitted, formula (35) yields the Toupin ‘equation of molecular equilibrium’ [64, 65].

3 Constitutive and kinematic relations

3.1 State equations

The local gradient theory of dielectrics predicts that the generalized free energy density f depends on five independent variables: the strain tensor, temperature, local electric field vector, modified chemical potential \({\upmu }'_{\uppi } \), and its gradient \({\nabla }{\upmu }'_{\uppi } \). The gradient-type constitutive equations of the local gradient electro-thermo-elasticity can be expressed in terms of this energy in the form as follows:

$$\begin{aligned} \upsigma _{ij}^{*} =\uprho \frac{\partial f}{\partial \upvarepsilon _{ij} }, s=-\frac{\partial f}{\partial T}, \uppi _{i}^{e} =-\frac{\partial f}{\partial E_{i}^{L} }, \uprho _{m} =-\frac{\partial f}{\partial {\upmu }'_{\uppi } }, \uppi _{i}^{m} =\frac{\partial f}{\partial (\nabla _{i} {\upmu }'_{\uppi } )}. \end{aligned}$$
(36)

These constitutive equations incorporate the LMD effect and its coupling with electro-thermo-mechanical fields and are consistent with the balance laws. It follows from (36) that within the considered model, the set of conjugate variables is complemented by two supplementary couples of variables (\(\uprho _{m} \),\({\upmu }'_{\uppi } )\) and (\({\varvec{{\uppi }}}^{m}\), \({\varvec{\nabla }}{\upmu }'_{\uppi })\) related to the LMD.

3.2 The generalized Fourier law

Within the context of formula (34), the second principle of thermodynamics can be verbalized as:

$$\begin{aligned} \upsigma _{s} =\left[ {\nabla _{i} \left( {\frac{1}{T}} \right) +\left( {\nabla _{j} Q_{ji} } \right) } \right] J_{i}^{q} +\nabla _{j} \left( {J_{i}^{q} } \right) Q_{ij} \ge 0. \end{aligned}$$

In order to satisfy the above dissipation inequality, we assume the following:

$$\begin{aligned} J_{i}^{q}= & {} m_{1} \left[ {\nabla _{i} \left( {\frac{1}{T}} \right) +\left( {\nabla _{j} Q_{ji} } \right) } \right] ,\,\,\,\,m_{1} >0, \end{aligned}$$
(37)
$$\begin{aligned} Q_{ij}= & {} m_{2} \nabla _{j} \left( {J_{i}^{q} } \right) ,\,\,\,\,m_{2} >0, \end{aligned}$$
(38)

where \(m_{1} \) and \(m_{2} \) are unknown constants. Equations (37) and (38) yield the following expression for the heat flux:

$$\begin{aligned} J_{i}^{q} =-\frac{m_{1} }{T^{2}}\nabla _{i} T+m_{1} m_{2} \Delta J_{i}^{q}. \end{aligned}$$
(39)

Here, \(\Delta \) denotes the Laplace operator. The linear constituent of Eq. (39) presents the generalized Fourier law of heat conduction:

$$\begin{aligned} J_{i}^{q} -\upzeta ^{2}\Delta J_{i}^{q} =-\uplambda \nabla _{i} T, \end{aligned}$$
(40)

where \(\uplambda =m_{1} /T_{0}^{2} \) is the coefficient of heat conductivity and \(\upzeta ^{2}=m_{1} m_{2} \). The term \(\upzeta ^{2}\Delta J_{i}^{q} \) represents the non-local heat conduction law [56]. For the macroscale problems with low heat flux, this term is relatively small and thus can be omitted. For such problems, Eq. (40) yields the classical Fourier law: \(J_{i}^{q} =-\uplambda \nabla _{i} T\).

Balance Eqs. (5), (16), (27), (28), Maxwell equations (6)–(9), differential relation (35), constitutive Eqs. (10), (36), kinematic expression (39) for heat flux, and the ‘strain–displacement’ relations (30)\(_{1}\) constitute the complete system of equations of the local gradient electro-thermo-elasticity with incorporating the non-classical Fourier law, the polarization inertia, and the flexodynamic effect. In general, the obtained balance and constitutive equations are nonlinear. Further, we consider their linear approximation.

4 Linear approximation

4.1 Balance and constitutive equations for linear isotropic continuum

For the linear problems, tensor \({\varvec{\upsigma }^{*}}\) can be replaced by the ordinary Cauchy stress tensor \({\varvec{\upsigma }}\) as well as: \(\uprho =\uprho _{0} \), \({{\textbf {E}}}^{*}={{\textbf {E}}}\), and \({d...}/ {dt}={\partial ...}/{\partial t}\). In the case of piezoelectric materials, the time rate of the magnetic induction can be neglected [68]. For electrostatic approximation, the electromagnetic field equations reduce to Eq. (6) and the electric field vector can be written as:

$$\begin{aligned} E_{i} =-\nabla _{i} \upvarphi _{e}, \end{aligned}$$
(41)

where \(\upvarphi _{e} \) is the electric potential. For dielectrics without free electric charges (\(\uprho _{e} =\) 0), the balance equations (5), (16), (27), and Gauss law (6) can be transformed to:

$$\begin{aligned}{} & {} \nabla _{j} \upsigma _{ij} +\uprho _{0} F_{i} =\uprho _{0} \frac{\partial ^{2}u_{i} }{\partial t^{2}}+\uprho _{0} M_{ij} \frac{\partial ^{2}\uppi _{j}^{e} }{\partial t^{2}}, \end{aligned}$$
(42)
$$\begin{aligned}{} & {} \uprho _{0} T_{0} \frac{\partial s}{\partial t}=-\nabla _{i} J_{i}^{q} +\uprho _{0} \Re , \end{aligned}$$
(43)
$$\begin{aligned}{} & {} \nabla _{i} D_{i} =0, \uprho _{m} =-\nabla _{i} \uppi _{i}^{m}. \end{aligned}$$
(44)

In order to obtain the linear constitutive equations, we convolute the free energy density into Taylor series with respect to the small (comparing to the natural state of homogenous medium) perturbations of the constitutive parameters with \(\upvarepsilon _{ij} =0\), \(\upsigma _{ij} =0\), \(T=T_{0} \), \(s=s_{0} \), \(E_{i}^{L} =0\), \(\uppi _{i}^{e} =0\), \(\uprho _{m} =0\), \({\upmu }'_{\uppi } ={\upmu }'_{\uppi 0} \), \(\nabla _{i} {\upmu }'_{\uppi } =0\), and \(\uppi _{i}^{m} =0\). Assume that \(\upvarepsilon _{ij} \ll 1\), \((T-T_{0} )/T_{0} \ll 1\), \(E_{i}^{L} \ll 1\), \(\bar{{{\upmu }'}}_{\uppi } ={\upmu }'_{\uppi } -{\upmu }'_{\uppi 0} \ll 1\), and \(\nabla _{i} \bar{{{\upmu }'}}_{\uppi } \ll 1\). Then, the free energy density for centrosymmetric isotropic materials can be written in the following quadratic form:

$$\begin{aligned} f=&{} f_{0} -s_{0} \,\uptheta -\frac{C_{V} }{2T_{0} }\,\uptheta ^{2}+\frac{\uplambda }{2\uprho _{0} }\upvarepsilon _{ii} \upvarepsilon _{jj} +\frac{\upmu }{\uprho _{0} }\upvarepsilon _{ij} \upvarepsilon _{ij} -\frac{\upchi _{E} }{2}\left( {E_{i}^{L} } \right) ^{2}-\frac{d_{\upmu }}{2}{\bar{{\upmu }}}_{\uppi }^{'\,2}-\frac{\upchi _{m} }{2}\left( {\nabla _{i} \bar{{{\upmu }}}_{\uppi }'}\right) ^{\,2}\nonumber \\{}&{} \quad -\frac{\upgamma _{T} }{\uprho _{0} }\,\uptheta \upvarepsilon _{ii} -\frac{\upalpha _{m} }{\uprho _{0} }\,\,{\bar{{\upmu }}}'_{\uppi } \upvarepsilon _{ii} -\upbeta _{T\upmu } \uptheta \,\,{\bar{{\upmu }}}'_{\uppi } +\,\upchi _{Em} E_{i}^{L} \,\nabla _{i} \bar{{{\upmu }}}_{\uppi }'. \end{aligned}$$
(45)

Here, \(\uptheta =T-T_{0} \). Within the framework of the considered model, the five additional material parameters \(d_{\upmu } \), \(\upalpha _{m} \), \(\upchi _{m} \,\), \(\upchi _{Em} \), and \(\upbeta _{T\upmu } \) are involved into expression (45) in addition to the conventional classical constants \(\uplambda \), \(\upmu \), \(C_{V} \), \(\upgamma _{T} \), and \(\upchi _{E} \). These material constants appear in the mathematical model due to the introduction of the modified chemical potential and its gradients in the free energy density function. Then, inserting expression (45) into formulae (36) results in linear constitutive equations:

$$\begin{aligned} \upsigma _{ij}= & {} 2\upmu \upvarepsilon _{ij} +\left( {\uplambda \upvarepsilon _{kk} -\upgamma _{T} \,\uptheta -\upalpha _{m} \,\bar{{{\upmu }}}_{\uppi }' } \right) \updelta _{ij}, \end{aligned}$$
(46)
$$\begin{aligned} s= & {} s_{0} +\frac{\upgamma _{T} }{\uprho _{0} }\upvarepsilon _{ii} +\frac{C_{V} }{T_{0} }\,\uptheta +\,\,\upbeta _{T\upmu } \,\bar{{{\upmu }}}_{\uppi }', \end{aligned}$$
(47)
$$\begin{aligned} \uppi _{i}^{e}= & {} \upchi _{E} E_{i}^{L} -\upchi _{Em} \nabla _{i} \bar{{{\upmu }}}_{\uppi }', \end{aligned}$$
(48)
$$\begin{aligned} \uprho _{m}= & {} \frac{\upalpha _{m} }{\uprho _{0} }\upvarepsilon _{ii} +\,\,\upbeta _{T\upmu } \,\uptheta +d_{\upmu } \bar{{{\upmu }}}_{\uppi }', \end{aligned}$$
(49)
$$\begin{aligned} \uppi _{i}^{m}= & {} \upchi _{Em} E_{i}^{L} -\upchi _{m} \,\nabla _{i} \bar{{{\upmu }}}_{\uppi }'. \end{aligned}$$
(50)

Here, i, j, k \(\in \) {1, 2, 3}. For centrosymmetric isotropic materials, expression (35) takes the form

$$\begin{aligned} E_{i} -E_{i}^{L} =\upgamma _{11} \frac{\partial ^{2}\uppi _{i}^{e} }{\partial t^{2}}+M_{11} \frac{\partial ^{2}u_{i} }{\partial t^{2}}. \end{aligned}$$
(51)

Note that Eqs. (48) and (50) yield the formula:

$$\begin{aligned} \upchi _{Em} \uppi _{i}^{e} -\upchi _{E} \uppi _{i}^{m} =\Theta \nabla _{i} \bar{{{\upmu }}}{'}_{\!\!\uppi },\qquad \Theta =\upchi _{m} \upchi _{E} \,-\upchi _{Em}^{2}. \end{aligned}$$

Then, combining Eqs. (48), (50), and (51), we arrive at

$$\begin{aligned} \left[ {1+\upgamma _{11} \upchi _{E} \frac{\partial ^{2}}{\partial t^{2}}} \right] \uppi _{i}^{e}=&{} \upchi _{E} E_{i} -\upchi _{Em} \nabla _{i} \bar{{{\upmu }}}_{\uppi }' -M_{11} \upchi _{E} \frac{\partial ^{2}u_{i} }{\partial t^{2}}, \end{aligned}$$
(52)
$$\begin{aligned} \left[ {1+\upgamma _{11} \upchi _{E} \frac{\partial ^{2}}{\partial t^{2}}} \right] \uppi _{i}^{m}=&{} \upchi _{Em} E_{i} -\upchi _{m} \nabla _{i} \bar{{{\upmu }}}_{\uppi }' -\upgamma _{11} \Theta \frac{\partial ^{2}\nabla _{i} \bar{{{\upmu }}}_{\uppi }' }{\partial t^{2}}-M_{11} \upchi _{Em} \frac{\partial ^{2}u_{i} }{\partial t^{2}}. \end{aligned}$$
(53)

Hence, due to accounting for the polarization inertia terms in expression for kinematic energy function, we get the rheological constitutive equations for polarization and the LMD vectors. If the contribution of the dynamics of polarization is dismissed (\(\upgamma _{11} =\) 0), the constitutive equations for the polarization vector and the LMD vector can be simplified and take the following form:

$$\begin{aligned} \uppi _{i}^{e}=&{} \upchi _{E} E_{i} -\upchi _{Em} \nabla _{i} \bar{{{\upmu }}}_{\uppi }' -M_{11} \upchi _{E} \frac{\partial ^{2}u_{i} }{\partial t^{2}}, \end{aligned}$$
(54)
$$\begin{aligned} \uppi _{i}^{m}=&{} \upchi _{Em} E_{i} -\upchi _{m} \,\nabla _{i} \bar{{{\upmu }}}_{\uppi }' -M_{11} \upchi _{Em} \frac{\partial ^{2}u_{i} }{\partial t^{2}}. \end{aligned}$$
(55)

4.2 The first system of governing equations

Employing balance equations (42)–(44), constitutive equations (10), (46), (47), (49), (52), (53) along with geometric relation (30)\(_{1}\), and kinematic expressions (40) and (41), the governing equations can be written in terms of the displacement components \(u_{i} \), temperature \(\uptheta \), electric potential \(\upvarphi _{e} \), and modified chemical potential \(\bar{{{\upmu }}}_{\uppi }'\) in the form as follows:

$$\begin{aligned} {}&{} \left[ {1+\upgamma _{11} \upchi _{E} \frac{\partial ^{2}}{\partial t^{2}}} \right] \left[ {\upmu u_{i,jj} +\left( {\uplambda +\upmu } \right) u_{j,ji} -\upgamma _{T} \,\uptheta _{,i} -\upalpha _{m} \bar{{{\upmu }}}_{\uppi ,i}' +\uprho _{0} F_{i} } \right] \nonumber \\{}&{} \quad =\uprho _{0} \frac{\partial ^{2}u_{i} }{\partial t^{2}}+\uprho _{0} \upchi _{E} \left( {\upgamma _{11} -M_{11}^{2} } \right) \frac{\partial ^{4}u_{i} }{\partial t^{4}}-\uprho _{0} M_{11} \left( {\upchi _{E} \frac{\partial ^{2}\upvarphi _{e,i} }{\partial t^{2}}+\upchi _{Em} \frac{\partial ^{2}\bar{{{\upmu }}}_{\uppi ,i}' }{\partial t^{2}}} \right) , \end{aligned}$$
(56)
$$\begin{aligned} \uplambda \uptheta _{,ii} {}&{} +\uprho _{0} \left( {\Re -\upzeta ^{2}\Re _{,ii} } \right) =\uprho _{0} C_{V} \,\left( {\frac{\partial \uptheta }{\partial t}-\upzeta ^{2}\frac{\partial \uptheta _{,ii} }{\partial t}} \right) \nonumber \\{}&{} \qquad +T_{0} \upgamma _{T} \left( {\frac{\partial u_{i,i} }{\partial t}-\upzeta ^{2}\frac{\partial u_{i,ijj} }{\partial t}} \right) +\,\uprho _{0} T_{0} \upbeta _{T\upmu } \,\left( {\frac{\partial \bar{{{\upmu }}}_{\uppi }' }{\partial t}-\upzeta ^{2}\frac{\partial \bar{{{\upmu }}}_{\uppi ,ii}' }{\partial t}} \right) , \end{aligned}$$
(57)
$$\begin{aligned} {}&{} \upvarepsilon \upvarphi _{e,ii} +\upvarepsilon _{0} \upchi _{E} \upgamma _{11} \frac{\partial ^{2}\upvarphi _{e,ii} }{\partial t^{2}}+\uprho _{0} \upchi _{Em} \bar{{{\upmu }}}_{\uppi ,ii}' +\uprho _{0} \upchi _{E} M_{11} \frac{\partial ^{2}u_{i,i} }{\partial t^{2}}=0, \end{aligned}$$
(58)
$$\begin{aligned} {}&{} \upchi _{m} \,\bar{{{\upmu }}}_{\uppi ,ii}' -d_{\upmu } \bar{{{\upmu }}}_{\uppi }' -d_{\upmu } \upgamma _{11} \upchi _{E} \frac{\partial ^{2}\bar{{{\upmu }}}_{\uppi }' }{\partial t^{2}}+\upgamma _{11} \Theta \frac{\partial ^{2}\bar{{{\upmu }}}_{\uppi ,ii}' }{\partial t^{2}}=\nonumber \\{}&{} \quad =\frac{\upalpha _{m} }{\uprho _{0} }u_{i,i} +\left( {\upgamma _{11} \upchi _{E} \frac{\upalpha _{m} }{\uprho _{0} }-M_{11} \upchi _{Em} } \right) \frac{\partial ^{2}u_{i,i} }{\partial t^{2}}+\upbeta _{T\upmu } \uptheta +\upgamma _{11} \upchi _{E} \upbeta _{T\upmu } \frac{\partial ^{2}\uptheta }{\partial t^{2}}\,-\upchi _{Em} \upvarphi _{e,ii}. \end{aligned}$$
(59)

Here, \(\upvarepsilon =\upvarepsilon _{0} +\uprho _{0} \upchi _{E} \), and a comma followed by a subscript denotes partial differentiation with respect to the coordinate associated with the subscript.

In contrast to the classical electro-thermo-elasticity, additional equation (59) appears in the system of governing equations due to consideration of the LMD. Since the polarization inertia and flexodynamic effects are incorporated into the mathematical model, equation of motion (56) additionally contains the third and fourth-order derivatives of functions \(u_{i} \), \(\uptheta \), \(\upvarphi _{e} \) and \(\bar{{{\upmu }}}_{\uppi }' \). The mixed time-spatial derivatives appear in this equation as a result of the polarization inertia effect. Also, because of the non-local expression for the heat flux, we arrived at the rather complex heat conduction equation (57), which includes the higher-order mixed time-spatial derivatives of the temperature field, dilatation, and modified chemical potential. This equation does not directly include the electric field terms. However, due to the connection of the LMD with the temperature field and the electric field (see Eqs. (59) and (58)), the derived system of governing equations (56)–(59) predicts the coupling between the temperature field and the electric field. This means that the current mathematical model of dielectrics describes the effect of the temperature gradient on the electric field and vice versa. The appearance of a polarization proportional to a temperature gradient when the macroscopic field is zero is known as the thermal polarization effect. It can be concluded that the developed local gradient theory of dielectrics covers the thermopolarization effect and accommodates an electro-thermo-mechanical interaction in isotropic centrosymmetric materials. In Eq. (58), the summands \(\uprho _{0} \upchi _{Em} {\bar{\upmu }'}_{\uppi ,ii} \) and \(\uprho _{0} \upchi _{E} M_{11} \ddot{{u}}_{i,i} \) are the microstructural and the flexodynamic terms, respectively. Note also that assuming parameters \(\upzeta \) and \(M_{11} \) are equal to zero, the governing equations (56)–(59) coincide with the results obtained in [28] within the local gradient theory of dielectric media which incorporates the inertia of polarization.

4.3 The second system of governing equations

Governing equations (56)–(59) are coupled with respect to the displacement, temperature, and modified chemical potential and electric potential fields. Let us now write the governing equations taking the electric polarization as a key function instead of the electric potential. In this case, the heat conduction equation (57) does not change, while Eqs. (56), (58), and (59) are transformed as follows:

$$\begin{aligned} {}&{} \upmu u_{i,jj} +\left( {\uplambda +\upmu } \right) u_{j,ji} -\upgamma _{T} \,\uptheta _{,i} -\upalpha _{m} \bar{{{\upmu }}}_{\uppi ,i}' +\uprho _{0} F_{i} =\uprho _{0} \frac{\partial ^{2}u_{i} }{\partial t^{2}}+\uprho _{0} M_{11} \frac{\partial ^{2}\uppi _{i}^{e} }{\partial t^{2}},\end{aligned}$$
(60)
$$\begin{aligned} {}&{} \frac{\upvarepsilon }{\upvarepsilon _{0} }\uppi _{i,i}^{e} +\upgamma _{11} \upchi _{E} \frac{\partial ^{2}\uppi _{i,i}^{e} }{\partial t^{2}}+\upchi _{Em} \bar{{{\upmu }}}_{\uppi ,ii}' +\upchi _{E} M_{11} \frac{\partial ^{2}u_{i,i} }{\partial t^{2}}=0, \end{aligned}$$
(61)
$$\begin{aligned} {}&{} \frac{\Theta }{\upchi _{E} }\bar{{{\upmu }}}_{\uppi ,ii}' -d_{\upmu } \bar{{{\upmu }}}_{\uppi }' =\frac{\upalpha _{m} }{\uprho _{0} }u_{i,i} +\,\,\upbeta _{T\upmu } \,\uptheta +\frac{\upchi _{Em} }{\upchi _{E} }\uppi _{i,i}^{e}.\end{aligned}$$
(62)

It can be easily seen that we get the second-order differential equation (60) for the displacement vector. Thus, it can be concluded that the system of governing equation in terms of the displacement components, temperature, electric polarization, and modified chemical potential is more appropriate to study dynamically coupled fields in dielectric media with polarization inertia and flexodynamic effects.

Governing systems of equations (56)–(59) or (57) and (60)–(62) take into account the additional contribution to the polarization response due to the accelerated motion of the medium. Such effects cannot be covered within the framework of the classical theory of dielectrics. Note that if polarization inertia and dynamic flexoelectric effect are neglected, then Eqs. (58), (59), and (61) for the electric field and the LMD became stationary. In this case, the mechanical equation and the heat conduction equation are dynamic, while the equations for electric field and the LMD are static and are not dynamically coupled.

4.4 Governing equations: particular sets

Particular sets of governing equations can be obtained from Eqs. (56)–(62) by setting the appropriate coefficients in the above formulae to equal zero. Below, we consider two special cases.

  1. 1.

    No inertia of polarization.

    In this case, the governing equations (56), (58), and (59) are simplified as:

    $$\begin{aligned} {}&{} \upmu u_{i,jj} +\left( {\uplambda +\upmu } \right) u_{j,ji} -\upgamma _{T} \,\uptheta _{,i} -\upalpha _{m} \bar{{{\upmu }}}_{\uppi ,i}' +\uprho _{0} F_{i} \nonumber \\{}&{} \quad =\uprho _{0} \frac{\partial ^{2}u_{i} }{\partial t^{2}}-\uprho _{0} M_{11} \left( {\upchi _{E} M_{11} \frac{\partial ^{4}u_{i} }{\partial t^{4}}+\upchi _{E} \frac{\partial ^{2}\upvarphi _{e,i} }{\partial t^{2}}+\upchi _{Em} \frac{\partial ^{2}\bar{{{\upmu }}}_{\uppi ,i}' }{\partial t^{2}}} \right) , \end{aligned}$$
    (63)
    $$\begin{aligned} {}&{} \upvarepsilon \upvarphi _{e,ii} +\uprho _{0} \upchi _{Em} \bar{{{\upmu }}}_{\uppi ,ii}' +\uprho _{0} \upchi _{E} M_{11} \frac{\partial ^{2}u_{i,i} }{\partial t^{2}}=0, \end{aligned}$$
    (64)
    $$\begin{aligned} {}&{} \upchi _{m} \bar{{{\upmu }}}_{\uppi ,ii}' -d_{\upmu } \bar{{{\upmu }}}_{\uppi }' =\frac{\upalpha _{m} }{\uprho _{0} }u_{i,i} -M_{11} \upchi _{Em} \frac{\partial ^{2}u_{i,i} }{\partial t^{2}}+\,\upbeta _{T\upmu } \,\uptheta -\upchi _{Em} \upvarphi _{e,ii}. \end{aligned}$$
    (65)

    For such approximation in governing system of equations (60)–(62), Eq. (61) should be replaced with the following one:

    $$\begin{aligned} \frac{\upvarepsilon }{\upvarepsilon _{0} }\uppi _{i,i}^{e} +\upchi _{Em} {{\bar{\upmu }'}}_{\uppi ,ii} +\upchi _{E} M_{11} \frac{\partial ^{2}u_{i,i} }{\partial t^{2}}=0. \end{aligned}$$
    (66)
  2. 2.

    No flexodynamic effect.

    In this case, governing equations (56), (58), and (59) are simplified as follows:

    $$\begin{aligned}&\left[ {1+\upgamma _{11} \upchi _{E} \frac{\partial ^{2}}{\partial t^{2}}} \right] \left[ {\upmu u_{i,jj} +\left( {\uplambda +\upmu } \right) u_{j,ji} -\upgamma _{T} \,\uptheta _{,i} -\upalpha _{m} \bar{{{\upmu }}}_{\uppi ,i}' +\uprho _{0} F_{i} } \right] = \uprho _{0} \frac{\partial ^{2}u_{i} }{\partial t^{2}}+\uprho _{0} \upchi _{E} \upgamma _{11} \frac{\partial ^{4}u_{i} }{\partial t^{4}},\nonumber \\ \end{aligned}$$
    (67)
    $$\begin{aligned}&\upvarepsilon \upvarphi _{e,ii} +\uprho _{0} \upchi _{Em} \bar{{{\upmu }}}_{\uppi ,ii}' +\upvarepsilon _{0} \upchi _{E} \upgamma _{11} \frac{\partial ^{2}\upvarphi _{e,ii} }{\partial t^{2}}=0, \end{aligned}$$
    (68)
    $$\begin{aligned}&\upchi _{m} \,\bar{{{\upmu }}}_{\uppi ,ii}' -d_{\upmu } \bar{{{\upmu }}}_{\uppi }' -\upgamma _{11} d_{\upmu } \upchi _{E} \frac{\partial ^{2}\bar{{{\upmu }}}_{\uppi }' }{\partial t^{2}}+\upgamma _{11} \Theta \frac{\partial ^{2}\bar{{{\upmu }}}_{\uppi ,ii}' }{\partial t^{2}} \nonumber \\&\quad =\frac{\upalpha _{m} }{\uprho _{0} }u_{i,i} +\upbeta _{T\upmu } \uptheta -\upchi _{Em} \upvarphi _{e,ii} +\upgamma _{11} \upchi _{E} \left( {\frac{\upalpha _{m} }{\uprho _{0} }\frac{\partial ^{2}u_{i,i} }{\partial t^{2}}+\upbeta _{T\upmu } \frac{\partial ^{2}\uptheta }{\partial t^{2}}} \right) . \end{aligned}$$
    (69)

    In the system of governing equations (60)–(62), Eq. (62) remains the same, whereas Eqs. (60) and (61) should be replaced by following ones:

    $$\begin{aligned}{} & {} \upmu u_{i,jj} +\left( {\uplambda +\upmu } \right) u_{j,ji} -\upgamma _{T} \,\uptheta _{,i} -\upalpha _{m} {{\bar{\upmu }'}}_{\uppi ,i} +\uprho _{0} F_{i} =\uprho _{0} \frac{\partial ^{2}u_{i} }{\partial t^{2}}, \end{aligned}$$
    (70)
    $$\begin{aligned}{} & {} \frac{\upvarepsilon }{\upvarepsilon _{0} }\uppi _{i,i}^{e} +\upchi _{Em} {{\bar{\upmu }'}}_{\uppi ,ii} +\upgamma _{11} \upchi _{E} \frac{\partial ^{2}\uppi _{i,i}^{e} }{\partial t^{2}}=0. \end{aligned}$$
    (71)

Note that in both cases I and II, the heat conduction equation (57) holds.

4.5 Validation of the model

For the simplicity sake, we restrict ourselves to consideration of the isothermal approximation. In the absence of body forces (\(F_{i} \) \(=\) 0), the gradient of modified chemical potential can be obtained from the equation of motion (60) as a function of the strain gradients and the second-order time derivatives of the displacement and polarization vectors:

$$\begin{aligned} \bar{{{\upmu }}}_{\uppi ,i}' =2\frac{\upmu }{\upalpha _{m} \,}\upvarepsilon _{ij,j} +\frac{\uplambda }{\upalpha _{m} \,}\upvarepsilon _{jj,i} -\frac{\uprho _{0} }{\upalpha _{m} }\frac{\partial ^{2}u_{i} }{\partial t^{2}}-\frac{\uprho _{0} M_{11} }{\upalpha _{m} }\frac{\partial ^{2}\uppi _{i}^{e} }{\partial t^{2}}.\end{aligned}$$
(72)

Then, combining the constitutive equation (52) and formula (72), we may write the electric field vector as:

$$\begin{aligned} E_{i}= & {} \frac{1}{\upchi _{E} }\uppi _{i}^{e} +2\frac{\upchi _{Em} }{\upchi _{E} }\frac{\upmu }{\upalpha _{m} \,}\upvarepsilon _{ij,j} +\frac{\upchi _{Em} }{\upchi _{E} }\frac{\uplambda }{\upalpha _{m} \,}\upvarepsilon _{jj,i} +M_{11} \left( {1-\frac{\uprho _{0} \upchi _{Em} }{M_{11} \upalpha _{m} \upchi _{E} }} \right) \frac{\partial ^{2}u_{i} }{\partial t^{2}}\\ {}{} & {} +\upgamma _{11} \left( {1-\frac{M_{11} \uprho _{0} \upchi _{Em} }{\upgamma _{11} \upalpha _{m} \upchi _{E} }} \right) \frac{\partial ^{2}\uppi _{i}^{e} }{\partial t^{2}}. \end{aligned}$$

In the above relation, the first term is classical. The second and third terms reflect the contribution of the strain gradients into the electric field vector. The last two terms correspond to the contribution of the flexodynamic effect and the inertia of polarization into the electric field. The foregoing relation complies with formula (53) in [23] obtained by Yudin and Tagantsev within a higher-grade theory of dielectric media with dynamic flexoelectricity. Hence, it can be concluded that the excluding the quantities related to the LMD from the state equation for electric field vector, the constitutive equation of strain gradient theory of dielectrics with dynamic flexoelectric effect is obtained.

5 Harmonic plane wave in an unbounded dielectric medium

In this section, the developed theory of dielectrics is verified though solving a coupled problem of electro-elasticity, where the propagation of harmonic plane waves in the context of the newly formulated model will be studied and discussed. For the simplicity sake, the effect of polarization inertia and temperature field is neglected. Therefore, we will now consider Eqs. (60), (62) and (66) in this section.

5.1 Governing equations in terms of potential and solenoidal parts of displacements

Let us decompose the vectors of displacement \({{\textbf {u}}}\) and mass force \({{\textbf {F}}}\) as the sum of their potential \(\upchi _{u} \), \(\upchi _{F} \) and solenoidal \({\varvec{\uppsi }}_{u} \), \({\varvec{\uppsi }}_{F} \) components. Following Maranganti et al. [69], for electrostatic approximation we can write:

$$\begin{aligned} {{{\textbf {u}}}}={\varvec{\nabla }}\upchi _{u} +{\varvec{\nabla }}\times {\varvec{\uppsi }}_{u}, {{\varvec{\uppi }}}^{e}={\varvec{\nabla }}\upchi _{\uppi }, {{{\textbf {F}}}}={\varvec{{\nabla }}}\upchi _{F} +{\varvec{\nabla }}\times {\varvec{\uppsi }}_{F}, \end{aligned}$$
(73)

where \({\varvec{\nabla }}\cdot \varvec{\uppsi }_{u} {=}0\) and \({\varvec{\nabla }}\cdot {\varvec{\uppsi } }_{F} {=}0\), and \(\upchi _{\uppi } \) is the potential part of polarization vector \({{\varvec{\uppi }}}^{e}\).

In terms of wave propagation, the scalar components \(\upchi _{u} \), \(\upchi _{\uppi } \), and \(\upchi _{F} \) correspond to longitudinal waves, while solenoidal components \(\varvec{\uppsi }_{u} \), \(\varvec{\uppsi }_{F} \) represent the shear waves propagating through the electro-elastic polarized medium. Substituting the decomposition (73) into governing equations (60), (62), and (66), we arrive at the following system of differential equations:

$$\begin{aligned} {}&{} c_{1}^{2} \Delta \upchi _{u} -\frac{\partial ^{2}\upchi _{u} }{\partial t^{2}}+\upchi _{F} -\frac{\upalpha _{m} }{\uprho _{0} }\bar{{{\upmu }}}_{\uppi }' -M_{11} \frac{\partial ^{2}\upchi _{\uppi } }{\partial t^{2}}=0, \end{aligned}$$
(74)
$$\begin{aligned} {}&{} c_{2}^{2} \Delta {\varvec{\uppsi }}_{u} +{\varvec{\uppsi }}_{F} -\frac{\partial ^{2}{\varvec{\uppsi }}_{u} }{\partial t^{2}}=0, \end{aligned}$$
(75)
$$\begin{aligned} {}&{} \Delta \upchi _{\uppi } +\frac{\upvarepsilon _{0} }{\upvarepsilon }\upchi _{Em} \Delta \bar{{{\upmu }}}_{\uppi }' +\frac{\upvarepsilon _{0} }{\upvarepsilon }\upchi _{E} M_{11} \frac{\partial ^{2}\left( {\Delta \upchi _{u} } \right) }{\partial t^{2}}=0, \end{aligned}$$
(76)
$$\begin{aligned} {}&{} \frac{\Theta }{\upchi _{E} }\Delta \bar{{{\upmu }}}_{\uppi }' -d_{\upmu } \bar{{{\upmu }}}_{\uppi }' =\frac{\upalpha _{m} }{\uprho _{0} }\Delta \upchi _{u} +\frac{\upchi _{Em} }{\upchi _{E} }\Delta \upchi _{\uppi }. \end{aligned}$$
(77)

Here, \(c_{1} \) and \(c_{2} \) are the velocities of propagation of longitudinal and transverse elastic waves:

$$\begin{aligned} c_{1} =\sqrt{{(\uplambda +2\upmu )}/{\uprho _{0} }},\qquad c_{2} =\sqrt{\upmu /{\uprho _{0} }}. \end{aligned}$$

The shear motion is characterized by vector \({\varvec{\uppsi }}_{u} \). For this vector, we get Eq. (75), which is identical to the equation of transverse waves in classical theory. The transverse wave is not modified by the LMD and the electrostatic electric field. Evidently, only the longitudinal wave is coupled with the electric field and modified chemical potential. This means that the LMD and flexodynamic effect can influence the velocity of propagation of longitudinal waves in isotropic media.

5.2 Problem formulation

In this subsection, we consider an elastic longitudinal wave propagating in an isotropic dielectric medium. Let a harmonic longitudinal plane monochromatic wave propagate in an infinite electro-elastic space along the axis Ox of the Cartesian rectangular coordinate system \((x,\,y,\,z)\). Assume that the mass forces are absent, i.e., \({{\textbf {F}}}=0\). All the considered functions are supposed to depend only on the spatial coordinate x and time t. In order to find functions \(\upchi _{u} \), \(\upchi _{\uppi } \), and \({{\bar{\upmu }'}}_{\uppi } \), from (74), (76), and (77), for the one-dimensional case we get:

$$\begin{aligned} {}&{} c_{1}^{2} \frac{\partial ^{2}\upchi _{u} }{\partial x^{2}}-\frac{\partial ^{2}\upchi _{u} }{\partial t^{2}}-\frac{\upalpha _{m} }{\uprho _{0} }\bar{{{\upmu }}}_{\uppi }' -M_{11} \frac{\partial ^{2}\upchi _{\uppi } }{\partial t^{2}}=0,\\{}&{} \frac{\partial ^{2}\upchi _{\uppi } }{\partial x^{2}}+\frac{\upvarepsilon _{0} }{\upvarepsilon }\upchi _{Em} \frac{\partial ^{2}\bar{{{\upmu }}}_{\uppi }' }{\partial x^{2}}+\frac{\upvarepsilon _{0} }{\upvarepsilon }\upchi _{E} M_{11} \frac{\partial ^{2}}{\partial t^{2}}\left( {\frac{\partial ^{2}\upchi _{u} }{\partial x^{2}}} \right) =0,\\{}&{} \left( {\,\upchi _{m} -\upchi _{Em} \upkappa _{E} } \right) \frac{\partial ^{2}\bar{{{\upmu }}}_{\uppi }' }{\partial x^{2}}-d_{\upmu } \bar{{{\upmu }}}_{\uppi }' =\frac{\upalpha _{m} }{\uprho _{0} }\frac{\partial ^{2}\upchi _{u} }{\partial x^{2}}-\upchi _{Em} M_{11} \frac{\upvarepsilon _{0} }{\upvarepsilon }\frac{\partial ^{2}}{\partial t^{2}}\left( {\frac{\partial ^{2}\upchi _{u} }{\partial x^{2}}} \right) . \end{aligned}$$

Eliminating the functions of \({{\bar{\upmu }'}}_{\uppi } \) and \(\upchi _{\uppi } \) from the first equation, we can obtain the following equation for the longitudinal wave:

$$\begin{aligned}{} & {} \frac{\partial ^{2}}{\partial x^{2}}\left\{ {c_{1}^{2} \left( {1+\textrm{m}} \right) \frac{\partial ^{2}\upchi _{u} }{\partial x^{2}}-\frac{\partial ^{2}\upchi _{u} }{\partial t^{2}}-c_{1}^{2} l_{*}^{2} \frac{\partial ^{4}\upchi _{u} }{\partial x^{4}}+\left( {l_{*}^{2} -2M_{11} \upchi _{Em} \frac{\upalpha _{m} }{\uprho _{0} d_{\upmu } }\frac{\upvarepsilon _{0} }{\upvarepsilon }} \right) \frac{\partial ^{4}\upchi _{u} }{\partial t^{2}\partial x^{2}}+M_{11}^{2} \frac{\upvarepsilon _{0} }{\upvarepsilon }\left( {\upchi _{E} \frac{\partial ^{4}\upchi _{u} }{\partial t^{4}}-\frac{\Theta }{d_{\upmu } }\frac{\partial ^{6}\upchi _{u} }{\partial t^{4}\partial x^{2}}} \right) } \right\} \\ {}{} & {} \quad =0. \end{aligned}$$

Here,

$$\begin{aligned} l_{*} =\sqrt{\frac{\upchi _{m} -\upchi _{Em} \upkappa _{E} }{d_{\upmu } }}, \textrm{m}=\frac{\upalpha _{m}^{2} }{\uprho _{0} d_{\upmu } (\uplambda +2\upmu )}, \upkappa _{E} =\frac{\uprho _{0} \upchi _{Em} }{\upvarepsilon }. \end{aligned}$$

Note that \(l_{*} \) is the material length-scale parameter, \(\textrm{m}\) is the coupling factor between the processes of mechanical deformation and the LMD. These parameters are small quantities [28].

The solutions to the above differential equations are taken in the form of a plane harmonic wave:

$$\begin{aligned} (\upchi _{u},\upchi _{\uppi },\bar{\upmu }_{\uppi }' )=(\underline{\upchi }_{u},\underline{\upchi }_{\uppi },\underline{\overline{\upmu }}_{\uppi }' )\exp (-ikx+i\upomega t), \end{aligned}$$

where k is the wavenumber, \(\upomega \) is the frequency of plane wave, and \(i=\sqrt{-1} \). Hence, for longitudinal wave in dielectrics we get the following dispersion relation:

$$\begin{aligned} k^{4}+\left[ {\frac{1}{l_{*}^{2} }(1+\textrm{m}+q)-\frac{\upomega ^{2}}{c_{1}^{2} }} \right] k^{2}-\frac{\upomega ^{2}}{l_{*}^{2} \,c_{1}^{2} }(1+q_{0} )=0, \end{aligned}$$
(78)

where

$$\begin{aligned} q(M_{11},\upomega )=M_{11} \frac{\upvarepsilon _{0} \upomega ^{2}}{\upvarepsilon \,d_{\upmu } c_{1}^{2} }\left( {2\upchi _{Em} \frac{\upalpha _{m} }{\uprho _{0} }-M_{11} \Theta \upomega ^{2}} \right) , q_{0} (M_{11},\upomega )=M_{11}^{2} \upchi _{E} \upomega ^{2}\frac{\upvarepsilon _{0} }{\upvarepsilon }. \end{aligned}$$

For the case of dielectric materials without considering the dynamic flexoelectric effect (\(M_{11} =0)\), dispersive relation (78) can be reduced to

$$\begin{aligned} k^{4}+\left[ {\frac{1}{l_{*}^{2} }\left( {1+\textrm{m}} \right) -\frac{\upomega ^{2}}{c_{1}^{2} }} \right] k^{2}-\frac{\upomega ^{2}}{l_{*}^{2} \,c_{1}^{2} }=0. \end{aligned}$$
(79)

Equation (79) is the same as that obtained in [70] for local gradient electro-elasticity. Further, for the case without the LMD effect (\(l_{*} =0\) and \(\textrm{m}=0)\), the dispersive relation (79) reduces to the classical equation: \(k^{2}-{\upomega ^{2}} /{c_{1}^{2} }=0\).

For the wave propagating in the positive direction of \(x-\)axis, biquadratic equation (78) yields:

$$\begin{aligned} k^{2}=\frac{\upomega ^{2}}{\,2c_{1}^{2} }-\frac{1}{2l_{*}^{2} }(1+\textrm{m}+q)+\frac{1}{2}\sqrt{\left[ {\frac{1}{l_{*}^{2} }(1+\textrm{m}+q)-\frac{\upomega ^{2}}{\,c_{1}^{2} }} \right] ^{2}+4\frac{\upomega ^{2}}{l_{*}^{2} c_{1}^{2} }(1+q_{0} )}. \end{aligned}$$
(80)

In view of the following estimations for the material parameters: \(c_{1}\sim 10^{3}\,\,\left[ {\text{ m/s }} \right] \), \(\uprho \sim 10^{3}\,\,\,[{\text{ kg/m}^{3}}]\), \(l_{*} \sim 10^{-9}\,\left[ {\text{ m }} \right] \), \(d_{\upmu } \sim 10^{-5}\,\,\left[ {\text{ s}^{2}/\text{m}^{2}} \right] \), \(\upchi _{m} =10^{-23}\,\left[ {s^{2}} \right] \), \(\upalpha _{m} \sim 10^{3}\,\,\left[ {\text{ kg/m}^{3}} \right] \), \(\upchi _{E} \sim 10^{-9}\,\,\left[ {\text{ F }\times \text{ m}^{2}/\text{kg }} \right] \), \(\upchi _{Em} \sim 10^{-17}\,\,\left[ {\text{ m}^{2}/\text{V }} \right] \) [28], and \(M_{11} \sim 10^{-8}\div 10^{-7}\,\,\left[ {\text{ Vs}^{2}/\text{m}^{2}} \right] \) [38], expression (80) can be simplified as follows:

$$\begin{aligned} k\approx \frac{\upomega }{c_{1} }\sqrt{1-\frac{\textrm{m}+q\left( {M_{11},\upomega ,c_{1} } \right) -q_{0} \left( {M_{11},\upomega } \right) }{1+\textrm{m}+q\left( {M_{11},\upomega ,c_{1} } \right) +{l_{*}^{2} \upomega ^{2}} / {c_{1}^{2} }\,}}. \end{aligned}$$

Since k is real, the wave is not damped. Within the framework of the developed theory, the phase velocity \(c_{p} =\upomega /k\) of propagation of the elastic longitudinal wave is

$$\begin{aligned} c_{p} (\upomega ,\textrm{m},l_{*},M_{11} )\approx {c_{1} }\bigg / {\sqrt{1-\frac{\textrm{m}+q(M_{11},\upomega )-q_{0} (M_{11},\upomega )}{1+\textrm{m}+q(M_{11},\upomega )+{l_{*}^{2} \upomega ^{2}}/{c_{1}^{2} }\,}} }. \end{aligned}$$
(81)

The phase velocity \(c_{p} \) of the longitudinal wave differs from its group velocity: \(c_{g} =d\upomega /dk\). Equation (81) shows that, unlike the classical theory characterized by the constant velocity of the longitudinal wave, the local gradient electro-elasticity with flexodynamic effect is characterized by velocity for longitudinal wave, which is a function of the frequency. Hence, this wave is dispersive. The dispersion of the longitudinal elastic wave is due to both the LMD and the flexodynamic effect. It is easy to see that dispersion is absent when the dynamic flexoelectric effect and the coupling between the LMD and mechanical fields are neglected. In this case, by setting \(M_{11} =0\), \(l_{*} =0\) and \(\textrm{m}=0\), one finds from (81) that the result of classical electro-elasticity with a constant velocity of the longitudinal wave is recovered.

5.3 Influence of dynamic flexoelectric effect on phase velocity of the longitudinal elastic wave

In order to distinguish between the microstructural and dynamic flexoelectric effects, in this subsection the effect of the LMD is omitted (i.e., \(\textrm{m}=\) 0 and \(l_{*} =\) 0). In this case, Eqs. (80) and (81) are simplified and can be written as follows:

$$\begin{aligned} k=\frac{\upomega }{c_{1} }\sqrt{1+\upchi _{E} M_{11}^{2} \frac{\upvarepsilon _{0} }{\upvarepsilon }\upomega ^{2}}, c_{p} (\upomega ,M_{11} )=\frac{c_{1} }{\sqrt{1+{M_{11}^{2} \upomega ^{2}\upchi _{E} \upvarepsilon _{0} }/\upvarepsilon } }. \end{aligned}$$
(82)

In Fig. 2, the non-dimensional phase velocity of the longitudinal elastic wave is computed from Eq. (82)\(_{2}\) and compared with the results, predicted by classical theory. For the computations, the following material parameters were used: \(\uprho _{0} =\,\,1986\,\,{\text{ kg }}/{\text{ m}^{3}}\) and \(\upchi _{E} =10^{-7}\,\,\text{ F }\times \text{ m}^{2}\text{/kg }\). In order to capture the electromechanical behavior of the flexoelectric media, the flexodynamic material parameter \(M_{11} \) is to be imposed. For isotropic dielectrics, however, such data are not yet available in the literature. Thus, we investigated the non-dimensional phase velocity of a longitudinal elastic wave for several values of flexodynamic coefficient \(M_{11} \). In Fig. 2, dynamic flexoelectric coefficient is assumed to be \(1.6\times 10^{-5}\,\text{ Vs}^{2}/\text{m}^{2},\,\,3.2\times 10^{-5}\,\text{ Vs}^{2}/\text{m}^{2},\,\,4.8\times 10^{-5}\,\text{ Vs}^{2}/\text{m}^{2}\) and \(7.7\times 10^{-5}\,\text{ Vs}^{2}/\text{m}^{2}\) (the dotted, dashed, dash-dotted, and solid lines, respectively).

From Fig. 2, it is found that for sufficiently high wave frequencies, increasing \(M_{11}\) results in decreasing value of phase wave velocity (i.e., the influence of dynamic flexoelectric effect on the wave velocity becomes more prominent). Note that the classic theory does not cover the experimentally observed phenomenon of high-frequency dispersion of longitudinal elastic waves [71, 72]. Figure 2 shows that such dispersion in the high-frequency region can be described using the developed theory of dielectrics which predicts a decrease in wave velocity.

Fig. 2
figure 2

Non-dimensional phase velocity of the longitudinal elastic wave versus wave frequency for different values of flexodynamic coefficient

Full size image

6 Conclusion

Using the continuum-thermodynamic approach, the advanced theory of electro-thermo-elasticity is suggested. The theory takes into account the non-diffusive and non-convective mass fluxes associated with the changes in the material microstructure (the local displacement of mass), the non-classical heat conduction law, polarization inertia, and flexodynamic effect. The gradient-type constitutive equations, the kinematic expression for non-classical heat flux, and generalized equation of balance of linear momentum are derived. It is shown that the non-classical law of heat conduction is defined by the phenomenological expression which connects the entropy and heat fluxes. Due to accounting for the polarization inertia and dynamic flexoelectricity terms, the rheological constitutive equations for polarization and the LMD vectors are obtained. The theory developed in this study predicts the dynamic flexoelectric effect in isotropic dielectrics and provides a basis for the investigation of electro-thermo-mechanical coupling phenomena in materials of arbitrary symmetry, including the isotropic centrosymmetric crystals. The obtained results are general and can be helpful for modeling new devices based on size and thermopolarization effects. The theory is expected to be useful for modeling coupled processes in polarized systems with heterogeneous inner structure, in nanodielectrics, etc.

Within the context of the local gradient electro-elasticity model, the propagation of the plane harmonic wave in an isotropic dielectric medium is analyzed. The dispersion relation of longitudinal elastic waves in the elastic dielectrics is derived. For dynamic problem, it is found that the plane longitudinal wave becomes dispersive at high frequencies through the coupling of the LMD, mechanical deformation, and electric polarization. The dispersion is more pronounced when the waves are short. It is found that dynamic flexoelectricity can affect the electromechanical behavior of dielectrics. It is shown that the numerical results for phase velocity agree with the experimental predictions. The obtained results can be efficiently used for theoretical analysis of high-frequency surface and plane waves propagation in polarized elastic structures.