Rigid–flexible–thermal coupling dynamics of a hub and multiplate system considering frictional contact

Abstract

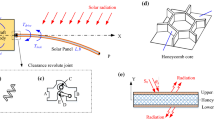
A geometric nonlinear modeling approach for strong rigid–flexible–thermal coupling dynamics of a hub and multiplate system considering frictional contact is proposed. Based on the absolute nodal coordinate formulation (ANCF), an ANCF thin-plate element with thermoelasticity is developed, where the temperature field is expressed with Taylor polynomials to yield heat-conduction equations. In contrast to the traditional coupling formulations, the influences of the attitude motion and structural deformation on the intensity of the solar radiation, the geometric nonlinearity of the plate as well as the frictional contact are taken into account. The frictional-contact formulations for a thin plate and a rigid body are presented, which can capture the stick–slip transition and address the multiple-point contact scenarios. To solve the strong rigid–flexible–thermal coupling equations, a novel numerical approach combining the generalized-$\alpha$ method and the modified central-difference method is proposed. Two validations are performed to verify the proposed model, which proves the importance of considering the geometric nonlinearity and reveals the phenomena of thermally induced vibrations. Then, the thermal–dynamic coupling analysis for the satellite and solar-array multibody system in a thermal environment is carried out. The dynamic characteristics of the thermally induced vibration can be successfully revealed by the rigid–flexible–thermal coupling model. Furthermore, it is indicated that the influence of contact and thermal load on the nonlinear behavior of the solar-array deployment is essential, which demonstrates the feasibility of the proposed approach.

Appendix. Solution scheme for the rigid–flexible–thermal coupling equations

The solution scheme for the rigid–flexible–thermal coupling equations is divided into the following three steps:

• Step1: Prediction of the initial value

Assuming that $\ddot{\mathbf{q}}_{d}^{t + \Delta t} = \mathbf{0}$, we combine Taylor’s formula, the generalized-$\alpha$ method, and a modified central-difference method to predict $\mathbf{a}_{d}^{t + \Delta t}$, $\mathbf{q}_{d}^{t + \Delta t}$, $\dot{\mathbf{q}}_{d}^{t + \Delta t}$, $\boldsymbol{\lambda}^{t + \Delta t}$, $\mathbf{p}^{t + \Delta t}$, as follows:

$$ \mathbf{a}_{d}^{t + \Delta t} = \frac{\alpha _{f}}{1 - \alpha _{m}}\ddot{\mathbf{q}}_{d}^{t} - \frac{\alpha _{m}}{1 - \alpha _{m}}\mathbf{a}_{d}^{t}, $$

(56)

$$ \mathbf{q}_{d}^{t + \Delta t} = \mathbf{q}_{d}^{t} + \Delta t\dot{\mathbf{q}}_{d}^{t} + \Delta t^{2}\left ( 0.5 - \beta \right )\mathbf{a}_{d}^{t} + \Delta t^{2}\beta \mathbf{a}_{d}^{t + \Delta t}, $$

(57)

$$ \dot{\mathbf{q}}_{d}^{t + \Delta t} = \dot{\mathbf{q}}_{d}^{t} + \Delta t\left ( 1 - \gamma \right )\mathbf{a}_{d}^{t} + \Delta t\gamma \mathbf{a}_{d}^{t + \Delta t}, $$

(58)

$$ \boldsymbol{\lambda}^{t + \Delta t} = \boldsymbol{\lambda}^{t}, $$

(59)

$$ \mathbf{p}^{t + \Delta t} = \theta \mathbf{p}^{t + \Delta t} + \left ( 1 - \theta \right )\mathbf{p}^{t}, $$

(60)

where

$$ \alpha _{m} = \frac{2\rho _{\infty} - 1}{\rho _{\infty} + 1},\quad \alpha _{f} = \frac{\rho _{\infty}}{\rho _{\infty} + 1}, $$

(61)

$$ \gamma = 0.5 + \alpha _{f} - \alpha _{m},\quad \beta = 0.25 \left ( \gamma + 0.5 \right )^{2}, $$

(62)

and the numerical parameters $\rho _{\infty}, \theta \in [0, 1]$. The numerical parameters in this paper are taken as $\rho _{\infty} = 0.6$, $\theta = 0.5$.

• Step2: Transformation into nonlinear algebraic equations

The dynamic equations can be transformed into nonlinear algebraic equations using the generalized-$\alpha$ method [53]

$$ \left [ \textstyle\begin{array}{c} \mathbf{M}_{d}\ddot{\mathbf{q}}_{d}^{t + \Delta t} + \mathbf{C}_{d}\dot{\mathbf{q}}_{d}^{t + \Delta t} + \boldsymbol{\Phi}_{\mathbf{q}_{d}}^{\mathrm{T}}\left ( \mathbf{q}_{d}^{t + \Delta t} \right )\boldsymbol{\lambda}^{t + \Delta t} - \mathbf{Q}_{d}(\mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t}) \\ \boldsymbol{\Phi} (\mathbf{q}_{d}^{t + \Delta t},t + \Delta t) \end{array}\displaystyle \right ] = \mathbf{0}, $$

(63)

where

$$ \frac{\partial \ddot{\mathbf{q}}_{d}^{t + \Delta t}}{\mathbf{q}_{d}^{t + \Delta t}} = \beta ' \mathbf{I},\quad \frac{\partial \dot{\mathbf{q}}_{d}^{t + \Delta t}}{\mathbf{q}_{d}^{t + \Delta t}} = \gamma ' \mathbf{I}, $$

(64)

$$ \beta ' = \frac{1 - \alpha _{m}}{\left ( 1 - \alpha _{f} \right )\beta \Delta t^{2}},\quad \gamma ' = \frac{\gamma}{\beta \Delta t}. $$

(65)

The heat-conduction equations in Eq. (48) are transformed into nonlinear algebraic equations by a modified central-difference method [49]

$$ \bar{\mathbf{K}} \mathbf{p}^{t + \Delta t} - \bar{\mathbf{Q}}(\mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t}) = \mathbf{0}, $$

(66)

where

$$ \bar{\mathbf{K}} = \frac{\mathbf{M}_{T}}{\Delta t} + \theta \mathbf{K}_{T}, $$

(67)

$$ \bar{\mathbf{Q}} = \left [ \frac{\mathbf{M}_{T}}{\Delta t} - \left ( 1 - \theta \right ) \mathbf{K}_{T} \right ]\mathbf{p}^{t} + \left ( 1 - \theta \right )\mathbf{F}_{T}^{t} + \theta \mathbf{F}_{T}^{t + \Delta t}. $$

(68)

• Step3: Solution of the combined nonlinear algebraic equations

According to Eqs. (A8) and (A11), the combined nonlinear algebraic equations are rewritten as

$$ \textstyle\begin{array}{l} \boldsymbol{\Psi} \left ( \mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t},\boldsymbol{\lambda}^{t + \Delta t},t + \Delta t \right ) \\ = \left [ \textstyle\begin{array}{c} \mathbf{M}_{d}\ddot{\mathbf{q}}_{d}^{t + \Delta t} + \mathbf{C}_{d}\dot{\mathbf{q}}_{d}^{t + \Delta t} + \boldsymbol{\Phi}_{\mathbf{q}_{d}}^{\mathrm{T}}\left ( \mathbf{q}_{d}^{t + \Delta t} \right )\boldsymbol{\lambda}^{t + \Delta t} - \mathbf{Q}_{d}(\mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t}) \\ \boldsymbol{\Phi} (\mathbf{q}_{d}^{t + \Delta t},t + \Delta t) \\ \bar{\mathbf{K}} \mathbf{p}^{t + \Delta t} - \bar{\mathbf{Q}}(\mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t}) \end{array}\displaystyle \right ] = \mathbf{0}. \end{array} $$

(69)

The Newton–Raphson algorithm is used to find a solution of Eq. (A14). At an iteration step $k$, the following equation is solved for a correction $\Delta \mathbf{q}_{(k)}^{t + \Delta t}$:

$$ \Delta \mathbf{q}_{(k)}^{t + \Delta t} = \left [ \textstyle\begin{array}{c} \Delta \mathbf{p}_{(k)}^{t + \Delta t} \\ \Delta \mathbf{q}_{d(k)}^{t + \Delta t} \\ \Delta \boldsymbol{\lambda}_{(k)}^{t + \Delta t} \end{array}\displaystyle \right ] = - \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c}\displaystyle \frac{\partial \boldsymbol{\Psi}}{\partial \mathbf{p}^{t + \Delta t}} & \displaystyle\frac{\partial \boldsymbol{\Psi}}{\partial \mathbf{q}_{d}^{t + \Delta t}} &\displaystyle \frac{\partial \boldsymbol{\Psi}}{\partial \boldsymbol{\lambda}^{t + \Delta t}} \end{array}\displaystyle \right ]^{ - 1}\boldsymbol{\Psi}, $$

(70)

where

$$ \frac{\partial \boldsymbol{\Psi}}{\partial \mathbf{p}^{t + \Delta t}} = \left [ \textstyle\begin{array}{c}\displaystyle - \frac{\partial \mathbf{Q}_{d}(\mathbf{q}_{d(k)}^{t + \Delta t},\mathbf{p}_{(k)}^{t + \Delta t})}{\partial \mathbf{p}^{t + \Delta t}} \\ \mathbf{0} \\ \displaystyle\bar{\mathbf{K}} - \frac{\partial \bar{\mathbf{Q}}(\mathbf{q}_{d(k)}^{t + \Delta t},\mathbf{p}_{(k)}^{t + \Delta t})}{\partial \mathbf{p}^{t + \Delta t}} \end{array}\displaystyle \right ], $$

(71)

$$ \frac{\partial \boldsymbol{\Psi}}{\partial \mathbf{q}_{d}^{t + \Delta t}} = \left [ \textstyle\begin{array}{c}\displaystyle \alpha '\mathbf{M}_{d} + \beta '\mathbf{C}_{d} + \frac{\partial \left ( \boldsymbol{\Phi}_{\mathbf{q}_{d}}^{\mathrm{T}}\left ( \mathbf{q}_{d(k)}^{t + \Delta t} \right )\boldsymbol{\lambda}_{(k)}^{t + \Delta t} \right )}{\partial \mathbf{q}_{d}^{t + \Delta t}} - \frac{\partial \left ( \mathbf{Q}_{d}(\mathbf{q}_{d(k)}^{t + \Delta t},\mathbf{p}_{(k)}^{t + \Delta t}) \right )}{\partial \mathbf{q}_{d}^{t + \Delta t}} \\ \boldsymbol{\Phi}_{\mathbf{q}_{d}}\left ( \mathbf{q}_{d(k)}^{t + \Delta t} \right ) \\ \displaystyle- \frac{\partial \bar{\mathbf{Q}}(\mathbf{q}_{d(k)}^{t + \Delta t},\mathbf{p}_{(k)}^{t + \Delta t})}{\partial \mathbf{q}_{d}^{t + \Delta t}} \end{array}\displaystyle \right ], $$

(72)

$$ \frac{\partial \boldsymbol{\Psi}}{\partial \boldsymbol{\lambda}^{t + \Delta t}} = \left [ \textstyle\begin{array}{c}\displaystyle \boldsymbol{\Phi}_{\mathbf{q}_{d}}^{\mathrm{T}}\left ( \mathbf{q}_{d(k)}^{t + \Delta t} \right ) \\ \mathbf{0} \\ \mathbf{0} \end{array}\displaystyle \right ]. $$

(73)

An improved estimate can be obtained as

$$ \mathbf{q}_{(k + 1)}^{t + \Delta t} = \mathbf{q}_{(k)}^{t + \Delta t} + \Delta \mathbf{q}_{(k)}^{t + \Delta t},\quad k = 0, 1,\ldots, $$

(74)

until the precision condition $\left \| \Delta \mathbf{q}_{(k)}^{t + \Delta t} \right \| \le \delta$ is satisfied, in which $\delta$ is the precision error.