1 Introduction

Mean elements are useful in a variety of aerospace engineering tasks, like maneuver design or fast-orbit propagation. They are roughly understood as the result of an averaging process whose aim is to isolate the long-trend variations of the osculating orbit, which are modulated with short-period fluctuations. While the averaging ensues from a particular transformation of variables it happens that different transformations can be applied, a fact that raises recurrent concern since the early days of the space era (Walter 1967; Ely 2015; Lara 2021b; Izzo et al. 2022; Arnas 2022). Therefore, the “mean elements” terminology is loosely used with the meaning of elements that are free from short-period effects, a vague definition that may cause misunderstandings in the implementation and use of available perturbation solutions in the literature—refer to the caveats in pp. 616, 690, and 695 of Vallado (2013).

Ideally, the transformation from mean to osculating elements should be purely periodic in the mean anomaly, so that the resulting mean elements comprise all the secular and long-period variations of the osculating orbit. But this is not often the case, and the mean-to-osculating transformation of different satellite theories may involve non-periodic and long-period terms in addition to the short-period terms. This is, in particular, the case of common analytical solutions in closed form of the eccentricity, in which some long-period terms remain hidden in the mean-to-osculating transformation due to the implicit dependence of the true anomaly on the mean anomaly and eccentricity through Kepler’s equation (Kozai 1962). Because of that, the mean orbit will depart from the average osculating orbit in long-period displacements of small amplitude.

The lack of agreement between mean and average dynamics is not a concern in usual analytical or semi-analytical orbit theories, a case in which the osculating solution is obtained after recovering the periodic effects using the mean-to-osculating transformation. This is the case of usual solutions computed by canonical-perturbation theory (Brouwer 1959; Kozai 1959; Coffey et al. 1996; Lara 2021). However, the disagreement may be unwanted in those cases in which the information provided by the mean elements alone is crucial for the problem at hand, as may happen in some space geodesy applications (Wagner et al. 1974; Métris and Exertier 1995) or when high accuracy is needed in preliminary orbit and maneuver design (Bhat et al. 1990; Guinn 1992). Conversely, the reported aim of some non-canonical perturbation methods is to achieve the removal of only the short-period fluctuations from the mean orbit (see McClain 1977; Danielson et al. 1994, and references therein). In this way, it is expected that the mean-to-osculating transformation is free from long-period terms, and, therefore, the resulting mean elements accurately represent the average behavior of the osculating orbit (Métris and Exertier 1995).

Taking these facts into account is of primordial importance when comparing canonical and non-canonical solutions (Lara et al. 2011, 2014). Moreover, special attention must be paid to the correct computation of the short-period elimination when Hamiltonian-simplification techniques are involved in the computation of the canonical solution (Lara et al. 2014b, a). On top on that some confusion is added since canonical-perturbation methods have been reported to be particularizations of non-canonical methods for the appropriate choice of the arbitrary integration functions of the slow variables that arise in the solution of each different approach (Morrison 1966). But this connection between canonical and non-canonical perturbation theories simply recalls the obvious: that canonical transformations are very particular instances of the wider field of transformation theory. Remarkably, the mean-to-osculating transformation that produces the exact separation between short- and long-period variations has been recognized as non-canonical for perturbed-Keplerian motion (Métris and Exertier 1995). More precisely, the exact separation of terms that are purely periodic in the mean anomaly can only be guaranteed up to the first order of the small parameter when using Hamiltonian methods (Ferraz-Mello 1999).

Regarding artificial-satellite theory, this issue is mainly relevant in the computation of second-order effects of the zonal harmonic of the second degree, hereafter noted \(J_2\). Indeed, for Earth-like bodies, the second-order effects of \(J_2\) are comparable to those produced by the higher-order harmonics of the gravitational potential, and, therefore, are routinely incorporated into operational software (Coffey and Alfriend 1984; Coffey et al. 1996; Folcik and Cefola 2012; Lara et al. 2018).

The generalized method of averaging (see Nayfeh 2004 p. 168 and ff., for instance) is a suitable, non-canonical option when approaching semi-analytically the solution of non-trivial perturbation models, which may include both Hamiltonian and non-Hamiltonian perturbations (McClain 1977). Rather, we focus on the simple \(J_2\) perturbation and resort to the versatile method of Lie transforms to compute explicit expressions of the mean variations as well as their concomitant periodic corrections. Beyond its original goal of dealing with perturbed Hamiltonian flows (Hori 1966; Deprit 1969), the Lie transforms method generally applies to systems of ordinary differential equations with minor modifications of the original formulation, and is readily implemented by means of efficient recursive algorithms (Kamel 1970; Henrard 1970). Most notably, the method allows for the explicit computation of the inverse, osculating-to-mean transformation, in addition to the direct, mean-to-osculating one. The former, we will see, is fundamental for understanding the consequences of choosing a mean-to-osculating transformation that is purely periodic in the mean anomaly in order to obtain the mean frequencies of the motion.

To clearly illustrate the non-canonical nature of a mean-to-osculating transformation that is purely periodic in the mean anomaly, we strip the formulation of non-essential complexities stemming from the closed-form integration of implicit functions of the mean anomaly. That is, we base our exposition on a \(J_2\)-type potential in which the implicit dependence of the \(J_2\)-problem on the mean anomaly is avoided by resorting to the usual expansions of the elliptic motion (Brouwer and Clemence 1961). Furthermore, we truncate these expansions to the lower orders of the eccentricity to shorten the length of printed expressions.

The toy model is assumed exact in the computation of the mean variations so that the mandatory analytical tests carried out to ensure the correctness of the theory provide immediate insight without need of making additional expansions. In particular, at each order of the perturbation approach we checked that the successive composition of the mean-to-osculating and osculating-to-mean analytic transformations yields formally the identity up to the truncation order of the theory. We also checked that replacing the transformation equations of the short-period elimination in the original, osculating variation equations, leads to mean variation equations that match term for term the mean frequencies obtained with the perturbation approach up to the truncation order of the perturbation solution. These tests and model also serve us to illustrate the paradox that the inverse of a non-canonical transformation that is purely periodic in the fast angle may bear long-period as well as non-periodic terms.

Moreover, the toy model permits the computation of high orders of the perturbation approach with relatively little computational effort. We need to compute them to show that, for a mean-to-osculating transformation that is purely periodic in the mean anomaly, the mean variation of the semimajor axis ceases to vanish at the third order. This is in clear contrast with the canonical-transformation approach, in which making the mean anomaly ignorable in the Hamiltonian definitely results in a constant mean semimajor axis at any order. Because of that, we may anticipate the inadequacy of a perturbation theory based on a purely periodic mean-to-osculating transformation for long-term propagation. Indeed, because the more important source of errors of a perturbation solution is related to the truncation of the mean frequencies, the neglected long-period effects in the variation of the semimajor axis unavoidably introduce long-period errors that will become dominant in the long term. Tests carried out to check the accuracy of perturbation solutions based on different choices of the mean-to-osculating transformation confirm this conjecture.

For the same reasons of simplicity and insight, we constructed the perturbation solution in Keplerian orbital elements, which are singular for circular orbits as well as for equatorial orbits. The implementation of alternative non-singular solutions useful for operational purposes can be approached analogously.

The paper is organized as follows. For completeness, the basic equations of the Lie-transforms method are summarized in Sect. 2. Then, the toy model is formulated in usual orbital elements in Sect. 3. Also in this section we discuss the two basic instances in which the computation of the m-th-order terms of the mean variations can be decoupled from the computation of the mean-to-osculating transformation of the same order, and illustrate the paradox that the inverse of a purely periodic transformation may yield long-period effects of higher order than the first. The perturbation solution based on a mean-to-osculating transformation that is purely periodic in the mean anomaly is described in Sect. 4, showing that the appearance of long-period terms in the variation of the mean semimajor axis starts at the third order. Section 5 deals with the case of a perturbation solution based on the purely periodic character of the vectorial generator of the Lie-transforms method, which, like in the Hamiltonian case, results in null mean variation of the semimajor axis at any order. Finally, selected propagations that illustrate the main features of each perturbation approach are presented in Sect. 6.

2 The Lie transforms method for vectorial flows

In this section, we present the basic formulation that should allow interested readers to reproduce our computations. Full details in the derivation of the algorithms can be consulted in the original reference of Kamel (1970), as well as in the reformulation by Henrard (1970), to which we rather adhere.

A Lie transformation \(x_j=x_j(y_k,\epsilon )\), with j and k integers ranging from 1 to l, is defined as the solution of the differential system

$$\begin{aligned} \frac{\textrm{d}{x}_j}{\textrm{d}\epsilon }=W_j(x_k,\epsilon ), \qquad j,k=1,2,\dots ,l, \end{aligned}$$
(1)

where \(\epsilon \) is the independent variable and \(W_j\) denote the l components of some vectorial generating function, for the initial conditions

$$\begin{aligned} y_j=x_j(y_k,0). \end{aligned}$$
(2)

When such kind of transformation is applied to an analytical function \(F=F(x_j,\epsilon )\) given by its Taylor-series expansion

$$\begin{aligned} F=\sum _{m\ge 0}\frac{\epsilon ^m}{m!}\,\left. \frac{\partial ^mF}{\partial \epsilon ^m}\right| _{\epsilon =0} =\sum _{m\ge 0}\frac{\epsilon ^m}{m!}\,F_{m,0}(x_j), \end{aligned}$$
(3)

the transformed function \(F^*=F(x_j(y_k,\epsilon ),\epsilon )\) can be directly obtained as a Taylor series in the new variables

$$\begin{aligned} F^*=\sum _{m\ge 0}\frac{\epsilon ^m}{m!}\, \left. \frac{\textrm{d}^mF}{\textrm{d}\epsilon ^m}\right| _{\epsilon =0} =\sum _{m\ge 0}\frac{\epsilon ^m}{m!}\,F_{0,m}(y_k), \end{aligned}$$
(4)

by the recursive computation of the coefficients \(F_{0,m}\) from Deprit’s triangle

$$\begin{aligned} F_{m,q+1}=F_{m+1,q}+\sum _{i=0}^m{m\atopwithdelims (){i}}{\mathcal {L}}_{i+1}(F_{m-i,q}), \end{aligned}$$
(5)

in which \({\mathcal {L}}\) denotes the linear, scalar operator

$$\begin{aligned} {\mathcal {L}}_{m}(\psi )=\sum _{k=1}^{l}\frac{\partial \psi }{\partial {x}_k}{W}_{k,m}, \end{aligned}$$
(6)

and \({W}_{k,m}\) are the coefficients of the Taylor-series expansion of the vectorial generator. Namely,

$$\begin{aligned} W_j=\sum _{m\ge 0}\frac{\epsilon ^m}{m!}\,W_{j,m+1}(x_k), \qquad j,k=1,2,\dots ,l. \end{aligned}$$
(7)

On the other hand, the formulation of a differential system, say

$$\begin{aligned} \frac{\textrm{d}x_j}{\textrm{d}t}=X_j(x_k,\epsilon )\equiv \sum _{m\ge 0}\frac{\epsilon ^m}{m!}\Phi _{j,m,0}(x_k), \quad \Phi _{j,m,0}=\left. \frac{\partial ^m{X}_j}{\partial \epsilon ^m} \right| _{\epsilon =0}, \end{aligned}$$
(8)

in the new variables \(y_j=y_j(x_k,\epsilon )\) needs to take the Jacobian of the transformation into account. Thus,

$$\begin{aligned} \frac{\textrm{d}y_j}{\textrm{d}t} =\sum _{k=1}^l\frac{\partial {y}_j}{\partial {x}_k}X_j (x_k,\epsilon )=Y_j(x_k,\epsilon ), \end{aligned}$$
(9)

whose series expansion in the new variables is

$$\begin{aligned} \frac{\textrm{d}y_j}{\textrm{d}t}=Y_j(x_k(y_i,\epsilon ),\epsilon ) \equiv \sum _{m\ge 0}\frac{\epsilon ^m}{m!}\Phi _{j,0,m}(y_k), \quad \Phi _{j,0,m}=\left. \frac{\textrm{d}^m{Y}_j}{\textrm{d} \epsilon ^m}\right| _{\epsilon =0}. \end{aligned}$$
(10)

Now, the coefficients \(\Phi _{j,0,n}\) are obtained directly in the new variables from the new recursion

$$\begin{aligned} \Phi _{j,m,q+1}=\Phi _{j,m+1,q}+\sum _{i\ge 0}^{m} {m\atopwithdelims (){i}}{\mathcal {L}}^*_{j,i+1}(\Phi _{k,m-i,q}), \quad j,k=1,2,\dots ,l, \end{aligned}$$
(11)

which still adheres to the structure of Deprit’s triangle but with a different, vectorial operator under the summations. To wit,

$$\begin{aligned} {\mathcal {L}}^*_{j,i}(\Phi _k)=\sum _{k=1}^l \left( \frac{\partial \Phi _j}{\partial {x}_k}W_{k,i} -\frac{\partial {W}_{j,i}}{\partial {x}_k}\Phi _k\right) , \quad j,k=1,2,\dots ,l. \end{aligned}$$
(12)

In a perturbation approach, we search for a generator that transforms the vectorial flow (8) to some desired, simplified form given by (10)—commonly with one of the variables removed up to a given order of the small parameter \(\epsilon \). For this task, the first order of recursion (11) yields

$$\begin{aligned} {\mathcal {L}}^*_{j,1}(\Phi _{k,0,0})=\Phi _{j,0,1}-{{\tilde{\Phi }}}_{j,0,1}, \end{aligned}$$
(13)

where \({{\tilde{\Phi }}}_{j,0,1}=\Phi _{j,1,0}\). After choosing the terms \(\Phi _{j,0,1}\) in agreement with our needs, Eq. (13) is solved for the \(W_{j,1}\) from the system of partial differential equations obtained replacing \({\mathcal {L}}^*_{j,1}\) from Eq. (12). Analogously, at the second order repeated iterations of Eq. (11) yield

$$\begin{aligned} {\mathcal {L}}^*_{j,2}(\Phi _{k,0,0})=\Phi _{j,0,2}-{{\tilde{\Phi }}}_{j,0,2}, \end{aligned}$$
(14)

where \({{\tilde{\Phi }}}_{j,0,2}=\Phi _{j,2,0}+{\mathcal {L}}^*_{j,1}(\Phi _{k,1,0})+{\mathcal {L}}^*_{j,1}(\Phi _{k,0,1})\) depends only on first-order terms, and hence is computable. Then, after choosing \(\Phi _{j,0,2}\) at our convenience, we solve Eq. (14) for \(W_{j,2}\). That is, in general, Eq. (11) is rearranged as the homological equation

$$\begin{aligned} {\mathcal {L}}^*_{j,m}(\Phi _{k,0,0}) =\Phi _{j,0,m}-{{\tilde{\Phi }}}_{j,0,m}, \qquad j=1,\dots ,l, \end{aligned}$$
(15)

in which the terms \({{\tilde{\Phi }}}_{j,0,m}\) are known from previous computations, whereas those \(\Phi _{j,0,m}\) are chosen in agreement with some desired objective. Therefore, everything becomes known in the homological equation save for the m-components of the vectorial generating function (7), which are then solved from the corresponding partial differential system.

The direct transformation

$$\begin{aligned} x_j=x_j(y_k,\epsilon )\equiv \sum _{m\ge 0}\frac{\epsilon ^m}{m!}x_{j,0,m}(y_k), \qquad j,k=1,\dots ,l, \end{aligned}$$
(16)

is derived from the vectorial generating function W as a particular instance of the scalar recursion (5) for the functions \(x_j=\sum _{m\ge 0}(\epsilon ^m/m!)\,x_{j,m,0}(x_k)\), in which \(x_{j,0,0}=x_j\) and \(x_{j,m,0}=0\) for \(m\ge 1\). The inverse transformation \(y_j=y_j(x_k,\epsilon )\) is analogously obtained from the vectorial generating function \(V_j=-W_j\), which in turn must be written in the \(y_k\) variables. Because W is itself a vectorial flow, the reformulation of \(W=W(x_k(y_k,\epsilon ),\epsilon )\) as a power series in the \(y_k\) variables is done based on Eq. (11), which is readily implemented replacing \(B_{j,i,0}=W_{j,i+1}(x_k)\). Once the terms \(B_{j,0,i}\) are computed recursively from Eq. (11), the inverse transformation

$$\begin{aligned} V_j=\sum _{m\ge 0}\frac{\epsilon ^m}{m!}\,V_{j,m+1}(y_k), \end{aligned}$$
(17)

is obtained by making \(V_{j,i+1}=V_{j,i+1}(y_k)\equiv -B_{j,0,i}(x_k)\vert _{\epsilon =0}\). In particular, \(V_1=V_1(y_k)\equiv -W_1(x_k)\vert _{\epsilon =0}\), from which it follows that the first-order terms of direct and inverse transformations are formally opposite—yet they are evaluated in distinct sets of variables. On the other hand, making \(m=q=0\) in Eq. (11) immediately yields \(B_{j,0,1}=B_{j,1,0}=W_{j,2}\), and hence \(V_2=V_2(y_k)\equiv -W_2(x_k)\vert _{\epsilon =0}\). Remark that this trivial equivalence between direct and inverse generating function terms no longer applies beyond the second order of \(\epsilon \).

3 A \(J_2\)-type perturbed Keplerian model

The \(J_2\) non-spherical term exerts the dominant gravitational perturbation of the Keplerian motion on Earth-orbiting, artificial satellites. This is the reason why this perturbation model is known as the “main problem” in the theory of artificial satellites (Brouwer 1959). For this problem, the only disturbance of the two-body potential \({\mathcal {V}}=-\mu /r\) is due to the term

$$\begin{aligned} {\mathcal {D}}=-\frac{\mu }{r}J_2\frac{R_{\oplus }^2}{r^2}\frac{1}{4}\left[ 2-3\sin ^2I+3\sin ^2I\cos 2(f+\omega )\right] , \end{aligned}$$
(18)

where \(r=a(1-e^2)/(1+e\cos {f})\) is the distance from the center of mass of the attracting body, a, e, I, \(\Omega \), \(\omega \), and M are usual Keplerian elements, denoting semimajor axis, eccentricity, inclination, right ascension of the ascending node, argument of the periapsis, and mean anomaly, respectively, whereas the true anomaly f is an implicit function of M and involves the solution of the Kepler equation. For a given body, the disturbing potential (18) is particularized by the physical parameters \(\mu \), \(R_{\oplus }\), and \(J_2\), standing for the gravitational parameter, the equatorial radius, and the oblateness coefficient, respectively.

The fact that the mean anomaly M, which is the fast angle to be removed in the computation of the mean variations, appears implicitly in Eq. (18) as a function of the true anomaly f, introduces additional complications in the solution of the integrals involved in the perturbation approach if the closed form is wanted. Therefore, in order to focus on the relevant facts of the solution in mean elements we rely on the usual expansions of the elliptic motion (Brouwer and Clemence 1961), which, besides, are truncated to the lower orders of the eccentricity. In this way, we not only sidestep many of the difficulties arising in the computation of the closed-form solution, but also shorten higher-order expressions stemming from the perturbation solution to a manageable extent.

Therefore, we replace the disturbing potential of the main problem in Eq. (18), by the substitute

$$\begin{aligned} {\mathcal {T}}&= \frac{\mu }{2a}J_2\frac{R_{\oplus }^2}{a^2}\frac{1}{4}\Big [ 2(3s^2-2)(1+3e\cos {M}) + 3es^2\cos (M+2\omega ) \nonumber \\&\quad -6s^2\cos (2M+2\omega ) -21es^2\cos (3M+2\omega ) \Big ], \end{aligned}$$
(19)

that depends explicitly on the mean anomaly, in which we abbreviate \(s\equiv \sin {I}\). Then, the variations of the osculating orbital variables are cast in the form of Eq. (8), where \(\epsilon =J_2\), and \(\textrm{d}x_j/\textrm{d}t\) denote the time variations of a, e, I, \(\Omega \), \(\omega \), and M, for \(j=1,\dots 6\), respectively. In particular,

$$\begin{aligned} \Phi _{j,0,0}&= 0, \qquad j<6, \end{aligned}$$
(20)
$$\begin{aligned} \Phi _{6,0,0}&= n, \end{aligned}$$
(21)
$$\begin{aligned} \Phi _{1,1,0}&= an\frac{R_{\oplus }^2}{a^2}\frac{3}{4}\big [ (6s^2-4)e\sin {M} +es^2\sin (M+2\omega ) -4s^2\sin (2M+2\omega ) \nonumber \\&\quad -21es^2\sin (3M+2\omega ) \big ], \end{aligned}$$
(22)
$$\begin{aligned} \Phi _{2,1,0}&= n\frac{R_{\oplus }^2}{a^2}\frac{\eta }{e}\frac{3}{8}\big [ e\eta (6s^2-4)\sin {M} +e(\eta -2)s^2\sin (M+2\omega ) \nonumber \\&\quad -4(\eta -1)s^2\sin (2M+2\omega ) -7e(3\eta -2)s^2\sin (3M+2\omega ) \big ], \end{aligned}$$
(23)
$$\begin{aligned} \Phi _{3,1,0}&= n\frac{R_{\oplus }^2}{a^2}\frac{cs}{\eta } \frac{3}{4}\big [ e\sin (M+2\omega ) -2\sin (2M+2\omega ) -7e\sin (3M+2\omega )\big ], \end{aligned}$$
(24)
$$\begin{aligned} \Phi _{4,1,0}&= -n\frac{R_{\oplus }^2}{a^2}\frac{c}{\eta } \frac{3}{4}\big [ 2 +6e\cos {M} +e\cos (M+2\omega ) -2\cos (2M+2\omega ) \nonumber \\&\quad -7e\cos (3M+2\omega )\big ], \end{aligned}$$
(25)
$$\begin{aligned} \Phi _{5,1,0}&= -n\frac{R_{\oplus }^2}{a^2}\frac{1}{e\eta }\frac{3}{8}\Big \{ 4e(s^2-1)\big [1-\cos (2M+2\omega )\big ] \nonumber \\&\quad +\big [e^2(6s^2-8)+6s^2-4\big ]\cos {M} +\big [e^2(s^2-2)+s^2\big ]\cos (M+2\omega ) \nonumber \\&\quad -7\big [e^2(s^2-2)+s^2\big ]\cos (3M+2\omega ) \Big \}, \end{aligned}$$
(26)
$$\begin{aligned} \Phi _{6,1,0}&= -n\frac{R_{\oplus }^2}{a^2}\frac{1}{e}\frac{3}{8}\Big \{ 4e\big [(3s^2-2-3s^2\cos (2M+2\omega )\big ] +(7e^2-1) \nonumber \\&\quad \times \big [(6s^2-4)\cos {M}+ s^2\cos (M+2\omega ) -7s^2\cos (3M+2\omega ) \big ] \Big \}. \end{aligned}$$
(27)

where \(n=(\mu /a^3)^{1/2}\) denotes the Keplerian mean motion, \(\eta =(1-e^2)^{1/2}\), and we also abbreviate \(c\equiv \cos {I}\). Terms \(\Phi _{j,m,0}\) vanish for \(m\ge 2\). The appearance of the eccentricity in denominators of the first-order terms of the variations of the argument of the periapsis and the mean anomaly given in Eqs. (26) and (27), respectively, may cause trouble in the integration of low-eccentricity orbits. However, because the toy model is chosen just for illustrative purposes this is not a concern, and we simply will take care in our numerical experiments of choosing initial conditions far away enough from problematic cases. Certainly, a perturbation solution intended for operational purposes should rather be implemented in some set of non-singular variables.

Remarkably, for perturbed Keplerian motion the homological equation of the Lie transforms method can be solved by indefinite integration. More precisely, for the m-th term, Eq. (15) turns into

$$\begin{aligned} W_{j,m}&=\frac{1}{n}\int \big ({{\tilde{\Phi }}}_{j,0,m} -\Phi _{j,0,m}\big )\textrm{d}M, \qquad j=1,\dots 5, \end{aligned}$$
(28)
$$\begin{aligned} W_{6,m}&=\frac{1}{n}\int \Big ({{\tilde{\Phi }}}_{6,0,m}-\Phi _{6,0,m}+\frac{\partial n}{\partial {a}}W_{1,m}\Big )\textrm{d}M, \end{aligned}$$
(29)

where \(\partial {n}/\partial {a}=-3n/(2a)\), as follows from the definition of the mean motion of a Keplerian flow. An attentive reader will have noticed the similarities between Eqs. (28)–(29) and Eqs. (55)–(58) of (Hori 1971).

It is important to note that \(\Phi _{j,0,m}\) should be chosen in such a way that it cancels the average of the known, tilde terms over the mean anomaly, namely, \(\langle {{\tilde{\Phi }}}_{j,0,m}\rangle _M\), in this way preventing the appearance of secular terms in the solution of the homological equation for \(j=1,\dots 5\). On the other hand, the choice of such \(\Phi _{6,0,m}\) that cancels the terms \(\langle {{\tilde{\Phi }}}_{6,0,m}-\frac{3}{2}(n/a)W_{1,m}\rangle _M\), thus avoiding the undesired secular terms, relies on the previous computation of \(W_{1,m}\). More precisely, we only need to know \(\langle {W}_{1,m}\rangle _M=C_{1,m}(a,e,I,\Omega ,\omega ,-)\), which can be chosen in advance in two relevant cases due to the freedom provided by the arbitrary integration function that arises in the integration of Eq. (28). In particular, imposing \(W_{1,m}\) to be purely periodic in the mean anomaly makes \(C_{1,m}=0\) trivially, and hence we can choose \(\Phi _{6,0,m}=\langle {{\tilde{\Phi }}}_{6,0,m}\rangle _M\) like in the other cases. Alternatively, imposing the mean-to-osculating transformation of the semimajor axis to be purely periodic in the mean anomaly, allows for the direct computation of \(C_{1,m}\) from previous orders of the perturbation solution.

For the last case, the mean-to-osculating transformation in Eq. (16) of the semimajor axis \(a=a'+J_2a_{0,1}+\frac{1}{2}J_2^2a_{0,2}+\dots \) is recursively computed from Eq. (5) as follows. At the first order \(a_{0,1}={\mathcal {L}}_{1}(a)=W_{1,1}\), as follows from the definition of the scalar operator in Eq. (6). Then,

$$\begin{aligned} C_{1,1}=0, \end{aligned}$$
(30)

and hence \(\Phi _{6,0,1}=\langle {{\tilde{\Phi }}}_{6,0,1}\rangle _M\). At the second order, \(a_{0,2}=a_{1,1}+{\mathcal {L}}_{1}(a_{0,1})\), where \(a_{1,1}=W_{1,2}\), as follows from Eq. (5). Hence \(W_{1,2}=a_{0,2}-{\mathcal {L}}_{1}(a_{0,1})\), where, for a purely periodic mean-to-osculating transformation \(\langle {a}_{0,2}\rangle _M=0\). Therefore, the computation of \(C_{1,2}=\langle {W}_{1,2}\rangle _M\) yields

$$\begin{aligned} C_{1,2}=-\langle {\mathcal {L}}_{1}(a_{0,1})\rangle _M =-\sum _{k=1}^6\Big \langle \frac{\partial {a}_{0,1}}{\partial {x}_k}W_{k,1}\Big \rangle _M, \end{aligned}$$
(31)

that only relies on first-order terms. Then, \(\Phi _{6,0,2}=\langle {{\tilde{\Phi }}}_{6,0,2}\rangle _M-\frac{3}{2}(n/a)C_{1,2}\). Analogously, at the third order, Eq. (5) leads to the sequence

$$\begin{aligned} \begin{aligned} a_{2,1}&= W_{1,3}, \\ a_{1,2}&= {\mathcal {L}}_{2}(a_{0,1}) +{\mathcal {L}}_{1}(a_{1,1}) +a_{2,1}, \\ a_{0,3}&= {\mathcal {L}}_{1}(a_{0,2}) +a_{1,2}, \end{aligned} \end{aligned}$$

from which \(W_{1,3}=a_{0,3}-{\mathcal {L}}_{1}(a_{0,2})-{\mathcal {L}}_{2}(a_{0,1})-{\mathcal {L}}_{1}(a_{1,1})\). Therefore, the requirement that \(\langle {a}_{0,3}\rangle _M=0\) yields

$$\begin{aligned} C_{1,3}=-\langle {\mathcal {L}}_{1}(a_{0,2})\rangle _M -\langle {\mathcal {L}}_{2}(a_{0,1})\rangle _M -\langle {\mathcal {L}}_{1}(a_{1,1})\rangle _M, \end{aligned}$$
(32)

and the long-period terms \(\langle {{\tilde{\Phi }}}_{6,0,3}\rangle _M-\frac{3}{2}(n/a)C_{1,3}\) that should be cancelled by \(\Phi _{6,0,3}\) are computed with the only knowledge of second-order terms and so on.

In a paradox, the choice of arbitrary functions that make the mean-to-osculating transformation purely periodic may prevent the inverse transformation from having the same nature. Using vectors, we denote \({\varvec{x}}={\varvec{x}}'+\epsilon {\varvec{x}}_{0,1}({\varvec{x}}')+\frac{1}{2}\epsilon ^2{\varvec{x}}_{0,2}({\varvec{x}}')+{\mathcal {O}}(\epsilon ^3)\) the mean-to-osculating transformation, and \( {\varvec{x}}'={\varvec{x}}+\epsilon {\varvec{x}}'_{0,1}({\varvec{x}})+\frac{1}{2}\epsilon ^2{\varvec{x}}_{0,2}'({\varvec{x}})+{\mathcal {O}}(\epsilon ^3)\) its inverse. Neglecting terms \({\mathcal {O}}(\epsilon ^3)\) and higher, their sequential composition yields

$$\begin{aligned} {\varvec{x}}=\Big [{\varvec{x}}+\epsilon {\varvec{x}}'_{0,1}({\varvec{x}}) +\frac{1}{2}\epsilon ^2{\varvec{x}}_{0,2}'({\varvec{x}})\Big ] +\epsilon {\varvec{x}}_{0,1}({\varvec{x}}+\epsilon {\varvec{x}}'_{0,1}({\varvec{x}})) +\frac{1}{2}\epsilon ^2{\varvec{x}}_{0,2}({\varvec{x}}), \end{aligned}$$
(33)

where the term \(\epsilon {\varvec{x}}_{0,1}\) still needs to be expanded. That is,

$$\begin{aligned} {\varvec{0}}= \epsilon \left[ {\varvec{x}}'_{0,1}({\varvec{x}})+{\varvec{x}}_{0,1} ({\varvec{x}})\right] +\frac{1}{2}\epsilon ^2\left[ {\varvec{x}}_{0,2}'({\varvec{x}}) +2{\varvec{x}}'_{0,1}({\varvec{x}})\frac{\partial {\varvec{x}}_{0,1}({\varvec{x}})}{\partial {\varvec{x}}} +{\varvec{x}}_{0,2}({\varvec{x}})\right] , \end{aligned}$$
(34)

in which \({\varvec{x}}'_{0,1}({\varvec{x}})\) and \({\varvec{x}}_{0,1}({\varvec{x}})\) cancel each other out because they are just opposite. Hence,

$$\begin{aligned} {\varvec{x}}_{0,2}'=-2{\varvec{x}}_{0,1}({\varvec{x}}) \frac{\partial {\varvec{x}}_{0,1}({\varvec{x}})}{\partial {\varvec{x}}} -{\varvec{x}}_{0,2}({\varvec{x}}), \end{aligned}$$
(35)

where \({\varvec{x}}_{0,2}\) is purely periodic in M by our choice of the arbitrary integration functions. However, the product \({\varvec{x}}_{0,1}\partial {\varvec{x}}_{0,1}/\partial {\varvec{x}}\) may give rise—and it certainly does for the \(J_2\) problem—to constant and long-period terms in spite of each factor is purely periodic in the mean anomaly.

Details on the construction of perturbation theories based in these two noteworthy cases are provided in the two following Sections.

4 Theory 1

In this Section, we obtain the perturbation solution based on a mean-to-osculating transformation that is purely periodic in the mean anomaly, which we label as “Theory 1”.

At first order, \(n=0\) and \(q=0\) in Eq. (11), and hence \({{\tilde{\Phi }}}_{j,0,1}=\Phi _{j,1,0}\). Besides, \(C_{1,1}=0\), as follows from Eq. (30), and we choose \(\Phi _{j,0,1}=\langle {{\tilde{\Phi }}}_{j,0,1}\rangle _M\). We obtain \(\Phi _{1,0,1}=\Phi _{2,0,1}=\Phi _{3,0,1}=0\), and

$$\begin{aligned} \Phi _{4,0,1}=-n\frac{R_{\oplus }^2}{a^2}\frac{3c}{2\eta }, \quad \Phi _{5,0,1}=-c\Phi _{4,0,1}, \quad \Phi _{6,0,1}=n\frac{R_{\oplus }^2}{a^2}\frac{3}{2}(3c^2-1). \end{aligned}$$
(36)

Then, the trivial integration of Eqs. (28)–(29) for \(m=1\) provides the first-order terms \(W_{j,1}\) of the vectorial generating function, each of which will depend on an arbitrary integration function \(C_{j,1}\equiv {C}_{j,1}(a,e,I,\Omega ,\omega ,-)\) save for \(C_{1,1}\), whose value has already been fixed.

The mean-to-osculating transformation is of the form of Eq. (16) and is computed using recursion (5) in which \(F_{m,0}=0\) for \(m\ge 1\) and F is successively replaced by each orbital element \(x_j\in (a,e,I,\Omega ,\omega ,M)\). In these equations, the arbitrariness of the functions \(C_{j,1}\) is suppressed by imposing that the transformation from mean elements to osculating elements be purely periodic in the mean anomaly, which yields \(C_{j,1}=0\). Then, we obtain

$$\begin{aligned} W_{1,1}&=a_{0,1}= -a\frac{R_{\oplus }^2}{a^2}\frac{3}{4}\big [ e(6s^2-4)\cos {M} +es^2\cos (M+2\omega ) -2s^2\nonumber \\&\quad \times \cos (2M+2\omega ) -7es^2\cos (3M+2\omega ) \big ], \end{aligned}$$
(37)
$$\begin{aligned} W_{2,1}&=e_{0,1}\nonumber \\&=-\frac{R_{\oplus }^2}{a^2}\frac{1}{8}\Big [6\eta ^2(3s^2-2)\cos {M} +3\eta (\eta -2)s^2\cos (M+2\omega ) \nonumber \\&\quad +\frac{6e\eta s^2}{1+\eta }\cos (2M+2\omega ) -7\eta (3\eta -2)s^2\cos (3M+2\omega ) \Big ], \end{aligned}$$
(38)
$$\begin{aligned} W_{3,1}&=I_{0,1}\nonumber \\&= -\frac{R_{\oplus }^2}{a^2}\frac{cs}{4\eta }\big [ 3e\cos (M+2\omega ) -3\cos (2M+2\omega ) \nonumber \\&\quad -7e\cos (3M+2\omega )\big ], \end{aligned}$$
(39)
$$\begin{aligned} W_{4,1}&=\Omega _{0,1}\nonumber \\&= -\frac{R_{\oplus }^2}{a^2}\frac{c}{4\eta }\big [ 18e\sin {M} +3e\sin (M+2\omega ) -3\sin (2M+2\omega )\nonumber \\&\quad -7e\sin (3M+2\omega )\big ], \end{aligned}$$
(40)
$$\begin{aligned} W_{5,1}&=\omega _{0,1}\nonumber \\&= -\frac{R_{\oplus }^2}{a^2}\frac{1}{e\eta }\frac{1}{8}\Big \{ 6[e^2(3s^2-4) +3s^2-2]\sin {M} \nonumber \\&\quad +3[e^2(s^2-2)+s^2]\sin (M+2\omega ) -6 e(s^2-1) \nonumber \\&\quad \times \sin (2M+2\omega ) -7[e^2(s^2-2)+s^2]\sin (3M+2\omega ) \Big \} \end{aligned}$$
(41)
$$\begin{aligned} W_{6,1}&=M_{0,1}\nonumber \\&= -\frac{R_{\oplus }^2}{a^2}\frac{1}{8e}\Big \{ (4e^2-1)\big [6(3s^2-2)\sin {M} +3s^2\sin (M+2\omega ) \nonumber \\&\quad -7s^2\sin (3M+2\omega )\big ]-9es^2\sin (2M+2\omega ) \Big \}. \end{aligned}$$
(42)

The reader will forgive the abuse of notation with the aim of reducing the number of printed expressions, for the components of the generator \(W_{j,m}\) depend on the osculating orbital variables, whereas the periodic corrections are functions of the mean variables. This change of the osculating variables by the mean ones in the periodic corrections, which also affects the mean variations, should be carried out at the end of the whole procedure in order to run the perturbation theory in a semi-analytical way. On the other hand, the first-order terms of the inverse, osculating-to-mean transformation, are formally the opposite of those in Eqs. (37)–(42), but they are evaluated in the original, osculating variables.

At the second order, the solution of Eqs. (28)–(29) needs the previous computation of the tilde terms \({{\tilde{\Phi }}}_{j,0,2}\). Repeated application of Eq. (11) yields

$$\begin{aligned} {{\tilde{\Phi }}}_{j,0,2}=\Phi _{j,2,0}+\sum _{k=1}^6\left[ W_{k,1}\frac{\partial (\Phi _{j,0,1}+\Phi _{j,1,0})}{\partial {x}_k} -(\Phi _{k,0,1}+\Phi _{k,1,0})\frac{\partial {W}_{j,1}}{\partial {x}_k}\right] , \end{aligned}$$
(43)

whose evaluation only involves straightforward operations. Then, the second-order terms of the mean variations of a, e, I, \(\Omega \), and \(\omega \) are chosen by averaging, to get

$$\begin{aligned}&\qquad \qquad \qquad \qquad \qquad \Phi _{1,0,2}= 0, \end{aligned}$$
(44)
$$\begin{aligned} \Phi _{2,0,2}&=-n\frac{R_{\oplus }^4}{a^4}\frac{9}{16} \frac{s^2e}{1+\eta }\left[ 11\eta ^2(3s^2-2)+3\eta (13s^2 -10)+12(s^2-1)\right] \sin 2\omega , \end{aligned}$$
(45)
$$\begin{aligned} \Phi _{3,0,2}&= n\frac{R_{\oplus }^4}{a^4}\frac{9}{16} \frac{1}{\eta ^2}\frac{cse^2}{1+\eta }\left[ 11\eta ^2 (3s^2-2)+3\eta (13s^2-10)+12(s^2-1)\right] \sin 2\omega , \end{aligned}$$
(46)
$$\begin{aligned} \Phi _{4,0,2}&= n\frac{R_{\oplus }^4}{a^4}\frac{3c}{16\eta ^2}\big \{ 33\eta ^3(43s^2-12)+104\eta ^2(s^2-1)-81\eta (15s^2-4) \nonumber \\&\quad -116(2s^2-1)+6\left[ 11\eta ^2(3s^2-1)+3\eta (13s^2-5)+6(2s^2-1)\right] \nonumber \\&\quad \times (\eta -1)\cos 2\omega \big \} , \end{aligned}$$
(47)
$$\begin{aligned} \Phi _{5,0,2}&= n\frac{R_{\oplus }^4}{a^4}\frac{3}{32\eta ^2}\big \{ 33\eta ^3(43s^4-86s^2+16) +52\eta ^2(3s^4-6s^2+4) -162\eta \nonumber \\&\quad \times (s^2-1)(15s^2-4) -116(s^2-1)(5s^2-2) +6\big [11\eta ^3(3s^4-6s^2+2) \nonumber \\&\quad +\eta ^2(9s^4-16s^2+8) -18\eta (s^2-1)(3s^2-1) -6(s^2-1)(5s^2-2) \big ] \nonumber \\&\quad \times \cos 2\omega \big \}. \end{aligned}$$
(48)

Finally, we compute \(C_{1,2}=\langle {W}_{1,2}\rangle _M\) from Eq. (31), to obtain

$$\begin{aligned} C_{1,2}&= -a\frac{R_{\oplus }^4}{a^4}\frac{3}{32\eta } \big \{ 21\eta ^3(43s^4-24s^2+8) +104\eta ^2s^2(s^2-2) \nonumber \\&\quad -15\eta (45s^4-24s^2+8) -232s^2(s^2-1) \nonumber \\&\quad +6(\eta -1)\left[ 7\eta ^2(3s^2-2) +\eta (27s^2-22)-12c^2\right] s^2\cos 2\omega \big \}, \end{aligned}$$
(49)

from which \(\Phi _{6,0,2}=\langle {{\tilde{\Phi }}}_{6,0,2}\rangle _M-\frac{3}{2}(n/a)C_{1,2}\), and hence

$$\begin{aligned} \Phi _{6,0,2}&= n\frac{R_{\oplus }^4}{a^4}\frac{3}{64\eta }\big \{ 459\eta ^3(43s^4-24s^2+8) +1456\eta ^2s^2(s^2-2) -315\eta \nonumber \\&\quad \times (45s^4-24s^2+8) -2784s^2(s^2-1) +6s^2\big [153\eta ^3(3s^2-2) \nonumber \\&\quad +28\eta ^2(3s^2-4) -105\eta (3s^2-2) -144(s^2-1)\big ]\cos 2\omega \big \}. \end{aligned}$$
(50)

It follows the solution of Eqs. (28) and (29) for \(m=2\) to obtain the components of the vectorial generator \(W_{j,2}\), which again introduce arbitrary integration functions that are particularized for obtaining a purely periodic, mean-to-osculating transformation. In addition to the function \(C_{1,2}\) in Eq. (49), for \(j\ge 2\) we readily obtain \(C_{j,2}=0\).

For instance, for the semimajor axis we obtain

$$\begin{aligned} a_{0,2}=a\frac{R_{\oplus }^4}{a^4}\frac{3}{32}\frac{1}{1+\eta } \sum _{i=0}^2\sum _{j=1+\delta _{2,i}}^{2i+2} \sum _{k=\delta _{2,i}}^{2+2\delta _{2i,j}}P_{i,j,k} \eta ^{k-1}e^{|{j}-2i|}s^{2i}\cos (2i\omega +jM), \end{aligned}$$
(51)

where \(\delta _{i,j}\) denotes the Kronecker delta and the inclination polynomials \(P_{i,j,k}\) are presented in Table 1. That \(a_{0,2}\) is purely periodic in the mean anomaly results from the subindex \(j\ge 1\). On the contrary, the inverse, osculating-to-mean correction to the semimajor axis takes the form

$$\begin{aligned} a_{0,2}'=a_{0,2,\textrm{long}}'+a\frac{R_{\oplus }^4}{a^4} \frac{3}{16}\sum _{i=0}^2\sum _{j=1}^{2i+2} \sum _{k=1-\delta _{2,i}}^{1+2\delta _{2i,j}}P'_{i,j,k} \eta ^{k-1}e^{|{j}-2i|}s^{2i}\cos (2i\omega +jM), \end{aligned}$$
(52)

with the new inclination polynomials \(P'_{i,j,k}\) of Table 2, and the long-period terms

$$\begin{aligned} a_{0,2,\textrm{long}}'= a\frac{R_{\oplus }^4}{a^4}\frac{3}{16}\sum _{i=0}^1 \sum _{k=0}^{3}P'_{i,0,k}\eta ^{k-1}s^{2i}\cos 2i\omega , \end{aligned}$$
(53)

with coefficients \(P'_{i,0,k}\) in the same table, which clearly show the non-purely periodic nature of the osculating-to-mean transformation announced in Eq. (35). Indeed, it is immediate to see that \(\langle {a}_{0,2}'\rangle _M=a_{0,2,\textrm{long}}'\). The same features are also observed in the direct and inverse corrections to the other orbital variables.

Table 1 Inclination polynomials \(P_{i,j,k}\) in Eq. (51)
Full size table
Table 2 Non-null coefficients \(P'_{i,j,k}\) in Eqs. (52) and (53)
Full size table

This apparent inconsistency in the osculating-to-mean transformation does not corrupt the solution, which, as desired, is made of the mean elements resulting from the numerical integration of the mean frequencies, and the analytic purely periodic corrections. Still, this kind of solution may be not the best one when the theory is intended for accurate long-term orbit propagation. To show that, we compute the third-order terms of the mean variations. Recalling that \(\Phi _{j,k,0}=0\) for \(k\ge 2\), from repeated iterations of recursion (11) we obtain

$$\begin{aligned} \begin{aligned} \Phi _{j,0,3}&= {\mathcal {L}}^*_{j,1}\left( \Phi _{j,0,2}\right) +\Phi _{j,1,2}, \\ \Phi _{j,1,2}&= {\mathcal {L}}^*_{j,2}\left( \Phi _{j,0,1}\right) +{\mathcal {L}}^*_{j,1}\left( \Phi _{j,1,1}\right) +\Phi _{j,2,1}, \\ \Phi _{j,2,1}&={\mathcal {L}}^*_{j,3}\left( \Phi _{j,0,0}\right) +2{\mathcal {L}}^*_{j,2}\left( \Phi _{j,1,0}\right) +\Phi _{j,3,0}, \end{aligned} \end{aligned}$$

where, from the same recursion, \(\Phi _{j,1,1}=\Phi _{j,0,2}-{\mathcal {L}}^*_{j,1}\left( \Phi _{j,0,1}\right) \). Then, the computable terms are \({{\tilde{\Phi }}}_{j,0,3}={\mathcal {L}}^*_{j,1}\left( \Phi _{j,0,2}+\Phi _{j,1,1}\right) +{\mathcal {L}}^*_{j,2}\left( \Phi _{j,0,1}+2\Phi _{j,1,0}\right) \), and, like before, we compute the third-order components of the mean variations as \(\Phi _{j,0,3}=\langle {{\tilde{\Phi }}}_{j,0,3}\rangle _M\) for \(j<6\), whereas the computation of \(\Phi _{6,0,3}=\langle {{\tilde{\Phi }}}_{6,0,3}-\frac{3}{2}(n/a)W_{1,3}\rangle _M\) requires the preliminary computation of \(C_{1,3}=\langle {W}_{1,3}\rangle _M\) from Eq. (32). For \(j=1\) we obtain

$$\begin{aligned} \Phi _{1,0,3}&= an\left( \frac{R_{\oplus }}{a}\right) ^6 \frac{c^2s^2e^2}{\eta ^2(1+\eta )}\frac{81}{16}\left[ 7\eta ^2(3s^2-2)+\eta (27 s^2-22)+12(s^2-1) \right] \sin 2\omega . \end{aligned}$$
(54)

The non-vanishing character of the mean variation of the semimajor axis is a crucial fact that remains hidden when the perturbation approach is truncated to the lower orders. Indeed, due to the Lyapunov instability of the Keplerian motion, the semimajor axis is the more sensitive element in the propagation of errors. So neglecting these terms of the variation of the mean semimajor axis, how tiny they may be, sooner or later will introduce observable errors in the mean elements propagation. This feature of Theory 1 will be clearly illustrated in the semi-analytical propagations presented in Sect. 6.

Finally, it is worth mentioning that the formulation of Theory 1 in a different set of variables, as for instance, non-singular ones based on the semi-equinoctial elements \(\kappa =e\cos \omega \), \(\sigma =e\sin \omega \), while feasible, will lose the purely periodic character of the mean-to-osculating transformation as soon as we reach the second order. The reason is the same stated above that the product of two purely periodic terms yields, in general, non-periodic terms. Thus, for instance, up to second-order terms \(\kappa =(e'+\epsilon {e}_{0,1}+\frac{1}{2}\epsilon ^2e_{0,2})\cos (\omega '+\epsilon \omega _{0,1}+\frac{1}{2}\epsilon ^2\omega _{0,2}) \), which, after expansion and truncation to \({\mathcal {O}}(\epsilon ^3)\) yields

$$\begin{aligned} \kappa&= e'\cos \omega ' +\epsilon \left( e_{0,1}\cos \omega '-\omega _{0,1}e'\sin \omega '\right) +\frac{1}{2} \epsilon ^2\left( e_{0,2}\cos \omega '-\omega _{0,2}e'\sin \omega '\right) \nonumber \\&\quad -\frac{1}{2}\epsilon ^2\left( 2e_{0,1}\omega _{0,1}\sin \omega '+\omega _{0,1}^2e'\cos \omega '\right) , \end{aligned}$$
(55)

where the products \(e_{0,1}\omega _{0,1}\) and \(\omega _{0,1}^2\) will naturally spring long-period terms that will remain after reformulation of the orbital elements into semi-equinoctial variables. Therefore, Theory 1 should be recomputed in the new variables from scratch if we want to preserve the purely periodic character in the fast variable of the mean-to-osculating transformation.

5 Theory 2

Other case in which the successive order of the mean variations can be computed based only on previous orders of the vectorial generator is when we prescribe the vectorial generating function to be purely periodic in the mean anomaly. That is, the arbitrary integration functions \(C_{j,m}=\langle {W}_{j,m}\rangle _M\) vanish at any order of the perturbation theory. We label this case as Theory 2.

To the first order, both approaches match and the results in Sect. 4 apply also to this case. At the second order, for \(j<6\) the mean frequencies \(\Phi _{j,0,2}\) are the same as those given in Eqs. (44)–(48), but the integration function \(C_{1,2}\) in Eq. (49) must be replaced by \(C_{1,2}=0\). Hence,

$$\begin{aligned} \Phi _{6,0,2}&= n\frac{R_{\oplus }^4}{a^4}\frac{3}{32\eta }\big \{ 198\eta ^3(43s^4-24s^2+8) +572\eta ^2s^2(s^2-2) -135\eta (45s^4 \nonumber \\&\quad -24s^2+8)-1044s^2(s^2-1)+6s^2\big [ 66\eta ^3(3s^2-2) +11\eta ^2(3s^2-4) \nonumber \\&\quad -45\eta (3s^2-2)-54(s^2-1) \big ]\cos 2\omega \big \}, \end{aligned}$$
(56)

whose structure is analogous to Eq. (50) but with different coefficients. The second-order terms of the vectorial generator \(W_{j,2}\) are consequently the same as before for \(j<6\), but change for \(W_{6,2}\). Since they all are involved in the computation of each transformation equation, now all of them are affected of long-period terms, which at this order are exactly the same in the direct and inverse transformations.

In particular, now

$$\begin{aligned} a_{0,2}=a_{0,2,\textrm{short}}+a_{0,2,\textrm{long}}, \end{aligned}$$
(57)

where \(a_{0,2,\textrm{short}}\) is the same as Eq. (51), which only comprises short-period terms, and the long-period terms \(a_{0,2,\textrm{long}}\) are exactly one half of those reported in Eq. (53). Analogously, now

$$\begin{aligned} a'_{0,2}=a'_{0,2,\textrm{short}}+a'_{0,2,\textrm{long}}, \end{aligned}$$
(58)

where the short-period terms \(a'_{0,2,\textrm{short}}\) are those obtained from Eq. (52) as \(a_{0,2}'-a_{0,2,\textrm{long}}'\), whereas \(a'_{0,2,\textrm{long}}=a_{0,2,\textrm{long}}\). The same happens to the other variables, in which the long-period terms appearing in the osculating-to-mean transformations of the previous approach are now distributed in equal parts between the direct and inverse transformation.

Contrary to Theory 1, the current choice of a purely short-periodic vectorial generator makes that now the variation of the mean semimajor axis vanishes at each order. Besides, since there are not special requisites related to the periodic character of the short-period elimination, Theory 2 can be reformulated in a different set of variables without need of approaching the Lie transformations from scratch, as it also happens in the Hamiltonian case (Lyddane 1963; Deprit and Rom 1970).

6 Semi-analytical propagations: A test case

The aim of this section is just to illustrate the different behavior of the two non-canonical perturbation theories described in the previous sections. The actual relevance of the differences observed between both kinds of solutions regarding the implementation of operational software falls out of the scope of the current study. Therefore, we are satisfied with running our tests for a favorable case in the orbital variables used, which we borrow from (Coffey and Alfriend 1984). In particular, we limit the reported tests to the case of an elliptical orbit with \(e=0.2\), \(I=20^\circ \), \(a=9500\) km, \(\Omega =0.1\) rad, \(\omega =274.56^\circ \), and \(M=0\). The gravity-field parameters used in the propagations are \(\mu =398600.4415\;\mathrm {km^3/s^2}\), \(R_{\oplus }=6378.1363\) km, and \(J_2=0.001082634\).

First of all, we recall that a semi-analytic propagation is made of three parts. The osculating-to-mean transformation is applied first to the initial conditions in order to get the initial state in mean variables, as well as, more importantly, to initialize the mean frequencies of the motion. Next, the mean variations are integrated numerically for the mean initial conditions, which is achieved with very long steps. Finally, osculating elements are obtained at each evaluation step from the mean-to-osculating transformation. Because the more important source of errors stems from the mean-elements propagation, usual perturbation theories include a higher order of the mean variations than the order of the periodic corrections (Brouwer 1959; Kozai 1959; Deprit and Rom 1970; McClain 1977). On the other hand, the initialization process is crucial to avoiding the abnormal growth of errors in the along-track direction, so the osculating-to-mean transformation is commonly patched including higher-order information related to the semimajor axis conversion (Lyddane and Cohen 1962; Breakwell and Vagners 1970; Lara 2021a, 2022). In this fashion, we denote as m-th order a theory that comprises the \((m+1)\)-th-order effects of the mean frequencies and the m-th-order effects of the transformation equations, but in which the osculating-to-mean transformation is patched with the \((m+1)\)-th-order effects of the semimajor axis. The usual calibration of the solution using the energy equation is not used in this case to strictly adhere to the general formulation of a non-Hamiltonian problem.

The first-order effects of both distinct perturbation approaches yield identical terms. However, in our notation of a first-order theory they disagree in \(a'_{0,2}\), cf. Eqs. (52)–(53) and Eq. (58), as well as in \(\Phi _{6,0,2}\), cf. Eqs. (50) and (56). These small differences in the formulation produce small but significant changes in the time-history of the errors resulting from each perturbation theory, which are computed with respect to a reference orbit obtained from the numerical integration of the osculating variations provided by Eqs. (20)–(27).

The time-histories of the root sum square (RSS) of the position errors for a three-day semi-analytic propagation of the test case with each theory are shown in Fig. 1, where we observe that the RSS errors remain of the same order and present the same behavior. This kind of representation is useful in illustrating the accuracy of each theory for orbit-prediction purposes, but does not illustrate relevant differences between the two distinct perturbation approaches.

Fig. 1
figure 1

Test case. Position errors of the first order of Theory 1 (left) and 2 (right)

Full size image

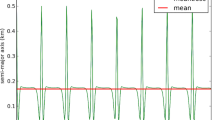
More precisely, Theory 1 yields mean elements that strictly adhere to the average behavior of the osculating orbit, as expected, which is not the case of Theory 2. This is illustrated in Fig. 2  for the semimajor axis, which shows that the propagation errors are of the same order and behave almost identically, with periodic oscillations of the same amplitude. However, the average of the errors, depicted by horizontal black lines in each plot of Fig. 2, nearly vanishes for Theory 1, averaging to about 1 cm in this example, whereas it is affected of a clear shift from the zero average in the case of Theory 2, of about 3 m in this particular propagation. Differences in the time-histories of the errors of the other orbital elements obtained with each theory, as well as in their respective averages, are of minor nature and are not presented. In particular, with both theories the errors of the eccentricity average to \(\sim 10^{-6}\) for the test case, and to values below one tenth of arc second for the orbital angles.

Fig. 2
figure 2

Test case. Semimajor axis errors of the first order of Theory 1 (left) and 2 (right)

Full size image

Taking additional terms clearly improves the accuracy of each perturbation theory, whose position errors reduce from tens of meters to several centimeters when propagating the test case with second-order theories, in agreement with a \({\mathcal {O}}(J_2)\) improvement. This is shown in Fig. 3, where we also note the lower amplitude of the RSS errors resulting from Theory 1. Nevertheless, in view of the RSS errors that remain in both cases with values of the expected order of the truncation of the perturbation theory, we consider that both theories are of comparable accuracy for the test case along the 3-day interval. In particular, in both propagations the errors are \({\mathcal {O}}(10^{-8})\) relative to distance.

Fig. 3
figure 3

Test case. Position errors of the second order of Theory 1 (left) and 2 (right)

Full size image

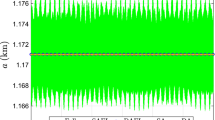
Correspondingly, the propagation errors of the semimajor axis reduce their amplitude from the meter to the centimeter level, as depicted in Fig. 4, also in agreement with the expected improvement provided by an additional order of the perturbation theories. As shown in the right plot of Fig. 4, the shift from the zero-average in Theory 2 remains, but now reduced to less than 1 cm due to the general improvements of the perturbation solution. The semimajor axis’ errors stemming from the semi-analytical propagation using Theory 1 fall now below the mm level. Regarding the errors of the other orbital elements, they remain small as well as similar in both cases, like it happened to the lower-order solutions.

Fig. 4
figure 4

Test case. Semimajor axis errors of the first order of Theory 1 (left) and 2 (right)

Full size image

On the other hand, as already pointed out in the text, the apparent superiority of Theory 1 must be better qualified. For the truncation of the non-vanishing mean variation of the semimajor axis, additional errors mainly affecting the mean motion and hence the mean-anomaly propagation turn this perturbation theory into a less accurate tool for long-term propagation. This is illustrated for the second-order versions of the perturbation theories in Fig. 5, in which the propagation interval of the test case is extended from 3 days to 3 weeks. Now, rather than RSS errors, we display the projections of the position error in the intrinsic (along-track, radial, and cross-track) directions, which better illustrate the nature of the resulting errors. Thus, we clearly see that along-track errors resulting from Theory 1 notably deteriorate passed one week and a half, whereas those of Theory 2 only worsen slightly (top plots of Fig. 5). This is the expected consequence of the truncation error of the mean motion in the propagation of the mean anomaly, which does not affect Theory 2 as far as the mean variation of the semimajor axis vanishes at any order. Due to the elliptic character of the test orbit, this error in the mean anomaly propagation is also observed in the radial errors, yet with less adverse effects (center plots of Fig. 5), but barely affects the errors in the cross-track direction (bottom plots of Fig. 5).

Fig. 5
figure 5

Intrinsic errors of a 3-week semi-analytical propagation of the test case with second-order Theory 1 (left) and Theory 2 (right)

Full size image

Still, there is no doubt that Theory 1 is certainly correct. To check that, we patched both second-order theories with the fourth-order terms of the mean variation of the semimajor axis, which changes nothing in Theory 2 for the vanishing of the mean semimajor axis in this approach, but clearly refines Theory 1. These additional corrections bring both theories again to comparable accuracy for orbit propagation purposes, as shown in Fig. 6, in which the plots in the right column are the same as corresponding ones in the right column of Fig. 5 but represented in different scales to ease comparison. It is worth to mention that in this last case, the second-order patched Theory 1 provides errors of the semimajor axis that average to just a few hundredths of mm, whereas the average of the semimajor axis error of Theory 2 remains in the cm level in spite of the expanded propagation interval. As before, the errors of the other orbital elements presented by each distinct theory are analogous and very small. On the other hand, the amplitude of the errors remain similar to the previous case because the patched theories still rely only on second-order direct corrections.

Fig. 6
figure 6

Intrinsic errors of a 3-week semi-analytical propagation of the test case with second-order patched Theory 1 (left) and Theory 2 (right)

Full size image

For reference, the relative RSS error between both different semi-analytical solutions is presented in Fig. 7  for the last case, showing that they remain within \(10^{-8}\) of the satellite’s distance (corresponding to the cm level) in the chosen time interval.

Fig. 7
figure 7

Relative RSS position errors between the second-order patched theories 1 and 2

Full size image

The choice of the step size for the numerical integration of the mean variations obviously affects the accuracy of both perturbation theories. For this particular example, we checked that the accuracy of the semi-analytical solutions using the standard Runge–Kutta method of the Mathematica 12 software, does not suffer significant changes for constant integration step sizes as long as 2 days, which amounts to about 19 orbital periods. Undeniably, patching the mean variation of the semimajor axis with additional terms increases the computational burden of Theory 1. However, the increase is just slight, and due to the small number of steps needed in the numerical-integration part, this fact should not be taken as a critical shortcoming of patched-Theory 1.

Finally, we must mention that, beyond the illustration purposes of this Section, both perturbation solutions of the toy model have been also obtained in non-singular variables—recomputed for Theory 1, to preserve the purely periodic character of the mean-to-osculating transformation, and simply reformulated in the case of Theory 2—in this way allowing us to carry out additional tests for less elliptical orbits that, while non-exhaustive, confirm the reported characteristics of each distinct perturbation approach.

7 Conclusions

For perturbed Keplerian motion, a non-canonical perturbation theory based on a mean-to-osculating transformation that is purely periodic in the fast angle has the advantage of providing mean elements that strictly adhere to the average evolution of the osculating orbit. On the other hand, extending this kind of perturbation theory to higher orders shows that the mean variation of the semimajor axis only vanishes up to second order of \(J_2\) effects. Because the accuracy of a perturbation solution for a given time is essentially related to the truncation order of the mean frequencies, and on account of the Lyapunov instability that is inherent to Keplerian motion, the non-vanishing of the mean variation of the semimajor axis turns the theory based on the purely periodic, mean-to-osculating transformation less accurate for long-term propagation than classical perturbation approaches due to increasing errors in the along-track direction. Therefore, there is not an always-best perturbation approach, and the choice of the proper kind of perturbation theory must be done depending on the user’s particular needs.

For didactic purposes, the exposition avoids the use of implicit functions of the mean anomaly and relies on a toy model in common orbital elements, which has been derived from the \(J_2\) problem by means of usual expansions of the elliptic motion. Computing an analogous theory in closed form requires to confront the solution of non-trivial integrals. Still, most of the solutions of these integrals are already reported in the literature or can be approached with known techniques of integral calculus. The computation of such kind of perturbation solution is under development and will be published elsewhere when fully completed and tested.