Presence-Only for Marked Point Process Under Preferential Sampling

Abstract

Preferential sampling models have garnered significant attention in recent years. Although the original model was developed for geostatistics, it founds applications in other types of data, such as point processes in the form of presence-only data. While this has been recognized in the Statistics literature, there is value in incorporating ideas from both presence-only and preferential sampling literature. In this paper, we propose a novel model that extends existing ideas to handle a continuous variable collected through opportunistic sampling. To demonstrate the potential of our approach, we apply it to sardine biomass data collected during commercial fishing trips. While the data is intuitively understood, it poses challenges due to two types of preferential sampling: fishing events (presence data) are non-random samples of the region, and fishermen tend to set their nets in areas with a high quality and value of catch (i.e., bigger schools of the target species). We discuss theoretical and practical aspects of the problem, and propose a well-defined probabilistic approach. Our approach employs a data augmentation scheme that predicts the number of unobserved fishing locations and corresponding biomass (in kg). This allows for evaluation of the Poisson Process likelihood without the need for numerical approximations. The results of our case study may serve as an incentive to use data collected during commercial fishing trips for decision-making aimed at benefiting both ecological and economic aspects. The proposed methodology has potential applications in a variety of fields, including ecology and epidemiology, where marked point process model are commonly used.

1 Introduction

Quantitative ecology faces a significant challenge in the form of Species Distribution Models (SDMs), which involve methodologies with a twofold objective. The first objective is to explain the occurrence of species in relation to geological, ecological, and climactic factors. The second objective is to predict the occurrence of these species in a specified region. SDMs have broad applications in fields, such as conservation and reserve planning, evolution, epidemiology, and invasive-species management (Phillips et al. 2006).

Collecting ecological data scientifically is often costly, requiring meticulous planning, consideration of study objectives, and the use of specialized equipment and personnel. Consequently, researchers rely on other sources of information, particularly data that has not been randomly or systematically collected. Such cases are known as opportunistic sampling and can result in biased information. However, if the model accounts for the bias, it can provide accurate estimates of scientifically relevant quantities.

Presence-only data arises from opportunistic sampling, where only the observed locations of the object of study are collected. A point process, as described by Cressie (1993), is appropriate for analyzing this type of data, but sampling bias can result in higher intensity in locations that are more easily accessible to observers. For instance, a group of biologists studying a particular species may only record its presence in areas that are readily accessible to them. This is a typical case of a presence-only point process for which the event locations are acquired in a preferential manner. Moreira and Gamerman (2022) addressed this issue by incorporating suitable covariates into the intensity function to mitigate the bias associated with data collection. These authors employed exact inference on an inhomogeneous Poisson process (IPP) and tackled identifiability issues mentioned in Fithian and Hastie (2013) and Dorazio (2014).

The problem becomes more complex when there is a measured variable associated with the observed locations. For instance, in fishery-dependent data, the amount of fish caught (in kg) is often recorded along with the fishing location. In such cases, the point process model proposed by Moreira and Gamerman (2022) is inadequate. In this work, we present a novel model by extending the approach in the aforementioned paper to a marked point process model. Additionally, fishing trips are likely to favor locations with higher fish biomass, leading to biased sampling. In such cases, the preferential sampling approach described by Diggle et al. (2010) is appropriate, but requires an adjustment to the presence-only field. This work combines these concepts to handle opportunistically sampled marked point processes. Note that this implies preferentiality occurs in two ways: in the acquisition of presence-only data and in the biased collection of the marks.

There have been previous attempts to deal with presence-only data in the context of preferential sampling, such as the approach taken by Gelfand and Shirota (2019) to model the sampling bias of presence-only data. However, the literature lacks methods that consider the case where preferential sampling of a continuous measurement occurs in addition to presence-only sampling. This is often the case in fishery data collected during fishing trips.

Fishermen often select areas associated with high quality and value of catch (e.g., larger schools of the target species), although they may occasionally prefer smaller catches if there are strict catch limits imposed by conservation laws. It is also assumed that fish abundance is a variable that exhibits spatial smoothness, which is modeled using a Gaussian Process as described in Cressie (1993). Therefore, it is reasonable to assume that this process can also be used to measure the sampling bias derived from the measured variable abundance.

The inclusion of a Gaussian Process in the intensity function extends Moreira and Gamerman (2022) presence-only model. This idea draws inspiration from the doubly stochastic process of Gonçalves and Gamerman (2018). To enhance computational efficiency, the recent nearest neighbor approach of Datta et al. (2016b) has been adapted for the point process context and discussed in the work of Shirota and Banerjee (2019). The proposed model aims to probabilistically define the spatially biased sampling of fish locations, along with their preferentially collected biomass, while avoiding approximations that are typical of Poisson process models.

This manuscript is divided into five main sections. Section 2 presents the motivating dataset and proposes a method to accurately estimate the point process intensity and marks while accounting for preferential sampling. In Sect. 3, we present a brief study using an artificial dataset. In Sect. 4, we apply the model to real-world data from a fishery case study in the south of Portugal. Lastly, Sect. 5 provides a discussion of the results, their implications, and limitations.

2 Proposal

2.1 Motivation

The motivation for the development proposed in this manuscript is supported by data from the sardine purse-seine fishery on the Portuguese south coast for the years 2011–2013. During this period, restrictions on sardine fishing were similar between years and lower than in subsequent years (ICES 2018). To obtain the data, vessel monitoring system (VMS) and logbook data from purse-seine vessels (>15 m) were merged based on the date-time of the start and end of a fishing trip and fishing vessel. Fishing sets were identified by analyzing vessel speed patterns. The start of a set was indicated by a rapid drop in velocity, followed by a 30–60 min period of low speed while the net was set and hauled. The end of a set was signaled by a rapid increase in velocity. Consecutive drops and increases in speed were used to identify the beginning and end of fishing sets (Katara and Silva 2017). To avoid bias, fishing trips with only one fishing set were selected since there is no information on how total catches are distributed by fishing set when a fishing trip has more than one fishing set. The final dataset consisted of N = 1211 fishing sets and included information, such as vessel ID, landing harbor, year, month, fishing set location (latitude, longitude), and sardine catch (in kg). It is important to note that the data on fishing set location and respective catches/biomass may be considered presence-only data since there are no records of fishing sets with zero catches.

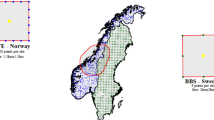
The left-hand side of Fig. 1 shows the locations of all fishing sets. As fishermen are likely to favor areas with higher abundance, this illustrates an example of preferential sampling. To accurately model this case study, a model parameter is required to quantify the degree of preferentiality, which should have a positive estimate significantly different from zero. Depth is a significant driver of sardine occurrence, as shown in Fig. 1. This species prefers coastal shelf waters, particularly at depths above 150 m, where it forms dense schools during the day. Purse seine daily fishing trips are typically short, lasting between 2 and 18 h. The duration of trips and the distances traveled to fishing grounds vary across the country. In the south, fishing trips extend into the morning, and usually involve one or two fishing sets in the evening. The number of sets per trip is directly related to the abundance and volume of the target species. Fishermen prefer to fish near the port and within the shallower half of the continental shelf to reduce fuel use and travel time. In Portugal’s south coast, water depth can be used as a proxy for the distance from the coast. Therefore, the proposed method must be able to handle correlated explanatory variables that explain both the occurrence of fish and the volume caught by fishermen.

Fig. 1

Water depth and fishing sets locations for sardine catches in the southern coast of Portugal during the period between 2011 and 2013. Portugal is identified with the letter ‘P’ and Spain with ‘S’. Left-hand side: Wider region. Right-hand side: Zoom on the studied region, south coast of Portugal

Figure 1 indicates that the points are more concentrated near shallow areas, as expected. However, without a model, it is nearly impossible to determine the extent to which this phenomenon is due to sardines preferring shallow waters or fishermen preferring proximity to ports. The proposed model takes into account the sampling issues illustrated in this case study, which we believe are representative of many other case studies.

2.2 Model and Notation

The proposed model uses a data augmentation scheme to achieve exact computation of the Inhomogeneous Poisson Process likelihood, similarly to Adams et al. (2009), Gonçalves and Gamerman (2018) and Moreira and Gamerman (2022).

The available data is composed of an unordered set of paired variables observed in a closed region $\mathcal {D}$ and denoted $(X, Z) = \{(x_1, z_1), \ldots , (x_{n_x}, z_{n_x})\}$. The component $x_i$ represents the i-th location of sardines fishing sets and $z_i$ represents its recorded catch (in biomass, kg). Catch in each location is also denoted as a process in the form $Z(s), s\in x$.

The data are modeled as a marked point process based on the Inhomogeneous Point Process (IPP). In addition, a data augmentation scheme is used to avoid performing approximations of the likelihood function.

$$\begin{aligned} \begin{aligned} X&\sim IPP(q(\cdot )p(\cdot )\lambda ^*)\\ X'&\sim IPP(q(\cdot )(1-p(\cdot ))\lambda ^*)\\ U&\sim IPP((1-q(\cdot ))\lambda ^*)\\ Z(s)\mid s\in x\cup x'&\sim logNormal(W_z(s) \beta _z + S(s), \tau ^2),\hspace{0.1cm} s\in \mathcal {D}\\ logit\hspace{0.1cm} q(s)&= W_{int}(s)\beta _{int},\hspace{0.1cm} s\in \mathcal {D}\\ logit\hspace{0.1cm} p(s)&= W_{obs}(s)\beta _{obs} + \gamma S(s),\hspace{0.1cm} s\in \mathcal {D}\\ S(\cdot )&\sim NNGP\left( 0, \sigma ^2\rho (\cdot )\right) ,\\ \end{aligned} \end{aligned}$$

(1)

where $W_z(\cdot ), W_{int}(\cdot )$ and $W_{obs}(\cdot )$ are sets of covariates, needed to correctly model the distribution of the marks, the probability of occurrence and the probability of observation, respectively.

Similarly to Moreira and Gamerman (2022), the process $X'$ represents the unobserved occurrences of the species. Process U does not have a direct physical interpretation. It is included purely to achieve the result which allows exact analytical computation of the likelihood function, as initially proposed by Adams et al. (2009). Note that the data augmentation is done not only with regards to point processes, in the form of $X'$ and U, but also for $Z(s), s\in x'$. Also note that the inclusion of the S(s) process extends the work of Moreira and Gamerman (2022). The adjustment not only adds further spatial dependence to the process, but also computational complexity which must be addressed.

Process $NNGP(\cdot , \cdot )$ stands for Nearest Neighbor Gaussian Process, initially proposed in Datta et al. (2016b). It is also discussed by Datta et al. (2016a), Banerjee (2017), Finley et al. (2019) and is used in the context of exact inference of Poisson Processes by Shirota and Banerjee (2019). The set of parameters which index this distribution is collected under the notation of $\theta$.

Parameter $\gamma$ measures the preferentiality of the biomass sampling procedure. The complete infinite-dimensional vector of unknown quantities is $\Theta = \left( \beta _z, \beta _{int}, \beta _{obs}, \gamma , \lambda ^*, X', Z(\cdot ), U, S(\cdot ), \theta \right)$. Note that, although $Z(\cdot )$ is mathematically defined in the whole region $\mathcal {D}$, it only makes physical sense to exist in the respective observed and latent locations of X and $X'$.

An intuitive visualization of the modeled intensities can be done. For simplicity and without loss of generality, suppose that $\mathcal {D}$ has only one dimension. Then the intensity functions can be plotted in a simple manner, as illustrated in Fig. 2.

Fig. 2

Simplified visualization of an example of one-dimensional intensity functions under the proposed model. The process of observations X, when superposed with the unobserved occurrences $X'$, yields the process of all occurrences in the region. Process U is necessary to complete the occurrences to achieve a total homogeneous process

Notice that the intensities of X, $X'$ and U, when added together, conveniently yield the constant $\lambda ^*$. This is what permits the proposal to avoid approximations of the likelihood, as the integral of the joint intensity is the integral of a constant in the region. This simply equals the constant times the area of the region, that is, $\lambda ^*|\mathcal {D}|$. Additionally, X and $X'$ sum up to acquire the occurrences intensity. This way, it is intuitive to separate the observed and unobserved occurrences.

2.3 Inference

The inference is done under the Bayesian paradigm on the posterior distribution (see Gelman et al. 2013) $\pi (\Theta \mid x, z)\propto L_x(\Theta )\pi (\Theta )$, where $L_x(\Theta )$ is the likelihood function and $\pi (\Theta )$ is the prior distribution. A prior distribution has been chosen so that the parameters are assumed to be independent. Equation (2) displays the prior distribution choices for the model parameters.

$$\begin{aligned} \begin{aligned} \lambda ^*&\sim Gamma(a_\lambda , b_\lambda )\\ \beta _{(k)}&\sim \mathcal {N}(0, \Sigma _{(k)}),\quad k = z, int, obs\\ \gamma&\sim \mathcal {N}(0, \sigma _\gamma ^2)\\ \tau ^2&\sim InvGamma(a_\tau , b_\tau )\\ \sigma ^2&\sim InvGamma(a_\sigma , b_\sigma ). \end{aligned} \end{aligned}$$

(2)

These choices are based on sound reasoning. The Gamma prior for $\lambda ^*$ is natural for a positive parameter, and it also simplifies the sampling of its full conditional since it is also Gamma-distributed. Similarly, the Normal prior for the regression effects $\beta _{(k)}$ induces L2 regularization, which is particularly useful in the Bayesian context, given the Pólya-Gamma data augmentation technique described below. The same can be said for the preferentiability parameter $\gamma$, which can be informally treated as a regression effect. Finally, the variances $\tau ^2$ and $\sigma ^2$ are assigned inverse Gamma priors, which again helps with the sampling of the full conditional since they are also inverse Gamma-distributed.

Furthermore, the parameters in the correlation function $\rho (\cdot )$ are selected to match its respective support, ensuring their appropriateness. Consequently, Equation (3) presents the posterior distribution for the model.

$$\begin{aligned} \begin{aligned} \pi (\Theta \mid x, z)\propto&\frac{e^{-(|\mathcal {D}| + b_\lambda )\lambda ^*} \lambda ^{*a_\lambda + n_x + n_{x'} + n_u - 1}}{n_{x'}!n_u!}&\\ \times&\prod _{s\in x}(1 + \exp \{-W_{int}(s)\beta _{int}\})^{-1}(1 + \exp \{-W_{obs}(s)\beta _{obs}-\gamma S(s)\})^{-1}\\ \times&\prod _{s\in x'}(1 + \exp \{-W_{int}(s)\beta _{int}\})^{-1}(1 + \exp \{W_{obs}(s)\beta _{obs}+\gamma S(s)\})^{-1}\\ \times&\prod _{s\in u}(1 + \exp \{W_{int}(s)\beta _{int}\})^{-1}\\ \times&\tau ^{2 - \frac{n_x + n{x'}}{2} - a_\tau - 1}e^{-\frac{b_\tau }{\tau ^2}}\prod _{s\in x\cup x'}\frac{1}{z(s)}\exp \left\{ -\frac{1}{2\tau ^2}\left( \log (z(s)) - W_z(s) \beta _z - S(s)\right) ^2\right\} \\ \times&\sigma ^{2 - \frac{n_x + n{x'}}{2} - a_\sigma - 1}e^{-\frac{b_\sigma }{\sigma ^2}}|\Sigma |^{-\frac{1}{2}}\exp \left\{ -\frac{1}{2\sigma ^2}S'\Sigma ^{-1}S\right\} \\ \times&\pi (\beta _z)\pi (\beta _{int})\pi (\beta _{obs})\pi (\theta ), \end{aligned} \end{aligned}$$

(3)

where $n_x$, $n_{x'}$ and $n_u$ are the number of points in their respective processes and $\Sigma$ is the NNGP correlation matrix.

The posterior is not known in closed form. An MCMC sampling scheme allows inference to be made. A Metropolis-within-Gibbs, see Gamerman and Lopes (2006), sampling procedure using concepts from Moreira and Gamerman (2022) and Shirota and Banerjee (2019) is employed to achieve the sampling.

The choice of the logNormal distribution for the marks in Eq. (1) simplifies the sampling algorithm. The full conditional distributions of all parameters but $\theta$ are thus known in closed form, which allows for a Gibbs sampler to be used for nearly the whole program.

Similarly to Moreira and Gamerman (2022), the sampling of $\beta _{int}$ and $\beta _{obs}$ is done via a logistic regression analogy. Its Gibbs sampler is possible via the data augmentation scheme proposed by Polson et al. (2012). Note that the respective Pólya-Gamma random variables have been excluded from Eq. (3). In order for the analogy to happen, two logistic regressions are considered, as in Moreira and Gamerman (2022).

The first analogy is for $\beta _{int}$, for which the successes are the points in x and $x'$ and failures are u. The second is for $\beta _{obs}$, for which the successes are x and the failures are $x'$. Also note that, conditional on $S(\cdot )$, parameter $\gamma$ can also be considered a regression coefficient where $S(s), s\in x\cup x'$ is its respective covariate.

Then, conditional on the Pólya-Gamma data augmentation vector $\omega$ described in Polson et al. (2012), the full conditional for the regression coefficient, generically denominated $\beta$ in each analogy is

$$\begin{aligned} \begin{aligned} \pi (\beta |\cdot )\propto&\pi (\beta )\prod _{s\in \text {success}}\exp \left\{ -\frac{1}{2}(0.5 - W(s)\beta )'\Omega (0.5 - W(s)\beta )\right\} \\ \times&\prod _{s\in \text {failure}}\exp \left\{ -\frac{1}{2}(-0.5 - W(s)\beta )'\Omega (-0.5 - W(s)\beta )\right\} , \end{aligned} \end{aligned}$$

(4)

where $\Omega$ is a diagonal matrix composed of $\omega$.

Equation (4) is useful to update the regression coefficients $\beta _{int}$ and $\beta _{obs}$, and consequently $\gamma$ as well.

It is also useful to update $S(\cdot )$ since its full conditional ends up being a normal distribution. This is especially important as the added complexity from the marks can be addressed with normality.

2.4 Updating the Spatial Smooth Process

Similarly to Gonçalves and Gamerman (2018) and Shirota and Banerjee (2019), process $S(\cdot )$ is updated in two separate steps. First only the process values in $X'$ are sampled in order to actually have their locations. Then the whole process is updated, which implies a second update of the values in $X'$. The introduction of the marks can present some complication, as detailed below. Note that the joint full conditional of $S(\cdot )$ and $Z(s), s\in x'$ is detailed in Eq. (5), also considering the Pólya-Gamma data augmentation.

$$\begin{aligned} \begin{aligned} \pi (S(\cdot ), Z(\cdot )|\cdot )\propto&\prod _{s\in x}\exp \left\{ -\frac{\gamma ^2}{2}\left( S - \left( \frac{0.5 - W_{obs}(s))\beta _{obs}}{\gamma }\right) \right) '\Omega \left( S - \left( \frac{0.5 - W_{obs}(s))\beta _{obs}}{\gamma }\right) \right) \right\} \\ \times&\prod _{s\in x'}\exp \left\{ -\frac{\gamma ^2}{2}\left( S - \left( \frac{-0.5 - W_{obs}(s))\beta _{obs}}{\gamma }\right) \right) '\Omega \left( S - \left( \frac{-0.5 - W_{obs}(s))\beta _{obs}}{\gamma }\right) \right) \right\} \\ \times&\prod _{s\in x\cup x'}\frac{1}{z(s)}\exp \left\{ -\frac{1}{2\tau ^2}\left( \log (z(s)) - W_z(s) \beta _z - S(s)\right) ^2\right\} \\ \times&\exp \left\{ -\frac{1}{2\sigma ^2}S'\Sigma ^{-1}S\right\} . \end{aligned} \end{aligned}$$

(5)

The proposal of Gonçalves and Gamerman (2018) for the sampling of $S(\cdot )$ in $X'$ is based on a acceptance-rejection algorithm based on the marginal distribution of $S(\cdot )$. In this case, due to the third line of Eq. (5), the values of $S(\cdot )$ are tied to the values of $Z(\cdot )$, which are unknown in new unobserved locations. For the same logic to be applied, then, it is necessary to sample jointly from a distribution whose density is proportional to

$$\begin{aligned} \prod _{s\in x\cup x'}\exp \left\{ -\frac{1}{2\tau ^2}\left( \log (z(s)) - W_z(s) \beta _z - S(s)\right) ^2\right\} \exp \left\{ -\frac{1}{2\sigma ^2}S'\Sigma ^{-1}S\right\} . \end{aligned}$$

The resulting values of $S(\cdot )$ are to be accepted or rejected similarly to Gonçalves and Gamerman (2018).

This sampling can be achieved with a simple variable transformation. Sample the auxiliary variables as in Eq. (6). In its notation, consider m and V the conditional mean and variance of $S(s), s\in x'$ given $S(s), s\in x$.

$$\begin{aligned} \begin{aligned} T&\sim \mathcal {N}\left( m\frac{\tau ^2}{\tau ^2+V}, \frac{\tau ^2V}{\tau ^2+V}\right) \\ R&\sim \mathcal {N}\left( -m\frac{\tau ^2}{\tau ^2+2V}, (\tau ^2+V)\frac{\tau ^2}{\tau ^2+2V}\right) . \end{aligned} \end{aligned}$$

(6)

Then the transformation $S = T + \frac{VR}{\tau ^2+V}$ and $Z = \exp \{R + W_z(\cdot )\beta _z\}$ achieves the desired sampling, which is verified by the Jacobian method. Note that the acceptance-rejection algorithm makes it so that the sampling of T and R is more efficient if done sequentially. This is because otherwise the rejection of any given point would require the whole vector to be discarded. Conveniently, the representation of the NNGP with the sparse precision matrix is particularly useful in this instance. See Datta et al. (2016a) and Finley et al. (2019) for more details.

The resampling step of $S(s), s\in x\cup x'$ can be achieved by resampling $Z(s), s\in x'$ from the logNormal distribution given known $S(s), s\in x'$, then the $S(s), s\in x\cup x'$ themselves from the Normal distribution in Eq. (5).

2.5 MCMC Algorithm

The procedure to acquire MCMC samples according to the details described in previous sections is presented for convenience in Algorithm 1 found below. An implementation in C++ with an associated wrapper in the form of an R (R Core Team 2022) package in CRAN called pompp, see https://cran.r-project.org/package=pompp.

Algorithm 1

MCMC procedure

A few notes can be made about Algorithm 1. First, the procedure to sample from $U, X', S(\cdot ), Z(\cdot )$ is done so that the uniform random variable $\mathcal {U}$ can be initially compared with q(s), then with q(s)p(s) in the log-scale, to provide numerical stability. Additionally, note that if a candidate point s is assigned to the set U, then there is no need to simulate from the smooth process S(s). This improves computation time, especially if the studied occurrences occur seldom in the region or only happens often in a relatively small sub-region. This happens since the majority of points from the superposed homogeneous Poisson Process, namely $X\cup X'\cup U$, belong to U in this scenario.

Another note is that the most computational intensive step in Algorithm 1 is sampling $S(s), Z(s)\mid \{S(t), t\in T\}$, that is, finding the NNGP conditional distribution at each point. This is why the choice of the NNGP is made. The conditional construction of Datta et al. (2016b) is particularly useful in this case since the points sampling happens one point at a time. To achieve optimum performance gain, an efficient choice for the neighborhood size is recommended. A choice of 20 neighbors should be enough for a smooth process. See Datta et al. (2016a) and Finley et al. (2019) for discussions about this.

Additionally, the sampling of the spatial correlation parameters in $\theta$ can further increase the computational cost meaningfully. Since the most expensive step is the calculation of the conditional distributions of $S(s), Z(s)\mid \{S(t), t\in T\}$, recalculating the precision matrix for a potential Metropolis proposal of the correlation parameters can prove too expensive for practice. In these cases, it may be worthwhile to estimate these parameters before the MCMC procedure and perform the simulations conditionally to the estimated values.

Finally, an object of great interest in this model is the distribution of the marks, particularly the ones in the unobserved presences. It can become very memory intensive to store all unobserved marks at every iteration, as each iteration can contain hundreds or thousands of values. It is recommended to store summaries of the sampled marks, such as sums and sums of squares. This may be used to calculate means and variances, for example.

3 Artificial Data

In order to fully understand the capabilities and pitfalls of the proposal, a comprehensive simulation study should be performed. To provide a wider range of scenarios for this study, a case of model misspecification was considered. For this case, a complementary log-log link was considered for the intensity of the species presences. That is, in (1), the equation for $q(\cdot )$ is replaced by

$$\begin{aligned} \log (-\log (1-q(s))) = W_{int}(s)\beta _{int}, s\in \mathcal {D}, \end{aligned}$$

(7)

to simulate data and fit it with a misspecified model. This function was chosen since it is very different from the logit link, being even asymmetric around zero.

Results are available using 30 datasets for a correctly specified model, and another 30 for misspecified ones. The [0, 1] square was chosen for the region $\mathcal {D}$ in all simulations.

The regression $W_z(s) \beta _z$ is reduced to only its intercept, which has been denoted $\mu$. The intensity regression $W_{int}(s) \beta$, that is, the one defining the probability of occurrence $q(\cdot )$, has been generated with 3 covariates, each from a Gaussian Process independent from each other. The observability regression $W_{obs}(s) \delta$, needed to define the probability of observation $p(\cdot )$, was generated with 2 covariates also with Gaussian Processes. For readability, $\beta _{int}$ has been renamed $\beta$ while $\beta _{obs}$ has been renamed $\delta$. All generated Gaussian Processes, including $S(\cdot )$, were generated with the exponential correlation function parameterized as in Eq. (8).

$$\begin{aligned} \rho (s, s') = \rho (||s - s'||) = \exp \left\{ -\frac{||s - s'||}{\phi }\right\} , \end{aligned}$$

(8)

The values used for the simulations are displayed in Table 1. The resulting number of observations in all datasets are summarized in Table 2.

Table 1 Values used for the data simulation

Table 2 Summary of number of observations generated in all simulated datasets

The covariance parameters $\sigma ^2$ and $\phi$ were estimated previously to the MCMC procedure using the observations via maximum likelihood. This is done to minimize the times that the MCMC procedure must calculate the precision matrix from the NNGP and its determinant. The resulting maximum likelihood estimates acquired for each run are shown in Fig. 3.

Fig. 3

Maximum likelihood estimates of the covariance function parameters using only the observed data for the simulated datasets. The value used for data generation is highlighted with a horizontal line

For prior information, all regression effects, including $\gamma$ were considered independent with mean 0 and variance 100. The same is true for parameter $\mu$. For the Gamma and inverse Gamma distributions, the values 0.001 were used for both parameters.

To summarize the information from all 30 simulations in each scenario (correctly specified and misspecified), the violin plot was chosen as it provides a detailed visualization of the posterior’s distributions. Figures 4 and 5 present an overview of the marginal posterior densities for each dataset and parameter.

Fig. 4

Marginal posterior distributions for the correctly specified model simulated exercise. Horizontal lines highlight the true values for the parameters. For visualization purposes, the $\beta _{int}$ vector is referred to as $\beta$ and $\beta _{obs}$ as $\delta$

Fig. 5

Marginal posterior distributions for the misspecified model simulated exercise. Horizontal lines highlight the true values for the parameters. For visualization purposes, the $\beta _{int}$ vector is referred to as $\beta$ and $\beta _{obs}$ as $\delta$

In addition, the models produce certain generated parameters that vary randomly and cannot be consistently replicated across different datasets. These parameters include the number of points in the unobserved processes, denoted as $n_U$ and $n_{X'}$. Moreover, it is also valuable to consider summary statistics related to the unobserved marks, such as their sum and variance. To ensure uniformity across all generated datasets, the bias is taken into account, with the true value represented as zero. Figure 6 shows the violin plots for the bias of these generated parameters.

Fig. 6

Marginal posterior distributions bias of each generated parameters. Horizontal lines highlight the true values, that is, no bias. Left: Correctly specified model. Right: Misspecified model

There are a few noteworthy observations to mention about these figures. Firstly, the model appears to accurately estimate its own parameters. Notably, there is less inconsistency in estimating $\mu$ and $\delta _0$, which is equivalent to $\beta _{obs, 0}$.

Another significant observation is that the posterior distributions exhibit heavy tails for all parameters. Although some effects may be slightly overestimated, the true values consistently fall within the posterior mass, indicating a close proximity. Furthermore, the preferentiability parameter $\gamma$ has been adequately estimated.

Even in the case of the misspecified model, it was able to recover the model’s parameters; however, the results show even heavier tails compared to the correctly specified model. In particular, $\lambda ^*$ shows heavy tails for high values in both cases, which increases the computational burden of the procedure. This could be remedied with a more informative prior, as discussed in Gonçalves and Gamerman (2018), but possibly also with smaller variance for the intercept terms from $\beta _{int}$ and $\beta _{obs}$.

Figure 6 shows more interesting results from the scientific perspective. While model parameters are relevant, they are more important to determine quantities of interest about the unobserved species occurrences. One can see that both scenarios have very similar posteriors for the number of points in processes $X'$ and U. Additionally, it is important to highlight that accurately estimating the number of points in $X'$ holds significant importance as it reflects the correct estimation of species observability. This particular quantity carries greater interest in the analysis. Regarding the summary statistics for the unobserved marks, it is evident that heavy tails are present; however, the majority of the posterior distribution is centered around the true values.

Finally, it is often of interest to correctly estimate the effect of different variables on the species occurrence or observability. This is reflected in $\beta _1$, $\beta _2$, $\beta _3$, $\delta _1$ and $\delta _2$. All these parameters were correctly estimated with little uncertainty.

For the presented simulation study, the model adequately estimates its parameters. Even under model misspecification, the proposal is useful to answer the relevant scientific questions.

4 Application

The model is applied to the data discussed in Sect. 2.1 and displayed in Fig. 1. Note that depth is denoted in negative values, meaning the more negative, the deeper the water. This means a positive effect is expected from the water depth in both the intensity and observability regressions.

It is also worth noting that the covariate has been standardized for stability. Standardizing is very important when dealing with regression models with nonlinear scale, such as the logit or the log. This is also useful for setting prior information on its effects. A prior variance of 10 was set for each $\beta$.

No covariates are being used to model the biomass. That is to say, in Eq. (1), the linear predictor $W_z(s) \beta _z$ reduces to its intercept which has been denoted $\mu$. Note that $\mu$ is not the marginal mean of the process Z, but rather of $\log \hspace{0.1cm}Z$. The spatial covariance parameters were estimated through a variogram function in a former step to Algorithm 1, for reasons of efficiency, as they are not of primary interest.

The dataset has 1,211 rows. The pre-processing involved removing rows with zero biomass, being interpreted as an observed absence. One location has also been recorded twice with different biomasses. This is a problem for the model since the smooth process $S(\cdot )$ depends on a covariance matrix built on points distances. Having a null distance between two points yields a non-invertible matrix, causing numerical instability. Thus the row with larger biomass has been removed. The resulting dataset used by the model had 1,024 rows.

Small changes in the prior are considered in relation to the ones mentioned for the artificial data. The prior variance for the regression parameters, including $\gamma$, is 10, following the recommendation in Moreira and Gamerman (2022). The results of the model can be seen in Fig. 7.

Fig. 7

Marginal distribution of all parameters of the application of Presence-only for Marked Point Process under Preferential Sampling on fishery data. Biomass was recorded in each sampled location. Each graphic is labeled with its respective parameter

Several noteworthy observations emerge from the marginal distributions. Firstly, the depth effect is positive for the intensity, as expected. However, the observability effect shows no discernible mass away from zero, showing little impact of the depth on the fishermen’s movement. The effects for the depth in the intensity and observability regressions are not strongly correlated (estimated posterior correlation = $-$0.023). The intercept for the observability regression is very low, indicating a very low probability of observing occurrences. These values are even more exceptional after comparing them with the prior, that is, a $\mathcal {N}(0, 10)$ distribution, which has negligible mass in this region. Secondly, parameter $\gamma$ is strongly positive, showing a strong preference of the fishermen towards higher biomass.

Parameters $\mu$ and $\tau ^2$ have the most stable Markov chains and have been well estimated. The chains for the $\beta$ parameters are slower to converge, which is an issue that is also observed in the simpler model from Moreira and Gamerman (2022).

Of utmost significance is the posterior distribution derived for $n_{x'}$. It predicts that there are between 22,500 and 30,500 schools of sardines which have not been observed by the fishermen during the study period. This could be a very large number, especially since the observed data has only 1,024 points. On the other hand, it is viable that there are many undetected sardine presences in an area as large as the southern Portuguese coast. Due to this large amount of unobserved occurrences, the sum of the unobserved biomass is very large, between 19,860 and 35,383 tonnes. The variance of the unobserved marks is also very large, with occasional extremely large values.

5 Discussion

Preferential sampling refers to a data collection method that, if the stochastic dependence between points and marks processes is overlooked, can lead to potentially misleading information. The pioneering work of Diggle et al. (2010) addresses this issue by providing corrective measures for such data. Presence-only data is a type of preferential sampling, which the method proposed in 2 deals with in two ways. Not only are the data collected as presence-only, but the associated marks are also collected preferentially.

The code to replicate the results in this paper can be found in https://github.com/GuidoAMoreira/pompp_article. However, note that restrictions apply to the availability of the data for the application in Sect. 4, which were used under license from Portuguese fisheries authority “DGRM - Direcção Geral dos Recursos Marinhos, Segurança e Serviços Marinhos” for the current study, and so are not publicly available. Data are available from the third author upon reasonable request and with permission from the DGRM.

The complexity of the proposed model is reflected in the computation time, which can be long due to the need to calculate the conditional distribution of each NNGP point. Additionally, the model’s fitting procedure can have slow convergence rates. Thus the computational cost can be pointed as the main drawback of the proposed model. One way to try to reduce the computational time by brute force, similarly to Wu et al. (2022), is to calculate the precision matrix $\Sigma ^{-1}$ for a fine lattice over the entire region and sample/resample the process on the entire region. Then, the S necessary values in X and $X'$ could just be taken from the nearest point in this lattice. This approach still needs consideration in terms of viability, as it might be very memory demanding.

Nevertheless, the method successfully fulfills its promises. It estimates both types of preferential sampling and accurately estimates regression coefficients and unobserved features. The likelihood function is evaluated exactly, and there is better identification between intensity and observability effects than with a traditional log-linear intensity link. The model is also equivalent to the traditional log-linear intensity link under limiting conditions of $\lambda ^*$ and the intercept term of $\beta _{int}$. Furthermore, the method estimates the number and locations of unobserved occurrences of the studied object. All of this is accomplished under a partially Bayesian approach that provides a comprehensive assessment of uncertainty. Currently, sampling of the NNGP parameters $\theta$ has not yet been incorporated into the MCMC procedure, which means that there is potentially reduced uncertainty for the results.

Our proposed method has broad applicability, as long as the marks can be expected to affect the observability of the point occurrences. Our approach is also an extension of previous works, since we consider presence-only data in conjunction with marks. This not only increases the theoretical complexity of the model, but also its computational aspects as mentioned earlier.

Despite the complexity of the proposed model, there are other features that could be included in it. The most prominent one is regarding the time dimension. In the case study presented, fishery observations are heavily influenced by legal and organizational limitations, which can change over time due to various factors. This presents a challenging problem, as it can be difficult to determine how to incorporate time into the model in a meaningful way.

Another important feature to consider is expanding the range of possible values for the marks. If the marks are not exclusively positive continuous values, a different distribution for $Z(\cdot )$ may be more appropriate. Real-valued, count, and binomial/multinomial responses are straightforward extensions, but appropriate treatments in the MCMC procedure are required.

Lastly, it may be worthwhile to consider cases where information about the studied object is available from multiple sources. For example, if a systematic survey has been done for the studied fish species, this information could be used to insert unbiased data into the model, potentially leading to more precise estimates. However, care should be taken when combining information from different sources, as it can be challenging to fuse data collected under different and incompatible domains. For further discussion on the Presence-only and Presence-absence cases, see Gelfand and Shirota (2019).