Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-02T07:50:12.968Z Has data issue: false hasContentIssue false
  • English
  • Français

Game semantics of Martin-Löf type theory

Published online by Cambridge University Press:  31 July 2023

Norihiro Yamada Open the ORCID record for Norihiro Yamada [Opens in a new window]
Norihiro Yamada*
Affiliation:
School of Mathematics, University of Minnesota, Minneapolis, MN, USA
*
Email: yamad041@umn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

This work presents game semantics of Martin-Löf type theory (MLTT) equipped with the One, the Zero, the N, Pi, Sigma and Id types. Game semantics interprets a wide range of logic and computation, even the polymorphic 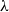$\lambda$-calculus; however, it has remained a well-known challenge in the past 25 years to achieve game semantics of dependent type theories such as MLTT, and past attempts lack directness or generality. For instance, the approach taken by Abramsky et al. interprets Sigma types indirectly by formal lists, not by games, making an interpretation of universes hopeless, and it is limited to a very specific class of dependent types. The difficulty of this challenge comes from a conflict between the extensionality of dependent types and the intensionality of game semantics. We overcome the challenge by inventing a novel variant of games, while we keep strategies unchanged, in such a way that this variant inherits the strong points of conventional game semantics. Also, our method enables an interpretation of subtyping on dependent types for the first time as game semantics. We finally give a new, game-semantic proof of the independence of Markov’s principle from MLTT. This proof illustrates an advantage of our intensional model over extensional ones such as Hyland’s effective topos.

Keywords

Game semanticsMartin-Löf type theoryConstructive mathematicsDependent types
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 33 , Issue 7 , August 2023 , pp. 605 - 646
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramsky, S. (2002). Algorithmic game semantics. In: Proof and System-Reliability, Springer, 21–47.CrossRefGoogle Scholar
Abramsky, S. (1997). Semantics of interaction: an introduction to game semantics. In: Semantics and Logics of Computation, Publications of the Newton Institute, 1–31.CrossRefGoogle Scholar
Abramsky, S., Honda, K. and McCusker, G. (1998). A fully abstract game semantics for general references. In: Proceedings. Thirteenth Annual IEEE Symposium on Logic in Computer Science (Cat. No. 98CB36226), IEEE, 334–344.CrossRefGoogle Scholar
Abramsky, S. and Jagadeesan, R. (1994). Games and full completeness for multiplicative linear logic. The Journal of Symbolic Logic 59 (02) 543–574.CrossRefGoogle Scholar
Abramsky, S. and Jagadeesan, R. (2005). A game semantics for generic polymorphism. Annals of Pure and Applied Logic 133 (1) 3–37.CrossRefGoogle Scholar
Abramsky, S., Jagadeesan, R. and Malacaria, P. (2000). Full abstraction for PCF. Information and Computation 163 (2) 409–470.10.1006/inco.2000.2930CrossRefGoogle Scholar
Abramsky, S., Jagadeesan, R. and Vákár, M. (2015). Games for dependent types. In: Automata, Languages, and Programming, Berlin, Heidelberg, Springer, 31–43.CrossRefGoogle Scholar
Abramsky, S. and McCusker, G. (1997). Linearity, sharing and state: a fully abstract game semantics for idealized algol with active expressions. In: Algol-like Languages, Springer, 297–329.Google Scholar
Abramsky, S. and McCusker, G. (1999a). Full abstraction for idealized algol with passive expressions. Theoretical Computer Science 227 (1–2) 3–42.CrossRefGoogle Scholar
Abramsky, S. and McCusker, G. (1999b). Game semantics. In: Computational Logic: Proceedings of the 1997 Marktoberdorf Summer School, Berlin, Heidelberg, Springer, 1–55.CrossRefGoogle Scholar
Aczel, P. (1986). The type theoretic interpretation of constructive set theory: inductive definitions. In: Studies in Logic and the Foundations of Mathematics, vol. 114, Elsevier, 17–49.CrossRefGoogle Scholar
Amadio, R. M. and Curien, P.-L. (1998). Domains and Lambda-Calculi. vol. 46, Cambridge University Press, Cambridge. https://www.amazon.com/Domains-Lambda-Calculi-Cambridge-Theoretical-Computer/dp/0521622778 CrossRefGoogle Scholar
Berry, G. and Curien, P.-L. (1982). Sequential algorithms on concrete data structures. Theoretical Computer Science 20 (3) 265–321.CrossRefGoogle Scholar
Blot, V. and Laird, J. (2018). Extensional and intensional semantic universes: a denotational model of dependent types. In: Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, ACM, 95–104.CrossRefGoogle Scholar
Chroboczek, J. (2000). Game semantics and subtyping. In: Proceedings Fifteenth Annual IEEE Symposium on Logic in Computer Science (Cat. No. 99CB36332), IEEE, 192–203.CrossRefGoogle Scholar
Church, A. (1940). A formulation of the simple theory of types. The Journal of Symbolic Logic 5 (02) 56–68.CrossRefGoogle Scholar
Clairambault, P. and Dybjer, P. (2014). The biequivalence of locally Cartesian closed categories and Martin-Löf type theories. Mathematical Structures in Computer Science 24 (05) e240501.CrossRefGoogle Scholar
Clairambault, P. and Harmer, R. (2010). Totality in arena games. Annals of Pure and Applied Logic 161 (5) 673–689.CrossRefGoogle Scholar
Constable, R. L., Allen, S. F., Bromley, H. M., Cleaveland, W. R., Cremer, J. F., Harper, R. W., Howe, D. J., Knoblock, T. B., Mendler, N. P., Panangaden, P., Sasaki, J. T. and Smith, S. F. (1986). Implementing mathematics with the nuprl proof development system.Please provide all the author names in the place of “et al.” in “Constable et al. (1986)”.Google Scholar
Coquand, T. (1995). A semantics of evidence for classical arithmetic. The Journal of Symbolic Logic 60 (1) 325–337.CrossRefGoogle Scholar
Curien, P.-L. (1998). Abstract Böhm trees. Mathematical Structures in Computer Science 8 (06) 559–591.CrossRefGoogle Scholar
Curien, P.-L. (2007). Definability and full abstraction. Electronic Notes in Theoretical Computer Science 172 301–310.CrossRefGoogle Scholar
Dybjer, P. (1996). Internal type theory. In: Types for Proofs and Programs, Springer, 120–134.CrossRefGoogle Scholar
Dybjer, P. and Palmgren, E. (2016). Intuitionistic type theory. Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/type-theory-intuitionistic/ Google Scholar
Fraenkel, A. (1922). Zu den grundlagen der cantor-zermeloschen mengenlehre. Mathematische Annalen 86 (3–4) 230–237.CrossRefGoogle Scholar
Girard, J.-Y. (1987). Linear logic. Theoretical Computer Science 50 (1) 1–101.CrossRefGoogle Scholar
Girard, J.-Y., Taylor, P. and Lafont, Y. (1989). Proofs and Types, vol. 7, Cambridge, Cambridge University Press.Google Scholar
Hofmann, M. (1997). Syntax and semantics of dependent types. In: Extensional Constructs in Intensional Type Theory, Springer, 13–54.Google Scholar
Hofmann, M. and Streicher, T. (1998). The groupoid interpretation of type theory. In: Twenty-Five Years of Constructive Type Theory (Venice, 1995), vol. 36, 83–111.CrossRefGoogle Scholar
Hyland, J. M. E. (1982). The effective topos. In: Studies in Logic and the Foundations of Mathematics, vol. 110, Elsevier, 165–216.CrossRefGoogle Scholar
Hyland, J. M. E. and Ong, C.-H. (2000). On full abstraction for PCF: I, II, and III. Information and Computation 163 (2) 285–408.CrossRefGoogle Scholar
Laird, J. (1997). Full abstraction for functional languages with control. In: Proceedings of Twelfth Annual IEEE Symposium on Logic in Computer Science, IEEE, 58–67.CrossRefGoogle Scholar
Laird, J. (2013). Game semantics for a polymorphic programming language. Journal of the ACM (JACM) 60 (4) 1–27.CrossRefGoogle Scholar
Laurent, O. (2002). Polarized games. In: Proceedings of the 17th Annual IEEE Symposium on Logic in Computer Science, IEEE, 265–274.CrossRefGoogle Scholar
Mannaa, B. and Coquand, T. (2017). The independence of markov’s principle in type theory. Logical Methods in Computer Science 13 (3:10) 1–28.Google Scholar
Markov, A. A. (1962). On constructive mathematics. Trudy Matematicheskogo Instituta imeni VA Steklova 67 8–14.Google Scholar
Martin-Löf, P. (1975). An intuitionistic theory of types: predicative part. Studies in Logic and the Foundations of Mathematics 80 73–118.CrossRefGoogle Scholar
Martin-Löf, P. (1982). Constructive mathematics and computer programming. Studies in Logic and the Foundations of Mathematics 104 153–175.CrossRefGoogle Scholar
Martin-Löf, P. (1984). Intuitionistic Type Theory: Notes by Giovanni Sambin of a series of lectures given in Padova, June 1980.Google Scholar
Martin-Löf, P. (1998). An intuitionistic theory of types. In: Twenty-Five Years of Constructive Type Theory, vol. 36, 127–172.CrossRefGoogle Scholar
McCusker, G. (1998). Games and Full Abstraction for a Functional Metalanguage with Recursive Types, London, Springer Science & Business Media.CrossRefGoogle Scholar
Nickau, H. (1994). Hereditarily sequential functionals. In: International Symposium on Logical Foundations of Computer Science, Springer, 253–264.Google Scholar
Palmgren, E. and Stoltenberg-Hansen, V. (1990). Domain interpretations of martin-löf’s partial type theory. Annals of Pure and Applied Logic 48 (2) 135–196.CrossRefGoogle Scholar
Plotkin, G. and Power, J. (2004). Computational effects and operations: an overview. Electronic Notes in Theoretical Computer Science 73 149–163.CrossRefGoogle Scholar
Rogers, H. H. (1967). Theory of Recursive Functions and Effective Computability, vol. 5, New York, McGraw-Hill.Google Scholar
Scott, D. (1970). Outline of a Mathematical Theory of Computation. Oxford University Computing Laboratory, Programming Research Group Oxford.Google Scholar
Seely, R. A. (1984). Locally Cartesian closed categories and type theory. Mathematical Proceedings of the Cambridge Philosophical Society 95 33–48, Cambridge, Cambridge University Press.CrossRefGoogle Scholar
Shoenfield, J. R. (1967). Mathematical Logic, vol. 21, Reading, Addison-Wesley.Google Scholar
Sørensen, M. H. and Urzyczyn, P. (2006). Lectures on the Curry-Howard Isomorphism, Elsevier, Amsterdam.Google Scholar
Streicher, T. (1993). Investigations into Intensional Type Theory (Doctoral dissertation, Habilitationsschrift, Ludwig-Maximilians-Universität München).Google Scholar
Streicher, T. (2012). Semantics of Type Theory: Correctness, Completeness and Independence Results, Springer Science & Business Media, New York.Please provide publisher location for “Streicher (2012)”.Google Scholar
Tarski, A. (1954). Contributions to the theory of models. i. In: Indagationes Mathematicae (Proceedings), vol. 57, Elsevier, 572–581.Google Scholar
Troelstra, A. S. and Schwichtenberg, H. (2000). Basic Proof Theory, vol. 43, Cambridge University Press, Cambridge. https://www.amazon.com/Theory-Cambridge-Theoretical-Computer-Science/dp/0521779111?asin=0521779111&revisionId=&format=4&depth=1 CrossRefGoogle Scholar
Troelstra, A. S. and van Dalen, D. (1988). Constructivism in Mathematics. Vol. I , Studies in Logic and the Foundations of Mathematics, vol. 121, 26.Google Scholar
Univalent Foundations Program, T. (2013). Homotopy Type Theory: Univalent Foundations of Mathematics. https://homotopytypetheory.org/book, Institute for Advanced Study.Google Scholar
Vákár, M., Jagadeesan, R. and Abramsky, S. (2018). Game semantics for dependent types. Information and Computation 261 401–431.CrossRefGoogle Scholar
Yamada, N. (2019). A game-semantic model of computation. Research in the Mathematical Sciences 6 (1) 3.CrossRefGoogle Scholar
Yamada, N. (2022). Game semantics of universes. arXiv preprint arXiv:2203.13069.Google Scholar
Zermelo, E. (1908). Untersuchungen über die grundlagen der mengenlehre. i. Mathematische Annalen 65 (2) 261–281.Google Scholar