1 Introduction

Lattice materials are a class of multiscale materials with periodic architecture at the microscale. The structural arrangement at the microscale determines the macroscopic characteristics of the material. The advancements in additive manufacturing have made it possible to fabricate complex micro-architectures resulting in engineered materials with effective properties that are not found in nature, e.g. auxetic behavior [1] tailored anisotropy [2] and mechanical coupling [3]. These are interesting features for engineering applications but when it comes to integration of these materials into products, the question arises whether the length ratio of macroscopic component and its micro-architecture affect the overall performance or not Various studies provided evidence that such length ratio influences the mechanics of samples composed of microstructure, e.g. [4,5,6,7,8,9,10]. This is referred to as size effects.

Full-field simulations of lattice materials with detailed microstructure are computationally expensive. Instead, considering the phenomenon to be captured (e.g. mechanics, thermomechanics, or in general multi-physics), the heterogenous media can be replaced by a homogenous continuum with equivalent properties using proper homogenization techniques. In mechanics, classical homogenization theories based on Cauchy continuum are valid under the assumption of scales separation, they fail when the size of micro- and macro-structure are comparable giving rise to e.g. size effects. For this, the generalization of the classical continuum towards either higher-order or higher-grade continua is required. Higher-order theory includes local rotations as additional degrees of freedom, e.g. Cosserat [11], while higher-grade theory extends the definition of strain energy to the higher gradients of kinematic or internal variables, e.g. strain gradient continuum in [12, 13]. While higher-order theories have been employed for homogenization of architectured materials in the literature e.g. [8, 14,15,16,17,18], strain gradient model offers some advantages over higher-order continua [19]. For instance, strain gradient elasticity can describe the length-scale effect without including large number of parameters as in micromorphic elasticity. Moreover, the anisotropic features of strain gradient elasticity are well understood [20]. Thus, in this paper, we focus on strain gradient elastic continuum model as described by Mindlin [12].

In the context of homogenization based on strain gradient theory, two general approaches exist: quadratic boundary conditions (QBC) and asymptotic analysis. The approach based on asymptotic analysis uses a series expansion—including higher-order terms in case of weak scale separation—to approximate the solution and solves a set of elasticity problems, e.g. see [21]. This is a promising approach for homogenization towards strain gradient continua, as demonstrated in [22,23,24] to name a few. Previous models based on asymptotic analysis suffer from persistence of strain gradient parameters when the material is fully homogeneous. This shortcomings is resolved using correction terms suggested in [25], and has been numerically implemented using fast Fourier transform (FFT) [26] and finite element method [27]. Following that, an alternative approach for the derivation of the correction terms was proposed in [28]. The proposed model was later implemented and verified in [29] for a range 3-D architectured materials. More recently, a boundary layer correction model was presented in [30] to include local effects at the vicinity of the boundaries in higher-order asymptotic homogenization.

The method based on quadratic boundary condition (QBC) is an extension of classical kinematic boundary conditions, in which displacements resulting from a uniform strain field are applied to the boundary of a representative volume element (RVE). This method is simpler as compared to asymptotic analysis which requires a set of auxiliary variables for the derivation of effective properties, e.g. see [28] for details. Indeed, in QBC method the effective strain gradient parameters are directly obtained from displacement field with no need for additional variables. The simplicity of QBC has made it a popular model for homogenization towards strain-gradient continua, e.g. [31,32,33]. But there has been a major flaw in this model (as noted by [24, 34]), that is the persistence of spurious gradient parameters when the material is homogenous. To resolve this, corrective body forces were introduced in the microscale equilibrium equations in [35]. Later, the proposed method was employed in [19] to numerically analyze anisotropic composite materials. Despite its success in the elimination of spurious gradient effects, it turned out that the model in [19] and [35] cannot evaluate composites with soft inclusions or lattices materials (with inclusion being a void—extreme case of soft inclusion). More recently, [36] and [37] extended QBC method to periodic boundary condition (PBC) and combined it with variational formulation for homogenization towards strain gradient continua. But the authors in [36] and [37] did not include the corrective body forces and neither discussed whether the gradient terms vanish in the case of homogenous material or not. In another work [38], the authors employed second-gradient approach based on PBC to investigate the deformation behavior of 2-D voided materials.

The literature in the field of strain gradient homogenization has mainly focused on composite materials, and there has been far less attention towards architectured materials. Studies on lattice materials are mainly limited to 2-D topologies, and very few studies considered 3-D geometries, e.g. [29] and [37] (the case studies are mainly dedicated to composites). The authors in [29] employed asymptotic homogenization and investigated the behavior of various composite materials and a 3-D foam with cuboid voids followed by a numerical validation. Also, the case of 3-D lattice is investigated in a limited context in [37], where the authors briefly discussed the elastic gradient parameters for a thin-walled lattice but no further validation nor a discussion on the influence of cell length is provided. Finally, literature lacks a comprehensive validation study because the majority of the works in the field either provided only qualitative validations or solely relied on numerical validation with no further experiments.

There is a need for a 3-D homogenization model based on PBC-approach (as an extension to QBC-approach) addressing voided materials with complex geometries, followed by a thorough verification study. We contribute to the field by tackling this problem and developing a 3-D numerical scheme based on strain gradient theory. The developed model uses periodic boundary conditions (PBC) along with variational formulation and is more practical compared to previous ones in a sense that no material should be assigned to the voided region and this makes the analysis of complex 3-D lattice materials possible. Additionally, rigorous mathematical derivation based on Hill–Mandel lemma is provided which guarantees vanishing strain gradient parameters when the material is homogenous or when strict scale separation is valid Finally, a comprehensive validation study based on full-field analysis, isogeometric (IGA) simulations and experimental tests is carried out.

The paper is structured as follows. First in the following section, the strain gradient homogenization theory is elaborated at micro-scale and macro-scale, and the scales are bridged using Hill–Mandel lemma. Next, Sect. 3 presents the practical numerical implementation and algorithm behind the homogenization scheme. Following this, the model is used to study the behavior of a range of 2-D square and 3-D cubic lattice materials in Sect. 4. Then, in Sect. 5, the homogenized results for the case of 3-D cubic lattices are validated using full-field simulations, isogeometric analysis, and experimental three-point bending tests. Finally, concluding remarks on the applicability of homogenization model based of strain gradient theory for different cell architectures and/or load conditions are provided.

2 Strain gradient homogenization

We deal with a multi-scale problem which is homogenized at the global (macro-) scale and heterogenous at the local (micro-) scale. At the microscale, the material follows classical Cauchy elasticity, while the homogenized macroscopic material acts as strain gradient continuum. The proposed scheme employs two length-scales: (1) a global coordinate, \({{\varvec{x}}}\), describing global (slow changing) variables, and (2) a local coordinate, \({{\varvec{y}}}\), describing local (fast changing) variables. The length-scales are related using a scaling factor \(\epsilon ={{\varvec{x}}}/ {{\varvec{y}}}\), which allows for arbitrary selection of local coordinates of an RVE. To introduce the continuum formulation of macroscale and microscale, the superscripts “\(\textrm{M}\)” and “\(\textrm{m}\)” denote macroscopic and microscopic variables, respectively.

(i) Macroscale

Aiming for a second-order homogenization, we use a truncated Taylor expansion to approximate the macroscopic strain field at a material point coinciding with the geometric center of an RVE, i.e. point \({{\varvec{x}}}_{{{\varvec{c}}}}\). This reads

$$\begin{aligned} {\varvec{\varepsilon }}_{{\varvec{(x)}}}^{\text {M}} ={\varvec{\varepsilon }}_{{\varvec{(}}{{\varvec{x}}}_{{{\varvec{c}}}}{\varvec{)}}} +\mathrm {\nabla }{\varvec{\varepsilon }} _{{\varvec{(}}{{\varvec{x}}}_{{{\varvec{c}}}}{\varvec{)}}}.({{\varvec{x}}}-{{\varvec{x}}}_{{{\varvec{c}}}}) \end{aligned}$$
(1)

where \({\varvec{\varepsilon }}_{{\varvec{(}}{{\varvec{x}}}_{{{\varvec{c}}}}{\varvec{)}}}\) and \(\mathrm {\nabla }{\varvec{\varepsilon }}_{{\varvec{(}}{{\varvec{x}}}_{{{\varvec{c}}}}{\varvec{)}}}\) are, respectively, the applied uniform macroscopic strain and uniform macroscopic gradient of strain. Over the selected RVE we write \({\varvec{\varepsilon }}_{\left( {{\varvec{x}}}_{{{\varvec{c}}}} \right) }={\bar{\varvec{\varepsilon }}}\) and \(\mathrm {\nabla }{\varvec{\varepsilon }}_{{\varvec{(}}{{\varvec{x}}}_{{{\varvec{c}}}}{\varvec{)}}}={\bar{\varvec{\mathcal {K}}}}\). By conveniently locating the coordinate system at the center of the RVE, the macroscopic strain field and its gradient simplify as

$$\begin{aligned} {\varvec{\varepsilon }}_{\left( {{\varvec{x}}} \right) }^{\text {M}} ={\bar{\varvec{\varepsilon }}}+{\bar{\varvec{\mathcal {K}}}}.{{\varvec{x}}} \; ; \mathrm {\nabla }{\varvec{\varepsilon }}_{\left( {{\varvec{x}}} \right) } ^{\text {M}}={\bar{\varvec{\mathcal {K}}}} \end{aligned}$$
(2)

where \(\mathrm {\nabla ()}\) is the gradient operator.

The macroscopic material is assumed to be a second-order strain gradient continua with the following equilibrium equation

$$\begin{aligned} \mathrm {\nabla }. (\varvec{\sigma }^{\textrm{M}}_{{\varvec{(x)}}}{} -{\mathrm {\nabla }.({{\varvec{S}}}}^{\textrm{M}}_{\left( {{\varvec{x}}} \right) }{})+ {{\varvec{f}}}=0 \end{aligned}$$
(3)

where \({{\varvec{f}}}\) is the body force \(\mathrm {\nabla }. \mathrm {()}\) is the divergence operator,   \(\varvec{\sigma }_{{\varvec{(x)}}}^{\text {M}} \)  is the second-order macroscopic stress tensor, and \({{\varvec{S}}}_{{\varvec{(x)}}}^{\text {M}} \) is the third-order hyperstress tensor. The stress and hyperstress tensors are defined as

$$\begin{aligned} \varvec{\sigma }^{\textrm{M}}_{{\varvec{(x)}}}{}= & {} {{\varvec{C}}}^{\textrm{M}}:{\varvec{\varepsilon }}^{\textrm{M}}_{{\varvec{(x)}}}{} + {{\varvec{B}}}^{\textrm{M}}\vdots {\mathrm {\nabla }{\varvec{\varepsilon }}}^{\textrm{M}}_{{\varvec{(x)}}}{} \end{aligned}$$
(4)
$$\begin{aligned} {{\varvec{S}}}^{\textrm{M}}_{{\varvec{(x)}}}{}= & {} {{({{\varvec{B}}}}^{\textrm{M}})}^{T}:{\varvec{\varepsilon }}^{\textrm{M}}_{{\varvec{(x)}}}{} + {{\varvec{D}}}^{\textrm{M}}\vdots {\mathrm {\nabla }{\varvec{\varepsilon }}}^{\textrm{M}}_{{\varvec{(x)}}}{} \end{aligned}$$
(5)

where “:” is a double contraction operator, \({{\varvec{C}}}^{\textrm{M}}\) is the macroscopic fourth-order elastic tensor, \({{\varvec{B}}}^{\textrm{M}}\) is the macroscopic fifth-order coupling tensor, and \({{\varvec{D}}}^{\textrm{M}}\) is the macroscopic sixth-order strain-gradient elasticity tensor. Inserting Eqs. (4, 5) into (3) leads to

$$\begin{aligned} \mathrm {\nabla }. \left( {{\varvec{C}}}^{\text {M}}:{\varvec{\varepsilon }}_{\left( {{\varvec{x}}} \right) }^{\text {M}}+ {{\varvec{B}}}^{\text {M}}\vdots {\mathrm {\nabla }{\varvec{\varepsilon }}}_{\left( {{\varvec{x}}} \right) }^{\text {M}}-\mathrm {\nabla }. \left( {{({{\varvec{B}}}}^{\text {M}})}^{T}:{\varvec{\varepsilon }}_{\left( {{\varvec{x}}} \right) }^{\text {M}}+ {{\varvec{D}}}^{\text {M}}\vdots {\mathrm {\nabla }{\varvec{\varepsilon }}}_{\left( {{\varvec{x}}} \right) }^{\text {M}} \right) \right) + {{\varvec{f}}}= 0 \end{aligned}$$
(6)

Inserting the macroscopic strain \({\varvec{\varepsilon }}_{\left( {{\varvec{x}}} \right) }^{\text {M}}\) and macroscopic strain gradient \(\mathrm {\nabla }{\varvec{\varepsilon }}_{\left( {{\varvec{x}}} \right) }^{\text {M}}\) fields defined in Eq. (2) into the above expression and following the mathematical operations yields

$$\begin{aligned} \mathrm {\nabla }. ({{\varvec{C}}}^{\textrm{M}}:({\bar{\varvec{\varepsilon }}}+{\bar{\varvec{\mathcal {K}}}}.{{\varvec{x}}}))+{{\varvec{f}}}=0 \end{aligned}$$
(7)

This equation motivates the presence of body forces in a strain-gradient continuum. The body forces are scale-independent and identical at both micro- and macroscale. In the limit case of a homogeneous RVE (governed by classical elasticity, i.e. \({{\varvec{B}}}^{\textrm{M}}=0\) and \({{\varvec{D}}}^{\textrm{M}}=0)\), the above relation simplifies to Cauchy equilibrium equation, in which the body forces disappear, and continuum body is self-equilibrated

$$\begin{aligned} \mathrm {\nabla }. \left( {{\varvec{C}}}^{\textrm{M}}:{\bar{\varvec{\varepsilon }}} \right) = 0 \end{aligned}$$
(8)

(ii) Microscale

We assume the microscopic strain is the superposition of macroscopic strain, \({\varvec{\varepsilon }}_{{\varvec{(x)}}}^{\text {M}} \), and microscale fluctuations, \({\varvec{\varepsilon }}_{{\varvec{(x,y)}}}^{*}\) (accounting for the heterogeneities). That is

$$\begin{aligned} {\varvec{\varepsilon }}_{\varvec{(x,y)}}^{\text {m}} ={\varvec{\varepsilon }}_{{\varvec{(x)}}}^{\text {M}} +{\varvec{\varepsilon }}_{{\varvec{(x,y)}}}^{*} ={\bar{\varvec{\varepsilon }}} +{\bar{\varvec{\mathcal {K}}}}.{{\varvec{x}}} +{\varvec{\varepsilon }}_{{\varvec{(x,y)}}}^{*} \end{aligned}$$
(9)

Following the classical Cauchy elasticity at the micro-scale, the equilibrium equation at micro-scale reads

$$\begin{aligned} \mathrm {\nabla }. \left( \varvec{\sigma }_{\left( {\varvec{x,y}} \right) }^{\text {m}} \right) + {{\varvec{f}}}=0 \end{aligned}$$
(10)

Having above introduced the governing continuum formulation of macroscale and microscale, to prepare for numerical retreatment, we now derive the elasticity weakform formulation of the following two cases:

Problem 1

\(({\bar{\varvec{\varepsilon }}}\mathrm {\ne 0}\) and \({\bar{\varvec{\mathcal {K}}}}\mathrm {=0})\)

This is the classical Cauchy elastic problem, in which the weak form appears as

$$\begin{aligned} \int \limits _\mathrm {\Omega } {\varvec{\sigma }_{{\varvec{(x,y)}}}^{\text {m}}:\delta {\varvec{\varepsilon }}_{{\varvec{(x,y)}}}^{\text {m}}\mathrm {\Omega }} =0 \end{aligned}$$
(11)

where \(\delta \varepsilon _{(x,y)}\) is the virtual strain, and is chosen to only vary at the microscale, i.e. \({\delta {\varvec{\varepsilon }}}_{{\varvec{(x,y)}}}^{\text {m}}=\delta {\varvec{\varepsilon }}_{{\varvec{(x,y)}}}^{*}\). Using the Hooke’s law along with Eq. (9) the above weak form reads

$$\begin{aligned} \int \limits _\mathrm {\Omega } {\delta {\varvec{\varepsilon }}_{\left( {\varvec{x,y}} \right) }^{*}:{{\varvec{C}}}_{{\varvec{(x)}}}^{\text {m}}:({\bar{\varvec{\varepsilon }}} +{\varvec{\varepsilon }}_{{\varvec{(x,y)}}}^{*})\text {d}\mathrm {\Omega }}=0 \end{aligned}$$
(12)

where \({{\varvec{C}}}_{{\varvec{(x)}}}^{\text {m}} \)is the elasticity tensor of the material at the local (micro) scale.

Problem 2

\(({\bar{\varvec{\varepsilon }}}\mathrm {=0}\) and \({\bar{\varvec{\mathcal {K}}}}\mathrm {\ne 0})\)

In this case, considering Eq. (7), the body forces also appear in the formulation (see Appendix A). Employing Eq. (9), the weak form reads

$$\begin{aligned} \int \limits _\mathrm {\Omega } {{\delta {\varvec{\varepsilon }}_{\left( {\varvec{x,y}} \right) }^{*}:{{\varvec{C}}}}_{{\varvec{(x)}}}^{\text {m}}:\left( {\bar{\varvec{\mathcal {K}}}}.{{\varvec{x}}}+{\varvec{\varepsilon }}_{{\varvec{(x,y)}}}^{*} \right) \text {d}\mathrm {\Omega }} -\int \limits _\mathrm {\Omega } {\delta {\varvec{\varepsilon }}_{\left( {\varvec{x,y}} \right) }^{*}:{{\varvec{C}}}{}^{\text {M}}:\left( {\bar{\varvec{\mathcal {K}}}}.{{\varvec{x}}} \right) \text {d}\mathrm {\Omega }} =0 \end{aligned}$$
(13)

We use Eqs. (12) and (13) along with periodic boundary conditions to solve the elastic and gradient elastic problems. The solution to these equations yields the strain fluctuations, \({\varvec{\varepsilon }}_{\left( {\varvec{x,y}} \right) }^{*}\), from which we can build the local strain fields, i.e. \({\varvec{\varepsilon }}^{{\textbf {1}}}_{{\left( {\varvec{x,y}}\right) }}{\!}^\text {m}\) and \({\varvec{\varepsilon }}^{{{\textbf {2}}}}_{{\left( {\varvec{x,y}}\right) }}{\!}^\text {m}\) using Eq. (9). Since the problem is linear, we form the local strain field using the superposition principle as

$$\begin{aligned} \varvec{\varepsilon }_{\varvec{(x,y)}}^{\text {m}} =\varvec{\varepsilon }^{{\textbf {1}}}_{\left( \varvec{x,y} \right) }{\!}^\text {m} +=\varvec{\varepsilon }^{{\textbf {2}}}_{\left( \varvec{x,y}\right) }{\!}^\text {m} =\mathbb {A}^{{\textbf {1}}}{}_{{\varvec{(x,y)}}}{\varvec{:}}{\bar{\varvec{\varepsilon }}} +{\mathbb {A}}^{{{\textbf {2}}}}{}_{{\varvec{(x,y)}}}\vdots {\bar{\varvec{\mathcal {K}}}} \end{aligned}$$
(14)

where \({\mathbb {A}}^{{\textbf{1}}}\) and \({\mathbb {A}}^{{\textbf{2}}}\) are, respectively, the fourth- and fifth- order localization tensors (strain solutions) obtained by solving Eqs. (12) and (13).

2.1 Effective properties

To bridge between scales, we work with the strain energy densities at both scales. In one hand, taking the volume average of the microscopic strain energy over the RVE yields

$$\begin{aligned} {<W}^{\text {m}}>=\frac{1}{2}<\varvec{\sigma }^{\text {m}}:{\varvec{\varepsilon }}^{\text {m}}>=\frac{1}{2}<{({\varvec{\varepsilon }}^{\text {m}})}^{T}:{{\varvec{C}}}^{{{\varvec{\text {m}}}}}:{\varvec{\varepsilon }}^{\text {m}}> \end{aligned}$$
(15)

where \(<>\) is the volume average operator defined as < \(\blacksquare >=\frac{1}{V_{\varOmega }}\int \limits _\varOmega {\blacksquare \mathrm {d\Omega }} \) over domain \(\varOmega \) of the RVE. Replacing total strain field, Eq. (14), into the above equation results

$$\begin{aligned} {<W}^{\text {m}}>=\frac{1}{2}<\left( {\mathbb {A}}^{{{\textbf {1}}}}:{\bar{\varvec{\varepsilon }}}+A^{2}\vdots {\bar{\varvec{\mathcal {K}}}} \right) ^{T}:C^{\text {m}}:\left( {\mathbb {A}}^{{{\textbf {1}}}}:{\bar{\varvec{\varepsilon }}}+{\mathbb {A}}^ {{{\textbf {2}}}}\vdots {\bar{\varvec{\mathcal {K}}}} \right) > \end{aligned}$$
(16)

Following the mathematical operations, this becomes

$$\begin{aligned} {<W}^{\text {m}}>= & {} {} \frac{1}{2} \left\{ {\bar{\varvec{\varepsilon }}}^{T}:{{<({\mathbb {A}}}^{{{\textbf {1}}}})}^{T}:{{\varvec{C}}}^{\text {m}}:{\mathbb {A}}^{{{\textbf {1}}}}>:{\bar{\varvec{\varepsilon }}} \right\} +\left\{ {\bar{\varvec{\varepsilon }}}^{T}:<{{({\mathbb {A}}}^{{{\textbf {1}}}})}^{T}:{{\varvec{C}}}^{\text {m}}:{\mathbb {A}}^{{{\textbf {2}}}}>\vdots {\bar{\varvec{\mathcal {K}}}} \right\} \nonumber \\ {}{} & {} +\frac{1}{2} {\bar{\varvec{\mathcal {K}}}}^{T}\vdots <{({\mathbb {A}}^{{{\textbf {2}}}})}^{T}:{{\varvec{C}}}^{\text {m}}:{\mathbb {A}}^{{{\textbf {2}}}}>\vdots {\bar{\varvec{\mathcal {K}}}} \end{aligned}$$
(17)

On the other hand at the macroscale, the Mindlin II [13] formulation of the energy for a homogenized strain-gradient material reads

$$\begin{aligned} W^{\text {M}}=\frac{1}{2}\left( \left( {\varvec{\varepsilon }}^{\text {M}} \right) ^{T}:{{\varvec{C}}}^{\text {M}}:{\varvec{\varepsilon }}^{\text {M}}\right) +{\varvec{\varepsilon }}^{\text {M}}:{{\varvec{B}}}^{\text {M}}\vdots {\mathrm {\nabla }{\varvec{\varepsilon }}}^{\text {M}}+ \frac{1}{2}\left( \left( {\mathrm {\nabla }{\varvec{\varepsilon }}}^{\text {M}} \right) ^{T}\vdots {{\varvec{D}}}^{\text {M}}\vdots {\mathrm {\nabla }{\varvec{\varepsilon }}}^{\text {M}}\right) \end{aligned}$$
(18)

Inserting Eq. (2) into the above energy expression results in

$$\begin{aligned} W^{\text {M}}= \frac{1}{2}\{\left( {\bar{\varvec{\varepsilon }}}+{\bar{\varvec{\mathcal {K}}}}.{{\varvec{x}}} \right) ^{T}: {{\varvec{C}}}^{\text {M}}:\left( {\bar{\varvec{\varepsilon }}}+{\bar{\varvec{\mathcal {K}}}}.{{\varvec{x}}} \right) \}+ \left( {\bar{\varvec{\varepsilon }}}+{\bar{\varvec{\mathcal {K}}}}.{{\varvec{x}}} \right) :{{\varvec{B}}}^{\text {M}}\vdots {\bar{\varvec{\mathcal {K}}}}+ \frac{1}{2}({\bar{\varvec{\mathcal {K}}}}^{T}\vdots {{\varvec{D}}}^{\text {M}}\vdots {\bar{\varvec{\mathcal {K}}}}) \end{aligned}$$
(19)

Following mathematical operations this leads to

$$\begin{aligned} W^{\text {M}}=\frac{1}{2}\{{\bar{\varvec{\varepsilon }}}^{T}: {{\varvec{C}}}^{\text {M}}:{\bar{\varvec{\varepsilon }}} \}+ {\bar{\varvec{\varepsilon }}}:({{\varvec{B}}}^{\text {M}}+{{\varvec{C}}}^{\text {M}}\otimes {{\varvec{x}}})\vdots {\bar{\varvec{\mathcal {K}}}}+ \frac{1}{2} \{{\bar{\varvec{\mathcal {K}}}}^{T}\vdots ({{\varvec{D}}}^{\text {M}}+{{\varvec{C}}}^{\text {M}}\otimes {{{\varvec{x}}}}{{{\varvec{x}}}})\vdots {\bar{\varvec{\mathcal {K}}}}\}\qquad \end{aligned}$$
(20)

Employing the principle of energy equivalency at micro-scale (Eq. 17) and macro-scale (Eq. 20), i.e. Hill–Mandel lemma \(W^{\text {M}}={<W}^{\text {m}}>\), we obtain the effective elasticity tensors of a homogenized second-order continua as

$$\begin{aligned} {{\varvec{C}}}^{\text {M}}=&{} <(\mathbb {A}^{{{\textbf {1}}}})^{T}:{{\varvec{C}}}^{\text {m}}:{\mathbb {A}}^{{{\textbf {1}}}}>\end{aligned}$$
(21)
$$\begin{aligned} {{\varvec{B}}}^{\text {M}}+{{\varvec{C}}}^{\text {M}}\otimes {{\varvec{x}}}=&{} <{({\mathbb {A}}^{{{\textbf {1}}}})}^{T}:{{\varvec{C}}}^{\text {m}}:{\mathbb {A}}^{{{\textbf {2}}}}> \end{aligned}$$
(22)
$$\begin{aligned} {{\varvec{D}}}^{\text {M}}+{{\varvec{C}}}^{\text {M}}\otimes {{{\varvec{x}}}}{{{\varvec{x}}}}=&{} <\left( {\mathbb {A}}^{{{\textbf {2}}}} \right) ^{T}:{{\varvec{C}}}^{\text {m}}:{\mathbb {A}}^{{{\textbf {2}}}}> \end{aligned}$$
(23)

Substituting expression for \(C^{\text {M}}\), Eq. (21), into Eqs. (22–23) yields

$$\begin{aligned} {{\varvec{B}}}^{\text {M}}+{<(\mathbb {A}^{{{\textbf {1}}}})}^{T}:{{\varvec{C}}}^{{{\text {m}}}}:{\mathbb {A}}^{{{\textbf {1}}}}\otimes {{\varvec{x}}}>= & {} <{\mathbb {A}}^{{{\textbf {1}}}}:{{\varvec{C}}}^{\text {m}}:{\mathbb {A}}^{{{\textbf {2}}}}> \end{aligned}$$
(24)
$$\begin{aligned} {{\varvec{D}}}^{\text {M}}+{<\left( {\mathbb {A}}^{{{\textbf {1}}}}\otimes {{\varvec{x}}} \right) }^{T}:{{\varvec{C}}}^{\text {m}}:{\mathbb {A}}^{{{\textbf {1}}}}\otimes {{\varvec{x}}}>= & {} <\left( {\mathbb {A}}^{{{\textbf {2}}}} \right) ^{T}:{{\varvec{C}}}^{\text {m}}:{\mathbb {A}}^{{{\textbf {2}}}}> \end{aligned}$$
(25)

Thus, the homogenized coupling and strain gradient tensors read as

$$\begin{aligned} {{\varvec{B}}}^{\text {M}}=< & {} ({\mathbb {A}}^{{{\textbf {1}}}})^{T}:{{\varvec{C}}}^{\text {m}}:({\mathbb {A}}^{{{\textbf {2}}}}-{\mathbb {A}}^{{{\textbf {1}}}}\otimes {{\varvec{x}}})> \end{aligned}$$
(26)
$$\begin{aligned} {{\varvec{D}}}^{\text {M}}=< & {} ({\mathbb {A}}^{{{\textbf {2}}}}-{\mathbb {A}}^{{{\textbf {1}}}}\otimes {\varvec{x}})^{T}:{{\varvec{C}}}^{\text {m}}:({\mathbb {A}}^{{{\textbf {2}}}}-{\mathbb {A}}^{{{\textbf {1}}}}\otimes {{\varvec{x}}})> \end{aligned}$$
(27)

Similar expressions for \({{\varvec{B}}}^{\text {M}}\) and \({{\varvec{D}}}^{\text {M}}\) are provided in the work of [19], where the authors modified the second localization tensor (\(\tilde{A^{2}}={{\mathbb {A}}^{{\textbf{2}}}-{\mathbb {A}}}^{{\textbf{1}}}\otimes {{\varvec{x}}})\) to eliminate spurious gradient terms. Their conclusion was based on the analysis of a special case of homogenous material, but here we provided a generic approach and mathematically derived this based on the equivalency of energies.

3 Numerical implementation

We use the finite element method along with periodic boundary condition to numerically solve Eqs. (12) and (13). For this following the Voight notation, Eqs. (12–13) are rewritten as

$$\begin{aligned} \int \limits _\mathrm {\Omega } {\left[ \delta \varepsilon ^{*} \right] \left[ C^{\text {m}} \right] (\left[ {\bar{\varvec{\varepsilon }}} \right] +[\varepsilon ^{*}])\text {d}\mathrm {\Omega }}=&{} 0 \end{aligned}$$
(28)
$$\begin{aligned} \int \limits _\mathrm {\Omega } {\left[ \delta \varepsilon ^{*} \right] ^{T}\left[ C^{\text {m}} \right] (\mathbf {[}g\mathbf {]}+[\varepsilon ^{*}])\text {d}\mathrm {\Omega }} -\int \limits _\mathrm {\Omega } {\left[ \delta \varepsilon ^{*} \right] ^{T}\left[ C^{\text {m}} \right] \mathbf {[}g\mathbf {]} \mathrm {\Omega }}=&{} 0 \end{aligned}$$
(29)

where \([\varepsilon ^{*}]\) and \(\left[ {\bar{\varvec{\varepsilon }}} \right] \) are, respectively, strain fluctuation and macroscopic strain in vector form, while \(\left[ C^{\text {m}} \right] \) and \(\left[ C^{\text {M}} \right] \)are, respectively, matrix representation of micro and macro elasticity tensors. In Voigt notation, the vector \([\mathcal {G}]\) reads

$$\begin{aligned} \left[ \mathcal {G} \right]= & {} \left[ {\begin{array}{*{20}c} {\bar{\varvec{\mathcal {K}}}}_{111}x_{1}+ {\bar{\varvec{\mathcal {K}}}}_{112}x_{2}\\ {\bar{\varvec{\mathcal {K}}}}_{221}x_{1}+ {\bar{\varvec{\mathcal {K}}}}_{222}x_{2}\\ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{121}{+{\bar{\varvec{\mathcal {K}}}}_{211})x}_{1} + {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{122}{+{\bar{\varvec{\mathcal {K}}}}_{212})x}_{2}\\ \end{array} } \right] \text {in 2-D} \nonumber \\ \left[ \mathcal {G} \right]= & {} \left[ {\begin{array}{*{20}c} {\bar{\varvec{\mathcal {K}}}}_{111}x_{1}+ {\bar{\varvec{\mathcal {K}}}}_{112}x_{2}+{\bar{\varvec{\mathcal {K}}}}_{113}x_{3}\\ {\bar{\varvec{\mathcal {K}}}}_{221}x_{1}+ {\bar{\varvec{\mathcal {K}}}}_{222}x_{2}+{\bar{\varvec{\mathcal {K}}}}_{223}x_{3}\\ {\bar{\varvec{\mathcal {K}}}}_{331}x_{1}+ K_{332}x_{2}+{\bar{\varvec{\mathcal {K}}}}_{333}x_{3}\\ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{231}{+{\bar{\varvec{\mathcal {K}}}}_{321})x}_{1}+ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{232}{+{\bar{\varvec{\mathcal {K}}}}_{322})x}_{2}+ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{233}{+K_{323})x}_{3}\\ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{131}{+{\bar{\varvec{\mathcal {K}}}}_{311})x}_{1}+ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{132}{+{\bar{\varvec{\mathcal {K}}}}_{312})x}_{2}+ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{133}{+{\bar{\varvec{\mathcal {K}}}}_{313})x}_{3}\\ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{121}{+{\bar{\varvec{\mathcal {K}}}}_{211})x}_{1}+ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{122}{+{\bar{\varvec{\mathcal {K}}}}_{212})x}_{2}+ {\frac{1}{2}({\bar{\varvec{\mathcal {K}}}}}_{123}{+{\bar{\varvec{\mathcal {K}}}}_{213})x}_{3}\\ \end{array} } \right] \text { in }3-D \end{aligned}$$
(30)

Note that the strain gradient components have minor symmetry with respect to the first two indices, e.g. \({\bar{\varvec{\mathcal {K}}}}_{123}={\bar{\varvec{\mathcal {K}}}}_{213}\)

To compute all the effective elastic and strain gradient parameters, one should solve Eqs. (28) and (29) for all the possible macroscopic strain and strain gradient loads. That is

$$\begin{aligned} {\bar{\varvec{\varepsilon }}}^{(ij)}= & {} \frac{1}{2} (\left( e_{i}\otimes e_{j} \right) +(e_{j}\otimes e_{i})) \end{aligned}$$
(31)
$$\begin{aligned} {\bar{\varvec{{K}}}}^{(klm)}= & {} \frac{1}{2}(\left( e_{k}\otimes e_{l} \right) +(e_{l}\otimes e_{k}))\otimes e_{m} \end{aligned}$$
(32)

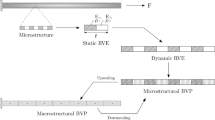
where \(e_{i,j,k,l,m}\) are unit basis vectors in 2- or 3-D space We write the above tensors as column vectors in Voight notation—following Tables 1, 2, 3 and 4 and build \(\left[ {\bar{\varvec{\varepsilon }}} \right] \) and \(\left[ {\bar{\varvec{\mathcal {K}}}} \right] \) for each load case. Once these are formed, we follow the algorithm described in Fig. 1.

Table 1 Voigt notation used for 2-D classic strain vector
Full size table
Table 2 Voigt notation used for 3-D classic strain vector
Full size table
Table 3 Voigt notation used for 2-D strain gradient vector
Full size table
Table 4 Voigt notation used for 3-D strain gradient vector
Full size table
Fig. 1
figure 1

Computational homogenization scheme

Full size image

4 Numerical studies

In the following, we employ the developed scheme and derive the classical and strain gradient elastic material parameters for various 2- and 3-D lattice materials. For 2-D plane-strain case, the whole process of model generation, meshing and analysis is done in the open-source software FreeFEM\(++\) [39]. But due to the complexity of models in 3-D, we use dedicated software for each stage. That is, CAD modelling is carried out in PTC Creo, mesh generation is performed in SALOME, and finite element computations are conducted in FreeFEM\(++\). A projection algorithm (in SALOME) is used to assure that the mesh nodes on opposite faces of the RVE boundary are identical to facilitate the implementation of periodic boundary conditions.

4.1 Two-dimensional lattices

We consider a 2-D square lattice as in Fig. 2, with the cell length of L and wall thickness of t. The lattice is made of a classical elastic material with Young’s modulus of 100 MPa and Poisson’s ratio of 0.3.

Fig. 2
figure 2

Unit cell of 2-D square lattice geometry

Full size image

The geometry of the square lattice is centro-symmetric meaning that the effective coupling matrix, \({{\varvec{B}}}^{\text {M}}\), vanishes. Additionally, this geometry implies a specific symmetry class with the following matrices of material properties.

$$\begin{aligned} {{\varvec{C}}}^{\text {M}}={} & {} {} \left[ {\begin{array}{*{20}c} C_{1111} &{}{} C_{1122} &{}{} 0\\ C_{2211} &{}{} C_{1111} &{}{} 0\\ 0 &{}{} 0 &{}{} C_{1212}\\ \end{array} } \right] \end{aligned}$$
(33)
$$\begin{aligned} {{\varvec{D}}}^{\text {M}}={} & {} {} \left[ {\begin{array}{*{20}c} D_{111111} &{}{} D_{111221} &{}{} \text { }D_{111122} &{}{} \text {0} &{}{} \text {0} &{}{} \text {0}\\ D_{221111} &{}{} D_{221221} &{}{} D_{221122} &{}{} 0 &{}{} 0 &{}{} 0\\ D_{122111} &{}{} D_{122221} &{}{} D_{122122} &{}{} 0 &{}{} 0 &{}{} 0\\ 0 &{}{} 0 &{}{} 0 &{}{} D_{111111} &{}{} D_{111221} &{}{} D_{111122}\\ 0 &{}{} 0 &{}{} 0 &{}{} D_{112222} &{}{} D_{221221} &{}{} D_{221122}\\ 0 &{}{} 0 &{}{} 0 &{}{} D_{122111} &{}{} D_{122221} &{}{} D_{122122}\\ \end{array} } \right] \end{aligned}$$
(34)

Considering the symmetry of \({{\varvec{C}}}^{\text {M}}\) and \({{\varvec{D}}}^{\text {M}}\) matrices, this material is characterized with only 3 classical and 6 strain gradient elastic parameters.

To evaluate the validity of the model against the basic understanding of strain gradient elasticity, we consider the three following test scenarios:

(i) Relative density

We assess the elastic and strain gradient parameters with respect to the relative density of the lattice by varying the wall thickness as in Table 5. As expected, the gradient material parameters initially increase with increasing solid volume fraction, but they start to reduce at \(\bar{\rho }=0.75\) and completely vanish when the material is fully homogenous (see Fig. 3a). This confirms that in the current approach, the spurious strain gradient parameters disappear when the material is fully solid. The presence of such an extremum for the D matrix motivates the possibility of extremizing the size effect as a material engineering tool. The classical elastic parameters monotonically increase with the relative density and reach the properties of the base material at \({\bar{\rho }}=1\).

Table 5 Variation of the unit-cell relative density (\(L=1\textrm{mm}\))
Full size table
Fig. 3
figure 3

Classical and strain gradient elastic material parameters at different relative densities

Full size image

(ii) Size effect

We now study the variation of elastic properties with respect to the cell size by changing the wall thickness and cell length (see Table 6), while keeping the relative density constant at \({\bar{\rho }}=0.19\). We observed that as expected, the parameters of classical elasticity, i.e. \({{\varvec{C}}}^{\text {M}}\), are size-independent and do not change with the cell size. However, one can see in Fig. 4 that the parameters of gradient elasticity are size-dependent, while all the parameters of \({{\varvec{D}}}^{\text {M}}\) approaches zero as the cell size decreases. This is true because as the unit-cell becomes smaller, the size effects become less dominant, and strain gradient parameters vanish. Moreover, we note that the strain gradient parameters in \({{\varvec{D}}}^{\text {M}}\) scale with \(\epsilon ^{2}\). For instance, the parameter \(D_{111111}\) in cell with \(L=1\) mm is, respectively, 4 times and 25 times higher than its counterparts in cells with \(L=0.5\) mm and \(L=0.2\) mm. This shows that the current model can accurately capture the size effects, e.g. see also [19, 21, 28].

Table 6 Variation of the unit-cell size \((\bar{\rho =0.19})\)
Full size table

The above scaling of strain gradient parameters with the cell size can also be mathematically verified. By writing Eq. (13) in local coordinate, i.e., \({{\varvec{x}}}=\epsilon {{\varvec{y}}}\), the solution to the problem (Eq. (14)) reads as: \({\varvec{\varepsilon }}_{\left( {\varvec{x,y}} \right) }={\mathbb {A}}^{{\textbf{1}}}_{{\varvec{(x,y)}}}:{\bar{\varvec{\varepsilon }}} +\epsilon \tilde{A^{2}}_{{\varvec{(x,y)}}}\vdots {\bar{\varvec{\mathcal {K}}}}\). Next, using this form of solution and following the same steps as described in Sect. 2, the homogenized coupling and strain gradient matrices in local coordinate read as

$$\begin{aligned} {{\varvec{B}}}^{\text {M}}=&{} \epsilon <{({\mathbb {A}}^{{{\textbf {1}}}})}^{T}:{{\varvec{C}}}^{\text {m}}:{\tilde{\mathbb {A}}}^{{{\textbf {2}}}}> \end{aligned}$$
(35)
$$\begin{aligned} {{\varvec{D}}}^{\text {M}}=&{} \epsilon ^{2}<({\tilde{\mathbb {A}}} ^{{{\textbf {2}}}})^{T}:{{\varvec{C}}}^{\text {m}}:{\tilde{A}}^{{{\textbf {2}}}}> \end{aligned}$$
(36)

This further confirms the validity of the model in predicting the size effects.

Fig. 4
figure 4

Variation of strain gradient parameters with the cell size (\({\bar{\rho }}=0.19\))

Full size image

(iii) Window of analysis

In this test, we check the influence of selection of the analysis window on classical and gradient elastic parameters. We do so by evaluating these parameters using three different RVEs consisting of one cell, four cells and nine cells, as shown in Fig. 5. In all cases, the cell length (L) and wall thickness (t) are 1 mm and 0.1 mm (\({\bar{\rho }}=0.19\)), respectively. Here, we refer to “analysis window” as the number of cells included in the RVE.

The classical elastic parameters are insensitive to the choice of analysis window, while the gradient elastic parameters change with the number of cells included in the RVE. We see in Fig. 6 that the parameter \(D_{111111}\) linearly varies with the total number of cells (or with \(N^{2}\) if we consider each RVE contains \(N\times N\) cells). Such trend was also observed in previous works, e.g. [35] and [36]. To further investigate this from an energy perspective, we applied macroscopic strain gradient load corresponding to\( {\bar{\varvec{\mathcal {K}}}}^{(111)}\), solved the microscopic problem and evaluated the energy density contribution of the gradient part, i.e. \(\frac{1}{{2V}_{\Omega }}\smallint {({\tilde{A}}^{{{\textbf {2}}}})}^{T}:{{\varvec{C}}}^{\text {m}}:{\tilde{A}}^{{{\textbf {2}}}}\mathrm {\Omega }\)—since the classical elastic parameters are identical in all cases. The results in Table 7 show that the energy density of the above-mentioned RVEs differs, and this is the reason behind variation of strain gradient parameters. We remind that the equivalency of energy between micro- and macro-scale is still valid for each individual case, i.e. each homogenized RVE and its microstructure. Yet, the value of energy varies in RVEs with different cell numbers

Fig. 5
figure 5

Different RVEs made of: a 1 cell, b 4 cells, and c 9 cells

Full size image
Fig. 6
figure 6

Variation of the effective strain gradient parameter with the number of cells in an RVE (Each RVE contains \(N\times N\) cells)

Full size image

Such variation between the obtained results for different RVEs has also been reported in [40], where the authors noticed the value of equivalent von Mises stress is higher for RVEs containing more number of cells. Thus, we argue that in the proposed method, one should choose the RVE as an irreducible cell (1 cell) specifying accordingly the scale ratio. Otherwise, the effective strain gradient properties should be scaled as in Fig. 6. Such a simple scaling is valid for linear elastic assumption, and the situation becomes more complicated when the material is nonlinear, e.g. large deformation or plasticity. Thus, we suggest selecting the analysis window as a single irreducible cell.

4.2 Three-dimensional lattices

We study a 3-D lattice material known as cubic lattice, see Fig. 7. Four cells with circular strut cross-section and various cell sizes are designed at the constant relative density of \({\bar{\rho }}=0.25\), see Table 8 for dimensions We homogenize the cells towards higher-grade continua using the algorithm described in Sect. 3 and examine the size effect of microstructure on the effective properties.

Table 7 Gradient strain energy density of RVEs with various cell numbers
Full size table
Fig. 7
figure 7

3-D cubic lattice materials with various cell sizes

Full size image

The base material used for the fabrication of lattices is polyamide PA-12. To quantify the properties of the base material, we conducted tensile tests—3 mm/min displacement rate—on two additively manufactured PA-12 dogbone samples that are produced with the same printing parameters used for the fabrication of lattice structures (see Sect. 5 for more details on 3D-printing). The averaged value of the experimentally measured parameters turned out to be 1.58 GPa for the elastic modulus and 0.4 for the Poisson’s ratio, see Appendix B for stress–strain plots.

These experimentally characterized properties are used as inputs for simulations. We discretize the unit-cells with linear elements and approximate the solution over the elements with second-order (P2) finite element space. In the literature, the convergence criterion for homogenization is not well-defined. Recently, Yang et al. [29] used the symmetry class of the material as a basis for convergence analysis. This approach is applicable only when the material symmetry is already known and is not practical for exploring new advanced materials. Additionally, assessing the convergence based on a few selected components of the elasticity matrices may not be representative of the overall behavior of the material. Therefore, we propose the strain energy of the homogenized cell, \(W^{\text {M}}\) in Eq. (19), to be used as the convergence criterion.

Table 8 Cell dimensions for cubic lattices (\({\bar{\rho }}=0.25\))
Full size table

We note that the convergence for classical elasticity (components of \({{\varvec{C}}}^{\text {M}})\) is easily achieved, even when relatively large mesh sizes are used. But this is not the case for gradient elastic parameters, so we base our assessment on convergence of \({{\varvec{D}}}^{\text {M}}\) components (note that \({{\varvec{B}}}^{\text {M}}\) is zero because the studied unit-cell is centro-symmetric). We assess the energy of the strain gradient part of \({{\varvec{W}}}^{\text {M}}\) in Eq. (19), \({\bar{\varvec{\mathcal {K}}}}^{T}\vdots {{\varvec{D}}}^{\text {M}}\vdots {\bar{\varvec{\mathcal {K}}}}\), by applying an arbitrary load case to the homogenized material. In this loading, to activate all the components of macroscopic strain gradient tensor, all the elements of \({\bar{\varvec{\mathcal {K}}}}\) are set to be 1. This allows for the contribution of all computed parameters of \({{\varvec{D}}}^{\text {M}}\) in the energy value. The convergence is reached when the difference between computed energy values from homogenized \({{\varvec{D}}}^{\text {M}}\) matrices is less than 1%. This is achieved when the mesh size is 1/10th of strut diameter, e.g. mesh size of 0.7 mm for cubic lattice in case 1.

As an example, the computed homogenized \({{\varvec{D}}}^{\text {M}}\) matrix for the cubic lattice with 20 mm cell size is shown in Fig. 8. The homogenized matrix follows the structure of a cubic symmetric material in strain gradient elasticity. Here, \({{\varvec{D}}}^{\text {M}}\) is a block-diagonal matrix composed of three identical \(5\times 5\) (blue, green, and yellow in Figure 8) and one \(3\times 3\) (orange in Fig. 8) block matrices, while other components of the matrix are negligible. Additionally, some of the components in the highlighted block matrices are equal, resulting in only 11 independent elastic parameters in this strain gradient matrix. For more details about the structure of a cubic symmetric material in strain gradient elasticity see [29, 41].

The obtained \({{\varvec{D}}}^{\text {M}}\) matrix is positive definite and it results in a positive strain energy value, see [42] for more details. Despite its fundamental importance, the positive definiteness of \({{\varvec{D}}}^{\text {M}}\) as well as positivity of strain energy is sometimes overlooked in other works related to strain gradient homogenization.

Fig. 8
figure 8

Homogenized \({{\varvec{D}}}^{\text {M}}\) matrix (in kN) for the cubic lattice following the cubic symmetry class in strain gradient elasticity, consisting of three \(5\times 5\) (in blue, green, and yellow), and one \(3\times 3\) (in orange) block matrices (colour figure online)

Full size image

Once the effective gradient elasticity matrix is computed for one cell, we may skip the costly computations for other cells using the scaling ratio \(\epsilon \) (as discussed in Sect. 4-(iii)). Having \({{\varvec{D}}}^{\text {M}}\) for 20 mm cell size, we obtain the effective gradient elasticity matrix corresponding to 10 mm, 5 mm, and 2.5 mm cell size by, respectively, scaling the computed \({{\varvec{D}}}^{\text {M}}\) with \(\epsilon ^{2}\)=1/4,1/16. and 1/64 The classical elasticity matrix \({{\varvec{C}}}^{\text {M}}\) is size-independent and remains constants for all the cells. This is obtained as

$$\begin{aligned} \left[ {\begin{array}{*{20}c} 196 &{} 28 &{} 28 &{} 0 &{} 0 &{} 0\\ 28 &{} 196 &{} 28 &{} 0 &{} 0 &{} 0\\ 28 &{} 28 &{} 196 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 15 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 15 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 15\\ \end{array} } \right] (\mathrm {MPa)} \end{aligned}$$
(37)

Note that the components of \({{\varvec{C}}}^{\text {M}}\) also follow the structure of a cubic symmetric material in classical elasticity, see also [2].

5 Validation

To validate the homogenization scheme and quantify the size effect, we consider the application of designed lattices in beam structures under three-point bending load. This beam structure is then analyzed via (i) full-field simulation of the beam with detailed microstructure, (ii) isogeometric analysis (IGA) of the homogenized higher-grade continua, and (iii) experimental tests on additively manufactured lattice structures.

5.1 Full-field simulations

We simulate three-point bending tests on beams with detailed microstructure, see Fig. 9. The beams are 140 mm long with 20 mm\( \times \) 20 mm square cross-section and are made of cells with different sizes as listed in Table 8.

Fig. 9
figure 9

Beam structures made of cubic lattice with various cell sizes

Full size image

We perform quasi-static displacement-controlled numerical tests in Abaqus CAE. Only quarter of the beam is modelled using x-symmetry and y-symmetry boundary conditions that are, respectively, applied to the middle yz-section and middle xz-section of the beam. The beam is constrained by setting \(u_{z}=0\) over the bottom edge of the end cross-section. We then displace the beam by coupling degrees of freedom in z-direction on the top edge of the middle cross-section to a reference point and apply a displacement in the negative z-direction to this point. This setup is schematically shown in Fig. 10.

For full-field simulations, the beam structures are discretised by C3D10 (a 10-node quadratic tetrahedron) finite elements. For lattices with different cell size, the ratio of approximate element size to strut diameter is kept as \(\approx \) 0.1. The base material of the microstructure follows the classical isotropic elasticity with the material properties stated in Sect. 4.2.

Fig. 10
figure 10

Deformed shape and distribution of z-component of the displacement field for: a quarter of the beam with detailed cubic microstructure, and b half of the homogeneous beam with effective properties modelled via IGA. Red point shows position of a reference point (RP) (colour figure online)

Full size image

5.2 Isogeometric analysis

We model the bending behaviour in the framework of strain gradient elasticity theory by representing the lattice beams as homogeneous continuum with effective elastic moduli given in \({{\varvec{C}}}^{\text {M}}\) and \({{\varvec{D}}}^{\text {M}}\), see Fig. 10. For the homogeneous 140 mm \(\times \) 20 mm \(\times \) 20 mm beams, only half of the domain is modelled using the x-symmetry boundary condition on the middle cross-section, which along with zero normal displacement (\(u_{x}=0)\) implies also zero normal derivative of tangent displacements (\(\frac{{\partial u}_{y}}{\partial x}=\frac{{\partial u}_{z}}{\partial x}=0)\) [43]. The other end of beam is constrained by setting \(u_{z}=0\) over the bottom edge of the end cross-section. We then displace the beam by coupling degrees of freedom in z-direction on the top edge of the middle cross-section (the cross-section where symmetry is implied, see Fig. 10) to a reference point and apply a displacement in the negative z-direction to this point.

We utilize Isogeometric analysis [44] for numerically solving the higher-grade continua problems [43, 45] and discretise the domain by \(32 \times 8 \times 8\) three-dimensional elements (knot spans) with B-splines of degree \(p=q=r=3\) and \(C^{2}\) global continuity. The conforming isogeometric Galerkin method is implemented using a 3-D UEL subroutine within a commercial software Abaqus, see [46,47,48].

5.3 Experiments

We 3D-print the lattice structures with HP MFJ 580 machine using multi jet fusion technology with monochrome cosmetic setting and HP PA-12 powder as the base material. To minimize the influence of build direction, all samples (including dogbone) are printed vertically with respect to the build plate, see also [49]. Moreover, the samples were auto-cooled to minimize the warpage resulting from temperature gradient. The printed lattice structures are shown in Fig. 11.

Fig. 11
figure 11

Additively manufactured dogbone specimen and lattice beam structures made of PA-12

Full size image
Fig. 12
figure 12

Three-point bending test setup for a cubic lattice beam-like structure

Full size image

We carry out two sets of three-point bending tests by applying a constant 3 mm/min displacement (identical to what was applied in tensile test for characterization of the base material) on the middle of a simply supported beam structure with 20 mm \(\times \) 20 mm square cross-section. The beams are 170 mm long, but they rest on two supports located at the distance of 140 mm. To exclude machine compliance, we use a video extensometer for displacement measurements. That is, we track the relative displacement between the two markers that are attached to a stationary cylinder (as a reference for measurements) and the loading nose, see Fig. 12. We continue the tests until the samples break but only use the data at early loading stage where the material behavior is assumed to be linear elastic. The tests are repeated twice.

Although the experiments were conducted on lattice beams with different cell sizes, only the data for 20 mm cell size (case 1) is used for comparison with numerical simulations. This is because the input material data in simulations are based on tensile tests conducted on 3 mm-thick dogbone specimens, but the strut radius in designed lattice structures spans between 3.7 to 0.46 mm. The change in mechanical properties of additively manufactured materials with print length-scale challenges the experimental quantification of size effects. The variation of material properties with the print thickness has been extensively investigated for some materials like Ti-64, e.g. see [5, 50, 51], but very few studies addressed the issue for PA-12, e.g. see [52]. Thus, we excluded the beam-like lattice structures with cell size less than 20 mm from the experimental analysis in Sect. 5.4. However, for the reader’s reference, the force-displacement plots of all the tested specimens along with their averaged experimental values and standard deviations are reported in Appendix C.

5.4 Results and discussion

Table 9 summarizes the simulations and experimental results for three-point bending tests. The most dominant size effect is observed in case 1, where the size of micro-structure is 1/7\(^{\textrm{th}}\) of the size of macro-structure (beam length). Here, classical elasticity underestimates the bending rigidity by 21%, while the IGA simulations based on homogenized stiffness matrices (\({{\varvec{C}}}^{\text {M}}\) and \({{\varvec{D}}}^{\text {M}})\) improve the predictions and show a 14% difference with the full-field simulations. In case 2, we further refine the micro-structure size by half so the micro- to macro-length ratio reads as 1/14. Even in this case, the classical solution fails to accurately predict the mechanical behavior—with 13% underestimation of bending rigidity compared to full-field data—, while IGA simulations show a good agreement with only 2% difference. The results for cases 3 and 4 confirm that as we further reduce the size of micro-structure, both full-field and IGA simulations converge towards classical elastic solution. This is because at the small unit-cell sizes (e.g. case 4 with micro- to macro-length ratio of 1/56, the assumption of strict scale separation is valid and strain gradient parameters in \({{\varvec{D}}}^{\text {M}}\) vanish

Table 9 Reaction forces (N) resulting from 1 mm displacement in three-point bending
Full size table

The difference between IGA and full-field results could be primarily due to boundary effects, which are not included in the current homogenization scheme, see also [30]. In fact, the application of periodic boundary conditions in the homogenization assumes infinite repetition of a unit-cell in 3-dimensional space, while we have a beam-like structure which is only tessellated in 1-direction with few unit-cells and is restricted to traction and/or displacement boundary conditions from all sides. This could lead to some discrepancies, especially when the unit-cell size is close to the size of macro-structure (case 1: with only 7 cells along the beam length) as the structural arrangement differs from the infinite tessellation assumption.

Moreover, the value of experimental three-point bending tests agrees with the obtained reaction force from full-field simulations with only 7% difference. Such a difference could be due to issues such as the influence of print direction on mechanical properties or pre-curvature arising from temperature gradient during fabrication process.

6 Conclusion

In this work, a computational homogenization scheme based on second-order strain gradient theory is proposed. While the literature in the field is mainly devoted to 2-D models with focus on composite materials, the current study targets 3-D lattice materials with void as their inclusion. This study, as the first one of its kind, provides in-depth validation using experiments, IGA, and full-field simulations of complex 3-D lattice materials. Additionally, the modifications suggested in [19] for the removal of spurious gradient effects, are mathematically derived based on the Hill–Mandel lemma. Finally, a new criterion based on macroscopic energy is proposed for the convergence analysis of homogenized strain gradient matrix.

The proposed methodology is generic and can be applied to any micro-architectured material. However, the identification of the form of the generalized continua (such as strain gradient, Cosserat, etc.) for the mechanical behavior of a specific micro-architectured material is yet an open question, see [53,54,55]. We validated the proposed second-order homogenization scheme by homogenizing cubic lattice material toward gradient elasticity, and the result seems promising, but this may not be necessarily the case for other lattices with different unit-cell architecture as their deformation behavior may be best quantified by a different generalized continuum theory. In other words, one homogenization theory might be suitable in describing the mechanics of a specific micro-architecture or even a specific load case, but it may not be able to accurately address all the deformation behaviors for a range of cell topologies. The identification of the most suitable continuum theory (and deriving a corresponding homogenization technique) based on the topology of an architectured material and the applied loading conditions is a subject that needs to be investigated in the future studies. Additionally, despite the advances in additive manufacturing for the production of complex micro-architectures, the lack of an optimized process resulting in stable properties across different print length-scales limits the possibility for experimental characterization of lattice materials. Nevertheless, the fast progress of additive manufacturing is believed to provide such controlled printability in the near future.