A weak version of the Mond conjecture

Abstract

We prove that a map germ $f:(\mathbb {C}^n,S)\rightarrow (\mathbb {C}^{n+1},0)$ with isolated instability is stable if and only if $\mu _I(f)=0$, where $\mu _I(f)$ is the image Milnor number defined by Mond. In a previous paper we proved this result with the additional assumption that f has corank one. The proof here is also valid for corank $\ge 2$, provided that $(n,n+1)$ are nice dimensions in Mather’s sense (so $\mu _I(f)$ is well defined). Our result can be seen as a weak version of a conjecture by Mond, which says that the $\mathscr {A}_e$-codimension of f is $\le \mu _I(f)$, with equality if f is weighted homogeneous. As an application, we deduce that the bifurcation set of a versal unfolding of f is a hypersurface.

1 Introduction

In the context of Thom-Mather theory (deformation theory) for map germs $f:(\mathbb {C}^n,S)\rightarrow (\mathbb {C}^{p},0)$, the cases $p<n+1$, $p=n+1$ and $p>n+1$ present different traits and behaviours. In particular, the case $p=n+1$ has several open questions that are understood for the other cases. Here we solve two of them: one regarding the homotopy type of a generic fiber and the other regarding the bifurcation set.

A hypersurface (X, 0) with isolated singularity has a well known invariant given by its Milnor fiber, the Milnor number $\mu (X,0)$. D. Mond introduced a similar invariant for map germs $f:(\mathbb {C}^n,S)\rightarrow (\mathbb {C}^{n+1},0)$ with isolated instability in [21]. Indeed, the image of a stable perturbation of f has the homotopy type of a wedge of spheres of dimension n, whose number is independent of the stable perturbation. This number of spheres is the image Milnor number of f, denoted by $\mu _I(f)$, and its stable perturbation plays the role of Milnor fiber of a hypersurface as before. However, this is only well defined when f has corank one or, alternatively, $(n,n+1)$ are nice dimensions in Mather’s sense (cf. [19]).

On the other hand, the $\mathscr {A}_e$-codimension of a germ as above is the equivalent of the Tjurina number $\tau (X)$ of a hypersurface with isolated singularity, because they control the space of deformations of map germs and germs of hypersurfaces, respectively.

The easy relation between the Tjurina and Milnor number for hypersurfaces inspired D. Mond to conjecture in [21] that the relation is reproduced in the case of map germs with isolated instability. More precisely:

Conjecture 1.1

(The Mond conjecture) Given a germ $f:(\mathbb {C}^n,S)\rightarrow (\mathbb {C}^{n+1},0)$ with finite $\mathscr {A}_e$-codimension such that it has corank one or $(n,n+1)$ are nice dimensions (i.e., $n<15$),

$$\begin{aligned} \mu _I(f)\ge \mathscr {A}_e\text {-}{\text {codim}}(f), \end{aligned}$$

with equality in the quasi-homogeneous case.

This question remains open in general (see [4, Theorem 4.2] and [22, Theorem 2.3] for the cases $n=1,2$).

In this paper we show a basic result on both invariants of map germs, the $\mu _I$ and the $\mathscr {A}_e\text {-}{\text {codim}}$. In Sect. 2 we deal with the image Milnor number an prove that it is positive if the germ is, indeed, unstable. This is a weak version of Conjecture 1.1 (i.e., when $\mu _I(f)=0$ we have $\mathscr {A}_e\text {-}{\text {codim}}(f)=0$) but it implies this conjecture in the case of $\mathscr {A}_e$-codimension one and the case of augmentations of such germs. In order to prove these results we also introduce new objects such as LC(G), a version of Saito’s characteristic variety $LC(\mathcal {X})$, to control the image Milnor number. Furthermore, a deep understanding of LC(G) allows us to prove that, if it is Cohen–Macaulay, the Mond conjecture is true for germs with a one parameter stable unfolding.

The bifurcation set is the set of parameters of a versal unfolding such that the corresponding perturbations have instabilities. In Sect. 3 we prove that the bifurcation set of a germ $f:(\mathbb {C}^n,S)\rightarrow (\mathbb {C}^{n+1},0)$ is a pure dimensional hypersurface. Its relevance is also put into perspective by explaining that the methods used to prove a similar fact in other settings fail in our case. Furthermore, a profound understanding of the space of unstable perturbations could lead to a proof of the Mond conjecture (see the program to solve this conjecture in the first author’s thesis, [9, Section 7.3]). Knowing that the bifurcation set is of codimension one is the first step in that direction.

We refer to the modern reference [23] for the definitions and properties about singularities of mappings such as stability, finite determinacy, versal unfoldings, and other basic concepts.

2 Unstable germs and the image Milnor number

Throughout this section we assume that $f:(\mathbb {C}^{n},S)\rightarrow (\mathbb {C}^{n+1},0)$ is an $\mathscr {A}$-finite germ such that it has corank one or $(n,n+1)$ are nice dimensions.

We fix a representative $f:U\rightarrow V$ which is a finite mapping (i.e., finite-to-one and closed) and denote by $X=f(U)$ its image. The germ of f at the point $y\in X$ is denoted by

$$\begin{aligned} (f)_{y}:\big (\mathbb {C}^n,f^{-1}(y)\big )\rightarrow (\mathbb {C}^{n+1},y). \end{aligned}$$

There is a natural stratification on an $\mathscr {A}$-finite germ f, which is straightforward in the case of a stable germ.

Definition 2.1

Suppose f is stable. The isosingular locus of f at a point $y_0$ in the image X is the set

$$\begin{aligned} {\text {Iso}}\big (f;y_0\big ){:}{=}\left\{ y\in X: (f)_y \text { is }\mathscr {A}\text {-equivalent to } (f)_{y_0}\right\} . \end{aligned}$$

Moreover, the stratification by stable types of the image of f is given by the isosingular loci of all points $y_0\in X$. There is an induced stratification in the source of f, these two stratifications are the stratification by stable types of f.

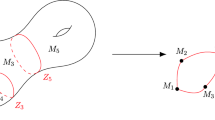
We refer to [23, Definition 7.2] for details and properties of this stratification. In fact, the hypothesis that f has corank one or $(n,n+1)$ are in the nice dimensions guarantees that we have a finite number of strata. The name of stable types is taken because, obviously, this stratification identifies stable singularities of the same $\mathscr {A}$-class (cf. Fig. 1). Indeed, there is an analogous definition of the stratification by stable types of a locally stable map.

In contrast, it could happen that $f:(\mathbb {C}^{n},S)\rightarrow (\mathbb {C}^{n+1},0)$ has instabilities. However, it has isolated instability if it is $\mathscr {A}$-finite (by Mather-Gaffney criterion). We can assume $f:U-S\rightarrow V-0$ is locally stable and extend its stratification by stable types just by adding the strata S and 0 in source and target, respectively. We call this stratification stratification by stable types of f as well (see Fig. 1).

Fig. 1

Stratification by stable types of an unstable bigerm given by a crosscap and an immersion. Observe that the transverse double points are in the same stratum

Let $F(x,s)=(f_s(x),s)$ be a stabilisation of $f:(\mathbb {C}^{n},S)\rightarrow (\mathbb {C}^{n+1},0)$. Then, F is also $\mathscr {A}$-finite, considered as a germ $(\mathbb {C}^n\times \mathbb {C},S\times 0)\rightarrow (\mathbb {C}^{n+1}\times \mathbb {C},0)$. We denote by $(\mathcal X,0)$ the image of F in $(\mathbb {C}^{n+1}\times \mathbb {C},0)$ and by $\pi :(\mathcal X,0)\rightarrow (\mathbb {C},0)$ the restriction of the projection onto the parameter space. For each s close to 0 in $\mathbb {C}$, the fibre $\pi ^{-1}(s)$ is $X_s$, the image of $f_s$.

We remark that F still has a well defined stratification by stable types on its image $\mathcal X$, although now $(n+1,n+2)$ could be in the boundary of the nice dimensions. In fact, if $(y,s)\in \mathcal X-0$, then the germ of $f_s$ at y is stable. Therefore, the germ of F at (y, s) is a trivial unfolding of the germ of $f_s$ at y. Since $(n,n+1)$ are nice dimensions or the germ has corank one, only a finite number of stable types of germs from $\mathbb {C}^n$ to $\mathbb {C}^{n+1}$ can appear. Thus, the family of isosingular loci ${\text {Iso}}\big (F;(y,s)\big )$ at points $(y,s)\in \mathcal X-\{0\}$ is finite. By adding the origin if necessary as a new stratum, we get the stratification by stable types of $\mathcal X$ (see Fig. 2).

Fig. 2

Stratification by stable types of the image of an unfolding $(f_s,s)$ of the unstable bigerm $f_0$ given by a crosscap and an immersion. Observe that, in contrast to Fig. 1, the stratum of dimension zero in now stable as a germ from $\mathbb {C}^3$ to $\mathbb {C}^4$. In a general unfolding this stratum could be unstable

Definition 2.2

(cf. [25, Lemma 3.2 and Definitions 3.3 and 3.9]) The logarithmic stratification of the hypersurface Y is the unique stratification $\left\{ D_\alpha , \alpha \in \mathcal {I}\right\}$ such that:

• (i) each $D_\alpha$ is a smooth connected immersed submanifold of Y and Y is the disjoint union $\coprod _\alpha D_\alpha$;

• (ii) if p is a point of $D_\alpha$, then the tangent space $T_p D_\alpha$ coincides with the space that the ${\text {Der}}(-\log Y)$ spans at p, i.e., $T_p D_\alpha ={\text {Der}}(-\log Y)(p)$; and

• (iii) if $D_\alpha \cap \overline{D_\beta }\ne \varnothing$ for some $\alpha ,\beta \in \mathcal {I}$ and $\alpha \ne \beta$, then $D_\alpha \subset \partial D_\beta$.

Furthermore, a logarithmic stratification is holonomic if each small enough open neighbourhood of any point intersects a finite number of strata.

Lemma 2.3

The (connected components of the) stratification by stable types of the hypersurface $(\mathcal X,0)$ coincides with the logarithmic stratification. In particular, $(\mathcal X,0)$ is holonomic.

Proof

Given two points (y, s) and $(y',s')$ in $\mathcal X$ in the same connected component of the stratification by stable types, the germs of F at (y, s) and $(y',s')$ are $\mathscr {A}$-equivalent. In particular, the germs of $\mathcal X$ at (y, s) and $(y',s')$ are equivalent by a biholomorphism $\Psi$ of the ambient space $\mathbb {C}^{n+1}\times \mathbb {C}$ and, furthermore, the stratification is analytically trivial along this stratum (cf. [6, Theorem 0.2] and [25, Paragraph 3.6]). Thus, by connectivity (y, s) and $(y',s')$ belong to the same stratum in the logarithmic stratification of $\mathcal X$.

But the converse also holds. Indeed, the germ F at each point is the normalisation of $\mathcal X$ at that point. If the germs of $\mathcal X$ at (y, s) and $(y',s')$ are equivalent by a biholomorphism $\Psi$ of $\mathbb {C}^{n+1}\times \mathbb {C}$, there exists a unique biholomorphism $\Phi$ in $\mathbb {C}^n\times \mathbb {C}$ so that $(\Phi ,\Psi )$ gives an $\mathscr {A}$-equivalence between the germs of F at (y, s) and $(y',s')$. Modulo connectivity, this shows that the stratification by stable types coincides with the logarithmic stratification. $\square$

The next result characterizes instabilities in terms of the previous stratification. Recall that when we say critical points in the stratified sense we mean critical points of the restriction to each stratum.

Lemma 2.4

The projection $\pi :(\mathcal X,0)\rightarrow (\mathbb {C},0)$ has isolated critical points in the stratified sense. Moreover, it has a critical point if, and only if, f is not stable.

Proof

As above, we fix a representative $\mathcal X$ and take $(y,s)\in \mathcal X-\{0\}$. Since the germ of $f_s$ at y is stable, the germ of F at (y, s) is a trivial unfolding of the germ of $f_s$ at y. Hence, there exist biholomorphisms $\Phi$ and $\Psi$ in $\mathbb {C}^n\times \mathbb C$ and $\mathbb {C}^{n+1}\times \mathbb C$, respectively, which are unfoldings of the identities and such that $\Psi \circ F\circ \Phi ^{-1}=f_s\times {\text {id}}_{\mathbb {C}}$ in a neighbourhood of (y, s). This gives a commutative diagram

so (y, s) is a regular point of $\pi$ in the stratifed sense.

Assume now that the origin 0 is also a regular point of $\pi$ in the stratifed sense. Let $S_0={\text {Iso}}(F;0)$ be the stratum of $\mathcal X$ which contains 0. Obviously, we must have $S_0\ne \{0\}$, and since F is stable at any point $(y,s)\in S_0-\{0\}$, F is also stable at 0. As $0\in S_0$ is a regular point of the restriction $\pi :S_0\rightarrow \mathbb C$, we deduce that the hyperplane $\pi ^{-1}(0)=\mathbb {C}^{n+1}\times \{0\}$ is transverse to $S_0$. By [24, Proposition 2.22], $f_0=f$ is stable at 0. The converse is obvious, as any unfolding is trivial and has the form $F(x,t)=\big (f_t(x),t\big )$ up to $\mathscr {A}$-equivalence. $\square$

Example 2.5

In Fig. 2 we have represented an unfolding $(f_s,s)$ of the unstable bigerm $f_0:\big (\mathbb {C}^2,\left\{ p,q\right\} \big )\rightarrow (\mathbb {C}^3,0)$ given by a crosscap and an immersion (see also Fig. 1), where $f_s$ is a stable perturbation of $f_0$ (i.e., $(f_s,s)$ is a stabilisation).

It is easy to see that Lemma 2.4 holds in this case. Indeed, the unique stratum of dimension zero is also the unique critical point of the projection to the parameter s.

The fact that this point is stable as a germ induced by the unfolding $(f_s,s)$ (i.e., as a germ from $\mathbb {C}^3$ to $\mathbb {C}^4$) plays no role in this fact. In general, if we begin with an unstable $f_0$ then, in the unfolding, we need to add as a stratum the point where the instability of $f_0$ is located, regardless whether it is stable or unstable as a germ induced by the unfolding.

Let $\theta _{n+2}$ be the ${\mathscr {O}}_{n+2}$-module of germs of vector fields on $\mathbb {C}^{n+2}\equiv \mathbb {C}^{n+1}\times \mathbb {C}$ at the origin. We denote by ${\text {Der}}(-\log \mathcal X)$ the submodule of logarithmic vector fields. We recall that $\xi \in {\text {Der}}(-\log \mathcal X)$ if and only if $\xi _p\in T_p\mathcal X$, for all $p\in \mathcal X_{reg}$, the regular part of $\mathcal X$. Equivalently, $\xi \in {\text {Der}}(-\log \mathcal X)$ if and only if $dG(\xi )\in (G)$, where $G\in {\mathscr {O}}_{n+2}$ such that $G=0$ is a reduced equation of $\mathcal X$.

Take a representative $\mathcal X$ in some open neighbourhood U of the origin in $\mathbb {C}^{n+2}$. We extend the stratification of $\mathcal X$ to U by adding the open stratum $U-\mathcal X$. The projection $\pi :U\rightarrow \mathbb {C}$ has also an isolated stratified critical point at the origin and, hence, the Bruce-Roberts number of the pair $(\mathcal {X},\pi )$

$$\begin{aligned} \mu _{BR}(\mathcal X,\pi ):={\text {dim}}_\mathbb {C}\frac{\mathscr {O}_{n+2}}{d\pi \big ({\text {Der}}(-\log \mathcal X)\big )} \end{aligned}$$

is always finite (see [1, Definition 2.4] and the previous comments) and is not zero when $\pi$ has a critical point at the origin, that is, when f is not stable (by Lemma 2.4). It seems natural to ask about the relationship between this number and $\mu _I(f)$, which gives the rank of the vanishing homology of the fiber $X_s=\pi ^{-1}(s)$. However, the following example shows that these two numbers are not equal in general.

Example 2.6

Let $f:(\mathbb C^2,0)\rightarrow (\mathbb C^3,0)$ be given by $f(x,y)=(x^2,y^2,xy+x^3+y^3)$ with stabilisation

$$\begin{aligned} F(x,y,s)=(x^2+sy,y^2-sx,xy+y^3+x^3+s(x-y),s). \end{aligned}$$

We have $\mu _I(f)=7$ (see [18, Section 3.1]) and a computation with Singular (see [5]) gives that $\mu _{BR}(\mathcal X,\pi )=8$.

Instead of ${\text {Der}}(-\log \mathcal X)$ we will consider the submodule ${\text {Der}}(-\log G)$, defined as the set of vector fields $\xi$ such that $dG(\xi )=0$. Roughly speaking, the difference between these modules is disregarding the fiber $G^{-1}(0)=\mathcal X$ as special and considering the tangency at every fiber of G. Obviously, we have the inclusion ${\text {Der}}(-\log G)\subset {\text {Der}}(-\log \mathcal X)$. Moreover, when $\mathcal X$ is weighted homogeneous, we also have that

$$\begin{aligned} {\text {Der}}(-\log \mathcal X)={\text {Der}}(-\log G)\oplus \mathscr {O}_{n+2}\cdot \{\epsilon \}, \end{aligned}$$

(1)

where $\epsilon$ is the Euler vector field

$$\begin{aligned} \epsilon = w_1 \frac{\partial }{\partial x_1}+\cdots +w_{n+1}\frac{\partial }{\partial x_{n+1}}+w_s\frac{\partial }{\partial s}, \end{aligned}$$

$w_\bullet$ denoting the corresponding weights of the variables. Moreover, since $d\pi (\epsilon )=w_{s}s$, we obtain the equality

$$\begin{aligned} d\pi \big ({\text {Der}}(-\log \mathcal X)\big )=d\pi \big ({\text {Der}}(-\log G)\big )+(s). \end{aligned}$$

(2)

The ideal $d\pi \big ({\text {Der}}(-\log G)\big )\subset \mathscr {O}_{n+2}$ contains relevant information we want to analyse. Observe that if, at a point p, the tangent space of the fiber of G(p) coincides with the tangent space of the fiber of $\pi (p)$, i.e., if

$$\begin{aligned} T_p G^{-1}\big (G(p)\big )=T_p \pi ^{-1}\big (\pi (p)\big ), \end{aligned}$$

then p will be in the set of zeros of $d\pi \left( {\text {Der}}(-\log G)\right) \subset \mathscr {O}_{n+2}$ (see Fig. 3). Hence, at least, this ideal contains the information of the failure of the transversality between the fibers of $\pi$ and G. For this reason, we use the notation

$$\begin{aligned} FT(\pi ,G){:}{=}d\pi \big ({\text {Der}}(-\log G)\big ). \end{aligned}$$

Note, however, that if we consider the points where the fibers of G are not smooth we do not have a tangent space at the singular locus. Therefore, in singular fibers, one should consider the space that ${\text {Der}}(-\log G)$ spans at each point instead of the tangent space and check transversality between these spaces and the fibers of $\pi$; this is similar to the notion of logarithmically transverse defined in [23, p. 282], but with ${\text {Der}}(-\log \mathcal {X})$ instead of ${\text {Der}}(-\log G)$. In this sense, $FT(\pi ,G)$ is a refinement of the failure of the transversality between the fibers of G and $\pi$.

Fig. 3

Representation of the set of zeros of the ideal $FT(\pi ,G)= d\pi \big ({\text {Der}}(-\log G)\big )$. Observe that it has two components in this representation

In the following lemma, we consider the general case where $\mathcal X$ is not necessarily weighted homogeneous. For each $s\in \mathbb {C}$ close enough to the origin, we denote by $g_s$ the function $g_s(y)=G(y,s)$.

Lemma 2.7

The zero locus $V\big (FT(\pi ,G)\big )$ of $FT(\pi ,G)$ in $(\mathbb {C}^{n+2},0)$ is the set-germ of points (y, s) such that either:

• (1) $(y,s)=0$ and f is not stable, or

• (2) $G(y,s)\ne 0$ and y is a critical point of $g_s$.

Moreover, in the second case, $FT(\pi ,G)$ is generated by $\frac{\partial G}{\partial y_1},\dots ,\frac{\partial G}{\partial y_{n+1}}$ in a neighbourhood of (y, s).

Proof

By the curve selection lemma, G has isolated critical value at the origin. We fix a representative in some open neighbourhood U of the origin in $\mathbb {C}^{n+2}$ such that $f_s$ is stable at y, for all $(y,s)\in \mathcal X-\{0\}$ and 0 is the only critical value of G.

Let $p=(y_0,s_0)\in U$. We first consider the case $G(p)=0$, so $p\in \mathcal X$.

If $f_{s_0}$ is stable at $y_0$ (in particular, if $p\ne 0$), then p is not a critical point of $\pi :U\rightarrow \mathbb {C}$, by Lemma 2.4. Hence, $p\notin V\big (d\pi \big ({\text {Der}}(-\log \mathcal X)\big )\big )$. On the other hand, at p, F is a trivial unfolding of the germ $(f_{s_0})_{y_0}$, as it is stable. Since we deal with corank one germs or $(n,n+1)$ are nice dimensions, the germ $(f_{s_0})_{y_0}$ is weighted homogeneous, up to $\mathscr {A}$-equivalence (see [23, Theorem 7.6]). In particular, $\mathcal X$ is weighted homogeneous in a neighbourhood of p, up to a coordinate change which preserves the parameter s. It follows from Eq. (2) that

$$\begin{aligned} d\pi \big ({\text {Der}}(-\log \mathcal X)\big )=d\pi \big ({\text {Der}}(-\log G)\big )+(s-s_0)=FT(\pi ,G)+(s-s_0), \end{aligned}$$

in a neighbourhood of p. Hence, $p\notin V\big (FT(\pi ,G)\big )$ because $p\in V(s-s_0)$.

If $p=0$ and f is unstable at that point, then 0 is a critical point of $\pi :U\rightarrow \mathbb {C}$ (by Lemma 2.4) and, hence,

$$\begin{aligned} 0\in V(d\pi \big ({\text {Der}}(-\log \mathcal X)\big )\subset V\big (FT(\pi ,G)\big ). \end{aligned}$$

Now we consider the case $G(p)\ne 0$. By assumption, G is regular at p. Assume that $\frac{\partial G}{\partial y_i}(p)\ne 0$, for some $i=1,\dots ,n+1$. We can suppose, for simplicity, that $i=1$. The map

$$\begin{aligned} \Phi (y,s)=\big (G(y,s),y_2,\dots ,y_{n+1},s\big ) \end{aligned}$$

is a biholomorphism in a neighbourhood of p and

$$\begin{aligned} G\circ \Phi ^{-1}(z,y_2\dots ,y_{n+1},s)=z, \end{aligned}$$

in a neighbourhood of $\Phi (p)$. The module ${\text {Der}}\big (-\log (G\circ \Phi ^{-1})\big )$ is generated at $\Phi (p)$ by the vector fields $\frac{\partial }{\partial y_2},\dots ,\frac{\partial }{\partial y_{n+1}},\frac{\partial }{\partial s}$. Composing by the differential of $\Phi$ we reverse the coordinate change, so ${\text {Der}}(-\log G)$ is generated at p by

$$\begin{aligned} \hspace{2cm}\xi _i&=\frac{\partial }{\partial y_{i}}+\frac{\partial G}{\partial y_i}\frac{\partial }{\partial y_{1}},\quad i=2,\dots ,n+1,\\ \xi _{n+2}&=\frac{\partial }{\partial s}+\frac{\partial G}{\partial s}\frac{\partial }{\partial y_{1}}. \end{aligned}$$

We have $d\pi (\xi _{n+2})=1$, so $p\notin V\big (FT(\pi ,G)\big )$.

The case $\frac{\partial G}{\partial s}(p)\ne 0$ has to be analysed separately. We proceed analogously and arrive to that ${\text {Der}}(-\log G)$ is generated at p by

$$\begin{aligned} \eta _i=\frac{\partial }{\partial y_{i}}+\frac{\partial G}{\partial y_i}\frac{\partial }{\partial s},\quad i=1,\dots ,n+1. \end{aligned}$$

In this case $d\pi (\eta _i)=\frac{\partial G}{\partial y_i}$. Hence, $FT(\pi ,G)$ is generated at p by $\frac{\partial G}{\partial y_1},\dots ,\frac{\partial G}{\partial y_{n+1}}$, and $p\in V\big (FT(\pi ,G)\big )$ if and only if $y_0$ is a critical point of $g_{s_0}$. $\square$

Corollary 2.8

The number

$$\begin{aligned} {\text {dim}}_\mathbb {C}\frac{{\mathscr {O}}_{n+2}}{FT(\pi ,G)+(s)} \end{aligned}$$

is always finite and is not zero if and only if f is not stable.

Proof

By shrinking the neighbourhood U if necessary, we can assume that 0 is the only critical value of $g_0$. Hence, by Lemma 2.7, we have that

$$\begin{aligned} V\big (FT(\pi ,G)+(s)\big )\subset \{0\}, \end{aligned}$$

with equality if and only if f is not stable. The results follows now from the analytic Nullstellensatz. $\square$

Example 2.9

Going back to the map germ given in Example 2.6, we have

$$\begin{aligned} {\text {dim}}_\mathbb {C}\frac{{\mathscr {O}}_{n+2}}{FT(\pi ,G)+(s)}=7, \end{aligned}$$

which coincides with $\mu _I(f)$. This anticipates Corollary 2.12, Theorem 2.21.

In the next theorem, we consider ${\mathscr {O}}_{n+2}/FT(\pi ,G)$ as an ${\mathscr {O}}_1$-module via the morphism $\pi ^*:\mathscr {O}_1\rightarrow {\mathscr {O}}_{n+2}$. By Corollary 2.8, $\mathscr {O}_{n+2}/FT(\pi ,G)$ is always finitely generated over ${\mathscr {O}}_1$.

Theorem 2.10

The image Milnor number of f equals the Samuel multiplicity of ${\mathscr {O}}_{n+2}/FT(\pi ,G)$ with respect to the maximal ideal (s), i.e.,

$$\begin{aligned} \mu _I(f)=e\left( (s); \frac{{\mathscr {O}}_{n+2}}{FT(\pi ,G)}\right) . \end{aligned}$$

Proof

Take $s_0\ne 0$ close enough to the origin in $\mathbb {C}$. By the conservation of the multiplicity (see, for example, [23, Corollary E.5]),

$$\begin{aligned} e\left( (s); \frac{\mathscr {O}_{n+2}}{FT(\pi ,G)}\right)&=\sum _{(y,s_0)\in V(FT(\pi ,G))} e\left( (s-s_0); \frac{{\mathscr {O}}_{n+2,(y,s_0)}}{FT(\pi ,G)}\right) \\&=\sum _{(y,s_0)\in V(FT(\pi ,G))} e\left( (s-s_0); \frac{\mathscr {O}_{n+2,(y,s_0)}}{\left( \frac{\partial G}{\partial y_1},\dots ,\frac{\partial G}{\partial y_{n+1}}\right) }\right) \\&=\sum _{y\notin X_{s_0}} {\text {dim}}_\mathbb {C}\frac{\mathscr {O}_{n+1,y}}{\left( \frac{\partial g_{s_0}}{\partial y_1},\dots ,\frac{\partial g_{s_0}}{\partial y_{n+1}}\right) }\\&=\sum _{y\notin X_{s_0}} \mu (g_{s_0};y)\\ {}&=\mu _I(f). \end{aligned}$$

The second equality follows from Lemma 2.7, the third one holds because

$$\begin{aligned} \frac{{\mathscr {O}}_{n+2,(y,s_0)}}{\left( \frac{\partial G}{\partial y_1},\dots ,\frac{\partial G}{\partial y_{n+1}}\right) } \end{aligned}$$

is Cohen–Macaulay, and the last one is a consequence of a theorem due to Siersma, [26, Theorem 2.3]. $\square$

Remark 2.11

The multiplicity $e\left( (s); \frac{{\mathscr {O}}_{n+2}}{FT(\pi ,G)}\right)$ can be interpreted geometrically as a local intersection number

$$\begin{aligned} e\left( (s); \frac{\mathscr {O}_{n+2}}{FT(\pi ,G)}\right) =i\left( j,V\big (FT(\pi ,G)\big )\right) , \end{aligned}$$

where $j:(\mathbb {C}^{n+1},0)\rightarrow (\mathbb {C}^{n+2},0)$ is the embedding $y\mapsto (y,0)$. We refer to Fulton’s book [8, Example 7.1.2] for details about the connection between the algebraic multiplicity and the local intersection number.

An alternative explanation of this equality can be given as we know that the points of $V\big (FT(\pi ,G)\big )$ are precisely the instability of $f_0$ and the critical points of $g_s$, where $g_s$ is the equation of ${\text {Im}}(f_s)$, that are not contained in the image of $f_s$, by Lemma 2.7. Moreover, we have already mentioned that a result of Siersma (see [26, Theorem 2.3]) says that the sum of the Milnor numbers of these critical points is equal to the image Milnor number of $f_0$. In other words,

$$\begin{aligned} \sum _{y\notin X_{s_0}} \mu (g_{s_0};y)=\mu _I(f), \end{aligned}$$

which is equal to the intersection multiplicity $i\big (j,V\big (FT(\pi ,G)\big )\big )$ and, in turn, equal to the Samuel multiplicity $e\big ((s); \frac{\mathscr {O}_{n+2}}{FT(\pi ,G)}\big )$ (by Theorem 2.10 above). See Remark 2.16 and Fig. 4 below.

Corollary 2.12

In terms of Theorem 2.10,

$$\begin{aligned} \mu _I(f)\le {\text {dim}}_\mathbb {C}\frac{{\mathscr {O}}_{n+2}}{FT(\pi ,G)+(s)}, \end{aligned}$$

with equality if and only if ${\mathscr {O}}_{n+2}/FT(\pi ,G)$ is Cohen–Macaulay of dimension 1.

The following definition is an adaptation of the definition of the logarithmic characteristic variety $LC(\mathcal X)$ introduced by Saito in [25], where we consider the module ${\text {Der}}(-\log G)$ instead of ${\text {Der}}(-\log \mathcal X)$.

Let $T^*\mathbb {C}^{n+2}$ be the cotangent bundle of $\mathbb {C}^{n+2}$. Given an open set $U\subset \mathbb {C}^{n+2}$, $T_U^*\mathbb {C}^{n+2}$ is the restriction of $T^*\mathbb {C}^{n+2}$ to U. An element of $T_U^*\mathbb {C}^{n+2}$ will be of the form $(y,s;\alpha )$, where $(y,s)\in U$ and $\alpha :\mathbb {C}^{n+2}\rightarrow \mathbb {C}$ is a linear form.

Given a holomorphic function $h:U\rightarrow \mathbb {C}$ (or a germ $h:(\mathbb {C}^{n+2},0)\rightarrow \mathbb {C}$), we denote by $Dh:U\rightarrow T^*\mathbb {C}^{n+2}$ (resp. $Dh:(\mathbb {C}^{n+2},0)\rightarrow T^*\mathbb {C}^{n+2}$) the differential, that is, the section of $T^*\mathbb {C}^{n+2}$ given by $Dh(y,s)=\big (y,s;dh_{(y,s)}\big )$.

Definition 2.13

Let U be some open neighbourhood of the origin in $\mathbb {C}^{n+2}$. Then, the logarithmic characteristic variety of G is defined as follows:

$$\begin{aligned} LC_U(G)=\left\{ (y,s;\alpha )\in T_U^*\mathbb {C}^{n+2}:\ \alpha (\xi )=0,\ \forall \xi \in {\text {Der}}(-\log G)\right\} . \end{aligned}$$

The variety LC(G) is the germ of $LC_U(G)$ along $T_0^*\mathbb {C}^{n+2}$.

It is easy to see that

$$\begin{aligned} D\pi ^{-1}\big (LC(G)\big )=V\big (FT(\pi ,G)\big ). \end{aligned}$$

(3)

To give the equations of LC(G), suppose that the module ${\text {Der}}(-\log G)$ is generated by germs of vector fields $\xi _1,\dots ,\xi _r$ and that

$$\begin{aligned} \xi _i=\sum _{i=1}^{n+1}a_j^i \frac{\partial }{\partial y_j}+b_i \frac{\partial }{\partial s}, \end{aligned}$$

for some $a_j^i,b_i\in {\mathscr {O}}_{n+2}$. Denote by $(y_1,\dots ,y_{n+1},s,p_1,\dots ,p_{n+1},q)$ the coordinates of $T^*\mathbb {C}^{n+2}$. Then LC(G) has equations $\xi ^*_i=0$, $i=1,\dots ,r$, where

$$\begin{aligned} \xi _i^*=\sum _{i=1}^{n+1}a_j^i p_j+b_i q\in {\mathscr {O}}_{n+2}[p_1,\dots ,p_{n+1},q]. \end{aligned}$$

This shows that LC(G) is independent of the choice of the neighbourhood U. It is not difficult to see that it is also independent of the choice of the generators. We remark that LC(G) is considered with the possibly non-reduced structure given by the ideal generated by $\xi ^*_i$, $i=1,\dots ,r$.

We know that $LC(\mathcal X)$ has dimension $n+2$, for $(\mathcal X,0)$ is holonomic (see [1, Proposition 1.14]). We compute the dimension of LC(G) in the next proposition.

Proposition 2.14

The variety LC(G) has dimension $n+3$. Furthermore, the variety $V\big (FT(\pi ,G)\big )$ has dimension 1 if, and only if, f is not stable and is empty otherwise.

Proof

By Corollary 2.8,

$$\begin{aligned} {\text {dim}}_\mathbb {C}\frac{{\mathscr {O}}_{n+2}}{FT(\pi ,G)+(s)}<\infty , \end{aligned}$$

so ${\text {codim}}V\big (FT(\pi ,G)\big )\ge n+1$, and, by Eq. (3), ${\text {codim}}LC(G)\ge n+1$. Hence, ${\text {dim}}V\big (FT(\pi ,G)\big )\le 1$ and ${\text {dim}}LC(G)\le n+3$.

On the other hand, G has isolated critical value at the origin by the curve selection Lemma. We take a small enough open neighbourhood U of the origin in $\mathbb {C}^{n+2}$ such that 0 is the only critical value of G on U. For each $(y,s)\in U- \mathcal X$, G is regular at (y, s). We use the argument given in the proof of Lemma 2.7 and deduce that ${\text {Der}}(-\log G)$ is generated in a neighbourhood of (y, s) by $n+1$ vector fields $\xi _1,\dots ,\xi _{n+1}$. It follows that LC(G) is given in a neighbourhood of (y, s) by $n+1$ equations $\xi ^*_i=0$, $i=1,\dots ,n+1$, so ${\text {codim}}LC(G)\le n+1$. Hence, ${\text {dim}}LC(G)=n+3$ and ${\text {dim}}V\big (FT(\pi ,G)\big )=1$ whenever it is not empty. However, by Corollary 2.8, $FT(\pi ,G)$ contains the constants if, and only if, f is stable, and $V\big (FT(\pi ,G)\big )$ would be empty. $\square$

Now we prove a weak version of the Mond conjecture Conjecture 1.1 for the case $\mu _I(f)=0$. This is a generalization of [10, Theorem 3.9], which is stated for corank one germs.

Theorem 2.15

We have that $\mu _I(f)=0$ if and only if f is stable.

Proof

Assume that f is not stable. We know from Proposition 2.14 that ${\text {dim}}LC(G)=n+3$ and ${\text {dim}}V\big (FT(\pi ,G)\big )= 1$. In other words,

$$\begin{aligned} {\text {dim}}{\mathscr {O}}_{n+2}/FT(\pi ,G)=1={\text {dim}}\mathscr {O}_1 \end{aligned}$$

and, hence,

$$\begin{aligned} \mu _I(f)=e\left( (s);\frac{{\mathscr {O}}_{n+2}}{FT(\pi ,G)}\right) \ge 1, \end{aligned}$$

(see, for instance, [20, Formula 14.2]). $\square$

Remark 2.16

There is an equivalent way of proving this result using the geometry of $V\big (FT(\pi ,G)\big )$. On one hand, we know that

$$\begin{aligned} \mu _I(f)=i\left( j,V\big (FT(\pi ,G)\big )\right) , \end{aligned}$$

as shown in Remark 2.11. On the other, this intersection number is positive, because $V\big (FT(\pi ,G)\big )$ is a curve (see Proposition 2.14), so the result follows. See Fig. 4 for a general overview of this reasoning.

Fig. 4

The curve $V\big (FT(\pi ,G)\big )$ and the intersection number $i\left( j,V\big (FT(\pi ,G)\big )\right)$

Corollary 2.17

The Mond conjecture is true for germs of $\mathscr {A}_e$-codimension 1 (see Conjecture 1.1).

Proof

The general case follows from Theorem 2.15. If f is quasi-homogeneus then its $\mathscr {A}_e$-codimension coincides with the dimension as vector space of the Jacobian module M(g), see [7], hence

$$\begin{aligned} 0<\mu _I(f)\le {\text {dim}}_\mathbb CM(g)=1, \end{aligned}$$

by [7, Proof of Theorem 6.1]. $\square$

Cooper, Mond and Wik Atique proved this result for corank one germs in [2, Theorem 7.2]. Actually, they proved that, in corank one, germs with $\mathscr {A}_e$-codimension 1 have image Milnor number equal to 1. This fact led Houston to prove that the Mond conjecture holds for a class of germs called augmentations of corank one germs that have $\mathscr {A}_e$-codimension one (see [15, Corollary 6.8]). We can generalize the proof to germs of any corank using the same ideas.

Definition 2.18

(cf. [12] and [14, Definition 3.1]) Let $f:(\mathbb {C}^n,S)\rightarrow (\mathbb {C}^p,0)$ be a germ with a one parameter stable unfolding (opsu) $F(x,\lambda )=\big (f_\lambda (x),\lambda \big )$. Let $g:(\mathbb {C}^q,0)\rightarrow (\mathbb {C},0)$ be a germ of holomorphic function. Then, the augmentation of f by F and g is the map germ

$$\begin{aligned} A_{F,g}(f)(x,z){:}{=}\big (f_{g(z)}(x),g(z)\big ). \end{aligned}$$

Corollary 2.19

Suppose that $A_{F,g}(f)$ is an augmentation with g of a germ $f:(\mathbb {C}^{n},S)\rightarrow (\mathbb {C}^{n+1},0)$ that satisfies the Mond conjecture. If f or g are quasi-homogeneous, $A_{F,g}(f)$ satisfies the Mond conjecture and, more precisely,

$$\begin{aligned} \mathscr {A}_e\text {-}{\text {codim}}\big (A_{F,g}(f)\big )=\mathscr {A}_e\text {-}{\text {codim}}(f)\tau (g)\le \mu _I(f)\mu (g)=\mu _I\big (A_{F,g}(f)\big ), \end{aligned}$$

where $\tau$ denotes the Tjurina number, with equality if f and g are quasi-homogeneous. In particular, this holds for germs f of $\mathscr {A}_e$-codimension one.

Proof

The result is a consequence of Corollary 2.17 and [15, Theorem 6.7] (see also [14, Theorem 3.3], which controls the $\mathscr {A}_e$-codimension of augmentations). There is, however, a small consideration to be made: the equality

$$\begin{aligned} \mu (g)\mu _I(f)=\mu _I\big (A_{F,g}(f)\big ) \end{aligned}$$

is stated for corank one monogerms in [15, Corollary 6.4]. One can give the same proof for multigerms of any corank, using the well known fact that the image of a stable perturbation of any f with our hypothesis has the homotopy type of a wedge of spheres (see, for example, [23, Proposition 8.3]). $\square$

Theorem 2.20

Let $f:(\mathbb {C}^n,S)\rightarrow (\mathbb {C}^{n+1})$ be a germ such that $(n,n+1)$ are nice dimensions or it has corank one. Then,

$$\begin{aligned} \mu _I(f)=i\big (D\pi \circ j, LC(G)\big ), \end{aligned}$$

where $j(y)=(y,0)$, as in Remark 2.11.

Proof

In fact, we have

$$\begin{aligned} i\big (D\pi \circ j,LC(G)\big )=e\left( \mathfrak m_{n+3,(0,\pi )};{\mathscr {O}}_{LC(G),D\pi (0)}\right) , \end{aligned}$$

where we consider ${\mathscr {O}}_{LC(G),D\pi (0)}$ as a module over ${\mathscr {O}}_{n+3,(0,\pi )}$ via the projection $T^*\mathbb {C}^{n+2}\rightarrow \mathbb {C}\times \mathbb {C}^{n+2}=\mathbb {C}^{n+3}$ given by $(y,s;\alpha )\mapsto (s;\alpha )$.

As in the proof of Theorem 2.10 we use the conservation of the multiplicity (see, for example, [23, Corollary E.5]). For $(s_0;\pi )$ with $s_0\ne 0$,

$$\begin{aligned} e\left( {\mathfrak {m}}_{n+3,(0,d\pi )};{\mathscr {O}}_{LC(G),D\pi (0)}\right) = \sum _{D\pi (y,s_0)\in LC(G)} e\left( \mathfrak m_{n+3,(s_0,\pi )};{\mathscr {O}}_{LC(G),D\pi (y,s_0)}\right) . \end{aligned}$$

Since G is regular at each $(y,s_0)$, ${\text {Der}}(-\log G)$ is generated by $n+1$ vector fields at $(y,s_0)$, therefore LC(G) is given by $n+1$ equations at $D\pi (y,s_0)$. So, LC(G) is Cohen–Macaulay at $D\pi (y,s_0)$ and, hence,

$$\begin{aligned} e\left( \mathfrak m_{n+3,(s_0,\pi )};\mathscr {O}_{LC(G),D\pi (y,s_0)}\right)&={\text {dim}}_\mathbb C\frac{\mathscr {O}_{LC(G),D\pi (y,s_0)}}{\mathfrak m_{n+3,(s_0,\pi )}\mathscr {O}_{LC(G),D\pi (y,s_0)}}\\&={\text {dim}}_\mathbb C\frac{\mathscr {O}_{V(FT(\pi ,G)),(y,s_0)}}{\mathfrak m_{1,s_0}\mathscr {O}_{V(FT(\pi ,G)),(y,s_0)}}\\&={\text {dim}}_\mathbb C\frac{\mathscr {O}_{n+2,(y,s_0)}}{FT(\pi ,G)+\mathfrak m_{1,s_0}}\\ {}&= \mu (g_{s_0};y); \end{aligned}$$

where the last equality is given by Lemma 2.7.

Using [26, Theorem 2.3] as in Theorem 2.10, this shows that

$$\begin{aligned} e\left( {\mathfrak {m}}_{n+3,(0,\pi )};\mathscr {O}_{LC(G),{D\pi }(0)}\right) =\mu _I(f), \end{aligned}$$

and the result follows. $\square$

Observe that, as we are using multiplicities in the proof of Theorem 2.20, the equality

$$\begin{aligned} \mu _I(f)={\text {dim}}_\mathbb {C}\frac{{\mathscr {O}}_{n+2}}{FT(\pi ,G)+(s)}, \end{aligned}$$

holds if and only if LC(G) is Cohen–Macaulay at $(0,\pi )$. This leads to the following result.

Theorem 2.21

The Mond conjecture is true for germs f with an opsu F and such that LC(G) is Cohen–Macaulay, for G given by F (see Conjecture 1.1).

Proof

As we were saying, we have conservation of the multiplicity, since LC(G) is Cohen–Macaulay, so

$$\begin{aligned} \mu _I(f)={\text {dim}}_\mathbb {C}\frac{{\mathscr {O}}_{n+1}}{FT(\pi ,G)+(s)}. \end{aligned}$$

(4)

Now, by [23, Theorem 8.7] (see the original version in [3]),

$$\begin{aligned} T^1\mathscr {A}_e(f)\cong \frac{\theta (i)}{ti(\theta _{n+1})+i^*\big ({\text {Der}}(-\log \mathcal {X})\big )}, \end{aligned}$$

where i is given by the commutative diagram

and i is transverse to F. However, we can do the identifications $\theta (i)/di(\theta _Y)\cong \theta (\pi )/\mathfrak {m}_1\theta (\pi )$ and $\theta (\pi )\cong \mathscr {O}_{n+1}$, so

$$\begin{aligned} \begin{aligned}T^1\mathscr {A}_e(f)&\cong \frac{\theta (\pi )}{d\pi \big ({\text {Der}}(-\log \mathcal {X})\big )+\mathfrak {m}_1\theta (\pi )}\\&\cong \frac{\mathscr {O}_{n+1}}{d\pi \big ({\text {Der}}(-\log \mathcal {X})\big )+(s)}.\end{aligned} \end{aligned}$$

(5)

Recall that, by definition, $FT(G,\pi )=d\pi \big ({\text {Der}}(-\log G)\big )$, and the decomposition

$$\begin{aligned} d\pi \big ({\text {Der}}(-\log \mathcal X)\big )=d\pi \big ({\text {Der}}(-\log G)\big )+(s) \end{aligned}$$

in the quasi-homogeneous case given in Eq. (2). Hence, comparing Eqs. (4) and (5), the result follows. $\square$

Remark 2.22

With the notation of Theorem 2.21, by Eq. (3), Cohen–Macaulayness of LC(G) implies Cohen–Macaulayness of the ring

$$\begin{aligned} \frac{\mathscr {O}_{n+1}}{FT(G,\pi )}=\frac{\mathscr {O}_{n+1}}{d\pi \big ({\text {Der}}(-\log G)\big )}, \end{aligned}$$

(6)

but the converse may be not true in general. Observe also that the ring (6) can be seen as the relative version of the normal space $T^1_{\mathscr {K}_{G,e}}i$ of the inclusion i with respect to Damon’s $\mathscr {K}_G$-equivalence.

It is well known that the conservation of multiplicity of $T^1_{\mathscr {K}_{G,e}}i$ implies the Mond conjecture, provided that G is a good defining equation of the image of F, that is, provided that $G\in J(G)$, the Jacobian ideal of G (see [23, Theorem 8.10]).

However, the existence of such a good defining equation G is guaranteed only when f is weighted homogeneous or when we allow the stable unfolding to have several parameters. Our Theorem 2.21 can be used without the hypothesis of good defining equation, which is more general when working with opsu.

The following conjecture is supported by many examples, in which G is a general function, not necessarily the equation of the image of a stable map germ.

Conjecture 2.23

For any reduced holomorphic function $G:(\mathbb {C}^N,0)\rightarrow (\mathbb {C},0)$, the variety LC(G) is Cohen–Macaulay.

3 Bifurcation set

In this section we prove that the bifurcation set of an $\mathscr {A}$-finite germ $f:(\mathbb {C}^{n},S)\rightarrow (\mathbb {C}^{n+1},0)$ is a hypersurface that has pure dimension. This is, indeed, the only case where it is not known whether the bifurcation set is a hypersurface (without any additional hypotheses).

For germs $f:(\mathbb {C}^{n},S)\rightarrow (\mathbb {C}^{p},0)$ with $n\ge p$, this property is shown in [23, Theorem 8.8], whose proof relies on the fact that the discriminant is a free divisor in this case (see [17, Corollary 6.13], cf. [23, Proposition 8.9]). This is no longer true for $p>n$. For germs with $p\ge n+2$ the bifurcation set can have greater codimension, see [23, Example 9.5]. Finally, when $p=n+1$, it was only known that the bifurcation set is a hypersurface for germs of corank one (see [23, Proposition 9.15]). This, in turn, relied in the good structure of the multiple point spaces, which lose this good behaviour when we study germs with greater corank.

Consider a map germ $f:(\mathbb {C}^n,S)\rightarrow (\mathbb {C}^{n+1},0)$ with $\mathscr {A}_e$-codimension $d>0$ and a miniversal unfolding (see Fig. 5)

$$\begin{aligned} F:\big (\mathbb {C}^n\times \mathbb {C}^d,S\times \{0\}\big )&\rightarrow (\mathbb {C}^{n+1}\times \mathbb {C}^d,0)\\ (x,\lambda )&\mapsto \big (f_\lambda (x),\lambda \big ). \end{aligned}$$

Fig. 5

Representation of the parameter space of the miniversal unfolding $F(x,a,b)=(x^2,x^5+ax^3+bx,a,b)$ of $f(x)=(x^2,x^5)$

We want to use some ideas Goryunov used in [13] to reach a version for more dimensions of his [13, Corollary] given for germs from $\mathbb {C}^2$ to $\mathbb {C}^3$, which relates the multiplicity of the bifurcation set with some image Milnor numbers. Indeed, it is implicit in Goryunov’s work the result given here as Theorem 2.15 or, as it is proven in those dimensions, the Mond conjecture (see [4, Theorem 4.2] and [22, Theorem 2.3]).

We can consider a generic line $\tilde{\ell }$ in $\mathbb {C}^d$ through the origin to compute the multiplicity of the bifurcation set $\mathscr {B}(F)$. Hence, when we shift the line $\tilde{\ell }$ to the new line $\ell$, the number $\nu$ of points in $\ell \cap \mathscr {B}(F)$ is the multiplicity of $\mathscr {B}(F)$ at the origin. Observe, however, that this multiplicity is positive if, and only if, $\mathscr {B}(F)$ is a hypersurface and, to prove that it is positive, we will use Theorem 2.15.

We can consider the pullback $F^\ell$ induced by $\ell$ and F, i.e., $F^\ell (x,t){:}{=}\big (f_{\ell (t)}(x),t\big )$ where $\ell (t)$ parametrizes the line $\ell$. Notice that this is a perturbation of the pullback $F^{\tilde{\ell }}$ induced by $\tilde{\ell }$ and F.

Theorem 3.1

If f has corank one or it is in the nice dimensions, the bifurcation set $\mathscr {B}(F)$ has components of codimension one.

Proof

We are going to use stratified Morse theory with a function induced from the projection $\pi$ to the parameter $\lambda$ in the image of $F^\ell$:

where $q_0$ is a generic point of $\ell$, which can be considered to lie in $\ell -\mathscr {B}(F)$. We also use the stratification given by the stable types (and the isolated unstable points) of $F^\ell$.

Observe that a critical point of $\pi$ induces a critical point of $\phi$. Furthermore, the points $p_i$ of the intersection $\ell \cap \mathscr {B}(F)$ are, precisely, the critical points of $\pi$ by Lemma 2.4 (or, to be more precise, a very easy adaptation of this result to $F^\ell$). By contradiction, if the intersection $\ell \cap \mathscr {B}(F)$ were empty, there would be no critical points, and, by Morse theory, the image of $F^\ell$ would have, as a deformation retract, the image of $f_{q_0}$. But this is absurd. Indeed, $F^\ell$ is a perturbation of $F^{\tilde{\ell }}$, and $f_{q_0}$ is a stable perturbation of f (so it has the homotopy type of a wedge of $\mu _I(f)$ spheres of dimension n). As f has an instability, the number $\mu _I(f)$ is positive (by Theorem 2.15), but the image of $F^\ell$ has only non-trivial homology in dimension zero and, possibly, in dimension $n+1$. $\square$

With these ideas, we can refine the result.

Theorem 3.2

In the conditions of Theorem 3.1,

$$\begin{aligned} m\big (\mathscr {B}(F)\big )\le \mu _I(f)+\mu _I\big (F^{\tilde{\ell }}\big ). \end{aligned}$$

Proof

Using the exact sequence of the pair,

$$\begin{aligned} 0\rightarrow H_{n+1}\big ( {\text {Im}}F^\ell \big )\rightarrow H_{n+1}\big ( {\text {Im}}F^\ell ,{\text {Im}}f_{q_0}\big )\rightarrow H_n(f_{q_0})\rightarrow 0, \end{aligned}$$

we only need to confirm that each point $p_i$ (i.e., each critical point of $\pi$) contributes with at least one copy of $\mathbb {Z}$ to $H_{n+1}\big ( {\text {Im}}F^\ell ,{\text {Im}}f_{q_0}\big )$. Indeed, if $\phi$ is not a stratified Morse function we can consider a Morsification, which has at least one critical point for each critical point of $\phi$ (hence $\pi$). As these images are analytic and $\phi$ is the module of a complex analytic function, the tangential Morse data is

$$\begin{aligned} (D^m,\partial D^m), \end{aligned}$$

where m is the dimension of the stratum that contains the critical point. Furthermore, as we deal with hypersurfaces, a theorem of Lê (see [16], but also the more easy to access [11, pp. 187–188]) says that the normal Morse data is homotopic to

$$\begin{aligned} \left( \vee D^{n+1-m},\partial \vee D^{n+1-m}\right) . \end{aligned}$$

Hence, the Morse data is

$$\begin{aligned} (D^m,\partial D^m)&\times \left( \vee D^{n+1-m};\partial \vee D^{n+1-m}\right) \\ {}&=\left( D^m\times \vee D^{n+1-m};\partial D^m\times \vee D^{n+1-m}\cup D^m\times \partial \vee D^{n+1-m} \right) \\ {}&\simeq \left( \vee D^{n+1};C_{<n+1}\right) , \end{aligned}$$

where $C_{< n+1}$ is a CW-complex of dimension lower than $n+1$. The result follows from here, counting the new cells per critical point. $\square$

Proposition 3.3

In the conditions of Theorem 3.1, the bifurcation set is pure dimensional (i.e., a hypersurface).

Proof

By contradiction, assume that $\mathscr {B}(F)$, with reduced structure, has a component that is not a hypersurface. We can consider a point $\lambda$ that lies in that component but not in the other components. By the openness of versality (see [27, Theorem 3.7], cf. [23, Theorem 5.6]), F is also a versal unfolding of $f_\lambda$ at each point. This is already a contradiction, as it is not a hypersurface. $\square$

Note 1 It is important to notice that the bifurcation set considered with the reduced structure is not, in general, irreducible. Indeed, in most cases it will have more than one irreducible component (see, for example, [23, Example 5.8]).

Remark 3.4

There is another approach to prove Theorem 2.15 and 3.1 and Proposition 3.3 from the better-known case of corank one. For those unstable germs that have a corank one unstable germ adjacent to it (i.e., with a perturbation with instabilities of corank one), one can use the conservation principle for the $\mu _I$ (see [10, Theorem 2.8]) to prove the weak form of the Mond conjecture in any corank, Theorem 2.15 above, from the corank one version (i.e., [10, Theorem 3.9]). One can give a similar approach to prove Theorem 3.1 and Proposition 3.3 from the corank one case shown in [23, Section 9.6]. Unfortunately, this is not true in general. The germ $f:(\mathbb {C}^5,0)\rightarrow (\mathbb {C}^6,0)$ given in [23, Example 9.7],

$$\begin{aligned} f(x_1,x_2,v_1,v_2,v_3)= \big (x_1^2+v_1x_2;\, x_1x_2+v_2x_1+v_2x_2;\, x_2^3+v_3x_1;\, v_1,v_2,v_3 \big ), \end{aligned}$$

is such that:

• (i) it is unstable of corank two,

• (ii) its stable deformations have corank two,

• (iii) has $\mathscr {A}_e$-codimension equal to one, and

• (iv) its bifurcation set of its miniversal unfolding is the origin.

However, this approach could be interesting for other contexts or other class of germs.