Hierarchy of generalized continua issued from micromorphic medium constructed by homogenization

Abstract

The present contribution provides a classification of generalized continua constructed by a micromechanical approach, relying on an extension of the Hill macrohomogeneity condition. The virtual power of equilibrium for a micromorphic effective medium is derived from the microscopic Cauchy balance equations, highlighting the classical and higher-order macroscopic stress tensors. The so-called homogeneous displacement associated with the micromorphic effective medium is derived from variational formulations. It allows establishing the extended Hill macrohomogeneity condition that prevails for the micromorphic continuum, wherein the higher-order stress tensors arise as the static variables conjugated to the selected macroscopic degrees of freedom. Suitable projections of the introduced kinematic micromorphic variables into degenerated kinematic variables lead to various subclasses of generalized continua: microstretch, micropolar, couple stress, microdilatation, microstrain, microshear, and strain gradient. An asymptotic ranking of the formulated generalized continua versus a small-scale parameter is formulated in the last part of the paper to quantify their relative importance. The micromorphic homogenization scheme is validated by comparing the predictions of the homogenized response at the macroscale for a double shear test to a reference exact solution. The proposed micromorphic homogenization method remedy most of the limitations of the existing schemes of the literature.

Appendices

Appendix A: determination of the microscopic displacement field for the effective micromorphic continuum

The micro displacement field in Eq. (50) incorporates five unknown coefficients that can be determined from the definitions of Eqs (35)–(37), and (5), and by recoursing to the averaging theorem together with the symmetry properties of the tensors (for centrosymmetric unit cells, $\left\langle {{\varvec{\underline{\upxi }}}^{n}} \right\rangle _{Y}$ is equal to zero for odd values of the exponent n):

$$\begin{aligned}{} & {} U_{i} \left( {\mathrm{\textbf{x}}} \right) =A_{i} +\frac{1}{2}C_{ijk} \left( {\mathrm{\textbf{x}}} \right) G_{jk} +\frac{1}{4}E_{ijklm} \left( {\mathrm{\textbf{x}}} \right) \left( {G_{4} } \right) _{jklm} \end{aligned}$$

(A 1)

$$\begin{aligned}{} & {} H_{ij}:=\left\langle {u_{i,j} } \right\rangle _{Y} =B_{ij} \left( {\mathrm{\textbf{x}}} \right) +\frac{1}{3}D_{imkl} \left( {\mathrm{\textbf{x}}} \right) \left[ {G_{kl} \left( {\textrm{I}_{2} } \right) _{mj} +G_{km} \left( {\textrm{I}_{2} } \right) _{lj} +G_{lm} \left( {\textrm{I}_{2} } \right) _{kj} } \right] \end{aligned}$$

(A 2)

$$\begin{aligned}{} & {} H_{ij} +\chi _{ij} =\left\langle {u_{i} \xi _{p} } \right\rangle _{Y} G_{pj}^{-1} =B_{ij} \left( {\mathrm{\textbf{x}}} \right) +\frac{1}{3}D_{inkl} \left( {\mathrm{\textbf{x}}} \right) \left( {G_{4} } \right) _{nklp} G_{pj}^{-1} \end{aligned}$$

(A 3)

$$\begin{aligned}{} & {} \begin{array}{l} \textrm{K}_{ijk} =2\left[ {\left\langle {u_{i} \xi _{p} \xi _{q} } \right\rangle _{Y} -\left\langle {u_{i} } \right\rangle _{Y} G_{pq} } \right] \left( {\left( {G_{4} } \right) _{pqjk} -G_{pq} G_{jk} } \right) ^{-1} \\ \qquad \quad =C_{ijk} \left( {\mathrm{\textbf{x}}} \right) +\frac{1}{2}E_{irlmn} \left( {\mathrm{\textbf{x}}} \right) \left[ {\left( {G_{6} } \right) _{rlmnpq} -\left( {G_{4} } \right) _{rlmn} G_{pq} } \right] \left( {\left( {G_{4} } \right) _{pqjk} -G_{pq} G_{jk} } \right) ^{-1} \\ \end{array} \end{aligned}$$

(A 4)

$$\begin{aligned}{} & {} \begin{array}{l} \mathop {\textbf{K}}\limits _{\simeq }={grad}_{{x}} {\mathop {\varvec{\chi }}\limits _{\thicksim }}=\left\langle {grad_{{y}} \left( {{{{{\underline{\varvec{u}}}}}}\otimes {\varvec{\underline{\upxi }}}} \right) } \right\rangle _{Y}.{{\mathop {\textbf{G}}\limits _{\thicksim }}}^{-1} -\left\langle {grad_{{y}} grad_{{y}} {{{{\underline{\varvec{u}}}}}}} \right\rangle _{Y} \\ K_{ijk} =U_{i} G_{jk}^{-1} -\frac{1}{4}E_{irlmn} \left[ {\begin{array}{l} G_{mn} \left( {\textrm{I}_{2} } \right) _{jr} \left( {\textrm{I}_{2} } \right) _{lk} +G_{\ln } \left( {\textrm{I}_{2} } \right) _{jr} \left( {\textrm{I}_{2} } \right) _{mk} +G_{ml} \left( {\textrm{I}_{2} } \right) _{jr} \left( {\textrm{I}_{2} } \right) _{nk} +G_{mn} \left( {\textrm{I}_{2} } \right) _{lj} \left( {\textrm{I}_{2} } \right) _{rk} + \\ G_{rn} \left( {\textrm{I}_{2} } \right) _{lj} \left( {\textrm{I}_{2} } \right) _{mk} +G_{rm} \left( {\textrm{I}_{2} } \right) _{lj} \left( {\textrm{I}_{2} } \right) _{nk} +G_{\ln } \left( {\textrm{I}_{2} } \right) _{mj} \left( {\textrm{I}_{2} } \right) _{rk} +G_{rn} \left( {\textrm{I}_{2} } \right) _{mj} \left( {\textrm{I}_{2} } \right) _{lk} + \\ G_{rl} \left( {\textrm{I}_{2} } \right) _{mj} \left( {\textrm{I}_{2} } \right) _{nk} +G_{lm} \left( {\textrm{I}_{2} } \right) _{nj} \left( {\textrm{I}_{2} } \right) _{rk} +G_{rm} \left( {\textrm{I}_{2} } \right) _{nj} \left( {\textrm{I}_{2} } \right) _{lk} +G_{rl} \left( {\textrm{I}_{2} } \right) _{nj} \left( {\textrm{I}_{2} } \right) _{mk} - \\ \left[ {\left( {G_{4} } \right) _{rlmp} \left( {\textrm{I}_{2} } \right) _{nk} +\left( {G_{4} } \right) _{rnlp} \left( {\textrm{I}_{2} } \right) _{mk} +\left( {G_{4} } \right) _{rmnp} \left( {\textrm{I}_{2} } \right) _{lk} +\left( {G_{4} } \right) _{lmnp} \left( {\textrm{I}_{2} } \right) _{rk} } \right] G_{pj}^{-1} \\ \end{array}} \right] \quad \\ \Rightarrow E_{irlmn} T_{rlmnjk}^{6} =4\left( {U_{i} G_{jk}^{-1} -K_{ijk} } \right) \\ \end{array} \end{aligned}$$

(A 5)

In Eq. (A 1), the first coefficient should be a true constant (independent of the macroscopic coordinate), so by eliminating macroscopic rigid body motions, it is selected to be nil, $A_{i} \left( {\mathrm{\textbf{x}}} \right) =0$.

It should be noted that the second moment of area tensor ${{\mathop {\textbf{G}}\limits _{\thicksim }}}$ is a diagonal matrix (for a square) [11] which can be written as

$$\begin{aligned} G_{pj} =G_{2}^{0} \left( {\textrm{I}_{2} } \right) _{pj} \end{aligned}$$

(A 6)

where $G_{2}^{0}$ is a constant depending on the unit cell shape.

Subtracting Eq. (A 2) from Eq. (A 3), leads to the evaluation of the coefficient ${\mathop {\textbf{e}}\limits _{\thicksim }}$ (a fourth-order tensor) as

$$\begin{aligned} \chi _{ij} \left( {\mathrm{\textbf{x}}} \right) =\frac{1}{3}D_{iklm} \left( {\mathrm{\textbf{x}}} \right) \left[ {\left( {G_{2}^{0} } \right) ^{-1}\left( {G_{4} } \right) _{klmq} -G_{kl} \left( {\textrm{I}_{2} } \right) _{mq} -G_{km} \left( {\textrm{I}_{2} } \right) _{lq} -G_{lm} \left( {\textrm{I}_{2} } \right) _{kq} } \right] \end{aligned}$$

(A 7)

Implementing the expression in Eq. (A 6), the coefficient $D_{inkl}$ can be written as

$$\begin{aligned} D_{iklm} \left( {\mathrm{\textbf{x}}} \right) =3\chi _{iq} \left( {\mathrm{\textbf{x}}} \right) \left[ {\left( {G_{2}^{0} } \right) ^{-1}\left( {G_{4} } \right) _{klmq} -G_{kl} \left( {\textrm{I}_{2} } \right) _{mq} -G_{km} \left( {\textrm{I}_{2} } \right) _{lq} -G_{lm} \left( {\textrm{I}_{2} } \right) _{kq} } \right] ^{-1} \end{aligned}$$

(A 8)

The previous relation has the following tensor format

$$\begin{aligned} {\mathop {\textbf{D}}\limits _{\approx }}\left( {\mathrm{\textbf{x}}} \right) =3{\mathop {\varvec{\chi }}\limits _{\thicksim }}\left( {\mathrm{\textbf{x}}} \right) \cdot {\mathop {\mathbf {\Upsilon }}\limits _{\approx }} \end{aligned}$$

(A 9)

In Eq. (A 9), ${\mathop {\mathbf {\Upsilon }}\limits _{\approx }}$ is the fourth-order tensor of the higher-order moments of unit cell area, which is defined as

$$\begin{aligned} \Upsilon _{klmq}:=\left[ {\left( {G_{2}^{0} } \right) ^{-1}\left( {G_{4} } \right) _{klmq} -G_{kl} \left( {\textrm{I}_{2} } \right) _{mq} -G_{km} \left( {\textrm{I}_{2} } \right) _{lq} -G_{lm} \left( {\textrm{I}_{2} } \right) _{kq} } \right] ^{-1} \end{aligned}$$

By substituting Eq. (A 9) into Eq. (A 2), the coefficient ${\mathop {\textbf{B}}\limits _{\thicksim }}$ expresses as

$$\begin{aligned} \begin{array}{l} B_{ij} \left( {\mathrm{\textbf{x}}} \right) =H_{ij} \left( {\mathrm{\textbf{x}}} \right) -\chi _{iq} \left( {\mathrm{\textbf{x}}} \right) \left[ {\left( {G^{0}} \right) ^{-1}\left( {G_{4} } \right) _{klmq} -G_{kl} \left( {\textrm{I}_{2} } \right) _{mq} -G_{km} \left( {\textrm{I}_{2} } \right) _{lq} -G_{lm} \left( {\textrm{I}_{2} } \right) _{kq} } \right] ^{-1}. \\ \left[ {G_{kl} \left( {\textrm{I}_{2} } \right) _{mj} +G_{km} \left( {\textrm{I}_{2} } \right) _{lj} +G_{lm} \left( {\textrm{I}_{2} } \right) _{kj} } \right] \\ \end{array} \end{aligned}$$

(A 10)

which receives the following tensor format

$$\begin{aligned} {\mathop {\textbf{B}}\limits _{\thicksim }}\left( {\mathrm{\textbf{x}}} \right) =\mathop {\textbf{H}}\limits _{\thicksim }\left( {\mathrm{\textbf{x}}} \right) -{\mathop {\varvec{\chi }}\limits _{\thicksim }}\left( {\mathrm{\textbf{x}}} \right) \cdot {\mathop {\mathbf {\Gamma }}\limits _{\thicksim }} \end{aligned}$$

(A 11)

with the second-order tensor ${\mathop {\mathbf {\Gamma }}\limits _{\thicksim }}$ defined in index format as

$$\begin{aligned} \Gamma _{qj}:=\left[ {\left( {G^{0}} \right) ^{-1}\left( {G_{4} } \right) _{klmq} -G_{kl} \left( {\textrm{I}_{2} } \right) _{mq} -G_{km} \left( {\textrm{I}_{2} } \right) _{lq} -G_{lm} \left( {\textrm{I}_{2} } \right) _{kq} } \right] ^{-1}\left[ {G_{kl} \left( {\textrm{I}_{2} } \right) _{mj} +G_{km} \left( {\textrm{I}_{2} } \right) _{lj} +G_{lm} \left( {\textrm{I}_{2} } \right) _{kj} } \right] \end{aligned}$$

To facilitate the calculation of the remaining coefficients, the left-hand side in next Eq. (A 12) can be simplified:

$$\begin{aligned} \left( {\left( {G_{4} } \right) _{pqjk} -G_{pq} G_{jk} } \right) ^{-1}G_{jk} =G_{4}^{0} \left( {\textrm{I}_{2} } \right) _{pq} \end{aligned}$$

(A 12)

where $G_{4}^{0}$ is a constant related to the fourth and second moment of areas. Using Eqs. (A 1), (A 5), we obtain:

$$\begin{aligned} \begin{array}{l} E_{ipqlm} T_{pqlmjk}^{6} =2C_{ipq} \left( {\mathrm{\textbf{x}}} \right) G_{pq} G_{jk}^{-1} +E_{ipqlm} \left( {\mathrm{\textbf{x}}} \right) \left( {G_{4} } \right) _{pqlm} G_{jk}^{-1} -K_{ijk} \\ \Rightarrow E_{ipqlm} \left( {T_{pqlmjk}^{6} -\left( {G_{4} } \right) _{pqlm} G_{jk}^{-1} } \right) =2C_{ipq} \left( {\mathrm{\textbf{x}}} \right) G_{pq} G_{jk}^{-1} -K_{ijk} \\ T_{rlmnjk}^{6} =\left[ {\begin{array}{l} G_{mn} \left( {\textrm{I}_{2} } \right) _{jr} \left( {\textrm{I}_{2} } \right) _{lk} +G_{\ln } \left( {\textrm{I}_{2} } \right) _{jr} \left( {\textrm{I}_{2} } \right) _{mk} +G_{ml} \left( {\textrm{I}_{2} } \right) _{jr} \left( {\textrm{I}_{2} } \right) _{nk} +G_{mn} \left( {\textrm{I}_{2} } \right) _{lj} \left( {\textrm{I}_{2} } \right) _{rk} + \\ G_{rn} \left( {\textrm{I}_{2} } \right) _{lj} \left( {\textrm{I}_{2} } \right) _{mk} +G_{rm} \left( {\textrm{I}_{2} } \right) _{lj} \left( {\textrm{I}_{2} } \right) _{nk} +G_{\ln } \left( {\textrm{I}_{2} } \right) _{mj} \left( {\textrm{I}_{2} } \right) _{rk} +G_{rn} \left( {\textrm{I}_{2} } \right) _{mj} \left( {\textrm{I}_{2} } \right) _{lk} + \\ G_{rl} \left( {\textrm{I}_{2} } \right) _{mj} \left( {\textrm{I}_{2} } \right) _{nk} +G_{lm} \left( {\textrm{I}_{2} } \right) _{nj} \left( {\textrm{I}_{2} } \right) _{rk} +G_{rm} \left( {\textrm{I}_{2} } \right) _{nj} \left( {\textrm{I}_{2} } \right) _{lk} +G_{rl} \left( {\textrm{I}_{2} } \right) _{nj} \left( {\textrm{I}_{2} } \right) _{mk} - \\ \left[ {\left( {G_{4} } \right) _{rlmp} \left( {\textrm{I}_{2} } \right) _{nk} +\left( {G_{4} } \right) _{rnlp} \left( {\textrm{I}_{2} } \right) _{mk} +\left( {G_{4} } \right) _{rmnp} \left( {\textrm{I}_{2} } \right) _{lk} +\left( {G_{4} } \right) _{lmnp} \left( {\textrm{I}_{2} } \right) _{rk} } \right] G_{pj}^{-1} \\ \end{array}} \right] \\ \end{array} \end{aligned}$$

(A 13)

Multiplying Eqs. (A 4) and (A 5) by $G_{jk}$ and using expression of $U_{i} \left( {\mathrm{\textbf{x}}} \right)$ from Eq. (A1) assuming no rigid body motion delivers the algebraic system:

$$\begin{aligned}{} & {} \left| {\begin{array}{l} E_{irlmn} T_{rlmnjk}^{6} G_{jk} =4\left( {C_{ijk} G_{jk} +\frac{1}{2}E_{irlmn} \left( {G_{4} } \right) _{rlmn} -K_{ijk} G_{jk} } \right) \\ 4\textrm{K}_{ijk} G_{jk} =4C_{ijk} G_{jk} +2E_{irlmn} \left( {\mathrm{\textbf{x}}} \right) \left[ {\left( {G_{6} } \right) _{rlmnpq} -\left( {G_{4} } \right) _{rlmn} G_{pq} } \right] \left( {\left( {G_{4} } \right) _{pqjk} -G_{pq} G_{jk} } \right) ^{-1}G_{jk} \\ \end{array}} \right. \nonumber \\{} & {} \Rightarrow 3\textrm{K}_{ijk} G_{jk} =E_{irlmn} \left\{ \left[ {\left( {G_{6} } \right) _{rlmnpq} -\left( {G_{4} } \right) _{rlmn} G_{pq} } \right] \left( {\left( {G_{4} } \right) _{pqjk} -G_{pq} G_{jk} } \right) ^{-1}G_{jk}\right. \nonumber \\{} & {} \left. +T_{rlmnjk}^{6} G_{jk} -\frac{1}{2}\left( {G_{4} } \right) _{rlmn} \right\} \nonumber \\{} & {} \left| {\begin{array}{l} G_{jk} =G_{2}^{0} \left( {\textrm{I}_{2} } \right) _{jk} \\ \left( {\left( {G_{4} } \right) _{pqjk} -G_{pq} G_{jk} } \right) ^{-1}G_{jk} =G_{4}^{0} \left( {\textrm{I}_{2} } \right) _{pq} \\ \end{array}} \right. \nonumber \\{} & {} \Rightarrow 3G_{2}^{0} \textrm{K}_{ijj} =E_{irlmn} \left\{ \left[ {\left( {G_{6} } \right) _{rlmnpp} -2G_{2}^{0} \left( {G_{4} } \right) _{rlmn} } \right] G_{4}^{0} \right. \nonumber \\{} & {} \left. +T_{rlmnjk}^{6} G_{jk} -\frac{1}{2}\left( {G_{4} } \right) _{rlmn} \right\} \nonumber \\{} & {} T_{rlmnjk}^{6} G_{jk} =\left[ {\begin{array}{l} 4G_{mn} G_{rl} +4G_{\ln } G_{rm} +4G_{ml} G_{rn} \\ -\left[ {\left( {G_{4} } \right) _{rlmp} \delta _{pn} +\left( {G_{4} } \right) _{rnlp} \delta _{pm} +\left( {G_{4} } \right) _{rmnp} \delta _{pl} +\left( {G_{4} } \right) _{lmnp} \delta _{pr} } \right] \\ \end{array}} \right] \nonumber \\{} & {} =\left[ {4G_{mn} G_{rl} +4G_{\ln } G_{rm} +4G_{ml} G_{rn} -\left[ {\left( {G_{4} } \right) _{rlmn} +\left( {G_{4} } \right) _{rnlm} +\left( {G_{4} } \right) _{rmnl} +\left( {G_{4} } \right) _{lmnr} } \right] } \right] \nonumber \\{} & {} \Rightarrow T_{rlmnjk}^{6} G_{jk} =T_{rlmn}^{4} \nonumber \\{} & {} \Rightarrow 3G_{2}^{0} \textrm{K}_{itt} =E_{irlmn} \left\{ {\left[ {\left( {G_{6} } \right) _{rlmnpp} -2G_{2}^{0} \left( {G_{4} } \right) _{rlmn} } \right] G_{4}^{0} +T_{rlmn}^{4} -\frac{1}{2}\left( {G_{4} } \right) _{rlmn} } \right\} \equiv E_{irlmn} \Omega _{rlmn} \nonumber \\{} & {} \Rightarrow E_{irlmn} =3G_{2}^{0} \textrm{K}_{itt} \left( {\Omega ^{-1}} \right) _{rlmn} \end{aligned}$$

(A 14)

Inserting the last relation into Eq. (A 4) leads to

$$\begin{aligned} \begin{array}{l} C_{ijk} \left( {\mathrm{\textbf{x}}} \right) =\textrm{K}_{ijk} -\frac{3}{2}G_{2}^{0} \textrm{K}_{itt} \left( {\mathrm{\textbf{x}}} \right) P_{jk} \\ P_{jk}:=\left( {\Omega ^{-1}} \right) _{rlmn} \left[ {\left( {G_{6} } \right) _{rlmnpq} -\left( {G_{4} } \right) _{rlmn} G_{pq} } \right] \left( {\left( {G_{4} } \right) _{pqjk} -G_{pq} G_{jk} } \right) ^{-1} \\ \end{array} \end{aligned}$$

(A 15)

Substituting the coefficients ${\mathop {\textbf{B}}\limits _{\thicksim }}$, ${\mathop {\textbf{C}}\limits _{\simeq }}$, ${\mathop {\textbf{D}}\limits _{\thickapprox }}$, and ${\mathop {\textbf{E}}\limits _{\approxeq }}$ into the previous Eq. (50) gives the total homogenous microscopic displacement as the following fourth-order polynomial expression of the relative microscopic position, expressed successively in the zoomed domain and physical domain versus the small-scale parameter for this last expression:

$$\begin{aligned} u_{i}^{\hom } \left( {{\varvec{\upxi }},\mathrm{\textbf{x}}} \right){} & {} =\left( {H_{ij} -\chi _{ip} \left( {\mathrm{\textbf{x}}} \right) \varvec{\Gamma }_{pj} } \right) \xi _{j} +\frac{1}{2}\left\{ {{\textbf{K}}_{ijk} -\frac{3}{2}G_{2}^{0} P_{jk} {\textbf{K}}_{itt} \left( {\mathrm{\textbf{x}}} \right) } \right\} \xi _{j} \xi _{k} +\chi _{ip} \left( {\mathrm{\textbf{x}}} \right) \varvec{\Upsilon }_{pjkl} \xi _{j} \xi _{k} \xi _{l} \nonumber \\{} & {} \quad +\frac{3}{4}G_{2}^{0} {\textbf{K}}_{itt} \left( {\mathrm{\textbf{x}}} \right) \left( {{\varvec{\Omega }}^{-1}} \right) _{jklm} \xi _{j} \xi _{k} \xi _{l} \xi _{m} \text{ in } \text{ non-dimensional } \text{ domain } \nonumber \\ \Rightarrow u_{i}^{\hom } \left( {{\varvec{\upxi }},\mathrm{\textbf{x}}} \right){} & {} =\left( {H_{ij} -\chi _{ip} \left( {\mathrm{\textbf{x}}} \right) \varvec{\Gamma }_{pj} } \right) \varepsilon \xi _{j} +\frac{1}{2}\left\{ {{\textbf{K}}_{ijk} -\frac{3}{2}G_{2}^{0} P_{jk} {\textbf{K}}_{itt} \left( {\mathrm{\textbf{x}}} \right) } \right\} \varepsilon ^{2}\xi _{j} \xi _{k} +\chi _{ip} \left( {\mathrm{\textbf{x}}} \right) \varvec{\Upsilon }_{pjkl} \varepsilon ^{3}\xi _{j} \xi _{k} \xi _{l} \nonumber \\{} & {} \quad +\frac{3}{4}G_{2}^{0} {\textbf{K}}_{itt} \left( {\mathrm{\textbf{x}}} \right) \left( {{\varvec{\Omega }}^{-1}} \right) _{jklm} \varepsilon ^{4}\xi _{j} \xi _{k} \xi _{l} \xi _{m} \text{ in } \text{ physical } \text{ domain } \end{aligned}$$

(A 16)

The displacement term depending on the micro deformation is odd in the micro position. Thus, the stress will be an even function of the micro deformation, which justifies a posteriori the assumption made in section 2.

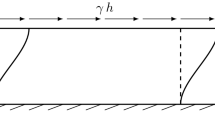
Appendix B: derivation of a closed form solution for the double shear problem

The boundary value problem to be solved for the effective micromorphic continuum includes the balance of linear momentum and the constitutive law written in Eq. (56), which specializes in the case of centrosymmetric microstructures and in the absence of body forces at the microlevel to:

$$\begin{aligned} \begin{array}{l} \left| {\begin{array}{l} {\textrm{div}}_{\textrm{x}} {\mathop {\varvec{\Sigma }}\limits _{\thicksim }}=\mathrm{\textbf{0}} \\ \left( {{\mathop {\varvec{\Sigma }}\limits _{\thicksim }}-{\mathop {\textbf{s}}\limits _{\thicksim }}} \right) +{\textrm{div}}_{\textrm{x}} {\mathop {\textbf{s}}\limits _{\simeq }}=0 \\ \end{array}} \right. \\ \left| {\begin{array}{l} {\mathop {\varvec{\Sigma }}\limits _{\thicksim }}={\mathop {\textbf{C}}\limits _{\thickapprox }}^{\hom }:\mathop {\textbf{H}}\limits _{\thicksim } \\ {\mathop {\textbf{s}}\limits _{\thicksim }}={\mathop {\textbf{H}}\limits _{\approx }}^{\hom }:{\mathop {\varvec{\chi }}\limits _{\thicksim }} \\ {\mathop {\textbf{s}}\limits _{\simeq }}={{\mathop {\textbf{K}}\limits _{\mathop {\thickapprox }\limits _{\thicksim }}}}^{\hom }\mathop {\textbf{K}}\limits _{\simeq } \\ \end{array}} \right. \\ \end{array} \end{aligned}$$

(B1)

The micromorphic constitutive law writes in full generality for an orthotropic material symmetry:

$$\begin{aligned} \left( {{\begin{array}{*{20}c} {{\textrm{S}}_{111} } \\ {{\textrm{S}}_{122} } \\ {{\textrm{S}}_{212} } \\ {{\textrm{S}}_{112} } \\ {{\textrm{S}}_{112} } \\ {{\textrm{S}}_{121} } \\ {{\textrm{S}}_{211} } \\ {{\textrm{S}}_{222} } \\ \end{array} }} \right) =\left( {{\begin{array}{*{20}c} {{\textrm{K}}_{11}^{\hom } } &{} {{\textrm{K}}_{12}^{\hom } } &{} {{\textrm{K}}_{13}^{\hom } } &{} {{\textrm{K}}_{14}^{\hom } } &{} &{} &{} &{} \\ {{\textrm{K}}_{12}^{\hom } } &{} {{\textrm{K}}_{22}^{\hom } } &{} {{\textrm{K}}_{24}^{\hom } } &{} {{\textrm{K}}_{24}^{\hom } } &{} &{} &{} &{} \\ {{\textrm{K}}_{13}^{\hom } } &{} {{\textrm{K}}_{23}^{\hom } } &{} {{\textrm{K}}_{33}^{\hom } } &{} {{\textrm{K}}_{34}^{\hom } } &{} &{} &{} &{} \\ {{\textrm{K}}_{14}^{\hom } } &{} {{\textrm{K}}_{24}^{\hom } } &{} {{\textrm{K}}_{34}^{\hom } } &{} {{\textrm{K}}_{44}^{\hom } } &{} &{} &{} &{} \\ &{} &{} &{} &{} {{\textrm{K}}_{55}^{\hom } } &{} {{\textrm{K}}_{56}^{\hom } } &{} {{\textrm{K}}_{57}^{\hom } } &{} {{\textrm{K}}_{58}^{\hom } } \\ &{} &{} &{} &{} {{\textrm{K}}_{65}^{\hom } } &{} {{\textrm{K}}_{66}^{\hom } } &{} {{\textrm{K}}_{67}^{\hom } } &{} {{\textrm{K}}_{68}^{\hom } } \\ &{} &{} &{} &{} {{\textrm{K}}_{75}^{\hom } } &{} {{\textrm{K}}_{76}^{\hom } } &{} {{\textrm{K}}_{77}^{\hom } } &{} {{\textrm{K}}_{78}^{\hom } } \\ &{} &{} &{} &{} {{\textrm{K}}_{85}^{\hom } } &{} {{\textrm{K}}_{86}^{\hom } } &{} {{\textrm{K}}_{87}^{\hom } } &{} {{\textrm{K}}_{88}^{\hom } } \\ \end{array} }} \right) \left( {{\begin{array}{*{20}c} {{\textrm{K}}_{111} } \\ {{\textrm{K}}_{122} } \\ {{\textrm{K}}_{212} } \\ {{\textrm{K}}_{112} } \\ {{\textrm{K}}_{112} } \\ {{\textrm{K}}_{121} } \\ {{\textrm{K}}_{211} } \\ {{\textrm{K}}_{222} } \\ \end{array} }} \right) \end{aligned}$$

(B2)

The considered BVP has been completely solved in [67] so we indicate the used Ansatz for the displacement and microdeformation and the obtained solution for an orthotropic micromorphic medium. The kinematic variables, the displacement and microdeformation, express versus the sole vetical position as follows:

$$\begin{aligned} \begin{array}{l} \mathrm{\textbf{u}}={\textrm{u}}\left( {\textrm{x}_{2} } \right) \mathrm{\textbf{e}}_{1} \\ {\varvec{\upchi }}={\varvec{\upchi }}\left( {x_{2} } \right) =\chi _{12} \left( {\textrm{x}_{2} } \right) \left( {\mathrm{\textbf{e}}_{1} \otimes \mathrm{\textbf{e}}_{2} +\mathrm{\textbf{e}}_{2} \otimes \mathrm{\textbf{e}}_{1} } \right) \\ \mathrm{\textbf{K}}:={\varvec{\upchi }}\otimes \nabla _{\textrm{X}} =\chi '_{12} \mathrm{\textbf{e}}_{1} \otimes \mathrm{\textbf{e}}_{2} \otimes \mathrm{\textbf{e}}_{2} +\chi '_{21} \mathrm{\textbf{e}}_{1} \otimes \mathrm{\textbf{e}}_{1} \otimes \mathrm{\textbf{e}}_{2} \\ \end{array} \end{aligned}$$

(B3)

In which the prime denotes the derivative with respect to the space variable ${\textrm{x}}_{2}$.

The boundary conditions are those of imposed displacement and clamped higher order kinematic conditions, thus it holds the six constraints:

$$\begin{aligned} \left| {\begin{array}{l} {\textrm{u}}\left( {\textrm{h}} \right) ={\textrm{u}}\left( {-{\textrm{h}}} \right) =\delta /2 \\ \chi _{12} \left( {\pm {\textrm{h}}} \right) =0 \\ \chi _{21} \left( {\pm {\textrm{h}}} \right) =0 \\ \end{array}} \right. \end{aligned}$$

(B4)

According to the kinematic assumptions in Eq. (B3), the constitutive law in Eq. (B1) takes the form

$$\begin{aligned} \left\{ {\begin{array}{l} \upsigma _{12} =2{\textrm{C}}_{1212} {\textrm{u}}' \\ {\textrm{s}}_{12} ={\textrm{B}}_{1212} \left( {{\textrm{u}}'-\upchi _{12} } \right) +{\textrm{B}}_{1221} \left( {-\upchi _{21} } \right) \\ {\textrm{s}}_{21} ={\textrm{B}}_{2112} \left( {{\textrm{u}}'-\upchi _{12} } \right) +{\textrm{B}}_{2121} \left( {-\upchi _{21} } \right) \\ {\textrm{S}}_{122} ={\textrm{A}}_{22} \upchi '_{12} +{\textrm{A}}_{23} \upchi '_{21} \\ {\textrm{S}}_{212} ={\textrm{A}}_{23} \upchi '_{12} +{\textrm{A}}_{33} \upchi '_{21} \end{array}} \right. \end{aligned}$$

(B5)

The solution for the micromorphic shear deformations have been obtained in [67], and write in terms of hyperbolic functions:

$$\begin{aligned} \left\{ {\begin{array}{l} \chi _{12} \left( {{\textrm{x}}_{2} } \right) =\frac{1}{\upomega _{1} }{\textrm{C}}{ }_{2}\cosh \left( {\upomega _{1} {\textrm{x}}_{2} } \right) +\frac{1}{\upomega _{2} }{\textrm{C}}{ }_{4}\cosh \left( {\upomega _{2} {\textrm{x}}_{2} } \right) +{\textrm{C}}_{9} \\ \chi _{21} \left( {{\textrm{x}}_{2} } \right) =\frac{\tau _{1} }{\upomega _{1} }{\textrm{C}}{ }_{2}\cosh \left( {\upomega _{1} {\textrm{x}}_{2} } \right) +\frac{\tau _{2} }{\upomega _{2} }{\textrm{C}}{ }_{4}\cosh \left( {\upomega _{2} {\textrm{x}}_{2} } \right) \\ u\left( {{\textrm{x}}_{2} } \right) =\frac{\eta _{1} +\eta _{2} \tau _{1} }{\upomega _{1} ^{2}}{\textrm{C}}{ }_{2}\cosh \left( {\upomega _{1} {\textrm{x}}_{2} } \right) +\frac{\eta _{1} +\eta _{2} \tau _{2} }{\upomega _{2}^{2}}{\textrm{C}}{ }_{4}\cosh \left( {\upomega _{2} {\textrm{x}}_{2} } \right) +{\textrm{C}}_{9} {\textrm{x}}_{2} \end{array}} \right. \end{aligned}$$

(B6)

with the constants therein ${\textrm{C}}{ }_{2},{\textrm{C}}{ }_{4},{\textrm{C}}{ }_{9}$ expressing from the three remaining boundary conditions:

$$\begin{aligned} \left| {\begin{array}{l} {\textrm{C}}_{4} =\frac{\delta }{2\left\{ {\frac{\eta _{1} +\eta _{2} \tau _{2} }{\upomega _{2}^{2}}\sinh \left( {\upomega _{2} h} \right) -h\frac{\cosh \left( {\upomega _{2} h} \right) }{\upomega _{2} }-\left( {\frac{\eta _{1} +\eta _{2} \tau _{1} }{\upomega _{1}^{2}}-h\frac{\cosh \left( {\upomega _{1} h} \right) }{\upomega _{1} }} \right) \frac{\tau _{2} }{\upomega _{2} }\sinh \left( {\upomega _{2} h} \right) \frac{\upomega _{1} }{\tau _{1} \cosh \left( {\upomega _{1} h} \right) }} \right\} } \\ {\textrm{C}}_{2} =-\frac{\tau _{2} }{\upomega _{2} }\sinh \left( {\upomega _{2} h} \right) \frac{\upomega _{1} }{\tau _{1} \cosh \left( {\upomega _{1} h} \right) }{\textrm{C}}_{4}, \\ {\textrm{C}}_{9} =-\frac{\cosh \left( {\upomega _{1} h} \right) }{\upomega _{1} }{\textrm{C}}_{2} -\frac{\cosh \left( {\upomega _{2} h} \right) }{\upomega _{2} }{\textrm{C}}_{4} \\ {\textrm{C}}_{5} =\frac{-\upalpha _{1} +\upalpha _{2} \upomega _{1}^{2}}{\upbeta _{1} +\upbeta _{2} \upomega _{1}^{2}}{\textrm{C}}_{1} =\tau _{1} {\textrm{C}}_{1}, {\textrm{C}}_{6} =\frac{-\upalpha _{1} +\upalpha _{2} \upomega _{1}^{2}}{\upbeta _{1} +\upbeta _{2} \upomega _{1}^{2}}{\textrm{C}}_{2} =\tau _{1} {\textrm{C}}_{2} \\ {\textrm{C}}_{7} =\frac{-\upalpha _{1} +\upalpha _{2} \upomega _{1}^{2}}{\upbeta _{1} +\upbeta _{2} \upomega _{1}^{2}}{\textrm{C}}_{3} =\tau _{2} {\textrm{C}}_{3}, {\textrm{C}}_{8} =\frac{-\upalpha _{1} +\upalpha _{2} \upomega _{1}^{2}}{\upbeta _{1} +\upbeta _{2} \upomega _{1}^{2}}{\textrm{C}}_{3} =\tau _{2} {\textrm{C}}_{4} \\ \end{array}} \right. \end{aligned}$$

(B7)

with $\upomega _{1}^{2},\upomega _{2}^{2}$ therein the solution (in terms of their square) of the characteristic equation

$$\begin{aligned} \begin{array}{l} \upalpha _{1} \left( {\upbeta _{3} -\upbeta _{1} } \right) +\left( {\upalpha _{2} \upbeta _{3} +\upalpha _{1} \upbeta _{4} -\upbeta _{1} \upalpha _{3} -\upalpha _{1} \upbeta _{2} } \right) x+\left( {\upalpha _{2} \upbeta _{4} -\upbeta _{2} \upalpha _{3} } \right) x^{2}=0 \\ \upalpha _{1}:=-\frac{{\textrm{C}}_{1212} }{{\textrm{C}}_{1212} +{\textrm{B}}_{1212} },\upalpha _{2}:=-\frac{{\textrm{A}}_{22} }{{\textrm{B}}_{1212} },\upalpha _{2}:=-\frac{{\textrm{A}}_{23} }{{\textrm{B}}_{2112} } \\ \upbeta _{1}:=\left( {\frac{{\textrm{B}}_{1221} }{{\textrm{C}}_{1212} +{\textrm{B}}_{1212} }-\frac{{\textrm{B}}_{1221} }{{\textrm{B}}_{1212} }} \right) ,\upbeta _{2}:=\frac{{\textrm{A}}_{23} }{{\textrm{B}}_{1212} },\upbeta _{3}:=\left( {\frac{{\textrm{B}}_{1221} }{{\textrm{C}}_{1212} +{\textrm{B}}_{1212} }-\frac{{\textrm{B}}_{2121} }{{\textrm{B}}_{2112} }} \right) ,\upbeta _{4}:=\frac{{\textrm{A}}_{33} }{{\textrm{B}}_{2112} } .\\ \end{array} \end{aligned}$$

(B8)