A look at endemic equilibria of compartmental epidemiological models and model control via vaccination and mitigation

Abstract

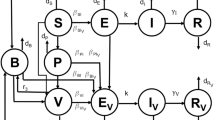
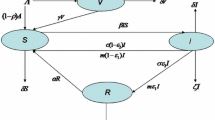
Compartmental models have long served as important tools in mathematical epidemiology, with their usefulness highlighted by the recent COVID-19 pandemic. However, most of the classical models fail to account for certain features of this disease and others like it, such as the ability of exposed individuals to recover without becoming infectious, or the possibility that asymptomatic individuals can indeed transmit the disease but at a lesser rate than the symptomatic. In the first part of this paper, we propose two new compartmental epidemiological models and study their equilibria, obtaining an endemic threshold theorem for the first model. In the second part of the paper, we treat the second model as an affine control system with two controls: vaccination and mitigation. We show that this system is static feedback linearizable, presents some simulations, and investigates an optimal control version of the problem. We conclude with some open problems and ideas for future research.

Appendix: Proof of Proposition 7

To find endemic equilibria of the SVE(R)IRS system, we need to solve the following system:

$$\begin{aligned} 0&= -\beta S (I+\alpha E)/n + \omega (n-S-E-I-V) -\phi S + \psi V \\ 0&= \beta S (I+\alpha E)/n - (\sigma + \delta ) E + \rho \beta V(I+\alpha E)/n \\ 0&= \sigma E - \gamma I \\ 0&=- \rho \beta V(I+\alpha E)/n + \phi S - \psi V. \end{aligned}$$

The third of the above equations readily yields $I=(\sigma /\gamma )E$. Plugging this into the rest of the equations and setting $\kappa = \frac{\sigma +\alpha \gamma }{n\gamma }$, we obtain

$$\begin{aligned} 0&= -\beta \kappa S E + \omega \left( n-S-\left( 1+\frac{\sigma }{\gamma }\right) E-V\right) -\phi S + \psi V \\ 0&= \beta \kappa S E - (\sigma + \delta ) E + \rho \beta \kappa V E \\ 0&=- \rho \beta \kappa V E + \phi S - \psi V. \end{aligned}$$

Note that $E=0$ yields the disease-free equilibrium, so we may assume that $E\ne 0$. Adding the bottom two equations to the first one and dividing the second equation by $\beta \kappa E$, we get

$$\begin{aligned} 0&= \omega \left( n-S-\left( 1+\frac{\sigma }{\gamma }\right) E-V\right) - (\sigma +\delta )E \\ 0&= S - \frac{\sigma + \delta }{\beta \kappa } + \rho V \\ 0&=- \rho \beta \kappa V E + \phi S - \psi V. \end{aligned}$$

From the first two equations, we easily find that

$$\begin{aligned} S&= -c + \rho a E \\ V&= b - a E, \end{aligned}$$

where

$$\begin{aligned} a&= \frac{1}{1-\rho }\left( 1+\frac{\sigma }{\gamma } + \frac{\sigma + \delta }{\omega }\right) \\ b&= \frac{1}{1-\rho }\left( n - \frac{\sigma + \delta }{\beta \kappa }\right) \\ c&= \frac{1}{1-\rho }\left( \rho n - \frac{\sigma + \delta }{\beta \kappa }\right) . \end{aligned}$$

Using the expressions for S and V in terms of E, we obtain the following quadratic equation:

$$\begin{aligned} \rho \beta \kappa a E^2 +(\rho \phi a+\psi a - \rho \beta \kappa b) E - (\phi c + \psi b) = 0, \end{aligned}$$

which yields the following two roots

$$\begin{aligned} E_{+,-}&= \frac{1}{2\rho \beta \kappa a}\Big ( -(\rho \phi a+\psi a - \rho \beta \kappa b) \\&\quad \pm \sqrt{(\rho \phi a+\psi a - \rho \beta \kappa b)^2+4\rho \beta \kappa a(\phi c + \psi b )} \Big ). \end{aligned}$$

Note that

$$\begin{aligned} \phi c + \psi b&= \frac{\phi }{1-\rho }\left( \rho n - n\frac{\gamma (\sigma +\delta )}{\beta (\sigma +\alpha \gamma )}\right) + \frac{\psi }{1-\rho }\left( n - n\frac{\gamma (\sigma +\delta )}{\beta (\sigma +\alpha \gamma )}\right) \\&= \frac{n}{1-\rho }\left( \rho \phi +\psi -(\phi +\psi )\frac{\gamma (\sigma +\delta )}{\beta (\sigma +\alpha \gamma )}\right) = \frac{n(\rho \phi +\psi )}{1-\rho }\left( 1-\frac{1}{\mathfrak {R}_0}\right) . \end{aligned}$$

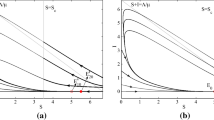
We thus see that if $\mathfrak {R}_0>1$, then both roots are real, and $E_{+}>0$, while $E_{-}<0$. The latter gives a biologically irrelevant state. Computing the values of S and V from $E_+$, we obtain

$$\begin{aligned} V_{+}&= b-a E_{+} = \frac{1}{2\rho \beta \kappa }\Big (\rho \beta \kappa b + \rho \phi a+\psi a \\&\quad - \sqrt{(\rho \phi a+\psi a - \rho \beta \kappa b)^2+4\rho \beta \kappa a(\phi c + \psi b )} \Big ).\\ S_{+}&= -c+\rho a E_{+} = \frac{1}{2\beta \kappa }\Big (-2\beta \kappa c -(\rho \phi a+\psi a -\rho \beta \kappa b) \\&\quad + \sqrt{(\rho \phi a+\psi a - \rho \beta \kappa b)^2+4\rho \beta \kappa a(\phi c + \psi b )} \Big ). \end{aligned}$$

Rather than showing directly from these expressions that $S_{+}$ and $V_{+}$ are positive, we proceed as follows. Note that instead of expressing S and V in terms of E, we could as easily express any two of these variables in terms of the remaining one. Hence, we can obtain quadratic equations for S and V. We do not need the whole equations, but we note that both of them have a positive factor in front of the quadratic term, while the free constant term in the equation for V is $\phi (\rho b -c)$, and in the equation for S, it is $-(\rho b -c)(\beta \kappa c/a+\psi )/\rho$. Now, $\rho b-c = \frac{\sigma +\delta }{\beta \kappa }>0$. Thus, the two roots of the equation for V have the same sign. Since $E_{-}<0$ when $\mathfrak {R}_0>1$, we see that one of such roots is $b-a E_{-}>0$; hence, we also have $V_{+}=b-a E_{+}>0$. Similarly, we note that if $c\ge 0$, the two roots of the equation for S have opposite signs, and since one of them is $-c+\rho a E_{-}<0$, we have $S_{+}=-c+\rho a E_{+}>0$. The latter inequality is obvious when $c<0$.

Finally, noting that $I_{+}=(\sigma /\gamma )E_{+}>0$, we see that having $\mathfrak {R}_0>1$ yields a single biologically relevant endemic equilibrium.