Homogenised governing equations for pre-stressed poroelastic composites

Abstract

We propose the governing equations for a pre-stressed poroelastic composite material. The structure that we investigate possesses a porous elastic matrix with embedded elastic subphases with an incompressible Newtonian fluid flowing in the pores. Both the matrix and individual subphases are assumed to be linear elastic and pre-stressed. We are able to apply the asymptotic homogenisation technique by exploiting the length-scale separation that exists between the porescale and the overall size of the material (the macroscale). We derive the novel macroscale model which describes a poroelastic composite material where the elastic phases possess a pre-stress. We extend the current literature for poroelastic composites by addressing the role of the pre-stresses in the functional form of the new system of derived partial differential equations and its coefficients. The latter are computed by solving appropriate periodic cell differential problems which encode the specific contribution related to the pre-stresses. The model in the first instance is derived in the most general scenario and then specified for a variety of particular cases which are associated with different macroscale behaviour of materials.

1 Introduction

A material comprising a porous elastic matrix with fluid flowing in the pore space can be described as poroelastic and is modelled using the theory of poroelasticity. This was first developed by Biot in [1,2,3,4] after conducting a variety of experiments. The theory can only be applied if there exists a scale at which the interactions taking place between the elastic matrix and the fluid can be resolved together with the interactions occurring in the matrix and in the fluid. This is a widely applied modelling framework with many real-world problems of interest. These problems include, but are not limited to, hard hierarchical tissues (undergoing small deformations), such as bones and tendons [5, 6] or the interstitial matrix in healthy and tumorous biological tissues [7]. It is also applicable to the heart (myocardium) such as in [8, 9] or artery walls (see e.g [10,11,12,13]). The theory of poroelasticity does not just have applications within human biology, it has also been used to model artificial constructs and biomaterials [14,15,16], and as in the original theory of Biot, it can be applied to soil and rock mechanics [17, 18].

We are considering materials that are characterised by a variety of structural features that are generally found over multiple microstructural levels (scales). Since we are modelling porous media, it is appropriate to consider a scale where the interactions between the various solid phases and the fluid flowing in the pores take place. This scale is called the porescale. The porescale is a fine microstructural level and has associated length much smaller than the whole domain. The whole material can be described by a scale which we will denote the macroscale.

Since we have a material that comprises multiple scales, we wish to find a model that is both detailed in the characterisation of the effective properties of the material and computationally feasible. In order to do this, we aim to relate the macroscale governing equations to properties and interactions taking place on the porescale. The first step in this process is to create a fluid–structure interaction (FSI) problem for the interactions that are taking place on the porescale. This problem can then be used in an upscaling process to obtain the macroscale governing equations. The upscaling process can be carried out by a variety of techniques proposed in the literature. These methods can be described as homogenisation techniques. These homogenisation techniques can be some of the following, including mixture theory, effective medium theory, volume averaging and asymptotic homogenisation. Each of the techniques have a variety of differences and should be selected based upon both the intended application and the type of information that one wishes to encode or have available from the resulting macroscale model. For a review and discussion of each of these techniques, see [19, 20].

Within this article, we employ the asymptotic homogenisation technique. This technique is popularly used in the context of poroelasticity and has been applied to derive Biot’s equations in [18, 21,22,23]. The theory of poroelasticity has been extended to more complicated dynamics, such as to include growth and remodelling and transport of solute, see, for example, [24, 25] by using the asymptotic homogenisation technique. Developments in the theory also include the vascularisation of poroelastic materials [26]. In recent years, the technique has also been used to consider elastic composites such as in [27] and poroelastic materials with more complicated microstructures such as poroelastic composites [28] and double poroelastic materials [29]. It has also been considered to determine how non-local diffusion affects the transport of chemical species in a composite material in [30]. Despite its main use residing in the linear setting being a critique of the technique, it has recently also been used in the context of poroelastic materials undergoing large deformations such as active poroelastic materials [25] and nonlinear poroelastic composites [31]. The resulting models derived via asymptotic homogenisation are also computationally feasible. In [32], the role of porosity and microscale solid matrix compressibility on the mechanical behaviour of poroelastic materials is considered. This was then further developed to consider the macroscale behaviour in [33]. More recently, a micromechanical analysis of the effective stiffness of poroelastic composites has been investigated in [34], and the results presented therein have then been further specialised to investigate the structural changes involved in myocardial infarction [35], thereby making a first step towards the use of a piecewise linear elastic asymptotic homogenisation model in the study of myocardial infarction.

We are applying the asymptotic homogenisation technique to the fluid–structure interaction (FSI) problem that we set up to describe the behaviour of a pre-stressed porous elastic matrix and subphases, with an incompressible Newtonian fluid flowing in the pores. This setting means that both the elastic matrix and the various subphases are in contact with the fluid flow. Structures of this type are applicable to many physical scenarios, particularly biological tissues. For example, this setting could be considered for artery wall models. In [36, 37], the authors present FSI problems in pre-stressed tubes to model the artery walls. Our structure investigated can be applicable for this scenario as we can identify the matrix portion with the extra cellular matrix and the elastic subphases with the embedded collagen and elastic fibres found in the artery wall microstructure [38]. Pre-stresses have also been considered when investigating the nonlinear stability analysis of thick, incompressible, isotropic elastic bodies subject to finite strains in [39].

We consider the components of the material at a scale where clearly visible and distinct from the matrix are the various solid subphases and the pores. We call this scale the microscale. This scale is much smaller than the entire material (where the pores or subphases are no longer distinctly visible), and so, we call it the macroscale. We then apply the asymptotic homogenisation technique to upscale the FSI problem, accounting for the continuity of tractions, displacements and velocities across the fluid–solid and solid–solid interfaces, that is, between the matrix and the fluid, the subphases and the fluid, and the matrix and the subphases. The novel macroscale model which is presented in the quasi-static case, for a general pre-stress, is of Biot type and is an extension of [28] for poroelastic composites. Our model contains additional terms to account for the different pre-stresses of each of the elastic phases. We are able to recover [28] by assuming that the matrix and the subphases have no pre-stress. The coefficients of the model encode the properties of the microstructure. These are computed by solving the microscale differential problems that arise as a result of applying the asymptotic homogenisation technique. These cell problems are of the type of [28] for poroelastic composites plus additional problems to account for the differences in pre-stresses among all the elastic phases.

We are able to make a comparison between the formalisms of our model and that of [40] on electrostrictive composites in the absence of the fluid phase. The model in [40] investigates the application of the asymptotic homogenisation technique to a linear elastic composite whose deformations are driven by the divergence of the generalised Maxwell stress tensor.

The paper is organised as follows. We begin by introducing the fluid–structure interaction problem that describes the material domain that we are considering in Sect. 2. This problem describes the interactions between the pre-stressed porous elastic matrix and subphases, and the fluid that flows in the pores. In Sect. 3, we then perform the multiscale analysis of the FSI problem that is given in Sect. 2. By doing this, we derive the new macroscale model describing the homogenised mechanical behaviour of pre-stressed poroelastic composites. In Sect. 4, we present the new macroscale model and discuss it for a variety of choices of the pre-stress. We also present a scheme for solving the macroscale model and compare the results derived here with [40] in the absence of a fluid compartment. In Sect. 5, we provide the conclusions to our work as well as further perspectives. We also have Appendix. A which contains all the cell problems presented herein in components notation that will be useful for carrying out the numerical simulations.

2 The fluid–structure interaction problem

We begin by considering a set $\Omega \in \mathbb {R}^3$, where $\Omega$ represents the union of a solid porous matrix $\Omega _{\scriptscriptstyle \textrm{p}}$, a connected fluid compartment $\Omega _{\textrm{f}}$ and a collection $\Omega _{\scriptscriptstyle \textrm{c}}$ of N disjoint subphases (which could represent either inclusions or fibres) $\Omega _{\alpha }$, such that

$$\begin{aligned} \Omega _{\scriptscriptstyle \textrm{c}}=\displaystyle \bigcup ^N_{i=1}\Omega _{\alpha }, \end{aligned}$$

(1)

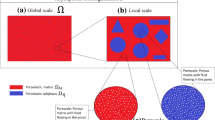
and ${\bar{\Omega }}={\bar{\Omega }}_{\scriptscriptstyle \textrm{c}} \cup {\bar{\Omega }}_{\scriptscriptstyle \textrm{p}} \cup \bar{\Omega }_{\textrm{f}}$. A sketch of a cross section of the three-dimensional domain $\Omega$ is shown in Fig. 1.

Before describing the equations that govern each of the domains in our structure, we first wish to clarify the notation that will be used throughout this manuscript.

Remark 1

(Notation) We use the following for a generic field, F. For a scalar, we use ordinary lowercase letters, e.g. f, for a vector we use boldface, e.g. $\textbf{f}$, and then, ${\textsf{F}}$ is used for second-rank tensor. We use ${\mathcal {F}}$ for third-rank tensors, and finally, $\mathbb {F}$ is used for fourth-rank tensors. We define the operations that will take place between each of these quantities such as the double contraction of a fourth-rank tensor with a second-rank tensor in components in Appendix. A. There are some exceptions to this notation in the final macroscale model in order to keep the style consistent with classical notation used for the Biot’s modulus and the Biot’s tensor of coefficients as well as porosity. In these cases, the Biot’s modulus is ${\hat{M}}$, the Biot’s tensor is $\hat{\varvec{\alpha }}$ and the porosity is $\phi$ as used in [21, 41].

The balance equations in the solid domains $\Omega _{\alpha }$ and $\Omega _{\scriptscriptstyle \textrm{p}}$, by neglecting volume forces and inertia, then read $\forall \, \alpha =1,...,N$

$$\begin{aligned} \nabla \cdot {{\textsf{T}}}_{\alpha }=0 \quad \text{ in } \quad \Omega _{\alpha }, \end{aligned}$$

(2)

and

$$\begin{aligned} \nabla \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{p}}=0 \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

(3)

The symbols ${\textsf{T}}_{\alpha }$ and ${\textsf{T}}_{\scriptscriptstyle \textrm{p}}$ that appear in relationships (2–3) denote the solid Cauchy stress tensors corresponding to each subphase $\Omega _{\alpha }$ and the one corresponding to the matrix $\Omega _{\scriptscriptstyle \textrm{p}}$, respectively. We then assume that both the matrix and each subphase are general linear elastic solids, and since we admit the presence of pre-stresses, we express ${\textsf{T}}_{\alpha }$ and ${\textsf{T}}_{\scriptscriptstyle \textrm{p}}$ as

$$\begin{aligned} {\textsf{T}}_{\alpha }&= \mathbb {C}^{\alpha } \nabla \textbf{u}_{\alpha }+\varvec{\sigma }_{\scriptscriptstyle {\textrm{0}\alpha }}, \end{aligned}$$

(4a)

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}&= \mathbb {C}^{\scriptscriptstyle \textrm{p}} \nabla \textbf{u}_{\scriptscriptstyle \textrm{p}}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}, \end{aligned}$$

(4b)

where $\textbf{u}_{\alpha }$ and $\textbf{u}_{\scriptscriptstyle \textrm{p}}$ are the elastic displacement in each subphase and the matrix, respectively, and $\varvec{\sigma }_{\scriptscriptstyle {\textrm{0}\alpha }}$ and $\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}$ are pre-stresses in both the subphase and the matrix. The first term in each of (4a) and (4b) is the constitutive expression of the Cauchy stresses.

Fig. 1

A 2D sketch showing the three-dimensional domain $\Omega$ and two different levels of magnification. In the most magnified (the microscale), the fluid phase is represented in blue, the porous matrix in pink and the subphases in orange. The inclusions and/or fibres can potentially be in contact with both the matrix and the fluid flowing in the pores, or alternatively, they can be fully embedded in the matrix. Note that the different sizes given to the dots representing the fluid and the inclusions/fibres do not mean that these phases intersect with each other. Rather, it simply means that the subphases and fluid channels have a variety of geometries and elastic properties

The fourth-rank tensors $\mathbb {C}^{\alpha }$ and $\mathbb {C}^{\scriptscriptstyle \textrm{p}}$ are the elasticity tensors in each subphase and the matrix, respectively, with corresponding components $C^{\alpha }_{ijkl}$ and $C^{\scriptscriptstyle \textrm{p}}_{ijkl}$, for $i,j,k,l=1,2,3$. We note that each $\mathbb {C}^{\alpha }$ and $\mathbb {C}^{\scriptscriptstyle \textrm{p}}$ are equipped with right minor and major symmetries, namely

$$\begin{aligned}&C^{\alpha }_{ijkl}=C^{\alpha }_{ijlk};\quad C^{\scriptscriptstyle \textrm{p}}_{ijkl}=C^{\scriptscriptstyle \textrm{p}}_{ijlk}, \end{aligned}$$

(5a)

$$\begin{aligned}&C^{\alpha }_{ijkl}=C^{\alpha }_{klij};\quad C^{\scriptscriptstyle \textrm{p}}_{ijkl}=C^{\scriptscriptstyle \textrm{p}}_{klij}, \end{aligned}$$

(5b)

and therefore, also left minor symmetries follow by combining (5a–5b). In particular, by applying right minor symmetries we can equivalently rewrite equations (4a–4b) as

$$\begin{aligned} {\textsf{T}}_{\alpha }=&\, \mathbb {C}^{\alpha } \xi (\textbf{u}_{\alpha })+\varvec{\sigma }_{\scriptscriptstyle {\textrm{0}\alpha }}, \end{aligned}$$

(6a)

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}=&\, \mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi (\textbf{u}_{\scriptscriptstyle \textrm{p}})+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}, \end{aligned}$$

(6b)

where

$$\begin{aligned} \xi (\bullet )=\frac{\nabla (\bullet )+({\nabla (\bullet )})^T}{2} \end{aligned}$$

(7)

is the symmetric part of the gradient operator.

The balance equation in the fluid compartment reads

$$\begin{aligned} \nabla \cdot {\textsf{T}}_{\textrm{f}}=0\quad \text{ in } \quad \Omega _{\textrm{f}}, \end{aligned}$$

(8)

where ${\textsf{T}}_{\textrm{f}}$ is the fluid stress tensor. We assume that the fluid compartment is an incompressible Newtonian fluid, so that the constitutive equation for ${\textsf{T}}_{\textrm{f}}$ is given by

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}=-p{\textsf{I}}+2\mu \xi ({\textbf{v}})\quad \text{ in } \quad \Omega _{\textrm{f}}, \end{aligned}$$

(9)

where $\mathbf{{v}}$ denotes fluid velocity, p the pressure and $\mu$ the viscosity, together with the incompressibility constraint

$$\begin{aligned} \nabla \cdot \textbf{v}=0\quad \text{ in } \quad \Omega _{\textrm{f}}. \end{aligned}$$

(10)

Substituting relationship (9) in (8) and using the divergence-free condition (10) yields the Stokes’ problem

$$\begin{aligned} \mu \nabla ^2 \textbf{v}=\nabla p\quad \text{ in } \quad \Omega _{\textrm{f}}. \end{aligned}$$

(11)

In order to close the fluid-structure interaction problem in the whole domain $\Omega$, we also require interface conditions between the fluid and the solid phases. We first define the interface between the fluid phase and the $\alpha$ inclusion/fibre as

$$\begin{aligned} \Gamma _{\alpha } =\partial \Omega _{\alpha }\cap \partial \Omega _{\textrm{f}} \end{aligned}$$

(12)

and the one between the matrix and the fluid phase as

$$\begin{aligned} \Gamma _{\scriptscriptstyle \textrm{p}} =\partial \Omega _{\scriptscriptstyle \textrm{p}} \cap \partial \Omega _{\textrm{f}}. \end{aligned}$$

(13)

We then impose continuity of velocities and stresses across each $\Gamma _{\alpha }$ and $\Gamma _{\scriptscriptstyle \textrm{p}}$, namely

$$\begin{aligned} \dot{\textbf{u}}_{\alpha }= \textbf{v}&\quad \text{ on }\quad \Gamma _{\alpha }, \end{aligned}$$

(14a)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}{} \textbf{n}_{\alpha }={\textsf{T}}_{\alpha }{} \textbf{n}_{\alpha }&\quad \text{ on }\quad \Gamma _{\alpha }, \end{aligned}$$

(14b)

$$\begin{aligned} \dot{\textbf{u}}_{{\scriptscriptstyle \textrm{p}}}= \textbf{v}&\quad \text{ on }\quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(14c)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}\textbf{n}_{\scriptscriptstyle \textrm{p}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}\textbf{n}_{\scriptscriptstyle \textrm{p}}&\quad \text{ on }\quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(14d)

$\forall \, \alpha =1...N$, where $\dot{\textbf{u}}_{\alpha }$ and $\dot{\textbf{u}}_{\scriptscriptstyle \textrm{p}}$ are the solid velocities in each subphase $\Omega _{\alpha }$ and the matrix $\Omega _{\scriptscriptstyle \textrm{p}}$, respectively. The unit outward (i.e. pointing into the fluid domain $\Omega _{\textrm{f}}$) vectors normal to the interfaces $\Gamma _{\alpha }$ and $\Gamma _{\scriptscriptstyle \textrm{p}}$ are denoted by $\textbf{n}_{\alpha }$ and $\textbf{n}_{\scriptscriptstyle \textrm{p}}$, respectively.

Finally, we require continuity of stresses and displacements across the interface between each solid subphase and the matrix. We define this boundary as $\Gamma _{\alpha \scriptscriptstyle \textrm{p}} =\partial \Omega _{\alpha } \cap \partial \Omega _{\scriptscriptstyle \textrm{p}}$, so that

$$\begin{aligned} {\textsf{T}}_{\alpha }{} \textbf{n}_{ \alpha \scriptscriptstyle \textrm{p}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}\textbf{n}_{\alpha \scriptscriptstyle \textrm{p}}&\quad \text{ on }\quad \Gamma _{\alpha \scriptscriptstyle \textrm{p}}. \end{aligned}$$

(15a)

$$\begin{aligned} \textbf{u}_{\alpha }=\textbf{u}_{\scriptscriptstyle \textrm{p}}&\quad \text{ on }\quad \Gamma _{\alpha \scriptscriptstyle \textrm{p}}, \end{aligned}$$

(15b)

$\forall \, \alpha =1,...,N$, where $\textbf{n}_{ \alpha \scriptscriptstyle \textrm{p}}$ is the unit vector normal to the interface $\Gamma _{\alpha \scriptscriptstyle \textrm{p}}$ pointing into the inclusion $\Omega _{\alpha }$.

In the next section, we perform a multiscale analysis. This involves (i) non-dimensionalising the partial differential equations (PDEs) (2), (3), (8) and (10) as well as interface conditions (14a)–(15b) that we have described in this section, (ii) introducing two well-separated length scales, (iii) applying the asymptotic homogenisation technique to the resulting non-dimensional systems of PDEs and (iv) deriving the effective governing equations for the material as a whole.

3 Multiscale analysis

We now perform a multiscale analysis of the fluid–structure interaction problem introduced in the previous section, which is summarised below

$$\begin{aligned} \nabla \cdot {\textsf{T}}_{\alpha }=0&\quad \text{ in } \quad \Omega _{\alpha }, \end{aligned}$$

(16a)

$$\begin{aligned} \nabla \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{p}}=0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(16b)

$$\begin{aligned} \nabla \cdot {\textsf{T}}_{\textrm{f}}=0&\quad \text{ in } \quad \Omega _{\textrm{f}}, \end{aligned}$$

(16c)

$$\begin{aligned} \nabla \cdot \textbf{v}=0&\quad \text{ in } \quad \Omega _{\textrm{f}}, \end{aligned}$$

(16d)

$$\begin{aligned} \dot{\textbf{u}}_{\alpha }= \textbf{v}&\quad \text{ on }\quad \Gamma _{\alpha }, \end{aligned}$$

(16e)

$$\begin{aligned} \dot{\textbf{u}}_{\scriptscriptstyle \textrm{p}}= \textbf{v}&\quad \text{ on }\quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(16f)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}{} \textbf{n}_{\scriptscriptstyle \alpha }={\textsf{T}}_{\alpha }{} \textbf{n}_{\scriptscriptstyle \alpha }&\quad \text{ on }\quad \Gamma _{\alpha }, \end{aligned}$$

(16g)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}&\quad \text{ on }\quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(16h)

$$\begin{aligned} {\textsf{T}}_{\alpha }{} \textbf{n}_{\scriptscriptstyle \alpha \textrm{p}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}{} \textbf{n}_{\scriptscriptstyle \alpha \textrm{p}}&\quad \text{ on }\quad \Gamma _{\alpha \scriptscriptstyle \textrm{p}}, \end{aligned}$$

(16i)

$$\begin{aligned} \textbf{u}_{\alpha }=\textbf{u}_{\scriptscriptstyle \textrm{p}}&\quad \text{ on }\quad \Gamma _{\alpha \scriptscriptstyle \textrm{p}}, \end{aligned}$$

(16j)

where, by means of the stress relationships (6a), (6b) and (9), together with the incompressibility constraint (16d), the balance equations (16a), (16b) and (16c) can also be rewritten as

$$\begin{aligned} \nabla \cdot (\mathbb {C}^{\alpha } \xi ( \textbf{u}_{\alpha }))+\nabla \cdot \varvec{\sigma }_{\scriptscriptstyle {\textrm{0}\alpha }}=0&\quad \text{ in } \quad \Omega _{\alpha } \end{aligned}$$

(17a)

$$\begin{aligned} \nabla \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi ( \textbf{u}_{\scriptscriptstyle \textrm{p}}))+\nabla \cdot \varvec{\sigma }_{\scriptscriptstyle {\textrm{0p}}} =0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(17b)

$$\begin{aligned} \mu \nabla ^2\textbf{v}=\nabla p&\quad \text{ in } \quad \Omega _{\textrm{f}} , \end{aligned}$$

(17c)

$\forall \, \alpha =1,...,N$. The problem (16a–16j) is then to be closed by prescribing suitable external boundary conditions on $\partial \Omega$.

3.1 Non-dimensional form of the equations

Our system is multiscale in nature. In particular, we denote the average size of the whole domain $\Omega$ by L (the macroscale), while d refers to the porescale (the microscale), which here is assumed to be comparable with the distance between adjacent subphases interacting with the matrix and the fluid domain. In order to emphasise the difference between such scales, it is helpful to perform a non-dimensional analysis of the system of PDEs (16a–16j). We carry out the non-dimensional analysis by assuming that the system is characterised by a reference pressure gradient C and that the characteristic (reference) fluid velocity is given by the typical parabolic profile proportional to that of a Newtonian fluid slowly flowing in a cylinder of radius d.

Therefore, in our case we have

$$\begin{aligned} \begin{aligned} {\textbf{x}}&=L \mathbf {x^*},\quad \mathbb {C}^{\alpha }=CL\mathbb {C}^{\alpha *},\quad \mathbb {C}^{\scriptscriptstyle \textrm{p}}=CL\mathbb {C}^{\scriptscriptstyle \mathrm {p*}}, \\ \textbf{u}_{\alpha }&=L\textbf{u}_{\alpha }^*, \quad \textbf{u}_{\scriptscriptstyle \textrm{p}}=L\textbf{u}_{\scriptscriptstyle \textrm{p}}^*, \quad \textbf{v}=\frac{Cd^2}{\mu }{} \textbf{v}^*,\quad p=CLp^*. \end{aligned} \end{aligned}$$

(18)

We then exploit (18) and observe that

$$\begin{aligned} \nabla =\frac{1}{L}\nabla ^* \end{aligned}$$

(19)

to obtain the non-dimensional form of the system of PDEs (16a–16j), namely

$$\begin{aligned} \nabla \cdot {\textsf{T}}_{\alpha }=0&\quad \text{ in } \quad \Omega _{\alpha } \end{aligned}$$

(20a)

$$\begin{aligned} \nabla \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{p}}=0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(20b)

$$\begin{aligned} \nabla \cdot {\textsf{T}}_{\textrm{f}}=0&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(20c)

$$\begin{aligned} \nabla \cdot \textbf{v}=0&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(20d)

$$\begin{aligned} \dot{\textbf{u}}_{\alpha }= \textbf{v}&\quad \text{ on }\quad \Gamma _{\alpha } \end{aligned}$$

(20e)

$$\begin{aligned} \dot{\textbf{u}}_{\scriptscriptstyle \textrm{p}}= \textbf{v}&\quad \text{ on }\quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(20f)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}} \textbf{n}_{\scriptscriptstyle \alpha }={\textsf{T}}_{\alpha }{} \textbf{n}_{\scriptscriptstyle \alpha }&\quad \text{ on }\quad \Gamma _{\alpha } \end{aligned}$$

(20g)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}} \textbf{n}_{\scriptscriptstyle \textrm{p}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}&\quad \text{ on }\quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(20h)

$$\begin{aligned} {\textsf{T}}_{\alpha }{} \textbf{n}_{\scriptscriptstyle \alpha \textrm{p}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}{} \textbf{n}_{\scriptscriptstyle \alpha \textrm{p}}&\quad \text{ on }\quad \Gamma _{\alpha \scriptscriptstyle \textrm{p}} \end{aligned}$$

(20i)

$$\begin{aligned} \textbf{u}_{\alpha }=\textbf{u}_{\scriptscriptstyle \textrm{p}}&\quad \text{ on }\quad \Gamma _{\alpha \scriptscriptstyle \textrm{p}} \end{aligned}$$

(20j)

$\forall \, \alpha =1,...,N$, where we have dropped the $^*$ for the sake of simplicity of notation. The non-dimensionalised counterparts of the stress tensors (6a), (6b) and (9) are given by

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}=-p{\textsf{I}}+\epsilon ^2 (\nabla \textbf{v}+(\nabla \textbf{v})^{\mathrm T})&\end{aligned}$$

(21a)

$$\begin{aligned} {\textsf{T}}_{\alpha }=\mathbb {C}^{\alpha }\xi (\textbf{u}_{\alpha })+\varvec{\sigma }_{\scriptscriptstyle {\textrm{0}\alpha }}&\end{aligned}$$

(21b)

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}=\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi (\textbf{u}_{\scriptscriptstyle \textrm{p}})+\varvec{\sigma }_{\scriptscriptstyle {\textrm{0p}}}&, \end{aligned}$$

(21c)

so that the balance equations (20a–20c) rewrite

$$\begin{aligned} \epsilon ^2 \nabla ^2\textbf{v}=\nabla p&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(22a)

$$\begin{aligned} \nabla \cdot (\mathbb {C}^{\alpha } \xi (\textbf{u}_{\alpha }))+\nabla \cdot \varvec{\sigma }_{\scriptscriptstyle {\textrm{0}\alpha }}=0&\quad \text{ in } \quad \Omega _{\alpha } \end{aligned}$$

(22b)

$$\begin{aligned} \nabla \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi (\textbf{u}_{\scriptscriptstyle \textrm{p}}))+\nabla \cdot \varvec{\sigma }_{\scriptscriptstyle {\textrm{0p}}}=0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} , \end{aligned}$$

(22c)

where

$$\begin{aligned} \epsilon =\frac{d}{L}. \end{aligned}$$

(23)

In the next section, we introduce the asymptotic homogenisation technique which is used to upscale the non-dimensional system of PDEs (20a–20j) by formally assuming that the microscale and the macroscale are well separated.

3.2 The asymptotic homogenisation technique

In this section, we introduce the two-scale asymptotic homogenisation technique which is used to derive a macroscale model for the equations (20a−20j). We first assume that the characteristic length of the microscale, denoted by d, and representing the length scale at which the pores and the individual inclusions/fibres are clearly resolved, is small compared to average size of the domain L, i.e.

$$\begin{aligned} \epsilon \ll 1. \end{aligned}$$

(24)

We then introduce a local spatial variable to capture microscale variations of the field via setting

$$\begin{aligned} \textbf{y}=\frac{\textbf{x}}{\epsilon }. \end{aligned}$$

(25)

The spatial variables $\textbf{x}$ and $\textbf{y}$ are to be considered formally independent and represent the macroscale and the microscale, respectively. The gradient operator then transforms as

$$\begin{aligned} \nabla \mapsto \nabla _\textbf{x}+\frac{1}{\epsilon }\nabla _\textbf{y}, \end{aligned}$$

(26)

with the symmetric part of the gradient operator transforming as

$$\begin{aligned} \xi \mapsto \xi _\textbf{x}+\frac{1}{\epsilon }\xi _\textbf{y}. \end{aligned}$$

(27)

We further assume that all the fields $\textbf{u}_{\scriptscriptstyle \textrm{p}}, \textbf{u}_{\alpha }, \textbf{v}, p, {\textsf{T}}_{\textrm{f}}, {\textsf{T}}_{\alpha }, {\textsf{T}}_{\scriptscriptstyle \textrm{p}}$, $\varvec{\sigma }_{\scriptscriptstyle {\textrm{0}\alpha }}$ and $\varvec{\sigma }_{\scriptscriptstyle {\textrm{0p}}}$ as well as the elasticity tensors $\mathbb {C}^{\scriptscriptstyle \textrm{p}}$ and $\mathbb {C}^{\alpha }$, $\forall \, \alpha =1,...,N$, are functions of both $\textbf{x}$ and $\textbf{y}$. We also assume that the fields $\textbf{u}_{\scriptscriptstyle \textrm{p}}, \textbf{u}_{\alpha }, \textbf{v}, p, {\textsf{T}}_{\textrm{f}}, {\textsf{T}}_{\alpha }, {\textsf{T}}_{\scriptscriptstyle \textrm{p}}$, $\varvec{\sigma }_{\scriptscriptstyle {\textrm{0}\alpha }}$ and $\varvec{\sigma }_{\scriptscriptstyle {\textrm{0p}}}$ can be represented in terms of a series expansion in powers of $\epsilon$, i.e.

$$\begin{aligned} \varphi ^{\epsilon }(\textbf{x,y},t)=\sum _{l=0}^\infty \varphi ^{(l)}(\textbf{x,y},t)\epsilon ^l, \end{aligned}$$

(28)

where $\varphi$ collectively denotes each field involved in the present analysis.

Remark 2

(Porescale Periodicity) In order to carry out the analysis of the microstructure, we wish to focus on a single periodic cell. To do this, we make the assumption that every field $\varphi ^{(l)}$ in our present analysis is $\textbf{y}$-periodic. This assumption allows for the microscale differential problems that arise from the asymptotic homogenisation technique to be solved on a finite subset (periodic cell) of the domain.

However, the assumption that all fields are $\textbf{y}$-periodic is not necessary to continue with the analysis. We instead could proceed by assuming local boundedness of fields only. This approach means we are only able to determine the functional form of the macroscale model. The coefficients obtained by assuming local boundedness are related to microscale problems which are to be solved on the whole microstructure of the material. This is virtually impossible if not prohibitive computationally. Some examples where the assumption of local boundedness is made are found in [21, 42].

Remark 3

(Macroscopic Uniformity) The microscale geometry of a given material can vary with respect to individual points on the macroscale. Such variation of the microstructure has been considered in the following [21, 24, 43,44,45] and results in the presence of additional terms in the final macroscale model by proper application of the Reynolds transport theorem. To simplify the derivation of the model, this dependence of the microstructure on the macroscale point is generally neglected. That is, we assume that at every macroscale point the microscale will be the same. This is equivalent to say that the microscale geometry does not depend on $\textbf{x}$. We call this property macroscopic uniformity. We make this assumption here. We therefore have the following result for differentiation under the integral sign

$$\begin{aligned} \int _{\Omega }\nabla _\textbf{x} \cdot (\bullet )\text{ d }\textbf{y}=\nabla _\textbf{x}\cdot \int _{\Omega }(\bullet )\text{ d }{} \textbf{y}, \end{aligned}$$

(29)

where $(\bullet )$ is a tensor or a vector quantity.

Remark 4

(Porescale geometry) For clarity of presentation and without loss of generality with respect to the properties of the model, we can restrict our analysis by assuming that only one subphase is contained in each periodic cell, as shown in Fig. 2. The model can be easily extended to a number of subphases within the periodic cell if necessary for a particular application. Therefore, the index $\alpha$ is no longer needed and we adjust the notation accordingly. We identify the domain $\Omega$ with its corresponding periodic cell, with fibre/inclusion, matrix and fluid cell portions denoted by $\Omega _{\scriptscriptstyle \textrm{c}}$, $\Omega _{\scriptscriptstyle \textrm{p}}$ and $\Omega _{\textrm{f}}$, respectively. The interfaces between the different phases are then denoted by $\Gamma _{\scriptscriptstyle \textrm{c}} =\partial \Omega _{\scriptscriptstyle \textrm{c}}\cap \partial \Omega _{\textrm{f}}$, $\Gamma _{\scriptscriptstyle \textrm{p}} =\partial \Omega _{\scriptscriptstyle \textrm{p}} \cap \partial \Omega _{\textrm{f}}$ and $\Gamma _{\scriptscriptstyle \textrm{cp}} =\partial \Omega _{\scriptscriptstyle \textrm{c}}\cap \partial \Omega _{\scriptscriptstyle \textrm{p}}$, with corresponding unit normal vectors ${\textbf{n}}_{\scriptscriptstyle \textrm{c}}$, ${\textbf{n}}_{\scriptscriptstyle \textrm{p}}$ and ${\textbf{n}}_{\scriptscriptstyle \textrm{cp}}$.

Fig. 2

A sketch of a 2D cross section of the periodic cell which we focus on. We have one subphase/fibre shown in orange that is in contact with the matrix shown in pink and the fluid shown in blue. We also highlight the interfaces $\Gamma _{\scriptscriptstyle \textrm{c}}$, $\Gamma _{\scriptscriptstyle \textrm{p}}$ and $\Gamma _{\scriptscriptstyle \textrm{cp}}$ among the phases

3.3 Derivation of the macroscale model

We apply the asymptotic homogenisation assumptions (26) and (28) to equations (20a–22c) to obtain, accounting for periodicity, the following multiscale system of PDEs

$$\begin{aligned} \nabla _\textbf{y} \cdot {{\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{\epsilon }}+\epsilon \nabla _\textbf{x} \cdot {{\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{\epsilon }}=0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(30a)

$$\begin{aligned} \nabla _\textbf{y} \cdot {{\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{\epsilon }}+\epsilon \nabla _\textbf{x} \cdot {{\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{\epsilon }}=0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(30b)

$$\begin{aligned} \nabla _\textbf{y} \cdot {{\textsf{T}}_{\textrm{f}}^{\epsilon }}+\epsilon \nabla _\textbf{x} \cdot {{\textsf{T}}_{\textrm{f}}^{\epsilon }}=0&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(30c)

$$\begin{aligned} \nabla _\textbf{y} \cdot \mathbf{v^{\epsilon }}+\epsilon \nabla _\textbf{x} \cdot \mathbf{v^{\epsilon }}=0&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(30d)

$$\begin{aligned} \dot{\textbf{u}}_{\scriptscriptstyle \textrm{c}}^{\epsilon }= \mathbf{v^{\epsilon }}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(30e)

$$\begin{aligned} \dot{\textbf{u}}_{\scriptscriptstyle \textrm{p}}^{\epsilon }= \mathbf{v^{\epsilon }}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(30f)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}^{\epsilon }{} \textbf{n}_{\scriptscriptstyle \textrm{c}}={\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{\epsilon }{} \textbf{n}_{\scriptscriptstyle \textrm{c}}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(30g)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}^{\epsilon }{} \textbf{n}_{\scriptscriptstyle \textrm{p}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{\epsilon }{} \textbf{n}_{\scriptscriptstyle \textrm{p}}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(30h)

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{\epsilon }{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{\epsilon }{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(30i)

$$\begin{aligned} \textbf{u}_{\scriptscriptstyle \textrm{c}}^{\epsilon }=\textbf{u}_{\scriptscriptstyle \textrm{p}}^{\epsilon }&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(30j)

equipped with multiscale expressions for ${\textsf{T}}_{\textrm{f}}^{\epsilon }$, ${\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{\epsilon }$, ${\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{\epsilon }$, given by

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}^{\epsilon }=-p^{\epsilon }{\textsf{I}}+\epsilon (\nabla _\textbf{y}{} \mathbf{v^{\epsilon }}+(\nabla _\textbf{y}{} \mathbf{v^{\epsilon }})^{\mathrm T})+\epsilon ^2(\nabla _\textbf{x}{} \mathbf{v^{\epsilon }}+(\nabla _\textbf{x}{} \mathbf{v^{\epsilon }})^{\mathrm T})&\end{aligned}$$

(31a)

$$\begin{aligned} \epsilon {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{\epsilon }=\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _y(\textbf{u}_{\scriptscriptstyle \textrm{c}}^{\epsilon })+\epsilon \mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _x(\textbf{u}_{\scriptscriptstyle \textrm{c}}^{\epsilon })+\epsilon \varvec{\sigma }_{\scriptscriptstyle {\textrm{0c}}}^{\epsilon }&\end{aligned}$$

(31b)

$$\begin{aligned} \epsilon {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{\epsilon }=\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _y(\textbf{u}_{\scriptscriptstyle \textrm{p}}^{\epsilon })+\epsilon \mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _x(\textbf{u}_{\scriptscriptstyle \textrm{p}}^{\epsilon })+\epsilon \varvec{\sigma }_{\scriptscriptstyle {\textrm{0p}}}^{\epsilon },&\end{aligned}$$

(31c)

while the balance equations in terms of $\textbf{u}^{\epsilon }_{\scriptscriptstyle \textrm{p}}$, $\textbf{u}^{\epsilon }_{\scriptscriptstyle \textrm{c}}$, $\textbf{v}^{\epsilon }$, $p^{\epsilon }$ read

$$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y( \textbf{u}_{\scriptscriptstyle \textrm{c}}^{\epsilon }))+\epsilon \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _x (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{\epsilon }))+\epsilon \nabla _\textbf{y}\cdot \varvec{\sigma }_{\scriptscriptstyle {\textrm{0c}}}^{\epsilon }+\epsilon \nabla _\textbf{x} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{\epsilon }))\nonumber \\&\qquad + \epsilon ^2\nabla _\textbf{x} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _x (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{\epsilon }))+\epsilon ^2\nabla _\textbf{x}\cdot \varvec{\sigma }_{\scriptscriptstyle {\textrm{0c}}}^{\epsilon }=0\qquad \qquad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(32a)

$$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{\epsilon }))+\epsilon \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _x (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{\epsilon }))+\epsilon \nabla _\textbf{y}\cdot \varvec{\sigma }_{\scriptscriptstyle {\textrm{0p}}}^{\epsilon }+\epsilon \nabla _\textbf{x} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{\epsilon }))\nonumber \\&\qquad + \epsilon ^2\nabla _\textbf{x} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _x (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{\epsilon }))+\epsilon ^2\nabla _\textbf{x}\cdot \varvec{\sigma }_{\scriptscriptstyle {\textrm{0p}}}^{\epsilon }=0\qquad \qquad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(32b)

$$\begin{aligned}&\epsilon ^3 \nabla _\textbf{x}^2\textbf{v}^{\epsilon }+\epsilon ^2 \nabla _\textbf{x} \cdot (\nabla _\textbf{y} \textbf{v}^{\epsilon })+\epsilon ^2\nabla _\textbf{y} \cdot (\nabla _\textbf{x} \textbf{v}^{\epsilon })+\epsilon \nabla _\textbf{y}^2\textbf{v}^{\epsilon }\nonumber \\&\quad =\nabla _\textbf{y} p^{\epsilon }+\epsilon \nabla _\textbf{x} p^{\epsilon } \qquad \qquad \qquad \qquad \qquad \quad \qquad \text{ in } \quad \Omega _{\textrm{f}}. \end{aligned}$$

(32c)

We can now substitute power series of the type (28) into the relevant fields in (30a−32c). Then by equating the coefficients of $\epsilon ^l$ for $l=0,1,...$ we derive the macroscale model for the material in terms of the relevant leading (zeroth)-order fields. Whenever a component in the asymptotic expansion retains a dependence on the microscale, we can take the integral average, which we define as

$$\begin{aligned} \langle \varphi \rangle _i:=\frac{1}{|\Omega |}\int _{\Omega _i}\varphi (\textbf{x,y},t)\text{ d }{} \textbf{y} \quad i=\textrm{f}, \textrm{c}, \textrm{p} \end{aligned}$$

(33)

where the integral average can be performed over one representative cell due to ${\textbf{y}}$-periodicity and $|\Omega |$ is the volume of the domain and the integration is performed over the microscale. We note that $|\Omega |:=|\Omega _{\textrm{f}}|+|\Omega _{\scriptscriptstyle \textrm{c}}|+|\Omega _{\scriptscriptstyle \textrm{p}}|$. Due to the assumption of $\textbf{y}$-periodicity, the integral average can be performed over one representative cell. Therefore, (33) represents a cell average. For the sake of brevity, we also introduce the notation

$$\begin{aligned} \langle \varphi _{\scriptscriptstyle \textrm{c}}+\varphi _{\scriptscriptstyle \textrm{p}}\rangle _s:=\frac{1}{|\Omega |}\left( \int _{\Omega _{\scriptscriptstyle \textrm{c}}}\varphi _{\scriptscriptstyle \textrm{c}}(\textbf{x,y},t)\text{ d }{} \textbf{y} +\int _{\Omega _{\scriptscriptstyle \textrm{p}}}\varphi _{\scriptscriptstyle \textrm{p}}(\textbf{x,y},t)\text{ d }{} \textbf{y} \right) , \end{aligned}$$

(34)

for fields $\varphi$ with restrictions $\varphi _{\scriptscriptstyle \textrm{c}}$ and $\varphi _{\scriptscriptstyle \textrm{p}}$ defined in the solid cell portions $\Omega _{\scriptscriptstyle \textrm{c}}$ or $\Omega _{\scriptscriptstyle \textrm{p}}$, respectively.

Equating coefficients of $\epsilon ^0$ in (30a−30j), we obtain

$$\begin{aligned} \nabla _\textbf{y} \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}=0&\qquad \qquad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(35a)

$$\begin{aligned} \nabla _\textbf{y} \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}=0&\qquad \qquad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(35b)

$$\begin{aligned} \nabla _\textbf{y} \cdot {\textsf{T}}_{\textrm{f}}^{(0)}=0&\qquad \qquad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(35c)

$$\begin{aligned} \nabla _\textbf{y} \cdot \textbf{v}^{(0)}=0&\qquad \qquad \text{ in }\quad \Omega _{\textrm{f}} \end{aligned}$$

(35d)

$$\begin{aligned} \dot{\textbf{u}}_{\scriptscriptstyle \textrm{c}}^{(0)}= \textbf{v}^{(0)}&\qquad \qquad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(35e)

$$\begin{aligned} \dot{\textbf{u}}_{\scriptscriptstyle \textrm{p}}^{(0)}= \textbf{v}^{(0)}&\qquad \qquad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(35f)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}^{(0)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}={\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}&\qquad \qquad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(35g)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}^{(0)}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}&\qquad \qquad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(35h)

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \qquad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(35i)

$$\begin{aligned} \textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)}=\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)}&\qquad \qquad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(35j)

and the stress equations (31a−31c) for ${\textsf{T}}_{\textrm{f}}^{\epsilon }$, ${\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{\epsilon }$, ${\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{\epsilon }$ have coefficients of $\epsilon ^0$

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}^{(0)}=-p^{(0)}{\textsf{I}}&\qquad \qquad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(36a)

$$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _y(\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)})=0&\qquad \qquad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(36b)

$$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _y(\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)})=0&\qquad \qquad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(36c)

while the balance equations (32a−32c) have coefficients of $\epsilon ^0$

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)}))=0&\qquad \qquad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(37a)

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y( \textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)}))=0&\qquad \qquad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(37b)

$$\begin{aligned} \nabla _\textbf{y} p^{(0)}=0&\qquad \qquad \text{ in }\quad \Omega _{\textrm{f}}. \end{aligned}$$

(37c)

Similarly we now wish to equate the coefficients of $\epsilon ^1$ in equations (30a–30j), which gives

$$\begin{aligned} \nabla _\textbf{y} \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(1)}+\nabla _\textbf{x} \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}=0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(38a)

$$\begin{aligned} \nabla _\textbf{y} \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(1)}+\nabla _\textbf{x} \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}=0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(38b)

$$\begin{aligned} \nabla _\textbf{y} \cdot {\textsf{T}}_{\textrm{f}}^{(1)}+\nabla _\textbf{x} \cdot {\textsf{T}}_{\textrm{f}}^{(0)}=0&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(38c)

$$\begin{aligned} \nabla _\textbf{y} \cdot \textbf{v}^{(1)}+\nabla _\textbf{x} \cdot \textbf{v}^{(0)}=0&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(38d)

$$\begin{aligned} \dot{\textbf{u}}_{\scriptscriptstyle \textrm{c}}^{(1)}= \textbf{v}^{(1)}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(38e)

$$\begin{aligned} \dot{\textbf{u}}_{\scriptscriptstyle \textrm{p}}^{(1)}= \textbf{v}^{(1)}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(38f)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}={\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(38g)

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(38h)

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}={\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(38i)

$$\begin{aligned} \textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}=\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(38j)

and the stress equations (31a−31c) for ${\textsf{T}}_{\textrm{f}}^{\epsilon }$, ${\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{\epsilon }$, ${\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{\epsilon }$ have coefficients of $\epsilon ^1$

$$\begin{aligned} {\textsf{T}}_{\textrm{f}}^{(1)}=-p^{(1)}{\textsf{I}}+(\nabla _\textbf{y}{} \textbf{v}^{(0)}+(\nabla _\textbf{y}{} \textbf{v}^{(0)})^{\mathrm T})&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

(39a)

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}=\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _y(\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)})+\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _x(\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)})+\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(39b)

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}=\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _y(\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)})+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _x(\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)})+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(39c)

while the balance equations (32a−32c) have coefficients of $\epsilon ^1$

$$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}))+\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _x (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)}))+\nabla _\textbf{x} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)}))\nonumber \\&\quad +\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}=0\qquad ~~ \text{ in } ~~ \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(40a)

$$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}))+\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _x (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)}))+\nabla _\textbf{x} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)}))\nonumber \\&\quad +\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}=0\qquad ~~ \text{ in } ~~ \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(40b)

$$\begin{aligned}&\nabla _\textbf{y}^2\textbf{v}^{(0)}=\nabla _\textbf{y} p^{(1)}+\nabla _\textbf{x} p^{(0)} \qquad ~~ \text{ in } ~~ \Omega _{\textrm{f}}. \end{aligned}$$

(40c)

We can now see from (35c) and (36a) that $p^{(0)}$ does not depend on the microscale variable $\textbf{y}$. That is,

$$\begin{aligned} p^{(0)}=p^{(0)}(\textbf{x},t). \end{aligned}$$

(41)

From (36b) and (36c) and the periodicity conditions, we also have that ${\textbf{u}}_{\scriptscriptstyle \textrm{c}}^{(0)}$ and ${\textbf{u}}_{\scriptscriptstyle \textrm{p}}^{(0)}$ are independent of the microscale variable ${\textbf{y}}$, although they do still depend, in general, on the macroscale variable ${\textbf{x}}$ and time t, see [21, 23]. That is,

$$\begin{aligned} \textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)}&=\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)}(\textbf{x},t) \end{aligned}$$

(42a)

$$\begin{aligned} \textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)}&=\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)}(\textbf{x},t). \end{aligned}$$

(42b)

Since we have the boundary condition $\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)}=\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)}$ on $\Gamma _{\scriptscriptstyle \textrm{cp}}$, we can define

$$\begin{aligned} \textbf{u}^{(0)}=\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)}=\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)}, \end{aligned}$$

(43)

which we will use throughout the following sections.

3.4 Fluid flow on the macroscale

We now wish to investigate the leading order of the velocity which we denoted $\textbf{v}^{(0)}$. We can define the relative fluid–solid displacement, ${\textbf{w}}$, by

$$\begin{aligned} {\textbf{w}}(\textbf{x}, \textbf{y}, t)=\textbf{v}^{(0)}(\textbf{x}, \textbf{y}, t)-\dot{\textbf{u}}^{(0)}(\textbf{x}, t). \end{aligned}$$

(44)

Using equations (36a), (35e), (35f), (38c) and (39a), exploiting notation (43), we have a boundary value problem of Stokes’ type, which is given by

$$\begin{aligned} \nabla _\textbf{y}^2\textbf{w}-\nabla _\textbf{y}p^{(1)}-\nabla _\textbf{x}p^{(0)}=\textbf{0},&\qquad \quad \text{ in } \quad \Omega _{\textrm{f}}, \end{aligned}$$

(45a)

$$\begin{aligned} \nabla _\textbf{y} \cdot {\textbf{w}}={ 0},&\qquad \quad \text{ in } \quad \Omega _{\textrm{f}}, \end{aligned}$$

(45b)

$$\begin{aligned} {\textbf{w}}=\textbf{0},&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

(45c)

Now exploiting linearity and using (41), we can propose the following ansatz for the Stokes-type boundary value problem (45a–45c),

$$\begin{aligned} {\textbf{w}}= & {} -{\textsf{W}}\nabla _\textbf{x} p^{(0)}, \end{aligned}$$

(46)

$$\begin{aligned} p^{(1)}= & {} -\textbf{P}\nabla _\textbf{x} p^{(0)}+c(\textbf{x}), \end{aligned}$$

(47)

where $p^{(1)}$ is defined up to an arbitrary $\textbf{y}$-constant function. Equation (47) is the solution to the problem (45a−45c) provided that second-rank tensor ${\textsf{W}}$ and vector $\textbf{P}$ satisfy the following cell problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \nabla _\textbf{y}^2 {\textsf{W}}^{\mathrm T}-\nabla _\textbf{y} \textbf{P} +{\textsf{I}}={\textsf{0}}&{} \quad \text{ in } \quad \Omega _{\textrm{f}}\\ \nabla _\textbf{y} \cdot {\textsf{W}}^{\mathrm T}=\textbf{0}&{} \quad \text{ in } \quad \Omega _{\textrm{f}}\\ {\textsf{W}}^{\mathrm T}={\textsf{0}}&{} \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned} \end{array}\right. } \end{aligned}$$

(48)

where periodic conditions apply on the boundary $\partial \Omega _{\textrm{f}}\backslash \Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{p}}$ and a further condition is to be placed on $\textbf{P}$ for the solution to be unique (for example zero average on the fluid cell portion). Taking the integral average of (46) over the fluid domain leads to

$$\begin{aligned} \langle \textbf{w}\rangle _{\textrm{f}}=-\langle {\textsf{W}}\rangle _{\textrm{f}}\nabla _\textbf{x}p^{(0)}, \end{aligned}$$

(49)

meaning that the fluid flow is described by Darcy’s law in the macroscale.

3.5 Poroelasticity on the macroscale

We now require the macroscale equations for the elastic displacement $\textbf{u}^{(0)}$ and $p^{(0)}$. Summing up the integral averages of Eqs. (38a), (38b) and (38c), we have

$$\begin{aligned}&\int _{\Omega _{\scriptscriptstyle \textrm{c}}} \nabla _\textbf{y}\cdot {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(1)}\text{ d }\textbf{y} +\int _{\Omega _{\scriptscriptstyle \textrm{p}}} \nabla _\textbf{y}\cdot {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(1)}\text{ d }\textbf{y} + \int _{\Omega _{\textrm{f}}}\nabla _\textbf{y}\cdot {\textsf{T}}_{\textrm{f}}^{(1)}\text{ d }{} \textbf{y} ~\nonumber \\&\quad +\int _{\Omega _{\scriptscriptstyle \textrm{c}}} \nabla _\textbf{x} \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}\text{ d }{} \textbf{y} + \int _{\Omega _{\scriptscriptstyle \textrm{p}}} \nabla _\textbf{x} \cdot {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}\text{ d }{} \textbf{y} + \int _{\Omega _{\textrm{f}}} \nabla _\textbf{x}\cdot {\textsf{T}}_{\textrm{f}}^{(0)}\text{ d }{} \textbf{y} =0. \end{aligned}$$

(50)

Applying the divergence theorem to the first three integrals and rearranging the last three integrals using macroscopic uniformity, we obtain

$$\begin{aligned}&\int _{\partial \Omega _{\scriptscriptstyle \textrm{c}}\setminus {\Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{cp}}}} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(1)}{} \textbf{n}_{\Omega _{\scriptscriptstyle \textrm{c}}\setminus {\Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{cp}}}}\textrm{dS }+\int _{\Gamma _{\scriptscriptstyle \textrm{c}}} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}\textrm{dS } -\int _{\Gamma _{\scriptscriptstyle \textrm{cp}}} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}\textrm{dS }~ \nonumber \\&\quad +\int _{\partial \Omega _{\scriptscriptstyle \textrm{p}}\setminus {\Gamma _{\scriptscriptstyle \textrm{p}}}\cup \Gamma _{\scriptscriptstyle \textrm{cp}}} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(1)}{} \textbf{n}_{\Omega _{\scriptscriptstyle \textrm{p}}\setminus {\Gamma _{\scriptscriptstyle \textrm{p}}}\cup \Gamma _{\scriptscriptstyle \textrm{cp}}}\textrm{dS } +\int _{\Gamma _{\scriptscriptstyle \textrm{p}}} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}\textrm{dS }+\int _{\Gamma _{\scriptscriptstyle \textrm{cp}}} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}\textrm{dS }~\nonumber \\&\quad +\int _{\partial \Omega _{\textrm{f}}\setminus \Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{p}}} {\textsf{T}}_{\textrm{f}}^{(1)}{} \textbf{n}_{\Omega _{\textrm{f}}\setminus \Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{p}}}\textrm{dS} -\int _{{\Gamma }_{\scriptscriptstyle \textrm{p}}} {\textsf{T}}_{\textrm{f}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}\textrm{dS} -\int _{{\Gamma }_{\scriptscriptstyle \textrm{c}}} {\textsf{T}}_{\textrm{f}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}\textrm{dS}~\nonumber \\&\quad + \nabla _\textbf{x} \cdot \int _{\Omega _{\scriptscriptstyle \textrm{c}}} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}\text{ d }{} \textbf{y} +\nabla _\textbf{x} \cdot \int _{\Omega _{\scriptscriptstyle \textrm{p}}} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}\text{ d }{} \textbf{y} + \nabla _\textbf{x}\cdot \int _{\Omega _{\textrm{f}}} {\textsf{T}}_{\textrm{f}}^{(0)}\text{ d }{} \textbf{y} =0, \end{aligned}$$

(51)

where $\textbf{n}_{\scriptscriptstyle \textrm{c}}$, $\textbf{n}_{\scriptscriptstyle \textrm{p}}$, $\textbf{n}_{\scriptscriptstyle \textrm{cp}}$, $\textbf{n}_{\Omega _{\scriptscriptstyle \textrm{c}}{\setminus }{\Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{cp}}}}$, $\textbf{n}_{\Omega _{\scriptscriptstyle \textrm{p}}{\setminus }{\Gamma _{\scriptscriptstyle \textrm{p}}\cup \Gamma _{\scriptscriptstyle \textrm{cp}}}}$ and $\textbf{n}_{\Omega _{\textrm{f}}{\setminus }{\Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{p}}}}$ are the unit normals corresponding to $\Gamma _{\scriptscriptstyle \textrm{c}}$, $\Gamma _{\scriptscriptstyle \textrm{p}}$, $\Gamma _{\scriptscriptstyle \textrm{cp}}$, $\partial \Omega _{\scriptscriptstyle \textrm{c}}{\setminus }\Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{cp}}$, $\partial \Omega _{\scriptscriptstyle \textrm{p}}{\setminus }\Gamma _{\scriptscriptstyle \textrm{p}}\cup \Gamma _{\scriptscriptstyle \textrm{cp}}$ and $\partial \Omega _{\textrm{f}}{\setminus }\Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{p}}$. Since the contributions over the external boundaries of $\Omega _{\scriptscriptstyle \textrm{c}}$, $\Omega _{\scriptscriptstyle \textrm{p}}$ and $\Omega _{\textrm{f}}$ cancel out due to $\textbf{y}$-periodicity, Equation (51) becomes

$$\begin{aligned}&\int _{\Gamma _{\scriptscriptstyle \textrm{c}}} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}\text{ dS } +\int _{\Gamma _{\scriptscriptstyle \textrm{p}}} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{p}}\text{ dS }- \int _{\Gamma _{\scriptscriptstyle \textrm{c}}} {\textsf{T}}_{\textrm{f}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}} \text{ dS }~\nonumber \\&\quad -\int _{\Gamma _{\scriptscriptstyle \textrm{p}}}{\textsf{T}}_{\textrm{f}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{p}} \text{ dS }-\int _{\Gamma _{\scriptscriptstyle \textrm{cp}}} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}\textrm{dS }+\int _{\Gamma _{\scriptscriptstyle \textrm{cp}}} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(1)}{} \textbf{n}_{\scriptscriptstyle \textrm{cp}}\textrm{dS }~\nonumber \\&\quad + \nabla _\textbf{x} \cdot \int _{\Omega _{\textrm{I}}} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}\text{ d }{} \textbf{y} +\nabla _\textbf{x} \cdot \int _{\Omega _{\scriptscriptstyle \textrm{p}}} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}\text{ d }{} \textbf{y} +\nabla _\textbf{x}\cdot \int _{\Omega _{\textrm{f}}} {\textsf{T}}_{\textrm{f}}^{(0)}\text{ d }{} \textbf{y} =0. \end{aligned}$$

(52)

The first six integrals in (52) cancel out due to (38g), (38h) and (38i), and the final three terms can be written as

$$\begin{aligned} \nabla _\textbf{x} \cdot \langle {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}+ {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}\rangle _s -\phi \nabla _\textbf{x} p^{(0)}=0, \end{aligned}$$

(53)

where $\phi =|\Omega _{\textrm{f}}|/|\Omega |$ is the porosity of the material.

By exploiting (41) and (43), and using (35a), (35b), (35g), (35h), (35i), (36a), (38j), (39b) and (39c), we can write the following problem for $\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(0)}$ and $\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(0)}$

$$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}))+ \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _x (\textbf{u}^{(0)}))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}=0 \quad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(54a)

$$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}))+ \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _x (\textbf{u}^{(0)}))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}=0 \quad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(54b)

$$\begin{aligned}&\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)})\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)})\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\mathbb {C}^{\scriptscriptstyle \textrm{p}}-\mathbb {C}^{\scriptscriptstyle \textrm{c}})\xi _x (\textbf{u}^{(0)})\textbf{n}_{\scriptscriptstyle \textrm{cp}}\nonumber \\&\quad +( \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}- \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)})\textbf{n}_{\scriptscriptstyle \textrm{cp}}~~ \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(54c)

$$\begin{aligned}&\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}=\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}~~ \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(54d)

$$\begin{aligned}&(\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)})+\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _x (\textbf{u}^{(0)})+\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)})\textbf{n}_{\scriptscriptstyle \textrm{c}}=-p^{(0)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(54e)

$$\begin{aligned}&(\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)})+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _x (\textbf{u}^{(0)})+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)})\textbf{n}_{\scriptscriptstyle \textrm{p}}=-p^{(0)}\textbf{n}_{\scriptscriptstyle \textrm{p}}\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

(54f)

The solution to the problem given by (54a−54f), exploiting linearity is given as

$$\begin{aligned}&\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}={\mathcal {A}}^{\scriptscriptstyle \textrm{c}} \xi _x (\textbf{u}^{(0)})+\textbf{a}^{\scriptscriptstyle \textrm{c}}p^{(0)}+\textbf{b}^{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(55)

$$\begin{aligned}&\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}={\mathcal {A}}^{\scriptscriptstyle \textrm{p}} \xi _x (\textbf{u}^{(0)})+\textbf{a}^{\scriptscriptstyle \textrm{p}}p^{(0)}+\textbf{b}^{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(56)

where ${\mathcal {A}}^{\scriptscriptstyle \textrm{c}}$ and ${\mathcal {A}}^{\scriptscriptstyle \textrm{p}}$ are third-rank tensors and $\textbf{a}^{\scriptscriptstyle \textrm{c}}$, $\textbf{a}^{\scriptscriptstyle \textrm{p}}$, $\textbf{b}^{\scriptscriptstyle \textrm{c}}$ and $\textbf{b}^{\scriptscriptstyle \textrm{p}}$ are vectors. The auxiliary fields ${\mathcal {A}}^{\scriptscriptstyle \textrm{c}}$, ${\mathcal {A}}^{\scriptscriptstyle \textrm{p}}$, $\textbf{a}^{\scriptscriptstyle \textrm{c}}$, $\textbf{a}^{\scriptscriptstyle \textrm{p}}$, $\textbf{b}^{\scriptscriptstyle \textrm{c}}$ and $\textbf{b}^{\scriptscriptstyle \textrm{p}}$ solve the following cell problems

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{c}}))+\nabla _\textbf{y} \cdot \mathbb {C}^{\scriptscriptstyle \textrm{c}}=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(57a)

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{p}}))+\nabla _\textbf{y} \cdot \mathbb {C}^{\scriptscriptstyle \textrm{p}}=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(57b)

$$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{c}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{p}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\mathbb {C}^{\scriptscriptstyle \textrm{p}}-\mathbb {C}^{\scriptscriptstyle \textrm{c}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(57c)

$$\begin{aligned} {\mathcal {A}}^{\scriptscriptstyle \textrm{c}}={\mathcal {A}}^{\scriptscriptstyle \textrm{p}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(57d)

$$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{c}}))\textbf{n}_{\scriptscriptstyle \textrm{c}}+ \mathbb {C}^{\scriptscriptstyle \textrm{c}}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(57e)

$$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y({\mathcal {A}}^{\scriptscriptstyle \textrm{p}}))\textbf{n}_{\scriptscriptstyle \textrm{p}}+ \mathbb {C}^{\scriptscriptstyle \textrm{p}}\textbf{n}_{\scriptscriptstyle \textrm{p}}=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(57f)

and

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{c}}))=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(58a)

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{p}}))=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(58b)

$$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{c}}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y( \textbf{a}^{\scriptscriptstyle \textrm{p}}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(58c)

$$\begin{aligned} \textbf{a}^{\scriptscriptstyle \textrm{c}}=\textbf{a}^{\scriptscriptstyle \textrm{p}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(58d)

$$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{c}}))\textbf{n}_{\scriptscriptstyle \textrm{c}}+ \textbf{n}_{\scriptscriptstyle \textrm{c}}=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(58e)

$$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{p}}))\textbf{n}_{\scriptscriptstyle \textrm{p}}+ \textbf{n}_{\scriptscriptstyle \textrm{p}}=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(58f)

and

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{b}^{\scriptscriptstyle \textrm{c}}))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(59a)

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{b}^{\scriptscriptstyle \textrm{p}}))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

(59b)

$$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{b}^{\scriptscriptstyle \textrm{c}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{b}^{\scriptscriptstyle \textrm{p}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}-\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)})\textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(59c)

$$\begin{aligned} \textbf{b}^{\scriptscriptstyle \textrm{c}}=\textbf{b}^{\scriptscriptstyle \textrm{p}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

(59d)

$$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{b}^{\scriptscriptstyle \textrm{c}}))\textbf{n}_{\scriptscriptstyle \textrm{c}}+ \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

(59e)

$$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y(\textbf{b}^{\scriptscriptstyle \textrm{p}}))\textbf{n}_{\scriptscriptstyle \textrm{p}}+ \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}\textbf{n}_{\scriptscriptstyle \textrm{p}}=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

(59f)

We now consider the leading-order solid stress tensors. Since from (39b) and (39c) we have that $\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}$ and $\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}$ are related to ${\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}$ and ${\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}$, respectively, we can write

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}=\mathbb {C}^{\scriptscriptstyle \textrm{c}}\mathbb {M}^{\scriptscriptstyle \textrm{c}}\xi _x (\textbf{u}^{(0)})+\mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{Q}}^{\scriptscriptstyle \textrm{c}}p^{(0)}+\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _x(\textbf{u}^{(0)})+\mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{R}}^{\scriptscriptstyle \textrm{c}}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)} \end{aligned}$$

(60)

and

$$\begin{aligned} {\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}=\mathbb {C}^{\scriptscriptstyle \textrm{p}}\mathbb {M}^{\scriptscriptstyle \textrm{p}}\xi _x (\textbf{u}^{(0)})+\mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{Q}}^{\scriptscriptstyle \textrm{p}}p^{(0)}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _x(\textbf{u}^{(0)})+\mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{R}}^{\scriptscriptstyle \textrm{p}}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}, \end{aligned}$$

(61)

where we define

$$\begin{aligned} \mathbb {M}^{\scriptscriptstyle \textrm{c}}=\xi _y({\mathcal {A}}^{\scriptscriptstyle \textrm{c}}), \quad \mathbb {M}^{\scriptscriptstyle \textrm{p}}=\xi _y({\mathcal {A}}^{\scriptscriptstyle \textrm{p}}),&\nonumber \\ {\textsf{Q}}^{\scriptscriptstyle \textrm{c}}=\xi _y(\textbf{a}^{\scriptscriptstyle \textrm{c}}), \quad {\textsf{Q}}^{\scriptscriptstyle \textrm{p}}=\xi _y(\textbf{a}^{\scriptscriptstyle \textrm{p}})&\nonumber \\ {\textsf{R}}^{\scriptscriptstyle \textrm{c}}=\xi _y(\textbf{b}^{\scriptscriptstyle \textrm{c}}), \quad {\textsf{R}}^{\scriptscriptstyle \textrm{p}}=\xi _y(\textbf{b}^{\scriptscriptstyle \textrm{p}}).&\end{aligned}$$

(62)

Adding (60) and (61) and taking the integral average over the solid domain gives

$$\begin{aligned} \langle {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}+{\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}\rangle _s&=\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}\mathbb {M}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{c}}+ \mathbb {C}^{\scriptscriptstyle \textrm{p}}\mathbb {M}^{\scriptscriptstyle \textrm{p}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\rangle _s \xi _x(\textbf{u}^{(0)})+\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{Q}}^{\scriptscriptstyle \textrm{p}}\rangle _sp^{(0)}\nonumber \\&\quad +\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{R}}^{\scriptscriptstyle \textrm{c}} + \mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{R}}^{\scriptscriptstyle \textrm{p}}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}\rangle _s. \end{aligned}$$

(63)

From (53), we have that

$$\begin{aligned} \nabla _\textbf{x} \cdot {\textsf{T}}_{\textrm{Eff}}=0 \end{aligned}$$

(64)

where

$$\begin{aligned} {\textsf{T}}_{\textrm{Eff}}&=\langle {\textsf{T}}_{\scriptscriptstyle \textrm{c}}^{(0)}+{\textsf{T}}_{\scriptscriptstyle \textrm{p}}^{(0)}\rangle _s-\phi p^{(0)} {\textsf{I}}\nonumber \\&=\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}\mathbb {M}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{c}}+ \mathbb {C}^{\scriptscriptstyle \textrm{p}}\mathbb {M}^{\scriptscriptstyle \textrm{p}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\rangle _s \xi _x(\textbf{u}^{(0)})\nonumber \\&\quad +(\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{Q}}^{\scriptscriptstyle \textrm{p}}\rangle _s-\phi {\textsf{I}})p^{(0)}+\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{R}}^{\scriptscriptstyle \textrm{c}} + \mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{R}}^{\scriptscriptstyle \textrm{p}}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}\rangle _s. \end{aligned}$$

(65)

We are able to describe (64) and (65) as the average force balance equations for our poroelastic composite material.

We now return to (38d), the incompressibility condition and integrate to obtain

$$\begin{aligned} 0=\int _{\Omega _{\textrm{f}}} \nabla _\textbf{y} \cdot \textbf{v}^{(1)}\text{ d }{} \textbf{y}+\int _{\Omega _{\textrm{f}}} \nabla _\textbf{x} \cdot \textbf{v}^{(0)}\text{ d }{} \textbf{y} \end{aligned}$$

(66)

Applying the divergence theorem twice to the first integral and using (38e) and (38f) and also rearranging the second integral, we obtain

$$\begin{aligned} 0&=-\int _{\Omega _{\scriptscriptstyle \textrm{c}}} \nabla _\textbf{y}\cdot {\dot{\textbf{u}}}_{\scriptscriptstyle \textrm{c}}^{(1)}\text{ d }\textbf{y}-\int _{\Omega _{\scriptscriptstyle \textrm{p}}} \nabla _\textbf{y}\cdot {\dot{\textbf{u}}}_{\scriptscriptstyle \textrm{p}}^{(1)}\text{ d }{} \textbf{y}+\nabla _\textbf{x} \cdot \langle \textbf{v}^{(0)} \rangle _{\textrm{f}} \end{aligned}$$

(67)

$$\begin{aligned}&=-\int _{\Omega _{\scriptscriptstyle \textrm{c}}}\text{ Tr }( \xi _y({\dot{\textbf{u}}}_{\scriptscriptstyle \textrm{c}}^{(1)}))\text{ d }\textbf{y}-\int _{\Omega _{\scriptscriptstyle \textrm{p}}} \text{ Tr }(\xi _y({\dot{\textbf{u}}}_{\scriptscriptstyle \textrm{p}}^{(1)}))\text{ d }\textbf{y}+\nabla _\textbf{x} \cdot \langle \textbf{v}^{(0)} \rangle _{\textrm{f}}. \end{aligned}$$

(68)

Therefore, we have

$$\begin{aligned} \langle \text{ Tr }(\xi _y({\dot{\textbf{u}}}_{\scriptscriptstyle \textrm{c}}^{(1)})+\xi _y({\dot{\textbf{u}}}_{\scriptscriptstyle \textrm{p}}^{(1)}))\rangle _s=\nabla _\textbf{x} \cdot \langle \textbf{v}^{(0)} \rangle _{\textrm{f}}. \end{aligned}$$

(69)

Using (55) and (56) with (62), we have that

$$\begin{aligned} \xi _y({\dot{\textbf{u}}}_{\scriptscriptstyle \textrm{c}}^{(1)})+\xi _y({\dot{\textbf{u}}}_{\scriptscriptstyle \textrm{p}}^{(1)})=(\mathbb {M}^{\scriptscriptstyle \textrm{c}}+\mathbb {M}^{\scriptscriptstyle \textrm{p}})\xi _x({\dot{\textbf{u}}}^{(0)}) +({\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+{\textsf{Q}}^{\scriptscriptstyle \textrm{p}}){\dot{p}}^{(0)}+ {\textsf{R}}^{\scriptscriptstyle \textrm{c}}+{\textsf{R}}^{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

(70)

So using (70), then equation (69) becomes

$$\begin{aligned} \nabla _\textbf{x} \cdot \langle \textbf{v}^{(0)} \rangle _{\textrm{f}}=\langle \text{ Tr }(\mathbb {M}^{\scriptscriptstyle \textrm{c}}+\mathbb {M}^{\scriptscriptstyle \textrm{p}})\rangle _s \xi _x({\dot{\textbf{u}}}^{(0)})+\langle \text{ Tr }({\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+{\textsf{Q}}^{\scriptscriptstyle \textrm{p}})\rangle _s{{\dot{p}}}^{(0)}+\langle \text{ Tr }({\textsf{R}}^{\scriptscriptstyle \textrm{c}}+{\textsf{R}}^{\scriptscriptstyle \textrm{p}})\rangle _s. \end{aligned}$$

(71)

Now returning to (44), the expression for relative fluid–solid displacement and taking the integral average over the fluid domain, we obtain

$$\begin{aligned} \langle \textbf{w}\rangle _{\textrm{f}}=\langle \textbf{v}^{(0)}\rangle _{\textrm{f}} - \phi \dot{\textbf{u}}^{(0)}, \end{aligned}$$

(72)

where $\phi$ is the porosity of the material. Then rearranging in terms of the average of $\textbf{v}^{(0)}$, we obtain

$$\begin{aligned} \langle \textbf{v}^{(0)}\rangle _{\textrm{f}}=\langle \textbf{w}\rangle _{\textrm{f}} +\phi \dot{\textbf{u}}^{(0)}. \end{aligned}$$

(73)

We will then use this relation to rewrite (71) as

$$\begin{aligned} \nabla _\textbf{x} \cdot (\langle \textbf{w}\rangle _{\textrm{f}} +\phi \dot{\textbf{u}}^{(0)})&=\langle \text{ Tr }(\mathbb {M}^{\scriptscriptstyle \textrm{c}}+\mathbb {M}^{\scriptscriptstyle \textrm{p}})\rangle _s \xi _x({\dot{\textbf{u}}}^{(0)})+\langle \text{ Tr }({\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+{\textsf{Q}}^{\scriptscriptstyle \textrm{p}})\rangle _s{{\dot{p}}}^{(0)} +\langle \text{ Tr }({\textsf{R}}^{\scriptscriptstyle \textrm{c}}+{\textsf{R}}^{\scriptscriptstyle \textrm{p}})\rangle _s. \end{aligned}$$

(74)

We can expand the left hand side of (74) and then rearrange to obtain the following expression for ${{\dot{p}}}^{(0)}$. We note that we are able to express $\phi \nabla _\textbf{x}\cdot {\dot{\textbf{u}}}^{(0)}$ as $\phi \textbf{I} \xi _x ({\dot{\textbf{u}}}^{(0)})$. Then

$$\begin{aligned} {{\dot{p}}}^{(0)}&=\frac{1}{\langle \text{ Tr }({\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+{\textsf{Q}}^{\scriptscriptstyle \textrm{p}})\rangle _s}\bigg ( \nabla _\textbf{x} \cdot \langle \textbf{w} \rangle _{\textrm{f}} +(\phi \textbf{I}-\langle \text{ Tr }(\mathbb {M}^{\scriptscriptstyle \textrm{c}}+\mathbb {M}^{\scriptscriptstyle \textrm{p}})\rangle _s) \xi _x({\dot{\textbf{u}}}^{(0)})-\langle \text{ Tr }({\textsf{R}}^{\scriptscriptstyle \textrm{c}}+{\textsf{R}}^{\scriptscriptstyle \textrm{p}})\rangle _s\bigg ). \end{aligned}$$

(75)

We can then define

$$\begin{aligned} {{\hat{M}}} =\frac{-1}{\langle \text{ Tr }({\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+{\textsf{Q}}^{\scriptscriptstyle \textrm{p}})\rangle _s} \quad \text{ and } \quad \hat{\varvec{\alpha }} =\phi {\textsf{I}}-\langle \text{ Tr }(\mathbb {M}^{\scriptscriptstyle \textrm{c}}+\mathbb {M}^{\scriptscriptstyle \textrm{p}})\rangle _s, \end{aligned}$$

(76)

and then, we can use (76) to write (75) as

$$\begin{aligned} {{\dot{p}}}^{(0)}=-{{\hat{M}}}( \nabla _\textbf{x} \cdot \langle \textbf{w} \rangle _{\textrm{f}}+\hat{\varvec{\alpha }} \xi _x({\dot{\textbf{u}}}^{(0)})-\langle \text{ Tr }({\textsf{R}}^{\scriptscriptstyle \textrm{c}}+{\textsf{R}}^{\scriptscriptstyle \textrm{p}})\rangle _s). \end{aligned}$$

(77)

Finally dividing through by ${{\hat{M}}}$, we obtain

$$\begin{aligned} \frac{{{\dot{p}}}^{(0)}}{{{\hat{M}}}}=-\nabla _\textbf{x} \cdot \langle \textbf{w} \rangle _{\textrm{f}}-\hat{\varvec{\alpha }} \xi _x({\dot{\textbf{u}}}^{(0)})+\langle \text{ Tr }({\textsf{R}}^{\scriptscriptstyle \textrm{c}}+{\textsf{R}}^{\scriptscriptstyle \textrm{p}})\rangle _s. \end{aligned}$$

(78)

We have now derived all the equations required to be able to state our macroscale model for a poroelastic composite.

4 The macroscale model

The equations in the macroscale model describe the effective poroelastic behaviour of the material in terms of the pore pressure, the average fluid velocity and the elastic displacement in a quasi-static regime. The macroscale model is then given by

$$\begin{aligned}&\langle \textbf{w}\rangle _{\textrm{f}}=-\langle {\textsf{W}}\rangle _{\textrm{f}}\nabla _\textbf{x}p^{(0)}, \end{aligned}$$

(79a)

$$\begin{aligned}&\nabla _\textbf{x} \cdot {\textsf{T}}_{\textrm{Eff}}=0 , \end{aligned}$$

(79b)

$$\begin{aligned}&{\textsf{T}}_{\textrm{Eff}}=\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}\mathbb {M}^{\scriptscriptstyle \textrm{c}} +\mathbb {C}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\mathbb {M}^{\scriptscriptstyle \textrm{p}} +\mathbb {C}^{\scriptscriptstyle \textrm{p}}\rangle _s\xi _x(\textbf{u}^{(0)})+(\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{Q}}^{\scriptscriptstyle \textrm{p}}\rangle _s-\phi {\textsf{I}})p^{(0)}\nonumber \\&\qquad \qquad +\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{R}}^{\scriptscriptstyle \textrm{c}} + \mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{R}}^{\scriptscriptstyle \textrm{p}}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}\rangle _s, \end{aligned}$$

(79c)

$$\begin{aligned}&\frac{{\dot{p}}^{(0)}}{{{\hat{M}}}}=-\nabla _\textbf{x} \cdot \langle \textbf{w}\rangle _{\textrm{f}}-\hat{\varvec{\alpha }} \xi _x(\dot{\textbf{u}}^{(0)})+\langle \text{ Tr }({\textsf{R}}^{\scriptscriptstyle \textrm{c}}+{\textsf{R}}^{\scriptscriptstyle \textrm{p}})\rangle _s, \end{aligned}$$

(79d)

where we have that $p^{(0)}$ is the macroscale pressure, $\textbf{u}^{(0)}$ is the leading-order solid displacement and $\dot{\textbf{u}}^{(0)}$ is the leading-order solid velocity. The novel model comprises the equation governing the fluid flow (79a). This equation is Darcy’s Law and is not impacted by the pre-stressed elastic phases. We have that (79b) is the balance equation for our material with the constitutive law given by (79c). The constitutive law incorporates the influence of the pre-stresses by including the leading-order pre-stresses, $\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}$ and $\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}$, in each phase and the additional terms, $\mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{R}}^{\scriptscriptstyle \textrm{c}}$ and $\mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{R}}^{\scriptscriptstyle \textrm{p}}$ that arise from solving the cell problem (59a)–(59f) that account for the difference in pre-stress at different points in the microstructure. The final equation (79d) is the conservation of mass equation which is that of poroelastic composites but with the additional term, $\langle \text{ Tr }({\textsf{R}}^{\scriptscriptstyle \textrm{c}}+{\textsf{R}}^{\scriptscriptstyle \textrm{p}})\rangle _s$ that accounts for the difference in pre-stress at different points in the microstructure.

4.1 Choices of the pre-stress

The macroscale model has been derived without specifying any details about the pre-stress in each elastic phase. We will now consider the following cases and discuss in detail the effect that each of these cases has on the macroscale model and the cell problems used to compute the model coefficients.

• Dependence on both scales

  In the case that the pre-stresses $\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}(\textbf{x,y})$ and $\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}(\textbf{x,y})$ depend on both the microscale and the macroscale, we derive exactly the macroscale model (79a)–(79d). The cell problems for the fluid do not involve the pre-stresses so remain as (48). In the case of the solid portion of the cell, then we have that problems (57a)–(57f) and (58a)–(58f) are unaffected by the pre-stresses; however, (59a)–(59f) is affected. We can see that in (59a)–(59f) we have the pre-stresses $\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}(\textbf{x,y})$ and $\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}(\textbf{x,y})$. If we are assuming that these tensors depend on both the microscale and macroscale, then the porescale periodic cell problems have a dependence on the macroscale and therefore cannot be easily solved. These pre-stresses depending on both scales means that the two scales are not fully decoupled, and therefore, this dramatically increases the computational complexity. There are, of course, emerging techniques that can be used to try to address solving coupled problems numerically [46]. The technique involves using artificial neural networks (ANNs) for quick, accurate upscaling and localisation of problems. This is carried out via an incremental numerical approach where there is a rearrangement of the cell properties relating to the current deformation or stress, and this means that there is a remodelling of the macroscopic model after each incremental time step. This method is applicable to finite strain and large deformation problems, whilst there will only be infinitesimal deformation or change in stress within each incremental time step. In the case that the material is an elastic composite comprising pre-stresses (no pores), then an approach similar to the one outlined in [47] for stratified layered elastic materials, whose material properties only change along one direction, can be used. This approach can, however, not be used in this model due to the pores. The case that the pre-stress depends on both scales is the most likely case found in biological tissues such as in the case of artery walls or the myocardium [36,37,38] where there are pre-stressed microscale collagen and elastic fibres contributing to the macroscale residual stress of the material.

• Decompositions of pre-stress into two components with variation on one scale

  Another way in which we can potentially tackle the coupling of the two scales, is to propose a decomposition of the pre-stress into two parts, one depending on the macroscale and the other depending on only the microscale. We make the following assumptions: firstly, the elasticity tensor depends only on the microscale

  $$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{c}}=\mathbb {C}^{\scriptscriptstyle \textrm{c}}(\textbf{y}) \quad \text{ and } \quad \mathbb {C}^{\scriptscriptstyle \textrm{p}}=\mathbb {C}^{\scriptscriptstyle \textrm{p}}(\textbf{y}), \end{aligned}$$

  (80)

  and secondly, the leading-order pre-stresses have the following decomposition

  $$\begin{aligned}&(\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)})_{ij}=(\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{L(0)}(\textbf{y}))_{ijkl}(\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{G(0)}(\textbf{x}))_{kl} \end{aligned}$$

  (81a)
  $$\begin{aligned}&(\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)})_{ij}=(\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{L(0)}(\textbf{y}))_{ijkl}(\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{G(0)}(\textbf{x}))_{kl}, \end{aligned}$$

  (81b)

  where the new superscripts L and G represent Local (microscale) and Global (macroscale), respectively. Here we have decomposed in such a way that the second-rank pre-stress arises from the double contraction of a fourth-rank microscale component with a second-rank macroscale component. We need to take this decomposition into account in the ansatz that we propose for elastic problem (54a)–(54f). The new solution that we propose is given as

  $$\begin{aligned} \textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}(\textbf{x}, \textbf{y})&={\mathcal {A}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}) \xi _x (\textbf{u}^{(0)}(\textbf{x}))+\textbf{a}^{\scriptscriptstyle \textrm{c}}(\textbf{y})p^{(0)}(\textbf{x})+{\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}) \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{G(0)}(\textbf{x})+{\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}) \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{G(0)}(\textbf{x}) \end{aligned}$$

  (82a)
  $$\begin{aligned} \textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}(\textbf{x}, \textbf{y})&={\mathcal {A}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}) \xi _x (\textbf{u}^{(0)}(\textbf{x}))+\textbf{a}^{\scriptscriptstyle \textrm{p}}(\textbf{y})p^{(0)}(\textbf{x})+{\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}) \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{G(0)}(\textbf{x}) +{\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}) \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{G(0)}(\textbf{x}), \end{aligned}$$

  (82b)

  where ${\mathcal {A}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})$, ${\mathcal {A}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})$, ${\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})$, ${\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})$, ${\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})$ and ${\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})$ are third-rank tensors with a dependence on only the microscale variable $\textbf{y}$ and $\textbf{a}^{\scriptscriptstyle \textrm{c}}(\textbf{y})$ and $\textbf{a}^{\scriptscriptstyle \textrm{p}}(\textbf{y})$ are vectors depending on the microscale variable $\textbf{y}$. There are now two choices that can be made that will result in different cell problems. If we assume that the second-rank tensors $\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{G(0)}(\textbf{x})\ne \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{G(0)}(\textbf{x})$, then we obtain the following cell problems that do not retain any macroscale dependency

  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))+\nabla _\textbf{y} \cdot \mathbb {C}^{\scriptscriptstyle \textrm{c}}=0&\quad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (83a)
  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))+\nabla _\textbf{y} \cdot \mathbb {C}^{\scriptscriptstyle \textrm{p}}=0&\quad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (83b)
  $$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\mathbb {C}^{\scriptscriptstyle \textrm{p}}-\mathbb {C}^{\scriptscriptstyle \textrm{c}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}&\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (83c)
  $$\begin{aligned} {\mathcal {A}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})={\mathcal {A}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})&\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (83d)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{c}}+ \mathbb {C}^{\scriptscriptstyle \textrm{c}}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}=0&\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (83e)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y({\mathcal {A}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{p}}+ \mathbb {C}^{\scriptscriptstyle \textrm{p}}\textbf{n}_{\scriptscriptstyle \textrm{p}}=0&\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (83f)

  and

  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))=\textbf{0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (84a)
  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))=\textbf{0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (84b)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y( \textbf{a}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (84c)
  $$\begin{aligned} \textbf{a}^{\scriptscriptstyle \textrm{c}}(\textbf{y})=\textbf{a}^{\scriptscriptstyle \textrm{p}}(\textbf{y})&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (84d)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{c}}+ \textbf{n}_{\scriptscriptstyle \textrm{c}}=\textbf{0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (84e)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{a}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{p}}+ \textbf{n}_{\scriptscriptstyle \textrm{p}}=\textbf{0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (84f)

  which are the cell problems (57a)–(57f) and (58a)–(58f) which are now $\textbf{y}$-dependent only since we make assumption (80). We have the change in the cell problems which include the pre-stresses which we have decomposed and these are

  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{L(0)}(\textbf{y})={ 0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (85a)
  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))={ 0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (85b)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}))-\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{cp}}=-\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{L(0)}(\textbf{y})\textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (85c)
  $$\begin{aligned} {\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})={\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (85d)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{c}}+ \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{L(0)}(\textbf{y})\textbf{n}_{\scriptscriptstyle \textrm{c}}={0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (85e)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{p}}={ 0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (85f)

  and

  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))={ 0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (86a)
  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{L(0)}(\textbf{y})={0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (86b)
  $$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}=\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{L(0)}(\textbf{y})\textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (86c)
  $$\begin{aligned} {\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})={\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (86d)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{c}}={0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (86e)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y({\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{p}}+ \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{L(0)}(\textbf{y})\textbf{n}_{\scriptscriptstyle \textrm{p}}={0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

  (86f)

  These cell problems can be solved completely on the microscale.

  If we instead make the assumption that the second-rank tensors

  $$\begin{aligned} \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{G(0)}(\textbf{x})=\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{G(0)}(\textbf{x})=\varvec{\sigma }_{\scriptscriptstyle \textrm{0}}^{G(0)}(\textbf{x}), \end{aligned}$$

  (87)

  then we can rewrite the ansatz (82a)–(82b) as

  $$\begin{aligned}&\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}(\textbf{x}, \textbf{y})={\mathcal {A}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}) \xi _x (\textbf{u}^{(0)}(\textbf{x}))+\textbf{a}^{\scriptscriptstyle \textrm{c}}(\textbf{y})p^{(0)}(\textbf{x})+{\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}) \varvec{\sigma }_{\scriptscriptstyle \textrm{0}}^{G(0)}(\textbf{x}) \end{aligned}$$

  (88a)
  $$\begin{aligned}&\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}(\textbf{x}, \textbf{y})={\mathcal {A}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}) \xi _x (\textbf{u}^{(0)}(\textbf{x}))+\textbf{a}^{\scriptscriptstyle \textrm{p}}(\textbf{y})p^{(0)}(\textbf{x})+{\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}) \varvec{\sigma }_{\scriptscriptstyle \textrm{0}}^{G(0)}(\textbf{x}), \end{aligned}$$

  (88b)

  where again ${\mathcal {A}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})$, ${\mathcal {A}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})$, ${\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})$ and ${\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})$ are third-rank tensors with a dependence on only the microscale variable $\textbf{y}$ and $\textbf{a}^{\scriptscriptstyle \textrm{c}}(\textbf{y})$ and $\textbf{a}^{\scriptscriptstyle \textrm{p}}(\textbf{y})$ are vectors that depend only on the microscale. This allows us to obtain the following cell problems that do not retain any macroscale dependency. We have exactly (83a)–(83f) and (84a)–(84f) and the following different microscale cell problem

  $$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{L(0)}(\textbf{y})=0 \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (89)
  $$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{L(0)}(\textbf{y})=0 \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (90)
  $$\begin{aligned}&\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{L(0)}(\textbf{y})\nonumber \\&\quad -\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{L(0)}(\textbf{y}))\textbf{n}_{\scriptscriptstyle \textrm{cp}} \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (91)
  $$\begin{aligned}&{\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})={\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}) \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (92)
  $$\begin{aligned}&(\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{c}}+ \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{L(0)}(\textbf{y})\textbf{n}_{\scriptscriptstyle \textrm{c}}=0 \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (93)
  $$\begin{aligned}&(\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y({\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{p}}+ \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{L(0)}(\textbf{y})\textbf{n}_{\scriptscriptstyle \textrm{p}}=0 \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

  (94)

  These different decompositions and assumptions lead to us having well-posed cell problems that when supplemented with the periodic conditions on the cell boundary, an additional condition for uniqueness can be easily solved to determine the coefficients of the macroscale model. Here we have introduced a more complicated notation that emphasises the scale that the quantity has a dependence on and shows the decomposition of the pre-stress into the local and global components. Despite this increased complexity in the notation, the resulting model can actually be solved at a reduced computational cost than when assuming that the pre-stresses depend on both the microscale and macroscale in full. We actually find that the decomposition of the pre-stresses leads to a complete decoupling between the macroscale and the microscale problems eliminating the issues discussed in the previous bullet point of this subsection. Since we have this decoupling, we then solve the six elastic-type cell problems (83a)–(83f), the vector problems (84a)–(84f) and then either vector problems (85a)–(85f) and (86a)–(86f) or (89)–(94).

• Microscopically varying pre-stress

  If we make the assumption that the pre-stresses $\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}(\textbf{y})$ and $\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}(\textbf{y})$ depend only on the microscale, then we derive exactly the macroscale model (79a)–(79d); however, we can notice that the effective stress,

  $$\begin{aligned} {\textsf{T}}_{\textrm{Eff}}&=\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}\mathbb {M}^{\scriptscriptstyle \textrm{c}} +\mathbb {C}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\mathbb {M}^{\scriptscriptstyle \textrm{p}} +\mathbb {C}^{\scriptscriptstyle \textrm{p}}\rangle _s\xi _x(\textbf{u}^{(0)})+(\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{Q}}^{\scriptscriptstyle \textrm{p}}\rangle _s-\phi {\textsf{I}})p^{(0)}\nonumber \\&\quad +\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{R}}^{\scriptscriptstyle \textrm{c}} + \mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{R}}^{\scriptscriptstyle \textrm{p}}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}\rangle _s, \end{aligned}$$

  (95)

  contains the pre-stresses as terms. This means that when we use this effective stress in our macroscale balance equation then these pre-stress terms will disappear as they only depend on the microscale. That is,

  $$\begin{aligned} \nabla _\textbf{x}\cdot {\textsf{T}}_{\textrm{Eff}}&=\nabla _\textbf{x}\cdot \big (\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}\mathbb {M}^{\scriptscriptstyle \textrm{c}} +\mathbb {C}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\mathbb {M}^{\scriptscriptstyle \textrm{p}} +\mathbb {C}^{\scriptscriptstyle \textrm{p}}\rangle _s\xi _x(\textbf{u}^{(0)})+(\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{Q}}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{Q}}^{\scriptscriptstyle \textrm{p}}\rangle _s\nonumber \\&\quad -\phi \textbf{I})p^{(0)}+\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{R}}^{\scriptscriptstyle \textrm{c}} + \mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{R}}^{\scriptscriptstyle \textrm{p}}\rangle _s\big )=0. \end{aligned}$$

  (96)

  The cell problems for the fluid, as before, do not involve the pre-stresses so remain as (48). Again for the solid cell portion, we have that problems (57a)–(57f) and (58a)–(58f) are unaffected by the pre-stresses; however, (59a)–(59f) is affected. We can see that in (59a)–(59f) we have the pre-stresses $\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}$ and $\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}$. In this cell problem, we take the microscale divergence of the pre-stress tensors and also have the difference in pre-stresses as the driving force of the cell problem. Since those pre-stresses depend solely on the microscale, then the two scales are fully decoupled. Then the cell problem is of the general asymptotic homogenisation type, where it only depends on the microscale and therefore can be solved in a straightforward way. For example, for linear elastic composites [27] the porescale asymptotic homogenisation cell problems were solved in [44]. The problems for linear poroelasticity were solved in [32] to investigate the role of porosity and microscale solid matrix compressibility on the mechanical behaviour of poroelastic materials. More recently, the cell problems for a poroelastic composite have been solved in [34] to perform a micromechanical analysis of the effective stiffness of poroelastic composites. The case where the pre-stress is depending on the microscale only could be applicable to additively manufactured metallic materials, such as stainless steel, which commonly possess substantial microscale residual or pre-stresses [48].

• Macroscopically varying pre-stress

  Finally we consider the case where the pre-stresses $\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}(\textbf{x})$ and $\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}(\textbf{x})$ depend only on the macroscale. We have the same macroscale model (79a)–(79d). Again all but cell problem (59a)–(59f) remain unchanged. We write the leading-order pre-stresses using the following decomposition

  $$\begin{aligned}&(\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)})_{ij}=\delta _{ik}\delta _{jl} (\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{G(0)}(\textbf{x}))_{kl} \end{aligned}$$

  (97a)
  $$\begin{aligned}&(\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)})_{ij}=\delta _{ik}\delta _{jl} (\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{G(0)}(\textbf{x}))_{kl}. \end{aligned}$$

  (97b)

  In this case, we see that the elastic problem (54a)–(54f) can be written as the following, since $\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}$ and $\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}$ have no $\textbf{y}$ dependence,

  $$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}))+ \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _x (\textbf{u}^{(0)}))=0 ~~ \text{ in } ~~ \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (98a)
  $$\begin{aligned}&\nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}))+ \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _x (\textbf{u}^{(0)}))=0 \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (98b)
  $$\begin{aligned}&\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)})\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)})\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\mathbb {C}^{\scriptscriptstyle \textrm{p}}-\mathbb {C}^{\scriptscriptstyle \textrm{c}}) \xi _x (\textbf{u}^{(0)})\textbf{n}_{\scriptscriptstyle \textrm{cp}}\nonumber \\&\quad +( \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}(\textbf{x})- \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}(\textbf{x}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}~~~\text{ on } ~~~ \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (98c)
  $$\begin{aligned}&\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)}=\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)}~~ \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (98d)
  $$\begin{aligned}&(\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{c}}^{(1)})+\mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _x (\textbf{u}^{(0)})+\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{G(0)}(\textbf{x}))\textbf{n}_{\scriptscriptstyle \textrm{c}}=-p^{(0)}{} \textbf{n}_{\scriptscriptstyle \textrm{c}}\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (98e)
  $$\begin{aligned}&(\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{u}_{\scriptscriptstyle \textrm{p}}^{(1)})+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _x (\textbf{u}^{(0)})+\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{G(0)}(\textbf{x}))\textbf{n}_{\scriptscriptstyle \textrm{p}}=-p^{(0)}\textbf{n}_{\scriptscriptstyle \textrm{p}}\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (98f)

  We also need to take this decomposition (97a) and (97b) into account in the ansatz that we propose for elastic problem (98a)–(98f). We are able to use (82a) and (82b) and we obtain (57a)–(57f) and (58a)–(58f) which are now $\textbf{y}$-dependent only since we make assumption (80) and we also obtain the two following cell problems

  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))={ 0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (99a)
  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))={0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (99b)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}))-\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{cp}}=-{{\textsf{I}}}\otimes \textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (99c)
  $$\begin{aligned} {\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})={\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (99d)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{c}}+ \mathbb {I})\textbf{n}_{\scriptscriptstyle \textrm{c}}={ 0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (99e)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{p}}={0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (99f)

  and

  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))={0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (100a)
  $$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))={0}&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}} \end{aligned}$$

  (100b)
  $$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y}))\textbf{n}_{\scriptscriptstyle \textrm{cp}}={\textsf{I}}\otimes \textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (100c)
  $$\begin{aligned} {\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})={\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}} \end{aligned}$$

  (100d)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {D}}^{\scriptscriptstyle \textrm{c}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{c}}={0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}} \end{aligned}$$

  (100e)
  $$\begin{aligned} (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y({\mathcal {B}}^{\scriptscriptstyle \textrm{p}}(\textbf{y})))\textbf{n}_{\scriptscriptstyle \textrm{p}}+\mathbb {I} \textbf{n}_{\scriptscriptstyle \textrm{p}}={ 0}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

  (100f)

  This decomposition is a special case of (81a) and (81b). These different decompositions and assumptions lead to us having well-posed cell problems that when supplemented with the periodic conditions on the cell boundary, as well as an additional condition for uniqueness can be easily solved to determine the coefficients of the macroscale model. The case where the pre-stress is depending on the macroscale only could be applicable to constitutive models of shear damage of pre-stressed anchored jointed rocks [49].

4.2 Scheme for solving the macroscale model

We now propose a scheme for solving the full macroscale model (79a)–(79d). The model is solvable using the following scheme for the suggested decompositions of the pre-stress, when the pre-stress only depends on the microscale, or when it only depends on the macroscale as discussed in Sect. 4.1. We provide a clear step-by-step guide on how to find the effective coefficients of the model and then how those are used when solving the macroscale model (79a)–(79d). The model coefficients encode the structural details such as geometry and elastic properties. In this guide, we include particular references that will assist the readers understanding of the type of numerical simulations that are to be carried out to find both the coefficients and solve the final model such as [32, 34].

We have made the assumption of global-scale uniformity of the material and assumed that the two scales are fully decoupled via one of the scenarios discussed in Sect. 4.1; then, we can propose the following steps to solve the model. The process is as follows:

• 1. The first step is to fix the original material properties of the elastic matrix and the elastic subphases at the microscale. We make the assumption of isotropy of each of the elastic phases. This means that we fix two parameters for the matrix and the subphase. These are two independent elastic constants such as the Poisson ratio and Young’s modulus (or alternatively depending on the experimental measurements available, the Lamé constants). We could, however, not make the assumption of isotropy and just provide the elasticity tensor with components depending on the symmetry that exists in each elastic phase.

• 2. We then must fix the microscale geometry, and this means we determine the specific geometry of a single periodic cell including the volume fraction of each of the phases.

• 3. The next step is then to find the macroscale model coefficients. We begin with the solid (elastic) coefficients. We solve the elastic-type cell problems (57a)–(57f), (58a)–(58f), (59a)–(59f) to obtain the auxiliary tensors $\mathbb {M}^{\scriptscriptstyle \textrm{c}}$, $\mathbb {M}^{\scriptscriptstyle \textrm{p}}$, ${\textsf{Q}}^{\scriptscriptstyle \textrm{c}}$, $\mathbb {Q}_{\scriptscriptstyle \textrm{p}}$, ${\textsf{R}}^{\scriptscriptstyle \textrm{c}}$ and ${\textsf{R}}^{\scriptscriptstyle \textrm{c}}$ which appear in the macroscale model coefficients. The cell problems to be solved are, in components

  $$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{c}})\bigg )+\frac{\partial C^{\scriptscriptstyle \textrm{c}}_{ijkl}}{\partial y_j}=0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

  (101a)
  $$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{p}})\bigg )+\frac{\partial C^{\scriptscriptstyle \textrm{p}}_{ijkl}}{\partial y_j}=0&\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

  (101b)
  $$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{cp}}_j-C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{cp}}_j=(C^{\scriptscriptstyle \textrm{p}}-C^{\scriptscriptstyle \textrm{c}})_{ijkl}n^{\scriptscriptstyle \textrm{cp}}_j&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

  (101c)
  $$\begin{aligned} {\mathcal {A}}^{\scriptscriptstyle \textrm{c}}_{ikl}={\mathcal {A}}^{\scriptscriptstyle \textrm{p}}_{ikl}&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

  (101d)
  $$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{c}}_j +C^{\scriptscriptstyle \textrm{c}}_{ijpq}n^{\scriptscriptstyle \textrm{c}}_j=0&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

  (101e)
  $$\begin{aligned} C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{p}}_j +C^{\scriptscriptstyle \textrm{p}}_{ijpq}n^{\scriptscriptstyle \textrm{p}}_j=0&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

  (101f)

  and

  $$\begin{aligned} \frac{\partial }{\partial y_j}\bigg (C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}(\textbf{a}^{\scriptscriptstyle \textrm{c}})\bigg )=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

  (102a)
  $$\begin{aligned} \frac{\partial }{\partial y_j}\bigg (C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}(\textbf{a}^{\scriptscriptstyle \textrm{p}})\bigg )=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

  (102b)
  $$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}(\textbf{a}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{cp}}_j=C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}(\textbf{a}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{cp}}_j&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

  (102c)
  $$\begin{aligned} a_i^{\scriptscriptstyle \textrm{c}}=a_i^{\scriptscriptstyle \textrm{p}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

  (102d)
  $$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}(\textbf{a}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{c}}_j +n^{\scriptscriptstyle \textrm{c}}_j=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

  (102e)
  $$\begin{aligned} C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}(\textbf{a}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{p}}_j +n^{\scriptscriptstyle \textrm{p}}_j=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

  (102f)

  and

  $$\begin{aligned}&\frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}(\textbf{b}^{\scriptscriptstyle \textrm{c}})\bigg )+\frac{\partial (\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0c})_{ij}}{\partial y_j}=0 \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

  (103a)
  $$\begin{aligned}&\frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}(\textbf{b}^{\scriptscriptstyle \textrm{p}})\bigg )+\frac{\partial (\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0p})_{ij}}{\partial y_j}=0 \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

  (103b)
  $$\begin{aligned}&C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}(\textbf{b}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{cp}}_j-C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}(\textbf{b}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{cp}}_j=(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0p}\nonumber \\&\quad -\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0c})_{ij}n^{\scriptscriptstyle \textrm{cp}}_j\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

  (103c)
  $$\begin{aligned}&b^{\scriptscriptstyle \textrm{c}}_{i}=b^{\scriptscriptstyle \textrm{p}}_{i} \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

  (103d)
  $$\begin{aligned}&C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}(\textbf{b}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{c}}_j +(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0c})_{ij}n^{\scriptscriptstyle \textrm{c}}_j=0\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

  (103e)
  $$\begin{aligned}&C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}(\textbf{b}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{p}}_j +(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0p})_{ij}n^{\scriptscriptstyle \textrm{p}}_j=0\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

  (103f)

  where we have used the notation

  $$\begin{aligned}&\xi _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{c}})=\frac{1}{2}\bigg (\frac{\partial {\mathcal {A}}^{\scriptscriptstyle \textrm{c}}_{pkl}}{\partial y_{q}}+\frac{\partial {\mathcal {A}}^{\scriptscriptstyle \textrm{c}}_{qkl}}{\partial y_{p}}\bigg ); ~ \xi _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{p}})=\frac{1}{2}\bigg (\frac{\partial {\mathcal {A}}^{\scriptscriptstyle \textrm{p}}_{pkl}}{\partial y_{q}}+\frac{\partial {\mathcal {A}}^{\scriptscriptstyle \textrm{p}}_{qkl}}{\partial y_{p}}\bigg ), \end{aligned}$$

  (104a)
  $$\begin{aligned}&\xi _{pq}(\textbf{a}^{\scriptscriptstyle \textrm{c}})=\frac{1}{2}\bigg (\frac{\partial a^{\scriptscriptstyle \textrm{c}}_{p}}{\partial y_{q}}+\frac{\partial a^{\scriptscriptstyle \textrm{c}}_{q}}{\partial y_{p}}\bigg ); \quad \xi _{pq}(\textbf{a}^{\scriptscriptstyle \textrm{p}})=\frac{1}{2}\bigg (\frac{\partial a^{\scriptscriptstyle \textrm{p}}_{p}}{\partial y_{q}}+\frac{\partial a^{\scriptscriptstyle \textrm{p}}_{q}}{\partial y_{p}}\bigg ), \end{aligned}$$

  (104b)
  $$\begin{aligned}&\xi _{pq}(\textbf{b}^{\scriptscriptstyle \textrm{c}})=\frac{1}{2}\bigg (\frac{\partial b^{\scriptscriptstyle \textrm{c}}_{p}}{\partial y_{q}}+\frac{\partial b^{\scriptscriptstyle \textrm{c}}_{q}}{\partial y_{p}}\bigg ); \quad \xi _{pq}(\textbf{b}^{\scriptscriptstyle \textrm{p}})=\frac{1}{2}\bigg (\frac{\partial b^{\scriptscriptstyle \textrm{p}}_{p}}{\partial y_{q}}+\frac{\partial b^{\scriptscriptstyle \textrm{p}}_{q}}{\partial y_{p}}\bigg ). \end{aligned}$$

  (104c)

  The solution of the problem (101a)–(101f) is found by solving six elastic-type cell problems by fixing the couple of indices $k, l = 1, 2, 3$. When we do this, we can see that we have strains $\zeta _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{c}})$ and $\zeta _{pq}^{kl}({\mathcal {A}}^{\scriptscriptstyle \textrm{p}})$ so that for each fixed couple of indices k, l we have a linear elastic problem. For more details on this process, see [32, 34]. The problems (102a)–(102f) and (103a)–(103f) are vector problems. These have driving forces of the normals to the interface between either the matrix and the void or the subphase and the void or the matrix and the subphase and the difference in the leading-order pre-stresses depending on which problem you are solving. The normal encodes the geometry of the voids and is used to compute the solution. We note that here we are providing the most general cell problems and that depending on the properties of the pre-stress it may be appropriate to use the modified versions of the cell problems appearing in Sect. 4.1, see Appendix A for all the cell problems in components.

• 4. To ensure uniqueness of solution, we require one additional condition. We choose to enforce that the cell averages of the cell problem solutions are zero, i.e.

  $$\begin{aligned} \begin{aligned} \langle {\mathcal {A}}^{\scriptscriptstyle \textrm{c}} \rangle _{\scriptscriptstyle \textrm{c}}&=0, \quad \langle {\mathcal {A}}^{\scriptscriptstyle \textrm{p}} \rangle _{\scriptscriptstyle \textrm{p}}=0, \quad \langle \textbf{a}^{\scriptscriptstyle \textrm{c}} \rangle _{\scriptscriptstyle \textrm{c}}=0, \quad \langle \textbf{a}^{\scriptscriptstyle \textrm{p}} \rangle _{\scriptscriptstyle \textrm{p}}=0, \\ \langle \textbf{b}^{\scriptscriptstyle \textrm{c}} \rangle _{\scriptscriptstyle \textrm{c}}&=0, \quad \langle \textbf{b}^{\scriptscriptstyle \textrm{p}} \rangle _{\scriptscriptstyle \textrm{p}}=0. \end{aligned} \end{aligned}$$

  (105)

• 5. We also have coefficients related to the fluid flow in the material. We have the fluid cell problem (48), which is solved to obtain the tensor ${\textsf{W}}$ and the vector $\textbf{P}$ which appear in the macroscale coefficients. The cell problem to be solved is, in components

  $$\begin{aligned} \frac{\partial ^2{\textsf{W}}_{ij}}{\partial y_k\partial y_k}-\frac{\partial P_i}{\partial y_j}+{\delta _{ij}}=0&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

  (106)
  $$\begin{aligned} \frac{\partial {\textsf{W}}_{ij}}{\partial y_i}=0&\quad \text{ in } \quad \Omega _{\textrm{f}} \end{aligned}$$

  (107)
  $$\begin{aligned} {\textsf{W}}_{ij}=0&\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}\cup \Gamma _{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

  (108)

• 6. The auxiliary second-rank tensors arising form the cell problems ($\mathbb {M}^{\scriptscriptstyle \textrm{c}}$, $\mathbb {M}^{\scriptscriptstyle \textrm{p}}$, ${\textsf{Q}}^{\scriptscriptstyle \textrm{c}}$, ${\textsf{Q}}^{\scriptscriptstyle \textrm{p}}$, ${\textsf{W}}$, ${\textsf{R}}^{\scriptscriptstyle \textrm{c}}$ and ${\textsf{R}}^{\scriptscriptstyle \textrm{p}}$) are then used to obtain the coefficients of the macroscale model.

• 7. The macroscale structure and geometry must be prescribed. We also set boundary conditions for the homogenised cell and provide initial conditions for the macroscale solid displacement and pressure.

• 8. Finally, our macroscale model can then be solved. For further details, consider [33]

4.3 Comparison of our work with [40]

We finally wish to compare the macroscale model (79a)–(79d) with the macroscale model for electrostrictive composites found in [40]. In the work of [40], the asymptotic homogenisation technique is used to derive a macroscale model that captures the behaviour of a linear elastic composite whose deformations are driven by the divergence of a given tensor, which is therein identified with the Maxwell stress tensor. The formal results of [40] can be compared with our ones in the absence of the fluid phase. Since in [40] there is no fluid contribution, then we can first consider the reduction of (79a)–(79d) to the case where there is no fluid. We will retain only the balance equation (79b) and will have a modified constitutive law (79c). That is, our reduced model is given by

$$\begin{aligned}&\nabla _\textbf{x} \cdot {\textsf{T}}_{\textrm{Eff}}=0 , \end{aligned}$$

(109a)

$$\begin{aligned}&{\textsf{T}}_{\textrm{Eff}}=\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}\mathbb {M}^{\scriptscriptstyle \textrm{c}} +\mathbb {C}^{\scriptscriptstyle \textrm{c}}+\mathbb {C}^{\scriptscriptstyle \textrm{p}}\mathbb {M}^{\scriptscriptstyle \textrm{p}} +\mathbb {C}^{\scriptscriptstyle \textrm{p}}\rangle _s\xi _x(\textbf{u}^{(0)})+\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{R}}^{\scriptscriptstyle \textrm{c}} + \mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{R}}^{\scriptscriptstyle \textrm{p}} +\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}\rangle _s, \end{aligned}$$

(109b)

In order for a more precise comparison, we can use the notation (34) that we introduced in Sect. 3.3 to rewrite the constitutive law as

$$\begin{aligned} {\textsf{T}}_{\textrm{Eff}}&=\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}\mathbb {M}^{\scriptscriptstyle \textrm{c}} +\mathbb {C}^{\scriptscriptstyle \textrm{c}}\rangle _{\scriptscriptstyle \textrm{c}} \xi _x(\textbf{u}^{(0)})+\langle \mathbb {C}^{\scriptscriptstyle \textrm{p}}\mathbb {M}^{\scriptscriptstyle \textrm{p}} +\mathbb {C}^{\scriptscriptstyle \textrm{p}}\rangle _{\scriptscriptstyle \textrm{p}} \xi _x(\textbf{u}^{(0)})+\langle \mathbb {C}^{\scriptscriptstyle \textrm{c}}{\textsf{R}}^{\scriptscriptstyle \textrm{c}} + \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}\rangle _{\scriptscriptstyle \textrm{c}}+\langle \mathbb {C}^{\scriptscriptstyle \textrm{p}}{\textsf{R}}^{\scriptscriptstyle \textrm{p}}+\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}\rangle _{\scriptscriptstyle \textrm{p}}. \end{aligned}$$

(110)

We can then see that the balance equation (79b) and the constitutive law (110) are exactly (60), (61a) and (61b) that are found in [40] when we make the following identifications in the notation. We have

$$\begin{aligned}&\mathbb {C}^{\scriptscriptstyle \textrm{c}}=\mathbb {C}_{\textrm{S}}, \quad \mathbb {C}^{\scriptscriptstyle \textrm{p}}=\mathbb {C}_{\textrm{M}}, \quad \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{c}})=\mathbb {M}^{\scriptscriptstyle \textrm{c}}=\mathbb {X}_y(\chi _{\textrm{S}}),\nonumber \\&\xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{p}})=\mathbb {M}^{\scriptscriptstyle \textrm{p}}=\mathbb {X}_y(\chi _{\textrm{M}}),\quad \xi _y (\textbf{b}^{\scriptscriptstyle \textrm{c}})={\textsf{R}}^{\scriptscriptstyle \textrm{c}}=\varvec{\xi }_y(\varvec{\omega }_{\textrm{S}}), \nonumber \\&\xi _y (\textbf{b}^{\scriptscriptstyle \textrm{p}})={\textsf{R}}^{\scriptscriptstyle \textrm{p}}=\varvec{\xi }_y(\varvec{\omega }_{\textrm{M}}),\quad \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}=\varvec{\sigma }_{\textrm{S}}^{(e)}. \quad \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}=\varvec{\sigma }_{\textrm{M}}^{(e)} \end{aligned}$$

(111)

where the tensors that we call the pre-stresses, $\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}$ and $\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}$, are identified with $\varvec{\sigma }_{\textrm{S}}^{(e)}$ and $\varvec{\sigma }_{\textrm{M}}^{(e)}$ which [40] uses as the generalised Maxwell stress tensor.

We can also compare the cell problems that we obtain here with those in [40]. We again will only need the solid elastic cell problems since there is no fluid involved in the formulation of [40]. This means that we will only require (57a)–(57f) and (59a)–(59f) modified for the case of no fluid. This means that these cell problems will become

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{c}}))+\nabla _\textbf{y} \cdot \mathbb {C}^{\scriptscriptstyle \textrm{c}}=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(112)

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{p}}))+\nabla _\textbf{y} \cdot \mathbb {C}^{\scriptscriptstyle \textrm{p}}=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(113)

$$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{c}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _y ({\mathcal {A}}^{\scriptscriptstyle \textrm{p}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\mathbb {C}^{\scriptscriptstyle \textrm{p}}-\mathbb {C}^{\scriptscriptstyle \textrm{c}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(114)

$$\begin{aligned} {\mathcal {A}}^{\scriptscriptstyle \textrm{c}}={\mathcal {A}}^{\scriptscriptstyle \textrm{p}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(115)

and

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{c}} \xi _y (\textbf{b}^{\scriptscriptstyle \textrm{c}}))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)}=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(116)

$$\begin{aligned} \nabla _\textbf{y} \cdot (\mathbb {C}^{\scriptscriptstyle \textrm{p}} \xi _y (\textbf{b}^{\scriptscriptstyle \textrm{p}}))+\nabla _\textbf{y} \cdot \varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(117)

$$\begin{aligned} \mathbb {C}^{\scriptscriptstyle \textrm{c}}\xi _y (\textbf{b}^{\scriptscriptstyle \textrm{c}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}-\mathbb {C}^{\scriptscriptstyle \textrm{p}}\xi _y (\textbf{b}^{\scriptscriptstyle \textrm{p}})\textbf{n}_{\scriptscriptstyle \textrm{cp}}=(\varvec{\sigma }_{\scriptscriptstyle \textrm{0p}}^{(0)}-\varvec{\sigma }_{\scriptscriptstyle \textrm{0c}}^{(0)})\textbf{n}_{\scriptscriptstyle \textrm{cp}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(118)

$$\begin{aligned} \textbf{b}^{\scriptscriptstyle \textrm{c}}=\textbf{b}^{\scriptscriptstyle \textrm{p}}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}. \end{aligned}$$

(119)

Using the identifications in notation that we made above, we can see that these are exactly the cell problems (44a-44d) and (45a-45d), respectively, found in [40].

5 Conclusion

Throughout this work, we have carried out the derivation, in a quasi-static regime, of a novel system of partial differential equations that describe the effective mechanical behaviour of a poroelastic composite that is subjected to pre-stresses. We investigate materials with a microstructure comprising a porous elastic matrix and subphases with an incompressible Newtonian fluid flowing in the pores. The elastic matrix and individual subphases are assumed to be linear elastic but are pre-stressed. Materials with this microstructure have many real-world applications, including modelling of biological tissues such as the artery walls. Another problem of biological interest that can be studied by using the multiscale approach developed in the present manuscript is that of focal adhesions, by extending, for instance, the analysis proposed in [50, 51], where non-elastic processes have been considered.

In order to derive the new model for this type of microstructure, we create a fluid–structure interaction (FSI) problem that appropriately describes each component of the geometry. The problem is closed by applying some interface conditions on the three different interfaces that exist in the structure. We apply the continuity of tractions and velocities on the interfaces between matrix and the fluid and on the interface between the subphase and the fluid. We also apply the continuity of tractions and displacements between the different elastic subphases and the matrix. We know that there is a sharp length-scale separation between the microscale (where all individual phases are clearly visible) and the macroscale (average length of the material) so due to this we are able to apply the asymptotic homogenisation technique to derive the novel model that governs the material behaviour. The coefficients of the newly obtained governing equations encode the precise microstructural details of geometry and material properties. We are able to compute the model coefficients by solving the periodic cell problems that arise as a result of using the asymptotic homogenisation technique. We then investigate different choices of the pre-stress that will influence the overall macroscale model and the cell problems that will determine the model coefficients. We provide a scheme for solving the macroscale model and state all possible arising cell problems in components in appendix. Finally we make the assumption that our model does not have a fluid phase and we recover the model of [40] on electrostrictive elastic composites.

The novel model obtained in this manuscript is an important extension of [28] and can be considered a useful advancement of the existing models for poroelastic materials with detailed microstructures such as biological tissues. The key novelty of this work resides in considering the influence of an existing pre-stress in each of the elastic phases. By considering the pre-stresses, we derive the model of [28] with additional terms and coefficients that encode these stresses. We have that the leading-order term in the asymptotic expansion of the pre-stress appears in the macroscale constitutive law for the material and is the driving force in the novel cell problem (59a)–(59f). This cell problem, along with (57a)–(57f) and (58a)–(58f), can be solved to find the coefficients which encode the details of the geometry and stiffness of the microstructure as well as the tensors, ${\textsf{R}}^{\scriptscriptstyle \textrm{c}}$ and ${\textsf{R}}^{\scriptscriptstyle \textrm{p}}$, which appear in the constitutive law and the conservation of mass equation in the macroscale model and account for the changes in pre-stress at different parts in the microstructure. Due to these cell problems, we are directly able to account for the microscale complexity within the macroscale governing equations.

The model that we have derived is subject to some limitations that can easily be amended if the desired application requires. We have formulated a quasi-static and linearised macroscale model. This means that we have not taken linearised inertia into consideration. However, it would be very possible to relax this assumption and this would give rise to additional terms in our macroscale model effective balance equation (79b). The addition of these inertial terms can be useful to applications of lung modelling where the acoustic properties can be used to aid the diagnosis of pulmonary diseases [52, 53].

We also have formulated this model in a linear elastic setting. The theoretical model can be extended to nonlinear elasticity and would be a special extension of [31]. By extending to the nonlinear setting, we create the complication in carrying out the numerical simulations. This complication arises because the two length scales in the system remain coupled leading to an increased computational load. There are emerging techniques that can potentially solve these models whilst not being computationally too expensive, such as using artificial neural networks [46, 54].

The theory could also be applicable in the context of viscoelasticity. The recent work [55] considers an underlying microstructure comprising several elastic phases and a fluid phase which when upscaled via asymptotic homogenzation gives a Kelvin–Voigt-type model for viscoelastic composites. It would be possible to extend this to assume that the solid phases were indeed pre-stressed. Fractional viscoelasticity has recently been used to analyse experimental data that describe the behaviour of a variety of heterogeneous biological materials. In [56], the effective properties of a composite with viscoelastic constitutive response is considered where each constituent is described by a fractional viscoelastic model. This could be further developed to include a pre-stress within each constituent of the composite.

In order to progress the model further, it would be necessary to obtain solutions to the model using a specific microstructure with the parameters chosen by real-world data. These data could relate to a wide variety of biological examples including artery walls and the myocardium. In the literature, the macroscale model of standard Biot’s poroelasticity has been solved by [33] and the microscale cell problems for poroelasticity have been solved by [32] and those for poroelastic composites solved by [34].

Appendix

In this appendix, we provide both the notation used throughout as well the cell problems for the different choices of pre-stresses discussed in Sect. 4.1 in components.

1.1 Notation

In this section, we will define exactly what is meant by the operations carried out between all the tensor and vector fields in our computations.

When we have the double contraction between a general fourth-rank tensor $\mathbb {F}$ and a second-rank tensor ${\textsf{F}}$ written as $\mathbb {F}{\textsf{F}}$, then in components this is given by

$$\begin{aligned} (\mathbb {F})_{ijkl}({\textsf{F}})_{kl}, \end{aligned}$$

(120)

where sum over repeated indices is understood. Similarly when we have the double contraction between a third-rank tensor ${\mathcal {F}}$ and a second-rank tensor ${\textsf{F}}$ which is written as ${\mathcal {F}}{\textsf{F}}$, we write

$$\begin{aligned} ({\mathcal {F}})_{ikl}({\textsf{F}})_{kl}, \end{aligned}$$

(121)

and again sum over repeated indices is understood. For the operation between a second-rank tensor ${\textsf{F}}$ and a vector $\textbf{f}$, we use the notation ${\textsf{F}}{} \textbf{f}$ which in components is

$$\begin{aligned} ({\textsf{F}})_{ik}(\textbf{f})_k, \end{aligned}$$

(122)

again with sum over repeated indices. Finally we have the scalar product between two vectors, say $\textbf{f}$ and $\textbf{p}$, which is written $\textbf{fp}$, and in components will be

$$\begin{aligned} (\textbf{f})_k(\textbf{p})_k, \end{aligned}$$

(123)

with the sum over k.

1.2 Pre-stress depends on both microscale and macroscale

When we have the decomposition of the pre-stress in each solid phase into a macroscale component and a microscale component (81a)–(81b), we have four sets of cell problems (83a)–(83f), (84a)–(84f), (85a)–(85f) and (86a)–(86f). The first two kinds in components are given by (101a)–(101f) and (102a)–(102f). We then must write (85a)–(85f) and (86a)–(86f) in components. That is,

$$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{c}})\bigg )+\frac{\partial (\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0c}(y))_{ijkl}}{\partial y_j}=0&\quad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(124a)

$$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{p}})\bigg )=0&\quad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(124b)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{cp}}_j-C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{cp}}_j=-(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0c}(y))_{ijkl}n^{\scriptscriptstyle \textrm{cp}}_j&\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(124c)

$$\begin{aligned} {\mathcal {B}}^{\scriptscriptstyle \textrm{c}}_{ikl}={\mathcal {D}}^{\scriptscriptstyle \textrm{p}}_{ikl}&\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(124d)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{c}}_j +(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0c}(y))_{ijkl}n^{\scriptscriptstyle \textrm{c}}_j=0&\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(124e)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{p}}_j =0&\quad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(124f)

and

$$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{c}})\bigg )=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(125a)

$$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{p}})\bigg )+\frac{\partial (\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0p}(y))_{ijkl}}{\partial y_j}=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(125b)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{cp}}_j-C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{cp}}_j=(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0p}(y))_{ijkl}n^{\scriptscriptstyle \textrm{cp}}_j&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(125c)

$$\begin{aligned} {\mathcal {D}}^{\scriptscriptstyle \textrm{c}}_{ikl}={\mathcal {B}}^{\scriptscriptstyle \textrm{p}}_{ikl}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(125d)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{c}}_j =0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(125e)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{p}}_j +(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0p}(y))_{ijkl}n^{\scriptscriptstyle \textrm{p}}_j=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(125f)

We make the assumption that the notation for the gradient of the third-rank tensors ${\mathcal {B}}^{\scriptscriptstyle \textrm{c}}$, ${\mathcal {B}}^{\scriptscriptstyle \textrm{p}}$, ${\mathcal {D}}^{\scriptscriptstyle \textrm{c}}$ and ${\mathcal {D}}^{\scriptscriptstyle \textrm{p}}$ is the same as the notation used for ${\mathcal {A}}^{\scriptscriptstyle \textrm{c}}$ and ${\mathcal {A}}^{\scriptscriptstyle \textrm{p}}$ in (104a).

We also consider the case that when we decompose the pre-stresses we have the continuity of the macroscale component between the two phases (87). This means that we obtain the cell problems (83a)–(83f), (84a)–(84f) and (89)–(94). We have already written the problems (83a)–(83f) and (84a)–(84f) in components in equations (101a)–(101f) and (102a)–(102f). So we can just write the different problem (89)–(94) in components as

$$\begin{aligned}&\frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{c}})\bigg )+\frac{\partial (\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0c}(y))_{ijkl}}{\partial y_j}=0\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(126a)

$$\begin{aligned}&\frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{p}})\bigg )+\frac{\partial (\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0p}(y))_{ijkl}}{\partial y_j}=0\quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(126b)

$$\begin{aligned}&C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{cp}}_j-C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{cp}}_j=((\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0p}(y))_{ijkl}\nonumber \\&\quad -(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0c}(y))_{ijkl})n^{\scriptscriptstyle \textrm{cp}}_j\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(126c)

$$\begin{aligned}&{\mathcal {B}}^{\scriptscriptstyle \textrm{c}}_{ikl}={\mathcal {B}}^{\scriptscriptstyle \textrm{p}}_{ikl}\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(126d)

$$\begin{aligned}&C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{c}}_j +(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0c}(y))_{ijkl}n^{\scriptscriptstyle \textrm{p}}_j =0\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(126e)

$$\begin{aligned}&C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{p}}_j +(\sigma ^{\scriptscriptstyle \mathrm {(0)}}_{0p}(y))_{ijkl}n^{\scriptscriptstyle \textrm{p}}_j=0\quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(126f)

1.3 Pre-stress depends only on the macroscale

The final cell problems we need to consider are for the case that the pre-stresses depend only on the macroscale. This is the pre-stresses are given by (97a) and (97b). This leads to the cell problems (83a)–(83f), (84a)–(84f), (99a)–(99f) and (100a)–(100f). We have already written the problems (83a)–(83f) and (84a)–(84f) in components in equations (101a)–(101f) and (102a)–(102f). So we can just write the different problems (99a)–(99f) and (100a)–(100f) in components as

$$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{c}})\bigg )=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(127a)

$$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{p}})\bigg )=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(127b)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{cp}}_j-C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{cp}}_j=-\delta _{ik}\delta _{jl}n^{\scriptscriptstyle \textrm{cp}}_j&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(127c)

$$\begin{aligned} {\mathcal {B}}^{\scriptscriptstyle \textrm{c}}_{ikl}={\mathcal {D}}^{\scriptscriptstyle \textrm{p}}_{ikl}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(127d)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{c}}_j +\delta _{ik}\delta _{jl}n^{\scriptscriptstyle \textrm{c}}_j=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(127e)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{p}}_j =0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(127f)

and

$$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{c}})\bigg )=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(128a)

$$\begin{aligned} \frac{\partial }{\partial y_{j}}\bigg (C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{p}})\bigg )=0&\qquad \quad \text{ in } \quad \Omega _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(128b)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{cp}}_j-C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{cp}}_j=\delta _{ik}\delta _{jl}n^{\scriptscriptstyle \textrm{cp}}_j&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(128c)

$$\begin{aligned} {\mathcal {D}}^{\scriptscriptstyle \textrm{c}}_{ikl}={\mathcal {B}}^{\scriptscriptstyle \textrm{p}}_{ikl}&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{cp}}, \end{aligned}$$

(128d)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{c}}_{ijpq}\xi _{pq}^{kl}({\mathcal {D}}^{\scriptscriptstyle \textrm{c}})n^{\scriptscriptstyle \textrm{c}}_j =0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{c}}, \end{aligned}$$

(128e)

$$\begin{aligned} C^{\scriptscriptstyle \textrm{p}}_{ijpq}\xi _{pq}^{kl}({\mathcal {B}}^{\scriptscriptstyle \textrm{p}})n^{\scriptscriptstyle \textrm{p}}_j +\delta _{ik}\delta _{jl}n^{\scriptscriptstyle \textrm{p}}_j=0&\qquad \quad \text{ on } \quad \Gamma _{\scriptscriptstyle \textrm{p}}, \end{aligned}$$

(128f)