Evaluation of reservoir subsidence due to hydrocarbon production based on seismic data

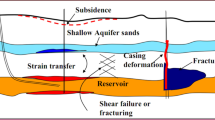
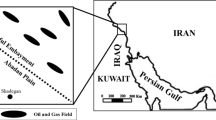
Abstract

Environmental problems associated with depleted oil and gas reservoirs upon long-term production from them are likely to become important challenges in future decades. With the increasing trend of production from hydrocarbon reservoirs, more and more reservoirs across the world are reaching the second half of their life—a fact that places an emphasis on the necessity of investigating what is known as reservoir subsidence. Different analytical and numerical approaches have been introduced for analyzing the subsidence on the basis of the elasticity theory but in the form of case studies, leaving a comprehensive model yet to be proposed. In this work, a formulation was introduced for estimating reservoir subsidence by integrating the rock physics, rock mechanics, and thermo-poroelasticity theories. Then, a modified version of this formulation was developed to calculate compaction in an actively producing reservoir that is suspect of subsidence, as a case study. For this purpose, triaxial hydrostatic tests were carried out on core plugs obtained from the considered reservoir, and then, compaction parameters (i.e., compression index and coefficient of deformation) were obtained at a laboratory scale. In order to evaluate the subsidence at a reservoir scale, the laboratory-scale results and in situ reservoir properties were integrated with well-logging and 3D seismic data at well location to come up with 3D cubes of compaction information. Continuing with the research, time-dependent inelastic deformation was modeled considering continued production for different future periods. The field observations showed that the estimated compaction is not visible at the surface in the form of subsidence due to the high depth and stiffness of the studied reservoir. However, collapse of casing at some of wells drilled into the studied reservoir could be attributed to the reservoir subsidence. Finally, variations of compaction with pore pressure were investigated to propose a model for predicting the subsidence in future periods. Findings of this research can be used to forecast subsidence at well location to take the required measures for avoiding possible casing collapse and/or relevant environmental issues.

Introduction

The knowledge of deformation mechanisms associated with the reservoir compaction and subsidence phenomena plays a vital role in environmental management of hydrocarbon production. The loss of pore pressure upon depletion of a hydrocarbon reservoir can lead to increased effective pressure and hence reservoir compaction. In extreme cases, this deformation of reservoir can end up with subsidence (Geertsma 1973; Chan and Zoback 2002; Doornhof et al. 2006; Sayers et al. 2007; Zhukov et al. 2021; Pei et al. 2023). Indeed, the dramatic decrease in pore pressure as a result of hydrocarbon production can impose significant impacts on the physical and mechanical properties of the reservoir rock. Referring to a form of deformation, reservoir compaction can cause porosity loss, wellbore instability, fault reactivation, earthquakes, and even subsidence at surface (Gurevich and Chilingarian 1995; Settari 2002; Hagin and Zoback 2004; Jelmert and Toverud 2018; Gazzola et al. 2023). During the recent century, numerous examples of reservoir subsidence have been reported across the world, including those in Goose Creek oil and gas field (Harris County, Texas), Wilmington field (Los Angeles), Valhall and Ekofisk fields (North Sea), the Field X (Gulf of Mexico), Bolivar Coast oil reservoirs (Venezuela), and Groningen gas reservoir (the Netherlands) (Sulak 1991; Doornhof et al. 2006). Then, scientists started to investigate depletion-induced reservoir compaction and subsidence across the world. Perhaps the first discussion on reservoir compaction was given by Geertsma (1973) who investigated the subsidence by defining uniaxial compaction coefficient. Later on, Addis (1997) investigated the changes in pore pressure and minimum stress upon reservoir depletion and the effect of such changes on the wellbore stability. Chan and Zoback (2002) proposed a formalism known as deformation analysis in reservoir space (DARS) for evaluating production-induced faulting and reservoir compaction. Hagin and Zoback (2004) investigated the application of viscous deformation of unconsolidated sandstone reservoirs considering attenuation parameters and time-dependent deformation. Höök et al. (2014) demonstrated that the size of an oilfield has significant influences on the decline and depletion rates. Yuan et al. (2013) investigated the production-induced reduction in horizontal stress and its effect on borehole stability along both the reservoir and cap rock using the geophysical logging data. Jelmert and Toverud (2018) and Mahajan et al. (2018) proposed analytical methods for modeling reservoir compaction and studied the impact of depletion on permeability. Shahbazi et al. (2020) predicted the effect of production-induced pressure drop on wellbore stability and sand control design. Gazzola et al. (2023) developed a robust workflow for subsidence prediction at reduced levels of uncertainty. Many works have reported on subsidence (e.g., Newman 1973; Sulak 1991; Gurevich et al. 1995; Nagel 2001; Ong et al. 2001; Doornhof et al. 2006; Taherynia et al. 2013; Ferronato et al. 2020; Zhukov et al. 2021; Kusolsong et al. 2023), the majority of which has approached the subsidence as an elastic behavior of rock, largely ignoring the plastic (collapse), creeping, and thermal properties of the rock. Moreover, most of research works on reservoir subsidence has seen it as sensible physical deformation at surface (e.g., Goose Creek oil and gas field, Wilmington field, Valhall and Ekofisk fields), leaving the compaction behavior and modeling of other reservoirs, where such physical deformation is still not observable at the surface, yet to be evaluated and rather remain challenging. Accordingly, considering the increasing rate of production from hydrocarbon reservoirs during the past century, it seems necessary to develop a comprehensive model for analyzing the reservoir subsidence, with outputs that can be conveniently incorporated into reservoir characterization schemes. In the soil engineering, the settlement (and consolidation) analysis represents a well-established area that is routinely used in construction projects (Terzaghi 1943; Das 1999). From an engineering point of view, unlike soil, a deep hydrocarbon reservoir is made up of a dense rock frame and undergoes physical and chemical compactions due to extremely high overburden pressures to which it is exposed (Brady and Brown 1985; Goodman 1989). Furthermore, it is known that the overburden pressure cannot normally increase during the production life of a reservoir, but the reservoir depletion leads to a reduction in pore pressure, thereby increasing the effective stress. This reveals that production-induced compression and plastic deformation of reservoir are inevitable to any reservoir, although to variable degrees—significant phenomena that can bring about a wide spectrum of side effects ranging from wellbore instability to subsidence at surface.

The present research is aimed at developing an approach for modeling the reservoir subsidence. For this, a review was carried out with relevant theories in the field of soil mechanics, rock physics, rock mechanics, and poromechanics. Then, modifications were made to the theories to introduce an analytic approach to reservoir subsidence estimation. Considering the significant impact of compressibility on rock deformation, the compaction was herein simulated using the results of triaxial hydrostatic tests on core samples. For this purpose, 10 core plugs were acquired from a reservoir that was suspected of subsidence. Next, based on the modified theoretical framework, laboratory-scale compaction analysis was performed and compaction rate was evaluated. Eventually, the laboratory-scale results were upscaled to reservoir scale by incorporating seismic and well-logging data.

Reservoir compaction modeling

In construction engineering, the terms compaction and consolidation have been interchangeably used for describing permanent deformation of rock/soil. In this respect, the compaction (consolidation) refers to a form of deformation that occurred upon expulsion of air (water/hydrocarbon) from pores. The settlement is a consequence of compaction/consolidation and can develop to subsidence in extreme cases (Terzaghi 1943; Bowles 1996; Das 1999). Indeed, the settlement is defined as vertical movement of the ground due to changes in the stress field within the earth, while the subsidence is simply defined as the sinking of the earth surface, which may not be necessarily related to stress changes. The term compaction has been used instead of settlement in reservoir engineering. Geologically speaking, the term compaction refers to a set of physical and/or chemical processes that occurred as part of the lithification of soil into rock and then diagenesis of the rock unit. As a reservoir gets depleted upon production, an increase in effective stress occurs due to decreased pore pressure. This leads the rock mass toward progressive compaction. Reservoir subsidence can be evaluated in terms of total compaction and the compaction rate (time-dependent deformation).

Compaction simulation using hydrostatic test

A rock sample can be modeled as a porous medium that is made up of minerals and pores with a complex geometry. Focusing on the pores, one can distinguish different classes of them, including compliant, soft, and stiff pores, which can be saturated with brine, oil, or gas (e.g., Avseth et al 2005; Zhao et al. 2013). When a rock specimen is subjected to non-deviatoric stress in a triaxial (or uniaxial oedometer cell), the effective stress applied to the grains increases, leading to some permanent decrease in the inter-grain volume upon the collapse of the pores (Brady and Brown 1985; Das 1999). Figure 1 shows the diagram of hydrostatic stress versus volumetric deformation, indicating four clear regions.

Fig. 1

Diagram of hydrostatic pressure versus volumetric strain (modified after Goodman 1989). Four regions can be distinguished along the curve, referring to plastic (crack closing), elastic, failure (pore collapse), and creep regions, respectively. K_ϕP, K_ϕE, K_ϕF, and K_ϕC denote the pore-space stiffness in different regions

In the first stage of loading, preexisting compliant pores (e.g., cracks and fissures) are closed and the soft pores (e.g., inter-grain pores in poorly compacted sandstone) are slightly compressed. In this stage, compliant pores remain closed even if the applied load is removed, exhibiting some plastic behavior. In the second stage, the soft pores are closed and the stiff pores are deformed, resulting in compression at an approximately linear rate. The slope of the diagram in this region is known as the bulk modulus (or compressibility). In the third stage (or post-elastic stage), the pores in porous rocks (e.g., sandstone and weak limestone) start to collapse under the effect of concentrated stress around them. In well-cemented rocks, such a collapse of pore space may not occur unless the confining stress goes beyond 100 MPa (~ 14,400 psi), while it begins at much lower pressure levels in loosely cemented rocks. Upon closure of all pores, a fourth stage emerges where only matrix or grains are remaining and compressibility becomes progressively low (Walsh 1965; Goodman 1989; Ashena et al. 2020a, b; Nourifard et al. 2020; Sharifi et al. 2020; Malki et al. 2023). The value of compressibility in different stages is related to pore-space stiffness. In the crack closing region, the pore-space stiffness is determined by the compressibility of cracks (pore-space stiffness of the plastic region, K_ϕP). In the same way, pore-space stiffness in the elastic and the failure regions are controlled by soft and stiff pores, respectively (K_ϕE and K_ϕF, respectively). In the creep stage, the effective pore stiffness is associated with the rock matrix (K_ϕC). During a drained triaxial test on a saturated carbonate rock specimen with vuggy pores, pore-space stiffness (K_ϕ) may further include the effect of fluid compressibility for stiffness measurement (Mavko et al. 2009; Sharifi et al. 2023).

Therefore, the compaction that occurred to a specimen in different stages of a triaxial test can be physically measured using axial and radial strain gauges installed around the specimen. Considering the overall compression occurred in the four mentioned stages, total compaction, C_T, can be defined as the algebraic summation of the reduction in the sample height (e.g., in cm), as follows:

$${C}_{\mathrm{T}}={C}_{\mathrm{P}}+{C}_{\mathrm{E}}+{C}_{F}+{C}_{\mathrm{C}}$$

(1)

where C_P is the first plastic compaction due to the closure of cracks and fissures, C_E is the elastic compaction resulted as soft pores are closed (i.e., stiff pores are compressed), C_F is the stiff pore collapse-induced compaction, and C_C refers to matrix compression or creep (i.e., a time-depended phenomenon). Unlike creep-induced compaction, the deformations that occurred during the crack closing, elastic, and pore collapse stages are time-invariant.

Subsidence evaluation using analytic method

After evaluating the deformation on the triaxial/uniaxial apparatus in laboratory conditions, the results can be upscaled to the entire reservoir interval to measure total compaction. In order to calculate the compaction in the elastic region due to water expulsion from the sample (resembling reservoir depletion), one should calculate the change in porosity (ϕ) due to changes in bulk volume of the sample, including the minerals and pore space, as follows:

$$\phi =\frac{{V}_{\mathrm{p}}}{{V}_{\mathrm{b}}}=\frac{{V}_{\mathrm{b}}-{V}_{\mathrm{m}}}{{V}_{\mathrm{b}}}=1-\frac{{V}_{\mathrm{m}}}{{V}_{\mathrm{b}}} ,$$

(2a)

$${V}_{\mathrm{b}}={V}_{\mathrm{p}}+{V}_{\mathrm{m}}$$

(2b)

where V_p is pore volume, V_b is bulk volume, and V_m is matrix/mineral/solid volume. In civil engineering, the common practice is to use the dimensionless quantity of void ratio (e), instead of porosity, with the following definition (Das 1999):

$$e = \frac{{V_{{\text{p}}} }}{{V_{{\text{m}}} }} = \frac{{V_{{\text{p}}} }}{{V_{{\text{b}}} - V_{{\text{p}}} }} = \frac{\phi }{1 - \phi } \Rightarrow \phi = \frac{{V_{{\text{p}}} }}{{V_{{\text{p}}} + V_{{\text{m}}} }} = \frac{e}{e + 1}$$

(3)

Consider an initial mass of rock volume of V_b1 which is compressed to a final volume of V_b2 during a compression test. Assuming that any change in the rock volume is solely caused by a reduction in the volume of the voids, the relationship between volumetric changes of the rock mass and the void ratio can be obtained as follows:

$$\Delta V=\frac{{V}_{\mathrm{b}1}{- V}_{\mathrm{b}2}}{{V}_{\mathrm{b}1}}=\frac{\left({V}_{\mathrm{p}1}+{V}_{m}\right)-\left({V}_{\mathrm{p}2}+{V}_{\mathrm{m}}\right)}{\left({V}_{\mathrm{p}1}+{V}_{\mathrm{m}}\right)} ,$$

(4)

dividing both numerator and denominator by V_m gives:

$$\Delta V=\frac{\left({e}_{1}+1\right)-({e}_{2}+1)}{{e}_{1}+1}=\frac{{e}_{1}{- e}_{2}}{{e}_{1}+1}=\frac{\Delta e}{1+{e}_{1}}$$

where ΔV is the volumetric change (in cm³) and e₁ and e₂ are initial and final void ratios during the compaction test. Volumetric change of the sample due to the applied pressure is defined as coefficient of volume compressibility (m_v) and measures the compression of a rock or soil sample per unit original thickness upon unit increase in pressure, as follows:

$${C}_{\mathrm{C}}=\sum_{i=1}^{n}{{H}_{3i}\sigma }^{\prime}_{vi}{C}_{m}$$

(5)

where m_v is in m²/kN, the reciprocal of m_V has the units of stress modulus (kPa or MPa) which is often referred to as the constrained modulus (Bowles 1996). Accordingly, should the sample area be fixed (ΔV/V = ΔH/H) in the uniaxial oedometer cell (or in hydrostatic compression), volumetric change of the sample is completely translated into a thickness change from H₁ to H₂. Then, variations of sample thickness can be derived from Eq. (4) as:

$$\Delta V=\frac{{V}_{\mathrm{b}1}{- V}_{\mathrm{b}2}}{{V}_{\mathrm{b}1}}=\frac{{H}_{1}{- H}_{2}}{{H}_{1}}=\frac{\Delta e}{1+{e}_{1}}$$

(6)

Once finished with measuring the porosity changes due to changes in the effective stress in a compression test under reservoir condition, the laboratory data could be upscaled to match the full scale of the whole reservoir. As a reservoir is being depleted, the level of stress acting onto the rock mass increases, subjecting the reservoir to vertical compaction or what is known as settlement (S) in the geotechnics. Skempton and Bjerrum (1957) were the first to formulate a methodology for settlement (plastic compaction) analysis in soil-based foundation studies, as below:

$$S={\int }_{0}^{Z}{\varepsilon }_{z}\mathrm{d}z={\int }_{0}^{Z}\frac{\Delta e}{1+{e}_{1}}\mathrm{d}z={\int }_{0}^{Z}{m}_{V}\Delta u\mathrm{d}z$$

(7a)

$$\Delta u=B\left[\Delta {\sigma }_{3}+A(\Delta {\sigma }_{1}-\Delta {\sigma }_{3})\right]$$

(7b)

where z is height of the studied layer (in cm), ε_z is vertical strain, σ₁ and σ₃ are maximum and minimum stress components (in MPa), respectively, u is pore pressure (in MPa), A is pore pressure coefficient, and B is Skempton coefficient (Terzaghi 1943; Sowers 1979; Barnes 2000). For a reservoir rock, one may ignore the effect of lateral strain (Eq. 6) and assume ΔP equal to Δσ₁, Δσ₃, and Δu to come up with the following expression of the general compaction theory for the reservoir rock:

$$\mathrm{S}=\frac{{\Delta eH}_{1}}{1+{e}_{1}}$$

(8)

Once finished with calculating the void ratio for each sample upon hydrostatic tests, a typical semi-logarithmic laboratory compressibility diagram can be developed, as presented in Fig. 2, by plotting the void ratio versus effective pressure. Drawn in semi-logarithmic scale, this laboratory compressibility curve is approximately double linear and delineates over-compacted and normally-compacted ranges by its slope, referring to the dimensionless quantities of recompression (C_r) indices and compression indices (I_c), respectively.

Fig. 2

A simplified diagram showing the results of hydrostatic laboratory tests in the plastic and elastic regions. Vertical axis is void ratio and horizontal axis indicates effective pressure in logarithmic scale. The compression (I_c) and recompression indices (C_r) are also indicated. Modified after Bowles (1996) and Das (1999)

As shown in Fig. 2, the recompression segment slope is relatively slower than the original compression segment. Considering the slope of the recompression segment of the diagram, the over-compaction/coring-induced deformation can be seen in the initial stage of loading (crack closing region), as follows (Sowers 1979; Bowles 1996):

$${C}_{\mathrm{P}}=\sum_{i=1}^{n}\frac{{{C}_{ri}H}_{1i}}{1+{e}_{1i}}\mathrm{log}\left(\frac{{\sigma }_{vi}{\prime}}{{\sigma }_{v0i}{\prime}}\right)$$

(9)

where H₁ and e₁ are initial height and void ratio of ith layer, respectively. Moreover, σ'_v0i is initial stress and σ'_vi denotes in situ stress. In the same way, elastic loading-induced compaction can be expressed as follows:

$${C}_{\mathrm{E}}=\sum_{i=1}^{n}\frac{{{I}_{ci}H}_{1i}}{1+{e}_{1i}}\mathrm{log}\left(\frac{{\sigma }_{\mathrm{vfi}}{\prime}}{{\sigma }_{\mathrm{vi}}{\prime}}\right)$$

(10)

where σ´_vfi is final stress under hydrostatic loading. Sample compressibility in the crack closing and elastic regions is estimated from Fig. 1. As an alternative to the derived equation (Eq. 10) and confirming this model, the Geertsma (1973) formulation proposes the same approach for estimating the compaction in the elastic region for reservoir subsidence:

$$\Delta h=\underset{0}{\overset{h}{\int }}\left(\frac{1+v}{3(1-v)}(1-\beta ){C}_{\mathrm{b}}\right)(z)\Delta P\left(z\right)\mathrm{d}z$$

(11)

where Δh is the change in compaction of a given layer (in cm), z is depth of layer (in cm), P refers to effective stress (in MPa), which is herein equal to in situ stress (σ'_v), υ is Poisson’s ratio, C_b denotes hydrostatically determined bulk compressibility (in MPa⁻¹), and β is the ratio between rock matrix (C_m) and bulk rock compressibility (C_m/C_b). With increasing the effective pressure beyond the stiffness of stiff pores, elastic compaction is surpassed and pores start to collapse, converting the rock to some zero-porosity matrix. In this condition, ultimate compaction equals the reduction in total porosity (pore collapse):

$${C}_{\mathrm{F}}=\sum_{i=1}^{n}\frac{{{e}_{2i}H}_{2i}}{1+{e}_{2i}}$$

(12)

in which H₂ is the final sample height, where the sample compressibility is much lower than those measured in other stages of testing. In the failure stage, however, the compressibility increases to a maximum value due to the pore collapse.

During a compression test, variations of porosity in relation to bulk and matrix strains can be obtained by Zimmerman’s (2017) equation. He combined the matrix and bulk strains with pore volume (Eqs. 2–3) during volumetric deformation to obtain the porosity variations as follows:

$$d\phi =-\frac{{dV}_{\mathrm{m}}}{{V}_{\mathrm{b}}}+\frac{{V}_{\mathrm{m}}}{{V}_{\mathrm{b}}^{2}}\mathrm{d}{V}_{\mathrm{b}}=-\frac{{V}_{\mathrm{m}}}{{V}_{b}}\frac{{dV}_{\mathrm{m}}}{{V}_{\mathrm{m}}}+\frac{{V}_{\mathrm{m}}}{{V}_{\mathrm{b}}}\frac{d{V}_{\mathrm{b}}}{{V}_{\mathrm{b}}}=-\left(1-\phi \right)\left({\varepsilon }_{\mathrm{b}}-{\varepsilon }_{\mathrm{m}}\right)$$

(13)

where ε_b denotes the bulk volume strain and ε_m is volumetric strain of the matrix. As the applied pressure increases, the rock matrix undergoes changes, and the resultant matrix strain versus pore pressure can be found by starting with the following general equation for the solid mineral phase strain, which holds true under hydrostatic stresses (Geertsma 1973; Jalalh 2006; Zimmerman 2017):

$${\varepsilon }_{\mathrm{b}}=-\frac{(1+v)}{(1-v)} {T\alpha }_{T}$$

(14a)

$$\varepsilon_{{\text{m}}} = C_{{\text{m}}} \left( {\frac{P - \phi u}{{1 - \phi }}} \right)$$

(14b)

where T is temperature, α_T refers to linear thermal expansion coefficient, and P is confining stress, which is herein equal to in situ stress (σ'_v) in reservoir condition. Assuming zero porosity and pore pressure in the end of the failure stage, Eq. (5) and Eq. (13) can be rewritten according to the matrix strain and creep equation, as follows:

$${C}_{\mathrm{C}}=\sum_{i=1}^{n}{{H}_{3i}}\sigma^{\prime}_{\mathrm{vi}}{C}_{\mathrm{m}}$$

(15)

where H₃ is the ultimate sample height in the last stage. The creep-driven compaction also can be expressed based on the poroelastic theory of Geertsma (1973), further confirming Eq. (15):

$$\frac{\Delta H}{{H}_{0}}=\Delta P\alpha {C}_{\mathrm{m}}\Rightarrow \Delta H={H}_{1}\Delta P{C}_{\mathrm{m}}$$

(16)

where α is the Biot coefficient and is presumably equal to 1 in zero-porosity condition.

In order to come up with a comprehensive study of the compaction behaviour of a porous rock, one needs some knowledge about temporal variations of not only pressure but also temperature. As an extension to the theory of poromechanics, the theory of thermoelasticity can be used to study pore pressure variations (du) as a function of changes in temperature (T) and confining pressure (dσ) in undrained condition, as follows:

$$du=Bd\sigma +\mathrm{\Lambda d}T$$

(17)

where Λ is the thermal pressurization and B is Skempton coefficient. Introducing poromechanics parameters into Eq. (17), one can evaluate porosity variations as below (Coussy 2004; Ghabezloo et al. 2009; Salimzadeh et al. 2018):

$$\frac{\mathrm{d}\phi }{\phi }=-\frac{1}{{\phi }_{0}}\left(\frac{1-{\phi }_{0}}{{K}_{\mathrm{dry}}}-\frac{1}{{K}_{\mathrm{m}}}\right)\mathrm{d}{\sigma }_{d}+\left(\frac{1}{{K}_{\mathrm{m}}}-\frac{1}{{K}_{\phi }}\right)\mathrm{d}u-\left({\alpha }_{\mathrm{d}}-{\alpha }_{\phi }\right)\mathrm{d}T$$

(18)

where K_m, K_dry, and K_fl denote the matrix, frame (dry), and fluid moduli (in GPa), respectively. Also dσ_d is differential pressure, K_ϕ is the dry pore-space stiffness (in GPa), ϕ represents total porosity, α_ϕ is pore volume thermal expansion coefficient, and α_d refers to volumetric drained thermal expansion coefficient. So, considering the thermoelasticity theory for compaction and Eq. (5), effect of temperature in each step of compaction can be obtained in the face of thermal expansion equation:

$$-\frac{\mathrm{d}H}{{H}_{1}}=\frac{\mathrm{d}{\sigma }_{d}}{{K}_{\mathrm{dry}}}+\frac{\mathrm{d}u}{{K}_{\mathrm{m}}}-{\alpha }_{d}\mathrm{d}T$$

(19)

$${\text{d}}H = C_{{\text{T}}} \alpha_{{\text{d}}} {\text{d}}T = H_{1} \alpha_{{\text{d}}} {\text{d}}T\, ({\text{d}}\sigma_{d} \,{\text{and \,d}}u = 0)$$

(19a)

where H₁ is the sample height in the first/last stage. Equation (19a) is another derivation for a case where variations of deviatoric stress and pore pressure are zero. Both sides of Eq. (19) are always negative, indicating expansion, as opposed to a compaction.

Rate of compaction

The progress of compaction is directly related to the dissipation of excess pore pressure during the course of hydrostatic test. In this regard, the most common approach to the prediction of the compaction rate is to use one-dimensional classical theory of Terzaghi (1943), as follows:

$${c}_{\mathrm{v}}=\frac{k}{{\gamma }_{f}{m}_{v}}=\frac{k(1+{e}_{0})}{{\gamma }_{f}{a}_{v}}$$

(20a)

$$a_{{\text{v}}} = \frac{\Delta e}{{\Delta P}}$$

(20b)

where k is hydraulic conductivity (in m/s), a_v denotes coefficient of compressibility (in m²/kN), γ_f is unit weight of water (in kN/m³), and c_v

In the foregoing theory, z is measured from the top of the studied layer and complete drainage is assumed at both the upper and lower surfaces, the thickness of the layer being taken as 2H, the initial excess pore pressure being expressed as Δu =− ΔP, and the boundary conditions being mathematically expressed as [z = 0, u = 0], [z = 2H, u = 0], and [t = 0, u = Δu], so that one can write:

$${c}_{v}\frac{{\partial }^{2}u}{{\partial z}^{2}}=\frac{\partial u}{\partial t}$$

(21)

In general, c_v is not a constant value as its constituting parameters vary throughout the compaction process. As a compaction-induced decrease in thickness may alter the permeability, coefficients of compaction can be of great help (Jelmert and Toverud 2018; Mahajan et al. 2018). The classical Terzaghi theory assumes constant permeability and applicability of the Darcy's law of saturated flow. It also considers soil as being a homogeneous and saturated medium and attributes variations in the sample volume to changes in the void ratio. Other assumptions made under this theory include one-dimensional nature of the compression phenomenon and single-direction nature of the water flow in the sample. Provided the above assumptions are admitted, the Fourier series can be used to solve the compaction equation analytically through defining the following dimensionless quantities:

$$Z=\frac{z}{{H}_{\mathrm{dr}}}$$

(22)

$${U}_{z}=1-\frac{u}{{u}_{t}}$$

(23)

where z is the depth of compressible stratum (in cm), H_dr is the pore fluid drainage length, u is excess pore pressure at time t (in s) and position z, and u_i is initial excess pore pressure at position z. Moreover, Z is the dimensionless depth within the compacting layer and U_z is the compaction ratio (in percent). Using a Taylor series expansion (Bowles, 1996), the u parameter in Eq. (21) can be rewritten as:

$$u=\sum_{n=1}^{n=\infty }\left(\frac{1}{H}{\int }_{0}^{2H}{u}_{i}\mathrm{sin}\frac{n\pi z}{2H}\mathrm{d}z\right)\left(sin\frac{n\pi z}{2H}\right)\mathrm{exp}\left(\frac{{n}^{2}{\pi }^{2}{c}_{\mathrm{v}}t}{4{H}^{2}}\right)$$

(24)

Then, average compaction of U_z after some elapsed time can be obtained as follows:

$${U}_{i}=1-\frac{\mathrm{Area \,of\, current \,excess \,pore \,pressure \,}}{\mathrm{Area \,of \,initial \,excess \,pore \,pressure \,}}=1-\frac{{u}_{i}}{{u}_{0}}=1-\sum_{m=0}^{m=\infty }\frac{2}{{M}^{2}}\mathrm{exp}(-{M}^{2}{T}_{t})$$

(25)

where

$$M=\frac{\pi }{2}\left(2m+1\right)$$

(25a)

$$n = \left( {2m + 1} \right)$$

(25b)

where m is a constant and positive integer value (varying from 0 to ∞) and T_t is the time factor and serves as a measure of dimensionless time. Eventually, dimensionless parameter of time factor is obtained as below:

$${T}_{t}=\frac{{c}_{\mathrm{v}}t}{{H}_{dr}^{2}}$$

(26)

where t is the elapsed time of compaction (in s).

Case study

With the theory of compaction explained (by modification the consolidation theory in soil mechanics and rock physics), this section verifies the proposed methodology on a real case study. For this, a workflow was developed to carry out experimental tests and compaction analysis on a given reservoir, as demonstrated in Fig. 3. The workflow covers investigations at two scales, namely laboratory and reservoir scales, with the results related to one another through a handful of coefficients and indices. That is, the coefficients and indices were obtained in the laboratory using core samples and then generalized to the reservoir scale.

Fig. 3

Workflow of the present research covering in-lab experiments and other investigations at reservoir scale. The relationships between core-scale and reservoir-scale analyses in all stages are further indicated. The indicated coefficients and indices were obtained from laboratory testing and then used for reservoir simulation

Geological framework and reservoir dataset

The case study is a carbonate oilfield in SW of Iran (Fig. 4) where an exploratory and several production wells were drilled. It produces oil from Cretaceous Sarvak Formation (deposited during Santonian—Campanian). The Sarvak Formation overlies the Kazhdumi Formation—a dominantly shaly stratum that is well known for serving the local reservoirs as source rock (Nabavi 1976; Asl and Aleali 2016). Geologically speaking, the study area is located in the Abadan Plain (north of Persian Gulf), a part of the Dezful Embayment along the Zagros Mountain Chain, where three-dimension (3D) seismic data (normal moveout-corrected pre-stack migrated CMP gathers processed using the Kirchhoff prestack time migration) were available across the study area. The seismic dataset included five partial-angle stacks at five angles ranging from 5° (i.e., near-angle stack) to 35° (i.e., far-angle stack). To begin, the data were interpreted to identify underground geological structure. Existing geological maps and seismic-based structural interpretations indicated no major fault in the study area. Preparing a horizon map of Sarvak Formation, it was found that this formation exhibits a thickness of about 500 m and ranges 3200–3700 m in depth from mean sea level (MSL). Figure 5 presents a schematic view of the underground geological structure. The reservoir has been producing oil at a rate of 250,000 bbl per day through four wells since after 1980 (A.D.).

Fig. 4

Location map of the study area in south west of Iran. Written in brown are the geological subdivisions of Iran. The green arrow indicates the location of the selected geophysical anticline (AZ oilfield) in the Abadan Plain, Dezful Embayment

Fig. 5

Schematic view of the stratigraphy of the study area in the Abadan Plain. Cross section of geological structures and production well locations are further indicated (AZ-07, AZ-03, and AZ-15). The wells are vertical and the Sarvak Formation serves as reservoir in this area, with the oil trap shown in red

Coring interval and well data

In the current field, exploration and production wells have been drilled into the Sarvak Formation. One of the wells located in this area named Well AZ-15 was chosen for experimental study, and two wells were used for reservoir-scale modeling (AZ-03 and AZ-07). Penetrating the reservoir by some 100 m, the Well AZ-15 was touching a crude with an API of 23 and a density of 0.945 g/cc. Furthermore, coring from the Sarvak Formation was successfully performed along a total length of 120 m at a core recovery ratio of 99%. Then, 10 core plugs were cut out of the whole core in such a way to ensure their representativeness of the studied interval, and zonation was carried out to have a core plug from each zone (Fig. 6). All along the well, a full suite of well logs was available, including porosity, density, sonic, and gamma-ray logs—that are fundamental for reservoir modeling.

Fig. 6

Coring interval and well-logging data along the Well AZ-15. From left to right, these logs represent core zonation interval, vertical stress/well test data (pore pressure estimation log), porosity (NPHI), density (RHOB), gamma ray/water saturation, and lithology, respectively. On this figure, H₀ refers to the height of each zone and T denotes the measured temperature at the time of well test

In order to simulate the reservoir conditions in the laboratory and come up with realistic compaction modeling results, poroelastic formulae were used to build mechanical earth model (MEM); then, in situ stress was estimated along the selected depth interval at points corresponding to the studied core plugs. Based on the results, the effective stress was found to increase by about 1.35 MPa for each 0.1 km increase in the depth of burial. Tectonic activity of the study area was evaluated as low, and the minimum horizontal stress-to-pore pressure ratio (σ_hmin/u) was calculated to range between 1.80 and 1.90. Details of in situ stress estimation were in accordance with Rajabi et al. (2010), Kidambi and Kumar (2016), and Sharifi et al. (2019). Furthermore, Drill Stem Test (DST) was conducted at some points along the studied interval of the Sarvak formation at Well AZ-15. The results showed hydrocarbon temperatures in the range of 97-99 °C and a pore pressure of 29 MPa in 2020 down from an initial pore pressure of 37 MPa at the time of exploration in 1980. Also, field reports at Wells AZ-03 and AZ-07 revealed that casing collapse and production string damage (stretching and thinning) had happened in an upper layer above the Sarvak Formation, interrupting the production (Table 1). Eventually, cubes of porosity, geomechanical parameters (i.e., effective pressure and overburden stress), and pore pressure were calculated by combining the seismic and well-logging data according to Gray et al. (2012) and Gholami et al. (2021).

Table 1 Detail of casing collapse includes the well data, casing information, and collapse information along the Wells AZ-03 and AZ-07

Sample preparation and characterization

Accurate depths of selected core samples were determined by gamma-ray measurements in the laboratory. Then, cores plugs were cut from the core in vertical direction in lengths and diameters in the ranges of 10–12 cm and 5–6 cm, respectively. Next, the plugs were prepared in reservoir saturation conditions based on the methods described by Amalokwu et al. (2016) and Alhosani et al. (2020). They were then kept in a desiccator at a relative humidity of about 90%. Spectral gamma logger instrument was used for measuring the bulk density of the samples. The samples were further subjected to porosity and air permeability measurements by helium injection on a porosimeter apparatus and a permeameter operating under the Darcy’s law, respectively. Results of physical measurements are shown in Fig. 6 and Table 2.

Table 2 Result of compaction analysis

Hydrostatic compression test

In order to investigate compaction variations with pressure under reservoir conditions, hydrostatic compression tests were carried out. The test was performed on cylindrical core samples in a triaxial low-frequency cell of a fully servo-controlled apparatus made by CSIRO. For this purpose, the specimen was heated to a predefined temperature (up to 100 °C) and an effective confining pressure of up to 80 MPa to simulate reservoir conditions. Three independent syringe pumps were used to apply the confining pressure, axial stress, and pore pressure, respectively, onto the sample, thereby simulating the reservoir pressure. The hydrostatic stress-induced strain was measured by radial and axial strain gauges installed around the sample. Figure 7 gives a schematic view of the triaxial loading frame and the test cell. Once finished with setting up the apparatus and mounting the sample inside the cell, hydrostatic compression was applied to the sample by increasing axial and confining pressures at constant deviatoric stress (Kim and Ko 1979; Khosravi 2012; Najibi and Asef 2014; Yurikov et al. 2021). In this regard, Fig. 7b, c shows the test design and stress variations with elapsed time for all samples. Accordingly, the effective confining pressure was increased to 60 MPa at 0.5 MPa/min. Here, the maximum axial stress (i.e., confining pressure, a function of the applied load) was set to be equivalent to a burial depth of 4–4.5 km. In the oil-saturated tests (drained test), only small amounts of pore pressure were developed, which were measured by a pore pressure sensor.

Fig. 7

a Schematic view of the triaxial loading frame and test cell. Several internal electronic and hydraulic feed-through transducers were installed in the load cell. b Diagrams of effective axial stress versus applied effective confining/deviatoric stress and pore pressure, c diagrams of stress versus elapsed time

Continuing with the research, variations of sample volume with effective confining pressure were noticed and rock compressibility was obtained as the slope of the sample volume-versus-effective confining pressure diagram (Fig. 8). Results showed an increase in strain together with a decrease in porosity with increasing the applied pressure, with all samples showing more or less the same trends and behaviors.

Fig. 8

Hydrostatic test results: variation of the effective hydrostatic pressure against the volumetric strain for selected samples at a depth of a 3058 m, b 3087 m, and c 3088 m. The color code shows porosity changes during the test, which is obtained from initial porosity and volumetric changes of the samples during the test

Equation (4) was utilized to evaluate porosity variations in the course of the hydrostatic test. According to the results, the first segment of the stress-versus-strain curve exhibited a slope (the bulk modulus, i.e., inverse of compressibility) in the range of 0.5–1 GPa, representing the pore compaction. Describing the closure of soft pores and compression of stiff pores, the second segment of the curve exhibited a slope in the range of 10–15 GPa. Expectedly, the third segment exhibited the lowest bulk modulus (< 0.42 GPa) as it referred to pore collapse. In order to study the behavior of matrix compressibility in the creep stage, the sample must be loaded by more than 200 MPa in the hydrostatic cell, which was well beyond the feasible capacity of the apparatus (so, it modeled theoretically). Accordingly, the theoretical matrix compressibility of 0.000013 GPa⁻¹ (corresponding to a bulk modulus of 76.72 GPa) was used for the limestone according to Mavko et al. (2009).

Figure 9a presents variations of porosity with confining stress during the hydrostatic test. Figure 9b shows the changes in porosity in the failure and creep stage, as modeled using Eqs. (13) and (14) for the bulk and matrix strains, respectively. The figures show that, upon starting the loading, instantaneous porosity reaches the in situ porosity and then the sample exhibits some elastic behavior. Once the effective pressure exceeds 80 MPa, the weak sample (H₀₄ in Fig. 6) fails and proceeds to creeping, showing some behavior that can be expressed using Eqs. (12) and (15), respectively. In the creep stage, the sample undergoes matrix compression and hence a decrease in its volume. This ends up with a sub-zero total porosity. In the creep stage, the sample compressibility is equal to the matrix compressibility.

Fig. 9

a Actual (blue line) and b schematic model (dash line) of effective stress versus porosity in the hydrostatic test for the sample corresponding to a depth of 3036 m. The star symbol marks the ultimate pressure tested in the laboratory. The loading starts from an initial porosity of 7.34%. With increasing the applied load (corresponding to an increase in depth) beyond the in-situ stress (37.95 MPa), no more significant drop of porosity was observed. The red and green arrows show the effects of stress buildup and strain on the microstructure, respectively

Compaction measurements

In the previous section, variations of effective hydrostatic pressure with volumetric strain were obtained for different samples. In this section, the porosity was converted to void ratio using Eq. (3) (Fig. 10). For a better view, a logarithmic horizontal axis was adopted. Detailed properties of a particular sample are shown in Fig. 10a. The compression index (I_c) was then obtained for each sample. The figure further shows in situ stress curves, highlighting the pre-yield and post-yield directions. That is, once the applied stress to the sample reaches the in situ stress, gradient of the void ratio increased significantly. The compression index can then be estimated as the slope of the tangent line (post-yield curve). Table 2 reports the compression index and other details of the samples.

Fig. 10

a Semi-logarithmic curves of void ratio (e) against effective confining stress (in MPa) for the sample corresponding to a depth of 3058 m. Two stages can be identified on the curve, namely pre-yield and post-yield stages. Calculation of the compression index (I_c) is also indicated. Furthermore, water saturation (S_w), initial porosity (ϕ), and height of sample (H) are further shown. b–e) Void ratio curves for samples corresponding to depths of 3072, 3043, 3036, and 3078 m, respectively

Once the compressibility index was estimated for each sample in the related zone, formation thickness variations with the effective confining stress in each zone were determined using Eq. (10). Then, the sum of deformation obtained for different zones was reported as cumulative compaction in the elastic stage, as shown in Fig. 11. Here, total compaction of the studied 100-m interval of the formation in the elastic stage and at an effective pressure of 70 MPa was evaluated as 16 cm. At the peak effective confining stress (here 80 MPa), however, transition to post-elastic stage was expectedly observed. Creep-induced deformation and expansion due to thermal behavior of reservoir were calculated, as reported in Table 2.

Fig. 11

Cumulative compaction versus effective confining pressure at the Well AZ-15. For example, a total compaction of 8 cm occurred in all zones comprising the studied 100-m interval of the Sarvak Formation as the effective pressure reached 40 MPa. Water saturation (S_w), average initial porosity (ϕ), average void ratio (e), and height (H) of the Sarvak Formation are also indicated

Rate of compaction

The compaction rate provides a measure of the dissipation of excess pore pressure. In this work, it was evaluated through the methodology described in Sect. "Reservoir compaction modeling" (Fig. 12). This began by monitoring the variations of the sample height with the elapsed time. In general, the time it takes for compaction to occur in the triaxial test gives a good indication of the necessary rate of strain for the considered sample. As a second step for estimating the rate of compaction, t₅₀ was determined and T_t values were calculated using the relevant table. This was followed by final calculation of the compaction rate, as reported in Table 2 for all samples. The one-dimensional theory of Terzaghi is the most common basis for predicting the compaction rate.

Fig. 12

Compaction rate estimation based on the time – compaction curve for the sample corresponding to a depth of 3043 m. Vertical axis is the compaction in mm and horizontal axis is the logarithm of time in min. Herein assume one-way drainage, with the time of each stage further indicated on the diagram. The D₀, D₅₀, and D₁₀₀ are sample displacement at initial condition, 50%, and ultimate condition

Reservoir-scale subsidence estimation

In the previous sections, hydrostatic triaxial test was used as a basis for calculating total compaction and compaction rate at the Well AZ-15. In this section, the compaction/subsidence and its rate were estimated across the 3D volume of the reservoir. For this, a 3D cube of porosity corresponding to the study area was obtained through seismic inversion (Hampson et al. 2005; Sen 2006; Sengupta et al. 2011; Dai et al. 2022; Sharifi 2023). In the same way, pore pressure and in situ stress were determined by combining well test data, well-logging data, and seismic impedance information (Fig. 13). Porosity estimation from the seismic inversion was done according to Hampson et al. (2005), Gray et al. (2012), and Ashraf et al. (2022). Time-to-depth conversion was then conducted through the Al-Chalabi (2014) approach. A subsequent quality control showed that the estimated porosity, pore pressure, and in situ stress values were in very good agreement with measured values at well location. As a first step, the porosity data were converted to void ratio via Eq. (3).

Fig. 13

Preparation of input 3D data for the proposed methodology: a acoustic impedance (in g/cc m/s), b total porosity (in %), c void ratio, and d pore pressure (in MPa). The z-axis is depth (in millisecond, ms), x-axis refers to crossline number, and y-axis is the inline number. The Sarvak Formation is located in time depths ranging from 1850 to 2100 ms

Next, total compaction was calculated via Eq. (1) by incorporating in situ stress, reservoir thickness, and compression indices obtained from the laboratory tests. Finally, the rate of compaction was computed across the entire volume of reservoir according to Eqs. (25) and (26), with the compaction factor obtained from hydrostatic tests. Total compaction and compaction rate were calculated in similar ways to those used at the well location. All computations were done using an author-developed code on seismic data in SEGY format. The compaction parameters were obtained according to Table 2. Eventually, total compaction was obtained in not only initial reservoir condition, but also in the present conditions and for 60 and 100 years later, as shown in Fig. 14. Based on obtained findings, stretching and thinning of casing and damage of production string could be attributed to compaction beyond 12 cm around the Wells AZ-03 and AZ-07 (see Table 1).

Fig. 14

Total compaction obtained a at the time of seismic acquisition (in year 2000), b present (in 2020), c, and 60 (in 2040), and d 100 (in 2080) years later. The color bar is in cm and and all years are in A.D

Discussion

Compaction analysis

In this work, total compaction and compaction rate were analyzed according to variations of pore pressure with effective confining pressure (Fig. 15). In this section, the lowest and highest parameters in the laboratory were analyzed to define two boundaries covering any possible situation. That is, considering the ranges of variations of compression index and coefficient of deformation, ultimate compaction was obtained for the studied 100-m interval of Sarvak Formation. The results showed an average plastic compaction of 10 cm and pore pressure drop of 8 MPa (from 37 down to 29 MPa) after 40 years of production. Reports of casing (and production string) collapse at two wells near the Well AZ-15 (i.e., AZ-03 and AZ-07) indicated the reliability of the results. The fact that no surface subsidence is currently observable in the studied field shows that the maximum compaction is less than enough for a subsidence to occur at the surface, although it has been high enough to induce damages to production string and other surface facilities. Notably, the ultimate compaction is expected upon complete depletion of the pore pressure—an event that has much to do with the production and enhanced oil recovery (EOR) plans. With the gas cap drive being the primary mechanism of production in this reservoir, ultimate recovery factor has been estimated to range between 20 and 40%. However, one can improve the ultimate recovery factor to as high as 80% by combining the gas cap drive with EOR, pushing the reservoir much closer to complete depletion condition. At a constant permeability, the combination of compaction with plastic-induced compaction may end up developing a subsidence-driven production mechanism, which results in improved production rate at larger compaction. This reflects the necessity of investigating possible interactions among the compaction, permeability, and production rate (Chan and Zoback 2002; Zoback 2007).

Fig. 15

Compaction model of the Sarvak Formation upon production at the current rates in the future. The right and left vertical axes refer to total compaction (in cm) and compaction ratio (in %), respectively, while the upper and lower horizontal axes indicate pore pressure and lithostatic effective stress, respectively. The two boundaries shown in blue and red mark the lower and upper limits of compaction parameters around the measured data, and all years are in A.D

Reliability and uncertainties of measured compaction

In practice, limited availability of core samples, anisotropic and heterogeneous nature of carbonates, apparatus limitations, and the modeling theory can introduce different errors and uncertainties into the obtained results. Although herein expanded the use of direct laboratory measurements, the proposed methodology is largely dependent on the availability of core samples, discrete value representation, and cost and time effectiveness, introducing a major limitation of the current methodology. The laboratory measurement of relevant parameters is another source of uncertainty in the present research. As other sources of uncertainty, human errors in performing the laboratory tests and apparatus limitation tend to constraint the applicability of this method, which can be the case for any laboratory test. In addition to common triaxial uncertainty analyses, the sample preparation and testing conditions may also introduce some errors. Heterogeneity introduces some other uncertainty concerns related to the association of anisotropy with even small-scale heterogeneities. Heterogeneity and anisotropy are scale-dependent factors that can be seen differently under the impact of measurement frequency (Avseth et al. 2005; Bazargan et al. 2021; Lin et al. 2022; Sharifi 2022; Purnomo et al. 2023). Accordingly, major levels of uncertainty may arise from the compaction equation and modeling to estimate the ultimate compaction and compaction rate. The uniaxial compaction parameters that were obtained by an odometer cell were used in this research (e.g., Terzaghi 1943; Mondol et al. 2007; Fjær 2009). Therefore, an underlying assumption made in this research was the purely triaxial nature of the compaction, thereby ignoring the lateral compaction. The assumptions made for the Terzaghi settlement’s theory represent another source of error. In this research, a simple and forward method was introduced to model the compaction. In future, one may develop other methods for reservoir compaction modeling to overcome the limitations and uncertainties of the proposed methodology while improving its results.

Conclusions

In the present research, poromechanics principles were combined with rock mechanics theories to present a novel theoretical foundation for analyzing and predicting hydrocarbon reservoir subsidence upon depletion. Findings of this research can be grouped along four main dimensions:

• 1. In contrast to previous studies, an analytic formulation was proposed for modeling the compaction in different stages (i.e., crack closing, elastic, post-elastic, and creep).

• 2. Reservoir compaction was obtained by incorporating pore pressure and porosity reduction using petrophysical data at well location.

• 3. Reservoir-scale evaluation/estimation of compaction was performed on 3D cubes using seismic data.

• 4. Compared to the conventional theories (e.g., Terzaghi’s consolidation theory, Geertsma, and Zimmerman), it further incorporated the effects of temperature, plastic compaction, and matrix compressibility into the model.

Furthermore, the results on the case study showed that the total compaction calculated via the proposed method is still below the threshold for occurring surface subsidence to such stiff framework of the carbonate rock. In the meantime, the subsurface compaction that occurred at the reservoir depth was more than enough to cause a casing collapse and relevant damages to well-site production facilities.