Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-28T01:44:00.268Z Has data issue: false hasContentIssue false
  • English
  • Français

Disjoint hypercyclicity, Sidon sets and weakly mixing operators

Part of: General theory of linear operators Topological dynamics Sequences and sets

Published online by Cambridge University Press:  22 August 2023

RODRIGO CARDECCIA Open the ORCID record for RODRIGO CARDECCIA [Opens in a new window]
RODRIGO CARDECCIA*
Affiliation:
Instituto Balseiro, Universidad Nacional de Cuyo – C.N.E.A. and CONICET, Av. Bustillo 9500, San Carlos de Bariloche, R8402AGP, Argentina
*
e-mail: rodrigo.cardeccia@ib.edu.ar
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that a finite set of natural numbers J satisfies that 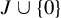$J\cup \{0\}$ is not Sidon if and only if for any operator T, the disjoint hypercyclicity of 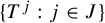$\{T^j:j\in J\}$ implies that T is weakly mixing. As an application we show the existence of a non-weakly mixing operator T such that 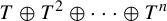$T\oplus T^2\oplus\cdots \oplus T^n$ is hypercyclic for every n.

Keywords

Sidon setsdisjoint hypercyclicitynon-weakly mixing operators

MSC classification

Primary: 47A16: Cyclic vectors, hypercyclic and chaotic operators 37B99: None of the above, but in this section
Secondary: 11B99: None of the above, but in this section
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 5 , May 2024 , pp. 1315 - 1329
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bayart, F. and Matheron, E.. Hypercyclic operators failing the hypercyclicity criterion on classical Banach spaces. J. Funct. Anal. 250(2) (2007), 426–441.CrossRefGoogle Scholar
Bayart, F. and Matheron, E.. Dynamics of Linear Operators (Cambridge Tracts in Mathematics, 179). Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Bayart, F. and Matheron, E.. (Non-)weakly mixing operators and hypercyclicity sets. Ann. Inst. Fourier (Grenoble) 59(1) (2009), 1–35.CrossRefGoogle Scholar
Bernal-González, L.. Disjoint hypercyclic operators. Studia Math. 182(2) (2007), 113–131.CrossRefGoogle Scholar
Bès, J., Martin, O., Peris, A. and Shkarin, S.. Disjoint mixing operators. J. Funct. Anal. 263(5) (2012), 1283–1322.CrossRefGoogle Scholar
Bès, J., Menet, Q., Peris, A. and Puig, Y.. Recurrence properties of hypercyclic operators. Math. Ann. 366(1–2) (2016), 545–572.CrossRefGoogle Scholar
Bès, J., Menet, Q., Peris, A. and Puig, Y.. Strong transitivity properties for operators. J. Differential Equations 266(2–3) (2019), 1313–1337.CrossRefGoogle Scholar
Bès, J. and Peris, A.. Hereditarily hypercyclic operators. J. Funct. Anal. 167(1) (1999), 94–112.CrossRefGoogle Scholar
Bès, J. and Peris, A.. Disjointness in hypercyclicity. J. Math. Anal. Appl. 336(1) (2007), 297–315.CrossRefGoogle Scholar
Bonilla, A. and Grosse-Erdmann, K.-G.. Upper frequent hypercyclicity and related notions. Rev. Mat. Complut. 31(3) (2018), 673–711.CrossRefGoogle Scholar
Bonilla, A., Grosse-Erdmann, K.-G., López-Martínez, A. and Peris, A.. Frequently recurrent operators. J. Funct. Anal. 283(12) (2022), 109713.CrossRefGoogle Scholar
Cardeccia, R. and Muro, S.. Arithmetic progressions and chaos in linear dynamics. Integral Equations Operator Theory 94 (2022), 11.CrossRefGoogle Scholar
Cardeccia, R. and Muro, S.. Multiple recurrence and hypercyclicity. Math. Scand. 128 (2022), 133256.CrossRefGoogle Scholar
Cilleruelo, J., Sidon sets in ${\mathbb{N}}^d$ . J. Combin. Theory Ser. A 117(7) (2010), 857–871.CrossRefGoogle Scholar
De La Rosa, M. and Read, C.. A hypercyclic operator whose direct sum $T\oplus T$ is not hypercyclic. J. Operator Theory 61(2) (2009), 369–380.Google Scholar
Desch, W. and Schappacher, W.. On products of hypercyclic semigroups. Semigroup Forum 71(2) (2005), 301–311.CrossRefGoogle Scholar
Erdős, P.. Some problems in number theory, combinatorics and combinatorial geometry. Math. Pannon. 5(2) (1994), 261–269.Google Scholar
Erdős, P. and Turán, P.. On a problem of Sidon in additive number theory, and on some related problems. J. Lond. Math. Soc. (2) 16 (1941), 212–215.CrossRefGoogle Scholar
Ernst, R., Esser, C. and Menet, Q.. $\mathbf{\mathcal{U}}$ -frequent hypercyclicity notions and related weighted densities. Israel J. Math. 241(2) (2021), 817–848.CrossRefGoogle Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981. M. B. Porter Lectures.CrossRefGoogle Scholar
Grosse-Erdmann, K.-G. and Peris Manguillot, A.. Linear Chaos. Springer, Berlin, 2011.CrossRefGoogle Scholar
Herrero, D. A.. Hypercyclic operators and chaos. J. Operator Theory 28(1) (1992), 93–103.Google Scholar
Lindström, B.. An inequality for ${B}_2$ -sequences. J. Combin. Theory 6 (1969), 211–212.CrossRefGoogle Scholar
Moothathu, T. K. S.. Diagonal points having dense orbit. Colloq. Math. 120(1) (2010), 127–138.CrossRefGoogle Scholar
Sanders, R. and Shkarin, S.. Existence of disjoint weakly mixing operators that fail to satisfy the disjoint hypercyclicity criterion. J. Math. Anal. Appl. 417(2) (2014), 834–855.CrossRefGoogle Scholar
Shkarin, S.. A short proof of existence of disjoint hypercyclic operators. J. Math. Anal. Appl. 367(2) (2010), 713–715.CrossRefGoogle Scholar
Singer, J.. A theorem in finite projective geometry and some applications to number theory. Trans. Amer. Math. Soc. 43(3) (1938), 377–385.CrossRefGoogle Scholar