Superfair Stochastic Games

Abstract

A two-person zero-sum stochastic game with a nonnegative stage reward function is superfair if the value of the one-shot game at each state is at least as large as the reward function at the given state. The payoff in the game is the limit superior of the expected stage rewards taken over the directed set of all finite stop rules. If the game has countable state and action spaces and if at least one of the players has a finite action space at each state, then the game has a value. The value of the stochastic game is obtained by a transfinite algorithm on the countable ordinals.

1 Introduction

A two-person zero-sum stochastic game is played in stages $n = 0,1,2,\ldots$ and has a nonnegative reward function defined on the state space. At each stage n of the game the players simultaneously select actions from their actions sets. These actions together with the current state determine the distribution of the next state. The payoff from player 2 to player 1 is the limit superior over finite stop rules t of the expectation of the reward function at stage t. The state space and the actions sets at each state are assumed to be countable with at least one of the action sets finite. The game is assumed to be superfair in the sense that, at every state, the value of the one-shot game in which the payoff is the expectation of the reward in the next state is at least as large as the reward in the current state. Superfair stochastic games could be seen as a game-theoretic analogue of a submartingale. Superfair stochastic games encompass for example all positive zero-sum stochastic games (cf. Flesch et al. [3]). Superfair games also include the leavable games of Maitra and Sudderth [6]. Leavable games are obviously superfair since player 1 is allowed to stop and receive the value of the reward function at any stage. In the special case when the reward function is bounded and the action sets are finite, superfair games can be viewed as limsup games in the sense of [6].

The game is shown to have a value that can be obtained by a transfinite algorithm over the countable ordinals. This generalizes a similar result for positive zero-sum stochastic games in Flesch et al. [3].

Player 2 is proved to have an $\varepsilon$-optimal Markov strategy for every $\varepsilon > 0$. Whether such strategies exist for player 1 is an open question. If all the action sets of player 2 are finite then player 2 has an optimal stationary strategy and, for every state and every $\varepsilon > 0$, player 1 has a stationary strategy that is $\varepsilon$-optimal if the game starts in the given state.

Organization of the Paper: In Sect. 2, we present our model. In Sect. 3, we discuss an illustrative example. In Sect. 4, we state our main result and provide an outline of the proof. In Sect. 5 we present an algorithm, which we use in Sects. 6 and 7 to prove the two main steps of the proof on the upper value and the lower value, respectively. In Sect. 8, we prove our results on the value of the game. In Sect. 9, we discuss optimal strategies of the players. In Sect. 10, we make some concluding remarks.

2 The Model

2.1 The Game

We consider zero-sum stochastic games with countable state and action spaces such that, in each state, at least one of the players has only finitely many actions.

Definition 1

A zero-sum stochastic game (with countable state and action spaces) is a tuple $\Gamma =(S,A,B,(A(s))_{s\in S},(B(s))_{s\in S},p,r)$, where:

• 1. S is a nonempty and countable state space.

• 2. A and B are nonempty and countable action sets for player 1 and player 2, respectively.

• 3. In each state $s\in S$, the sets $A(s)\subseteq A$ and $B(s)\subseteq B$ are nonempty, such that at least one of the sets A(s) and B(s) is finite. The elements of A(s) and B(s) are called the available actions in state s for player 1 and player 2, respectively.

• 4. p is a transition law: to every state $s\in S$ and actions $a\in A(s)$, $b\in B(s)$, the function p assigns a probability measure $p(s,a,b)=(p(s'|s,a,b))_{s'\in S}$ on S.

• 5. $r: S \rightarrow [0,\infty )$ is a non-negative reward function.

The game is played at stages in ${\mathbb {N}}=\{0,1,2,\ldots \}$ and begins at some state $s_0\in S$. At every stage $n\in \mathbb {N}$, the play is in a state $s_n\in S$. In this state, player 1 chooses an action $a_n\in A(s_n)$ and simultaneously player 2 chooses an action $b_n\in B(s_n)$. Then, player 1 receives the reward $r(s_n)$ from player 2, and the state $s_{n+1}$ is drawn according to the probability measure $p(s_n,a_n,b_n)$, where the play of the game continues at stage $n+1$.

2.2 Histories and Plays

A history at stage  $n\in {\mathbb {N}}$ is a sequence $(s_0,a_0,b_0,\ldots ,s_{n-1},a_{n-1},b_{n-1},s_n)\in (S\times A\times B)^n\times S$ where $a_k\in A(s_k)$ and $b_k\in B(s_k)$ for each $k=1,\ldots ,n-1$. Let $H_n$ denote the set of histories at stage n, and let $H=\cup _{n\in {\mathbb {N}}} H_n$ denote the set of all histories. For each history $h\in H$, let $s_h$ denote the final state in h.

A play is a sequence of the form $(s_0,a_0,b_0,s_1,\ldots )\in (S\times A\times B)^{\infty }$ where $a_k\in A(s_k)$ and $b_k\in B(s_k)$ for each $k\in {\mathbb {N}}$. Let $H_\infty$ denote the set of plays.

We endow the set $(S\times A\times B)^{\infty }$ with the product topology, where each of the sets S, A, and B has its discrete topology. The set $H_\infty$ of plays is a closed subset of $(S\times A\times B)^{\infty }$, which we endow with the induced subspace topology.

2.3 Strategies

A mixed action for player 1 in state $s\in S$ is a probability measure $x(s)=(x(s,a))_{a\in A(s)}$ on A(s). Similarly, a mixed action for player 2 in state $s\in S$ is a probability measure $y(s)=(y(s,b))_{b\in B(s)}$ on B(s). The respective sets of mixed actions in state s are denoted by $\Delta (A(s))$ and $\Delta (B(s))$.

A strategy for player 1 is a map $\pi$ that to each history $h\in H$ assigns a mixed action $\pi (h)\in \Delta (A(s_h))$. Similarly, a strategy for player 2 is a map $\sigma$ that to each history $h\in H$ assigns a mixed action $\sigma (h)\in \Delta (B(s_h))$. The set of strategies is denoted by $\Pi$ for player 1 and by $\Sigma$ for player 2.

2.4 Stop Rules

A finite stop rule is a mapping $t:H_\infty \rightarrow {\mathbb {N}}$ with the following property: if for some play $h_\infty =(s_0,a_0,b_0,s_1,\ldots )\in H_\infty$ we have $t(h_\infty )=n$, and $h'_\infty \in H_\infty$ is another play that begins with the history $(s_0,a_0,b_0,s_1,\ldots ,s_n)$, then $t(h_\infty )=t(h'_\infty )$. Intuitively, t assigns a stage to each play in such a way that the assigned stage only depends on the history in that stage. For finite stop rules t and $t'$ we write $t\ge t'$ if $t(h_\infty )\ge t'(h_\infty )$ for every play $h_\infty \in H_\infty$. The set of finite stop rules equipped with the relation $\ge$ is a partially ordered directed set.¹

2.5 Payoffs

An initial state $s\in S$ and a pair of strategies $(\pi ,\sigma )\in \Pi \times \Sigma$ determine, by Kolmogorov’s extension theorem, a unique probability measure ${\mathbb {P}}_{s,\pi ,\sigma }$ on $H_\infty$. The corresponding expectation operator² is denoted by $\mathbb {E}_{s,\pi ,\sigma }$.

The payoff for a pair of strategies $(\pi ,\sigma )\in \Pi \times \Sigma$, when the initial state is $s\in S$, is defined as

$$\begin{aligned} u(s,\pi ,\sigma )=\limsup _{t}\,\mathbb {E}_{s,\pi ,\sigma }[r(s_t)]=\inf _{t'}\sup _{t\ge t'}\,\mathbb {E}_{s,\pi ,\sigma }[r(s_t)], \end{aligned}$$

(1)

where t and $t'$ range over the directed set of finite stop rules. This payoff was introduced by Dubins and Savage ([2], p. 39) and several of its properties are explained in Section 4.2 of Maitra and Sudderth [6]. Player 1’s objective is to maximize the payoff given by u, and player 2’s objective is to minimize it.

For a discussion of alternative payoffs, we refer to Sect. 10.

2.6 Superfair Games

A zero-sum stochastic game $\Gamma$ is called superfair if, in each state, player 1 can play so that the expectation of the reward in the next state is at least as large as the reward in the current state. To make this notion precise, we introduce an associated one-shot game.

For a function $\phi :S \rightarrow [0,\infty ]$ and state $s \in S$, the one-shot game $M_\phi (s)$ is the zero-sum game in which player 1 selects an action $a\in A(s)$ and simultaneously player 2 selects an action $b\in B(s)$, and then player 2 pays player 1 the amount $\sum _{s'\in S}\phi (s')p(s'|s,a,b)$. For mixed actions $x(s)\in \Delta (A(s))$ and $y(s)\in \Delta (B(s))$, let the expected payoff in the one-shot game $M_\phi (s)$ be denoted by

$$\begin{aligned} U\phi (s,x(s),y(s))=\sum _{a\in A(s),\,b\in B(s)}\sum _{s'\in S}\phi (s')\, p(s'|s,a,b)\, x(s,a)\, y(s,b). \end{aligned}$$

The game $M_\phi (s)$ has a value, denoted by $G\phi (s)$, by Theorems 2 and 3 in Flesch et al. [3]. Thus

$$\begin{aligned} G\phi (s)&= \sup _{x(s) \in \Delta (A(s))}\inf _{y(s) \in \Delta (B(s))}U\phi (s,x(s),y(s)) \\&=\inf _{y(s) \in \Delta (B(s))}\sup _{x(s) \in \Delta (A(s))}U\phi (s,x(s),y(s)). \end{aligned}$$

Note that, generally, the supremum and infimum cannot be replaced with maximum and minimum, because the action set of one of the players can be infinite.

The zero-sum stochastic game $\Gamma$ is called superfair if $Gr(s) \ge r(s)$ for all states $s\in S$.

2.7 Value and Optimality

Consider a zero-sum stochastic game $\Gamma$. The lower value for the initial state $s\in S$ is defined as

$$\begin{aligned}\alpha (s)=\sup _{\pi \in \Pi }\inf _{\sigma \in \Sigma } u(s,\pi ,\sigma ).\end{aligned}$$

Similarly, the upper value for the initial state $s\in S$ is defined as

$$\begin{aligned} \beta (s)=\inf _{\sigma \in \Sigma }\sup _{\pi \in \Pi } u(s,\pi ,\sigma ). \end{aligned}$$

The inequality $\alpha (s)\le \beta (s)$ always holds. If $\alpha (s)=\beta (s)$, then this quantity is called the value for the initial state s and it is denoted by v(s). Then, for $\varepsilon \ge 0$, a strategy $\pi \in \Pi$ for player 1 is called $\varepsilon$-optimal for the initial state s if $u(s,\pi ,\sigma )\ge v(s)-\varepsilon$ for every strategy $\sigma \in \Sigma$ for player 2. Similarly, a strategy $\sigma \in \Sigma$ for player 2 is called $\varepsilon$-optimal for the initial state s if $u(s,\pi ,\sigma )\le v(s)+\varepsilon$ for every strategy $\pi \in \Pi$ for player 1.

If the value exists for every initial state, then for every $\varepsilon >0$, each player has a strategy that is $\varepsilon$-optimal for every initial state. We call these strategies $\varepsilon$-optimal. A 0-optimal strategy is simply called optimal.

3 An Illustrative Example

In this section we discuss an illustrative example, which is based on Examples (6.6), p. 183 and (9.1), p. 191 in Maitra and Sudderth [6].

Example 1

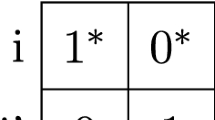
Let $S={\mathbb {N}}= \{0,1,2\ldots \}$. The state 0 is absorbing. For $s \ge 1$, the action sets are $A(s) = B(s) = \{1,2\}$ and the transition law satisfies

$$\begin{aligned} p_{ab}=p(s+1|s,a,b) = 1- p(s-1|s,a,b) \end{aligned}$$

where $p_{ab}\in [0,1]$ for every $a,b\in \{1,2\}$. Let the reward function be $r(0)=1$ and $r(s)=0$ for all $s\ge 1$. The game is superfair because $r(0)=Gr(0)=1$, $r(1)=0\le Gr(1)$, and $r(s)=Gr(s)=0$ for all $s\ge 2$.

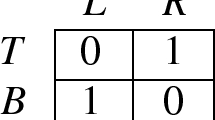
In view of the reward function r, it is clear that, from any state $s \ge 1$, player 1 wants to move to $s-1$ and player 2 to move to $s+1$. So it is not surprising, and is proved in [6], that optimal (stationary) strategies $\pi$ and $\sigma$ for players 1 and 2, respectively, are to play, at every stage and at every state $s \ge 1$, optimal mixed actions in the matrix game:

$$\begin{aligned} \begin{bmatrix} 1-p_{11} &{} 1-p_{12}\\ 1-p_{21} &{} 1-p_{22}\\ \end{bmatrix}. \end{aligned}$$

Let w be the value of this matrix game. Then, for $s \ge 1$, the distribution ${\mathbb {P}}_{s,\pi ,\sigma }$ of the process $s,s_1,s_2, \ldots$ of states is that of a simple random walk that moves to the right with probability $1-w$ and to the left with probability w at every positive state, and is absorbed at state 0.

The value v(s) of the stochastic game is exactly the ${\mathbb {P}}_{s,\pi ,\sigma }$-probability of reaching state 0, namely:

$$\begin{aligned} v(s) =\left\{ \begin{array}{ll} \big (\frac{w}{1-w}\big )^s &{} \ \ \ \text {if } w < 1/2,\\ \ 1 &{} \ \ \ \text {if } w \ge 1/2;\\ \end{array}\right. \end{aligned}$$

for a proof we refer to [6].

Now suppose that the reward function is the identity $r(s) = s$ for all $s \in {\mathbb {N}}$. Because r is an increasing function on S, from any state $s\ge 1$, player 1 wants to maximize and player 2 wants to minimize the chance of moving to $s+1$. Let $w'$ be the value of the matrix game

$$\begin{aligned} M = \begin{bmatrix} p_{11} &{} p_{12}\\ p_{21} &{} p_{22}\\ \end{bmatrix}. \end{aligned}$$

Assume also that $w' > 1/2$. Then the game is superfair because, for each state $s \ge 1$ (cf. also p. 183 in [6]):

$$\begin{aligned} Gr(s)&= w'\cdot r(s+1)+(1-w')\cdot r(s-1)\\&= w'\cdot (s+1)+(1-w')\cdot (s-1)\\&\ge s \,=\, r(s). \end{aligned}$$

Optimal (stationary) strategies $\pi$ and $\sigma$ for the players in the stochastic game are now to play optimally in the matrix game M at every stage and at every state $s \ge 1$. The distribution ${\mathbb {P}}_{s,\pi ,\sigma }$ of the process of states is then that of a simple random walk that moves right with probability $w'$ and left with probability $1-w'$ at every positive state, and is absorbed at state 0. Because $w' > 1/2$, there is positive probability that the random walk will converge to infinity starting from any state $s \ge 1$. Hence, the value function is

$$\begin{aligned} v(s) =\left\{ \begin{array}{ll} 0 &{} \ \ \ \text {if } s=0,\\ \infty &{} \ \ \ \text {if } s\ge 1.\\ \end{array}\right. \end{aligned}$$

If $1/2<w' < 1$, then there is also positive probability of being absorbed at state 0. $\Diamond$

4 Main Result

The main result of the paper is the following theorem.

Theorem 1

Every superfair zero-sum stochastic game has a value v(s) for every initial state $s\in S$. Moreover, there is a transfinite algorithm for calculating the value function $v=(v(s))_{s\in S}$.

A similar result was proven for so-called positive zero-sum stochastic games in Flesch et al. [3]. A positive zero-sum stochastic game is defined as a game in Definition 1, but instead of Eq. (1), the payoff is defined as the sum of the expected stage rewards. Because every positive zero-sum stochastic game can be transformed³ into an equivalent zero-sum stochastic game as in Definition 1 with the payoff given in Eq. (1), and because this latter game is by construction superfair, Theorem 1 above generalizes Theorem 1 in Flesch et al. [3] for positive zero-sum stochastic games.⁴

There is also a transfinite algorithm for calculating the value of a limsup game in Maitra and Sudderth [6]. Unlike the algorithms for superfair games and for positive games, the algorithm for a limsup game is not, in general, monotone. It may require infinitely many steps both increasing and decreasing.

The proof of Theorem 1 consists of the following steps. In Sect. 5, we present a transfinite algorithm that results in a function $r^*:S\rightarrow [0,\infty ]$. In Sect. 6 we show that $r^*$ is bounded from below by the upper value $\beta$ of the game, while in Sect. 7 we show that $r^*$ is bounded from above by the lower value $\alpha$ of the game: thus, $\beta \le r^*\le \alpha$. Since $\alpha \le \beta$, this will imply that $r^*$ is the value of the game.

5 The Algorithm

In this section, we consider the following transfinite algorithm on the countable ordinals. Let $r_0 =r$ and define, for each countable ordinal $\xi$,

$$\begin{aligned} r_{\xi } =\left\{ \begin{array}{ll} Gr_{\xi -1} &{} \ \ \ \text {if } \xi \, \,\text {is a successor ordinal},\\ \sup _{\eta < \xi }r_{\eta } &{} \ \ \ \text {if } \xi \, \,\text {is a limit ordinal}.\\ \end{array}\right. \end{aligned}$$

We remark that the first use of a transfinite algorithm to calculate the value of a stochastic game was by Blackwell [1]. Other examples are in Maitra and Sudderth [5, 6], and Flesch et al. [3].

Lemma 1

For all countable ordinals $\xi$ and $\eta$:

• 1. $Gr_{\xi } \ge r_{\xi }$.

• 2. $\eta \le \xi$ implies $r_{\eta } \le r_{\xi }$.

• 3. There exists a countable ordinal $\xi ^*$ such that $r_{\xi ^*} = r_{\xi ^*+1} = Gr_{\xi ^*}$.

Proof

First, we prove Claim 1 by transfinite induction on $\xi$. If $\xi =0$, then $r_0 = r$ and $Gr_0 = Gr \ge r =r_0$ because the game is superfair. For the inductive step, assume that $\xi > 0$ and that Claim 1 holds for all $\eta < \xi$. If $\xi$ is a successor ordinal, then $r_{\xi } = Gr_{\xi -1} \ge r_{\xi -1}$, and hence $Gr_{\xi } \ge Gr_{\xi -1} = r_{\xi }$. If $\xi$ is a limit ordinal, then $r_{\xi } = \sup _{\eta < \xi }r_{\eta }$, which implies that $Gr_{\xi } \ge Gr_{\eta } \ge r_{\eta }$ for all $\eta < \xi$, and hence $Gr_{\xi } \ge \sup _{\eta < \xi }r_{\eta } = r_{\xi }$.

Now we prove Claim 2, also by transfinite induction on $\xi$. Claim 2 is trivially true for $\xi =0$. For the inductive step, assume that $\xi > 0$ and that Claim 2 holds for $\eta < \xi$. If $\xi$ is a successor ordinal, then $r_{\xi } = Gr_{\xi -1} \ge r_{\xi -1} \ge r_{\eta }$ for all $\eta \le \xi -1$. If $\xi$ is a limit ordinal, then Claim 2 follows from the definition of $r_{\xi }$.

Finally, Claim 3 follows from a standard cardinality argument. Indeed, for every state $s\in S$, the sequence $(r_\xi (s))_\xi$ is a nondecreasing sequence of real numbers. Hence, the sequence $(r_\xi (s))_\xi$ can only have countably many different elements.⁵ Thus, for state $s\in S$, there exists a countable ordinal $\xi _s$ such that $r_{\xi _s}(s) = r_{\xi }(s)$ for every $\xi \ge \xi _s$. Now take $\xi ^*=\sup _{s\in S} \xi _s$. Because S is countable, $\xi ^*$ is a countable ordinal. $\square$

To simplify notation, let $r^* = r_{\xi ^*}$ where $\xi ^*$ is from Lemma 1.

Lemma 2

The function $r^*$ is the least function $\phi :S \mapsto [0,\infty ]$ such that (a) $G\phi \le \phi$ and (b) $\phi \ge r$.

Proof

The function $r^*$ satisfies condition (a) by Claim 3 of Lemma 1. The function $r^*$ also satisfies condition (b) because, by Claim 2 of Lemma 1, we have $r^* = r_{\xi ^*} \ge r_0 = r$.

Now assume that $\phi$ satisfies conditions (a) and (b). We will show that $\phi \ge r_{\xi }$ for all $\xi$ by transfinite induction, and so $\phi \ge r^* =r_{\xi ^*}$.

By condition (b), for $\xi =0$ we have $\phi \ge r =r_0$. For the inductive step, assume that $\xi > 0$ and that $\phi \ge r_{\eta }$ for all $\eta < \xi$. If $\xi$ is a successor ordinal, then $r_{\xi } = Gr_{\xi -1} \le G\phi \le \phi$ by condition (a). If $\xi$ is a limit ordinal, then $r_{\xi } = \sup _{\eta < \xi } r_{\eta } \le \phi$ by the inductive assumption. $\square$

The next two sections will show that the value of the superfair game $\Gamma$ is $r^*(s)$ for every initial state $s \in S$.

6 The Upper Value

In this section we show that $r^*$, which we defined below Lemma 1, is at least as large as the upper value of the game.

Lemma 3

Let $\varepsilon >0$, and, for every stage $n\in {\mathbb {N}}$ and every state $s \in S$, let $y_n(s) \in \Delta (B(s))$ be a mixed action for player 2 that is $\varepsilon /2^{n+1}$-optimal for player 2 in the one-shot game $M_{r^*}(s)$. Define $\sigma$ to be the strategy for player 2 such that, for every stage $n\in {\mathbb {N}}$ and every history $h_n=(s_0,a_0,b_0,\ldots ,s_{n-1},a_{n-1},b_{n-1},s_n)\in H_n$, it holds that $\sigma (h_n) = y_n(s_n)$, i.e., for every mixed action $x(s_n) \in \Delta (A(s_n))$ of player 1,

$$\begin{aligned} U r^*(s_n,x(s_n),y_n(s_n))\ \le \ Gr^*(s_n)+\frac{\varepsilon }{2^{n+1}}\ =\ r^*(s_n)+\frac{\varepsilon }{2^{n+1}}. \end{aligned}$$

(2)

Then, for every initial state $s\in S$ and every strategy $\pi$ for player 1, we have

$$\begin{aligned} u(s,\pi ,\sigma )\,\le \,r^*(s)+\varepsilon . \end{aligned}$$

(3)

Consequently, for every initial state $s \in S$, we have $\beta (s) \le r^*(s)$.

Proof

Let $\varepsilon > 0$, and choose a strategy $\sigma$ for player 2 as in the lemma. Fix an initial state $s=s_0 \in S$ and a strategy $\pi$ for player 1.

By Eq. (2), the process

$$\begin{aligned} r^*(s_0),\ r^*(s_1)-\frac{\varepsilon }{2},\ r^*(s_2)-\frac{\varepsilon }{2}-\frac{\varepsilon }{2^2},\ \ldots \end{aligned}$$

is a ${\mathbb {P}}_{s,\pi ,\sigma }$-supermartingale, possibly with infinite values. By an optional sampling theorem (cf. Maitra and Sudderth [6], Section 2.4),

$$\begin{aligned} \mathbb {E}_{s,\pi ,\sigma }[r^*(s_t)-\varepsilon ]\, \le \, \mathbb {E}_{s,\pi ,\sigma }\Big [r^*(s_t) -\frac{\varepsilon }{2}-\cdots -\frac{\varepsilon }{2^t}\Big ]\,\le \, r^*(s) \end{aligned}$$

for every finite stop rule t. Using Eq. (1) and $r^* \ge r$ (cf. Claim 2 of Lemma 1), we have

$$\begin{aligned} u(s,\pi ,\sigma ) = \limsup _t\, \mathbb {E}_{s,\pi ,\sigma }[r(s_t)] \,\le \, \limsup _t\,\mathbb {E}_{s,\pi ,\sigma }[r^*(s_t)]\, \le \, r^*(s)+ \varepsilon , \end{aligned}$$

which completes the proof. $\square$

7 The Lower Value

In this section we show that $r^*$ is at most as large as the lower value of the game.

Lemma 4

For every initial state $s \in S$, we have $\alpha (s) \ge r^*(s)$.

Proof

It is sufficient to verify that the function $\alpha$ satisfies conditions (a) and (b) of Lemma 2.

Step 1 First we verify that $\alpha$ satisfies condition (b) of Lemma 2. Let $\varepsilon > 0$, and choose a strategy $\pi$ for player 1 such that for every stage $n\in {\mathbb {N}}$ and every history $h_n =(s_0,a_0,b_0,s_1,\ldots ,s_{n-1},a_{n-1},b_{n-1},s_n)\in H_n$ at stage n, the mixed action $\pi (h_n)$ is $\varepsilon /2^{n+1}$-optimal for player 1 in the one-shot game $M_r(s_n)$, i.e., for every mixed action $y(s_n)\in \Delta (B(s_n))$ of player 2,

$$\begin{aligned} U r(s_n,\pi (h_n),y(s_n))\ \ge \ Gr(s_n)-\frac{\varepsilon }{2^{n+1}}. \end{aligned}$$

(4)

Fix an initial state $s = s_0 \in S$ and a strategy $\sigma$ for player 2.

Then, by Eq. (4) and Claim 1 of Lemma 1, for every history $h_n\in H_n$ at stage $n\in {\mathbb {N}}$ we have

$$\begin{aligned} \mathbb {E}_{s,\pi ,\sigma }[r(s_{n+1})\mid h_n]\, \ge \, Gr(s_n) - \frac{\varepsilon }{2^{n+1}}\, \ge \, r(s_n) - \frac{\varepsilon }{2^{n+1}}. \end{aligned}$$

Thus, the process

$$\begin{aligned} r(s),\ r(s_1)+\frac{\varepsilon }{2},\ r(s_2)+\frac{\varepsilon }{2}+\frac{\varepsilon }{2^2},\ \ldots \end{aligned}$$

is a ${\mathbb {P}}_{s,\pi ,\sigma }$-submartingale. By an optional sampling theorem (cf. Maitra and Sudderth [6], Section 2.4),

$$\begin{aligned} \mathbb {E}_{s,\pi ,\sigma }[r(s_t)+\varepsilon ]\,\ge \, \mathbb {E}_{s,\pi ,\sigma }\Bigg [r(s_t)+\frac{\varepsilon }{2}\cdots + \frac{\varepsilon }{2^t}\Bigg ]\,\ge \, r(s) \end{aligned}$$

for every finite stop rule t. Hence, by Eq. (1),

$$\begin{aligned} u(s,\pi ,\sigma )\, =\, \limsup _t\,\mathbb {E}_{s,\pi ,\sigma }[r(s_t)]\, \ge \, r(s)- \varepsilon , \end{aligned}$$

and therefore $\alpha (s)\, \ge \, r(s)-\varepsilon$. Because $\varepsilon$ is an arbitrary positive number, $\alpha$ satisfies condition (b).

Step 2 Now we verify that $\alpha$ satisfies condition (a) of Lemma 2. Fix an initial state $s=s_0 \in S$ and let $R < G\alpha (s)$. Because $G\alpha (s)$ is the value of the one-shot game $M_{\alpha }(s)$, there exists a mixed action $x^*(s) \in \Delta (A(s))$ for player 1 such that, for every action $b\in B(s)$ for player 2,

$$\begin{aligned} U \alpha (s,x^*(s),b)\,=\,\sum _{a\in A(s)}\sum _{s'\in S} \alpha (s')\,p(s'|s,a,b)\,x^*(s,a)\ >\ R. \end{aligned}$$

Hence, by the monotone convergence theorem, for every action $b\in B(s)$ of player 2, there is some $m(b)\in {\mathbb {N}}$ such that

$$\begin{aligned} \sum _{a\in A(s)}\,\sum _{s'\in S}\, \min \{\alpha (s'),m(b)\}\,p(s'|s,a,b)\,x^*(s,a)\ >\ R. \end{aligned}$$

(5)

The reason for taking the minimum with m(b) is that some values of $\alpha (s')$ may be infinite.

Let $\varepsilon >0$. By the definition of $\alpha$, for each state $s' \in S$ and each $m\in {\mathbb {N}}$, there is a strategy $\pi _{s'}^m$ for player 1 such that, for every strategy $\sigma$ for player 2, we have

$$\begin{aligned} u(s',\pi _{s'}^m,\sigma ) \,\ge \, \min \{\alpha (s'),m\} - \varepsilon . \end{aligned}$$

(6)

Now let $\pi$ be the following strategy for player 1: (i) in stage 0, in state $s=s_0$, the strategy $\pi$ plays the mixed action $x^*(s)$, (ii) from stage 1 on, from state $s_1$, the strategy $\pi$ follows the strategy $\pi _{s_1}^{m(b_0)}$, where $b_0$ denotes the action chosen by player 2 in stage 0.

Then, for every strategy $\sigma$ of player 2,

$$\begin{aligned} u(s,\pi ,\sigma )&= \sum _{a_0\in A(s),\,b_0\in B(s)}\sum _{s_1\in S}\,u\big (s_1,\pi _{s_1}^{m(b_0)},\sigma [h_1]\big ) \\&\quad \cdot p(s_1|s,a_0,b_0)\,x^*(s,a_0)\,\sigma (s)(b_0)\\&\,\ge \, \sum _{a_0\in A(s),\,b_0\in B(s)}\sum _{s_1\in S}\,\min \{\alpha (s_1),m(b_0)\} \\&\quad \cdot p(s_1|s,a_0,b_0)\,x^*(s,a_0)\,\sigma (s)(b_0) -\varepsilon \\&=\sum _{b_0\in B(s)}\left[ \sum _{a_0\in A(s)}\sum _{s_1\in S}\,\min \{\alpha (s_1),m(b_0)\}\cdot p(s_1|s,a_0,b_0)\,x^*(s,a_0)\right] \\&\quad \cdot \sigma (s)(b_0) -\varepsilon \\&\ge \,R-\varepsilon , \end{aligned}$$

where $\sigma [h_1]$ denotes the continuation strategy of $\sigma$ from stage 1 onward. The first equality in this calculation follows from Theorem 2.12, p. 64, in Maitra and Sudderth [6] when both sides are finite, and the proof of that result can be modified to handle the case when there are infinite values. The first inequality follows from Eq. (6), and the last inequality follows because Eq. (5) holds for every action $b_0\in B(s)$.

Therefore,

$$\begin{aligned} \alpha (s)\,\ge \,\inf _{\sigma \in \Sigma }u(s,\pi ,\sigma )\,\ge \,R-\varepsilon . \end{aligned}$$

As the number $R < G\alpha (s)$ is otherwise arbitrary and $\varepsilon$ is an arbitrary positive number, we conclude that $\alpha (s)\ge G\alpha (s)$. This implies that $\alpha$ satisfies condition (a). $\square$

8 The Value

Theorem 1 now follows from Lemmas 3 and 4. It also follows that $r^*$ is equal to the value function v of the game.

We have two additional results on the value of the game in the following special cases: when the game is fair and when the action sets of player 2 are finite.

A zero-sum stochastic game as in Definition 1 is called fair if $Gr = r$.

Corollary 1

If the zero-sum stochastic game is fair, then $v=r$.

Proof

It is clear from the algorithm that $r_{\xi } = r$ for all $\xi$. Thus $v = r^* =r$. $\square$

If all the action sets for player 2 are finite, then the algorithm for the value function reaches a fixed point not later than at ordinal $\omega$ (i.e., $\xi ^*\le \omega )$, where $\omega$ denotes the first infinite ordinal.

Theorem 2

If all the action sets $B(s), s\in S$, of player 2 are finite, then $v = r_{\omega } = \lim _n r_n$.

Proof

By Claim 2 of Lemma 1, $r_{\omega } \ge r$. So, by Lemma 2, it suffices to show that $Gr_{\omega } \le r_{\omega }$.

Fix $s \in S$ and $\varepsilon > 0$. Let $R < Gr_{\omega }(s)$. Because $Gr_{\omega }(s)$ is the value of the one-shot game $M_{r_{\omega }}(s)$, there exists a mixed action $x(s) \in \Delta (A(s))$ for player 1 such that, for all actions $b \in B(s)$ of player 2,

$$\begin{aligned} Ur_\omega (s,x(s),b)=\sum _{a\in A(s)}\sum _{s'\in S}r_{\omega }(s')\,p(s'|s,a,b)\,x(s,a)\, >\, R. \end{aligned}$$

As $r_{\omega }(s)$ is the increasing limit of $r_n(s)$ as $n\rightarrow \infty$, by the monotone convergence theorem, we have for n sufficiently large and all $b \in B(s)$

$$\begin{aligned} Ur_n(s,x(s),b)=\sum _{a\in A(s)}\sum _{s'\in S}r_{n}(s')\,p(s'|s,a,b)\,x(s,a)\, >\, R; \end{aligned}$$

here we rely on the assumption that the set B(s) is finite. Thus, for large n,

$$\begin{aligned} r_{\omega }(s)\,\ge \,r_{n+1}(s)\,=\,Gr_n(s)\, >\, R. \end{aligned}$$

Since R was an arbitrary number smaller that $G_{r_{\omega }}(s)$, we can conclude that $r_{\omega }(s) \ge Gr_{\omega }(s)$, as desired. $\square$

It can happen that $r_{\omega } < v$ if player 2 has an infinite action set. The following example is a slight variation on Example 6 in Flesch et al. [3].

Example 2

Let $S = \{0,1,2,\ldots \}$ and let the reward r be such that $r(1) =1$ and $r(n)=0$ for all states $n\in S{\setminus }\{1\}$. Player 1 is a dummy (i.e., A is a singleton) and player 2’s action set in state 0 is $B(0) = \{1,2,\ldots \}$. The transitions are as follows: (i) In state 0, playing action n leads to state n, (ii) state 1 is absorbing, and (iii) in each state $n\ge 2$, regardless the action of player 2, play moves to state $n-1$. Let the initial state be state 0.

In this game, by choosing an initial action $b > n+1$, player 2 can guarantee a reward of 0 for the first n stages. This implies that $r_n(0) = (G^nr)(0) = 0$ for each $n\in {\mathbb {N}}$, and hence $r_{\omega }(0) = \sup _n r_n(0) = 0$. However, as state 1 is absorbing, the value of the game with initial state 0 is $v(0)=1$. In fact, in this game, the value function v is equal to $r_{\omega +1} = Gr_{\omega }$. $\Diamond$

9 Markov Strategies and Stationary Strategies

In this section we examine the optimal and $\varepsilon$-optimal strategies of the players in the superfair zero-sum stochastic game.

A selector for player 2 is a mapping $y:S \mapsto \Delta (B)$ such that, for every $s\in S$, $y(s) \in \Delta (B(s))$. A strategy $\sigma$ for player 2 is called stationary if there is a selector y such that $\sigma (h) = y(s_h)$ for every history $h\in H$; recall that $s_h$ denotes the final state of the history h. Thus a stationary strategy ignores the past and the current stage of the game when choosing an action.

A strategy $\sigma$ for player 2 is called Markov if there is a sequence of selectors $y_0,y_1,\ldots$ for player 2 such that $\sigma (h) = y_n(s_h)$ for every history $h\in H_n$ in every stage $n\in {\mathbb {N}}$. So a Markov strategy ignores the past but may make use of the current stage of the game.

Stationary and Markov strategies for player 1 are defined similarly.

Theorem 3

In every superfair zero-sum stochastic game, player 2 has an $\varepsilon$-optimal Markov strategy for every $\varepsilon > 0$. If all the action sets B(s), $s\in S$, of player 2 are finite, then player 2 has an optimal stationary strategy.

Proof

The strategy $\sigma$ in the statement of Lemma 3 is Markov. It is also $\varepsilon$-optimal by Eq. (3) because $r^* = v$ is the value function for the game. This proves the first assertion.

Now assume that the action sets B(s), $s\in S$, are all finite. By Theorem 2 in Flesch et al. [3], player 2 has, for every state $s\in S$, an optimal mixed action $y(s) \in \Delta (B(s))$ for the one-shot game $M_v(s)$. The argument for Lemma 3 can be repeated with $y_n = y$ for all n and $\varepsilon = 0$ to show that the stationary strategy $\sigma$ corresponding to the selector y is optimal. $\square$

We do not know whether the first assertion of Theorem 3 holds for player 1; that is, whether $\varepsilon$-optimal Markov strategies exist for player 1 for all $\varepsilon > 0$. Kiefer et al. [7] constructed a very nice and delicate Markov decision problem on a countable state space, with a so-called Büchi payoff, in which the decision maker has no $\varepsilon$-optimal Markov strategies for small $\varepsilon >0$. This illustrates that Markov strategies are not always sufficient when the state space is countable. Their Markov decision problem, however, is not superfair in our sense.

The second assertion of Theorem 3 is false for player 1. Indeed, there is an example in Kumar and Shiau [4] with three states and two actions for each player in which player 1 has no optimal strategy. (The example is also on p. 192 in Maitra and Sudderth [6].)

Here is a positive result for player 1 under further assumptions.

Theorem 4

If the reward function r is bounded and all the actions sets B(s), $s \in S$, of player 2 are finite, then, for every $\varepsilon > 0$ and every state $s \in S$, player 1 has a stationary strategy that is $\varepsilon$-optimal for the initial state s.

Proof

This follows from Theorem 2 and the argument for Corollary 3.9 in Secchi [8]. $\square$

10 Concluding Remarks

10.1 Related Payoff Functions

In our model, the payoff function u was defined in Eq. (1). There are a few related payoff functions that we briefly discuss here: for every pair of strategies $(\pi ,\sigma )\in \Pi \times \Sigma$ and initial state $s\in S$, define

$$\begin{aligned} k(s,\pi ,\sigma )\,=\,\limsup _n\, \mathbb {E}_{s,\pi ,\sigma }[r(s_n)],\qquad \ell (s,\pi ,\sigma )\,=\,\mathbb {E}_{s,\pi ,\sigma }\left[ \limsup _n\,r(s_n)\right] \end{aligned}$$

where as before, n denotes a stage of the game. The connection between k and $\ell$ and the payoff function u stems from the fact that stage n can be seen as the outcome of the stop rule that is constant n (i.e., always stops in stage n). In the specific case when the reward function r is bounded, we have $k\le \ell =u$, where the inequality follows by Fatou’s lemma and the equality follows from Theorem 2.2 in Maitra and Sudderth [6]. However, when the reward function r is unbounded, this is no longer true. Consider the following example, in which $\ell <k=u$.

Example 3

(Double-or-Nothing) Let $S =\{0,1,2,2^2,\ldots ,2^n,\ldots \}$ and $r(s) =s$ for every state $s \in S$. Assume that both players are dummies (i.e., A and B are singletons), and therefore, to simplify the notation, we omit the strategies from the notations. The transitions are as follows: state 0 is an absorbing state, and $p(2\,s|s) = p(0|s) =1/2$ for every state $s > 0$. Let the initial state be state 1. Note that the game is superfair and even fair.

In this game, $s_n$ eventually reaches state 0 with probability 1. Hence, the payoff function $\ell$ gives payoff 0 (recall that we follow the convention that $0\cdot \infty =0$). On the other hand,

$$\begin{aligned} \mathbb {E}_1[r(s_n)] = 2^n\cdot {\mathbb {P}}_1[s_1=2,s_2 = 2^2,\ldots ,s_n =2^n] =2^n\cdot \frac{1}{2^n}\, =\,1, \end{aligned}$$

which implies that the payoff function k gives payoff 1. One can similarly deduce that u also gives payoff 1 (this also follows directly from Corollary 1). $\Diamond$

We do not know if the statement of Theorem 1 holds for the payoff function $\ell$: when the reward function r is unbounded, we do not know, in general, how to calculate the value of the game for the payoff function $\ell$, or even whether the game has a value. We are also not aware of a paper where an algorithm is given for calculating the value of the game for the payoff function k, or even where it is proven that the game with the payoff function k admits a value.

10.2 Approximating the Reward Function with Bounded Functions

In games with unbounded reward functions, it is a frequently used technique to approximate the reward function with bounded functions and investigate what happens when the mistake in the approximation tends to zero. In our case, it is natural to consider the reward function $r_m:S\rightarrow [0,\infty )$, for every $m\in \mathbb {N}$, defined by $r_m(s)=\min \{r(s),m\}$ for every state $s\in S$.

For every $m\in \mathbb {N}$, and for every pair of strategies $(\pi ,\sigma )\in \Pi \times \Sigma$ and initial state $s\in S$, define the payoff as

$$\begin{aligned}u_m(s,\pi ,\sigma )\,=\,\limsup _t\, \mathbb {E}_{s,\pi ,\sigma }[r_m(s_t)];\end{aligned}$$

the payoff is similar to Eq. (1) but the reward function $r_m$ is used instead of the original r. Let $v_m$ denote the value function of the game with respect to the payoff function $u_m$. As $v_m$ is non-decreasing in m, it converges to some $v_\infty \in [0,\infty ]^S$ as m tends to infinity.

One may wonder whether $v_\infty$ is always equal to the value function of the game v [with respect to the original payoff in Eq. (1)]. This is not true, as in Example 3 for the initial state 1 we have $v_m(1)=0$ for every $m\in \mathbb {N}$ and hence $v_\infty (1)=0$, whereas the value is $v(1)=1$.

10.3 Rewards that also Depend on the Actions

In our model of zero-sum stochastic games (cf. Definition 1), the reward function r only depends on the current state. One could extend the model by allowing the reward function to depend on the current actions well, and have the form $r:S\times A\times B\rightarrow [0,\infty )$. However, in this extended model, it is not clear how to define the notion “superfair” without this notion being too restrictive. One natural idea would be to transform a zero-sum stochastic game in which the rewards depend on the current state and the current actions into a zero-sum stochastic game in which the rewards only depend on the current state (by extending the state space so that each state in the latter game corresponds to a triple consisting of a state of the former game and an action for each player). As it turns out, after applying such a transformation, the latter game is only superfair under rather restrictive conditions on the former game. It remains an open problem to find an appealing definition of the notion “superfair” when the reward function may also depend on the current actions.

Appendix

As mentioned in Sect. 4, every positive zero-sum stochastic game can be transformed into an equivalent zero-sum stochastic game as in Definition 1, which is superfair. Here we describe this transformation in detail, and explain what the equivalence between these games exactly means.

A positive zero-sum stochastic game $\Gamma ^+$ is a game

$$\begin{aligned}\Gamma ^+=(S^+,A^+,B^+,(A^+(s))_{s\in S},(B^+(s))_{s\in S},p^+,r^+)\end{aligned}$$

as in Definition 1, but with a reward function $r^+:S^+\times A^+\times B^+\rightarrow [0,\infty )$ depending on states and actions. The payoff is defined as the expectation of the infinite sum of the stage rewards. Thus, for each strategy pair $(\pi ^+,\sigma ^+)$ and initial state $s^+\in S^+$

$$\begin{aligned} u^+(s^+,\pi ^+,\sigma ^+) =\mathbb {E}_{s^+,\pi ^+,\sigma ^+}\left[ \sum _{n=0}^{\infty } r^+(s^+_n,a^+_n,b^+_n)\right] . \end{aligned}$$

(7)

The positive zero-sum stochastic game $\Gamma ^+$ can be transformed into a zero-sum stochastic game $\Gamma$ as in Definition 1 with the payoff function given in Eq. (1). Indeed, in the game $\Gamma$, (i) let the state space be the set of histories of $\Gamma ^+$, i.e., $S=H^+$, (ii) let the action spaces be $A=A^+$, $B=B^+$, and for each history $s=h^+\in S=H^+$ ending in state $s^+\in S^+$ let $A(s)=A^+(s^+)$, $B(s)=B^+(s^+)$, (iii) let the transition law p be defined as follows: from each $h^+=(s^+_0,a_0,b_0,\ldots ,s^+_{n-1},a_{n-1},b_{n-1},s^+_n)$, under actions $a_n\in A^+(s_n^+)$ and $b_n\in B^+(s_n^+)$, transition occurs to $g^+=(s^+_0,a_0,b_0,\ldots ,s^+_n,a_n,b_n,s^+_{n+1})$ with probability $p^+(s^+_{n+1}|s^+_n,a_n,b_n)$, and (iv) let the reward function r be defined as follows: for each $s=h^+\in S=H^+$, say $h^+=(s^+_0,a_0,b_0,\ldots ,s^+_{n-1},a_{n-1},b_{n-1},s^+_n)$, if $n=0$ then we let $r(s)=r(h^+)=0$ and if $n\ge 1$ we let

$$\begin{aligned}r(s)=r(h^+) = \sum _{k=0}^{n-1}r^+(s^+_k,a_k,b_k).\end{aligned}$$

Thus, the reward in $\Gamma$ at a state $h^+\in S=H^+$ is the sum of the rewards in $\Gamma ^+$ along the history $h^+$ of $\Gamma ^+$.

Note that $\Gamma$ is superfair by construction. Indeed, if the transition law p places a positive probability for moving from $h\in S$ to $h'\in S$, then $h'$ extends h with an additional stage. Therefore, $r(h)\le r(h')$. In particular, r is nondecreasing during the entire play of the game $\Gamma$ (with probability 1, regardless the strategies of the players).

There is a natural one-to-one correspondence between the histories of $\Gamma$ and $\Gamma ^+$: Consider an initial state $s^+$ of $\Gamma ^+$, which corresponds to the initial state $(s^+_0)$ of $\Gamma$. Given these initial states, a history $h^+=(s^+_0,a_0,b_0,\ldots ,s^+_{n-1},a_{n-1},b_{n-1},s^+_n)$ of $\Gamma ^+$ corresponds to the history of $\Gamma$ of the form $(h^+_0,a_0,b_0,\ldots ,h^+_{n-1},a_{n-1},b_{n-1},h^+)$, where $h^+_j$ denotes the initial part of $h^+$ up to state $s^+_j$ in stage j.

Based on this one-to-one correspondence between the histories, there is also a one-to-one correspondence between strategies. Finally, a strategy pair $(\pi ^+,\sigma ^+)$ in $\Gamma ^+$ induces the same payoff as the corresponding strategy pair $(\pi ,\sigma )$ in $\Gamma$: by Eqs. (1) and (7), for every strategy pair ($\pi ,\sigma )$ and initial state $s\in S$,

$$\begin{aligned} u^+(s^+,\pi ^+,\sigma ^+)&=\mathbb {E}_{s^+,\pi ^+,\sigma ^+}\left[ \sum _{n=0}^{\infty } r^+(s^+_n,a_n,b_n)\right] \\&= \mathbb {E}_{s^+,\pi ^+,\sigma ^+}\left[ \lim _{t\rightarrow \infty }\left[ \sum _{n=0}^{t-1} r^+(s^+_n,a_n,b_n)\right] \right] \\&= \lim _{t\rightarrow \infty }E_{s^+,\pi ^+,\sigma ^+}\left[ \sum _{n=0}^{t-1} r^+(s^+_n,a_n,b_n)\right] \\&=\lim _{t\rightarrow \infty }\, \mathbb {E}_{s,\pi ,\sigma }[r(s_t)]=u(s,\pi ,\sigma ). \end{aligned}$$

The third equality is by Theorem 4.2.7, p. 62 in Maitra and Sudderth [6]. We also used that in $\Gamma$ the stage rewards are nondecreasing during the play, so the limit superior over finite stop rules can be replaced with the limit.