Augmented Lagrangian index-3 semi-recursive formulations with projections

Abstract

Sensitivity analysis represents a powerful tool for the optimization of multibody system dynamics. The performance of a gradient-based optimization algorithm is strongly tied to the dynamic and the sensitivity formulations considered. The accuracy and efficiency are critical to any optimization problem, thus they are key factors in the selection of the dynamic and sensitivity analysis approaches used to compute an objective function gradient. Semi-recursive methods usually outperform global methods in terms of computational time, even though they involve sometimes demanding recursive procedures. Semi-recursive methods are well suited to be combined with different constraints enforcement schemes as the augmented Lagrangian index-3 formulation with velocity and acceleration projections (ALI3-P), taking advantage of the robustness, accurate fulfillment of constraint equations and the low computational burden. The sensitivity analysis of the semi-recursive ALI3-P formulation is studied in this document by means of the direct differentiation method. As a result, a semi-recursive ALI3-P sensitivity formulation is developed for an arbitrary reference point selection, and then two particular versions are unfolded and implemented in the general purpose multibody library MBSLIM, using as reference point the center of mass (RTdyn0) or the global origin of coordinates (RTdyn1). Besides, the detailed derivatives of the recursive terms are provided, which will be useful not only for the direct sensitivity formulation presented herein, but also for other sensitivity formulations relying on the same recursive expressions. The implementation has been tested in two numerical experiments, a five-bar benchmark problem and a buggy vehicle.

1 Introduction

Since the onset of the first multibody dynamic simulations, the optimization of the dynamic response of a multibody system has attracted the attention of several multibody researchers, and, despite the continuous publications of new methods, it is still an open problem. Optimal design and control can be addressed following different paths, such as look-up-tables based on experiment design, gradient-based methods or stochastic methods, among others. However, for multibody systems, optimization algorithms that handle objective function gradients usually perform better than others based on the mere evaluation of the objective function [1]. For the assessment of a gradient involving the dynamic response of a system, a sensitivity analysis is required [2–4].

The sensitivity analysis of dynamic formulations can be addressed by means of diverse differentiation techniques, such as numerical differentiation [5], symbolic differentiation [6], automatic differentiation [7–10], analytical differentiation [10] or their combinations [11]. Frequently, analytical differentiation methods are the most computationally efficient for the evaluation of any derivative, even though they are not broadly used in the multibody community due to the enormous implementation effort that they require. On the contrary, automatic and numerical differentiations are much simpler to implement, but this usually comes at the price of a higher computational expense.

The efficiency of a sensitivity analysis is strongly related to the performance of the dynamic simulation. In this regard, the selection of a set of coordinates is not trivial but it has a direct impact in the composition of the equations of motion (EoM) as well as in the computational effort required to solve them [12]. Although there is no set of coordinates or formulation universally better than others for any mechanism [13], relative coordinates are usually the most computationally efficient.

Relative or joint coordinate models are based on the type and sequence of joints linking the bodies of a multibody system. The generation of the set of EoM in relative coordinate models can be tackled by means of a semi-recursive composition of mass matrices and generalized force vectors [14–18], or through a fully-recursive technique [19–21]. With the semi-recursive approach, open-loop systems can be readily combined with kinematic constraints using one of many well-known constrained multibody dynamic formulations [22]. One efficient, accurate and robust constraint-enforcement scheme is the augmented Lagrangian index-3 formulation with velocity and acceleration projections (ALI3-P). The combination of the semi-recursive method with the ALI3-P formulation, studied in [16–18, 23, 24], combines the reduced number of coordinates and constraints of the semi-recursive process with the advantages of the ALI3-P constraint enforcement scheme.

Two of the most recent works studying the sensitivity analysis of multibody dynamic formulations refer to the ALI3-P formulation [25, 26]. The first work [25] presents the application of the direct differentiation method (DDM) to the ALI3-P equations of motion, delivering a set of sensitivity systems that can be solved analogously to and jointly with the dynamic equations. The second work [26] is committed to the application of the continuous adjoint variable method (AVM) to the ALI3-P equations with the aim of reducing the computational burden of the sensitivity analysis for large sets of parameters. However, the sensitivity analysis of semi-recursive ALI3-P formulations has not been addressed yet, either with a direct or an adjoint approach.

In the current work, the DDM is applied to the semi-recursive ALI3-P equations of motion following an analytical differentiation procedure both for the differentiation of the sensitivity expressions and for derivatives of kinematic recursive relations and accumulation procedures. The sensitivity equations reached are analog to those presented in [25], but the recursive nature, the composition of the equations of motion and the use of relative coordinates make semi-recursive ALI3-P sensitivity formulations intrinsically different.

The main novelty of this work relies on the development of the optimized analytical derivatives of each dynamic and kinematic term involved in semi-recursive methods. The expressions of the derivatives are presented for an arbitrary reference point (general expressions) and also particularized for the most usual choices of reference points, giving rise to the RTdyn0 formulation (centre of mass as reference point) and RTdyn1 formulation (origin of coordinates as reference point). The effect of the different reference points is studied in terms of sensitivity to determine if RTdyn1 performs better than RTdyn0 (like it happens in the dynamics [27]). Moreover, the particular RTdyn0 and RTdyn1 expressions allow some simplifications which make them more efficient compared to the general expressions.

A rigorous comparison of the herein presented analytical derivatives with automatic differentiation may be the objective of a separate work, but the authors do not expect superior efficiency of automatic differentiation based on their previous experience [10].

The semi-recursive sensitivity analyses developed in this paper have been implemented as general formulations in the general purpose multibody library MBSLIM [28], which includes different forward dynamic formulations, inverse dynamics, kinematics and sensitivity analysis of multibody systems, among other capabilities. The library, originally based on natural coordinates, now supports kinematic, dynamic and sensitivity analyses of relative coordinate models.

This work is structured into 11 sections: Sects. 1 and 2 are devoted to the introduction and the description of the notation used along the paper; Sect. 3 presents a brief description of the semi-recursive ALI3-P formulation; Sect. 4 covers the development of the set of semi-recursive ALI3-P sensitivity equations; Sects. 5 and 6 are focused on the analytical derivatives of the mass matrix and generalized forces vector; the constraint derivatives involved in this sensitivity formulation are introduced in Sect. 7; Sects. 8 and 9 explore the derivatives of natural coordinates and the recursive kinematic relations; in Sect. 10, the semi-recursive ALI3-P sensitivity formulation is tested in two numerical experiments. Finally, Sect. 11 gathers the main conclusions of the work. Moreover, four additional appendices are included to shed light on the particularization of the general semi-recursive ALI3-P sensitivity formulation to RTdyn0 and RTdyn1.

This paper is regarded as a continuation of the former paper [24] in which the semi-recursive ALI3-P formulation is thoroughly described. Here, a brief description of the formulation is presented, while the reader is referred to [24] for further details.

2 Notation

Derivatives in semi-recursive formulations involve several concatenations of matrices and multi-dimensional matrix products. The explosion of terms leads to large expressions which can be clarified using the convenient notation and a new rule of differentiation. Let us consider a model described by ${\mathbf{z}}\in \mathbb{R}^{n}$ relative coordinates, with ${\mathbf{q}}\in \mathbb{R}^{n_{q}}$ natural (or fully-Cartesian) coordinates referred to points and vectors, and with ${\boldsymbol{\rho} }\in \mathbb{R}^{p}$ system parameters. Given a function $f$ depending on ${\mathbf{z}}$, ${\dot{\mathbf{z}}}$, ${\ddot{\mathbf{z}}}$, ${\mathbf{q}}$, ${\dot{\mathbf{q}}}$, ${\ddot{\mathbf{q}}}$ and ${\boldsymbol{\rho} }$, the following differentiation rule is considered:

$$ f_{\hat{\mathbf{x}}}= \dfrac{\partial f}{\partial {\mathbf{q}}} \dfrac{\partial {\mathbf{q}}}{\partial \mathbf{x}} + \dfrac{\partial f}{\partial {\dot{\mathbf{q}}}} \dfrac{\partial {\dot{\mathbf{q}}}}{\partial \mathbf{x}} + \dfrac{\partial f}{\partial {\ddot{\mathbf{q}}}} \dfrac{\partial {\ddot{\mathbf{q}}}}{\partial \mathbf{x}} + \dfrac{\partial f}{\partial \mathbf{x}}= {f}_{{\mathbf{q}}} {{\mathbf{q}}}_{\mathbf{x}} + {f}_{{ \dot{\mathbf{q}}}} {{\dot{\mathbf{q}}}}_{\mathbf{x}} + {f}_{{\ddot{\mathbf{q}}}} {{ \ddot{\mathbf{q}}}}_{\mathbf{x}} + {f}_{\mathbf{x}}{,} $$

(1)

with ${\mathbf{x}}$ being any of the dependencies of function $f$. As it was mentioned in the nomenclature, this notation indicates the derivative of a function with respect to ${\mathbf{x}}$ considering all the explicit dependencies of the function on natural coordinates, and the dependencies of natural coordinates on ${\mathbf{x}}$. This notation is also valid for the differentiation of vectors or matrices.

Besides, it is convenient to define the operator $(\; \tilde{} \;)$ as the skew-symmetric matrix of a vector. For an arbitrary vector ${\mathbf{v}}= \begin{bmatrix} v_{x} & v_{y} & v_{z} \end{bmatrix} ^{\mathrm{T}} \in \mathbb{R}^{3}$, this function yields

$$ \tilde{\mathbf{v}}= \begin{bmatrix} 0 & -v_{z} & v_{y} \\ v_{z} & 0 & -v_{x} \\ -v_{y} & v_{x} & 0 \end{bmatrix} {.} $$

(2)

Similarly, the skew-symmetric multi-dimensional matrix of a matrix ${\mathbf{A}} \in \mathbb{R}^{3 \times n}$ can be defined as the multi-dimensional matrix ${\tilde{\mathbf{A}}} \in \mathbb{R}^{3 \times 3 \times n}$ composed of the skew-symmetric matrices of each column of the matrix ${\mathbf{A}}$,

$$ {\tilde{\mathbf{A}}}= \begin{bmatrix} {\tilde{\mathbf{A}}}_{1} & {\tilde{\mathbf{A}}}_{2} & \ldots & {\tilde{\mathbf{A}}}_{n} \end{bmatrix} {,} $$

(3)

where ${\mathbf{A}}_{i}$ represents the column $i$ of the matrix ${\mathbf{A}}$.

3 Description of the multibody formulation

The semi-recursive ALI3-P formulation is briefly outlined in this section, and the reader is referred to [24] to gain insight into the composition of the EoM, recursive relations and assembly procedures. The semi-recursive relations presented can be regarded as a generalization of other works like [19, 29] to an arbitrary reference point, and the reader might also have useful information in [13, 30] for ALI3-P formulations. Additional information can be found in [18]

Let us consider a multibody system composed of $n_{{{\mathrm{b}}}}$ bodies with $n_{{{\mathrm{b}}}}$ kinematic joints relating the motion of the bodies, and $n$ joint coordinates ${\mathbf{z}}$ parameterizing the motion. In the case of unconstrained open-loop systems, the kinematics of the multibody system can be described by means of the following set of recursive relations:

$$\begin{aligned} {\mathbf{V}}_{i}&= {\mathbf{B}}_{i}^{\mathrm{v}} {\mathbf{V}}_{i-1}+{\mathbf{b}}_{i}^{\mathrm{v}} {{ \dot{\mathbf{z}}}_{i}} {,} \end{aligned}$$

(4a)

$$\begin{aligned} {\dot{\mathbf{V}}}_{i} &= {\mathbf{B}}_{i}^{\mathrm{v}} {\dot{\mathbf{V}}}_{i-1}+ {\mathbf{b}}_{i}^{ \mathrm{v}} {{\ddot{\mathbf{z}}}_{i}} + {\mathbf{d}}_{i}^{\mathrm{v}} {,} \end{aligned}$$

(4b)

$$\begin{aligned} {\mathbf{B}}_{i}^{\mathrm{v}} &= \begin{bmatrix} {\mathbf{I}} & {\tilde{\mathbf{r}}}_{i-1} - {\tilde{\mathbf{r}}}_{i} \\ {\mathbf{0}} & {\mathbf{I}} \end{bmatrix} {,} \end{aligned}$$

(4c)

$$\begin{aligned} {\dot{\mathbf{B}}}_{i}^{\mathrm{v}} &= \begin{bmatrix} {\mathbf{0}} & {\dot{\tilde{\mathbf{r}}}}_{i-1} - {\dot{\tilde{\mathbf{r}}}}_{i} \\ {\mathbf{0}} & {\mathbf{0}} \end{bmatrix}{,} \end{aligned}$$

(4d)

$$\begin{aligned} {\mathbf{d}}_{i}^{\mathrm{v}}&= {\dot{\mathbf{B}}}_{i}^{\mathrm{v}} {\mathbf{V}}_{i-1} + { \dot{\mathbf{b}}}_{i}^{\mathrm{v}} {{\dot{\mathbf{z}}}_{i}}{,} \end{aligned}$$

(4e)

wherein ${\mathbf{V}}_{i}= \begin{bmatrix} {\dot{\mathbf{r}}}_{i}^{{\mathrm{T}}} & {\boldsymbol{\omega} }_{i}^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}$, ${\dot{\mathbf{V}}}_{i}= \begin{bmatrix} {\ddot{\mathbf{r}}}_{i}^{{\mathrm{T}}} & {\dot{\boldsymbol{\omega} }}_{i}^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}}$, and with ${\mathbf{b}}_{i}^{\mathrm{v}}$ being a recursive term reliant on the joint type describing the relative motion between body $i$ and its preceding body (see Appendix D). The previous relations can be gathered in a matrix form as

$$\begin{aligned} {\mathbf{V}} &= {\mathbf{R}}^{\mathrm{v}} {{\dot{\mathbf{z}}}} {,} \end{aligned}$$

(5)

$$\begin{aligned} {\dot{\mathbf{V}}} &= {\mathbf{R}}^{\mathrm{v}} {\ddot{\mathbf{z}}} + {\dot{\mathbf{R}}}^{ \mathrm{v}} {\dot{\mathbf{z}}}{.} \end{aligned}$$

(6)

Applying the virtual power principle to the dynamic equations expressed in terms of reference point coordinates and considering (5) and (6), the EoM of an unconstrained open-loop system can be described with the following matrix equation:

$$ \left ( {\mathbf{R}}^{\mathrm{v{\mathrm{T}}}} {\mathbf{M}}^{\mathrm{v}} {\mathbf{R}}^{\mathrm{v}} \right ) {\ddot{\mathbf{z}}} = {\mathbf{R}}^{\mathrm{v{\mathrm{T}}}} \left ( {\mathbf{Q}}^{ \mathrm{v}} - {\mathbf{M}}^{\mathrm{v}} {\dot{\mathbf{R}}}^{\mathrm{v}} {\dot{\mathbf{z}}} \right ) {,} $$

(7)

which can be reformulated as

$$ {\mathbf{M}}^{\mathrm{d}} {\ddot{\mathbf{z}}} = {\mathbf{Q}}^{\mathrm{d}} {,} $$

(8)

where ${{\mathbf{R}}^{\mathrm{v}}}\in \mathbb{R}^{6 n_{{{\mathrm{b}}}} \times n}$ is the topology matrix used for the semi-recursive accumulation and ${{\dot{\mathbf{R}}}^{\mathrm{v}}}\in \mathbb{R}^{6 n_{{{\mathrm{b}}}} \times n}$ is its time derivative, ${\mathbf{M}}^{\mathrm{v}}\in \mathbb{R}^{6 n_{{{\mathrm{b}}}} \times 6 n_{{{\mathrm{b}}}}}$ and ${\mathbf{Q}}^{\mathrm{v}} \in \mathbb{R}^{6 n_{{{\mathrm{b}}}}}$ are, respectively, the mass matrix and generalized vector of forces referred to reference point coordinates, and ${\mathbf{M}}^{\mathrm{d}}\in \mathbb{R}^{n \times n}$ and ${\mathbf{Q}}^{\mathrm{d}} \in \mathbb{R}^{n}$ are, respectively, the accumulated mass matrix and generalized forces vector.

If the mechanism has closed loops or other kinematic relations not described by kinematic joints, some constraint equations ${{\boldsymbol{\Phi } }}\in \mathbb{R}^{m}$ must be added to the open-loop system. These constraints can be enforced using different formulations. One possibility is to use the augmented Lagrangian index-3 formulation with projections recently reviewed in [18, 24], also used in [13] and originated from [30]. The semi-recursive augmented Lagrangian part of the formulation takes the form

$$\begin{aligned} {\mathbf{{M}}}^{\mathrm{d}} {\ddot{\mathbf{z}}}^{*} &+ {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{ \mathrm{T}} \left ( {{\boldsymbol{\lambda}}^{*\{i\}}} + {\boldsymbol{\alpha}} {{ \boldsymbol{\Phi } }}\right ) = {\mathbf{{Q}}}^{\mathrm{d}}{,} \end{aligned}$$

(9a)

$$\begin{aligned} {\boldsymbol{\lambda}}_{n+1}^{*\{i\}} &= {\boldsymbol{\lambda}}_{n+1}^{*\{i-1\}} + { \boldsymbol{\alpha}} {{\boldsymbol{\Phi } }}_{n+1}^{\{i\}} ; \quad i>1 {,} \end{aligned}$$

(9b)

where $\boldsymbol{\alpha}$ is a diagonal matrix containing the penalty factors associated with the constraints, $n$ is the time step index and $i$ is the iteration index of the approximate Lagrange multipliers ${\boldsymbol{\lambda}}_{n+1}^{*} \in \mathbb{R}^{m}$.

In this formulation, constraints in velocities and accelerations are enforced by means of velocity and acceleration projections. For the projection of the velocities:

$$\begin{aligned} \left ( \bar{\mathbf{{P}}} + {\varsigma} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{ \mathrm{T}} {\boldsymbol{\alpha}} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} \right ) {{ \dot{\mathbf{z}}}}^{\{i\}} &=\bar{\mathbf{{P}}} {{{\dot{\mathbf{z}}}}^{*}} - {{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{\mathrm{T}} \left ( {\boldsymbol{\sigma}}^{\{i\}} + { \varsigma} {\boldsymbol{\alpha}} {{{\boldsymbol{\Phi } }}_{t}} \right ){,} \end{aligned}$$

(10a)

$$\begin{aligned} {\boldsymbol{\sigma}}^{\{i\}} &= {\boldsymbol{\sigma}}^{\{i-1\}} + {\varsigma} { \boldsymbol{\alpha}} \dot{{\boldsymbol{\Phi } }}; \quad i>1{,} \end{aligned}$$

(10b)

where $\bar{\mathbf{{P}}} \in \mathbb{R}^{n \times n}$ is a symmetric projection matrix, ${\varsigma}$ is a weighting constant and ${\boldsymbol{\sigma}} \in \mathbb{R}^{m}$ the Lagrange multipliers related to the velocity projection. Observe that the penalty factor for the velocity projection is actually ${\varsigma}{\boldsymbol{\alpha}}$. The selection of the most convenient projection matrix and penalty is out of the scope of this work, but there is some previous research about how to choose these parameters based on the energy conserving or decaying properties of the projection (see, e.g. [31]).

Analogously, for the acceleration projection,

$$\begin{aligned} \left ( \bar{\mathbf{{P}}} + {\varsigma} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{ \mathrm{T}} {\boldsymbol{\alpha}} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} \right ) {{ \ddot{\mathbf{z}}}}^{\{i\}} &= \bar{\mathbf{{P}}} {{{\ddot{\mathbf{z}}}}^{*}} - {{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{\mathrm{T}} \left ( {\boldsymbol{\kappa}}^{\{i\}} + { \varsigma} {\boldsymbol{\alpha}} \left ( \dot{{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} { \dot{\mathbf{z}}}+ {\dot{{\boldsymbol{\Phi } }}_{t}}\right ) \right ) {,} \end{aligned}$$

(11a)

$$\begin{aligned} {\boldsymbol{\kappa}}^{\{i\}} &= {\boldsymbol{\kappa}}^{\{i-1\}} + {\varsigma} { \boldsymbol{\alpha}} \ddot{{\boldsymbol{\Phi } }}; \quad i>1{,} \end{aligned}$$

(11b)

with ${\boldsymbol{\kappa}} \in \mathbb{R}^{m}$ being the Lagrange multipliers associated with the acceleration projections. Observe that the same projection matrix and penalty are assumed for the acceleration projection in order to obtain identical leading matrices for the systems of velocity and acceleration projections, (10a) and (11a), thus reducing the computational time needed for solving the systems.

This formulation gathers the advantages of relative coordinates modelling, such as the reduced number of variables and small systems of equations, with the robustness and efficiency of an augmented Lagrangian index-3 formulation.

4 Direct sensitivity analysis

Let us consider an objective function expressed in terms of ${\mathbf{z}}$, ${\dot{\mathbf{z}}}$, ${\ddot{\mathbf{z}}}$, ${\mathbf{q}}$, ${\dot{\mathbf{q}}}$, ${\ddot{\mathbf{q}}}$, ${\boldsymbol{\lambda} ^{*}}$ and ${ \boldsymbol{\rho} }$, with ${\boldsymbol{\rho} }\in \mathbb{R}^{p}$ being the set of parameters of the system, and also in terms of the Lagrange multipliers of the velocity and acceleration projections ${\boldsymbol{\sigma}}$ and ${\boldsymbol{\kappa}}$,

$$ {\boldsymbol{\psi}} = \int _{t_{0}}^{t_{{{\mathrm{F}}}}} {{\mathbf{g}} \left ( {\mathbf{z}}, { \dot{\mathbf{z}}}, {\ddot{\mathbf{z}}}, {\mathbf{q}}, {\dot{\mathbf{q}}}, {\ddot{\mathbf{q}}}, { \boldsymbol{\lambda} ^{*}}, {\boldsymbol{\sigma}}, {\boldsymbol{\kappa}}, {\boldsymbol{\rho}}\right )}\, { \mathrm{d}} t {.} $$

(12)

Considering the differentiation rule (1), the gradient of the objective function ${\boldsymbol{\psi}}$ can be expressed as

$$ \begin{aligned} {\boldsymbol{\psi}}'=\nabla {\boldsymbol{\psi}}^{{\mathrm{T}}}= \int _{t_{0}}^{t_{{{ \mathrm{F}}}}} {\left ({\mathbf{g}}_{\hat{\mathbf{z}}} {\mathbf{z}}' + {\mathbf{g}}_{ \hat{\dot{\mathbf{z}}}} {\dot{\mathbf{z}}}' + {\mathbf{g}}_{\hat{\ddot{\mathbf{z}}}} { \ddot{\mathbf{z}}}' + {\mathbf{g}}_{\boldsymbol{\lambda} ^{*}} {\boldsymbol{\lambda} ^{*}}' + { \mathbf{g}}_{\boldsymbol{\sigma}} {\boldsymbol{\sigma}}' + {\mathbf{g}}_{\boldsymbol{\kappa}} { \boldsymbol{\kappa}}' + {\mathbf{g}}_{\boldsymbol{\rho}}\right )}\, {\mathrm{d}} t {.} \end{aligned} $$

(13)

The unknown sensitivities, i.e. ${\mathbf{z}}'$, ${\dot{\mathbf{z}}}'$, ${\ddot{\mathbf{z}}}'$, ${\boldsymbol{\lambda} ^{*}}'$, ${\boldsymbol{\sigma}}'$ and ${\boldsymbol{\kappa}}'$, can be obtained from the sensitivity analysis of the formulation used to solve the dynamics. The direct differentiation of the semi-recursive ALI3-P formulation leads to a set of $p$ systems of differential algebraic equations (DAE) related to the ALI3 part of the dynamics, additional $p$ systems of equations for the sensitivity of the velocity projections, and $p$ systems for the sensitivities of the acceleration projections.²

Taking derivatives of (9a), (9b) with respect to the set of parameters of the system ${\boldsymbol{\rho} }$, the following sensitivity equations for the augmented Lagrangian part of the ALI3-P formulation are reached:

$$\begin{gathered} \Big[ {\mathbf{M}}^{\mathrm{d}} {{{\ddot{\mathbf{z}}}{}}^{* \prime \{ i \} } } +{{ \mathbf{C}} {{{\dot{\mathbf{z}}}{}}^{* \prime \{ i \} } } } +\bar{\mathbf{K}} {{ \mathbf{z}}'}^{\{ i \} } +{{{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{\mathrm{T}}} {{ \boldsymbol{\lambda}}^{* \prime \{ i \} } } \Big] = \bar{\mathbf{{Q}}}^{\boldsymbol{\rho}}{,} \end{gathered}$$

(14a)

$$\begin{gathered} {{\boldsymbol{\lambda}}}^{* \prime \{i\} }={{\boldsymbol{\lambda}}}^{* \prime \{i - 1 \} } +{\boldsymbol{\alpha}} {{\boldsymbol{\Phi } }}'{,} \end{gathered}$$

(14b)

$$\begin{gathered} \bar{\mathbf{K}}= {{\mathbf{M}}_{\hat{\mathbf{z}}}^{\mathrm{d}} {{\ddot{\mathbf{z}}}}^{*}} +{{{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}^{\mathrm{T}}} \left ({{\boldsymbol{\lambda}}^{ \mathrm{*}}}+{\boldsymbol{\alpha} {\boldsymbol{\Phi } }} \right )+{{{\boldsymbol{\Phi } }}_{ \hat{\mathbf{z}}}^{\mathrm{T}}}\boldsymbol{\alpha} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} +{\mathbf{{K}}}{,} \end{gathered}$$

(14c)

$$\begin{gathered} \bar{\mathbf{{Q}}}^{{\boldsymbol{\rho} }} = {\mathbf{{Q}}}_{{\hat{\boldsymbol{\rho} }}}^{\mathrm{d}}-{{ \mathbf{M}}_{{\hat{\boldsymbol{\rho} }}}^{\mathrm{d}} {{\ddot{\mathbf{z}}}}^{*}} -{{{{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{{\hat{\boldsymbol{\rho} }}}}^{\mathrm{T}}}} \left ({{ \boldsymbol{\lambda}}^{*}}+{\boldsymbol{\alpha} {\boldsymbol{\Phi } }} \right )-{{{\boldsymbol{\Phi } }}_{ \hat{\mathbf{z}}}^{\mathrm{T}}}\boldsymbol{\alpha} {{\boldsymbol{\Phi } }}_{{\hat{\boldsymbol{\rho} }}}{,} \end{gathered}$$

(14d)

$$\begin{gathered} {{\boldsymbol{\Phi } }}' = {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} {\mathbf{z}}' + {{ \boldsymbol{\Phi } }}_{{\hat{\boldsymbol{\rho} }}}{,} \end{gathered}$$

(14e)

wherein ${\mathbf{K}}$ (equivalent stiffness matrix), ${\mathbf{C}}$ (equivalent damping matrix), $\bar{\mathbf{K}}$ and ${\mathbf{M}}^{\mathrm{d}} \in \mathbb{R}^{n \times n}$ in (14a)–(14e) are square matrices, while $\bar{\mathbf{{Q}}}^{\boldsymbol{\rho}} \in \mathbb{R}^{n \times p}$ is a matrix with the same dimensions of ${{\mathbf{z}}'}^{\{ i \} }$. In the calculation of these matrices, the following multi-dimensional matrix-vector products are used:³${{\mathbf{M}}_{\hat{\mathbf{z}}}^{\mathrm{d}} {{\ddot{\mathbf{z}}}}^{*}} ={{\mathbf{M}}_{ \hat{\mathbf{z}}}^{\mathrm{d}} \otimes {{\ddot{\mathbf{z}}}}^{*}}$, ${{{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}^{\mathrm{T}}} \left ({{ \boldsymbol{\lambda}}^{\mathrm{*}}}+{\boldsymbol{\alpha} {\boldsymbol{\Phi } }} \right )={{{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}^{\mathrm{T}}} \otimes \left ({{ \boldsymbol{\lambda}}^{\mathrm{*}}}+{\boldsymbol{\alpha} {\boldsymbol{\Phi } }} \right )$, ${{\mathbf{M}}_{{\hat{\boldsymbol{\rho} }}}^{\mathrm{d}} {{\ddot{\mathbf{z}}}}^{*}}={{\mathbf{M}}_{{ \hat{\boldsymbol{\rho} }}}^{\mathrm{d}} \otimes {{\ddot{\mathbf{z}}}}^{*}}$ and ${{{{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}^{\mathrm{T}}}} \left ({{ \boldsymbol{\lambda}}^{*}}+{\boldsymbol{\alpha} {\boldsymbol{\Phi } }} \right )={{{{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}^{\mathrm{T}}}} \otimes \left ({{ \boldsymbol{\lambda}}^{*}}+{\boldsymbol{\alpha} {\boldsymbol{\Phi } }} \right )$.

The dynamics of an ALI3-P formulation involves the projection of velocities and accelerations, and, consequently, this effect has to be included in the sensitivity analysis. Considering $\bar{\mathbf{P}} \in \mathbb{R}^{n \times n}$, a symmetric projection matrix, the sensitivity of the iterative velocity projections yields:

$$\begin{aligned} \begin{aligned} \left ( \bar{\mathbf{P}} + {\varsigma} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{\mathrm{T}} {\boldsymbol{\alpha}} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} \right ) {\dot{\mathbf{z}}}^{\prime \, \{i\} } &={\bar{\mathbf{P}} {\dot{\mathbf{z}}}^{* \prime}} + \bar{\mathbf{{P}}}' \left ( { \dot{\mathbf{z}}}^{*} - {\dot{\mathbf{z}}}\right ) -{{\boldsymbol{\Phi } }}_{ \hat{\mathbf{z}}\hat{\mathbf{z}}}^{\mathrm{T}} \left ( {\boldsymbol{\sigma}} + {\varsigma} { \boldsymbol{\alpha}} \dot{{\boldsymbol{\Phi } }}\right ) {\mathbf{z}}' \\ &\quad -{{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}^{\mathrm{T}} \left ( {\boldsymbol{\sigma}} + {\varsigma} {\boldsymbol{\alpha}} \dot{{\boldsymbol{\Phi } }}\right ) -{{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{\mathrm{T}} \left ( {\boldsymbol{\sigma}}^{\prime \,\{ i \}} + {\varsigma} {\boldsymbol{\alpha}} {\mathbf{b}}^{{\boldsymbol{\rho} }} \right ){,} \end{aligned} \end{aligned}$$

(15a)

$$\begin{aligned} {\boldsymbol{\sigma}}^{\prime \, \{i \}} &= {\boldsymbol{\sigma}}^{\prime \, \{i-1 \}}+ {\varsigma} { \boldsymbol{\alpha}} \dot{{\boldsymbol{\Phi } }}' ; \quad i>1{,} \end{aligned}$$

(15b)

with

$$ {\mathbf{b}}^{{\boldsymbol{\rho} }} = \dot{{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} {\mathbf{z}}^{ \prime} + \dot{{\boldsymbol{\Phi } }}_{{\hat{\boldsymbol{\rho} }}}{.} $$

(16)

In (15a), (15b), the following multi-dimensional matrix–vector products appear:

$$ \begin{aligned} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}^{\mathrm{T}} \left ( { \boldsymbol{\sigma}} + {\varsigma} {\boldsymbol{\alpha}} \dot{{\boldsymbol{\Phi } }}\right ) { \mathbf{z}}' &= \left ( {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}^{\mathrm{T}} \otimes \left ( {\boldsymbol{\sigma}} + {\varsigma} {\boldsymbol{\alpha}} \dot{{\boldsymbol{\Phi } }}\right ) \right ) {\mathbf{z}}', \\ {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}^{\mathrm{T}} \left ( { \boldsymbol{\sigma}} + {\varsigma} {\boldsymbol{\alpha}} \dot{{\boldsymbol{\Phi } }}\right ) &={{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}^{\mathrm{T}} \otimes \left ( { \boldsymbol{\sigma}} + {\varsigma} {\boldsymbol{\alpha}} \dot{{\boldsymbol{\Phi } }}\right ) . \end{aligned} $$

Following the aforementioned procedure, the sensitivity of the acceleration projections takes the form:

$$\begin{aligned} \begin{aligned} \left ( \bar{\mathbf{P}} + {\varsigma} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{\mathrm{T}} {\boldsymbol{\alpha}} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} \right ) {\ddot{\mathbf{z}}}^{\prime \,\{ i\} } &={\bar{\mathbf{P}} {\ddot{\mathbf{z}}}^{* \prime}} + \bar{\mathbf{{P}}}' \left ( { \ddot{\mathbf{z}}}^{*} - {\ddot{\mathbf{z}}}\right ) -{{\boldsymbol{\Phi } }}_{ \hat{\mathbf{z}}\hat{\mathbf{z}}}^{\mathrm{T}} \left ( {\boldsymbol{\kappa}} + {\varsigma} { \boldsymbol{\alpha}} \ddot{{\boldsymbol{\Phi } }}\right ) {\mathbf{z}}' \\ &\quad -{{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}^{\mathrm{T}} \left ( {\boldsymbol{\kappa}} + {\varsigma} {\boldsymbol{\alpha}} \ddot{{\boldsymbol{\Phi } }}\right ) -{{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}^{\mathrm{T}} \left ( {\boldsymbol{\kappa}}^{\prime \,\{ i \} } + {\varsigma} {\boldsymbol{\alpha}} {\mathbf{c}}^{{\boldsymbol{\rho} }} \right ){,} \end{aligned} \end{aligned}$$

(17a)

$$\begin{aligned} {\boldsymbol{\kappa}}^{\prime \,\{ i \}} &= {\boldsymbol{\kappa}}^{\prime \,\{ i-1 \}}+ {\varsigma} { \boldsymbol{\alpha}} \ddot{{\boldsymbol{\Phi } }}' ; \quad i>1{,} \end{aligned}$$

(17b)

with

$$ \begin{aligned} {\mathbf{c}}^{{\boldsymbol{\rho} }} = 2\dot{{\boldsymbol{\Phi } }}_{ \hat{\mathbf{z}}} {\dot{\mathbf{z}}}^{\prime} + \ddot{{\boldsymbol{\Phi } }}_{ \hat{\mathbf{z}}} {\mathbf{z}}^{\prime} + \ddot{{\boldsymbol{\Phi } }}_{{ \hat{\boldsymbol{\rho} }}}{} \end{aligned} $$

(18)

and the following multi-dimensional matrix–vector products:

$$ \begin{aligned} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}^{\mathrm{T}} \left ( { \boldsymbol{\kappa}} + {\varsigma} {\boldsymbol{\alpha}} \ddot{{\boldsymbol{\Phi } }}\right ) { \mathbf{z}}' &= \left ( {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}^{\mathrm{T}} \otimes \left ( {\boldsymbol{\kappa}} + {\varsigma} {\boldsymbol{\alpha}} \ddot{{\boldsymbol{\Phi } }}\right ) \right ) {\mathbf{z}}', \\ {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}^{\mathrm{T}} \left ( { \boldsymbol{\kappa}} + {\varsigma} {\boldsymbol{\alpha}} \ddot{{\boldsymbol{\Phi } }}\right ) &={{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}^{\mathrm{T}} \otimes \left ( { \boldsymbol{\kappa}} + {\varsigma} {\boldsymbol{\alpha}} \ddot{{\boldsymbol{\Phi } }}\right ). \end{aligned} $$

Equations (14a)–(14e) provide the sensitivities of the relative coordinates in positions ${\mathbf{z}}^{\prime}$, the sensitivities of the Lagrange multipliers ${\boldsymbol{\lambda}}^{*\prime}$ and the sensitivities of the unprojected velocities and accelerations of the states, ${\dot{\mathbf{z}}}^{* \prime}$ and ${\ddot{\mathbf{z}}}^{* \prime}$. Equations (15a), (15b) use the sensitivities of the unprojected velocities obtained in (14a)–(14e) to compute the sensitivities of the projected velocities of the states ${\dot{\mathbf{z}}}^{\prime}$ and the Lagrange multipliers $\boldsymbol{\sigma} ^{\prime}$. Similarly, equations (17a), (17b) produce the sensitivities of the projected accelerations from the sensitivities of the unprojected ones and the Lagrange multipliers sensitivities associated with this projection ${\boldsymbol{\kappa}}^{\prime}$.

5 Mass matrix derivatives

Considering the implicit dependencies of the mass matrix in a given instant of time, its derivative with respect to a set of sensitivity parameters can be obtained as

$$ \frac{{\mathrm{d}}{\mathbf{M}}^{\mathrm{d}}}{ \mathrm{d\boldsymbol{\rho}}}={\mathbf{M}}_{\hat{\mathbf{z}}}^{ \mathrm{d}} {{\mathbf{z}}'} + {\mathbf{M}}_{{\hat{\boldsymbol{\rho} }}}^{\mathrm{d}}{.} $$

(19)

In semi-recursive methods, the mass matrix can be fragmented in blocks with the form ${\mathbf{M}}_{i,j}^{\mathrm{d}}={\mathbf{b}}_{i}^{\mathrm{v{\mathrm{T}}}} {\mathbf{M}}_{i}^{\mathrm{v}\Sigma } {\mathbf{b}}_{i,j}^{\mathrm{v}}$, with ${\mathbf{b}}_{i}^{\mathrm{v}} \in \mathbb{R}^{6 \times n_{{v_{i}}}}$ being the relative recursive term of joint $i$, ${\mathbf{M}}_{i}^{\mathrm{v}\Sigma } \in \mathbb{R}^{6 \times 6}$ the accumulated mass matrix on body $i$, ${\mathbf{b}}_{i,j}^{\mathrm{v}} \in \mathbb{R}^{6 \times n_{{v_{j}}}}$ the accumulated relative recursive term of joint $j$ referred to the reference point of body $i$, and with $n_{{v_{i}}}$ and $n_{{v_{j}}}$ the number of coordinates of joints $i$ and $j$, respectively.

Following the structure of the mass matrix, its derivative with respect to ${\mathbf{z}}$ or ${\boldsymbol{\rho} }$ using (1) can be obtained as the assembly of the derivatives of each block, with the form

$$ \begin{aligned} \Bigl({\mathbf{M}}_{i,j}^{\mathrm{d}} \Bigr)_{\hat{\mathbf{x}}} = \Bigl({\mathbf{b}}_{i}^{ \mathrm{v{\mathrm{T}}}} {\mathbf{M}}_{i}^{\mathrm{v}\Sigma }{} {\mathbf{b}}_{i,j}^{\mathrm{v}} \Bigr)_{\hat{\mathbf{x}}} =\Bigl({\mathbf{b}}_{i}^{\mathrm{v{\mathrm{T}}}}\Bigr)_{ \hat{\mathbf{x}}} {\mathbf{M}}_{i}^{\mathrm{v}\Sigma }{} {\mathbf{b}}_{i,j}^{\mathrm{v}} +{ \mathbf{b}}_{i}^{\mathrm{v{\mathrm{T}}}} \Bigl({\mathbf{M}}_{i}^{\mathrm{v}\Sigma }{}\Bigr)_{ \hat{\mathbf{x}}} {\mathbf{b}}_{i,j}^{\mathrm{v}} +{\mathbf{b}}_{i}^{\mathrm{v{\mathrm{T}}}} {\mathbf{M}}_{i}^{ \mathrm{v}\Sigma }{} \Bigl({\mathbf{b}}_{i,j}^{\mathrm{v}}\Bigr)_{\hat{\mathbf{x}}} {,} \end{aligned} $$

(20)

with ${\mathbf{x}}$ being either ${\mathbf{z}}$ or ${\boldsymbol{\rho} }$, depending on which derivative is considered. Derivatives of relative recursive terms ${ \mathbf{b}}_{i}^{\mathrm{v}}$ and ${\mathbf{b}}_{i,j}^{\mathrm{v}}$ depend on the type of joint, while the derivatives of the accumulated mass matrix ${\mathbf{M}}_{i}^{\mathrm{v}\Sigma }{}$ rely on the topology of the mechanism and the derivatives of the elemental mass matrix of each body and they can be obtained as

$$ \begin{aligned} \Bigl( {\mathbf{M}}_{i}^{\mathrm{v}\Sigma }{} \Bigr)_{\hat{\mathbf{x}}}&= \Bigl( {\mathbf{M}}_{i}^{\mathrm{v}} + \displaystyle \sum _{{s}=1}^{n_{s}^{i}} \left ( {{\mathbf{B}}_{s}^{\mathrm{v}}}^{\mathrm{T}} {\mathbf{M}}_{s}^{\mathrm{v}\Sigma } { \mathbf{B}}_{s}^{\mathrm{v}}\right ) \Bigr)_{\hat{\mathbf{x}}} \\ &= \Bigl( {\mathbf{M}}_{i}^{\mathrm{v}}\Bigr)_{\hat{\mathbf{x}}} + \displaystyle \sum _{s=1}^{n_{s}^{i}} \left ( \Bigl( {{\mathbf{B}}_{s}^{\mathrm{v}}}^{\mathrm{T}} \Bigr)_{\hat{\mathbf{x}}} {\mathbf{M}}_{s}^{\mathrm{v}\Sigma } {\mathbf{B}}_{s}^{\mathrm{v}} +{{ \mathbf{B}}_{s}^{\mathrm{v}}}^{\mathrm{T}} \Bigl( {\mathbf{M}}_{s}^{\mathrm{v}\Sigma } \Bigr)_{ \hat{\mathbf{x}}} {\mathbf{B}}_{s}^{\mathrm{v}} +{{\mathbf{B}}_{s}^{\mathrm{v}}}^{\mathrm{T}} {\mathbf{M}}_{s}^{ \mathrm{v}\Sigma } \Bigl( {\mathbf{B}}_{s}^{\mathrm{v}} \Bigr)_{\hat{\mathbf{x}}} \right ){,} \end{aligned} $$

(21)

where $n_{s}^{i}$ is the number of children of body $i$, and ${\mathbf{B}}_{s}^{\mathrm{v}} \in \mathbb{R}^{6 \times 6}$ is a recursive transformation matrix between body $s$ and its preceding body.

The derivative of the elemental mass matrix of a body ${\mathbf{M}}_{i}^{\mathrm{v}}$ is determined by the reference point selected. The derivatives of this matrix for the RTdyn0 and RTdyn1 versions are explained in Appendix A (observe that both approaches involve important simplifications with respect to generic reference point formulas). Furthermore, the term $\Bigl({\mathbf{b}}_{i}^{\mathrm{v{\mathrm{T}}}} {\mathbf{M}}_{i}^{\mathrm{v}\Sigma }{} {\mathbf{b}}_{i,j}^{ \mathrm{v}} \Bigr)_{\hat{\mathbf{x}}}$ can be efficiently computed reusing terms and exploiting multi-dimensional matrix symmetries.

6 Force derivatives

First of all, the elemental force vector for each body can be decomposed into two terms, one related to each external force applied to the body and the other referred to velocity-dependent inertia forces:⁴

$$\begin{aligned} {\mathbf{Q}}_{i}^{\mathrm{v}} &=\displaystyle \sum _{j=1}^{n_{f}^{i}} {\mathbf{Q}}_{i,j}^{ \mathrm{v (e)}} +{{\mathbf{Q}}_{i}^{\mathrm{v}}}^{\mathrm{(I)}}{,} \end{aligned}$$

(22a)

$$\begin{aligned} {\mathbf{Q}}_{i,j}^{\mathrm{v (e)}}&= \begin{bmatrix} {\mathbf{f}}_{j} \\ {\mathbf{n}}_{j}^{\mathrm{G}} + \left ({\tilde{\mathbf{r}}}_{\mathrm{G}}^{i}-{ \tilde{\mathbf{r}}}_{i}\right ) {\mathbf{f}}_{j} \end{bmatrix}{,} \end{aligned}$$

(22b)

$$\begin{aligned} {{\mathbf{Q}}_{i}^{\mathrm{v}}}^{\mathrm{(I)}}&= \begin{bmatrix} - m_{i} {\tilde{\boldsymbol{\omega} }}_{i} {\tilde{\boldsymbol{\omega} }}_{i} \left ( { \mathbf{r}}_{\mathrm{G}}^{i} - {\mathbf{r}}_{i} \right ) \\ - {\tilde{\boldsymbol{\omega} }}_{i} {\mathbf{J}}_{i}^{\mathrm{G}} {\boldsymbol{\omega} }_{i} - \left ({\tilde{\mathbf{r}}}_{\mathrm{G}}^{i}-{\tilde{\mathbf{r}}}_{i}\right ) \left (m_{i} {\tilde{\boldsymbol{\omega} }}_{i} {\tilde{\boldsymbol{\omega} }}_{i} \left ( {\mathbf{r}}_{\mathrm{G}}^{i} - {\mathbf{r}}_{i} \right )\right ) \end{bmatrix} {.} \end{aligned}$$

(22c)

Herein, $n_{f}^{i}$ represents the number of external forces applied to the body $i$, ${\mathbf{f}}_{j} \in \mathbb{R}^{3}$ is an external force applied on body $i$, ${\mathbf{n}}_{j}^{\mathrm{G}} \in \mathbb{R}^{3}$ denotes the equivalent torque of ${\mathbf{f}}_{j}$ on the centre of mass, ${\mathbf{r}}_{\mathrm{G}}^{i} \in \mathbb{R}^{3}$ is the position of the centre of mass of body $i$, ${\mathbf{r}}_{i} \in \mathbb{R}^{3}$ identifies the reference point of body $i$, ${\boldsymbol{\omega} }_{i} \in \mathbb{R}^{3}$ is the angular velocity of body $i$ and the operator $(\; \tilde{} \;)$ indicates the skew-symmetric matrix of a vector of dimension 3, such as in ${\tilde{\boldsymbol{\omega} }}_{i} \in \mathbb{R}^{3 \times 3}$. Thanks to this division, the terms related to each external force ${\mathbf{f}}_{j}$ can be evaluated separately from the inertial component of the elemental force.

Finally, the elemental force vectors referred to each body (22a)–(22c) have to be assembled in order to build the vector of generalized forces ${\mathbf{Q}}^{\mathrm{d}}$:

$$\begin{aligned} {\mathbf{Q}}_{i}^{\mathrm{d}} &= {\mathbf{R}}_{i}^{\mathrm{v{\mathrm{T}}}} \left ( {\mathbf{Q}}^{ \mathrm{v}} - {\mathbf{M}}^{\mathrm{v}} {\dot{\mathbf{R}}}^{\mathrm{v}} {\dot{\mathbf{z}}} \right ) = {\mathbf{b}}_{i}^{\mathrm{v{\mathrm{T}}}} {\mathbf{Q}}_{i}^{\mathrm{v}\Sigma } {,} \end{aligned}$$

(23a)

$$\begin{aligned} {\mathbf{Q}}_{i}^{\mathrm{v}\Sigma } &= {\mathbf{Q}}_{i}^{\mathrm{v}} - {\mathbf{M}}_{i}^{\mathrm{v}} {\mathbf{d}}_{i}^{\mathrm{v}\Sigma } + \sum _{s=1}^{n_{s}^{i}}{}{\mathbf{B}}_{s}^{ \mathrm{v{\mathrm{T}}}} {\mathbf{Q}}_{s}^{\mathrm{v}\Sigma }{,} \end{aligned}$$

(23b)

where $n_{s}^{i}$ is again the number of children of body $i$, and ${\mathbf{d}}_{i}^{\mathrm{v}\Sigma }$ is the recursive accumulation of the joint-dependent term ${\mathbf{d}}_{i}^{\mathrm{v}}$ following the topology of the mechanism,

$$ {\mathbf{d}}_{i}^{\mathrm{v}\Sigma } = {\mathbf{d}}_{i}^{\mathrm{v}} + {\mathbf{B}}_{i}^{\mathrm{v}} {\mathbf{d}}_{h}^{\mathrm{v}\Sigma } .$$

(24)

6.1 Matrix ${\mathbf{K}}$

The equivalent stiffness matrix ${\mathbf{K}}$ is defined as ${\mathbf{K}}=-\Bigl( {\mathbf{Q}}^{\mathrm{d}} \Bigr)_{\hat{\mathbf{z}}}$. It can be obtained following the aforementioned procedure of division of the generalized forces vector. Taking derivatives on (23a) and (23b) yields

$$\begin{aligned} {\mathbf{K}}_{i} &= -\Bigl( {\mathbf{Q}}_{i}^{\mathrm{d}} \Bigr)_{\hat{\mathbf{z}}} = { \mathbf{b}}_{i}^{\mathrm{v{\mathrm{T}}}} {\mathbf{K}}_{i}^{\mathrm{v}\Sigma } - \Bigl( {\mathbf{b}}_{i}^{ \mathrm{v{\mathrm{T}}}} \Bigr)_{\hat{\mathbf{z}}} {\mathbf{Q}}_{i}^{\mathrm{v}\Sigma }, \end{aligned}$$

(25a)

$$\begin{aligned} {\mathbf{K}}_{i}^{\mathrm{v}\Sigma } &=-\Bigl( {\mathbf{Q}}_{i}^{\mathrm{v}\Sigma }\Bigr)_{ \hat{\mathbf{z}}} = {\mathbf{K}}_{i}^{\mathrm{v}} + \Bigl( {\mathbf{M}}_{i}^{\mathrm{v}} \Bigr)_{\hat{\mathbf{z}}} {\mathbf{d}}_{i}^{\mathrm{v}\Sigma } + {\mathbf{M}}_{i}^{\mathrm{v}} \Bigl( {\mathbf{d}}_{i}^{\mathrm{v}\Sigma } \Bigr)_{\hat{\mathbf{z}}} + \sum _{s=1}^{n_{s}^{i}}{} \left ( {\mathbf{B}}_{s}^{\mathrm{v{\mathrm{T}}}} {\mathbf{K}}_{s}^{\mathrm{v}\Sigma } - \Bigl( {\mathbf{B}}_{s}^{\mathrm{v{\mathrm{T}}}} \Bigr)_{\hat{\mathbf{z}}} {\mathbf{Q}}_{s}^{ \mathrm{v}\Sigma } \right ){,} \end{aligned}$$

(25b)

where $n_{s}^{i}$ is again the number of children of body $i$. The derivative of the accumulated kinematic term ${\mathbf{d}}_{i}^{\mathrm{v}\Sigma }$ involved in (25b) will be described in Sect. 9.7.

Before addressing the analytical expressions of the elemental force derivatives involved in (25b), it is convenient to introduce the derivatives of the position and velocity of a point belonging to body $i$ (fixed in its local reference frame) and the angular velocity. For the sake of brevity, the final results will be directly used avoiding the intermediate developments:

$$\begin{aligned} \left ( {\mathbf{r}}_{j}\right )_{{\mathbf{z}}} &= \left ( {\dot{\mathbf{r}}}_{j} \right )_{{\dot{\mathbf{z}}}} = \begin{bmatrix} {\mathbf{I}} & \; {\tilde{\mathbf{r}}}_{i} - {\tilde{\mathbf{r}}}_{j} \end{bmatrix} {\mathbf{R}}_{i}^{\mathrm{v}}{,} \end{aligned}$$

(26)

$$\begin{aligned} \left ( {\dot{\mathbf{r}}}_{j}\right )_{{\mathbf{z}}} &= \dfrac{{\mathrm{d}} }{{\mathrm{d}} t} \left ( {\mathbf{r}}_{j}\right )_{{\mathbf{z}}} = \begin{bmatrix} {\mathbf{0}} & \; {\dot{\tilde{\mathbf{r}}}}_{i} - {\dot{\tilde{\mathbf{r}}}}_{j} \end{bmatrix} {\mathbf{R}}_{i}^{\mathrm{v}} + \begin{bmatrix} {\mathbf{I}} & \; {\tilde{\mathbf{r}}}_{i} - {\tilde{\mathbf{r}}}_{j} \end{bmatrix} {\dot{\mathbf{R}}}_{i}^{\mathrm{v}}{,} \end{aligned}$$

(27)

$$\begin{aligned} \left ({\boldsymbol{\omega} }_{i} \right )_{\hat{\mathbf{z}}} &= \begin{bmatrix} {\mathbf{0}} & {\mathbf{I}} \end{bmatrix} \left ( {\mathbf{R}}_{i}^{\mathrm{v}} \right ) _{\hat{\mathbf{z}}} { \dot{\mathbf{z}}}= \begin{bmatrix} {\mathbf{0}} & {\mathbf{I}} \end{bmatrix} {\dot{\mathbf{R}}}_{i}^{\mathrm{v}} - \begin{bmatrix} {\mathbf{0}} & {{\tilde{\boldsymbol{\omega} }}_{i}} \end{bmatrix} {\mathbf{R}}_{i}^{\mathrm{v}}{.} \end{aligned}$$

(28)

In order to compute (25a) and (25b), ${\mathbf{K}}_{i}^{\mathrm{v}}$ have to be determined. Taking derivatives of (22a)–(22c) and applying (26) and (28) gives

$$\begin{aligned} {\mathbf{K}}_{i}^{\mathrm{v}} &=-\Bigl( {\mathbf{Q}}_{i}^{\mathrm{v}} \Bigr)_{\hat{\mathbf{z}}}= \displaystyle \sum _{j=1}^{{n_{f}^{i}}} {\mathbf{K}}_{i,j}^{\mathrm{v (e)}} + {{ \mathbf{K}}_{i}^{\mathrm{v}}}^{\mathrm{(I)}}{,} \end{aligned}$$

(29a)

$$\begin{aligned} {\mathbf{K}}_{i,j}^{\mathrm{v (e)}}&= \begin{bmatrix} -\Bigl( {\mathbf{f}}_{j} \Bigr)_{\hat{\mathbf{z}}} \\ {\tilde{\mathbf{f}}}_{j} \left ( \begin{bmatrix} {\mathbf{I}} & \;{\tilde{\mathbf{r}}}_{i} -{\tilde{\mathbf{r}}}_{j} \end{bmatrix}{\mathbf{R}}_{i}^{\mathrm{v}} - \Bigl({\mathbf{r}}_{i}\Bigr)_{{\mathbf{z}}} \right ) - \Bigl( {\mathbf{n}}_{j}^{\mathrm{G}} \Bigr)_{\hat{\mathbf{z}}}+ \left ( { \tilde{\mathbf{r}}}_{i} -{\tilde{\mathbf{r}}}_{j} \right ) \Bigl( {\mathbf{f}}_{j} \Bigr)_{\hat{\mathbf{z}}} \end{bmatrix}{,} \end{aligned}$$

(29b)

$$\begin{aligned} \begin{aligned} {{\mathbf{K}}_{i}^{\mathrm{v}}}^{\mathrm{(I)}}&= \begin{bmatrix} {\mathbf{t}}_{\hat{\mathbf{z}}} \\ \left ( {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i}-{\tilde{\mathbf{r}}}_{i} \right ) { \mathbf{t}}_{\hat{\mathbf{z}}} - \tilde{\mathbf{t}} \left ( \begin{bmatrix} {\mathbf{I}} & \;{\tilde{\mathbf{r}}}_{i}-{\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \end{bmatrix} {\mathbf{R}}_{i}^{\mathrm{v}} - \Bigl( {\mathbf{r}}_{i}\Bigr)_{{ \mathbf{z}}} \right ) \end{bmatrix} \\ &\quad + \begin{bmatrix} {\mathbf{0}} \\ \left ( \tilde{{\boldsymbol{\omega} }_{i}}{\mathbf{J}}_{i}^{\mathrm{G}} - \widetilde{{ \mathbf{J}}_{i}^{\mathrm{G}} {\boldsymbol{\omega} }_{i}} \right ) \Bigl( {{\boldsymbol{\omega} }_{i}} \Bigr)_{\hat{\mathbf{z}}} +\tilde{{\boldsymbol{\omega} }_{i}} \Bigl( {\mathbf{J}}_{i}^{ \mathrm{G}} \Bigr)_{\hat{\mathbf{z}}} {\boldsymbol{\omega} }_{i} \end{bmatrix}{,} \end{aligned} \end{aligned}$$

(29c)

where

$$\begin{aligned} {\mathbf{t}}&=m_{i} {\tilde{\boldsymbol{\omega} }}_{i} \left ( {\tilde{\boldsymbol{\omega} }}_{i} \left ( {\mathbf{r}}_{\mathrm{G}}^{i} - {\mathbf{r}}_{i} \right ) \right ) {,} \end{aligned}$$

(30a)

$$\begin{aligned} {\mathbf{t}}_{\hat{\mathbf{z}}} &=m_{i} \tilde{{\boldsymbol{\omega} }_{i}} \tilde{{\boldsymbol{\omega} }_{i}} \left ( \begin{bmatrix} {\mathbf{I}} & \;{\tilde{\mathbf{r}}}_{i} -{\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \end{bmatrix} {\mathbf{R}}_{i}^{\mathrm{v}} - \Bigl( {\mathbf{r}}_{i} \Bigr)_{{ \mathbf{z}}}\right ) - m_{i} \left ( \tilde{\mathbf{h}}- \tilde{{\boldsymbol{\omega} }_{i}} \left ({\tilde{\mathbf{r}}}_{i} -{ \tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \right ) \right ) \Bigl( {{\boldsymbol{\omega} }_{i}} \Bigr)_{\hat{\mathbf{z}}} {,} \end{aligned}$$

(30b)

$$\begin{aligned} {\mathbf{h}}&= \tilde{{\boldsymbol{\omega} }_{i}}\left ({\mathbf{r}}_{\mathrm{G}}^{i} -{\mathbf{r}}_{i} \right ) {.} \end{aligned}$$

(30c)

The obtained expressions can be further particularized for a given selection of reference points. Appendix B covers their reformulation for RTdyn0 and RTdyn1.

6.2 Matrix ${\mathbf{C}}$

Matrix ${\mathbf{C}}$ can be regarded as a damping matrix since it measures the variation of the generalized forces vector with the velocities of the relative coordinates, ${\mathbf{C}}=-\left ( {\mathbf{Q}}^{\mathrm{d}} \right )_{\hat{\dot{\mathbf{z}}}}$. Taking derivatives on the forces assembly scheme introduced in (23a) and (23b) gives

$$\begin{aligned} {\mathbf{C}}_{i} &= {\mathbf{b}}_{i}^{\mathrm{v{\mathrm{T}}}} {\mathbf{C}}_{i}^{\mathrm{v}\Sigma }, \end{aligned}$$

(31a)

$$\begin{aligned} {\mathbf{C}}_{i}^{\mathrm{v}\Sigma } &= {\mathbf{C}}_{i}^{\mathrm{v}} + {\mathbf{M}}_{i}^{\mathrm{v}} \Bigl( {\mathbf{d}}_{i}^{\mathrm{v}\Sigma } \Bigr)_{\hat{\dot{\mathbf{z}}}} + \sum _{s=1}^{n_{s}^{i}}{} {\mathbf{B}}_{s}^{\mathrm{v{\mathrm{T}}}} {\mathbf{C}}_{s}^{\mathrm{v}\Sigma }{,} \end{aligned}$$

(31b)

with $n_{s}^{i}$ being the number of children of body $i$. The derivatives of the term ${\mathbf{d}}_{i}^{\mathrm{v}\Sigma }$ with respect to velocities will be introduced in Sect. 9.6.

Taking derivatives of (22a)–(22c) with respect to ${\dot{\mathbf{z}}}$ according to (1) yields

$$\begin{aligned} {\mathbf{C}}_{i}^{\mathrm{v}} &=- \Bigl( {\mathbf{Q}}_{i}^{\mathrm{v}} \Bigr)_{ \hat{\dot{\mathbf{z}}}}=\displaystyle \sum _{j=1}^{{n_{f}^{i}}}{\mathbf{C}}_{i,j}^{ \mathrm{v (e)}} + {{\mathbf{C}}_{i}^{\mathrm{v}}}^{\mathrm{(I)}}{,} \end{aligned}$$

(32a)

$$\begin{aligned} {\mathbf{C}}_{i,j}^{\mathrm{v (e)}}&= - \begin{bmatrix} \mathbf{{I} }\\ {\tilde{\mathbf{r}}}_{j}- {\tilde{\mathbf{r}}}_{i} \end{bmatrix}\Bigl( {\mathbf{f}}_{j} \Bigr)_{\hat{\mathbf{z}}} - \begin{bmatrix} \mathbf{{0} }\\ \Bigl( {\mathbf{n}}_{j}^{\mathrm{G}} \Bigr)_{\hat{\mathbf{z}}} \end{bmatrix} {,} \end{aligned}$$

(32b)

$$\begin{aligned} {{\mathbf{C}}_{i}^{\mathrm{v}}}^{\mathrm{(I)}}&= \begin{bmatrix} {\mathbf{0}} & {-} m_{i} \left ( \tilde{\mathbf{h}}-\tilde{{\boldsymbol{\omega} }_{i}} \left ( {\tilde{\mathbf{r}}}_{i} -{\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \right ) \right ) \\ {\mathbf{0}} & \tilde{{\boldsymbol{\omega} }_{i}}{\mathbf{J}}_{i}^{\mathrm{G}} - \widetilde{{ \mathbf{J}}_{i}^{\mathrm{G}} {\boldsymbol{\omega} }_{i}} {-} m_{i} \left ( { \tilde{\mathbf{r}}}_{\mathrm{G}}^{i} - {\tilde{\mathbf{r}}}_{i} \right )\left ( \tilde{\mathbf{h}}-\tilde{{\boldsymbol{\omega} }_{i}}\left ( {\tilde{\mathbf{r}}}_{i} - {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \right )\right ) \end{bmatrix}{\mathbf{R}}_{i}^{\mathrm{v}}{,} \end{aligned}$$

(32c)

with ${\mathbf{h}}$ given by (30c). Appendix C includes the particular expressions of matrix ${\mathbf{C}}$ for RTdyn0 and RTdyn1.

6.3 Evaluation of ${\mathbf{Q}}^{\mathrm{d}}_{{\hat{\boldsymbol{\rho} }}}$

Sensitivity parameters can affect both the magnitude of a single force (e.g. a stiffness coefficient of a spring force) and the topology of the multibody system (e.g. a local coordinate of a point or vector defining a joint). Differentiating (23a), (23b), the derivative of the generalized forces vector becomes:

$$\begin{aligned} \Bigl( {{\mathbf{Q}}^{\mathrm{d}}_{i}}\Bigr)_{{\hat{\boldsymbol{\rho} }}} &= {\mathbf{b}}_{i}^{ \mathrm{v{\mathrm{T}}}} \Bigl( {{\mathbf{Q}}^{\mathrm{v}\Sigma }_{i}}\Bigr)_{{ \hat{\boldsymbol{\rho} }}} + \Bigl( {\mathbf{b}}_{i}^{\mathrm{v{\mathrm{T}}}} \Bigr)_{{ \hat{\boldsymbol{\rho} }}} {\mathbf{Q}}_{i}^{\mathrm{v}\Sigma }, \end{aligned}$$

(33a)

$$\begin{aligned} \Bigl( {{\mathbf{Q}}^{\mathrm{v}\Sigma }_{i}}\Bigr)_{{\hat{\boldsymbol{\rho} }}} &= \Bigl( {{\mathbf{Q}}^{\mathrm{v}}_{i}}\Bigr)_{{\hat{\boldsymbol{\rho} }}} + \Bigl( {\mathbf{M}}_{i}^{ \mathrm{v}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} {\mathbf{d}}_{i}^{\mathrm{v}\Sigma } + {\mathbf{M}}_{i}^{ \mathrm{v}} \Bigl( {\mathbf{d}}_{i}^{\mathrm{v}\Sigma } \Bigr)_{{\hat{\boldsymbol{\rho} }}} + \sum _{s=1}^{n_{s}^{i}}{} \left ( {\mathbf{B}}_{s}^{\mathrm{v{\mathrm{T}}}} \Bigl( {{ \mathbf{Q}}^{\mathrm{v}\Sigma }_{s}}\Bigr)_{{\hat{\boldsymbol{\rho} }}} + \Bigl( {\mathbf{B}}_{s}^{ \mathrm{v{\mathrm{T}}}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} {\mathbf{Q}}_{s}^{\mathrm{v}\Sigma } \right ){.} \end{aligned}$$

(33b)

The application of the rule of differentiation defined in (1) to the expressions of the generalized forces vector (22a)–(22c) generates:

$$\begin{aligned} \Bigl( {{\mathbf{Q}}^{\mathrm{v}}_{i}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} &= \displaystyle \sum _{j=1}^{{n_{f}^{i}}} \Bigl( {\mathbf{Q}}^{\mathrm{v (e)}}_{i,j} \Bigr)_{{\hat{\boldsymbol{\rho} }}} + \Bigl( {{\mathbf{Q}}^{\mathrm{v}}_{i}}^{\mathrm{(I)}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} {,} \end{aligned}$$

(34a)

$$\begin{aligned} \Bigl( {{\mathbf{Q}}^{\mathrm{v (e)}}_{i,j}} \Bigr)_{{\hat{\boldsymbol{\rho} }}}&= \begin{bmatrix} \Bigl( {\mathbf{f}}_{j} \Bigr)_{{\hat{\boldsymbol{\rho} }}} \\ \tilde{{\mathbf{f}}_{j}} \left ( \Bigl( {\mathbf{r}}_{j}\Bigr)_{{\boldsymbol{\rho} }} - \Bigl( {\mathbf{r}}_{i}\Bigr)_{{\boldsymbol{\rho} }} \right ) + \Bigl( {\mathbf{n}}_{j}^{ \mathrm{G}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} + \left ( {\tilde{\mathbf{r}}}_{j} -{ \tilde{\mathbf{r}}}_{i} \right ) \Bigl( {\mathbf{f}}_{j} \Bigr)_{{ \hat{\boldsymbol{\rho} }}} \end{bmatrix}{,} \end{aligned}$$

(34b)

$$\begin{aligned} \Bigl( {{\mathbf{Q}}^{\mathrm{v}}_{i}}^{\mathrm{(I)}} \Bigr)_{{\hat{\boldsymbol{\rho} }}}&= \begin{bmatrix} {\mathbf{t}}_{{\hat{\boldsymbol{\rho} }}} \\ \left ( {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i}-{\tilde{\mathbf{r}}}_{i} \right ) { \mathbf{t}}_{{\hat{\boldsymbol{\rho} }}} + \tilde{\mathbf{t}}\left ( \Bigl( {\mathbf{r}}_{i} \Bigr)_{{\boldsymbol{\rho} }} - \Bigl({\mathbf{r}}_{\mathrm{G}}^{i}\Bigr)_{{\boldsymbol{\rho} }} \right ) - \left ( \tilde{{\boldsymbol{\omega} }_{i}}{\mathbf{J}}_{i}^{\mathrm{G}} - \widetilde{{\mathbf{J}}_{i}^{\mathrm{G}} {\boldsymbol{\omega} }_{i}} \right ) \Bigl( {{ \boldsymbol{\omega} }_{i}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} - \tilde{{\boldsymbol{\omega} }_{i}} \Bigl( {\mathbf{J}}_{i}^{\mathrm{G}} \Bigr)_{{ \hat{\boldsymbol{\rho} }}} {\boldsymbol{\omega} }_{i} \end{bmatrix}{,} \end{aligned}$$

(34c)

where

$$ {\mathbf{t}}_{{\hat{\boldsymbol{\rho} }}} =-m_{i} \tilde{{\boldsymbol{\omega} }_{i}} \tilde{{\boldsymbol{\omega} }_{i}} \left ( \Bigl( {\mathbf{r}}_{\mathrm{G}}^{i}\Bigr)_{{ \boldsymbol{\rho} }} - \Bigl( {\mathbf{r}}_{i}\Bigr)_{{\boldsymbol{\rho} }} \right ) - m_{i} \left ( \tilde{\mathbf{h}}-\tilde{{\boldsymbol{\omega} }_{i}} \left ({\tilde{\mathbf{r}}}_{i} -{\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \right ) \right ) \Bigl( {{\boldsymbol{\omega} }_{i}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} ,$$

(35)

with ${\mathbf{t}}$ and ${\mathbf{h}}$ given by (30a) and (30a), respectively.

In equation (34a)–(34c), the derivatives of natural coordinates with respect to parameters have the known analytical expressions presented in Sect. 8.3. The partial derivatives of forces and torques can be directly obtained from their explicit dependencies on the parameters and natural coordinates applying the differentiation rule (1). The term $\left ( {\mathbf{J}}_{i}^{\mathrm{G}} \right )_{{\hat{\boldsymbol{\rho} }}}$ involves the variation of the global inertia tensor with respect to any set of parameters, for which the partial derivatives of rotation matrices should be considered (remember that ${\mathbf{J}}_{i}^{\mathrm{G}} = {\mathbf{A}}_{i} {\bar{\mathbf{J}}}_{i}^{\mathrm{G}} {\mathbf{A}}_{i}^{ \mathrm{T}}$). Moreover, the derivative of the angular velocity can be reached by means of different methods, one of them being the differentiation of the angular part of the recursive equations (4a),

$$ \Bigl( {\boldsymbol{\omega} }_{i} \Bigr)_{{\hat{\boldsymbol{\rho} }}}= \Bigl( { \boldsymbol{\omega} }_{i-1} \Bigr)_{{\hat{\boldsymbol{\rho} }}} + \begin{bmatrix} {\mathbf{0}}_{3} & {\mathbf{I}}_{3} \end{bmatrix} \Bigl({\mathbf{b}}_{i}^{\mathrm{v}}\Bigr)_{{\hat{\boldsymbol{\rho} }}} {{\dot{\mathbf{z}}}_{i}}{.} $$

(36)

Comparing this derivative with the expressions of the stiffness matrix, several analogies can be observed, both in the elemental derivatives and in the assembly, which makes it possible to reuse routines of computation for both terms.

7 Constraint derivatives

Derivatives of the constraints vector are ubiquitous in the dynamic solution of any constrained multibody model, and the same occurs on a sensitivity analysis. Constraints can be expressed in terms of coordinates of points and vectors, and therefore, a transformation from natural to relative coordinates have to be executed for each constraint derivative. In this regard, two types of derivatives are required in the differentiation of the constraints vector: explicit derivatives (see Table 1), involving explicit dependencies of each constraint equation; and topological derivatives (see Table 2), related to the variation of natural coordinates with respect to relative coordinates, and which do not depend on each particular constraint equation but on the type and sequence of joints.

Table 1 Explicit constraint derivatives involved in a sensitivity analysis

Table 2 Natural coordinates derivatives involved in a sensitivity analysis

In the following sections, the derivatives of the constraints vector needed in the current sensitivity analysis are introduced.

In this section, the following analytical expressions of the first order derivatives ${\boldsymbol{\Phi } }_{\hat{\mathbf{z}}}$ and $\dot{{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}$ are used as starting point for the calculation of second order derivatives:

$$\begin{aligned} {\boldsymbol{\Phi } }_{\hat{\mathbf{z}}}&={\boldsymbol{\Phi } }_{{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}} + {\boldsymbol{\Phi } }_{{\mathbf{z}}} {,} \end{aligned}$$

(37)

$$\begin{aligned} \dot{{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}}&=\dot{{\boldsymbol{\Phi } }}_{{\mathbf{q}}} {{ \mathbf{q}}}_{{\mathbf{z}}} + {\boldsymbol{\Phi } }_{{\mathbf{q}}} {{\dot{\mathbf{q}}}}_{{\mathbf{z}}} + \dot{{\boldsymbol{\Phi } }}_{{\mathbf{z}}} {.} \end{aligned}$$

(38)

7.1 Evaluation of ${{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}$

The second derivative of the constraints vector with respect to the relative coordinates can be computed as

$$ \begin{aligned} {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}= {\left ( {{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} \right )}_{\hat{\mathbf{z}}}= \left ( {{ \boldsymbol{\Phi } }}_{{\mathbf{q}}{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}} \right ) {{\mathbf{q}}}_{{ \mathbf{z}}} + {{\boldsymbol{\Phi } }}_{{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}{\mathbf{z}}} + 2 {{ \boldsymbol{\Phi } }}_{{\mathbf{z}}{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}} +{{\boldsymbol{\Phi } }}_{{ \mathbf{z}}{\mathbf{z}}} {.} \end{aligned} $$

(39)

Note that three new derivatives of the constraint vector appear in (39), involving the second partial derivative of the constraints with respect to the local coordinates ${{\boldsymbol{\Phi } }}_{{\mathbf{q}}{\mathbf{q}}} \in \mathbb{R}^{m \times n_{q} \times n_{q}}$, the second partial derivative with respect to relative coordinates ${{\boldsymbol{\Phi } }}_{{\mathbf{z}}{\mathbf{z}}} \in \mathbb{R}^{m \times n \times n}$ and the crossed derivatives with respect to the relative and natural coordinates ${{\boldsymbol{\Phi } }}_{{\mathbf{z}}{\mathbf{q}}} \in \mathbb{R}^{m \times n \times n_{q}}$. Natural coordinate derivatives ${{\mathbf{q}}}_{{\mathbf{z}}}$ and ${{\mathbf{q}}}_{{\mathbf{z}}{\mathbf{z}}}$ will be addressed in Sects. 8.1 and 8.2, respectively.

7.2 Evaluation of ${\dot{{\boldsymbol{\Phi } }}}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}$

This derivative can be calculated through direct differentiation of the expression of ${{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}$ given by (39) with respect to time:

$$ \begin{aligned} {\dot{{\boldsymbol{\Phi } }}}_{\hat{\mathbf{z}}\hat{\mathbf{z}}}&= \frac{{\mathrm{d}}}{{\mathrm{d}} t} \left ( \left ( {{\boldsymbol{\Phi } }}_{{\mathbf{q}}{ \mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}} \right ) {{\mathbf{q}}}_{{\mathbf{z}}} + {{ \boldsymbol{\Phi } }}_{{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}{\mathbf{z}}} + 2 {{\boldsymbol{\Phi } }}_{{ \mathbf{z}}{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}} +{{\boldsymbol{\Phi } }}_{{\mathbf{z}}{\mathbf{z}}} \right ) \\ &=\left ( {\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{q}}{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}} \right ) {{\mathbf{q}}}_{{\mathbf{z}}} +\left ( {{\boldsymbol{\Phi } }}_{{\mathbf{q}}{\mathbf{q}}} {{\dot{\mathbf{q}}}}_{{\mathbf{z}}} \right ) {{\mathbf{q}}}_{{\mathbf{z}}}+\left ( {{ \boldsymbol{\Phi } }}_{{\mathbf{q}}{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}} \right ) {{ \dot{\mathbf{q}}}}_{{\mathbf{z}}} + {\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{q}}} {{\mathbf{q}}}_{{ \mathbf{z}}{\mathbf{z}}} + {{\boldsymbol{\Phi } }}_{{\mathbf{q}}} {{\dot{\mathbf{q}}}}_{{\mathbf{z}}{ \mathbf{z}}} + 2 {\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{z}}{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}} + 2 {{\boldsymbol{\Phi } }}_{{\mathbf{z}}{\mathbf{q}}} {{\dot{\mathbf{q}}}}_{{\mathbf{z}}} +{ \dot{{\boldsymbol{\Phi } }}}_{{\mathbf{z}}{\mathbf{z}}}{.} \end{aligned} $$

(40)

The multi-dimensional matrices ${\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{q}}{\mathbf{q}}}$, ${\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{z}}{\mathbf{q}}}$ and ${\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{z}}{\mathbf{z}}}$ can be directly calculated for a particular constraint equation, but ${{\dot{\mathbf{q}}}}_{{\mathbf{z}}{\mathbf{z}}}$ is a general term dependent on the topology of the mechanism (see Sect. 8.2).

7.3 Evaluation of ${{\boldsymbol{\Phi } }}_{{\hat{\boldsymbol{\rho} }}}$

Since any constant or coefficient of a constraint can be selected as a parameter, the derivative of the constraint vector with respect to it can have multiple forms, all depending on the type of constraint and the type of parameter. Thus, the equations of each type of constraint have to be specifically differentiated with respect to the parameter selected.

7.4 Evaluation of ${{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}$

The derivative ${{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}$ can be calculated by means of the following expression:

$$ {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}} = \left ( {{ \boldsymbol{\Phi } }}_{{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}}+{{\boldsymbol{\Phi } }}_{{\mathbf{z}}} \right )_{{\hat{\boldsymbol{\rho} }}}= {{\boldsymbol{\Phi } }}_{{\mathbf{q}}{ \hat{\boldsymbol{\rho} }}} {{\mathbf{q}}}_{{\mathbf{z}}} + {{\boldsymbol{\Phi } }}_{{\mathbf{q}}} {{{ \mathbf{q}}}_{{\mathbf{z}}{\boldsymbol{\rho} }}} +{{\boldsymbol{\Phi } }}_{{\mathbf{z}}{ \hat{\boldsymbol{\rho} }}}{,} $$

(41)

in which the multi-dimensional matrices ${{\boldsymbol{\Phi } }}_{{\mathbf{q}}{\hat{\boldsymbol{\rho} }}} \in \mathbb{R}^{m \times n_{q} \times p}$ and ${{\boldsymbol{\Phi } }}_{{\mathbf{z}}{\hat{\boldsymbol{\rho} }}} \in \mathbb{R}^{m \times n \times p}$ are obtained from the particular expressions of each type of constraint, while ${{\mathbf{q}}}_{{\mathbf{z}}{\boldsymbol{\rho} }} \in \mathbb{R}^{n_{q} \times n \times p}$ is related to the topology of the mechanism (see Sect. 8.4).

If the parameters of the system are related to the local geometry of a body, this is, they condition the position of local coordinates, there will be a double explicit dependency in the derivatives of the constraint vector (with ${\mathbf{q}}$ and ${\boldsymbol{\rho} }$). In this case:

$$\begin{aligned} {{\boldsymbol{\Phi } }}_{{\mathbf{q}}{\hat{\boldsymbol{\rho} }}} &= {{\boldsymbol{\Phi } }}_{{\mathbf{q}}{ \mathbf{q}}} {{{\mathbf{q}}}_{{\boldsymbol{\rho} }}} + {{\boldsymbol{\Phi } }}_{{\mathbf{q}}{ \boldsymbol{\rho} }} {,} \end{aligned}$$

(42a)

$$\begin{aligned} {{\boldsymbol{\Phi } }}_{{\mathbf{z}}{\hat{\boldsymbol{\rho} }}} &= {{\boldsymbol{\Phi } }}_{{\mathbf{z}}{ \mathbf{q}}} {{{\mathbf{q}}}_{{\boldsymbol{\rho} }}} + {{\boldsymbol{\Phi } }}_{{\mathbf{z}}{ \boldsymbol{\rho} }} {.} \end{aligned}$$

(42b)

The derivative ${{\mathbf{q}}}_{{\boldsymbol{\rho} }}$ is a term dependent on the topology of the system, and will be tackled in Sect. 8.3.

7.5 Evaluation of ${\dot{{\boldsymbol{\Phi } }}}_{{\hat{\boldsymbol{\rho} }}}$

This derivative can be obtained by applying the rule of differentiation (1) to the time derivative of the constraints vector,

$$ \left ( {\dot{{\boldsymbol{\Phi } }}} \right )_{{\hat{\boldsymbol{\rho} }}} = \left ( {{ \boldsymbol{\Phi } }}_{\hat{\mathbf{z}}} {\dot{\mathbf{z}}}+ {{\boldsymbol{\Phi } }_{t}} \right )_{{\hat{\boldsymbol{\rho} }}} = {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{ \hat{\boldsymbol{\rho} }}} {\dot{\mathbf{z}}}+ {{\boldsymbol{\Phi } }}_{t {\hat{\boldsymbol{\rho} }}}{,} $$

(43)

where ${{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}} \in \mathbb{R}^{m \times n \times p}$ is a multi-dimensional matrix described in Sect. 7.4, and ${{\boldsymbol{\Phi } }}_{t {\hat{\boldsymbol{\rho} }}} \in \mathbb{R}^{m \times p}$ is a matrix obtained from the particular expressions of each type of constraint.

Observe that ${{\boldsymbol{\Phi } }}_{t {\hat{\boldsymbol{\rho} }}}$ can be decomposed into ${{\boldsymbol{\Phi } }}_{t {\hat{\boldsymbol{\rho} }}} = {{\boldsymbol{\Phi } }}_{t {\mathbf{q}}} {{{ \mathbf{q}}}_{{\boldsymbol{\rho} }}} + {{\boldsymbol{\Phi } }}_{t {\boldsymbol{\rho} }}$, with ${{ \mathbf{q}}}_{{\boldsymbol{\rho} }}$ computed using the expressions of Sect. 8.3.

7.6 Evaluation of ${\dot{{\boldsymbol{\Phi } }}}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}$

The term ${\dot{{\boldsymbol{\Phi } }}}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}} \in \mathbb{R}^{m \times n \times p}$ can be expressed in terms of partial derivatives as

$$ {\dot{{\boldsymbol{\Phi } }}}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}} = \left ( { \dot{{\boldsymbol{\Phi } }}}_{{\mathbf{q}}} {{\mathbf{q}}}_{{\mathbf{z}}}+{{\boldsymbol{\Phi } }}_{{ \mathbf{q}}} {{\dot{\mathbf{q}}}}_{{\mathbf{z}}}+{\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{z}}} \right )_{{\hat{\boldsymbol{\rho} }}} = {\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{q}}{ \hat{\boldsymbol{\rho} }}} {{\mathbf{q}}}_{{\mathbf{z}}} + {{\boldsymbol{\Phi } }}_{{\mathbf{q}}{ \hat{\boldsymbol{\rho} }}} {{\dot{\mathbf{q}}}}_{{\mathbf{z}}} + {\dot{{\boldsymbol{\Phi } }}}_{{ \mathbf{q}}} {{{\mathbf{q}}}_{{\mathbf{z}}{\boldsymbol{\rho} }}} + {{\boldsymbol{\Phi } }}_{{\mathbf{q}}} {{{ \dot{\mathbf{q}}}}_{{\mathbf{z}}{\boldsymbol{\rho} }}} +{\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{z}}{ \hat{\boldsymbol{\rho} }}}{.} $$

(44)

Once again, the terms of (44) with the subscript ${\hat{\boldsymbol{\rho} }}$ can be further decomposed as

$$\begin{aligned} {\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{q}}{\hat{\boldsymbol{\rho} }}} &= { \dot{{\boldsymbol{\Phi } }}}_{{\mathbf{q}}{\mathbf{q}}} {{{\mathbf{q}}}_{{\boldsymbol{\rho} }} }+ {{ \boldsymbol{\Phi } }}_{{\mathbf{q}}{\mathbf{q}}} {{{\dot{\mathbf{q}}}}_{{\boldsymbol{\rho} }}} + { \dot{{\boldsymbol{\Phi } }}}_{{\mathbf{q}}{\boldsymbol{\rho} }} {,} \end{aligned}$$

(45a)

$$\begin{aligned} {\dot{{\boldsymbol{\Phi } }}}_{{\mathbf{z}}{\hat{\boldsymbol{\rho} }}} &= { \dot{{\boldsymbol{\Phi } }}}_{{\mathbf{z}}{\mathbf{q}}} {{{\mathbf{q}}}_{{\boldsymbol{\rho} }}} + {{ \boldsymbol{\Phi } }}_{{\mathbf{z}}{\mathbf{q}}} {{{\dot{\mathbf{q}}}}_{{\boldsymbol{\rho} }}} + { \dot{{\boldsymbol{\Phi } }}}_{{\mathbf{z}}{\boldsymbol{\rho} }} {.} \end{aligned}$$

(45b)

Observe that most of the terms vanish for linear and quadratic constraint equations (quite usual in natural coordinates), with the consequent reduction in the computational burden.

7.7 Evaluation of ${\ddot{{\boldsymbol{\Phi } }}}_{{\hat{\boldsymbol{\rho} }}}$

The derivative ${\ddot{{\boldsymbol{\Phi } }}}_{{\hat{\boldsymbol{\rho} }}}$ is explicitly required to obtain ${\mathbf{c}}^{{\boldsymbol{\rho} }}$ in (18). It can be obtained differentiating (43) with respect to time:

$$ \left ( {\ddot{{\boldsymbol{\Phi } }}} \right )_{{\hat{\boldsymbol{\rho} }}} = \frac{\mathrm{d}}{\mathrm{d t}} \left ( {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{ \hat{\boldsymbol{\rho} }}} {\dot{\mathbf{z}}}+ {{\boldsymbol{\Phi } }}_{t {\hat{\boldsymbol{\rho} }}} \right ) = {\dot{{\boldsymbol{\Phi } }}}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}} { \dot{\mathbf{z}}}+ {{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}} { \ddot{\mathbf{z}}}+ {\dot{{\boldsymbol{\Phi } }}}_{t {\hat{\boldsymbol{\rho} }}}{,} $$

(46)

where ${\dot{{\boldsymbol{\Phi } }}}_{t {\hat{\boldsymbol{\rho} }}} = {\dot{{\boldsymbol{\Phi } }}}_{t {\mathbf{q}}} {{{\mathbf{q}}}_{{\boldsymbol{\rho} }}} + {{\boldsymbol{\Phi } }}_{t {\mathbf{q}}} {{{ \dot{\mathbf{q}}}}_{{\boldsymbol{\rho} }}} + {\dot{{\boldsymbol{\Phi } }}}_{t {\boldsymbol{\rho} }}$. The terms ${\dot{{\boldsymbol{\Phi } }}}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}$ and ${{\boldsymbol{\Phi } }}_{\hat{\mathbf{z}}{\hat{\boldsymbol{\rho} }}}$ have been described in Sects. 7.6 and 7.4, respectively.

8 Point and vector derivatives

Point and vector coordinates are ubiquitous in relative coordinate models. They are required for the assessment of forces and constraint equations but also for recursive relations, assemblies and derivatives. Therefore, an efficient derivative evaluation is crucial to reduce the computational expense both in the dynamics and in the sensitivity analysis.

Using as starting point the identity ${\mathbf{q}}_{{\mathbf{z}}}={\dot{\mathbf{q}}}_{{\dot{\mathbf{z}}}}$, a new set of expressions independent of the selection of reference points is conquered. Moreover, a new set of derivatives with respect to geometric parameters is also developed.

8.1 Elemental calculation of ${\mathbf{q}}_{{\mathbf{z}}}$, ${{\dot{\mathbf{q}}}}_{{\mathbf{z}}}$ and ${{\ddot{\mathbf{q}}}}_{{\mathbf{z}}}$

Let us consider

$$ {\mathbf{q}}_{{\mathbf{z}}} = \begin{bmatrix} {\mathbf{q}}_{{\mathbf{z}}_{1}} & {\mathbf{q}}_{{\mathbf{z}}_{2}} & \ldots & {\mathbf{q}}_{{ \mathbf{z}}_{n_{{{\mathrm{b}}}}}} \end{bmatrix} {,} $$

(47)

where ${n_{{{\mathrm{b}}}}}$ is the number of joints (or bodies) of the mechanism, and ${\mathbf{q}}_{{\mathbf{z}}_{j}}$ represents the partial derivative of a set of natural coordinates with respect to the relative coordinates of joint $j$, which has the expressions presented in Table 3 for each of the joint types studied (see Appendix D).

Table 3 Natural coordinates derivatives in positions with respect to relative coordinates

Furthermore, ${{\dot{\mathbf{q}}}}_{{\mathbf{z}}}$ and ${{\ddot{\mathbf{q}}}}_{{\mathbf{z}}}$ can be evaluated as the first and second time derivatives of ${{\mathbf{q}}}_{{\mathbf{z}}}$:

$$\begin{aligned} {{\dot{\mathbf{q}}}}_{{\mathbf{z}}} &= \begin{bmatrix} {{\dot{\mathbf{q}}}}_{{\mathbf{z}}_{1}} & {{\dot{\mathbf{q}}}}_{{\mathbf{z}}_{2}} & \ldots & {{\dot{\mathbf{q}}}}_{{\mathbf{z}}_{n_{{{\mathrm{b}}}}}} \end{bmatrix}{,} \end{aligned}$$

(48a)

$$\begin{aligned} {{\ddot{\mathbf{q}}}}_{{\mathbf{z}}} &= \begin{bmatrix} {{\ddot{\mathbf{q}}}}_{{\mathbf{z}}_{1}} & {{\ddot{\mathbf{q}}}}_{{\mathbf{z}}_{2}} & \ldots & {{\ddot{\mathbf{q}}}}_{{\mathbf{z}}_{n_{{{\mathrm{b}}}}}} \end{bmatrix}{,} \end{aligned}$$

(48b)

with ${{\dot{\mathbf{q}}}}_{{\mathbf{z}}_{j}}$ and ${{\ddot{\mathbf{q}}}}_{{\mathbf{z}}_{j}}$ being the partial derivatives of natural velocities and accelerations with respect to the relative coordinates of joint $j$, respectively, which can be easily evaluated as the time derivatives of expressions of Table 3.

The resulting joint dependent expressions are independent of the reference point selected, which simplifies the implementation of RTdyn0 and RTdyn1 formulations and reduces the computational effort devoted to second order derivatives.

8.2 Elemental calculation of ${\mathbf{q}}_{{\mathbf{z}}{\mathbf{z}}}$ and ${{\dot{\mathbf{q}}}}_{{\mathbf{z}}{\mathbf{z}}}$

Using the expressions presented in the previous section, the multi-dimensional matrix ${\mathbf{q}}_{{\mathbf{z}}{\mathbf{z}}}$ is straightforward to achieve. Let us consider the matrix ${\mathbf{q}}_{{\mathbf{z}}{\mathbf{z}}} {\mathbf{x}}$, defined as the product of the multi-dimensional matrix ${\mathbf{q}}_{{\mathbf{z}}{\mathbf{z}}} \in \mathbb{R}^{n_{q} \times n \times n}$ by a vector ${\mathbf{x}} \in \mathbb{R}^{n}$. Each of its elements can be evaluated as

$$ ( {\mathbf{q}}_{{\mathbf{z}}{\mathbf{z}}} {\mathbf{x}} ) (i,j) = \dfrac{\partial }{\partial {\mathbf{z}}} \left ( \dfrac{\partial{\mathbf{q}}_{i}}{\partial {\mathbf{z}}_{j}} \right ) {\mathbf{x}}_{j}{,} $$

(49)

with $i$ and $j$ being the indices of joints.

Observe that the terms $\dfrac{\partial }{\partial {\mathbf{z}}} \left ( \dfrac{\partial{\mathbf{q}}_{i}}{\partial {\mathbf{z}}_{j}} \right ) {\mathbf{x}}_{j}$ can be easily calculated taking derivatives of the expressions of Table 3. For brevity, this derivative will be only specified for a revolute joint, the extension to the other joints being almost straightforward.

• Revolute joint

  For a point,

  $$ \dfrac{\partial }{\partial {\mathbf{z}}} \left ( \dfrac{\partial{\mathbf{r}}_{k}}{\partial {\mathbf{z}}_{j}} \right ) {\mathbf{x}}_{j} =\left ({\tilde{\mathbf{r}}}_{j} - {{\tilde{\mathbf{r}}}_{k}}\right ) \dfrac{\partial {\mathbf{{w}}}_{j} }{\partial {\mathbf{z}}} {\mathbf{x}}_{j} + { \tilde{\mathbf{{w}}}}_{j} \left ( \dfrac{\partial {\mathbf{r}}_{k}}{\partial {\mathbf{z}}} - \dfrac{\partial {\mathbf{r}}_{j}}{\partial {\mathbf{z}}}\right ) {\mathbf{x}}_{j}{.} $$

  (50)

  For a vector,

  $$ \dfrac{\partial }{\partial {\mathbf{z}}} \left ( \dfrac{\partial {\mathbf{{u}}}_{k}{}}{\partial {\mathbf{z}}_{j}} \right ) {\mathbf{x}}_{j} =- {{\tilde{\mathbf{{u}}}}_{k}{}} \dfrac{\partial {\mathbf{{w}}}_{j} }{\partial {\mathbf{z}}} {\mathbf{x}}_{j} + { \tilde{\mathbf{{w}}}}_{j} \dfrac{\partial {\mathbf{{u}}}_{k}{}}{\partial {\mathbf{z}}} {\mathbf{x}}_{j}{.} $$

  (51)

The resulting elemental second derivatives are expressed in terms of single derivatives of natural coordinates, whose expressions have been introduced in Sect. 8.1. The scheme of differentiation presented enhances the efficiency of the computation of ${\mathbf{q}}_{{\mathbf{z}}{\mathbf{z}}}$ compared with the expressions depending on ${\mathbf{R}}^{\mathrm{v}}$.

The partial derivative ${{\dot{\mathbf{q}}}}_{{\mathbf{z}}{\mathbf{z}}}$ can be reached by assembling the time derivatives of the terms introduced in the current section.

8.3 Elemental calculation of ${{\mathbf{q}}}_{{\boldsymbol{\rho} }}$, ${{\dot{\mathbf{q}}}}_{{\boldsymbol{\rho} }}$ and ${{\ddot{\mathbf{q}}}}_{{\boldsymbol{\rho} }}$

For the sake of simplicity, let us consider here the case of a local coordinate of a point as a sensitivity parameter. The position of any point in an open chain system involving the joint types considered in this work (see Table 3) can be computed by means of

$$ {{\mathbf{r}}_{k}^{i}}= \sum \limits _{h=1}^{i} \left ( {{\mathbf{A}}_{h}} \left ({\bar{\mathbf{{r}}}}_{h}^{h}-{\bar{\mathbf{{r}}}}_{h-1}^{h}\right ) \right ) +{{\mathbf{A}}_{i}}\left ({\bar{\mathbf{{r}}}}_{k}^{i}-{\bar{\mathbf{{r}}}}_{i}^{i} \right ) + \sum \limits _{h=1}^{i} \left ( {\mathbf{{u}}}_{h}{} {z_{h}} \right ){,} $$

(52)

with $h$ being each of the preceding joints of body $i$ within the kinematic chain, ${\mathbf{{u}}}_{h}{}$ the axis of translation in prismatic, cylindrical and floating joints, and ${z_{h}}$ the translation coordinate. Observe that neither the axis nor the coordinate of a translational motion has direct dependencies with the local coordinate of any point.

From (52) it can be inferred that the local coordinates affecting ${{\mathbf{r}}_{k}^{i}}$ are those used in the definition of the preceding joints in the kinematic chain, this is, the group of joints that are between the base body and body $i$, as well as the local coordinates of point $k$ in body $i$. Considering that rotation matrices only involve local coordinates of vectors, their derivatives with respect to the local coordinates of a point are null.

The partial derivative of the position of any point is

$$ \dfrac{\partial{{\mathbf{r}}_{k}}}{\partial{{\bar{\mathbf{{r}}}}_{j}^{l}}} = \left \{ \textstyle\begin{array}{l@{\quad}l} {{\mathbf{A}}_{l}} & \text{{in} Case 1} {,} \\ -{{\mathbf{A}}_{l}} & \text{{in} Case 2} {,} \\ {\mathbf{0}} & \text{{in} Case 3} {,} \end{array}\displaystyle \right . $$

(53)

in which $l$ represents the body where the local coordinates of point $k$ are defined as parameters, and cases are:

• Case 1. Point $j$ is contained in the definition of a preceding joint and $l$ is the first body of the joint,⁵ or $k = j$.

• Case 2. Point $j$ is involved in the definition of a preceding joint and $l$ is the second body of the joint.

• Case 3. Point $j$ does not affect any joint previous to body $i$ and $k \neq j$.

If an axis of rotation can be only defined by a vector, as it is implemented in MBSLIM, the derivative of the position of a vector with respect to the local coordinates of a point is always zero because no local coordinates of points are included into an expression of a rotation matrix, ${\partial {{\mathbf{{u}}}_{k}{}}} / { \partial {{\bar{\mathbf{{r}}}}_{j}^{l}}} ={ \mathbf{0}}$.

Additionally, terms ${{\dot{\mathbf{q}}}}_{{\hat{\boldsymbol{\rho} }}}$ and ${{\ddot{\mathbf{q}}}}_{{\hat{\boldsymbol{\rho} }}}$ can be evaluated as the first and second temporal derivatives of ${{\mathbf{q}}}_{{\hat{\boldsymbol{\rho} }}}$, which for the case of local coordinates of points as parameters reduces to the mere evaluation of the time derivatives of a rotation matrix (see (53)).

8.4 Elemental calculation of ${{\mathbf{q}}}_{{\mathbf{z}}{\boldsymbol{\rho} }}$ and ${{\dot{\mathbf{q}}}}_{{\mathbf{z}}{\boldsymbol{\rho} }}$

Following the scheme of differentiation of the previous sections, the second derivative of ${\mathbf{q}}$ with respect to the relative coordinates and with respect to the parameters of the system can be obtained by taking derivatives of ${{\mathbf{q}}}_{{\boldsymbol{\rho} }}$ with respect to ${\mathbf{z}}$. The results are

$$ \dfrac{\partial }{\partial {\mathbf{z}}} \left ( \dfrac{\partial{{\mathbf{r}}_{k}}}{\partial{{\bar{\mathbf{{r}}}}_{j}^{l}}} \right ) = \left \{ \textstyle\begin{array}{l@{\quad}l} {\partial {\mathbf{A}}_{l}} / {\partial {\mathbf{z}}} & \text{{in} Case 1} {,} \\ -{\partial {\mathbf{A}}_{l}} / {\partial {\mathbf{z}}} & \text{{in} Case 2} {,} \\ {\mathbf{0}} & \text{{in} Case 3} {,} \end{array}\displaystyle \right . $$

(54)

where $l$ is the body where the local coordinates of point $k$ are defined as parameters. The cases have been defined in Sect. 8.3.

The derivative ${{\dot{\mathbf{q}}}}_{{\mathbf{z}}{\boldsymbol{\rho} }}$ can be easily obtained applying again a new time derivative to the expressions of ${{\mathbf{q}}}_{{\mathbf{z}}{\boldsymbol{\rho} }}$.

9 Derivatives of recursive kinematic relations

One of the most significant differences between global and topological formulations is the presence of recursive relations needed for the assemblies and accumulations in topological models. These terms rely on the relative coordinates and local coordinates of points and vectors defining each joint.

Recursive relations can be categorized in two groups: joint dependent terms, with ${\mathbf{A}}_{i}$, ${\mathbf{b}}_{i}^{\mathrm{v}}$ and ${\dot{\mathbf{b}}}_{i}^{\mathrm{v}}$; and joint independent terms, with ${{\mathbf{B}}_{i}^{\mathrm{v}}}$, ${{\dot{\mathbf{B}}}_{i}^{\mathrm{v}}}$ and ${{\mathbf{d}}_{i}^{\mathrm{v}}}$. Their derivatives are summarized in Table 4.

Table 4 Recursive relations derivatives involved in a sensitivity analysis

9.1 Evaluation of ${\left ({\mathbf{A}}_{i} \right )}_{{\mathbf{z}}}$

A rotation matrix of a body can be computed recursively as ${\mathbf{A}}_{i}={\mathbf{A}}_{i-1} {\mathbf{{A}}}_{i}^{i-1}$, with ${\mathbf{A}}_{i-1}$ being the rotation matrix of body $i-1$ and ${\mathbf{{A}}}_{i}^{i-1}$ a relative rotation matrix between bodies $i-1$ and $i$. Taking derivatives of this expression, ${\left ({\mathbf{A}}_{i} \right )}_{{\mathbf{z}}}$ becomes

$$ \left ( {\mathbf{A}}_{i} \right )_{{\mathbf{z}}}=\left ( {\mathbf{A}}_{i-1} \right )_{{\mathbf{z}}} {\mathbf{{A}}}_{i}^{i-1}+{\mathbf{A}}_{i-1} \left ( {\mathbf{{A}}}_{i}^{i-1} \right )_{{\mathbf{z}}}{.} $$

(55)

However, a more efficient expression is possible, involving only partial derivatives of relative rotation matrices without the need of accumulating terms as $\left ( {\mathbf{A}}_{i-1} \right )_{{\mathbf{z}}}$,

$$ \left ( {\mathbf{A}}_{i} \right )_{{\mathbf{z}}}=\left ( \sum \limits _{j=1}^{i} {\mathbf{{A}}}_{j-1} \left ( {\mathbf{A}}_{j}^{j-1} \right )_{{\mathbf{z}}} {{ \mathbf{{A}}}_{j}}^{\mathrm{T}} \right ) {\mathbf{{A}}}_{i} {.} $$

(56)

Observe that the relative rotation matrix derivatives involved in (56) only depend on the joint coordinates describing each relative motion. Those derivatives are listed in Table 5.

Table 5 Derivatives of ${\mathbf{A}}_{i}^{i-1}$ with respect to relative coordinates

9.2 Evaluation of ${\left ({\mathbf{A}}_{i} \right )}_{\boldsymbol{\rho}}$

The rotation matrix of a body can depend on a few parameters, like the local position of a vector, for example. Although the derivatives of each relative rotation matrix with respect of each parameter must be calculated individually, the following assembly is needed:

$$ \left ( {\mathbf{A}}_{i} \right )_{\boldsymbol{\rho}}=\left ( \sum \limits _{j=1}^{i} {\mathbf{{A}}}_{j-1} \left ( {\mathbf{A}}_{j}^{j-1}\right )_{\boldsymbol{\rho}} {{\mathbf{{A}}}_{j}}^{T} \right ) {\mathbf{{A}}}_{i}{.} $$

(57)

9.3 Evaluation of ${\left ({\mathbf{b}}_{i}^{\mathrm{v}}\right )}_{\hat{\mathbf{z}}}$ and ${\left ({\dot{\mathbf{b}}}_{i}^{\mathrm{v}}\right )}_{\hat{\mathbf{z}}}$

Even though each type of joint has a different expression for ${\mathbf{b}}_{i}^{\mathrm{v}}$ (see Appendix D), some patterns can be detected and harnessed to gather terms and reuse structures of computation. Basically, the derivatives of ${\mathbf{b}}_{i}^{\mathrm{v}}$ with respect to the relative coordinates can be divided in two types, those involving natural coordinates and those depending also on Euler parameters.

As a means to simplify the notation and make the final expressions clearer, a decomposition of the term ${\mathbf{b}}_{i}^{\mathrm{v}}$ is considered. On the one hand, ${\mathbf{b}}_{i}^{{\mathrm{v}}j}$ can be expressed as a combination of arrays ${\mathbf{b}}_{i}^{{\mathrm{v}}j} \in \mathbb{R}^{6}$, with each array ${\mathbf{b}}_{i}^{{\mathrm{v}}j}$ being the $j$th column of matrix ${\mathbf{b}}_{i}^{\mathrm{v}}$. On the other hand, each column can be further divided into arrays ${\mathbf{b}}_{i}^{{\mathrm{v}}{k,j}} \in \mathbb{R}^{3}$ corresponding to the linear and angular part of ${\mathbf{b}}_{i}^{{\mathrm{v}}j}$. Accordingly, the term ${\mathbf{b}}_{i}^{\mathrm{v}}$ of the spherical joint can be expressed with this notation as

$$ {\mathbf{b}}_{i}^{\mathrm{v}}= \begin{bmatrix} {\mathbf{b}}_{i}^{\mathrm{v1}} & {\mathbf{b}}_{i}^{\mathrm{v2}} & {\mathbf{b}}_{i}^{\mathrm{v3}} & { \mathbf{b}}_{i}^{\mathrm{v4}} \end{bmatrix} = \begin{bmatrix} {\mathbf{b}}_{i}^{\mathrm{v1},\mathrm{1}} & {\mathbf{b}}_{i}^{\mathrm{v1},\mathrm{2}} & {\mathbf{b}}_{i}^{\mathrm{v1},\mathrm{3}} & {\mathbf{b}}_{i}^{\mathrm{v1},\mathrm{4}} \\ {\mathbf{b}}_{i}^{\mathrm{v2},\mathrm{1}} & {\mathbf{b}}_{i}^{\mathrm{v2},\mathrm{2}} & {\mathbf{b}}_{i}^{\mathrm{v2},\mathrm{3}} & {\mathbf{b}}_{i}^{\mathrm{v2},\mathrm{4}} \end{bmatrix} {.} $$

(58)

These two divisions of ${\mathbf{b}}_{i}^{\mathrm{v}}$ make it possible to differentiate arrays instead of matrices and they allow taking derivatives separately on the linear part of the term (the first three rows) and on the angular part (from the fourth to sixth row). The present notation intends to make the differentiation more readable and to reflect the close relation of ${\mathbf{b}}_{i}^{\mathrm{v}}$ with its own derivatives.

In order to reduce the extension of this paper, only the final expressions are included (see Appendix D for the original expressions of ${\mathbf{b}}_{i}^{\mathrm{v}}$ for each joint).

In general, the partial derivative of the term ${\dot{\mathbf{b}}}_{i}^{\mathrm{v}}$ with respect to the relative coordinates in positions ${\mathbf{z}}$ can be calculated as the time derivative of the expressions of Table 6:

$$ {\dot{\mathbf{b}}}_{i}^{\mathrm{v}}= \dfrac{{\mathrm{d}} {\mathbf{b}}_{i}^{\mathrm{v}}}{{\mathrm{d}} \mathrm{t}} \Rightarrow { \left ({\dot{\mathbf{b}}}_{i}^{\mathrm{v}}\right )}_{{\mathbf{z}}}= \dfrac{{\mathrm{d}} {\left ({\mathbf{b}}_{i}^{\mathrm{v}}\right )}_{{\mathbf{z}}}}{{\mathrm{d}} \mathrm{t}}{.} $$

(59)

Table 6 Derivatives of ${\mathbf{b}}_{i}^{\mathrm{v}}$ with respect to relative coordinates

The time differentiation in this case is straightforward, thus the particular expression for each joint is omitted here.

9.4 Evaluation of ${\left ({\mathbf{b}}_{i}^{\mathrm{v}}\right )}_{{\hat{\boldsymbol{\rho} }}}$

The recursive kinematic relations are expressed as a combination of natural coordinates, relative coordinates (Euler parameters) and rotation matrices. Since rotation matrices and natural coordinates involve local coordinates of points and vectors, those local coordinates constitute a possible set of parameters that affect the recursive kinematic relations.

The term ${\left ({\mathbf{b}}_{i}^{\mathrm{v}}\right )}_{{\hat{\boldsymbol{\rho} }}}$ can be obtained for any kinematic joint by means of a two-stage process: first, derivatives can be taken with respect to the points and vectors that define the joint; the second stage consists in computing the derivative of the natural coordinates with respect to the parameters as explained in Sect. 8.3.

9.5 Evaluation of ${\left ({\mathbf{B}}_{i}^{\mathrm{v}}\right )}_{\hat{\mathbf{z}}}$ and ${\left ({\dot{\mathbf{B}}}_{i}^{\mathrm{v}}\right )}_{\hat{\mathbf{z}}}$

The term ${\mathbf{B}}_{i}^{\mathrm{v}}$ relates the position of the different reference points of each body [24]. The derivative of ${\mathbf{B}}_{i}^{\mathrm{v}}$ depends on the type of reference point selected, as it is patent in the following expression:

$$ {\left ({\mathbf{B}}_{i}^{\mathrm{v}}\right )}_{\hat{\mathbf{z}}} = \begin{bmatrix} {\mathbf{0}} & \left ( {\tilde{\mathbf{r}}}_{i-1} \right )_{\hat{\mathbf{z}}} - \left ( {\tilde{\mathbf{r}}}_{i} \right )_{\hat{\mathbf{z}}} \\ {\mathbf{0}} & {\mathbf{0}} \end{bmatrix} {,} $$

(60)

in which the particular expression of the corresponding reference point derivative has to be used.

Besides, ${\left ({\dot{\mathbf{B}}}_{i}^{\mathrm{v}}\right )}_{\hat{\mathbf{z}}}$ can be expressed as

$$ {\left ({\dot{\mathbf{B}}}_{i}^{\mathrm{v}}\right )}_{\hat{\mathbf{z}}} = \begin{bmatrix} {\mathbf{0}} & \left ( {\dot{\tilde{\mathbf{r}}}}_{i-1} \right )_{ \hat{\mathbf{z}}} - \left ( {\dot{\tilde{\mathbf{r}}}}_{i} \right )_{ \hat{\mathbf{z}}} \\ {\mathbf{0}} & {\mathbf{0}} \end{bmatrix} {.} $$

(61)

In the case of a set of reference points fixed in the local reference frame of the corresponding body, as in RTdyn0, expressions (60) and (61) can be reformulated. For the sake of clearness, Let us consider the product of these derivatives by a given array ${\mathbf{x}} \in \mathbb{R}^{6}$:

$$\begin{aligned} \begin{aligned} \left ( {\mathbf{B}}_{i}^{\mathrm{y}} \right )_{\hat{\mathbf{z}}} {\mathbf{x}}&= \left ( { \mathbf{B}}_{i}^{\mathrm{y}}\right )_{\hat{\mathbf{z}}} \begin{bmatrix} {\mathbf{x}}_{1} \\ {\mathbf{x}}_{2} \end{bmatrix} = \begin{bmatrix} \tilde{{\mathbf{x}}}_{2} \left ( \begin{bmatrix} {\mathbf{0}} & {\tilde{\mathbf{r}}}_{i-1} - {\tilde{\mathbf{r}}}_{i} \end{bmatrix} {\mathbf{R}}_{i-1}^{\mathrm{y}} + \begin{bmatrix} {\mathbf{I}} & {\mathbf{0}} \end{bmatrix} {\mathbf{b}}_{i}^{\mathrm{y0}} \right ) \\ {\mathbf{0}} \end{bmatrix} \end{aligned} {,} \end{aligned}$$

(62)

$$\begin{aligned} \begin{aligned} \left ({\dot{\mathbf{B}}}_{i}^{\mathrm{y}}\right )_{\hat{\mathbf{z}}} {\mathbf{x}}&= \left ({\dot{\mathbf{B}}}_{i}^{\mathrm{y}}\right )_{\hat{\mathbf{z}}} \begin{bmatrix} {\mathbf{x}}_{1} \\ {\mathbf{x}}_{2} \end{bmatrix} = \begin{bmatrix} \tilde{{\mathbf{x}}}_{2} \left ( \begin{bmatrix} {\mathbf{I}} & {\mathbf{0}} \end{bmatrix} {\dot{\mathbf{R}}}_{i}^{\mathrm{y}} - \begin{bmatrix} {\mathbf{I}} & {\mathbf{0}} \end{bmatrix} {\dot{\mathbf{R}}}_{i-1}^{\mathrm{y}} \right ) \\ {\mathbf{0}} \end{bmatrix}{,} \end{aligned} \end{aligned}$$

(63)

with ${\mathbf{b}}_{i}^{\mathrm{y0}} ={\mathbf{b}}_{i}^{\mathrm{y}} \dfrac{\partial{{\dot{\mathbf{z}}}_{k}}}{\partial {\dot{\mathbf{z}}}} = \begin{bmatrix} {\mathbf{0}} & \ldots & {\mathbf{0}} & {\mathbf{b}}_{i}^{\mathrm{y}} & {\mathbf{0}} & \ldots & { \mathbf{0}} \end{bmatrix}$.

If the reference point is fixed in the global frame, as it happens in RTdyn1, the derivative is more cumbersome,

$$ \begin{aligned} {\left ({\dot{\mathbf{B}}}_{i}^{\mathrm{z}}\right )}_{\hat{\mathbf{z}}} {\mathbf{x}}&= {\left ({\dot{\mathbf{B}}}_{i}^{\mathrm{z}}\right )}_{\hat{\mathbf{z}}} \begin{bmatrix} {\mathbf{x}}_{1} \\ {\mathbf{x}}_{2} \end{bmatrix} \\ &= \begin{bmatrix} \tilde{{\mathbf{x}}}_{2} \left ( \begin{bmatrix} {\mathbf{I}} & {\mathbf{0}} \end{bmatrix} {\dot{\mathbf{R}}}_{i}^{\mathrm{z}} - \begin{bmatrix} {{\tilde{\boldsymbol{\omega} }}_{i}} & {\mathbf{0}} \end{bmatrix} {\mathbf{R}}_{i}^{\mathrm{z}} - \begin{bmatrix} {\mathbf{I}} & {\mathbf{0}} \end{bmatrix} {\dot{\mathbf{R}}}_{i-1}^{\mathrm{z}} + \begin{bmatrix} {{\tilde{\boldsymbol{\omega} }}_{i-1}} & {\mathbf{0}} \end{bmatrix} {\mathbf{R}}_{i-1}^{\mathrm{z}} \right ) \\ {\mathbf{0}} \end{bmatrix}{.} \end{aligned} $$

(64)

9.6 Evaluation of ${\left ({\mathbf{d}}_{i}^{\mathrm{v}}\right )}_{\hat{\dot{\mathbf{z}}}}$

As long as ${\mathbf{d}}_{i}$ can be expressed in terms of ${\mathbf{b}}_{i}^{\mathrm{v}}$ and ${\dot{\mathbf{b}}}_{i}^{\mathrm{v}}$ according to (4e), its derivatives $\left ( {\mathbf{d}}_{i} \right )_{\hat{\mathbf{z}}}$ and $\left ( {\mathbf{d}}_{i}\right )_{\hat{\dot{\mathbf{z}}}}$ can be formulated as a combination of ${\mathbf{b}}_{i}$ and ${\dot{\mathbf{b}}}_{i}$, and their derivatives. The differentiation of the general expression of ${\mathbf{d}}_{i}^{\mathrm{v}}$ for any type of joint, and for any reference point yields

$$\begin{aligned} \begin{aligned} \left ( {\mathbf{d}}_{i}^{\mathrm{v}} \right )_{\hat{\dot{\mathbf{z}}}}&= { \begin{bmatrix} \left ( {\dot{\tilde{\mathbf{r}}}}_{i-1} - {\dot{\tilde{\mathbf{r}}}}_{i} \right ) \begin{bmatrix} {\mathbf{0}} & {\mathbf{I}} \end{bmatrix} {\mathbf{R}}_{i-1}^{\mathrm{v}} - {\tilde{\boldsymbol{\omega} }}_{i-1} \left ( \left ( { \dot{\mathbf{r}}}_{i-1}\right )_{{\dot{\mathbf{z}}}} - \left ( {\dot{\mathbf{r}}}_{i} \right )_{{\dot{\mathbf{z}}}}\right ) \\ {\mathbf{0}} \end{bmatrix} + \left ( {\dot{\mathbf{b}}}_{i}^{\mathrm{v}} \right )_{\hat{\dot{\mathbf{z}}}} {{ \dot{\mathbf{z}}}_{i}} + {\dot{\mathbf{b}}}_{i}^{\mathrm{v0}}} \end{aligned}{,} \end{aligned}$$

(65)

$$\begin{aligned} {\dot{\mathbf{b}}}_{i}^{\mathrm{v0}}&={\dot{\mathbf{b}}}_{i}^{\mathrm{v}} \dfrac{\partial{{\dot{\mathbf{z}}}_{k}}}{\partial {\dot{\mathbf{z}}}}= \begin{bmatrix} {\mathbf{0}} & \ldots & {\mathbf{0}} & {\dot{\mathbf{b}}}_{i}^{\mathrm{v}} & {\mathbf{0}} & \ldots & {\mathbf{0}} \end{bmatrix}{.} \end{aligned}$$

(66)

The accumulation term ${\mathbf{d}}_{i}^{\mathrm{v}\Sigma }$ evaluated in (24) can be differentiated with respect to joint coordinate velocities, which yields

$$ \left ( {\mathbf{d}}_{i}^{\mathrm{v}\Sigma } \right )_{\hat{\dot{\mathbf{z}}}} = \left ( {\mathbf{d}}_{i}^{\mathrm{v}}\right )_{\hat{\dot{\mathbf{z}}}} + {\mathbf{B}}_{i}^{ \mathrm{v}} \left ( {\mathbf{d}}_{h}^{\mathrm{v}\Sigma }\right )_{\hat{\dot{\mathbf{z}}}}{,} $$

(67)

where $h$ is the parent body of $i$. Accordingly, this derivative can be computed as a recursive accumulation of $\left ( {\mathbf{d}}_{i}^{\mathrm{v}}\right )_{\hat{\dot{\mathbf{z}}}}$ from the root to the leaves of the mechanism.

Equations (65) and (67) apply for any set of reference points. For RTdyn0 and RTdyn1, the particular derivatives of the reference points can be directly substituted, regarding also that ${\mathbf{B}}_{i}^{\mathrm{v}}$ becomes the identity in the RTdyn1 method.

9.7 Evaluation of ${\left ({\mathbf{d}}_{i}^{\mathrm{v}}\right )}_{\hat{\mathbf{z}}}$

This derivative can be obtained from the differentiation of $\left ( {\mathbf{d}}_{i}^{\mathrm{v}} \right )_{\hat{\dot{\mathbf{z}}}}$ with respect to time, but it is more direct to start from equation (4e). Taking derivatives of (4e) yields

$$ \begin{aligned} \left ( {\mathbf{d}}_{i}^{\mathrm{v}} \right )_{\hat{\mathbf{z}}}&= \begin{bmatrix} \left ( {{\dot{\tilde{\mathbf{r}}}}_{i-1} -{\dot{\tilde{\mathbf{r}}}}_{i}} \right )\left ( \begin{bmatrix} {\mathbf{0}} & {\mathbf{I}} \end{bmatrix} {\dot{\mathbf{R}}}_{i-1}^{\mathrm{v}} - \begin{bmatrix} {\mathbf{0}} & {{\tilde{\boldsymbol{\omega} }}_{i-1}} \end{bmatrix} {\mathbf{R}}_{i-1}^{\mathrm{v}} \right ) - {\tilde{\boldsymbol{\omega} }}_{i-1} \left ( \left ( {\dot{\tilde{\mathbf{r}}}}_{i-1}\right )_{\mathbf{{z}}} - \left ( {\dot{\tilde{\mathbf{r}}}}_{i} \right )_{\mathbf{{z}}} \right ) \\ {\mathbf{0}} \end{bmatrix} \\ &\quad {}+ \left ( {\dot{\mathbf{b}}}_{i}^{\mathrm{v}} \right )_{ \hat{\mathbf{z}}} {{\dot{\mathbf{z}}}_{i}}{.} \end{aligned} $$

(68)

Analogously to Sect. 9.6, the derivative of ${\mathbf{d}}_{i}^{\mathrm{v}\Sigma }$ with respect to ${\mathbf{z}}$ can be reached through an accumulative process,

$$ \left ( {\mathbf{d}}_{i}^{\mathrm{v}\Sigma }\right )_{\hat{\mathbf{z}}} =\left ( { \mathbf{d}}_{i}^{\mathrm{v}}\right )_{\hat{\mathbf{z}}} + \left ( {\mathbf{B}}_{i}^{\mathrm{v}} \right )_{\hat{\mathbf{z}}} {\mathbf{d}}_{h}^{\mathrm{v}\Sigma } + {\mathbf{B}}_{i}^{ \mathrm{v}} \left ( {\mathbf{d}}_{h}^{\mathrm{v}\Sigma }\right )_{\hat{\mathbf{z}}}{.} $$

(69)

Equations (68) and (69) can be further particularized for RTdyn0 and RTdyn1 substituting the corresponding expressions of the reference point derivatives. Moreover, it should be recalled that in the RTdyn1 method ${\mathbf{B}}_{i}^{\mathrm{z}}$ becomes the identity and $\left ( {\mathbf{B}}_{i}^{\mathrm{z}}\right )_{\hat{\mathbf{z}}}$ is null.

10 Numerical experiments

The sensitivity analysis proposed in this paper has been tested in two multibody systems. In these numerical experiments, the accuracy is compared with the equivalent formulation in natural coordinates, with a reference result. Moreover, the computational burden is also compared between semi-recursive and global ALI3-P forward sensitivity formulations. All the sensitivity analyses in relative and natural coordinates have been computed with the multibody library MBSLIM in an Intel Core i7-8700 CPU at 3.20 GHz running Windows 10 with Fortran Intel Parallel Studio XE 2018.

10.1 Sensitivity analysis of a five-bar mechanism

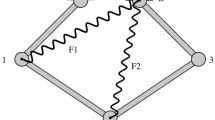
The first mechanism tested is the five-bar linkage sensitivity benchmark problem displayed in Fig. 1. A detailed description of the mechanism, initial conditions, simulation time, objective function and sensitivity parameters is included in the IFToMM benchmark library [32].

Fig. 1

Five-bar linkage

According to [32], an array of cost functions is considered ${\boldsymbol{\psi}} = \begin{bmatrix} {\psi}_{1} & {\psi}_{2} & {\psi}_{3} \end{bmatrix} ^{\mathrm{T}} \in \mathbb{R}^{3}$ for the sensitivity analysis, with

$$\begin{aligned} {\psi}_{1} &= \int ^{t_{{{\mathrm{F}}}}}_{t_{{{\mathrm{0}}}}} \left ( {\mathbf{r}}_{2} - {\mathbf{r}}_{20} \right )^{\mathrm{T}} \left ( {\mathbf{r}}_{2} - {\mathbf{r}}_{20} \right ) {\mathrm{d}}t{,} \end{aligned}$$

(70a)

$$\begin{aligned} {\psi}_{2} &= \int ^{t_{{{\mathrm{F}}}}}_{t_{{{\mathrm{0}}}}} {\dot{\mathbf{r}}}_{2}^{ \mathrm{T}} {\dot{\mathbf{r}}}_{2} {\mathrm{d}}t{,} \end{aligned}$$

(70b)

$$\begin{aligned} {\psi}_{3} &= \int ^{t_{{{\mathrm{F}}}}}_{t_{{{\mathrm{0}}}}} {\ddot{\mathbf{r}}}_{2}^{ \mathrm{T}} {\ddot{\mathbf{r}}}_{2} {\mathrm{d}}t{,} \end{aligned}$$

(70c)

in which ${\mathbf{r}}_{2}$ is the position of the point identified as 2 in Fig. 1, whereas the term ${\mathbf{r}}_{20}$ represents the initial position of point 2.

The group of parameters considered in the sensitivity analysis are the natural length of the springs, the mass of bar A1, the longitudinal coordinate of the local position of its center of mass and the length of the bar A1,

$$ {\boldsymbol{\rho} }= \begin{bmatrix} L_{{\mathrm{s1}}} & L_{{\mathrm{s2}}} & m_{{\mathrm{A1}}} & x^{{\mathrm{G}}}_{{\mathrm{A1}}} & L_{{ \mathrm{A1}}} \end{bmatrix} {,} $$

(71)

in which $x^{{\mathrm{G}}}_{{\mathrm{A1}}}$ constitutes a simplified notation of $\left ({\bar{\mathbf{{r}}}}_{{\mathrm{A1}}}^{{\mathrm{G}}}\right )_{x}$, with $X$ being the longitudinal local coordinate of the bar.

The numerical experiment consists in a 5-second dynamic simulation and sensitivity analysis of the mechanism subjected to gravitational and spring forces. All semi-recursive and global ALI3-P formulations are executed with a penalty factor $\alpha =10^{9}$ using non-iterative mass orthogonal projections, with $\varsigma =1.0$. Since the purpose of the document does not rely on the dynamic simulation of the mechanism but on its sensitivity analysis, dynamic graphs are omitted, and the reader is referred to the benchmark mechanism description in [32] for more information about the motion of the five-bar linkage.

The evolution of the objective functions (70a)–(70c) over time is displayed in Fig. 2, in which the results of global and semi-recursive ALI3-P formulations are compared with the reference result. This plot evidences a high level of accuracy of dynamic formulations, thus a similar accuracy level can be expected for the objective functions gradient.

Fig. 2

Evolution of each component of the objective function

The results for the gradient of the objective function (70a)–(70c) evaluated with the semi-recursive ALI3-P forward sensitivity formulation particularized for RTdyn0 and RTdyn1 are compared in Table 7 with the global ALI3-P forward sensitivity formulation and with the reference response included in the benchmark mechanism description in [32]. This table shows an excellent level of accuracy for all the sensitivity formulations compared.

Table 7 Comparison of the objective functions gradient evaluated with the global and semi-recursive ALI3-P forward sensitivity formulations and with the reference formulation

Looking at Table 8, it is obvious that the computation of the sensitivity analysis using relative coordinates models is slower than the calculation with the equivalent formulations in natural coordinates, even though the dynamics have similar computational times. For multibody models with a higher number of bodies, a better performance of semi-recursive methods is expected.

Table 8 CPU time (in seconds) of global and semi-recursive ALI3-P forward sensitivity formulations for the five-bar mechanism

Regarding the selection of reference points, Table 8 shows that both RTdyn0 and RTdyn1 lead to almost identical computational efforts, with the CPU time deviation being lower than 1 millisecond in this numerical example.

10.2 Sensitivity analysis of a buggy vehicle

As second numerical experiment, a more complex industrial multibody system is considered in order to prove both the validity of the semi-recursive ALI3-P sensitivity formulations and their performance in real life mechanisms. This model has been previously used to test semi-recursive dynamic formulations [24] and different sensitivity analysis methods [25, 26], among other topics [33, 34]. In this section, only the essential information of the mechanism and analysis conditions will be provided. For a more detailed description of the multibody system, maneuvers, objective functions and parameters, two new benchmark problems have been submitted to the IFToMM benchmark library [32].

The vehicle displayed in Fig. 3 is a four-wheeled buggy composed of 18 bodies and with four articulated suspensions. The mechanism has been modelled with 33 points, 25 vectors, 4 angles (one per wheel) and 5 distances (steering rack and one per spring–damper system). Moreover, a rheonomic constraint has been used for the guidance of the steering rack.

Fig. 3

Image of the buggy vehicle identifying the points and vectors defining the model

The natural coordinates model generated is composed of 180 mixed coordinates (171 coordinates of points and vectors and 9 relative to angles and distances) and it is provided with 178 constraint equations. The relative model coordinates automatically built by MBSLIM consist of 18 kinematic joints parameterized by a total of 36 joint coordinates. The opening of closed loops and the user defined constraints yield a total of 26 constraint equations.

The buggy vehicle is subjected to gravitational forces and a spring–damper force associated to each suspension. Moreover, the wheel–ground interaction has been modelled by means of tire contact-frictional forces.

In the initial position, the suspensions of the vehicle are not at the equilibrium configuration but slightly elevated, and therefore a stabilization of the suspensions occurs during the first second of simulation.

The behaviour of the semi-recursive sensitivity formulations introduced in this paper is assessed in two maneuvers performed with this multibody system. The dynamics of the two maneuvers considered here are studied and detailed in the benchmark problem descriptions [32] and in [24], thus hereinafter the focus will be primarily put on their sensitivity analysis.

10.2.1 First maneuver: step descent

The first maneuver consists in the descent of a step of 1 cm located at 5.5 m from the origin, with forward initial linear speed of 3 m/s and 11 rad/s for each wheel. With this velocity, the step is reached approximately at $t={2.0}\text{ s}$. The simulation lasts 4.5 seconds with a time step of 1 ms, no additional traction forces are applied and the steering system is blocked with the front wheels straight.

For the sensitivity analysis of this maneuver, the following objective function is considered:

$$ {\psi} = \int ^{t_{{{\mathrm{F}}}}}_{t_{{{\mathrm{0}}}}} \ddot{r}_{1_{z}}^{2} { \mathrm{dt}}{,} $$

(72)

in which ${\ddot{r}}_{1_{z}}{}$ denotes the $Z$ (vertical) component of the acceleration of point 1, located in the front of the chassis. This objective function represents a measure of comfort, since it is evaluating the accelerations that the driver would experiment during the descent of the step.

The parameters selected for this maneuver are the stiffness and damping coefficients of the four suspensions (equal values are considered for the spring-dampers of each axle) along with the mass of the chassis,

$$ {{\boldsymbol{\rho} }} = \begin{bmatrix} k_{{\mathrm{f}}} & c_{{\mathrm{f}}} & k_{{\mathrm{r}}} & c_{{\mathrm{r}}} & m_{{\mathrm{c}}} \end{bmatrix} {,} $$

(73)

where $k_{{\mathrm{f}}}$ and $c_{{\mathrm{f}}}$ are the stiffness and damping coefficients of the front suspensions, $k_{{\mathrm{r}}}$ and $c_{{\mathrm{r}}}$ denote the stiffness and damping coefficients of the rear suspensions and $m_{{\mathrm{c}}}$ represents the mass of the chassis.

Dynamic results are referred to [24], where the identical maneuver with the same semi-recursive and global ALI3-P formulations have been executed.

Figure 4 displays the value of the objective function gradient obtained with the two semi-recursive sensitivity formulations presented in this paper (for RTdyn0 and RTdyn1 semi-recursive methods), with the equivalent formulation in natural coordinates and with the reference values. The convergence of the results in this figure highlights the validity and accuracy of the new sensitivity formulations presented, which is even more relevant taking into account the totally different models being simulated.

Fig. 4

Objective function gradient for the step-descent maneuver

A comparison of CPU times of the sensitivity formulations displayed in Table 9 presents a superior efficiency of semi-recursive formulations, which are 15.8% faster than the equivalent formulation in natural coordinates for this particular maneuver.

Table 9 CPU time of relative coordinates sensitivity formulations (in seconds) compared with the equivalent one in natural coordinates for the step-descent maneuver

10.2.2 Second maneuver: double lane change

The second maneuver lasts 12 seconds and consists in a double lane change under the conditions specified in [24]. In this maneuver, the lateral and inertial forces entail a change in the roll $\phi$ of the chassis. For the sensitivity analysis, an objective function measuring the roll rate sum of squares over time is considered,

$$ {\boldsymbol{\psi}} = \int ^{t_{{{\mathrm{F}}}}}_{t_{{{\mathrm{0}}}}} \dot{\phi}^{2} { \mathrm{dt}}{.} $$

(74)

The sensitivities of this objective function will deliver the relevance of each one of the parameters in the roll rate, and they could be eventually used for minimizing the roll rate during this maneuver.

The set of parameters considered are the same as in the previous maneuver (73).

A double lane change is a smoother maneuver than the step descent since there are no impacts, collisions or abrupt changes in forces or constraints. Therefore, both the dynamics and its sensitivities can be computed increasing the time step. In this case, the semi-recursive and global ALI3-P formulations are executed with a time step of 10 milliseconds.

In Fig. 5, a small divergence of the objective function evolution over time assessed with the global ALI3-P formulation with respect to the reference result can be observed, while semi-recursive dynamic formulations are more accurate for this time step.

Fig. 5

Evolution of the objective function over time on a double lane change maneuver

According to the objective function gradients of Fig. 6, semi-recursive formulations display, as it happens in the dynamics, better behaviour than the equivalent global formulation in terms of accuracy. Moreover, it is especially remarkable that, even for 10 milliseconds of time step, the semi-recursive ALI3-P forward sensitivity results are very close to the reference.

Fig. 6

Objective function gradient for the double lane change maneuver

Comparing computational efforts of semi-recursive and global ALI3-P forward sensitivity formulations, Table 10 evidences that the first methods are $78.8 \%$ faster for the same time step. Therefore, is clear that semi-recursive methods outperform ALI3-P global formulations in this numerical experiment both in terms of accuracy and efficiency.

Table 10 CPU time of relative coordinates sensitivity formulations (in seconds) compared with the equivalent one in natural coordinates for the double lane change maneuver

The results of this maneuver demonstrate the low computational time required to compute the sensitivity analysis of this complex multibody model involving several bodies, types of joints, closed loops, types of constraints, types of forces and types of parameters. In fact, the dynamics and sensitivity analysis of a 12-second maneuver is executed in 2.578 seconds, which is 4.655 times faster than real time.

11 Conclusions

In this paper, the direct differentiation method has been successfully applied to the semi-recursive augmented Lagrangian index-3 formulation with velocity and acceleration projections (ALI3-P) recently reviewed in [24]. As a result, a semi-recursive ALI3-P forward sensitivity formulation has been developed for an arbitrary selection of reference points. In parallel, two specific sensitivity formulations have been developed and implemented in the general purpose multibody library MBSLIM, corresponding to the particularization of the general formulation to RTdyn0 and RTdyn1 semi-recursive methods. Additionally, the most important derivatives involved in this sensitivity formulation have been analytically obtained, including the mass matrix, generalized forces vector and constraint derivatives.

An important effort has been devoted to the efficient differentiation of natural coordinates due to its omnipresence in the derivatives of semi-recursive expressions. As a result, a set of expressions independent of the reference point selection have been developed. Furthermore, the case of a local coordinate of a point as a parameter has been studied, delivering a set of straightforward derivatives founded on the topology of the system.

Moreover, the semi-recursive ALI3-P forward sensitivity formulations for RTdyn0 and RTdyn1 have been tested in two numerical experiments. The semi-recursive sensitivity formulations have displayed excellent behaviour in terms of accuracy in the five-bar experiment, but they have showed worse efficiency than global methods. However, the two maneuvers executed with the buggy vehicle have proved that semi-recursive sensitivity formulations are well suited for branched multibody systems involving several bodies. In these maneuvers, the semi-recursive ALI3-P sensitivity formulations have required less computational effort than the equivalent global formulation.

Apart from the sensitivity formulation presented, the developments referred to derivatives of semi-recursive terms (i.e. mass matrix, generalized forces vector and constraints derivatives) are described in detail in order to establish the foundations for other semi-recursive constrained multibody sensitivity formulations.

Appendices

Appendix A: Derivatives of the mass matrix of a body

In a general formulation for any reference point, the body mass matrix can be expressed as the product of a mass matrix referred to the center of mass by a correction matrix ${\mathbf{D}}_{i}^{\mathrm{v}}$ (see [24]):

$$ {\mathbf{M}}_{i}^{\mathrm{v}} = \left ({\mathbf{D}}_{i}^{\mathrm{v}}\right )^{\mathrm{T}} { \mathbf{M}}_{i}^{\mathrm{y}} {\mathbf{D}}_{i}^{\mathrm{v}}, \hspace{0.3cm} \text{with} \ {\mathbf{D}}_{i}^{\mathrm{v}} = \begin{bmatrix} {\mathbf{I}} & {\tilde{\mathbf{r}}}_{i} - {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \\ {\mathbf{0}} & {\mathbf{I}} \end{bmatrix} {,} $$

(75)

with ${\mathbf{r}}_{i}$ being the position of the reference point of body $i$ and ${\mathbf{r}}_{\mathrm{G}}^{i}$ its centre of mass.

Applying the chain rule for differentiation, the multi-dimensional matrix $\Bigl( {\mathbf{M}}_{i}^{\mathrm{v}} \Bigr)_{\hat{\mathbf{z}}} \in \mathbb{R}^{6 \times 6 \times n}$, the result of the application of the differentiation rule (1) to the mass matrix with respect to the relative coordinates, can be calculated as

$$ \begin{aligned} \Bigl( {\mathbf{M}}_{i}^{\mathrm{v}} \Bigr)_{\hat{\mathbf{z}}} =m_{i} \left ( \Bigl( {\mathbf{D}}_{i}^{\mathrm{v{\mathrm{T}}}} \Bigr)_{\hat{\mathbf{z}}} {\mathbf{D}}_{i}^{ \mathrm{v}} + \left ({\mathbf{D}}_{i}^{\mathrm{v}}\right )^{\mathrm{T}} \Bigl({\mathbf{D}}_{i}^{ \mathrm{v}} \Bigr)_{\hat{\mathbf{z}}} \right ) + \begin{bmatrix} {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & \Bigl( {\mathbf{J}}_{i}^{\mathrm{G}} \Bigr)_{\hat{\mathbf{z}}} \end{bmatrix}{,} \end{aligned} $$

(76)

with $m_{i} \in \mathbb{R}^{1}$ being the mass of body $i$ and ${\mathbf{J}}_{i}^{\mathrm{G}} \in \mathbb{R}^{3 \times 3}$ its inertia tensor referred to its centre of mass.

Considering now the differentiation with respect of the parameters of the system, the multi-dimensional matrix $\Bigl( {\mathbf{M}}_{i}^{\mathrm{v}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} \in \mathbb{R}^{6 \times 6 \times p}$ takes the form

$$ \begin{aligned} \Bigl( {\mathbf{M}}_{i}^{\mathrm{v}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} = \dfrac{\partial m_{i}}{\partial \boldsymbol{\rho} } \left ( \left ({\mathbf{D}}_{i}^{ \mathrm{v}}\right )^{\mathrm{T}} {\mathbf{D}}_{i}^{\mathrm{v}} \right ) + m_{i} \left ( \Bigl( {\mathbf{D}}_{i}^{\mathrm{v{\mathrm{T}}}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} {\mathbf{D}}_{i}^{ \mathrm{v}} + \left ({\mathbf{D}}_{i}^{\mathrm{v}}\right )^{\mathrm{T}} \Bigl( {\mathbf{D}}_{i}^{ \mathrm{v}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} \right ) + \begin{bmatrix} {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & \Bigl( {\mathbf{J}}_{i}^{\mathrm{G}} \Bigr)_{{\hat{\boldsymbol{\rho} }}} \end{bmatrix}{.} \end{aligned} $$

(77)

The previous expressions can be applied to RTdyn0 and RTdyn1 (see [24]). First, for the RTdyn0 approach, with the centre of mass of each body as a reference point, the following simplifications apply: ${\mathbf{D}}_{i}^{\mathrm{y}}={\mathbf{I}}$, $\left ( {\mathbf{D}}_{i}^{\mathrm{y}} \right )_{ \hat{\mathbf{z}}}={\mathbf{0}}$ and $\left ( {\mathbf{D}}_{i}^{\mathrm{y}} \right )_{{\hat{\boldsymbol{\rho} }}}={\mathbf{0}}$. For the RTdyn1 approach, the following simplifications can be considered: ${\mathbf{B}}_{i}^{\mathrm{z}}={\mathbf{I}}$, $\left ( {\mathbf{B}}_{i}^{\mathrm{z}} \right )_{ \hat{\mathbf{z}}}={\mathbf{0}}$ and $\left ( {\mathbf{B}}_{i}^{\mathrm{z}} \right )_{{\hat{\boldsymbol{\rho} }}}={\mathbf{0}}$. The substitution in (21), (76) and (77) is straightforward, and for brevity omitted.

Appendix B: Equivalent stiffness matrix for RTdyn0 and RTdyn1

First, let us consider the RTdyn0 formulation. Substituting the reference point of this formulation into (29a)–(29c) yields

$$\begin{aligned} {\mathbf{K}}_{i}^{\mathrm{y}} &=-\Bigl({\mathbf{Q}}_{i}^{\mathrm{y}} \Bigr)_{\hat{\mathbf{z}}}= \displaystyle \sum _{j=1}^{{n_{f}^{i}}} {\mathbf{K}}_{i,j}^{\mathrm{y (e)}} + {{ \mathbf{K}}_{i}^{\mathrm{y}}}^{\mathrm{(I)}}{,} \end{aligned}$$

(78a)

$$\begin{aligned} {\mathbf{K}}_{i,j}^{\mathrm{y (e)}}&= \begin{bmatrix} -\Bigl( {\mathbf{f}}_{j} \Bigr)_{\hat{\mathbf{z}}} \\ {\tilde{\mathbf{f}}}_{j} \begin{bmatrix} {\mathbf{0}} & {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} - {\tilde{\mathbf{r}}}_{j} \end{bmatrix}{\mathbf{R}}_{i}^{\mathrm{y}} -\Bigl( {\mathbf{n}}_{j}^{\mathrm{G}} \Bigr)_{ \hat{\mathbf{z}}} + \left ( {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} - {\tilde{\mathbf{r}}}_{j} \right ) \Bigl( {\mathbf{f}}_{j} \Bigr)_{\hat{\mathbf{z}}} \end{bmatrix}{,} \end{aligned}$$

(78b)

$$\begin{aligned} {{\mathbf{K}}_{i}^{\mathrm{y}}}^{\mathrm{(I)}}&= \begin{bmatrix} {\mathbf{0}} \\ \left ( \tilde{{\boldsymbol{\omega} }_{i}}{\mathbf{J}}_{i}^{\mathrm{G}} - \widetilde{{ \mathbf{J}}_{i}^{\mathrm{G}} {\boldsymbol{\omega} }_{i}} \right ) \Bigl( {{\boldsymbol{\omega} }_{i}} \Bigr)_{\hat{\mathbf{z}}} +\tilde{{\boldsymbol{\omega} }_{i}} \Bigl( {\mathbf{J}}_{i}^{ \mathrm{G}} \Bigr)_{\hat{\mathbf{z}}} {\boldsymbol{\omega} }_{i} \end{bmatrix}{.} \end{aligned}$$

(78c)

The term of inertia ${{\mathbf{K}}_{i}^{\mathrm{y}}}^{\mathrm{(I)}}$ is substantially simpler than (29a)–(29c), which reduces the implementation effort. The assembly equations (25a) and (25b) can be directly applied to this method.

In RTdyn1, the composition of the stiffness matrix is slightly different since $\left ( {\mathbf{r}}_{0}^{i} \right )_{\hat{\mathbf{z}}} \neq \left ( { \dot{\mathbf{r}}}_{0}^{i} \right )_{\hat{\dot{\mathbf{z}}}}$:

$$\begin{aligned} {\mathbf{K}}_{i}^{\mathrm{z}} &=-\Bigl( {\mathbf{Q}}_{i}^{\mathrm{z}} \Bigr)_{\hat{\mathbf{z}}}= \displaystyle \sum _{j=1}^{{n_{f}^{i}}} {\mathbf{K}}_{i,j}^{\mathrm{z(e)}} + {{ \mathbf{K}}_{i}^{\mathrm{z}}}^{\mathrm{(I)}}{,} \end{aligned}$$

(79a)

$$\begin{aligned} {\mathbf{K}}_{i,j}^{\mathrm{z (e)}}&= \begin{bmatrix} -\Bigl( {\mathbf{f}}_{j} \Bigr)_{\hat{\mathbf{z}}} \\ {\tilde{\mathbf{f}}}_{j} \begin{bmatrix} {\mathbf{I}} & -{\tilde{\mathbf{r}}}_{j} \end{bmatrix}{\mathbf{R}}_{i}^{\mathrm{z}} - \Bigl( {\mathbf{n}}_{j}^{\mathrm{G}} \Bigr)_{ \hat{\mathbf{z}}} -{\tilde{\mathbf{r}}}_{j} \Bigl( {\mathbf{f}}_{j} \Bigr)_{ \hat{\mathbf{z}}} \end{bmatrix}{,} \end{aligned}$$

(79b)

$$\begin{aligned} {{\mathbf{K}}_{i}^{\mathrm{z}}}^{\mathrm{(I)}}&= \begin{bmatrix} {\mathbf{t}}_{\hat{\mathbf{z}}} \\ {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} {\mathbf{t}}_{\hat{\mathbf{z}}}+ \tilde{\mathbf{t}} \begin{bmatrix} -{\mathbf{I}} & {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \end{bmatrix} {\mathbf{R}}_{i}^{\mathrm{z}} + \left ( \tilde{{\boldsymbol{\omega} }_{i}}{ \mathbf{J}}_{i}^{\mathrm{G}} - \widetilde{{\mathbf{J}}_{i}^{\mathrm{G}} {\boldsymbol{\omega} }_{i}} \right ) \Bigl( {{\boldsymbol{\omega} }_{i}} \Bigr)_{\hat{\mathbf{z}}} + \tilde{{\boldsymbol{\omega} }_{i}} \Bigl( {\mathbf{J}}_{i}^{\mathrm{G}} \Bigr)_{ \hat{\mathbf{z}}} {\boldsymbol{\omega} }_{i} \end{bmatrix} {,} \end{aligned}$$

(79c)

$$\begin{aligned} {\mathbf{t}}&=m_{i} {\tilde{\boldsymbol{\omega} }}_{i} \left ( {\tilde{\boldsymbol{\omega} }}_{i} {\mathbf{r}}_{\mathrm{G}}^{i} \right ) {,} \end{aligned}$$

(79d)

$$\begin{aligned} {\mathbf{t}}_{\hat{\mathbf{z}}}&=m_{i} \tilde{{\boldsymbol{\omega} }_{i}} \tilde{{\boldsymbol{\omega} }_{i}} \begin{bmatrix} {\mathbf{I}} & -{\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \end{bmatrix} {\mathbf{R}}_{i}^{\mathrm{z}} - m_{i} \left ( \widetilde{ \tilde{{\boldsymbol{\omega} }_{i}}{\mathbf{r}}_{\mathrm{G}}^{i}}+ \tilde{{\boldsymbol{\omega} }_{i}}{\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \right ) \Bigl( {{ \boldsymbol{\omega} }_{i}} \Bigr)_{\hat{\mathbf{z}}} {.} \end{aligned}$$

(79e)

The application of the relation ${\mathbf{B}}_{i}^{\mathrm{z}}={\mathbf{I}}$, coming from the definition of the RTdyn1 approach, to the assembly equations of the stiffness matrix (25a) and (25b) brings about important simplifications:

$$\begin{aligned} {\mathbf{K}}_{i} &= {\mathbf{b}}_{i}^{\mathrm{z{\mathrm{T}}}} {\mathbf{K}}_{i}^{\mathrm{z}\Sigma } - \Bigl( {\mathbf{b}}_{i}^{\mathrm{z{\mathrm{T}}}} \Bigr)_{\hat{\mathbf{z}}} {\mathbf{Q}}_{i}^{ \mathrm{z}\Sigma }, \end{aligned}$$

(80a)

$$\begin{aligned} {\mathbf{K}}_{i}^{\mathrm{z}\Sigma } &= {\mathbf{K}}_{i}^{\mathrm{z}} + \Bigl( {\mathbf{M}}_{i}^{ \mathrm{z}} \Bigr)_{\hat{\mathbf{z}}} {\mathbf{d}}_{i}^{\mathrm{z}\Sigma } + {\mathbf{M}}_{i}^{ \mathrm{z}} \Bigl( {\mathbf{d}}_{i}^{\mathrm{z}\Sigma } \Bigr)_{\hat{\mathbf{z}}} + \sum _{s=1}^{{n_{s}^{i}}}{} {\mathbf{K}}_{s}^{\mathrm{z}\Sigma }. \end{aligned}$$

(80b)

Appendix C: Equivalent damping matrix for RTdyn0 and RTdyn1

Considering the centre of mass of each body as reference point (RTdyn0), the damping matrix can be formulated as follows:

$$\begin{aligned} {\mathbf{C}}_{i}^{\mathrm{y}} &=-\Bigl( {\mathbf{Q}}_{i}^{\mathrm{y}} \Bigr)_{ \hat{\dot{\mathbf{z}}}}=\displaystyle \sum _{j=1}^{{n_{f}^{i}}}{\mathbf{C}}_{i,j}^{ \mathrm{y (e)}} + {{\mathbf{C}}_{i}^{\mathrm{y}}}^{\mathrm{(I)}}{,} \end{aligned}$$

(81a)

$$\begin{aligned} {\mathbf{C}}_{i,j}^{\mathrm{y (e)}}&= - \begin{bmatrix} \mathbf{{I} }\\ {\tilde{\mathbf{r}}}_{j}- {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \end{bmatrix}\Bigl( {\mathbf{f}}_{j} \Bigr)_{\hat{\mathbf{z}}} - \begin{bmatrix} \mathbf{{0} }\\ \Bigl( {\mathbf{n}}_{j}^{\mathrm{G}} \Bigr)_{\hat{\mathbf{z}}} \end{bmatrix} \; , \quad {{\mathbf{C}}_{i}^{\mathrm{y}}}^{\mathrm{(I)}}= \begin{bmatrix} {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & \tilde{{\boldsymbol{\omega} }_{i}}{\mathbf{J}}_{i}^{\mathrm{G}} - \widetilde{{ \mathbf{J}}_{i}^{\mathrm{G}} {\boldsymbol{\omega} }_{i}} \end{bmatrix}{\mathbf{R}}_{i}^{\mathrm{y}}. \end{aligned}$$

(81b)

In analogy to what happens with the stiffness matrix, the elemental damping matrices related to the inertial terms are simplified, while the other terms and assemblies (31a) and (31b) remain unaltered.

In the RTdyn1 approach, the corresponding equations are:

$$\begin{aligned} {\mathbf{C}}_{i}^{\mathrm{z}} &=-\Bigl( {\mathbf{Q}}_{i}^{\mathrm{z}} \Bigr)_{ \hat{\dot{\mathbf{z}}}}=\displaystyle \sum _{j=1}^{{n_{f}^{i}}}{\mathbf{C}}_{i,j}^{ \mathrm{z (e)}} + {{\mathbf{C}}_{i}^{\mathrm{z}}}^{\mathrm{(I)}}{,} \end{aligned}$$

(82a)

$$\begin{aligned} {\mathbf{C}}_{i,j}^{\mathrm{z (e)}}&= - \begin{bmatrix} \mathbf{{I} }\\ {\tilde{\mathbf{r}}}_{j} \end{bmatrix}\Bigl( {\mathbf{f}}_{j} \Bigr)_{\hat{\mathbf{z}}} - \begin{bmatrix} \mathbf{{0} }\\ \Bigl( {\mathbf{n}}_{j}^{\mathrm{G}} \Bigr)_{\hat{\mathbf{z}}} \end{bmatrix} {,} \end{aligned}$$

(82b)

$$\begin{aligned} {{\mathbf{C}}_{i}^{\mathrm{z}}}^{\mathrm{(I)}}&= \begin{bmatrix} {\mathbf{0}} & {-} m_{i} \left ( \widetilde{\tilde{{\boldsymbol{\omega} }_{i}}{\mathbf{r}}_{ \mathrm{G}}^{i}}+\tilde{{\boldsymbol{\omega} }_{i}}{\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \right ) \\ {\mathbf{0}} & \tilde{{\boldsymbol{\omega} }_{i}}{\mathbf{J}}_{i}^{\mathrm{G}} - \widetilde{{ \mathbf{J}}_{i}^{\mathrm{G}} {\boldsymbol{\omega} }_{i}} {-}m_{i} {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i} \left (\widetilde{\tilde{{\boldsymbol{\omega} }_{i}}{\mathbf{r}}_{\mathrm{G}}^{i}}+ \tilde{{\boldsymbol{\omega} }_{i}} {\tilde{\mathbf{r}}}_{\mathrm{G}}^{i}\right ) \end{bmatrix}{\mathbf{R}}_{i}^{\mathrm{z}}{.} \end{aligned}$$

(82c)

In this case, the assembly is also simplified:

$$ {\mathbf{C}}_{i} = {\mathbf{b}}_{i}^{\mathrm{z{\mathrm{T}}}} {\mathbf{C}}_{i}^{\mathrm{z}\Sigma }\; , \quad {\mathbf{C}}_{i}^{\mathrm{z}\Sigma } = {\mathbf{C}}_{i}^{\mathrm{z}} + {\mathbf{M}}_{i}^{\mathrm{z}} \Bigl( {\mathbf{d}}_{i}^{\mathrm{z}\Sigma } \Bigr)_{\hat{\dot{\mathbf{z}}}} + \sum _{s=1}^{{n_{s}^{i}}}{} {\mathbf{C}}_{s}^{\mathrm{z}\Sigma }{.} $$

(83)

Appendix D: Summary of kinematic joints considered

The main kinematic relations of the kinematic joints considered in this work are summarize in Table 11.

Table 11 Summary of kinematic joints

Appendix E: Evaluation of ${\left ({\mathbf{b}}_{i}^{\mathrm{v}}\right )}_{\hat{\mathbf{z}}}$ for RTdyn0 and RTdyn1

The derivatives are presented in Table 12 for RTdyn0 and Table 13 for RTdyn1.

Table 12 Derivatives of ${\mathbf{b}}_{i}^{\mathrm{y}}$ with respect to relative coordinates for RTdyn0

Table 13 Derivatives of ${\mathbf{b}}_{i}^{\mathrm{z}}$ with respect to relative coordinates for RTdyn1