Improving neural network’s robustness on tabular data with D-layers

Abstract

Artificial neural networks (${{{\texttt {ANN}}}}$) are widely used machine learning models. Their widespread use has attracted a lot of interest in their robustness. Many studies show that ANN’s performance can be highly vulnerable to input manipulation such as adversarial attacks and covariate drift. Therefore, various techniques that focus on improving ${{{\texttt {ANN}}}}$’s robustness have been proposed in the last few years. However, most of these works have mostly focused on image data. In this paper, we investigate the role of discretization in improving ${{{\texttt {ANN}}}}$’s robustness on tabular datasets. Two custom ${{{\texttt {ANN}}}}$ layers– D1-Layer and D2-Layer (collectively called D-Layers) are proposed. The two layers integrate discretization during the training phase to improve ${{{\texttt {ANN}}}}$’s ability to defend against adversarial attacks. Additionally, D2-Layer integrates dynamic discretization during testing phase as well, to provide a unified strategy to handle adversarial attacks and covariate drift. The experimental results on 24 publicly available datasets show that our proposed D-Layers add much-needed robustness to ${{{\texttt {ANN}}}}$ for tabular datasets.

1 Introduction

The widespread use of ${{{\texttt {ANN}}}}$ models has attracted a lot of interest in their robustness (Goodfellow et al. 2014; Kurakin et al. 2017). Typically, one measure of ANN’s robustness is to see whether it can maintain performance with the changes in input data. These changes can be driven by either malicious or benign intent. An example of malicious intent change is adversarial attacks that manipulate input data to sway the model output towards a desirable outcome (Akhtar and Mian 2018). An example of benign intent change is data variation over time due to covariate drift. With the ever-changing facet of adversarial attack methods and datasets drifting over time, how to add robustness to ${{{\texttt {ANN}}}}$ on tabular datasets remains an open, yet fundamental question. This work is motivated to address the issue of robustness in ${{{\texttt {ANN}}}}$ models by proposing new novel layers in standard ${{{\texttt {ANN}}}}$ architecture.

Traditionally, adversarial attacks constitute imperceptible perturbations on the input image to control ${{{\texttt {ANN}}}}$’s output. Many studies have demonstrated that the perturbed images that fail one model can also fail other models trained on different datasets with different architectures (Goodfellow et al. 2014), highlighting the severity of the problem. In the past few years, plenty of research efforts have been exerted in designing appropriate defence mechanisms for ANNmodels on image datasets (Kurakin et al. 2017; Shafahi et al. 2019). However, image datasets are not the only datasets susceptible to adversarial attacks. Tabular datasets that are commonly used in various ${{{\texttt {ANN}}}}$ applications domains such as finance and medicine are as vulnerable to adversarial attacks as image datasets (Cartella et al. 2021). Tabular datasets have one trait, i.e., the presence of categorical features that can serve as a natural defence against adversarial attacks, as the adversarial perturbations on categorical features can be easily observed. For instance, in a loan approval scenario, the level-of-education is bachelor, master, and doctorate (normally represented as integers like 1, 2, and 3), it is easy for bank managers to find the fraudulent modification when a customer modifies her education level from 2 to 2.5 or from 3 to 4, to obtain a loan. However, numeric features in tabular datasets are as vulnerable to adversarial attacks as pixel values in images (Cartella et al. 2021). Considering the natural defence capability of categorical features, recently, various discretization-based defence methods have been proposed (Buckman et al. 2018).

Covariate drift which informally refers to the situation where testing distribution is different from training distribution can also adversely affect ${{{\texttt {ANN}}}}$ models’ performance (Nado et al. 2020). Several studies in domain adaptation and causal inference aim to tackle the covariate drift issue by taking advantage of the information on testing distribution (Magliacane et al. 2017). Discretization can serve as a natural defence against some forms of covariate drifts as well. For example, if the Salary feature (at the training time) is discretized with equal frequency discretization into three bins {A, B, C}—even with covariate drift resulting in the monotonic transformation of the testing data—discretization on the transformed Salary feature (at the testing time) can result in a similar allocation of the bins.

Given the pivotal role that discretization can play as a defence mechanism against adversarial attacks and covariate drift, there is a need to integrate discretization into ${{{\texttt {ANN}}}}$’s models for increasing their robustness. In this work, we propose two customized new layers for ${{{\texttt {ANN}}}}$ – named D1-Layer ‘Discretization’) and D2-Layer (‘Dynamic Discretization’)—collectively called D-Layers, to address this need. The main motivations of these two layers are:

• Existing discretization-based adversarial attack defence methods (Buckman et al. 2018; Zhou et al. 2022) normally discretize data prior to training the model. Despite their effectiveness, if some part of the training data is changed (e.g., as part of adversarial training), the discretization results will be incorrect, as the discretization boundaries are learned beforehand. Furthermore, any time the model is to be re-trained requires re-discretizing the dataset. The seamless integration of discretization in ANN(during model training) and exploiting its benefits is the main motivation for our proposed D-Layers.

• Once the model is trained, there is no way to update the discretization boundaries. However, if the distribution of testing data is changed due to covariate drift or adversarial attack, there is a strong need to update discretization boundaries to accommodate this distribution change. In other words, we need dynamic discretization at the testing phase to resist potential distribution changes caused by covariate drift or adversarial attack. The seamless integration of such dynamic discretization in ANN(during model testing) is the main motivation for our proposed D2-Layer.

The main contributions of this paper are:

• We have proposed two new layers for adding robustness to ${{{\texttt {ANN}}}}$ models. Specifically, D1-Layer integrates discretization during the training phase to improve ${{{\texttt {ANN}}}}$’s ability to defend against adversarial attacks. Whereas, D2-Layer integrates discretization during the training phase, as well as during the testing phase to provide a unified strategy for ${{{\texttt {ANN}}}}$ to handle covariate drift and adversarial attacks.

• We demonstrate that our proposed D1-Layer lead to the state-of-the-art (SOTA) defence mechanism against a range of standard attacks on various publicly available tabular datasets.

• We demonstrate that our proposed D2-Layer offers an effective unified strategy to address adversarial attacks and covariate drift at the same time.

The rest of this paper is organized as follows. In Sect. 2, we review the related works. In Sect. 3, we present our proposed formulations namely D-Layers. Section 4 provides an empirical evaluation of our proposed formulations. In Sect. 5, we conclude the paper with pointers to future works.

2 Related work

2.1 Adversarial attack methods

To highlight the robustness of ${{{\texttt {ANN}}}}$ models, a large number of adversarial attack models have been proposed in the literature in the past few years. Broadly, these existing adversarial attack models can be divided into white-box attack models and black-box attack models (Kumová and Pilát 2021). Attack models that require access to information of the original ${{{\texttt {ANN}}}}$ model such as parameters, gradient, or structure to conduct attacks are referred to as white-box attack models, otherwise black-box attack models (Huang et al. 2020). Our study focuses on white-box attack models and hence we will mainly review popular white-box attack models. A more comprehensive literature review can be found in (Kong et al. 2021; Huang et al. 2020).

FGSM (Fast Gradient Sign Method) (Goodfellow et al. 2014) is the most classic white-box attack model for both image and tabular data. It creates adversarial samples by adding gradients to the original instance. FGSM is easy to implement but normally has a relatively low success rate, as the adversarial samples created by adding gradient may be insufficient to cross the decision boundary (Shafahi et al. 2019). A direct extension of FGSM is BIM (Basic Iterative Method) which iteratively conduct FGSM multiple times with a small step size to achieve better attack performance (Kurakin et al. 2016). PGD (Projected Gradient Descent) is also a popular white-box attack model built on top of  FGSM (Madry et al. 2017). Different from BIM that directly iteratively conducts FGSM from the original sample, PGD initializes the start of the adversarial attack from a random distribution to add variations to the attack to further improve the attack’s success rate.

Another popular white-box attack model is DeepFool (Moosavi-Dezfooli et al. 2016). It works by iteratively linearizing the model to generate unperceivable adversarial examples. Compared with other gradient-based white-box attack models, DeepFool is more efficient as it can always generate adversarial examples that are close to the decision boundary. LowProFool is the state-of-the-art white-box attack model on tabular data (Ballet et al. 2019). It induces parameter updates toward the targeted class by utilizing the gradient of adversarial noise. The importance weights of features are evaluated to ensure large perturbations only exist on irrelevant or less important features, such that the generated examples are imperceptible to expert scrutiny.

2.2 Adversarial defence methods

Madry et al. (2017) is the most straightforward defence method—it takes advantage of adversarial training to minimize models’ adversarial risk to defend against adversarial attacks. Despite its effectiveness, one critical issue of this adversarial-training-based defence model is overfitting to attacks that generate adversarial samples (Kurakin et al. 2017). For example, the models that were adversarially trained to resist FGSM frequently failed to resist L-BFGS and BIM attacks. Thereby, recent studies have started to advocate input discretization as the defence mechanism. Thermometer encoding (Buckman et al. 2018) is one of the most popular discretization-based defence models as it defends against adversarial attacks by discretizing the numeric inputs to [0, 1] vectors. For example, discretizes 0.23 to [0, 0, 1, 1, 1, 1, 1, 1, 1, 1], 0.34 to [0, 0, 0, 1, 1, 1, 1, 1, 1, 1], etc. Thermometer’s formulation is very similar to one-hot encoding, but it can preserve the order of input after discretization, thus having better performance than one-hot encoding. In the context of deep ANN models implemented via Keras,¹ one can utilize Keras discretization layer.² It offers another method to discretize neural network input. It is important to note that unlike other discretization methods which are feature-based (i.e., different cut-points are learned for different features)—the discretization strategy in this layer learns one set of cut-points for all the features—i.e., data across all features is used to compute the quantiles—which are later used as the cut-points to discretize. Little efforts have been made to investigate the effectiveness of keras discretization layer in defending against adversarial attacks. We will explore this direction together by proposing two discretization-inspired algorithms in this work.

D2A3 and D2A3N (Zhou et al. 2022) are state-of-the-art defence models on tabular data. D2A3 defends against adversarial attacks by exploiting both input discretization and adversarial training. In D2A3, the numeric input features are discretized to train a discretized model—this model is then improved by taking advantage of adversarial training. The main limitation of D2A3 is the requirement for accessing input data and changing it from numeric to discrete, which may be impossible in many application scenarios. In D2A3N, the numerical input features are discretized by the cut-points directly learned from the training data—data close to cut-points are considered adversarial samples and are replaced by the median of the bin to defend against adversarial attacks. Although these existing studies demonstrated the effectiveness of input discretization as a defence mechanism against tabular data adversarial attacks, their performance can be further improved by integrating flexible within model cut-points learning strategies as well as dynamic discretization—strategies that we will study in this work. Note, D2A3 and D2A3N are state-of-the-art adversarial defence approaches in the context of deep ANN. Therefore, we will consider these approaches as the baseline when comparing the adversarial defence capability of the proposed methods in this work. The main advantage of our proposed D-Layers over D2A3 and its variant is that the defence mechanism does not include adversarial training. Secondly, and importantly, our proposed method integrates discretization in the learning of an ANN model, unlike a pre-discretization strategy of D2A3. We will discuss in the following, that this trait is one of the reasons for the superior performance of D-Layers. One limitation of our proposed approach in handling covariate drift is its inability to handle non-monotonic transformations (or drifts). This is because, as we will also discuss below, D-Layers are based on equal frequency discretization, and hence assumes that order is preserved during the drift. However, if the order is not preserved, our proposed layers will not be effective. We are working on how to handle non-monotonic drifts as well as concept drift as an extension of this research.

2.3 Covariate drift

Covariate drift also known as covariate shift represents a typical model drift scenario that occurs when the distribution of the testing data is different from the training data (Sugiyama et al. 2007). In covariate drift, the distribution change only lies in the input features, whilst the labels of testing data remain the same (Bickel et al. 2009). The case in which the labels of the testing data change as well is called concept drift (Gama et al. 2014)—which is outside the scope of this work. Covariate drift can significantly compromise the performance of a well-trained ${{{\texttt {ANN}}}}$, therefore, a bunch of studies on domain adaptation (Chen et al. 2020) and transfer learning (Wang et al. 2019) have been conducted to address the covariate drift problem through the alignment of training and testing distributions (Wilson and Cook 2020). For example, (Gretton et al. 2009) proposed a kernel mean matching-based method to match the training and testing distributions by reweighting the training distribution in a reproducing kernel Hilbert space. Li et al. (2020) proposed an important weighting method for addressing the covariate drift by reweighting the residuals of kernel mean matching and non-parametric regression. Zhang et al. (2020) proposed a strategy that learns the weights required to address covariate shifts in only one step. Pathak et al. (2022) proposed a new measurement to measure the distribution mismatch between training and testing data based on the integrated ratio of probabilities of balls at a given radius, and demonstrated its effectiveness in addressing covariate drift in non-parametric regression. The main limitation of these approaches is the dependence on the prior knowledge of testing data that is not always available at the training stage (Nair et al. 2019). Although some recent studies on causal inference have tackled this issue by utilizing the stability of causal graphs (Yu et al. 2020), the proposed models are complicated due to the difficulty of capturing causal relations in the data. This paper will show that simple input discretization can be an effective method to handle some forms of covariate drift, i.e., monotonic covariate drift.

Covariate and concept drift have been widely studied in machine learning, however, most of this work aims to develop models that have a built-in mechanism to handle either concept or covariate drift, e.g., Pfahringer et al. (2007); Bifet and Gavaldà (2009), Oza and Russell (2001). Our work, in this paper, is different from various existing works, as we specifically are interested to address covariate drift in deep ANN models. Therefore, we have not conducted a comparison with the existing concept or covariate drift method in this work, as it does not offer a meaningful comparison. We, however, are interested to do this analysis as part of future works for this research. Note, the baseline for measuring the effectiveness of our proposed method in handling covariate drift is a vanilla deep ANN model.

3 Methodology

In this section, we start by formulating the problem of robust ${{{\texttt {ANN}}}}$, followed by discussing the motivations for using discretization to improve ${{{\texttt {ANN}}}}$’s robustness. Later, we present in detail our proposed D1-Layer and D2-Layer.

3.1 Problem formulation

Definition 1

(Adversarial Attack on Tabular Data) Let $({\mathbb {X}}, {\mathbb {Y}}) = \{(X^1, Y^1), (X^2, Y^2),\ldots , (X^{n}, Y^{n})\}$ be a dataset with n samples, where ${\mathbb {X}}$ is defined by a set of features $j \in {\mathbb {J}}$, ${\mathbb {Y}} = [Y^1, Y^2,\ldots , Y^n]$ denotes the corresponding labels. Let $f: {\mathbb {R}}^D \rightarrow {\mathbb {Y}}$ be the trained ${{{\texttt {ANN}}}}$ model. For a given sample $(X^i, Y^i) \in ({\mathbb {X}}, {\mathbb {Y}})$, the adversarial attack aims to generate an adversarial sample $X^i_{\text {adv}} = (X^i +r^*)$ such that

$$\begin{aligned} \begin{aligned}&f(X^i_{\text {adv}}) = Y^t \ne f(X^i)= Y^i \\&\text {s.t.} \ X^i_{\text {adv}} \in {\mathbb {R}}^D \ \text {and} \ r^* = \arg \min _r d(r), \end{aligned} \end{aligned}$$

(1)

where $Y^t$ is the target label, $d(r) = \Vert r \Vert _p$ is the perceptibility value that indicates the quantity of the changes in $X^i$ after adding adversarial perturbation r. $r^*$ is perturbation r that achieves minimum d(r).

Definition 2

(Covariate Drift) For a model $f: {\mathbb {X}} \rightarrow {\mathbb {Y}}$ covariate drift refers to the case where $P_{\text {train}} (Y \mid X) = P_{\text {test}} (Y \mid X)$, while $P_{\text {train}} (X) \ne P_{\text {test}} (X)$.

Here, $P_{\text {train}}(X)$ is the distribution of the training data (without labels), $P_{\text {test}}(X)$ is the distribution of the testing data (without labels), $P_{\text {train}} (Y \mid X)$ is the conditional distribution of training data, and $P_{\text {test}} (Y \mid X)$ is the conditional distribution of testing data.

Given Definitions 1 and 2, we have the following definition for robust ${{{\texttt {ANN}}}}$:

Definition 3

(Robust ${{{\texttt {ANN}}}}$) For a model $f: {\mathbb {X}} \rightarrow {\mathbb {Y}}$ trained on the training dataset ${\mathcal {S}}_{\text {data-train}} = ({\mathbb {X}}, {\mathbb {Y}})$, suppose its performance on the testing dataset ${\mathcal {S}}_{\text {data-test}}$ is $D\%$. For a perturbed dataset $\tilde{{\mathcal {S}}}_{\text {data-test}}$ (based on Definitions 1 and 2), f is robust if its performance on $\tilde{{\mathcal {S}}}_{\text {data-test}}$ is not less than $D\%-\delta$, where $\delta$ is a user-specified confidence interval.

We will make use of this definition to evaluate (and compare) the effectiveness of our proposed formulations.

3.2 Rationales

Discretization is performed by sorting the data and separating the numeric features into different bins according to the learned cut-points (also known as discretization boundaries).³

Fig. 1

Rationale of discretization-based defence models

Figure 1 demonstrates the rationale of discretization-based adversarial attack defence methods. As shown in Fig. 1a, in the original numeric feature space, there is no way to differentiate adversarial example $x_{\text {adv}}$ and other data. However, after discretization, the numeric features will be separated into different bins according to specific cut-points (see Fig. 1b). The bin number (e.g., 1, 2, 3, 4) or the median/mean of bin values will be used to train the ${{{\texttt {ANN}}}}$ models. It can be seen that after discretization the adversarial example $x_{\text {adv}}$ has been scaled back to a value that is expected by ${{{\texttt {ANN}}}}$ (in our example, they are 1, 2, 3, 4). That means, whatever the attacker’s intent was, discretization is able to convert adversarial samples back to the values that have a consistent format with training samples. The efficacy of this approach depends on the number of discretized values that cross the bin boundaries. For example, if $x_{\text {adv}}$ in Fig. 1b moves to the right of $\delta _3$—its discretized value will be incorrect (see Fig. 2a), thereby leading to performance degradation. Furthermore, as shown in Fig. 2b, a small drift of the data on the x-axis (covariate drift) will result in many data points being assigned to the wrong bins or even invalid bins. Based on this analysis, the following observations can be drawn:

• 1. Pre-discretizing the data is not an effective defence strategy,⁴ as the pre-learned cut-points are learned on original data, and are static.

  Every time data is modified, we must re-compute the cut-points and re-train the model (which can be expensive), to make discretization work as a defence strategy. Note, we are assuming that we have access to some adversarial or drifted data at the training time. There is a need for cut-points to be adjusted based on updated data during the training—we will call this dynamic discretization.

  Our proposed D-Layers are aimed at incorporating dynamic discretization for adding robustness to the ${{{\texttt {ANN}}}}$ model.

• 2. Cut-points should be dynamically updated from the data even during the testing time. If the data distribution is changed during the testing time (i.e., covariate drift), the cut-points should be changed accordingly to accommodate the changes to maintain discretization accuracy. Similar to batch normalization (Ioffe and Szegedy 2015), our proposed D2-Layer aims to address this issue by taking advantage of the statistical information of testing data.

Fig. 2

Illustration of limitations of stationary cut-points in case of adversarial attack and covariate drift

3.3 D1-Layer

Let us start by formulating our problem. Ideally, we are interested in discretizing an input feature’s numeric value, in an ${{{\texttt {ANN}}}}$ model, i.e., a value say 23.5 is transformed into value say 3, based on some cut-points—$\delta _1, \ldots , \delta _k$. Our problem constitutes learning the cut-points in an end-to-end fashion, such that the whole process remains differentiable. For this, we have proposed a novel layer named D1-Layer, that does exactly that. The idea of D1-Layer is inspired by VQ-VAE (Vector Quantized Variational Auto-Encoder) that discretizes the encoder’s output via a codebook to improve the quality of image generation (Van Den Oord et al. 2017). In D1-Layer, we aim to learn a cut-point space. We denote this space as—${\mathcal {C}}$, also known as the codebook. This codebook will be used to discretize the input features. For example, the simplest way to discretize a data point is by doing a nearest neighbour search in the codebook, i.e., the input data is represented by the index of the nearest codebook vector.

The salient feature of D1-Layer is that it actually aims to learn the codebook space which is basically the representation of the cut-points, i.e., the cut-point $\delta _i$ is actually represented by a D-dimensional vector. The number of cut-points has to be specified in advance, e.g., if we have K cut-points, we have ${\mathcal {C}} \in {\mathbb {R}}^{K \times D}$. An issue that originates from enforcing the dimensions of the cut-point to be $1 \times D$, is the dimensionality mismatch between an input data feature (a scale) and the cut-point representation (a vector of size D). This renders the comparison between input data feature and codebook vector (or nearest neighbour search) invalid. D1-Layer utilizes three strategies to address this dimensionality mismatch.⁵ Let us discuss these strategies in the following.

3.3.1 Duplicate expansion search (DES)

The first strategy that D1-Layer employs is to duplicate the scalar value D-times to convert it into a D-dimensional vector. This is depicted in Fig. 3a. Let ${\mathcal {Z}}(\cdot )$ indicate an operator that takes a scalar value as input and returns a vector of size D. Formally, for the j-th feature of the data i, the duplicate expansion search can be defined as:

$$\begin{aligned} {\mathcal {Z}}(X_j^{i})= & {} \underbrace{[X_j^{i}, X_j^{i}, \ldots , X_j^{i}]}_{D}. \end{aligned}$$

3.3.2 Taylor series expansion search (TSES)

Considering simple duplication may have less variation on the input representations, D1-Layer also employs a Taylor series expansion of $\frac{1}{1-{X_j^{i}}}$ to expand the scalar value (as shown in Fig. 3b). Formally, the Taylor series expansion search can be defined as:

$$\begin{aligned} {\mathcal {Z}}(X_j^{i}) = [X_j^{i}, (X_j^{i} + {X_j^{i}}^2), \ldots (X_j^{i} + {X_j^{i}}^2 +\ldots + {X_j^{i}}^D)]. \end{aligned}$$

For simplicity, we ignored the constant 1 in the Taylor series expansion.

For DES and TSES, after aligning the dimensionality of input features and codebook, the nearest neighbor search can be defined as:

$$\begin{aligned} q(X_j^{i}) = \text {argmin}_k \; \Vert {\mathcal {Z}}(X^i_{j}) - {\mathcal {C}}_{k} \Vert _2. \end{aligned}$$

(2)

3.3.3 Direct cut-point search (DCS)

Other than expanding our input values to match the size of the cut-point space, one can also reduce the dimensionality of the cut-point space to match the input size. As shown in Fig. 3c, in DCS, we set the dimensionality of the cut-point space to $1 \times K$. The discretized value $q(X_j^{i})$ can then be determined as:

$$\begin{aligned} q(X_j^{i}) = \text {argmin}_k \; \Vert X_j^{i} - {\mathcal {C}}_{k} \Vert _2. \end{aligned}$$

(3)

3.3.4 Learning in D1-Layer

The output of D1-Layer is the discretized data— $q(X^{i}_{j})$, that is passed through to the next layer for further processing. The forward pass through D1-Layer can be seen as the clustering of the input feature values—the index of each cluster center served as the discretized value.

The main challenge in training D1-Layer is that Eq. (2) (or 3) is non-differentiable due to the presence of the $\text {argmin}$ operation. Similar to VQ-VAE, the simple gradient estimator strategy is adopted to address this issue (Bengio et al. 2013). That is, in the backward pass, gradients of the numeric representations are approximated by directly copying the gradient of the discretized representations (see Fig. 3). The loss function of our proposed D1-Layer-based ${{{\texttt {ANN}}}}$ is:

$$\begin{aligned} L = L_c(Y^{i}, X^{i}) + \sum _{j=1}^{\mid {\mathbb {J}} \mid }\Vert \textbf{sg}[Z(X^{i}_{j})] - {\mathcal {C}}_k \Vert ^2_2, \end{aligned}$$

(4)

where $L_c(Y^{i}, X^{i})$ represents the standard classification loss such as cross-entropy, MSE, etc. $\mid {\mathbb {J}}\mid$ represents the number of features, $\sum _{j=1}^{\mid {\mathbb {J}} \mid }\Vert \textbf{sg}[q(X^{i}_{j})] - {\mathcal {C}}_k \Vert ^2_2$ represents the codebook learning loss of data $X^i$, which directs the codebook embedding ${\mathcal {C}}_k$ toward the corresponding data value. Note, $\textbf{sg}[\cdot ]$ is the stop gradient operator that has zero partial derivatives.

We have summarized the learning process of D1-Layer-based ${{{\texttt {ANN}}}}$ in Algorithm 1. In the training phase, D1-Layer first discretizes the input data of each mini-batch—we denote discretized data as $q(X)_b$ (Algorithm 1, lines 1–12). Note, we provide algorithm for TSES representation. Discretized data $q(X)_b$ is then used in subsequent layers to train the network with parameters $\Theta$ and codebook ${\mathcal {C}}$ (Algorithm 1, lines 13–20). In the testing phase, the learned codebook ${\mathcal {C}}$ is used to discretize the input data, which is then fed into the network parameterized by parameter $\Theta$, for inference (Algorithm 1, lines 21–30).

Fig. 3

Illustration of the discretization in D1-Layer. The numeric input in each feature is discretized by the codebook. The gradient of discretized feature representation will be directly copied to the numeric feature representation in the backward pass (straight-through estimator)

3.4 D2-Layer

D1-Layer utilizes an objective function of the form of Eq. (4) to learn a representation of the cut-points. A simpler strategy could be to use the statistical information present in each mini-batch of the data and adjust cut-points accordingly. Our proposed D2-Layer does exactly that. It takes advantage of the statistical information of each mini-batch to dynamically update the cut-points (which can be applied at training as well as testing time).

Let ${\mathcal {B}} = [{\mathbb {X}}_{1},\ldots ,{\mathbb {X}}_{B}]$ represent a mini-batch of size B. D2-Layer sorts the data in each mini-batch and calculates the cut-points using Equal Frequency (EF) discretization. Other forms of discretization can be used, however, we argue that EF discretization has desirable properties that can lead to some robustness in the model.

Let $\Phi _{{\texttt {EF}}}({\mathbb {X}})$ represent a discretization function that returns a set of K cut-points (based on EF discretization), learned on mini-batch ${\mathbb {X}}$:

$$\begin{aligned} \Phi _{{\texttt {EF}}}({\mathbb {X}})&\sim [\delta _{1},\ldots ,\delta _{K}]. \end{aligned}$$

(5)

We have discretized value $q(X^{i}_{j}) = {\mathbb {O}}({\hat{\Phi }} (X^i_{j}))$. Here, ${\hat{\Phi }}(.)$ is the function that applies the learned cut-points $\Phi _{{\texttt {EF}}}({\mathbb {X}})$ to the data, and ${\mathbb {O}}(.)$ is the function that represents the discretized value, e.g., one-hot-encoding, bin-number, etc. The discretized value $q(X^{i}_{j})$ is then used in subsequent layers of ${{{\texttt {ANN}}}}$ to train the network. Let us discuss some salient features of D2-Layer:

• 1. The mean and variance of the output of the D2-Layer are guaranteed to be stationary and, therefore, the covariate drift can be largely eliminated (in cases where drift is due to monotonic transformation).

• 2. The discretization operator used in D2-Layer is not differentiable, hence, the gradient-based attacking for original input $X^{i}$ will not be effective. Thus providing a defence against many forms of adversarial attacks.

• 3. D2-Layer can be deployed at the testing time— i.e., the cut-points can be adjusted based on testing data distribution—making it perfect to address covariate drift even after the model is trained. Note, one can re-train a codebook in ${\texttt {D1-Layer}}$ at testing time, but this might not be effective, as learning a codebook representation of size $K \times D$ requires much larger data and hence larger size of the batch. On the contrary, D2-Layer makes use of simpler statistics from the data, which can be obtained from a few test data points.

We have summarized the learning of the D2-Layer-based ${{{\texttt {ANN}}}}$ at Algorithm 2.

In the training phase of D2-Layer, equal frequency discretization is used to learn the cut-points of each training batch (Algorithm 2, lines 1–12). The discretized values resulting from the learned cut-points are used to train the entire network (Algorithm 2, lines 13–20). The selection of feature-specific equal-frequency discretization is critical to the working of D2-Layer’s algorithm—i.e., in handling covariate drift, and in warding-off adversarial attack. As we mentioned earlier, Keras discretization layer also learns cut-points but based on the quantiles of the whole input data rather than separately for each feature. We will integrate this quantiles-based discretization strategy in D2-Layer and compare it with other forms of discretizations later in Sect. 4.

In the testing phase, different from D1-Layer and other existing defence methods that use cut-points learned from training data, D2-Layer uses equal frequency discretization to learn new cut-points from each testing batch to ensure the cut-points are suitable for testing data (Algorithm 2, lines 21–32). This dynamic discretization strategy makes sure that D2-Layer can handle distribution drifts during the testing phase.

4 Experiments

In this section, we start by presenting the details of our experimental settings followed by the results and detailed analysis.

4.1 Experimental settings

4.1.1 Datasets

We have used 24 classification datasets from UCI machine learning dataset repository.⁶ All of these datasets have more than 1000 samples. Of the considered datasets, there are 5 datasets with more than 100,000 samples and are denoted as Large, 9 datasets with between 10,000 and 100,000 samples and are denoted as Medium, 10 datasets with between 1000 and 10,000 samples and are denoted as Small. The statistics information of these datasets is shown in Table 1, where n, $m_{\text {n}}$, and $m_{\text {c}}$ represent the number of samples, numeric features, and categorical features individually.

Table 1 Statistic information of datasets

4.1.2 Baseline methods and evaluation metric

In terms of adversarial attacks, three of the most commonly used white-box attack models, namely, FGSM, DeepFool (DPF), and LowProFool (LPF) have been adopted in our experiments. The parameters of these models are set as the values suggested in the respective original papers, e.g., the step size of FGSM is set to 0.1, the maximum iteration of LowProFool and DeepFool is set to 50, the trade-off factor of LowProFool is set to 10.

For defence, the state-of-the-art tabular data adversarial attack defence model D2A3N and Madry are selected as the baselines to test D-Layers embedded ${{{\texttt {ANN}}}}$’s robustness. The ${{{\texttt {ANN}}}}$ model without any defence method (denoted as Clean) is used as the baseline to demonstrate the severity of the robustness problem. The standard evaluation metric Robust Accuracy is used to evaluate our proposed D-Layers’ performance in defending against adversarial attacks. Similar to Standard Accuracy that measures the ratio of correct predictions and total data points, Robust Accuracy measures model’s accuracy under unsettled conditions such as attack and covariate drift (Zhou et al. 2022)—the higher the Robust Accuracy, the more robust the model, and vice-versa.

4.1.3 Implementations

D-Layers and all baselines are implemented with PyTorch. D1-Layer and D2-Layer are integrated into the first layer of an ${{{\texttt {ANN}}}}$ that has 5 hidden layers with ReLu activation function and Softmax as the output layer. Each of the hidden layers has 100 neurons. The training epochs, batch size, and learning rate is set to 500, 100, and 0.0001 respectively. The number of bins K is set to 5 for both D1-Layer and D2-Layer. Embedding dimensions – D, in D1-Layer is set to 10. For the implementation of adversarial attack models, we use the code released in the original papers, which is available on GitHub.⁷ For D2A3N, we implement the Equal Frequency discretization-based version without adversarial training for fair comparison (i.e., denoted as D2A3N-EF in the original paper). The parameters of D2A3N and referred attack models are set to the default values as provided in the paper. All the experiments were conducted on an $i7-10750$ desktop PC with 16 GB RAM and single NVIDIA GeForce GTX 1660 Ti GPU.

4.1.4 Evaluation scenario

To evaluate the effectiveness of our proposed D-Layers in improving ${{{\texttt {ANN}}}}$’s robustness, we split the data into training set and testing set. The testing data is attacked via three attack methods as presented in Sect. 4.1.2 or modified with covariate drift. We will discuss the details of concept drift in the later section. Nonetheless, we call the data modified testing data. The proposed D-Layers formulation and other baselines are trained with training data. The performance of the trained model is evaluated on the modified testing data. The two-fold cross-validation is adopted for the train-test split, and the average robust accuracy results over five rounds are reported. The evaluation framework is illustrated in Fig. 4.

Fig. 4

The evaluation framework of the experiments

4.2 Experimental results

4.2.1 Comparison of D1-Layer search strategies

Before comparing the defence performance (robust accuracy) against adversarial attacks of our proposed D-Layers with baselines, we need to determine the best search strategy for D1-Layer. For this, we compared the performance of D1-Layer embedded ${{{\texttt {ANN}}}}$ with three different search strategies, i.e., DES, TSES, and DCS. The average robust accuracies are presented in Fig. 5, where the results are broken across all, large, medium and small categories of datasets. Three attack methods of FGSM, LPF and DPF are used. It can be seen that in most cases TSES has higher robust accuracy than DES and DCS in defending all baseline attack methods (especially, in face of LPF attack). The pattern is consistent across Large and Medium datasets. On Small datasets, DCS performs better than other search strategies. For sake of simplicity, in the remainder of this paper, we only present D1-Layer results with TSES as representative of the three search techniques. The potential of ${{{\texttt {ANN}}}}$ models is best-achieved with Large datasets. This is because on Medium and Small datasets, they can overfit the data. Our selection of TSES as representative is motivated by its extremely good performance of itself on Large collection of datasets.

Fig. 5

Robust accuracy comparison of different search strategies for D1-Layer, under adversarial attacks

4.2.2 Defence against adversarial attacks

Let us now compare the performance of our proposed D-Layers with other baselines in terms of defending against adversarial attacks. The average robust accuracies of these methods are shown in Fig. 6.

Fig. 6

Robust Accuracy of D1-layer, D2-layer and baselines under adversarial attacks

From Fig. 6a, we can see that both D1-Layer and D2-Layer demonstrate higher robust accuracies than baselines on all datasets. This demonstrates the effectiveness of our proposed D-Layers in defending against adversarial attacks. The average robust accuracies of Clean ${{{\texttt {ANN}}}}$ on all 24 datasets under FGSM, LPF, and DPF attacks are merely 0.37, 0.24, and 0.26 respectively. These alarming lower robust accuracies demonstrate that white-box adversarial attacks are quite effective in degrading the performance of ${{{\texttt {ANN}}}}$ models. The higher average robust accuracy of D2A3N and Madry compared to Clean ANN demonstrates their effectiveness in defending against adversarial attacks. It is important to note that D2A3N is the state-of-the-art defence model. Let us compare the performance of D-Layers with D2A3N and Clean ANN in the following.

It is encouraging to see that D2-Layer leads to a performance improvement of 12, 9, and 14% on FGSM, LPF, and DPF attacks respectively over D3A3N. Compared with Clean ${{{\texttt {ANN}}}}$, the average robust accuracy improvement of D2-Layer on these three attacks reaches 34, 48, and 42% respectively.

It can be seen that D1-Layer achieves the highest average robust accuracy when compared with all other baselines. The average robust accuracy improvement of D1-Layer defence against FGSM, LPF, and DPF attacks compared to D2A3N reaches 18, 17, and 17% respectively; and that robust accuracy improvement compared to Clean ANN reaches 34, 48, and 42% respectively.

From Fig. 6b–d, we can see that D1-Layer wins against all baselines on almost all categories of datasets, the exception is Large with DPF attack. D2-Layer also shows superior performance on almost all categories of datasets, exceptions are Medium with FGSM and LPF attacks. Generally, we can conclude that in most cases D1-Layer and D2-Layer show significant performance improvement than all other baselines on Large, Medium, and Small datasets. Also, D1-Layer has better performance in defending against adversarial attacks than D2-Layer and of cause other baselines.

Let us now demonstrate the effectiveness of our proposed D-Layers’ robustness by utilizing the robustness definition from Definition 3. In particular, we summarize the number of times a method’s robust accuracy wins against the standard accuracy of an ${{{\texttt {ANN}}}}$ by a certain margin— denoted as $\delta$, under LPF attack in Table 2.⁸ The results are reported for varying values of $\delta$. It can be seen that D1-Layer and D2-Layer outperform all other baselines on all values of $\delta$, with D1-Layer (as we found earlier) is more robust than D2-Layer.

Table 2 Number of wins of D1-Layer, D2-layer, D2A3N, and Madry with varying the value of $\delta$

4.2.3 Handling covariate drift

The typical way of evaluating the covariate drift handling ability of models is to simulate the drift artificially in the data, then test the models’ performance on the drifted data (Nair et al. 2019). For doing this, we followed the following procedures:

• We split each dataset into training set and testing set (as described in Sect. 4.1.4). We will refer to these sets as training data and original test data respectively, in the following discussions.

• We apply a non-linear transformation to all features ($X^i_j=\alpha X^{i^5}_j+ \beta X^i_j+ \gamma$) on the testing set. The values of $\alpha , \beta$, and $\gamma$ are set to 1, 1, 300 for the transformation. We call this dataset as drifted test data in the following.

• The D1-Layer, D2-Layer, D2A3N, and Clean ${{{\texttt {ANN}}}}$ are trained on the training set and tested on the drifted test data.

The average robustness of our proposed D2-Layer and baselines under monotonic covariate drift are presented in Fig. 7.⁹ We can see that D2-Layer achieves the highest average robust accuracy (0.89) and wins against all baselines on Large, Medium, and Small datasets. The average performance improvement of D2-Layer compared to Clean ${{{\texttt {ANN}}}}$ is $29\%$ (which is quite impressive). This demonstrates the superiority of D2-Layer in handling monotonic covariate drift. It can be seen that D1-Layer and D2A3N can not address monotonic covariate drift at all.

Fig. 7

Robust accuracy of D1-Layer, D2-Layer, D2A3N and ANNunder covariate drift

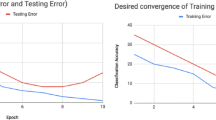
To further demonstrate the effectiveness of D2-Layer in handling monotonic covariate drift, we visualize the accuracies of clean ${{{\texttt {ANN}}}}$ and D2-Layer with and without drift on various datasets in Fig. 8. In particular, we plot the accuracies on modified testing data and testing data. For the sake of completeness, we also plot the model’s performance during the training as well. From Fig. 8, we can see that during the covariate drift phase, there is a significant performance degradation of clean ${{{\texttt {ANN}}}}$ (green line). However, the performance of the D2-Layer-based ${{{\texttt {ANN}}}}$ model (red line) is maintained, which clearly demonstrates D2-Layer’s ability in handling covariate drift. The inclusion of training accuracies in the results reveals that D2-Layer has a different convergence profile as compared to clean ${{{\texttt {ANN}}}}$.

Fig. 8

Illustration of accuracy (with and without covariate drift) on various datasets. Plots show accuracy on the training data (during the training process), followed by accuracy of the trained model on the drifted testing data, followed by the accuracy of the trained model on original testing data

4.2.4 Selection of discretization strategies in D2-Layer

As we discussed in Sect. 3, D2-Layer can accommodate various discretization strategies. So far, in this work, we have constrained D2-Layer with equal frequency discretization. In this section, we will study the performance of D2-Layer with two other discretization techniques namely—Equal Width discretization (denoted as EW) and Quantile-based discretization technique based on Keras discretization layer (denoted as Quan). Note, Equal Frequency discretization is denoted as EF in the results. We have not tested the performance of D2-Layer with supervised methods such as MDL discretization, because, it is not possible to fix the number of bins with MDL discretization. That is, different batches in the data will lead to different numbers of bins. The inclusion of MDL discretization in D2-Layer has been left as a future work.

The average robust accuracy of D2-Layer with the three discretization methods (namely EF—default option in D2-Layer, EW, and Quan) under adversarial attacks and covariate drift is shown in Fig. 9.¹⁰ We can see that D2-Layer with EF discretization (D2-EF) achieves better performance than that with EW discretization (D2-EW) and quantile-based discretization (D2-Quan).

Fig. 9

Robust accuracy of D2-Layer under different discretization strategies (EF, EW and Quan)

4.2.5 One strategy for two problems

Based on the experimental results in Sects. 4.2.2 and 4.2.3, we can establish that D2-Layer is efficient in terms of providing a defence against adversarial attacks as well as handling covariate drift. To clearly demonstrate this property, we plot the performance of D2-Layer under covariate drift and adversarial attack simultaneously, on two datasets, in Fig. 10. It can be seen that D2-Layer-based ${{{\texttt {ANN}}}}$ has a consistent performance under the three attack methods and covariate shift. Its performance is consistently maintained within the $\pm 25\%$ degradation boundaries (shown by orange lines in the figure). In contrast, there is significant performance degradation in the performance of the clean ${{{\texttt {ANN}}}}$ model (green line).

Fig. 10

Illustration of the robustness of D2-Layer to adversarial attacks and covariate drift by demonstrating its performance under various forms of attacks as well as covariate drift. Horizontal orange lines depict $\delta = 25\%$. The two models are applied on testing data, followed by drifted testing data, followed by modified testing data (due to FGSM, DPF and LPF attacks)

5 Conclusions

In this paper, we proposed two ANNlayers - D1-Layer and D2-Layer (collectively referred to as D-Layers) to improve the robustness of typical ANNmodels on tabular datasets. This is an extension of research focusing on the use of discretization in improving ANN’s robustness (Zhou et al. 2022, 2023). The two layers are motivated by the need of adding discretization within the training of ANNmodels and, therefore, learn cut-point for discretizing the input data during the training phase. Furthermore, D2-Layer is motivated by the need for dynamic cut-point adjustment at the testing time. Through empirical evaluations, we demonstrated that D1-Layer and D2-Layer can be easily integrated into existing ${{{\texttt {ANN}}}}$ models and provides an excellent mechanism for defending against adversarial attacks and for addressing some forms of covariate drift. Our experimental results revealed that:

• 1. D1-Layer leads to state-of-the-art (SOTA) defence performance against major forms of adversarial attacks on various tabular datasets.

• 2. D2-Layer leads to an effective strategy to address covariate drift and adversarial attacks at the same time.

Our future work entails:

• Studying the application of D-Layers to the hidden layers of the network: This will result in obtaining a discrete ANN and can lead to a network that is more robust to attacks and covariate drift. However, it can result in significant performance degradation. How to maintain a good performance while maintaining robustness is a question of great value, and we are currently investigating this.

• Studying the impact of the nature of input data: That is, how the number of features, the number of categorial/numerical features, data size, etc. influence the performance of D-Layers in defending against adversarial attacks and addressing co-variate shifts.

• Studying the efficacy of D2-Layer for other forms of drift: Currently, the proposed D2-Layer can only be effective against the monotonic drift in the data. We are currently exploring the effectiveness of D2-Layer against non-monotonic transformations as well as concept drifts.

Appendices

Appendix A: Code

The code of D-Layers, as well as the data used in this paper, along with experimental scripts, is available to be used at: https://github.com/allwenau/DLayers.

Appendix B: Detailed results

The detailed results of all the experiments done in this paper can be found in Tables 3, 4, 5, 6.

Table 3 Robust accuracy comparison of different search strategies for D1-Layer

Table 4 Robust accuracy of D1-layer, D2-layer and baselines under adversarial attacks

Table 5 Robust accuracy of D1-Layer, D2-Layer, D2A3N and clean ANN  under covariate drift

Table 6 Robust accuracy of D2-layer with different discretiztaion strategy under adversarial attacks or covariate shift