Spillover Effects in Irrigated Agriculture from the Groundwater Commons

Abstract

This study examines irrigation spillover effects within the groundwater commons of the San Luis Valley in Colorado. We investigate the common pool competition predicted by a theoretical model of crop production through water-use intensity, acreage size choices, and production intensity among irrigators. By specifying Spatial Probit and regular Spatial Durbin Models, we empirically measure not only the effects of these choices on neighbors, but also the effect of other factors that affect water use and cultivation choices at neighboring farming units. For all three response variables, the results show that irrigators consider neighbors’ responses, with the strength of spatial dependency being highest for production intensity. Additionally, there are significant spillover effects from changes in key covariates, demonstrating the inadequacy of estimating direct effects only. For example, a one-foot increase in depth-to-water has both direct and indirect positive effects on water-use intensity, but the indirect effect constitutes over 81% of the total effect.

1 Introduction

One of the burning issues in water resource management continues to concern global environmental change and its impact on water resources. Much of the economic literature on the groundwater commons underscores the fact that, wherever underlying aquifer material permits seepage, groundwater commons tend to be a non-excludable resource. Like many common-pool resources (CPRs), groundwater commons have been considered susceptible to the “tragedy of commons” prediction by Hardin (1968): CPRs are prone to over-use and are highly likely to become extinct when access to them is unrestricted and there is lack of effective maintenance. In this paper, we provide evidence that groundwater competition not only affects pumping responses but also permeates the production decisions of neighboring farmers; we also show the existence of local spillovers arising from other water related and non-water factors that affect general cultivation choices. These spatial externalities should be considered in policy-making, particularly if imposing a pumping fee, which will be misspecified if such spillovers are not included.

To examine spillover effects in irrigated agriculture within the groundwater commons of the San Luis Valley (SLV) of Colorado, we investigate the presence of competitive water-use intensity, acreage size choices and production (land use) intensity among irrigators. By specifying Spatial Probit and regular Spatial Durbin Models, we are able to empirically measure not only the effects of these responses on neighbors, but also the effect of other factors such as depth-to-water, surface water availability, crop types and acreages, as well as some irrigating unit-specific characteristics that affect water use and cultivation choices at neighboring farming units. We find evidence that irrigators consider neighbors’ pumping relative to these variables, with the strength of spatial dependency being highest (i.e., spatial autocorrelation parameter $\rho = 0.72$) for production intensity.

Furthermore, we break down the effects on pumping from changes in key covariates into direct and spillover (indirect) effects (Table 1), finding important significant spillovers for a number of covariates. For instance, we find that a one-foot increase in depth-to-water has both a direct and an indirect positive effect on water-use intensity, but the indirect effect constitutes over $81\%$ of the total effect. A direct effect estimate looks at the change in the dependent variable due strictly to a change in that particular independent variable: in this case, if the depth-to-water increases and we hold all else equal—crop choice, neighbor choice, etc.—what happens to that irrigator’s water use decision? Meanwhile, the indirect effect captures the feedback loop of a neighbor adjusting to the water table and the original irrigator reacting to that adjustment, ad infinitum à la Nash equilibrium. In this case, that feedback interaction constitutes the majority of the adjustment in water use owing to increased scarcity. For another example, an additional acre-foot of groundwater use by neighbors and a one-foot increase in depth-to-water respectively constitute up to $86.5$ and $92.3\%$ of the total effects on the choice of acreage size. In a policy context, this implies it is inadequate to rely on direct effects estimates only—these sizable indirect effects would be missed and the total effects understated if a regular, non-spatial model is used. As policymakers begin to implement fees like in the SLV, achieving efficiency requires calculating the right fee, or, if second-best measures are chosen, then decision makers need a bound of what improvements to expect and measure success by.

Table 1 Explanation of direct vs indirect effect

The rest of this paper is structured as follows. Section 2 describes some of the background of the types of externalities seen in the groundwater commons, and the context of this paper in the wider economic literature on pumping. Section

3 develops a game theoretic model that demonstrates the spillovers in groundwater use and the inefficiency of competitive equilibrium. Section 4 gives a brief description of the study area, the associated irrigated agriculture, and the data used. In Sect. 5, we present the empirical estimation framework, with results in Sect. 6. Section 7 concludes.

2 Background

Economists have long tried to capture the nature of groundwater externalities, such as the “stock externality” and the “pumping cost externality” (Provencher and Burt 1993). Negative stock externalities arise as a user’s withdrawal increases the pumping lift—i.e., the distance the water has to travel from aquifer to surface—and thereby limits pumping options available for all other users (Wang and Segarra 2011). Positive stock externalities arise when a user attempts to conserve groundwater; this action is unrewarded when other users are able to lay claim to the stock and withdraw at least some units without appropriate compensation. A negative pumping cost externality (also called a congestion externality), on the other hand, arises even during simultaneous withdrawal owing to the “cone of depression” that occurs from the change in water pressure in the aquifer (Theis 1938), so more energy must be applied to pull water out until the cone dissipates. Provencher and Burt (1993) argue that this pumping cost externality is essentially equivalent to the stock externality. If one acre-foot of water pumped by a user lowers the stock level for other users, then their depth-to-water increases, leading to higher lift costs, regardless of timing.

Negri (1989) had characterized a “strategic externality,” i.e. that it is an optimal strategy for neighboring users to not conserve water but rather pump more now because any rise in groundwater stock level from conservation only leads to more pumping by their neighbors. However, Negri’s intuitive explanation of the strategic externality essentially reduces to the stock externality as well. Noting this, Provencher and Burt (1993) do not consider the strategic externality as separate, but rather introduce the “risk externality” which speaks to the variability in income that all farmers suffer due to unexpected changes in the level of groundwater stock. A depleted stock makes incomes more susceptible to variations in recharge and surface water supplies, if any. Thus, as far as individual irrigators do not factor the private cost of income risk to others in their pumping decisions, pumping will not be at the socially optimal level.

Groundwater is non-infinite, owing to potentially slow recharge rates and losses to the system, and the afore-mentioned sources of inefficiency stem from the lack of exclusion for well-defined property rights. Where a shared aquifer’s hydrological system is such that a user’s withdrawal can affect other users’ pumping alternatives, there is bound to be competitive pumping among users. Rouhi Rad et al. (2021) find evidence of a short-term decrease in pumping near recently retired wells, indicating that committed lower usage of water (a well out of commission into the future) further decreases pumping competition for wells remaining. Groundwater competition can thus seem like an “arms race” and has the potential for welfare loss (Dasgupta and Heal 1979; Eswaran and Lewis 1984; Msangi 2004). One notable welfare result, identified by Gisser and Sanchez (1980), is that the social benefits from optimal control in groundwater management are not significant, especially when the aquifer is relatively large. This paradoxical result is called Gisser-Sanczhez’s effect (GSE). Empirical studies attempting to further verify the nature and quantify the magnitude of this spatial externality have split along two major lines—those that confirm the GSE (for example, Gisser and Sanchez 1980; Gisser1983; Rubio and Casino 2003) and those that do not (for example, Koundouri 2004; Noel et al. 1980; Burness and Brill2001; Bredehoeft and Young 1970). More recent work by Edwards (2016) finds that aquifer characteristics very much affect the benefit to groundwater management, notably that “one standard deviation increase in [the hydrologic communication] variable increases land value by 5–8% after management is implemented.”

Most of these studies rely on mathematical programming, both analytical and simulation methods. Even in the last decade when economic anyalysis began to incorporate more relevant and reliable physical hydrological variables in their models (for example, Saak and Peterson 2007; Brozović 2010), similar non-econometric approaches have been used. Pfeiffer and Lin (2012) first adopt econometric estimation of the economic relationship among users and find evidence of the existence of significant spatial externalities and increased pumping between neighboring groundwater irrigators in the High Plains Aquifer system of Western Kansas. Smith (2018) utilizes a similar econometric framework in estimating the impact of the spatial externality on neighborhood pumping in the San Luis Valley (SLV) of Colorado by estimating the effect of pumping on groundwater height at own and neighboring wells. Both Pfeiffer and Lin (2012) and Smith (2018) find neighborhood pumping reduces water height for users.

Perhaps one of the reasons econometric studies on spatial externality in groundwater extraction are few and far between is the fact that for many such models to be meaningful and reliable, they require actual non-simulated data on very important agro-climatic and hydrogeological variables, some of which can be hard to acquire. In examining neighboring farmers in Western Kansas, Pfeiffer and Lin (2012) make use of a unique spatial dataset that includes hydraulic conductivity measures. This enables spatial weights based on the equation of Darcy’s Law on seepage of fluid through porous materials to directly test the below-ground relationship among wells. They also note the importance of instrumenting for neighboring water usage due to simultaneity concerns, something we address as well.

Unfortunately, transmisivity data is not available in all areas—it requires studies conducted by hydrogeologists, often in the form of reports through the U.S. Geological Survey. Due to the non-availability of similar transmisivity/hydraulic conductivity data for the San Luis Valley in Colorado, Smith (2018) was able to study only the “above-ground” response to a pumping fee policy and water withdrawals by neighbors. This observable response, however, only occurs because of an underlying physical connection. Despite the lack of transmisivity data,¹$^,$² the SLV is an interesting study area from a public goods point of view because part of it comprises a closed basin.

A closed basin is an aquifer system that does not have outside runoff: its waters do not flow to the ocean.³ From an economic point of view, this geologic characteristic would limit the number of stakeholders and could increase the efficacy of collective action. The potential “free-riders” of groundwater conservation are only local neighbors, and not downstream entities, and so a management system can form without leakage (Ostrom 1990). This characteristic is important enough that it lends its name to the Closed Basin Project, established in 1972 by the U.S. federal government and remains operated by the U.S. Bureau of Reclamation until today (Simonds 2015; Ivers 2022). Recognizing that the water would stay in the closed aquifer, the Closed Basin Project creates a limited “downstream” by adding a major stakeholder. The project pulls groundwater out of the closed basin for delivery to the Rio Grande watershed, the abutting water-stressed region that contains the rest of the SLV, with beneficiaries in and outside Colorado. Unlike a typical downstream scenario, however, the water taken by the Bureau of Reclamation is bound by constant lump sum of water rights and a commitment to surrounding well depth levels: previously the Bureau had rights to 117,000 acre-feet of water per year, now only 83,000, with only about 17,300 delivered per year since 2000 (Ivers 2022).⁴

Owing to dropping water levels, the state of Colorado mandated water conservation on irrigators in the SLV: irrigators face a complete loss of water rights if levels are insufficient in the future. To avoid this, irrigators within Rio Grande Water Conservation district embarked on a project to regulate themselves and bring down the levels of withdrawals as a group with the creation of six subdistricts that would regulate pumping (Smith et al. 2017). Special Groundwater Subdistrict No.1—the closed basin portion—was first to be legally recognized in 2006, implementing a ${\$}$ 45 fee per acre-foot of water pumped in 2011. The fee was further increased to ${\$}$75 per acre-foot of water pumped in 2012, and subtracts a “Surface Water Credit” for irrigators who use surface water from outside the district (water that would not have otherwise gone into the aquifer) (RGWCD Subdistrict 2017).

The other five subdistricts were formed later (2016–2018) and delayed implementation, generating a a rare quasi-experiment in which the Subdistrict No.1 serves as treated group while the other five sub-districts serve as a control group. Our paper considers data from 2009 until 2013, so we investigate only this first initiation of the fee in Subdistrict 1. However, conservation work has continued: Subdistrict Nos. 2 and 3 implemented fees in May 2019, No. 6 in September 2019, and Nos. 4 and 5 in June 2020 (RGWCD 2022).⁵

This study analyzes similar data and from the same source as Smith et al. (2017) and Smith (2018) but differs significantly from both Pfeiffer and Lin (2012) and Smith (2018) in the approach and extent of analyzing possible externalities in irrigated agriculture in groundwater commons. First, with respect to Smith (2018), this analysis is not within a difference-in-difference framework as it does not seek to analyze the impact of the pricing policy as a one-time implementation. Rather the fee is included directly as a level predictor variable, and we focus on interpretation of the spatial coefficients. Second and more importantly, we extend the analysis with respect to the presence of externalities to cover not only the possible response of irrigators in terms of their water use to changes in neighboring irrigators’ water use. We adopt a relatively more comprehensive approach by analyzing how changes in other relevant variables and farming choices by neighbors affect each other.

In irrigated agriculture within the context of groundwater commons, as in the SLV, neighboring irrigators may or may not necessarily have clear knowledge of the porosity levels of the ground material of their wells (as opposed to the porosity of the soil in the fields themselves). Additionally, they may or may not observe the pumping habits and other above-ground choices of their neighbors, though Smith (2018) notes “it is reasonable that neighbors would have a general idea of the their neighbors’ water use” (pg. 155). Regardless of observation, neighbors’ choices can have local or global spillover effects. For example, given a change in the depth-to-water level, an irrigator may respond to the increased lift cost in a way that this local response would then affect the outcomes of neighbors, which in turn affect outcomes of their neighbors, including the initial irrigator. Thus, in the empirical formulation, while the global effect works through the spatial lag of the outcome variable, changes in relevant covariates affect outcomes of local neighbors through spatial lags of such covariates (Gibson 2019). These effects are likely to be different for each pair or group of neighbors; as such we consider the average effects which we can break down into direct and indirect marginal impacts (LeSage 2008).

3 Theoretical Model

3.1 Individual Irrigators and the Nash Equilibrium

In this section, we consider a one-shot game between irrigating farmers with multi-crop agricultural production functions. In particular, the irrigators operate in an environment which already has water stress measures, like a Pigouvian tax, in place. Thus, the marginal cost of water is dependent on scarcity s, modeled as depth-to-water from the surface, and on the Pigouvian tax b. For simplicity, we assume that irrigators first make their initial individual-level optimal land allocations, $n^{i*}_k$, simultaneously; they then subsequently choose water use to maximize expected profits.

Water use as a choice variable is expected to be the main source of interaction or competition since irrigators share the same aquifer in a water-stressed region. While it is clear that the real-world situation has dynamic components, dynamic games are much more complicated.⁶ A calibrated dynamic game in this scenario would benefit from a hydrogeologic model of recharge, possibly supplemented with sophisticated weather and price forecasting. Koundouri and Xepapadeas (2004) examine a dynamic market in which irrigators are small and thus find an open loop (non-game theoretic) equilibrium of the system; they also note their “doubt that the use of an alternative equilibrium concept such as the closed loop (feedback-subgame perfect) changes the substantive conclusions or the methodological advances” of their paper. Using a distance-function approach, they estimate the shadow price of groundwater, provide evidence of stock effects increasing with scarcity, and support the result that irrigators have inefficient water withdrawal compared to collective management. Pfeiffer and Lin (2012) also examine a continuous dynamic game of pumping volumes, finding that “To capture the water before it can flow out and extract it at a lower marginal cost, [irrigator] i would increase pumping.” Thus, with prior literature on resource stocks confirming a dynamic tragedy of the commons, our model focuses on the single stage interaction between agents and more fully describes the profit and land allocation decisions as functions of water withdrawal.

Consider two neighboring irrigators, i and j. Depending on the hydrology of the aquifer that sits the neighboring wells, the amount of water w extracted by irrigator j may affect the water levels in irrigator i’s well, and thus the depth-to-water. The same in reverse holds for irrigator i. Without loss of generality, the depth-to-water of irrigator i’s well at any given time during the growing season can be considered a function of withdrawals by i as well as neighboring j’s withdrawals: $s^i = s^i (w^i, w^j)$, where $w^i = \sum _{k=0}^K w^i_k$ represents i’s total water withdrawal for all their crops $k\in [0,K]$. Thus $s^i(w^i, w^j)$ captures the stock/pumping cost externalities described in Sect. 2 and incorporates the physical connection between irrigators and their shared aquifer into the model. As such, we can write the non-constant per unit water cost for irrigator i as $B^i = B^i(s^i(w^i, w^j), b)$, which is a function of depth-to-water and b, the existing constant monetary price per unit water pumped.

Irrigators/farmers choose how to allocate land among k growable crops according to $n^{i*}_k\left( {\textbf {p}}, {\textbf {r}}, B^i\left( s^i\left( w^i, w^j\right) ,b\right) , N^i; {\textbf {x}}\right)$, with total per unit cost of water $\textit{B}$, prices of other non-water inputs ${\textbf {r}}$, output prices ${\textbf {p}}$, land constraints $N^i$, and other variables ${\textbf {x}}$ relating to hydrogeological, climate, weather, and soil conditions. Taking this land decision function into account, an irrigator’s expected crop-level profit is $\varvec{\pi }^{i*}_k \left( p_k, {\textbf {r}}, B^i\left( s^i\left( w^i, w^j\right) ,b\right) , n^{i*}_k; {\textbf {x}} \right)$. Producers behave as price takers, and we assume $\varvec{\pi }^i_k(.)$ is twice-continuously differentiable, convex and closed in output and input prices ($p_k, {\textbf {r}}$, and $B^i$) in the non-negative orthant, homogeneous of degree one in output and input prices, strictly decreasing in ${\textbf {r}}$ and $B^i$, and non-decreasing in $n^i_k$ and $p_k$.

Water is the ultimate short-run variable. To study the interaction between the irrigators, we consider their water withdrawal choices in maximizing their respective profits. The enterprise-wide profit maximization problem for irrigator i can be stated as:

$$\begin{aligned} \begin{aligned} \varvec{\Uppi }^{i}&\varvec{\big (}{} {\textbf {p}}, {\textbf {r}}, B^i(s^i(w^i, w^j),b), N^i; {\textbf {x}} \varvec{\big )}\\&= \max _{\{w_0 \ldots w_K\}} \, \, \sum _{k=0}^{K} \varvec{\pi }^{i*}_k\varvec{\bigg (}p_k, {\textbf {r}}, B^i\left( s^i{\left( \sum _{\ell = 0}^K w_\ell ^i, \sum _{\ell =0}^K w_\ell ^j\right) },b\right) , n^{i*}_k(\cdot ); {\textbf {x}}\varvec{\bigg )} \\ \end{aligned} \end{aligned}$$

(1)

Taking j’s total withdrawal $w^j$ as given, the first order condition for agent i’s withdrawal for an individual crop $w^i_k$, for all $k \in [0, K]$, is derived as follows:

$$\begin{aligned} \begin{aligned} \frac{\partial {\varvec{\Uppi }^{i}}}{\partial w^i_k}&= \sum _{\ell =0}^{K} \frac{\partial \varvec{\pi }^{i*}_\ell \big (p_\ell , {\textbf {r}}, B^i(s^i(w^i, w^j),b), n^{i*}_\ell (\cdot ); {\textbf {x}}\big )}{\partial w^i_k} \\&= \sum _{\ell =0}^{K} \left( \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial B^i(\cdot )} \cdot \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} + \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot ) }\cdot \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) \\&= \sum _{\ell =0}^{K} \left[ \left( \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial B^i(\cdot )} + \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )}\cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot ) } \right) \left( \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) \right] \le 0 \\ \end{aligned} \end{aligned}$$

(2)

with equality if water withdrawal is positive, i.e. $w_k^i > 0$, which we expect for all crops with the exception of dry fallow. Agent j’s first order conditions are symmetric and stated in Appendix 1 as Eq. (9). The crop level water withdrawal amounts $({\hat{w}}^{i}_0,\ldots , {\hat{w}}^{i}_K, {\hat{w}}^{j}_0,\ldots , {\hat{w}}^{j}_K)$ that simultaneously solve Eqs. (2) and (9) constitute the Nash equilibrium.

We can use the first order conditions and the Implicit Function Theorem to examine the impact of agent j’s withdrawal for crop m on agent i’s withdrawal for crop k. Equation (13) derived in Appendix 1.1 gives a complicated formula that compares the curvature of profits due to the opponent’s water withdrawal and own water withdrawal. The sign of $\frac{d w_k^i}{d w_m^j}$ is indeterminate without further functional assumptions, but we note that it depends very much on reallocation of crops based on total water cost, $\frac{\partial n_\ell ^{i*}}{\partial B^i}$, and on the physical interdependency of neighboring units’ water withdrawals on scarcity, $\frac{\partial ^2 s^i}{\partial w^j_m \partial w^i_k}$. Consider the case where this cross-partial is very large in comparison to other terms, and so is the own second derivative of withdrawal on scarcity, $\frac{\partial ^2 s_i}{\partial {w_k^i}^2}$, i.e. acceleration of depth-to-water due to withdrawal.⁷ If own withdrawal is convex while transmissive seepage is concave, then we could see a positive strategic effect even in a one-stage scenario. If, on the other hand, the second order effect of scarcity on water cost is stronger than transmission—as it might be if the well is close to inoperability—then we would expect a negative strategic effect. Thus the model captures how the simultaneous physical interrelationship between wells ($w^j$ and its entry into $s^i$) affects cropping and watering decisions.

3.2 Social Optimum

In the Nash equilibrium, each irrigator can control only their own water withdrawals. Under cooperative management, the irrigators choose water withdrawals together to maximize the sum of their profits:

$$\begin{aligned} \begin{aligned} \varvec{\Uppi }^{sp}\varvec{\bigg (}{} {\textbf {p}}, {\textbf {r}},&B^{sp}(s^{sp}(w^i, w^j),b), N^{sp}; {\textbf {x}} \varvec{\bigg )} \\ = \max _{\{w_0 \ldots w_K\}}&\Bigg [ \sum _{k=0}^{K} \varvec{\pi }^i_k\varvec{\Bigg (}p_k, {\textbf {r}}, B^i\left( s^i\left( \sum _{\ell = 0}^K w^i_\ell , \sum _{\ell = 0}^K w^j_\ell \right) ,b\right) , n^{i*}_k; {\textbf {x}}\varvec{\Bigg )} \\&+ \sum _{k=0}^{K} \varvec{\pi }^j_k\varvec{\Bigg (}p_k, {\textbf {r}}, B^j\left( s^j\left( \sum _{\ell =0}^K w^j_\ell , \sum _{\ell =0}^K w^i_\ell \right) ,b\right) , n^{j*}_k; {\textbf {x}}\varvec{\Bigg )}\Bigg ]. \\ \end{aligned} \end{aligned}$$

(3)

We present the full derivation of the first order conditions with respect to both agents’ withdrawals in Appendix 1.2; however, we note that the following socially efficient condition contains the individual FOC from Eq. (2) and adds an externality term, denoted $E^i$:

$$\begin{aligned} \begin{aligned} \frac{\partial {\varvec{\Uppi }^{sp}}}{\partial w^i_k}&= \sum _{\ell =0}^{K} \left( \frac{\partial \varvec{\pi }^i_\ell (\cdot )}{\partial B^i(\cdot )} + \frac{\partial \varvec{\pi }^i_\ell (\cdot )}{\partial n^{i*} _\ell (\cdot )} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot ) } \right) \left( \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) \\& \quad\;\;+ \sum _{\ell =0}^{K} \hspace{-5.69054pt}\underbrace{ \left( \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial B^j(\cdot )} + \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial n^{j*} _\ell (\cdot )} \cdot \frac{\partial n^{j*}_\ell (\cdot )}{\partial B^j(\cdot ) } \right) \left( \frac{\partial B^j(\cdot )}{\partial s^j(\cdot )} \cdot \frac{\partial s^j(\cdot )}{\partial w^i_k} \right) }_{ E^i_k }\le 0 \end{aligned} \end{aligned}$$

(4)

From the individual FOCs, we note that individual irrigators do not internalize the impact of their withdrawals on the extraction cost of neighbors via the impact on depth-to-water. The socially efficient solution includes such an impact: the term labeled $E^i_k$ is a scaling of the chain effect of an irrigator’s water withdrawal for crop k on neighbor’s depth-to-water, cost of water, crop-land choice and profit levels. Therefore the crop level water withdrawal amounts (${\tilde{w}}^{i}_k$, ${\tilde{w}}^{j}_k$) from the cooperative problem are efficient compared to (${\hat{w}}^{i}_k$, ${\hat{w}}^{j}_k$). To ensure socially optimal levels of withdrawal in a period, we could set an individual tax for each irrigator such that irrigator i faces a per unit withdrawal tax of $t^i = - \sum _{k=0}^K E^i_k$ and irrigator j faces a per unit withdrawal tax of $t^j = - \sum _{k=0}^K E^j_k$.

Unlike the existing per unit tax b, E is non-constant: it is clearly a function of depth-to-water of own and neighboring wells, as well as water withdrawal levels by self and neighboring irrigators. Furthermore, unlike b, E is not uniform as $E^i$ is not necessarily equal to $E^j$.⁸ Additionally, this model also raises the possibility of taxing water withdrawal per crop, with $t^i_k = -E^i_k$, instead of the summation. If all crops are taxed, then this equates with the earlier total and efficiency. However, taxing the most water-intensive crops only would alleviate some of the externality, discourage those crops in Pigouvian fashion, and perhaps be more politically palatable in certain areas.

Irrigator i’s effect on j contains three derivatives of just j’s terms and one with respect to i’s action. The expected sign of $E^i$ thus depends on the individual signs and magnitudes of its components. As mentioned earlier, an increase in the total marginal cost of water decreases profits, $\frac{\partial \varvec{\pi }^i_k(\cdot )}{\partial B^i(\cdot )} < 0$, land weakly increases profits, $\frac{\partial \varvec{\pi }^i_k(\cdot )}{\partial n^{i*}_k(\cdot )} \ge 0$, an increase depth-to-water increases total marginal cost, $\frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} > 0$, water withdrawals weakly increase scarcity, $\frac{\partial s^i(\cdot )}{\partial w^i_k(\cdot )}\ge 0$ and $\frac{\partial s^j(\cdot )}{\partial w^i_k} \ge 0$, and how total marginal cost of water affects crop allocation, $\frac{\partial n^{i*}_k (\cdot )}{\partial B^i(\cdot )}$, differs per crop. The sign of $E^i$ could therefore be negative or positive and is thus mainly determined empirically (see Moore et al. 1994; Schoengold et al. 2006; Smith et al. 2017).

Typically, the impact of total marginal cost on optimal crop-land is a long-term response involving land reallocation (a so-called extensive margin adjustment). Thus, in a single stage $E^i$ will be negative unless $\frac{\partial n^{j*}_\ell (\cdot )}{\partial B^j(\cdot )}$ is positive with a large enough magnitude to make $\left( \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial B^j(\cdot )} + \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial n^{j*}_\ell (\cdot )} \cdot \frac{\partial n^{j*}_\ell (\cdot )}{\partial B^j(\cdot ) } \right)$ positive for a substantial majority of crops $\ell$. Indeed, a positive $E^i$ would imply a negative tax—or subsidy—needs to be imposed on irrigator i to restore social efficiency. All told, as long as transmissivity is non-zero, then a spatial externality exists.

4 Study Region and Data Description

4.1 Data Source and Description

A spatial data set on irrigated agriculture in the San Luis Valley (SLV) of Colorado offers the opportunity to empirically explore the spatial externality characterized by the theoretical model. While agriculture remains a major contributor to the economy of the SLV, its rainfall receipt averages only about 7.5 inches annually. Where surface water has become insufficient, farmers have become increasingly reliant on groundwater irrigation. As a consequence, water levels in wells, mostly in what is now the Special Improvement District No.1, began to drop quickly, raising sustainability concerns. However, it was not until 2009 that the reporting of groundwater pumping at most wells became effective with the installation of meters. Although there are some data dating back to 1936 (especially on irrigated parcels), data from 2009 are more complete and reliable.

The raw data are available from the Colorado Decision Support System (CDSS), a data section of the Colorado Division of Natural Resources (CDNR). The spatially referenced pumping data of the annual amount of water pumped for irrigation at the well and surface ditch levels, and well-specific features, such as the decreed flow rate, well depth, and the irrigator, are downloadable from the CDSS’s HydroBase. The data on irrigated acres with unique identification numbers for wells and ditches serving the parcels of land cultivated, irrigation technology, amount pumped, and crops grown are also available in shapefiles on CDNR’s website for download. Our data cover the five-year period from 2009 to 2013. There are around 3,000 wells for which complete records are available during this time; these wells were aggregated into irrigator-units for analysis.

Using individual parcels themselves as the unit of analysis would be very difficult: when matching the well data with the irrigated parcels, some parcels are irrigated with water from more than one well per season. Additionally, sometimes a single well irrigates two or more parcels in a season. Thus, the aggregation of the data for analysis follows Smith et al. (2017) and involves linking of all parcels irrigated by the same well to form initial irrigation units. Given no record of how much water was directly applied to each parcel, we assume equal division for parcels irrigated by the same well and for the parcels irrigated by more than one well. The aggregation of those equally divided amounts (shares) for a particular parcel is then considered as the amount of water used in irrigating it.

Aside from amount of groundwater, another variable that may be important in groundwater irrigation decision making is the amount of surface water available. These are extracted from the geospatial database. The Irrigated Land Geospatial database provides a link between surface water identifiers and the parcels they serve. However, just with the case of the wells, we do not have a direct record of how much water from each ditch is used to irrigate each parcel. As such, we apply the same equal share method that we adopted in the well-to-parcel analysis. The resulting means of 99,207.52 acre-feet of surface water inflows per irrigator-unit and 227.29 surface water AF per acre are thus rather large. The interpretation of these variables is the surface water that is available to an irrigator-unit during the season. This is not necessarily equivalent to surface water applied, as there is no measure of return flow. Because our study focuses on groundwater usage, surface water available is the relevant variable of concern, as it captures the other main source an irrigator could turn to.

The second stage involves the linking of the initial units to those that have parcels in common to produce one final unit. The process is repeated across time to produce a panel of time-consistent irrigation units that comprise a set of wells and all the parcels they irrigate. Thus, it is important to note that the unit of analysis is neither individual wells/ditches nor individual parcels, but rather these irrigator-units described above as a panel of time-consistent fixed units that encompass a set of wells and all the parcels they irrigate.

4.2 Summary Statistics

Summary statistics are presented in Tables 2 and 3 for the data at the irrigator-unit level, not individual parcel level. As stated earlier an irrigator-unit is composed of several individual parcels. Therefore, the average values reported in the data summary statistics table below should be read as average per irrigator-unit per year (growing season) and not average per acre or per parcel. Irrigating units apply 790 acre-ft of groundwater and have 99, 207 acre-ft of surface water available on average per year, irrigating on average 221.5 acres. Groundwater-use intensity averages 2.55 acre-ft/acre per year while land-use intensity, which measures the proportion of irrigator’s total available acres cultivated, is around 0.86 each year. The largest crop is alfalfa (68.64 acres), for which the acreage constitutes one third of the 221.5 average acres cultivated. The “Other” crops category, which includes sorghum, blue grass, vegetables, cover crop, corn, and wheat, constitutes only about $5\%$ of mean acres cultivated. In particular relation to per acre variables, acre-feet per acre (which defines groundwater acre-feet per acre pumped) and surface water available per acre are variables that have been defined at the parcel level before the irrigator unit aggregation; the latter variable is not used in our later regression analysis, but is presented for context of the surface water inflows per irrigator-unit variable that is used.

Table 2 Summary statistics, yearly totals/percentages (except depth-to-water, which is the difference between well elevation and annual interpolated groundwater height at monitoring stations)

Table 3 Summary statistics of key spatial variables

Aside from using mean crop acres to proxy irrigator-unit specific characteristics such irrigator preferences, specialty, soil and landscape suitability, we also consider some physical features unique to associated wells or the land parcels. These include permitted flow rates, well depth, presence of sprinkler technology, and whether the unit is also served by a surface water ditch. Average permitted flow rate is about 10 ft$^3$ per second with a standard deviation of 74.4, indicating large variation across units.

Table 3 shows summary statistics for some of the spatial variables. The mean and standard deviations indicate significant variance across space. Neighboring units within a half-mile radius use an average of 391 acre-ft of groundwater, irrigating about 176 acres per season, while those within a five-mile radius cultivate an average of 222 acres using 746 acre-ft of groundwater on average per year. These differences can be attributed to the clustering of smaller acreage units in the bottom of the valley, closer to groundwater, with larger acreage units spaced out from each other and often up the sides of the valley.

The assumption of equal water distribution and the process of amalgamating parcels irrigated by the same wells has one main shortcoming, in that large outliers cannot truly be excluded. Removing one parcel from the construction of its irrigation-unit would skew results, and removing a well entirely would misrepresent the hydrogeology of the region. We do test the removal of high-irrigating outliers by also running specifications deleting observations above the 95th percentile for all main variables of interest, including surface water availability, acre-feet of ground water pumped, acres, and acre-ft/acre. This leads to a reduction of 2,985 fewer observations for analysis. While deleting the outliers does not alter the results qualitatively, the large reduction in observations affects 597 irrigator-units, leading to their being dropped also. Given the spatial nature of our analysis, we believe this at best would reduce the strength any spatial relationships that may exist among the irrigator-units, and at worst leaves a hole in the map, essentially.

5 Empirical Estimation

5.1 Spillovers in Water Use and Production Competitiveness

We test whether the water used by neighboring irrigating units, defined by a neighborhood weight matrix, has any spillover effects on the amount of water used by an irrigating unit. In order to account for possible differences in the sizes of irrigating units, the unit of observation is the amount of groundwater (acre-feet) used per acre by an irrigating unit in a growing season. We do not directly test the physical relationship between wells, i.e. the effect that withdrawal of water from one well has on the withdrawal amount from a neighboring well, which would require hydrogeologic data on the aquifer (Sears et al. 2018). However, any outward response stems from the shared hydrogeology between neighbors.

Thus, instead of using individual wells as the unit of analysis, we use the irrigating/farm units (linked with wells that irrigate them) as units of analysis and the amount of water (acre-feet) withdrawn from the associated wells for irrigating an acre of these farm units as the units of observation. Spillover effects due to spatial interdependencies among wells are rather felt through depth-to-water levels and the resulting changes in lift cost during the growing season. As such, an irrigator’s response to neighborhood pumping can be captured indirectly by the amount of groundwater used per acre irrigated after controlling for other well- and irrigating-unit-specific features and crop/farming factors. Aside from agro-climatic factors that might be time-variant, some of these unit-specific and time-invariant factors may have additional interest.

We estimate a Spatial Durbin Model (SDM) with correlated random effects, a generalization of the Spatial Auto-regressive Model (SAR) which includes spatially weighted independent variables as explanatory variables (Miranda et al. 2018) and also involves the use of the Mundlak device (Chamberlain 1984; Mundlak 1978; Wooldridge 2010, 2019). This model allows the estimation of unit’s responses to changes in their own variables directly and unit’s responses to changes in neighboring units’ choices and variables indirectly. The regression specification is:

$$\begin{gathered} y_{{nt}} = \alpha _{0} \imath _{n} + \rho W_{n} y_{{nt}} + X_{{nt}} \beta _{1} + W_{n} X_{{nt}} \beta _{2} + \bar{X}_{n} \theta _{1} + W_{n} \bar{X}_{n} \theta _{2} \hfill \\ \quad\quad\;\; + \lambda _{{1^{\prime}}} c_{n} + W_{n} \lambda _{{2^{\prime}}} c_{n} + \nu _{n} + W_{n} \nu _{n} + \epsilon _{{nt}} , \hfill \\ \end{gathered}$$

(5)

where $y_{nt}$ is the $n \times 1$ vector of outcomes, $X_{nt}$ is an $n \times K$ matrix of measured time-varying regressors⁹ for n irrigating units at time $t = 1, \ldots , T$, that vary within and between clusters (units), ${\bar{X}}_{nt}$ is the vector of time-means (clustered means) of the time-varying regressors, and $c_n$ are time-invariant unit-specific factors. In this model, $W_n$ is an $n\times n$ inverse-distance spatial weighting matrix whose $(i, j)^\textrm{th}$ element is the inverse of the distance between units i and j with diagonal elements set to zero and $\rho$ is the corresponding spatial parameter.

In this modified random-intercept spatial panel model, the error term is composed of the intra-cluster error $\mu _n$ with spillovers $W_n\mu _n$ and error $\epsilon _{nt}$, which is considered white noise if it is completely independent of the regressors. The clustered means ${\bar{X}}_n$ account for any correlations between the intra-cluster error ($\mu _n$) and $X_{nt}$, where $\mu _n = \alpha {_0}\imath _n + {{\bar{X}}}_n \theta + \nu _n$ with $\nu _n$ being the part of $\mu _n$ which is uncorrelated with $X_{nt}$ (Schunck 2013; Halaby 2003). The spatial spillovers of the intra-cluster error therefore take the form $W_n\mu _n= W_n {{\bar{X}}}_n \theta + W_n\nu _n$.¹⁰ As such, CRE does not strictly require $\mu _n$ to be uncorrelated with $X_{nt}$. Under these circumstances, the parameter $\rho$ measures the strength of the spatial interaction in terms of the amount by which outcomes are affected by neighboring outcomes, $W_n y_{nt}$ (Anselin 2002). The parameter vector $\beta _1$ measures the direct effects of the exogenous regressors, whereas $\beta _2$ measures the strength of the spatial spillover between the irrigating units due to the exogenous regressors. Note that $\beta _1$ and $\beta _2$ are the equivalent of the “within” fixed effects in the fixed-effects specification of the SDM model. The difference of the between and within effects are estimated by $\theta _1$ and $\theta _2$. Finally, the $\lambda _1$ and $\lambda _2$ parameters are the coefficients associated with individual time-invariant unit effects and their spillovers respectively.

The inclusion of WX in the model lets changes in X affect outcomes of immediate neighbors. As Gibson (2019) noted, since the effects of a change in the value of a covariate in unit i on outcomes in unit j may differ for each i–j combination due to spillover and feedback effects, the evaluation of such impacts is done by considering average marginal effects of a change in average value of the given covariate. These average marginal effects are decomposed into direct and indirect effects, summing up to the total average marginal effects. LeSage and Pace (2009) provide a framework for this decomposition such that the outcome from unit i depends on own-unit factors in the covariate matrix, plus the same factors averaged over all the neighboring units.¹¹

There is an overt and delicate case of reverse causality to consider: we propose that scarcity (depth-to-water) affects pumping rates, but pumping clearly can affect depth-to-water as well, as prior literature already mentioned has shown. In a previous study without the spatial interactions, we use time-lagged depth-to-water as an instrumental variable and find that own scarcity does increase pumping.¹² When including the weight matrix of neighbor’s characteristics, however, using last year’s depth-to-water quickly creates an issue, greatly reducing the number of observations and loss of vital spatial information.¹³

Thus, we proceed with concurrent depth-to-water, very cautiously. First, we note that the regressor $\ln$Depth_to_water is constructed as the difference of yearly averages: we take the year average groundwater height and elevation for all wells that serve an irrigator-unit, average those to obtain the elevation and groundwater height of the irrigator unit, and then use the natural log of the difference as logged depth-to-water. In this way, the depth-to-water variable contains the scarcity signals of the whole year. Meanwhile, the dependent variables, particularly intensity of groundwater use (acre-feet/acre pumped), are all totals for the year. Therefore, we argue that our measure of depth-to-water is a “predetermined” regressor and is thus sequentially, or weakly, exogenous. A predetermined regressor is one where only its future values are affected by the current value of the dependent variable (please see Wooldridge (2010) or Chapter 8 of Arellano (2003) for a fuller discussion of predetermined regressors). While pumping throughout the year no doubt changed groundwater height later into the year, the total year’s pumping cannot have affected the starting values included in the average scarcity.

Second, the earlier described cluster means are a known and successful method of mitigating reverse causality as well. In a dynamic simulation, Leszczensky and Wolbring (2022) find that demeaning the data and thus relaxing strict exogeneity requirements outperforms pooled OLS or random effects models which must otherwise incorporate lags. One particular issue is that of specifying the correct lagged variables to include: should the variable go back one period, or two? With regard to irrigation, anecdotally farmers may remember and react to severe droughts that occurred years prior. Thus, we believe our CRE approach including the clustered means ${\bar{X}}$ further assists with correct identification.

Third, the concern of spatial endogeneity/reverse causality warrants specialized approaches, such as instrumental variables or maximum likelihood estimation techniques to estimate the model parameters (Anselin 2002). Since the IV approach was not feasible, we adopt a quasi-maximum likelihood approach to estimate the correlated random effects model (Yu et al. 2008; Wooldridge 2014), which addresses the endogeneity problem by explicitly taking into account the structural form of the endogeneity of the model’s variables. We utilize the Stata routine, xsmle, by Belotti et al. (2017) for Spatial Durbin Models (SDM) panel models to compute these effects.

In our first set of specifications, the dependent variable $y_{nt}$ is water use, while in the second we use cultivated acreage. The intensity of groundwater use is of primary interest, as it is the direct unit of consumption of the groundwater commons. However, because we are cognizant of the earlier mentioned simultaneity concerns, we consider the second specification of cultivated acreage as a production competitiveness proxy, to demonstrate how the availability of the input from the commons affects the unit’s total production. Doing so means that we can include acre-feet pumped as one of the time-varying predictors in the cultivated acreage specification as a robustness check. The other time-varying predictors in both models include the depth-to-water, amount of surface water available, acres of various crops cultivated and their lags.

The unit-specific factors in this study that may affect water use and cultivation decisions can arise from two main sources: time-invariant factors specific to the wells that irrigate the land parcels and those specific to irrigator and/or the parcels (i.e., the irrigating unit) that may inform cultivation practices. Some of the well-specific factors we assume may be a source of heterogeneity include well depth, decreed rate of flow and an indicator of whether or not the well falls within the special Subdistrict No.1. Irrigator/parcel-specific factors are difficult to measure, so we assume that these factors drive observable, consistent irrigator decisions. For example, we use the type of irrigation technology as a proxy for time-invariant parcel-specific factors such as slope and soil characteristics. To account for the possibility of changes in irrigation technology type, we also include the cluster mean values of acres irrigated by irrigation type. By the same analogy, we include the cluster means of all the time-variant regressors to account any unmeasured heterogeneity, including using cluster mean values of acres of each cultivated crop as a proxy for an irrigator’s consistent preferences. The only other unit-specific factor we consider is an indicator whether the unit is also served by a surface ditch. As mentioned earlier, we proxy for irrigator-unit specific characteristics with crop choice: specifically, we include the previous season’s crop and fallow choices. Crop decisions are commonly linked over years, and while this year’s crop may not be observable at the beginning of the season, last year’s crop span is known. Thus, we include the natural logs of last year’s crop acreages as a control for irrigator-unit preferences that can serve as a signal of this year’s plans.

5.2 Spillovers in Production (Land-Use) Intensity

Another measure we study is production intensity, not just in terms of the yearly acreage cultivated as described above, but as the share of potential acreage. An irrigator’s cultivated area in a particular growing season may be greater than a neighbor’s solely based on the relative difference in how much land each has to begin with. The data from SLV show that units cultivated the largest irrigated acres in 1998. We therefore rely on these maximum irrigated acres observed for each farmer or irrigating unit in 1998 as total capacity acres for that irrigator. We then define land-use intensity propacre as the proportion of each season’s cultivated acreage relative to the 1998 total capacity.¹⁴ In addition to the earlier specification of cultivated acreage itself which provides estimates for production competitiveness, this proportion better captures production intensity in a variable more directly comparable among irrigators. We follow Papke and Wooldridge (2008) and specify a fractional response model, in which the unobserved effects are allowed for and modeled using the Mundlak (1978) and Chamberlain (1980) device conditional on the exogenous covariates.

Consider we have available T observations, $t = 1, \ldots , T$ for each random cross-sectional observation i at time t such that the response variable $0 \le propacre_{it} \le 1$. If we define a $1\times K$ vector of explanatory variables ${\textbf {X}}_{it}$, then the non-spatial fractional probit model with the correlated random effects specification (Papke and Wooldridge 2008) has the form:

$$\begin{aligned} \begin{aligned} \varvec{\textrm{E}}\left( propacre_{it} \mid {\varvec{X}}_{it}, c_i, \nu _i \right)&= \Phi \left( \alpha {_0} + {\varvec{X}}_{it} \varvec{\beta } + \bar{\varvec{X}}_{i} \varvec{\theta } + c_i \lambda + \nu _i \right) , \end{aligned} \end{aligned}$$

(6)

where $\Phi (\cdot )$ represents the standard normal cumulative distribution function (cdf), $c_i$ is the vector of time-invariant, unit-specific variables, and $\varvec{{\bar{X}}}$ is defined by its relationship with the cluster error: $\mu _i = \alpha {_0} + \varvec{{{\bar{X}}}}_i \varvec{\theta } + \nu _i$, with $\nu _i\mid \varvec{X}_i \sim N(0,\sigma ^2_\nu )$ (Papke and Wooldridge 2008; Chamberlain 1980).

To examine the spillover effects, we include spatial lags of the explanatory variables, as well as the spatial lag of the response variable propacre, into Eq. (6). Specifically, we estimate a spatial probit model of the form:

$$\begin{aligned} \begin{aligned} \varvec{\textrm{E}}\left( propacre_{it} \mid {\varvec{X}}_{it}, c_i, \nu _i, W \right) &= \Phi \big (\alpha {_0} + \rho W propacre_{it} + {\textbf {X}}_{it} \varvec{\beta _1} + W{\textbf {X}}_{it}\varvec{\beta _2} + \bar{{\textbf {X}}}_{i} \varvec{\theta _1} \\& \quad\;+ W\bar{{\textbf {X}}}_{i}\varvec{\theta _2}+ c_i \lambda _1 + W c_i \lambda _2 + \nu _i + W\nu _i \big ), \end{aligned} \end{aligned}$$

(7)

where W is the spatial inverse distance weight matrix as described above. As before, the parameter $\rho$ measures the strength of the spatial interaction in terms of the amount by which outcomes are affected by neighboring outcomes ($W propacre_{it}$).

Regarding interpretation, there are two facts worth highlighting. First, the estimates of $\varvec{\beta }$ and $\varvec{\theta }$ parameters only provide information on the direction of the partial effects—same as in a typical, non-spatial probit model—and thus are not comparable to the marginal effects estimates from standard regression models (Papke and Wooldridge 2008; LeSage 2008). The comparable marginal effect from (6) is expressed:

$$\begin{aligned} \begin{aligned} \frac{\partial {\varvec{\textrm{E}}}\left( propacre_{t} \mid {\varvec{X}_{t}}, c, \mu \right) }{\partial X_{tk}}&= \beta _k \Phi \left( {\varvec{X}}_t \varvec{\beta } + c + \mu \right) . \\ \end{aligned} \end{aligned}$$

(8)

Thus the size of the effect of changes on the expected probability varies with the levels of $X_k$. To obtain comparable marginal effects for our model in Eq. (7), Average Partial Effects (APEs) are computed by averaging the partial effects over the entire sample on $\varvec{X}_{it}$ and the distributions of c and $\mu$. The APEs are thus interpreted as the effect that a change in the average sample observation of a covariate has on the expected probability.

Second, with respect to the spatial probit model, the same direct, indirect and total effects intepretation for spatial models holds in the context of the probit model APEs interpretation. That is, a change in the average value of the kth observation of the covariate vector would have the own-direct APE on its outcome $propacre_k$ in addition to spillover (indirect) APE on other units $propacre_l$, where $k \ne l$ (LeSage 2008).

6 Results

6.1 Intensity of Groundwater Use

Table 4 reports the direct, indirect and total average marginal effects from the range of local and global spillovers based on our first specification (Eq. 5) for 0.5-mile and 1-mile radius neighborhood weight matrices. The dependent variable is the intensity of irrigation: how many acre-feet of water were used per acre of land (i.e. acre-ft/acre). Due to space constraints, only estimates key variables are reported. Results for 2- and 5-mile radii stated in the Appendix for all specifications, with Table 7 as the counterpart to Table 4.

Across all radii, we find a positive, significant $\rho$, which is the spatial coefficient on $W y_{it}$, demonstrating there is indeed spatial dependence in the response variable, ${\text {acre-feet/acre}}$, among the irrigating units. Though the degree of this interdependency seems small across the various radii, it is important to recognize that $\rho$ captures the net (marginal) effect from the feedback loop. The effects from or to a neighbor could individually be large, but the counterbalancing of these effects gives the small, positive coefficient.

The sign on all key covariates reported remains the same across all radii, showing that the relationship between these variables and the outcome variable remains the same and ubiquitous throughout the system (i.e., San Luis Valley groundwater irrigated agriculture). The positive direct effect of a given variable on its own indicates that a change in that variable, all else equal including neighbor response, increases the irrigator’s own pumping.

Table 4 Direct, indirect and total effects for water use (acre-foot/acre) for 0.5- and 1-mile radii

The own-unit direct effect of a 1-dollar increase in pumping fee is to reduce acre-feet/acre of water use irrespective of where irrigating units are located. The direct effect of a 1-percent increase in depth-to-water is to increase acre-feet/acre of water use, while the direct effect of a 1-percent increase in surface-water availability is to reduce groundwater use. Additionally, for almost all covariates, the signs of their direct and total effect are the same. This means that either the indirect effect has the same sign as well or, when it is opposite, the size of the indirect effect is not large enough to alter the overall effect of the covariate on the outcome for a given irrigating unit.

Turning to indirect effects, the results show varied strength, significance, and range of spillover effects across the neighborhood definitions. A positive indirect effect would mean that a change in that variable indicates additional adjustments to neighborhood pumping, including neighbors’ reactions to the irrigator’s direct effect, increase the irrigator’s response. For most key variables, the indirect effects decrease as the neighborhood radius increases, indicating units are more affected by covariate changes of a nearby unit than by a unit farther away. In other words, the interactions satisfy Tobler’s first law—“everything is related to everything else, but near things are more related than distant things” (Tobler 1970).

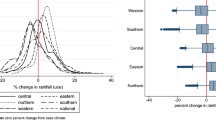
The total effect is the impact of a given change in the covariate for all neighboring units on the outcome variable in unit i, average over all units. Since the indirect effect is the difference between the total and direct effects, an insignificant indirect effect implies there is not a strong local effect given a change in the covariate. However, where the indirect effect is significant and greater than the direct effect, models that do not consider spillovers would underestimate the effect on outcomes of changes in the covariate (Gibson 2019). Within the half-mile radius (Column 2 of Table 4), we see see large indirect effects of the pumping fee, depth-to-water, surface water availability, and even sprinkler technology; all four are significant and larger in magnitude than their respective direct effects. For the depth-to-water variable, for example, the direct effect captures only about $18.7\%$ of its total effect on acre-feet/acre, missing a significant $81.3\%$ of the total effects. Figure 1 demonstrates this for depth-to-water and surface water availability with the actual estimated effects.

Fig. 1

Direct and indirect effects of depth-to-water and surface water availability on water-use intensity. Note. depth-to-water here is measured as log feet and surface water as log acre-feet

For instance, depth-to-water has a positive direct effect, meaning the irrigator does not scale back irrigation when they observe a higher depth-to-water, but rather, increases their watering intensity (acre-foot per acre). Because this is separated from the indirect effect, we interpret the meaning of this direct effect as own response to the situation only, meaning groundwater depth seems to be something like a Giffen input, likely because of the lift cost structure and the potential for extinction. The positive indirect effect of depth-to-water is what indicates competition, regardless of the sign of the direct effect: when neighbors increase water use intensity as a response to their own scarcity and the irrigator’s direct effect, that in turn increases the irrigator’s water use intensity as well.

Regarding the nature of the spillovers and the underlying interaction, the positive indirect effect of depth-to-water provides an important clue. Neighboring irrigating units interpret increasing depth-to-water levels as signal of increased pumping by neighbors or a general rise in water scarcity levels. Their response might then indicate a reaction to the cone of depression, with irrigators hoping to extend the cone around their well so as to direct the flow of water into their well at a faster rate, creating further spillovers and feedback effects. In essence, this type of competitive pumping would lead to increased water use per acre, and hence the positive relationship even though increased depth-to-water is expected translate into increased extraction cost. The other three variables—fee, surface water availability, and sprinkler technology—may indicate conservation/decreased pumping by neighbors and thus give the opposite. In the San Luis Valley, regulations require irrigators with access to surface water to only use groundwater if they exhaust their surface water supplies, expect for ditches with a special recharge decree (Smith et al. 2017). Column (1) of Table 4 implies that a $100\%$ increase in surface water availability leads to a direct effect of reducing groundwater use per acre by 0.18 acre-foot, which is bolstered by an indirect effect of 0.71 acre-feet reduction in groundwater use. Irrigating units within the half-mile radius neighborhood who have surface water rights appear to be observing regulations, signaling a competitive posture working through the global effects of the reduction in groundwater use by those units with increased availability of surface water.

Surprisingly, acres of land fallowed in a previous growing season do not have spillover effects on groundwater use. Fallowing land in a previous season increases own water use a bit, indicating that areas are not likely to be fallowed two seasons in a row, but the indirect and total effects are insignificant. We also show that acres of land committed to various crop types the preceding season also do not induce statistically significant spillover effects, though cultivating grass or alfalfa last year raises own pumping more than other crops. Finally, the site-specific variables of permitted flow rate, well depth, and lack of surface ditch all have the expected sign of direct effect, but do not have any significant spillovers.

6.2 Production Competitiveness (Acreage Irrigated)

While the previous specification examined the externality in terms of competitive groundwater use, we also examine whether irrigating units respond to neighboring units’ productivity. Put differently, are irrigating units’ outcomes in terms of productivity affected by changes in neighbors’ productivity and their covariates? In the absence of data on yield per acre, we proxy productivity by total acreage cultivated per season as the response variable in Eq. (5). Table 5 reports the average marginal effects for the 0.5-mile and 1-mile radius neighborhoods, while Table 8 reports for 2 and 5 miles.

Table 5 Direct, indirect and total effects for acreage irrigated for 0.5- and 1-mile radii

Cross-unit spillovers are positive and large for groundwater used in the 0.5-mile radius. This indicates competitiveness in choosing acreage size relative to neighbors’ water use, and so own cropping efforts increase. Unlike in the previous specification, however, an increase in depth-to-water level predicates a reduction in acreage cultivated. Thus, it would seem that when irrigators’ decision relates to water use, they tend to interpret increasing depth-to-water in terms of being at the risk of facing stock externality and thus apply the “rule of capture,” increasing their groundwater use in the process. However, when their decision relates to how much acreage to cultivate, increasing depth-to-water is seen as a prohibitive factor in terms high extraction cost. This may seem initially contradictory, but given the data, it could well be that irrigators’ response to increasing depth-to-water is to reduce acres cultivated but plant more water-intensive and more profitable crops.

Across all radii, we find the spatial autoregressive parameter $\rho$ positive and highly significant, providing evidence of strategic interaction. This demonstrates the spillover framework developed by Brueckner (2003) in which agent i determines the acreage cultivated by considering the acreage cultivated by other irrigating units in the neighborhood. Our results suggest that an increase in acreage cultivated by neighboring irrigating units leads to an increase in unit’s i acreage cultivated by a positive value, $\rho$W—a global effect. Units may interpret this positive spillover as increased groundwater use by neighbors and then seek to lessen the earlier-mentioned pumping cost/risk externalities (Provencher and Burt 1993).

The effect of sprinkler technology changes sign as well. This is not surprising as irrigators are likely to want to leverage the efficiency of the sprinkler technology—water and cost savings—to cultivate more acres. Use of sprinklers by the neighbors may or may not leave more groundwater available—the coefficient on sprinkler technology in the the groundwater intensity specification was insignificant. However, both direct and indirect effects of sprinkler technology on production intensity are positive. This result may indicate a version of Jevons’ Paradox: “a technology that enhances the efficiency of using a natural resource does not necessarily lead to less consumption of that resource” (Sears et al. 2018, p. 5). This paradox may thus explain both the positive direct and indirect effects on sprinkler technology, in that its availability increases both own and neighborhood acreage irrigated, separately from the indirect decrease in pumping intensity indicated in Table 4. Total groundwater use of neighbors may not decrease as a result of sprinkler technology, but the same amount may be spread over a larger number of acres.

For all the spillover effects in Table 5, we again see that the indirect effects are larger than the direct effects. The direct effect of a $100\%$ increase in the amount of groundwater use is to increase acreage cultivated by some 0.212 acres. The indirect effect of the same change in groundwater use is to increase acreage cultivated by 1.36 acres. Given that the total effect of this change in groundwater use is 1.57 acres, the direct effect contributes only $13.5\%$ while the indirect effects constitute a significant $86.5\%$. The same analysis holds true for depth-to-water where the indirect effect constitutes $92.3\%$ of the total effects.

We also see significant negative spillovers associated with lagged crops and lagged fallowing. Each crop choice other than small grains leads to decreases in cultivated acres. This is less relevant in our context of the groundwater commons, but provides an interesting look at the competition associated with various crops. A neighbor that fallowed land last season is unlikely to do so this season, and thus is expected to produce more, thus perhaps inducing an irrigator to decrease their own acreage in response.

6.3 Proportional Production Intensity

Our final specification tests production intensity as the proportion of total available acres irrigated. Results of the fractional spatial Probit regression model in Eq. (7) are presented in Table 6 for the 0.5- and 1-mile radius neighborhood specifications and in Table 9 for 2 and 5 miles. Across all these neighborhood definitions, the spatial lag of the fractional response variable Wpropacre is highly statistically significant. This confirms that a standard Probit model would ignore the spatial dependence in the response variable, propacre, and also an indication of spatial dependence in land-use intensity. This implies that resource management failing to account for this spatial interdependence will not achieve full efficiency. The positive $\rho$ implies the propensity of an irrigating unit increasing its land-use intensity increases when neighboring units also have a high propensity; pricing schemes ignoring this effect will thus undercharge for groundwater and overcultivate land. A commonly discussed example of such overcultivation outside of the SLV is that of almonds in California, which have a high water footprint in relation to their calorie content and other crops (Fulton et al. 2019). Relative to the two previous models, the magnitude of $\rho$ estimated in the production intensity model (7) is large across all four neighborhood specifications with the half-mile radius being the neighborhood with the biggest size of the spatial parameter estimate of 0.7227. The strength decays as the radius is increased.

The direct and indirect effects reported in Table 6 (and 9 in the Appendix) are average partial effects (APEs) and reflect the direction and magnitude of the own-unit and cross-unit effects of a change in the average value of the covariate. Using the 0.5- and 1-mile neighboring results, we show that, in terms of direct effects, higher groundwater use, lower pumping fee, smaller depth-to-water, higher amount of surface water availability, and sprinkler technology all increase a unit’s proportional production intensity. For instance, with respect to the 0.5-mile radius, a $10\%$ increase in the amount of groundwater used leads to a direct APE of increasing the proportion of acre cultivated by 0.00268 (0.268 percentage points). A $\$10$ increase in pumping fee reduces the proportion of land cultivated by 0.008 while a $10\%$ increase depth-to-water reduces production intensity by 0.00643.

Table 6 Average partial direct and indirect effects for proportion of total available acres irrigated for 0.5- and 1-mile radii

Regarding the indirect effects, just as seen in the two previous models, the strength and extent of the spillover effects from changes in the covariates vary and decay across the neighborhood definitions. Notably, the direction (sign) of the impact reverses for a few of the covariates once we move out of the 0.5-mile radius neighborhood. Within the 0.5-mile radius, the indirect APE of a $10\%$ increase of groundwater use is an increase in proportion of land cultivated by 0.22 percentage points. However, expanding the neighborhood range to 1, 2, and 5 miles, the indirect APE of a $10\%$ increase of groundwater use rather decreases the proportion of land cultivated by 0.13, 0.084, and 0.037 percentage points, respectively. The response variable is such that, even if increased groundwater use by neighbors elicits the same by unit i, this may not necessarily translate into higher proportion of available acres cultivated. The increased groundwater use response may go in the direction of increasing water-use intensity (i.e., increasing water use per acre of land in the first specification).

Both depth-to-water and sprinkler technology have statistically significant, negative indirect APE across the neighborhood specifications. A $10\%$ increase in depth-to-water has a spillover effect reducing a unit’s proportion of acres cultivated by 0.63 percentage points within the 0.5-mile radius (decreasing over the larger radii). Similarly as in the previous specifications, because sprinkler technology may be considered water-saving technology (or at least a water-effectiveness boosting technology), sprinkler use allows agents to increase their own acreage intensity, while sprinkler use by neighbors encourages agents to reduce the proportion of acres cultivated, all else equal.

6.4 Robustness of Results

The pumping fee implemented in the Subdistrict No.1 (serving as the Pigouvian tax b in the theoretical model) is likely to change water use habits relative to irrigators in other subdistricts. If this is the case, it may be that the estimates from these spatial models may be different if they are run separately on subdistricts with pumping fee and on those without pumping fee. Estimating the models on the split data, we show that the responses among irrigators in the two separate groups is qualitatively similar. Table 10 in the Appendix presents results for the land-use intensity model (the third specification) for a 0.5-mile radius neighborhood for units in Subdistrict No.1 only, while Table 11 shows that of the other subdistricts. For both subdistrict groups, the spatial autocorrelation parameter remains positive as in the full sample results. The direct and indirect effects of change in acre-ft of groundwater use also remain positive and the indirect effect of depth-to-water maintains the negative sign. The implication therefore, is that irrespective of the pumping fee, competitiveness among irrigating units persists.

Finally, there may be some concern regarding the responses of irrigators that fall under the special recharge decree, and how their reactions to increased surface water availability may differ from irrigators not under the same decree. Per our analysis about 3743 out of our 10,525 observations are affected by the ditches with the special recharge decree. Taking cognizance of this, we ran several specifications including an interaction variable of surface water interacted with those ditches with special recharge decrees. The coefficients of this interaction variable (both direct and indirect effects) were not statistically significant, and the signs of the other coefficients did not differ from the reported models. Our results largely align with Smith et al. (2017), which reported the coefficient of the interaction between surface water and the special decree ditches as having a negative sign (see Smith et. al. 2017’s online appendix Table C4: Unit-Year Robustness Checks; Acre Feet Extracted). Only when this interaction is further interacted with post-intervention years membership of Subdistrict No. 1 does a positive coefficient result. We do not replicate this third level interaction as our analysis does not use this difference-in-difference framework.

7 Conclusions

Previous studies have discussed whether use of the groundwater commons can be socially efficient where individual irrigators seek to maximize their own welfare. Some support imposition of financial incentives and increased participation in decentralized commons in order to yield outcomes closer to the social optimum and sustainability (for example, Provencher and Burt 1993; Koundouri 2004; Ito 2012). Others suggest the social optimum may not necessarily differ from the competitive solution, or that its benefits are tempered by spatial externalities (for example, Gisser and Sanchez 1980; Gisser 1983; Rubio and Casino 2003).

In this paper, we investigate the extent to which the presence of a stock externality induces competition among irrigators who share the same aquifer. Using a spatial dataset on irrigating units from the San Luis Valley (SLV) in Colorado, we find that in addition to water-use intensity, neighboring irrigators also seem to compete in terms of the size of acreage they choose to cultivate and the proportion of their cultivable land they choose to put into production each season. Furthermore, not only are irrigators affected by their neighbors’ choices of these three outcome variables, but they are also affected by key variables like depth-to-water (which proxies scarcity and extraction cost), surface water availability, and sprinkler technology. We also control for fallowed acreage and crop choices in preceding years, which show the effect of switching costs and competition in planting efforts.

In terms of water-use intensity, the results show that one-percent increase in depth-to-water level has both direct and indirect (spillover) effects of increasing acre-ft/acre of ground water use, but the spillover effect constitutes a significant greater share of the total effects. For example, within a half-mile radius neighborhood, the spillover effect is over $81\%$ of the total effect of a rise in depth-to-water. Increases in surface water availability on the other hand have both direct and spillover effects of reducing amount of groundwater use, with spillovers again constituting about $80\%$ of the total effect.

We draw two main conclusions from these results. First, models that do not include spatial lags of these covariates would fail to capture these spillover effects from neighboring irrigating units, thus understating the total effects. Second, positive spillovers from depth-to-water imply competitive water usage: when irrigating units attribute a longer depth-to-water to increased groundwater use by neighbors, they tend to respond by increasing their own groundwater use in return. In the same light, where surface water availability increases, irrigation units reasonably associate this with a reduction in neighborhood pumping and respond by also reducing groundwater use. These two responses are characteristic of commons competition or a strategic interaction of the kind where irrigating units increase water-use intensity when they believe neighbors are doing same and vice versa.

This effect is mainly seen on irrigation intensity, as increased pumping has only small negative spillover effects of choosing smaller acreage or lower land-use intensity. The positive own-unit direct effect, however, is generally large enough to ensure total effects are positive. Furthermore, when irrigating units associate high extraction cost to increasing depth-to-water, they respond by reducing both acreage and proportional land-use intensity. At the core of this competitive and strategic response is, as noted earlier, the stock or pumping cost/congestion externality. Given these results obtain even under a pumping fee, it remains to be seen if price incentive policies can effectively reduce competitive pumping as much as required on a long-term basis to ensure sustainable extraction in groundwater commons.¹⁵

With regard to policy, the constant across-the-board pumping fee as implemented in the SLV assumes that irrigators exert equal externality on each other, irrespective of the depth-to-water from which individuals withdraw water. Given our analysis, the fact that depth-to-water has a positive spillover effects implies competitive water use: when irrigating units attribute increasing depth-to-water to increased groundwater use by neighbors, they could respond by also increasing groundwater use, even in the face of the constant marginal fee. If we consider depth-to-water as a cost-metric measure of groundwater scarcity, then better knowledge of the nature of the spatial spillovers could be used to design a more user-specific pumping fee, in a bid to account for the net externality generated by individual irrigators and achieve efficiency. This is of particular import to the SLV, given that the irrigators’ will lose usage rights if the Conservation District cannot increase conservation.

These results are obtained using land mass irrigating units and not the locations of the physical wells as unit of analysis. If hydraulic conductivity data measures become available and the physical well locations are used as units of analysis, the strength of these results may even be bolstered. Additionally, the combination of confined and unconfined aquifer sources in the SLV region should be considered. If driven by Subdistrict No. 1’s closed basin aspect, then the results from this area present somewhat of an “upper bound” on the potential efficacy of intervention. Conservation in areas where the aquifer flows out of the region may have lower local incentives, as the commons flow to downstream stakeholders. Finally, while we cannot speak to the exact hydraulic conductivity of the region, we expect our results regarding the misspecficiation of a constant groundwaterwater tax without consideration of spatial externalities will hold for water stressed regions with any positive amount of transmissivity between fields, be the area similar to or different from the SLV. The search for a policy mix that would address the spatial externality must therefore continue to engage the attention of researchers, policymakers, and users.

Appendices

Appendix 1 Additional Derivations

1.1 Individual Problem

The first order conditions from irrigator j’s Nash equilibrium problem are as follows:

$$\begin{aligned} \begin{aligned} \frac{\partial {\varvec{\Uppi }^{j}}}{\partial w^j_k}&= \sum _{\ell =0}^K \frac{\partial \varvec{\pi }^{j*}_\ell \big (p_\ell , {\textbf {r}}, B^j(s^j(w^j, w^i),b), n^{j*}_\ell (\cdot ); {\textbf {x}}\big )}{\partial w^j_k} \\&= \sum _{\ell =0}^{K} \left[ \left( \frac{\partial \varvec{\pi }^{j*}_\ell (\cdot )}{\partial B^j(\cdot )} + {\frac{\partial \varvec{\pi }^{j*}_\ell (\cdot )}{\partial n^{j*}_\ell (\cdot )} \cdot } \frac{\partial n^{j*}_\ell (\cdot )}{\partial B^j(\cdot ) } \right) \left( \frac{\partial B^j(\cdot )}{\partial s^j(\cdot )} \cdot \frac{\partial s^j(\cdot )}{\partial w^j_k} \right) \right] \le 0 \\ \end{aligned} \end{aligned}$$

(9)

with equality if water withdrawal is positive, i.e. $w_k^j > 0$.

Using the Implicit Function Theorem, we see:

$$\begin{aligned} \frac{d w^i_k}{d w^j_m} = - \frac{ \displaystyle \frac{\partial }{\partial w^j_m}\left[ \frac{\partial {\varvec{\Uppi }^{i}}}{\partial w^i_k}\right] }{\displaystyle \frac{\partial }{\partial w^i_k}\left[ \frac{\partial {\varvec{\Uppi }^{i}}}{\partial w^i_k}\right] } = - \frac{\displaystyle \frac{\partial ^2 {\varvec{\Uppi }^{i}}}{\partial w^i_k \partial w^j_m }}{\displaystyle \frac{\partial ^2 {\varvec{\Uppi }^{i}}}{\partial {w^i_k}^2}}. \end{aligned}$$

(10)

The strategic effect of j’s total withdrawal will be made up of these individual effects, which are the cross-partial and the second order condition of own withdrawal on profits. Because of the external negative sign, the strategic effect will be positive if either numerator or denominator (but not both) is positive, while it would be negative if numerator and denominator match in sign. The effect will be small in absolute terms if the own second order condition is larger in magnitude than that due to the opponent, while the effect will be large if the other-directed second order condition is larger. The full second order conditions, with respect to $w^j_m$ and $w^i_k$ are as follows:

$$\begin{aligned}& \frac{\partial }{\partial w^j_m} \left[ \frac{\partial {\varvec{\Uppi }^{i}}}{\partial w^i_k}\right]= \sum _{\ell =0}^K \Bigg \{ \left( \frac{\partial ^2 \varvec{\pi }^{i*}_\ell (\cdot )}{ \partial B^i(\cdot )^2 } + \frac{\partial ^2 \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )^2} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot )} + \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )}\cdot \frac{\partial ^2 n^{i*}_\ell (\cdot )}{\partial B^i(\cdot )^2 } \right) \nonumber \\ &\quad\quad\quad\quad\quad\quad\; \cdot \left( \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \right) ^2 \left( \frac{\partial s^i(\cdot )}{\partial w^j_m} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) + \left( \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial B^i(\cdot )} + \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot ) } \right) \\ &\quad\quad\quad\quad\quad\quad\; {\cdot} \left. {\left( {\frac{{\partial ^{2} B^{i} ( \cdot )}}{{\partial s^{i} ( \cdot )^{2} }} \cdot \frac{{\partial s^{i} ( \cdot )}}{{\partial w_{m}^{j} }} \cdot \frac{{\partial s^{i} ( \cdot )}}{{\partial w_{k}^{i} }} + \frac{{\partial B^{i} ( \cdot )}}{{\partial s^{i} ( \cdot )}} \cdot \frac{{\partial ^{2} s^{i} ( \cdot )}}{{\partial w_{m}^{j} \partial w_{k}^{i} }}} \right)} \right\} \end{aligned}$$

(11)

$$\begin{aligned}\frac{\partial }{\partial w^i_k} \left[ \frac{\partial {\varvec{\Uppi }^{i}}}{\partial w^i_k}\right]&= \sum _{\ell =0}^K \Bigg \{ \left( \frac{\partial ^2 \varvec{\pi }^{i*}_\ell (\cdot )}{ \partial B^i(\cdot )^2 } + \frac{\partial ^2 \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )^2} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot )} + \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )}\cdot \frac{\partial ^2 n^{i*}_\ell (\cdot )}{\partial B^i(\cdot )^2 } \right) \nonumber \\& \quad\;\cdot \left( \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) ^2 + \left( \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial B^i(\cdot )} + \frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot ) } \right) \nonumber \\&\quad\;\cdot \left( \frac{\partial ^2 B^i(\cdot )}{\partial s^i(\cdot )^2} \left( \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) ^2 + \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial ^2 s^i(\cdot )}{\partial {w^i_k}^2} \right) \Bigg \} \end{aligned}$$

(12)

Using Eqs. (11) and (12), we can write $-\frac{d w^i_k}{d w^j_m}$ as:

$$\frac{{ {\sum\limits_{{l = 0}}^{K} \begin{gathered} \left\{ {\left( {\frac{{\partial ^{2} \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )^{2} }} + \frac{{\partial ^{2} \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial n_{\ell }^{{i*}} ( \cdot )^{2} }} \cdot \frac{{\partial n_{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )}} + \frac{{\partial \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial n_{\ell }^{{i*}} ( \cdot )}} \cdot \frac{{\partial ^{2} n_{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )^{2} }}} \right)\left( {\frac{{\partial B^{i} ( \cdot )}}{{\partial s^{i} ( \cdot )}}} \right)^{2} \left( {\frac{{\partial s^{i} ( \cdot )}}{{\partial w_{m}^{j} }} \cdot \frac{{\partial s^{i} ( \cdot )}}{{\partial w_{k}^{i} }}} \right)} \right. \hfill \\ \left. {\quad \quad + \left( {\frac{{\partial \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )}} + \frac{{\partial \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial n_{\ell }^{{i*}} ( \cdot )}} \cdot \frac{{\partial n_{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )}}} \right)\left( {\frac{{\partial ^{2} B^{i} ( \cdot )}}{{\partial s^{i} ( \cdot )^{2} }} \cdot \frac{{\partial s^{i} ( \cdot )}}{{\partial w_{m}^{j} }} \cdot \frac{{\partial s^{i} ( \cdot )}}{{\partial w_{k}^{i} }} + \frac{{\partial B^{i} ( \cdot )}}{{\partial s^{i} ( \cdot )}} \cdot \frac{{\partial ^{2} s^{i} ( \cdot )}}{{\partial w_{m}^{j} \partial w_{k}^{i} }}} \right)} \right\} \hfill \\ \end{gathered} } }}{{ {\sum\limits_{{l = 0}}^{K} \begin{gathered} \left\{ {\left( {\frac{{\partial ^{2} \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )^{2} }} + \frac{{\partial ^{2} \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial n_{\ell }^{{i*}} ( \cdot )^{2} }} \cdot \frac{{\partial n_{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )}} + \frac{{\partial \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial n_{\ell }^{{i*}} ( \cdot )}} \cdot \frac{{\partial ^{2} n_{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )^{2} }}} \right)\left( {\frac{{\partial B^{i} ( \cdot )}}{{\partial s^{i} ( \cdot )}} \cdot \frac{{\partial s^{i} ( \cdot )}}{{\partial w_{k}^{i} }}} \right)^{2} } \right. \hfill \\ \left. {\quad \quad \left( {\frac{{\partial \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )}} + \frac{{\partial \pi _{\ell }^{{i*}} ( \cdot )}}{{\partial n_{\ell }^{{i*}} ( \cdot )}} \cdot \frac{{\partial n_{\ell }^{{i*}} ( \cdot )}}{{\partial B^{i} ( \cdot )}}} \right)\left( {\frac{{\partial ^{2} B^{i} ( \cdot )}}{{\partial s^{i} ( \cdot )^{2} }}\left( {\frac{{\partial s^{i} ( \cdot )}}{{\partial w_{k}^{i} }}} \right)^{2} + \frac{{\partial B^{i} ( \cdot )}}{{\partial s^{i} ( \cdot )}} \cdot \frac{{\partial ^{2} s^{i} ( \cdot )}}{{\partial w_{k}^{{i2}} }}} \right)} \right\} \hfill \\ \end{gathered} } }}$$

(13)

With regard to the individual first derivative terms, we assumed for all crops k that an increase in the total marginal cost of water decreases profits, $\frac{\partial \varvec{\pi }^i_k(\cdot )}{\partial B^i(\cdot )} < 0$, while profits are non-decreasing in land allocation, $\frac{\partial \varvec{\pi }^i_k(\cdot )}{\partial n^{i*}_k(\cdot )} \ge 0$. Because of lift cost, increasing depth-to-water increases total marginal cost, $\frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} > 0$. We assume that an agent’s own water use weakly increases their scarcity measure, $\frac{\partial s^i(\cdot )}{\partial w^i_k(\cdot )}\ge 0$; we also assume that another agent’s water use weakly increases¹⁶ agent i’s scarcity, $\frac{\partial s^i(\cdot )}{\partial w^j_m} \ge 0$. Less obvious, however, is how total marginal cost of water affects the land dedicated to various crops, $\frac{\partial n^{i*}_k (\cdot )}{\partial B^i(\cdot )}$: the farmer may decrease land for water-intensive crops and increase the allocation for fallowing or other crops, or there may be no reaction at all. In a particular growing season, it is unlikely the farmer will be able to purchase land quickly enough to grow additional crops that season. If we also assume that land is sold outside of the growing season (listed after a previous season), then we can see that in a particular game, total land is fixed, $\sum _{k=0}^K n^i_k = N^i$. Thus, when examining the derivatives, we know that their sum must add up to a constant, which is zero in the case of the one-stage game¹⁷ with no land sale: $\sum _{k=0}^K \frac{\partial n^i_k}{\partial B^i} = 0$.

With regard to the second derivative terms, we assumed convex profits, meaning $\frac{\partial ^2 \pi ^{i*}_k(\cdot )}{\partial B^i(\cdot )^2} \ge 0$. Resource cost functions are often convex, i.e. accelerating in cost (Schworm 1983; Kotani et al. 2008), and so we assume $\frac{\partial ^2 B^i(\cdot )}{\partial s^i(\cdot )^2} \ge 0$. Unfortunately, a priori, we cannot say much about the remaining second derivatives. There are two derivatives about the second order effect of water withdrawal—both i’s and j’s—on i’s depth-to-water. While we are comfortable assuming the first derivative is weakly positive (taking out water increases scarcity), we are unsure whether this effect is increasing, constant, or decreasing. The own second order effect, $\frac{\partial ^2\,s^i(\cdot )}{\partial w^i_k(\cdot )^2}$, reflects the curvature with regard to water withdrawal for only the farmer in question, while the cross-partial, $\frac{\partial ^2\,s^i(\cdot )}{\partial w^j_m \partial w^i_k(\cdot )}$, reflects how another farmer’s withdrawals change the marginal cost of withdrawal for farmer i. Additionally, we will remain agnostic on the second derivative of land allocation for crop k with respect to water cost, $\frac{\partial ^2 n^{i*}_k (\cdot )}{\partial B^i(\cdot )^2}$.

Examining the numerator of Eq. (13), an individual term in the summation is:

$$\begin{aligned} \begin{aligned}&\left( \underbrace{\frac{\partial ^2 \varvec{\pi }^{i*}_\ell (\cdot )}{\partial B^i(\cdot )^2 }}_{\ge 0} + \frac{\partial ^2 \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )^2} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot )} + \underbrace{\frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )}}_{\ge 0}\cdot \frac{\partial ^2 n^{i*}_\ell (\cdot )}{\partial B^i(\cdot )^2 } \right) \underbrace{\left( \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \right) ^2}_{>0} \underbrace{\left( \frac{\partial s^i(\cdot )}{\partial w^j_m} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) }_{>0} \\&\quad+ \left( \underbrace{\frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial B^i(\cdot )}}_{<0} + \underbrace{\frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )}}_{\ge 0} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot ) } \right) \left( \underbrace{\frac{\partial ^2 B^i(\cdot )}{\partial s^i(\cdot )^2}}_{\ge 0} \cdot \underbrace{\frac{\partial s^i(\cdot )}{\partial w^j_m} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k}}_{>0} + \underbrace{\frac{\partial B^i(\cdot )}{\partial s^i(\cdot )}}_{>0} \cdot \frac{\partial ^2 s^i(\cdot )}{\partial w^j_m \partial w^i_k} \right) \end{aligned} \end{aligned}$$

(14)

Meanwhile, an individual term in the denominator is:

$$\begin{aligned} \begin{aligned}&\left( \underbrace{\frac{\partial ^2 \varvec{\pi }^{i*}_\ell (\cdot )}{\partial B^i(\cdot )^2 }}_{\ge 0} + \frac{\partial ^2 \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )^2} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot )} + \underbrace{\frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )}}_{\ge 0}\cdot \frac{\partial ^2 n^{i*}_\ell (\cdot )}{\partial B^i(\cdot )^2 } \right) \underbrace{\left( \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) ^2}_{>0} \\&\quad+ \left( \underbrace{\frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial B^i(\cdot )}}_{<0} + \underbrace{\frac{\partial \varvec{\pi }^{i*}_\ell (\cdot )}{\partial n^{i*}_\ell (\cdot )}}_{\ge 0} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot ) } \right) \left( \underbrace{\frac{\partial ^2 B^i(\cdot )}{\partial s^i(\cdot )^2}}_{\ge 0} \underbrace{\left( \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) ^2}_{>0} + \underbrace{\frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} }_{>0} \cdot \frac{\partial ^2 s^i(\cdot )}{\partial {w^i_k}^2} \right) \end{aligned} \end{aligned}$$

(15)

The first thing to note is that the sign of $\frac{d w^i_k}{d w^j_m}$ will depend on the signs of in Eqs. (14) and (15) added up over K. For each crop, these only differ according to curvature of profits with respect to land allocation and land reallocation with respect to water cost. The first terms of both Eqs. (14) and (15) will match in sign, so the second term that will determine the sign of the strategic effect. This second term is the change in profits per crop scaled by the adjustments in scarcity due to withdrawals and water’s cost due to scarcity.

The second thing to note is how these two expressions differ from each other: the denominator has a squared term $\left( \frac{\partial s^i(\cdot )}{\partial w^i_k}\right) ^2$, where the numerator has a product of matching signs but potentially not magnitudes, $\frac{\partial s^i(\cdot )}{\partial w^j_m} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k}$. Additionally, the final term in the numerator has the cross-partial of withdrawal, while that term in the denominator has the own second order effect. These terms are where potential differences in sign and magnitude arise.

1.2 Coordinated Problem

The first order conditions of the coordinated problem with respect to i’s water choices are as follows:

$$\begin{aligned}\begin{aligned} & \frac{\partial {\varvec{\Uppi }^{sp}}}{\partial w^i_k}= \sum _{\ell =0}^{K} \left( \frac{\partial \varvec{\pi }^i_\ell \big (p_\ell , {\textbf {r}}, B^i(s^i(w^i, w^j),b), n^{i*}_\ell (\cdot ); {\textbf {x}}\big )}{\partial w^i_k} + \frac{\partial \varvec{\pi }^j_\ell \big (p_\ell , {\textbf {r}}, B^j(s^j(w^i, w^j),b), n^{j*}_\ell (\cdot ); {\textbf {x}}\big )}{\partial w^i_k} \right) \\& \quad\quad\;= \sum _{\ell =0}^{K} \left( \frac{\partial \varvec{\pi }^i_\ell (\cdot )}{\partial B^i(\cdot )} \cdot \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} + \frac{\partial \varvec{\pi }^i_\ell (\cdot )}{\partial n^{i*} _\ell (\cdot )} \cdot \frac{\partial n^{i*} _\ell (\cdot )}{\partial B^i(\cdot ) }\cdot \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) \\&\quad\quad\quad\;+\sum _{\ell =0}^{K} \left( \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial B^j(\cdot )} \cdot \frac{\partial B^j(\cdot )}{\partial s^j(\cdot )} \cdot \frac{\partial s^j(\cdot )}{\partial w^i_k} + \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial n^{j*} _\ell (\cdot )} \cdot \frac{\partial n^{j*} _\ell (\cdot )}{\partial B^j(\cdot ) }\cdot \frac{\partial B^j(\cdot )}{\partial s^j(\cdot )} \cdot \frac{\partial s^j(\cdot )}{\partial w^i_k} \right) \\&\quad\quad\;= \sum _{\ell =0}^{K} \left( \frac{\partial \varvec{\pi }^i_\ell (\cdot )}{\partial B^i(\cdot )} + \frac{\partial \varvec{\pi }^i_\ell (\cdot )}{\partial n^{i*} _\ell (\cdot )} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot ) } \right) \left( \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^i_k} \right) \\&\quad\quad\quad\;+ \sum _{\ell =0}^{K} \hspace{-5.69054pt}\underbrace{ \left( \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial B^j(\cdot )} + \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial n^{j*} _\ell (\cdot )} \cdot \frac{\partial n^{j*}_\ell (\cdot )}{\partial B^j(\cdot ) } \right) \left( \frac{\partial B^j(\cdot )}{\partial s^j(\cdot )} \cdot \frac{\partial s^j(\cdot )}{\partial w^i_k} \right) }_{ E^i_k } \le 0 \\ \end{aligned} \end{aligned}$$

(16)

with equality if water withdrawal is positive, i.e. $w_k^i > 0$.

Again, assuming the irrigators are symmetric, we have for $w^j_k$

$$\begin{aligned} \begin{aligned} & \frac{\partial {\varvec{\Uppi }^{sp}}}{\partial w^j_k}= \sum _{\ell =0}^{K} \left( \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial B^j(\cdot )} + \frac{\partial \varvec{\pi }^j_\ell (\cdot )}{\partial n^{j*} _\ell (\cdot )} \cdot \frac{\partial n^{j*}_\ell (\cdot )}{\partial B^j(\cdot ) } \right) \left( \frac{\partial B^j(\cdot )}{\partial s^j(\cdot )} \cdot \frac{\partial s^j(\cdot )}{\partial w^j_k} \right) \\& \quad\quad\quad\;\;+ \sum _{\ell =0}^{K} \hspace{-5.69054pt}\underbrace{ \left( \frac{\partial \varvec{\pi }^i_\ell (\cdot )}{\partial B^i(\cdot )} + \frac{\partial \varvec{\pi }^i_\ell (\cdot )}{\partial n^{i*} _\ell (\cdot )} \cdot \frac{\partial n^{i*}_\ell (\cdot )}{\partial B^i(\cdot ) } \right) \left( \frac{\partial B^i(\cdot )}{\partial s^i(\cdot )} \cdot \frac{\partial s^i(\cdot )}{\partial w^j_k} \right) }_{ E^j_k } \le 0 \\ \end{aligned} \end{aligned}$$

(17)

with equality if water withdrawal is positive, i.e. $w_k^j > 0$.

Appendix 2 Additional Tables

We include tables for results for the larger 2- and 5-mile radii for all three regression specifications, as well as production intensity (share of acreage cropped) broken out by subdistrict. See Table 7, 8, 9, 10 and 11.

Table 7 Direct, Indirect and Total Effects for Water Use (acre-foot/acre) for 2- and 5-mile radii

Table 8 Direct, indirect and total effects for acreage irrigated for 2- and 5-mile radii

Table 9 Average partial direct and indirect effects for proportion of total available acres irrigated for 2- and 5-mile radii

Table 10 Production intensity for subdistrict with pumping fee—half-mile radius

Table 11 Production intensity for subdistrict with no pumping fee—half-mile radius