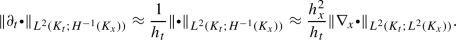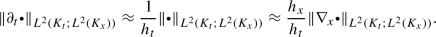Interpolation operators for parabolic problems

Abstract

We introduce interpolation operators with approximation and stability properties suited for parabolic problems in primal and mixed formulations. We derive localized error estimates for tensor product meshes (occurring in classical time-marching schemes) as well as locally in space-time refined meshes.

1 Introduction

In recent years simultaneous space-time variational formulations for parabolic problems became more and more popular. Besides practical aspects like highly parallelizable computations [4, 19, 24, 33] the ansatz offers analytical advantages including quasi-optimality of the discrete solution [31] (also called symmetric error estimates in [3, 6]). This property motivates adaptive time stepping [12], adaptive wavelet schemes [25], adaptive wavelet-in-time and finite-element-in-space approaches [28], and even adaptive mesh refinements locally in space-time [7, 18, 22, 23]. While numerical experiments suggest superiority of the latter approach for singular solutions, theoretical results are restricted to plain convergence [17] but do not verify optimal convergence rates as they do for elliptic problems [2, 27]. Motivated by the extension of such optimality results to parabolic problem, this paper introduces and investigates a main ingredient in the analysis of adaptive schemes for parabolic problems like the heat equation in a time-space cylinder $Q = \mathcal {J} \times \Omega$, namely interpolation operators suited for the norm

Additionally, we introduce an interpolation operator for first-order formulations of the heat equation satisfying a beneficial commuting diagram property. On tensor product meshes the interpolation operators are stable and have optimal approximation properties. We give upper bounds for the interpolation errors and emphasize the need of parabolic scaling if the solution is rough in time. The localization of the interpolation error in space leads to unavoidable weights in terms of negative powers of the local mesh size. Under realistic regularity assumptions we can overcome these negative powers due to parabolic scaling. Unfortunately, this strategy cannot be applied to the interpolation error of adaptively refined meshes. In fact, we illustrate that any (local) interpolation operator experiences these difficulties. Overall, this paper’s main contributions are the following.

• We present approximation properties suited for parabolic problems in Sects. 3 and 4.

• We introduce an interpolation operator with optimal approximation properties on tensor product meshes in Sect. 5.1.

• We introduce an interpolation operator suited for first-order formulations with optimal approximation properties on tensor product meshes and a commuting diagram property in Sect. 5.2.

• We introduce an interpolation operator for locally in space-time refined meshes and discuss its stability in Sect. 6.

2 Bochner spaces and their discretization

This section introduces Bochner spaces, suitable discretizations by finite elements, and their underlying partitions.

2.1 Bochner spaces

Our analysis is motivated by the approximation of parabolic problems like the heat equation. Given a time-space cylinder with bounded time interval $\mathcal {J} = [0,T] \subset \mathbb {R}^d$ and bounded Lipschitz domain $\Omega \subset \mathbb {R}^d$, this problem seeks with given right-hand side $f:Q\rightarrow \mathbb {R}$ and initial data $u_0 :\Omega \rightarrow \mathbb {R}$ the solution $u :Q \rightarrow \mathbb {R}$ to

$$\begin{aligned} \partial _t u - \Delta _x u = f\text { in }Q,\qquad u = 0 \text { on }\mathcal {J} \times \partial \Omega ,\qquad u(0) = u_0\text { in }\Omega . \end{aligned}$$

(1)

A suitable analytical setting relies on Sobolev-Bochner spaces. Therefore, we set the space $H^{-1}(\Omega )$ as the dual of the Sobolev space $H^1_0(\Omega )$ equipped with norm and dual pairing which equals the $L^2$ inner product for smooth functions. Given $V \in \lbrace H^1_0(\Omega ), L^2(\Omega ),H^{-1}(\Omega ) \rbrace$, we set

$$\begin{aligned} \begin{aligned} \Vert p \Vert _{L^2(\mathcal {J};V)}^2&\,{:}{=}\, \int _\mathcal {J} \Vert p(s)\Vert _V^2\,\textrm{d}s\qquad \qquad \text {for all }p:\mathcal {J} \rightarrow V,\\ \Vert v \Vert _{H^1(\mathcal {J};V)}^2&\,{:}{=}\,\Vert v \Vert _{L^2(\mathcal {J};V)}^2 + \Vert \partial _t v \Vert _{L^2(\mathcal {J};V)}^2 \qquad \qquad \text {for all }v:\mathcal {J} \rightarrow V.\\ \end{aligned} \end{aligned}$$

The Bochner spaces read

$$\begin{aligned} \begin{aligned} L^2(\mathcal {J};V)&\,{:}{=}\, \lbrace p:\mathcal {J} \rightarrow V:\Vert p \Vert _{L^2(\mathcal {J};V)}< \infty \rbrace ,\\ H^1(\mathcal {J};V)&\,{:}{=}\, \lbrace v :\mathcal {J} \rightarrow V :\Vert v \Vert _{H^1(\mathcal {J};V)} < \infty \rbrace . \end{aligned} \end{aligned}$$

We can identify $L^2(\mathcal {J};L^2(\Omega )) = L^2(Q)$. Moreover, we have the following.

Remark 1

(Tensor spaces) Bochner spaces can be seen as closure of algebraic tensor product spaces [11, Rem. 64.24], i.e., for $V \in \lbrace H^1_0(\Omega ), L^2(\Omega ),H^{-1}(\Omega )\rbrace$

$$\begin{aligned} L^2(\mathcal {J}) \otimes V&\,{:}{=}\, span \lbrace v_tv_x :v_t\in L^2(\mathcal {J})\text { and }v_x \in V\rbrace{} & {} \text { is dense in }L^2(\mathcal {J};V),\\ H^1(\mathcal {J}) \otimes V&\,{:}{=}\, span \lbrace v_tv_x :v_t\in H^1(\mathcal {J})\text { and }v_x \in V\rbrace{} & {} \text { is dense in }H^1(\mathcal {J};V). \end{aligned}$$

We are particularly interested in the space

$$\begin{aligned} X \,{:}{=}\, L^2(\mathcal {J};H^1_0(\Omega )) \cap H^1(\mathcal {J};H^{-1}(\Omega )). \end{aligned}$$

(2)

Lemma 2

(Embedding) We have for all $v\in X$ and $t\in \mathcal {J} = [0,T]$

$$\begin{aligned} \Vert v(t) \Vert _{L^2(\Omega )}^2 \le T^{-1} \Vert v\Vert _{L^2(Q)}^2 + \Vert \nabla _x v\Vert _{L^2(Q)}^2 + \Vert \partial _t v \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2. \end{aligned}$$

Proof

This is a known result which we prove to stress the dependency on T often hidden in textbooks. Let $v\in X$ and $t\in \mathcal {J}$. The fundamental theorem of calculus [11, Thm. 64.31] reveals for all $\tau \in \mathcal {J}$

$$\begin{aligned} \Vert v(t) \Vert _{L^2(\Omega )}^2&= \Vert v(\tau ) \Vert _{L^2(\Omega )}^2 + 2 \int ^t_\tau \langle \partial _t v,v\rangle _\Omega \,\textrm{d}s\\&\le \Vert v(\tau ) \Vert _{L^2(\Omega )}^2 +\left| \int ^t_\tau \big ( \Vert \partial _t v(s) \Vert _{H^{-1}(\Omega )}^2 + \Vert \nabla _x v(s) \Vert _{L^2(\Omega )}^2 \big ) \,\textrm{d}s\right| \\&\le \Vert v(\tau ) \Vert _{L^2(\Omega )}^2 + \Vert \partial _t v \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2 + \Vert \nabla _x v\Vert _{L^2(Q)}^2. \end{aligned}$$

An integration of the inequality over all $\tau \in \mathcal {J}$ concludes the proof. $\square$

Given a right-hand side $f\in L^2(\mathcal {J};H^{-1}(\Omega ))$ and initial data $u_0\in L^2(\Omega )$, the problem in (1) has a unique solution $u\in X$ [26, Thm. 5.1]. More precisely, the mapping $(f,u_0) \mapsto u$ is a linear isomorphism and so the norm of u depends continuously on the data, that is,

$$\begin{aligned} \begin{aligned} \Vert u \Vert _X^2&:= \Vert u \Vert _{L^2(\mathcal {J};H^1_0(\Omega ))}^2 + \Vert \partial _t u \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2\\&= \Vert \nabla _x u \Vert _{L^2(Q)}^2 + \Vert \partial _t u \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2 \eqsim \Vert f \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2 + \Vert u_0 \Vert ^2_{L^2(\Omega )}. \end{aligned} \end{aligned}$$

(3)

If the right-hand side is slightly smoother in space, that is $f \in L^2(\mathcal {J};L^2(\Omega ))$, we have for initial data $u_0 \in H^1_0(\Omega )$ the additional regularity property [5, Sec. 4]

$$\begin{aligned} \Vert \Delta _x u \Vert _{L^2(Q)}^2 + \Vert \partial _t u \Vert _{L^2(Q)}^2 \lesssim \Vert f \Vert ^2_{L^2(Q)} + \Vert \nabla _x u_0 \Vert _{L^2(\Omega )}^2. \end{aligned}$$

(4)

If $f \in H^1(\mathcal {J};H^{-1}(\Omega ))$ and $f(0) + \Delta _x u_0 \in L^2(\Omega )$, then $\xi = \partial _t u$ solves

$$\begin{aligned} \partial _t \xi - \Delta _x \xi = \partial _t f\text { in }Q,\qquad \xi = 0 \text { on }\mathcal {J} \times \partial \Omega ,\qquad \xi (0) = f(0) + \Delta _x u_0\text { in }\Omega . \end{aligned}$$

Thus, (3) leads to the bound

$$\begin{aligned} \begin{aligned}&\Vert \partial _t \nabla _x u \Vert _{L^2(Q)}^2 + \Vert \partial _t^2 u \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2\\&\quad \lesssim \Vert \partial _t f \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2 + \Vert f(0) + \Delta _x u_0\Vert _{L^2(\Omega )}^2. \end{aligned} \end{aligned}$$

(5)

Notice that elliptic regularity results imply for convex or smooth domains $\Omega$

$$\begin{aligned} \Vert \nabla ^2_x u \Vert _{L^2(Q)} \lesssim \Vert \Delta _x u \Vert _{L^2(Q)}. \end{aligned}$$

(6)

The estimates in (4)–(6) provide some reasonable regularity assumptions.

2.2 Triangulation

Rather than using simplicial partitions of the time-space cylinder $Q = \mathcal {J} \times \Omega \subset \mathbb {R}^{d+1}$, we use partitions $\mathcal {T}$ of Q into cylindrical closed time-space cells $K=K_t\times K_x$ with time interval $K_t\subset \mathbb {R}$ and simplices $K_x\subset \mathbb {R}^{d}$ as in [7, 18]. The following considerations motivate the use of such partitions.

• A special case of cylindrical partitions are tensor product meshes which typically occur in time-marching schemes and are thus of great interest.

• The parabolic Poincaré inequality in Theorem 4 suggests the use of parabolically scaled meshes for irregular solutions. Thus, we want to allow for local mesh refinements such that the diameter of local cells in space direction $h_x$ and the length of cells in time direction $h_t$ satisfy

  $$\begin{aligned} \begin{aligned} h_t&\eqsim h_x^2{} & {} \text {if we scale parabolically},\\ h_t&\eqsim h_x{} & {} \text {if we scale equally}. \end{aligned} \end{aligned}$$

  Such refinements can easily be achieved with cylindrical meshes.

• The faces of each time-space cell in a cylindrical partition $\mathcal {T}$ are either parallel or perpendicular to the time axis. This allows for the design of finite elements that are better suited for approximations in spaces like $L^2(\mathcal {J};H(div _x,\Omega )) = \lbrace \tau \in L^2(Q;\mathbb {R}^d):div _x\, \tau \in L^2(Q)\rbrace$, where $div _x$ denotes the divergence in space. This leads to significantly improved rates of convergence compared to finite elements on simplicial meshes; see [18].

Throughout this paper we suppose that the partition $\mathcal {T}$ of $Q = \mathcal {J} \times \Omega$ consists of time-space cells $K = K_t \times K_x \subset \mathbb {R}^{d+1}$ with shape regular d-simplices $K_x$. A special class of meshes satisfying these assumptions are tensor-product meshes. Given conforming partitions $\mathcal {T}_t$ and $\mathcal {T}_x$ of the time interval $\mathcal {J}$ and the domain $\Omega$ into shape-regular simplices, these meshes read

$$\begin{aligned} \mathcal {T}_\otimes = \mathcal {T}_t \otimes \mathcal {T}_x = \lbrace K_t \times K_x:K_t\in \mathcal {T}_t\text { and }K_x\in \mathcal {T}_x\rbrace . \end{aligned}$$

(7)

Besides these tensor product meshes, we discuss adaptively refined meshes with hanging vertices in Sect. 6.

2.3 Finite element spaces

Let $\mathcal {T}$ be a partition of Q as described in the previous subsection. For all cells $K=K_t \times K_x \in \mathcal {T}$ and polynomial degrees $k\in \mathbb {N}_0$ we set for $L \in \lbrace K,K_t,K_x\rbrace$ the space of polynomials

$$\begin{aligned} \mathbb {P}_k(L)\,{:}{=}\, \lbrace v_h \in L^2(L):v_h\text { is a polynomial of maximal degree }k\rbrace . \end{aligned}$$

Given polynomial degrees $k,\ell \in \mathbb {N}$, we discretize the space X in (2) by

$$\begin{aligned} X_h \,{:}{=}\, X_h^{k,\ell } \,{:}{=}\, \lbrace v_h \in X:v_h|_K \in \mathbb {P}_k(K_t)\otimes \mathbb {P}_\ell (K_x)\text { for all }K_t\times K_x \in \mathcal {T}\rbrace . \end{aligned}$$

(8)

A special class of meshes included in our analysis are tensor product meshes $\mathcal {T}_\otimes = \mathcal {T}_t \otimes \mathcal {T}_x$ introduced in (7). We set the spaces

$$\begin{aligned} \begin{aligned} \mathcal {L}^0_k(\mathcal {T}_t)&\,{:}{=}\, \lbrace p_t \in L^2(\mathcal {J}):p_t|_{K_t} \in \mathbb {P}_k(K_t)\text { for all }K_t \in \mathcal {T}_t\rbrace ,\\ \mathcal {L}^1_k(\mathcal {T}_t)&\,{:}{=}\, \lbrace v_t \in H^1(\mathcal {J}):v_t|_{K_t} \in \mathbb {P}_k(K_t)\text { for all }K_t \in \mathcal {T}_t\rbrace ,\\ \mathcal {L}^1_{\ell }(\mathcal {T}_x)&\,{:}{=}\, \lbrace v_x \in H^1(\Omega ):v_x|_{K_x} \in \mathbb {P}_\ell (K_x)\text { for all }K_x \in \mathcal {T}_x\rbrace ,\\ \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)&\,{:}{=}\, \lbrace v_x \in H^1_0(\Omega ):v_x|_{K_x} \in \mathbb {P}_\ell (K_x)\text { for all }K_x \in \mathcal {T}_x\rbrace . \end{aligned} \end{aligned}$$

(9)

If $\mathcal {T}= \mathcal {T}_\otimes$ is a tensor product mesh, the ansatz space in (8) equals

$$\begin{aligned} X_h = X_h^{k,\ell } = \mathcal {L}^1_k(\mathcal {T}_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)) \,{:}{=}\, \mathcal {L}^1_k(\mathcal {T}_t)\otimes \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x). \end{aligned}$$

3 Local estimates

In this section we introduce several local estimates for functions on a time-space cell $K = K_t \times K_x$. The cell consists of a bounded time-interval $K_t \subset \mathbb {R}$ of length $h_t {:}{=}|K_t| >0$ and a simplex $K_x \subset \mathbb {R}^d$ with diameter $h_x {:}{=}diam (K_x)$. The space $H^{-1}(K_x)$ is defined as the dual of $H^1_0(K_x)$ with dual pairing and dual norm

$$\begin{aligned} \Vert \xi \Vert _{H^{-1}(K_x)} \,{:}{=}\, \sup _{w\in H^1_0(K_x)} \frac{\langle \xi ,w\rangle _{K_x}}{\Vert \nabla _x w\Vert _{L^2(K_x)}}\qquad \text {for all }\xi \in H^{-1}(K_x). \end{aligned}$$

This definition and Friedrichs’ inequality lead to the upper bound

$$\begin{aligned} \Vert f \Vert _{H^{-1}(K_x)} \lesssim h_x \Vert f \Vert _{L^2(K_x)}\qquad \text {for all }f \in L^2(K_x). \end{aligned}$$

(10)

The following lemma shows that these two terms are equivalent for polynomials.

Lemma 3

(Inverse estimate) Let $k\in \mathbb {N}_0$. We have the upper bound

$$\begin{aligned} \Vert f_h \Vert _{L^2(K_x)} \lesssim h_x^{-1} \Vert f_h\Vert _{H^{-1}(K_x)}\qquad \text {for all }f_h \in \mathbb {P}_k(K_x). \end{aligned}$$

The hidden constant depends solely on the degree k and the shape regularity of $K_x$.

Proof

The proof can be found in [13, Lem. 1]. $\square$

The following result is of crucial importance for the analysis of parabolic problems. It involves the integral mean, with volume |K| of K,

The result is stated in a very general formulation in [8, Lem. 2.9]. Rather than using the more general result, we give an alternative direct proof.

Theorem 4

(Parabolic Poincaré inequality) All functions $v\in L^2(K_t;H^1(K_x)) \cap H^1(K_t;H^{-1}(K_x))$ satisfy

$$\begin{aligned} \Vert v - \langle v \rangle _K \Vert _{L^2(K)} \lesssim h_x\, \Vert \nabla _x v \Vert _{L^2(K)} + \frac{h_t}{h_x}\, \Vert \partial _t v\Vert _{L^2(K_t;H^{-1}(K_x))}. \end{aligned}$$

More general, we have for $k,\ell \in \mathbb {N}_0$

$$\begin{aligned} \min _{v_h \in \mathbb {P}_k(K_t;\mathbb {P}_\ell (K_x))}\Vert v - v_h \Vert _{L^2(K)}&\lesssim h_x\, \min _{v_x \in L^2(K_t;\mathbb {P}_\ell (K_x))} \Vert \nabla _x (v-v_x) \Vert _{L^2(K)}\\&\quad + \frac{h_t}{h_x}\, \min _{v_t\in \mathbb {P}_k(K_t;H^{-1}(K_x))} \Vert \partial _t (v-v_t)\Vert _{L^2(K_t;H^{-1}(K_x))}. \end{aligned}$$

The hidden constant depends solely on the polynomial degrees k and $\ell$ as well as the shape regularity of $K_x$.

The proof of the theorem splits the approximation of v by a polynomial on K into the approximation by a polynomial in time and a polynomial in space. While approximation properties of the latter are well understood, we state approximation properties of functions in $\mathbb {P}_k(K_t;H^{-1}(K_x)) = \mathbb {P}_k(K_t) \otimes H^{-1}(K_x)$.

Lemma 5

(Averaged Taylor polynomial in time) Let $\xi \in H^k(K_t;V)$ with $k \in \mathbb {N}_0$ and one of the two spaces $V \in \lbrace L^2(K_x),H^{-1}(K_x)\rbrace$. There exists a polynomial $\xi _h \in \mathbb {P}_k(K_t;V)$ with

$$\begin{aligned} \Vert \partial _t^m (\xi - \xi _h)\Vert _{L^2(K_t;V)} \lesssim h_t^{k-m}\, \Vert \partial _t^k \xi \Vert _{L^2(K_t;V)}\qquad \text {for all }m=0,\dots ,k. \end{aligned}$$

Proof

This result follows directly from the tensor product structure in Remark 1 and approximation properties of polynomials in $H^m(K_t)$. A detailed proof (for general $L^p$ spaces with $p \in [1,\infty ]$) can be found in the appendix of [9]. $\square$

Let $\mathcal {I}^{L^2}_t :L^2(K_t) \rightarrow \mathbb {P}_k(K_t)$ be an $L^2(K_t)$ stable projection onto the space of polynomials of maximal degree $k\in \mathbb {N}_0$ in time. Its application everywhere in space leads to a mapping for functions on the entire time-space cell K, that is,

$$\begin{aligned} \mathcal {I}^{L^2}_t:L^2(K_t;H^{-1}(K_x)) \rightarrow \mathbb {P}_k(K_t;H^{-1}(K_x)). \end{aligned}$$

Lemma 6

(Approximability in $L^2(K_t;H^{-1}(K_x))$) The mapping $\mathcal {I}^{L^2}_t:L^2(K) \rightarrow \mathbb {P}_k(K_t;H^{-1}(K_x))$ satisfies for all $v \in H^m(K_t;H^{-1}(K_x))$ and $m=0,\dots ,k$

$$\begin{aligned} \Vert \partial _t^m (v - \mathcal {I}^{L^2}_t v) \Vert _{L^2(K_t;H^{-1}(K_x))} \eqsim \min _{v_t \in \mathbb {P}_k(K_t;H^{-1}(K_x))} \Vert \partial _t^m (v - v_t) \Vert _{L^2(K_t;H^{-1}(K_x))}. \end{aligned}$$

Proof

This result follows by classical arguments using Lemma 5. See [9, Thm. 4.3] for more details. $\square$

With these two results we are able to verify Theorem 4.

Proof of Theorem 4

We denote the $L^2(K_t)$ orthogonal projection in time and the $H^{-1}(K_x)$ orthogonal projection in space onto constant functions by

$$\begin{aligned} \Pi _{L^2(K_t)}:L^2(K_t) \rightarrow \mathbb {P}_0(K_t)\qquad \text {and}\qquad \Pi _{H^{-1}(K_x)}:H^{-1}(K_x)\rightarrow \mathbb {P}_0(K_x). \end{aligned}$$

By applying them everywhere in time or space they extend to semi-discrete maps

$$\begin{aligned} \Pi _{L^2(K_t)}&:L^2(K_t;L^2(K_x)) \rightarrow \mathbb {P}_0(K_t;L^2(K_x)),\\ \Pi _{H^{-1}(K_x)}&:L^2(K_t;H^{-1}(K_x))\rightarrow L^2(K_t;\mathbb {P}_0(K_x)). \end{aligned}$$

Since their composition maps onto constant functions, we have for all $f\in L^2(K)$

$$\begin{aligned} \begin{aligned}&\Vert f - \langle f \rangle _K\Vert _{L^2(K)} \le \Vert f - \Pi _{H^{-1}(K_x)}\Pi _{L^2(K_t)} f \Vert _{L^2(K)}\\&\quad \le \Vert f - \Pi _{H^{-1}(K_x)} f \Vert _{L^2(K)} + \Vert \Pi _{H^{-1}(K_x)} (f - \Pi _{L^2(K_t)} f )\Vert _{L^2(K)}. \end{aligned} \end{aligned}$$

(11)

Set . The first addend is bounded by

$$\begin{aligned} \Vert f - \Pi _{H^{-1}(K_x)} f \Vert _{L^2(K)} \le \Vert f - \langle f\rangle _{K_x} \Vert _{L^2(K)} + \Vert \Pi _{H^{-1}(K_x)} (f - \langle f\rangle _{K_x}) \Vert _{L^2(K)}. \end{aligned}$$

The inverse estimate in Lemma 3 yields $L^2$ stability of $\Pi _{H^{-1}(K_x)}$ in the sense that

$$\begin{aligned} \Vert \Pi _{H^{-1}(K_x)} g \Vert _{L^2(K)}&\lesssim h_x^{-1} \Vert \Pi _{H^{-1}(K_x)} g \Vert _{L^2(K_t;H^{-1}(K_x))} \\&\le h_x^{-1} \Vert g \Vert _{L^2(K_t;H^{-1}(K_x))} \lesssim \Vert g \Vert _{L^2(K)}\qquad \text {for all }g\in L^2(K). \end{aligned}$$

These two estimates (with $g = f - \langle f\rangle _{K_x}$) and Poincaré’s inequality show

$$\begin{aligned} \Vert f - \Pi _{H^{-1}(K_x)} f \Vert _{L^2(K)} \lesssim h_x\, \Vert \nabla _x f \Vert _{L^2(K)}. \end{aligned}$$

(12)

The second addend in (11) is bounded due to the inverse estimate in Lemma 3, stability of $\Pi _{H^{-1}(K_x)}$ in $H^{-1}(K_x)$, and approximation properties in Lemma 5–6 by

$$\begin{aligned} \begin{aligned} \Vert \Pi _{H^{-1}(K_x)} (f - \Pi _{L^2(K_t)} f )\Vert _{L^2(K)}&\lesssim h_x^{-1} \Vert f - \Pi _{L^2(K_t)} f \Vert _{L^2(K_t;H^{-1}(K_x))} \\&\lesssim h_t h^{-1}_x \Vert \partial _t f\Vert _{L^2(K_t;H^{-1}(K_x))}. \end{aligned} \end{aligned}$$

(13)

Combining (11)–(13) concludes the proof of the first inequality in the theorem. Similar arguments yield the second inequality. $\square$

If the function v in Theorem 4 satisfies additionally that $\partial _t v \in L^2(K)$, an application of (10) to the first estimate leads to the Poincaré inequality

$$\begin{aligned} \Vert v - \langle v \rangle _K\Vert _{L^2(K)} \lesssim h_x\, \Vert \nabla _x v \Vert _{L^2(K)} + h_t\, \Vert \partial _t v \Vert _{L^2(K)}. \end{aligned}$$

(14)

In this regard Theorem 4 can be seen as a weaker version of Poincaré’s inequality that is better suited for parabolic problems. For example, the regularity stated in (4) does not yield $\partial _t \nabla _x u\in L^2(K)$ for the solution to the heat equation, preventing an application of (14). However, Theorem 4 applies and yields with parabolic scaling $h_t \eqsim h_x^2$ and the estimate

$$\begin{aligned} \Vert \partial _t \nabla _x u \Vert ^2_{L^2(K_t;H^{-1}(K_x))}&= \int _{K_t} \sup _{v(s)\in H^1_0(K_x;\mathbb {R}^d)\setminus \lbrace 0 \rbrace } \frac{\langle \nabla _x \partial _t u(s),v(s)\rangle _{K_x}^2}{\Vert \nabla _x v(s) \Vert ^2_{L^2(K_x)}}\,\textrm{d}s\\&= \int _{K_t} \sup _{v(s)\in H^1_0(K_x;\mathbb {R}^d)\setminus \lbrace 0 \rbrace } \frac{\langle \partial _t u(s),div \, v(s)\rangle ^2_{K_x}}{\Vert \nabla _x v(s) \Vert ^2_{L^2(K_x)}}\,\textrm{d}s\le \Vert \partial _t u \Vert ^2_{L^2(K)}. \end{aligned}$$

the convergence result

$$\begin{aligned} \Vert \nabla _x u - \langle \nabla _x u\rangle _K\Vert _{L^2(K)}&\lesssim h_x\, \Vert \nabla _x^2 u \Vert _{L^2(K)} + \frac{h_t}{h_x}\, \Vert \partial _t \nabla _x u \Vert _{L^2(K_t;H^{-1}(K_x))} \\&\lesssim h_x\, (\Vert \nabla _x^2 u \Vert _{L^2(K)} + \Vert \partial _t u \Vert _{L^2(K)}). \end{aligned}$$

The need of parabolic scaling for irregular solutions is further illustrated by the numerical experiment in [7, Sec. 7.4].

Remark 7

(Sharp estimate) Inverse estimates show that the bound in Theorem 4 must be sharp. More precisely, let $v = v_t v_x$ with polynomials $v_t\in \mathbb {P}_k(K_t)$ and $v_x\in \mathbb {P}_\ell (K_x)$ with $\langle v\rangle _K = 0$ for $K=K_t\times K_x$. Then inverse estimates reveal

$$\begin{aligned} h_x\, \Vert \nabla _x v \Vert _{L^2(K)} + \frac{h_t}{h_x} \Vert \partial _t v \Vert _{L^2(K_t;H^{-1}(K_x))} \lesssim \Vert v\Vert _{L^2(K)} + h_t\, \Vert \partial _t v\Vert _{L^2(K)} \lesssim \Vert v \Vert _{L^2(K)}. \end{aligned}$$

4 Interpolation in space or time

The main idea in this paper’s design of interpolation operators in space-time is to exploit the tensor product structure of Bochner spaces like $H^1(\mathcal {J};H^{-1}(\Omega )) = H^1(\mathcal {J}) \otimes H^{-1}(\Omega ) \supset X$. This allows us to apply an interpolation operator in time to the $H^1(\mathcal {J})$ component and in space to the $H^{-1}(\Omega )$ component.

4.1 Interpolation operator in space

We utilize the $H^{-1}(\Omega )$ stable interpolation operator $\mathcal {I}_x:H^{-1}(\Omega ) \rightarrow \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)$ introduced in [9] for conforming and shape-regular partitions $\mathcal {T}_x$ of $\Omega$ with $\ell \in \mathbb {N}$. Throughout this subsection we assume that $\mathcal {T}_x$ is such a partition. Let $\mathcal {N}_x$ denote the set of vertices in $\mathcal {T}_x$ and set for all $j\in \mathcal {N}_x$ the corresponding vertex patch

$$\begin{aligned} \omega _{x,j} \,{:}{=}\, \bigcup \lbrace K_x\in \mathcal {T}_x:j\in K_x\rbrace . \end{aligned}$$

We denote the nodal basis functions by $\phi _{x,j} \in \mathcal {L}^1_1(\mathcal {T}_x)$ with $\phi _{x,j}(i) = \delta _{i,j}$ for all vertices $i,j\in \mathcal {N}_x$.

Lemma 8

(Localization of $H^{-1}(\Omega )$) Let $\xi \in H^{-1}(\Omega )$. Then we have

$$\begin{aligned} \sum _{j\in \mathcal {N}_x} \Vert \xi \Vert _{H^{-1}(\omega _{x,j})}^2 \lesssim \Vert \xi \Vert _{H^{-1}(\Omega )}^2 \lesssim \sum _{j\in \mathcal {N}_x} h_{x,j}^{-2} \Vert \xi \Vert _{H^{-1}(\omega _{x,j})}^2. \end{aligned}$$

Proof

Let $\xi \in H^{-1}(\Omega )$. The partition of unity $1 = \sum _{j\in \mathcal {N}_x} \phi _{x,j}$ leads for all $w\in H^1_0(\Omega )$ to the upper bound

$$\begin{aligned} \langle \xi ,w\rangle _\Omega= & {} \sum _{j\in \mathcal {N}_x} \langle \xi , \phi _{x,j} w\rangle _\Omega \nonumber \\\le & {} \sum _{j\in \mathcal {N}_x} h_{x,j}^{-1}\Vert \xi \Vert _{H^{-1}(\omega _{x,j})} h_{x,j}\Vert \nabla _x( \phi _{x,j} w)\Vert _{L^2(\omega _{x,j})}\nonumber \\\lesssim & {} \Big (\sum _{j\in \mathcal {N}_x} h_{x,j}^{-2} \Vert \xi \Vert _{H^{-1}(\omega _{x,j})}^2\Big )^{1/2} \bigg (\Big (\sum _{j\in \mathcal {N}_x} h_{x,j}^2 \Vert \nabla _x w \Vert _{L^2(\omega _{x,j})}^2\Big )^{1/2}\nonumber \\{} & {} + \Big (\sum _{j\in \mathcal {N}_x} \Vert w \Vert _{L^2(\omega _{x,j})}^2\Big )^{1/2}\bigg ) \nonumber \\\lesssim & {} \Big (\sum _{j\in \mathcal {N}_x} h_{x,j}^{-2} \Vert \xi \Vert _{H^{-1}(\omega _{x,j})}^2\Big )^{1/2} \Vert \nabla _x w \Vert _{L^2(\Omega )}. \end{aligned}$$

(15)

This concludes the proof of the upper bound. The lower bound follows with standard arguments (see for example [9, Lem. 11]). $\square$

The upper bound in Lemma 8 is indeed sharp, as one can see by localizing the $H^{-1}(\Omega )$ norm of the constant function $\xi = 1 \in H^{-1}(\Omega )$. The operator $\mathcal {I}_x$ allows for a localization of the $H^{-1}(\Omega )$ norm without any additional weights. In particular, we have the following result involving the patches

$$\begin{aligned} \begin{aligned} \omega _{x,j}^2&\,{:}{=}\, \bigcup \Big \lbrace \omega _{x,i}:i \in \omega _{x,j} \rbrace{} & {} \text {for all }j\in \mathcal {N}_x,\\ \omega _{K_x}&\,{:}{=}\, \bigcup \Big \lbrace K_x'\in \mathcal {T}_x :K_x \cap K_x'\ne \emptyset \rbrace{} & {} \text {for all }K_x \in \mathcal {T}_x. \end{aligned} \end{aligned}$$

Theorem 9

(Interpolation operator $\mathcal {I}_x$) The operator $\mathcal {I}_x :H^{-1}(\Omega ) \rightarrow \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)$ is a linear projection onto $\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)$. It satisfies for all $\xi \in H^{-1}(\Omega )$

$$\begin{aligned} \Vert \xi - \mathcal {I}_x \xi \Vert ^2_{H^{-1}(\Omega )}&\eqsim \sum _{j\in \mathcal {N}_x} \Vert \xi - \mathcal {I}_x \xi \Vert _{H^{-1}(\omega _{x,j})}^2\eqsim \sum _{j\in \mathcal {N}_x} \min _{\xi _h\in \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)} \Vert \xi - \xi _h\Vert _{H^{-1}(\omega _{x,j}^2)}^2. \end{aligned}$$

Moreover, it satisfies for all $\xi \in L^2(\Omega )$ and $K_x\in \mathcal {T}_x$

$$\begin{aligned} \Vert \xi - \mathcal {I}_x \xi \Vert _{L^2(K_x)} \eqsim \min _{\xi _h \in \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)} \Vert \xi - \xi _h\Vert _{L^2(\omega _{K_x})}. \end{aligned}$$

If in addition $\xi \in H^1_0(\Omega )$, we have the equivalence

$$\begin{aligned} \Vert \nabla _x( \xi - \mathcal {I}_x \xi )\Vert _{L^2(K_x)} \eqsim \min _{\xi _h \in \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)} \Vert \nabla _x( \xi - \xi _h)\Vert _{L^2(\omega _{K_x})}. \end{aligned}$$

Proof

The first statement is shown in [9, Thm. 2.1]. The second in follows from the local stability of the operator shown in [9, Thm. 2.1]. More precisely, the projection and stability property of $\mathcal {I}_x$ imply for $\xi _h \in \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)$ and $\xi \in L^2(\Omega )$

$$\begin{aligned} \Vert \xi - \mathcal {I}_x \xi \Vert _{L^2(K_x)} = \Vert \xi - \xi _h - \mathcal {I}_x (\xi - \xi _h) \Vert _{L^2(K_x)} \lesssim \Vert \xi - \xi _h \Vert _{L^2(\omega _{K_x})}. \end{aligned}$$

This yields the second statement. Similar arguments imply the third statement. $\square$

Remark 10

(Boundary data) It is possible to modify the design of $\mathcal {I}_x$ in order to replace the space $\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)$ equipped with zero boundary data by the space $\mathcal {L}^1_{\ell }(\mathcal {T}_x)$ without zero boundary data; see [9] for details.

An application of $\mathcal {I}_x$ everywhere in time extends the operator to a mapping $\mathcal {I}_x :L^2(\mathcal {J};H^{-1}(\Omega )) \rightarrow L^2(\mathcal {J};\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))$ in the sense that for all $v\in L^2(\mathcal {J};H^{-1}(\Omega ))$

$$\begin{aligned} (\mathcal {I}_x v)(s) = \mathcal {I}_x v(s)\qquad \text {for almost all }s \in \mathcal {J}. \end{aligned}$$

(16)

4.2 Interpolation operators in time

Besides the interpolation operator $\mathcal {I}_x$ in space introduced in the previous subsection, we utilize an interpolation operator $\mathcal {I}_t:H^1(\mathcal {J}) \rightarrow \mathcal {L}^1_k(\mathcal {T}_t)$ with polynomial degree $k\in \mathbb {N}$ and partition $\mathcal {T}_t$ of the time interval $\mathcal {J}$. We set the operator locally for each for time interval $K_t = [a,b] \in \mathcal {T}_t$. Its definition involves the bubble function $b_{K_t} \in \mathbb {P}_2(K_t)$ with $\int _{K_t} b_{K_t} \,\textrm{d}s= 1$ and $b_{K_t}(a) = 0 = b_{K_t}(b)$. For $v\in H^1(K_t)$ we set the operator as follows. Let $\mathcal {I}_{K_t}^1 v\in \mathbb {P}_1(K_t)$ denote the nodal interpolation defined by

$$\begin{aligned} \mathcal {I}_{K_t}^1 v(a)= v(a)\qquad \text {and}\qquad \mathcal {I}_{K_t}^1 v(b) = v(b). \end{aligned}$$

Let $\mathcal {I}_{K_t}^2v = 0$ for $k=1$ and for $k\ge 2$ let $\mathcal {I}_{K_t}^2 v \in \mathbb {P}_{k-2}(K_t)$ be the solution to

$$\begin{aligned} \int _{K_t} b_{K_t} (\mathcal {I}_{K_t}^2 v)\, w_{k-2} \,\textrm{d}s= \int _{K_t} (v-\mathcal {I}_{K_t}^1 v)\, w_{k-2} \,\textrm{d}s\qquad \text {for all }w_{k-2}\in \mathbb {P}_{k-2}(K_t). \end{aligned}$$

We set the interpolation of v as

$$\begin{aligned} \mathcal {I}_{K_t} v \,{:}{=}\, \mathcal {I}_{K_t}^1 v + b_{K_t} \mathcal {I}_{K_t}^2 v. \end{aligned}$$

(17)

Moreover, we denote the $L^2(K_t)$ orthogonal projection onto $\mathbb {P}_{r}(K_t)$ by

$$\begin{aligned} \Pi _{\mathbb {P}_r(K_t)}:L^2(K_t) \rightarrow \mathbb {P}_r(K_t)\qquad \text {for all }r\in \mathbb {N}_0. \end{aligned}$$

(18)

Theorem 11

(Interpolation operator $\mathcal {I}_{K_t}$) The operator $\mathcal {I}_{K_t}:H^{1}(K_t) \rightarrow \mathbb {P}_k(K_t)$ is a linear projection onto $\mathbb {P}_k(K_t)$ satisfying the commuting diagram property

$$\begin{aligned} \partial _t \mathcal {I}_{K_t} = \Pi _{\mathbb {P}_{k-1}(K_t)} \partial _t. \end{aligned}$$

(19)

For all $v\in H^1(K_t)$ the difference $v- \mathcal {I}_{K_t} v\in H^1_0(K_t)$ has zero boundary values and

$$\begin{aligned} \Vert \partial _t (v - \mathcal {I}_{K_t} v) \Vert _{L^2(K_t)}&= \min _{v_h \in \mathbb {P}_k(K_t)} \Vert \partial _t (v - v_h) \Vert _{L^2(K_t)}. \end{aligned}$$

Proof

Let $v\in H^1(K_t)$. Since by definition $v- \mathcal {I}_{K_t} v\in H^1_0(K_t)$, an integration by parts and the definition of $\mathcal {I}_{K_t}^2$ yield for all $w_h\in \mathbb {P}_{k-1}(K_t)$

$$\begin{aligned} \int _{K_t} \partial _t (v- \mathcal {I}_{K_t} v)\, w_h\,\textrm{d}s&= -\int _{K_t} (v- \mathcal {I}_{K_t}v)\, \partial _t w_h \,\textrm{d}s\\&= \int _{K_t} b_{K_t} (\mathcal {I}^2_{K_t} v)\, \partial _t w_h \,\textrm{d}s-\int _{K_t} (v- \mathcal {I}^1_{K_t} v)\, \partial _t w_h \,\textrm{d}s= 0. \end{aligned}$$

This proves the commuting diagram property. The commuting diagram property yields the best-approximation property and leads to the projection property. $\square$

By applying the operator everywhere in $\Omega$, the operator extends to a mapping

$$\begin{aligned} \mathcal {I}_{K_t} :H^1(K_t;H^{-1}(\Omega )) \rightarrow \mathbb {P}_k(K_t;H^{-1}(\Omega )). \end{aligned}$$

Applying $\mathcal {I}_{K_t}$ on each time cell $K_t\in \mathcal {T}_t$ leads to the operator $\mathcal {I}_t :L^2(\mathcal {J};H^{-1}(\Omega )) \rightarrow \mathcal {L}_k^1(\mathcal {T}_t;H^{-1}(\Omega ))$ with

$$\begin{aligned} (\mathcal {I}_t v)|_{K_t} \,{:}{=}\, \mathcal {I}_{K_t} v|_{K_t}\qquad \text {for all }v\in H^1(\mathcal {J};H^{-1}(\Omega ))\text { and }K_t\in \mathcal {T}_t. \end{aligned}$$

(20)

5 Tensor product meshes

This section introduces interpolation operators for special cylindrical partitions of Q, namely tensor product meshes $\mathcal {T}= \mathcal {T}_t \otimes \mathcal {T}_x$ with a partition $\mathcal {T}_t$ of the time interval $\mathcal {J}$ and a conforming simplicial partition $\mathcal {T}_x$ of the domain $\Omega$. Such partitions are of special interest since classical time-marching schemes can be seen as a space-time ansatz using such meshes and ansatz spaces $X_h = \mathcal {L}^1_\ell (\mathcal {T}_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))$ as well as some specific discretization of the test space $L^2(\mathcal {J};H^1_0(\Omega ))$; see for example [12, 32] for the Crank-Nicolson scheme. We introduce and investigate a suitable interpolation operator in the first subsection. The second subsection introduces and investigates an interpolation operator for mixed schemes.

5.1 Interpolation operator $\mathcal {I}_X^\otimes$

Due to the tensor product structure of the mesh $\mathcal {T}= \mathcal {T}_t\otimes \mathcal {T}_x$, the discrete space $X_h$ defined in (8) equals $X_h = \mathcal {L}^1_\ell (\mathcal {T}_t) \otimes \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)$. This allows for the direct application of the operators

$$\begin{aligned} \begin{aligned}&\mathcal {I}_x:L^2(\mathcal {J};H^{-1}(\Omega )) \rightarrow L^2(\mathcal {J};\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)){} & {} \text { defined in } (16),\\&\mathcal {I}_t :H^1(\mathcal {J};H^{-1}(\Omega )) \rightarrow \mathcal {L}^1_k(\mathcal {T}_t;H^{-1}(\Omega )){} & {} \text { defined in } (20). \end{aligned} \end{aligned}$$

More precisely, we set the interpolation operator $\mathcal {I}_X^\otimes :X \rightarrow X_h$ as the composition

$$\begin{aligned} \mathcal {I}_X^\otimes \,{:}{=}\, \mathcal {I}_x \circ \mathcal {I}_t = \mathcal {I}_t \circ \mathcal {I}_x. \end{aligned}$$

(21)

This operator has the following beneficial properties involving the local mesh sizes $h_x(K) \,{:}{=}\, diam (K_x)$ and $h_t(K) \,{:}{=}\, |K_t|$ for all $K = K_t \times K_x \in \mathcal {T}$.

Theorem 12

(Interpolation operator $\mathcal {I}_X^\otimes$) The operator $\mathcal {I}_X^\otimes$ satisfies for all $v\in X$

$$\begin{aligned} \Vert \nabla _x (v-\mathcal {I}_X^\otimes v)\Vert _{L^2(Q)}^2&\lesssim \sum _{K\in \mathcal {T}} \left( \min _{v_{x}\in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))} \Vert \nabla _x (v-v_{x})\Vert _{L^2(K_t;L^2(\omega _{K_x}))}^2 \right. \\&\quad \left. + \frac{h_t(K)^2}{h_x(K)^4} \min _{v_{t}\in \mathbb {P}_k(K_t;H^{-1}(\omega _{K_x}))} \Vert \partial _t (v-v_{t}) \Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2\right) . \end{aligned}$$

Moreover, we have for all $v\in H^1(\mathcal {J};H^{-1}(\Omega ))$ the upper bound

$$\begin{aligned} \Vert \partial _t (v - \mathcal {I}_X^\otimes v)\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2&\lesssim \sum _{K\in \mathcal {T}} \min _{\xi _{x}\in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))} \Vert \partial _t v - \xi _{x} \Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2 \\&\quad + \sum _{K_t\in \mathcal {T}_t} \min _{v_{t} \in \mathbb {P}_k(K_t;H^{-1}(\Omega ))} \Vert \partial _t (v-v_{t})\Vert _{L^2(K_t;H^{-1}(\Omega ))}^2. \end{aligned}$$

Proof

Let $v\in X$. The triangle inequality yields

$$\begin{aligned} \Vert \nabla _x (v-\mathcal {I}_X^\otimes v)\Vert _{L^2(Q)}&\le \Vert \nabla _x (v - \mathcal {I}_x v)\Vert _{L^2(Q)} + \Vert \nabla _x \mathcal {I}_x (v-\mathcal {I}_t v)\Vert _{L^2(Q)}. \end{aligned}$$

(22)

The approximation properties displayed in Theorem 9 yield for the first addend

$$\begin{aligned} \Vert \nabla _x (v - \mathcal {I}_x v)\Vert _{L^2(Q)}^2 \eqsim \sum _{K\in \mathcal {T}} \min _{v_{x}\in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))} \Vert \nabla _x (v-v_{x})\Vert _{L^2(K_t;L^2(\omega _{K_x}))}^2. \end{aligned}$$

Due to inverse estimates (Lemma 3) and Theorem 11 the second addend satisfies

$$\begin{aligned} \begin{aligned} \Vert \nabla _x \mathcal {I}_x (v-\mathcal {I}_t v)\Vert _{L^2(Q)}^2&= \sum _{K\in \mathcal {T}} \Vert \nabla _x \mathcal {I}_x (v-\mathcal {I}_t v)\Vert _{L^2(K)}^2\\&\quad \lesssim \sum _{K\in \mathcal {T}} h_x(K)^{-4} \Vert v-\mathcal {I}_t v\Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2\\&\quad \lesssim \sum _{K\in \mathcal {T}} \frac{h_t(K)^2}{h_x(K)^4} \min _{v_{t}\in \mathbb {P}_k(K_t;H^{-1}(\Omega ))} \Vert \partial _t (v-v_{t}) \Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2. \end{aligned} \end{aligned}$$

(23)

This proves the first inequality in the theorem.

Let $v\in L^2(\mathcal {J};H^{-1}(\Omega ))$. Since $\mathcal {I}_x \partial _t = \partial _t\mathcal {I}_x$, we have

$$\begin{aligned} \Vert \partial _t( v -\mathcal {I}_X v) \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}&\le \Vert \partial _t v - \mathcal {I}_x \partial _t v\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}\\&\quad + \Vert \mathcal {I}_x \partial _t (v - \mathcal {I}_t v) \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}. \end{aligned}$$

An application of Theorem 9 to the first addend yields

$$\begin{aligned} \Vert \partial _t v - \mathcal {I}_x \partial _t v\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2 \lesssim \sum _{K\in \mathcal {T}} \min _{\xi _{x}\in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))} \Vert \partial _t v - \xi _{x} \Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2. \end{aligned}$$

The $H^{-1}(\Omega )$ stability of $\mathcal {I}_x$ and the approximation properties of $\mathcal {I}_t$ yield

$$\begin{aligned} \Vert \mathcal {I}_x \partial _t (v - \mathcal {I}_t v) \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2&\lesssim \Vert \partial _t (v - \mathcal {I}_t v) \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2\\&= \sum _{K_t\in \mathcal {T}_t} \min _{v_{t}\in \mathbb {P}_k(K_t;H^{-1}(\Omega ))} \Vert \partial _t (v - v_{t}) \Vert _{L^2(K_t;H^{-1}(\Omega ))}^2. \end{aligned}$$

Combining the estimates concludes the proof. $\square$

Due to the continuous embedding $X\hookrightarrow C^0(\mathcal {J};L^2(\Omega ))$ in Lemma 2, we have for all $v\in X$ and $t\in \mathcal {J} = [0,T]$ the upper bound

$$\begin{aligned}&\Vert v(t) - (\mathcal {I}_X^\otimes v)(t) \Vert _{L^2(\Omega )}\\&\qquad \lesssim (1+T^{-1})\Vert \nabla _x (v-\mathcal {I}_X^\otimes v)\Vert _{L^2(Q)} + \Vert \partial _t (v-\mathcal {I}_X^\otimes v)\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}. \end{aligned}$$

The following result improves this bound. We set the diameters $h_t(K_t) \,{:}{=}\, |K_t|$ and $h_x(K_x) \,{:}{=}\, diam (K_x)$ for all $K_t\in \mathcal {T}_t$ and $K_x\in \mathcal {T}_x$.

Theorem 13

(Interpolation error in $C^0(\mathcal {J};L^2(\Omega ))$) Let $t\in K_t\in \mathcal {T}_t$ and $v\in X$. Then we have

$$\begin{aligned}&\Vert (v - \mathcal {I}_X^\otimes v)(t) \Vert _{L^2(\Omega )}^2 \lesssim \min _{v_t\in \mathbb {P}_k(K_t;H^{-1}(\Omega ))} \Vert \partial _t (v-v_t)\Vert ^2_{L^2(K_t;H^{-1}(\Omega ))} \\&\qquad + \sum _{K_x\in \mathcal {T}_x} \left( 1+\frac{h_x(K_x)^2}{h_t(K_t)}\right) \min _{v_{x}\in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))} \Vert \nabla _x( v - v_{x}) \Vert _{L^2(K_t;L^2(\omega _{K_x}))}^2\\&\qquad + \sum _{K_x\in \mathcal {T}_x} \left( \frac{h_t(K_t)}{h_x(K_x)^2} + \frac{h_t(K_t)^2}{h_x(K_x)^4}\right) \min _{v_{t} \in \mathbb {P}_k(K_t;H^{-1}(\Omega ))} \Vert \partial _t (v-v_{t})\Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2 \\&\qquad + \sum _{K_x\in \mathcal {T}_x} \min _{\xi _x \in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)))} \Vert \partial _t v-\xi _x \Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2\\&\qquad + \min _{v_{t} \in \mathbb {P}_k(K_t;H^{-1}(\Omega ))} \Vert \partial _t (v-v_{t})\Vert _{L^2(K_t;H^{-1}(\Omega ))}^2. \end{aligned}$$

Proof

Let $t\in K_t\in \mathcal {T}_t$ and $v\in X$. Lemma 2 reveals that

$$\begin{aligned} \Vert (v - \mathcal {I}_X^\otimes v)(t) \Vert _{L^2(\Omega )}^2&\le \frac{1}{h_t(K_t)}\, \Vert v - \mathcal {I}_X^\otimes v \Vert _{L^2(K_t;L^2(\Omega ))}^2 + \Vert \nabla _x( v - \mathcal {I}_X^\otimes v) \Vert _{L^2(K_t;L^2( \Omega ))}^2\\&\quad + \Vert \partial _t (v - \mathcal {I}_X^\otimes v) \Vert ^2_{L^2(K_t;H^{-1}(\Omega ))}. \end{aligned}$$

The arguments in the proof of Theorem 12 lead to the bound

$$\begin{aligned}&\frac{1}{h_t(K_t)}\Vert v - \mathcal {I}_X^\otimes v \Vert _{L^2(K_t;L^2(\Omega ))}^2 = \sum _{K_x\in \mathcal {T}_x} \frac{1}{h_t(K_t)} \Vert v - \mathcal {I}_X^\otimes v \Vert _{L^2(K_t;L^2(K_x))}^2 \\&\quad \lesssim \sum _{K_x\in \mathcal {T}_x} \frac{h_x(K_x)^2}{h_t(K_t)} \min _{v_{x}\in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))} \Vert \nabla _x( v - v_{x}) \Vert _{L^2(K_t;L^2(\omega _{K_x}))}^2\\&\quad + \sum _{K_x\in \mathcal {T}_x} \frac{h_t(K_t)}{ h_x(K_x)^2} \min _{v_{t} \in \mathbb {P}_k(K_t;H^{-1}(\Omega ))} \Vert \partial _t (v-v_{t})\Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2. \end{aligned}$$

Combining this estimate with the approximation properties displayed in Theorem 12 concludes the proof. $\square$

We conclude this subsection with two remarks.

Remark 14

(Stability in $L^2(\mathcal {J};H^1_0(\Omega ))$) While the operator $\mathcal {I}_X^\otimes$ is always stable in $H^1(\mathcal {J};H^{-1}(\Omega ))$, its (uniform) stability in X requires the parabolic scaling $h_t(K) \eqsim h_x(K)^2$ for all $K\in \mathcal {T}$. This is due to the change of the norm to in (23). It is possible to avoid this change of norms when $\mathcal {I}_t$ is replaced by some $L^2$ stable projection operator $\mathcal {I}_t^{L^2}:L^2(\mathcal {J}) \rightarrow \mathcal {L}^1_k(\mathcal {T}_t)$ like the Scott-Zhang interpolation operator [30] as done in [9, Sec. 4.2]. Set $(\mathcal {I}_X^\otimes )' \,{:}{=}\, \mathcal {I}_x \circ \mathcal {I}_t^{L^2}$ and assume that neighboring time cells $K_t,K_t'\in \mathcal {T}_t$ are of equivalent size. A similar proof as in Theorem 12 leads for all $v\in L^2(\mathcal {J};H^1_0(\Omega ))$ to

$$\begin{aligned}&\Vert \nabla _x (v-(\mathcal {I}_X^\otimes )' v)\Vert _{L^2(Q)}^2\\&\lesssim \sum _{K\in \mathcal {T}} \min _{v_{x}\in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))} \Vert \nabla _x (v-v_{x})\Vert _{L^2(K_t;L^2(\omega _{K_x}))}^2 \\&\quad + \min _{W_{t}\in \mathcal {L}^1_k(\mathcal {T}_t;L^2(\Omega ;\mathbb {R}^d))} \Vert \nabla _x v- W_{t} \Vert _{L^2(\omega _{K_t};L^2(\omega _{K_x}))}^2. \end{aligned}$$

Furthermore, it satisfies for all $v\in H^1(\mathcal {J};H^{-1}(\Omega ))$

$$\begin{aligned}&\Vert \partial _t (v - (\mathcal {I}_X^\otimes )' v)\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2\\&\quad \lesssim \sum _{K\in \mathcal {T}} \min _{\xi _{x}\in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))} \Vert \partial _t v - \xi _{x} \Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2 \\&\quad + \sum _{K_t\in \mathcal {T}_t} \min _{v_{t} \in \mathcal {L}^1_k(\mathcal {T}_t;H^{-1}(\Omega ))} \Vert \partial _t (v-v_{t})\Vert _{L^2(\omega _{K_t};H^{-1}(\Omega ))}^2. \end{aligned}$$

Note that this operator has increased the domain of dependence with respect to the time direction compared to the operator in Theorem 12.

Remark 15

(Localization of the $H^1(K_t;H^{-1}(\Omega ))$ norm) While the interpolation error for $\Vert \nabla _x (v-\mathcal {I}_X^\otimes v)\Vert _{L^2(Q)}$ decomposes into localized norms, the interpolation error $\Vert \partial _t (v - \mathcal {I}_X^\otimes v)\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}$ localizes only in time. Lemma 8 shows that it is possible to localize further but at the cost of negative powers of the local mesh size, that is for all $v\in H^1(\mathcal {J};H^{-1}(\Omega ))$

$$\begin{aligned}&\sum _{K_t\in \mathcal {T}_t} \min _{v_{t} \in \mathbb {P}_k(K_t;H^{-1}(\Omega ))} \Vert \partial _t (v-v_{t})\Vert _{L^2(K_t;H^{-1}(\Omega ))}^2\\&\quad \lesssim \sum _{K\in \mathcal {T}} h_x(K)^{-2} \min _{v_{t} \in \mathbb {P}_k(K_t;H^{-1}(\omega _{K_x}))} \Vert \partial _t (v-v_{t})\Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2. \end{aligned}$$

This upper bound is indeed sharp, as the following consideration shows.

Suppose there exists for some $s<2$ and all $v\in H^1(\mathcal {J};H^{-1}(\Omega ))$ an estimate

$$\begin{aligned} \Vert \partial _t (v- \mathcal {I}_X^\otimes v)\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2&\lesssim \sum _{K\in \mathcal {T}} \min _{v_{x}\in L^2(K_t;\mathcal {L}^1_{\ell ,0}(\mathcal {T}_x))} \Vert \partial _t (v - v_{x}) \Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2\\&\quad + h_x(K)^{-s} \min _{v_{t}\in \mathbb {P}_k(K_t;H^{-1}(\omega _{K_x}))} \Vert \partial _t (v - v_{t}) \Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2. \end{aligned}$$

The estimate holds in particular for functions $w = w_t w_{x}$ with $w_t\in H^1(\mathcal {J})$ and $w_{x} \in \mathcal {L}^1_{\ell ,0}(\mathcal {T}_x)$, that is

$$\begin{aligned}&\Vert \partial _t (w_t - \mathcal {I}_t w_t) \Vert _{L^2(\mathcal {J})}^2 \Vert w_{x} \Vert _{H^{-1}(\Omega )}^2 = \Vert \partial _t (w - \mathcal {I}_X^\otimes w)\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}^2 \\&\quad \lesssim \sum _{K\in \mathcal {T}} h_x(K)^{-s} \min _{v_t \in \mathbb {P}_k(K_t;H^{-1}(\omega _{K_x}))} \Vert \partial _t (w - v_t) \Vert _{L^2(K_t;H^{-1}(\omega _{K_x}))}^2\\&\quad \lesssim \sum _{K\in \mathcal {T}} h_x(K)^{2-s} \Vert \partial _t w \Vert _{L^2(K_t;L^2(\omega _{K_x}))}^2. \end{aligned}$$

Hence, we have

$$\begin{aligned} \Vert \partial _t (w_t - \mathcal {I}_t w_t) \Vert _{L^2(\mathcal {J})}\Vert w_{x} \Vert _{H^{-1}(\Omega )} \lesssim \max _{K\in \mathcal {T}}\, h_x(K)^{1-s/2} \Vert \partial _t w_t \Vert _{L^2(\mathcal {J})} \Vert w_{x}\Vert _{L^2(\Omega )}. \end{aligned}$$

This yields convergence of $\Vert \partial _t (w_t - \mathcal {I}_t w_t) \Vert _{L^2(\mathcal {J})}$ independent of the time discretization, which cannot be possible.

5.2 Commuting interpolation operator $\mathcal {I}^\otimes _\Lambda$

Simultaneous space-time minimal residual methods [7, 14, 17, 18] and time marching schemes in mixed form [1, 20, 21] involve the time-space divergence $div \, (v,\tau ) \,{:}{=}\, \partial _t v + div _x \tau$ and the related space

$$\begin{aligned} \Lambda = \lbrace (v,\tau ) \in L^2(\mathcal {J};H^1_0(\Omega )) \times L^2(Q;\mathbb {R}^d):div \,(v,\tau ) \in L^2(Q)\rbrace . \end{aligned}$$

We set for all $(v,\tau ) \in \Lambda$ the squared norm

$$\begin{aligned} \Vert (v,\tau ) \Vert _\Lambda ^2 \,{:}{=}\, \Vert \nabla _x v \Vert _{L^2(Q)}^2 + \Vert \tau \Vert _{L^2(Q)}^2 + \Vert div \, (v,\tau )\Vert _{L^2(Q)}^2. \end{aligned}$$

Any function $(v,\tau ) \in \Lambda$ satisfies [17, Lem. 2.1]

$$\begin{aligned} \Vert \partial _t v \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))} \lesssim \Vert \tau \Vert _{L^2(Q)} + \Vert div \, (v,\tau )\Vert _{L^2(Q)} \lesssim \Vert (v,\tau )\Vert _\Lambda . \end{aligned}$$

(24)

In particular, we have with $\Sigma \,{:}{=}\, L^2(\mathcal {J};H(div _x,\Omega ))$ and $H(div _x,\Omega ) \,{:}{=}\, \lbrace q \in L^2(\Omega ;\mathbb {R}^d): div _x q \in L^2(\Omega )\rbrace$ with spacial divergence $div _x$ the inclusion

$$\begin{aligned} \Lambda = \lbrace (v,\tau ) \in X \times L^2(Q;\mathbb {R}^d):div \,(v,\tau ) \in L^2(Q)\rbrace \subset X \times \Sigma . \end{aligned}$$

Let $\mathcal {T}= \mathcal {T}_t \otimes \mathcal {T}_x$ be a tensor product mesh with conforming triangulations $\mathcal {T}_t$ of $\mathcal {J}$ and $\mathcal {T}_x$ of $\Omega$. Set the Raviart-Thomas finite element space $RT_\ell (\mathcal {T}_x)$, which reads with identity mapping $id :\Omega \rightarrow \Omega$

$$\begin{aligned} RT_\ell (\mathcal {T}_x) \,{:}{=}\, \lbrace \tau \in H(div _x,\Omega ):\tau |_{K_x} \in \mathbb {P}_\ell (K_x) + id \cdot \mathbb {P}_\ell (K_x;\mathbb {R}^d)\rbrace . \end{aligned}$$

Let $\Pi _{\mathcal {L}^0_{\ell }(\mathcal {T}_x)}:L^2(\Omega )\rightarrow \mathcal {L}^0_{\ell }(\mathcal {T}_x)$ be the $L^2(\Omega )$ orthogonal projector onto $\mathcal {L}^0_{\ell }(\mathcal {T}_x)$.

Theorem 16

(Commuting interpolation operator $\mathcal {I}_{RT}$) There exists an interpolation operator $\mathcal {I}_{RT}:L^2(\Omega ;\mathbb {R}^d) \rightarrow RT_\ell (\mathcal {T}_x)$ with the commuting diagram property

$$\begin{aligned} div _x \mathcal {I}_{RT} \tau = \Pi _{\mathcal {L}^0_{\ell }(\mathcal {T}_x)} div _x \tau \qquad \text {for all }\tau \in H(div _x,\Omega ). \end{aligned}$$

Moreover, it has for all $p\in L^2(\Omega ;\mathbb {R}^d)$ the approximation property

$$\begin{aligned} \Vert p - \mathcal {I}_{RT} p \Vert _{L^2(\Omega )}^2 \eqsim \sum _{K_x \in \mathcal {T}_x} \min _{p_h\in RT_\ell (\mathcal {T}_x)} \Vert p - p_h \Vert _{L^2(\omega _{K_x})}^2. \end{aligned}$$

Proof

A suitable operator is investigated for example in [10, Sec. 23]. $\square$

We set the discrete subspace

$$\begin{aligned} \Sigma _h \,{:}{=}\, \mathcal {L}^0_{k-1}(\mathcal {T}_t;RT_\ell (\mathcal {T}_x)) = \mathcal {L}^0_{k-1}(\mathcal {T}_t) \otimes RT_\ell (\mathcal {T}_x) \subset \Sigma . \end{aligned}$$

Moreover, we denote the $L^2$ orthogonal projections onto the space of piece-wise polynomials in time $\mathcal {L}^0_{k-1}(\mathcal {T}_t)$ and piece-wise polynomials in space $\mathcal {L}^0_\ell (\mathcal {T}_x)$ by

$$\begin{aligned} \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)}&:L^2(Q;\mathbb {R}^r)\rightarrow \mathcal {L}^0_{k-1}(\mathcal {T}_t;L^2(\Omega ;\mathbb {R}^r))\qquad \text {with }r\in \lbrace 1,d\rbrace ,\\ \Pi _{\mathcal {L}^0_\ell (\mathcal {T}_x)}&:L^2(Q)\rightarrow L^2(\mathcal {J};\mathcal {L}^0_\ell (\mathcal {T}_x)). \end{aligned}$$

We set the interpolation operator

$$\begin{aligned} \mathcal {I}^\otimes _\Sigma \,{:}{=}\, \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)} \circ \mathcal {I}_{RT} :L^2(Q) \rightarrow \Sigma _h. \end{aligned}$$

Theorem 17

(Commuting interpolation operator $\mathcal {I}^\otimes _\Sigma$) We have the commuting diagram property

$$\begin{aligned} div _x\mathcal {I}^\otimes _\Sigma = \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)} \Pi _{\mathcal {L}^0_{\ell }(\mathcal {T}_x)} div _x. \end{aligned}$$

Moreover, we have for all $p \in L^2(Q;\mathbb {R}^d)$ the approximation property

$$\begin{aligned} \Vert p - \mathcal {I}^\otimes _\Sigma p\Vert _{L^2(Q)}^2&\eqsim \sum _{K\in \mathcal {T}} \Big ( \min _{p_{x} \in L^2(K_t;RT_\ell (\mathcal {T}_x))} \Vert p - p_{x} \Vert _{L^2(K_t;L^2(\omega _{K_x}))}^2\\&\quad + \min _{p_t \in \mathbb {P}_{k-1}(K_t;L^2(K_x;\mathbb {R}^d))} \Vert p - p_{t} \Vert _{L^2(K_t;L^2(K_x))}^2\Big ). \end{aligned}$$

Proof

Let $p \in L^2(Q;\mathbb {R}^d)$. The triangle inequality yields

$$\begin{aligned} \Vert p - \mathcal {I}^\otimes _\Sigma p\Vert _{L^2(Q)}&\le \Vert p - \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)} p \Vert _{L^2(Q)} + \Vert \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)} (p - \mathcal {I}_{RT}p)\Vert _{L^2(Q)}\\&\le \Vert p - \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)} p \Vert _{L^2(Q)} + \Vert p - \mathcal {I}_{RT} p \Vert _{L^2(Q)}. \end{aligned}$$

The approximation properties of the semi-discrete operators $\Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)}$ and $\mathcal {I}_{RT}$ lead to the approximation property in the theorem. Theorem 16 implies the commuting diagram property. $\square$

We set the discrete subspace $\Lambda _h \,{:}{=}\, X_h \otimes \Sigma _h$. By exploiting the tensor product structure we can define for each $(v,\tau ) \in \Lambda$ an interpolation $(\mathcal {I}_X^\otimes v,\mathcal {I}^\otimes _\Sigma \tau ) \in \Lambda _h$ with good approximation properties. In fact, a similar interpolation operator has been suggested in [18]. We modify this ansatz to achieve additionally a commuting diagram property. The modification involves the application of the inverse Laplacian $(-\Delta _x)^{-1}:L^2(\mathcal {J};H^{-1}(\Omega )) \rightarrow L^2(\mathcal {J};H^1_0(\Omega ))$ everywhere in time defined for all $\xi \in L^2(\mathcal {J};H^{-1}(\Omega ))$ as solution operator to

$$\begin{aligned} \langle \nabla _x (-\Delta _x)^{-1} \xi , \nabla _x w\rangle _\Omega = \langle \xi ,w\rangle _\Omega \qquad \text {for all }w\in L^2(\mathcal {J};H^1_0(\Omega )). \end{aligned}$$

We set for all $(v,\tau )\in \Lambda$ the interpolation operator $\mathcal {I}^\otimes _\Lambda :\Lambda \rightarrow \Lambda _h$ as

$$\begin{aligned} \mathcal {I}^\otimes _{\Lambda }(v,\tau ) \,{:}{=}\, (\mathcal {I}_X^\otimes v, \mathcal {I}_2(v,\tau ))\text { with }\mathcal {I}_2(v,\tau ) = \mathcal {I}^\otimes _\Sigma \big (\tau -\nabla _x (-\Delta _x)^{-1} \partial _t (v - \mathcal {I}_X^\otimes v)\big ). \end{aligned}$$

Theorem 18

(Commuting diagram property and approximablity of $\mathcal {I}^\otimes _\Lambda$) The projection $\mathcal {I}^\otimes _\Lambda$ onto $\Lambda _h$ commutes in the sense that for all $(v,\tau )\in \Lambda$

$$\begin{aligned} div \, \mathcal {I}^\otimes _\Lambda (v,\tau ) = \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)} \Pi _{\mathcal {L}^0_\ell (\mathcal {T}_x)} \, div \, (v,\tau ). \end{aligned}$$

Moreover, we control for all $(v,\tau )\in X \times \Sigma$ the interpolation error by

$$\begin{aligned} \Vert \tau - \mathcal {I}_2(v,\tau )\Vert _{L^2(Q)} \lesssim \Vert \tau - \mathcal {I}^\otimes _\Sigma \tau \Vert _{L^2(Q)} + \Vert \partial _t (v-\mathcal {I}_X^\otimes v)\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}. \end{aligned}$$

(25)

Proof

Let $(v,\tau ) \in \Lambda$. The commuting diagram property of $\mathcal {I}^\otimes _\Sigma$ (Theorem 17) and $- div _x \nabla _x (-\Delta _x)^{-1} \partial _t (v -\mathcal {I}_X^\otimes v) = \partial _t (v -\mathcal {I}_X^\otimes v)$ yield

$$\begin{aligned} div _x \mathcal {I}_2(v,\tau )&= div _x \mathcal {I}^\otimes _\Sigma \big ( \tau -\nabla _x (-\Delta _x)^{-1} \partial _t (v - \mathcal {I}_X^\otimes v)\big )\\&= \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)} \Pi _{\mathcal {L}^0_\ell (\mathcal {T}_x)} div _x \big ( \tau - \nabla _x (-\Delta _x)^{-1} \partial _t (v -\mathcal {I}_X^\otimes v)\big )\\&= -\partial _t \mathcal {I}_X^\otimes v + \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)} \Pi _{\mathcal {L}^0_\ell (\mathcal {T}_x)} (\partial _t v + div _x \tau ). \end{aligned}$$

Hence, we have the commuting diagram property

$$\begin{aligned} div \, \mathcal {I}^\otimes _\Lambda (v,\tau )&= \partial _t \mathcal {I}_X^\otimes v + div _x \mathcal {I}_2(v,\tau ) = \Pi _{\mathcal {L}^0_{k-1}(\mathcal {T}_t)} \Pi _{\mathcal {L}^0_\ell (\mathcal {T}_x)} div \, (v,\tau ). \end{aligned}$$

The approximation property follows from an application of the triangle inequality and the $L^2$ stability of $\mathcal {I}^\otimes _\Sigma$, that is, for all $(v,\tau ) \in X \times \Sigma$

$$\begin{aligned} \Vert \tau - \mathcal {I}_2(v,\tau ) \Vert _{L^2(Q)}&\lesssim \Vert \tau - \mathcal {I}^\otimes _\Sigma \tau \Vert _{L^2(Q)} + \Vert \nabla _x (-\Delta _x)^{-1} \partial _t (v -\mathcal {I}_X^\otimes v) \Vert _{L^2(Q)}\\&= \Vert \tau - \mathcal {I}^\otimes _\Sigma \tau \Vert _{L^2(Q)} + \Vert \partial _t (v -\mathcal {I}_X^\otimes v) \Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))}. \end{aligned}$$

$\square$

Remark 19

(Smoothing rough-right hand sides) The papers [9, 13, 15] suggest smoothing of the right-hand side in least-squares and mixed formulations for the Poisson model problem to conclude optimal rates of convergence even with right-hand sides in $H^{-1}(\Omega )$. The key in the proof are suitable properties of the smoothing operator and the commuting diagram property of the operator $\mathcal {I}_{RT}$. Using the commuting diagram property of the operator $\mathcal {I}^\otimes _\Lambda$ and using a suitable smoother (which results from the composition of $\Pi _{\mathcal {L}^0_k(\mathcal {T}_t)}$ and the smoother for the Poisson model problem in space) lead to the same results for least-squares and mixed schemes for the heat equation.

6 Irregular meshes

In this section we introduce an operator $\mathcal {I}_X:X \rightarrow X_h$ with locally in space-time refined underlying triangulation $\mathcal {T}$. Such local refinements lead to irregular partitions as for example displayed in Fig. 1. Hence, there might be hanging nodes. More precisely, let $K = K_t \times K_x \in \mathcal {T}$ be a cylinder and let $\mathcal {N}(K_t) \subset K_t$ and $\mathcal {N}(K_x)\subset K_t$ denote the Lagrange nodes in $\mathbb {P}_k(K_t)$ and $\mathbb {P}_\ell (K_x)$, respectively. In other words, with Lagrange basis functions $(b_{j_t})_{j_t\in \mathcal {N}(K_t)} \subset \mathbb {P}_k(K_t)$ and $(b_{j_x})_{j_x\in \mathcal {N}(K_x)} \subset \mathbb {P}_\ell (K_x)$ we have

$$\begin{aligned} \begin{aligned} b^{K_t}_{j_t}(i_t)&= \delta _{j_t,i_t}\qquad \qquad \text {for all }j_t,i_t\in \mathcal {N}(K_t),\\ b^{K_x}_{j_x}(i_x)&= \delta _{j_x,i_x}\qquad \qquad \text {for all }j_x,i_x\in \mathcal {N}(K_x). \end{aligned} \end{aligned}$$

(26)

Hence, the local degrees of freedom in $\mathbb {P}_k(K_t) \otimes \mathbb {P}_\ell (K_x)$ read $\mathcal {N}(K) = \mathcal {N}(K_t) \times \mathcal {N}(K_x)$ and the basis functions are

$$\begin{aligned} b_j^K \,{:}{=}\, b^{K_t}_{j_t} b^{K_x}_{j_x}\quad \text {with }b_j^K(i) = \delta _{j,i} \qquad \text {for all }j = j_t \times j_x \in \mathcal {N}(K)\text { and }i \in \mathcal {N}(K). \end{aligned}$$

Let $\mathcal {N}(\mathcal {T}) \,{:}{=}\, \bigcup _{K\in \mathcal {T}}\mathcal {N}(K)$ denote the set of all local degrees of freedom. If $\mathcal {T}$ is an irregular partition, there exist hanging nodes, that is, local degrees of freedom that are no global degrees of freedom in the sense that they are contained in

$$\begin{aligned} \mathcal {H}(\mathcal {T}) \,{:}{=}\, \lbrace j \in \mathcal {N}(\mathcal {T}) :\exists K'\in \mathcal {T}\text { with }j\in K' \text { and }j\not \in \mathcal {N}(K')\rbrace . \end{aligned}$$

We define the set of free nodes by

$$\begin{aligned} \mathcal {F}(\mathcal {T}) \,{:}{=}\, \mathcal {N}(\mathcal {T}) \setminus \big (\mathcal {H}(\mathcal {T}) \cup (\mathcal {J} \times \partial \Omega )\big ). \end{aligned}$$

We assume that the mesh has some hierarchical structure in the sense that all cylinders $K,K'\in \mathcal {T}$ with $K \cap K' \ne \emptyset$ satisfy

$$\begin{aligned} \mathcal {N}(K) \cap K' \subset \mathcal {N}(K') \quad \text {or}\quad \mathcal {N}(K') \cap K \subset \mathcal {N}(K). \end{aligned}$$

(27)

Lemma 20

(Basis) Suppose (27) is true. Then for any $j\in \mathcal {N}(\mathcal {T})$ exist coefficients $\alpha _j(i) \in \mathbb {R}$ with uniform bound $|\alpha _j(i)| \le C < \infty$ depending on k, $\ell$, and d such that

$$\begin{aligned} v_h(j) = \sum _{i\in \mathcal {F}(\mathcal {T})} \alpha _j(i) v_h(i) \qquad \text {for all }v_h \in X_h. \end{aligned}$$

Moreover, the space $X_h$ is spanned by the basis $(\phi _j)_{j\in \mathcal {F}(\mathcal {T})}\subset X_h$ with functions $\phi _j \in X_h$ uniquely defined by the condition

$$\begin{aligned} \phi _j(i) = \delta _{j,i}\qquad \text {for all }j,i\in \mathcal {F}(\mathcal {T}). \end{aligned}$$

Proof

Straight forward modifications of [16, Thm. 3.1 and Lem. 3.2] yield the lemma. $\square$

In order to have some finite overlap of basis functions, we need additional assumptions like the 1-irregular rule in [18]. To avoid technicalities, we do not discuss the impact of these properties and rather state, besides (27), additionally the following assumption.

• (a) (Shape regularity) All d-simplices $K_x$ with $K = K_t\times K_x \in \mathcal {T}$ are shape regular.

• (b) (Local grading) Let $K\in \mathcal {T}$ and set $\mathcal {N}_K \,{:}{=}\, \lbrace j\in \mathcal {N}:K \subset supp (\phi _j) \rbrace$. We define the patch $\omega _K = \omega _{K,t} \times \omega _{K,x} \supset \bigcup _{j\in \mathcal {N}_K} supp (\phi _j)$ as the smallest cylinder that contains the support of all basis functions $\phi _j$ with $j\in \mathcal {N}_K$. We assume that cylinders $K'=K_t'\times K_x' \in \mathcal {T}$ with $K' \subset \omega _K$ are of equivalent size in the sense that $|K'_t|\eqsim |K_t| \eqsim |\omega _{K,t}|$ and $|K'_x|\eqsim |K_x| \eqsim |\omega _{K,x}|$.

Let $\Pi _K:X \rightarrow \mathbb {P}_k(K_t;\mathbb {P}_\ell (K_x))$ denote the $L^2(K)$ orthogonal projection onto the space $\mathbb {P}_k(K_t;\mathbb {P}_\ell (K_x))$ for all $K = K_t \times K_x\in \mathcal {T}$.

Lemma 21

(Operator $\Pi _K$) Let $K\in \mathcal {T}$ and $v \in X$. We have

$$\begin{aligned} \Vert \nabla _x (v - \Pi _K v)\Vert _{L^2(K)}&\eqsim \min _{v_x \in L^2(K_t;\mathbb {P}_\ell (K_x))} \Vert \nabla _x (v - v_x)\Vert _{L^2(K_t;L^2(K_x))}\\&\quad + \min _{V_t \in \mathbb {P}_k(K_t;L^2(K_x;\mathbb {R}^d))} \Vert \nabla _x v- V_t \Vert _{L^2(K_t;L^2(K_x))}. \end{aligned}$$

If additionally $\partial _t v \in L^2(K)$, we obtain

$$\begin{aligned} \Vert \partial _t (v - \Pi _K v)\Vert _{L^2(K)}&\eqsim \min _{\xi _x\in L^2(K_t;\mathbb {P}_{\ell }(K_x))} \Vert \partial _t v - \xi _x \Vert _{L^2(K_t;L^2(K_x))} \\&\quad + \min _{v_t \in \mathbb {P}_k(K_t;L^2(K_x))} \Vert \partial _t( v - v_t)\Vert _{L^2(K_t;L^2(K_x))}. \end{aligned}$$

Proof

Let $v\in X$ and let $K = K_t\times K_x\in \mathcal {T}$. Recall the $L^2(K_t)$ orthogonal projector $\Pi _{\mathbb {P}_k(K_t)}$ defined in (18). Let $\Pi _{\mathbb {P}_\ell (K_x)}$ denote the $L^2(K_x)$ orthogonal projection onto $\mathbb {P}_{\ell }(K_x)$. Since $\Pi _K v = \Pi _{\mathbb {P}_k(K_t)} \Pi _{\mathbb {P}_\ell (K_x)} v$, we have

$$\begin{aligned}&\Vert \nabla _x ( v - \Pi _K v)\Vert _{L^2(K)}\\&\qquad \le \Vert \nabla _x (v - \Pi _{\mathbb {P}_k(K_t)} v) \Vert _{L^2(K)} + \Vert \Pi _{\mathbb {P}_k(K_t)}\nabla _x (v - \Pi _{\mathbb {P}_\ell (K_x)} v) \Vert _{L^2(K)}\\&\qquad \le \Vert \nabla _x (v - \Pi _{\mathbb {P}_k(K_t)} v) \Vert _{L^2(K)} + \Vert \nabla _x (v - \Pi _{\mathbb {P}_\ell (K_x)} v) \Vert _{L^2(K)}. \end{aligned}$$

Using the approximation properties of the semi-discrete projection operators leads to the first estimate in the lemma. Similar arguments yield due to the identity $\Pi _K v = \Pi _{\mathbb {P}_\ell (K_x)} \Pi _{\mathbb {P}_k(K_t)} v$ the second estimate. $\square$

We assign to each degree of freedom $j\in \mathcal {N}$ a cylinder $K(j)\in \mathcal {T}$ that contains the node $j\in K(j)$ and set the operator $\mathcal {I}_X :X \rightarrow X_h$ with

$$\begin{aligned} (\mathcal {I}_X v)(j) \,{:}{=}\, (\Pi _{K(j)} v)(j)\qquad \text {for all }v\in X\text { and }j\in \mathcal {N}. \end{aligned}$$

(28)

Theorem 22

(Interpolation operator $\mathcal {I}_X$) The operator $\mathcal {I}_X$ is a projection onto $X_h$ that satisfies for all $v\in X$ with $\partial _t v \in L^2(\omega _K)$

$$\begin{aligned}&\Vert \nabla _x (v - \mathcal {I}_X v)\Vert _{L^2(K)} \lesssim \min _{v_h \in X_h} \Vert \nabla _x (v - v_h)\Vert _{L^2(\omega _K)} + \frac{h_t(K)}{h_x(K)}\, \Vert \partial _t v- \partial _t v_h \Vert _{L^2(\omega _K)}. \end{aligned}$$

Moreover, we have for all $v\in X$ with $\partial _t v \in L^2(\omega _K)$

$$\begin{aligned} \Vert \partial _t (v - \mathcal {I}_X v)\Vert _{L^2(K)}&\lesssim \min _{v_h \in X_h} \Vert \partial _t (v - v_h) \Vert _{L^2(\omega _K)} + \frac{h_x(K)}{h_t(K)} \Vert \nabla _x v - \nabla _x v_h\Vert _{L^2(\omega _K)}. \end{aligned}$$

Proof

The projection property of $\mathcal {I}_X$ follows directly by its definition. Let $K = K_t\times K_x\in \mathcal {T}$, let $v\in X$ with $\partial _t v \in L^2(\omega _K)$, and let $v_h \in X_h$. Since $(\Pi _K v_h - \mathcal {I}_X v_h)|_K = 0$, we have with $e \,{:}{=}\, v - v_h$

$$\begin{aligned} \Vert \nabla _x( v - \mathcal {I}_X v) \Vert _{L^2(K)} \le \Vert \nabla _x( v - \Pi _K v)\Vert _{L^2(K)} + \Vert \nabla _x(\Pi _K e - \mathcal {I}_X e) \Vert _{L^2(K)}. \end{aligned}$$

(29)

Let $\mathcal {N}(K_t) \subset K_t$ and $\mathcal {N}(K_x)\subset K_t$ denote the Lagrange nodes in $\mathbb {P}_k(K_t)$ and $\mathbb {P}_\ell (K_x)$ with Lagrange basis functions $(b_{j_t})_{j_t\in \mathcal {N}(K_t)} \subset \mathbb {P}_k(K_t)$ and $(b_{j_x})_{j_x\in \mathcal {N}(K_x)} \subset \mathbb {P}_\ell (K_x)$ as introduced in (26). For each of these functions exists (cf. [30, Eq. 2.9]) a dual basis $b_{j_t}^* \in \mathbb {P}_k(K_t)$ and $b_{j_x}^*\in \mathbb {P}_\ell (K_x)$ in the sense that

$$\begin{aligned} \begin{aligned} \langle b_{j_t},b_{i_t}^*\rangle _{K_t}&= \delta _{j_t,i_t}\qquad \qquad \text {for all }j_t,i_t\in \mathcal {N}(K_t),\\ \langle b_{j_x},b_{i_x}^*\rangle _{K_x}&= \delta _{j_x,i_x}\qquad \qquad \text {for all }j_x,i_x\in \mathcal {N}(K_x). \end{aligned} \end{aligned}$$

The basis and dual basis functions in $\mathbb {P}_{k}(K_t)\otimes \mathbb {P}_{\ell }(K_x)$ read

$$\begin{aligned} b_j \,{:}{=}\, b_{j_t} b_{j_x}\quad \text {and}\quad b^*_j \,{:}{=}\, b^*_{j_t} b^*_{j_x}\quad \text {for all }j = j_t\times j_x \in \mathcal {N}(K)= \mathcal {N}(K_t)\times \mathcal {N}(K_x). \end{aligned}$$

Indeed, these functions are bi-orthogonal in $L^2(K)$ in the sense that

$$\begin{aligned} \langle b_j , b^*_i\rangle _K = \delta _{j,i}\qquad \text {for all }j,i\in \mathcal {N}(K). \end{aligned}$$

We have for all $i\in \mathcal {N}(K)$ and $e = v - v_h$ the identity

$$\begin{aligned} \sum _{j\in \mathcal {N}(K)} \left\langle \langle e,b_j^*\rangle _K b_j,b^*_i\right\rangle _K = \langle e,b_i^*\rangle _K. \end{aligned}$$

Since $(b_i^*)_{i\in \mathcal {N}(K)}$ forms a basis of $\mathbb {P}_{k}(K_t)\otimes \mathbb {P}_{\ell }(K_x)$, this identity shows that

$$\begin{aligned} \Pi _K e = \sum _{j\in \mathcal {N}(K)} \langle e,b_j^*\rangle _K b_j. \end{aligned}$$

(30)

Hence, the triangle inequality reveals that

$$\begin{aligned}&\Vert \nabla _x( \Pi _K e - \mathcal {I}_X e) \Vert _{L^2(K)} \le \sum _{j \in \mathcal {N}(K)} |\langle e , b_j^* \rangle _Q - (\mathcal {I}_X e)(j) |\, \Vert \nabla _x b_j \Vert _{L^2(K)}. \end{aligned}$$

(31)

The values of $\mathcal {I}_X e$ at the local degree of freedom $j \in \mathcal {N}(K)$ read as follows.

• If $j\in \mathcal {N}(K)$ is not on the boundary $\mathcal {J}\times \partial \Omega$, Lemma 20 shows that the value of $\mathcal {I}_X$ at j depends on the values of $\mathcal {I}_X$ at some degrees of freedom $(i_j^m)_{m = 1}^{N_j}\subset \mathcal {F}(\mathcal {T})$ with $j\in supp (\phi _{i_j^m})$ for all $m=1,\dots ,N_j$ and some uniformly bounded number $N_j \in \mathbb {N}$, where the boundedness follows from the local grading assumption in (b). In other words, there exist coefficients $(\alpha ^m_j)_{m=1}^{N_j} \subset [-C,C] \subset \mathbb {R}$ with

  $$\begin{aligned} (\mathcal {I}_X w)(j) = \sum _{m=1}^{N_j} \alpha ^m_j (\mathcal {I}_Xw)(i_j^m)\qquad \text {for all }w\in X. \end{aligned}$$

  For any $i_j^m$ with $m\in \lbrace 1,\dots ,N_j\rbrace$ the definition in (28) states the existence of a cylinder $K(i_j^m)\in \mathcal {T}$ such that

  $$\begin{aligned} (\mathcal {I}_X e)(i_j^m) = (\Pi _{K(i_j^m)} e)(i_j^m). \end{aligned}$$

  Due to the arguments in (30), there exist dual basis functions $(b_j^m)^* = (b_{j_t}^m)^*(b_{j_x}^m)^*$ with $(b_{j_t}^m)^*\in \mathbb {P}_k(K_t(i_j^m))$ and $(b_{j_x}^m)^*\in \mathbb {P}_\ell (K_x(i_j^m))$ such that

  $$\begin{aligned} (\mathcal {I}_X w)(i_j^m) = \sum _{m=1}^{N_{j}} \alpha ^m_{j} \langle w, (b_{j}^m)^* \rangle _{K(i_j^m)} \qquad \text {for all }w\in X. \end{aligned}$$

• If the local degree of freedom j is on the boundary $\mathcal {J} \times \partial \Omega$, we have $(\mathcal {I}_X e)(j) = 0$ and set $N_j \,{:}{=}\, 0$.

Case 1 (Interior cylinder). Let $K\in \mathcal {T}$ be a cylinder with $\sum _{j \in \mathcal {F}(\mathcal {T})} \phi _j|_K= 1.$ Then the definition of $\mathcal {I}_X$ in (28) implies

$$\begin{aligned} (\mathcal {I}_X 1)|_K = \sum _{j \in \mathcal {F}(\mathcal {T})} \phi _j|_K= 1. \end{aligned}$$

In particular, we obtain for any local degree of freedom $j\in \mathcal {N}(K)$

$$\begin{aligned} 1 = (\mathcal {I}_X 1)(j) = \sum _{m=1}^{N_{j}} \alpha _j^m (\mathcal {I}_X 1)(i_j^m) = \sum _{m=1}^{N_{j}} \alpha _j^m. \end{aligned}$$

(32)

Set the integral means and . Combining the identity (32) with $\langle 1,b_{j,t}^*- (b^m_{j,t})^* \rangle _\mathcal {J} = 1-1 = 0 = \langle 1, (b^m_{j,x})^* - b_{j,x}^* \rangle _\Omega$ and scaling arguments yields for the addends in (31) and all $j\in \mathcal {N}(K)$

$$\begin{aligned} \begin{aligned}&|\langle e , b_j^* \rangle _Q - (\mathcal {I}_X e)(j)|\, \Vert \nabla _x b_j \Vert _{L^2(K)} = \Big |\sum _{m=1}^{N_j} \alpha ^m_j \langle e , b_j^* - (b_j^m)^* \rangle _Q \Big |\, \Vert \nabla _x b_j \Vert _{L^2(K)} \\&\quad \le \Big |\sum _{m=1}^{N_j} \alpha ^m_j \langle e - \langle e \rangle _{\omega _{K,t}}, b_{j,x}^* (b_{j,t}^*- (b^m_{j,t})^*)\rangle _Q \Big |\, \Vert \nabla _x b_j \Vert _{L^2(K)}\\&\quad + \Big | \sum _{m=1}^{N_j} \alpha ^m_j \langle e - \langle e \rangle _{\omega _{K,x}}, (b_{j,x}^*-(b_{j,x}^m)^* )(b^m_{j,t})^*\rangle _Q\Big | \, \Vert \nabla _x b_j \Vert _{L^2(K)}\\&\quad \le \sum _{m=1}^{N_j} |\alpha ^m_j| \,\Vert e - \langle e \rangle _{\omega _{K,t}} \Vert _{L^2(\omega _K)} \Vert b_{j,x}^* (b_{j,t}^*- (b^m_{j,t})^*)\Vert _{L^2(Q)} \Vert \nabla _x b_j \Vert _{L^2(K)}\\&\quad + \sum _{m=1}^{N_j} |\alpha ^m_j|\, \Vert e - \langle e \rangle _{\omega _{K,x}}\Vert _{L^2(\omega _K)} \Vert b_{j,x}^*-(b_{j,x}^m)^* )(b^m_{j,t})^*\Vert _{L^2(Q)} \Vert \nabla _x b_j \Vert _{L^2(K)}\\&\quad \lesssim \sum _{m=1}^{N_j} |\alpha ^m_j| \,\Vert e - \langle e \rangle _{\omega _{K,t}} \Vert _{L^2(\omega _K)} h_x(K)^{-1} + \sum _{m=1}^{N_j} |\alpha ^m_j|\, \Vert e - \langle e \rangle _{\omega _{K,x}}\Vert _{L^2(\omega _K)} h_x(K)^{-1}\\&\quad \lesssim \frac{h_t(K)}{h_x(K)} \Vert \partial _t e \Vert _{L^2(\omega _K)} + \Vert \nabla _x e \Vert _{L^2(\omega _K)}. \end{aligned} \end{aligned}$$

Case 2 (dof on boundary). Suppose that $\sum _{j \in \mathcal {F}(\mathcal {T})} \phi _j|_K \ne 1$. The patch $\omega _K$ shares a face with the boundary. Hence, scaling arguments and Friedrichs’ inequality lead for all $j \in \mathcal {N}(K)$ to

$$\begin{aligned}{} & {} |\langle e , b_j^* \rangle _Q - (\mathcal {I}_X e)(j)|\, \Vert \nabla _x b_j \Vert _{L^2(K)} \le \Big | \Big \langle e , b_j^* - \sum _{m=1}^{N_j} \alpha ^m_{j} (b_{j}^m)^* \Big \rangle _Q\Big |\, \Vert \nabla _x b_j \Vert _{L^2(K)} \nonumber \\{} & {} \quad \lesssim \Vert e \Vert _{L^2(\omega _K)} h_x(K)^{-1} \lesssim \Vert \nabla _x e \Vert _{L^2(K)}. \end{aligned}$$

(33)

Combining these estimates and Lemma 21 leads to the first bound in the lemma. The second follows similarly. $\square$

We proceed with a comparison of the interpolation error estimates on tensor product and irregular meshes. Let $K \in \mathcal {T}$ be a time-space cell with $h_t \,{:}{=}\, h_t(K)$ and $h_x \,{:}{=}\, h_x(K)$ in a tensor product mesh (if we apply $\mathcal {I}^\otimes _X$) or in an irregular mesh. Due to Theorem 4, 12, and 22 we have the stability and approximation properties

$$\begin{aligned} \begin{aligned}&\Vert \nabla _x( v - \mathcal {I} v)\Vert _{L^2(K)}\\&\quad \lesssim {\left\{ \begin{array}{ll} \Vert \nabla _x v \Vert _{L^2(K)} + \frac{h_t}{h_x^2} \Vert \partial _t v\Vert _{L^2(K_t;H^{-1}(\omega _{K,x}))}&{}\text {for }\mathcal {I} = \mathcal {I}_X^\otimes ,\\ h_x \Vert \nabla ^2_x v \Vert _{L^2(K)} + \frac{h^2_t}{h_x^2} \Vert \partial _t^2 v\Vert _{L^2(K_t;H^{-1}(\omega _{K,x}))}&{}\text {for }\mathcal {I} = \mathcal {I}_X^\otimes ,\\ \Vert \nabla _x v \Vert _{L^2(K)} + \frac{h_t}{h_x} \Vert \partial _t v\Vert _{L^2(\omega _K)}&{}\text {for }\mathcal {I} \in \lbrace \mathcal {I}_X^\otimes ,\mathcal {I}_X\rbrace ,\\ h_x\Vert \nabla ^2_x v \Vert _{L^2(K)} + \frac{h_t}{h_x} \Vert \partial _t v\Vert _{L^2(\omega _K)}&{}\text {for }\mathcal {I} \in \lbrace \mathcal {I}_X^\otimes ,\mathcal {I}_X\rbrace ,\\ h_x \Vert \nabla ^2_x v \Vert _{L^2(K)} + \frac{h^2_t}{h_x} \Vert \partial _t^2 v\Vert _{L^2(\omega _K)}&{}\text {for }\mathcal {I} \in \lbrace \mathcal {I}_X^\otimes ,\mathcal {I}_X\rbrace ,\\ h_x \Vert \nabla ^2_x v \Vert _{L^2(K)} + h_t \Vert \partial _t \nabla _x v\Vert _{L^2(\omega _K)}&{}\\ + \frac{h^2_t}{h_x^2} \Vert \partial _t^2 v\Vert _{L^2(K_t;H^{-1}(\omega _{K,x}))}&{}\text {for }\mathcal {I} \in \lbrace \mathcal {I}_X^\otimes ,\mathcal {I}_X\rbrace . \end{array}\right. } \end{aligned} \end{aligned}$$

(34)

Despite a smaller domain of dependency with respect to time (neglected in the comparison above), the advantages of the operator $\mathcal {I}_X^\otimes$ are restricted to stability properties in X rather than in $L^2(\mathcal {J};H^1_0(\Omega )) \cap H^1(\mathcal {J};L^2(\Omega ))$. However, under reasonable regularity assumptions like in (4) and (5) both operators lead to the same approximation properties. These properties suggest the following mesh scalings.

• If we only have (4), the results suggest the parabolic scaling $h_t \eqsim h_x^2$ and a tensor-product mesh, leading with the first inequality in (34) to the rate of convergence $h_x$.

• If we only have (4) and (5), the results suggest the scaling $h_t \eqsim h_x^{3/2}$, leading with the last inequality in (34) to the rate of convergence $h_x$.

• If we additionally have $\partial _t^2 v\in L^2(Q)$, the results suggest the scaling $h_t \eqsim h_x$, leading with the fourth inequality in (34) to the rate of convergence $h_x$.

While Theorem 12 investigates the error $\partial _t (v - \mathcal {I}_X^\otimes v)$ in the $L^2(\mathcal {J};H^{-1}(\Omega ))$ norm, Theorem 22 investigates the error $\partial _t (v - \mathcal {I}_X v)$ in the $L^2(Q)$ norm. Notice however, that similar arguments as in the proof of Theorem 12 allow us to conclude upper bounds for the $L^2(Q)$ norm of the interpolation error $\partial _t (v - \mathcal {I}_X^\otimes v)$ as well. This leads to the following comparison for $\mathcal {I} \in \lbrace \mathcal {I}_X^\otimes ,\mathcal {I}_X\rbrace$, where the values in brackets are solely needed if $\mathcal {I} = \mathcal {I}_X$:

$$\begin{aligned}&\Vert \partial _t (v-\mathcal {I}v)\Vert _{L^2(K)}\\&\quad \lesssim {\left\{ \begin{array}{ll} \Vert \partial _t v \Vert _{L^2(\omega _K)}&{} \big (+\frac{h_x}{h_t} \Vert \nabla _x v \Vert _{L^2(\omega _K)}\big ),\text { or}\\ h_x \Vert \partial _t \nabla _x v \Vert _{L^2(\omega _K)} + \frac{h_t}{h_x} \Vert \partial _t^2 v \Vert _{L^2(K_t;H^{-1}(\omega _{K,x}))} &{}\big (+\frac{h^2_x}{h_t} \Vert \nabla ^2_x v \Vert _{L^2(\omega _K)}\big ),\text { or} \\ h_x \Vert \partial _t \nabla _x v \Vert _{L^2(\omega _K)} + h_t \Vert \partial _t^2 v \Vert _{L^2(\omega _K)} &{}\big (+\frac{h_x^2}{h_t} \Vert \nabla _x^2 v \Vert _{L^2(\omega _K)}\big ). \end{array}\right. } \end{aligned}$$

Under the regularity assumptions in (4) and (5) the estimates show for both operators a reduced rate of convergence compared to (34). This can be expected, since we investigate the error with respect to the stronger $L^2(Q)$ norm. The combination of the error estimates with the regularity properties in (4) and (5) suggests a scaling $h_t \eqsim h_x^{3/2}$. If we grade the mesh too strongly, for example $h_t \eqsim h_x^2$, the operator $\mathcal {I}_X$ experiences, unlike the operator $\mathcal {I}_X^\otimes$, stability issues due to the terms

$$\begin{aligned} \frac{h_x}{h_t} \Vert \nabla _x v \Vert _{L^2(K)} \qquad \text {or}\qquad \frac{h_x^2}{h_t} \Vert \nabla _x^2 v \Vert _{L^2(K)}. \end{aligned}$$

(35)

Notice that unlike for operators on tensor meshes, such terms which do not depend on the time derivative $\partial _t v$ must occur in bounds for the interpolation error $\partial _t (v -\mathcal {I}_X v)$, since on irregular meshes the interpolated function $\mathcal {I}_X v$ might vary in time even so v might be constant in time, that is, the property $\partial _t v = 0$ does in general not imply $\partial _t \mathcal {I}_X v = 0$. The following remark investigates this aspect in more detail.

Fig. 1

Locally refined meshes

Remark 23

(Parabolic scaling vs.  local refinements)

Let $\mathcal {I}:X \rightarrow X_h$ be some locally defined interpolation operator with first order ansatz space $X_h = X_h^{1,1}$ and basis functions $(\phi _j)_{j\in \mathcal {N}}$. For simplicity we assume that the operator has weights $\phi _{j}^* \in X$ with $supp (\phi _j^*) \subset supp (\phi _j)$ and

$$\begin{aligned} \mathcal {I} v = \sum _{j\in \mathcal {N}} \langle v, \phi _{j}^*\rangle \phi _j\qquad \text {for all }v\in X. \end{aligned}$$

Moreover, we assume that these weights solely depend on the shape of the element patch. Let the underlying mesh result from refining a uniform tensor mesh $\mathcal {T}_t \otimes \mathcal {T}_x$ with $0<h_t = |K_t|$ for all $K_t\in \mathcal {T}_t$ and $0<h_x = diam (K_x)$ for all $K_x\in \mathcal {T}_x$ in every fourth time interval $K_t(4),K_t(8),K_t(12),\dots \in \mathcal {T}_t$ as depicted in Fig. 1. We can find a function $v\in X$ with $\partial _t v = 0$ such that $(\mathcal {I} v)|_{K_t(4\,m-2)\times \Omega } = 0$ equals zero on every $(4\,m-2)$-th time interval in $\mathcal {T}_t$ with $m\in \mathbb {N}$ and $(\mathcal {I} v)(j) = 1$ for all degrees of freedom $j\in \mathcal {N}$ inside the refined area, that is for all $j\in int (K_t(4m) \times \Omega )$. Scaling arguments lead to $\Vert \nabla _x v\Vert _{L^2(Q)} \eqsim h_x^{-1}$ and $\Vert \nabla ^2_x v\Vert _{L^2(Q)} \eqsim h_x^{-2}$. Since by definition $\Vert \partial _t \mathcal {I}v\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))} \eqsim \Vert \partial _t \mathcal {I}v\Vert _{L^2(Q))} \eqsim h_t^{-1}$, the interpolation error reads

$$\begin{aligned} \Vert \partial _t(v- \mathcal {I}v)\Vert _{L^2(\mathcal {J};H^{-1}(\Omega ))} \eqsim \Vert \partial _t (v-\mathcal {I}v) \Vert _{L^2(Q)} \eqsim \frac{h_x}{h_t} \Vert \nabla _x v\Vert _{L^2(Q)} \eqsim \frac{h^2_x}{h_t} \Vert \nabla ^2_x v\Vert _{L^2(Q)}. \end{aligned}$$

In this regard the terms in (35) cannot be avoided in interpolation error estimates for the time derivative on irregular meshes.

7 Conclusion

This paper introduces interpolation operators and investigates their stability and (localized) approximation properties displayed in Theorem 12, 18, and 22. Their derivation led to the following observations.

• While it is possible to localize interpolation errors in the $H^{-1}(\Omega )$ as for example done in [9], it is not possible to localize the $L^2(\mathcal {J};H^{-1}(\Omega ))$ error in space without introducing a negative power of the local mesh size as weight; see Remark 15.

• The parabolic Poincaré inequality in Theorem 4 suggests a parabolic scaling $h_t(K) \eqsim h_x^2(K)$ for the interpolation of irregular functions $v \in X$. This scaling occurs also when we change the norm in our interpolation error estimates like in (23). Roughly speaking, this change of norms reads

  

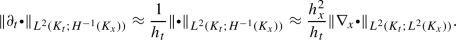
  On irregular meshes, we have to use the $L^2(\mathcal {J};L^2(\Omega ))$ norm to localize the error in the approximation of the time derivative. If we change the norm (which we have to do according to Remark 23), we observe roughly speaking

  

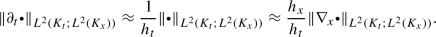
  This indicates that parabolic scaling occurs naturally for tensor product meshes but causes difficulties for irregular meshes. Remark 23 underlines the latter observation.

All in all, we have shown that the localization of the $L^2(\mathcal {J};H^{-1}(\Omega ))$ norm in space leads to some unavoidable difficulties, which can partially be overcome by assuming additional smoothness of the underlying function. However, interpolation operators $\mathcal {I}:X \rightarrow X_h$ cannot have the same beneficial properties as interpolation operators for elliptic problems. It is likely that similar difficulties occur in the numerical analysis of simultaneous space-time variational formulations, in particular when the underlying mesh is irregular. For example, to the authors’ knowledge there exists no numerical scheme that leads to quasi-optimal approximations with respect to the norm in X with underlying meshes that do not have some kind of tensor product structure; c.f. [29]. An exception are minimal residual methods [7, 14, 17], which are quasi-optimal in a slightly stronger norm. This might indicate that the norm in X is actually not well suited for adaptive numerical schemes and a remedy might be the use of alternative norms that are better suited for localization.