Abstract
We provide a non-Gentzen, though fully syntactical, cut-elimination algorithm for classical propositional logic. The designed procedure is implemented on \(\textsf{GS4}\), the one-sided version of Kleene’s sequent system \(\textsf{G4}\). The algorithm here proposed proves to be more ‘dexterous’ than other, more traditional, Gentzen-style techniques as the size of proofs decreases at each step of reduction. As a corollary result, we show that analyticity always guarantees minimality of the size of \(\textsf{GS4}\)-proofs.
Similar content being viewed by others
1 Introduction
In this paper we focus attention on \(\textsf{GS4}\), the one-sided version à la Tait of Kleene’s sequent system \(\textsf{G4}\) for classical propositional logic [7, 9, 13].Footnote 1 The proof-system \(\textsf{GS4}\) combines three specific technical features: (i) the logical rules are considered in their context-sharing (additive) formulation, (ii) the axiom-rule comes in its generalized version, and (iii) logical contexts are taken to be multisets of formulas. Besides, we crucially require that only clauses—i.e. sequents displaying solely literals—can be introduced as instances of the axiom-rule (cfr. Fig. 1).
We show that \(\textsf{GS4}\) admits a non-Gentzen cut-elimination algorithm considerably more efficient than other, more traditional, Gentzen-style reduction procedures as the size of proofs decreases at each reduction step. The algorithm proposed here relies on the observation that, if \(\vdash \Gamma \) is a provable sequent, then any proof \(\pi \) of \(\vdash \Gamma ,A\) can be turned into a proof \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) ending in \(\vdash \Gamma \) (Corollary 11) simply by ‘unthreading’ from the proof-tree \(\pi \) the formula A (Proposition 9 and Lemma 10). As a corollary result of our Hauptsatz (Theorem 12), we show that analyticity always guarantees minimality of the size of proofs (Corollary 13).
2 Notation, terminology, and preliminary results
We consider a language à la Tait comprising only two connectives: conjunction (\(\wedge \)) and disjunction (\(\vee \)) [13]. Negation comes as primitive on atomic sentences
and it extends to compound formulas by means of the following standard equivalences:
The set \(\mathcal {F}\) of well-formed formulas is defined according to the following grammar:
Logical contexts \(\Gamma ,\Delta ,\ldots \) are taken to be multisets of formulas from \(\mathcal {F}\). As usual, we write \(\Gamma ,A\) and \(\Gamma ,\Delta \) to simplify the expressions \(\Gamma \uplus [A]\) and \(\Gamma \uplus \Delta \), respectively.
The complexity \(\mathcal {C}(A)\) of a formula A is given by the number of occurrences of logical connectives in it. More formally: \(\mathcal {C}(A)=0\), for any \(A\in \textbf{AT}\), and \(\mathcal {C}(A\wedge B)=\mathcal {C}(A\vee B)=\mathcal {C}(A)\,+\,\mathcal {C}(B)+1\). For any multiset \(\Gamma =[A_{1},A_{2},\ldots ,A_{n}]\), we set \(\mathcal {C}(\Gamma )=\mathcal {C}(A_{1})+\mathcal {C}(A_{2})+\cdots +\mathcal {C}(A_{n})\). It is easy to check that \(\mathcal {C}(A)=\mathcal {C}(\overline{A})\), for any \(A\in \mathcal {F}\).
Following the standard terminology, a clause is a sequent displaying only atomic sentences [1, 3]. In particular, a clause \(\vdash \Gamma \) is said to be an identity clause just in case \(\Gamma \) contains at least one pair of dual atoms (\(\Gamma \) is an inconsistent multiset of literals), otherwise \(\vdash \Gamma \) is termed complementary (\(\Gamma \) is a consistent multiset of literals).Footnote 2
We call \(\textsf{GS4}\) the one-sided version of Kleene’s sequent system G4 whose rules are displayed in Fig. 1 [6, 7, 9, 12]. It is crucial to observe that, in the specific version of the \(\textsf{GS4}\) calculus adopted here, the axiom-rule is allowed to introduce only (identity) clauses. Hereafter, \(\textsf{GS4}\)-proofs are defined by passing through the more general notion of decomposition-tree.
Definition 1
(Decomposition-trees) Decomposition-trees are finite trees of sequents such that:
-
For any finite \(\Gamma \subset \textbf{AT}\), \(\vdash \Gamma \) is a decomposition-tree.
-
If \(\pi _{1}\), \(\rho _{1}\) and \(\rho _{2}\) are the three decomposition-trees reported below

then the following also qualify as decomposition-trees.

-
Nothing else is a decomposition-tree.
Definition 2
(\(\textsf{GS4}\)-proofs, direct subproofs) A decomposition-tree \(\pi \) qualifies as a \(\textsf{GS4}\)-proof just in case each of \(\pi \)’s top-sequents turns out to be an instance of the axiom-rule, i.e., an identity clause. A subproof \(\rho \) of a \(\textsf{GS4}\)-proof \(\pi \) is said to be direct if it delivers one of the premises of \(\pi \)’s last rule. We say that \(\textsf{GS4}\) proves the sequent \(\vdash \Gamma \) to mean that there is at least one \(\textsf{GS4}\)-proof ending in \(\vdash \Gamma \).
Proposition 1
Any multiset of formulas \(\Gamma \) admits a decomposition-tree ending in \(\vdash \Gamma \).
Proof
It suffices to start from \(\vdash \Gamma \) and keep decomposing it by applying upwards the logical rules till the leaves of the tree are all clauses (i.e. not further decomposable sequents). \(\square \)
We denote with \(\textsf{top}(\pi )\) the multiset of clauses occurring as top-sequents in a decomposition-tree \(\pi \). The size \(h\times w\) of a decomposition-tree \(\pi \) is measured by means of two parameters expressing \(\pi \)’s height and width. The height \(h(\pi )\) of \(\pi \) is given by the number of sequents occurring in one of its longest branches. The width \(w(\pi )\) counts the number of \(\pi \)’s top-sequents, that is \(w(\pi )=\#\textsf{top}(\pi )\).
Example 1
We report below a decomposition-tree \(\pi \) for the sequent \({\vdash }(p{\wedge } t){\vee } q,(p{\vee } q){\wedge } t\).

In this case, \(\textsf{top}(\pi )=\big [\, \hspace{-2pt}\vdash p,q,p,q,\,\vdash p,q,t,\,\vdash t,q,p,q,\,\vdash t,q,t\,\big ]\), \(h(\pi )=5\), and \(w(\pi )=4\).
The following lemma gathers some (already known) very important properties characterizing Kleene’s systems \(\textsf{G4}\) and \(\textsf{GS4}\) with respect to other equivalent sequent formulations for classical propositional logic [3, 9].
Lemma 2
(Size preserving permutability of the rules) Consider a decomposition-tree \(\pi \) for \(\vdash \Gamma ,A\) with \(\mathcal {C}(A)>0\). There is a decomposition-tree \(\rho \) ending in the same sequent as \(\pi \) and such that: (i) the formula A occurs as principal in \(\rho \)’s last inference, (ii) \(\pi \) and \(\rho \) have the same size, and (iii) \(\textsf{top}(\pi )=\textsf{top}(\rho )\).
Proof
Let \(A\equiv B\circ C\), with \(\circ \in \{\wedge ,\vee \}\). The argument goes by induction on the height \(h(\pi )\) of \(\pi \) and it consists in showing that the specific instance of the \(\circ \)-rule forming the compound \(B\circ C\) can be freely permuted downwards along \(\pi \) till it becomes the very last inference step. Then, it suffices to notice that the size of the decomposition-tree as well as the multiset of its top-sequents is not affected by such permutations. (The reader can find all the missing details in [9, Lemma 3]). \(\square \)
Invertibility of the logical rules is an immediate consequence of the previous lemma.
Corollary 3
(Invertibility of the logical rules) The logical rules of \(\textsf{GS4}\) are both invertible:
- (i):
-
If \(\textsf{GS4}\) proves \(\vdash \Gamma ,A\wedge B\), then it also proves both \(\vdash \Gamma ,A\) and \(\vdash \Gamma ,B\);
- (ii):
-
If \(\textsf{GS4}\) proves \(\vdash \Gamma ,A\vee B\), then \(\vdash \Gamma ,A,B\) is provable too.
Proof
As for point (i), by Lemma 2, the sequent \(\vdash \Gamma ,A\wedge B\) admits a proof \(\rho \) whose last inference is the specific instance of the \(\wedge \)-rule introducing the formula \(A\wedge B\). Then, it suffices to consider the two direct subproofs of \(\rho \) ending in \(\vdash \Gamma ,A\) and \(\vdash \Gamma ,B\) to get the desired conclusion. Point (ii) can be handled likewise. \(\square \)
Remark 1
Proposition 1 is enough to prove completeness. Since \(\textsf{GS4}\)’s logical rules are both invertible, validity is always preserved upwards, from the conclusion to the premise(s). This fact guarantees that each top-sequent in every decomposition-tree \(\pi \) associated with a valid sequent \(\vdash \Gamma \) will be an identity clause, that is, an instance of the ax-rule. Hence, \(\pi \) qualifies as a \(\textsf{GS4}\)-proof for \(\vdash \Gamma \).
The following theorem presents a strengthened version of some key results already obtained in [8, 9].
Theorem 4
If \(\pi \) and \(\rho \) are two decomposition-trees ending in the same sequent \(\vdash \Gamma \), then they have equal size and, notably, \(\textsf{top}(\pi )=\textsf{top}(\rho )\).
Proof
The proof is led by induction on \(\mathcal {C}(\Gamma )\). (Base) For \(\mathcal {C}(\Gamma )=0\), we clearly have \(\pi =\rho =\,\,\vdash \Gamma \), therefore \(h(\pi )=h(\rho )=1\), \(w(\pi )=w(\rho )=1\), and \(\textsf{top}(\pi )=\textsf{top}(\rho )=[\,\vdash \Gamma \,]\). (Step) When \(\mathcal {C}(\Gamma )>0\), we need to proceed by cases depending on \(\pi \)’s last rule.
-
(\(\wedge \)-rule) Let \(\Gamma =\Gamma ',B\wedge C\) and assume that \(\pi \) has this shape

Now we apply Lemma 2 to transform \(\rho \) into a decomposition-tree \(\rho '\):

and such that \(h(\rho )=max(h(\rho '_{1}),h(\rho '_{2}))+1\), \(w(\rho )=w(\rho '_{1})+w(\rho '_{2})\), and \(\textsf{top}(\rho )=\textsf{top}(\rho '_{1})\uplus \textsf{top}(\rho '_{2})\). By inductive hypothesis, we get the six equalities:
Now, it suffices to observe that \(h(\pi )=max(h(\pi _{1}),h(\pi _{2}))+1\), \(w(\pi )=w(\pi _{1})+w(\pi _{2})\), and \(\textsf{top}(\pi )=\textsf{top}(\pi _{1})\uplus \textsf{top}(\pi _{2})\) to get the desired conclusion.
-
(\(\vee \)-rule) Let \(\Gamma =\Gamma ', B\vee C\) and assume that \(\pi \) comes as follows.

As for the previous item, we use Lemma 2 to transform \(\rho \) into the decomposition-tree \(\rho '\):

and such that \(h(\rho )=h(\rho ')\), \(w(\rho )=w(\rho ')\), and \(\textsf{top}(\rho )=\textsf{top}(\rho ')\). By inductive hypothesis we have that \(h(\pi _{1})=w(\rho '_{1})\), \(w(\pi _{1})=w(\rho '_{1})\), and \(\textsf{top}(\pi _{1})=\textsf{top}(\rho '_{1})\). These facts allow us to conclude that \(\pi \) and \(\rho \) have the same size and, in particular, \(\textsf{top}(\pi )=\textsf{top}(\rho )\). \(\square \)
We observe that Theorem 4 brings us two important facts. First of all, it allows us to push our notation and write, if convenient, \(\textsf{top}(\Gamma )\) to directly refer to the set of top-sequents induced by any decomposition-tree ending in \(\vdash \Gamma \). Second, such a result guarantees that whatsoever decomposition (proof-search) strategy starting from a provable sequent will always prove successful in the sense that:
Corollary 5
The sequent \(\vdash \Gamma \) is provable in \(\textsf{GS4}\) if, and only if, every decomposition-tree \(\pi \) ending in \(\vdash \Gamma \) turns out to be a \(\textsf{GS4}\)-proof for \(\vdash \Gamma \).
Proof
Assume that \(\vdash \Gamma \) admits both a \(\textsf{GS4}\)-proof \(\pi \) and a decomposition-tree \(\rho \) which does not qualify as a \(\textsf{GS4}\)-proof. In this case we would have \(\textsf{top}(\pi )\ne \textsf{top}(\rho )\), against what established by Theorem 4. The opposite direction of the biconditional is trivial. \(\square \)
Remark 2
When sequent derivations are considered modulo permutations of the logical rules, the combination of Theorem 4 and Corollary 5 actually amounts to show that \(\textsf{GS4}\) admits exactly one proof for any derivable sequent.
The following is another straightforward consequence of Theorem 4 which will find application in the next section.
Proposition 6
For any multiset of formulas \(\Gamma \) and any atomic sentence p, if \(\textsf{top}(\Gamma )=\big [\vdash \Gamma _{1},\vdash \Gamma _{2},\ldots ,\vdash \Gamma _{n}\,\big ]\), then \(\textsf{top}(\Gamma ,p)=\big [\vdash \Gamma _{1},p, \vdash \Gamma _{2},p,\ldots ,\vdash \Gamma _{n},p\,\big ]\).
Proof
Any decomposition-tree \(\pi \) for \(\vdash \Gamma \) can be turned into a decomposition-tree \(\rho \) for \(\vdash \Gamma ,p\) simply by replacing each sequent \(\vdash \Delta \) occurring in \(\pi \) with the sequent \(\vdash \Delta ,p\). We apply Theorem 4 to conclude that \(\textsf{top}(\Gamma ,p)=\big [\vdash \Gamma _{1},p,\vdash \Gamma _{2},p, \ldots ,\vdash \Gamma _{n},p\,\big ]\). \(\square \)
We conclude this section by recalling a well-known result which proves a key ingredient in several cut-elimination procedures [9, 11, 13], including the one we shall be presenting in the next section.
Theorem 7
(Weakening admissibility) If \(\textsf{GS4}\) proves \(\vdash \Gamma \), then it also proves \(\vdash \Gamma ,A\), for any formula A.
Proof
The proof is by induction on \(\mathcal {C}(A)\). (Base) For \(A\in \textbf{AT}\), it suffices to observe that any proof \(\pi \) of \(\vdash \Gamma \) can be turned into a proof \(\rho \) of \(\vdash \Gamma ,p\) simply by replacing each sequent \(\vdash \Delta \) occurring in \(\pi \) with the sequent \(\vdash \Delta ,p\). (Step) We consider two cases.
-
\(A\equiv B\wedge C\). We observe that \(\mathcal {C}(B),\mathcal {C}(C)<\mathcal {C}(B\wedge C)\) and apply our inductive hypothesis twice so as to get two proofs \(\pi _{1}\) and \(\pi _{2}\) ending in \(\vdash \Gamma ,B\) and \(\vdash \Gamma ,C\), respectively. Then, we can easily get a proof \(\pi \) for \(\vdash \Gamma ,A\wedge B\) by connecting \(\pi _{1}\) and \(\pi _{2}\) through an application of the \(\wedge \)-rule.
-
\(A\equiv B\vee C\). This case can be handled likewise. \(\square \)
3 Reduction Lemma
We call \(\textsf{GS4}^{+}\) the sequent system obtained from \(\textsf{GS4}\) by adding the cut-rule in its context-sharing (additive) formulation:

We indicate with \(|\pi |\) the number of cut-applications occurring in a \(\textsf{GS4}^{+}\)-proof \(\pi \). Clearly, \(\pi \) turns out to be a \(\textsf{GS4}\)-proof whenever \(|\pi |=0\). According to the standard terminology, proofs displaying no cut-applications are called analytic.
Having settled these matters, we can now turn to the following quick version of the Reduction Lemma.
Lemma 8
(Reduction Lemma) If \(\textsf{GS4}\) proves both \(\vdash \Gamma ,A\) and \(\vdash \Gamma ,\overline{A}\), then it also proves the sequent \(\vdash \Gamma \).
Proof
We proceed by induction on \(\mathcal {C}(A)\).
(Base) Let \(A\equiv p\) and assume, by contradiction, that \(\vdash \Gamma \) is not provable. By Definition 2 and Corollary 5, there is at least one clause \(\vdash \Gamma _{i}\in \textsf{top}(\Gamma )\) which proves complementary. We apply Proposition 6, to derive \(\vdash \Gamma _{i},p\in \textsf{top}(\Gamma ,p)\) and \(\vdash \Gamma _{i},\overline{p}\in \textsf{top}(\Gamma ,\overline{p})\). Since \(\vdash \Gamma ,p\) and \(\vdash \Gamma ,\overline{p}\) are both provable in \(\textsf{GS4}\), again by Corollary 5, \(\vdash \Gamma _{i},p\) and \(\vdash \Gamma _{i},\overline{p}\) must be both identity clauses (i.e. instances of the axiom rule). To sum up, we have that \(\vdash \Gamma _{i}\) is a complementary clause, whereas \(\vdash \Gamma _{i},p\) and \(\vdash \Gamma _{i},\overline{p}\) are both identity clauses. Hence, it must be \(\overline{p}\in \Gamma _{i}\) and \(p\in \Gamma _{i}\). This latter conclusion is patently incompatible with our initial assumption that \(\vdash \Gamma _{i}\) is a complementary clause.
(Step) As for \(\mathcal {C}(A)>0\), let \(A\equiv B\wedge C\) and \(\overline{A}\equiv \overline{B}\vee \overline{C}\). We apply Lemma 2 to get the (cut-free) provability of the three sequents \(\vdash \Gamma ,B\), \(\vdash \Gamma ,C\), and \(\vdash \Gamma ,\overline{B},\overline{C}\). By Theorem 7, we have that the sequent \(\vdash \Gamma ,B,\overline{C}\) is also provable in \(\textsf{GS4}\). Let’s now observe that
and apply our inductive hypothesis twice. First, we combine the provability of \(\vdash \Gamma ,\overline{B},\overline{C}\) and that of \(\vdash \Gamma ,B,\overline{C}\) so as to get the provability of \(\vdash \Gamma ,\overline{C}\). Then, we combine the provability of \(\vdash \Gamma ,\overline{C}\) and \(\vdash \Gamma ,C\) to finally achieve the provability of \(\vdash \Gamma \). \(\square \)
4 A non-Gentzen cut-elimination algorithm
Before going into detail of our cut-elimination procedure, we need to draw up the ‘unthreading’ operation \((\,\,\hspace{-3pt}\upharpoonleft \hspace{-4pt}\,\,)\). In particular, given a decomposition-tree \(\pi \) for \(\vdash \Gamma ,A\), we want to produce another decomposition-tree \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) ending in \(\vdash \Gamma \) and obtained by ‘unthreading’ from \(\pi \) the formula A together with all the occurrences of its subformulas. The ‘unthreading’ operation is formally defined in two steps: Proposition 9 considers the case in which A is atomic, whilst Lemma 10 deals with formulas having non-zero complexity.
Proposition 9
If \(\pi \) is a decomposition-tree for \(\vdash \Gamma ,p\) with \(\Gamma \ne \varnothing \), then there is a decomposition-tree \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}\hspace{1pt}p\) ending in \(\vdash \Gamma \) having exactly the same size as \(\pi \).
Proof
Since \(\Gamma \ne \varnothing \), each sequent occurring in \(\pi \) will be of the form \(\vdash \Delta ,p\) with \(\Delta \ne \varnothing \). Therefore, the decomposition-tree \(\rho \) can be obtained from \(\pi \) simply by removing exactly one occurrence of p from each of the sequents displayed by \(\pi \). Moreover, we observe that \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}\hspace{1pt} p\) has exactly the same graph-theoretic structure as \(\pi \), thus we immediately get \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}\hspace{1pt} p)=h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}\hspace{1pt} p)=w(\pi )\). \(\square \)
Example 2
We report below a decomposition-tree \(\pi \) associated with the sequent \(\vdash \overline{p}\vee (p\wedge (t\vee \overline{q})),t\) together with its ‘unthreaded’ version \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}\hspace{1pt} t\) ending in \(\vdash \overline{p}\vee (p\wedge (t\vee \overline{q}))\). In particular, \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}t\) is obtained by applying the simple procedure illustrated in the proof of Proposition 9, namely by removing exactly one occurrence of the atom t from each of \(\pi \)’s sequents. The two decomposition-trees have the same size \(4\times 2\).

Lemma 10
Let \(\pi \) be a decomposition-tree for \(\vdash \Gamma ,A\) with \(\Gamma \ne \varnothing \) and \(\mathcal {C}(A)>0\). There is a decomposition-tree \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt} A\) for \(\vdash \Gamma \) such that \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant w(\pi )\).
Proof
We show how to manufacture \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) for any decomposition-tree \(\pi \) ending in \(\vdash \Gamma ,A\). The proof is led by induction on \(\mathcal {C}(\Gamma ,A)\).
(Base) For \(\mathcal {C}(\Gamma ,A)=1\), since \(\mathcal {C}(A)>0\), we have that \(\Gamma \subset \textbf{AT}\) and so A is either the disjunction or the conjunction of two atomic sentences. Let’s consider these two cases separately.
-
If \(A\equiv p\vee q\), then \(\pi \) is the decomposition-tree
 and so we can simply set \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A=\,\,\vdash \Gamma \). Since \(\Gamma \subset \textbf{AT}\), the single-point tree \(\vdash \Gamma \) turns out to be a decomposition-tree. Moreover, we clearly have \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)=w(\pi )=1\).
and so we can simply set \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A=\,\,\vdash \Gamma \). Since \(\Gamma \subset \textbf{AT}\), the single-point tree \(\vdash \Gamma \) turns out to be a decomposition-tree. Moreover, we clearly have \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)=w(\pi )=1\). -
If \(A\equiv p\wedge q\), then
 As in the previous case, we put \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A=\,\vdash \Gamma \) and observe that \(\vdash \Gamma \) is still a decomposition-tree. Besides, \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<w(\pi )\).
As in the previous case, we put \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A=\,\vdash \Gamma \) and observe that \(\vdash \Gamma \) is still a decomposition-tree. Besides, \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<w(\pi )\).
(Step) For \(\mathcal {C}(\Gamma ,A)>1\), we need to consider the following four cases separately.
-
\(A\equiv B\vee C\) and A occurs as the principal formula in \(\pi \)’s last inference. In other words, \(\pi \) comes with this shape:

Now we can set \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A=(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}B) \hspace{-3pt}\upharpoonleft \hspace{-4pt}C\) (or, equivalently, \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A=(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}C) \hspace{-3pt}\upharpoonleft \hspace{-4pt}B\)). The fact that \(\mathcal {C}(\Gamma ,C)<\mathcal {C}(\Gamma ,B,C)<\mathcal {C}(\Gamma ,B\vee C)\) guarantees that: (i) the operation \((\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}B) \hspace{-3pt}\upharpoonleft \hspace{-4pt}C\) is inductively well-defined, (ii) the tree of sequents \((\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}B) \hspace{-3pt}\upharpoonleft \hspace{-4pt}C\) is still a decomposition-tree, and (iii) \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant w(\pi )\).
-
\(\pi \)’s last inference is an application of the \(\vee \)-rule, but A is not the principal formula. In this case, we can write \(\pi \) as follows:

We obtain \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) by computing \(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) and then extending it by means of a final application of the \(\vee \)-rule as indicated below:

Since \(\mathcal {C}(\Gamma ,D,E,A)<\mathcal {C}(\Gamma ,D\vee E,A)\) the operation \(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) turns out to be inductively well-defined and this guarantees that \(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) actually qualifies as a decomposition-tree. Moreover, by inductive hypothesis, we have both \(h(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi _{1})\) and \(w(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant w(\pi _{1})\). From these latter facts we can easily conclude that \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant w(\pi )\).
-
\(A\equiv B\wedge C\) and A occurs as the principal formula in \(\pi \)’s last inference. Then, we can write \(\pi \) as follows:

In this case, there are two possible ways to define \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) as we can put either \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A=\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}B\) or \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A{=}\pi _{2}\hspace{-3pt}\upharpoonleft \hspace{-4pt}C\). Since \(\mathcal {C}(\Gamma ,B){<}\mathcal {C}(\Gamma ,B\wedge C)\) and \(\mathcal {C}(\Gamma ,C){<}\mathcal {C}(\Gamma ,B\wedge C)\), the decomposition-trees \(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}B\) and \(\pi _{2}\hspace{-3pt}\upharpoonleft \hspace{-4pt}C\) prove both inductively well-defined. Still by inductive hypothesis, we can derive the four inequalities \(h(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}B){<}h(\pi _{1})\), \(h(\pi _{2}\hspace{-3pt}\upharpoonleft \hspace{-4pt}C){<}h(\pi _{2})\), \(w(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}B)\leqslant w(\pi _{1})\), and \(w(\pi _{2}\hspace{-3pt}\upharpoonleft \hspace{-4pt}C)\leqslant w(\pi _{2})\). Thence, \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant w(\pi )\). (In this latter inequality, \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\) is actually strictly smaller than \(w(\pi )\), since \(w(\pi _{1})<w(\pi )\) and \(w(\pi _{2})<w(\pi )\).)
-
\(\pi \)’s last rule is an instance of the \(\wedge \)-rule, but A does not occur as the principal formula. In this case, \(\pi \) comes shaped as follows:

The decomposition-tree \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) is obtained by combining \(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) and \(\pi _{2}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) in this way:

Again, since \(\mathcal {C}(\Gamma ',D,A),\mathcal {C}(\Gamma ',E,A)<\mathcal {C}(\Gamma ',D\wedge E,A)\), the two decomposition-trees \(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) and \(\pi _{2}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) prove both inductively well-defined. By inductive hypothesis, we also have \(h(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi _{1})\), \(h(\pi _{2}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi _{2})\), \(w(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant w(\pi _{1})\), and \(w(\pi _{2}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant h(\pi _{2})\). These facts allow us to conclude that \(h(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)<h(\pi )\) and \(w(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant w(\pi )\). \(\square \)
Corollary 11
Let \(\pi \) be a \(\textsf{GS4}\)-proof ending in \(\vdash \Gamma ,A\) and \(\vdash \Gamma \) a provable sequent. Then \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) is a \(\textsf{GS4}\)-proof for \(\vdash \Gamma \).
Proof
By Definition 2, the sequent \(\vdash \Gamma \) is provable in \(\textsf{GS4}\) just in case it admits a decomposition-tree \(\rho \) whose top-sequents are all identity clauses. By Lemma 10, \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) turns out to be a decomposition-tree for \(\vdash \Gamma \). Furthermore, by Theorem 4, we have that \(\textsf{top}(\rho )=\textsf{top}(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\), namely all the sequents in \(\textsf{top}(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\) must be identity clauses. Thereby, \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) actually qualifies as a \(\textsf{GS4}\)-proof ending in \(\vdash \Gamma \). \(\square \)
Example 3
Here below the reader can see a decomposition-tree \(\pi \) for the sequent \(\vdash \overline{p}\vee (q\vee p),(p\vee q)\wedge t\) together with its ‘unthreaded’ version \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}(p\vee q)\wedge t\) ending in \(\vdash \overline{p}\vee (q\vee p)\). It this case, we unthread the formula \((p\vee q)\wedge t\) from our decomposition-tree by discarding the subproof of \(\pi \) delivering the right-premise of the \(\wedge \)-rule. Notice that \(\pi \) and \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}(p\vee q)\wedge t\) have size \(5\times 2\) and \(3\times 1\), respectively. According to Corollary 11, \(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}(p\vee q)\wedge t\) is actually a \(\textsf{GS4}\)-proof for \(\vdash \overline{p}\vee (q\vee p)\).

The cut-elimination algorithm we shall be furnishing in a moment takes shape from the combination of our Reduction Lemma (Lemma 8) and the ‘unthreading’ procedure described in the proofs of Proposition 9 and Lemma 10.
Theorem 12
(Hauptsatz) Any \(\textsf{GS4}^{+}\)-proof \(\pi \) of \(\vdash \Gamma \) can be turned into a \(\textsf{GS4}\)-proof \(\rho \) ending in the same sequent, such that \(h(\rho )\leqslant h(\pi )\) and \(w(\rho )<w(\pi )\).
Proof
The procedure is implemented by always applying the same reduction step. At each step, we need to focus attention on a subproof \(\lambda \) of \(\pi \) such that: (i) \(\lambda \)’s last inference-step is an application of the cut-rule, and (ii) at least one of \(\lambda \)’s direct subproofs is cut-free. In particular, we can assume without any loss of generality that \(\lambda \) comes shaped as follows, with \(\lambda _{1}\) cut-free:

Lemma 8 guarantees the provability of \(\vdash \Delta \) and, in particular, by Corollary 11, \(\lambda _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A\) turns out to be a \(\textsf{GS4}\)-proof ending in \(\vdash \Gamma \).
Consider now the \(\textsf{GS4}^{+}\)-proof \(\pi '\) obtained from \(\pi \) by replacing \(\lambda \) with \(\lambda _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A\). Clearly, \(|\pi '|<|\pi |\). Moreover, by Proposition 9 and Lemma 10, we have that \(h(\lambda _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant h(\lambda _{1})\) and \(w(\lambda _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}A)\leqslant w(\lambda _{1})\). We can also notice that \(w(\lambda _{1})<w(\lambda )\). By combining all these facts, we conclude that \(h(\pi ')\leqslant h(\pi )\) and \(w(\pi ')<w(\pi )\). \(\square \)
Example 4
We apply the just designated procedure to ‘extract’ from the \(\textsf{GS4}^{+}\)-proof \(\pi \) reported below one of its cut-free versions.

We follow the optimal strategy by selecting the direct cut-free subproof \(\pi _{1}\) of \(\pi \) delivering the left-premise of \(\pi \)’s lowermost cut-application. Then it suffices to compute \(\pi _{1}\hspace{-3pt}\upharpoonleft \hspace{-4pt}q\wedge t\) to get one of the final cut-free versions of \(\pi \).

Remark 3
The property established by Theorem 12 cannot be imported in multiplicative settings in which the cut-rule comes as a context-mixing inference pattern. The simplest counterexample is illustrated below.

In the following corollary we draw an immediate consequence of our Hauptsatz, namely that fact that, in the specific proof-theoretic setting offered by \(\textsf{GS4}\), analytic proofs always express the optimal deductive strategy.
Corollary 13
Let \(\pi \) and \(\rho \) be two proofs of the same sequent, such that \(|\pi |>0\) and \(|\rho |=0\). Then we have, \(h(\rho )\leqslant h(\pi )\) and \(w(\rho )<w(\pi )\).
Proof
Consider the \(\textsf{GS4}\)-proof \(\lambda \) of \(\vdash \Gamma \) obtained from \(\pi \) by applying the cut-elimination algorithm illustrated in the proof of Theorem 12. Theorem 12 also guarantees that \(h(\lambda )\leqslant h(\pi )\) and \(w(\lambda )<w(\pi )\). Since \(|{\lambda }|=|\rho |=0\), by Theorem 4, we have both \(h(\lambda )=h(\rho )\) and \(w(\lambda )=w(\rho )\). This latter fact allows us to conclude that \(h(\rho )\leqslant h(\pi )\) and \(w(\rho )<w(\pi )\). \(\square \)
Remark 4
(Use-check) Given a provable sequent \(\vdash \Gamma ,A\), the problem of checking whether \(\vdash \Gamma \) remains provable — i.e. the problem of checking A’s dispensability from the point of view of the provability of \(\vdash \Gamma ,A\) — is known in the proof-search literature as use-check [5]. In the present case, a very simple use-check algorithm can be straightforwardly obtained from the technical results established in this section.
In particular, given a \(\textsf{GS4}\)-proof \(\pi \) for \(\vdash \Gamma ,A\), we simply need to follow, from the root up, the decomposition-tree \(\pi \) so as to back trace each of A’s atomic components and then remove it from the top-sequents in which it occurs. When such a removal procedure is completed, if no identity axiom from \(\textsf{top}(\Gamma ,A)\) is turned into a complementary clause, then \(\vdash \Gamma \) is provable and, therefore, A proves to be actually dispensable. This is an immediate consequence of the fact that \(\textsf{top}(\pi \hspace{-3pt}\upharpoonleft \hspace{-4pt}A)=\textsf{top}(\Gamma )\), for any decomposition-tree \(\pi \) ending in \(\vdash \Gamma ,A\).
5 Concluding observations
One could wonder whether the algorithm proposed in the previous section actually seizes the simplest possible cut-elimination procedure for \(\textsf{GS4}\). In particular, one could go one step further by switching directly to proof-search. The interlacing between cut-elimination and proof-search have been already investigated, especially in the context of modal logic [2, 4]. In the case of \(\textsf{GS4}\), such a relation proves to be quite a trivial issue: given a \(\textsf{GS4}^{+}\)-proof \(\pi \), we could just retain from \(\pi \) its end-sequent and then keep decomposing it till a \(\textsf{GS4}\)-proof is fully accomplished. Proposition 1 guarantees termination; Corollary 5 keeps out the possibility to run into unsuccessful proof-search strategies. However, two warnings should be put forward.
First, the locution ‘cut-elimination’ standardly indicates a purely syntactical procedure that allows the user of a certain proof-system to rewrite a proof \(\pi \) with cuts into a cut-free proof \(\pi '\) of the same sequent. The fact that \(\pi '\) is obtained by applying a series of syntactical transformations to \(\pi \) is a key feature that distinguishes cut-elimination from mere cut-admissibility, namely the fact that dropping the cut-rule no theorem is lost. Having clarified this issue, proof-search leads to a syntactical proof of cut-admissibility, but it can hardly qualify as a cut-elimination procedure.
Second, as already observed, the logical rules of \(\textsf{GS4}\) are all invertible and, in addiction, the complexity of sequents (measured as the number of occurrences of the logical connectives) decreases as we move upwards along proofs. The combination of these two features brings about the fact that, in \(\textsf{GS4}\), proof-search simply parallels completeness to the extant that the very inductive procedure employed to prove completeness can be also read as a proof-search algorithm and vice versa (cf. Remark 1). That casts doubt upon the genuine syntactical nature of the procedure based on proof-search and shows that the method given in Sect. 4 represents the syntactical threshold beyond which cut-admissibility collapses into completeness itself.
Notes
The system \(\textsf{GS4}\) could be also presented as a slight propositional variant of GS3 as it is described in [14, Def. 3.6.2]
References
Avron, A.: Gentzen-type systems, resolution and tableaux. J. Autom. Reason. 10(2), 265–281 (1993)
Brighton, J.: Cut elimination for GLS using the terminability of its regress process. J. Philos. Logic 45, 147–153 (2016)
Gallier, J.H.: Logic for Computer Science: Foundations of Automatic Theorem Proving. Courier Dover Publications (2015)
Goré, R., Ramanayake, R., Shillito, I.: Cut-elimination for provability logic by terminating proof-search: formalised and deconstructed using Coq. In: Automated Reasoning with Analytic Tableaux and Related Methods: 30th International Conference, TABLEAUX 2021, Proceedings 30, pp. 299–313. Springer (2021)
Heuerding, A., Seyfried, M., Zimmermann, H.: Efficient loop-check for backward proof search in some non-classical propositional logics. In: Theorem Proving with Analytic Tableaux and Related Methods: 5th International Workshop, TABLEAUX\(^\prime \) 96, Proceedings 5, pp. 210–225. Springer (1996)
Hughes, D.: A minimal classical sequent calculus free of structural rules. Ann. Pure Appl. Logic 161(10), 1244–1253 (2010)
Kleene, S.C.: Mathematical Logic. Wiley (1967)
Piazza, M., Pulcini, G.: Fractional semantics for classical logic. Rev. Symb. Logic 13(4), 810–828 (2020)
Pulcini, G.: A note on cut-elimination for classical propositional logic. Arch. Math. Logic 61, 555–565 (2022)
Pulcini, G., Varzi, A.C.: Classical logic through rejection and refutation. In: Fitting, M. (ed.) Landscapes in Logic, vol. 2. College Publications (2021)
Schwichtenberg, H.: Proof theory: some applications of cut-elimination. In: Studies in Logic and the Foundations of Mathematics, vol. 90, pp. 867–895. Elsevier (1977)
Smullyan, R.M.: First-Order Logic. Courier Corporation (1995)
Tait, W.: Normal derivability in classical logic. In: The Syntax and Semantics of Infinitary Languages, pp. 204–236. Springer (1968)
Troelstra, A.S., Schwichtenberg, H.: Basic Proof Theory. Cambridge Tracts in Theoretical Computer Science, 2nd edn. Cambridge University Press (2000)
Varzi, A.C.: Complementary sentential logics. Bull. Sect. Logic 19(4), 112–116 (1990)
Funding
Open access funding provided by Università degli Studi di Roma Tor Vergata within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Contributions
As a unique author, GP wrote the entire paper.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pulcini, G. Cut elimination by unthreading. Arch. Math. Logic 63, 211–223 (2024). https://doi.org/10.1007/s00153-023-00892-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00153-023-00892-4



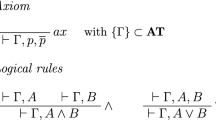


 and so we can simply set
and so we can simply set  As in the previous case, we put
As in the previous case, we put