The role of electron correlations in the electronic structure of putative Chern magnet TbMn₆Sn₆

Abstract

A member of the RMn₆Sn₆ rare-earth family materials, TbMn₆Sn₆, recently showed experimental signatures of the realization of a quantum-limit Chern magnet. In this work, we use quantum Monte Carlo (QMC) and density functional theory with Hubbard U (DFT + U) calculations to examine the electronic structure of TbMn₆Sn₆. To do so, we optimize accurate, correlation-consistent pseudopotentials for Tb and Sn using coupled-cluster and configuration–interaction (CI) methods. We find that DFT + U and single-reference QMC calculations suffer from the same overestimation of the magnetic moments as meta-GGA and hybrid density functional approximations. Our findings point to the need for improved orbitals/wavefunctions for this class of materials, such as natural orbitals from CI, or for the inclusion of multi-reference effects that capture the static correlations for an accurate prediction of magnetic properties. DFT + U with Mn magnetic moments adjusted to the experiment predict the Dirac crossing in bulk to be close to the Fermi level, within ~120 meV, in agreement with the experiments. Our non-stoichiometric slab calculations show that the Dirac crossing approaches even closer to the Fermi level, suggesting the possible realization of Chern magnetism in this limit.

Introduction

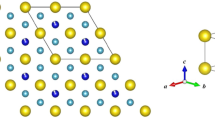
Rare-earth (R) material class RMn₆Sn₆ displays rich and intricate physical phenomena consisting of strong electron-electron correlations, spin–orbit effects, and supposedly topological behavior^{1,2,3,4,5,6,7,8,9,10}. These materials belong to the P6/mmm (#191) space group, where Mn atoms form 2D kagome layers interlaced with R and Sn layers, see Fig. 1. Although the RMn₆Sn₆ family of materials has been studied for more than three decades, recent experimental anomalous Hall effect (AHE) studies^1,9,11 inspired another wave of research^{2,3,4,5,6,7,8,12,13,14,15,16,17} on related materials.

Fig. 1: A supercell of TbMn₆Sn₆.

a Out-of-plane and b in-plane views are shown. The large red spheres are Tb atoms, medium blue spheres are Mn atoms, and small gray spheres are Sn atoms.

Experimental studies show that stable compounds form for R = {Sc, Y, Gd, Tb, Dy, Ho, Er, Tm, Yb, Ly}^{18,19,20,21,22,23,24,25}. In this study, R = Tb is of particular interest since it is the only element of the previous set that forms an out-of-plane spin system. In contrast, other R-element materials display either an in-plane or canted spin direction behavior^{1,2,8,18,23,24}. In particular, this case is interesting because the Chern magnetic phase predicted by Haldane’s model requires an out-of-plane spin alignment²⁶. Initially, Haldane considered a honeycomb lattice²⁶; however, the model was later extended to kagome systems²⁷. Therefore, the kagome lattice with out-of-plane spin alignment requirement seems to be met by Mn atoms of TbMn₆Sn₆ and therefore opens the possibility of realizing a Chern magnet in this material.

Indeed, a few years ago, Yin et al.¹ carried out experimental transport measurements using scanning tunneling microscopy (STM) in high-magnetic fields and observed a series of Landau quantization states in TbMn₆Sn₆. They conducted AHE measurements and observed a large intrinsic contribution due to the large Berry curvature of Chern-gapped Dirac fermions. Further edge-state conductivity measurements showed significant signals within the Chern gap energy scale. Therefore, they concluded that TbMn₆Sn₆ is close to realizing a quantum-limit Chern magnet, as predicted by the Haldane model. Indeed, kagome lattice geometry with an out-of-plane magnetization formed by the Mn atoms and the presence of strong spin–orbit coupling (SOC) stemming from the Tb and Sn atoms to open a Chern gap seems to suggest that TbMn₆Sn₆ could realize such an exotic phase.

However, the possibility of realizing the Chern phase hinges on the ability to align the Fermi level (E_F) in the Dirac crossing (DC) or the Chern gap, as seen in the Kagome systems^1,2,27. Yin and coworkers’ experiments show that the Chern gap is located at 130(4) meV above E_F¹. However, Lee and coworkers reported density functional theory with Hubbard U (DFT + U) calculations² predicting the quasi-2D DC to be 700 meV above E_F or at least 300 meV above E_F, suggesting that the Dirac crossing cannot be related to the observed AHE signal. Therefore, there seems to be a disagreement in the literature about the exact position of DC with respect to E_F and whether TbMn₆Sn₆ could realize a Chern phase. In this work, we focus on whether the DC is indeed close to the Fermi level using quantum Monte Carlo (QMC), DFT + U, and other correlated methods.

Clearly, accurately estimating the energetic level of DC with respect to E_F, which is on the order of a few hundred meV, would require a very accurate electronic structure treatment. Such a small energetic level could be affected by the accuracy of pseudopotentials²⁸, the level of electron correlation treatment, the accuracy of SOC effects, and the degree of multi-reference character intrinsic to the true electronic wave function of the system. In the following sections, we thoroughly investigate these aspects and try to enumerate their contributions and biases.

In the Section “Pseudopotentials,” we optimize the required Tb and Sn element pseudopotentials using correlated methods and evaluate their errors via transferability tests. Then in Section “QMC biases of elemental sub-species”, we carry out nearly exact energy calculations for related molecular systems to estimate the biases present in single-reference QMC calculations. We then apply the developed pseudopotentials to TbMn₆Sn₆ using DFT + U in Section “DFA sensitivity problem” and QMC in Section “Single-reference QMC” and demonstrate the issues with single-reference calculations. Section “DFT + U results” includes additional DFT + U results, which elucidate the position of DC. The findings are further analyzed and discussed in Section “Discussion.”

Results

Pseudopotentials

One of the major approximations used in correlated methods is the pseudopotential or effective core potential (ECP) approximation²⁹. High-accuracy correlated methods such as configuration interaction (CI) or coupled cluster (CC) are limited by the accuracy of the ECP as it modifies the Hamiltonian. Therefore, it’s crucial that ECPs be optimized in a correlation-consistent way, especially for correlated methods and systems. Here, we develop correlation-consistent ECPs (ccECP) for Sn and Tb elements using CC and CI methods and use a ccECP for Mn from a previously published work³⁰. In the next subsection, we show the results for the Tb element and compare its accuracy against fully correlated, relativistic, all-electron (AE) calculations. The full results for Sn, optimization methods, and further details are provided in Supplementary Note 2.

Tb ccECP

The optimization of the Tb ECP is more involved than Sn (Supplementary Note 2) or Mn³⁰. For instance, in Sn, the electrons can be easily partitioned by quantum principle number n into core and valence spaces by treating n ≥ 5 in the valence space (5s, 5p, 5d, ...). However, in Tb, core ↔ valence partitioning is not straightforward since 4f orbital eigenvalues are on the same order as n = 5 principal number orbitals (5s, 5p, 5d), suggesting it should be included in the valence space, see Supplementary Tables 7 and 8. To overcome this, one could include the whole n = 4 electrons in the valence and treat only n ≤ 3 electrons as the core; however, this results in a prohibitively high computational cost in many-body QMC calculations. Conversely, 4f electrons are sometimes included in the core, but this can result in poor results²⁸. In this work, we decided to include the 4f electrons in the valence (with ${N}_{{{{\rm{core}}}}}=46$e⁻) and treat them fully self-consistently, along with 5s, 5p, 5d, and 6s orbitals. However, the many-body accuracy of such partitioning is not well-known and must therefore be carefully tested. At least in 3d transition metals, similar large-core ECPs with valence spaces of 3d^k4s² (where the lowest n orbital is not an s) are well-known to produce inaccurate results^31,32,33.

Our extensive many-body calculations show that the chosen core choice for Tb ccECP should result in small errors once properly optimized. In fact, the accuracy of Tb ccECP is on par with the uncorrelated core AE (UC) where ${N}_{{{{\rm{core}}}}}=46$ electrons are not active. This is illustrated by the atomic gap errors in Fig. 2a and TbH₃, and TbO molecular binding energy errors in Fig. 2b, c. We observed that all atomic gap errors are below ~0.07 eV up to the third ionization potential level, see Supplementary Table 9. Higher-order ionizations result in significantly larger errors on the order of an eV, showing the limits of such an ECP. On the other hand, very high ionization potential errors are probably not relevant for condensed matter applications since rare-earth elements form either R²⁺ or R³⁺ compounds³⁴. Nevertheless, Tb ccECP is much more accurate than the existing ECPs with the same core choices, such as SBKJC³⁵ and an OPIUM-generated DFT-PBE³⁶ ECP using the Troullier–Martins scheme³⁷. In fact, the ccECP errors are below chemical accuracy for the low-lying states (Fig. 2a) and most of the bond lengths in hydride and oxide molecules (Fig. 2b, c). Tb and Sn ccECPs are available online in ref. ³⁸ for broader use.

Fig. 2: Scalar relativistic AE UCCSD(T) errors for various Tb core approximations.

a Tb atomic gap errors. Various mean absolute deviation (MAD) metrics are used (see Supplementary Note 2 for details). b TbH₃ and c TbO molecular binding energy discrepancies. The shaded region indicates the band of chemical accuracy. The dashed vertical line represents the equilibrium geometry. In TbH₃, only the bond lengths are varied, while the H–Tb–H angles of 120° are kept constant. The Tb atomic energy reference is [Xe] 4f⁸6s²5d¹ state.

The presented low biases of Tb and Sn ccECPs here and of Mn ccECP elsewhere³⁰ provide the opportunity to focus on the other systematic biases, such as the accuracy of the wavefunction and correlation treatment. Namely, we can assume that any deviations from the experiments are not due to the technical limitations of the representative Hamiltonians; rather, it has to be due to more fundamental reasons, such as inaccurate trial wave function in QMC or improper density functional approximation (DFA) and Hubbard U in DFT + U. These are the subjects of Sections “QMC biases of elemental sub-species” and “DFA sensitivity problem,” respectively.

QMC biases of elemental sub-species

It is beneficial to know the inherent systematic biases of single-reference QMC calculations for the system of interest by comparing the QMC energies to CI or CCSD(T) energies at the complete basis set limit (CBS). Although CI and CCSD(T) calculations have been recently applied with great success to periodic systems^{39,40,41,42,43,44,45}, they are still out of reach for large systems such as TbMn₆Sn₆^40,45. Therefore, we focus on constituent atoms and relevant molecular systems to estimate the QMC biases. Once the ECPs are made accurate, and other systematic errors such as timestep bias and walker population biases are under control, the main remaining errors are fixed-node and localization bias (if a nonlocal ECP is used as here). Usually, the fixed-node bias is the dominant of these two^46,47,48; however, both of them go to zero as the trial wave function approaches the exact form^47,49,50.

We enumerate the biases of fixed-node diffusion Monte Carlo (DMC)⁴⁹η as a percentage of the correlation energies in Fig. 3a using nearly-exact energies from CCSD(T) at CBS, and single-reference DMC calculations with PBE⁵¹, PBE0⁵², and Hartree–Fock (HF) references. This plot reveals a few insights about TbMn₆Sn₆ solid. First, the Sn atom has the smallest fixed-node bias, ~2% of the correlation energy. This error is close to the 1–2% errors of the iso-valent Si atom, Si_xH_y molecules, and diamond-structure bulk Si observed before^53,54. Second, Mn shows a sizable error, ~9% of the correlation energy missing in single-reference calculations, which also agrees with previous work⁵⁵. Finally, the largest errors occur for systems with Tb, where ~12% of the correlation energy is missing. However, we found that these large biases tend to cancel out for Tb when considering energy differences, such as the binding energies of TbH₃ and TbO molecules (see Supplementary Table 17).

Fig. 3: Element-resolved sources of errors.

a Estimation of combined FN and localization biases in single-reference DMC calculations for TbMn₆Sn₆ relevant systems. Here η represents the missing percentage of the correlation energy in such calculations, η = (E_exact − E_DMC)/(E_exact − E_ROHF) × 100%. b Density of states of bulk TbMn₆Sn₆. Note that Mn atomic states dominate in this small energy window while Tb states are minimal. LDA $+\,{U}_{{{{\rm{Mn}}}}}^{3d}$ (−0.5 eV) DFA was used.

In TbMn₆Sn₆, the leading Tb atomic density of states (DOS) is well below the Fermi level (E_F), and Mn atomic DOS is dominant near E_F, as shown in Fig. 3b. Given that the Sn atom DMC errors are small and Tb states are well below E_F, we argue that the largest errors in QMC will stem from an improper characterization of Mn atoms in our trial wave functions. In other words, low-lying conduction states near E_F might give rise to wave functions of multi-reference character due to sizable single-reference DMC error in the Mn atom. This is supported by calculated atomic moments from DFT + U, which show severe sensitivity when U is applied on Mn-3d orbitals (shown later) and insensitivity on Tb-4f, Tb-5d, and Sn-5p orbitals, see Supplementary Table 15. In addition, we observe no changes in the band structure when + U is applied to Tb-4f orbitals (Supplementary Fig. 3).

Another insight from Fig. 3a is that for a given magnetization, Tb systems with HF reference result in the lowest energies signifying the importance of localization in 4f orbitals. On the other hand, Mn and Sn seem to favor more delocalized orbitals when compared to HF for constrained magnetization. These aspects will be discussed later in detail by means of applying Hubbard U on Mn-3d orbitals.

DFA sensitivity problem

This work uses the DFT + U approach with an effective Hubbard repulsion (U_eff = U − J)^56,57 with the fully localized limit (FLL) double counting scheme^57,58,59,60 as implemented in QUANTUM ESPRESSO code^61,62,63. We explored two types of DFT + U calculations. In one case, the total magnetization of the cell was constrained to agree with the experimentally observed value of ~ M^s = 7μ_B in the SCF procedure (indicated with C-DFT, such as C-LDA or C-PBE). In the other case, the total magnetization was unconstrained and determined during the SCF cycles (simply indicated with the DFA name, such as LDA or PBE). Extended details of the employed DFT + U methodology are given in Supplementary Note 3.

TbMn₆Sn₆ ground state is a ferrimagnetic phase (FiM), where the Mn atoms align ferromagnetically, and the Tb spins point in the opposite direction²⁴. Figure 4 shows the bulk band structures using various DFAs for the FiM phase. For a pure 2D kagome lattice, tight binding models show that the DC occurs at E_F, k = K point, while the flat bands are above the E_F^1,27. Considering the LDA⁶⁴ band structure (Fig. 4a), we see the expected “flat” band in the minority spin channel at ~0.5 eV. In addition, a few DCs occur at k = K in the minority spin channel. These DCs were labeled for clarity in Fig. 4 and will be referred to as DCn, where n is the label. When LDA is switched to PBE DFA (Fig. 4b), the flat band and DC2 and DC3 shift up by around 200 meV. Introducing a small effective Hubbard ${U}_{{{{\rm{Mn}}}}}^{3d}=0.5$ eV to LDA (Fig. 4c) shifts the flat bands and DCs up even further. The upward shifts in the minority spin channel are accompanied by downward shifts in the majority spin channel. Obviously, this energetic sensitivity is a problem where one is interested in resolving an energy scale of ~150 meV.

Fig. 4: Band structures of TbMn₆Sn₆ using scalar relativistic (averaged spin–orbit) ECPs.

DFAs employed here are a LDA, b PBE, c LDA with $+{U}_{{{{\rm{Mn}}}}}^{3d}$ (+0.5 eV). Note how severely DC positions (labeled by numbers at k = K) shift as the DFA is changed.

Another related issue is demonstrated in Fig. 5 by considering the Mn magnetic moment and cell magnetization as ${U}_{{{{\rm{Mn}}}}}^{3d}$ is varied. Strikingly, the magnetizations are severely overestimated compared to the experimental green-shaded region once a small positive value of ${U}_{{{{\rm{Mn}}}}}^{3d}$ is introduced. In fact, the overestimation of magnetic moments with advanced DFAs or DFT + U is a well-known issue for metals displaying itinerant magnetism^2,65,66,67. Previous studies^65,66 showed that increasingly advanced DFAs in Jacob’s ladder of DFA ranks⁶⁸, such as GGA PBE⁵¹, meta-GGA SCAN⁶⁹, and hybrid PBE0⁵², tend to increasingly overestimate the magnetic moments in metallic ferromagnetic systems such as bcc Fe, hcp Co, and fcc Ni. Interestingly, even LDA could slightly overestimate the magnetic moments, such as in fcc Ni⁶⁶.

Fig. 5: Comparison of DFT $+\,{U}_{{{{\rm{Mn}}}}}^{3d}$ and experimental magnetizations.

a Mn atomic magnetic moments using Löwdin populations, b cell spin magnetization per formula unit. The green-shaded regions represent the envelope of various experimental measurements^{1,6,7,18,20,23,24}. In b, the experimental cell magnetization was added with the Tb orbital magnetization of ${M}_{{{{\rm{Tb}}}}}^{{{{\rm{orb}}}}}=2.96\,{\mu }_{{{{\rm{B}}}}}$² for a proper comparison, ${M}^{{{{\rm{s}}}}}={M}_{\exp }^{{{{\rm{total}}}}}+{M}_{{{{\rm{Tb}}}}}^{{{{\rm{orb}}}}}$.

In Fig. 5, it is evident that LDA + U requires a small negative ${U}_{{{{\rm{Mn}}}}}^{3d}$ value to agree with both experimental Mn atomic moment and overall cell magnetization. We note that utilization of a negative U was suggested^70,71 and applied^{72,73,74,75,76} before, especially on superconducting systems. Physically, this means that Hund’s exchange J dominates the on-site Coulomb repulsion U, resulting in a minor negative U_eff = U − J value. The result is more delocalization of orbitals and a tendency to pair electrons, which produce lower magnetic moments. The opposite extreme can be seen when using HF and hybrid DFA for metals, which over-localize the electrons and tend to unpair the electrons, resulting in overestimated magnetic moments. Even though DFT + (U > 0) physics is different than hybrid DFAs, the effect is a similar localization of orbitals⁷⁰. In this case, the proper delocalization could be achieved by a minor negative U_eff or a Hund’s J with a magnitude larger than U. In addition, previous studies showed that the employed double-counting scheme in DFT + U could significantly change the predicted magnetic moments^2,77. Ultimately, the key goal is to achieve a proper (de)localization of electrons and hence the correct magnetization driven by an appropriate tendency of electrons to pair. The difficulties of predicting magnetic moments using advanced DFAs raise the issue of whether single-reference QMC calculations can predict the correct magnetization in a complex correlated metal such as TbMn₆Sn₆.

Single-reference QMC

As kinetic energy sampling via k-mesh integration is crucial in metals^78,79,80,81, we use canonical twist-averaging (CTA) and a supercell with two formula units (Fig. 1) in all TbMn₆Sn₆ QMC calculations. To assess the validity of single-reference QMC, we consider results from two different QMC methods. These methods are fixed-node/fixed-phase DMC (captures most correlations), and σ² → 0 extrapolated VMC (VMC${}_{{{{\rm{extrap}}}}}^{{\sigma }^{2}\to 0}$, estimate of converged dynamic correlations) using single-reference Slater–Jastrow type trial wave functions. The VMC${}_{{{{\rm{extrap}}}}}^{{\sigma }^{2}\to 0}$ method uses two data points with the same determinantal form to extrapolate to the σ² = 0 limit, as shown in Fig. 6 for the TbO molecule where nearly-exact energies can be obtained via UCCSD(T)/CBS. Specifically, energies from the Slater trial wave function and Slater–Jastrow trial wave function with one-, two-, and three-body terms (SJ₁₂₃) were used in the extrapolation (black squares). In principle, as the variance goes to zero, the VMC energy should recover the exact correlation energy due to the zero-variance principal⁴⁹. However, since the Jastrow factor only captures the dynamic correlations⁸², we do not expect this estimator to recover the exact correlation, as the trial wave function is improved only in the symmetric term (due to Jastrow), while the antisymmetric term (due to Slater) remains as an approximation. Although one can not strictly distinguish between static and dynamic correlations, the above separation is clear —the Jastrow term is the source of “dynamic correlations,” while the fermionic term is the source of “static correlations.” In this sense, the VMC${}_{{{{\rm{extrap}}}}}^{{\sigma }^{2}\to 0}$ method is expected to give the energy for the “perfect Jastrow”. We would like to note that this is only an approximation, as σ² = 0 should only occur for the exact ground state.

Fig. 6: VMC energy vs. variance extrapolation for TbO molecule.

DMC/SJ₁₂₃ is a DMC calculation using HF Slater–Jastrow form with one-, two-, and three-body terms in the Jastrow. UCCSD(T)/CBS represents the nearly exact energy from basis set extrapolations. In J₁₂(n), n = (16, . . . , 100). All data points were optimized for energy. See the main text for details.

Provided that the trial wave function Ψ_T has a significant overlap with the exact ground state only, one can show that the VMC energy must linearly depend on the variance for σ² → 0⁸³:

$${E}_{{{{\rm{VMC}}}}}={E}_{{{{\rm{exact}}}}}+\alpha {\sigma }^{2}.$$

(1)

In practice, it can be difficult to achieve near-ideal linear extrapolations, for instance, as seen in multi-determinant extrapolations of high-pressure hydrogen⁵⁰. We investigated the convergence behavior of one- and two-body Jastrow (J₁₂(n)) and also three-body Jastrow (J₃(n)) as the number of optimizable parameters n is increased. A nonlinear convergence was observed for J₁₂(n) in all cases of Fig. 6. For large n, J₁₂(n) reaches a plateau where the energy is converged with respect to n. A linear behavior was observed when using these converged J₁₂ functions and including J₃(n) terms with various n values. The simple two-point extrapolations using the Slater trial wave function (free of Jastrow optimization imperfections) and the SJ₁₂₃ with the highest feasible optimizable parameters (the best Jastrow we could optimize) proved to be the most robust and consistent way to compare energies. The obtained VMC${}_{{{{\rm{extrap}}}}}^{{\sigma }^{2}\to 0}$ value would therefore represent the VMC energy of an SJ_{(123. . . ∞)}, i.e., Jastrow with up to M-body interactions where M → ∞.

In Fig. 6, even though VMC${}_{{{{\rm{extrap}}}}}^{{\sigma }^{2}\to 0}$ estimator energy is below the single-reference DMC, it is still significantly above the estimated exact energy since the estimator is mainly probing for the effect of dynamic correlations due to the single-reference form. We observed similar plots with the same energy ordering for the other molecules considered in this work; see Supplementary Fig. 14. The only exception to this was the Sn atom, where the VMC${}_{{{{\rm{extrap}}}}}^{{\sigma }^{2}\to 0}$ estimated energy goes slightly below the UCCSD(T)/CBS value (by about 10⁻⁴ Ha). This is not surprising since the fixed-node bias in the Sn atom is very small (~2% of the correlation energy), and thus we might expect that the static correlation is captured well by single-reference, and VMC${}_{{{{\rm{extrap}}}}}^{{\sigma }^{2}\to 0}$ should give close to exact energies. More information about VMC energy extrapolations and extended details of QMC methods are given in Supplementary Note 4.

In Fig. 7a, b, we plot the bulk energies with the above-described methods where the orbitals are generated from DFA = {LDA, PBE}. Specifically, LDA DFT calculations obtain magnetizations close to the experiments, so it is interesting to see whether QMC predicts the correct magnetization when the LDA orbitals are reused for various QMC magnetizations. Namely, in Fig. 7a, b, the same orbitals are used, but a different overall magnetization M^s is constructed in QMC calculations. Since QMC methods are variational, the lowest energy states correspond to the physical predictions from single reference QMC^84,85. As shown in these plots, the lowest energy for both estimators corresponds to ~15μ_B, approximately twice the correct value and well outside of the experimental region. This overestimation seems independent of the employed orbitals, as LDA and PBE results follow similar trends. In addition, extrapolating the dynamic correlations to the zero-variance limit does not change the energy curve, signifying a necessity for either significantly improved orbitals or including static correlations via multi-reference wavefunctions.

Fig. 7: QMC energies of various trial wave functions.

a, b QMC energies [Ha] using LDA and PBE trial wave functions for various QMC magnetizations M^s. The green-shaded regions represent the envelope of various experimental measurements^{1,6,7,18,20,23,24}. The experimental cell magnetization was added with the Tb orbital magnetization of ${M}_{{{{\rm{Tb}}}}}^{{{{\rm{orb}}}}}=2.96\,{\mu }_{{{{\rm{B}}}}}$² for a proper comparison, ${M}^{{{{\rm{s}}}}}={M}_{\exp }^{{{{\rm{total}}}}}+{M}_{{{{\rm{Tb}}}}}^{{{{\rm{orb}}}}}$. DFT-predicted magnetizations are also shown as vertical lines. c, d QMC energies [Ha] using DFT + U_eff^56,57 and e, f DFT + U + J⁶⁰ trial wave functions. The QMC spins in c–f are constrained at ${M}^{{{{\rm{s}}}}}={N}_{e}^{{{{\rm{up}}}}}-{N}_{e}^{{{{\rm{down}}}}}=7\,{\mu }_{{{{\rm{B}}}}}$ for each twist. QMC error bars correspond to one standard deviation and are either similar to or smaller than data symbols.

Next, we explore fixing the QMC cell magnetization to agree with experiments (at M^s = 7μ_B) and varying the orbitals by the introduction of Hubbard + U (Fig. 7c–f). In Fig. 7c, d, this is done for unconstrained DFT (M^s from SCF) and magnetization-constrained DFT (M^s = 7μ_B) using an effective Hubbard U as described in Section “DFA sensitivity problem”. In Fig. 7c, the DMC method obtains the lowest energy for unconstrained LDA at ${U}_{{{{\rm{Mn}}}}}^{3d}=1$ eV. The magnetization in this reference is severely overestimated in DFT with cell magnetization of ≈12μ_B and Mn moment of 3.38μ_B, see Fig. 5. On the other hand, the lowest DMC energy for the constrained reference occurs at a much larger value of ${U}_{{{{\rm{Mn}}}}}^{3d}=2$ eV. This is because in the constrained case, the Mn moments increase much more slowly as ${U}_{{{{\rm{Mn}}}}}^{3d}$ is increased (Fig. 5a), requiring a larger value of ${U}_{{{{\rm{Mn}}}}}^{3d}$. This suggests that the magnetization of Mn atoms dictates the QMC energy.

In Fig. 7d, similar plots are shown using the VMC${}_{{{{\rm{extrap}}}}}^{{\sigma }^{2}\to 0}$ method. The results are qualitatively similar to DMC in Fig. 7c, but the minima are shifted by about $\Delta {U}_{{{{\rm{Mn}}}}}^{3d}=0.5$ eV closer to zero. However, the corresponding DFT magnetizations are still considerably overestimated and outside the experimental measurements (see Fig. 5 for corresponding ${U}_{{{{\rm{Mn}}}}}^{3d}$ values). This shows that including the full dynamic correlations can improve the prediction of magnetic properties, but it is not enough for an accurate estimation in this case.

Finally, we explored the effect of J in the DFT + U + J formalism⁶⁰ in Fig. 7e, f. We consider LDA with ${U}_{{{{\rm{Mn}}}}}^{3d}=1.0$ eV, which results in the lowest energy in DMC for this DFA (Fig. 7c). In DMC/SJ₁₂₃ method, Fig. 7e, the energies increase as J is increased. This is because the effect of J is to discourage high-spin states, and we see a similar effect as in Fig. 7c. The VMC${}_{{{{\rm{extrap}}}}}^{\sigma \to 0}$ in Fig. 7e method predicts a value of ${J}_{{{{\rm{Mn}}}}}^{{{{\rm{3d}}}}}=0.6$ eV; however, the corresponding Mn moment of 2.61μ_B is still slightly overestimated relative to the experimental value of 2.39(8) μ_B²⁴ (see Supplementary Fig. 8).

It is evident from Fig. 7c–f that constraining the QMC cell magnetization seems to alleviate the overestimation problem. This is especially pronounced in the VMC${}_{{{{\rm{extrap}}}}}^{\sigma \to 0}$ case, where full dynamic correlations are expected to be captured. However, the lowest energies using constrained QMC cell magnetizations in Fig. 7c–f are still much higher than the unrestricted, M^s = 15μ_B case in Fig. 7a. This is true within each method, DMC/SJ₁₂₃ and VMC${}_{{{{\rm{extrap}}}}}^{{\sigma }^{2}\to 0}$. These calculations show that single-reference QMC overestimates the magnetic moments similar to meta-GGA SCAN and hybrid PBE0 DFAs. This overestimation trend persists even when the dynamic correlations are extrapolated to the zero-variance values, Fig. 7d. This points to a significant deficiency in static correlations, which possibly stem from a few sources:

• 1. Imperfect one-particle orbitals. Within the single-reference framework, the nodal surface is fully determined by the single-particle inputs. In case of the presence of static/multi-reference correlations, this can bias the expectations. Natural orbitals (NOs) from CI calculations can provide a better orbital set for improving the description within the single-reference model⁸⁶.

• 2. Lack of multi-reference trial wave function. Even with high-quality orbitals such as NOs, it is possible that multi-reference wave functions are needed to predict the magnetic moments correctly. This would not be surprising because systems with Mn elements are known to display multi-reference characters⁸⁷. For instance, a previous study of bulk MnO using CCSD found improvement in band gaps and magnetic moments on the overestimated values of UHF⁴⁵.

  An additional example where a similar problem occurs is the W atom. Its ground state is [Xe]4f¹⁴5d⁴6s² (⁵D) configuration, while the first excited state configuration is a higher spin [Xe]4f¹⁴5d⁵6s¹ (⁷S)⁸⁸. Fixed-phase spin–orbit DMC, with minimal expansion of determinants, incorrectly predicts the high-spin state ⁷S as the ground state⁸⁹. However, as the trial wave function is expanded with more determinants, the correct ⁵D ground state is recovered in agreement with the experiments⁸⁹.

• 3. Finite-size effects. In this work, we used a supercell with two formula units and CTA where each twist is occupied with the same M^s. Although CTA should reach the same TDL energy as grand-canonical twist averaging (GCTA) for the same magnetization, it could have a considerable impact on finite supercell sizes. This overlaps with the first point above as it is a one-body effect. However, it has a different origin since the change is across-twist rather than within-twist.

Although the above effects can be present, it is out of the scope of this work to study TDL convergence and to apply multi-reference approaches here since we are interested in the single-reference model and its accuracy limit for these types of materials. Therefore, we leave these aspects for future study.

Intuitively, the QMC overestimation issue could be explained as follows. Mn element in the atomic limit favors the ⁶S_5/2 high-spin state⁸⁸, and this localized atomic energy scale could dominate the QMC energy in the metallic solid. The energy due to bonding is partially captured in the single-reference case; however, it is not properly balanced with the localized energy scale, which skews the optimal energy to the Mn atomic high-spin state. Therefore, a balanced trial wave function would also need to capture the multi-reference effects stemming from crystal field and orbital hybridization so as to counterweight the pronounced atomic high-spin limit. Indeed, in the HF method, where there are no correlations by definition, the Mn moment is close to the fully unpaired limit of 5μ_B, see Table 1. Compared to insulators, the interactions must be significantly screened in metals⁹⁰, and HF or hybrid DFAs are well-known to result in poor screening^91,92, and other unphysical features in partially-filled band metals^93,94. We note that in the thermodynamic limit (TDL) of full-CI (FCI), the proper screening must be achieved in metallic systems due to the cancelation of static correlation effects and long-range interactions^92,93,94. Remarkably, the approximate correlations in LDA seem to capture the screening and multi-reference effects quite well, judging by the obtained magnetizations in Table 1. Indeed, a few previous studies found that LDA could mimic the long-range correlations due to multireference effects^95,96,97, which is facilitated by the larger self-interaction errors in LDA compared to hybrids.

Table 1 Mn moments and cell magnetizations M^s for various DFAs.

DFT + U results

In order to shed additional light on the intricate relationship of single-reference and magnetic order, we empirically adjust the magnetic moment of the Mn atom to the neutron diffraction experimental result of 2.39(8) μ_B²⁴. A recent muon spin rotation measurement, which is a highly powerful probe of local magnetism, also obtained an Mn moment of ~2.4μ_B at low temperatures⁶. We note that using the Mn moments as a reference is more robust than comparing against the overall cell magnetization or Tb atomic moments due to the orbital magnetic moment contribution of the localized and well-screened 4f orbitals³⁴. On the other hand, the 3d orbital magnetic moments are negligible due to orbital quenching^2,34, and the spin moments can be directly compared with the experiments. In addition, the Mn moments were shown to display much smaller spin fluctuations⁷, making Mn more suitable to compare against experiments. In fact, using muon spin rotation experiments, ref. ⁶ showed a critical slowing down of spin fluctuations below ${T}_{{{{\rm{C1}}}}}^{* }\simeq 120$ K. Further colling the systems below T_C1 ≃ 20 K resulted in freezing the spin fluctuations into static patches of ideal out-of-plane FiM ordering, which persisted down to the lowest measured 1.7 K temperature. Therefore, although our calculations are T = 0 K and collinear FiM, they can be directly compared with the Mn moments obtained from T < T_C1 ≃ 20 K without considering the effects of spin fluctuations which are seen in some other frustrated kagome materials^10,98,99. We find that employing LDA DFA and Löwdin population analysis, a small effective value ${U}_{{{{\rm{Mn}}}}}^{3d}\approx -0.5$ eV is required to approximately match with the neutron diffraction experimental value of 2.39(8) μ_B²⁴ (LDA$+{U}_{{{{\rm{Mn}}}}}^{3d}$ (−0.5 eV) results in Mn moment of 2.366μ_B). This value of ${U}_{{{{\rm{Mn}}}}}^{3d}$ is qualitatively corroborated by Fig. 3a, where Mn seems to favor more delocalized orbitals for the given magnetization, and previous studies show that even LDA, which presumably produces the smallest orbital localization, shows a tendency to overestimate the magnetic moments^65,66.

Having established an appropriate DFA for the study of TbMn₆Sn₆, we now plot the bulk band structure for the FiM phase using LDA $+\,{U}_{{{{\rm{Mn}}}}}^{3d}$ with ${U}_{{{{\rm{Mn}}}}}^{3d}=-0.5$ eV. In Fig. 8a, the bands are plotted with scalar relativistic pseudopotentials, namely, with averaged spin-orbit interactions. We find that the DC2 energetic level (E_DC2) with respect to E_F shifts down to about E_DC2 = 120 meV when compared with LDA (Fig. 4a). This is in excellent agreement with the experimental result of ${E}_{{{{\rm{DC}}}}}^{\exp }=130(4)$ meV from tunneling and quasiparticle scattering along the bulk crystal edge direction¹. In addition, the inclusion of explicit SOC results in the opening of the Chern gap in DC2 and DC3 seen at 120 meV above E_F, Fig. 8b. The Chern gap for DC2 is Δ = 25 meV, which is also in reasonable agreement with the experimental value of ${\Delta }^{\exp }=34(2)$ meV.

Fig. 8: Band structures using LDA $+\,{U}_{{{{\rm{Mn}}}}}^{3d}$ (−0.5 eV) with scalar relativity (averaged spin–orbit coupling, AREP) as well as full relativity (explicit spin–orbit coupling, SOREP).

a Bulk with AREP, b slab with AREP, c bulk with SOREP, d slab with SOREP. Labels “1”, “2”, and “3” at k = K indicate the DC positions in the minority spin channel.

Our calculations show that DC2 in bulk is close to E_F, which could affect the experimental AHE measurements. An important distinction between the bulk theory and experimental transport measurements is that the experiments were carried out in a cleaved bulk terminated with an Mn surface. Specifically, the Mn-terminated surface showed a significant modulation in the dI/dV line map at B = 9T, interpreted as a Landau quantization signature. On the other hand, the TbSn-terminated surface showed an almost homogenous dI/dV line map¹. This was attributed to a possible geometry reconstruction due to dangling Tb³⁺ bonds¹. The Mn termination could also modify the band structure near the surface. To explore this, we carried out DFT + U calculations of a TbMn₁₂Sn₁₀ non-stoichiometric semi-infinite slab terminated with Mn layers. In other words, the slab is periodic along in-plane directions, while a large vacuum is inserted in both out-of-plane ends, which are terminated with Mn layers, see Fig. 9. To demonstrate that the Mn surface effects can be appropriately modeled by this slab, we calculated the atomic moments and charges in these two settings. Table 2 provides these values for Tb and Mn in various environments. We observed that the Tb spin moments and charges are largely unchanged for bulk vs. slab, indicating that the relevant changes occur only in the surface and sub-surface Mn layers as well as Sn layers in between. The sub-surface Mn shows a moderate change in the moments. However, a significant change occurs near the Mn surface, where we see much larger Mn moments of 3.33μ_B, in quantitative agreement with previous findings². This shows that the surface effects can be reliably modeled by the constructed slab.

Fig. 9: A slab of TbMn₆Sn₆.

a Out-of-plane and b in-plane views are shown. The large red spheres are Tb atoms, medium blue spheres are Mn atoms, and small gray spheres are Sn atoms. The slab is Mn-terminated due to the observed intense modulation in the experimental dI/dV line map¹. The vacuum length between the periodic slabs is ≈13.5 Ang.

Table 2 Comparison of atomic moments and charges in bulk vs. slab.

Figure 8c, d shows the slab band structures. Compared to bulk bands, the notable differences are DC3 shifting up from ~120 meV to ~275 meV, while DC2 shifting down very close to E_F. The shift in DC2 is likely due to charge transfer from the surface Mn layer to the subsurface Mn layer (see Table 2 for atomic charges). In Fig. 8c, where the SOC is not explicitly included, the DC2 is ~15 meV below the E_F. However, once the SOC is included, the Chern gap of Δ = 26 meV opens up, and the Fermi level lies within this gap (Fig. 8d). In reality, the Fermi level in the cleaved bulk might or might not exactly lie in the Chern gap of 34(2) meV, as the ab initio methods used here combined with a level of experimental input could result in larger systematic bias than 34 meV. However, the change in E_DC2 going from the bulk to the surface, ΔE_DC2 = 135 meV, must be a more robust quantity, as this is an energy difference, and we expect it to be much less sensitive to the quality of DFA or trial wave functions.

To obtain further insights into the DCs’ origin, we investigated their orbital characters using projections onto the atomic Mn orbitals. In the bulk, there are two DCs near 120 meV (Fig. 8a, DC2 and DC3). DC3 has a heavy d_zx and d_zy character, while DC2 has a d_xy and ${d}_{{x}^{2}-{y}^{2}}$ character (see Supplementary Fig. 9). Since DC3 is significantly above the E_F in the slab (~275 meV), we focus on DC2 with d_xy, ${d}_{{x}^{2}-{y}^{2}}$ character and plot the band structures of the surface, subsurface, and bulk Mn layers projected onto atomic d_xy, ${d}_{{x}^{2}-{y}^{2}}$ orbitals in Fig. 10. The subsurface Mn bands look similar to the bulk Mn bands, but the DC2 appears closer to E_F. On the other hand, the surface bands look quite different, and the d_xy, ${d}_{{x}^{2}-{y}^{2}}$ DC2 signal near the E_F is very weak. We note that a DC2 near E_F can still be seen on the surface Mn layer, albeit with strong ${d}_{{z}^{2}}$, d_zx, and d_zy characters (Supplementary Fig. 11). Namely, the DC2 near E_F in the slab (Fig. 8c) is split between the surface and subsurface DCs in the d-orbital manifold with different characters. Perhaps it is not surprising that the surface DC2 takes on a substantial z character since it now faces the vacuum. Assuming that STM transport measurements involved conduction mainly in x and y directions (in-plane), the above DC2 split suggests that the experimental signal mainly consists of the bulk and subsurface layers with a stronger d_xy, ${d}_{{x}^{2}-{y}^{2}}$ character, and a weaker signal coming from the surface Mn d_zx, d_zy orbitals. This is corroborated by the fact that the STM Landau fan diagram obtained from an Mn-terminated bulk shows the Chern gap at 130(4) meV above E_F, not near E_F as we see for the surface.

Fig. 10: Minority spin band structures using projections on the atomic Mn $({d}_{xy}+{d}_{{x}^{2}-{y}^{2}})$ orbitals.

Projections in a bulk, b slab subsurface, and c slab surface are shown.

Another aspect of this material studied by ref. ² was the k_z dispersion of the bulk TbMn₆Sn₆. Specifically, the authors mentioned that the k_z-dispersion was too high in the bulk TbMn₆Sn₆, which is not desired for a 2D model. Indeed, we also find this to be true in bulk, and the band structure shows drastic changes as the k_z is slowly varied (Supplementary Fig. 12). In fact, the DC2 and DC3 occur only in k_z = 0 when looked at increments of Δk_z = 0.1 in reciprocal lattice units and disappears for higher values. The ‘flat’ band in k_z = 0 also gradually disperses for high k_z values. The non-ideal 2D nature of the bulk can be seen in the Fermi surface as well (see Supplementary Fig. 5). This demonstrates the additional challenge in realizing the Chern magnetism in the bulk Mn layers and motivates the experimental synthesis of TbMn₆Sn₆ thin films to eliminate the heavy k_z-dependance and to move the DC2 closer to E_F.

Finally, besides E_DC2, we have also calculated the Dirac velocity (v_D) to compare with experiments. To obtain v_D, we use the Dirac dispersion in the presence of a Chern gap due to SOC¹:

$${E}_{k}={E}_{{{{\rm{DC}}}}}\pm \sqrt{{(\Delta /2)}^{2}+{(\hslash {{{\bf{k}}}}{v}_{{{{\rm{D}}}}})}^{2}}.$$

(2)

The fit of Eq. (2) to the upper band of DC2 in Fig. 8b provides v_D = 2.25 × 10⁵ m/s (see Supplementary Fig. 4). This is only in qualitative agreement with the experimental value of ${v}_{{{{\rm{D}}}}}^{\exp }=4.2(3)\times 1{0}^{5}$ m/s which was obtained by a fit to the Landau fan diagram¹. In addition, the Dirac velocity extracted from tunneling data provided results close to ${v}_{{{{\rm{D}}}}}^{\exp }=4.2(3)\times 1{0}^{5}$ m/s¹. Therefore, LDA $+\,{U}_{{{{\rm{Mn}}}}}^{3d}$ seems to genuinely underestimate v_D (and relatedly, Fermi velocities). This v_D underestimation is only mildly sensitive to the value of $+{U}_{{{{\rm{Mn}}}}}^{3d}$, as the increase of v_D going from LDA $+\,{U}_{{{{\rm{Mn}}}}}^{3d}$ (−0.5 eV) to LDA $+\,{U}_{{{{\rm{Mn}}}}}^{3d}$ (+0.5 eV) is only Δv_D = 0.27 × 10⁵ m/s. Namely, the main effect of $+{U}_{{{{\rm{Mn}}}}}^{3d}$ in this material is to shift the band energies up/down while only moderately changing the dispersions (namely slopes or v_D). Therefore, we don’t expect LDA $+\,{U}_{{{{\rm{Mn}}}}}^{3d}$ (−0.5 eV) to obtain both E_DC2 and v_D correctly, nor do we expect it to produce accurate results for all other properties, such as optimized geometries. We note that the v_D underestimation is not only specific to TbMn₆Sn₆, and it has been observed in other materials such as graphene and Dirac semimetal Na₃Bi, where LDA underestimates the Fermi velocity while hybrid DFT or GW methods show considerable improvements^100,101. Ultimately, the inability to predict all properties using the same DFA shows the limitations of the single-particle picture, which supports our findings throughout this work.

To further investigate the nature of electron correlations and spin fluctuations in TbMn₆Sn₆, we carried out DFT + dynamical mean field theory (DMFT) calculations (see Supplementary Note 5 for DMFT methods). The preliminary results on the high-temperature paramagnetic (PM) phase of TbMn₆Sn₆ show strong orbital-dependent electron correlations. We find that in the PM phase, the electron occupation of the Mn 3d-subspace is 5.3e⁻ and the mean fluctuating local moments (〈m_z〉) of Mn 3d electrons to be ~3.7μ_B, which is in good agreement with a recent DFT + DMFT computation performed on YMn₆Sn₆¹⁰², a sister compound in this family. To compute the fluctuating moment, we use

$$< {m}_{z} > =2\mathop{\sum}\limits_{i}{P}_{i}| {S}_{z}{| }_{i}$$

(3)

where P_i is the probability of the ith multiplet in the continuous time Monte Carlo impurity solver and ∣S_z∣_i is the absolute value of the corresponding moment. The histogram plot (Supplementary Fig. 16) shows that the most probable spin states are high-spin states with S_z = 2.0, 2.5, and 1.5, indicating the correlation in the PM phase is likely due to Hund’s rule coupling¹⁰³. This prediction also agrees with other kagome metals, including YMn₆Sn₆^102,104. Hund’s metals were shown to display strong electron correlations¹⁰⁵, and this agrees with our QMC results, which show significant correlations due to multi-reference character. The underlying mechanism of the origin of ferromagnetism with the ordering of fluctuating moments is an important area for further studies and is beyond the scope of the present work.

Discussion

This study has made advancements in three distinct but related directions. First, an accurate, correlation-consistent ECP was generated for the Tb element with a valence space of 4f⁹5s²5p⁶6s². To the best of our knowledge, the accuracy of such a core-valence partitioning was not known for many-body methods such as CCSD(T) or DMC. In CCSD(T), we found that the low-lying atomic gaps and the binding energies of TbH₃ and TbO can be made chemically accurate (1 kcal/mol) with careful optimizations. In light of the obtained results, this seemingly too technical aspect of the effective core model is actually important for a clear delineation of subtle physical effects in the studied system. Single-reference DMC calculations showed that ≈12% of the correlation energy is missing in Tb, TbH₃, and TbO. We believe the promising results obtained for the Tb element indicate that similarly accurate ccECPs could be generated for other rare-earth elements. Such a set of rare-earth ccECPs would open further possibilities to study the broader family of RMn₆Sn₆ with significantly improved accuracy using many-body methods such as CCSD(T), CI, QMC, and DFT with appropriate DFAs. In fact, the current progress in applying real-space QMC to f-element systems seems to be hindered by the unavailability of accurate enough rare-earth ECPs^28,106, as we were able to find only a few QMC studies in the literature^{107,108,109,110}. Therefore, we hope this work will motivate further studies in this avenue.

Second, recent studies^65,66 showed that meta-GGA such as SCAN, hybrid DFT such as PBE0, and DFT + U methods overestimate the magnetic moments in simple elemental metals such as bcc Fe, hcp Co, fcc Ni, and other transition metals. Here, we observe a similar overestimation in Mn magnetic moments when using DFT + U. Importantly; we show that single-reference QMC calculations also severely overestimate the transition metal moments similar to the previously shown^65,66 advanced DFAs such as SCAN and PBE0. The overestimation persists even when the dynamic correlations are extrapolated to the zero-variance limit, suggesting that a multi-reference treatment is needed to predict the magnetic moments correctly. These results have broader implications for the ability of commonly used DFAs, such as LDA, to effectively capture the multi-reference effects and for the origins of effective weak interactions in metallic systems. A study of static correlation effects is possible for such systems with small primitive cells as multi-reference methods such as CCSD(T) and CI mature for use in periodic boundary conditions. We leave this aspect of the study to future work and hope that these findings will stimulate further research in this direction.

Finally, using a combination of ab initio and neutron diffraction experimental results, we reveal key insights about TbMn₆Sn₆ bulk and non-stoichiometric thin film limit. We show that DC2 is only ~120 meV above E_F in bulk, in agreement with experiments¹. However, the realization of Chern magnetism in bulk is complicated by the heavy k_z-dispersion as suggested previously^2,7. We show that in the slab, the DC2 shifts even closer to E_F. This motivates further experimental studies of TbMn₆Sn₆ in the thin film limit to eliminate the k_z-dispersion and to probe for the possible realization of Chern magnetism. Viable pathways to experimentally synthesize defect-free¹¹¹ thin films in a controlled manner to realize the Chern phase remain to be shown. Our work thus illuminates the aspects of TbMn₆Sn₆ both from theoretical and experimental viewpoints and opens the door for future studies of this exciting material.

Methods

DFT + U methods

DFT + U calculations were carried out using QUANTUM ESPRESSO package^61,62,63. DFT + U is well-known to converge to meta-stable states depending on the given initial guess for the Hubbard occupation matrix. To overcome this issue, we used a method similar to the ramping method described in Ref. ¹¹². Specifically, first, we converged a DFT + U calculation with a very small U value, such as 10⁻¹⁶ eV. Then, the converged charge density, orbitals, and Hubbard occupation matrices were directly provided as an initial guess for the desired value of U, skipping the adiabatic ramping of U. On a few occasions, we tested that this method indeed results in lower energies than the default values for Hubbard occupations.

QMC methods

QMC calculations were carried out using the QMCPACK package^113,114. Most calculations were driven by the NEXUS automation tool¹¹⁵. All bulk QMC calculations use canonical twist-averaging (CTA) with [8 × 4 × 8] twists to sample the kinetic energy. In this approach, every twist is charge-neutral. In addition, every twist (θ) is enforced to have the same cell magnetization:

$${M}^{{{{\rm{s}}}}}(\theta )={N}_{e}^{\uparrow }(\theta )-{N}_{e}^{\downarrow }(\theta )={{{\rm{Constant}}}}$$

(4)

namely, every twist has the same magnetization as the twist-averaged magnetization of the cell. At each twist, the orbitals are occupied using the lowest Kohn-Sham eigenvalues in each spin channel. All molecular and bulk Jastrow functions were optimized using energy minimization in VMC. For bulk calculations, the Jastrow was optimized at k = Γ twist and reused for other twists. This optimization was carried out for LDA orbitals at M^s = 7μ_B and reused for all other DFAs and M^s values. This was done to obtain improved energy differences originating from the determinantal part of the trial wave function.

The UCCSD(T) calculations were carried out using the MOLPRO package¹¹⁶. For COSCI calculations, we used the DIRAC code¹¹⁷.