Derivations of large classes of facet defining inequalities of the weak order polytope using ranking structures

Abstract

Ordering polytopes have been instrumental to the study of combinatorial optimization problems arising in a variety of fields including comparative probability, computational social choice, and group decision-making. The weak order polytope is defined as the convex hull of the characteristic vectors of all binary orders on n alternatives that are reflexive, transitive, and total. By and large, facet defining inequalities (FDIs) of this polytope have been obtained through simple enumeration and through connections with other combinatorial polytopes. This paper derives five new large classes of FDIs by utilizing the equivalent representations of a weak order as a ranking of n alternatives that allows ties; this connection simplifies the construction of valid inequalities, and it enables groupings of characteristic vectors into useful structures. We demonstrate that a number of FDIs previously obtained through enumeration are actually special cases of the large classes. This work also introduces novel construction procedures for generating affinely independent members of the identified ranking structures. Additionally, it states two conjectures on how to derive many more large classes of FDIs using the featured techniques.

Appendices

A Valid inequality proofs

1.1 A.1 T2-0 VI proof

Theorem 2

(T2-0 VI) Inequality (4) is a VI of $\textbf{P}^n_{WO}$, for any $n\ge 4$.

Proof

Inequality (4) is satisfied at equality by the characteristic vectors corresponding to the ranking structures listed in Table 3, which are justified as follows. Here, the positive and negative arc subsets are given by:

$$\begin{aligned} {\mathcal {A}}_{+}&=\{(i_2,i_1)\}\cup \{(i_1,j):j\in \hat{N}^c\} \cup \{(j,i_2):j\in \hat{N}^c\}, \\ {\mathcal {A}}_{-}&=\{(i_1,i_2)\}\cup \{(j,j'):j,j'\in \hat{N}^c, j\ne j'\}. \end{aligned}$$

Let W be an arbitrary weak order defined over the set of alternatives N, where the fixed alternatives $i_1$ and $i_2$ are tied with exactly $t_1\ge 0$ and $t_2\ge 0$ unfixed alternatives, respectively, such that $t_1 + t_2 \le n{\,-\,}2$. The structure of the weak orders generated by the different values of $t_1$ and $t_2$ can be encapsulated by the following cases:

Case 1

($t_1\le 1, t_2\le 1$) Suppose that the ranks of alternatives $i_1$ and $i_2$ are fixed as $r_{i_1}=k_1>0$ and $r_{i_2}=k_2>0$, respectively. Furthermore, let $\hat{N}^c_{<k_1}\subseteq \hat{N}^c$ denote the set of unfixed alternatives with rank $r< k_1$, and $\hat{N}^c_{>k_2}\subseteq \hat{N}^c$ denote the set of unfixed alternatives with rank $r'> k_2$. Note that $\hat{N}^c_{<k_1}\cap \hat{N}^c_{>k_2} = \emptyset$ only when either $k_1\le k_2$ or $k_1=k_2 + t_2$. Based on the relative values of $k_1$ and $k_2$, the weak orders can be further divided into the following two sub-cases:

• Case 1a ($k_1 < k_2$) For each $\hat{j}\in \hat{N}^c_{<k_1}$ and $\hat{j'}\in \hat{N}^c_{>k_2}$ add positive arcs $(i_1,\hat{j})$ and $(\hat{j'}, i_2)$, respectively, to W to obtain a weak order where alternative $i_1$ is in first place and alternative $i_2$ is in last place. This gives precisely $2(n{\,-\,}2)$ selected positive arcs: $n{\,-\,}2$ each from the ordering of the two fixed alternatives $i_1$ and $i_2$ with each unfixed alternative $j\in \hat{N}^c$. In the event of ties between $i_1$ and an unfixed alternative, say $j_1$ (i.e., $t_1=1$), or/and between $i_2$ and an unfixed alternative, say $j_2$ (i.e., $t_2=1$), it may be necessary to remove the corresponding arcs, specifically arcs $(j_1, i_1)$ and $(i_2, j_2)$, respectively, to maintain transitivity. Since these are zero arcs (i.e., $\pi _{j_1, i_1}=\pi _{i_2, j_2}=0$), their removal does not affect the values of $\Vert {\varvec{x}}_-^{W}\Vert$ or $\Vert {\varvec{x}}_+^{W}\Vert$. Next, break the ties (if any) between $j,j'\in \hat{N}^c$, where $j \ne j'$, by removing either negative arc $(j,j')$ or negative arc $(j',j)$ from W; denote the generated weak order as $W'$. This gives a total of $(n{\,-\,}2)(n{\,-\,}3)/2 {\, +\, }1$ selected negative arcs. Since all preceding operations do not increase the value of $\Vert {\varvec{x}}_-^{W}\Vert$ or decrease the value of $\Vert {\varvec{x}}_+^{W}\Vert$, we have that $\Vert {\varvec{x}}_+^{W}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W}\Vert \le \Vert {\varvec{x}}_+^{W'}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W'}\Vert$. For any member of the presented ranking structure, the value of $\Vert {\varvec{x}}_+^{W'}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W'}\Vert$ equals the right-hand side of inequality (4). Note that, since there must be at least one arc between every pair of alternatives to induce a total order, further reduction in negative arcs is not possible. Now, depending on the initial position of $i_1$ and $i_2$ and the value of $t_1$ and $t_2$, $W'$ attains one of four ranking structures: alternative $i_1$ is uniquely in first place and alternative $i_2$ is uniquely in last place (#1), an alternative $j_1\in \hat{N}^c$ is tied with $i_1$ for first place (#2), an alternative $j_2\in \hat{N}^c$ is tied with $i_2$ for the last available position, $n{\,-\,}1$ in this case (#3), or both of these ties occur, with $j_1\ne j_2$ (#4).

• Case 1b ($k_1 \ge k_2$) This case is addressed using the same arguments as in Case 1a with the addition that, to maintain transitivity, it is necessary either to replace positive arc $(i_2, i_1)$ with negative arc $(i_1, i_2)$ (when $k_1>k_2$) or to remove positive arc $(i_2, i_1)$ (when $k_1=k_2$) to place $i_1$ strictly in front of $i_2$; denote the generated weak order as $W'$. In this case, the relevant operations increase the value of $\Vert {\varvec{x}}_-^{W}\Vert$ by at most 1 and of $\Vert {\varvec{x}}_+^{W}\Vert$ by at least $n{\,-\,}3\ge 1$. As a result, we have that $\Vert {\varvec{x}}_+^{W}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W}\Vert \le \Vert {\varvec{x}}_+^{W'}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W'}\Vert$. This also leads to the same ranking structures as in Case 1a.

Case 2

($t_1\ge 2, t_2\le 1$) Let $[j_1, j_{t_1}]\subseteq \hat{N}^c$ denote those unfixed alternatives tied with $i_1$ in rank position $k_1$. First, break the ties between $\hat{j}$ and $j_{t_1}$ by removing arc $(j_{t_1}, \hat{j})$ from W, for each $\hat{j}\in \{i_1\}\cup [j_1, j_{t_1{\,-\,}1}]$; denote the generated weak order as $W_{t_1 {\,-\,}1, t_2}$. Since this removal decreases the value of $\Vert {\varvec{x}}_-^{W}\Vert$ by $(t_1{\,-\,}1)\ge 1$ and keeps the value of $\Vert {\varvec{x}}_+^{W}\Vert$ unchanged, we have that $\Vert {\varvec{x}}_+^{W}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W}\Vert <\Vert {\varvec{x}}_+^{W_{t_1{\,-\,}1, t_2}}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W_{t_1{\,-\,}1, t_2}}\Vert$. It is worth noting that, as $(j_{t_1}, i_1)$ is a zero arc, its removal does not affect the values of $\Vert {\varvec{x}}_-^{W}\Vert$ or $\Vert {\varvec{x}}_+^{W}\Vert$. Next, break the ties between each of $\hat{j}\in \{i_1\}\cup [j_1, j_{t_1{\,-\,}2}]$ with $j_{t_1{\,-\,}1}$ in $W_{t_1 {\,-\,}1, t_2}$ in a similar fashion to obtain a modified weak order, denoted as $W_{t_1{\,-\,}2, t_2}$. Repeat this process until arriving at a weak order, denoted as $W_{1, t_2}$, in which $i_1$ is tied with exactly one unfixed alternative $j_1$. At this point, apply the results of Case 1 by setting $W{:}{=}W_{1, t_2}$.

Case 3

($t_2\ge 2$) Let $[j_1, j_{t_2}]\subseteq \hat{N}^c$ denote those unfixed alternatives tied with alternative $i_2$ in rank position $k_2$. This case is addressed using the same arguments as in Case 2 by replacing $\{i_1\}\cup [j_1, j_{t'{\,-\,}1}]$ and $(j_{t'}, \hat{j})$ with $\{i_2\}\cup [j_1, j_{t'{\,-\,}1}]$ and $(\hat{j}, j_{t'})$, respectively, in each step, where $t'=t_2, t_2{\,-\,}1,\ldots ,2$. In the generated weak order, denoted as $W_{t_1, 1}$, $i_2$ is tied with exactly one unfixed alternative $j_1$. At this point, apply the results of Case 1 or 2 by setting $W{:}{=}W_{t_1, 1}$. $\square$

1.2 A.2 T2-3 VI proof

Theorem 5

(T2-3 VI) Inequality (7) is a VI of $\textbf{P}^n_{WO}$, for any $n\ge 4$.

Proof

Inequality (7) is satisfied at equality by the characteristic vectors corresponding to the ranking structures listed in Table 5. Here, the positive and negative arc subsets are given by:

$$\begin{aligned} {\mathcal {A}}_{+}&=\{(i_2,j):j\in \hat{N}^c\}\cup \{(i_1,j):j\in \hat{N}^c\} \cup \{(j,i_1):j\in \hat{N}^c\}, \\ {\mathcal {A}}_{-}&=\{(i_2,i_1)\}\cup \{(j,j'):j,j'\in \hat{N}^c, j\ne j'\}. \end{aligned}$$

Let W be an arbitrary weak order defined over the set of alternatives N, where the fixed alternatives $i_1$ and $i_2$ are tied with exactly $t_1\ge 0$ and $t_2\ge 0$ unfixed alternatives, respectively, such that $t_1 + t_2 \le n{\,-\,}2$. Now suppose that the ranks of these alternatives are fixed as $r_{i_1}=k_1>0$ and $r_{i_2}=k_2>0$. Additionally, let $\hat{N}^c_{<k_1}\subseteq \hat{N}^c$ denote the set of unfixed alternatives with rank $r< r_{i_1}$, and $\hat{N}^c_{<k_2}\subseteq \hat{N}^c$ denote the set of unfixed alternatives with rank $r'< r_{i_2}$. Note that, $\hat{N}^c_{<k_1}\cap \hat{N}^c_{<k_2} =\emptyset$ only when either $\hat{N}^c_{<k_1} =\emptyset$ or $\hat{N}^c_{<k_2} =\emptyset$ or both. The structure of the weak orders generated by the different values of $t_1$ and $t_2$ can be encapsulated by the following cases:

Case 1

($t_1=0, t_2\le 1$) For each $\hat{j}\in \hat{N}^c_{<k_1}$, replace positive arc $(\hat{j},i_1)$ with positive arc $(i_1,\hat{j})$ and for each $\hat{j'}\in \hat{N}^c_{<k_2}$, add positive arc $(i_2,\hat{j'})$ to W to obtain a weak order where alternatives $i_1$ and $i_2$ are placed in front of all $j\in \hat{N}^c$. This gives precisely $2(n{\,-\,}2)$ selected positive arcs: $n{\,-\,}2$ each from the strict ordering of the two fixed alternatives $i_1$ and $i_2$ with each unfixed alternative $j\in \hat{N}^c$. Next, break the ties (if any) between $j,j'\in \hat{N}^c$, where $j \ne j'$, by removing either negative arc $(j,j')$ or negative arc $(j',j)$ from W. Additionally, when $k_1 \ge k_2$, replace negative arc $(i_2, i_1)$ with zero arc $(i_1, i_2)$ to obtain a weak order, denoted as $W'$, in which $i_1$ is uniquely in first place and $i_2$ is uniquely in second place. This gives a total of $(n{\,-\,}3)(n{\,-\,}2)/2$ selected negative arcs. In the event of ties between $i_2$ and an unfixed alternative, say $j_1\in \hat{N}^c$ (i.e., $t_2=1$), it is also necessary to replace negative arc $(\hat{j'}, j_1)$ with negative arc $(j_1, \hat{j'})$ for each $\hat{j'} \in \hat{N}^c_{<k_2}$ to maintain the tie between $i_2$ and $j_1$. Furthermore, when $k_1 = k_2$ remove positive arc $(j_1, i_1)$, whereas when $k_1>k_2$ replace positive arc $(j_1, i_1)$ with positive arc $(i_1, j_1)$ to place $i_1$ strictly infront of $j_1$. Since all preceding operations neither increase the value of $\Vert {\varvec{x}}_-^{W}\Vert$ nor decrease the value of $\Vert {\varvec{x}}_+^{W}\Vert$, we have that $\Vert {\varvec{x}}_+^{W}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W}\Vert \le \Vert {\varvec{x}}_+^{W'}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W'}\Vert$. For any such weak order, equivalently characterized by either ranking structure #1, if $t_2=0$, or #2, if $t_2=1$, the value of $\Vert {\varvec{x}}_+^{W'}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W'}\Vert$ equals the right-hand side of inequality (7).

Case 2

($t_1=1, t_2\le 1$) Let $j_1\in \hat{N}^c$ denote the unfixed alternative tied with $i_1$ in rank position $k_1$. For each $\hat{j'}\in \hat{N}^c_{<k_2}\backslash \{j_1\}$, add positive arc $(i_2, \hat{j'})$ to W to place $i_2$ infront of all $j\in \hat{N}^c\backslash \{j_1\}$. Additionally, when $k_1\le k_2$, for each $\hat{j}\in \hat{N}^c_{<k_1}$, replace positive arc $(\hat{j}, i_1)$ with positive arc $(i_1, \hat{j})$ and negative arc $(\hat{j}, j_1)$ with negative arc $(j_1, \hat{j})$, to obtain a weak order where alternatives $i_1$, $j_1$, and $i_2$ are placed in front of all $j\in \hat{N}^c\backslash \{j_1\}$. In the event of tie between $i_2$ and an unfixed alternative, say $j_2\in \hat{N}^c\backslash \{j_1\}$ (i.e., $t_2=1$), it is also necessary to replace negative arc $(\hat{j'}, j_2)$ with negative arc $(j_2, \hat{j'})$ for each $\hat{j'} \in \hat{N}^c_{<k_2}\backslash \{j_1\}$ to maintain the tie between $i_2$ and $j_2$. Next the ties (if any) between $j,j'\in \hat{N}^c\backslash \{j_1\}$, where $j \ne j'$, are broken by removing either negative arc $(j,j')$ or negative arc $(j',j)$ from W; denote the generated weak order as $W'$. Since the preceding operations neither increase the value of $\Vert {\varvec{x}}_-^{W}\Vert$ nor decrease the value of $\Vert {\varvec{x}}_+^{W}\Vert$, we have that $\Vert {\varvec{x}}_+^{W}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W}\Vert \le \Vert {\varvec{x}}_+^{W'}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W'}\Vert$. Now, depending on the initial position of $i_1$ and $i_2$ and the value of $t_2$, $W'$ attains one of six ranking structures: $i_1$ is tied with $j_1$ for first place (#3); $i_1$ is tied with $j_1$ for first place and $i_2$ is tied with $j_2$ for third place (#4); $i_1$, $i_2$, and $j_1$ all remain tied for first place (#5); $i_1$, $i_2$, $j_1$, and $j_2$ all remain tied for first place (#6); $i_1$ and $j_1$ remain tied for any position but first, which is occupied by $i_2$ (#7); $i_1$ and $j_1$ remain tied for any position but first, which is occupied by $i_2$ jointly with $j_2$ (#8).

Case 3

($t_1=2, t_2\le 1$) Let $j_1, j_2\in \hat{N}^c$ denote the unfixed alternatives tied with $i_1$ in rank position $k_1$. For each $\hat{j'}\in \hat{N}^c_{<k_2}$, add positive arc $(i_2, \hat{j'})$ to W to place $i_2$ infront of all alternatives $j\in N$. Additionally, when $k_1 <k_2$, replace zero arc $(i_1, i_2)$ with negative arc $(i_2, i_1)$, whereas when $k_1 = k_2$ remove zero arc $(i_1, i_2)$ to place $i_2$ strictly infront of $i_1$. In the event of tie between $i_2$ and an alternative, say $j_3\in \hat{N}^c\backslash \{j_1, j_2\}$ (i.e., $t_2=1$), it is also necessary to replace negative arc $(\hat{j'}, j_3)$ with negative arc $(j_3, \hat{j'})$ for each $\hat{j'} \in \hat{N}^c_{<k_2}$ to maintain the tie between $i_2$ and $j_3$. Furthermore, when $k_1 < k_2$ replace arc $(\hat{j}, j_3)$ with arc $(j_3, \hat{j})$, whereas when $k_1=k_2$ remove arc $(\hat{j}, j_3)$ for each $\hat{j}\in \{i_1, j_1, j_2\}$. Next, the ties (if any) between $j,j'\in \hat{N}^c\backslash \{j_1, j_2\}$, where $j \ne j'$, are broken by removing either negative arc $(j,j')$ or negative arc $(j',j)$ from W; denote the generated weak order as $W'$. Since the preceding operations neither increase the value of $\Vert {\varvec{x}}_-^{W}\Vert$ nor decrease the value of $\Vert {\varvec{x}}_+^{W}\Vert$, we have that $\Vert {\varvec{x}}_+^{W}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W}\Vert \le \Vert {\varvec{x}}_+^{W'}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W'}\Vert$. Here, $W'$ is a member of ranking structure #9, if $t_2=0$, or #10, if $t_2=1$.

Case 4

($t_1\ge 3, t_2\le 1$) Let $[j_1, j_{t_1}]\subseteq \hat{N}^c$ denote the unfixed alternatives tied with $i_1$ in rank position $k_1$. First, break the tie between $\hat{j}$ and $j_{t_1}$ by removing arc $(j_{t_1}, \hat{j})$ from W, for each $\hat{j}\in \{i_1\}\cup [j_1,j_{t_1{\,-\,}1}]$ (when $k_1=k_2$, $\hat{j}\in \{i_1, i_2\}\cup [j_1,j_{t_1{\,-\,}1}]$); denote the generated weak order as $W_{t_1 {\,-\,}1, t_2}$. Since this removal decreases the value of $\Vert {\varvec{x}}_-^{W}\Vert$ and $\Vert {\varvec{x}}_+^{W}\Vert$ by at least $(t_1{\,-\,}1)\ge 1$ and at most 1, respectively, we have that $\Vert {\varvec{x}}_+^{W}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W}\Vert \le \Vert {\varvec{x}}_+^{W_{t_1 {\,-\,}1, t_2}}\Vert \hspace{-.5mm}-\hspace{-.5mm}\Vert {\varvec{x}}_-^{W_{t_1 {\,-\,}1, t_2}}\Vert$. Next, break the ties between each of $\hat{j}\in \{i_1\}\cup [j_1, j_{t_1{\,-\,}2}]$ (when $k_1=k_2$, $\hat{j}\in \{i_1, i_2\}\cup [j_1, j_{t_1{\,-\,}2}]$) with $j_{t_1{\,-\,}1}$ in $W_{t_1 {\,-\,}1, t_2}$ in a similar fashion to obtain a modified weak order, denoted as $W_{t_1 {\,-\,}2, t_2}$. Repeat this process until arriving at a weak order, denoted as $W_{2, t_2}$, in which $i_1$ is tied with exactly two unfixed alternatives, say $j_1$ and $j_2$ (when $k_1=k_2$, both $i_1$ and $i_2$ are tied with $j_1$ and $j_2$). At this point, apply the results of Case 3 by setting $W{:}{=}W_{2,t_2}$.

Case 5

($t_2\ge 2$) Let $[j_1, j_{t_2}]\subseteq \hat{N}^c$ denote the unfixed alternatives tied with $i_2$ in rank position $k_2$. This case is addressed using the same arguments as in Case 4 by replacing $\{i_1\}\cup [j_1, j_{t'{\,-\,}1}]$ with $\{i_2\}\cup [j_1, j_{t'{\,-\,}1}]$ in each step, where $t'=t_2, t_2{\,-\,}1,\ldots ,1$. In the generated weak order, denoted as $W_{t_1,1}$, $i_2$ is tied with exactly one unfixed alternative, say $j_1$. At this point, apply the results of Cases 1-4 by setting $W{:}{=}W_{t_1,1}$. $\square$

B Facet defining inequality proofs

1.1 B.1 T1 FDI differences matrix

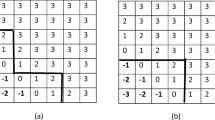
To introduce the differences matrix we fixed $i_1=1$ and $j_k=k{\, +\, }1$, for $k=1,\dots ,n{\,-\,}1$; note that the same relabeling was used in the proof. The difference matrix, $\bar{{\varvec{X}}}$ is generated after iteratively subtracting several rows of ${\varvec{X}}$ as described in the T1  FDI proof (see Theorem 8). For ease of visualization, $\bar{{\varvec{X}}}$ is partitioned into two matrices as,

$$\begin{aligned} \bar{{\varvec{X}}}=\left[ \begin{array}{cc} \bar{{\varvec{X}}}^1&\quad \bar{{\varvec{X}}}^2 \end{array}\right] \end{aligned}$$

(16)

where $\bar{{\varvec{X}}}_1\hspace{-1mm}\in \mathbb {Z}^{n(n{\,-\,}1)\times 2(n{\,-\,}1)}$ and $\bar{{\varvec{X}}}_2\hspace{-1mm}\in \mathbb {Z}^{n(n{\,-\,}1)\times (n{\,-\,}1)(n{\,-\,}2)}$ such that, the first $2n{\,-\,}2$ columns i.e., elements involving the comparison of alternative 1 with $j\in \hat{N}^c$ show up in $\bar{{\varvec{X}}}_1$ and, the last $(n{\,-\,}1)(n{\,-\,}2)$ columns i.e., all comparisons between $j,j'\in \hat{N}^c=N\backslash \{1\}$ appear in $\bar{{\varvec{X}}}_2$. Both of these matrices are illustrated as follows:

1.2 B.2 T2-1 FDI differences matrix and proof

To introduce the differences matrix for the T2-1 FDI proof we fixed $i_1=1$, $i_2=n$ and $j_k=k{\, +\, }1$, for $k=1,\dots ,n{\,-\,}2$. The difference matrix, $\bar{{\varvec{X}}}$ is generated after iteratively subtracting several rows of ${\varvec{X}}$ as described in the following proof. For ease of visualization, $\bar{{\varvec{X}}}$ is partitioned into two matrices as,

$$\begin{aligned} \bar{{\varvec{X}}}=\left[ \begin{array}{cc} \bar{{\varvec{X}}}^1&\quad \bar{{\varvec{X}}}^2 \end{array}\right] \end{aligned}$$

(17)

where $\bar{{\varvec{X}}}_1\hspace{-1mm}\in \mathbb {Z}^{n(n{\,-\,}1)\times 2(n{\,-\,}1)}$ and $\bar{{\varvec{X}}}_2\hspace{-1mm}\in \mathbb {Z}^{n(n{\,-\,}1)\times (n{\,-\,}1)(n{\,-\,}2)}$ such that, the first $2n{\,-\,}2$ columns i.e., elements involving the comparison of alternative 1 with $j\in N\backslash \{1\}$ show up in $\bar{{\varvec{X}}}_1$ and, the last $(n{\,-\,}1)(n{\,-\,}2)$ columns i.e., all comparisons between $j,j'\in N\backslash \{1\}$ appear in $\bar{\varvec{X}}_2$. Both of these matrices are illustrated as follows:

Theorem 9

(T2-1 FDI) T2-1 VI is an FDI of $\textbf{P}^n_{WO}$, for any $n\ge 4$.

Proof

In the T2-1  valid inequality expression, fix $i_1=1$ and $i_2=n$ for ease of exposition—or assume a corresponding relabeling of the alternatives is performed a priori. It is straightforward to verify that all points output by CPT2-1 belong to the six ranking structures given in Table 4 that satisfy the inequality at equality.

To obtain the difference matrix, $\bar{{\varvec{X}}}$, first shift rows 1,2 and 3 to the bottom of the matrix such that they become rows $n(n{\,-\,}1){\,-\,}2$, $n(n{\,-\,}1){\,-\,}1$ and $n(n{\,-\,}1)$ respectively; all other rows are shifted upward. Second, iteratively subtract row $i{\,-\,}1$ from row i, for $i=n(n{\,-\,}1){\,-\,}3,\dots ,2$. Third, subtract row $n(n{\,-\,}1)$ from row 1, row $n(n{\,-\,}1){\,-\,}1$ from row $n(n{\,-\,}1){\,-\,}2$ and row $n(n{\,-\,}1){\,-\,}2$ from row $n(n{\,-\,}1){\,-\,}1$. To proceed, set ${\varvec{A}}^0\in {\mathbb {R}}^{n(n{\,-\,}1)\times n(n{\,-\,}1)}$ with a rearranged column ordering of $\bar{{\varvec{X}}}$ such that, all comparisons between the alternatives $j,j'\in \hat{N}^c=N\backslash \{1,n\}$ appear in the first $(n{\,-\,}2)(n{\,-\,}3)$ columns, the next $2(n{\,-\,}2)$ columns involve the comparisons between $i_2=n$ and $j\in \hat{N}^c$ and the finally elements involving the comparison of $i_1=1$ with $j\in \hat{N}^c$ and $i_2=n$ shows up in the last $2(n{\,-\,}1)$ columns. The first thing to remark about the structure of ${\varvec{A}}^0$ is that for the submatrix involving the first $(n{\,-\,}1)(n{\,-\,}2)$ columns and the first $(n{\,-\,}1)^2{\,-\,}1$ rows, nearly all rows have either a 1 or a ${\,-\,}1$ as the only nonzero element and the nonzero occurs under a unique column. The only $n{\,-\,}2$ rows that do not fit this pattern are rows $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }2$, for $i=1,\dots ,n{\,-\,}2$ which have a 1 and a ${\,-\,}1$ under columns $(i{\, +\, }1,n)$ and $(n,i{\, +\, }1)$, respectively. The two consecutive vectors after each of these $n{\,-\,}2$ rows have a nonzero element of the opposite sign under the same columns. In particular, row $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }3$ has a 1 under column $(n,i{\, +\, }1)$ and row $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }4$ has a ${\,-\,}1$ under column $(i{\, +\, }1, n)$, where $1\le i\le n{\,-\,}2$. Another thing to note about ${\varvec{A}}^0$ is that, the binary values of its final row corresponds to the alternative-ordering in which items $\{1,n\}$ are tied for the first position and the remaining alternatives are in a lexicographical linear ordering occupying positions 2 to $(n{\,-\,}1)$. To eliminate the nonzero elements of the first $(n{\,-\,}1)(n{\,-\,}2)$ columns of this row add to it rows $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }2 j$, where, $1\le i \le n {\,-\,}2$ and $1\le j\le n{\,-\,}i$. As the next step, eliminate the first two nonzero entries of row $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }2$ by adding to it rows $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }3$ and $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }4$, for $i=1,\dots ,n{\,-\,}2$. Then shift these $n{\,-\,}2$ rows to the bottom of the matrix and denote the resulting matrix as $A^1$. More explicitly, row $(n{\,-\,}1)^2{\, +\, }i{\, +\, }1$ of ${\varvec{A}}^1$ receives row $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }2$ from ${\varvec{A}}^0$, for $1\le i\le n{\,-\,}2$; all other rows are shifted upwards. Afterwards, the structure of ${\varvec{A}}^1$ can be described via a partition with the same number of submatrices and related dimensions as defined by Eq. (11).

Similar to the proof of Theorem 8, it is only necessary to know a part of the contents of these submatrices to proceed. ${\varvec{B}}^1$ is comprised entirely of positive or negative unit vectors and, thus we have, $|\det ({\varvec{B}}^1)|=1$. ${\varvec{C}}^1$ is mostly a zero matrix, with the exception of row i whose values under columns $(n{\,-\,}i{\,-\,}1,n{\,-\,}1)$ and $(n{\,-\,}1,n{\,-\,}i{\,-\,}1)$ are 1 and  $-$ 1, respectively, for $i=1,..,n{\,-\,}3$ and row $n{\,-\,}2$ which has a ${\,-\,}1$ under column $(n{\,-\,}2,n{\,-\,}1)$ and a 1 under column $(n{\,-\,}1,n{\,-\,}2)$. To turn ${\varvec{C}}^1$ into a zero matrix first add to row i, where $1\le i\le n{\,-\,}3$, the two consecutive elementary vectors from ${\varvec{B}}^1$ that have nonzeroes of the opposite sign under columns $(n{\,-\,}i{\,-\,}1,n{\,-\,}1)$ and $(n{\,-\,}1,n{\,-\,}i{\,-\,}1)$. Next, to eliminate the entries of row $n{\,-\,}2$ subtract from it rows $(n{\,-\,}1)(n{\,-\,}2){\,-\,}4$ and $(n{\,-\,}1)(n{\,-\,}2){\,-\,}3$ of ${\varvec{B}}^1$. Similar to ${\varvec{B}}^1$, ${\varvec{D}}^1$ is comprised entirely of elementary vectors, more specifically, it consists of the following entries: a 1 under column (n, 1) and $(i{\, +\, }j{\, +\, }1,1)$ in row 1 and $(2n{\,-\,}i)(i{\,-\,}1){\,-\,}2(i {\,-\,}j){\, +\, }3$ respectively and a ${\,-\,}1$ under (1, n) and $(1, i{\, +\, }j{\, +\, }1)$ in row 2 and $(2n{\,-\,}i)(i{\,-\,}1){\,-\,}2(i {\,-\,}j){\, +\, }4$ respectively, where, $1\le i\le n{\,-\,}3$ and $1\le j\le n{\,-\,}i{\,-\,}1$. Finally, the structure of ${\varvec{E}}^1$ can be described as follows:

From the above structure we can see that, row n of ${\varvec{E}}^1$ in addition to having a 1 under column (1, i), where $1\le i\le n{\,-\,}1$, also has a non-increasing sequence of negative integers under column (j, 1), where, $3\,\hspace{-1mm}\le j \le \hspace{-1mm}\, n{\,-\,}2$. Upon completion of the elimination steps to convert ${\varvec{C}}^1$ into a zero matrix, the entries of ${\varvec{E}}^1$ change slightly and only affect the entries in columns $(1,n{\,-\,}1)$ and $(n{\,-\,}1,1)$. The structure of the new matrix, denoted as ${\varvec{E}}^2$, is given by:

Now, since the determinant of ${\varvec{B}}^1$ is 1 and ${\varvec{C}}^2$ has been turned into a zero matrix, we can write $|\det ({\varvec{A}}^1)|=|\det ({\varvec{E}}^2)|$. To simplify ${\varvec{E}}^2$, first add row $n{\,-\,}2$ to row i, where $1\le i\le n{\,-\,}3$. Second, add to row $n{\, +\, }i{\, +\, }1$ the updated rows j, where $1\le i \le n{\,-\,}4$ and $1\le j \le n{\,-\,}i{\,-\,}4$ and subtract from it row $n{\,-\,}2$. Third, add rows 1 to $n{\,-\,}4$ and rows $n{\, +\, }2$ to $2n{\,-\,}2$ to row $n{\, +\, }1$. Fourth, eliminate the nonzero entries of row n from column (1, 2) to $(n{\,-\,}2, 1)$ by following similar steps that was used to eliminate the entries of row $(2n{\,-\,}2)$ in the proof of Theorem 8. The resulting matrix ${\varvec{E}}^3$ from the above elimination steps possesses the following form:

where

$$\begin{aligned} \alpha ={\,-\,}n{\, +\, }4;\hspace{5mm}\beta =2-\sum _{k=1}^{n-4}(k{\,-\,}1)=\frac{(n{\,-\,}1){\,-\,}(n{\,-\,}3)(n{\,-\,}5)}{2}; \end{aligned}$$

Using the same reasoning as in the proof of Theorem 8, it can be concluded that the non-singularity of ${\varvec{E}}^3$ depends on the non-singularity of the following $4\hspace{-.5mm}\times \hspace{-.5mm}4$ matrix:

$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{}\quad {\,-\,}1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {\,-\,}1 \\ \beta &{}\quad \alpha &{}\quad 0 &{}\quad \alpha {\,-\,}1\\ 1 &{}\quad 0 &{}\quad {\,-\,}1 &{}\quad 0 \end{array}\right] . \end{aligned}$$

The symbolic determinant of this matrix is $\alpha {\, +\, }\beta$, which equals 0 when,

$$\begin{aligned} \alpha {\, +\, }\beta =0\Leftrightarrow n=\frac{7}{2}\pm \frac{\sqrt{17}}{2}\notin \mathbb {Z}. \end{aligned}$$

which implies that the characteristic vectors produced by CPT2-1  are affinely independent, thereby establishing that T2-1 VI is facet defining for $n\ge 4$. $\square$

1.3 B.3 T2-3 FDI differences matrix and proof

To introduce the differences matrix for the T2-3 FDI proof the same relabeling of alternatives was used as in the previous subsection. The difference matrix, $\bar{{\varvec{X}}}$ is then generated after iteratively subtracting several rows of ${\varvec{X}}$ as described in the proof below. Similar to the previous proof, for ease of visualization $\bar{{\varvec{X}}}$ is described via a partition with the same number of submatrices and related dimensions as defined by Eq. (17). Both of the partitioned matrices $\bar{\varvec{X}}_1$ and $\bar{\varvec{X}}_2$ are illustrated as follows:

Theorem 11

(T2-3 FDI) T2-3 VI is an FDI of $\textbf{P}^n_{WO}$, for any $n\ge 4$.

Proof

As in the previous theorem, fix $i_1=1$ and $i_2 = n$ or assume that a corresponding relabeling of the alternatives is performed a priori. It is straightforward to verify that all points yielded by the modified version of CPT2-1 , denoted here as CPT2-3 for ease of explanation (the details of which can be found in page 21 of the main paper), belong to the ten ranking structures of Table 5 satisfy inequality (7) at equality. The rest of this proof follows almost the same steps as in the proof of Theorem 9. Therefore we sketch below only minor differences and where a change in the structure occurs due to the differences between CPT2-1  and CPT2-3. First, most entries of the two difference matrices, both denoted by $\bar{{\varvec{X}}}$, are the same except those in rows $1, n(n{\,-\,}1){\,-\,}1$ and $n(n{\,-\,}1)$. The first row has only a 1 under column (2, 1) and a ${\,-\,}1$ under column (n, 2), row $n(n{\,-\,}1){\,-\,}1$ has a ${\,-\,}1$ under column (2, n) with no other nonzero entry and finally row $n(n{\,-\,}1)$ has a binary structure that corresponds to a alternative-ordering where, item $i_1=1$ is in the first position, items $\{2,n\}$ are tied in the second position and the rest of the alternatives follow a lexicographical linear ordering. Second, due to the difference between the entries in the first row of ${\varvec{A}}^0$ generated from CPT2-1  and CPT2-3, the following changes are needed to convert ${\varvec{A}}^0$ into ${\varvec{A}}^1$: eliminate the entries in the first $(n{\,-\,}1)(n{\,-\,}2)$ columns of row $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }2$ by first adding the second row to row 1 and then by adding rows $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }3$ and $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }4$ to row $2n(i {\,-\,}1){\,-\,}i^2{\, +\, }2$, for $i=2,\dots ,n{\,-\,}2$. Third, submatrix ${\varvec{C}}^1$ has an additional ${\,-\,}1$ in row $n{\,-\,}1$ under column (2, n), which can be eliminated by subtracting from it the second row of ${\varvec{B}}^1$. The final change is related to difference in the structure of ${\varvec{E}}^2$. The additional operations performed to eliminate the nonzero entry of ${\varvec{C}}^1$ only affects two rows of ${\varvec{E}}^2$; row $n{\,-\,}1$ which now consists of a 1 under column (1, n) and row $n{\, +\, }1$ which in addition to the 1 under column (2, 1) has another 1 under column (n, 1) instead of a ${\,-\,}1$ under column (1, n). After the same elimination steps are performed on ${\varvec{E}}^2$ as in the proof of Theorem 9 we get the following structure for ${\varvec{E}}^3$:

where $\alpha$ and $\beta$ have the same value as in the proof of Theorem 9. Now, applying the same reasoning for the non-singularity of $E^3$ as in the proof of the previous theorem, it can be concluded that the determinant of this sub-matrix depends only on the following $4\hspace{-.5mm}\times \hspace{-.5mm}4$ matrix:

$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{}\quad {\,-\,}1 &{} \quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ \beta &{}\quad \alpha &{}\quad 0 &{}\quad \alpha {\,-\,}1\\ 1 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{array}\right] . \end{aligned}$$

The determinant of this matrix is ${\,-\,}\beta {\,-\,}1$, which equals 0 when,

$$\begin{aligned} \beta {\, +\, }1= & {} 0\Leftrightarrow \frac{(n{\,-\,}1){\,-\,}(n{\,-\,}3)(n{\,-\,}5)}{2}{\, +\, }1\\= & {} {\,-\,}\frac{1}{2}(n^2{\,-\,}9n{\, +\, }14) = {\,-\,}\frac{1}{2}(n{\,-\,}2)(n{\,-\,}7)=0 \Leftrightarrow n=7\text { or }2. \end{aligned}$$

Therefore, for all $n\ge 4$, except $n=7$, the $n(n{\,-\,}1)$ characteristic vectors generated by CPT2-3 that satisfy inequality (7) at equality are linearly independent and, thus, affinely independent. To prove that the result holds for $n=7$ as well, subtract row $n(n{\,-\,}1)$ of matrix ${\varvec{X}}$ from row i, where $i=1,2\ldots n(n{\,-\,}1){\,-\,}1$, to yield a new matrix $\hat{\varvec{X}}$. It is straightforward to verify that the first 41 vectors of $\hat{\varvec{X}}$ are linearly independent (i.e., the row rank is 41) and, therefore, the 42 characteristic vectors are indeed affinely independent. Hence, the result also holds for $n=7$, and T2-3 VI is facet defining for any $n\ge 4$. $\square$