Effect of a canopy patch made of streamwise-oriented plates on turbulence in an open-channel flow

Abstract

The paper examines the flow through a highly porous canopy patch made of streamwise-oriented thin plates arranged in a staggered configuration and placed in a rough-bed open channel. This patch geometry contrasts with the patches made of bluff bodies, which are nearly exclusively used in the literature. Particle Image Velocimetry was used to measure the flow upstream, within and downstream of the patch. The canopy patch has the effect of drastically reducing the turbulence level of the incoming flow, especially the turbulence shear stress, which is reduced by 85%. Spectral analysis of the velocity shows that the reduction in turbulent kinetic energy occurs at all length scales. Yet, at the entrance of the patch, the energy from the smallest scales up to the scale of the water surface increases. This suggests a spectral shortcut mechanism by which the large-scale structures of the incoming flow are disintegrated by the group of plates instead of decaying through the energy cascade. The increased small-scale turbulent energy then dissipates through the patch.

1 Introduction

A canopy patch is an isolated group of solid elements in a flow. Such groups of elements are encountered for example as vegetation growing on a river bed, or as a group of trees or of buildings in atmospheric flows.

Investigations that were performed so far on canopy patches show that, similarly to solid bodies, canopy patches induce a wake having a velocity deficit and an increased turbulence. The wake of canopy patches can be divided into a steady-wake region, immediately downstream of the patch, characterised by an absence of vortex shedding, and a following von Karman vortex street characterised by alternative vortex formation, these vortices being on the scale of the patch width [1, 2]. The length of the steady-wake increases with decreasing patch density [1, 2]. In the case of very low density patches, for which the two shear layers on either side of the patch only weakly interact, the von Karman vortex street can be not existent [1] or be replaced by a symmetric vortex street in varicose mode [3]. Overall, the wake length of canopy patches, which can be quantified by the wake recovery length, i.e. the distance downstream of the patch where the streamwise velocity recovers 90% of its original magnitude upstream of the patch [4], is higher for porous patches compared to solid patches of same width. The wake recovery length increases with patch porosity, except for high porosities for which it decreases again [4].

Further, canopy patches distinguish themselves from solid bodies through the phenomenon called bleeding [4, 5], which refers to the flow that seeps out of the patch, not only from the rear, but also at the sides and at the top (in the case of immersed patches [4]) or at the bottom (in the case of suspended patches [6]) of the patch. It is the bleeding at the rear of the patch that is responsible for the much higher wake recovery length of canopy patches compared to solid bodies of same width [4].

Compared to emergent patches (patches spanning the whole flow depth), the flow around submerged patches is complicated by the presence of a shear layer at the top of the patch. This shear layer can interact with the two shear layers on either side of the patch [5].

Porous obstacles, and canopy patches in particular, have two opposite effects on the turbulence. On the one hand they produce turbulence at the length scale of the individual elements. On the other hand, they alter the turbulence of the incoming flow through a so-called spectral shortcut [7], whose global effect is to reduce the turbulence. Large-scale turbulent structures that pass through porous patches are disintegrated by the individual elements of the vegetation into smaller structures. In this way, the energy cascade is shortcut and the incoming large-scale structures dissipate faster. Green [8] for example proposed to model the effect of porous vegetation in the turbulent kinetic energy equation by adding both a source term and a sink term, respectively representing these two effects.

Until now, the patch elements that were used in laboratory studies for modelling vegetation were mostly circular cylinders [4, 6, 9]. For building aerodynamics, cubes are usually used [10, 11]. These elements are bluff bodies, which exert important drag on the flow and induce turbulence production. In such patches, the turbulence-reduction effect mentioned above is not noticeable and was also not especially investigated. However, vegetation patches are composed partly of leaves or blades, which depart significantly from the circular cylinder form. In view of these limitations relative to the bluff body based patch, the present study aims at investigating an alternative canopy patch, for which the turbulence-reduction effect would be maximised, whereas the turbulence-production effect would be minimised. To this aim, streamwise-oriented flat plates were used as patch elements. As streamlined bodies, these plates will induce little drag and turbulence, while they are expected to affect efficiently large-scale turbulent structures of the incoming flow. The objectives are (i) to assess in which extent a turbulence-reduction takes place, (ii) to observe where this turbulence-reduction occurs within the patch and (iii) to characterise the spectral shortcut associated to this turbulence-reduction thanks to velocity spectra measured along the patch. The plates are vertical, rigid and regularly arranged, such that important properties influencing the dynamics of real plants, as flexibility, varying shape and porosity in space, are not considered. Nevertheless, flow processes are expected to be observed, which can also be present in real vegetation patches or in other flow applications. To see the influence of submergence on this particular patch geometry, the canopy patch will be investigated in both emergent and lowly submerged conditions.

Previous experiments measuring flows in canopy patches have been restricted to measurements around the patch or to point measurements (ADV measurement) within the patch, since mechanical and optical access prevented spatially resolved measurements within the patch. The choice of taking streamwise-oriented clear glass plates as patch elements allowed to overcome this limitation by enabling full optical access within the patch. In this way, Particle Image Velocimetry (PIV) could be used to measure the turbulent flow characteristics within the patch, as well as upstream and downstream from the patch.

In a parallel study, a similar group of plates was investigated by means of Large Eddy Simulation (LES) by Gong et al. [12], which focused on the drag of the patch overall and of the individual plates. They showed that drag is mostly exerted by the plates located at the edge of the patch, whereas the plates within the patch have a much lower drag due to a sheltering effect.

The current paper presents the experimental results for two different incoming velocities and for the glass-plate patch being either emergent or lowly submerged. After describing the set-up and the flow parameters (Sect. 2), the experimental results are presented in Sect. 3, and discussed further in Sect. 4.

2 Experimental methodology

2.1 Patch geometry and flow conditions

The experiments took place in the Total Environment Simulator at the University of Hull (UK), a 10 m long and 6 m wide flume. The experiments were conducted in a central portion of the flume of width $B_0=3$ m and delimited by vertical side walls, which were transparent in the measurement section. The bed of the flume was covered with gravel having a median diameter of approximately 2 cm and was screeded flat. The slope of the bed was $S_0=0.0015$.

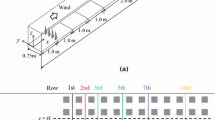
The canopy patch consists of 35 vertical glass plates arranged in a staggered configuration and was installed in the middle of the channel above the gravel bed and at 7 m from the flume inlet. Each plate is 1 mm thick, with a length of $l=4$ cm and a height of $k=20$ cm. The total length of the patch is $L=332$ mm and the width $B=264$ mm. The detailed geometric arrangement of the patch is sketched in Fig. 1. The plates were fixed onto a plate which was then covered by the gravel. The blocking ratio of the canopy patch, defined as the projected solid area divided by the total frontal area, is $BR=6.4$%. The patch density, defined as the ratio of the planar area of the patch’s elements and the total planar area of the patch, is $\phi =0.0166$ (computed on the basis of a repetitive pattern composed of one plate and of size $73\times 33$ mm$^2$). It is similar to the most porous patch used by Taddei et al. [4] ($BR=15$%, $\phi =0.0175$) and to one of the patch density used by Zhang et al. [2] ($\phi =0.013$).

Fig. 1

Geometrical arrangement of the canopy patch. On the bottom of the figure the fields of view (FOV) of the two measurements used for planes A and B (FOVs 1 and 2), which were then merged for the presentation of the results, and of the single measurement used for plane C (FOV 3), are indicated

The longitudinal axis is denoted by x and has its origin at the front edge of the patch, y is the lateral axis with origin on the symmetry line of the patch and z is the vertical axis with the origin at the crest of the gravel bed. The velocities in these three directions are denoted u, v and w respectively. An overbar denotes the time-averaging operator and primes the fluctuation part of a given flow quantity.

Three flow configurations were investigated by varying the incoming velocity and the flow depth: for test cases V1Full (velocity 1, full depth) and V2Full (velocity 2, full depth) the canopy patch extends through the full water depth $h=20$ cm, which is equal to the plate height k, and the bulk velocity of the incoming flow is $U=0.42$ m.s$^{-1}$ and $U=0.68$ m.s$^{-1}$ respectively. For test case V2Part (velocity 2, partial depth) the water depth is $h=30$ cm, such that the canopy patch extends through only the lower 2/3 of the water depth, and the velocity is the same as for test case V2Full. The flow conditions of the incoming flow are summarised in Table 1, where the Reynolds number, the Froude number and the shear velocity $u_*$ are given. The shear velocity $u_*$ was determined from the vertical profile of turbulent shear stress (see Fig. 2 later). The equivalent sand-grain size of the rough bed was estimated at $k_s=7$ mm, by fitting the vertical profile of velocity $\overline{u}(z)$ upstream of the patch with a logarithmic law.

Table 1 Incoming flow conditions for the three test cases: water depth h above the gravel crest, discharge Q, bulk velocity $U=Q/(hB)$, Reynolds number $\text {Re}=hU/\nu$, Froude number $\text {Fr}=U/\sqrt{gh}$ and shear velocity $u_*$ (based on the maximum of the turbulent shear stress profile)

2.2 PIV measurement

The velocity field was measured in three longitudinal-vertical planes (Fig. 1) using a 2D PIV set-up. The beam of a $2 \times 120$ mJ pulsed laser was guided through a light-tube beneath the water surface to illuminate the flow from downstream, generating a laser sheet of 5 mm effective thickness. A camera with a resolution of $2320 \times 1726$ px$^2$ and equipped with a 65 mm lens was placed in a torpedo immersed in the still water between the separation walls and the actual walls of the flume. The camera looked perpendicular to the laser sheet. Laser and camera were mounted on a carriage, which could be moved at different positions. As the plates were transparent and thin, the distortion they induced on the camera image was negligible and measurements could be carried out within the group of plates. The measurement planes were located on the left-side of the patch ($y>0$), as depicted in Fig. 1: Plane A is between the symmetry line and the adjacent row of plates on the left ($y=8$ mm), plane B is between the 3rd and 4th row left of the symmetry line ($y=58$ mm) and plane C is between the 7th and 8th row left of the symmetry line ($y=124$ mm).

For planes A and B, measurements were completed at two longitudinal positions with some overlap (FOVs 1 and 2 indicated in Fig. 1), and the velocity vector fields were then merged (in the overlap region of the two FOVs, an average of the two measurements was made). The measurement of planes C was performed at a single position (FOV 3). For each plane, 16000, 12800 and 24000 samples were recorded for V1Full, V2Full and V2Part respectively, with sample frequencies of 50 Hz, 50 Hz and 20 Hz respectively. This corresponds to a number of bulk time units (h/U) of 1000, 1100 and 1400 respectively. The water was seeded with 180 ${\upmu \textrm{m}}$ diameter particles of density 0.99 g.cm$^{-3}$ (Plascoat Talisman 20).

To eliminate thin laser reflections ($\approx 1$ mm wide) at the edges of the glass plates, the raw images were pre-processed with a morphological opening filter based on the Matlab function imopen, which detected the stripes due to the reflections and removed them. The images were then processed with the Davis10 PIV-software of LaVision using an interrogation window of $48 \times 48$ px$^2$ and an overlap of 50%, yielding a grid resolution of 4.3 mm ($=0.11 l$) in both x- and z-directions.

2.3 Characteristics of the flow upstream of the patch

Figure 2 shows the vertical profiles of the turbulent shear stress upstream of the canopy patch at $x/L=-0.5$ for the three test cases. Due to the presence of surface waves, the measurements could not be performed till the water surface. The profiles have their maximum above the gravels’ crest, which is common for boundary layers on rough beds (e.g. [13]), and can be explained by the presence of dispersive shear stresses [14, 15], i.e. spatial heterogeneity in the horizontal plane, which could not be measured here. Above the maximum, the turbulent shear stress profile is not linear, which could be explained by the presence of secondary currents. Indeed, secondary currents are known to induce convex and concave shapes of the turbulent shear stress profile for upward and downward flow regions respectively [16, 17]. The friction velocity $u_*$, used subsequently to normalise the turbulent stresses, was determined by the maximum value of the turbulent shear stress, since an extrapolation to the top of the gravel bed [15] was difficult to achieve due to the non-linearity of the turbulent shear stress profile.

Fig. 2

Vertical profiles of the turbulent shear stress upstream of the canopy patch at the position $x/L=-0.5$, normalised by the maximum value, for the three test cases

With respect to the aspect ratios $B_0/h$ and the bed roughness, the present flows would necessitate about 100h to become fully-developed [18, 19]. As the patch is located at 35h for V1Full and V2Full and at 23h for V2Part from the entry of the channel, we expect the flow arriving at the patch to be not fully-developed. However, the turbulent shear stress profile (Fig. 2) do not feature a zone of zero-value in the upper part, which would indicate that the boundary layer has not reached the water surface [20]. Therefore, the flows can still be considered as not too far from being fully-developed.

3 Results

The left-side panels in Fig. 3 show the normalised time-averaged longitudinal velocity $\overline{u}/U$ in plane A for the three test cases. Contrary to bluff body based patches, no significant velocity decrease is observed in the near wake of the patch. For the submerged case V2Part, a slight velocity increase occurs above the patch, of approximately +4% at $z/k=1.2$ (Fig. 3e).

Fig. 3

Time-averaged longitudinal (left column) and vertical (right column) velocities, normalised by the bulk velocity U, in plane A for the three test cases

The normalised time-averaged vertical velocity $\overline{w}/U$ in plane A is shown in the right-side panels of Fig. 3. The alternation of upwards and downwards flow close to the water surface for the two cases where the patch spans the full depth (V1Full and V2Full) reveals the presence of stationary surface waves. The wavelength of these standing waves increases with the flow velocity (approx. 0.3L for V1Full and 0.8L for V2Full). For the test case where the patch is submerged (Fig. 3f), no stationary waves are observed at the free-surface; instead, the flow is deflected upwards at the front tip of each plate, revealing vertical bleeding.

Such stationary waves associated with periodic solid elements can be explained by a resonance between natural free-surface waves and the wave length of the periodic solid elements [21]. The dispersion relation for deep water waves is $\lambda _0=2\pi c^2/g$, where $\lambda _0$ is the wave length, c the wave celerity, and g the gravity acceleration. For a stationary wave, the wave celerity is equal to the flow velocity: $c=U$. We thus obtain wavelengths $\lambda _0$ of 0.33L and of 0.90L for V1Full and V2Full respectively, which correspond fairly well to the wave lengths observed. Thus, it seems that the free-surface resonates with the length of two plates for V1Full and with the entire length of the patch for V2Full.

Figure 4 shows the normalised turbulent shear stress $-\overline{u'w'}/u_*^2$ (left panels) and the normalised longitudinal turbulent normal stress $\overline{u'u'}/u_*^2$ (right panels) in plane A for the three test cases. It can be seen that the passage through the patch induces a significant decrease in these turbulence stresses. This decrease takes place mostly in the first quarter of the patch ($x/L \approx 0.25$), over the span of about two plates. The turbulence reduction is not affected by the fact that the patch is emergent or submerged.

For test case V2Part (Fig. 4e), an additional source of turbulence occurs at the top of the plates, visible as a brighter trail in the contour plot of $-\overline{u'w'}$ above and mainly downstream of the patch. It corresponds to a shear layer that forms between the flow above the group of plates, which accelerates lightly as mentioned above, and the flow underneath, which slows down slightly, giving rise to a vertical profile of velocity with an inflection point (not shown). Such shear layers are characteristic of submerged canopy patches [4, 9]. The autocorrelation and the two-point correlation of the streamwise velocity within the shear layer (not shown) reveal that no large-scale quasi-periodic Kelvin-Helmholtz structures are present. The shear parameter of this shear layer, $\lambda =(U_2-U_1)/(U_2+U_2)$ – where $U_1$ and $U_2$ are the velocities at the edge of the shear layer on the low- and high-speed side respectively – is about 0.07 at $x/L=1.2$. It was shown in the case of lateral shear layers in shallow open-channel flows that Kelvin-Helmholtz structures appear only for shear parameters higher than a critical value of $\lambda _{\text {crit}} \approx 0.3$ [22, 23]. According to Dupuis et al. [23], below this critical value the ambient turbulence inhibits the Kelvin-Helmholtz structures formation. The same mechanism is expected to occur in shear layers at the top of submerged canopies.

Fig. 4

Turbulent shear stress (left column) and longitudinal normal stress (right column), normalised by $u_*^2$, at plane A for the three test cases

For a more quantitative analysis of the flow behaviour along the patch, Figs. 5a and b show the longitudinal profiles $\overline{u}(x)$ in plane A, at $z/k=0.2$ (left panels) and at $z/k=0.8$ (right panels), normalised by the value upstream of the patch at $x/L=-0.5$ and at the same elevation. For V2Full, a 5% increase in $\overline{u}$ is observed upstream to downstream of the patch at $z/k=0.2$ (Fig. 5a), whereas at $z/k=0.8$ (Fig. 5b), $\overline{u}$ reduces by 2%. The increase in velocity in the central plane of the patch implies that water is entering the patch from the sides, suggesting a suction effect of the patch, which is the opposite of what is usually observed in canopy patches (bleeding, i.e. flow outwards through the sides of the patch [4, 9]). The two other test cases feature a velocity reduction in plane A upstream to downstream of the patch, but always less than 5%.

For comparison, Taddei et al. [4] observed a velocity decrease of about 25% behind a canopy patch of density $\phi =0.0175$, Zhang et al. [2] a decrease of 20 to 60% (depending on the patch length) behind a canopy patch of density $\phi =0.013$ and Liu et al. [9] a decrease of about 25% behind a canopy patch of density $\phi =0.021$. The much lower velocity deficit in the wake of the present patch of density $\phi =0.0166$ can be explained by the streamlined shape of the canopy elements, which induce a very low drag, compared to the bluff bodies and high-drag inducing elements (circular cylinders) used in the above studies. The fact that for test case V2Full a slight velocity increase is even observed could be due to the reduced turbulence in the wake region. Indeed, the turbulent shear stress becoming much weaker, the flux of longitudinal momentum towards the bed is reduced, and this reduction of momentum sink leads to velocity increase. Why this increase was only observed for V2Full is not clear for now.

Within the patch, the presence of the plates induces a periodic local velocity increase in the lateral space between two plates (Fig. 5a and b). This is likely to be due to the contraction of the cross-section linked to the plate thickness and to the boundary layers that develop on the plates: Assuming a 1/7-power-law velocity profile for the turbulent boundary layer growing on the plates [24], the displacement thickness at the end of the plate is about $\delta ^*=0.02l/Re_l^{1/7}=0.2$ mm for each test case, such that the blocking ratio due to the plate thickness and the boundary layer is about 4%. The latter corresponds indeed to the local increase in $\overline{u}$ in the interstice between two plates (Fig. 5a and b). These local velocity variations in the interstices between plates can also be observed in the LES simulation of Gong et al. [12].

Figure 5c–h show the turbulent stresses profiles $-\overline{u'w'}(x)$, $\overline{u'u'}(x)$ and $\overline{w'w'}(x)$ at the same locations as in Fig. 5a and b and also normalised by their value upstream of the patch. Consider first the changes upstream to downstream of the patch. For the turbulent shear stress $-\overline{u'w'}$ (Fig. 5c and d), the reduction through the group of plates is drastic – about 85% at $z/k=0.2$ and close to 100% at $z/k=0.8$. The reduction of $\overline{u'u'}$ (Fig. 5e and f) is about 50% close to the bottom and about 15–35% close to the top of the plates, whereas for $\overline{w'w'}$ (Fig. 5g–h) it is about 80% and 50% respectively.

Fig. 5

Longitudinal profiles in plane A at $z/k=0.2$ (left column) and $z/k=0.8$ (right column) of the longitudinal velocity (a–b), of the turbulent shear stress (c–d), of the longitudinal (e–f) and the vertical (g–h) turbulent normal stress, all normalised by their values at $x/L=-0.5$

Consider now the evolution within the patch, starting with the position close to the bed, $z/k=0.2$ (left panels). The turbulent shear stress $-\overline{u'w'}$ (Fig. 5c) reduces continuously. It starts to decrease about 0.4L upstream of the patch and then drops drastically from the leading edge of the first plate to the leading edge of the second plate. From the third plate onwards, the reduction rate decreases significantly. For $\overline{u'u'}$ (Fig. 5e), and to a lesser extent for $\overline{w'w'}$ (Fig. 5g), a local increase is first observed at the leading edge of the first plate. This jump is lower when the plates are submerged. After the first plate, $\overline{u'u'}$ and $\overline{w'w'}$ reduce drastically, similarly to the turbulent shear stress at that position. The reduction rate of the two normal stresses then decreases along the group of plates but remains non negligible till the end and even downstream of the patch, particularly for $\overline{w'w'}$.

Close to the plates’ tip, at $z/k=0.8$ (Fig. 5d, f and h), the normalised profiles of the turbulent stresses display similar evolutions as at $z/k=0.2$, but with higher variability and differences between the three flow cases. This is likely due to free-surface effects, as the influence of waves. The turbulent shear stress $-\overline{u'w'}$ is reduced to almost zero downstream of the patch (Fig. 5d). For $\overline{u'u'}$, an increase occurs at the entry within the group of plates (Fig. 5f), but the maximum is reached in the gap between the first two plates, i.e. further downstream than what is observed at $z/k=0.2$ (Fig. 5e). $\overline{u'u'}$ then decreases till the end of the group of plates. $\overline{w'w'}$ (Fig. 5h) shows the same trend as $\overline{u'u'}$, but the peak also occurs a bit later, at the level of the second plate.

To analyse the flow variability in the transverse direction within the patch, Fig. 6 shows the turbulent stresses $-\overline{u'w'}$ and $\overline{u'u'}$ in planes A, B and C for test case V2Part. The general flow patterns in planes B and C are similar to the ones in plane A. However, the drop in turbulence through the patch decreases towards the edge of the patch: at $z/k=0.25$, the decrease in $-\overline{u'w'}$ is of 87%, 64% and 30% for planes A, B and C respectively and the decrease in $\overline{u'u'}$ is of 64%, 12% and 6% respectively.

Fig. 6

Turbulent shear stress (left column) and longitudinal turbulent normal stress (right column), normalised by $u_*^2$, for test case V2Part and in the three measured planes A, B and C

In plane C, a local increase in $\overline{u'u'}$ takes place at the location of the first plate (Fig. 6f), similarly to the observation for plane A (right panels in Fig. 4). However, an increase in $\overline{u'u'}$ at the first plate is not present for plane B (Fig. 6d). For test case V1Part (not shown), a similar increase in $\overline{u'u'}$ in planes A and C and an absence of increase in plane B was also observed (for test case V2Full, the planes B and C are not available). The increase in $\overline{u'u'}$ in plane A and C may be related to a lateral wake developing on the left-side of the plate due to a small lateral component of the incoming flow (possibly resulting from strong secondary currents). This would explain why in plane B, which is positioned on the right-side of the first plate, an increase in $\overline{u'u'}$ is not observed. From this perspective, the local peaks of the turbulent normal stresses observed at the entrance of the patch would not be a general feature of this type of patch, but due to a slight lateral component of the incoming flow.

In order to analyse how the passage of the flow through the patch affects turbulence at different length scales, the power spectral densities (PSD) of the longitudinal velocity fluctuation were computed for test case V1Full at $z/k=0.2$ (Fig. 7a) and $z/k=0.8$ (Fig. 7b) for different streamwise positions in plane A. The frequencies associated to different length scales (using a Taylor hypothesis with the convection velocity equal to the bulk velocity U) are also indicated in the figure: the water depth h, 10h, the plate length l and the lateral interstice within the patch, $s_y/2$. As can be seen, scales smaller than this lateral interstice could not be resolved. We also exclude from the following analysis the region $f<U/10h$, since these large length scales are physically less relevant, being probably affected by the dynamics of the hydraulic system. Note that in the high frequency region ($f>20$ Hz), the spectra are slightly affected by aliasing. Despite these limitations, some clear trends can be discerned. First, comparing the spectra upstream and downstream of the patch at $z/k=0.2$ (red and pink profiles in Fig. 7a), it can be seen that the reduction of turbulent energy occurs at all length scales between $s_y/2$ and 10h. Looking now to the evolution of the spectra between the two positions upstream of the patch at the same elevation (comparing the red and green profiles in Fig. 7a), it can be observed that the decrease in $\overline{u'u'}$ which occurs upstream of the group of plates (see Fig. 5e) is mostly due to a reduction of the energy in the length scales larger than the water depth ($f<U/h$). In parallel, the turbulent energy increases in the scales smaller than the plate length ($f>U/l$), while the region between U/h and U/l is nearly not affected. In the middle of the first plate (blue profile), where $\overline{u'u'}$ is at its maximum (see Fig. 5e), the energy has increased at all the scales between $s_y/2$ and 10h. From this position on, the energy decreases progressively along the canopy patch at all length scales between $s_y/2$ and 10h (yellow and pink profiles).

Fig. 7

Power spectral density (PSD) of the longitudinal velocity fluctuation for test case V1Full at a $z/k=0.2$ and b $z/k=0.8$ at different streamwise positions in plane A. Note that $x/L=0.05$ is at the middle of the first plate and $x/L=0.09$ at the middle between the first and the second plate, corresponding respectively to the maximum of $\overline{u'u'}$ at $z/k=0.2$ and $z/k=0.8$. Also indicated are the frequency associated to different length scales (using a Taylor hypothesis with convection velocity U): the water depth h, 10 times the water depth, the plate length l and the interstice within the group of plates $s_y/2$

Close to the plates’ tip, at $z/k=0.8$ (Fig. 7b), the evolution of the spectra is similar. However, overall there is no significant energy decrease upstream to downstream of the patch, as could also be seen in Fig. 5f (red curve). Moreover, compared to the spectra at $z/k=0.2$, the energy in the small length scales ($f>U/l$) are growing until $x/L=0.09$ (located in the gap between the first and second plate, i.e. where $\overline{u'u'}$ is maximum at this vertical position, see Fig. 5f) and the energy of these small scales remains higher than it was upstream of the patch even at the exit of the patch.

A similar behaviour was observed for the spectra of the vertical velocity fluctuation (not shown).

4 Discussion

The investigated highly porous canopy patch made of thin streamwise-oriented plates has the effect of drastically reducing the turbulence of the incoming flow. A striking observation is how the turbulence, and especially the turbulent shear stress, reduces very rapidly when entering the group of plates. After 0.25L (1.5 plates) the turbulent shear stress $-\overline{u'w'}$ drops by more than 80% and then remains quite constant. However, this does not imply that the plates further downstream do not play a significant role. In addition, the normal stresses continue to decrease after 0.25L.

The turbulence-reducing behaviour of the canopy patch appears to be similar to the one of turbulence-reducing devices that are commonly used in fluid mechanics. For example, in wind tunnel and water channel facilities, grids, screens and honeycombs are commonly placed upstream of the test section to ensure a low turbulence level of the flow entering in the test section [25]. In open-channel flow facilities, row of plates (also called guide vanes) are sometimes preferred [20], as they induce less flow resistance and therefore less free-surface perturbation. Turbulence manipulators have also been used in the context of skin drag reduction, especially Large-Eddy Breakup Devices (LEBU), which consist of one or several plates mounted parallel to the flow and placed close and parallel to the wall [26, 27].

As stated by Loehrke and Nagib [28], the main mechanism responsible for turbulence reduction through honeycombs is “the thwarting of the transverse velocity components by the honeycomb side walls”. Loehrke and Nagib [28], who were able to carry out some flow visualisation within honeycombs, also stated that “the major part of the damping and suppression of the upstream turbulence is achieved in the early section of the flow passages inside the [honeycomb]”, an observation we also made with the present canopy patch. Kulkarni et al. [29], who performed a CFD simulation of flows through honeycombs, confirmed that the reduction rate of turbulence decreases along the honeycomb. From a distance of eight times the honeycomb cell size, the decay rate of the turbulence becomes relatively low. Kulkarni et al. [29] revealed in addition that an increase in turbulence takes place just at the entrance of the honeycomb, as similarly observed in the present patch in plane A and C. However, as mentioned above, we are not sure that it is a characteristic behaviour of such patches, as it could be due to a lateral component of the incoming flow.

The present canopy patch resembles in its geometry some of these turbulence-reducing devices, especially the LEBU devices – except that the plates are normal to the channel bed and not parallel to it – and the guide vanes. The turbulence reduction factor, which is used to characterise the efficiency of grids or honeycombs in reducing turbulence [25], is defined as $f_i=(u_{i,\text {rms}})_d/(u_{i,\text {rms}})_u$ where $u_{i,\text {rms}}$ is the root mean square of the velocity in the i-th space direction and the indices u and d refer to the states upstream and downstream of the device (or with and without the device). The turbulence reduction factors of the present canopy patch in the three test cases are $f_u \approx 0.7$ and $f_w \approx 0.5$ at $z/k=0.2$, and $f_u \approx 0.9$ and $f_w \approx 0.7$ at $z/k=0.8$, and therefore similar to those of efficient screens and honeycombs [25].

Physically, the turbulence-reduction effect of the group of plates can be explained by the impingement of lateral turbulent movement against the individual plates. Figure 8 illustrates this for the case of a simpler canopy patch made of a unique row of parallel plates of length $L_x$, equally spaced by the distance s. Such a plate configuration would be effective for disintegrating vortices whose axes are in the plane of the plates (for example the ones with longitudinal or vertical axes, as sketched in Fig. 8). Consider a circular vortex with its axis in the plane of the plates (vertical, longitudinal, or between the two), with diameter d and maximum radial velocity $u_r$, which is convected with a convection velocity $U_c$ towards one plate (the plate being in the middle of the vortex). The vortex will be destroyed if the lateral flow induced by the vortex impinges against the plate. It can be considered that the plate is effective at destroying the vortex if the passage time through the plate is comparable to the time taken for one rotation of the vortex. If the passage time is much smaller, then the effect of the plate would be just to induce a slight distortion of the vortex due to the plate wake. The passage time of the centre of the vortex through the plate is given by $t_p=L_x/U_c$. The time for the vortex to turn once is $t_v \approx \pi d/u_r$. We can then consider that the plate will be effective to disintegrate the vortex if the number:

$$\begin{aligned} E=\frac{L_x}{d} \, \frac{u_r}{U_c} \end{aligned}$$

(1)

is large enough.

Fig. 8

A group of streamwise oriented plates interacts with circular vortices having their axes in the plane of the plates

In the present case, this number can only be estimated. The radial velocity $u_r$ can be roughly approximated by the root mean square of the streamwise velocity. At $z/k=0.2$, $u_{\text {rms}}$ is about 0.1 m.s$^{-1}$ for V2Full and V2Part and about 0.06 m.s$^{-1}$ for V1Full. The width d of the typical vortices can be estimated by the lateral correlation length of the velocity. To this end, we can rely on the study of Detert et al. [30], who computed the mean width of a streak based on the distance between zero-crossings of the two-point correlation in lateral direction. According to them, the streak width is about $3k_s$ close to the bottom, where $k_s$ is the equivalent sand roughness of the bed (estimated in the present case at $k_s=7$ mm). Taking as length $L_x$ the length within the patch from which the turbulence is drastically reduced, i.e. 0.25L, and as convection velocity $U_c$ the bulk velocity U, we obtain $E \approx 0.6$ for the three test cases. Thus, a E-value of this order seems to be enough for effectively reducing the turbulence of the incoming flow, and this corresponds to a rotation of approximately one-fifth turn ($E/\pi$) of the vortex. However, more investigations over a wider range of parameters would be necessary to confirm this simple scaling.

Concerning the lateral spacing of the plates s, an effective turbulence reduction is expected to take place if each vortex encounters at least one plate. This would require that $s \approx d/2$, where d is the typical size of the vortex.

The canopy patch investigated in this study was slightly different from the one sketched in Fig. 8, since the plates are discontinuous. The questions whether interrupted plates are advantageous or not to reduce turbulence, and what is the influence of the spatial configuration (square or staggered) need further investigation to be solved. The possible advantage of interrupted plates is to reduce the boundary layer growth and therefore the wake and the turbulence induced by the plates.

Concerning vortices whose axes are normal to the plates, the interaction mechanisms with the plates are likely to be different, but the disaggregation of the vortex can still be effective. Marshall [31] for instance showed how the cutting of a vortex by a blade placed normal to the vortex axis can lead to a breakup of the vortex.

The weaker reduction in turbulence measured at the edge of the canopy patch (plane B and C in Fig. 6) may have two non-exclusive explanations: (i) the reduction in length of the patch at this outer location (only three plates instead of five – this would then confirm the important role of the downstream plates), and (ii) an edge effect, since the vortices arriving near the last row of plates are only partly affected by the plates, and the vortices remaining outside of the patch retain their turbulent energy.

5 Conclusion

The effect of a highly porous canopy patch made of thin streamwise-oriented and bed-normal plates on a rough-bed turbulent open-channel flow was investigated by means of PIV measurements. Two incoming velocities were tested and the patch was either emergent or lowly submerged. The canopy patch affects only slightly the time-averaged streamwise velocity. In one test case (V2Full), it even induces an increase in streamwise velocity within the patch and in its wake, in opposition to what is usually observed in canopy patches. But the main feature of this patch is that it acts as a turbulence-reducer of the incoming flow, resembling the behaviour of turbulence-reduction devices like LEBU devices or very effective honeycombs.

Close to the bed, where the turbulence of the incoming flow is the highest, the group of plates reduces the turbulent shear stress by 85%, the longitudinal turbulent normal stress by 50% and the vertical turbulent normal stress by 80%. The drop of turbulence occurs mainly in the first quarter of the canopy patch. Yet, for the turbulent normal stresses, a local increase is detected at the entrance in the canopy patch, for reasons that are not fully understood. A possible explanation is a slight lateral component of the incoming flow, implying that this increase is not a general feature of such a patch.

Spectral analysis of the velocity shows that close to the bed (where the turbulence of the incoming flow is the highest), the energy upstream to downstream of the patch is reduced at all length scales ranging from the lateral interstice $s_y/2$ to ten times the water depth. However, inside the patch, an increase in energy occurs at the small length scales (especially at the length scales lower than the plate length l). The increased energy in the small scales then progressively dissipates along the group of plates. This suggests a spectral shortcut mechanism, meaning that turbulence dissipation does not occur through the direct energy cascade but through the action of solid elements which disintegrate the large structures.

The ability of such a highly porous canopy patch made of plates to reduce turbulence was characterised by a non-dimensional number, which compares the passage time of a vortex of typical size along the patch and the turning time of the vortex. If this number is high enough, then the lateral motion that the vortex creates impinges against the plate, leading to the destruction of the vortical structure. The pertinence of this number needs to be validated though by means of a parametric study.

The turbulence reduction is not significantly influenced by the submergence of the canopy patch, which affects more the free-surface and the time-averaged flow field. When the patch reaches the water surface, stationary surface waves form, whose wavelength increases with the flow velocity. These waves are absent when the patch is submerged. Instead, in this case, vertical bleeding is observed on the top of the patch, as well as the formation of a shear layer, which is typical for submerged canopy patches.