On strongly dependent zero-inflated INAR(1) processes

Abstract

We consider INAR(1) processes modulated by an unobserved strongly dependent $0-1$ process. The observed process exhibits zero inflation and long memory. A simple method is proposed for estimating the INAR-parameters without modelling the unobserved modulating process. Asymptotic results for the estimators are derived, and a zero-inflation test is introduced. Asymptotic rejection regions and asymptotic power under long-memory alternatives are derived. A small simulation study illustrates the asymptotic results.

1 Introduction

Time series that consist of counts often exhibit zero inflation (see e.g. Young et al. 2022 and references therein). For instance, instrumental detection limits can lead to an increased number of zeroes. Also ecological data sets tend to contain a large proportion of zeroes that are classified by ecologists as "false zero counts" (Martin et al. 2005). Examples can also be found in other areas such as medicine, psychology, traffic or insurance, among others (Young et al. 2022). In this paper we consider zero inflation generated by a long-memory process. This is in contrast to the statistical literature where zero inflation processes are usually assumed to be iid or at most weakly dependent. The issue of zeroes occuring in long batches has been discussed in the recent applied literature. In many applications, zero inflation is related to missing values due to faulty measurement devices, instrumental detection limits or biological reasons. Also, the occurence of batches of zeroes may be caused by other unobserved time series (see e.g. Che et al. 2018). A natural approach to handling such data is to use models that exhibit long-range dependence with respect to zero inflation. Note that, in a related paper, Möller et al. (2018) discuss models that tend to produce relatively long runs of zeroes (e.g. ZT-Bar(1) processes). However, asymptotically, the autocorrelation function of their models decays exponentially and is thus summable. In contrast, the models considered here have long memory in the sense that autocorrelations decay hyperbolically and are not summable. Note also that a long-memory INAR model, a so-called fractional INARFIMA, is suggested in Quoreshi (2014). However, the INARFIMA model, as specified by Quoreshi, is not well defined, because it relies on a fractional thinning operator that yields infinity when applied to non-negative sequences.

More specifically, we consider INAR(1) processes modulated in a multiplicative way by an unobserved strongly dependent $0-1$ process. Thus, the observed process is assumed to be of the form

$$\begin{aligned} Y_{j}=W\left( j\right) X_{j} \left( j=1,2,...\right) \end{aligned}$$

(1)

where the stationary 0–1-process W(j) ($j\in {\mathbb {N}}$) is independent of the INAR(1) process $X_{j}$ ($j\in {\mathbb {N}}$), and the autocovariances $\gamma _{W}(k)=cov(W(j),W(j+k))$ are such that

$$\begin{aligned} \gamma _{W}\left( k\right) \underset{k\rightarrow \infty }{\sim }c_{\gamma ,W}k^{2d-1}y \end{aligned}$$

(2)

for some constants $0<c_{\gamma ,W}<\infty$, $d\in (0,\frac{1}{2})$. Note that Eq. (2) implies that the spectral density

$$\begin{aligned} f_{W}\left( \lambda \right) =\frac{1}{2\pi }\sum _{k=-\infty }^{\infty } \gamma _{W}\left( \left| k\right| \right) e^{-ik\lambda } \end{aligned}$$

(3)

has a pole at the origin, of the form

$$\begin{aligned} f_{W}\left( \lambda \right) \underset{\lambda \rightarrow 0}{\sim } c_{f,W}\left| \lambda \right| ^{-2d} \end{aligned}$$

(4)

where $c_{f,W}=c_{\gamma ,W}\pi ^{-1}\Gamma (2d)\sin (\pi /2-\pi d)$ (Zygmund 1968; Beran et al. 2013, Theorem 1.3). We will use the notation

$$\begin{aligned} p_{0,W}=P\left( W(j)=0\right) =1-P\left( W\left( j\right) =1\right) \end{aligned}$$

(5)

More specifically, we will assume $X_{j}$ to be a Poisson INAR(1) process (McKenzie 1985; Al-Osh and Alzaid 1987) defined by

$$\begin{aligned} X_{j}=\alpha \circ X_{j-1}+\varepsilon _{j} \end{aligned}$$

where $\alpha \in (0,1)$, and $\varepsilon _{j}$ are iid Poisson variables with intensity $\lambda$. The thinning operator "$\circ$" (Steutel and Van Harn 1979; Gauthier and Latour 1994) means that, conditionally on $X_{j-1}$, $\alpha \circ X_{j-1}$ is a binomial random variable generated by $X_{j-1}$ Bernoulli trials with success probability $\alpha$. The unknown parameters are $\alpha$ and $\lambda$. Alternatively, one may also use the parameterization $\alpha$ and $\mu _{X}=E(X_{j})=\lambda /(1-\alpha )$.

Two questions regarding model Eq. (1) are addressed in this paper: a) estimation of the INAR(1) paramters $\alpha$ and $\mu _{X}$ without modelling the unobservable process W; b) testing for zero-inflation as specified by model Eq. (1).

Since the introduction of INAR models by McKenzie (1985) and Al-Osh and Alzaid (1987), the literature on integer-valued time series based on binomial thinning (Steutel and Van Harn 1979) has grown steadily. Some references are Du and Li (1991); Gauthier and Latour (1994); Da Silva and Oliveira (2004); Freeland and McCabe (2004, 2005); Gourieroux and Jasiak (2004); Jung et al. (2005); Puig and Valero (2007); Drost et al. (2008); Park and Kim (2012); Pedeli and Karlis (2013); Schweer and Weiss (2014); Pedeli et al. (2015) and Jentsch and Weiss (2019). Excellent overviews on integer-valued processes and references can be found for instance in Weiss (2018) and Davis et al. (2021). Testing for zero-inflation in INAR(1) models is discussed in a recent paper by Weiss et al. (2019). Also see Pavlopoulos and Karlis (2008); Barreto-Souza (2015); Weiss (2013), and Bourguignon and Weiss (2017) for over- and underdispersed INAR processes. References to long-memory processes can be found for instance in Beran (1994); Giraitis et al. (2012); Beran et al. (2013) and Pipiras and Taqqu (2017).

The paper is organized as follows. Basic results are established in Sect. 2. Question a) is addressed in Sect. 3. In Sect. 4, a test is developed for the null hypothesis of a non-inflated INAR(1) process against the alternative of a zero-inflated process as defined in Eq. (1). Asymptotic rejection regions are derived, as well as an asymptotic lower and upper bound for the power of the test. A small simulation study in Sect. 5 illustrates the results. Final remarks in Sect. 6 conclude the paper. Proofs are given in the appendix.

2 Basic results

2.1 Expected value and autocovariance function

Let $Y_{j}$ be generated by model Eq. (1) where $X_{j}$ is a Poisson INAR(1) process. We will use the notation ${\textbf{1}}\{A\}$ for the indicator function of a set (or event) A. Moreover, we define

$$\begin{aligned} p_{0,W}= & {} P\left( W\left( j\right) =0\right) \text {, }p_{0,Y}=P\left( Y_{j}=0\right) \text {, }p_{0,X}=P\left( X_{j}=0\right) , \\ \mu _{X}= & {} E\left( X_{j}\right) \text {, }\mu _{W}=E\left[ W\left( j\right) \right] \text {, }\mu _{Y}=E\left( Y_{j}\right) , \\ \gamma _{X}\left( k\right)= & {} cov\left( X_{j},X_{j+k}\right) \text {, } \gamma _{W}\left( k\right) \\= & {} cov\left( W\left( j\right) ,W\left( j+k\right) \right) \text {, }\gamma _{Y}\left( k\right) =cov\left( Y_{j},Y_{j+k}\right) \text { (}j,k\ge 0\text {).} \end{aligned}$$

Also, for $k<0$, we set $\gamma _{X}(k)=\gamma _{X}(-k)$, $\gamma _{W} (k)=\gamma _{W}(-k)$, $\gamma _{Y}(k)=\gamma _{Y}(-k)$, and, for $\lambda \in [-\pi ,\pi ]$,

$$\begin{aligned} f_{X}\left( \lambda \right)= & {} \frac{1}{2\pi }\sum _{k=-\infty }^{\infty } \gamma _{X}\left( k\right) e^{-ik\lambda } \\ f_{W}\left( \lambda \right)= & {} \frac{1}{2\pi }\sum _{k=-\infty }^{\infty } \gamma _{W}\left( k\right) e^{-ik\lambda } \\ f_{WX}\left( \lambda \right)= & {} \frac{1}{2\pi }\sum _{k=-\infty }^{\infty } \gamma _{W}\left( k\right) \gamma _{X}\left( k\right) e^{-ik\lambda } \\ f_{Y}\left( \lambda \right)= & {} \frac{1}{2\pi }\sum _{k=-\infty }^{\infty } \gamma _{Y}\left( k\right) e^{-ik\lambda } \end{aligned}$$

Due to mutual independence and stationarity of the two processes $X_{j}$ and W(j) we have

$$\begin{aligned} \mu _{Y}=\mu _{W}\mu _{X} \end{aligned}$$

and

$$\begin{aligned} \gamma _{Y}\left( k\right)&=E\left[ W\left( 0\right) W\left( k\right) \right] E\left[ X_{0}X_{k}\right] -\mu _{W}^{2}\mu _{X} ^{2} \nonumber \\&=\mu _{X}^{2}\gamma _{W}\left( k\right) +\mu _{W}^{2}\gamma _{X}\left( k \right) +\gamma _{W}\left( k\right) \gamma _{X}\left( k\right) \end{aligned}$$

(6)

Noting that

$$\begin{aligned} \gamma _{X}\left( k\right) =\alpha ^{k}\mu _{X} (k\ge 0) \end{aligned}$$

where $\mu _{X}=\lambda /(1-\alpha )$, assumption Eq. (2) implies

$$\begin{aligned} \gamma _{Y}\left( k\right) \underset{k\rightarrow \infty }{\sim }\mu _{X} ^{2}c_{\gamma ,W}k^{2d-1} \end{aligned}$$

(7)

and

$$\begin{aligned} f_{Y}\left( \lambda \right) =\mu _{X}^{2}f_{W}\left( \lambda \right) +\mu _{W}^{2}f_{X}\left( \lambda \right) +f_{WX}\left( \lambda \right) \underset{\lambda \rightarrow 0}{\sim }\mu _{X}^{2}c_{f,W}\left| \lambda \right| ^{-2d} \end{aligned}$$

(8)

Thus, although the original process $X_{j}$ has exponentially decaying autocovariances, the observed process $Y_{j}$ inherits long memory from the modulating process W(j).

Example 1

Let $Z_{j}$ ($j\in {\mathbb {Z}}$) be a stationary Gaussian process with zero mean, variance one and spectral density function $f_{Z}$ such that

$$\begin{aligned} f_{Z}\left( \lambda \right) \underset{\lambda \rightarrow 0}{\sim } c_{f,Z}\left| \lambda \right| ^{-2d} \end{aligned}$$

for some $0<c_{f,Z}<\infty$, $d\in (0,\frac{1}{2})$. Also, let $\kappa \ne 0$, and denote by $\Phi$ and $\phi$ the standard normal distribution and density function respectively. Then the process

$$\begin{aligned} W\left( j\right) ={\textbf{1}}\left\{ Z_{j}\le \kappa \right\} \text { (} j\in {\mathbb {Z}}\text {)} \end{aligned}$$

is stationary with expected value $\mu _{W}=\Phi (\kappa )$ and spectral density

$$\begin{aligned} f_{W}\left( \lambda \right) \underset{\lambda \rightarrow 0}{\sim } c_{f,W}\left| \lambda \right| ^{-2d} \end{aligned}$$

where $c_{f,W}=c_{f,Z}\varphi (\kappa )$.

Example 2

Another example of a modulating process with long memory can be obtained from a renewal reward process defined by

$$\begin{aligned} {\tilde{W}}\left( t\right) =\xi _{0}{\textbf{1}}\left\{ 0\le t<\tau _{0}\right\} +\sum _{j=-1}^{\infty }\xi _{j}{\textbf{1}}\left\{ \tau _{j-1}\le t<\tau _{j-1}+T_{j}\right\} \text { (}t>0\text {)} \end{aligned}$$

(9)

where $\tau _{j}$ ($j=1,2,...$) is a renewal process with intensity $\nu$, and $\xi _{j}\in \{0,1\}$ are iid random variables with $p_{\xi }=P(\xi _{j} =1)\in (0,1)$, independent of the process $\tau _{j}$. Moreover, the interarrival times $T_{j}=\tau _{j}-\tau _{j-1}$ are assumed to have a finite expected value $E(T)=\mu$ and a marginal distribution function $F_{T}$ such that

$$\begin{aligned} 1-F_{T}\left( u\right) \sim c_{F,T}u^{-a}\text { (}u\rightarrow \infty \text {)} \end{aligned}$$

for some constants $0<c_{F,T}<\infty$, $1<\alpha <2$. Finally, to achieve stationarity, the distribution function of $\tau _{0}$ is assumed to be given by $F_{\tau _{0}}(x)=\mu ^{-1}\int _{0}^{x}(1-F_{T}(u))du$. Then ${\tilde{W}}$ is a continuous time stationary process with expected value $\mu _{W}=p_{\xi }$ and autocovariance function

$$\begin{aligned} \gamma _{{\tilde{W}}}\left( u\right) =cov\left( {\tilde{W}}\left( 0\right) ,{\tilde{W}}\left( u\right) \right) =p_{\xi }\left( 1-p_{\xi }\right) P\left( \tau _{0}>u\right) \underset{u\rightarrow \infty }{\sim }c_{\gamma ,W}u^{2d-1} \end{aligned}$$

where

$$\begin{aligned} d=1-\frac{a}{2}\in \left( \frac{1}{2},1\right) \end{aligned}$$

Setting $W(j)={\tilde{W}}(j)$ ($j=1,2,...$), we obtain a discrete time stationary zero–one process with long memory as defined by Eq. (4) (see e.g. Beran et al. 2013, and references therein).

2.2 Sample mean and sample autocovariances

Standard methods for estimating the parameters of a Poisson INAR(1) process include moment and conditional least squares estimation. For both methods, estimators are functions of the sample mean and the lag-one sample autocorrelation. It is therefore of interest to study the effect of modulation on these statistics.

Consider first the sample mean ${\bar{y}}_{n}=n^{-1}\sum _{j=1}^{n}Y_{j}$ as an estimator of $\mu _{Y}$. With respect to the expected value we have $E(\bar{y}_{n})=\mu _{W}\mu _{X}$. Thus, ${\bar{y}}_{n}$ is biased, unless $P(W(t)=1)=1$. The asymptotic distribution of ${\bar{y}}_{n}$ follows from the asymptotic distribution of ${\bar{w}}_{n}=n^{-1}\sum _{j=1}^{n}W(j)$, as stated in the next theorem. We will use the notation

$$\begin{aligned} \nu \left( d\right) =\frac{2\sin \pi d}{d\left( 2d+1\right) }\Gamma \left( 1-2d\right) \end{aligned}$$

Also, "$\rightarrow _{d}$" and "$\rightarrow _{p}$" will denote convergence in distribution and in probability respectively.

Theorem 1

Let the process W be such that

$$\begin{aligned} Z_{n,W}=\frac{{\bar{w}}_{n}-\mu _{W}}{\sqrt{var\left( {\bar{w}}_{n}\right) } }\underset{d}{\rightarrow }Z_{W}\text { (}n\rightarrow \infty \text {)} \end{aligned}$$

where $Z_{W}$ is a standard normal random variable. Then, under the assumptions given above,

$$\begin{aligned} n^{\frac{1}{2}-d}\frac{{\bar{y}}_{n}-\mu _{W}\mu _{X}}{\sqrt{c_{f,W}\nu \left( d\right) }}\underset{d}{\rightarrow }\mu _{X}Z_{W} \end{aligned}$$

Remark 1

In Theorem 1, the assumption that $X_{t}$ is an INAR(1) process is not needed. More generally, the result holds whenever the modulating process W has the properties given above, the modulated process $Y_{t}$ is defined by Eq. (1), and $X_{t}$ is a weakly stationary process with expected value $\mu _{X}$ and summable autocovariances $\gamma _{X}(k)$.

An analogous result can be obtained for sample autocovariances. In particular,

$$\begin{aligned} {\hat{\gamma }}_{Y}\left( k\right) =n^{-1}\sum _{j=1}^{n-k}\left( Y_{j}-{\bar{y}}_{n}\right) \left( Y_{j+k}-{\bar{y}}_{n}\right) \text { (}k\ge 0\text {)} \end{aligned}$$

converges in probability to

$$\begin{aligned} \gamma _{Y}\left( k\right) =\mu _{X}^{2}\gamma _{W}\left( k\right) +\left( \mu _{W}^{2}+\gamma _{W}\left( k\right) \right) \gamma _{X}\left( k\right) \end{aligned}$$

Thus, the asymptotic bias of the unadjusted sample autocovariance is equal to

$$\begin{aligned} B_{\gamma }\left( k\right) =\gamma _{Y}\left( k\right) -\gamma _{X}\left( k\right) =\mu _{X}^{2}\gamma _{W}\left( k\right) +\left( \mu _{W}^{2} +\gamma _{W}\left( k\right) -1\right) \gamma _{X}\left( k\right) \end{aligned}$$

(10)

3 Conditional estimators

The modulating process W is usually not observable. Therefore the question arises whether consistent estimation of the INAR(1) parameters characterizing $X_{j}$ is possible, without having to model the unobserved process W. A simple approach is to make use of the fact that $P(Y_{j}=X_{j}|Y_{j}>0)=1$. For instance, we may consider conditional moment estimators.

More specifically, for a Poisson INAR(1) process with intensity $\lambda$, we have $\mu _{X}=E(X)=\lambda /(1-\alpha )$ and

$$\begin{aligned} E\left( X_{j}|X_{j}>0\right) =\frac{\mu _{X}}{1-\exp \left( -\mu _{X}\right) }=:g\left( \mu _{X}\right) \end{aligned}$$

Moreover,

$$\begin{aligned} E\left( {\textbf{1}}\left\{ Y_{j}>0\right\} Y_{j}\right)&=E\left( {\textbf{1}}\left\{ W\left( j\right) =1\right\} {\textbf{1}}\left\{ X_{j}>0\right\} X_{j}\right) \\&=\left( 1-p_{0,W}\right) \mu _{X} \end{aligned}$$

$$\begin{aligned} E\left( {\textbf{1}}\left\{ Y_{j}>0\right\} \right) =\left( 1-p_{0,W} \right) \left( 1-\exp \left( -\mu _{X}\right) \right) \end{aligned}$$

and hence

$$\begin{aligned} R=\frac{E\left( {\textbf{1}}\left\{ Y_{j}>0\right\} Y_{j}\right) }{E\left( {\textbf{1}}\left\{ Y_{j}>0\right\} \right) }=E\left( X_{j}|X_{j}>0\right) \end{aligned}$$

Therefore,

$$\begin{aligned} R_{n}=\frac{n^{-1}\sum _{j=1}^{n}{\textbf{1}}\left\{ Y_{j}>0\right\} Y_{j} }{n^{-1}\sum _{j=1}^{n}{\textbf{1}}\left\{ Y_{j}>0\right\} } \end{aligned}$$

provides a consistent nonparametric estimator of $E(X_{j}|X_{j}>0)$. This motivates the definition of a conditional moment estimator of $\mu _{X}$ as the solution ${\hat{\mu }}_{X}$ of

$$\begin{aligned} g\left( {\hat{\mu }}_{X} \right) = R_{n} \end{aligned}$$

(11)

It is straightforward to prove that Eq. (11) provides a consistent estimator:

Theorem 2

Let ${\hat{\mu }}_{X}$ be defined by Eq. (11 ). Then

$$\begin{aligned} {\hat{\mu }}_{X}\underset{p}{\rightarrow }\mu _{X}. \end{aligned}$$

Remark 2

In Theorem 2, the assumption that $X_{t}$ is an INAR(1) process is not needed. Suppose that $X_{t}$ is a nonnegative integer valued weakly stationary process with a summable autocovariance function $\gamma _{X}$. Then, calculating $E(X_{t}|X_{t}>0)$, the function g and the nonparametric estimator $R_{n}$ can be adapted accordingly to obtain a consistent estimator ${\hat{\mu }}_{X}$ via (??).

While consistency of ${\hat{\mu }}_{X}$ is not influenced by the modulating process, this is not true for the asymptotic distribution of ${\hat{\mu }}_{X}$. This is discussed in Theorem 4 (Sect. 4).

The usual moment estimator of the INAR(1)-parameter $\alpha$ is obtained by the lag-one sample autocorrelation. However, as we saw above, for the modulated process $Y_{j}$ sample autocovariances are asymptotically biased estimators of $\gamma _{X}$. We may therefore consider an estimator based on the conditional autocovariance $cov(Y_{j},Y_{j+1}|Y_{j},Y_{j+1}>0)$. By analogous arguments as above it is easy to see that

$$\begin{aligned} cov\left( Y_{j},Y_{j+1}|Y_{j},Y_{j+1}>0\right) =cov\left( X_{j},X_{j+1}|X_{j},X_{j+1}>0\right) . \end{aligned}$$

(12)

However, in terms of the INAR(1) parameters $\alpha$ and $\mu _{X}$, the right hand side of Eq. (12) is a rather complicated nonlinear function. As it turns out, a much simpler expression can be obtained for the noncentered conditional moment $E(X_{j}X_{j+1}|X_{j},X_{j+1}>0)$. Specifically, for a Poisson INAR(1) process the following formulas hold:

Lemma 1

Let $X_{j}$ be a Poisson INAR(1) process with parameters $\mu _{X}$ and $\alpha$. Then

$$\begin{aligned} P\left( X_{j}X_{j+1}>0\right) =1-2e^{-\mu _{X}}+e^{-2\mu _{X}}e^{\mu _{X} \alpha } \end{aligned}$$

and

$$\begin{aligned} E\left( X_{j}X_{j+1}|X_{j},X_{j+1}>0\right) =\frac{\alpha \mu _{X}+\mu _{X} ^{2}}{1-2\exp \left( -\mu _{X}\right) +\exp \left( -2\mu _{X}\right) \exp \left( \mu _{X}\alpha \right) } \end{aligned}$$

A consistent nonparametric estimator of $E(X_{j}X_{j+1}|X_{j},X_{j+1}>0)$ is given by

$$\begin{aligned} E_{n}=\frac{n^{-1}\sum _{j=1}^{n-1}{\textbf{1}}\left\{ Y_{j}Y_{j+1}>0\right\} Y_{j}Y_{j+1}}{n^{-1}\sum _{j=1}^{n-1}{\textbf{1}}\left\{ Y_{j}Y_{j+1}>0\right\} } \end{aligned}$$

Setting

$$\begin{aligned} h\left( \alpha ,\mu _{X}\right) =\frac{\alpha \mu _{X}+\mu _{X}^{2}}{1-2\exp \left( -\mu _{X}\right) +\exp \left( -2\mu _{X}\right) \exp \left( \mu _{X}\alpha \right) } \end{aligned}$$

we define ${\hat{\alpha }}$ by

$$\begin{aligned} h\left( {\hat{\alpha }},{\hat{\mu }}_{X}\right) =E_{n} \end{aligned}$$

(13)

where ${\hat{\mu }}_{X}$ is obtained from (11). Equation (13) provides a consistent estimator:

Theorem 3

Let ${\hat{\alpha }}$ be defined by Eq. (13). Then

$$\begin{aligned} {\hat{\alpha }}\underset{p}{\rightarrow }\alpha \end{aligned}$$

4 Testing for zero inflation

4.1 Definition of the test statistic

In this section, we consider the question how to test for zero-inflation due to modulation as specified by Eqs. (1), (5), (2) and (3). As before, we assume that the modulating process W is not observable. Using the notation

$$\begin{aligned} p_{0,X}=P\left( X_{j}=0\right) =\exp \left( -\mu _{X}\right) \text {, }p_{0,Y}=P\left( Y_{j}=0\right) \text {, }p_{0,W}=P\left( W\left( t\right) =0\right) \end{aligned}$$

we may formulate the null hypothesis $H_{0}$ and the alternative $H_{1}$ as

$$\begin{aligned} H_{0}:p_{0,Y}=p_{0,X}\text {, }H_{1}:p_{0,Y}>p_{0,X} \end{aligned}$$

For some general results on zero-inflation tests for INAR processes, see e.g. the recent paper by Weiss et al. (2019). Note that in our situation, we are testing explicitly for zero-inflation in the marginal distribution. We may therefore use a very simple statistic that compares the empirical relative frequency of zeroes with the frequency modelled by an INAR(1) process. Since $P(Y_{j}=X_{j}|Y_{j}>0)=1$, we suggest to use the consistent conditional estimator of $\mu _{X}$ defined in Eq. (11). Thus, let ${\hat{\mu }}_{X}$ be defined by Eq. (11), and let

$$\begin{aligned} {\hat{p}}_{0,X}=\exp \left( -{\hat{\mu }}_{X}\right) \end{aligned}$$

and

$$\begin{aligned} {\tilde{p}}_{0,Y}=\frac{1}{n}\sum _{t=1}^{n}{\textbf{1}}\left\{ Y_{t}=0\right\} \end{aligned}$$

We define the test statistic

$$\begin{aligned} T_{n}={\tilde{p}}_{0,Y}-{\hat{p}}_{0,X} \end{aligned}$$

Then, under $H_{0}$, $T_{n}$ converges to zero in probability, whereas under the alternative $H_{1}$, it converges to a positive constant. Asymptotic rejection regions are derived in the following section.

4.2 Asymptotic rejection regions

Before deriving the asymptotic distribution of $T_{n}$, we need to consider the joint asymptotic distribution of ${\hat{\mu }}_{X}$ and ${\tilde{p}}_{0,X}$. The following notation is adopted from Weiss et al. (2019):

$$\begin{aligned} \sigma _{11}= & {} \mu _{X}\frac{1+\alpha }{1-\alpha } \end{aligned}$$

(14)

$$\begin{aligned} \sigma _{22}= & {} e^{-\mu _{X}}\left[ 1-e^{-\mu _{X}}+2e^{-\mu _{X}}\sum _{j=1} ^{\infty }\frac{\mu _{X}^{j}}{j!}\frac{\alpha ^{j}}{1-\alpha ^{j}}\right] \end{aligned}$$

(15)

and

$$\begin{aligned} \sigma _{12}=-\mu _{X}e^{-\mu _{X}}\frac{1+\alpha }{1-\alpha } \end{aligned}$$

(16)

Also, denote by

$$\begin{aligned} r_{0,X}=\frac{p_{0,X}}{1-p_{0,X}} \end{aligned}$$

the odds ratio based on $p_{0,X}$.

Theorem 4

Let

$$\begin{aligned} \zeta _{n}=\sqrt{n}\left( {\hat{\mu }}_{X}-\mu _{X},{\tilde{p}}_{0,Y}-p_{0,X} \right) \end{aligned}$$

and suppose that $H_{0}$ holds. Then

$$\begin{aligned} \zeta _{n}\underset{d}{\rightarrow }\zeta \end{aligned}$$

where $\zeta =(\zeta _{1},\zeta _{2})$ is a zero mean bivariate normal random variable with covariance matrix $\Sigma _{\zeta }=(c_{ij})_{i,j=1,2}$. The entries in $\Sigma _{\zeta }$ are defined by

$$\begin{aligned} c_{11}= & {} \frac{\sigma _{11}+2\mu _{X}r_{0,X}p_{0,X}^{-1}\sigma _{12}+\mu _{X} ^{2}r_{0,X}^{2}p_{0,X}^{-2}\sigma _{22}}{\left( 1-\mu _{X}r_{0,X}\right) ^{2} } \end{aligned}$$

(17)

$$\begin{aligned} c_{22}= & {} \sigma _{22} \end{aligned}$$

(18)

$$\begin{aligned} c_{12}= & {} \frac{\sigma _{12}+\mu _{X}r_{0,X}p_{0,X}^{-1}\sigma _{22}}{1-\mu _{X}r_{0,X}} \end{aligned}$$

(19)

The asymptotic distribution of $T_{n}$ under $H_{0}$ is given by the following Theorem:

Theorem 5

Under $H_{0}$,

$$\begin{aligned} \sqrt{n}T_{n}\underset{d}{\rightarrow }\sigma _{T}Z_{T} \end{aligned}$$

where $Z_{T}$ is a standard normal variable,

$$\begin{aligned} \sigma _{T}^{2}=\frac{e^{-2\mu _{X}}\sigma _{11}+2e^{-\mu _{X}}\sigma _{12} +\sigma _{22}}{\left( 1-\mu _{X}r_{0,X}\right) ^{2}} \end{aligned}$$

and $\sigma _{ij}$ are given by Eqs. (14), (16), (15).

Based on Theorem 5, asymptotic rejection regions at a level of significance $\alpha \in (0,1)$ can be defined by

$$\begin{aligned} T_{n}>z_{1-\alpha }\frac{\sigma _{T}}{\sqrt{n}} \end{aligned}$$

(20)

where $z_{1-\alpha }$ denotes the $(1-\alpha )-$quantile of a standard normal variable.

4.3 Asymptotic power

We consider the asymptotic distribution of $T_{n}$ under the alternative as specified by Eqs. (1), (2), (4) and (5) with $0<p_{0,W}<1$. Note first that

$$\begin{aligned} {\tilde{p}}_{0,Y}=\frac{1}{n}\sum _{j=1}^{n}{\textbf{1}}\left\{ Y_{j}=1\right\} =\frac{1}{n}\sum _{j=1}^{n}{\textbf{1}}\left\{ X_{j}=0\right\} +\frac{1}{n} \sum _{j=1}^{n}{\textbf{1}}\left\{ Y_{j}=0,X_{j}>0\right\} \end{aligned}$$

converges in probability to

$$\begin{aligned} P\left( Y_{t}=0\right)&=p_{0,X}+P\left( W\left( t\right) =0,X_{t}>0\right) \\&=p_{0,X}+p_{0,W}\left( 1-p_{0,X}\right) \end{aligned}$$

On the other hand, ${\hat{p}}_{0,X}$ converges in probability to $p_{0,X}$. Therefore, under $H_{1}$,

$$\begin{aligned} T_{n}\underset{p}{\rightarrow }p_{0,W}\left( 1-p_{0,X}\right) >0 \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty }P\left( T_{n}>z_{1-\alpha }\frac{\sigma _{T}}{\sqrt{n}}\right) =1 \end{aligned}$$

A more detailed result is given by the following Theorem. We will use the notation

$$\begin{aligned} S_{n,1,W}= & {} \sum _{j=1}^{n}\left( {\textbf{1}}\left\{ W\left( j\right) =0\right\} -p_{0,W}\right) \\ \varphi \left( x\right)= & {} \frac{1}{\sqrt{2\pi }}e^{-\frac{1}{2}x^{2}} \\ \nu \left( d\right)= & {} \frac{2\sin \pi d}{d\left( 2d+1\right) }\Gamma \left( 1-2d\right) \end{aligned}$$

and

$$\begin{aligned} q=\frac{p_{0,X}}{\sqrt{c_{f,W}\nu \left( d\right) }} \end{aligned}$$

Theorem 6

Suppose that $H_{1}$ holds, as specified by Eqs. (1), (2), (4) and (5) with $0<p_{0,W}<1$. Moreover, assume that

$$\begin{aligned} \frac{S_{n,1,W}}{\sqrt{var\left( S_{n,1,W}\right) }}\underset{d}{\rightarrow }Z_{1,W} \end{aligned}$$

(21)

where $Z_{1,W}$ is a standard normal random variable. Then, for n large enough,

$$\begin{aligned} n^{d-\frac{1}{2}}\frac{1}{q+q^{-1}n^{2d-1}}\varphi \left( qn^{\frac{1}{2} -d}\right) \le 1-P\left( \sqrt{n}T_{n}>z_{1-\alpha }\right) \le n^{d-\frac{1}{2}}\frac{1}{q}\varphi \left( qn^{\frac{1}{2}-d}\right) \end{aligned}$$

(22)

Remark 3

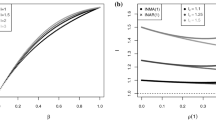
Note that the rate at which the two bounds in Eq. (22) tend to zero, as $n\rightarrow \infty$, is slower for larger values of d. Thus, the power of the test becomes weaker with increasing long memory in the modulating process W. Also note that, with increasing d, the bounds become less sharp.

5 Simulations

We consider the model $Y_{j}=W(j)X_{j}$ where $W(j)={\tilde{W}}(j)$ and ${\tilde{W}}$ is the renewal reward process defined in Eq. (9). The following INAR(1) parameters are used: a) $\mu _{W}=0.5$ with $\lambda =0.4$ and $\alpha =0.2$; b) $\mu _{W}=1$ with $\lambda =0.4$ and $\alpha =0.6$. For W we consider $\mu _{W}=p_{0,W}=$0.5, 0.9, 1, and $d=$0.1, 0.4. In the simulations of the zero-inflation test we also add a case of extreme long memory, with $d=0.49$. For each parameter combination and sample sizes $n=$100, 200, 400, 800 and 1000, ten thousand simulations were carried out. Simulated means and variances of the conditional moment estimates ${\hat{\mu }}_{X}$, as defined in Eq. (11) and ${\hat{\alpha }}_{cond}$, as defined in Eq. (13), are shown in Tables 1 ($\mu _{W}=1$), 2 and 3 ($\mu _{W}=$0.5, 0.9). For comparison, the unconditional estimates ${\bar{y}}$ and ${\hat{\alpha }}_{uncond}$ are also given. Under $H_{0}$, we observe an undisturbed INAR(1) process. As expected, the conditional estimates have a larger variance than the unconditional ones (Table 1). Under $H_{1}$, we have $\mu _{W}<1$, so that ${\bar{y}}$ underestimates $\mu _{X}$. Due to zero inflation, the absolute value of the bias increases as $\mu _{W}$ decreases. In contrast, no relevant finite sample bias is observed for the conditional estimator ${\hat{\mu }}_{X}$. For the unconditional estimator of $\alpha$, the effect of zero-inflation is much less clear. A noticeable bias of the unconditional estimator can only be observed for $p_{0,W}=0.5$ and $d=0.1$. A possible reason for the rather minor effect is that the potential bias under zero-inflation may be compensated by a modified lag-one autocorrelation of the observed process due to dependence in W.

Tables 4 show results for the zero-inflation test based on Eq. (20). Under $H_{0}$, the simulated levels are reasonably close to the nominal value of 0.05. As expected, for smaller values of $p_{0,W}$, the test has higher power. The effect of long memory is less obvious for mild zero-inflation ($p_{0,W}=0.9$). For $p_{0,W}=0.5$, the simulation results show a clearer picture, with a tendency for slightly lower power when d is large.

Finally, Table 5 shows results for the case where $X_{j}$ is generated by an INAR(2) process (Alzaid and Al-Osh 1990), but is misspecified as an INAR(1) model. Specifically, we simulate $X_{j}=\alpha _{1}\circ X_{j-1} + \alpha _{1}\circ X_{j-2} + \varepsilon _{j}$ where $(\alpha _{1},\alpha _{2})=(0.2,0.2)$ and (0.6, 0.2) respectively, and $\varepsilon _{j}$ are iid Poisson variables with $\lambda =0.4$. For $(\alpha _{1},\alpha _{2})=(0.6,0.2)$, the simulated rejection frequencies under $H_{0}$ are very close to the nominal level of 0.05. For $(\alpha _{1},\alpha _{2})=(0.2,0.2)$, rejection frequencies tend to be slightly too high. A possible explanation is that for $\alpha _{1}=0.6$ the relative influence of $X_{j-1}$ on $X_{j}$ is much stronger than for $\alpha _{1}=0.2$. In this sense, the INAR(2) process is closer to an INAR(1) process for larger values of the ratio $\alpha _{1}/\alpha _{2}$, and the misspecification is less noticeable. On the other hand, under $H_{1}$, rejection probabilities tend to be higher for $\alpha _{1}=0.2$. This may be explained, at least partially, by the fact that for this parameter setting the level of significance is higher than the nominal level of 0.05. Generally speaking, one may conjecture that the test is likely to be fairly robust to mild deviations from an INAR(1) model. If serious deviations from the ideal model are expected, a modification of the test may be preferable (see Remarks 1 and 2 ). An interesting task for future research is to develop adaptive tests for zero-inflation that are applicable without the need of specifying which member of a certain family of "ideal models" (e.g. the family of all INAR(p) models with $p=1,2,...$) generates the unmodulated process $X_{j}$.

6 Final remarks

In this paper, we introduced a zero-inflated INAR(1) model where zero-inflation is caused by a long-memory process. Parameter estimation and testing for zero-inflation was considered. Various extensions of this model are of interest. For instance, modulation may occur at the level of the innovations of the INAR(1) process. The structure of this type of modulated INAR(1) processes is much more complex, and will be considered elsewhere. Another obvious extension is to consider model (1), however replacing $X_{j}$ by a general INAR(p) process. It is expected that the methods considered here can be extended to this case using analogous arguments as for $p=1$.

Finally note that instead using the test statistic discussed in Sect. 4, one may consider the lengths of zero runs (for related results see e.g. Jazi et al. 2012, Qi et al. 2019). An advantage of the test considered here is its simplicity. In particular, under the alternative, the distribution of runs can be quite complicated. On the other hand, the estimator of $\mu _{X}$ used here, omits parts of the information that may be useful for detecting deviations from the null hypothesis. The development of more efficient tests, for instance based on runs, is an interesting task for future research.

Appendix—Proofs, Tables

1.1 Proofs

Proof of Theorem 1

First of all, $E({\bar{y}}_{n})=\mu _{W}\mu _{X}=p_{0,W}\mu _{X}$, because the two processes X and W are independent of each other. Moreover,

$$\begin{aligned} n^{-1}\sum _{j=1}^{n}Y_{j}&=n^{-1}\sum _{j=1}^{n}W\left( j\right) \left( X_{j}-\mu _{X}\right) +\mu _{X}n^{-1}\sum _{j=1}^{n}W\left( j\right) \\&=\mu _{W}\mu _{X}+n^{-1}\sum _{j=1}^{n}W\left( j\right) \left( X_{j} -\mu _{X}\right) +\mu _{X}n^{-1}\sum _{j=1}^{n}\left( W\left( j\right) -\mu _{W}\right) \\&=\mu _{W}\mu _{X}+n^{-1}S_{n,1}+\mu _{X}n^{-1}S_{n,2}. \end{aligned}$$

Now,

$$\begin{aligned} E\left[ W\left( j\right) \left( X_{j}-\mu _{X}\right) \right] =0 \end{aligned}$$

and

$$\begin{aligned} \left| cov\left( W\left( j\right) \left( X_{j}-\mu _{X}\right) ,W\left( j+k\right) \left( X_{j+k}-\mu _{X}\right) \right) \right|&=\left| \gamma _{W}\left( k\right) +\mu _{W}^{2}\right| \left| \gamma _{X}\left( k\right) \right| \\&\le c\left| \gamma _{X}\left( k\right) \right| \end{aligned}$$

for a suitable constant $0<c<\infty$. Therefore

$$\begin{aligned} n^{-1}\sum _{j=1}^{n}Y_{j}-\mu _{W}\mu _{X}=O_{p}\left( n^{-\frac{1}{2}}\right) \end{aligned}$$

Furthermore,

$$\begin{aligned} S_{n,2}={\bar{w}}_{n}-\mu _{W}=\sqrt{var\left( {\bar{w}}_{n}\right) }Z_{n,W} \end{aligned}$$

Now Eqs. (7) and (8) imply

$$\begin{aligned} var\left( {\bar{w}}_{n}\right) \underset{n\rightarrow \infty }{\sim }c_{f,W} \nu \left( d\right) n^{2d-1} \end{aligned}$$

(see e.g. Beran et al. 2013, Corollary 1.2). Since $d>0$, $n^{-1}S_{n,1}$ is asymptotically negligible and the result follows. $\square$

Proof of Theorem 2

The function g is monotonically increasing, with $\lim _{\mu \rightarrow 0}g\left( \mu \right) =1$ and $\lim _{\mu \rightarrow \infty }g\left( \mu \right) =\infty$. Since $R_{n}\ge 1$, Eq. (11) has a unique solution. Moreover, W is a stationary $0-1-$process, and

$$\begin{aligned} cov\left( {\textbf{1}}\left\{ Y_{j}>0\right\} Y_{j},{\textbf{1}}\left\{ Y_{j+k}>0\right\} Y_{j+k}\right)&=cov\left( Y_{j},Y_{j+k}\right) =\gamma _{Y}\left( k\right) \\&=\mu _{X}^{2}\gamma _{W}\left( k\right) +\mu _{W}^{2}\gamma _{X}\left( k\right) +\gamma _{W}\left( k\right) \gamma _{X}\left( k\right) \end{aligned}$$

Tschebyschev’s inequality then implies

$$\begin{aligned} n^{-1}\sum _{j=1}^{n}{\textbf{1}}\left\{ Y_{j}>0\right\} Y_{j}\rightarrow _{p}E\left( {\textbf{1}}\left\{ Y>0\right\} Y\right) =\left( 1-p_{0,W} \right) \mu _{X} \end{aligned}$$

and

$$\begin{aligned} n^{-1}\sum _{j=1}^{n}{\textbf{1}}\left\{ Y_{j}>0\right\} \rightarrow _{p}\left( 1-p_{0,W}\right) \left( 1-\exp (-\mu _{X})\right) \end{aligned}$$

so that

$$\begin{aligned} R_{n}\underset{p}{\rightarrow }\frac{\mu _{X}}{1-\exp \left( -\mu _{X}\right) } \end{aligned}$$

$\square$

Proof of Lemma 1

First of all,

$$\begin{aligned} P\left( X_{j}X_{j+1}>0\right)&=\sum _{k=1}^{\infty }\frac{\mu _{X}^{k}}{k!}e^{-\mu _{X}}\left[ 1-\left( 1-\alpha \right) ^{k}+\left( 1-e^{-\lambda }\right) \left( 1-\alpha \right) ^{k}\right] \\&=\sum _{k=1}^{\infty }\frac{\mu _{X}^{k}}{k!}e^{-\mu _{X}}\left[ 1-e^{-\lambda }\left( 1-\alpha \right) ^{k}\right] \\&=\left( 1-e^{-\mu _{X}}\right) -e^{-(\lambda +\mu _{X})+\mu _{X}(1-\alpha )}\sum _{k=1}^{\infty }\frac{\left[ \mu _{X}\left( 1-\alpha \right) \right] ^{k}}{k!}e^{-\mu _{X}(1-\alpha )}\\&=\left( 1-e^{-\mu _{X}}\right) -e^{-\mu _{X}}\left( 1-e^{-\mu _{X} (1-\alpha )}\right) \\&=1-2e^{-\mu _{X}}+e^{-2\mu _{X}}e^{\mu _{X}\alpha } \end{aligned}$$

Then

$$\begin{aligned} E\left( X_{j}X_{j+1}|X_{j},X_{j+1}>0\right)&=\frac{E\left( X_{j} X_{j+1}\right) }{P\left( X_{j}X_{j+1}>0\right) }=\frac{\gamma _{X}\left( 1\right) +\mu _{X}^{2}}{P\left( X_{j}X_{j+1}>0\right) }\\&=\frac{\alpha \mu _{X}+\mu _{X}^{2}}{1-2\exp \left( -\mu _{X}\right) +\exp \left( -2\mu _{X}\right) \exp \left( \mu _{X}\alpha \right) } \end{aligned}$$

$\square$

Proof of Theorem 3

First note that

$$\begin{aligned} E\left( {\textbf{1}}\left\{ Y_{j}Y_{j+1}>0\right\} Y_{j}Y_{j+1}\right)= & {} E\left( {\textbf{1}}\left\{ W\left( j\right) W\left( j+k\right)>0\right\} \right) \\{} & {} \quad E\left( {\textbf{1}}\left\{ X_{j}X_{j+1}>0\right\} X_{j}X_{j+k}\right) , \\ E\left( {\textbf{1}}\left\{ Y_{j}Y_{j+1}>0\right\} \right)= & {} E\left( {\textbf{1}}\left\{ W\left( j\right) W\left( j+k\right)>0\right\} \right) E\left( {\textbf{1}}\left\{ X_{j}X_{j+1}>0\right\} \right) \end{aligned}$$

so that

$$\begin{aligned} \frac{E\left( {\textbf{1}}\left\{ Y_{j}Y_{j+1}>0\right\} Y_{j}Y_{j+1}\right) }{E\left( {\textbf{1}}\left\{ Y_{j}Y_{j+1}>0\right\} \right) }&=\frac{E\left( {\textbf{1}}\left\{ X_{j}X_{j+1}>0\right\} X_{j} X_{j+k}\right) }{E\left( {\textbf{1}}\left\{ X_{j}X_{j+1}>0\right\} \right) }\\&=E(X_{j}X_{j+1}|X_{j},X_{j+1}>0) \end{aligned}$$

Then,

$$\begin{aligned} n^{-1}\sum _{j=1}^{n-1}{\textbf{1}}\left\{ Y_{j}Y_{j+1}>0\right\} Y_{j} Y_{j+1}\underset{p}{\rightarrow }E\left( {\textbf{1}}\left\{ Y_{j} Y_{j+1}>0\right\} Y_{j}Y_{j+1}\right) \end{aligned}$$

and

$$\begin{aligned} n^{-1}\sum _{j=1}^{n-1}{\textbf{1}}\left\{ Y_{j}Y_{j+1}>0\right\} \underset{p}{\rightarrow }E\left( {\textbf{1}}\left\{ Y_{j}Y_{j+1}>0\right\} \right) \end{aligned}$$

implies

$$\begin{aligned} E_{n}\underset{p}{\rightarrow }E(X_{j}X_{j+1}|X_{j},X_{j+1}>0) \end{aligned}$$

Now, for any fixed $\mu _{X}>0$, $h(\alpha ,\mu _{X})$ is monotonically increasing in $\alpha$ with

$$\begin{aligned} \lim _{\alpha \rightarrow 0}h\left( \alpha ,\mu _{X}\right)= & {} \frac{\mu _{X}^{2} }{\left( 1-\exp \left( -\mu _{X}\right) \right) ^{2}}=E^{2}\left( X|X>0\right) \\ \lim _{\alpha \rightarrow 1}h\left( \alpha ,\mu _{X}\right)= & {} \frac{\mu _{X}\left( \mu _{X}+1\right) }{1-\exp \left( -\mu _{X}\right) }=E\left( X^{2} |X>0\right) \end{aligned}$$

Hence, together with Theorem 2, we may conclude that, for n large enough, (13) has a unique solution and ${\hat{\alpha }}\rightarrow _{p}\alpha$. $\square$

Proof of Theorem 4

Recall that

$$\begin{aligned} {\tilde{p}}_{0,Y}=\frac{1}{n}\sum _{j=1}^{n}{\textbf{1}}\left\{ Y_{j}=0\right\} \end{aligned}$$

and

$$\begin{aligned} g\left( {\hat{\mu }}_{X}\right) =\frac{n^{-1}S_{n}}{1-{\tilde{p}}_{0,Y}} \end{aligned}$$

where

$$\begin{aligned} g\left( \mu \right) =\frac{\mu _{X}}{1-p_{0,X}}=\frac{\mu _{X}}{1-\exp \left( -\mu _{X}\right) }=E\left( X_{j}|X_{j}>0\right) \end{aligned}$$

and

$$\begin{aligned} S_{n}=\sum _{j=1}^{n}{\textbf{1}}\left\{ Y_{j}>0\right\} Y_{j}=\sum _{j=1} ^{n}Y_{j}=n{\bar{y}} \end{aligned}$$

Under $H_{0}$, we have

$$\begin{aligned} n^{-1}S_{n}={\bar{y}}={\bar{x}} \end{aligned}$$

so that

$$\begin{aligned} g\left( {\hat{\mu }}_{X}\right) =\frac{{\bar{x}}}{1-{\tilde{p}}_{0,Y}} \end{aligned}$$

(23)

Since ${\hat{\mu }}_{X}$ is consistent, we may use a Taylor expansion

$$\begin{aligned} g\left( {\hat{\mu }}_{X}\right) =g\left( \mu _{X}\right) +g^{\prime }\left( \mu _{X}\right) \left( {\hat{\mu }}_{X}-\mu _{X}\right) +o_{p}\left( \hat{\mu }_{X}-\mu _{X}\right) \end{aligned}$$

to obtain

$$\begin{aligned} {\hat{\mu }}_{X}-\mu _{X}=\frac{1}{g^{\prime }\left( \mu _{X}\right) }\left[ \frac{{\bar{x}}}{1-{\tilde{p}}_{0,Y}}-g\left( \mu _{X}\right) \right] +o_{p}\left( {\hat{\mu }}_{X}-\mu _{X}\right) \end{aligned}$$

(24)

Moreover, under $H_{0}$, we also have $p_{0,Y}=p_{0,X}$ and

$$\begin{aligned} \frac{1}{1-{\tilde{p}}_{0,Y}}=\frac{1}{1-p_{0,X}}\left[ 1+\frac{{\tilde{p}} _{0,Y}-p_{0,X}}{1-p_{0,X}}+o_{p}\left( {\tilde{p}}_{0,Y}-p_{0,X}\right) \right] \end{aligned}$$

Now

$$\begin{aligned} \frac{{\bar{x}}}{1-{\tilde{p}}_{0,Y}}-g\left( \mu _{X}\right)&=\frac{{\bar{x}}-\mu _{X}}{1-{\tilde{p}}_{0,Y}}+\left( \frac{\mu _{X}}{1-{\tilde{p}}_{0,Y} }-g\left( \mu _{X}\right) \right) \\&=A_{n}+B_{n} \end{aligned}$$

The second term can be written as

$$\begin{aligned} B_{n}&=\frac{\mu _{X}}{1-{\tilde{p}}_{0,Y}}-g\left( \mu _{X}\right) \\&=\frac{\mu _{X}}{1-p_{0,X}}\left[ 1+\frac{{\tilde{p}}_{0,Y}-p_{0,X} }{1-p_{0,X}}+o_{p}\left( {\tilde{p}}_{0,Y}-p_{0,X}\right) \right] -g\left( \mu _{X}\right) \\&=g\left( \mu _{X}\right) \frac{{\tilde{p}}_{0,Y}-p_{0,X}}{1-p_{0,X}} +o_{p}\left( {\tilde{p}}_{0,Y}-p_{0,X}\right) \end{aligned}$$

The first term can be simplified to

$$\begin{aligned} A_{n}=\frac{{\bar{x}}-\mu _{X}}{1-p_{0,X}}+o_{p}\left( {\tilde{p}}_{0,Y} -p_{0,X}\right) \end{aligned}$$

Thus,

$$\begin{aligned} {\hat{\mu }}_{X}-\mu _{X}&=\frac{1}{g^{\prime }\left( \mu _{X}\right) }\left( A_{n}+B_{n}\right) +o_{p}\left( {\hat{\mu }}_{X}-\mu _{X}\right) \\&=\frac{\left( {\bar{x}}-\mu _{X}\right) +g\left( \mu _{X}\right) \left( {\tilde{p}}_{0,Y}-p_{0,X}\right) }{g^{\prime }\left( \mu _{X}\right) \left( 1-p_{0,X}\right) }+o_{p}\left( {\hat{\mu }}_{X}-\mu _{X}\right) +o_{p}\left( {\tilde{p}}_{0,Y}-p_{0,X}\right) \end{aligned}$$

Applying Theorem 3.1.1 in Weiss et al. (2019), this can be simplified to

$$\begin{aligned} {\hat{\mu }}_{X}-\mu _{X}=\frac{Z_{1}+g\left( \mu _{X}\right) Z_{2}}{\left( 1-p_{0,X}\right) g^{\prime }\left( \mu _{X}\right) }n^{-\frac{1}{2}} +o_{p}\left( n^{-\frac{1}{2}}\right) \end{aligned}$$

where $Z=(Z_{1},Z_{2})$ is a zero mean bivariate random variable with covariance matrix $\Sigma =(\sigma _{ij})_{i,j=1,2}$, as defined by Eqs. (14), (16), (15). Note furthermore that $p_{0,X}=\exp (-\mu _{X})$,

$$\begin{aligned} g^{\prime }\left( \mu \right) =\frac{1-\left( \mu +1\right) \exp \left( -\mu \right) }{\left( 1-\exp \left( -\mu \right) \right) ^{2}} \end{aligned}$$

so that

$$\begin{aligned} \frac{1}{g^{\prime }\left( \mu _{X}\right) \left( 1-p_{0,X}\right) }&=\frac{1-\exp \left( -\mu _{X}\right) }{1-\left( \mu _{X}+1\right) \exp \left( -\mu _{X}\right) }\\&=\frac{1}{1-\mu _{X}r_{0,X}} \end{aligned}$$

and

$$\begin{aligned} \frac{g\left( \mu _{X}\right) }{g^{\prime }\left( \mu _{X}\right) \left( 1-p_{0,X}\right) }&=\frac{\mu _{X}}{1-\left( \mu _{X}+1\right) \exp \left( -\mu _{X}\right) }\\&=\frac{\mu _{X}}{1-p_{0,X}}\frac{1}{1-\mu _{X}r_{0,X}} \end{aligned}$$

Thus, we obtain

$$\begin{aligned} {\hat{\mu }}_{X}-\mu _{X}=\frac{1}{1-\mu _{X}r_{0,X}}\left( Z_{1}+\frac{\mu _{X} }{1-p_{0,X}}Z_{2}\right) n^{-\frac{1}{2}}+o_{p}\left( n^{-\frac{1}{2} }\right) \end{aligned}$$

Moreover, by definition,

$$\begin{aligned} {\tilde{p}}_{0,Y}-p_{0,X}=n^{-\frac{1}{2}}Z_{2}+o_{p}\left( n^{-\frac{1}{^{2}} }\right) \end{aligned}$$

Therefore

$$\begin{aligned} \zeta _{n}=\sqrt{n}\left( {\hat{\mu }}_{X}-\mu _{X},{\tilde{p}}_{0,Y}-p_{0,X} \right) \underset{d}{\rightarrow }\zeta \end{aligned}$$

where $\zeta$ has the covariance matrix $\Sigma _{\zeta }$ defined by Eqs. (17), (18) and (19). $\square$

Proof of Theorem 5

Note first that

$$\begin{aligned} {\hat{p}}_{0,X}&=\exp \left( -{\hat{\mu }}_{X}\right) =p_{0,X}\exp \left( -\left( {\hat{\mu }}_{X}-\mu _{X}\right) \right) \\&=p_{0,X}\left( 1-\left( {\hat{\mu }}_{X}-\mu _{X}\right) +o_{p}\left( {\hat{\mu }}_{X}-\mu _{X}\right) \right) \end{aligned}$$

Theorem 4 implies

$$\begin{aligned} {\hat{p}}_{0,X}-p_{0,X}=-p_{0,X}\zeta _{1}n^{-\frac{1}{2}}+o_{p}\left( n^{-\frac{1}{2}}\right) \end{aligned}$$

and

$$\begin{aligned} \sqrt{n}T_{n}&={\tilde{p}}_{0,Y}-{\hat{p}}_{0,X}\\&=\zeta _{2}+p_{0,X}\zeta _{1}+o_{p}\left( 1\right) \end{aligned}$$

where $\zeta$ is defined in Theorem 4. Then formulas Eqs. (17),(18),(19) lead to

$$\begin{aligned} \sigma _{T}^{2}&=\lim _{n\rightarrow \infty }n\cdot var\left( T_{n}\right) \\&=var\left( \zeta _{2}\right) +2p_{0,X}cov\left( \zeta _{1},\zeta _{2}\right) +p_{0,X}^{2}var\left( \zeta _{1}\right) \\&=\frac{\sigma _{22}+2p_{0,X}\sigma _{12}+\sigma _{11}p_{0,X}^{2}}{\left( 1-\mu _{X}r_{0,X}\right) ^{2}}\\&=\frac{e^{-2\mu _{X}}\sigma _{11}+2e^{-\mu _{X}}\sigma _{12}+\sigma _{22} }{\left( 1-\mu _{X}r_{0,X}\right) ^{2}} \end{aligned}$$

$\square$

Proof of Theorem 6

First note that

$$\begin{aligned} {\tilde{p}}_{0,Y}=A_{n}+B_{n} \end{aligned}$$

where

$$\begin{aligned} A_{n}=\frac{1}{n}\sum _{j=1}^{n}{\textbf{1}}\left\{ X_{j}=0\right\} =p_{0,X}+n^{-\frac{1}{2}}Z_{2}+o_{p}\left( n^{-\frac{1}{2}}\right) \end{aligned}$$

and

$$\begin{aligned} B_{n}&=\frac{1}{n}\sum _{j=1}^{n}{\textbf{1}}\left\{ Y_{j}=0,X_{j}>0\right\} \\&=p_{0,W}\left( 1-p_{0,X}\right) +n^{-1}S_{1,n}-n^{-1}S_{2,n} \end{aligned}$$

with

$$\begin{aligned} n^{-1}S_{1,n}= & {} n^{-1}\sum _{j=1}^{n}{\textbf{1}}\left\{ W\left( j\right) =0\right\} -p_{0,W} \\ n^{-1}S_{2,n}= & {} n^{-1}\sum _{j=1}^{n}{\textbf{1}}\left\{ W\left( j\right) =0\right\} {\textbf{1}}\left\{ X_{j}=0\right\} -p_{0,W}p_{0,X} \end{aligned}$$

Also note that

$$\begin{aligned}&cov\left( {\textbf{1}}\left\{ W\left( j\right) =0\right\} ,{\textbf{1}} \left\{ W\left( j+k\right) =0\right\} \right) \\&=cov\left( 1-W\left( j\right) ,1-W\left( j+k\right) \right) \\&=\gamma _{W}\left( k\right) \end{aligned}$$

By assumption,

$$\begin{aligned} \gamma _{W}\left( k\right) \underset{k\rightarrow \infty }{\sim }c_{\gamma ,1,W}k^{2d-1} \end{aligned}$$

where

$$\begin{aligned} c_{\gamma ,W}=2c_{f,W}\Gamma \left( 1-2d\right) \sin \pi d \end{aligned}$$

(see e.g. Beran et al. 2013, Theorem 1.3). Moreover,

$$\begin{aligned}&E\left[ {\textbf{1}}\left\{ W\left( j\right) =0\right\} {\textbf{1}} \left\{ X_{j}=0\right\} {\textbf{1}}\left\{ W\left( j+k\right) =0\right\} {\textbf{1}}\left\{ X_{j+k}=0\right\} \right] \\&=E\left[ {\textbf{1}}\left\{ W\left( j\right) =0\right\} {\textbf{1}} \left\{ W\left( j+k\right) =0\right\} \right] E\left[ {\textbf{1}}\left\{ X_{j}=0\right\} {\textbf{1}}\left\{ X_{j+k}=0\right\} \right] \\&=\left( \gamma _{1,W}\left( k\right) +p_{0,W}^{2}\right) \left( \gamma _{X}\left( k\right) +p_{0,X}^{2}\right) \end{aligned}$$

$$\begin{aligned} E^{2}\left[ {\textbf{1}}\left\{ W\left( j\right) =0\right\} {\textbf{1}} \left\{ X_{j}=0\right\} \right] =p_{0,W}^{2}p_{0,X}^{2}, \end{aligned}$$

and hence

$$\begin{aligned}&cov\left( {\textbf{1}}\left\{ W\left( j\right) =0\right\} {\textbf{1}} \left\{ X_{j}=0\right\} ,{\textbf{1}}\left\{ W\left( j+k\right) =0\right\} {\textbf{1}}\left\{ X_{j+k}=0\right\} \right) \\&=p_{0,X}^{2}\gamma _{W}\left( k\right) +p_{0,W}^{2}\gamma _{X}\left( k\right) +\gamma _{W}\left( k\right) \gamma _{X}\left( k\right) \end{aligned}$$

This implies

$$\begin{aligned} cov\left( {\textbf{1}}\left\{ W\left( j\right) =0\right\} {\textbf{1}} \left\{ X_{j}=0\right\} ,{\textbf{1}}\left\{ W\left( j+k\right) =0\right\} {\textbf{1}}\left\{ X_{j+k}=0\right\} \right) \underset{k\rightarrow \infty }{\sim }c_{\gamma ,W}k^{2d-1}p_{0,X}^{2} \end{aligned}$$

Also,

$$\begin{aligned}&E\left( {\textbf{1}}\left\{ W\left( j\right) =0\right\} {\textbf{1}} \left\{ W\left( j+k\right) =0\right\} {\textbf{1}}\left\{ X_{j+k} =0\right\} \right) \\&=p_{0,X}\left( \gamma _{W}\left( k\right) +p_{0,W}^{2}\right) \end{aligned}$$

and

$$\begin{aligned} E\left( {\textbf{1}}\left\{ W\left( j\right) =0\right\} \right) E\left( {\textbf{1}}\left\{ W\left( j+k\right) =0\right\} {\textbf{1}}\left\{ X_{j+k}=0\right\} \right) =p_{0,X}p_{0,W}^{2} \end{aligned}$$

so that

$$\begin{aligned} cov\left( {\textbf{1}}\left\{ W\left( j\right) =0\right\} ,{\textbf{1}} \left\{ W\left( j+k\right) =0\right\} {\textbf{1}}\left\{ X_{j+k} =0\right\} \right) =p_{0,X}\gamma _{W}\left( k\right) \end{aligned}$$

We then obtain

$$\begin{aligned} var\left( n^{-1}\left( S_{1}-S_{2}\right) \right) =n^{-2}\left[ var\left( S_{1}\right) +var\left( S_{2}\right) -2cov\left( S_{1},S_{2}\right) \right] \end{aligned}$$

with

$$\begin{aligned} var\left( S_{1}\right) =\sum _{k=-(n-1)}^{n-1}\left( n-\left| k\right| \right) \gamma _{W}\left( k\right) \underset{n\rightarrow \infty }{\sim }c_{f,W}\nu \left( d\right) n^{2d+1} \end{aligned}$$

$$\begin{aligned} var\left( S_{2}\right)&=p_{0,X}^{2}\sum _{k=-(n-1)}^{n-1}\left( n-\left| k\right| \right) \gamma _{W}\left( k\right) +p_{0,W} ^{2}\sum _{k=-(n-1)}^{np_{0,X}-1}\left( n-\left| k\right| \right) \gamma _{X}\left( k\right) \\&+2\sum _{k=-(n-1)}^{n-1}\left( n-\left| k\right| \right) \gamma _{W}\left( k\right) \gamma _{X}\left( k\right) \\&\underset{n\rightarrow \infty }{\sim }p_{0,X}^{2}c_{f,W}\nu \left( d\right) n^{2d+1} \end{aligned}$$

and

$$\begin{aligned} cov\left( S_{1},S_{2}\right) =p_{0,X}\sum _{k=-(n-1)}^{n-1}\left( n-\left| k\right| \right) \gamma _{1,W}\left( k\right) \underset{n\rightarrow \infty }{\sim }p_{0,X}c_{f,W}\nu \left( d\right) n^{2d+1} \end{aligned}$$

Thus, overall

$$\begin{aligned} var\left( n^{-1}\left( S_{1}-S_{2}\right) \right) \underset{n\rightarrow \infty }{\sim }c_{f,W}\nu \left( d\right) \left( 1-p_{0,X}\right) ^{2}n^{2d-1} \end{aligned}$$

Moreover, under the given assumptions, $n^{\frac{1}{2}-d}(S_{1,n},S_{2,n})$ are asymptotically jointly normal, so that

$$\begin{aligned} {\tilde{p}}_{0}\underset{d}{=}p_{0,X}+p_{0,X}\left( 1-p_{0,X}\right) +n^{d-\frac{1}{2}}\sqrt{c_{f,W}\nu \left( d\right) }\left( 1-p_{0,X}\right) Z_{3}+o_{p}\left( n^{d-\frac{1}{2}}\right) \end{aligned}$$

where $Z_{3}\sim N(0,1)$. Hence, we have

$$\begin{aligned} \sqrt{n}T_{n}&=\sqrt{n}\left( {\tilde{p}}_{0}-{\hat{p}}_{0}\right) \\&=\sqrt{n}p_{0,X}\left( 1-p_{0,X}\right) +n^{d}\sqrt{c_{f,W}\nu \left( d\right) }\left( 1-p_{0,X}\right) Z_{3}+o_{p}\left( n^{d-\frac{1}{2} }\right) \end{aligned}$$

For

$$\begin{aligned} \Delta _{n}=1-P\left( \sqrt{n}T_{n}>z_{1-\alpha }\right) \end{aligned}$$

this yields

$$\begin{aligned} \Delta _{n}&=1-P\left( \sqrt{n}p_{0,X}\left( 1-p_{0,X}\right) +n^{d} \sqrt{c_{f,W}\nu \left( d\right) }\left( 1-p_{0,X}\right) Z_{3}>z_{1-\alpha }\right) +o\left( \Delta _{n}\right) \\&=P\left( Z_{3}>n^{\frac{1}{2}-d}\frac{p_{0,X}}{\sqrt{c_{f,W}\nu \left( d\right) }}\right) +o\left( \Delta _{n}\right) \end{aligned}$$

Inequality (22) then follows from

$$\begin{aligned} \frac{\exp \left( -\frac{1}{2}x^{2}\right) }{\sqrt{2\pi }\left( x+x^{-1}\right) }<1-\Phi \left( x\right) <\frac{\exp \left( -\frac{1}{2}x^{2}\right) }{\sqrt{2\pi }x} \end{aligned}$$

(Gordon 1941) by plugging in

$$\begin{aligned} x+x^{-1}&=n^{\frac{1}{2}-d}\frac{p_{0,X}}{\sqrt{c_{f,W}\nu \left( d\right) }}+n^{d-\frac{1}{2}}\frac{\sqrt{c_{f,W}\nu \left( d\right) }}{p_{0,X}}\\&=n^{\frac{1}{2}-d}\left( q+q^{-1}n^{2d-1}\right) \end{aligned}$$

$\square$

1.2 Tables

See Tables 1, 2, 3 and 4.

Table 1 Simulated mean (first number) and variance (second number) of unconditional and conditional estimates of $\mu _{X}$ and $\alpha$ under $H_{0}$. For each combination of parameters and sample size, the results are based on 10,000 simulations

Table 2 Simulated mean (first number) and variance (second number) of unconditional and conditional estimates of $\mu _{X}$ and $\alpha$ under $H_{1}$ with $\mu _{X}=0.5$ ($\alpha$=0.2, $\lambda =0.4$). For each combination of parameters and sample size, the results are based on 10,000 simulations

Table 3 Simulated mean (first number) and variance (second number) of unconditional and conditional estimates of $\mu _{X}$ and $\alpha$ under $H_{1}$ with $\mu _{X}=1$ ($\alpha$=0.6, $\lambda =0.4$). For each combination of parameters and sample size, the results are based on 10,000 simulations

Table 4 Simulated relative rejection frequencies based on asymptotic rejection regions defined by Eq. (20) with a level of significance of 0.05. For each combination of parameters and sample size, the results are based on 10,000 simulations

Table 5 Simulated relative rejection frequencies under misspecification. The results are based on 10,000 simulations of an INAR(2) process with $(\alpha _{1},\alpha _{2})=(0.2,0.2)$ and (0.6, 0.2) respectively, and $\varepsilon _{j}$ iid Poisson variables with $\lambda =0.4$. The alternative considered here is $\mu _{W}=0.5$, with $d=0.1$ and $d=0.4$ respectively. For each simulated series, a (misspecified) INAR(1) model was fitted using the methods in Sect. 3 and the test defined in Sect. 4 was applied, at a nominal level of significance of 0.05