Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-28T11:40:51.082Z Has data issue: false hasContentIssue false
  • English
  • Français

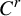$C^r$-chain closing lemma for certain partially hyperbolic diffeomorphisms

Part of: Smooth dynamical systems: general theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  11 October 2023

YI SHI  and
XIAODONG WANG
YI SHI*
Affiliation:
School of Mathematics, Sichuan University, Chengdu 610065, P. R. China
XIAODONG WANG
Affiliation:
School of Mathematical Sciences, CMA-Shanghai, Shanghai Jiao Tong University, Shanghai 200240, P. R. China (e-mail: xdwang1987@sjtu.edu.cn)
*
e-mail: shiyi@scu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

For every 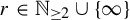$r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$, we prove a 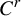$C^r$-orbit connecting lemma for dynamically coherent and plaque expansive partially hyperbolic diffeomorphisms with one-dimensional orientation preserving center bundle. To be precise, for such a diffeomorphism f, if a point y is chain attainable from x through pseudo-orbits, then for any neighborhood U of x and any neighborhood V of y, there exist true orbits from U to V by arbitrarily $C^r$-small perturbations. As a consequence, we prove that for 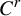$C^r$-generic diffeomorphisms in this class, periodic points are dense in the chain recurrent set, and chain transitivity implies transitivity.

Keywords

partially hyperbolic diffeomorphismchain closing lemmaperiodic orbitdynamical coherencechain recurrent set

MSC classification

Primary: 37D30: Partially hyperbolic systems and dominated splittings
Secondary: 37C20: Generic properties, structural stability 37C50: Approximate trajectories (pseudotrajectories, shadowing, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 22
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anosov, D. V.. Geodesic flows on closed Riemannian manifolds of negative curvature. Tr. Mat. Inst. Steklova 90 (1967), 209pp (in Russian).Google Scholar
Arnaud, M.-C.. Création de connexions en topologie ${C}^1$ . Ergod. Th. & Dynam. Sys. 21 (2001), 339–381.CrossRefGoogle Scholar
Asaoka, M. and Irie, K.. A ${C}^{\infty }$ closing lemma for Hamiltonian diffeomorphisms of closed surfaces. Geom. Funct. Anal. 26 (2016), 1245–1254.CrossRefGoogle Scholar
Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158 (2004), 33–104.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L.. Persistent nonhyperbolic transitive diffeomorphisms. Ann. of Math. (2) 143 (1996), 357–396.CrossRefGoogle Scholar
Brin, M.. Topological transitivity of a certain class of dynamical systems, and flows of frames on manifolds of negative curvature. Funktsional. Anal. i Prilozhen. 9 (1975), 9–19 (in Russian).CrossRefGoogle Scholar
Cristofaro-Gardiner, D., Prasad, R. and Zhang, B.. Periodic Floer homology and the smooth closing lemma for area-preserving surface diffeomorphisms. Preprint, 2022, arXiv:2110.02925.Google Scholar
Crovisier, S.. Periodic orbits and chain-transitive sets of ${C}^1$ -diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 104 (2006), 87–141.CrossRefGoogle Scholar
Crovisier, S.. Perturbation de la dynamique de difféomorphismes en petite régularité. Astérisque 354 (2013), 1–147.Google Scholar
Edtmair, O. and Hutchings, M.. PFH spectral invariants and ${C}^{\infty }$ closing lemmas. Preprint, 2022, arXiv:2110.02463.Google Scholar
Gan, S. and Shi, Y.. A chain transitive accessible partially hyperbolic diffeomorphism which is non-transitive. Proc. Amer. Math. Soc. 146 (2018), 223–232.CrossRefGoogle Scholar
Gan, S. and Shi, Y.. ${C}^r$ -closing lemma for partially hyperbolic diffeomorphisms with 1D-center bundle. Adv. Math. 407 (2022), Paper no. 108553.CrossRefGoogle Scholar
Gan, S. and Wen, L.. Heteroclinic cycles and homoclinic closures for generic diffeomorphisms. J. Dynam. Differential Equations 15 (2003), 451–471.CrossRefGoogle Scholar
Gourmelon, N.. Adapted metrics for dominated splittings. Ergod. Th. & Dynam. Sys. 27 (2007), 1839–1849.CrossRefGoogle Scholar
Gutierrez, C.. A counter-example to a ${C}^2$ closing lemma. Ergod. Th. & Dynam. Sys. 7 (1987), 509–530.CrossRefGoogle Scholar
Hammerlindl, A.. Leaf conjugacies on the torus. Ergod. Th. & Dynam. Sys. 33 (2013), 896–933.CrossRefGoogle Scholar
Hammerlindl, A. and Potrie, R.. Pointwise partial hyperbolicity in three-dimensional nilmanifolds. J. Lond. Math. Soc. (2) 89 (2014), 853–875.CrossRefGoogle Scholar
Hayashi, S.. Connecting invariant manifolds and the solution of the C1 stability and $\varOmega$ -stability conjectures for flows. Ann. of Math. (2) 145 (1997), 81–137.CrossRefGoogle Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer Verlag, Berlin, 1977.CrossRefGoogle Scholar
Hu, H., Zhou, Y. and Zhu, Y.. Quasi-shadowing for partially hyperbolic diffeomorphisms. Ergod. Th. & Dynam. Sys. 35 (2015), 412–430.CrossRefGoogle Scholar
Kryzhevich, S. and Tikhomirov, S.. Partial hyperbolicity and central shadowing. Discrete Contin. Dyn. Syst. 33 (2013), 2901–2909.CrossRefGoogle Scholar
Mañé, R.. An ergodic closing lemma. Ann. of Math. (2) 116 (1982), 503–540.CrossRefGoogle Scholar
Mañé, R.. On the creation of homoclinic points. Publ. Math. Inst. Hautes Études Sci. 66 (1988), 139–159.CrossRefGoogle Scholar
Mañé, R.. A proof of the ${C}^1$ stability conjecture. Publ. Math. Inst. Hautes Études Sci. 66 (1988), 161–210.CrossRefGoogle Scholar
Martinchich, S.. Global stability of discretized Anosov flows. Preprint, 2023, arXiv:2204.03825.CrossRefGoogle Scholar
Potrie, R.. Partial hyperbolicity and foliations in ${T}^3$ . J. Mod. Dyn. 9 (2015), 81–121.CrossRefGoogle Scholar
Pugh, C.. The closing lemma. Amer. J. Math. 89 (1967), 956–1009.CrossRefGoogle Scholar
Wen, L. and Xia, Z.. ${C}^1$ connecting lemmas. Trans. Amer. Math. Soc. 352 (2000), 5213–5230.CrossRefGoogle Scholar
Yoccoz, J.-C.. Recent developments in dynamics. Proc. Int. Congr. Math. 1(2) (1994), 246–265.Google Scholar